A Visual Odometry Pipeline for Real-Time UAS Geopositioning
Abstract
:1. Introduction
- Using an offline geospatial data structure for on-the-fly landmark set retrieval for matching. The database module uses a geospatial data structure to swiftly generate a list of landmarks from the look-up region while reducing computational and data bandwidths.
- Introducing a geometry control module to select appropriate scales that guarantee matching ground sampling distances across reference and UAS landmarks. This, in turn, enables the UAS to change its attitude and altitude during flight freely.
- Our approach achieves absolute UAS geopositioning with high accuracy in vertical and horizontal directions.
- In contrast to our earlier work [1], where the UAS was forced to fly at a fixed altitude and attitude, this paper provides an algorithm that removes fixed altitude and attitude constraints.
2. Related Works
2.1. SLAM-Based Solutions
2.2. Cross-View Deep Learning Approaches
3. Methodology
3.1. Geospatial Quad-Tree
3.2. Landmark Retrieval and Matching
3.3. Geometric Transformation
3.4. Attitude Control
| Algorithm 1 Attitude control module working process | |
| Input: Output: if then and else and | ▹ |
| and end if | |
4. Experiments
4.1. Datasets
4.2. Evaluation
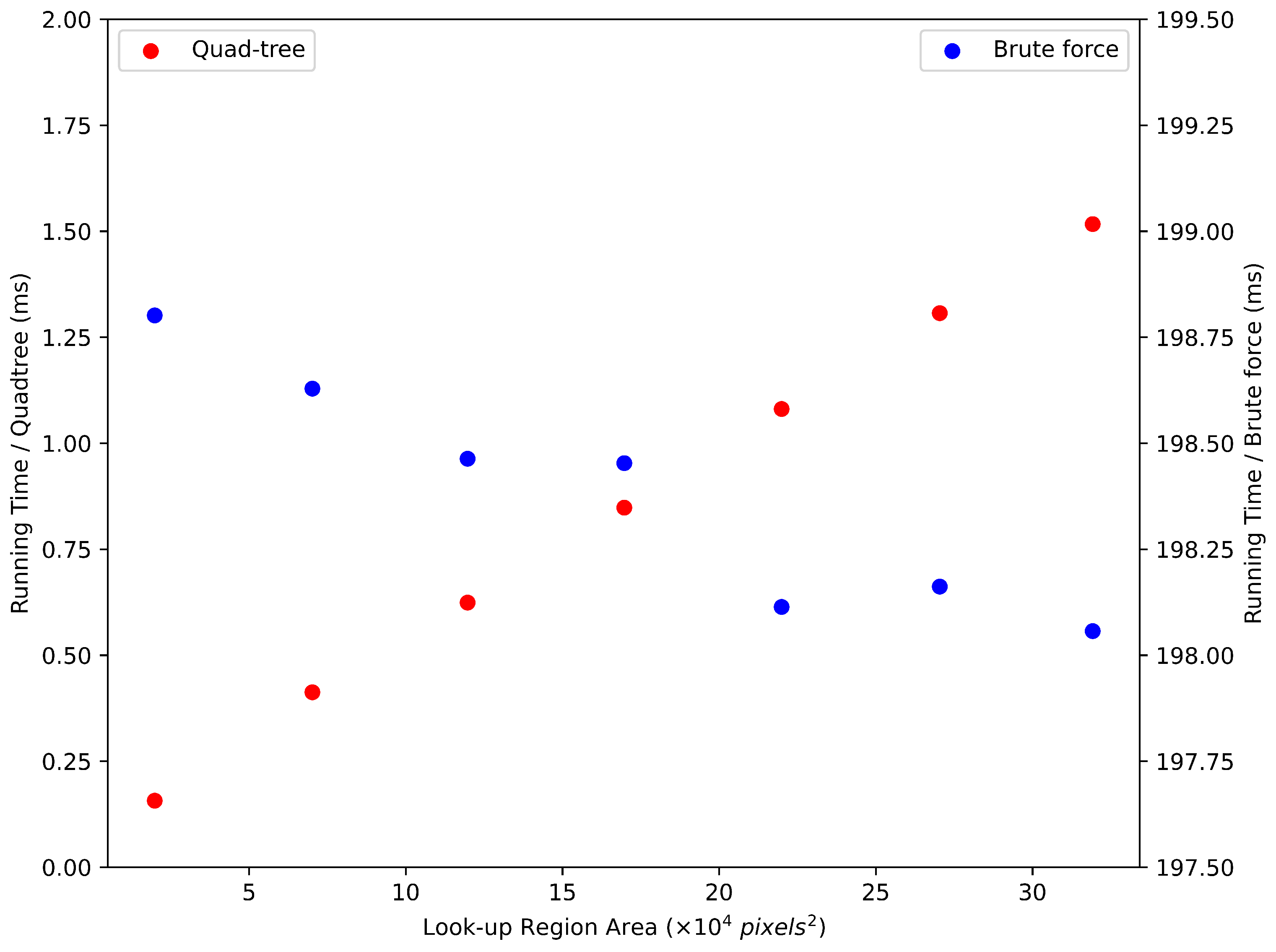
4.3. GIS Filtering and Its Effectiveness
4.4. SuperGlue vs. ORB
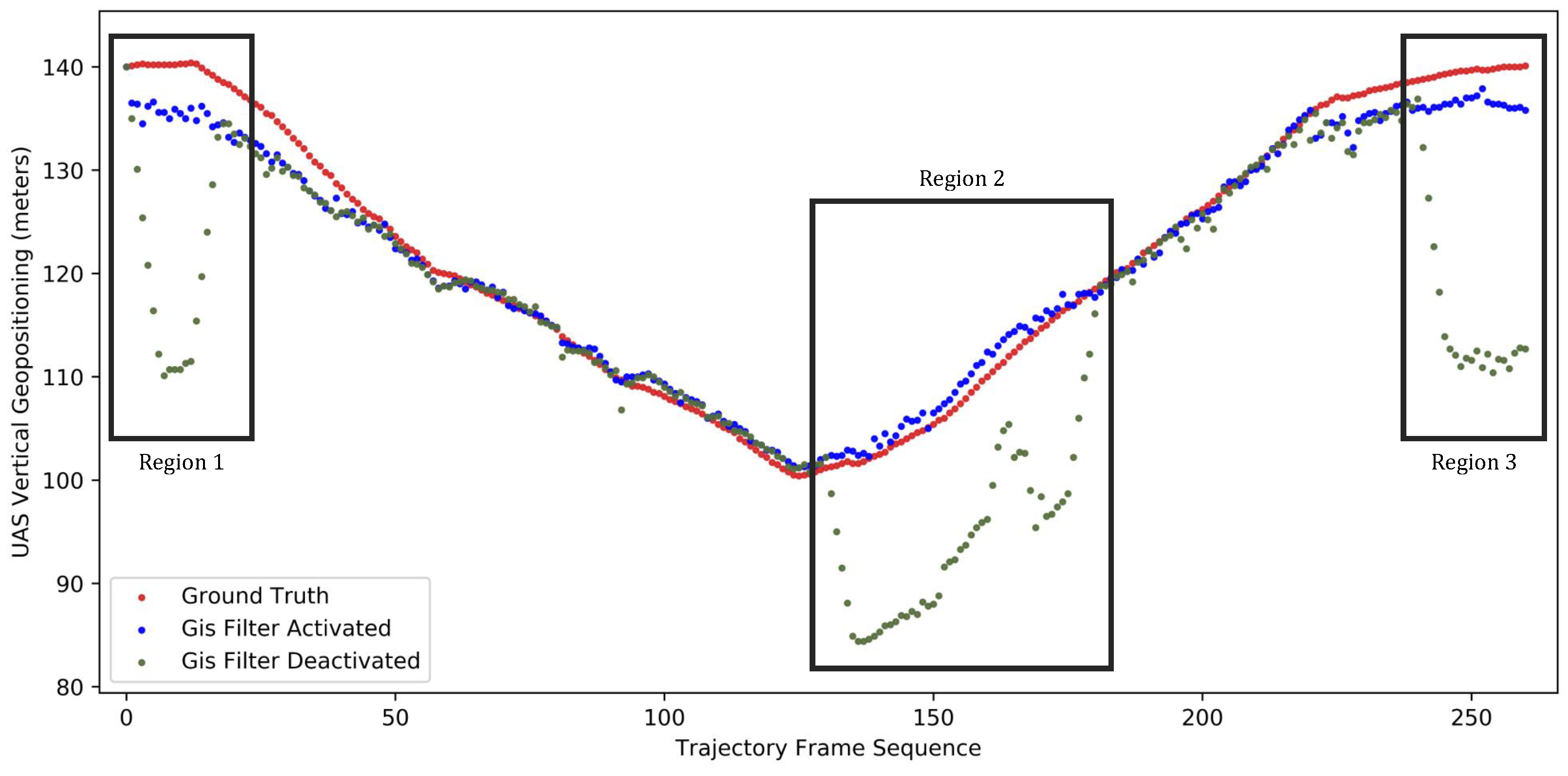
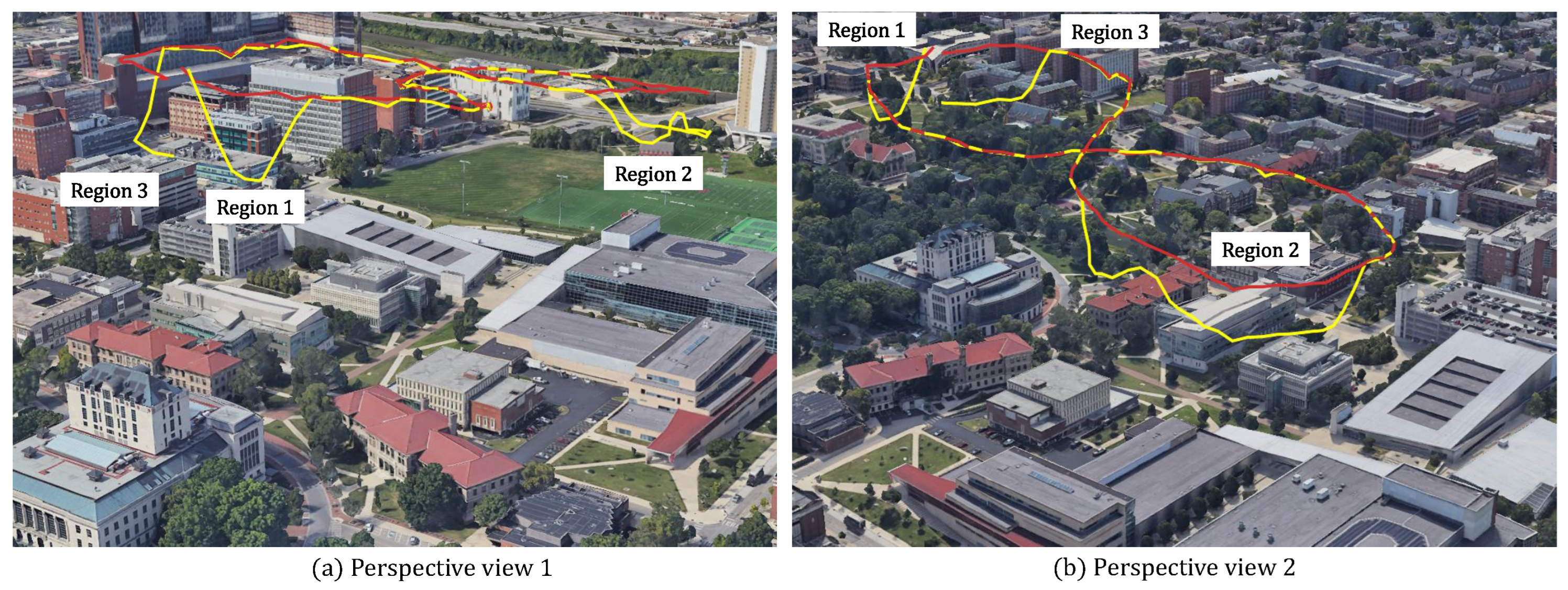

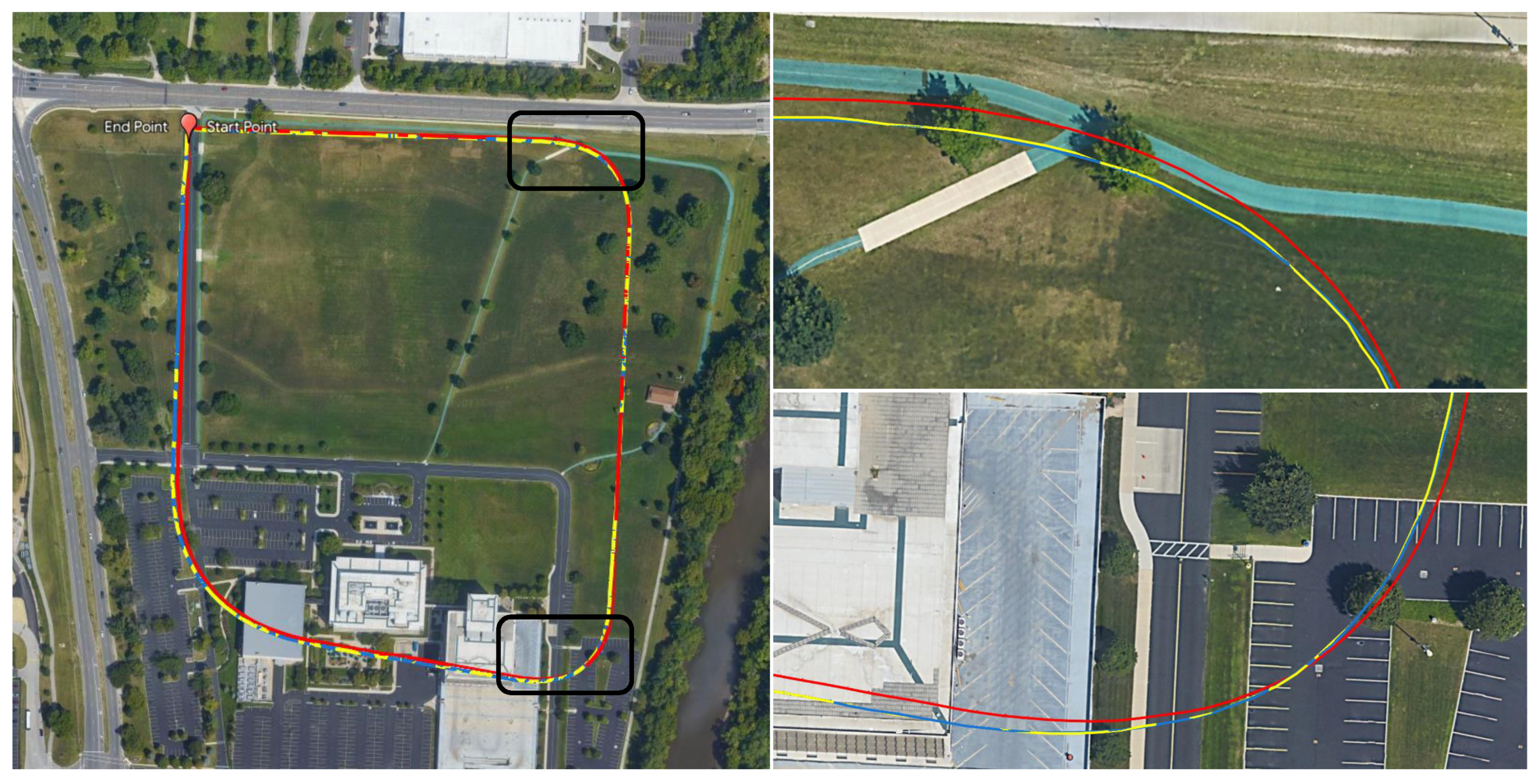

4.5. Comparison with SLAM
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| GCP | Ground Control Point |
| GIS | Geographic Information System |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| IMU | Inertial Measurement Unit |
| ORB | Oriented FAST and Rotated BRIEF |
| SLAM | Simultaneous Localization and Mapping |
| UAS | Unmanned Aerial System |
References
- Wei, J.; Karakay, D.; Yilmaz, A. A Gis Aided Approach for Geolocalizing an Unmanned Aerial System Using Deep Learning. In Proceedings of the 2022 IEEE Sensors, Dallas, TX, USA, 30 October–2 November 2022; pp. 1–4. [Google Scholar]
- Remondino, F.; Morelli, L.; Stathopoulou, E.; Elhashash, M.; Qin, R. Aerial triangulation with learning-based tie points. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2022, 43, 77–84. [Google Scholar] [CrossRef]
- Sarlin, P.E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 19–13 June 2020; pp. 4938–4947. [Google Scholar]
- Ahmad, N.; Ghazilla, R.A.R.; Khairi, N.M.; Kasi, V. Reviews on various inertial measurement unit (IMU) sensor applications. Int. J. Signal Process. Syst. 2013, 1, 256–262. [Google Scholar] [CrossRef]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-time single camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Hu, S.; Feng, M.; Nguyen, R.M.; Lee, G.H. CVM-net: Cross-view matching network for image-based ground-to-aerial geo-localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7258–7267. [Google Scholar]
- Zhuang, J.; Dai, M.; Chen, X.; Zheng, E. A Faster and More Effective Cross-View Matching Method of UAV and Satellite Images for UAV Geolocalization. Remote Sens. 2021, 13, 3979. [Google Scholar] [CrossRef]
- Macario Barros, A.; Michel, M.; Moline, Y.; Corre, G.; Carrel, F. A comprehensive survey of visual slam algorithms. Robotics 2022, 11, 24. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the Computer Vision—ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; Volume 13, pp. 834–849. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. Orb-slam3: An accurate open-source library for visual, visual–inertial, and multimap slam. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Shetty, A.; Gao, G.X. UAV pose estimation using cross-view geolocalization with satellite imagery. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 1827–1833. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 187. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Samet, H. The quadtree and related hierarchical data structures. ACM Comput. Surv. (CSUR) 1984, 16, 187–260. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–11 November 2011; pp. 2564–2571. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Chang, K.T. Geographic information system. In International Encyclopedia of Geography: People, the Earth, Environment and Technology; Wiley-Blackwell: Hoboken, NJ, USA, 2016; pp. 1–10. [Google Scholar]
- OpenStreetMap Contributors. Planet Dump. 2017. Available online: https://www.openstreetmap.org; (accessed on 9 August 2004).









| DoF | Matrix | Proprieties | |
|---|---|---|---|
| Pseudo-Perspective | 4 | Rotation, Translation, Scaling | |
| Affine | 6 | Pseudo-Perspective, Shearing | |
| Homography | 8 | Affine, non-Parallelism |
| Altitude (m) | Not Adjusted 1 | Adjusted | ||||
|---|---|---|---|---|---|---|
| Feat. 2 | Matches 3 | Pct. (%) 4 | Feat. | Matches | Pct. | |
| 50 | 3488 | 343 | 9.83 | 1059 | 301 | 28.42 |
| 60 | 3568 | 406 | 11.38 | 1459 | 343 | 23.51 |
| 70 | 3749 | 470 | 12.54 | 1947 | 396 | 20.34 |
| 80 | 3954 | 546 | 13.81 | 2434 | 510 | 20.95 |
| 90 | 4085 | 639 | 15.64 | 2956 | 604 | 20.43 |
| 100 | 4137 | 746 | 18.03 | 3489 | 700 | 20.06 |
| Altitude (m) | Not Adjusted 1 | Adjusted | ||||
|---|---|---|---|---|---|---|
| Feat. 2 | Matches 3 | Pct. (%) 4 | Feat. | Matches | Pct. | |
| 50 | 4000 | 838 | 20.95 | 2872 | 909 | 31.65 |
| 60 | 4000 | 968 | 24.20 | 3398 | 993 | 29.22 |
| 70 | 4000 | 953 | 23.83 | 3753 | 955 | 25.45 |
| 80 | 4000 | 996 | 24.90 | 3893 | 1008 | 25.89 |
| 90 | 4000 | 994 | 24.85 | 3965 | 931 | 23.48 |
| 100 | 4000 | 1000 | 25.00 | 4000 | 925 | 23.13 |
| Resi. | Campus | PKG. | Farm1 | Farm2 | |
|---|---|---|---|---|---|
| Dis. (km) | 2.2 | 0.78 | 1.4 | 2.1 | 1.4 |
| Init. Orien. 1 | |||||
| Init. Alt. (m) | 140 | 140 | 90 | 130 | 140 |
| Alt. Fluct. (m) 2 | 105–140 | 110–140 | 90–145 | 120–145 | 130–149 |
| Min. Err. (m) 3 | 1.5 | 2.1 | 3.9 | 0.1 | 1.0 |
| Max. Err. (m) 3 | 10.1 | 9.6 | 9.7 | 7.4 | 5.1 |
| MAE (m) 3 | 6.0 | 6.3 | 7.1 | 4.0 | 3.4 |
| Std (m) 4 | 1.74 | 1.74 | 1.07 | 1.54 | 1.07 |
| Min. Err. (m) 5 | 0.0 | 0.0 | 2.0 | 0.0 | 0.0 |
| Max. Err. (m) 5 | 12.3 | 6.4 | 6.1 | 5.30 | 4.1 |
| MAE (m) 5 | 2.9 | 1.8 | 4.5 | 1.8 | 1.2 |
| Std (m) 6 | 3.1 | 1.53 | 0.70 | 1.25 | 1.05 |
| GIS Filter | Transformation | Residential Area | University Campus | Parking | Farm1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | MAE | Std. | Min. | Max. | MAE | Std. | Min. | Max. | MAE | Std. | Min. | Max. | MAE | Std. | ||
| Activated | Pseudo-perspective | 1.5 | 10.1 | 6.0 | 1.74 | 2.1 | 9.6 | 6.3 | 1.74 | 3.9 | 9.7 | 7.1 | 1.07 | 0.1 | 7.4 | 4.0 | 1.54 |
| Affine | 1.6 | 10.4 | 6.0 | 1.69 | 2.4 | 9.7 | 6.3 | 1.71 | 3.9 | 9.5 | 7.1 | 1.06 | 0.1 | 7.6 | 4.1 | 1.55 | |
| Homography | 0.9 | 16.0 | 7.3 | 2.68 | 1.6 | 18.5 | 7.6 | 3.15 | 4.4 | 16.0 | 8.0 | 1.74 | 0.3 | 11.1 | 5.0 | 2.26 | |
| Deactivated | Pseudo-perspective | 1.5 | 10.1 | 6.0 | 1.71 | 1.9 | 9.8 | 5.7 | 1.61 | 3.9 | 9.7 | 7.1 | 1.08 | 0.1 | 7.7 | 4.0 | 1.54 |
| Affine | 1.7 | 10.3 | 6.0 | 1.70 | 2.4 | 9.8 | 5.7 | 1.57 | 3.7 | 9.5 | 7.1 | 1.08 | 0.1 | 7.8 | 4.1 | 1.54 | |
| Homography | 0.8 | 15.7 | 7.4 | 2.80 | 1.0 | 26.9 | 8.6 | 4.60 | 3.2 | 27.1 | 8.3 | 2.40 | 0.3 | 33.7 | 5.1 | 2.96 | |
| GIS Filter | Transformation | Residential Area | University Campus | Parking | Farm1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | MAE | Std. | Min. | Max. | MAE | Std. | Min. | Max. | MAE | Std. | Min. | Max. | MAE | Std. | ||
| Activated | Pseudo-perspective | 0.0 | 12.3 | 2.9 | 3.10 | 0.0 | 6.4 | 1.8 | 1.53 | 2.0 | 6.1 | 4.5 | 0.70 | 0.0 | 5.3 | 1.8 | 1.25 |
| Affine | 0.0 | 12.1 | 3.1 | 3.24 | 0.0 | 6.5 | 1.8 | 1.56 | 1.8 | 6.2 | 4.5 | 0.67 | 0.0 | 6.1 | 1.9 | 1.35 | |
| Deactivated | Pseudo-perspective | 0.0 | 12.0 | 3.4 | 3.40 | 0.0 | 29.5 | 6.2 | 8.28 | 2.1 | 6.0 | 4.5 | 0.66 | 0.0 | 5.5 | 1.8 | 1.25 |
| Affine | 0.0 | 12.2 | 3.4 | 3.38 | 0.0 | 33.7 | 6.6 | 8.59 | 0.6 | 6.1 | 4.4 | 0.68 | 0.0 | 5.7 | 1.9 | 1.30 | |
| Min. 1 | Max. 1 | MAE 1 | Std 1 | fps 2 | dist 3 | Max. Speed 4 | |
|---|---|---|---|---|---|---|---|
| SG 5 | 1.0 | 5.1 | 3.4 | 1.08 | 3.40 | 33 | 112 |
| ORB | 1.0 | 5.1 | 3.4 | 1.06 | 6.58 | 90 | 592 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Yilmaz, A. A Visual Odometry Pipeline for Real-Time UAS Geopositioning. Drones 2023, 7, 569. https://doi.org/10.3390/drones7090569
Wei J, Yilmaz A. A Visual Odometry Pipeline for Real-Time UAS Geopositioning. Drones. 2023; 7(9):569. https://doi.org/10.3390/drones7090569
Chicago/Turabian StyleWei, Jianli, and Alper Yilmaz. 2023. "A Visual Odometry Pipeline for Real-Time UAS Geopositioning" Drones 7, no. 9: 569. https://doi.org/10.3390/drones7090569
APA StyleWei, J., & Yilmaz, A. (2023). A Visual Odometry Pipeline for Real-Time UAS Geopositioning. Drones, 7(9), 569. https://doi.org/10.3390/drones7090569





