Abstract
The influence of entropy in multiple chemical equilibria is investigated for systems with two different types of sites for Langmuir’s condition, which means that the binding enthalpy of the species is the same for each type of sites and independent of those that are already bonded and that this holds for both types of sites independently. The analysis makes use of the particle distribution theory which holds for each type of sites separately. We provide physical insight by discussing an Xm{AB}Xn system with m = 0, 1, …, M and n = 0, 1, …, N in detail. The procedure and results are exemplified for an Xm{AB}Xn system with M = 3 and N = 2. A satisfactory consequence of the results is that the eleven equilibrium constants needed to describe such a system can be expressed as a function of two constants only. This is generally valid for any Xm{AB}Xn system where the [(M + 1)(N + 1) − 1] equilibrium constants can be expressed as a function of 2 constants only. This has also implication for quantum-theoretical studies in the sense that it is sufficient to model only two reactions instead of many in order to describe the system. We have observed that it is sufficient to have two different sites in a multiple equilibrium in order to observe a characteristic of isotherms that cannot be described by Langmuir’s equation. This is a result that may be useful for explaining experimental data which otherwise have not been explained satisfactory so far. Instead of inventing adsorption models it might often make sense of describing the system in terms of multiple equilibria.
1. Introduction
We explained the influence of entropy in multiple chemical equilibria by studying the particle distribution for the conditions that the binding enthalpy of the species is the same for all sites and that it is independent of those that are already bonded [1]. Consequences were discussed for the insertion of guests into the one dimensional channels of a host, for dicarboxylic acids, and for cation exchange of zeolites. The validity of the results is independent of the nature and the strength of the binding. The quantitative link between the description of multiple equilibria and Langmuir’s isotherm [2,3,4] was found to provide new insight. Multiple equilibria of objects with several equivalent binding, docking, coupling, or adsorption sites for neutral or charged species play an important role in all fields of chemistry [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. We now investigate systems with two different types of sites, which we name Xm{AB}Xn, for the condition that the binding enthalpy of the species is the same for each type of sites and independent of those that are already bonded and that this holds for both types of sites independently. The analysis makes use of the particle distribution theory as described in ref. [1], which holds for each type of sites separately. The condition that the binding enthalpy of the species is the same for all sites and that it is independent of those that are already bonded is equivalent to the condition I. Langmuir used one hundred years ago to derive the Langmuir isotherm [2,3]. We therefore name it Langmuir’s condition.
2. Results and Discussion
The number of distinguishable chemical objects of an Xm{AB}Xn (m = 0, 1, …, M and n = 0, 1, …, N) system is equal to (M + 1)(N + 1). From this follows that the number of equilibria with X is [(M + 1)(N + 1) − 1] which is also the number of equilibrium constants. We show that Langmuir’s condition in connection with the particle distribution function allows to express the (M + 1)(N + 1) − 1 equilibrium constants as a function of two different constants only. This is a simplification which allows studying systems quantitatively by experimental and theoretical means which otherwise might be difficult to handle. A numerical analysis of experimental data for a system with 5 different types of sites has been carried out based on this reasoning and has allowed to correct earlier reports on the reaction entropy of silver zeolite A [16]. We improve the physical insight by discussing a simple Xm{AB}Xn system in detail. The notation Xm{AB}Xn represents individual particles, a grid consisting of many sites, microporous objects, or other chemical systems. The procedure and results are exemplified for m = 0, 1, 2, 3 and n = 0, 1, 2. The 11 equilibria and the corresponding equilibrium constants Ki are collected in Table 1.

Table 1.
Equilibria of an Xm{AB}Xn system with m = 0, 1, 2, 3 and n = 0, 1, 2.
We apply the stoichiometrie-matrix expression for evaluating these equlilibria [9,10]. Details of this procedure are reported in the appendix. The result is given in Table 2. It is convenient to use the following notations to write the concentrations of the individual objects, namely Ci and also [Xm{AB}Xn], but only [X] for the concentration of X.

We have 11 equation available for expressing the 13 concentrations: Ci, i = 1, 2, …, 12 and [X]. An additional equation is available from the fact that in a closed system the total concentration of the Xm{AB}Xn species, which we name A0, is constant, as expressed in Equation (1). The concentration C12 = can, hence, be determined using Equation (1). The concentration [X] of the ligand X that can bind to the is the free variable.
We need to know 11 equilibrium constants in order to describe the evolution of the concentrations Ci of the twelve species as a function of the variable [X]. This is a difficult situation and may in many cases have as a consequence that a system cannot be handled in a satisfactory way. A very important simplification arises if Langmuir’s condition applies. This may often be the case sufficiently well. Langmuir’s condition implies in our example that K1, K4, and K7 are equal. The same holds for K2, K5, and K8 and also for K3, K6, and K9. From this follows a further simplification from the application of the particle distribution function f(n,r) [1,16,30], where n is the total number of equilibria of a set and r counts the individual equilibria in a set; r = 0, 1, …, n − 1:
The particle distribution function describes the entropy decrease in the corresponding reaction sets, as we have discussed in detail [1]. Applying Langmuirs’s condition and the particle distribution function we find the results reported in Table 3.

Table 3.
Relation between the equilibrium constants defined in Table 1 as a consequence of Langmuirs’s condition and the particle distribution function.
The very satisfactory consequence of the result shown in Table 3 is, that the eleven equilibrium constants can be expressed as a function of two constants only, namely K1 and K10. Inserting this in the equation shown in Table 2 we find the Equations (3) and (4), where C12(X) is the concentration of expressed as a function of the concentration of X. This is a nice and very useful result. It allows to study the concentration of the twelve species Ci, i = 1, 2, …, 12 as a function of the concentration X by considering only 2 parameters, namely K1 and K10, instead of eleven. This has also implication for quantum-theoretical studies in the sense that it is sufficient to model only two reactions instead of eleven, in order to describe the system.
We illustrate the meaning of this result by calculation the concentrations Ci for two sets of equilibrium constants K1 and K10, namely 50 and 1, and 1 and 50, as a function of the concentration of X. A comparison of the results shown in Figure 1 and Figure 2 with those reported in Figures 4, 5, and 7 in ref. [1] illustrates well that the behavior of the system with two types of sites is very different from that of a systems with only one type.
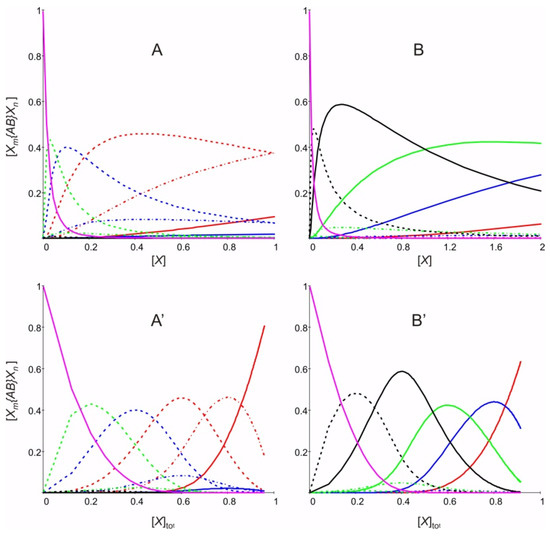
Figure 1.
Concentration of Xm{AB}Xn as a function of the concentration of X, (A,B), and versus the total concentration [X]tot of X in the system, (A’,B’). (A,A’) calculated for K1 = 50.0 and K10 = 1.0; (B,B’) calculated for K1 = 1.0 and K10 = 50.0. Red lines: [X3{AB}Xn] (solid: n = 2, dash: n = 1, dash dot: n = 0). Blue lines: [X2{AB}Xn] (solid: n = 2, dash: n = 1, dash dot: n = 0). Green lines: [X{AB}Xn] (solid: n = 2, dash: n = 1, dash dot: n = 0). Black lines: [{AB}X2] solid: [{AB}X] dash. Pink line: [{AB}] = C12 (solid).
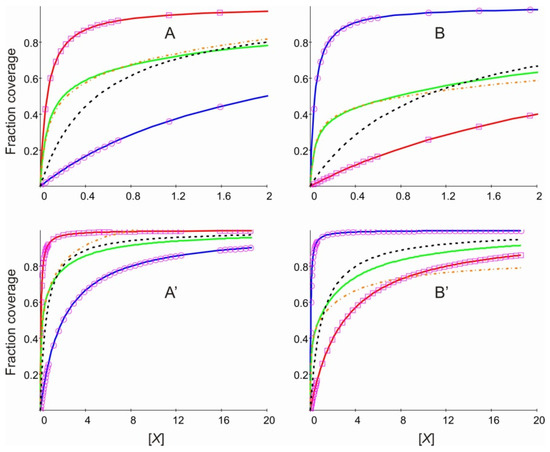
Figure 2.
Isotherms expressed as a function of the concentration of [X]. Left: Calculated for K1 = 50.0 and K10 = 1.0. Right: Calculated for K1 = 1.0 and K10 = 50.0. (A,B) in the range of [X] between 0 and 2, and (A’,B’) between 0 and 20. Solid lines: Amount of the objects Xm{AB}Xn. Red: m = 1,2,3, all n; divided by 3. Blue: {AB}Xn, n = 1,2; divided by 2. The rectangles and the circles correspond to Langmuir’s eqs. (29) and (29A) of ref. [1] with KL = K1/3 and KL = K10/2, respectively. Green: all Xm{AB}Xn, except {AB}, divided by 5. Black, dashed: Isotherm calculated using Langmuir’s eqs. (29) and (29A) of ref. [1] with optimized values for KL. Orange, dash dot: Sum of the red and the blue curves weighted by an optimized factor.
We see e.g., in Figure 1A, that the X{AB}Xn appear only at the beginning for small values of [X] and even more, that only X{AB}X shows temporally a value of larger than 0.05, while X{AB}X2 always stays very small. We note that {AB} vanishes soon and that the X3{AB}Xn become dominant. [{AB}X2] and [{AB}X] always remain small. The situation changes very much in Figure 1B. The symmetry of the plot of the concentrations Ci versus the total concentration [X]tot we have observed in Figure 4B of ref. [1] has completely disappeared, however, in both cases as seen in Figure 1A’,B’. We also observe that out of the 12 species Xm{AB}Xn only few manage to evolve significant concentrations. An example with different values of K1 and K10 is reported in the appendix.
The fractional coverage expressed as a function of the concentration [X] is of special interest, also because it can often be determined experimentally relatively easy. We show this in Figure 2.
It is interesting but not surprising that the amount of the objects Xm{AB}Xn (m = 1,2,3, all n; divided by 3) can be perfectly described by Langmuir’s isotherm equation. We observe the same for the concentration of {AB}Xn (n = 1,2; divided by 2). The sum of all objects Xm{AB}Xn (m = 0,1,2,3, all n), however, cannot be described by the Langmuir isotherm equation. This behaviour seems to be of general validity, as I have numerically tested for a number of representative examples. It should be possible to prove this analytically but such a proof is not yet known. If the numerical values of K1 and K10 are equal, the system simplifies to the situation we have discussed in ref. [1]. In the other extreme, when K1 and K10 differ by orders of magnitude, the system decomposes into separate parts.
Different types of explanations for isotherms that deviate from Langmuir isotherms have been developed. They are in many cases satisfactory because they have been linked to a microscopic phenomenon, but they seem to be arbitrary in other situation [6,11,18,24]. We find that it is sufficient to have two different sites in a multiple equilibrium in order to observe a characteristic that differs from Langmuir’s equation, despite of the fact that the latter applies for individual parts. Writing multiple chemical equilibria could therefore be useful for explaining experimental data and for making prediction. Instead of inventing adsorption models, it might make sense to describe a system in such terms. The system may consist of one set of equivalent sites [1], two sets, as reported here, or even of several sets of equivalent sites [16].
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We express the equilibrium equations of the reaction sin Table 1 by means of the stoichiometry matrix; see refs. [9,10], where the labels with a bar are the logarithm of the corresponding object: . This leads to Equation (A1).
Linear transformation of (A1) allows finding the solution (A2); see e.g., ref. [10].
Using this solution we can express the concentrations of the Xm{AB}Xn species as reported in Table A1. [X] is considered to be a parameter, while the concentration C12 = can be determined for the condition that in a closed system the total concentration of the Xm{AB}Xn species, which we name A0, is constant, a fact which we express in Equation (A3) as follows:

Table A1.
Concentrations Ci, calculated using Equation (A2).
Table A1.
Concentrations Ci, calculated using Equation (A2).
| C1 = | = | 5 K1 K2 K3 K10 K11 | |
| C2 = | = | 4 K1 K2 K10 K11 | |
| C3 = | = | 3 K1 K10 K11 | |
| C4 = | = | 4 K4 K5 K6 K10 | |
| C5 = | = | 3 K4 K5 K10 | |
| C6 = | = | 2 K4 K10 | |
| C7 = | = | 3 K7 K8 K9 | |
| C8 = | = | 2 K7 K8 | |
| C9 = | = | K7 | |
| C10 = | = | 2 K10 K11 | |
| C11 = | = | K10 |
Figure A1 and Figure A2 show an example calculate with different equilibrium constants, namely: (A,A’) K1 = 5 and K10 = 1; (B,B’) K1 = 1 and K10 = 5. We observe a different behavior with respect to Figure 1 and Figure 2, as expected.
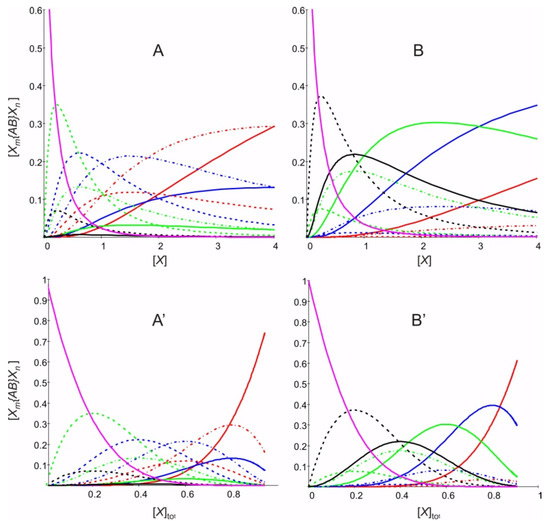
Figure A1.
Concentration of Xm{AB}Xn as a function of the concentration of X, (A,B), and versus the total concentration [X]tot of X in the system, (A’,B’). (A,A’) calculated for K1 = 5.0 and K10 = 1.0; (B,B’) calculated for K1 = 1.0 and K10 = 5.0. Red lines: [X3{AB}Xn] (solid: n = 2, dash: n = 1, dash dot: n = 0). Blue lines: [X2{AB}Xn] (solid: n = 2, dash: n = 1, dash dot: n = 0). Green lines: [X{AB}Xn] (solid: n = 2, dash: n = 1, dash dot: n = 0). Black lines: [{AB}X2] solid: [{AB}X] dash. Pink line: [{AB}] = C12 (solid).
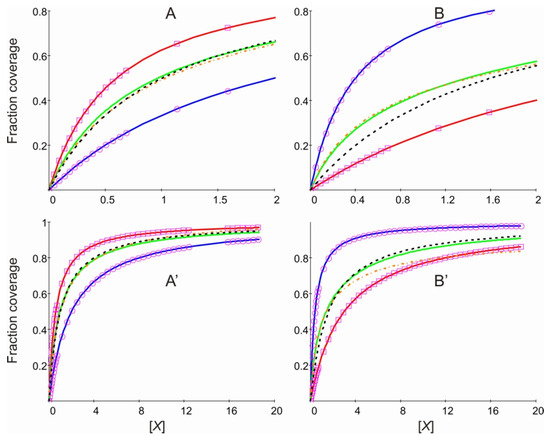
Figure A2.
Isotherms expressed as a function of the concentration of [X]. (A’) calculated for K1 = 5.0 and K10 = 1.0; (B’) calculated for K1 = 1.0 and K10 = 5.0. (A,B) in the range of X between 0 and 2 and (A’,B’) between 0 to 6. Solid lines: Amount of the objects Xm{AB}Xn. Red: m = 1,2,3, all n; divided by 3. Blue: {AB}Xn, n = 1,2; divided by 2. The rectangles and the circles correspond to Langmuir’s eqs. (29) and (29A) of ref. [1] with KL = K1/3 and KL = K10/2, respectively. Green: all Xm{AB}Xn, except {AB}, divided by 5. Black, dashed: Isotherm calculated using Langmuir’s eqs. (29) and (29A) of ref. [1] with optimized values for KL. Orange, dash dot: Sum of the red and the blue curves weighted by an optimized factor.
References
- Calzaferri, G. Entropy in multiple equilibria, theory and applications. Phys. Chem. Chem. Phys. 2017, 19, 10611–10621. [Google Scholar] [CrossRef] [PubMed]
- Langmuir, I. The constitution and fundamental properties of solids and liquids. Part I. Solids. J. Am. Chem. Soc. 1916, 38, 2221–2295. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Denbigh, K. The Principles of Chemical Equilibrium, 2rd ed.; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Tabacchi, G. Supramolecular organization and confined nanospaces. Chem. Phys. Chem. 2018, in press. [Google Scholar] [CrossRef]
- Barrer, R.M. Zeolites and Clay Minerals as Sorbents and Molecular Sieves; Academic: London, UK, 1978; ISBN 0-12-079350-4. [Google Scholar]
- Nagaj, J.; Stokowa-Sołtys, K.; Kurowska, E.; Frączyk, T.; Jeżowska-Bojczuk, M.; Bal, W. Revised coordination model and stability constants of Cu (II) complexes of tris buffer. Inorg. Chem. 2013, 52, 13927–13933. [Google Scholar] [CrossRef]
- David, C.; Companys, E.; Galceran, J.; Garcés, J.L.; Mas, F.; Rey-Castro, C.; Salvador, J.; Puy, J. Competitive Cd2+/H+ complexation to polyacrylic acid described by the stepwise and intrinsic stability constants. J. Phys. Chem. 2008, 112, 10092–10100. [Google Scholar] [CrossRef]
- Prigogine, I. Thermodynamics of Irreversible Processes, 3rd ed.; Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Dubler, T.; Maissen, C.; Calzaferri, G. Diskussion Chemischer Gleichgewichte. Z. Naturforsch. 1976, 31, 569–579. [Google Scholar] [CrossRef]
- Breck, D.W. Zeolite Molecular Sieves; John Wiley: New York, NY, USA, 1974; ISBN 0-471-09985-6. [Google Scholar]
- Schoonheydt, R.A.; Weckhuysen, B.M. Editorial Highlight: Molecules in confined spaces. Phys. Chem. Chem. Phys. 2009, 11, 2794–2798. [Google Scholar] [CrossRef]
- Schulz-Ekloff, G.; Wöhrle, D.; van Duffel, B.; Schoonheydt, R.A. Chromophores in porous silicas and minerals: Preparation and optical properties. Microporous Mesoporous Mater. 2002, 51, 91–138. [Google Scholar] [CrossRef]
- Craciun, G.; Feinberg, M. Multiple Equilibria in Complex Chemical Reaction Networks: Semiopen Mass Action Systems. SIAM J. Appl. Math. 2010, 70, 1859–1877. [Google Scholar] [CrossRef]
- Roduner, E.; Radhakrishnan, S.G. In command of non-equilibrium. Chem. Soc. Rev. 2016, 45, 2768–2784. [Google Scholar] [CrossRef] [PubMed]
- Meyer, M.; Leiggener, C.; Calzaferri, G. Particle distribution in a microporous material: Experiments with zeolite A. Chem. Phys. Chem. 2005, 6, 1071–1080. [Google Scholar] [CrossRef]
- Calzaferri, G.; Huber, S.; Maas, H.; Minkowski, C. Host-guest antenna materials. Angew. Chem. Int. Ed. 2003, 42, 3732–3758. [Google Scholar] [CrossRef] [PubMed]
- Valtchev, V.; Mintova, S.; Tsapatsis, M. (Eds.) Ordered Porous Solids, 1st ed.; Elsevier: Oxford, UK, 2009; ISBN 978-0-444-53189-6. [Google Scholar]
- Sola-Llano, R.; Martínez-Martínez, V.; Fujita, Y.; Hortigüela, L.G.; Alfayate, A.; Uji-I, H.; Fron, E.; Pérez-Pariente, J.; López-Arbeloa, I. Formation of a nonlinear optical host-guest hybrid material by tight confinement of LDS 722 into aluminophosphate 1D nanochannels. Chem. Eur. J. 2016, 22, 15700–15711. [Google Scholar] [CrossRef] [PubMed]
- Al-Aqar, R.; Atahan, A.; Benniston, A.C.; Perks, T.; Waddell, P.G.; Harriman, A. Exciton Migration and Surface Trapping for a Photonic Crystal Displaying Charge-Recombination Fluorescence. Chem. Eur. J. 2016, 22, 15420–15429. [Google Scholar] [CrossRef]
- Ramamurthy, V.; Inoue, Y. (Eds.) Supramolecular Photochemistry: Controlling Photochemical Processes; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-0-470-23053-4. [Google Scholar]
- Tabacchi, G.; Fois, E.; Calzaferri, G. Structure of Nanochannel Entrances in Stopcock-Functionalized Zeolite L Composites. Angew. Chem. Int. Ed. 2015, 54, 11112–11116. [Google Scholar] [CrossRef]
- Tabacchi, G.; Calzaferri, G.; Fois, E. One-dimensional self-assembly of perylene-diimide dyes by unidirectional transit of zeolite channel openings. Chem. Commun. 2016, 52, 11195–11198. [Google Scholar] [CrossRef]
- Cejka, J.; van Bekkum, H.; Corma, A.; Schüth, F. (Eds.) Studies in Surface Science and Catalysis, Vol. 168: Introduction to Zeolite Science and Practice, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2007; ISBN 978-0-444-53063-9. [Google Scholar]
- Gigli, L.; Arletti, R.; Vitillo, J.G.; Alberto, G.; Martra, G.; Devaux, A.; Vezzalini, G. Thionine dye confined in zeolite L: synthesis location and optical properties. J. Phys. Chem. C 2015, 119, 16156–16165. [Google Scholar] [CrossRef][Green Version]
- Getman, R.B.; Bae, J.S.; Wilmer, C.E.; Snurr, R.Q. Review and analysis of molecular simulations of methane, hydrogen, and acetylene storage in metal–organic frameworks. Chem. Rev. 2012, 112, 703–723. [Google Scholar] [CrossRef]
- Lencione, D.; Gehlen, M.H.; Trujillo, L.N.; Leitao, R.C.F.; Albuquerque, R.Q. The spatial distribution of the photostability of thionine in zeolite L nanochannels investigated by Photobleaching Lifetime Imaging Microscopy. Photochem. Photobiol. Sci. 2016, 15, 398–404. [Google Scholar] [CrossRef]
- Bussemer, B.; Dreiling, I.; Grummt, U.-W.; Mohr, G.J. Spectroscopic and quantum chemical study of the Brønsted acid sites in zeolite L channels with acidochromic cyanine dyes. J. Photochem. Photobiol. A Chem. 2009, 204, 90–96. [Google Scholar] [CrossRef]
- Woodtli, P.; Giger, S.; Müller, P.; Sägesser, L.; Zucchetto, N.; Reber, M.J.; Ecker, A.; Brühwiler, D. Indigo in the nanochannels of zeolite L: Towards a new type of colorant. Dyes Pigment. 2017. [Google Scholar] [CrossRef]
- Kunzmann, A.; Seifert, R.; Calzaferri, G. Particle distribution in a microporous material. J. Phys. Chem B 1999, 103, 18–26. [Google Scholar] [CrossRef]
- Van Speybroeck, V.; Hemelsoet, K.; Joos, L.; Waroquier, M.; Bell, R.G.; Catlow, C.R.A. Advances in theory and their application within the field of zeolite chemistry. Chem. Soc. Rev. 2015, 44, 7044–7111. [Google Scholar] [CrossRef]
- Gigli1, L.; Arletti, R.; Tabacchi, G.; Fabbiani, M.; Vitillo, J.G.; Gianmario, M.; Devaux, A.; Miletto, I.; Quartieri, S.; Calzaferri, G. Structure and Host-Guest Interactions of Perylene-Bisimide Dyes in Zeolite L Nanochannels. J. Phys. Chem. C in press. 2018. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).