Abstract
In this work, we present and discuss on the deflection estimation of a bi-dimensional panel by using Fiber Bragg Gratings (FBGs) as strain sensors embedded in the structure and a method based on the classical beam theory. The existing difficulties in the direct measure of the deflection are overcome thanks to the proposed technique and a real-time indirect structural monitoring is possible both on small and large structure. In many tests the estimated deflection with the proposed method has been compared with direct deflection measurements obtained with a mechanical comparator showing good agreement. A resolution of few tens of microns over a surface of the order of 1 m2 has been reached.
1. Introduction
In the last years, the maintenance and management of civil infrastructure frequently involve vast amounts of resources in terms of manual labor, materials and finance; therefore, the research of technologies for the deformation monitoring with cost-effectiveness and high performances is ongoing [1]. Indeed, several applications of the use of specific sensors for deformation monitoring, are present in the literature for monitoring bridges [2,3], marine piles [4], ground displacement [5], tunnel and pipelines [6,7], pavements and building structures [8].
Traditional deformation monitoring techniques, such as dial indicator, level gauge, tensional wire displacement and deflection gauge, are widely used for structure deformation measurement, but they don’t allow for a good real time monitoring. Indeed, more sophisticated techniques such as GPS, laser and photoelectric imaging are developed for real time measurements.
In the last few years, optical fiber sensor (OFS) technologies have become a suitable solution for structural health monitoring, thanks to their unique properties as: small in size, passive, immune to electromagnetic interference, intrinsic multiplexing, resistant to harsh environments and the capability to perform distributed sensing. In particular, among OFS, Fiber Bragg gratings (FBGs) are increasingly being used in sensing applications and are enjoying widespread acceptance and use [9].
In this context, here we present a deflection estimation of a bidimensional multilayer structures (shown in Figure 1) by using FBG strain sensors and a displacement-strain transformation, extending the approach that we have previously demonstrated for a beam structure [10].
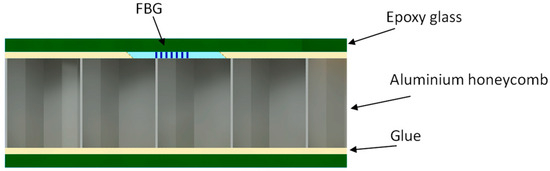
Figure 1.
Schematic of transversal section of the multilayer panel.
2. Materials and Methods
The method to estimate the deflection of a beam structure from the measured strain is based on the classical beam theory with small deformation assumption where a second derivative relationship exists between the displacement orthogonal to the surface and the strain component parallel to it. Indeed, if we consider a 1D structure, the surface strain component along the longitudinal direction, according to [10], is given by
where is the displacement profile. By integrating twice Equation (1), the vertical deflection can be expressed according to the following equation:
where represents the position of the neutral axis.
This method has been successfully used to estimate the beam deflection, thus on a one-dimensional structure. Aim of the work is to extend this approach to a two-dimensional panel (i.e., a structure with two dominant sides with respect to the third one), using the strain profile measured along more than one line of the structure, in order to create a 2D deflection map.
We have used a polynomial expression for the strain along the different lines in order to achieve a continuous function for the strain. The coefficients of a polynomial that fits the data has been find by means of a fitting algorithm in the least-squares sense. At this point, the deflection function along the different lines can be expressed in the polynomial form also, and the coefficient of the polynomial can be calculated directly from the ones of the strain polynomial. Finally, the 2D map is the result of a new polynomial fitting in two variables with the addition of the boundary conditions.
3. Results
In order to evaluate the proposed technique, a planar panel of 100 cm long, 40 cm wide and with a thickness of 0.95 ± 0.005 cm has been tested. It consists in a multilayer symmetric structure consisting of a central aluminum honeycomb, bonded between two layers of epoxy glass (composite material) through the epoxy resin Araldite 2011 as depicted in Figure 1. The panel has been instrumented with 15 commercial 10 mm long FBGs whose spectra are showed in Figure 2d.
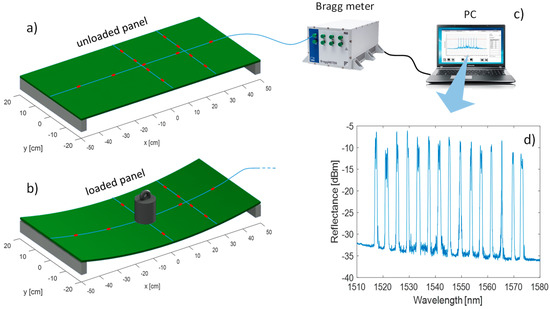
Figure 2.
Schematic (a) unloaded panel; (b) loaded panel; (c) interrogation setup; (d) reflectance spectrum of the FBGs embedded in the panel.
The FBGs are distributed in 3 straight arrays on the top of the panel positioned in two arrays of four and five FBGs respectively along the two main axes of symmetry (along the short and the long side, i.e., x and y axis respectively), while another array of four FBGs has been positioned along the short side of the panel in order to obtain additional measuring points, as it is possible to see in Figure 2a,b (in the unloaded and loaded case, respectively). The three arrays are connected to a commercial optoelectronic unit (Figure 2c) that measures the FBGs signal. Other two FBGs, are positioned on the opposite side of the honeycomb near to the center of the panel with orthogonal orientations. It is worth to note that the use of sensors on both side of the panel is useful for the position of the neutral axis estimation. Finally another FBG sensor has been used, in a strain-free configuration, for the monitoring of the environmental temperature and the subsequent compensation of the effects of the temperature on the sensors embedded in the structure.
In order to test the procedure, the panel has been loaded with increasing weights: 0 kg, 2 kg, 4 kg, 6 kg and then progressively returned to 0 kg. The procedure to pass from the strain values to the deflection function in a line by means of a polynomial fitting and others simple arithmetic calculations is showed synthetically in Figure 3.
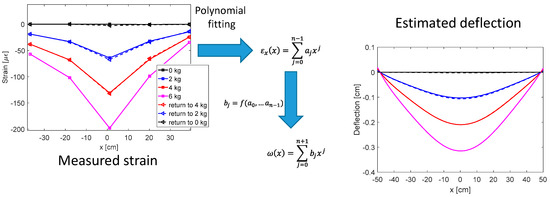
Figure 3.
Procedure to obtain the polynomial deflection function of a line.
Once calculated the vertical deflection along the arrays, it is possible to get the tridimensional profile of the deflection on the whole structure by means of polynomial fitting with two variables.
The deflection map of the panel loaded with 6 kg has been displayed in Figure 4, where the position of the FBGs strain sensors has been indicated with pink dots. The map shows that at the edges there are no significant variations while the panel flexes at the center with maximum deflection values of about −0.30 cm.
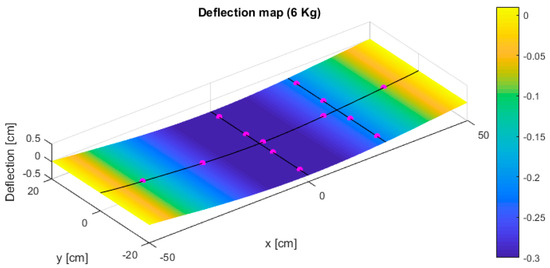
Figure 4.
Deflection map of the multilayer panel with a load of 6 kg.
In order to validate the proposed model, numerous tests have been performed, comparing the deflection estimated with the proposed algorithm with the direct deflection measurements carried out by a mechanical comparator (Mitutoyo ID-C125XB, uncertainty of 0.003 cm) showing a very good accordance.
4. Conclusions
In this work a multilayer panel has been instrumented with 15 FBGs arrayed along only few optical fibers, avoiding the complex wiring typical of strain gauges. From the strain measured by the FBGs, the curvature function has been evaluated as a polynomial function with the coefficients obtained by least mean square analysis; then the deflection is estimated by integrating twice the curvature function.
Experimental results show good agreement between the deflection indirectly measured by the FBGs and directly measured by a mechanical comparator, with a resolution of few tens of microns.
We have demonstrated that the proposed technique allows an effective real-time indirect structural monitoring in small and large structures solving the existing difficulties in measuring the deflection directly.
Author Contributions
Experiment design and supervision, M.D.P., A.I. and S.C.; sensorized panel construction V.C., M.A., M.D.P., A.I. and S.C.; numerical and experimental characterization P.D.P. and G.P.; paper writing, P.D.P.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University of Naples “Parthenope”, through the “Bando di sostegno alla ricerca individuale per il triennio 2015-2017, Annualità 2017”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, H.; Ren, W.-X.; Wang, Z.-C. Deflection Estimation of Bending Beam Structures Using Fiber Bragg Grating Strain Sensors. Adv. Struct. Eng. 2015, 18, 395–403. [Google Scholar] [CrossRef]
- Alampalli, S.; Fu, G.; Dillon, E.W. On the Use of Measured Vibration for Detecting Bridge Damage. In Proceedings of the Fourth International Bridge Engineering Conference, San Francisco, CA, USA, 28–30 August 1995; pp. 125–137. [Google Scholar]
- Tennyson, R.C.; Mufti, A.A.; Rizkalla, S.; Tadros, G.; Benmokrane, B. Structural health monitoring of innovative bridges in Canada with fiber optic sensors. Smart Mater. Struct. 2001, 10, 560–573. [Google Scholar] [CrossRef]
- Baldwin, C.S.; Salter, T.; Niemczuk, J.B.; Chen, P.C.; Kiddy, J.S. Structural monitoring of composite marine piles using multiplexed fiber Bragg grating sensors: In-field applications. In Proceedings of the Smart Structures and Materials 2002: Smart Systems for Bridges, Structures, and Highways, San Diego, CA, USA, 28 June 2002. [Google Scholar]
- Klar, A.; Dromy, I.; Linker, R. Monitoring tunneling induced ground displacements using distributed fiber-optic sensing. Tunn. Undergr. Sp. Technol. 2014, 40, 141–150. [Google Scholar] [CrossRef]
- Li, C.; Zhao, Y.G.; Liu, H.; Wan, Z.; Zhang, C.; Rong, N. Monitoring second lining of tunnel with mounted fiber Bragg grating strain sensors. Autom. Constr. 2008, 17, 641–644. [Google Scholar] [CrossRef]
- Majumder, M.; Gangopadhyay, T.K.; Chakraborty, A.K.; Dasgupta, K.; Bhattacharya, D.K. Fibre Bragg gratings in structural health monitoring-Present status and applications. Sens. Actuators, A Phys. 2008, 147, 150–164. [Google Scholar] [CrossRef]
- Leung, C.K.Y.; Wan, K.T.; Inaudi, D.; Bao, X.; Habel, W.; Zhou, Z.; Ou, J. Review: Optical fiber sensors for civil engineering applications. Mater. Struct. 2015, 48, 871–906. [Google Scholar] [CrossRef]
- Kashyap, R. Fiber Bragg Gratings; Academic press: San Diego, CA, USA, 1999. [Google Scholar]
- Iadicicco, A.; della Pietra, M.; Alviggi, M.; Canale, V.; Campopiano, S. Deflection monitoring method using fiber bragg gratings applied to tracking particle detectors. IEEE Photonics J. 2014, 6. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).