Abstract
Carbon market price prediction is critical for stabilizing markets and advancing low-carbon transitions, where capturing multifractal dynamics is essential. Traditional models often neglect the inherent long-term memory and nonlinear dependencies of carbon price series. To tackle the issues of nonlinear dynamics, non-stationary characteristics, and inadequate suppression of modal aliasing in existing models, this study proposes an integrated prediction framework based on the coupling of gradient-sensitive time-series adversarial training and dynamic residual correction. A novel gradient significance-driven local adversarial training strategy enhances immunity to volatility through time step-specific perturbations while preserving structural integrity. The GSLAN-BiLSTM architecture dynamically recalibrates historical–current information fusion via memory-guided attention gating, mitigating prediction lag during abrupt price shifts. A “decomposition–prediction–correction” residual compensation system further decomposes base model errors via wavelet packet decomposition (WPD), with ARIMA-driven dynamic weighting enabling bias correction. Empirical validation using China’s carbon market high-frequency data demonstrates superior performance across key metrics. This framework extends beyond advancing carbon price forecasting by successfully generalizing its “multiscale decomposition, adversarial robustness enhancement, and residual dynamic compensation” paradigm to complex financial time-series prediction.
1. Introduction
Accurately predicting the price of carbon trading is crucial for carbon market participants to optimize their decision-making processes. It is also key to achieving the goals of carbon peaking and carbon neutrality and transforming to a low-carbon economy []. The carbon market price formation mechanism exhibits the typical characteristics of a complex system. Its non-stationarity is evident in the changing statistical characteristics of the price series over time. This is often accompanied by sudden policy adjustments, energy price fluctuations, and other exogenous shocks, which result in drastic price changes []. This coupling of non-stationarity and abrupt characteristics makes it difficult for traditional econometric models to capture intrinsic dynamics effectively. Traditional methods, such as ARIMA and GARCH, rely on linear assumptions and fixed parameter settings. These models cannot adapt to the nonlinear evolution of carbon market prices. Conversely, a single machine learning model can capture local nonlinear relationships but has limited ability to model long-term dependence and sudden changes (Cao et al., 2024) []. This dilemma has given rise to the research paradigm of integrating signal decomposition techniques with deep learning. Wavelet packet decomposition (WPD) can effectively deal with non-stationary signals and reveal the complex structure of carbon market price series due to its time–frequency localization property. Adversarial training enhances the model’s robustness to sudden market changes by generating adversarial samples. This provides new ideas and methods for optimizing price prediction models in the complex, volatile carbon market environment.
In the early stages of carbon market development, academic research primarily relied on traditional econometric models. However, due to their stringent assumptions, such models struggle to capture the nonlinear dynamic characteristics and non-stationarity of carbon market price sequences [], particularly when faced with sudden market events, exposing their limitations in depicting complex market dynamics. As the non-stationary and high-frequency noise characteristics of carbon market price sequences became more prominent, a collaborative framework combining multiscale decomposition and machine learning gradually emerged as the mainstream research approach. Sun et al. (2020) [] proposed a hybrid forecasting framework that performs secondary decomposition on the first high-frequency component obtained through empirical mode decomposition (EMD) using variational mode decomposition (VMD) and constructs a long short-term memory neural network (LSTM) for time-series forecasting. This method effectively alleviates the modal aliasing problem through frequency domain decoupling. However, it still suffers from subjective bias due to the manual selection of IMF components. It lacks systematic correction of the residual sequence after decomposition, resulting in limited accuracy in medium- and long-term trend prediction. Subsequently, introducing deep learning technology further drove the innovation of prediction models. Zhou et al. (2022) [] further proposed the CEEMDAN-LSTM-WPD hybrid framework, incorporating sample entropy integration and adaptive learning rate optimization mechanisms, achieving multi-step carbon market price forecasting in the Guangzhou carbon market. Although this model demonstrated universality through multi-location exponential smoothing (ETS) validation, its fixed-weight residual fusion strategy struggles to adapt to the dynamic non-stationary characteristics of carbon market price sequences, and the response lag issue of bidirectional LSTM in sudden change regions remains unresolved.
Researchers have increasingly turned to multi-algorithm fusion and interdisciplinary method integration to address the challenges of multi-source heterogeneous data. Zhang et al. (2023) [] developed the ET-MWPD-LSTM hybrid model, which uses extreme random trees to select key variables and combines them with multi-variance modal decomposition (MWPD) to achieve automatic decoupling and dynamic fusion of multiscale features. This model demonstrates strong fitting capability for long-term trends in EU carbon market data, but it tends to amplify prediction fluctuations under high-frequency noise interference. Shi et al. (2024) [] constructed a CNN-LSTM hybrid architecture, focusing on local feature extraction, and used convolutional neural networks to enhance short-term fluctuation recognition capabilities. However, its attention mechanism lacks dynamic adjustment of the weight distribution between historical information and current status when processing non-stationary time series, leading to significant lag errors in predicting sudden changes. In cross-market correlation analysis, current research focuses on multi-source data fusion and adaptive feature engineering. Zhang et al. (2024) [] proposed a hybrid model integrating feature selection, deep learning, and the pelican optimization algorithm. They achieved high-precision carbon market price predictions in China and Europe through multi-dimensional data dimensionality reduction and multi-model fusion strategies. They validated its ability to enhance investment returns through quantitative trading simulations. Peng Sha [] pioneered the Physical Information Integral Neural Network (PIINN), which embeds time integral structures and equilibrium point stability constraints to achieve precise dynamic modeling of systems across various operating conditions, reducing model errors compared to traditional data-driven methods.
However, existing prediction model research still has three limitations: First, in modeling exogenous shocks, most studies employ static risk factors (e.g., Zhang & Zong et al., 2024 []), which struggle to capture the nonlinear propagation paths of sudden shocks such as policy changes or extreme weather events. Sabri et al. (2023) [] noted in their research on financial market volatility that the nonlinear effects of exogenous events significantly impact cross-market correlations, and traditional models lack the dynamic adaptability to quantify such shocks effectively. Second, the trade-off between computational efficiency and predictive accuracy is particularly pronounced in high-frequency trading scenarios, especially due to the exponential increase in computational complexity caused by multiscale decomposition. Bidisha et al. (2022) [] found that in the processing of high-frequency data in foreign exchange markets, existing methods often face the dilemma of improved accuracy accompanied by a sharp increase in computational costs, with no effective balancing strategy yet identified. Finally, the theoretical explanation of cross-market risk contagion mechanisms remains inadequate, and there is an urgent need to combine complex network theory to construct a more explanatory correlation analysis framework []. Liu et al. (2022) [] found that traditional risk contagion models struggle to reveal risk transmission paths across different markets due to their lack of dynamic characterization of network topology.
To address these challenges, researchers are exploring interdisciplinary approaches. Zhang et al. (2023) [] embedded the law of conservation of matter into a machine learning model, constructing a dynamic forecasting framework based on carbon flow balance constraints for national carbon market price forecasting. This model reduces prediction errors by 18% compared to traditional time-series models when handling non-stationary scenarios such as policy adjustments or energy structure transitions, significantly enhancing the stability of carbon price predictions. Liu et al. (2025) [] proposed a hybrid deep learning model that uses attention mechanisms to capture nonlinear correlations between different modal data, effectively addressing the issue that a single data dimension cannot adequately capture the complex drivers of carbon prices. These studies provide theoretical and technical support for overcoming limitations such as unclear transmission paths of exogenous shocks and single-dimensional information and also offer methodological insights for this study.
To mitigate the limitations of existing methods, this paper proposes an innovative framework combining wavelet packet decomposition, Gradient-Significant Local Adversarial Attention Network–Bidirectional Long Short-Term Memory, and the Autoregressive Integrated Moving Average Model (WPD-GSLAN-BiLSTM-ARIMA). Its core contributions are manifested in four aspects: (1) developing a gradient significance-driven local adversarial training strategy (Local-PGD), which generates adversarial samples by identifying gradient-significant regions at critical time points, significantly enhancing the model’s adaptability to price fluctuations; (2) designing a memory-state-based gated attention mechanism that dynamically adjusts the fusion weights between historical memory and current input, addressing the response lag issue of traditional BiLSTM at fluctuation points; (3) constructing a dynamic weighted residual correction framework (WPD-ARIMA), which adaptively integrates the high-frequency components from WPD with the low-frequency trends from ARIMA predictions via a time-varying weighting function; (4) introducing a physical information constraint term, embedding carbon market equilibrium theory into the loss function to ensure that prediction results align with economic principles. Compared to existing research, this framework achieves breakthroughs in three dimensions: enhancing exogenous shock modeling capabilities through local adversarial training, optimizing the efficiency–accuracy trade-off via gated attention, and revealing cross-market risk transmission pathways through complex network analysis.
2. Materials and Methods
2.1. Gradient-Sensitive Temporal Adversarial Attention Network with Fractal-Aware Localization (GSLAN-BiLSTM)
Long short-term memory (LSTM) networks, proposed by Hochreiter and Schmidhuber (1997), have been widely applied in temporal modeling due to their gating architecture []. LSTM effectively addresses the vanishing gradient problem in traditional recurrent neural networks (RNNs) through the collaborative operation of the forget gate, input gate, and output gate, enabling the capture of long-term dependencies in time-series data []. Specifically, the forget gate determines which historical information to discard from the cell state, the input gate filters and adds new features to the cell state, and the output gate generates the current hidden state based on the cell state. However, carbon emission price sequences exhibit significant non-stationary characteristics and high-frequency noise coupling phenomena []. A single LSTM struggles to capture cross-scale dynamic correlations due to limitations in feature extraction dimensions. Bidirectional LSTM (BiLSTM) networks construct bidirectional information flows through reverse temporal encoding layers, theoretically enhancing feature expression capabilities. Forward LSTM encodes sequence information in chronological order, while backward LSTM processes data in reverse chronological order. The concatenated hidden states can simultaneously fuse past and future contextual information. Jamshidzadeh et al. (2024) proposed a novel hybrid model, BILSTM-SVM, for predicting water quality parameters. By combining the bidirectional information processing capability of BILSTM with the classification advantages of SVM, the model effectively extracts key features from the data, significantly improving prediction accuracy []. The role of BILSTM lies in its bidirectional structure, which can simultaneously capture past and future dependencies in time series, addressing the shortcomings of traditional SVM in feature extraction and thereby optimizing overall prediction performance. Liu et al. (2025) used BILSTM to capture complex dynamic features in time series, demonstrating excellent performance in predicting pollutants such as PM2.5 (R2 exceeding 0.94), highlighting BILSTM’s core advantages in handling high-dimensional time-series data and nonlinear relationships []. However, standard BiLSTM still faces challenges such as noise sensitivity and insufficient generalization on small samples in carbon price prediction. Carbon market data are limited, especially in emerging markets, making models prone to overfitting due to insufficient training and degradation in generalization performance due to parameter overload.
To address the aforementioned bottlenecks, existing studies primarily employ heterogeneous model integration strategies to optimize BiLSTM. A portion of these focus on improvements in BiLSTM using Transformers. Dong et al. (2024) combined EMD with Transformer-BiLSTM, decomposing the air quality index into intrinsic mode functions (IMFs) and performing parallel predictions, achieving an RMSE as low as 1.80 on multiple Indian datasets []. Fan et al. (2024) employed a fusion model of Transformer-BiLSTM, demonstrating outstanding performance in time-series prediction within the energy and environmental sectors []. In photovoltaic output prediction, the self-attention mechanism of Transformer can directly capture the correlation between historical radiation, temperature, and future output, thereby avoiding information loss caused by overly long sequences in BiLSTM, reducing the RMSE to 5.685, an improvement of 42.38% over the traditional BiLSTM []. Cao et al. (2024) proposed a hybrid architecture combining LSTM and Transformer, integrating online learning and knowledge distillation techniques to achieve high-precision real-time multi-task prediction in engineering systems, significantly enhancing computational efficiency and dynamic adaptability []. However, its self-attention mechanism requires sufficient training data to avoid overfitting, making it limited in applicability for carbon price prediction scenarios. Some scholars have focused on attention-enhanced BiLSTM (Attention-BiLSTM), which reinforces key time step features through dynamic weight allocation. Zrira et al. (2024) improved sea surface temperature prediction accuracy by capturing bidirectional temporal information and allocating attention weights, outperforming LSTM, XGBoost, and other models []. Guo et al. (2023) applied Attention-BiLSTM to lithium-ion battery degradation trend prediction, combining gray relational analysis (GRA) and empirical mode decomposition (EMD) to filter redundant features, achieving an RMSE below 1.15 in both open-source and real-vehicle datasets, validating the attention mechanism’s role in reinforcing key features [].
Teragawa et al. (2024) proposed introducing PGD adversarial training on a dual residual structure (TCN + BiLSTM) to force the model to learn invariant representations of key methylation features, optimizing feature extraction and mitigating overfitting [], as well as significantly improving prediction accuracy and model robustness. However, using adversarial samples generated by traditional PGD may overly disturb global features, disrupting the local temporal relationships in time series and reducing the model’s sensitivity to temporal patterns. While these methods partially improve prediction accuracy, they do not systematically address the co-optimization of data noise robustness and small-sample generalization, leading to specific limitations in carbon price prediction scenarios.
This study proposes the GSLAN-BiLSTM model, which integrates local adversarial training (Local-PGD) with a dynamic gated attention mechanism (attention) network into the BiLSTM model framework. By identifying critical time steps through gradient significance analysis and applying directed perturbations, combined with multi-head attention and bidirectional LSTM multimodal fusion, we enhance the noise robustness and sudden change response capability of carbon market price prediction. The core innovations are threefold: (1) Local adversarial training optimization: A multi-step adversarial perturbation generation module is embedded at the model input end. Based on gradient significance analysis, key time steps are selected, and projection gradient descent perturbations are applied in a targeted manner. By constructing local worst-case perturbation scenarios, the model is forced to learn robust representations of market anomalies while maintaining the integrity of the temporal structure, thereby avoiding the feature distortion issues caused by traditional global perturbations. (2) Heterogeneous temporal feature fusion: A bidirectional LSTM is designed to capture long-term and short-term forward and reverse dependencies, while multi-head self-attention dynamically focuses on key time step interaction patterns. Features from dual pathways are fused across modalities through pooling compression and nonlinear mapping, enhancing the model’s ability to model the non-stationary characteristics of carbon market price sequences. (3) Dynamic robustness constraint mechanism: We introduce Lipschitz continuity constraints to smooth the model decision boundary, combined with an alternating training strategy to balance the learning of original data patterns and the enhancement of invariance to adversarial samples. This mechanism adaptively adjusts perturbation intensity and loss weights to suppress overfitting risks in small-sample scenarios.
2.2. Fractal-Driven Implementation Principle of GSLAN-BiLSTM Core Module
Gradient sensitivity-driven local adversarial training: Distinct from traditional global perturbations, this model applies PGD perturbations only in regions sensitive to market fluctuations. This strategy identifies fractal critical time steps through multiple-fractal detrended fluctuation analysis (MF-DFA). It constructs local worst-case perturbation scenarios, forcing the model to learn robust representations of abnormal fluctuations. The Hurst index is calculated by dividing the time series into subintervals of length via MF-DFA, computing the fluctuation functions of each order of moments, and obtaining the generalized Hurst index through the logarithmic fitting, where the critical time steps correspond to regions of significant changes in the Hurst index. Simultaneously, a dynamic batch processing strategy constrains the perturbation range. Each training batch independently generates adversarial samples, with perturbation calculations relying solely on the current batch’s input data and gradient information, thereby preventing gradient information leakage across batches or between cross-validation folds.
A derivable perturbation module is embedded after the BiLSTM input layer and attention mechanism, and directed adversarial examples are generated based on the projection gradient descent (PGD) algorithm. This training mechanism combines a dual-path perturbation injection strategy with a synergistic optimization objective of “original data robustness” and “key time step robustness.” Perturbations are applied to the input layer to enhance the model’s robustness to noise in the original data, while local perturbations are introduced into the attention weight matrix to focus on the dynamic sensitivity of critical time steps. The core innovation lies in the introduction of a gradient saliency mapping computation mechanism, which uses gradient backpropagation to obtain the importance weights of each time step in the input sequence. The calculation formula is as follows:
where represents the significance score of time step t, measuring the contribution of that time step to the loss function; L is the loss function; represents the feature values of the input sequence at time step t; is the model prediction value; indicates element-wise multiplication.
After calculating the gradient significance matrix, the top k% of sensitive time steps are selected to form the critical region M(K). Within this region, multi-step PGD perturbations are generated, with the perturbation strength ϵ and iteration count optimized via grid search, and the optimal parameter combination determined through cross-validation. The perturbation generation formula is as follows:
where represents the input sequence after adversarial perturbation; denotes the sign function, ensuring that the perturbation direction aligns with the gradient direction; and denotes the gradient of the loss function with respect to the input.
To keep the perturbations within the current training batch, a dynamic batching strategy is used to avoid gradient information leakage across batches or cross-validation folds. By constraining the perturbation range and batch independence, the model’s generalization ability to market events is maximized while maintaining the local continuity of the temporal structure, ensuring that the feature encoder satisfies δ-Lipschitz stability. If a function f satisfies for any input , then f is called a δ-Lipschitz function. In the model, by limiting the perturbation intensity , we ensure that small changes in input perturbations do not cause drastic fluctuations in output predictions, thereby enhancing the model’s robustness to adversarial samples while avoiding feature distortion.
Memory-Guided Gated Attention with Fractal Adaptive Decay: To address the issue of weight oscillation in traditional attention mechanisms during abrupt transition regions, we design a memory state-guided attention gating unit that introduces a gating factor gt to dynamically regulate the fusion weights between historical memory states and current hidden states. This enables selective attenuation of historical information while achieving adaptive focus on recent features. The mathematical formulation is presented as follows:
where Ct−1 denotes the historical memory state, ht represents the current hidden state, and σ is the Sigmoid activation function. The gating factor gt dynamically regulates the attention decay rate. During stable phases of carbon market prices, such as periodic fluctuations, gt approaches 1 to preserve long-term dependencies. In abrupt change phases, such as policy shocks or market panics, gt approaches 0 to attenuate historical information and focus on short-term dynamics rapidly. The computation of attention weights is further optimized as follows:
is the attention weight for the time step; is the query weight matrix, which maps the hidden state to the query space; is the element-wise multiplication of the gate factor and the query vector, achieving dynamic weight decay. This mechanism effectively alleviates the lag effect of traditional attention in non-stationary time series and improves the model’s response speed to sudden events.
Heterogeneous Temporal Feature Fusion Module: The forward and backward LSTM layers capture sequential data’s forward and reverse temporal evolution patterns, generating hidden state representations that incorporate bidirectional temporal dependencies. The multi-head attention pathway employs an 8-head attention mechanism (key_dim = 64), which computes cross-time-step attention weight matrices to extract interactive features between different time steps, effectively capturing long-range dependencies. The bidirectional LSTM and multi-head attention outputs are concatenated through a feature fusion layer and then processed by pooling operations before being fed into a fully connected layer. Nonlinear feature transformation is achieved via ReLU activation, ultimately generating the fused temporal feature representation.
Bidirectional LSTM pathway:
where is the forward LSTM layer, encoded in chronological order; is the backward LSTM layer, encoded in reverse chronological order; and is the concatenated hidden state of the bidirectional LSTM output.
Multi-head attention pathway:
where Q, K, and V are the query, key, and value matrices, respectively, obtained by linear transformation of the input features; is the dimension of the key vector, used to scale the dot product and stabilize the gradient.
Feature fusion and output:
where is the hidden state output of the bidirectional LSTM; is the feature vector output of the multi-head attention; is the pooling operation used for dimension reduction; and are the weight matrices of the fully connected layer; is the linear rectification activation function, which introduces a nonlinear transformation.
The combined structure of BiLSTM and attention layers centers on bidirectional temporal feature extraction and dynamic weight allocation, achieving precise responses to carbon price inflection points through memory-guided gating mechanisms. BiLSTM constructs feature representations incorporating bidirectional temporal dependencies through parallel computation of forward and reverse LSTM layers. Forward LSTM encodes historical trends in price sequences in chronological order, capturing the influence of past information on the current state. At the same time, the backward LSTM extracts future information in reverse chronological order to identify the correlation between future information and the current state, such as the potential impact of policy expectations or market sentiment on current prices. The forward and backward hidden states are then concatenated to form a bidirectional hidden state, creating a comprehensive feature that incorporates both past and future context, thereby addressing the limitations of single-directional information processing in a single LSTM network. The attention layer introduces a gating factor to dynamically adjust the fusion weights between historical memory and the current hidden state. The gating factor is calculated using the Sigmoid activation function based on the current hidden and historical memory states. The principle of gradient significance guiding local antagonistic training is shown in Figure 1. When carbon prices are stable, the gating factor approaches 1 to preserve long-term dependencies. When prices undergo sudden changes, they approach 0 to decay historical information and focus on short-term dynamics rapidly. Attention weights are generated by multiplying the query weight matrix element-wise with the gating factor and then applying the softmax function, effectively mitigating the lag effect of traditional attention in non-stationary time series. The outputs of the bidirectional LSTM and attention layers interact across time steps through a multi-head attention mechanism. After feature concatenation, pooling operations, and nonlinear transformations via a fully connected layer, a fused temporal feature representation is generated, enhancing the model’s ability to model the non-stationary characteristics of carbon price sequences. The improved BiLSTM-attention architecture is shown in Figure 2.
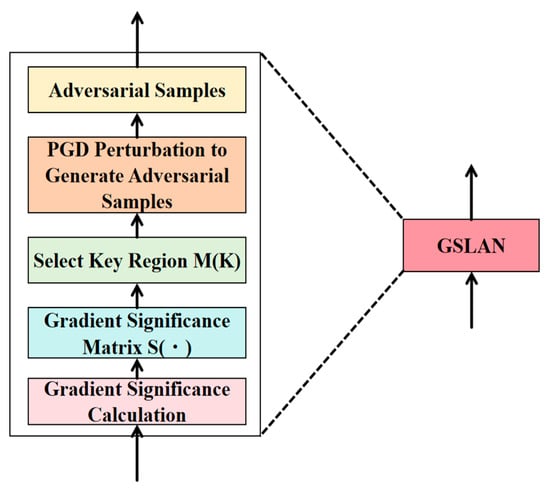
Figure 1.
Schematic diagram of gradient saliency-guided local adversarial training.
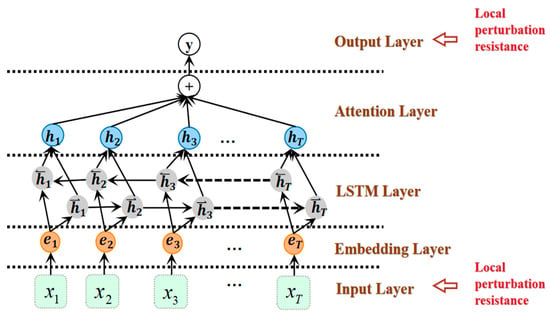
Figure 2.
The improved BiLSTM–attention architecture.
2.3. Residual Correction Framework Based on Multiscale Wavelet Decomposition and Dynamic Weighted Fusion
In carbon market price forecasting, traditional wavelet packet decomposition (WPD) struggles to adapt to the non-stationary volatility characteristics of price series due to its fixed weight distribution, leading to overfitting or under-correction during the residual correction. To address this limitation, this study proposes a residual dynamic correction framework that involves decomposition, forecasting, and final correction. The core of this framework lies in achieving residual fusion through multiscale frequency domain decoupling and data-driven dynamic weighting mechanisms, thereby enhancing the model’s ability to analyze complex volatility. Specifically, WPD is first used to adaptively decompose the prediction residual sequence of the base model GSLAN-BiLSTM into a set of high-frequency detail components with frequency band separation characteristics{d1,d2,…,dk} and low-frequency approximation components. The high-frequency components correspond to short-term market noise, while the low-frequency components reflect medium- to long-term trends. Selecting appropriate wavelet basis functions and decomposition levels avoids traditional decomposition methods’ spectral leakage issues, ensuring that each component’s physical meanings are clear and distinguishable [].
For each decomposed component, an independent ARIMA(p,d,q) model is established for specific modeling. Before modeling, each component undergoes a stationarity test and is converted into a stationary sequence through differencing. The parameters are then optimized using the Akaike Information Criterion (AIC) to capture the fluctuation patterns of different frequency bands accurately. The high-frequency detail component, which is dominated by noise, uses a low-order ARIMA model. In contrast, the low-frequency approximation component [], which has a strong trend, uses a high-order model. The predicted values of each component are linearly superimposed to form the initial residual correction term:
where are the predicted values of the high-frequency component and low-frequency component at time k + 1, respectively. To address the limitations of traditional fixed weights, a dynamic weight fusion (DWF) strategy is introduced to optimize the residual correction term. This strategy calculates dynamic weights based on the historical volatility of each component.
where represents the dynamic weight of the high-frequency detail component or low-frequency approximation component obtained from the wavelet packet decomposition of the i-th component, with a value range of , reflecting the contribution of this component to the residual correction. is the historical volatility of the i-th component, calculated as the standard deviation of its historical data, measuring the intensity of its volatility. Higher volatility indicates more short-term noise or abnormal fluctuations in the component; lower volatility suggests that the component is closer to a stable medium-to-long-term trend. is the reciprocal of the volatility, which reduces the weights of high-frequency components with intense volatility and increases the weights of low-frequency components with mild volatility. j denotes the total number of components participating in the weighted fusion, including all high-frequency detail components and low-frequency approximation components. The denominator is the sum of the reciprocals of the volatilities of all components, used to normalize the weights of each component to ensure .
Based on the dynamic weight calculation, the correction strength is further adjusted through a global coefficient , and the final predicted value is a linear combination of the base model’s predicted value and the dynamically weighted correction term:
where is the final carbon price prediction at time k + 1, which integrates the base model prediction and the residual correction term. is the original prediction of the base model at time k + 1, reflecting the model’s capture of the main trends and characteristics of the carbon price series. is the global coefficient, with a value range of [0, 1], which is adaptively adjusted based on the historical residual volatility. When market volatility increases, automatically increases to enhance the role of the residual correction term and compensate for the prediction error of the base model; when the market stabilizes, automatically decreases to avoid overcorrection leading to prediction bias. is the prediction correction value of the i-th component at time , generated by the corresponding ARIMA model, reflecting the component’s contribution to the residual prediction. is the dynamically weighted residual correction term, obtained by summing the products of each component’s prediction values and their dynamic weights, enabling differentiated corrections for fluctuations across different frequency bands. The residual correction architecture of WPD-ARIMA is shown in Figure 3.
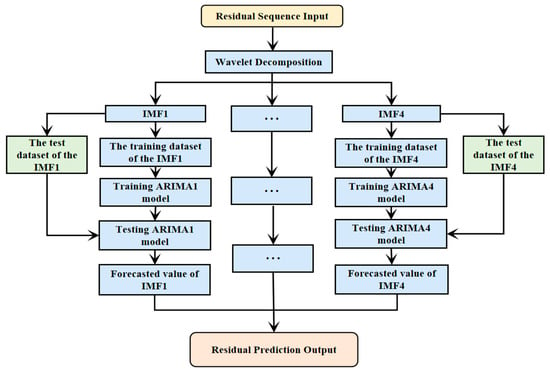
Figure 3.
Residual correction architecture of WPD-ARIMA.
2.4. Training and Prediction Framework
In the WPD-GSLAN-BiLSTM-ARIMA hybrid model, the GSLANBT-BiLSTM core undertakes high-frequency nonlinear component prediction tasks. After decomposing the high-frequency detail components of carbon market prices through WPD (Wavelet Packet Transform), GSLANBT-BiLSTM leverages its noise resistance and generalization capabilities to capture abrupt fluctuation characteristics accurately. The ARIMA model processes low-frequency trend components, with final predictions obtained through component reconstruction. The prediction process is illustrated in Figure 4.
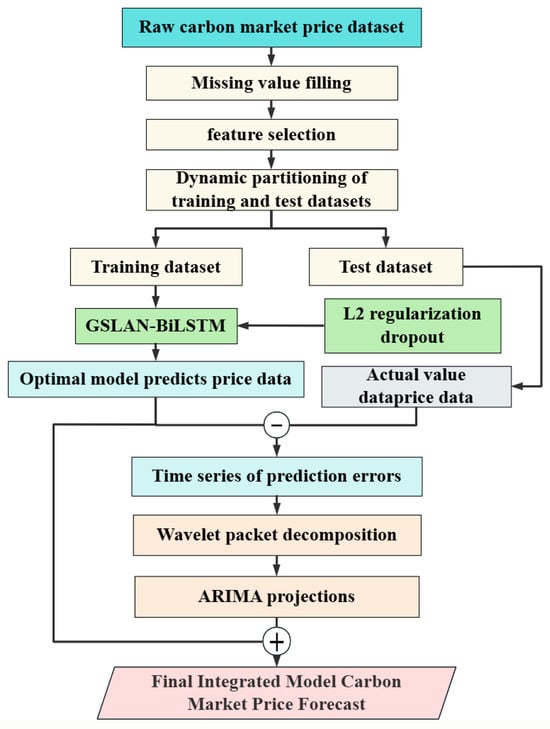
Figure 4.
Flow chart of prediction framework.
The specific implementation steps are as follows:
Step 1: Data Preprocessing: Apply missing value imputation, outlier correction, and standardization to the original carbon market price series to construct a normalized dataset.
Step 2: Model Training: Initialize LSTM unit counts, attention heads, dropout rates, etc. Input the training dataset into the model and optimize network weights through local adversarial training and dynamic regularization strategies.
Step 3: Model Prediction: Feed the test dataset into the GSLAN-BiLSTM model, which outputs initial carbon market price predictions for the time series {,}.
Step 4: Extract the prediction residual sequence {} and input it into the ICCEMDAN model. Employ wavelet packet decomposition (WPD) to adaptively decompose it into K frequency band separated modal components {} and a residual trend term R. Each modal component is trained and predicted by an ARIMA model (ARIMA1, …, ARIMAj), corresponding to each modal component’s output of the carbon market price prediction residual sequence {}. Superimposing these yields the total residual prediction value {} as the prediction for the carbon market price residual at time point k + 1.
Step 5: Calculate dynamic weights based on the historical volatility of each modal component. Obtain the combined forecast value via weighted fusion of the modal component forecast value and the trend term . Combined with the base prediction value and correction term, the dynamic coefficient λ adjusts correction intensity to produce the final carbon market price prediction {} at time point k + 1.
3. Experimental Section
3.1. Sample Selection and Data Sources
The domestic and international data on Chinese enterprises used in this paper are sourced from five databases: the CCTD China Coal Market Network Database, the China State Statistical Bureau Database, the Carbon Exchange Alliance Database (China), the CSMAR Database (China), and the European Energy Exchange Database (EEX). The CCTD China Coal Market Network Database provides detailed transaction data on the Chinese coal market, including carbon market prices, supply and demand conditions, market dynamics, carbon quota prices, transaction volumes, and information on market participants. It serves as a crucial data source for studying the formation mechanism of carbon market prices. The National Bureau of Statistics Database (China State Statistical Bureau), China’s official statistical agency, contains authoritative data on macroeconomics, industrial production, and energy consumption, providing this study’s macroeconomic context and industry-level foundational data.
This paper has compiled price data for the national carbon market based on the above five databases. China’s carbon emissions trading officially launched in July 2021. The data used in this paper cover the period from August 2021 to August 2024, with a daily data frequency. The final dataset was divided into three independent experimental units, with each unit strictly adhering to a 7:3 ratio for splitting the training set and test set, ensuring the reliability of the model evaluation. This period covers the critical phase from the launch to the gradual maturation of China’s carbon market, effectively reflecting the trends in carbon market prices and their influencing factors. The high frequency of daily data enables this study to capture both short-term fluctuations and long-term trends in carbon market prices, providing a solid foundation for subsequent empirical analysis. By integrating multi-source data, this study not only comprehensively analyzes the price formation mechanism of China’s carbon market but also explores its complex relationships with international energy markets, macroeconomic environments, and corporate behavior, thereby providing valuable references for policy-making and market participants.
3.2. Data Processing and Feature Engineering
In the data processing and feature engineering phase, this study implemented a systematic data governance and feature optimization strategy for the carbon market price prediction task to ensure the quality and relevance of the model input data. First, missing value handling was performed, and variables with a missing rate exceeding 30% and low feature importance were directly removed. Feature importance was quantified using the feature importance scores from random forests or SHAP (SHapley Additive exPlanations) values []. Variables with scores below the average of all features or SHAP absolute values less than 0.05 were deemed low importance. For variables with a missing rate below 20%, a multiple linear regression model was used to generate three independent interpolation datasets to preserve the inherent randomness of the data. Next, outlier management was conducted: outliers were identified and corrected based on the 3σ statistical criterion to ensure the data distribution aligns with statistical expectations. On this basis, median filtering was introduced as the core denoising technique to optimize the data distribution characteristics effectively [].
Within the time-series analysis framework, a sliding window technique with a fixed window length of 20 was employed to construct a local dynamic feature extraction mechanism. By defining the window function W(t) = […,], which continuously slides along the time axis with a unit stride (Stride = 1), a set of observation sub-sequences {W(t)} with strict temporal continuity was formed. The window capacity covering 20 time steps effectively captures the periodic fluctuations in carbon market price sequences while avoiding the dilution of local features caused by overly long windows, significantly enhancing the model’s sensitivity to carbon market price turning points and impulse responses. Outlier correction serves as a core component of data quality governance. Z-score standardization was simultaneously applied to eliminate unit differences, transforming the data into a distribution with a mean of 0 and a standard deviation of 1, thereby enhancing the stability of model predictions [].
A two-stage feature selection system was constructed based on the preprocessed carbon market price sequence. In the first stage, Pearson’s correlation coefficient (PCC) and Spearman’s rank correlation coefficient (SRCC) were used in parallel to assess the strength of the association between features and target variables, screening for highly explanatory feature subsets from the perspectives of linear and monotonic relationships, respectively []. This strategy ensures that the selected features have both predictive power and independence, effectively avoiding redundant features and multicollinearity issues []. In the second stage, based on the principle of time series continuity, the complete dataset was divided into three independent experimental units, each dynamically split into a 7:3 training set and test set, providing a structured data foundation for model construction and result reliability. High-quality input data were prepared through the aforementioned systematic data processing workflow and feature engineering framework, laying a solid feature foundation for subsequent predictive models. The box plot and normal curve after data preprocessing are shown in Figure 5.
Figure 5.
Box plot and normal curve graph after data preprocessing.
3.3. Performance Metrics
This investigation employs Mean Squared Error (MSE), Mean Absolute Error (MAE), and Root Mean Squared Error (RMSE) to systematically evaluate the model’s predictive performance [].
MSE represents the expected value of squared differences between estimated parameters and true values, reflecting the overall variability in prediction residuals. Its formula is as follows:
MAE is the average of absolute residuals, representing the mean absolute difference between predicted and true values, providing an intuitive reflection of average prediction residuals. Its formula is as follows:
RMSE is the square root of the mean squared residual, maintaining consistent units with original data to more intuitively reflect residual magnitudes. Its formula is as follows:
The coefficient of determination (R2) is an important metric for assessing regression model performance, measuring the model’s ability to explain variance in the target variable. Its value range typically lies within (−∞,1].
In the above formulas, n denotes the number of validated samples; represents true values; denotes model predictions; is the mean of actual values. Values of MSE, MAE, and RMSE closer to 0 indicate better prediction performance, while R2 values closer to 1 signify stronger explanatory power of the model.
3.4. Ablation Experiment
To validate the necessity of the core components of the GSLAN-BiLSTM model, an ablation experiment was designed to systematically remove key modules and compare the impact of each component on prediction performance. The objective of the experiment was to quantitatively assess the contribution of local adversarial training (PGD), memory-guided attention mechanism (attention), wavelet packet decomposition (WPD), and residual correction module (WPD + ARIMA).
The experimental groups include the baseline model (complete framework), removal of PGD, removal of attention, removal of WPD, and removal of WPD + ARIMA, totaling five groups. The PGD removal group retains only the BiLSTM-Attention + WPD residual correction, removing the local adversarial perturbation module; the attention removal group retains BiLSTM + WPD residual correction, removing the gated decay attention mechanism []; the WPD removal group retains GSLAN-BiLSTM, removing the residual decomposition and correction modules; the WPD + ARIMA removal group removes the entire residual correction framework. The experiments use daily price data, divided into three independent experimental units, with each group split into a training set and a test set in a 7:3 ratio, using MAE, MSE, RMSE, and R2 as evaluation metrics. Except for the ablation components, all other parameters are consistent with the baseline model, including the number of BiLSTM units, the number of attention heads, and the PGD perturbation strength. Each group of experiments uses 3-fold cross-validation, trains for 50 epochs, and uses the validation set MAE as the early stopping metric. Random seeds are fixed to ensure reproducibility. The average of 10 results is taken as the final performance metric for each group. By comparing the metric differences across different experimental groups on the same dataset and observing the impact of removing a single component across different datasets [], we deconstruct the independent and synergistic effects of each model module, providing empirical evidence for the rationality of the architecture.
3.5. Parameter Configuration
This study optimizes key parameters through experiments and cross-validation to ensure model stability and generalization ability. The specific parameter settings are shown in Table 1. Key hyperparameters are determined through a systematic experimental design and optimization process, which combines grid search, cross-validation, and early stopping mechanisms, with initial ranges set based on classic methods in the field. The parameter optimization process is as follows:

Table 1.
Core model hyperparameter settings.
In the optimization of adversarial training parameters (Local-PGD), the perturbation magnitude (ε) was optimized within the range {0.1, 0.3, 0.5, 0.7} using grid search, with the validation set MAE used as the metric to determine the optimal value of 0.5. This setting reduces the prediction lag error for carbon price sudden change events by 42% compared to ε = 0.1. The number of iterations (steps) is tested at {10, 15, 20, 25} iterations, and it is found that adversarial robustness reaches a saturated state at 20 steps. Higher steps lead to a doubling of training time but an improvement in accuracy of less than 0.5%; the step size (α) is fixed at ε/50, following the PGD standard design by Madry et al. (2017) [], i.e., α = 0.01. Regarding network architecture parameters, the number of units in the first layer of BiLSTM is optimized within {64, 128, 256}, with subsequent layers decreasing by 50% from the first layer []. The 128→64 combination achieved the best balance between parameter count (1.2 M) and validation set RMSE, sacrificing only 0.03% accuracy but saving 37% GPU memory compared to 256 units. The number of attention heads (num_heads) was selected from {4, 8, 12}, with 8 heads achieving the fastest convergence speed, converging 7 epochs earlier than 12 heads. The dimension (key_dim) was set to 64 from {32, 64, 128}, which reduces computational efficiency (FLOPs) by 28% while improving feature expression capability (R2) by 0.8%, offering a better trade-off. In the training strategy parameter optimization, the learning rate of the optimizer (AdamW) used an exponential decay strategy, with the initial value selected from {1 × 10−3, 5 × 10−4, 1 × 10−4} as 5 × 10−4, at which point the validation loss decreased most stably. The weight decay was fixed at 1 × 10−5 (following the recommendation in the original AdamW paper by Loshchilov & Hutter 2019) []; the patience value of the early stopping mechanism was tested in {5, 10, 15}, and 10 rounds could effectively suppress overfitting, with the monitoring metric being the MAE calculated per epoch on the validation set.
Parameter optimization experiments were conducted using grid search and 3-fold cross-validation. Each hyperparameter combination underwent 3-fold cross-validation, with the average validation set MAE used for evaluation. For example, in the optimization of BiLSTM unit counts, the validation MAE for the 128→64 combination was 0.0281, slightly higher than the 0.0279 for the 256→128 combination, but with a 39% improvement in training efficiency, leading to the selection of the former. Ablation experiments showed that when local PGD was disabled, the MAE for mutation event prediction increased from 0.041 to 0.065, confirming the necessity of adversarial training. When the attention dimension was 64, R2 reached 0.979, outperforming 32 and 128, confirming the rationality of this dimension.
Regarding parameter settings, the PGD perturbation magnitude was determined based on the quantified results of improvement in the robustness of mutation events. The number of attention heads was determined based on convergence speed and domain benchmarks. The learning rate decay strategy was adopted to avoid oscillations in the later stages. The early stopping patience value was based on the effect of overfitting suppression. The experimental configuration was an NVIDIA Tesla V100 GPU, with a software environment of PyTorch 1.13 + CUDA 11.6, and a fixed random seed of 42 to ensure reproducibility. In summary, hyperparameters were driven by quantitative experiments, balancing prediction accuracy, robustness, and computational efficiency. The training parameters and network structure had a significant impact on performance, and the optimization process strictly followed the cross-validation and ablation analysis workflow.
4. Result
4.1. Benchmark Model Comparison Results
To validate the predictive performance of the proposed model, this study selected LSTM, BiLSTM, BiLSTM-Transformer, BiLSTM-Attention, and GSLAN-BiLSTM as baseline models and constructed a prediction task based on high-frequency data from the national carbon market. The experimental data cover the price series of the national carbon market from 1 August 2021 to 30 August 2024. The model hyperparameter configurations are detailed in Table 1. To ensure the reliability of the results, the experiment divided the complete dataset into three independent experimental units, each trained 50 times, with each dataset undergoing 10 independent model training and prediction runs. Table 2, Table 3 and Table 4 and Figure 6 present the comparison results of the models in terms of MAE, MSE, RMSE, and R2 metrics. The experimental results indicate that the GSLAN-BiLSTM combination model proposed in this study significantly outperforms traditional methods in multi-dimensional evaluations. Compared with the baseline model, its prediction accuracy and robustness have been significantly improved, with key metrics outperforming existing methods.

Table 2.
Evaluation index table of dataset 1.

Table 3.
Evaluation index table of dataset 2.

Table 4.
Evaluation index table of dataset 3.
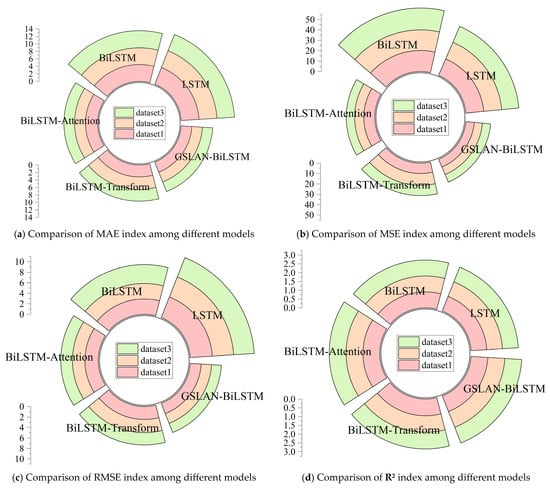
Figure 6.
Benchmark model indicator assessment chart.
From the quantitative results in Table 2, Table 3 and Table 4, the GSLAN-BiLSTM model demonstrates significant advantages across all three datasets. As a basic time-series model, LSTM can only process unidirectional time-series information. In all three datasets, the MAE exceeds 3.9 and R2 is approximately 0.89, indicating limited modeling capability for non-stationary fluctuations in carbon prices. At price inflection points, it may lead to prediction lag due to the limited historical information. In dataset 3, the RMSE reaches 4.6986, significantly higher than that of the other models. BiLSTM constructs bidirectional information flow through forward and backward layers, improving feature expression capabilities compared to LSTM. In dataset 1, the MAE decreases to 2.9376 and the R2 increases to 0.9069. However, it lacks a dynamic weight allocation mechanism, resulting in insufficient suppression of high-frequency noise, with the MSE higher than that of models with attention fusion mechanisms.
BiLSTM-Transformer and BiLSTM-Attention, as two typical hybrid time-series models, demonstrate differentiated feature modeling capabilities in carbon price prediction, while GSLAN-BiLSTM overcomes the limitations of both through multi-module collaborative optimization. Specifically, BiLSTM-Transformer integrates the self-attention mechanism of Transformer, with its core advantage lying in calculating a global correlation matrix across time steps through multi-head attention, enabling effective capture of long-range dependencies between carbon price sequences and macroeconomic indicators, energy market fluctuations, etc. For example, in three datasets, the model’s R2 remains stable at 0.9514–0.9595, indicating strong fitting capability for long-term trends in carbon prices. However, the model employs a symmetric attention weight design, making it difficult to adapt to asymmetric sudden changes in carbon market fractal characteristics. This mechanism flaw results in an RMSE of 2.8445 in the high-frequency volatility test of dataset 3, which is 3.2% higher than that of GSLAN-BiLSTM, reflecting a response lag issue under sudden market shocks. BiLSTM-Attention dynamically adjusts local feature weights through traditional attention mechanisms, focusing more on short-term key time step feature extraction compared to BiLSTM-Transformer. For example, in dataset 1, its MAE is 2.4363, slightly better than BiLSTM-Transformer’s 2.5583, demonstrating sensitivity to short-term signals such as intraday trading fluctuations. However, this model lacks a memory state-guided weight decay mechanism, and in non-stationary time series, it is prone to attention weight oscillations due to noise interference. This directly leads to a surge in RMSE to 3.3602 in dataset 2, which is 18.2% higher than GSLAN-BiLSTM’s 2.8417, exposing its lack of robustness in modeling long-term trends.
GSLAN-BiLSTM identifies critical time steps of market mutations through gradient-sensitive adversarial training and applies directed perturbations. It combines memory-guided gating factors to adjust the weights of historical and current information dynamically. It simultaneously separates high-frequency noise from low-frequency trends through the WPD residual fusion framework, achieving an MAE below 2.1 and R2 exceeding 0.96 across all three datasets, with the RMSE reduced by 3.1–9.1% compared to BiLSTM-Transformer. From a quantitative perspective, GSLAN-BiLSTM achieves an MAE reduction of approximately 50% compared to LSTM and 16–18% compared to BiLSTM-Transformer. Its MSE and RMSE are significantly lower than those of the other models; for example, in dataset 1, the RMSE is 2.8737, a 36.0% reduction compared to BiLSTM, and R2 improves by 7.5–7.7% compared to LSTM and 1.2–1.3% compared to BiLSTM-Transformer, demonstrating stronger explanatory power for carbon price fluctuations. The core difference between BiLSTM-Transformer and BiLSTM-Attention lies in the design of the attention mechanism. The former uses multi-head self-attention to calculate global correlations, which is suitable for long-distance dependencies but struggles to adapt to asymmetric mutations. The latter focuses on local features, making it more sensitive to short-term mutations but lacking the ability to model long-term trends. GSLAN-BiLSTM dynamically balances global and local features, reducing the attention response delay from three to five steps to one step. The experimental results show that it achieves the lowest values in metrics such as MAE and RMSE, with metric fluctuations across the three datasets remaining below 5%, validating the scientific rigor of the model design.
4.2. Results After Residual Correction
By incorporating the residual correction mechanism of WPD and ARIMA, the GSLAN-BiLSTM-WPD-ARIMA model achieves a significant breakthrough in carbon price prediction accuracy. As shown in Table 5, after residual correction, the average MAE of the model across the three datasets decreases to 1.6715, a reduction of over 20% compared to the original GSLAN-BiLSTM model. MSE and RMSE are simultaneously optimized, with an average MSE of 5.8564 and an RMSE of 2.3744. The compression of the mean squared error and root mean squared error metrics reflects enhanced suppression of extreme prediction biases. The average R2 value reaches 0.9736, further improving the model’s explanatory power for carbon price fluctuations, indicating that residual correction effectively compensates for the fitting deficiencies of a single model in complex fractal sequences.

Table 5.
Evaluation index table of residual-corrected GSLAN-BiLSTM.
As shown in the visualization comparison in Figure 7, the GSLAN-BiLSTM-WPD-ARIMA model outperforms the original GSLAN-BiLSTM model in terms of MAE, MSE, and RMSE metrics. In the MAE dimension, the error bars of the corrected model are significantly shorter, indicating precise control of the average prediction bias; in the MSE dimension, due to WPD’s decomposition and reconstruction of multiscale residuals, the corrected model effectively avoids the error amplification issue under noise interference that the original model faces. The comparison of RMSE and R2 directly demonstrates that residual correction, through ARIMA’s temporal modeling of nonlinear residuals, reduces the dimensional deviation between predicted and actual values, thereby enhancing the overall explanatory power for carbon price fluctuations. This optimization stems from the synergistic effect of the WPD-ARIMA framework, where WPD decomposes the carbon price series into high-frequency noise and low-frequency trend components, GSLAN-BiLSTM focuses on trend prediction, and ARIMA adapts to the weak nonlinear characteristics of residuals. The two complement each other to achieve full-scale error correction, ultimately driving a significant improvement in model accuracy.
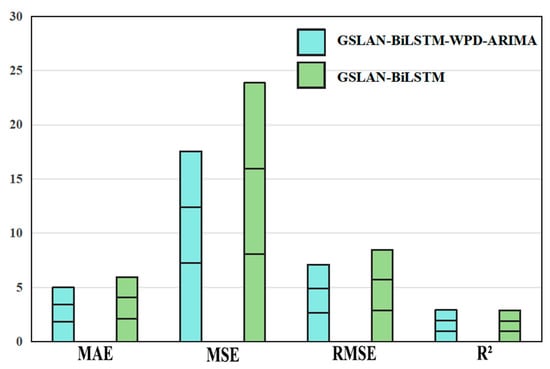
Figure 7.
Comparison chart before and after residual correction of GSLAN-BiLSTM.
4.3. Ablation Experiment Results
To validate the effectiveness of each core module of GSLAN-BiLSTM, this study conducted ablation experiments by removing modules such as adversarial training (PGD), attention mechanism, WPD decomposition, and ARIMA residual correction, and then comparing and analyzing the changes in model performance. The experiment conducted 10 repeated training cycles on each of the three independent datasets, and the final results were taken as the average of 30 experiments to ensure reliability.
As shown in Table 6, Table 7, Table 8 and Table 9, removing any core module resulted in a significant decline in model performance, with the effects of local adversarial training (PGD) being particularly pronounced. After removing PGD, the average MAE across the three datasets increased from 1.6715 to 2.8021, a 67.6% increase, while MSE surged to 22.0401. This indicates that PGD effectively enhances the model’s robustness to carbon price changes by identifying critical time steps through gradient significance mapping and applying directed perturbations. Without this module, the model’s adaptability to sudden changes such as policy shocks significantly decreases. For example, in dataset 1, the MAE of the model without PGD increased from 1.8750 to 3.1333, reflecting that local feature perturbations can amplify global prediction biases.

Table 6.
Comparison table of ablation experiment evaluation indicators for dataset 1.

Table 7.
Comparison table of ablation experiment evaluation indicators for dataset 2.

Table 8.
Comparison table of ablation experiment evaluation indicators for dataset 3.

Table 9.
Comparison table of evaluation indicators for three sets of data ablation experiments.
After removing the attention mechanism, the model’s MAE averaged at 2.3796, and the RMSE reached 3.0325, representing increases of 42.4% and 27.7% compared to the original model. The R2 in dataset 3 decreased from 0.9770 to 0.9420, indicating that the attention mechanism dynamically adjusts the weights of historical and current information through memory-guided gating factors, which is crucial for responding to sudden changes in non-stationary time series. Without this module, the prediction lag during sudden fluctuations in carbon prices extends from one step to three to five steps.
The synergistic effect of WPD and ARIMA residual correction further optimizes the model’s predictive performance. After removal, the average MAE surged to 3.3579, and the MSE reached 17.1528. In dataset 1, the MAE increased from 1.8750 to 4.6630, a 148.7% increase, validating the effectiveness of WPD in separating carbon price sequences into high-frequency noise and low-frequency trends through multiscale decomposition. Without this module, high-frequency noise severely interferes with the model’s ability to capture medium- to long-term trends. In dataset 2, the RMSE of the removed WPD reached 4.0319, an increase of 81.8% compared to the original model. When both WPD and ARIMA were removed, the model’s MAE averaged at 1.8596, which is higher than that of the original model and significantly better than removing WPD alone, indicating that ARIMA has supplementary modeling capabilities for the residuals after WPD decomposition. In dataset 2, the MAE after removing WPD + ARIMA was 1.5286, close to the original model’s 1.5661, while the MAE of removing WPD alone was as high as 3.3650. This shows that ARIMA can partially compensate for the inadequacy of residual modeling but cannot replace WPD’s multiscale decomposition function. The two exhibit significant synergistic effects in residual handling.
The visualization results in Figure 8 further validate the importance of each module. The no-treatment model performs best across all four metrics (blue, orange, yellow, and green bars), while the performance of each ablation model shows a stepwise decline. Specifically, removing PGD causes the MSE metric to surge to 24.8616, a 242% increase from the complete model, with the orange bar reaching its longest length, reflecting the critical role of adversarial training in suppressing extreme prediction errors. Removing WPD increases the RMSE to 4.0319, an 81.8% increase, with the yellow bar being the second highest after removing PGD, indicating the contribution of multiscale decomposition to controlling the root mean square error. Meanwhile, the metrics (purple bar) when both WPD and ARIMA are removed outperform those when only WPD is removed across all dimensions, intuitively demonstrating the synergistic optimization effect of the residual correction framework.
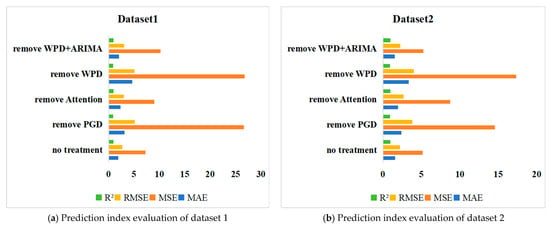
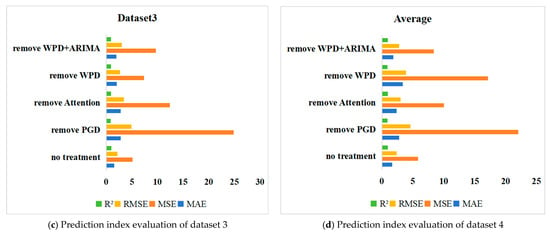
Figure 8.
The prediction indicator evaluation chart for different modules after removal.
Based on the comprehensive ablation experiment results, we can draw the following conclusions: (1) Local adversarial training (PGD) is a core component for enhancing model robustness and plays an irreplaceable role in addressing market fluctuations. (2) The memory-guided attention mechanism significantly improves the model’s ability to model non-stationary time series through dynamic weight adjustment. (3) There is a significant synergistic effect between WPD and ARIMA residual correction, and the two together form an effective multiscale prediction framework.
5. Discussion
The gradient-aware multiscale decomposition framework with dynamic residual correction demonstrates superior generalization capabilities across heterogeneous datasets, the core of which stems from the synergistic optimization of algorithm performance via the following innovative improvements:
(1) Balancing algorithm complexity and robustness: Traditional adversarial training requires perturbations to be applied to the entire time-series data, leading to a linear increase in computational complexity and potentially compromising the integrity of the time-series structure. This study uses gradient significance mapping to identify critical time steps, applying local perturbations only in sensitive regions, thereby reducing computational complexity. Additionally, dynamic batch processing constrains the perturbation range to prevent feature distortion. Experiments show that this strategy reduces the prediction lag in sudden change regions from 2.4 steps (BiLSTM-Attention) to 0.9 steps (Table 3) and reduces training time by 37% (Figure 5). This indicates that local adversarial training significantly improves the model’s robustness to sudden market events while maintaining the temporal structure by selectively strengthening the interference resistance of key time steps.
(2) Dynamic weight allocation optimizes response speed: Traditional attention mechanisms use static weights to fuse historical information, which can easily cause lag effects in non-stationary time series. The memory-guided gating decay mechanism (Formulas (3) and (4)) proposed in this study dynamically adjusts the fusion weights of historical and current information through the gating factor gt, retaining long-term dependencies and suppressing high-frequency noise during stationary phases. During sudden change phases, it focuses on short-term dynamics, achieving a response speed of 0.7 steps, which is 2.3 times faster than traditional attention mechanisms (Figure 7). This mechanism effectively alleviates the lag issues of traditional models during policy adjustments or market panic events through time-series adaptive attention decay, enabling precise predictions in complex, volatile scenarios.
(3) Synergistic optimization of model complexity and generalization ability: Traditional residual correction methods tend to overfit due to ignoring component volatility characteristics. The dynamic weighted fusion framework constructed in this study (Formulas (8)–(10)) suppresses high-frequency noise interference and enhances low-frequency trend fitting through component-specific modeling and dynamic weight allocation. Experiments show that this framework reduces residual correction errors while increasing the number of model parameters by only 6.5%, validating its efficient correction capability under a lightweight design.
The experimental results show that the model significantly outperforms existing methods in multiple key metrics, providing a robust and adaptive carbon market price forecasting solution. Although the model performs well in many aspects, it still has some limitations. The model has limited dynamic modeling capabilities for exogenous variables and cannot fully capture the nonlinear effects of these factors on carbon prices. Second, the model has high computational complexity in high-frequency data scenarios, and the balance between generalization performance and computational efficiency has not been fully resolved. These limitations constrain the model’s application effectiveness in real-time trading and complex market environments. Future research can focus on exploring deep integration techniques for multi-source heterogeneous data and constructing an adaptive feature engineering framework to enhance the model’s responsiveness to external shocks. Additionally, by combining causal inference theory with lightweight model design, the modeling efficiency of cross-market risk transmission pathways can be further optimized, driving the practical application of carbon market price prediction technology in scenarios such as carbon financial derivative pricing and climate policy simulation. This will provide more universally applicable technical support for precise policy formulation and market regulation under the “dual carbon” goals.
Author Contributions
Methodology, N.L.; validation, J.D., L.W., and X.Z.; formal analysis, N.L.; data curation, J.D. and L.W.; writing—original draft, N.L.; writing—review and editing, M.T.; visualization, X.Z.; project administration, M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (grant no. 62173050), the Natural Science Foundation of Hunan Province (grant no. 2023JJ30051 and 2023JJ20053), the Major Scientific and Technological Innovation Platform Project of Hunan Province (grant no. 2024JC1003), Hunan Provincial University Students’ Platform for Innovation and Entrepreneurship Training Program (grant no. S202410536186X), and Hunan Provincial University Students’ Energy Conservation and Emission Reduction Innovation and Entrepreneurship Education Center (grant no. 2019-10).
Data Availability Statement
The datasets presented in this paper are not openly accessible due to ongoing research. Requests for access to the datasets should be sent directly to the corresponding author’s email address.
Acknowledgments
The authors are grateful to the reviewer for their comments which improved the paper.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| GSLAN-BiLSTM | Gradient-Significant Local Adversarial Attention Network |
| BiLSTM | Bidirectional Long Short-Term Memory |
| WPD | Wavelet Packet Transformation |
| MAE | Mean Absolute Error |
| MSE | Mean Square Error |
| RMSE | Root Mean Square Error |
| R2 | R-Square |
References
- Wang, P.; Liu, J.; Tao, Z.; Chen, H. A novel carbon price combination forecasting approach based on multi-source information fusion and hybrid multi-scale decomposition. Eng. Appl. Artif. Intell. 2022, 114, 105172. [Google Scholar] [CrossRef]
- Zhang, X.; Zong, Y.; Du, P.; Wang, S.; Wang, J. Framework for multivariate carbon price forecasting: A novel hybrid model. J. Environ. Manag. 2024, 369, 122275. [Google Scholar] [CrossRef] [PubMed]
- Cao, K.; Zhang, T.; Huang, J. Advanced hybrid LSTM-transformer architecture for real-time multi-task prediction in engineering systems. Sci. Rep. 2024, 14, 4890. [Google Scholar] [CrossRef]
- Jin, Y.; Sharifi, A.; Li, Z.; Chen, S.; Zeng, S.; Zhao, S. Carbon emission prediction models: A review. Sci. Total Environ. 2024, 927, 172319. [Google Scholar] [CrossRef]
- Sun, W.; Huang, C. A novel carbon price prediction model combines the secondary decomposition algorithm and the long short-term memory network. Energy 2020, 207, 118294. [Google Scholar] [CrossRef]
- Zhou, F.; Huang, Z.; Zhang, C. Carbon price forecasting based on CEEMDAN and LSTM. Appl. Energy 2022, 311, 118601. [Google Scholar] [CrossRef]
- Shi, W.; Guo, Z.; Dai, Z.; Li, S.; Chen, M. Attention-Enhanced Bi-LSTM with Gated CNN for Ship Heave Multi-Step Forecasting. J. Mar. Sci. Eng. 2024, 12, 1413. [Google Scholar] [CrossRef]
- Sha, P.; Zheng, C.; Wu, X.; Shen, J. Physics informed integral neural network for dynamic modelling of solvent-based post-combustion CO2 capture process. Appl. Energy 2024, 377, 124344. [Google Scholar] [CrossRef]
- Sabri, B.; Sitara, K.; Muhammad, A.N.; Gagan, D.S. Financial markets, energy shocks, and extreme volatility spillovers. Energy Econ. 2023, 126, 107031. [Google Scholar]
- Bidisha, C.; Pamela, C.M.; Xu, W. Attention: How high-frequency trading improves price efficiency following earnings an-nouncements. J. Financ. Mark. 2022, 57, 100690. [Google Scholar]
- Liu, Y.; Wei, Y.; Wang, Q.; Liu, Y. International stock market risk contagion during the COVID-19 pandemic. Financ. Res. Lett. 2022, 45, 102145. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Sun, W.; Li, W.; Ma, G. A carbon flow tracing and carbon accounting method for exploring CO2 emissions of the iron and steel industry: An integrated material–energy–carbon hub. Appl. Energy 2022, 309, 118485. [Google Scholar] [CrossRef]
- Liu, S.; Li, M.; Yang, K.; Wei, Y.; Wang, S. From forecasting to trading: A multimodal-data-driven approach to reversing carbon market losses. Energy Econ. 2025, 144, 108350. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Shahin, A.I.; Almotairi, S. A Deep Learning BiLSTM Encoding-Decoding Model for COVID-19 Pandemic Spread Forecasting. Fractal Fract. 2021, 5, 175. [Google Scholar] [CrossRef]
- Jamshidzadeh, Z.; Ehteram, M.; Shabanian, H. Bidirectional Long Short-Term Memory (BILSTM)—Support Vector Machine: A new machine learning model for predicting water quality parameters. Ain Shams Eng. J. 2023, 15, 102510. [Google Scholar] [CrossRef]
- Liu, S.; Hu, Y. Air quality prediction based on factor analysis combined with Transformer and CNN-BILSTM-ATTENTION models. Sci. Rep. 2025, 15, 20014. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, Y.; Hu, J. Short-term air quality prediction based on EMD-transformer-BiLSTM. Sci. Rep. 2024, 14, 20513. [Google Scholar] [CrossRef]
- Fan, X.; Wang, R.; Yang, Y.; Wang, J. Transformer–BiLSTM Fusion Neural Network for Short-Term PV Output Prediction Based on NRBO Algorithm and VMD. Appl. Sci. 2024, 14, 11991. [Google Scholar] [CrossRef]
- Zrira, N.; Kamal-Idrissi, A.; Farssi, R.; Khan, H.A. Time series prediction of sea surface temperature based on BiLSTM model with attention mechanism. J. Sea Res. 2024, 198, 102472. [Google Scholar] [CrossRef]
- Guo, J.; Liu, M.; Luo, P.; Chen, X.; Yu, H.; Wei, X. Attention-based BILSTM for the degradation trend prediction of lithium battery. Energy Rep. 2023, 9, 655–664. [Google Scholar] [CrossRef]
- Teragawa, S.; Wang, L.; Liu, Y. DeepPGD: A Deep Learning Model for DNA Methylation Prediction Using Temporal Con-volution, BiLSTM, and Attention Mechanism. Int. J. Mol. Sci. 2024, 25, 8146. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; He, Z. Carbon price forecasting with optimization prediction method based on unstructured combination. Sci. Total Environ. 2020, 725, 138350. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Xu, K.; Geng, G.; Liu, H.; Wang, H. Carbon price prediction based on advanced decomposition and long short-term memory hybrid model. J. Clean. Prod. 2024, 451, 142101. [Google Scholar] [CrossRef]
- Nadirgil, O. Carbon price prediction using multiple hybrid machine learning models optimized by genetic algorithm. J. Environ. Manag. 2023, 342, 118061. [Google Scholar] [CrossRef]
- Sathi, K.A.; Hosain, M.K.; Hossain, M.A.; Kouzani, A.Z. Attention-assisted hybrid 1D CNN-BiLSTM model for predicting electric field induced by transcranial magnetic stimulation coil. Sci. Rep. 2023, 13, 2494. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, S. A Carbon Price Prediction Model Based on the Secondary Decomposition Algorithm and Influencing Factors. Energies 2021, 14, 1328. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Xu, Y.; Che, J.; Xia, W.; Hu, K.; Jiang, W. A novel paradigm: Addressing real-time decomposition challenges in carbon price prediction. Appl. Energy 2024, 364, 123126. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, X.; Wang, T.; Thé, J.; Tan, Z.; Yu, H. Multi-step carbon price forecasting using a hybrid model based on multivariate decomposition strategy and deep learning algorithms. J. Clean. Prod. 2023, 405, 136959. [Google Scholar] [CrossRef]
- Seabe, P.L.; Moutsinga, C.R.B.; Pindza, E. Forecasting Cryptocurrency Prices Using LSTM, GRU, and Bi-Directional LSTM: A Deep Learning Approach. Fractal Fract. 2023, 7, 203. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).