Fundamentals of Dual Basic Symmetric Quantum Calculus and Its Fractional Perspectives

Abstract

Taylor expansion is a remarkable tool with broad applications in analysis, science, engineering, and mathematics. In this manuscript, we derive a proof of generalized Taylor expansion for polynomials and write its particular case in symmetric quantum calculus. In addition, we define a novel type of calculus that is called symmetric $(\mathit{p},\mathit{q})$- or dual basic symmetric quantum calculus. Moreover, we derive a symmetric $(\mathit{p},\mathit{q})$-Taylor expansion for polynomials based on this calculus. After that, we investigate Taylor’s formulae through an example. Furthermore, we define symmetric definite $(\mathit{p},\mathit{q})$-integral and derive a fundamental law of symmetric $(\mathit{p},\mathit{q})$-calculus. Finally, we derive the symmetric $(\mathit{p},\mathit{q})$-Cauchy formula for integrals that enables us to construct the fractional perspectives of $(\mathit{p},\mathit{q})$-symmetric integrals.

1. Introduction

Taylor’s theorem is an essential part of calculus and analysis because it enables us to examine the nature of functions, including their derivatives. It provides information on the power series of $\mathfrak{g}\left(\mathfrak{u}\right)$ that contains all the orders of derivatives at $\mathfrak{u}=\beta$ and is expressed as follows:

$$\mathfrak{g}\left(\mathfrak{u}\right)=\sum _{\mathfrak{m}=0}^{\infty }{\mathfrak{g}}^{\left(\mathfrak{m}\right)}\left(\beta \right){\displaystyle \frac{{(\mathfrak{u}-\beta )}^{\mathfrak{m}}}{\mathfrak{m}!}},$$

(1)

where $\beta \in \mathbb{R}$ and $\mathfrak{m}$ is a non-negative integer. This is a method for approximating complex functions via less complicated polynomials and is essential for numerous applications in science and mathematics. It also significantly impacts computer science, economics, physics, engineering, scientific simulation, and error analysis. For instance, Taylor’s theorem plays a key role in the finite element methods (FEMs) [1] used for finding the numerical solutions of differential equations in mechanical and civil engineering. In 2021, L. Wei et al. explained neural tensor networks mathematically using Taylor’s formula [2]. L. Gabor and his co-authors used Taylor’s theorem to find the numerical solutions of kinetic differential equations [3]. In 2017, the Taylor expansion was utilized by Y. Ding et al. to identify emotion in faces from image frames [4]. For further readings regarding applications of Taylor’s theorem, see [5,6]. In short, we can approximate a continuous function with a discrete or piecewise continuous function through the Taylor expansion. As stated below, the Taylor expansion is studied in [7] as a generalized form for polynomials.

Theorem 1 

([7]). Let $\mathtt{D}$ be the linear operator defined on a space of polynomials $\mathtt{V}\left[\mathfrak{u}\right]=\{{\wp }_0\left(\mathfrak{u}\right),{\wp }_1\left(\mathfrak{u}\right),{\wp }_2\left(\mathfrak{u}\right),\dots ,{\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)\}$ and for any $\mathfrak{m}$, this list of polynomials satisfies the following conditions:

(i) 

${\wp }_0\left(\beta \right)=1$ and for any $\mathfrak{m}\ge 1,{\wp }_{\mathfrak{m}}\left(\beta \right)=0$,

(ii) 

$\mathfrak{m}$ is the degree of the polynomial ${\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)$,

(iii) 

for any $\mathfrak{m}\ge 1$, $\mathtt{D}{\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)={\wp }_{\mathfrak{m}-1}\left(\mathfrak{u}\right)$ and $\mathtt{D}\left(1\right)=0$.

Then, for any positive integer $\mathtt{N}$, the Taylor’s formula for any polynomial $\mathfrak{g}\left(\mathfrak{u}\right)$ of degree $\mathtt{N}$ is

$$\mathfrak{g}\left(\mathfrak{u}\right)=\sum _{\mathfrak{m}=0}^{\mathtt{N}}\left({\mathtt{D}}^{\mathfrak{m}}\mathfrak{g}\right)\left(\beta \right){\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right).$$

(2)

Throughout this paper, our concern about Taylor expansion is only for the polynomial perspective. The $\mathit{q}$-version of (1) is also studied in [7]. For this purpose, let the polynomial ${\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)={\displaystyle \frac{{(\mathfrak{u}-\beta )}_{\mathit{q}}^{\mathfrak{m}}}{\left[\mathfrak{m}\right]!}}$, which satisfies all conditions of Theorem 1, where $\left[\mathfrak{m}\right]!$ will be defined below later, and ${(\mathfrak{u}-\beta )}_{\mathit{q}}^{\mathfrak{m}}$ can be defined as

$${(\mathfrak{u}-\beta )}_{\mathit{q}}^{\mathfrak{m}}=\left\{\begin{array}{cc}(\mathfrak{u}-\beta )(\mathfrak{u}-\mathit{q}\beta )\dots (\mathfrak{u}-{\mathit{q}}^{\mathfrak{m}-1}\beta )\hfill & \mathrm{if}\mathfrak{m}\ge 1,\hfill \\ 1\hfill & \mathrm{if}\mathfrak{m}=0.\hfill \end{array}\right.$$

The $\mathit{q}$-Taylor formula for a polynomial is stated as.

Theorem 2 

([7]). For any number β and the polynomial $\mathfrak{g}\left(\mathfrak{u}\right)$ with degree $\mathtt{N}$, then

$$\mathfrak{g}\left(\mathfrak{u}\right)=\sum _{\mathfrak{m}=0}^{\mathtt{N}}\left({\mathtt{D}}^{\mathfrak{m}}\mathfrak{g}\right)\left(\beta \right){\displaystyle \frac{{(\mathfrak{u}-\beta )}_{\mathit{q}}^{\mathfrak{m}}}{\left[\mathfrak{m}\right]!}}$$

(3)

is called a $\mathit{q}$-Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$.

Many applications of the $\mathit{q}$-Taylor expansion can be seen in the literature. See [8,9,10]. The symmetric $\mathit{q}$-analogue or power of $(\mathfrak{u}-\beta )$ is also studied in [7], which can be written as

$${(\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}=\left\{\begin{array}{cc}(\mathfrak{u}-{\mathit{q}}^{\mathfrak{m}-1}\beta )(\mathfrak{u}-{\mathit{q}}^{\mathfrak{m}-3}\beta )\dots (\mathfrak{u}-{\mathit{q}}^{-\mathfrak{m}+1}\beta )\hfill & \mathrm{if}\mathfrak{m}\ge 1,\hfill \\ 1\hfill & \mathrm{if}\mathfrak{m}=0.\hfill \end{array}\right.$$

We can see that

$$\begin{array}{cc}\hfill {(\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}& =(\mathfrak{u}-\beta )\mathrm{if}\mathfrak{m}=1,\hfill \\ \hfill {(\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}& =(\mathfrak{u}-\mathit{q}\beta )(\mathfrak{u}-{\mathit{q}}^{-1}\beta )\mathrm{if}\mathfrak{m}=2,\hfill \\ \hfill {(\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}& =(\mathfrak{u}-{\mathit{q}}^2\beta )(\mathfrak{u}-\beta )(\mathfrak{u}-{\mathit{q}}^{-2}\beta )\mathrm{if}\mathfrak{m}=3.\hfill \end{array}$$

So, the degree of the polynomial ${(\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}$ is equal to $\mathfrak{m}$. In a similar fashion, one thing also noticed in [7] is that the polynomial ${\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)={\displaystyle \frac{{(\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}}{\widetilde{\left[\mathfrak{m}\right]}!}}$ does not satisfy the first condition of Theorem 1. The author of [7] later proposed another generalized form for the polynomial ${\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)={\displaystyle \frac{{(\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}}{\widetilde{\left[\mathfrak{m}\right]}!}}$ in [11] that we will mention in the next section. The author has suggested a method for proving the newly suggested result, but the proof is not yet in the literature. So, we will provide proof of the newly suggested result. But before proceeding, we will review some literature about $\mathit{q}$-, symmetric $\mathit{q}$-, and $(\mathit{p},\mathit{q})$-calculus that is the inspiration for deriving new results in mathematics.

Let an integer $\mathfrak{m}\in {\mathbb{Z}}^{+}$ and $0<\mathit{q}<1$; then, the $\mathit{q}$-analogue of $\mathfrak{m}$ can be defined as [7]

$${\left[\mathfrak{m}\right]}_{\mathit{q}}=\left[\mathfrak{m}\right]={\displaystyle \frac{1-{\mathit{q}}^{\mathfrak{m}}}{1-\mathit{q}}}=1+\mathit{q}+{\mathit{q}}^2+\dots +{\mathit{q}}^{\mathfrak{m}-1},$$

and ${\left[\mathfrak{m}\right]}_{\mathit{q}}$ is called the $\mathit{q}$-number. Similarly, for any number $\mathfrak{m}$, the symmetric $\mathit{q}$-analogue of $\mathfrak{m}$ (called the symmetric $\mathit{q}$-number) can be defined as [7]

$${\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{q}}=\widetilde{\left[\mathfrak{m}\right]}={\displaystyle \frac{{\mathit{q}}^{\mathfrak{m}}-{\mathit{q}}^{-\mathfrak{m}}}{\mathit{q}-{\mathit{q}}^{-1}}}.$$

The classical binomial coefficients can be written as

$$\left(\begin{array}{c}\mathfrak{m}\\ \eta \end{array}\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\mathfrak{m}!}{\eta !(\mathfrak{m}-\eta )!}},\hfill & \mathrm{if}0\le \eta \le \mathfrak{m},\hfill \\ 0,\hfill & \mathrm{if}\eta >\mathfrak{m},\hfill \end{array}\right.$$

and play a key role in combinatorics. Its $\mathit{q}$ and symmetric $\mathit{q}$ version are defined as [7]

$${\left[\begin{array}{c}\mathfrak{m}\\ \eta \end{array}\right]}_{\mathit{q}}={\displaystyle \frac{{\left[\mathfrak{m}\right]}_{\mathit{q}}!}{{\left[\eta \right]}_{\mathit{q}}!{[\mathfrak{m}-\eta ]}_{\mathit{q}}!}},\mathrm{if}0\le \eta \le \mathfrak{m}$$

(4)

and

$${\widetilde{\left[\begin{array}{c}\mathfrak{m}\\ \eta \end{array}\right]}}_{\mathit{q}}={\displaystyle \frac{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{q}}!}{{\widetilde{\left[\eta \right]}}_{\mathit{q}}!{\widetilde{[\mathfrak{m}-\eta ]}}_{\mathit{q}}!}},\mathrm{if}0\le \eta \le \mathfrak{m}$$

(5)

respectively. Here, ${\left[\mathfrak{m}\right]}_{\mathit{q}}!={\left[\mathfrak{m}\right]}_{\mathit{q}}\dots {\left[2\right]}_{\mathit{q}}.{\left[1\right]}_{\mathit{q}}$ and ${\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{q}}!={\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{q}}\dots {\widetilde{\left[2\right]}}_{\mathit{q}}.{\widetilde{\left[1\right]}}_{\mathit{q}}$.

Definition 1 

([7]). For any function $\mathfrak{g}\left(\mathfrak{u}\right)$, then

$${\mathtt{d}}_{\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)=\mathfrak{g}\left(\mathit{q}\mathfrak{u}\right)-\mathfrak{g}\left(\mathfrak{u}\right)$$

(6)

is called a $\mathit{q}$-differential of $\mathfrak{g}\left(\mathfrak{u}\right)$.

Its corresponding derivative can be defined as.

Definition 2 

([7]). For any function $\mathfrak{g}\left(\mathfrak{u}\right)$, then

$${\mathtt{D}}_{\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)={\displaystyle \frac{{\mathtt{d}}_{\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)}{{\mathtt{d}}_{\mathit{q}}\mathfrak{u}}}={\displaystyle \frac{\mathfrak{g}\left(\mathit{q}\mathfrak{u}\right)-\mathfrak{g}\left(\mathfrak{u}\right)}{(\mathit{q}-1)\mathfrak{u}}}$$

(7)

is called a $\mathit{q}$-derivative of $\mathfrak{g}\left(\mathfrak{u}\right)$.

For further details on quantum calculus, the readers can also see [12].

Definition 3 

([7]). For any function $\mathfrak{g}\left(\mathfrak{u}\right)$, then

$${\tilde{\mathtt{D}}}_{\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)=\mathfrak{g}\left(\mathit{q}\mathfrak{u}\right)-\mathfrak{g}\left({\mathit{q}}^{-1}\mathfrak{u}\right)$$

(8)

is called symmetric $\mathit{q}$-differential of $\mathfrak{g}\left(\mathfrak{u}\right)$.

Definition 4 

([7]). For any function $\mathfrak{g}\left(\mathfrak{u}\right)$, then

$${\tilde{\mathtt{D}}}_{\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)={\displaystyle \frac{{\tilde{\mathtt{D}}}_{\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)}{{\tilde{\mathtt{D}}}_{\mathit{q}}\mathfrak{u}}}={\displaystyle \frac{\mathfrak{g}\left(\mathit{q}\mathfrak{u}\right)-\mathfrak{g}\left({\mathit{q}}^{-1}\mathfrak{u}\right)}{(\mathit{q}-{\mathit{q}}^{-1})\mathfrak{u}}}$$

(9)

is called symmetric $\mathit{q}$-derivative of $\mathfrak{g}\left(\mathfrak{u}\right)$.

Cruz et al. have introduced a new approach to the study of quantum calculus in [13], namely q-symmetric variational calculus. As a result, they constructed the optimal conditions of the Euler–Lagrange type to study symmetrical variation problems. Many studies have been conducted on symmetric derivatives and integrals in order to get around the drawbacks of classical derivatives and integral operators. In [14], applications of symmetric quantum calculus to the class of harmonic functions, convexity, compactness, radii of $\mathsf{q}$ starlike and $\mathsf{q}$ convex functions of order $\alpha$, and extreme points for this recently described class of harmonic functions were among the novel conclusions they established. In [15], the authors investigated quantum-symmetric derivatives on finite intervals. They also introduced the concept of integral operators and right quantum symmetric derivatives and also examined a number of their features on inequality theory (see also [16]). Butt et al. in [17] presented some Hermite-Hadamard and midpoint-type inequalities in symmetric quantum calculus and extended them on a finite rectangular plane in [18] and for symmetric Hahn calculus in [19].

For any number $0<\mathit{p}<1$, R. Jagannathan et al. [20] extended the $\mathit{q}$-number into ($\mathit{p},\mathit{q}$)-number or basic twin number that is derived below:

$${\left[\mathfrak{m}\right]}_{\mathit{p},\mathit{q}}={\displaystyle \frac{{\mathit{p}}^{\mathfrak{m}}-{\mathit{q}}^{\mathfrak{m}}}{\mathit{p}-\mathit{q}}}.$$

If $\mathit{p}⟶1$, it becomes a $\mathit{q}$-number. They also extended (4) into a ($\mathit{p},\mathit{q}$)-binomial coefficient that is written below.

$${\left[\begin{array}{c}\mathfrak{m}\\ \eta \end{array}\right]}_{\mathit{p},\mathit{q}}={\displaystyle \frac{{\left[\mathfrak{m}\right]}_{\mathit{p},\mathit{q}}!}{{\left[\eta \right]}_{\mathit{p},\mathit{q}}!{[\mathfrak{m}-\eta ]}_{\mathit{p},\mathit{q}}!}},0\le \eta \le \mathfrak{m},$$

where ${\left[\mathfrak{m}\right]}_{\mathit{p},\mathit{q}}!={\left[\mathfrak{m}\right]}_{\mathit{p},\mathit{q}}.{[\mathfrak{m}-1]}_{\mathit{p},\mathit{q}}\dots {\left[2\right]}_{\mathit{p},\mathit{q}}.{\left[1\right]}_{\mathit{p},\mathit{q}}$, for $\mathfrak{m}=1,2,3,\dots$ and ${\left[0\right]}_{\mathit{p},\mathit{q}}!=1$. If $\mathit{p}⟶1$, it becomes (4).

P. Njionou Sadjang [21] extended the idea of (6) into a ($\mathit{p},\mathit{q}$)-differential of a function that is defined below.

Definition 5 

([21]). For any function $\mathfrak{g}\left(\mathfrak{u}\right)$, then

$${\mathtt{d}}_{\mathit{p},\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)=\mathfrak{g}\left(\mathit{p}\mathfrak{u}\right)-\mathfrak{g}\left(\mathit{q}\mathfrak{u}\right)$$

(10)

is called a ($\mathit{p},\mathit{q}$)-differential of $\mathfrak{g}\left(\mathfrak{u}\right)$.

The $(\mathit{p},\mathit{q})$-Taylor’s formula for a polynomial is studied in [21] and stated below.

Theorem 3 

([21]). For any number β and the polynomial $\mathfrak{g}\left(\mathfrak{u}\right)$ with degree $\mathtt{N}$, then

$$\mathfrak{g}\left(\mathfrak{u}\right)=\sum _{\mathfrak{m}=0}^{\mathtt{N}}{\mathit{p}}^{-\left(\begin{array}{c}\mathfrak{m}\\ 2\end{array}\right)}\left({\mathtt{D}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\right)\left({\mathit{p}}^{-\mathfrak{m}}\beta \right){\displaystyle \frac{{(\mathfrak{u}-\beta )}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}}{{\left[\mathfrak{m}\right]}_{\mathit{p},\mathit{q}}!}}$$

(11)

is called the $(\mathit{p},\mathit{q})$-Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$.

Corollary 1 

([21]). If $\mathfrak{g}\left(\mathfrak{u}\right)={\mathfrak{u}}^{\eta }$ in (11), it becomes

$${\mathfrak{u}}^{\eta }=\sum _{\mathfrak{m}=0}^{\eta }{\mathit{p}}^{-\left(\begin{array}{c}\mathfrak{m}\\ 2\end{array}\right)}{\left[\begin{array}{c}\eta \\ \mathfrak{m}\end{array}\right]}_{\mathit{p},\mathit{q}}{\left({\mathit{p}}^{-\mathfrak{m}}\beta \right)}^{\eta -\mathfrak{m}}{(\mathfrak{u}-\beta )}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}.$$

(12)

Inspired by the (7), R. Chakrabarti et al. [22] studied (7) at ($\mathit{p},\mathit{q}$)-level briefly. See [23,24,25] for more details about the $(\mathit{p},\mathit{q})$-calculus.

Definition 6 

([22]). For any function $\mathfrak{g}\left(\mathfrak{u}\right)$, then

$${\mathtt{D}}_{\mathit{p},\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)={\displaystyle \frac{{\mathtt{d}}_{\mathit{p},\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)}{{\mathtt{d}}_{\mathit{p},\mathit{q}}\mathfrak{u}}}={\displaystyle \frac{\mathfrak{g}\left(\mathit{p}\mathfrak{u}\right)-\mathfrak{g}\left(\mathit{q}\mathfrak{u}\right)}{(\mathit{p}-\mathit{q})\mathfrak{u}}}$$

(13)

is called the ($\mathit{p},\mathit{q}$)-derivative of $\mathfrak{g}\left(\mathfrak{u}\right)$.

If $\mathit{p}⟶1$ in (13), it becomes (7). This idea becomes the main reason for our motivation.

2. Preliminary Results in Symmetric Quantum Calculus

At the beginning of this section, we give the proof of the newly suggested result that is discussed above and can be written as

Theorem 4. 

Let $\mathtt{D}$ be the linear operator defined on a space of polynomials $\mathtt{V}=\mathtt{V}\left[\mathfrak{u}\right]=\{{\wp }_0\left(\mathfrak{u}\right),{\wp }_1\left(\mathfrak{u}\right),{\wp }_2\left(\mathfrak{u}\right),\dots ,{\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)\}$ and for any non-negative integer $\mathfrak{m}$, this list of polynomials satisfies the following conditions:

(i) 

${\wp }_0\left(\beta \right)=1$, and if $\mathfrak{m}$ is odd, then ${\wp }_{\mathfrak{m}}\left(\beta \right)=0$ and if $\mathfrak{m}$ is positive even, then ${\wp }_{\mathfrak{m}}\left(\mathit{q}\beta \right)={\wp }_{\mathfrak{m}}\left({\mathit{q}}^{-1}\beta \right)=0$;

(ii) 

$\mathfrak{m}$ is the degree of the polynomial ${\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)$;

(iii) 

for any $\mathfrak{m}\ge 1$, $\mathtt{D}{\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)={\wp }_{\mathfrak{m}-1}\left(\mathfrak{u}\right)$ and $\mathtt{D}\left(1\right)=0$.

Then, Taylor’s formula for any polynomial $\mathfrak{g}\left(\mathfrak{u}\right)$ of degree $\mathtt{N}$ is

$$\mathfrak{g}\left(\mathfrak{u}\right)=\sum _{\left(even\right)\mathfrak{m}\ge 0}^{\mathtt{N}}\left({\mathtt{D}}^{\mathfrak{m}}\mathfrak{g}\right)\left(\beta \right)\left({\mathit{q}}^{-\mathfrak{m}}{\wp }_{\mathfrak{m}}\left(\mathit{q}\mathfrak{u}\right)\right)+\sum _{\left(odd\right)\mathfrak{m}>0}^{\mathtt{N}}\left({\mathtt{D}}^{\mathfrak{m}}\mathfrak{g}\right)\left({\mathit{q}}^{-1}\beta \right)\left({\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)\right).$$

(14)

Proof. 

Let $\mathtt{V}\left[\mathfrak{u}\right]=\{{\wp }_0\left(\mathfrak{u}\right),{\wp }_1\left(\mathfrak{u}\right),{\wp }_2\left(\mathfrak{u}\right),\dots ,{\wp }_{\mathtt{N}}\left(\mathfrak{u}\right)\}$ be a space of polynomials of degree $\le \mathtt{N}$. Therefore, the dim$\mathtt{V}\left[\mathfrak{u}\right]=\mathtt{N}+1$. According to condition (ii), the degrees of the sequence of polynomials $\{{\wp }_0\left(\mathfrak{u}\right),{\wp }_1\left(\mathfrak{u}\right),{\wp }_2\left(\mathfrak{u}\right),\dots ,{\wp }_{\mathtt{N}}\left(\mathfrak{u}\right)\}$ are strictly increasing. Therefore, these polynomials are linearly independent and form the basis of $\mathtt{V}$. For any polynomial, $\mathfrak{g}\left(\mathfrak{u}\right)\in \mathtt{V}$ can be written as

$$\mathfrak{g}\left(\mathfrak{u}\right)=\sum _{m=0}^{\mathtt{N}}{\gamma }_m{\wp }_m\left(\mathfrak{u}\right).$$

We can split it into two parts, where ${\omega }_e$ is an even index and ${\omega }_o$ is an odd index term:

$$\begin{array}{cc}\hfill \mathfrak{g}\left(\mathfrak{u}\right)& =\sum _{{\omega }_e\ge 0}^{\mathtt{N}}{\gamma }_{{\omega }_e}{\wp }_{{\omega }_e}\left(\mathfrak{u}\right)+\sum _{{\omega }_o>0}^{\mathtt{N}}{\gamma }_{{\omega }_o}{\wp }_{{\omega }_o}\left(\mathfrak{u}\right)\hfill \\ \hfill & =\sum _{{\omega }_e\ge 0}^{\mathtt{N}}{\gamma }_{{\omega }_e}{\mathit{q}}^{-{\omega }_e}{\wp }_{{\omega }_e}\left(\mathit{q}\mathfrak{u}\right)+\sum _{{\omega }_o>0}^{\mathtt{N}}{\gamma }_{{\omega }_o}{\wp }_{{\omega }_o}\left(\mathfrak{u}\right).\hfill \end{array}$$

(15)

For any even $\mathfrak{m}$ and $1<\mathfrak{m}\le \mathtt{N}$, applying ${\mathtt{D}}^{\mathfrak{m}}$ on both sides of (15) and using the (iii) condition, we have

$$\begin{array}{cc}\hfill {\mathtt{D}}^{\mathfrak{m}}\mathfrak{g}\left(\mathfrak{u}\right)& =\sum _{{\omega }_e={\mathfrak{m}}_e}^{\mathtt{N}}{\gamma }_{{\omega }_e}{\mathit{q}}^{-{\omega }_e+\mathfrak{m}}{\wp }_{{\omega }_e-\mathfrak{m}}\left(\mathit{q}\mathfrak{u}\right)+\sum _{{\omega }_o={\mathfrak{m}}_o}^{\mathtt{N}}{\gamma }_{{\omega }_o}{\wp }_{{\omega }_o-\mathfrak{m}}\left(\mathfrak{u}\right),\hfill \end{array}$$

(16)

where ${\mathfrak{m}}_e\in \{\mathfrak{m},\mathfrak{m}+2,\dots \mathrm{all}\mathrm{evens}\le \mathtt{N}\}$ and ${\mathfrak{m}}_o\in \{\mathfrak{m}+1,\mathfrak{m}+3,\dots \mathrm{all}\mathrm{odds}\le \mathtt{N}\}$. If we put $\mathfrak{u}=\beta$ in (16), we obtain

$${\gamma }_{\mathfrak{m}}={\mathtt{D}}^{\mathfrak{m}}\mathfrak{g}\left(\beta \right).$$

(17)

For any odd $\mathfrak{m}$ and $1\le \mathfrak{m}\le \mathtt{N}$, applying ${\mathtt{D}}^{\mathfrak{m}}$ on both sides of (15) and using the (iii) condition, the even index terms of the polynomial become odd and odd index terms become even, and we have

$$\begin{array}{cc}\hfill {\mathtt{D}}^{\mathfrak{m}}\mathfrak{g}\left(\mathfrak{u}\right)& =\sum _{{\omega }_e={\mathfrak{m}}_e}^{\mathtt{N}}{\gamma }_{{\omega }_e}{\mathit{q}}^{-{\omega }_e+\mathfrak{m}}{\wp }_{{\omega }_e-\mathfrak{m}}\left(\mathit{q}\mathfrak{u}\right)+\sum _{{\omega }_o={\mathfrak{m}}_o}^{\mathtt{N}}{\gamma }_{{\omega }_o}{\wp }_{{\omega }_o-\mathfrak{m}}\left(\mathfrak{u}\right),\hfill \end{array}$$

(18)

where ${\mathfrak{m}}_e\in \{\mathfrak{m}+1,\mathfrak{m}+3,\dots \mathrm{all}\mathrm{evens}\le \mathtt{N}\}$ and ${\mathfrak{m}}_o\in \{\mathfrak{m},\mathfrak{m}+2,\dots \mathrm{all}\mathrm{odds}\le \mathtt{N}\}$. We put $\mathfrak{u}={\mathit{q}}^{-1}\beta$ in (18); then,

$${\gamma }_{\mathfrak{m}}={\mathtt{D}}^{\mathfrak{m}}\mathfrak{g}\left({\mathit{q}}^{-1}\beta \right).$$

(19)

Putting (17) and (19) in (15), we obtain (14). □

Since the polynomial ${\wp }_{\mathfrak{m}}\left(\mathfrak{u}\right)={\displaystyle \frac{{(\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}}{\widetilde{\left[\mathfrak{m}\right]}!}}$ satisfies all the conditions of Theorem 4, we can write $\mathit{q}$-symmetric Taylor’s or $\tilde{\mathit{q}}$-Taylor’s formula as follows.

Theorem 5. 

For any number β and polynomial $\mathfrak{g}\left(\mathfrak{u}\right)$ with degree $\mathtt{N}$, then

$$\mathfrak{g}\left(\mathfrak{u}\right)=\sum _{\left(even\right)\mathfrak{m}\ge 0}^{\mathtt{N}}{\tilde{\mathtt{D}}}_{\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\beta \right)\left({\mathit{q}}^{-\mathfrak{m}}\right){\displaystyle \frac{{(\mathit{q}\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}}{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{q}}!}}+\sum _{\left(odd\right)\mathfrak{m}>0}^{\mathtt{N}}{\tilde{\mathtt{D}}}_{\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left({\mathit{q}}^{-1}\beta \right){\displaystyle \frac{{(\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}}{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{q}}!}}$$

(20)

is called the symmetric $\mathit{q}$-Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$.

Corollary 2. 

If we let $\mathfrak{g}\left(\mathfrak{u}\right)={\mathfrak{u}}^{\eta }$ in (20), we have the following result:

$${\mathfrak{u}}^{\eta }=\sum _{\left(even\right)\mathfrak{m}\ge 0}^{\mathtt{N}}{\mathit{q}}^{-\mathfrak{m}}{\widetilde{\left[\begin{array}{c}\eta \\ \mathfrak{m}\end{array}\right]}}_{\mathit{q}}{\left(\beta \right)}^{\eta -\mathfrak{m}}{(\mathit{q}\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}+\sum _{\left(odd\right)\mathfrak{m}>0}^{\mathtt{N}}{\widetilde{\left[\begin{array}{c}\eta \\ \mathfrak{m}\end{array}\right]}}_{\mathit{q}}{\left({\mathit{q}}^{-1}\beta \right)}^{\eta -\mathfrak{m}}{(\mathfrak{u}-\beta )}_{\tilde{\mathit{q}}}^{\mathfrak{m}}.$$

(21)

3. New Definitions and Results

For any non-negative integer $\mathfrak{m}$, we can define a symmetric ($\mathit{p},\mathit{q}$)-number or a dual basic symmetric number and write it as

$${\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}:={\displaystyle \frac{{\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}-{\mathit{p}}^{-\mathfrak{m}}{\mathit{q}}^{-\mathfrak{m}}}{\mathit{p}\mathit{q}-{\mathit{p}}^{-1}{\mathit{q}}^{-1}}}.$$

If $\mathit{p}⟶1$, it becomes a symmetric $\mathit{q}$-number. In addition, we can also extend the symmetric $\mathit{q}$-binomial coefficients into a symmetric ($\mathit{p},\mathit{q}$)-version that can be defined as

$${\widetilde{\left[\begin{array}{c}\mathfrak{m}\\ \eta \end{array}\right]}}_{\mathit{p},\mathit{q}}:={\displaystyle \frac{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}{{\widetilde{\left[\eta \right]}}_{\mathit{p},\mathit{q}}!{\widetilde{[\mathfrak{m}-\eta ]}}_{\mathit{p},\mathit{q}}!}},\mathrm{if}0\le \eta \le \mathfrak{m}$$

(22)

where ${\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!:={\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}\dots {\widetilde{\left[2\right]}}_{\mathit{p},\mathit{q}}.{\widetilde{\left[1\right]}}_{\mathit{p},\mathit{q}}$.

Now, let us introduce a dual basic symmetric differential of a function.

Definition 7. 

For any function $\mathfrak{g}\left(\mathfrak{u}\right)$, then

$${\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)=\mathfrak{g}\left(\mathit{p}\mathit{q}\mathfrak{u}\right)-\mathfrak{g}\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)$$

(23)

is called a symmetric ($\mathit{p},\mathit{q}$)-differential or dual basic symmetric differential of $\mathfrak{g}\left(\mathfrak{u}\right)$.

If $\mathfrak{g}\left(\mathfrak{u}\right)=\mathfrak{u}$, then (23) becomes ${\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}=(\mathit{p}\mathit{q}-{\mathit{p}}^{-1}{\mathit{q}}^{-1})\mathfrak{u}$. Moreover, if $\mathit{p}⟶1$ (23), then it is reduced to (8).

Proposition 1. 

For any two functions ${\mathfrak{g}}_1\left(\mathfrak{u}\right)$ and ${\mathfrak{g}}_2\left(\mathfrak{u}\right)$, then

$${\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right){\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)={\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)+{\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right)$$

(24)

is called the product rule of a symmetric ($\mathit{p},\mathit{q}$)-differential.

Proof. 

$$\begin{array}{cc}\hfill {\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right){\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)& ={\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\mathfrak{g}}_2\left(\mathit{p}\mathit{q}\mathfrak{u}\right)-{\mathfrak{g}}_1\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)\hfill \\ & ={\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\mathfrak{g}}_2\left(\mathit{p}\mathit{q}\mathfrak{u}\right)-{\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)+{\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)\hfill \\ & -{\mathfrak{g}}_1\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)\hfill \\ & ={\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right)\left({\mathfrak{g}}_2\left(\mathit{p}\mathit{q}\mathfrak{u}\right)-{\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)\right)+{\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)({\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right)-{\mathfrak{g}}_1\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right))\hfill \\ & ={\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)+{\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right).\hfill \end{array}$$

□

Induced by the symmetric ($\mathit{p},\mathit{q}$)-differential, we can also define the symmetric ($\mathit{p},\mathit{q}$)-derivative.

Definition 8. 

For any function $\mathfrak{g}\left(\mathfrak{u}\right)$, then

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)={\displaystyle \frac{{\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)}{{\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}}}={\displaystyle \frac{\mathfrak{g}\left(\mathit{p}\mathit{q}\mathfrak{u}\right)-\mathfrak{g}\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)}{(\mathit{p}\mathit{q}-{\mathit{p}}^{-1}{\mathit{q}}^{-1})\mathfrak{u}}}$$

(25)

is called symmetric ($\mathit{p},\mathit{q}$)-derivative or dual basic symmetric derivative of $\mathfrak{g}\left(\mathfrak{u}\right)$.

If $\mathit{p}⟶1$ in (25), it will become a symmetric $\mathit{q}$-derivative.

Example 1. 

Let $\mathfrak{g}\left(\mathfrak{u}\right)={\mathfrak{u}}^{\mathfrak{m}}$, where $\mathfrak{m}$ is a positive integer, and its symmetric ($\mathit{p},\mathit{q}$)-derivative is

$$\begin{array}{cc}\hfill {\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)& ={\displaystyle \frac{{\left(\mathit{p}\mathit{q}\mathfrak{u}\right)}^{\mathfrak{m}}-{\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)}^{\mathfrak{m}}}{(\mathit{p}\mathit{q}-{\mathit{p}}^{-1}{\mathit{q}}^{-1})\mathfrak{u}}}\hfill \\ \hfill & ={\displaystyle \frac{{\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}-{\mathit{p}}^{-\mathfrak{m}}{\mathit{q}}^{-\mathfrak{m}}}{\mathit{p}\mathit{q}-{\mathit{p}}^{-1}{\mathit{q}}^{-1}}}{\mathfrak{u}}^{\mathfrak{m}-1}\hfill \\ \hfill & ={\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}{\mathfrak{u}}^{\mathfrak{m}-1}.\hfill \end{array}$$

Proposition 2. 

For any two functions ${\mathfrak{g}}_1\left(\mathfrak{u}\right)$ and ${\mathfrak{g}}_2\left(\mathfrak{u}\right)$, then there exist two integers ${\mathfrak{m}}_1$ and ${\mathfrak{m}}_2$ such that the

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}({\mathfrak{m}}_1{\mathfrak{g}}_1\left(\mathfrak{u}\right)+{\mathfrak{m}}_2{\mathfrak{g}}_2\left(\mathfrak{u}\right))={\mathfrak{m}}_1{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right)+{\mathfrak{m}}_2{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)$$

equality holds.

Proof. 

This is obvious from the definition of the symmetric ($\mathit{p},\mathit{q}$)-derivative. □

Proposition 3. 

For any two functions ${\mathfrak{g}}_1\left(\mathfrak{u}\right)$ and ${\mathfrak{g}}_2\left(\mathfrak{u}\right)$, then

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right){\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)={\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)+{\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right)$$

(26)

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right){\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)={\mathfrak{g}}_2\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right)+{\mathfrak{g}}_1\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)$$

(27)

are called the product rules of symmetric ($\mathit{p},\mathit{q}$)-derivatives.

Proof. 

Using (25) and (24),

$$\begin{array}{cc}\hfill {\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right){\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)& ={\displaystyle \frac{{\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right){\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)}{{\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}}}={\displaystyle \frac{{\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)+{\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right)}{(\mathit{p}\mathit{q}-{\mathit{p}}^{-1}{\mathit{q}}^{-1})\mathfrak{u}}}\hfill \\ & ={\mathfrak{g}}_1\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)+{\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right).\hfill \end{array}$$

Also, we can prove (27) in a similar way. □

Proposition 4. 

For any two functions ${\mathfrak{g}}_1\left(\mathfrak{u}\right)$ and ${\mathfrak{g}}_2\left(\mathfrak{u}\right)$ with ${\mathfrak{g}}_2\left(\mathfrak{u}\right)\ne 0$, then

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\displaystyle \frac{{\mathfrak{g}}_1\left(\mathfrak{u}\right)}{{\mathfrak{g}}_2\left(\mathfrak{u}\right)}}\right)={\displaystyle \frac{{\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right)-{\mathfrak{g}}_1\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)}{{\mathfrak{g}}_2\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)}}$$

(28)

is called the quotient rule of symmetric ($\mathit{p},\mathit{q}$)-derivatives.

Proof. 

Since ${\mathfrak{g}}_2\left(\mathfrak{u}\right)\ne 0$, we have

$$\begin{array}{c}\hfill {\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right)={\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right){\displaystyle \frac{{\mathfrak{g}}_1\left(\mathfrak{u}\right)}{{\mathfrak{g}}_2\left(\mathfrak{u}\right)}}\right)\end{array}$$

Applying (26),

$$\begin{array}{cc}\hfill {\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right)& ={\mathfrak{g}}_2\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\displaystyle \frac{{\mathfrak{g}}_1\left(\mathfrak{u}\right)}{{\mathfrak{g}}_2\left(\mathfrak{u}\right)}}\right)+\left({\displaystyle \frac{{\mathfrak{g}}_1\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)}{{\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)}}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)\hfill \\ \hfill {\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\displaystyle \frac{{\mathfrak{g}}_1\left(\mathfrak{u}\right)}{{\mathfrak{g}}_2\left(\mathfrak{u}\right)}}\right)& ={\displaystyle \frac{{\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_1\left(\mathfrak{u}\right)\right)-{\mathfrak{g}}_1\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left({\mathfrak{g}}_2\left(\mathfrak{u}\right)\right)}{{\mathfrak{g}}_2\left(\mathit{p}\mathit{q}\mathfrak{u}\right){\mathfrak{g}}_2\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)}}.\hfill \end{array}$$

□

Definition 9. 

The symmetric ($\mathit{p},\mathit{q}$)-power can be written as

$${(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}=(\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{\mathfrak{m}-1}\beta )(\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{\mathfrak{m}-3}\beta )(\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{\mathfrak{m}-5}\beta )\dots (\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{-\mathfrak{m}+1}\beta ),$$

(29)

with ${(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^0=1$.

If $\mathit{p}⟶1$ in (29), it will become a symmetric $\mathit{q}$-power, which is described in [7].

Proposition 5. 

If

$${(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}=(\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{\mathfrak{m}-1}\beta )(\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{\mathfrak{m}-3}\beta )(\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{\mathfrak{m}-5}\beta )\dots (\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{-\mathfrak{m}+1}\beta )$$

with any positive integer $\mathfrak{m}$, then

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}={\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}-1}.$$

(30)

Proof. 

Use induction on $\mathfrak{m}$.

• Since it is true for $\mathfrak{m}=1$, now assume that it is true for $\mathfrak{m}=\mathfrak{s}$ with $\mathfrak{s}\ge 1$.

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}}={\widetilde{\left[\mathfrak{s}\right]}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}-1}.$$

(31)

Let ${\mathfrak{g}}_1\left(\mathfrak{u}\right)={(\mathfrak{u}-\mathit{p}\mathit{q}\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}}$ and ${\mathfrak{g}}_2\left(\mathfrak{u}\right)=(\mathfrak{u}-{\mathit{p}}^{-\mathfrak{s}}{\mathit{q}}^{-\mathfrak{s}}\beta )$; then using (26), we can infer that

$$\begin{array}{cc}\hfill {\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}+1}& ={\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left[{(\mathfrak{u}-\mathit{p}\mathit{q}\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}}(\mathfrak{u}-{\mathit{p}}^{-\mathfrak{s}}{\mathit{q}}^{-\mathfrak{s}}\beta )\right]\hfill \\ \hfill & ={(\mathit{p}\mathit{q}\mathfrak{u}-\mathit{p}\mathit{q}\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}}+({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}-{\mathit{p}}^{-\mathfrak{s}}{\mathit{q}}^{-\mathfrak{s}}\beta ){\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-\mathit{p}\mathit{q}\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}}\hfill \\ \hfill & ={\mathit{p}}^{\mathfrak{s}}{\mathit{q}}^{\mathfrak{s}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}}+{\mathit{p}}^{-1}{\mathit{q}}^{-1}(\mathfrak{u}-{\mathit{p}}^{-\mathfrak{s}+1}{\mathit{q}}^{-\mathfrak{s}+1}\beta ){\widetilde{\left[\mathfrak{s}\right]}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-\mathit{p}\mathit{q}\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}-1}\hfill \\ \hfill & =\{{\mathit{p}}^{\mathfrak{s}}{\mathit{q}}^{\mathfrak{s}}+{\mathit{p}}^{-1}{\mathit{q}}^{-1}{\widetilde{\left[\mathfrak{s}\right]}}_{\mathit{p},\mathit{q}}\}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}}\hfill \\ \hfill & ={\widetilde{[\mathfrak{s}+1]}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{s}},\hfill \end{array}$$

is proved. □

Remark 1. 

It is obvious that if $\mathfrak{m}=0$; then ${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^0={\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left(1\right)=0$.

Proposition 5 can be extended to higher-order derivatives.

Proposition 6. 

If

$${(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}=(\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{\mathfrak{m}-1}\beta )(\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{\mathfrak{m}-3}\beta )(\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{\mathfrak{m}-5}\beta )\dots (\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{-\mathfrak{m}+1}\beta ),$$

then for any integer $0\le \eta \le \mathfrak{m}$,

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\eta }{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}={\displaystyle \frac{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}{{\widetilde{[\mathfrak{m}-\eta ]}}_{\mathit{p},\mathit{q}}!}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}-\eta }.$$

(32)

Proof. 

We are applying induction on $\eta$. Since it is obvious for $\eta =0$, we start induction from $\eta \ge 1$. Since for $\eta =1$, it becomes (30), now, suppose that it is true for $\eta =\mathfrak{s}$ with $\mathfrak{s}\ge 1$.

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{s}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}={\displaystyle \frac{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}{{\widetilde{[\mathfrak{m}-\mathfrak{s}]}}_{\mathit{p},\mathit{q}}!}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}-\mathfrak{s}}.$$

As

$$\begin{array}{cc}\hfill {\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{s}+1}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}& ={\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left[{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{s}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}\right]\hfill \\ \hfill & ={\displaystyle \frac{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}{{\widetilde{[\mathfrak{m}-\mathfrak{s}]}}_{\mathit{p},\mathit{q}}!}}{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\left[{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}-\mathfrak{s}}\right]\hfill \\ \hfill & ={\displaystyle \frac{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}{{\widetilde{[\mathfrak{m}-\mathfrak{s}]}}_{\mathit{p},\mathit{q}}!}}{\widetilde{[\mathfrak{m}-\mathfrak{s}]}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}-\mathfrak{s}-1}\hfill \\ \hfill & ={\displaystyle \frac{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}{{\widetilde{[\mathfrak{m}-\mathfrak{s}-1]}}_{\mathit{p},\mathit{q}}!}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}-\mathfrak{s}-1}.\hfill \end{array}$$

□

Now, we construct the symmetric $(\mathit{p},\mathit{q})$-Taylor’s formula for polynomials.

Theorem 6. 

For any real number β and a polynomial $\mathfrak{g}\left(\mathfrak{u}\right)$ with degree $\mathtt{N}$, then

$$\mathfrak{g}\left(\mathfrak{u}\right)=\sum _{\left(even\right)\mathfrak{m}\ge 0}^{\mathtt{N}}{\mathit{p}}^{-\mathfrak{m}}{\mathit{q}}^{-\mathfrak{m}}{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\beta \right){\displaystyle \frac{{(\mathit{p}\mathit{q}\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}}{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}}+\sum _{\left(odd\right)\mathfrak{m}>0}^{\mathtt{N}}{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\beta \right){\displaystyle \frac{{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}}{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}}$$

(33)

is called symmetric $(\mathit{p},\mathit{q})$-Taylor’s or $\left(\widetilde{\mathit{p},\mathit{q}}\right)$-Taylor’s expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$.

Proof. 

Suppose a polynomial $\mathfrak{g}\left(\mathfrak{u}\right)$ with degree $\mathtt{N}$, then

$$\mathfrak{g}\left(\mathfrak{u}\right)=\sum _{m=0}^{\mathtt{N}}{\gamma }_m{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}.$$

This can be split into two parts: ${\omega }_e$ is an even index and ${\omega }_o$ is an odd index term.

$$\begin{array}{cc}\hfill \mathfrak{g}\left(\mathfrak{u}\right)& =\sum _{{\omega }_e\ge 0}^{\mathtt{N}}{\gamma }_{{\omega }_e}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{{\omega }_e}+\sum _{{\omega }_o>0}^{\mathtt{N}}{\gamma }_{{\omega }_o}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{{\omega }_o}\hfill \\ \hfill & =\sum _{{\omega }_e\ge 0}^{\mathtt{N}}{\gamma }_{{\omega }_e}{\mathit{p}}^{-{\omega }_e}{\mathit{q}}^{-{\omega }_e}{(\mathit{p}\mathit{q}\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{{\omega }_e}+\sum _{{\omega }_o>0}^{\mathtt{N}}{\gamma }_{{\omega }_o}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{{\omega }_o}.\hfill \end{array}$$

(34)

For any even $\mathfrak{m}$ and $0\le \mathfrak{m}\le \mathtt{N}$, applying ${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}$ on both sides of (34) and using (32), we have

$$\begin{array}{cc}\hfill {\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\mathfrak{u}\right)& =\sum _{{\omega }_e={\mathfrak{m}}_e}^{\mathtt{N}}{\gamma }_{{\omega }_e}{\mathit{p}}^{-{\omega }_e+\mathfrak{m}}{\mathit{q}}^{-{\omega }_e+\mathfrak{m}}{(\mathit{p}\mathit{q}\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{{\omega }_e-\mathfrak{m}}+\sum _{{\omega }_o={\mathfrak{m}}_o}^{\mathtt{N}}{\gamma }_{{\omega }_o}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{{\omega }_o-\mathfrak{m}},\hfill \end{array}$$

(35)

where ${\mathfrak{m}}_e\in \{\mathfrak{m},\mathfrak{m}+2,\dots \mathrm{all}\mathrm{evens}\le \mathtt{N}\}$ and ${\mathfrak{m}}_o\in \{\mathfrak{m}+1,\mathfrak{m}+3,\dots \mathrm{all}\mathrm{odds}\le \mathtt{N}\}$. If we put $\mathfrak{u}=\beta$ in (35), we obtain

$${\gamma }_{\mathfrak{m}}={\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\beta \right).$$

(36)

For any odd $\mathfrak{m}$ and $1\le \mathfrak{m}\le \mathtt{N}$, applying ${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}$ on both sides of (34) and using (32), then, the even index terms of the polynomial becomes odd and odd index terms become even, and we have

$$\begin{array}{cc}\hfill {\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\mathfrak{u}\right)& =\sum _{{\omega }_e={\mathfrak{m}}_e}^{\mathtt{N}}{\gamma }_{{\omega }_e}{\mathit{p}}^{-{\omega }_e+\mathfrak{m}}{\mathit{q}}^{-{\omega }_e+\mathfrak{m}}{(\mathit{p}\mathit{q}\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{{\omega }_e-\mathfrak{m}}+\sum _{{\omega }_o={\mathfrak{m}}_o}^{\mathtt{N}}{\gamma }_{{\omega }_o}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{{\omega }_o-\mathfrak{m}},\hfill \end{array}$$

(37)

where ${\mathfrak{m}}_e\in \{\mathfrak{m}+1,\mathfrak{m}+3,\dots \mathrm{all}\mathrm{evens}\le \mathtt{N}\}$ and ${\mathfrak{m}}_o\in \{\mathfrak{m},\mathfrak{m}+2,\dots \mathrm{all}\mathrm{odds}\le \mathtt{N}\}$. If we put $\mathfrak{u}={\mathit{p}}^{-1}{\mathit{q}}^{-1}\beta$ in (37), then,

$${\gamma }_{\mathfrak{m}}={\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\beta \right).$$

(38)

Putting (36) and (38) in (34), we obtain (33). □

Corollary 3. 

If we let $\mathfrak{g}\left(\mathfrak{u}\right)={\mathfrak{u}}^{\eta }$ in (33), we have the following result:

$${\mathfrak{u}}^{\eta }=\sum _{\left(even\right)\mathfrak{m}\ge 0}^{\mathtt{N}}{\mathit{p}}^{-\mathfrak{m}}{\mathit{q}}^{-\mathfrak{m}}{\widetilde{\left[\begin{array}{c}\eta \\ \mathfrak{m}\end{array}\right]}}_{\mathit{p},\mathit{q}}{\left(\beta \right)}^{\eta -\mathfrak{m}}{(\mathit{p}\mathit{q}\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}+\sum _{\left(odd\right)\mathfrak{m}>0}^{\mathtt{N}}{\widetilde{\left[\begin{array}{c}\eta \\ \mathfrak{m}\end{array}\right]}}_{\mathit{p},\mathit{q}}{\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\beta \right)}^{\eta -\mathfrak{m}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}.$$

(39)

Now, we provide an example that differentiates the classical, quantum, and newly obtained Taylor’s formulae for an arbitrary polynomial function. In addition, this example will be useful for finding new approximations of other functions in quantum, post-quantum, and their symmetric versions in upcoming research.

Example 2. 

Let $\mathfrak{g}\left(\mathfrak{u}\right)={\mathfrak{u}}^3$ and $\beta =1$.

Case 1. 

Classical Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$: The classical Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$ around $\mathfrak{u}=1$ is

$$\begin{array}{cc}\hfill \mathfrak{g}\left(\mathfrak{u}\right)& =\mathfrak{g}\left(1\right)+{\mathfrak{g}}^{\prime }\left(1\right){\displaystyle \frac{(\mathfrak{u}-1)}{1!}}+{\mathfrak{g}}^{″}\left(1\right){\displaystyle \frac{{(\mathfrak{u}-1)}^2}{2!}}+{\mathfrak{g}}^{‴}\left(1\right){\displaystyle \frac{{(\mathfrak{u}-1)}^3}{3!}}\hfill \\ \hfill & =1+3(\mathfrak{u}-1)+3{(\mathfrak{u}-1)}^2+{(\mathfrak{u}-1)}^3.\hfill \end{array}$$

Its graphical representation is given below; see Figure 1, Figure 2 and Figure 3.

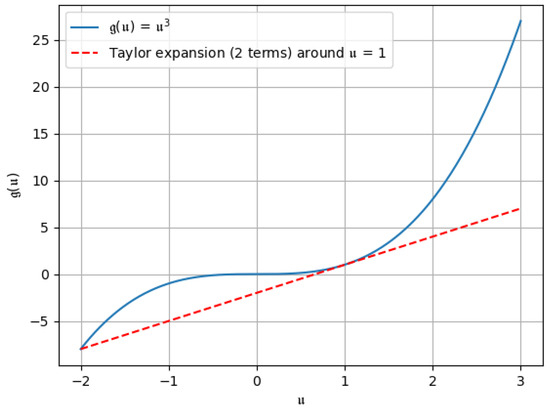Figure 1. Taylor expansion up to the 1st two terms, i.e., $\mathfrak{g}\left(\mathfrak{u}\right)\approx 1+3(\mathfrak{u}-1)$.

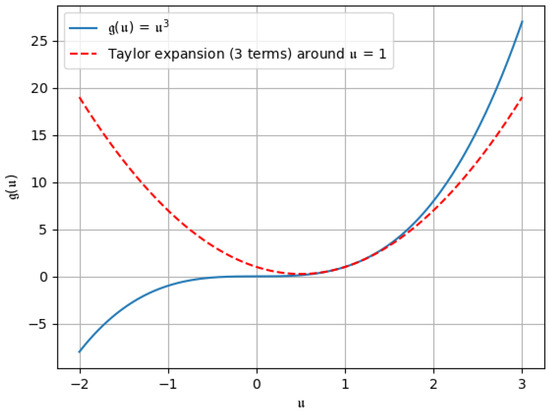Figure 2. Taylor expansion up to the 1st three terms, i.e., $\mathfrak{g}\left(\mathfrak{u}\right)\approx 1+3(\mathfrak{u}-1)+3{(\mathfrak{u}-1)}^2$.

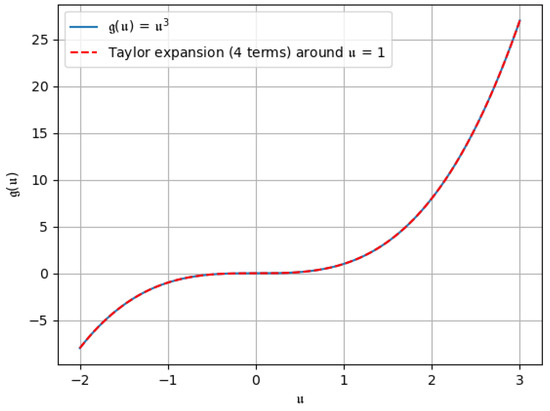Figure 3. Taylor expansion up to all four terms.

Case 2. 

The $\mathit{q}$-Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$: The $\mathit{q}$-Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$ around $\mathfrak{u}=1$ with $\mathit{q}=0.5$ is

$$\begin{array}{cc}\hfill \mathfrak{g}\left(\mathfrak{u}\right)& =\mathfrak{g}\left(1\right)+{\mathtt{D}}_{\mathit{q}}\mathfrak{g}\left(1\right){\displaystyle \frac{{(\mathfrak{u}-1)}_{\mathit{q}}}{\left[1\right]!}}+{\mathtt{D}}_{\mathit{q}}^2\mathfrak{g}\left(1\right){\displaystyle \frac{{(\mathfrak{u}-1)}_{\mathit{q}}^2}{\left[2\right]!}}+{\mathtt{D}}_{\mathit{q}}^3\mathfrak{g}\left(1\right){\displaystyle \frac{{(\mathfrak{u}-1)}_{\mathit{q}}^3}{\left[3\right]!}}\hfill \\ \hfill & =1+\left[3\right]{(\mathfrak{u}-1)}_{\mathit{q}}+\left[3\right]{(\mathfrak{u}-1)}_{\mathit{q}}^2+{(\mathfrak{u}-1)}_{\mathit{q}}^3\hfill \\ \hfill & =1+(1+\mathit{q}+{\mathit{q}}^2)(\mathfrak{u}-1)+(1+\mathit{q}+{\mathit{q}}^2)(\mathfrak{u}-1)(\mathfrak{u}-\mathit{q})+(\mathfrak{u}-1)(\mathfrak{u}-\mathit{q})(\mathfrak{u}-{\mathit{q}}^2)\hfill \\ \hfill & =1+\left(1.75\right)(\mathfrak{u}-1)+\left(1.75\right)(\mathfrak{u}-1)(\mathfrak{u}-0.5)+(\mathfrak{u}-1)(\mathfrak{u}-0.5)(\mathfrak{u}-0.25).\hfill \end{array}$$

The graphical representation of this expansion is given in Figure 4, Figure 5 and Figure 6.

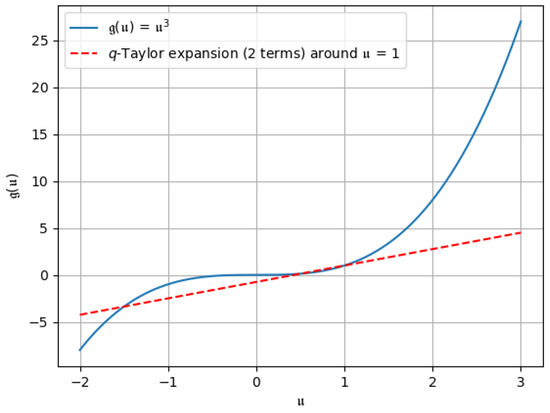Figure 4. $\mathit{q}$-Taylor expansion up to the first two terms, i.e., $\mathfrak{g}\left(\mathfrak{u}\right)\approx 1+1.75{(\mathfrak{u}-1)}_{\mathit{q}}$.

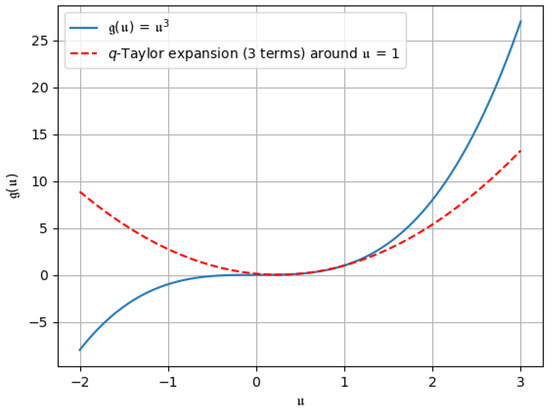Figure 5. $\mathit{q}$-Taylor expansion up to the first three terms, i.e., $\mathfrak{g}\left(\mathfrak{u}\right)\approx 1+1.75{(\mathfrak{u}-1)}_{\mathit{q}}+1.75{(\mathfrak{u}-1)}_{\mathit{q}}^2$.

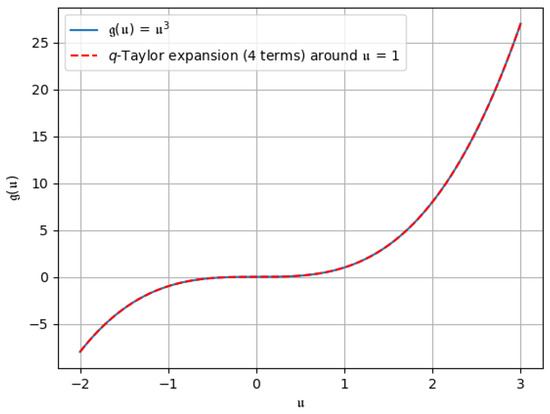Figure 6. $\mathit{q}$-Taylor expansion up to all four terms.

Case 3. 

The $\mathit{q}$-symmetric Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$: Using Corollary 2, put $\eta =3$ and $\beta =1$ in (21), we obtain the $\mathit{q}$-symmetric Taylor expansion of ${\mathfrak{u}}^3$ and write it as

$$\begin{array}{cc}\hfill {\mathfrak{u}}^3& ={\widetilde{\left[\begin{array}{c}3\\ 0\end{array}\right]}}_{\mathit{q}}+{\widetilde{\left[\begin{array}{c}3\\ 1\end{array}\right]}}_{\mathit{q}}{\mathit{q}}^{-2}{(\mathfrak{u}-1)}_{\tilde{\mathit{q}}}+{\widetilde{\left[\begin{array}{c}3\\ 2\end{array}\right]}}_{\mathit{q}}{\mathit{q}}^{-2}{(\mathit{q}\mathfrak{u}-1)}_{\tilde{\mathit{q}}}^2+{\widetilde{\left[\begin{array}{c}3\\ 3\end{array}\right]}}_{\mathit{q}}{(\mathfrak{u}-1)}_{\tilde{\mathit{q}}}^3\hfill \\ \hfill & =1+\widetilde{\left[3\right]}{\mathit{q}}^{-2}{(\mathfrak{u}-1)}_{\tilde{\mathit{q}}}+\widetilde{\left[3\right]}{\mathit{q}}^{-2}{(\mathit{q}\mathfrak{u}-1)}_{\tilde{\mathit{q}}}^2+{(\mathfrak{u}-1)}_{\tilde{\mathit{q}}}^3\hfill \\ \hfill & =1+(1+{\mathit{q}}^{-2}+{\mathit{q}}^{-4})(\mathfrak{u}-1)+(1+{\mathit{q}}^{-2}+{\mathit{q}}^{-4})(\mathit{q}\mathfrak{u}-\mathit{q})(\mathit{q}\mathfrak{u}-{\mathit{q}}^{-1})+(\mathfrak{u}-{\mathit{q}}^2)(\mathfrak{u}-1)(\mathfrak{u}-{\mathit{q}}^{-2})\hfill \\ \hfill & =1+21(\mathfrak{u}-1)+21(0.5\mathfrak{u}-0.5)(0.5\mathfrak{u}-2)+(\mathfrak{u}-0.25)(\mathfrak{u}-1)(\mathfrak{u}-4).\hfill \end{array}$$

The graphical representation of the $\mathit{q}$-symmetric Taylor expansion of ${\mathfrak{u}}^3$ is provided in Figure 7, Figure 8 and Figure 9.

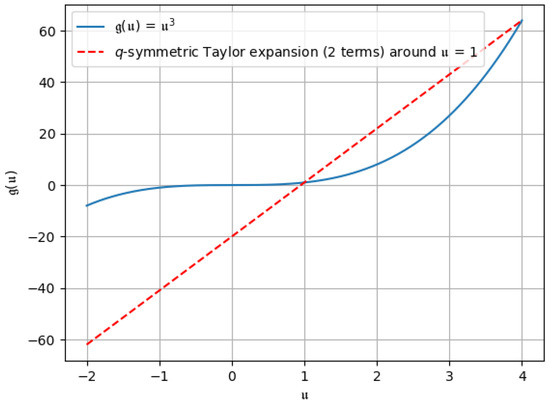Figure 7. $\mathit{q}$-symmetric Taylor expansion up to the first two terms.

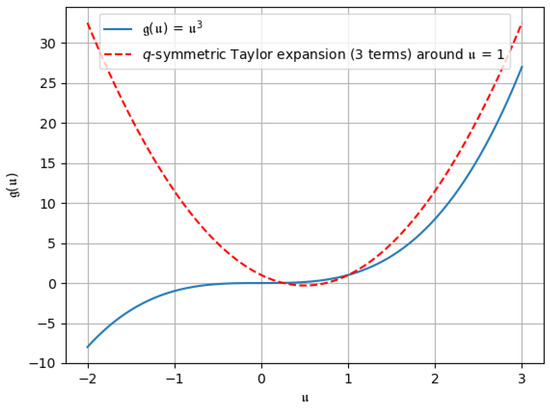Figure 8. $\mathit{q}$-symmetric Taylor expansion up to the first three terms.

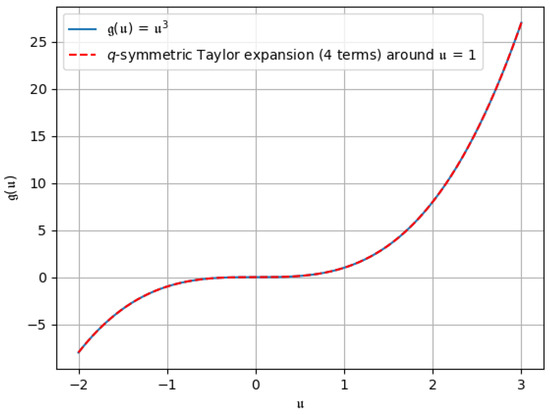Figure 9. $\mathit{q}$-symmetric Taylor expansion up to all four terms.

Case 4. 

The $(\mathit{p},\mathit{q})$-Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$: Put $\eta =3$ and $\beta =1$ in Corollary 1; the $(\mathit{p},\mathit{q})$-Taylor expansion of ${\mathfrak{u}}^3$ is

$$\begin{array}{cc}\hfill {\mathfrak{u}}^3& ={\left[\begin{array}{c}3\\ 0\end{array}\right]}_{\mathit{p},\mathit{q}}+{\left[\begin{array}{c}3\\ 1\end{array}\right]}_{\mathit{p},\mathit{q}}{\mathit{p}}^{-2}{(\mathfrak{u}-1)}_{\mathit{p},\mathit{q}}+{\left[\begin{array}{c}3\\ 2\end{array}\right]}_{\mathit{p},\mathit{q}}{\mathit{p}}^{-3}{(\mathfrak{u}-1)}_{\mathit{p},\mathit{q}}^2+{\left[\begin{array}{c}3\\ 3\end{array}\right]}_{\mathit{p},\mathit{q}}{\mathit{p}}^{-3}{(\mathfrak{u}-1)}_{\mathit{p},\mathit{q}}^3\hfill \\ \hfill & =1+{\left[3\right]}_{\mathit{p},\mathit{q}}{\mathit{p}}^{-2}(\mathfrak{u}-1)+{\left[3\right]}_{\mathit{p},\mathit{q}}{\mathit{p}}^{-3}(\mathfrak{u}-1)(\mathit{p}\mathfrak{u}-\mathit{q})+{\mathit{p}}^{-3}(\mathfrak{u}-1)(\mathit{p}\mathfrak{u}-\mathit{q})({\mathit{p}}^2\mathfrak{u}-{\mathit{q}}^2)\hfill \\ \hfill & =1+(1+{\mathit{p}}^{-1}\mathit{q}+{\mathit{p}}^{-2}{\mathit{q}}^2)(\mathfrak{u}-1)+(1+{\mathit{p}}^{-1}\mathit{q}+{\mathit{p}}^{-2}{\mathit{q}}^2)(\mathfrak{u}-1)(\mathfrak{u}-{\mathit{p}}^{-1}\mathit{q})\hfill \\ \hfill & +{\mathit{p}}^{-3}(\mathfrak{u}-1)(\mathit{p}\mathfrak{u}-\mathit{q})({\mathit{p}}^2\mathfrak{u}-{\mathit{q}}^2).\hfill \end{array}$$

Let us set $\mathit{p}=0.7$ and $\mathit{q}=0.5$; then, the above expansion will become

$$\begin{array}{c}\hfill {\mathfrak{u}}^3=1+2.225(\mathfrak{u}-1)+2.225(\mathfrak{u}-1)(\mathfrak{u}-0.7143)+2.916(\mathfrak{u}-1)(0.7\mathfrak{u}-0.5)(0.5\mathfrak{u}-0.25).\end{array}$$

The graphical representation of $(\mathit{p},\mathit{q})$-Taylor expansion of ${\mathfrak{u}}^3$ around $\mathfrak{u}=1$ is given below in the Figure 10, Figure 11 and Figure 12.

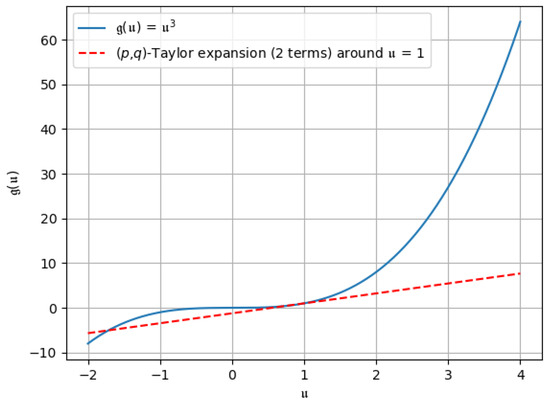Figure 10. $(\mathit{p},\mathit{q})$-Taylor expansion up to the first two terms.

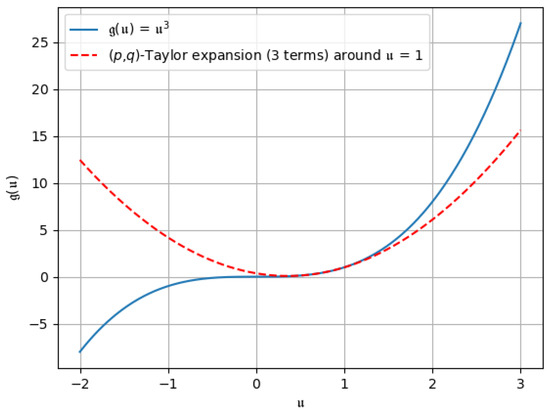Figure 11. $(\mathit{p},\mathit{q})$-Taylor expansion up to the first three terms.

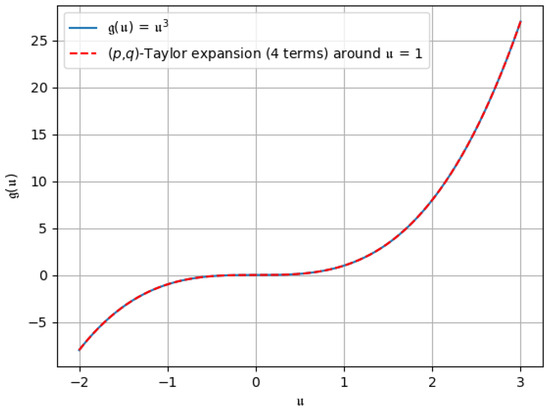Figure 12. $(\mathit{p},\mathit{q})$-Taylor expansion up to all four terms.

Case 5. 

The symmetric $(\mathit{p},\mathit{q})$-Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$: If we put $\eta =3$ and $\beta =1$ in (39), then the symmetric $(\mathit{p},\mathit{q})$-Taylor expansion of ${\mathfrak{u}}^3$ can be derived as

$$\begin{array}{cc}\hfill {\mathfrak{u}}^3& ={\widetilde{\left[\begin{array}{c}3\\ 0\end{array}\right]}}_{\mathit{p},\mathit{q}}+{\widetilde{\left[\begin{array}{c}3\\ 1\end{array}\right]}}_{\mathit{p},\mathit{q}}{\mathit{p}}^{-2}{\mathit{q}}^{-2}{(\mathfrak{u}-1)}_{\widetilde{\mathit{p},\mathit{q}}}+{\widetilde{\left[\begin{array}{c}3\\ 2\end{array}\right]}}_{\mathit{p},\mathit{q}}{\mathit{p}}^{-2}{\mathit{q}}^{-2}{(\mathit{p}\mathit{q}\mathfrak{u}-1)}_{\widetilde{\mathit{p},\mathit{q}}}^2+{\widetilde{\left[\begin{array}{c}3\\ 3\end{array}\right]}}_{\mathit{p},\mathit{q}}{(\mathfrak{u}-1)}_{\widetilde{\mathit{p},\mathit{q}}}^3\hfill \\ \hfill & =1+{\widetilde{\left[3\right]}}_{\mathit{p},\mathit{q}}{\mathit{p}}^{-2}{\mathit{q}}^{-2}(\mathfrak{u}-1)+{\widetilde{\left[3\right]}}_{\mathit{p},\mathit{q}}{\mathit{p}}^{-1}{\mathit{q}}^{-1}(\mathfrak{u}-1)(\mathit{p}\mathit{q}\mathfrak{u}-{\mathit{p}}^{-1}{\mathit{q}}^{-1})\hfill \\ \hfill & +(\mathfrak{u}-{\mathit{p}}^2{\mathit{q}}^2)(\mathfrak{u}-1)(\mathfrak{u}-{\mathit{p}}^{-2}{\mathit{q}}^{-2})\hfill \\ \hfill & =1+(1+{\mathit{p}}^{-2}{\mathit{q}}^{-2}+{\mathit{p}}^{-4}{\mathit{q}}^{-4})(\mathfrak{u}-1)+({\mathit{p}}^2{\mathit{q}}^2+1+{\mathit{p}}^{-2}{\mathit{q}}^{-2})(\mathfrak{u}-1)(\mathfrak{u}-{\mathit{p}}^{-2}{\mathit{q}}^{-2})\hfill \\ \hfill & +(\mathfrak{u}-{\mathit{p}}^2{\mathit{q}}^2)(\mathfrak{u}-1)(\mathfrak{u}-{\mathit{p}}^{-2}{\mathit{q}}^{-2}).\hfill \end{array}$$

Here, put $\mathit{p}=0.7$ and $\mathit{q}=0.5$; then, the symmetric $(\mathit{p},\mathit{q})$-Taylor expansion becomes

$$\begin{array}{c}\hfill {\mathfrak{u}}^3=1+75.80(\mathfrak{u}-1)+9.2858(\mathfrak{u}-1)(\mathfrak{u}-8.1633)+(\mathfrak{u}-0.123)(\mathfrak{u}-1)(\mathfrak{u}-8.1633).\end{array}$$

The graphical representation of the symmetric $(\mathit{p},\mathit{q})$-Taylor expansion of ${\mathfrak{u}}^3$ around $\mathfrak{u}=1$ can be seen in Figure 13, Figure 14 and Figure 15.

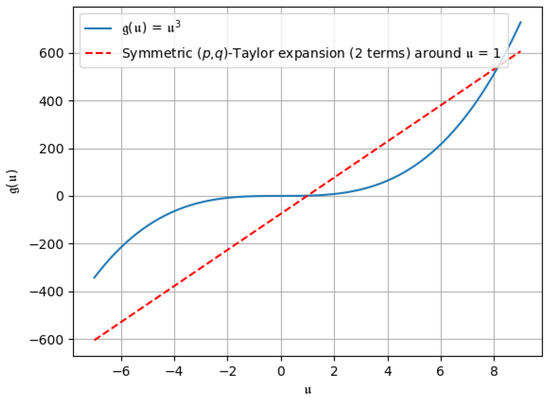Figure 13. The symmetric $(\mathit{p},\mathit{q})$-Taylor expansion up to the first two terms.

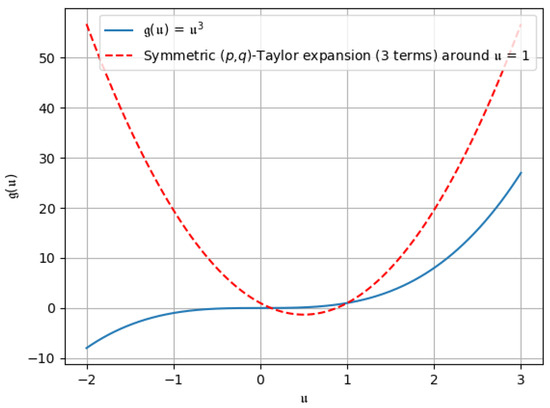Figure 14. The symmetric $(\mathit{p},\mathit{q})$-Taylor expansion up to the first three terms.

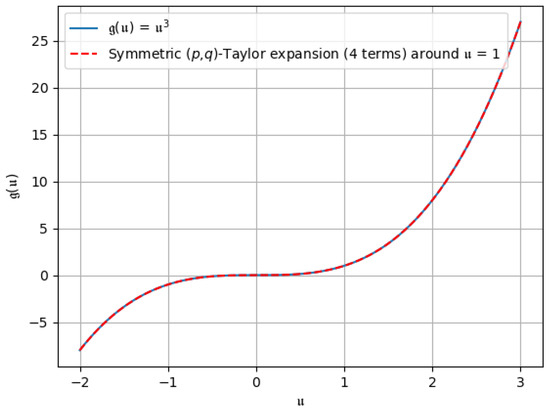Figure 15. The symmetric $(\mathit{p},\mathit{q})$-Taylor expansion up to all four terms.

It can therefore be seen that all of Taylor’s formulae for the cubic function $\mathfrak{g}\left(\mathfrak{u}\right)={\mathfrak{u}}^3$ give different approximations (term to term) and converge to the original curve.

Remark 2. 

It can be seen that ${(\beta -\mathfrak{u})}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}={(-1)}^{\mathfrak{m}}{(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}$.

Proposition 7. 

For any integer $\mathfrak{m}$,

$$\tilde{\mathtt{D}}{(\beta -\mathfrak{u})}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}=-{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}{(\beta -\mathfrak{u})}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}-1}.$$

Proof. 

The proof is the same as Proposition 5. □

The Proposition 7 can also be generalized for higher-order derivatives.

Proposition 8. 

If

$${(\beta -\mathfrak{u})}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}=(\beta -{\mathit{p}}^{\mathfrak{m}-1}{\mathit{q}}^{\mathfrak{m}-1}\mathfrak{u})(\beta -{\mathit{p}}^{\mathfrak{m}-3}{\mathit{q}}^{\mathfrak{m}-3}\mathfrak{u})(\beta -{\mathit{p}}^{\mathfrak{m}-5}{\mathit{q}}^{\mathfrak{m}-5}\mathfrak{u})\dots (\beta -{\mathit{p}}^{-\mathfrak{m}+1}{\mathit{q}}^{-\mathfrak{m}+1}\mathfrak{u})$$

with any non-negative integer $\mathfrak{m}$, then for any integer $0\le \eta \le \mathfrak{m}$,

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\eta }{(\beta -\mathfrak{u})}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}={\displaystyle \frac{{(-1)}^{\eta }{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}{{\widetilde{[\mathfrak{m}-\eta ]}}_{\mathit{p},\mathit{q}}!}}{(\beta -\mathfrak{u})}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}-\eta }.$$

Proof. 

The proof is similar to Proposition 6. □

Theorem 7. 

For any real number β and the polynomial $\mathfrak{g}\left(\mathfrak{u}\right)$ with degree $\mathtt{N}$, then

$$\mathfrak{g}\left(\mathfrak{u}\right)=\sum _{\left(even\right)\mathfrak{m}\ge 0}^{\mathtt{N}}{\mathit{p}}^{-\mathfrak{m}}{\mathit{q}}^{-\mathfrak{m}}{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\beta \right){\displaystyle \frac{{(\mathit{p}\mathit{q}\beta -\mathfrak{u})}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}}{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}}-\sum _{\left(odd\right)\mathfrak{m}>0}^{\mathtt{N}}{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\beta \right){\displaystyle \frac{{(\beta -\mathfrak{u})}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}}{{\widetilde{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!}}$$

(40)

is called symmetric $(\mathit{p},\mathit{q})$-Taylor or $\left(\widetilde{\mathit{p},\mathit{q}}\right)$-Taylor expansion of $\mathfrak{g}\left(\mathfrak{u}\right)$.

Proof. 

We can prove it the same as (33). □

Corollary 4. 

If we put $\mathfrak{g}\left(\mathfrak{u}\right)={\mathfrak{u}}^{\eta }$ in (40), then we have

$${\mathfrak{u}}^{\eta }=\sum _{\left(even\right)\mathfrak{m}\ge 0}^{\mathtt{N}}{\mathit{p}}^{-\mathfrak{m}}{\mathit{q}}^{-\mathfrak{m}}{\widetilde{\left[\begin{array}{c}\eta \\ \mathfrak{m}\end{array}\right]}}_{\mathit{p},\mathit{q}}{\left(\beta \right)}^{\eta -\mathfrak{m}}{(\mathit{p}\mathit{q}\beta -\mathfrak{u})}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}-\sum _{\left(odd\right)\mathfrak{m}>0}^{\mathtt{N}}{\widetilde{\left[\begin{array}{c}\eta \\ \mathfrak{m}\end{array}\right]}}_{\mathit{p},\mathit{q}}{\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\beta \right)}^{\eta -\mathfrak{m}}{(\beta -\mathfrak{u})}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}.$$

Now, we introduce the symmetric $(\mathit{p},\mathit{q})$-integration. For this, we have to define some operators, which are described below.

Definition 10. 

Let $\check{\mathfrak{u}}$ and ${\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}$ be the two linear operators in the field of polynomials that are defined as

$$\check{\mathfrak{u}}\left(\mathfrak{g}\left(\mathfrak{u}\right)\right)=\mathfrak{u}\mathfrak{g}\left(\mathfrak{u}\right);{\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}\left(\mathfrak{g}\left(\mathfrak{u}\right)\right)=\mathfrak{g}\left(\mathit{p}\mathit{q}\mathfrak{u}\right).$$

Proposition 9. 

If $\check{\mathfrak{u}}$ and ${\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}$ are the linear operator in the field of polynomials, then

(i) 

${\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}\check{\mathfrak{u}}=\mathit{p}\mathit{q}\check{\mathfrak{u}}{\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}$

(ii) 

${\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}{\check{\mathcal{N}}}_{{\mathit{p}}^{-1},{\mathit{q}}^{-1}}={\check{\mathcal{N}}}_{{\mathit{p}}^{-1},{\mathit{q}}^{-1}}{\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}$

(iii) 

${\check{\mathcal{N}}}_{{\mathit{p}}^{-1},{\mathit{q}}^{-1}}={\left({\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}\right)}^{-1}$.

Proof. 

(i) Since for any polynomial $\mathfrak{g}\left(\mathfrak{u}\right)$, we have

$$\begin{array}{cc}\hfill {\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}\check{\mathfrak{u}}\left(\mathfrak{g}\left(\mathfrak{u}\right)\right)& ={\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}\left(\mathfrak{u}\mathfrak{g}\left(\mathfrak{u}\right)\right)\hfill \\ \hfill & =\mathit{p}\mathit{q}\mathfrak{u}\mathfrak{g}\left(\mathit{p}\mathit{q}\mathfrak{u}\right)\hfill \\ \hfill & =\mathit{p}\mathit{q}\check{\mathfrak{u}}{\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}\left(\mathfrak{g}\left(\mathfrak{u}\right)\right).\hfill \end{array}$$

which endorses our desired result. Similarly, we can verify (ii) and (iii). □

Let $\mathtt{G}\left(\mathfrak{u}\right)$ be the symmetric $(\mathit{p},\mathfrak{q})$-antiderivative of $\mathfrak{g}\left(\mathfrak{u}\right)$. Then by using ${\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}$, we can write

$$\begin{array}{cc}\hfill ({\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}-{\displaystyle \frac{1}{{\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}}})\mathtt{G}\left(\mathfrak{u}\right)& =\mathtt{G}\left(\mathit{p}\mathit{q}\mathfrak{u}\right)-\mathtt{G}\left({\mathit{p}}^{-1}{\mathit{q}}^{-1}\mathfrak{u}\right)\hfill \\ \hfill & =(\mathit{p}\mathit{q}-{\mathit{p}}^{-1}{\mathit{q}}^{-1})\mathfrak{u}\mathfrak{g}\left(\mathfrak{u}\right)\hfill \\ \hfill \mathtt{G}\left(\mathfrak{u}\right)& =({\mathit{p}}^{-1}{\mathit{q}}^{-1}-\mathit{p}\mathit{q}){\displaystyle \frac{{\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}}{1-{\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}^2}}\mathfrak{u}\mathfrak{g}\left(\mathfrak{u}\right)\hfill \\ \hfill & =({\mathit{p}}^{-1}{\mathit{q}}^{-1}-\mathit{p}\mathit{q})[{\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}+{\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}^3+{\check{\mathcal{N}}}_{\mathit{p},\mathit{q}}^5+\dots ]\mathfrak{u}\mathfrak{g}\left(\mathfrak{u}\right).\hfill \end{array}$$

Hence

$$\mathtt{G}\left(\mathfrak{u}\right)=\mathfrak{u}({\mathit{p}}^{-1}{\mathit{q}}^{-1}-\mathit{p}\mathit{q})\sum _{\mathfrak{m}=1}^{\infty }{\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left({\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}\mathfrak{u}\right),$$

(41)

where $\mathfrak{m}$ is an odd integer. It is obvious that if the R.H.S. of (41) converges, then $\mathtt{G}\left(\mathfrak{u}\right)$ is the symmetric $(\mathit{p},\mathit{q})$-antiderivative of $\mathfrak{g}\left(\mathfrak{u}\right)$, and it becomes zero at $\mathfrak{u}=0$. As a consequence, we define the symmetric definite $(\mathit{p},\mathit{q})$-integrals that are mentioned below.

Definition 11. 

For any arbitrary function $\mathfrak{g}\left(\mathfrak{u}\right):\mathtt{I}=[\mathfrak{a},\mathfrak{b}]⟶\mathtt{R}$, then

$${\int }_{\mathfrak{a}}^{\mathfrak{b}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}={\int }_0^{\mathfrak{b}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}-{\int }_0^{\mathfrak{a}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u},$$

(42)

where

$${\int }_0^{\mathfrak{a}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}=\mathfrak{a}({\mathit{p}}^{-1}{\mathit{q}}^{-1}-\mathit{p}\mathit{q})\sum _{\mathfrak{m}=1,3,5,\dots }{\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left({\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}\mathfrak{a}\right)$$

(43)

is called a symmetric definite $(\mathit{p},\mathfrak{q})$-integral or definite $\left(\widetilde{\mathit{p},\mathfrak{q}}\right)$-integral of $\mathfrak{g}\left(\mathfrak{u}\right)$.

If $\mathit{p}⟶1$ in (42), it reduces to the definite $\tilde{\mathfrak{q}}$-integral that is mentioned in [7].

Theorem 8 

(Fundamental theorem of symmetric $(\mathit{p},\mathit{q})$-calculus). For any arbitrary continuous function, where $\mathfrak{g}\left(\mathfrak{u}\right):\mathtt{I}⟶\mathtt{R}$ and $\mathtt{G}\left(\mathfrak{u}\right)$ is its symmetric $(\mathit{p},\mathfrak{q})$-antiderivative, then

$${\int }_{\mathfrak{a}}^{\mathfrak{b}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}=\mathtt{G}\left(\mathfrak{b}\right)-\mathtt{G}\left(\mathfrak{a}\right)$$

(44)

where $0\le \mathfrak{a}<\mathfrak{b}<\infty$.

Proof. 

Since $\mathtt{G}\left(\mathfrak{u}\right)$ is symmetric $(\mathit{p},\mathfrak{q})$-antiderivative and $\mathtt{G}\left(0\right)=0$, then, using (41), we have

$$\begin{array}{cc}\hfill \mathtt{G}\left(\mathfrak{u}\right)& =\mathfrak{u}({\mathit{p}}^{-1}{\mathit{q}}^{-1}-\mathit{p}\mathit{q})\sum _{\mathfrak{m}=1,3,5,\dots }{\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left({\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}\mathfrak{u}\right)+\mathtt{G}\left(0\right)\hfill \\ \hfill \mathtt{G}\left(\mathfrak{a}\right)& =\mathfrak{a}({\mathit{p}}^{-1}{\mathit{q}}^{-1}-\mathit{p}\mathit{q})\sum _{\mathfrak{m}=1,3,5,\dots }{\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left({\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}\mathfrak{a}\right)+\mathtt{G}\left(0\right).\hfill \end{array}$$

(45)

Since, by (43), we have

$${\int }_0^{\mathfrak{a}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}=\mathfrak{a}({\mathit{p}}^{-1}{\mathit{q}}^{-1}-\mathit{p}\mathit{q})\sum _{\mathfrak{m}=1,3,5,\dots }{\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left({\mathit{p}}^{\mathfrak{m}}{\mathit{q}}^{\mathfrak{m}}\mathfrak{a}\right).$$

then (45) becomes

$$\begin{array}{c}\hfill {\int }_0^{\mathfrak{a}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}=\mathtt{G}\left(\mathfrak{a}\right)-\mathtt{G}\left(0\right).\end{array}$$

(46)

Similarly, we have

$$\begin{array}{c}\hfill {\int }_0^{\mathfrak{b}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}=\mathtt{G}\left(\mathfrak{b}\right)-\mathtt{G}\left(0\right).\end{array}$$

(47)

Subtracting (46) from (47), we obtain the desired result. □

4. Fractional Dual Basic Symmetric Quantum Integral

In this section, we define another $(\mathit{p},\mathit{q})$-number, which can be written as

$${\left[\mathfrak{m}\right]}_{{\mathit{p}}^2,{\mathit{q}}^2}={\overline{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}={\displaystyle \frac{1-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}}}{1-{\left(\mathit{p}\mathit{q}\right)}^2}}.$$

(48)

The factorial of this number can be defined as

$${\overline{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}!=\left\{\begin{array}{cc}{\overline{\left[\mathfrak{m}\right]}}_{\mathit{p},\mathit{q}}{\overline{[\mathfrak{m}-1]}}_{\mathit{p},\mathit{q}}\dots {\overline{\left[1\right]}}_{\mathit{p},\mathit{q}}\hfill & \mathrm{if}\mathfrak{m}\ge 1,\hfill \\ 1\hfill & \mathrm{if}\mathfrak{m}=0.\hfill \end{array}\right.$$

Another $(\mathit{p},\mathit{q})$-symmetric analogue of ${(\mathfrak{u}-\beta )}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}$ can be written as

$${\overline{(\mathfrak{u}-\beta )}}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}=\left\{\begin{array}{cc}\prod _{\mathfrak{s}=0}^{\mathfrak{m}-1}(\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{s}+1}\beta )\hfill & \mathrm{if}\mathfrak{m}>0,\hfill \\ 1\hfill & \mathrm{if}\mathfrak{m}=0.\hfill \end{array}\right.$$

It can be extended to $\mathfrak{m}\in \mathbb{R}$ and written as

$${\overline{(\mathfrak{u}-\beta )}}_{\widetilde{\mathit{p},\mathit{q}}}^{\mathfrak{m}}={\mathfrak{u}}^{\mathfrak{m}}{\displaystyle \frac{{\prod }_{\mathfrak{s}=0}^{\infty }(1-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{s}+1}\frac{\beta }{\mathfrak{u}})}{{\prod }_{\mathfrak{s}=0}^{\infty }(1-{\left(\mathit{p}\mathit{q}\right)}^{2(\mathfrak{s}+\mathfrak{m})+1}\frac{\beta }{\mathfrak{u}})}},\mathfrak{u}\ne 0.$$

(49)

For $\mathfrak{u}\in \mathbb{R}\setminus \{0,-1,-2,\dots \}$, the $(\mathit{p},\mathit{q})$-symmetric gamma function can be derived as

$${\tilde{\Gamma }}_{\mathit{p},\mathit{q}}\left(\mathfrak{u}\right)={\displaystyle \frac{{\prod }_{\mathfrak{s}=0}^{\infty }(1-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{s}+2})}{{\prod }_{\mathfrak{s}=0}^{\infty }(1-{\left(\mathit{p}\mathit{q}\right)}^{2(\mathfrak{s}+\mathfrak{u}-1)+2})}}{(1-{\left(\mathit{p}\mathit{q}\right)}^2)}^{1-\mathfrak{u}}.$$

The definite $\widetilde{(\mathit{p},\mathit{q})}$-integral can also be written as

$${}_{\mathfrak{a}}\tilde{\mathtt{I}}_{\mathit{p},\mathit{q}}^{ }\mathfrak{g}\left(\mathfrak{u}\right)={\int }_{\mathfrak{a}}^{\mathfrak{s}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}={\int }_0^{\mathfrak{s}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}-{\int }_0^{\mathfrak{a}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u},$$

here

$${}_0\tilde{\mathtt{I}}_{\mathit{p},\mathit{q}}^{ }\mathfrak{g}\left(\mathfrak{u}\right)={\int }_0^{\mathfrak{s}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}=\mathfrak{s}(1-{\left(\mathit{p}\mathit{q}\right)}^2)\sum _{\mathfrak{m}=0}^{\infty }{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}}\mathfrak{g}\left({\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}\mathfrak{s}\right).$$

Moreover, for a nonnegative integer $\mathfrak{m}$, ${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\mathfrak{u}\right)$ is called the higher-order $\widetilde{(\mathit{p},\mathit{q})}$-derivative of $\mathfrak{g}\left(\mathfrak{u}\right)$. Therefore, it is obvious that

$${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^0\mathfrak{g}\left(\mathfrak{u}\right)=\mathfrak{g}\left(\mathfrak{u}\right),{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\mathfrak{u}\right)={\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}-1}\mathfrak{g}\left(\mathfrak{u}\right).$$

Furthermore, we can define the ${\tilde{\mathtt{I}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}$ operator for these derivatives, and the following results exist:

(i) 

${\tilde{\mathtt{I}}}_{\mathit{p},\mathit{q}}^0\mathfrak{g}\left(\mathfrak{u}\right)=\mathfrak{g}\left(\mathfrak{u}\right)$,

(ii) 

${\tilde{\mathtt{I}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\mathfrak{u}\right)={\tilde{\mathtt{I}}}_{\mathit{p},\mathit{q}}{\tilde{\mathtt{I}}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}-1}\mathfrak{g}\left(\mathfrak{u}\right)$,

(iii) 

${\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}{\tilde{\mathtt{I}}}_{\mathit{p},\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)=\mathfrak{g}\left(\mathfrak{u}\right)$,

(iv) 

${\tilde{\mathtt{I}}}_{\mathit{p},\mathit{q}}{\tilde{\mathtt{D}}}_{\mathit{p},\mathit{q}}\mathfrak{g}\left(\mathfrak{u}\right)=\mathfrak{g}\left(\mathfrak{u}\right)-\mathfrak{g}\left(0\right)$.

Now, we derive a lemma that is very useful to construct the $(\mathit{p},\mathit{q})$-symmetric Cauchy’s formula.

Lemma 1. 

For any positive integer η,

$${\displaystyle \frac{(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}}{{\left(\mathit{p}\mathit{q}\right)}^{\eta }}}\sum _{\mathfrak{m}=0}^{{\mathfrak{m}}_1}{\overline{({\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2})}}^{\eta -1}={\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1})}}^{\eta }$$

(50)

holds.

Proof. 

Expanding the summation of the left side of (50), we have

$$\begin{array}{c}{\displaystyle \frac{(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}}{{\left(\mathit{p}\mathit{q}\right)}^{\eta }}}\sum _{\mathfrak{m}=0}^{{\mathfrak{m}}_1}{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}{\overline{({\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2})}}^{\eta -1}\hfill \\ ={\displaystyle \frac{(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}}{{\left(\mathit{p}\mathit{q}\right)}^{\eta }}}\left[\left(\mathit{p}\mathit{q}\right){\overline{(\left(\mathit{p}\mathit{q}\right)-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2})}}^{\eta -1}+{\left(\mathit{p}\mathit{q}\right)}^3{\overline{({\left(\mathit{p}\mathit{q}\right)}^3-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2})}}^{\eta -1}+\cdots \right.\hfill \\ +\left.{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1}{\overline{({\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1}-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2})}}^{\eta -1}\right]\hfill \\ =(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}\left[{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1})}}^{\eta -1}+{\left(\mathit{p}\mathit{q}\right)}^{2\eta }{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1-1})}}^{\eta -1}+\cdots \right.\hfill \\ +\left.{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1\eta }{\overline{(1-(\mathit{p}\mathit{q}\left)\right)}}^{\eta -1}\right]\hfill \\ =(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}\left[{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1\eta }{\overline{(1-(\mathit{p}\mathit{q}\left)\right)}}^{\eta -1}+{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-1)\eta }{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^3)}}^{\eta -1}+\cdots \right.\hfill \\ +\left.{\left(\mathit{p}\mathit{q}\right)}^{2\eta }{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1-1})}}^{\eta -1}+{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1})}}^{\eta -1}\right]\hfill \\ =(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}\left[{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-1)\eta }\left({\left(\mathit{p}\mathit{q}\right)}^{2\eta }{\overline{(1-(\mathit{p}\mathit{q}\left)\right)}}^{\eta -1}+{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^3)}}^{\eta -1}\right)\right.\hfill \\ +\left.{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-2)\eta }{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^5)}}^{\eta -1}+\cdots +{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1})}}^{\eta -1}\right]\hfill \\ =(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}\left[{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-1)\eta }\left({\left(\mathit{p}\mathit{q}\right)}^{2\eta }\prod _{\mathfrak{s}=0}^{\eta -2}(1-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{s}+2})+\prod _{\mathfrak{s}=0}^{\eta -2}(1-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{s}+4})\right)\right.\hfill \\ +\left.{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-2)\eta }{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^5)}}^{\eta -1}+\cdots +{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1})}}^{\eta -1}\right]\hfill \\ =(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}\left[{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-1)\eta }(1-{\left(\mathit{p}\mathit{q}\right)}^{2\eta +2})\prod _{\mathfrak{s}=0}^{\eta -3}(1-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{s}+4})\right.\hfill \\ +\left.{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-2)\eta }{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^5)}}^{\eta -1}+\cdots +{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1})}}^{\eta -1}\right]\hfill \\ =(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}\left[{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-2)\eta }\left({\left(\mathit{p}\mathit{q}\right)}^{2\eta }(1-{\left(\mathit{p}\mathit{q}\right)}^{2\eta +2})\prod _{\mathfrak{s}=0}^{\eta -3}(1-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{s}+4})+\prod _{\mathfrak{s}=0}^{\eta -2}(1-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{s}+6})\right)\right.\hfill \\ +\left.{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-3)\eta }{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^7)}}^{\eta -1}+\cdots +{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1})}}^{\eta -1}\right]\hfill \\ =(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}\left[{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-2)\eta }(1-{\left(\mathit{p}\mathit{q}\right)}^{2\eta +2})(1-{\left(\mathit{p}\mathit{q}\right)}^{2\eta +4})\prod _{\mathfrak{s}=0}^{\eta -4}(1-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{s}+6})\right.\hfill \\ +\left.{\left(\mathit{p}\mathit{q}\right)}^{2({\mathfrak{m}}_1-3)\eta }{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^7)}}^{\eta -1}+\cdots +{\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1})}}^{\eta -1}\right]\hfill \\ ⋮\hfill \\ =(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}\left[(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2})(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+4})\cdots (1-{\left(\mathit{p}\mathit{q}\right)}^{2\eta -2})(1-{\left(\mathit{p}\mathit{q}\right)}^{2\eta +2})\cdots \right.\hfill \\ \times \left.(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2\eta })\right]\hfill \\ ={\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1})}}^{\eta }.\hfill \end{array}$$

            □

Theorem 9. 

Let ${}_0\tilde{\mathtt{I}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}={\int }_0^{\mathfrak{u}}{\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{s}{\int }_0^{\mathfrak{s}}{\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}{\mathfrak{s}}_{\mathfrak{m}-1}{\int }_0^{{\mathfrak{s}}_{\mathfrak{m}-1}}{\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}{\mathfrak{s}}_{\mathfrak{m}-2}\dots {\int }_0^{{\mathfrak{s}}_2}{\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}{\mathfrak{s}}_1$ be denoted as multiple definite $\widetilde{(\mathit{p},\mathit{q})}$-integrals; then,

$${}_0\tilde{\mathtt{I}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\mathfrak{u}\right)={\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\mathfrak{m}\\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\mathfrak{m}\\ 2\end{array}\right)}}{{\overline{[\mathfrak{m}-1]}}_{\mathit{p},\mathit{q}}}}{\int }_0^{\mathfrak{u}}{\overline{(\mathfrak{u}-\mathfrak{s})}}^{\mathfrak{m}-1}\mathfrak{g}\left(\mathfrak{s}{\mathit{p}}^{\mathfrak{m}-1}{\mathit{q}}^{\mathfrak{m}-1}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{s}$$

(51)

exists, where $\left(\begin{array}{c}\mathfrak{m}\\ 2\end{array}\right)={\displaystyle \frac{\Gamma (\mathfrak{m}+1)}{\Gamma \left(3\right)\Gamma (\mathfrak{m}-1)}}$.

Proof. 

Using induction on $\mathfrak{m}$. For $\mathfrak{m}=1$,

$${}_0\tilde{\mathtt{I}}_{\mathit{p},\mathit{q}}^{ }\mathfrak{g}\left(\mathfrak{u}\right)={\int }_0^{\mathfrak{s}}\mathfrak{g}\left(\mathfrak{u}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{u}.$$

Hence, (51) is true for $\mathfrak{m}=1$. Suppose it is true for $\mathfrak{m}=\eta$. As

$$\begin{array}{cc}\hfill {}_0\tilde{\mathtt{I}}_{\mathit{p},\mathit{q}}^{\eta +1}\mathfrak{g}\left(\mathfrak{u}\right)& ={}_0\tilde{\mathtt{I}}_{\mathit{p},\mathit{q}}^{ }\left({}_0\tilde{\mathtt{I}}_{\mathit{p},\mathit{q}}^{\eta }\mathfrak{g}\left(\mathfrak{u}\right)\right)\hfill \\ & ={}_0\tilde{\mathtt{I}}_{\mathit{p},\mathit{q}}^{ }\left({\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}}{{\overline{[\eta -1]}}_{\mathit{p},\mathit{q}}}}{\int }_0^{\mathfrak{u}}{\overline{(\mathfrak{u}-{\mathfrak{u}}_1)}}^{\eta -1}\mathfrak{g}\left({\mathfrak{u}}_1{\mathit{p}}^{\eta -1}{\mathit{q}}^{\eta -1}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}{\mathfrak{u}}_1\right)\hfill \\ & ={\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}}{{\overline{[\eta -1]}}_{\mathit{p},\mathit{q}}}}{\int }_0^{\mathfrak{u}}{\int }_0^{\mathfrak{s}}{\overline{(\mathfrak{s}-{\mathfrak{u}}_1)}}^{\eta -1}\mathfrak{g}\left({\mathfrak{u}}_1{\mathit{p}}^{\eta -1}{\mathit{q}}^{\eta -1}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}{\mathfrak{u}}_1{\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{s}\hfill \\ & ={\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}}{{\overline{[\eta -1]}}_{\mathit{p},\mathit{q}}}}\mathfrak{u}(1-{\left(\mathit{p}\mathit{q}\right)}^2)\sum _{\mathfrak{m}=0}^{\infty }{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}}\hfill \\ & \times {\int }_0^{{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}\mathfrak{u}}{\overline{({\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}\mathfrak{u}-{\mathfrak{u}}_1)}}^{\eta -1}\mathfrak{g}\left({\mathfrak{u}}_1{\mathit{p}}^{\eta -1}{\mathit{q}}^{\eta -1}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}{\mathfrak{u}}_1\hfill \\ & ={\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}}{{\overline{[\eta -1]}}_{\mathit{p},\mathit{q}}}}{\mathfrak{u}}^2{(1-{\left(\mathit{p}\mathit{q}\right)}^2)}^2\sum _{\mathfrak{m}=0}^{\infty }\sum _{{\mathfrak{m}}_1=0}^{\infty }{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}}{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1+2{\mathfrak{m}}_1}\hfill \\ & \times {\overline{({\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1+2{\mathfrak{m}}_1+1}\mathfrak{u})}}^{\eta -1}\mathfrak{g}\left(\mathfrak{u}{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1+2{\mathfrak{m}}_1+1}{\left(\mathit{p}\mathit{q}\right)}^{\eta -1}\right)\hfill \\ & ={\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}}{{\overline{[\eta -1]}}_{\mathit{p},\mathit{q}}}}{\mathfrak{u}}^2{(1-{\left(\mathit{p}\mathit{q}\right)}^2)}^2\sum _{\mathfrak{m}=0}^{\infty }\sum _{{\mathfrak{m}}_1=\mathfrak{m}}^{\infty }{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}}{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1}\hfill \\ & \times {\overline{({\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}\mathfrak{u}-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2}\mathfrak{u})}}^{\eta -1}\mathfrak{g}\left(\mathfrak{u}{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2}{\left(\mathit{p}\mathit{q}\right)}^{\eta -1}\right)\hfill \\ & ={\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}}{{\overline{[\eta -1]}}_{\mathit{p},\mathit{q}}}}{\mathfrak{u}}^{\eta +1}{(1-{\left(\mathit{p}\mathit{q}\right)}^2)}^2\sum _{\mathfrak{m}=0}^{\infty }\sum _{{\mathfrak{m}}_1=\mathfrak{m}}^{\infty }{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}}{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1}\hfill \\ & \times {\overline{({\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2})}}^{\eta -1}\mathfrak{g}\left(\mathfrak{u}{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2}{\left(\mathit{p}\mathit{q}\right)}^{\eta -1}\right)\hfill \\ & ={\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\eta \\ 2\end{array}\right)}}{{\overline{[\eta -1]}}_{\mathit{p},\mathit{q}}}}{\mathfrak{u}}^{\eta +1}{(1-{\left(\mathit{p}\mathit{q}\right)}^2)}^2\sum _{{\mathfrak{m}}_1=0}^{\infty }{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1}\mathfrak{g}\left(\mathfrak{u}{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2}{\left(\mathit{p}\mathit{q}\right)}^{\eta -1}\right)\hfill \\ & \times \sum _{\mathfrak{m}=0}^{{\mathfrak{m}}_1}{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}{\overline{({\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2})}}^{\eta -1}\hfill \\ & ={\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\eta +1\\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\eta +1\\ 2\end{array}\right)}}{{\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}}}{\mathfrak{u}}^{\eta +1}(1-{\left(\mathit{p}\mathit{q}\right)}^2)\sum _{{\mathfrak{m}}_1=0}^{\infty }{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1}\mathfrak{g}\left(\mathfrak{u}{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2}{\left(\mathit{p}\mathit{q}\right)}^{\eta -1}\right)\hfill \\ & \times {\displaystyle \frac{(1-{\left(\mathit{p}\mathit{q}\right)}^2){\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}}{{\left(\mathit{p}\mathit{q}\right)}^{\eta }}}\sum _{\mathfrak{m}=0}^{{\mathfrak{m}}_1}{\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}{\overline{({\left(\mathit{p}\mathit{q}\right)}^{2\mathfrak{m}+1}-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2})}}^{\eta -1}.\hfill \end{array}$$

Using Lemma 1,

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\eta +1\\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\eta +1\\ 2\end{array}\right)}}{{\overline{\left[\eta \right]}}_{\mathit{p},\mathit{q}}}}{\mathfrak{u}}^{\eta +1}(1-{\left(\mathit{p}\mathit{q}\right)}^2)\sum _{{\mathfrak{m}}_1=0}^{\infty }{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1}\mathfrak{g}\left(\mathfrak{u}{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+2}{\left(\mathit{p}\mathit{q}\right)}^{\eta -1}\right)\hfill \\ & \times {\overline{(1-{\left(\mathit{p}\mathit{q}\right)}^{2{\mathfrak{m}}_1+1})}}^{\eta }.\hfill \end{array}$$

Thus, it is also true for $\mathfrak{m}=\eta +1$. □

Remark 3. 

If we fix $\mathit{p}=1$, then (51) is reduced to the $\mathit{q}$-symmetric Cauchy’s formula, which is discussed in [26].

Now, we introduce the fractional $\widetilde{(\mathit{p},\mathit{q})}$-integral formula.

Definition 12. 

For any positive real number $\mathfrak{m}$, then

$${}_0\tilde{\mathtt{I}}_{\mathit{p},\mathit{q}}^{\mathfrak{m}}\mathfrak{g}\left(\mathfrak{u}\right)={\displaystyle \frac{{\mathit{p}}^{\left(\begin{array}{c}\mathfrak{m}\\ 2\end{array}\right)}{\mathit{q}}^{\left(\begin{array}{c}\mathfrak{m}\\ 2\end{array}\right)}}{{\tilde{\Gamma }}_{\mathit{p},\mathit{q}}\left(\mathfrak{m}\right)}}{\int }_0^{\mathfrak{u}}{\overline{(\mathfrak{u}-\mathfrak{s})}}^{\mathfrak{m}-1}\mathfrak{g}\left(\mathfrak{s}{\mathit{p}}^{\mathfrak{m}-1}{\mathit{q}}^{\mathfrak{m}-1}\right){\tilde{\mathtt{d}}}_{\mathit{p},\mathit{q}}\mathfrak{s}$$

is said to be a fractional $\widetilde{(\mathit{p},\mathit{q})}$-integral formula. Moreover, it is obvious that it shrinks into a fractional $\mathit{q}$-symmetric integral formula when $\mathit{p}=1$.

5. Conclusions

In this work, we wrote out the specific case of generalized Taylor expansions for polynomials in symmetric quantum calculus and derived a proof for it. Furthermore, we established a new kind of calculus known as dual basic symmetric quantum calculus or symmetric $(\mathit{p},\mathit{q})$-calculus. Furthermore, using this calculus, we obtained the symmetric $(\mathit{p},\mathit{q})$-Taylor expansion for polynomials. Next, we examined Taylor’s formulas for classical, quantum, symmetric quantum, $(\mathit{p},\mathit{q})$-, and dual basic symmetric quantum calculus using an example. Moreover, we defined symmetric definite $(\mathit{p},\mathit{q})$-integral and deduced the fundamental law of symmetric $(\mathit{p},\mathit{q})$-calculus. Lastly, we derived the symmetric $(\mathit{p},\mathit{q})$-Cauchy formula for integrals, and using this notion, we introduced fractional $(\mathit{p},\mathit{q})$-symmetric integrals. In upcoming papers, this new calculus might be more useful in obtaining new results in mathematics and engineering. For example, it can be used to create several integral inequalities and to obtain new findings for Z-Transforms in engineering and physics. Furthermore, this kind of calculus will provide fresh perspectives on the field of fractional calculus.