On Product Neutrosophic Fractal Spaces and α-Density Theory with Arbitrarily Small and Controlled Error

Abstract

In this manuscript, we present the classical Hutchinson–Barnsley theory on the product neutrosophic fractal spaces by utilizing an iterated function system, which is enclosed by neutrosophic Edelstein contractions and a finite number of neutrosophic b-contractions. Further, we provide a sequence of sets that, under appropriate conditions and in terms of the Hausdorff neutrosophic metric, converge to the attractor set of specific neutrosophic iterated function systems. Furthermore, we present a fuzzy variant of α-dense curves that can accurately approximate the attractor set of certain iterated function systems with barely noticeable and controlled errors. In the end, we make a connection between the above-discussed concepts of neutrosophic theory and α-density theory.

1. Introduction

Fractals have a wide range of applications in biomedicine [1], quantum physics [2], computer graphics [3], and several other areas of science. Extensive usage of the theory of discrete dynamical systems, which is explicitly known as the idea of iterated function system (IFS), was started by ancient mathematicians, and it is used to construct fractal and self-similar sets. Self-similarity is not only an asset of a fractal set, but it may also be used to define the fractal and self-similar sets. A stable compact subset of a complete metric space (MS) produced by the iterated function system of contractive mappings was configured by Hutchinson [4], who developed a theory called the Hutchinson–Barnsley (HB) theory by employing the Banach contraction principle. A very well-known application of fractal theory, especially the utilization of self-similarity property, is encountered in fractal image compression, which is also termed fractal image encoding. One of the primary goals of this perception is to consider the fractal transform operator that is directly gained from the perception by considering the fractal transform maps, and the undertaken image function will be approximated by the attractor of the associated contractive operator. Rajkumar and Uthayakumar [5] constructed a distance function of fuzzy points, and using this metric, they presented a complete MS via fuzzy-valued image functions. Subsequently, they defined a fractal transform operator on the newly produced complete MS.

Zadeh [6] initiated the theory of fuzzy sets (FSs) and several notions of fuzzy MSs (FMSs), and their properties have been analyzed by several mathematicians; see [7,8]. Then, Park [9] provided the notion of intuitionistic FMSs (IFMSs), which is a common idea of FMS introduced by George and Veeramani [10]. Similar to FMSs, there are several research papers available on the concept of generalized fuzzy topological spaces. Twenty-five years back, FSs and fuzzy topology were generalized to a new concept that includes the non-membership function, called intuitionistic FS and intuitionistic fuzzy topology. Especially, Coker [11] introduced the notion of an intuitionistic fuzzy topological space.

Further, an analysis of the fuzzy fractal space and intuitionistic fuzzy fractal space was performed by Easwaramoorthy and Uthayakumar [12,13,14]. In their work, they investigated the attractors constructed by the IFS of fuzzy contractive mappings in both FMS and IFMS by generalizing the HB theory. Additionally, they discussed several naming theorems, such as the Collage theorem and the falling leaves theorem, in the setting of standard FMS and standard Hausdorff MS. A generalized fuzzy Hausdorff distance on the set of compact subsets of a generalized FMS can be constructed utilizing the technique that is described by Alihajimohammad and Saadati [15]. Additionally, they defined the concept of generalized fuzzy fractal spaces. Alaca et al. [16] used the idea of intuitionistic FS and defined the concept of IFMSs. Secelean [17] investigated the IFS composed of generalized contractions and several fixed point (FP) theorems from the classical HB theory of IFS involving the Banach contraction principle. Barnsley and Vince [18] established that a projective IFS has at most one attractor. García, [19] introduced a novel method to approximate the attractor set of a countable IFS with an arbitrarily barely noticeable and controlled error. Schweizer and Sklar [20] introduced the concept of statistical MSs. Rahmat and Noorani [21] generalized the notion of the product of probabilistic MSs and extended it to the family of FMS.

The concept of neutrosophic sets (NSs) was first presented by Smarandache [22]. Das et al. [23] discussed a multi-criteria group decision-making model via NSs, and Das et al. [24] worked on certain algebraic operations and neutrosophic matric spaces (NMSs). The notion of NMS and their topological structure was investigated by Kirisci and Simsek [25]. The notion of neutrosophic bitopological spaces (NbTSs) was proposed by Das and Tripathy [26] while pursuing pairwise neutrosophic-b-open sets. The pairwise neutrosophic b-continuous function in NbTSs was established by Tripathy and Das [27]. The concept of neutrosophic multiset topological space was proposed by Das and Tripathy [28]. Multivalued fractals’ numerical aspects were discussed by Fiser [29]. Using an iterated multifunction system that includes a finite number of neutrosophic B-contractions and neutrosophic Edelstein contractions, Saleem et al. [30] established the idea of multivalued fractals in NMSs. The HB operator on the product FMS and fuzzy B-contraction was presented by Uthayakumar and Gowrisankar [31]. See for more related results [32,33].

Bounemeur et al. [34] discussed the fuzzy fault-tolerant control using fuzzy systems for a class of uncertain SISO systems with unknown control gain sign and actuator faults. Bounemeur and Chemachema [35] presented an adaptive fuzzy fault-tolerant tracking control for a class of unknown multi-variable nonlinear systems, with external disturbances, unknown control signs, and actuator faults. Bey and Chemachema [36] introduce a decentralized event-triggered fault-tolerant echo-state network (ESN) direct adaptive controller for uncertain interconnected nonlinear systems in pure-feedback form. Bounemeur and Chemachema [37] present a finite-time fault-tolerant fuzzy adaptive controller for uncertain interconnected nonlinear systems in strict-feedback form.

Barnsley [38] introduced how fractal geometry can be used to model real objects in the physical world. Sagan [39] discussed Peano’s Space-Filling Curve. Mora, and Cherruault [40] introduced the $\alpha$-dense curve and also discussed the $r$-stochastically independent functions.

In this study, we use an iterated function and present the classical HB theory on the product neutrosophic fractal space, which is enclosed by neutrosophic Edelstein contractions and a finite number of neutrosophic b-contractions. Further, we provide a sequence of sets that, under appropriate conditions and in terms of the Hausdorff NMS, converge to the attractor set of specific neutrosophic IFS. Moreover, we present a fuzzy variant of α-dense curves that can accurately approximate the attractor set of certain iterated function systems with barely noticeable and controlled errors. In addition, we make a connection between the above-discussed concepts of neutrosophic theory and α-density theory.

This manuscript is organized as follows. In Section 2, we present some definitions of Hausdorff metric spaces and their completeness, IFS, HP operator, CTN, CTCN, intuitionistic fuzzy metric space, intuitionistic IFS, product fuzzy metric spaces, and neutrosophic metric spaces. In Section 3, we discuss fuzzy comparison functions, $\alpha$ dense curves, and densifiable sets. In Section 4, we use densifiable techniques and approximate the neutrosophic fractals. In Section 5, we extend this notion to a finite number of NMS having neutrosophic B-contraction and neutrosophic Edelstein contraction as the neutrosophic IFS.

2. Preliminaries

In this section, we present some definitions and results from the existing literature that help to understand the main results.

Definition 1 

([18]). The Hausdorff metric $H_d :k\left(\Omega \right)\times k\left(\Omega \right)\to [0,+\infty )$ is defined by

$$H_d\left(A,B\right)=\mathit{max}\{\underset{\omega \in A}{\mathit{sup}}\underset{\varpi \in B}{\mathit{inf}}d\left(\omega ,\varpi \right),\underset{\omega \in B}{\mathit{sup}}\underset{\varpi \in A}{\mathit{inf}}d\left(\omega ,\varpi \right)\}$$

for each  $A, B\in k\left(\Omega \right).$

It is generally known that $\left(k\right(\Omega ), H_d)$ is a complete MS (for instance, see [6]). A mapping ${\rm Y}:(\Omega , d)\to (\Omega , d)$ is said to be an  $r$-contraction, if for some $0<r<1$ satisfies

$$d\left({\rm Y}\left(\omega \right), {\rm Y}\left(\varpi \right)\right)\le rd\left(\omega , \varpi \right)$$

for all  $\omega , \varpi \in \Omega$.

Definition 2 

([17]). Suppose ${{\rm Y}}_i :\Omega \to \Omega$ is an  $r_i$-contraction for some  $r_i\in \left(\mathrm{0,1}\right)$, where  $1\le i\le n.$ Then,  $F:=\{\Omega ; {{\rm Y}}_1, \cdots , {{\rm Y}}_n\}$is said to be an IFS.

Definition 3 

([14]). Suppose $F:=\left\{\Omega ;{{\rm Y}}_1, \cdots , {{\rm Y}}_n\right\},$ is an IFS. A map (set-valued)  $F:k\left(\Omega \right)\to k\left(\Omega \right)$ given as

$$F\left(K\right)=\bigcup _{i=1}^n{{\rm Y}}_i\left(K\right) \forall K\in k\left(\Omega \right),$$

is called an HB operator.

Theorem 1 

([17]). Let $F$ be an HB operator and  $F :=\left\{\Omega ; {{\rm Y}}_1, \cdots , {{\rm Y}}_n\right\},$ be an IFS. Then, for  $r:=max\{r_i:i=1, \cdots , n\},$  $F$ is an  $r$-contraction, its (unique) FP,  $A$ is called a fractal (or attractor set) of the IFS  $F$ and

$$\underset{k}{\lim }{F}^k\left(B\right)=A,$$

for  $B\in k\left(\Omega \right),$ Furthermore, for each  $B \in k\left(\Omega \right),$ we can write

$$H_d\left(A,B\right)\le {\displaystyle \frac{H_d\left(B,F\left(B\right)\right)}{1-r}}.$$

Definition 4 

([9]). A binary operation $\ast :I^2\to I \left(I=\left[\mathrm{0,1}\right]\right)$ is said to be a continuous t-norm (CTN) if it fulfills the below axioms:

(i) 

$a\ast b=b\ast a;$

(i) 

$a\ast \left(b\ast c\right)=\left(a\ast b\right)\ast c;$

(iii) 

$\ast$ is continuous;

(iv) 

$a\ast 1=a \forall a\in I;$

(v) 

$a\ast b\le c\ast d whenever a\le c and b\le d \forall a,b,c,d\in I.$

Definition 5 

([9]). A binary operation $\odot : I^2 \to I$ is said to be a continuous t-conorm (CTCN) if it satisfies properties (i), (ii), (iii), and (v) with respect to  $\odot$ instead of  $\ast$ and (vi)  $a\odot 0=a for all a\in I$ instead of (iv) in the above definition.

Definition 6 

([21]). A 5-tuple $(\Omega , \Psi , \Phi , \ast , \odot )$is said to be an IFMS if  $\ast$ is a CTN,  $\odot$ is a CTCN, and  $\Psi , \Phi$ are FSs on  ${\Omega }^2\times (0,+\infty )$ verifying the below assertions:

(i) 

$\Psi \left(\omega , \varpi , m\right)>0, \Phi \left(\omega , \varpi , m\right)<1, and 0\le \Psi \left(\omega , \varpi , m\right)+\Phi \left(\omega , \varpi , m\right)\le 1;$

(ii) 

$\Psi \left(\omega , \varpi , m\right)=1 if and only if \omega =\varpi ;$

(iii) 

$\Phi \left(\omega , \varpi , m\right)=0 if and only if \omega =\varpi ;$

(iv) 

$\Psi \left(\omega , \varpi , m\right)=\Psi \left(\varpi , \omega , m\right) and \Phi \left(\omega , \varpi , m\right)=\Phi \left(\varpi , \omega , m\right);$

(v) 

$\Psi \left(\omega , \varpi , m\right)\ast \Psi \left(\varpi , z, s\right)\le \Psi \left(\omega , z, m+s\right);$

(vi) 

$\Phi \left(\omega , \varpi , m\right)\odot \Phi \left(\varpi , z, s\right)\ge \Phi \left(\omega , z, m+s\right);$

(vi) 

$\Psi (\omega , \varpi , ·), \Phi (\omega , \varpi , ·):(0,+\infty )\to (0, 1]$ are continuous;

for  $s, m>0$ and for each  $\omega , \varpi , z\in \Omega$. Then the pair  $(\Psi , \Phi )$ is said to be an IFM on  $\Omega$.

Definition 7 

([14]). For each$A, B\in k_0\left(\Omega \right)$ and  $m>0,$ let

$$\begin{gathered} \Psi \left(A,B,m\right)=\underset{\omega \in A}{\inf }\underset{\varpi \in B}{\sup }\Psi \left(\omega ,\varpi ,m\right), \\ \Phi \left(A,B,m\right)=\underset{\omega \in A}{\sup }\underset{\varpi \in B}{\inf }\Phi \left(\omega ,\varpi ,m\right). \end{gathered}$$

Then, the Hausdorff IFM  $(H_{\Psi }, H_{\Phi })$ is defined as

$$H_{\Psi }\left(A, B, m\right)≔\min \left\{\Psi \left(A, B, m\right), \Psi \left(B, A, m\right)\right\},$$

and

$$H_{\Phi }\left(A, B, m\right):=\max \left\{\Phi \left(A, B, m\right), \Phi \left(B, A, m\right)\right\}.$$

Clearly,  $(H_{\Psi }, H_{\Phi })$ is an IFM on  $k_0\left(\Omega \right)$ and hence  $\left(k_0\right(\Omega ), H_{\Psi }, H_{\Phi }, \ast , \odot )$ is an IFMS, called the Hausdorff IFMS.

Proposition 1 

([33]). The following axioms are equivalent:

(i) 

$(\Omega , d)$ is complete;

(ii) 

The standard IFMS induced by $d, (\Omega , {\Psi }_d, {\Phi }_d, \ast , \odot ),$ is complete;

(iii) 

The IFMS $\left(k_0\right(\Omega ), H_{\Psi }d , H_{\Phi }d , \ast , \odot )$is complete.

Proposition 2. 

([33]). The Hausdorff IFM $(H_{{\Psi }_d}, H_{{\Phi }_d})$ of the standard IFM  $({\Psi }_d, {\Phi }_d)$ coincides with the standard IFM  $({\Psi }_{H_d} , {\Phi }_{H_d})$ of the Hausdorff metric on  $k_0\left(\Omega \right),$ we write

$$\begin{gathered} H_{{\Psi }_d}\left(A,B,m\right)={\Psi }_{H_d}\left(A,B,m\right)={\displaystyle \frac{m}{m+H_d(A,B)}}, \\ {H}_{{\Phi }_d}\left(A,B,m\right)={\Phi }_{H_d}\left(A,B,m\right)={\displaystyle \frac{H_d(A,B)}{m+H_d(A,B)}}, \end{gathered}$$

for every  $A, B \in k_0\left(\Omega \right)$ and  $m>0$.

In the next definitions, we study the notions of IFS in IFMSs.

Definition 8 

([14]). Given ${\rm Y}:\Omega \to \Omega . {\rm Y}$ is said to be an intuitionistic fuzzy  $r$-contraction (IF$r$C) in  $(\Omega , \Psi , \Phi , \ast , \odot )$ for  $r\in \left(\mathrm{0,1}\right)$, if

$$\begin{gathered} {\displaystyle \frac{1}{\Psi ({\rm Y}\left(\omega \right),{\rm Y}\left(\varpi \right),m)}}-1\le r\left({\displaystyle \frac{1}{\Psi \left(\omega ,\varpi ,m\right)}}-1\right), \\ {\displaystyle \frac{1}{\Phi ({\rm Y}\left(\omega \right),{\rm Y}\left(\varpi \right),m)}}-1\ge {\displaystyle \frac{1}{r}}\left({\displaystyle \frac{1}{\Phi \left(\omega ,\varpi ,m\right)}}-1\right), \end{gathered}$$

for each  $\omega , \varpi \in \Omega$ and  $m>0$. If  ${{\rm Y}}_i :\Omega \to \Omega$, for  $1\le i\le n,$ is an IF$r_i$C, for some  $r_i\in \left(\mathrm{0,1}\right)$, then  $F:=\left\{\Omega ;{{\rm Y}}_1, \cdots , {{\rm Y}}_n\right\},$ is said to be an intuitionistic fuzzy IFS (IF-IFS) in the context of  $\left(\Omega , \Psi , \Phi , \ast , \odot \right).$

Proposition 3. 

An  $F:=\left\{\Omega ;{{\rm Y}}_1, \cdots , {{\rm Y}}_n\right\},$ is said to be an IFS if and only if  $F$ is an IF-IFS in the context of  $(\Omega , {\Psi }_d, {\Phi }_d, \ast , \odot ).$

The HB operator in the setting of the Hausdorff IFMS $\left(k_0\right(\Omega ), H_{\Psi }, H_{\Phi }, \ast , \odot )$ is defined in [14] as follows:

Definition 9 

([14]). Suppose $F:=\left\{\Omega ;{{\rm Y}}_1, \cdots , {{\rm Y}}_n\right\},$ is an IF-IFS in the context of  $\left(\Omega , \Psi , \Phi , \ast , \odot \right).$ Then, the intuitionistic fuzzy HB operator (IF-HB operator), is a map (set-valued)  $F:k_0\left(\Omega \right)\to k_0\left(\Omega \right)$ defined by

$$F\left(k\right)=\bigcup _{i=1}^n{{\rm Y}}_i\left(k\right) \forall k\in k_0\left(\Omega \right).$$

Definition 10 

([21]). Let $\left({\Omega }_1,A_1,\ast \right)$ and  $\left({\Omega }_2,A_2,\ast \right)$ be two FMSs and  $\mathcal{X}={\Omega }_1\times {\Omega }_2.$ For

$$a=\left(a_1,a_2\right), b=\left(b_1,b_2\right)\in \mathcal{X},$$

and  $m>0,$ we write

$$A_{\mathcal{X}}\left(a,b,m\right)=A_1\left(a_1,b_1,m\right)\ast A_2\left(a_2,b_2,m\right).$$

Then,  $\left(A_{\mathcal{X}},\ast \right)$ is a fuzzy metric on  $\mathcal{X}$ and the triple  $\left(\mathcal{X},A_{\mathcal{X}},\ast \right)$ is called the product FMS of  ${\Omega }_1$ and  ${\Omega }_2$.

Definition 11 

([29]). Let $\left(\mathcal{X},d^{\prime }\right)$ be a product space. Define  $a\ast b=a.b$ and suppose  $A_{{\mathcal{X}}_{d^{\prime }}}$ be the function on  $\mathcal{X}\times \mathcal{X}\times \left(0,\infty \right)$ given by

$$A_{{\mathcal{X}}_{d^{\prime }}}={\displaystyle \frac{m}{m+d^{\prime }\left(a,b\right)}} \forall a,b\in \mathcal{X} \mathrm{a}\mathrm{n}\mathrm{d} m>0.$$

Then,  $\left(\mathcal{X},A_{\mathcal{X}},\ast \right)$ is an FMS said to be a standard product FMS and  $A_{{\mathcal{X}}_{d^{\prime }}}$ be the standard product fuzzy metric induced by the metric  $d^{\prime }$.

Definition 12 

([29]). Let $\left(\Omega , A, \ast \right)$ be a FMS. Let  $\phi$ be a fuzzy B-contraction on  $\Omega$ and  $\left(\mathcal{X},A_{\mathcal{X}},\ast \right)$ be a product FMS of  $\Omega$ and  ${\psi }_n:\mathcal{X}\to \mathcal{X},n=\mathrm{1,2},\cdots ,\Phi \left(\Phi \in \mathbb{N}\right),$ be N-fuzzy B-contraction mappings defined by

$${\psi }_n\left(a,b\right)=\left({\phi }_n\left(a\right),{\phi }_n\left(b\right)\right).$$

Then, the system  $\left\{\mathcal{X};{\psi }_n, n=\mathrm{1,2},\cdots ,\Phi ;\Phi \in \mathbb{N}\right\},$ is said to be a fuzzy IFS of fuzzy B-contraction on the product FMS  $\left(\mathcal{X},A_{\mathcal{X}},\ast \right).$

Definition 13 

([29]). Let $\left(\mathcal{X},A_{\mathcal{X}},\ast \right)$ be a product FMS. Let  $\left\{\mathcal{X};{\psi }_n, n=\mathrm{1,2},\cdots ,\Phi ;\Phi \in \mathbb{N}\right\},$ be a fuzzy IFS of fuzzy B-contraction on  $\left(\mathcal{X},A_{\mathcal{X}},\ast \right).$ Let  $\left\{\mathcal{X};{\psi }_n, n=\mathrm{1,2},\cdots ,\Phi ;\Phi \in \mathbb{N}\right\},$ be a fuzzy IFS of fuzzy B-contraction on  $\left(\mathcal{X},A_{\mathcal{X}},\ast \right).$ Let  $\varrho \left(\mathcal{X}\right)$ be the set of all non-empty compact subsets of  $\mathcal{X}.$ Then, the fuzzy HB operator of the fuzzy IFS of fuzzy B-contraction on  $\left(\mathcal{X},A_{\mathcal{X}},\ast \right)$ is a function  ${\Phi }^{\prime }:\varrho \left(\mathcal{X}\right)\to \varrho \left(\mathcal{X}\right),$ defined by

$${\mathsf{\Phi }}^{\prime }\left(A_1\right)=\bigcup _{n=1}^{\Phi }{\psi }_n\left(A_1\right) \forall A_1\in \varrho \left(\mathcal{X}\right).$$

That is,

$${\mathsf{\Phi }}^{\prime }\left(A_1\right)=\bigcup _{n=1}^{\Phi }\left({\phi }_n\left(a\right),{\phi }_n\left(b\right)\right)\forall \omega =\left(a,b\right)\in A_1\in \varrho \left(\mathcal{X}\right).$$

Definition 14 

([29]). Let $\left(\mathcal{X},A_{\mathcal{X}},\ast \right)$be a complete FMS. Let  $\left\{\mathcal{X};{\psi }_n, n=\mathrm{1,2},\cdots ,\Phi ;\Phi \in \mathbb{N}\right\},$ be a fuzzy IFS of fuzzy B-contraction on  $\left(\mathcal{X},A_{\mathcal{X}},\ast \right)$ and  ${\Phi }^{\prime }$ be the fuzzy HB operator of the fuzzy IFS of fuzzy B-contraction on  $\left(\mathcal{X},A_{\mathcal{X}},\ast \right).$ The set  $A_{\infty }\in \varrho \left(\mathcal{X}\right),$ is the product fuzzy attractor (product fuzzy fractal) of the given fuzzy IFS of fuzzy B-contractions; if is a unique FP of the fuzzy HB operator  ${\Phi }^{\prime }.$ $A_{\infty }$ is also called as product fuzzy fractal generated by the fuzzy IFS of fuzzy B-contraction.

Definition 15 

([25]). A 6-tuple $(\Omega , \Psi , \Phi ,O, \ast , \odot )$is said to be an NMS, if  $\ast$ is a CTN,  $\odot$ is a CTCN and  $\Psi , \Phi$ and  $O$ are NSs defined on  ${\Omega }^2\times (0,+\infty )$ satisfying the following conditions:

(i) 

$\Psi \left(\omega , \varpi , m\right)+\Phi \left(\omega , \varpi , m\right)+O\left(\omega , \varpi , m\right)\le 3;$

(ii) 

$\Psi \left(\omega , \varpi , m\right)>0.$

(iii) 

$\Psi \left(\omega , \varpi , m\right)=1 \mathrm{i}\mathrm{f} \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{o}\mathrm{n}\mathrm{l}\mathrm{y} \mathrm{i}\mathrm{f} \omega =\varpi ;$

(iv) 

$\Psi \left(\omega , \varpi , m\right)=\Psi \left(\varpi , \omega , m\right);$

(v) 

$\Psi \left(\omega , \varpi , m\right)\ast \Psi \left(\varpi , z, s\right)\le \Psi \left(\omega , z, m+s\right);$

(vi) 

$\Psi (\omega , \varpi , ·) : (0,+\infty ) \to (0, 1]$ is continuous;

(vii) 

$\Phi \left(\omega , \varpi , m\right)<1;$

(viii) 

$\Phi \left(\omega , \varpi , m\right)=0 if and only if \omega =\varpi ;$

(iv) 

$\Phi \left(\omega , \varpi , m\right)=\Phi \left(\varpi , \omega , m\right);$

(x) 

$\Phi \left(\omega , \varpi , m\right)\odot \Phi \left(\varpi , z, s\right)\ge \Phi \left(\omega , z, m+s\right);$

(xi) 

$\Phi (\omega , \varpi , ·) : (0,+\infty )\to (0, 1]$ is continuous;

(xii) 

$O\left(\omega , \varpi , m\right)<1;$

(xiii) 

$O\left(\omega , \varpi , m\right)=0 if and only if \omega =\varpi ;$

(xiv) 

$O\left(\omega , \varpi , m\right)=O\left(\varpi , \omega , m\right);$

(xv) 

$O\left(\omega , \varpi , m\right)\odot \Phi \left(\varpi , z, s\right)\ge O\left(\omega , z, m+s\right);$

(xvi) 

$O(\omega , \varpi , ·) :(0,+\infty ) \to (0, 1]$ is continuous;

for each  $\omega , \varpi , z\in \Omega$ and  $s, m>0.$ The three tuple  $(\Psi , \Phi ,O)$ is said to be a neutrosophic metric on  $\Omega$.

Definition 16 

([25]). Assume $\left(\Omega ,{\Psi }_d,{\Phi }_d,O_d,\ast , \odot \right)$ is a standard NMS and if there is  $r\in \left(\mathrm{0,1}\right), m>0$ and  $a\in \Omega .$ The family

$$\overline{B_r}\left(a,m\right)=\left\{b\in \Omega :\Psi \left(a,b,m\right)>1-r, \Phi \left(a,b,m\right)<r, O\left(a,b,m\right)<r\right\},$$

is entitled as the open ball having center  $a$ and radius  $r$ with respect to  $m.$

Definition 17 

([25]). Assume that $(\Omega ,\Psi ,\Phi ,O,\ast , \odot )$ is an NMS and  ${\tau }_{\left(\Psi ,\Phi ,O\right)}$ is the topology on  $\Omega$ produced by the neutrosophic metric  $\left(\Psi ,\Phi ,O\right)$ on  $\Omega$. Then

(1) 

A sequence $\left\{{\omega }_n\right\},$ converges to  $\omega \in \Omega ,$ if  $\Psi \left({\omega }_n,\Omega ,m\right)\to 1, \Phi \left({\omega }_n,\Omega ,m\right)\to 0,$ and  $O\left({\omega }_n,\Omega ,m\right)\to 0,$ as  $n\to \infty .$

(2) 

A sequence $\left\{{\omega }_n\right\}$ is known as a Cauchy sequence if for each  $\epsilon >0$ and each  $m>0,$ there exists  $\Phi \in \mathbb{N}$ such that  $\Psi \left( {\omega }_{n_1},{\omega }_{n_2},m\right)>1-\epsilon , \Phi \left( {\omega }_{n_1},{\omega }_{n_2},m\right)<\epsilon ,$ and  $O\left( {\omega }_{n_1},{\omega }_{n_2},m\right)<\epsilon ,$ for all  ${\omega }_{n_1},{\omega }_{n_2}\ge \Phi .$

(3) 

If every Cauchy sequence is convergent in  $(\Omega ,\Psi ,\Phi ,O,\ast , \odot )$ with respect to  ${\tau }_{\left(\Psi ,\Phi ,O\right)}.$ Then, it is known as complete NMS.

(4) 

$(\Omega ,\Psi ,\Phi ,O,\ast , \odot )$ is said to be compact if every sequence has a convergent subsequence.

Definition 18 

([30]). For each $A, B\in k_0\left(\Omega \right)$ and  $m>0,$ let

$$\begin{gathered} \Psi \left(A,B,m\right)=\underset{\omega \in A}{\inf }\underset{\varpi \in B}{\sup }\Psi \left(\omega ,\varpi ,m\right), \\ \Phi \left(A,B,m\right)=\underset{\omega \in A}{\sup }\underset{\varpi \in B}{\inf }\Phi \left(\omega ,\varpi ,m\right), \\ O\left(A,B,m\right)=\underset{\omega \in A}{\sup }\underset{\varpi \in B}{\inf }\Phi \left(\omega ,\varpi ,m\right). \end{gathered}$$

Then, the Hausdorff NM  $(H_{\Psi }, H_{\Phi }, H_O)$ is defined as

$$\begin{gathered} H_{\Psi }\left(A, B, m\right)≔\min \left\{\Psi \left(A, B, m\right), \Psi \left(B, A, m\right)\right\}, \\ {H}_{\Phi }\left(A, B, m\right):=\max \left\{\Phi \left(A, B, m\right), \Phi \left(B, A, m\right)\right\}, \end{gathered}$$

and

$$H_O\left(A, B, m\right):=\max \left\{O\left(A, B, m\right), O\left(B, A, m\right)\right\}.$$

Clearly,  $(H_{\Psi }, H_{\Phi })$ is an NM on  $k_0\left(\Omega \right)$ and hence  $\left(k_0\right(\Omega ), H_{\Psi }, H_{\Phi }, H_O, \ast , \odot )$ is an NMS, called the Hausdorff NMS.

Theorem 2. 

Let  $(\Omega , d)$ be a complete MS,  $F:=\left\{\Omega ;{{\rm Y}}_1, \cdots , {{\rm Y}}_n\right\},$ a NIFS in  $(\Omega , {\Psi }_d, {\Phi }_d,O_d, \ast , \odot )$, and the neutrosophic HB operator. Then,  $F$ is a  $r$-contraction, with  $r:=\mathit{max}\{r_i:i=1, \cdots ,n\},$ its (unique) FP  $A$ is called the attractor of the NIFS  $F$ and

$$\underset{k}{\lim }{F}^k\left(B\right)=A,$$

for every  $B\in k\left(\Omega \right).$ Furthermore, for each  $B\in k_0\left(\Omega \right):$

$$\begin{gathered} H_{{\Psi }_d}\left(A, B, m\right)\ge H_{{\Psi }_d}\left(B, F\left(B\right), m\left(1-r\right)\right), \\ {H}_{{\Phi }_d}\left(A, B, m\right)\le H_{{\Phi }_d}\left(B, F\left(B\right), m\left(1-r\right)\right), \\ {H}_{O_d}\left(A, B, m\right)\le H_{O_d}\left(B, F\left(B\right), m\left(1-r\right)\right). \end{gathered}$$

Example 1. 

Let  $\Omega =\left[\mathrm{0,1}\right]$, CTN  $a\ast b=a\cdot b$ and CTCN  $a\odot b=\mathit{max}\left\{a,b\right\}.$ Define  ${\Psi }_d, {\Phi }_d,$ and  $O_d$ by

$$\begin{gathered} \left\{\begin{array}{c}{\Psi }_d\left(\omega , \varpi , m\right)=e^{-{\displaystyle \frac{\left(\omega +\varpi \right)}{m}}}, if \omega ,\varpi \in \Omega \backslash \left\{0\right\}\\ {\Psi }_d\left(\omega , 0, m\right)={\Psi }_d\left(0,\omega , m\right)=e^{-{\displaystyle \frac{\omega }{3m}}}, \omega \in \Omega ,\end{array}\right. \\ \left\{\begin{array}{c}{\Phi }_d\left(\omega , \varpi , m\right)=1-e^{-{\displaystyle \frac{{\left(\omega +\varpi \right)}^2}{m}}}, if \omega ,\varpi \in \Omega \backslash \left\{0\right\}\\ {\Phi }_d\left(\omega , 0, m\right)={\Phi }_d\left(0,\omega , m\right)=1-e^{-{\displaystyle \frac{\omega }{3m}}}, \omega \in \Omega ,\end{array}\right. \\ \left\{\begin{array}{c}{O}_d\left(\omega , \varpi , m\right)=1-e^{-{\displaystyle \frac{\left(\omega +\varpi \right)}{m}}}, if \omega ,\varpi \in \Omega \backslash \left\{0\right\}\\ O_d\left(\omega , 0, m\right)={\Phi }_d\left(0,\omega , m\right)=1-e^{-{\displaystyle \frac{{\omega }^2}{3m}}}, \omega \in \Omega .\end{array}\right. \end{gathered}$$

Then,  $\left(\Omega , {\Psi }_d, {\Phi }_d,O_d, \ast , \odot \right)$ is an NMS. Assume that  ${{\rm Y}}_1={\displaystyle \frac{\omega }{2}},$  ${{\rm Y}}_2={\displaystyle \frac{\omega +1}{2}},$ are self-mappings, and  $r={\displaystyle \frac{1}{2}},$ then the unique FP (attractor)

$$A=\bigcap _{k=1}^{\infty }{F}^k\left(B\right).$$

If  $B=\left[0, 1\right],$ so

$$F\left(B\right)={{\rm Y}}_1\left(B\right)\cup {{\rm Y}}_2\left(B\right)=\left[0,{\displaystyle \frac{1}{2}}\right]\cup \left[{\displaystyle \frac{1}{2}}, 1\right],$$

continue this process the  $F^k\left(B\right)$ converges to an attractor  $A=\left\{\mathrm{0,1}\right\}.$ This shows that NIFS  $F$ fulfills all the conditions of Theorem 2.

3. α-Dense Curves and Densifiable Sets

In this part, we introduce and discuss some definitions and results from the existing literature.

Definition 19 

([33]). A function $\phi$ (continuous) is said to be a fuzzy comparison function (FCF), if  $\phi :(0,+\infty )\times [0,+\infty )\to I$ satisfies the below assertions for each  $m>0:$

(i) 

$\phi (m, ·)$ is decreasing;

(ii) 

$\phi (m, \alpha )=1\iff \alpha =0;$

(iii) 

$\underset{\alpha \to +\infty }{\mathit{lim}}\phi (m,\alpha )=0.$

Definition 20 

([33]). Let $(\Omega , \Psi , \ast )$ be an FMS,  $B\subseteq \Omega \ne \varphi ,\alpha \ge 0$ and  $\phi$ a FCF. A map (continuous)  $\gamma :I\to \Omega$ is called a fuzzy  $\alpha$-dense curve in  $B$ with respect to the FCF  $\phi ,$ if it verifies the below assertions:

(i) 

$\gamma \left(I\right)\subset B;$

(ii) 

for each  $\omega \in B$ there is  $\varpi \in \gamma \left(I\right)$ such that  $\Psi \left(\omega , \varpi , m\right)\ge \phi \left(m, \alpha \right)$ for every  $m>0.$

Proposition 4 

([33]). Let $(\Omega , {\Psi }_d, \ast )$ be a standard FMS induced by  $d, B\subseteq \Omega \ne \varphi ,$ bounded. Suppose  $\gamma :I\to \Omega$ is a curve that is  $\alpha$-dense in  $B$ for some  $\alpha >0.$ Then,  $\gamma$ is a fuzzy curve that is  $\alpha$-dense in  $B$ with respect to the  $\phi (m, \alpha ):=m/(m+\alpha ).$ Therefore,  $B$ is fuzzy densifiable with respect to the  $\phi ,$ if it is densifiable.

Definition 21 

([40]). Set $\alpha \ge 0, B\subseteq \Omega \ne \varphi ,$ and bounded. A map (continuous)  $\gamma :I\to (\Omega , d)$ is called a curve that is  $\alpha$-dense in  $B$, if verifies the below assertions:

(i) 

$\gamma \left(I\right)\subset B;$

(ii) 

for any  $\omega \in B,$ there is  $\varpi \in \gamma \left(I\right)$ such that  $d\left(\omega , \varpi \right)\le \alpha .$

The  $B$ is called densifiable if there is a curve that is  $\alpha$-dense in  $B$ for each  $\alpha >0.$

Noticeably, given a bounded  $B\subseteq \Omega \ne \varphi ,$ always, we get a curve that is  $\alpha$-dense in  $B$ for some  $\alpha \ge diameter\left(B\right)\left(Diam\left(B\right)\right).$ Therefore, for fixed  ${\omega }_0\in B, \gamma \left(\tau \right):={\omega }_0\forall \tau \in I,$ is a curve that is an  $\alpha$-dense in  $B$ when  $\alpha \ge Diam\left(B\right).$

Example 2. 

A mapping  ${\gamma }_m:I\to {\mathbb{R}}^d$ for each positive integer  $m$ and  $d>0$ given by

$$\gamma \left(\tau \right)=\left(\tau ,{\displaystyle \frac{1}{2}}\left(1-\cos \left(m\pi \tau \right)\right) , \cdots ,{\displaystyle \frac{1}{2}}\left(1-\cos \left(m^{d-1}\pi \tau \right)\right)\right)$$

for all  $\tau \in I,$ is a  ${\displaystyle \frac{\sqrt{d-1}}{m}}$ dense curve in  $I^d,$ called the cosine curve.

Proposition 5 

([26]). Under the above conditions, we have

$$H_d\left(A,B_k\right)\le r^k\left({\displaystyle \frac{\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{m}\left(\Omega \right)}{1-r^k}}+{\alpha }_k\right) \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} k\ge n.$$

Since, in the context of standard IFMS $\left(\Omega , {\Psi }_d, {\Phi }_d, \ast ,\odot \right),$  $F$ is an IF-IFS formed by $d$ by Proposition 3, the following conclusion is obtained when we examine an IF-HB operator $F$ and its FP $A$ (i.e., the intuitionistic fuzzy fractal of $F$).

Proposition 6. 

The Hausdorff neutrosophic metric $(H_{{\Psi }_d}, H_{{\Phi }_d}, H_{O_d})$ of the standard neutrosophic metric  $({\Psi }_d, {\Phi }_d, O_d)$ coincides with the standard neutrosophic metric  $({\Psi }_{H_d}, {\Phi }_{H_d}, O_{H_d})$ of the Hausdorff metric on  $k_0\left(\Omega \right),$ we have

$$\begin{gathered} H_{{\Psi }_d}\left(A,B,m\right)={\Psi }_{H_d}\left(A,B,m\right)={\displaystyle \frac{m}{m+H_d(A,B)}}, \\ {H}_{{\Phi }_d}\left(A,B,m\right)={\Phi }_{H_d}\left(A,B,m\right)={\displaystyle \frac{H_d(A,B)}{m+H_d(A,B)}}, \\ {H}_{O_d}\left(A,B,m\right)=O_{H_d}\left(A,B,m\right)={\displaystyle \frac{H_d(A,B)}{m}}, \end{gathered}$$

for every  $A, B\in k_0\left(\Omega \right)$ and  $m>0$.

The below results establish important bounds on the relationships between a sequence of sets$B_k$ and a fixed set $A$ within a densifiable metric space $(\Omega ,d).$ These bounds are expressed in terms of specific Hausdorff-type measures $H_{{\Psi }_d}, H_{{\Phi }_d}$ and $H_{O_d}$ which are fundamental in analyzing the geometric and topological properties of sets in a metric space.

Theorem 3. 

Let $(\Omega , d)$be densifiable and suppose  ${\left(B_k\right)}_{k\ge 1}\subset \Omega ,$ is a sequence given in Proposition (5). Then,  $\forall m>0,$ the inequalities

$$H_{{\Psi }_d}\left(A,B_k,m\right)\ge {\displaystyle \frac{m\left(1-r^k\right)}{m\left(1-r^k\right)+{\rho }_k}},$$

(1)

$$H_{{\Phi }_d}\left(A,B_k,m\right)\le {\displaystyle \frac{{\rho }_k}{{\rho }_k+m\left(1-r^k\right)}},$$

(2)

$$H_{O_d}\left(A,B_k,m\right)\le {\displaystyle \frac{m\left(1-r^k\right)}{{\rho }_k}},$$

(3)

hold for every  $k\ge n,$ where  ${\rho }_k:=r^k \left(Diam\right(\Omega )+\left(1-r^k\right){\alpha }_k).$

Proof. 

Fixed $k\ge n,$ by Proposition 5, we have

$$H_d\left(A,B_k\right)\le r^k\left({\displaystyle \frac{\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{m}\left(\Omega \right)}{1-r^k}}+{\alpha }_k\right) \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} k\ge n.$$

(4)

Next, given $m>0,$ by Proposition 6 and noticing (4) we have

$$\begin{gathered} H_{{\Psi }_d} \left(A, Bk, m\right)={\Psi }_{H_d} \left(A, Bk, m\right)={\displaystyle \frac{m}{m+H_d\left(A,B_k\right)}} \\ \ge {\displaystyle \frac{m\left(1-r^k\right)}{m\left(1-r^k\right)+\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{m}\left(\Omega \right)+{\left(1-r^k\right)}_{{\alpha }_k}\right)}}={\displaystyle \frac{m(1-r^k)}{m\left(1-r^k\right)+{\rho }_k}}, \end{gathered}$$

and, as

$$\begin{gathered} H_{{\Phi }_d}\left(A, B_k, m\right)={\Phi }_{H_d}\left(A, B_k, m\right)={\displaystyle \frac{H_d\left(A,B_k\right)}{m+H_d\left(A,B_k\right)}} \\ \le {\displaystyle \frac{\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{m}\left(\Omega \right)+{\left(1-r^k\right)}_{{\alpha }_k}\right)}{m\left(1-r^k\right)+\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{m}\left(\Omega \right)+{\left(1-r^k\right)}_{{\alpha }_k}\right)}}={\displaystyle \frac{{\rho }_k}{m\left(1-r^k\right)+{\rho }_k}}, \end{gathered}$$

and given $m>0,$ by Proposition 6 and noticing (4), we have

$$\begin{gathered} H_{O_d}\left(A, B_k, m\right)=O_{H_d}\left(A, B_k, m\right)={\displaystyle \frac{H_d\left(A,B_k\right)}{m}} \\ \le {\displaystyle \frac{\left(\mathrm{D}\mathrm{i}\mathrm{a}\mathrm{m}\left(\Omega \right)+{\left(1-r^k\right)}_{{\alpha }_k}\right)}{m\left(1-r^k\right)}}={\displaystyle \frac{{\rho }_k}{m\left(1-r^k\right)}}, \end{gathered}$$

and the result follows.

We obtain a sequence from the preceding result for the approximation (small and controlled error) of the neutrosophic fractal of $F$ as we can say that the degree of membership function between $A$ and $B_k, H_{{\Psi }_d} (A, B_k, m),$rises with $k$ even though the degree of non-membership function $H_{{\Phi }_d}(A, B_k, m)$ falls and $H_{O_d}(A, B_k, m)$ degree of neutral function for each $m>0.$ Correctly:

$$\underset{k}{\mathrm{l}\mathrm{i}\mathrm{m}} H_{{\Psi }_d} \left(A, B_k, m\right)=1,$$

(5)

$$\underset{k}{\mathrm{l}\mathrm{i}\mathrm{m}} H_{{\Phi }_d} \left(A, B_k, m\right)=0,$$

(6)

$$\underset{k}{\mathrm{l}\mathrm{i}\mathrm{m}} H_{O_d} \left(A, B_k, m\right)=0,$$

(7)

for all $m>0.$ Furthermore, each $B_k$ be a set that is finite, and consequently, by utilizing the appropriate software it can be drawable. □

Example 3. 

Let  $\Omega =\left[\mathrm{0,2}\right],$ and CTN  $a\ast b=a\cdot b,$ CTCN is  $a\odot b=\mathit{max}\left\{a,b\right\},$

$$\begin{gathered} {\Psi }_d\left(\omega , \varpi , m\right)={\displaystyle \frac{m}{m+d\left(\omega , \varpi \right)}}, \\ {\Phi }_d\left(\omega , \varpi , m\right)={\displaystyle \frac{d(\omega ,\varpi )}{m+d(\omega , \varpi )}}, \\ {O}_d\left(\omega , \varpi , m\right)={\displaystyle \frac{d(\omega ,\varpi )}{m}}, \end{gathered}$$

Then,  $\left(\Omega , {\Psi }_d, {\Phi }_d,O_d, \ast , \odot \right)$ is an NMS, where  $d\left(\omega ,\varpi \right)=\left|\omega -\varpi \right|$. Assume that NIFS  $\left\{I^2; {{\rm Y}}_1, {{\rm Y}}_2, {{\rm Y}}_3\right\},$ has the attractor set that is sierpinsky triangle  $T$ as shown in Figure 1, where

$${{\rm Y}}_1\left(\omega ,\varpi \right)=\left({\displaystyle \frac{\omega }{2}}, {\displaystyle \frac{\varpi }{2}}\right), {{\rm Y}}_2\left(\omega ,\varpi \right)=\left({\displaystyle \frac{\omega }{2}}+{\displaystyle \frac{1}{2}}, {\displaystyle \frac{\varpi }{2}}\right), {{\rm Y}}_3\left(\omega ,\varpi \right)=\left({\displaystyle \frac{\omega }{2}}+{\displaystyle \frac{1}{4}}, {\displaystyle \frac{\varpi }{2}}+{\displaystyle \frac{1}{2}}\right),$$

For every  $\omega ,\varpi \in I.$ Then in Figure 2 we use the so-called chaos game (see [38]) for the approximation of ${\rm Y}.$ We start with  ${\omega }_1=\left(\mathrm{0,0}\right),$ and generate some points with a cosine curve (see [39]) and Proposition 5.

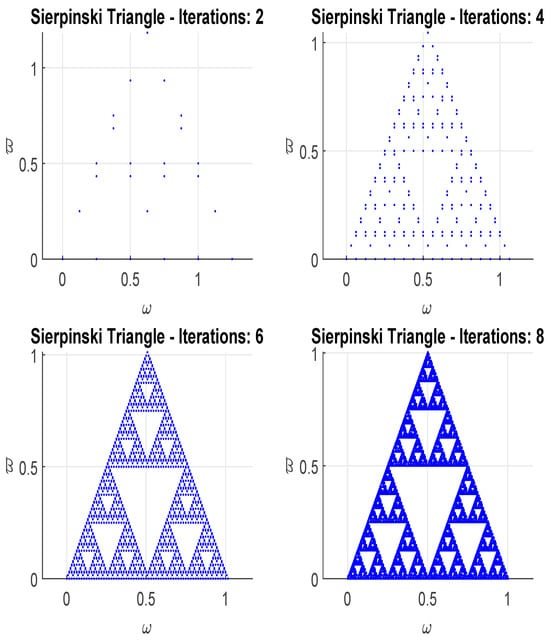
Figure 1. Shows the approximation of ${\rm Y}.$

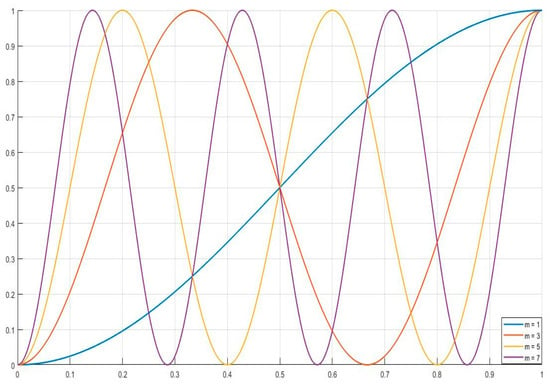
Figure 2. Shows the graphical behavior of dense curve for different values of $m.$

In this case $Diam \left(I^2\right)=\sqrt{2}, r={\displaystyle \frac{1}{2}},$ and ${\alpha }_k={\displaystyle \frac{1}{k}},$ for every $k\ge 1.$ Therefore, all the inequalities of Theorem 3 are held.

4. Approximating Neutrosophic Fractals by Densifiability Techniques

In this section, we discuss some results in NMSs and define the concept of neutrosophic $r$-contraction (N$r$C).

Definition 22. 

Given  ${\rm Y}:\Omega \to \Omega ,$ and  $r\in \left(\mathrm{0,1}\right), {\rm Y}$ is said to be an N$r$C in  $(\Omega , \Psi , \Phi ,O, \ast , \odot )$ if

$$\begin{gathered} {\displaystyle \frac{1}{\Psi ({\rm Y}\left(\omega \right),{\rm Y}\left(\varpi \right),m)}}-1\le r\left({\displaystyle \frac{1}{\Psi \left(\omega ,\varpi ,m\right)}}-1\right), \\ {\displaystyle \frac{1}{\Phi \left({\rm Y}\left(\omega \right),{\rm Y}\left(\varpi \right),m\right)}}-1\ge {\displaystyle \frac{1}{r}}\left({\displaystyle \frac{1}{\Phi \left(\omega ,\varpi ,m\right)}}-1\right), \\ O\left({\rm Y}\left(\omega \right),{\rm Y}\left(\varpi \right),m\right)\le rO\left(\omega ,\varpi ,m\right), \end{gathered}$$

for each  $\omega , \varpi \in \Omega$ and  $m>0.$ If  ${{\rm Y}}_i:\Omega \to \Omega ,$ for  $i=1, \cdots , n,$ is an N$r_i$C, for some  $r_i\in \left(\mathrm{0,1}\right),$ then  $F:=\left\{\Omega ;{{\rm Y}}_1, \cdots , {{\rm Y}}_n\right\},$ is said to be a neutrosophic IFS, shortly NIFS, in  $\left(\Omega , \Psi , \Phi ,O, \ast , \odot \right).$

For an IFS, the following lemma is provided in Lemma 2 of [9], however, it is also valid for a NIFS.

Lemma 1. 

For each  $k\ge n,$ we have

$$A=F^k\left(A\right)=\bigcup _{j_1,...,j_k}{{\rm Y}}_{j_1,\dots ,j_k}\left(A\right),$$

the union being performed over all possible  $j_1, \cdots , j_k\in {\Phi }_n:=\{1, 2, \cdots , n\}$ and  ${{\rm Y}}_{j_1···j_k}:={{\rm Y}}_{j_1}◦\cdots ◦{{\rm Y}}_{j_k}$

We will also require the following lemmas, which are simply proved by applying the inequalities and definitions involved as follows:

$$0\le H_{\Psi }\left(A, C, m\right)+H_{\Phi }\left(A, C, m\right)+H_O\left(A, C, m\right)\le 3,$$

and

$$0\le \Psi (\omega , \varpi , m)+\Phi (\omega , \varpi , m)+O(\omega , \varpi , m)\le 3,$$

for every  $m>0, A, B\in k_0\left(\Omega \right)$ and  $\omega , \varpi \in \Omega .$

Lemma 2. 

For each  $A, B, C\in k_0\left(\Omega \right)$ and  $m>0,$ we have the inequalities

$$\begin{gathered} H_{\Psi }\left(A, C, 2m\right)\ge H_{\Psi }\left(A, B, m\right)\ast H_{\Psi }\left(B, C, m\right), \\ {H}_{\Phi }\left(A, C, 2m\right)\le H_{\Phi }\left(A, B, m\right)\odot H_{\Phi }\left(B, C, m\right), \\ {H}_O(A, C, 2m)\le H_O(A, B, m)\odot H_O(B, C, m). \end{gathered}$$

Lemma 3. 

Let  $(\Omega , \Psi , \ast )$ be an FMS and  $\gamma$ a fuzzy curve that is  $\alpha$-dense in  $\Omega$, for some  $\alpha >0$ with respect to the function  $\phi$ that is also fuzzy comparison. Then, in  $(\Omega , \Psi , \Phi ,O, \ast , \odot ),$ for each  $\omega \in \Omega$ there is  $\varpi \in \gamma \left(I\right)$ following:

$$\begin{gathered} \Psi \left(\omega , \varpi , m\right)\ge \phi \left(m, \alpha \right), \\ \Phi (\omega , \varpi , m) \le 1-\phi (m, \alpha ), \\ O(\omega , \varpi , m) \le 1-\phi (m, \alpha ), \end{gathered}$$

for every  $m>0.$

The next theorem extends approximation and convergence concepts into the fuzzy set theory framework by incorporating fuzzy structures and measures. It provides recursive bounds on the proximity between a set$A$ and a sequence of fuzzy-constructed sets $B_k$ within a fuzzy densifiable space $(\Omega ,\Psi ,\ast )$ relative to a fuzzy comparison function.

Theorem 4. 

Let  $(\Omega , \Psi , \ast )$ is fuzzy densifiable with respect to function (fuzzy comparison)  $\phi ,$ and suppose  ${\gamma }_k$ is a fuzzy curve that is  ${\alpha }_k$-dense in  $\Omega$, for every  $k\ge 1$ with respect to the function  $\phi$ as  ${\alpha }_k\to 0$ and  $0<\phi (m, {\alpha }_k)<1$ for all  $m>0$ and  $k\ge 1.$ For fixed  ${\omega }_1\in \Omega ,$ assume  $B_1:=\left\{{{\rm Y}}_1\right({\omega }_1\left)\right\}$ and for  $k>1$ define

$$B_k :={{\rm Y}}_{j_1···j_k}\left({\varpi }_k\right): \Psi \left({\omega }_{\left(i_1···i_{k-1}\right)} , {\varpi }_k, m\right)\ge \phi \left(m, {\alpha }_k\right),$$

for all  $m>0$, for each  ${\omega }_{\left(i_1···i_{k-1}\right)}\in B_{k-1}$ and some  ${\varpi }_k\in {\gamma }_k\left(I\right),$ where  $j_1, \cdots , j_k\in {\Phi }_k$ and  $i_1, \cdots , i_k-1\in {\Phi }_{k-1},$ where  ${\Phi }_k:=\{1, \cdots , k\}$ for  $1<k<n$ and  ${\Phi }_k:=\{1, \cdots , n\}$ for  $k\ge n.$ Then, we have

$$\begin{gathered} H_{\Psi }\left(A, B_k, 2m\right)\ge {\displaystyle \frac{H_{\Psi }\left(A, B_{k-1}, m\right)}{H_{\Psi }\left(A, B_{k-1}, m\right)+r^k\left(1-H_{\Psi }\left(A, B_{k-1}, m\right)\right)}} \\ \ast {\displaystyle \frac{\phi \left(m, {\alpha }_k\right)}{\phi \left(m, {\alpha }_k\right)+r^k\left(1-\phi \left(m, {\alpha }_k\right)\right)}}, \end{gathered}$$

(8)

$$H_{\Phi }\left(A, B_k, 2m\right)\le {\displaystyle \frac{r^k{H}_{\Phi }\left(A, B_{k-1}, m\right)}{r^k{H}_{\Phi }\left(A, B_{k-1}, m\right)+1-H_{\Phi }\left(A, B_{k-1}, m\right)}}\odot {\displaystyle \frac{r^k\left(1-\phi \left(m, {\alpha }_k\right)\right)}{\phi \left(m, {\alpha }_k\right)}},$$

(9)

and

$$H_O\left(A, B_k, 2m\right)\le r^k{H}_O\left(A, B_{k-1}, m\right)\odot r^k\left(1-\phi \left(m, {\alpha }_k\right)\right),$$

(10)

for every  $k\ge n$ and  $m>0.$

Proof. 

Let any $m>0$ and $k\ge n.$ As $A$ and $B_k,$ belong to $k_0\left(\Omega \right),$ by Lemmas 1 and 2, we have

$$\begin{gathered} H_{\Psi }\left(A, B_k, 2m\right)\ge H_{\Psi }(A, F^k(B_{k-1}, m)\ast H_{\Psi }(F^k\left(B_{k-1}\right), B_k, m) \\ =H_{\Psi }\left(F^k\left(A\right),F^k\left(B_{k-1}\right), m\right)\ast H_{\Psi }\left(F^k\left(B_{k-1}\right), B_k, m\right), \end{gathered}$$

(11)

also, in view of Definition 22, as

$${\displaystyle \frac{1}{\Psi \left({{\rm Y}}_{j_1\dots j_k}\left(\omega \right),{{\rm Y}}_{j_1\dots j_k}\left(\varpi \right),m\right)}}-1\le r^k\left({\displaystyle \frac{1}{\Psi \left(\omega ,\varpi ,m\right)}}-1\right),$$

for every $j_1, \cdots , j_k\in {\Phi }_k$ and $\omega \in F^k\left(A\right), \varpi \in F^k\left(B_{k-1}\right)$, we infer that

$${\displaystyle \frac{1}{H_{\Psi }\left(F^k\left(\omega \right),F^k\left(B_{k-1}\right),m\right)}}-1\le r^k\left({\displaystyle \frac{1}{H_{\Psi }\left(A,B_{k-1},m\right)}}-1\right),$$

and therefore,

$$H_{\Psi }\left(F^k\left(\omega \right),F^k\left(B_{k-1}\right),m\right)\ge {\displaystyle \frac{H_{\Psi }\left(A,B_{k-1},m\right)}{H_{\Psi }\left(A,B_{k-1},m\right)+r^k\left(1-H_{\Psi }\left(A,B_{k-1},m\right)\right)}}.$$

(12)

So, by replacing (12) with (11), we find

$$\begin{gathered} H_{\Psi }\left(A, B_k, 2m\right)\ge {\displaystyle \frac{H_{\Psi }\left(A,B_{k-1},m\right)}{H_{\Psi }\left(A,B_{k-1},m\right)+r^k\left(1-H_{\Psi }\left(A,B_{k-1},m\right)\right)}} \\ \ast H_{\Psi }\left(F_k\left(B_{k-1}\right), B_k,m\right). \end{gathered}$$

(13)

Next, we need to estimate $H_{\Psi }\left(F_k\right(B_{k-1}), B_k, m).$ Let $\omega \in F_k\left(B_{k-1}\right),$ put $\omega :={{\rm Y}}_{j_1...j_k}\left({\omega }_0\right)$ for some $j_1, \cdots , j_k\in {\Phi }_k,$ and ${\omega }_0\in B_{k-1}$, and take (by virtue of Lemma 3) $\varpi :={{\rm Y}}_{j_1\dots j_k}\left({\varpi }_0\right)$ with ${\varpi }_0\in {\gamma }_k\left(I\right)$such that $\Psi (\omega , \varpi , m)\ge \phi (m, {\alpha }_k).$ Then, from this and noticing Definition 22, we have

$$\Psi \left(\omega , \varpi , m\right)=\Psi \left({{\rm Y}}_{j_1...j_k}\left({\omega }_0\right), {{\rm Y}}_{j_1...j_k}\left({\varpi }_0\right),m\right)\ge {\displaystyle \frac{\phi \left(m, {\alpha }_k\right)}{\phi \left(m, {\alpha }_k\right)+r^k\left(1-\phi \left(m, {\alpha }_k\right)\right)}}.$$

From the arbitrariness of $\omega \in F_k\left(B_{k-1}\right),$ we conclude

$$\underset{\omega \in F^k\left(B_{k-1}\right)}{\inf }\underset{\varpi \in B_k}{\sup }\Psi (\omega ,\varpi ,m)\ge {\displaystyle \frac{\phi \left(m, {\alpha }_k\right)}{\phi \left(m, {\alpha }_k\right)+r^k\left(1-\phi \left(m, {\alpha }_k\right)\right)}},$$

Likewise, we can prove that

$$\underset{\omega \in \left(B_k\right)}{\inf }\underset{\varpi \in F^k\left(B_{k-1}\right)}{\sup }\Psi (\omega ,\varpi ,m)\ge {\displaystyle \frac{\phi \left(m, {\alpha }_k\right)}{\phi \left(m, {\alpha }_k\right)+r^k\left(1-\phi \left(m, {\alpha }_k\right)\right)}},$$

and therefore

$$H_{\Psi }\left(F^k\left(B_{k-1}\right), B_k, m\right)\ge {\displaystyle \frac{\phi \left(m, {\alpha }_k\right)}{\phi \left(m, {\alpha }_k\right)+r^k\left(1-\phi \left(m, {\alpha }_k\right)\right)}}.$$

(14)

So, replacing (14) in (13) the inequality (8) follows. Therefore, by applying the Lemmas 1 and 2, we get

$$\begin{gathered} H_{\Phi }\left(A, B_k, 2m\right)\le H_{\Phi } \left(A, F^k\left(B_{k-1}\right), m\right)\odot H_{\Phi }\left(F^k\left(B_{k-1}\right), B_k, m\right) \\ =H_{\Phi }\left(F^k\left(A\right), F^k\left(B_{k-1}\right), m\right)\odot H_{\Phi }\left(F^k\left(B_{k-1}\right), B_k, m\right), \end{gathered}$$

(15)

and similarly, as above, we can write

$$H_{\Phi }\left(F^k\left(A\right), F^k\left(B_{k-1}\right), m\right)\le {\displaystyle \frac{r^k\left(H_{\Phi }\left(A, B_{k-1}, m\right)\right)}{{r^{k}H}_{\Phi }\left(A, B_{k-1}, m\right)+1-H_{\Phi }\left(A, B_{k-1}, m\right)}}.$$

(16)

Then, replacing (16) in (15), we deduce

$$\begin{gathered} H_{\Phi }\left(A, B_k, 2m\right)\le {\displaystyle \frac{r^k\left(H_{\Phi }\left(A, B_{k-1}, m\right)\right)}{{r^{k}H}_{\Phi }\left(A, B_{k-1}, m\right)+1-H_{\Phi }\left(A, B_{k-1}, m\right)}} \\ \odot H_{\Phi }\left(F^k\left(B_{k-1}\right), B_k, m\right). \end{gathered}$$

(17)

To estimate $H_{\Phi }\left(F^k\right(B_{k-1}), B_k, m)$, noticing Lemma 3 and on the same lines as in the inequality (14), we examine that

$$H_{\Phi }\left(F^k\left(B_{k-1}\right), B_k, m\right)\le {\displaystyle \frac{r^k\left(1-\phi \left(m, {\alpha }_k\right)\right)}{\phi \left(m, {\alpha }_k\right)}},$$

(18)

and combining (18) and (17), the inequality (9) follows. As $A$ and $B_k$ belong to $k_0\left(\Omega \right),$ by Lemmas 1 and 2, we have

$$\begin{gathered} H_O\left(A, B_k, 2m\right)\le H_O(A, F^k (B_{k-1}, m) \odot H_O(F^k \left(B_{k-1}\right), B_k, m) \\ =H_O\left(F^k\left(A\right),F^k\left(B_{k-1}\right), m\right)\odot H_O\left(F^k\left(B_{k-1}\right), B_k, m\right), \end{gathered}$$

(19)

also, in view of Definition 22, we can write

$$O\left({{\rm Y}}_{j_1\dots j_k}\left(\omega \right),{{\rm Y}}_{j_1\dots j_k}\left(\varpi \right),m\right)\le r^{k}O\left(\omega ,\varpi ,m\right),$$

for every $j_1, \cdots , j_k\in {\Phi }_k$ and $\omega \in F^k\left(A\right), \varpi \in F^k\left(B_{k-1}\right),$ we infer that

$$H_O\left(F^k\left(\omega \right),F^k\left(B_{k-1}\right),m\right)\le r^k{H}_O\left(A,B_{k-1},m\right).$$

(20)

So, replacing (20) in (19), we find

$$H_O\left(A, B_k, 2m\right)\le r^k{H}_O\left(A,B_{k-1},m\right)\odot H_O\left(F_k\left(B_{k-1}\right), B_k,m\right).$$

(21)

Next, we need to estimate $H_O\left(F_k\right(B_{k-1}), B_k, m).$ Let $\omega \in F_k\left(B_{k-1}\right),$ put $\omega :={{\rm Y}}_{j_1...j_k}\left({\omega }_0\right)$ for some $j_1, \cdots , j_k\in {\Phi }_k$ and ${\omega }_0\in B_{k-1},$ and take (by virtue of Lemma 3) $\varpi :={{\rm Y}}_{j_1...j_k}\left({\varpi }_0\right)$ with ${\varpi }_0\in {\gamma }_k\left(I\right)$ such that$O\left(\omega , \varpi , m\right)\le 1-\phi (m, {\alpha }_k).$ Then, from this and noticing Definition 22, we have

$$O\left(\omega , \varpi , m\right)=O\left({{\rm Y}}_{j_1\dots j_k}\left({\omega }_0\right), {{\rm Y}}_{j_1\dots j_k}\left({\varpi }_0\right),m\right)\le r^k\left(1-\phi \left(m, {\alpha }_k\right)\right).$$

From the arbitrariness of $\omega \in F_k\left(B_{k-1}\right),$ we conclude

$$\underset{\omega \in F^k\left(B_{k-1}\right)}{\inf }\underset{\varpi \in B_k}{\sup }O(\omega ,\varpi ,m)\le r^k\left(1-\phi \left(m, {\alpha }_k\right)\right).$$

Likewise, we can prove that

$$\underset{\omega \in \left(B_k\right)}{\inf }\underset{\varpi \in F^k\left(B_{k-1}\right)}{\sup }O(\omega ,\varpi ,m)\le r^k\left(1-\phi \left(m, {\alpha }_k\right)\right),$$

and therefore

$$H_O\left(F^k\left(B_{k-1}\right), B_k, m\right)\le r^k\left(1-\phi \left(m, {\alpha }_k\right)\right).$$

(22)

So, replacing (22) in (21), the inequality (10) follows. This completes the proof. □

Clearly, the limits obtained in (5)–(7) of Theorem 3 are held in the preceding result as follows:

$$\begin{gathered} \underset{k}{\lim }{\displaystyle \frac{H_{\Psi }\left(A,B_{k-1},m\right)}{H_{\Psi }\left(A,B_{k-1},m\right)+r^k\left(1-H_{\Psi }\left(A,B_{k-1},m\right)\right)}} \\ =\underset{k}{\lim }{\displaystyle \frac{\phi (m, {\alpha }_k)}{\phi \left(m, {\alpha }_k\right)+r^k(1-\phi (m, {\alpha }_k\left)\right)}}=1, \\ \underset{k}{\lim }{\displaystyle \frac{r^k\left(H_{\Phi }\left(A, B_{k-1}, m\right)\right)}{{r^{k}H}_{\Phi }\left(A, B_{k-1}, m\right)+1-H_{\Phi }\left(A, B_{k-1}, m\right)}} \\ =\underset{k}{\lim }{\displaystyle \frac{r^k\left(1-\phi \left(m, {\alpha }_k\right)\right)}{\phi \left(m, {\alpha }_k\right)}}=0, \end{gathered}$$

and

$$\begin{gathered} \underset{k}{\lim }{r}^k\left(H_O\left(A, B_{k-1}, m\right)\right) \\ =\underset{k}{\lim }{r}^k\left(1-\phi \left(m, {\alpha }_k\right)\right)=0. \end{gathered}$$

By applying the CTN $\ast$and CTCN $\odot$ for each $m>0,$ we get

$$\begin{gathered} \underset{k}{\lim } H_{\Psi }\left(A, B_k, 2m\right)=1, \\ \underset{k}{\lim }{H}_{\Phi }\left(A, B_k, 2m\right)=0, \\ \underset{k}{\lim }{H}_O(A, B_k, 2m)=0. \end{gathered}$$

5. Product Neutrosophic Fractal Space

Product FMS was investigated by Uthayakumar and Gowrisankar [31]. They implemented the idea of fuzzy IFS consisting of fuzzy B-contraction in the product FMS. Now, we extend this notion to a finite number of NMS having neutrosophic B-contraction and neutrosophic Edelstein contraction as the neutrosophic IFS.

Definition 23. 

Let  $(\Omega ,\Psi ,\Phi ,O,\ast ,\odot )$ be an NMS. Denote  $\varrho \left(\Omega \right)$ as the set of all non-empty compact subsets of  $\Omega$. We give the definition of the Hausdorff neutrosophic metric represented by  $\left({\mathcal{H}}_{\Psi },{\mathcal{H}}_{\Phi }, {\mathcal{H}}_O,\ast ,\odot \right)$ as

$$\begin{gathered} {\mathcal{H}}_{\Psi }\left({\Psi }_1,{\Phi }_1,m\right)=\min \left\{\Psi \left({\Psi }_1,{\Phi }_1,m\right),\Psi \left({\Phi }_1,{\Psi }_1,m\right)\right\}, \\ {\mathcal{H}}_{\Phi }\left({\Psi }_1,{\Phi }_1,m\right)=\min \left\{\Phi \left({\Psi }_1,{\Phi }_1,m\right),\Phi \left({\Phi }_1,{\Psi }_1,m\right)\right\}, \\ {\mathcal{H}}_O\left({\Psi }_1,{\Phi }_1,m\right)=\min \left\{O\left({\Psi }_1,{\Phi }_1,m\right),O\left({\Phi }_1,{\Psi }_1,m\right)\right\}, \end{gathered}$$

where

$$\begin{gathered} \Psi \left({\Psi }_1,{\Phi }_1,m\right)=\underset{a_1\in {\Psi }_1}{\inf }\Psi \left(a_1,{\Phi }_1,m\right),\Psi \left(a_1,{\Phi }_1,m\right)=\underset{b_1\in {\Phi }_1}{\sup }\Psi \left(a_1,b_1,m\right), \\ \Phi \left({\Psi }_1,{\Phi }_1,m\right)=\underset{a_1\in {\Psi }_1}{\sup }\Phi \left(a_1,{\Phi }_1,m\right),\Phi \left(a_1,{\Phi }_1,m\right)=\underset{b_1\in {\Phi }_1}{\inf }\Phi \left(a_1,b_1,m\right), \\ O\left({\Psi }_1,{\Phi }_1,m\right)=\underset{a_1\in {\Psi }_1}{\sup }O\left(a_1,{\Phi }_1,m\right),O\left(a_1,{\Phi }_1,m\right)=\underset{b_1\in {\Phi }_1}{\inf }O\left(a_1,b_1,m\right) \end{gathered}$$

for all  $m\in \Omega$ and  ${\Psi }_1,{\Phi }_1\in \varrho \left(\Omega \right)$. Here,  $({\mathcal{H}}_{\Psi },{\mathcal{H}}_{\Phi },{\mathcal{H}}_O)$ is a Hausdorff neutrosophic metric on the hyperspace of compact sets,  $\varrho \left(\Omega \right)$. Accordingly,  $\left(\varrho \left(\Omega \right),{\mathcal{H}}_{\Psi },{\mathcal{H}}_{\Phi }, {\mathcal{H}}_O,\ast ,\odot \right)$ is said to be a Hausdorff NMS.

Theorem 5. 

Let  $(\Omega ,\Psi ,\Phi ,O,\ast ,\odot )$ be an NMS. Then,  $\left(\varrho \left(\Omega \right),{\mathcal{H}}_{\Psi },{\mathcal{H}}_{\Phi }, {\mathcal{H}}_O,\ast ,\odot \right)$ is complete if  $(\Omega ,\Psi ,\Phi ,O,\ast ,\odot )$ is compact.

Theorem 6. 

Suppose  $(\Omega ,\Psi ,\Phi ,O,\ast ,\odot )$ is an NMS. Then  $\left(\varrho \left(\Omega \right),{\mathcal{H}}_{\Psi },{\mathcal{H}}_{\Phi }, {\mathcal{H}}_O,\ast ,\odot \right)$ is complete if  $(\Omega ,\Psi ,\Phi ,O,\ast ,\odot )$ is compact.

Definition 24. 

Take  $\left({\Omega }_1,{\Psi }_1,{\Phi }_1,O_1,\ast ,\odot \right),\cdots , \left({\Omega }_{\omega },{\Psi }_{\Phi },{\Phi }_{\omega }, O_{\omega },\ast ,\odot \right)$ be NMS and let  $\mathcal{X}={\Omega }_1\times {\Omega }_2\times {\Omega }_3,\cdots , {\Omega }_{\omega }$. For each  $a=a_1\times a_2\times a_3,\cdots , a_{\omega }, b=b_1\times b_2\times b_3,\cdots , b_{\omega }$ and  $m>0,$ consider

$${\Psi }_{\mathcal{X}}\left(a,b,m\right)=\left\{\begin{array}{c}{\Psi }_{{\Omega }_1}\left(a_1,b_1,m\right)\ast {\Psi }_{{\Omega }_2}\left(a_2,b_2,m\right)\\ \ast {\Psi }_{{\Omega }_3}\left(a_3,b_3,m\right)\ast ,\cdots ,\ast {\Psi }_{{\Omega }_{\omega }}\left(a_{\omega },b_{\omega },m\right)\end{array}\right\},$$

(23)

$${\Phi }_{\mathcal{X}}\left(a,b,m\right)=\left\{\begin{array}{c}{\Phi }_{{\Omega }_1}\left(a_1,b_1,m\right)\odot {\Phi }_{{\Omega }_2}\left(a_2,b_2,m\right)\\ \odot {\Phi }_{{\Omega }_3}\left(a_3,b_3,m\right)\odot ,\cdots ,\odot {\Phi }_{{\Omega }_{\omega }}\left(a_{\omega },b_{\omega },m\right)\end{array}\right\},$$

(24)

$$O_{\mathcal{X}}\left(a,b,m\right)=\left\{\begin{array}{c}{O}_{{\Omega }_1}\left(a_1,b_1,m\right)\odot O_{{\Omega }_2}\left(a_2,b_2,m\right)\\ \odot O_{{\Omega }_3}\left(a_3,b_3,m\right)\odot ,\cdots ,\odot O_{{\Omega }_{\omega }}\left(a_{\omega },b_{\omega },m\right)\end{array}\right\}.$$

(25)

Then,  $\left({\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}},O_{\mathcal{X}},\ast ,\odot \right)$ is a neutrosophic metric on  $\mathcal{X}$, and the  $6-$tuple  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ is called the product NMS of  ${\Omega }_1,{\Omega }_2,{\Omega }_3,\cdots , {\Omega }_{\omega }.$

Definition 25. 

Suppose  $\left(\mathcal{X},d^{\prime }\right)$ is a product space. Define  $a\ast b=a.b,$ where  $a.b$ is the usual real number multiplication for all  $a,b\in \left[\mathrm{0,1}\right]$ and  $a\odot b=1-\left[\left(1-a\right)\ast \left(1-b\right)\right]$. Take  ${\Psi }_{{\mathcal{X}}_{d^{\prime }}}{\Phi }_{{\mathcal{X}}_{d^{\prime }}}$ and  $O_{{\mathcal{X}}_{d^{\prime }}}$ be the mappings defined on  $\mathcal{X}\times \mathcal{X}\to \left(0,\infty \right)$ by

$$\begin{gathered} {\Psi }_{{\mathcal{X}}_{d^{\prime }}}={\displaystyle \frac{m}{m+d^{\prime }\left(a,b\right)}}, \\ {\Phi }_{{\mathcal{X}}_{d^{\prime }}}={\displaystyle \frac{d^{\prime }\left(a,b\right)}{m+d^{\prime }\left(a,b\right)}}, \end{gathered}$$

and

$$O_{{\mathcal{X}}_{d^{\prime }}}={\displaystyle \frac{d^{\prime }\left(a,b\right)}{m}},$$

for all  $a,b\in \Omega$ and  $m>0.$ Then  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ is known as the standard product neutrosophic metric produced by the metric space, and  $\left({\Psi }_{{\mathcal{X}}_{d^{\prime }}}, {\Phi }_{{\mathcal{X}}_{d^{\prime }}}, O_{{\mathcal{X}}_{d^{\prime }}}\right)$ is said to be the standard product neutrosophic metric produced by the metric  $d’.$

Hereafter, we assume that  $\mathcal{X}=\Omega \times \Omega \times \Omega ,\cdots ,\times \Omega ,$ where  $\left(\Omega ,\Psi ,\Phi ,O,\ast ,\odot \right)$ is an NMS, unless otherwise mentioned.

Definition 26. 

Suppose  $\left(\Omega ,\Psi ,\Phi , O,\ast ,\odot \right)$ is a NMS and  $\psi$ is a self-mapping on $\Omega .$ The function $\psi$ is said to be a neutrosophic B-contraction on  $\Omega ,$ if there exist  $\overline{p}\in \left(0, 1\right)$ such that

$$\begin{gathered} \Psi \left(\psi \left(a\right),\psi \left(b\right),\overline{p}m\right)\ge \Psi \left(a, b,\overline{p}m\right), \\ \Phi \left(\psi \left(a\right),\psi \left(b\right),\overline{p}m\right)\le \Phi \left(a, b,m\right), \end{gathered}$$

and

$$O\left(\psi \left(a\right),\psi \left(b\right),\overline{p}m\right)\le O\left(a, b,m\right),$$

for every  $a,b\in \Omega ,$ and  $m>0.$ Therefore,  $\overline{p}$ is a neutrosophic B-contractions ratio of  $\psi .$

The function $\psi$ is said to ba a neutrosophic Edelstein contraction on  $\Omega ,$ if there exist  $\overline{p}\in \left(0, 1\right)$ such that

$$\begin{gathered} \Psi \left(\psi \left(a\right),\psi \left(b\right),\ast \right)\ge \Psi \left(a, b,\ast \right), \\ \Phi \left(\psi \left(a\right),\psi \left(b\right),\odot \right)\le \Phi \left(a, b,\odot \right), \end{gathered}$$

and

$$O\left(\psi \left(a\right),\psi \left(b\right),\odot \right)\le O\left(a, b,\odot \right),$$

for every  $a,b\in \Omega ,$ and  $m>0.$ Therefore,  $\overline{p}$ is a neutrosophic Edelstein contractions ratio of  $\psi .$The below theorem shows that neutrosophic B-contractions remain preserved under product structures in NMS.

Theorem 7. 

Suppose  $\left(\Omega ,\Psi ,\Phi , O,\ast ,\odot \right)$ is an NMS and  $\phi$ be a neutrosophic B-contraction on  $\Omega$. Assume that  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},B_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ is a product NMS of  $\Omega$. Then the function  $\psi : \mathcal{X}\to \mathcal{X}$ defined by

$$\psi \left(a\right)=\left(\phi \left(a_1\right),\phi \left(a_2\right),\cdots ,\phi \left(a_{\omega }\right)\right), a=\left(a_1,a_2,a_3,\cdots ,a_{\omega }\right)\in \mathcal{X},$$

is a neutrosophic B-contraction on  $\mathcal{X}$.

Proof. 

Take $\mathcal{X}=\Omega \times \Omega \times \Omega \times \cdots \times \Omega$ and let $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ be the product NMS. Then for any $\overline{p}\in \left(\mathrm{0,1}\right), a,b\in \mathcal{X},$ and $m>0$ , by using the assumption that $\phi$ is a neutrosophic B-contraction, we have

$$\begin{gathered} {\Psi }_{\mathcal{X}}\left(\psi \left(a\right),\psi \left(b\right),\overline{p}m\right)={\Psi }_{\mathcal{X}}\left(\left(\phi \left(a_1\right),\phi \left(a_2\right),\cdots ,\phi \left(a_{\omega }\right)\right),\left(\phi \left(b_1\right),\phi \left(b_2\right),\cdots ,\phi \left(b_{\omega }\right)\right),\overline{p}m\right) \\ ={\Psi }_{\Omega }\left(\phi \left(a_1\right),\phi \left(b_1\right),\overline{p}m\right)\ast {\Psi }_{\Omega }\left(\phi \left(a_2\right),\phi \left(b_2\right),\overline{p}m\right)\ast ,\cdots ,{\ast \Psi }_{\Omega }\left(\phi \left(a_{\omega }\right),\phi \left(b_{\omega }\right),\overline{p}m\right) \\ \ge {\Psi }_{\Omega }\left(a_1,b_1,m\right)\ast {\Psi }_{\Omega }\left(a_2,b_2,m\right)\ast ,\cdots ,{\ast \Psi }_{\Omega }\left(a_{\omega },b_{\omega },m\right)={\Psi }_{\mathcal{X}}\left(a,b,m\right), \end{gathered}$$

(26)

and

$$\begin{gathered} {\Phi }_{\mathcal{X}}\left(\psi \left(a\right),\psi \left(b\right),\overline{p}m\right)={\Phi }_{\mathcal{X}}\left(\left(\phi \left(a_1\right),\phi \left(a_2\right),\cdots ,\phi \left(a_{\omega }\right)\right),\left(\phi \left(b_1\right),\phi \left(b_2\right),\cdots ,\phi \left(b_{\omega }\right)\right),\overline{p}m\right) \\ ={\Phi }_{\Omega }\left(\phi \left(a_1\right),\phi \left(b_1\right),\overline{p}m\right)\odot {\Phi }_{\Omega }\left(\phi \left(a_2\right),\phi \left(b_2\right),\overline{p}m\right)\odot ,\cdots ,{\odot \Phi }_{\Omega }\left(\phi \left(a_{\omega }\right),\phi \left(b_{\omega }\right),\overline{p}m\right) \\ \le {\Phi }_{\Omega }\left(a_1,b_1,m\right)\odot {\Phi }_{\Omega }\left(a_2,b_2,m\right)\odot ,\cdots ,{\odot \Phi }_{\Omega }\left(a_{\omega },b_{\omega },m\right)={\Phi }_{\mathcal{X}}\left(a,b,m\right), \end{gathered}$$

(27)

and in a similar way, we obtain

$$\begin{gathered} O_{\mathcal{X}}\left(\psi \left(a\right),\psi \left(b\right),\overline{p}m\right)=O_{\mathcal{X}}\left(\left(\phi \left(a_1\right),\phi \left(a_2\right),\cdots ,\phi \left(a_{\omega }\right)\right),\left(\phi \left(b_1\right),\phi \left(b_2\right),\cdots ,\phi \left(b_{\omega }\right)\right),\overline{p}m\right) \\ =O_{\Omega }\left(\phi \left(a_1\right),\phi \left(b_1\right),\overline{p}m\right)\odot O_{\Omega }\left(\phi \left(a_2\right),\phi \left(b_2\right),\overline{p}m\right)\odot ,\cdots ,{\odot O}_{\Omega }\left(\phi \left(a_{\omega }\right),\phi \left(b_{\omega }\right),\overline{p}m\right) \\ \le O_{\Omega }\left(a_1,b_1,m\right)\odot O_{\Omega }\left(a_2,b_2,m\right)\odot ,\cdots ,{\odot O}_{\Omega }\left(a_{\omega },b_{\omega },m\right)=O_{\mathcal{X}}\left(a,b,m\right). \left(28\right) \end{gathered}$$

(28)

From the inequalities (26)–(28), we get the required result. □

Example 4. 

Let  $\Omega =\left[\mathrm{0,4}\right],$ and CTN  $a\ast b=a\cdot b,$ CTCN is  $a\odot b=\mathit{max}\left\{a,b\right\},$ and  $(X,d_{\omega })$ and  $(Y, d_{\varpi })$ are two usual metric spaces and their product is  $\left(X\times Y, d\right),$ with metric  $d$ is  $d\left(p,q\right)=\mathit{max}\left\{d_{\omega }\left({\omega }_1, {\omega }_2\right), d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)\right\},$ for each  $p=\left({\omega }_1, {\varpi }_1\right),$ and  $q=\left({\omega }_2, {\varpi }_2\right),$ in  $X\times Y.$

$$\begin{gathered} {\Psi }_{\omega }\left(p, q, m\right)={\displaystyle \frac{m}{m+d(p,q)}}, \\ {\Phi }_{\mathcal{X}}\left(p, q, m\right)={\displaystyle \frac{d(p,q)}{m+d(p,q)}}, \\ {O}_{\mathcal{X}}\left(p, q, m\right)={\displaystyle \frac{d(p,q)}{m}}, \end{gathered}$$

Then,  $\left(\mathcal{X}, {\Psi }_d, {\Phi }_d,O_d, \ast , \odot \right)$ is a product of NMS. Assume that  $\psi : \mathcal{X}\to \mathcal{X},$ is mapping so

$$\psi \left(a\right)=\left(\psi \left(p\right), \psi \left(q\right)\right)=\left({\displaystyle \frac{p}{2}},{\displaystyle \frac{q}{2}}\right),$$

where  $p,q\in \mathcal{X},$ and  $\overline{p}\in \left(\mathrm{0,1}\right)$ such that

$$\begin{gathered} {\Psi }_{\mathcal{X}}\left(\psi \left(p\right),\psi \left(q\right),\overline{p}m\right)={\displaystyle \frac{\overline{p}m}{\overline{p}m+d\left(\psi \right(p),\psi (q\left)\right) }}={\displaystyle \frac{\overline{p}m}{\overline{p}m+\max \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\}, }} \\ ={\displaystyle \frac{\overline{p}m}{\overline{p}m+\max \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\}, }} \\ \ge {\displaystyle \frac{m}{m+d_{\omega }({\omega }_1, {\omega }_2) }}\cdot {\displaystyle \frac{m}{m+d_{\varpi }({\varpi }_1, {\varpi }_2) }} \\ ={\displaystyle \frac{m}{m+d_{\omega }({\omega }_1, {\omega }_2) }}\ast {\displaystyle \frac{m}{m+d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)}}={\Psi }_{\mathcal{X}}\left(p, q, m\right). \end{gathered}$$

For better understanding, we show its graphical behavior in Figure 3.

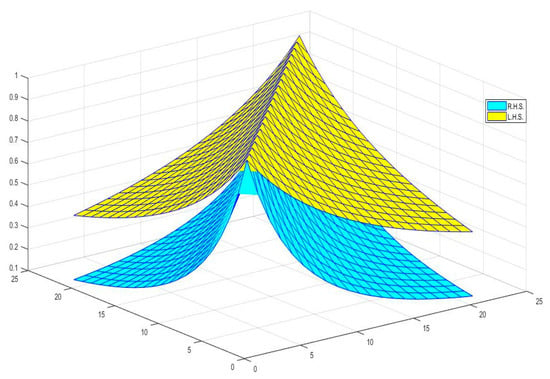
Figure 3. Shows the graphical behavior of the inequality ${ \Psi }_{\mathcal{X}}\left(\psi \left(p\right),\psi \left(q\right),\overline{p}m\right)\ge {\Psi }_{\mathcal{X}}\left(p, q, m\right),$ for $m=2,$ and $\overline{p}=0.7.$

$$\begin{gathered} {\Phi }_{\mathcal{X}}\left(\psi \left(p\right),\psi \left(q\right),\overline{p}m\right)={\displaystyle \frac{d\left(\psi \right(p),\psi (q\left)\right)}{\overline{p}m+d\left(\psi \right(p),\psi (q\left)\right) }}={\displaystyle \frac{\max \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\},}{\overline{p}m+\max \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\}, }} \\ ={\displaystyle \frac{\max \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\},}{\overline{p}m+\max \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\}, }} \\ \le \max \left\{{\displaystyle \frac{d_{\omega }\left({\omega }_1, {\omega }_2\right)}{m+d_{\omega }\left({\omega }_1, {\omega }_2\right)}},{\displaystyle \frac{d_{\varpi }({\varpi }_1, {\varpi }_2)}{m+d_{\varpi }({\varpi }_1, {\varpi }_2) }}\right\} \\ ={\displaystyle \frac{d_{\omega }\left({\omega }_1, {\omega }_2\right)}{m+d_{\omega }\left({\omega }_1, {\omega }_2\right)}}\mathsf{\Delta }{\displaystyle \frac{d_{\varpi }({\varpi }_1, {\varpi }_2)}{m+d_{\varpi }({\varpi }_1, {\varpi }_2) }}={\Phi }_{\mathcal{X}}\left(p, q, m\right). \end{gathered}$$

For better understanding, we show its graphical behavior in Figure 4.

$$\begin{gathered} O_{\mathcal{X}}\left(\psi \left(p\right),\psi \left(q\right),\overline{p}m\right)={\displaystyle \frac{d\left(\psi \right(p),\psi (q\left)\right)}{\overline{p}m }}={\displaystyle \frac{\max \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\},}{\overline{p}m }} \\ ={\displaystyle \frac{\max \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\},}{\overline{p}m }} \\ \le \max \left\{{\displaystyle \frac{d_{\omega }\left({\omega }_1, {\omega }_2\right)}{m}},{\displaystyle \frac{d_{\varpi }({\varpi }_1, {\varpi }_2)}{m }}\right\} \\ ={\displaystyle \frac{d_{\omega }\left({\omega }_1, {\omega }_2\right)}{m}}\mathsf{\Delta }{\displaystyle \frac{d_{\varpi }({\varpi }_1, {\varpi }_2)}{m }}=O_{\mathcal{X}}\left(p, q, m\right). \end{gathered}$$

For better understanding, we show its graphical behavior in Figure 5.

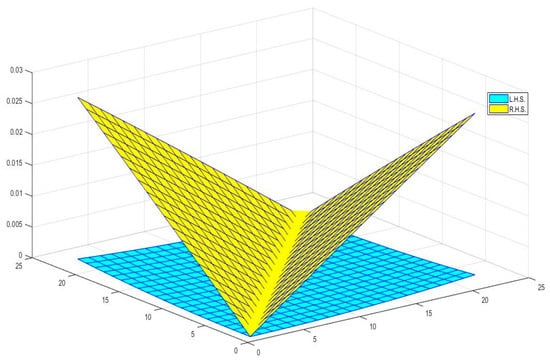
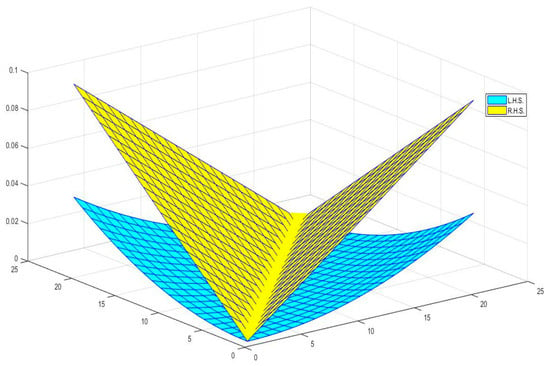
Figure 4. Shows the graphical behavior of the inequality ${\Phi }_{\mathcal{X}}\left(\psi \left(p\right),\psi \left(q\right),\overline{p}m\right)\le {\Phi }_{\mathcal{X}}\left(p, q, m\right),$ for $m=2,$ and $\overline{p}=0.7.$

Figure 5. Shows the graphical behavior of the inequality $O_{\mathcal{X}}\left(\psi \left(p\right),\psi \left(q\right),\overline{p}m\right)\le O_{\mathcal{X}}\left(p, q, m\right),$ for $m=2,$ and $\overline{p}=0.7.$

Therefore, all the conditions of Theorem 7 are satisfied, so the mapping $\psi ,$ is a neutrosophic B-contraction on $\mathcal{X}.$

We demonstrate that a neutrosophic Edelstein contraction defined on an NMS $\left(\Omega ,\Psi ,\Phi ,O,\ast ,\odot \right)$ naturally extends to its product space in the below theorem.

Theorem 8. 

Assume that  $\left(\Omega ,\Psi ,\Phi ,O,\ast ,\odot \right)$ is a NMS and  $\phi$ is a neutrosophic Edelstein contraction on  $\Omega .$ Let  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ be the corresponding product NMS of  $\Omega .$ Then the function  $\psi :\mathcal{X}\to \mathcal{X},$ represented by

$$\psi \left(a\right)=\left(\phi \left(a_1\right),\phi \left(a_2\right),\cdots ,\phi \left(a_{\omega }\right)\right),$$

(29)

 $for all a=\left(a_1,a_2,a_3,\cdots ,a_{\omega }\right)\in \mathcal{X}$ is a neutrosophic Edelstein contraction on  $\mathcal{X}$.

Proof. 

Let $\mathcal{X}=\Omega \times \Omega \times \Omega \times ,\cdots ,\times \Omega$ and$\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}},\ast ,\odot \right)$ be the product NMS. For each $\overline{p}\in \left(\mathrm{0,1}\right), a,b\in \mathcal{X},$ such that $a\ne b,$ by using the result that $\phi$ is a neutrosophic Edelstein contraction, we have

$$\begin{gathered} {\Psi }_{\mathcal{X}}\left(\psi \left(a\right),\psi \left(b\right),\ast \right)={\Psi }_{\mathcal{X}}\left(\left(\phi \left(a_1\right),\phi \left(a_2\right),\cdots ,\phi \left(a_{\omega }\right)\right),\left(\phi \left(b_1\right),\phi \left(b_2\right),\cdots ,\phi \left(b_{\omega }\right)\right),\ast \right) \\ ={\Psi }_{\Omega }\left(\phi \left(a_1\right),\phi \left(b_1\right),\ast \right)\ast {\Psi }_{\Omega }\left(\phi \left(a_2\right),\phi \left(b_2\right),\ast \right)\ast ,\cdots ,{\ast \Psi }_{\Omega }\left(\phi \left(a_{\omega }\right),\phi \left(b_{\omega }\right),\ast \right) \\ \ge {\Psi }_{\Omega }\left(a_1,b_1,\ast \right)\ast {\Psi }_{\Omega }\left(a_2,b_2,\ast \right)\ast ,\cdots ,{\ast \Psi }_{\Omega }\left(a_{\omega },b_{\omega },\ast \right)={\Psi }_{\mathcal{X}}\left(a,b,\ast \right), \end{gathered}$$

(30)

and

$$\begin{gathered} {\Phi }_{\mathcal{X}}\left(\psi \left(a\right),\psi \left(b\right),\odot \right)={\Phi }_{\mathcal{X}}\left(\left(\phi \left(a_1\right),\phi \left(a_2\right),\cdots ,\phi \left(a_{\omega }\right)\right),\left(\phi \left(b_1\right),\phi \left(b_2\right),\cdots ,\phi \left(b_{\omega }\right)\right),\odot \right) \\ ={\Phi }_{\Omega }\left(\phi \left(a_1\right),\phi \left(b_1\right),\odot \right)\odot {\Phi }_{\Omega }\left(\phi \left(a_2\right),\phi \left(b_2\right),\odot \right)\odot ,\cdots ,{\odot \Phi }_{\Omega }\left(\phi \left(a_{\omega }\right),\phi \left(b_{\omega }\right),\odot \right) \\ \le {\Phi }_{\Omega }\left(a_1,b_1,\odot \right)\odot {\Phi }_{\Omega }\left(a_2,b_2,\odot \right)\odot ,\cdots ,{\odot \Phi }_{\Omega }\left(a_{\omega },b_{\omega },\odot \right)={\Phi }_{\mathcal{X}}\left(a,b,\odot \right), \end{gathered}$$

(31)

and in a similar way, we obtain

$$\begin{gathered} O_{\mathcal{X}}\left(\psi \left(a\right),\psi \left(b\right),\odot \right)=O_{\mathcal{X}}\left(\left(\phi \left(a_1\right),\phi \left(a_2\right),\cdots ,\phi \left(a_{\omega }\right)\right),\left(\phi \left(b_1\right),\phi \left(b_2\right),\cdots ,\phi \left(b_{\omega }\right)\right),\odot \right) \\ =O_{\Omega }\left(\phi \left(a_1\right),\phi \left(b_1\right),\odot \right)\odot O_{\Omega }\left(\phi \left(a_2\right),\phi \left(b_2\right),\odot \right)\odot ,\cdots ,{\odot O}_{\Omega }\left(\phi \left(a_{\omega }\right),\phi \left(b_{\omega }\right),\odot \right) \\ \le O_{\Omega }\left(a_1,b_1,\odot \right)\odot O_{\Omega }\left(a_2,b_2,\odot \right)\odot ,\cdots ,{\odot O}_{\Omega }\left(a_{\omega },b_{\omega },\odot \right)=O_{\mathcal{X}}\left(a,b,\odot \right). \end{gathered}$$

(32)

From formulas (30)–(32), we get the required result as follows. □

Example 5. 

Let  $\Omega =\left[\mathrm{0,1}\right],$ and CTN  $a\ast b=a\cdot b,$ CTCN is  $a\odot b=\mathit{max}\left\{a,b\right\},$ and  $(X,d_{\omega })$ and  $(Y, d_{\varpi })$ are two usual metric spaces, and their product is  $\left(X\times Y, d\right),$ with  $d\left(p,q\right)=\mathit{max}\left\{d_{\omega }\left({\omega }_1, {\omega }_2\right), d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)\right\},$ and  $d^{\prime }\left(p,q\right)=\mathit{min}\left\{d_{\omega }\left({\omega }_1, {\omega }_2\right), d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)\right\},$ for each  $p=\left({\omega }_1, {\varpi }_1\right),$ and  $q=\left({\omega }_2, {\varpi }_2\right),$ in  $X\times Y.$

$$\begin{gathered} {\Psi }_{\omega }\left(p, q, m\right)={\displaystyle \frac{d^{\prime }\left(p,q\right)+m}{d\left(p,q\right)+m}}, \\ {\Phi }_{\mathcal{X}}\left(p, q, m\right)=1-{\displaystyle \frac{d^{\prime }\left(p,q\right)+m}{d\left(p,q\right)+m}}, \\ {O}_{\mathcal{X}}\left(p, q, m\right)={\displaystyle \frac{d\left(p,q\right)-d^{\prime }\left(p,q\right)}{d\left(p,q\right)+m}}. \end{gathered}$$

Then,  $\left(\mathcal{X}, {\Psi }_d, {\Phi }_d,O_d, \ast , \odot \right)$ is a products of NMS. Assume that  $\psi : \mathcal{X}\to \mathcal{X},$ is mapping so

$$\psi \left(a\right)=\left(\psi \left(p\right), \psi \left(q\right)\right)=\left({\displaystyle \frac{p}{2}},{\displaystyle \frac{q}{2}}\right),$$

where  $\overline{p}\in \left(\mathrm{0,1}\right), p,q\in \mathcal{X},$ such that

$$\begin{gathered} {\Psi }_{\mathcal{X}}\left(\psi \left(p\right),\psi \left(q\right),\overline{p}m\right)={\displaystyle \frac{d^{\prime }\left(\psi \left(p\right),\psi \left(q\right)\right)+\overline{p}m}{d\left(\psi \left(p\right),\psi \left(q\right)\right)+\overline{p}m }}={\displaystyle \frac{\min \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\},+\overline{p}m}{\max \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\}+\overline{p}m }} \\ ={\displaystyle \frac{\min \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\},+\overline{p}m}{\max \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\}+\overline{p}m }} \\ \ge {\displaystyle \frac{d_{\omega }^{\prime }\left({\omega }_1, {\omega }_2\right)+m}{d_{\omega }\left({\omega }_1, {\omega }_2\right)+m }}\cdot {\displaystyle \frac{d_{\varpi }^{\prime }\left({\varpi }_1, {\varpi }_2\right)+m}{d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)+m }} \\ {\displaystyle \frac{d_{\omega }^{\prime }\left({\omega }_1, {\omega }_2\right)+m}{d_{\omega }\left({\omega }_1, {\omega }_2\right)+m}}\ast {\displaystyle \frac{d^{\prime }\left({\varpi }_1, {\varpi }_2\right)+m}{d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)+m}}={\Psi }_{\mathcal{X}}\left(p, q, m\right), \\ {\Phi }_{\mathcal{X}}\left(\psi \left(p\right),\psi \left(q\right),\overline{p}m\right)=1-{\displaystyle \frac{d^{\prime }\left(\psi \left(p\right),\psi \left(q\right)\right)+\overline{p}m}{d\left(\psi \left(p\right),\psi \left(q\right)\right)+\overline{p}m }}, \\ =1-{\displaystyle \frac{\min \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\},+\overline{p}m}{\max \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\}+\overline{p}m }}, \\ =1-{\displaystyle \frac{\min \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\},+\overline{p}m}{\max \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\}+\overline{p}m }} \\ \le \max \left\{1-{\displaystyle \frac{d_{\omega }^{\prime }\left({\omega }_1, {\omega }_2\right)+m}{d_{\omega }\left({\omega }_1, {\omega }_2\right)+m }}, 1-{\displaystyle \frac{d_{\varpi }^{\prime }\left({\varpi }_1, {\varpi }_2\right)+m}{d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)+m }}\right\}, \\ ={\displaystyle \frac{d_{\omega }^{\prime }({\omega }_1, {\omega }_2)+m}{d_{\omega }\left({\omega }_1, {\omega }_2\right)+m}}\mathsf{\Delta }{\displaystyle \frac{d^{\prime }\left({\varpi }_1, {\varpi }_2\right)+m}{d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)+m}}={\Phi }_{\mathcal{X}}\left(p, q, m\right), \end{gathered}$$

and

$$\begin{gathered} O_{\mathcal{X}}\left(\psi \left(p\right),\psi \left(q\right),\overline{p}m\right)={\displaystyle \frac{d^{\prime }\left(\psi \left(p\right),\psi \left(q\right)\right)+\overline{p}m}{\overline{p}m }}, \\ ={\displaystyle \frac{\max \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\},-\min \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\},}{\max \left\{d_{\omega }\left(\psi \left({\omega }_1\right), \psi \left({\omega }_2\right)\right), d_{\varpi }\left({\psi (\varpi }_1), \psi ({\varpi }_2)\right)\right\},+\overline{p}m }}, \\ ={\displaystyle \frac{\max \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\}-\min \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\}}{\min \left\{\left|\frac{{\omega }_1}{2}-\frac{{\omega }_2}{2}\right|, \left|\frac{{\varpi }_1}{2}-\frac{{\varpi }_2}{2}\right|\right\}+\overline{p}m }} \\ \le \max \left\{{\displaystyle \frac{d_{\omega }\left({\omega }_1, {\omega }_2\right)-d_{\omega }^{\prime }\left({\omega }_1, {\omega }_2\right)}{d_{\omega }\left({\omega }_1, {\omega }_2\right)+m }}, {\displaystyle \frac{d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)-d_{\varpi }^{\prime }\left({\varpi }_1, {\varpi }_2\right)}{d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)+m }}\right\}, \\ ={\displaystyle \frac{d_{\omega }({\omega }_1, {\omega }_2)-d_{\omega }^{\prime }({\omega }_1, {\omega }_2)}{d_{\omega }\left({\omega }_1, {\omega }_2\right)+m}}\mathsf{\Delta }{\displaystyle \frac{d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)-d^{\prime }\left({\varpi }_1, {\varpi }_2\right)}{d_{\varpi }\left({\varpi }_1, {\varpi }_2\right)+m}}=O_{\mathcal{X}}\left(p, q, m\right), \end{gathered}$$

Therefore, all the conditions of Theorem 8 are satisfied, so the mapping  $\psi ,$ is a neutrosophic B-contraction on  $\mathcal{X}.$

Definition 27. 

Let  $\left(\Omega ,\Psi ,\Phi ,O,\ast ,\odot \right)$ be an NMS. Suppose  ${\phi }_n:\Omega \to \Omega$ and  $n=\mathrm{1,2},\cdots ,\omega \left(\omega \in \mathbb{N}\right)$ are N-neutrosophic B-contraction (respectively N-neutrosophic Edelstein contraction) on  $\Omega ,$ and  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}},\ast ,\odot \right)$ is the product NMS of  $\Omega .$ Assume  ${\psi }_n:\mathcal{X}\to \mathcal{X},n=\mathrm{1,2},\cdots ,\omega ,$ are N-neutrosophic B-contraction (respectively N-neutrosophic Edelstein contraction) on the product space given by

$${\psi }_n\left(a_1,a_2,\cdots ,a_{\omega }\right)=\left({\phi }_n\left(a_1\right),{\phi }_n\left(a_2\right),\cdots ,{\phi }_n\left(a_{\omega }\right)\right).$$

(33)

Then the collection  $\left\{\Omega ; {\psi }_n, n=\mathrm{1,2},\cdots ,\omega , \omega \in \mathbb{N}\right\},$ is called a neutrosophic IFS of the neutrosophic B-contraction (respectively neutrosophic Edelstein contraction) on the product NMS.

Definition 28. 

Assume that  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ is the product NMS. Let  $\left\{\mathcal{X};{\psi }_n, n=\mathrm{1,2},\cdots ,\omega , \omega \in \mathbb{N}\right\},$ be a neutrosophic IFS of the neutrosophic B-contraction (similarly neutrosophic Edelstein contractions) on  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right).$ Take  $\varrho \left(\mathcal{X}\right)$ as the set of all non-empty compact subsets of  $\mathcal{X}.$ Then the neutrosophic HB operator of the neutrosophic IFS of neutrosophic B-contractions (respectively neutrosophic Edelstein contractions) on  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ is a function  ${\Phi }^{\prime }: \varrho \left(\mathcal{X}\right)\to \varrho \left(\mathcal{X}\right)$ defined by

$${\mathsf{\Phi }}^{\prime }\left(\Psi \right)=\bigcup _{n=1}^{\omega }{\psi }_n\left(\Psi \right),$$

for all  $\Psi \in \varrho \left(\mathcal{X}\right)$. That is,

$${\mathsf{\Phi }}^{\prime }\left(\Psi \right)=\bigcup _{n=1}^{\omega }\left({\phi }_n\left(a_1\right),{\phi }_n\left(a_2\right),\cdots ,{\phi }_n\left(a_{\omega }\right)\right),$$

for all  $a=\left(a_1,a_2,\cdots ,a_{\omega }\right)\in \Psi \in \varrho \left(\mathcal{X}\right).$

In the next study, we extend neutrosophic B-contractions to the Hausdorff product NMS, ensuring controlled contraction behavior between set-valued mappings.

Theorem 9. 

Let  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ be a product NMS. If  $(\varrho \left(\mathcal{X}\right),{\mathcal{H}}_{{\Psi }_{\mathcal{X}}},{\mathcal{H}}_{{\Phi }_{\mathcal{X}}}, {\mathcal{H}}_{O_{\mathcal{X}}},\ast ,\odot )$ is the associated Hausdorff product NMS. Suppose  $\psi :\mathcal{X}\to \mathcal{X},$ is a neutrosophic B-contraction on  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right).$ Then for  $\overline{p}\in \left(\mathrm{0,1}\right),$

$${\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left(\psi \left({\Psi }_1\right),\psi \left({\Phi }_1\right),\overline{p}m\right)\ge {\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right),$$

(34)

$${\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left(\psi \left({\Psi }_1\right),\psi \left({\Phi }_1\right),\overline{p}m\right)\le {\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right),$$

(35)

$${\mathcal{H}}_{O_{\mathcal{X}}}\left(\psi \left({\Psi }_1\right),\psi \left({\Phi }_1\right),\overline{p}m\right)\le {\mathcal{H}}_{O_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right),$$

(36)

for all  ${\Psi }_1,{\Phi }_1\in \varrho \left(\mathcal{X}\right),$ and  $m>0.$

Proof. 

For any fixed $m>0.$ Take all ${\Psi }_1,{\Phi }_1\in \varrho \left(\mathcal{X}\right).$ Usage of Theorem 7 implies for any $\overline{p}\in \left(\mathrm{0,1}\right),$

$${\Psi }_{\mathcal{X}}\left(\psi \left(a_1\right),\psi \left(b_1\right),\overline{p}m\right)\ge {\Psi }_{\mathcal{X}}\left(a_1,b_1,m\right),$$

for all $a_1,b_1\in \mathcal{X}\ge {\Psi }_{\mathcal{X}}\left(a_1,b_1,m\right)$ for all $a_1\in \Psi$ and $b_1\in {\Phi }_1,$

$$\begin{gathered} \underset{b_1\in {\Phi }_1}{\sup }{\Psi }_{\mathcal{X}}\left(\psi \left(a_1\right),\psi \left(b_1\right),\overline{p}m\right)\ge {\underset{b_1\in {\Phi }_1}{\mathrm{s}\mathrm{u}\mathrm{p}}\Psi }_{\mathcal{X}}\left(a_1,b_1,m\right) \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} a_1\in {\Psi }_1, \\ {\Psi }_{\mathcal{X}}\left(\psi \left(a_1\right),\psi \left({\Phi }_1\right),\overline{p}m\right)\ge {\Psi }_{\mathcal{X}}\left(a_1,{\Phi }_1,m\right) \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} a_1\in {\Psi }_1, \\ \underset{a_1\in {\Psi }_1}{\inf }{\Psi }_{\mathcal{X}}\left(\psi \left(a_1\right),\psi \left({\Phi }_1\right),\overline{p}m\right)\ge {\underset{b_1\in {\Phi }_1}{\mathrm{s}\mathrm{u}\mathrm{p}}\Psi }_{\mathcal{X}}\left(a_1,{\Phi }_1,m\right) \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} a_1\in {\Psi }_1, \\ {\Psi }_{\mathcal{X}}\left(\psi \left(a_1\right),\psi \left({\Phi }_1\right),\overline{p}m\right)\ge {\Psi }_{\mathcal{X}}\left(a_1,{\Phi }_1,m\right). \end{gathered}$$

Similarly, we can get

$${\Psi }_{\mathcal{X}}\left(\psi \left({\Phi }_1\right),\psi \left({\Psi }_1\right),\overline{p}m\right)\ge {\Psi }_{\mathcal{X}}\left({\Phi }_1,{\Psi }_1,m\right).$$

Now

$$\begin{gathered} \min \left\{{\Psi }_{\mathcal{X}}\left(\psi \left({\Psi }_1\right),\psi \left({\Phi }_1\right), \overline{p}m\right),{\Psi }_{\mathcal{X}}\left(\psi \left({\Phi }_1\right),\psi \left({\Psi }_1\right), \overline{p}m\right)\right\} \\ \ge \min \left\{{\Psi }_{\mathcal{X}}\left({\Psi }_1,{\Phi }_1,m\right),{\Psi }_{\mathcal{X}}\left({\Phi }_1,{\Psi }_1,m\right)\right\}, \end{gathered}$$

i.e.,

$${\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left(\psi \left({\Psi }_1\right),\psi \left({\Phi }_1\right),\overline{p}m\right)\ge {\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right).$$

(37)

By replacing ${\Psi }_{\mathcal{X}}$ by ${\Phi }_{\mathcal{X}}$ and $O_{\mathcal{X}}$ sup by inf, and changing the corresponding inequality, we have the following:

$${\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left(\psi \left({\Psi }_1\right),\psi \left({\Phi }_1\right),\overline{p}m\right)\le {\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right),$$

(38)

$${\mathcal{H}}_{O_{\mathcal{X}}}\left(\psi \left({\Psi }_1\right),\psi \left({\Phi }_1\right),\overline{p}m\right)\le {\mathcal{H}}_{O_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right).$$

(39)

From inequalities (37)–(39), we have the required inequality. □

Next, the theorem extends the neutrosophic Edelstein contraction to the Hausdorff product NMS, ensuring that the contraction property holds for set-valued mappings.

Theorem 10. 

Let  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ be a product NMS. Suppose  $(\varrho \left(\mathcal{X}\right),{\mathcal{H}}_{{\Psi }_{\mathcal{X}}},{\mathcal{H}}_{{\Phi }_{\mathcal{X}}}, {\mathcal{H}}_{O_{\mathcal{X}}},\ast ,\odot )$ is the related Hausdorff product NMS. Suppose  $\psi :\mathcal{X}\to \mathcal{X},$ is a neutrosophic Edelstein contraction on  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}},O_{\mathcal{X}},\ast ,\odot \right).$ Then for  $\overline{p}\in \left(\mathrm{0,1}\right),$

$${\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left(\psi \left({\Psi }_1\right),\psi \left({\Phi }_1\right),\ast \right)\ge {\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left(a_1,b_1,\ast \right),$$

(40)

$${\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left(\psi \left({\Psi }_1\right),\psi \left({\Phi }_1\right),\odot \right)\le {\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,\odot \right),$$

(41)

$${\mathcal{H}}_{O_{\mathcal{X}}}\left(\psi \left({\Psi }_1\right),\psi \left({\Phi }_1\right),\odot \right)\le {\mathcal{H}}_{O_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,\odot \right),$$

(42)

for all  ${\Psi }_1,{\Phi }_1\in \varrho \left(\mathcal{X}\right),$ such that  ${\Psi }_1\cap {\Phi }_1=\varnothing .$

Proof. 

The proof of the current Theorem will occur by retracting the proof of Theorem 9 for any two disjoint set ${\Psi }_1,{\Phi }_1\in \varrho \left(\mathcal{X}\right),$ and for any constant$\overline{p}\in \left(\mathrm{0,1}\right).$ □

In the below theorem, the HB operator formed from a sequence of N-neutrosophic B-contractions ${\psi }_n$ retains the B-contraction property in the Hausdorff product NMS.

Theorem 11. 

If  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ is a product of NMS. Let  $\left(\varrho \left(\mathcal{X}\right),{\mathcal{H}}_{{\Psi }_{\mathcal{X}}},{\mathcal{H}}_{{\Phi }_{\mathcal{X}}},\ast ,\odot \right),$ is the related Hausdorff product NMS. Assume  ${\psi }_n:\mathcal{X}\to \mathcal{X},n=\mathrm{1,2},\cdots ,\omega ,$ are N-neutrosophic B-contraction on  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right).$ Then the HB operator is a neutrosophic B-contraction on  $\left(\varrho \left(\mathcal{X}\right),{\mathcal{H}}_{{\Psi }_{\mathcal{X}}},{\mathcal{H}}_{{\Phi }_{\mathcal{X}}}, {\mathcal{H}}_{O_{\mathcal{X}}},\ast ,\odot \right).$

Proof. 

Fix $m>0,$ take ${\Psi }_1,{\Phi }_1\in \varrho \left(\mathcal{X}\right),$ then for a given $\overline{p}\in \left(\mathrm{0,1}\right).$ Using Theorem 7, we get

$$\begin{gathered} {\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left({\mathsf{\Phi }}^{\prime }\left({\Psi }_1\right),{\mathsf{\Phi }}^{\prime }\left({\Phi }_1\right),\overline{p}m\right)={\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left(\bigcup _{n=1}^{\omega }{\psi }_n\left({\Psi }_1\right),\bigcup _{n=1}^{\omega }{\psi }_n\left({\Phi }_1\right),\overline{p}m\right) \\ \ge \underset{1\le n\le \omega }{\min }{\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left({\psi }_n\left({\Psi }_1\right),{\psi }_n\left({\Phi }_1\right),\overline{p}m\right)\ge {\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right) \\ \ge {\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left({\mathsf{\Phi }}^{\prime }\left({\Psi }_1\right),{\mathsf{\Phi }}^{\prime } \left({\Phi }_1\right),\overline{p}m\right)\ge {\mathcal{H}}_{{\Psi }_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right). \end{gathered}$$

and

$$\begin{gathered} {\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left({\mathsf{\Phi }}^{\prime }\left({\Psi }_1\right),{\mathsf{\Phi }}^{\prime } \left({\Phi }_1\right),\overline{p}m\right)={\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left(\bigcup _{n=1}^{\omega }{\psi }_n\left({\Psi }_1\right),\bigcup _{n=1}^{\omega }{\psi }_n\left({\Phi }_1\right),\overline{p}m\right) \\ \le \underset{1\le n\le \omega }{\max }{\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left({\psi }_n\left({\Psi }_1\right),{\psi }_n\left({\Phi }_1\right),\overline{p}m\right)\le {\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right) \\ \le {\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left({\mathsf{\Phi }}^{\prime }\left({\Psi }_1\right),{\mathsf{\Phi }}^{\prime } \left({\Phi }_1\right),\overline{p}m\right)\le {\mathcal{H}}_{{\Phi }_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right). \end{gathered}$$

Proceeding on the similar lines, we have

$$\begin{gathered} \left({\mathsf{\Phi }}^{\prime }\left({\Psi }_1\right),{\mathsf{\Phi }}^{\prime } \left({\Phi }_1\right),\overline{p}m\right)={\mathcal{H}}_{O_{\mathcal{X}}} \left(\bigcup _{n=1}^{\omega }{\psi }_n\left({\Psi }_1\right),\bigcup _{n=1}^{\omega }{\psi }_n\left({\Phi }_1\right),\overline{p}m\right) \\ \le \underset{1\le n\le \omega }{\max }{\mathcal{H}}_{O_{\mathcal{X}}}\left({\psi }_n\left({\Psi }_1\right),{\psi }_n\left({\Phi }_1\right),\overline{p}m\right)\le {\mathcal{H}}_{O_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right) \\ \le {\mathcal{H}}_{O_{\mathcal{X}}}\left({\mathsf{\Phi }}^{\prime }\left({\Psi }_1\right),{\mathsf{\Phi }}^{\prime } \left({\Phi }_1\right),\overline{p}m\right)\le {\mathcal{H}}_{O_{\mathcal{X}}}\left({\Psi }_1,{\Phi }_1,m\right). \end{gathered}$$

Therefore, ${\mathsf{\Phi }}^{\prime }$ is a neutrosophic B-contraction. □

The next result ensures convergence and stability in iterative processes involving complex systems with uncertainty and indeterminate data.

Theorem 12. 

If  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ is a product of NMS. Assume  $\left(\varrho \left(\mathcal{X}\right),{\mathcal{H}}_{{\Psi }_{\mathcal{X}}},{\mathcal{H}}_{{\Phi }_{\mathcal{X}}}, {\mathcal{H}}_{O_{\mathcal{X}}},\ast ,\odot \right)$ is the associated Hausdorff product NMS. Suppose  ${\psi }_n:\mathcal{X}\to \mathcal{X},n=\mathrm{1,2},\cdots ,\omega ,$ are N-neutrosophic Edelstein contraction on  $\left(\mathcal{X},{\Psi }_{{\mathcal{X}}_{d^{\prime } } },{\Phi }_{{\mathcal{X}}_{d^{\prime } }},O_{{\mathcal{X}}_{d^{\prime } }},\ast ,\odot \right).$ Then the HB operator is a neutrosophic Edelstein contraction on  $\left(\varrho \left(\mathcal{X}\right),{\mathcal{H}}_{{\Psi }_{\mathcal{X}}},{\mathcal{H}}_{{\Phi }_{\mathcal{X}}}, {\mathcal{H}}_{O_{\mathcal{X}}},\ast ,\odot \right).$

Proof. 

On the same steps in the proof of Theorem 11 examined this theorem for any ${\Psi }_1,{\Phi }_1\in \varrho \left(\mathcal{X}\right)$. □

The following results guarantee the existence and uniqueness of a compact invariant set ${\Psi }_{\infty }$ as a fixed point of the neutrosophic HB operator in a complete NMS.

Theorem 13. 

Suppose  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ is a complete NMS. Let  $\left\{\mathcal{X};{\psi }_n, n=\mathrm{1,2},\cdots ,\omega , \omega \in \mathbb{N}\right\},$ be a neutrosophic IFS of neutrosophic B-contractions on  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}},O_{\mathcal{X}},\ast ,\odot \right)$ and ${\mathit{\Phi }}^{\mathit{\prime }}$ be the neutrosophic HB operator of the neutrosophic IFS. Then, there exists only one compact invariant set  ${\Psi }_{\infty }\in \varrho \left(\mathcal{X}\right),$ of the HB operator or, equivalently,  ${\Phi }^{\prime }$ has a unique FP namely ${\Psi }_{\infty }\in \varrho \left(\mathcal{X}\right).$

Proof. 

Since $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ is a complete NMS and by Theorem 3, we have $\left(\varrho \left(\mathcal{X}\right),{\mathcal{H}}_{{\Psi }_{\mathcal{X}}},{\mathcal{H}}_{{\Phi }_{\mathcal{X}}},{\mathcal{H}}_{O_{\mathcal{X}}},\ast ,\odot \right),$ is also complete Hausdorff NMS. It can be easily shown that the HB operator ${\Phi }^{\prime }$ is a neutrosophic B-contraction by Theorem 9. Then by the neutrosophic Banach contraction theorem (Theorem 7 in Ref. [30]) and with reference of Definition 28, we say that ${\Phi }^{\prime }$ has a unique FP namely${\Psi }_{\infty }\in \varrho \left(\mathcal{X}\right).$ □

Theorem 14. 

Suppose  $\left(\mathcal{X},{\Psi }_{\mathcal{X}},{\Phi }_{\mathcal{X}}, O_{\mathcal{X}},\ast ,\odot \right)$ is a complete NMS. Let  $\left\{\mathcal{X};{\psi }_n, n=\mathrm{1,2},\cdots ,\omega , \omega \in \mathbb{N}\right\},$ be a neutrosophic IFS of neutrosophic Edelstein contraction and  ${\Phi }^{\prime }$ be the neutrosophic HB operator of neutrosophic Edelstein contraction. Then, there exists only one compact invariant set  ${\Psi }_{\infty }\in \varrho \left(\mathcal{X}\right)$ of the HB operator or, equivalently, ${\Phi }^{\prime }$ has a unique FP namely ${\Psi }_{\infty }\in \varrho \left(\mathcal{X}\right).$

Proof. 

The same arguments of Theorems 6, 12, and 13 are concluded as the proof. □

Now, we conclude that the neutrosophic attractor or fractal on complete space (respectively, compact space) as the set ${\Psi }_{\infty }\in \varrho \left(\mathcal{X}\right)$ which is obtained in Theorem 11 for complete space (respectively Theorem 14 for compact space). Such ${\Psi }_{\infty }\in \varrho \left(\mathcal{X}\right)$ is also called a fractal generated by the neutrosophic IFS of neutrosophic B-contractions (respectively neutrosophic Edelstein contractions) and so-called neutrosophic fractals on complete space (compact space).

6. Conclusions

In this study, we implemented the idea of product neutrosophic fractal space in the sense of neutrosophic B-contraction and neutrosophic Edelstein contraction. We studied the HB theory in this new fractal space and proved that the HB operator is a neutrosophic B-contraction, and neutrosophic Edelstein contraction on the corresponding Hausdorff product neutrosophic metric space having neutrosophic B-contraction and neutrosophic Edelstein contraction as the neutrosophic IFS. Further, we provided the definition for the product neutrosophic fractal produced by the neutrosophic IFS consisting of neutrosophic B-contractions and neutrosophic Edelstein contractions. Furthermore, we introduced a fuzzy version of an α-dense curve that was used by the author to approximate (with arbitrarily small and controlled error) the attractor set of certain IFSs. This work is extendable in the context of neutrosophic controlled metric spaces, neutrosophic partial metric spaces, neutrosophic product partial metric spaces, and many other similar structures.