A Distributed-Order Fractional Hyperchaotic Detuned Laser Model: Dynamics, Multistability, and Dual Combination Synchronization

Abstract

The aim of this article is to introduce the distributed-order hyperchaotic detuned (DOHD) laser model. Its dissipative dynamics, invariance, and fixed points (FPs) and their stability are investigated. Numerical solutions of the DOHD laser model are computed using the modified Predictor–Corrector approach. Its viscoelasticity is described by the so-called DO derivative, allowing for the study of different technical systems and materials, and the model is found to have a whole circle of FPs as a hyperchaotic attractor. We discuss the coexistence of more attractors under various initial conditions and the same sets of parameters for our model (multistability). We also introduce the notion of dual combination synchronization (DCS), using four integer-order drive models and two DO response models. A theorem is stated and proved to obtain an analytical control function that ensures DCS for our models. Numerical simulations are presented to support these analytical results. Regarding the use of the well–known Caputo derivative, the results are very similar to those of DO, except when the Caputo order, $0<\sigma \le 1$, is very close to 1, where the dynamics shows a “spiralling behavior” towards a fixed point. In all other cases, both Caputo and DO exhibit a very similar behavior.

1. Introduction

The distributed-order (DO) fractional calculus was discussed for the first time in 1969 in [1]. It was argued then that the DO derivative is a generalization of fractional and integer-order derivatives. Caputo and others, in [2,3], developed what they called the DO calculus. In viscoelasticity, the DO operator provides a flexible framework to interpolate between different fractional orders, thereby modeling a broad spectrum of hereditary behaviors in materials. Furthermore, we emphasize the model’s improved performance in terms of richer dynamical behaviors, enhanced sensitivity to initial conditions, and the ability to generate more complex attractors. We have also noted the computational benefits, as the DO approach allows for efficient numerical integration by balancing accuracy and stability [4,5,6,7,8].

DO differential equations have several uses in the fields of secure communication, image encryption, physics, and circuit implementation [9,10,11,12]. Aboelenen [13] proposed a local discontinuous Galerkin finite element approach for DO time, Riesz space-fractional convection–diffusion, and Schrödinger-type problems. Chaos synchronization of the DO Lorenz model using chaotic masking is presented. Secure communications using DO hyperchaotic masking for a text that consists of symbols, spaces, numbers, and alphabets are examined in [9]. Abed-Elhameed et al. [12] introduced a scheme for image encryption based on adaptive synchronization.

The authors of [14] proposed the complex detuned lasers model as follows:

$$\begin{array}{c}\dot{u}=av-a(1-ic)u,\hfill \\ \dot{v}=(d-w)u-(1+ic)v,\hfill \\ \dot{w}=-bw+{\displaystyle \frac{1}{2}}(\overline{u}v+u\overline{v}),\hfill \end{array}$$

(1)

where $u=w_{11}+i{w}_{12}$, $v=w_{13}+i{w}_{14}$, $i=\sqrt{-1}$, $w=w_{15}$, the positive real parameters are a, b, c, and d, the complex conjugate variable is denoted by $\left(\overline{\dots }\right)$, and the time derivatives are represented by dots. The state variables w, v, and u in a ring laser system of two-level atoms are related to population inversion, polarization, and electric field amplitude, respectively, as illustrated in [15]. The dynamics and synchronization characteristics of complex detuned lasers (1) were investigated by Mahmoud et al. [16], and in this five-dimensional model [16] only chaotic attractors were found to exist. Using a novel image cryptosystem for high security, Li et al. [17] discussed the seven-dimensional fractional-order hyperchaotic detuned laser model.

The real form of (1) is written as

$$\begin{array}{c}{\dot{w}}_{11}=a(w_{13}-w_{11})-ab{w}_{12},\hfill \\ {\dot{w}}_{12}=a(w_{14}-w_{12})+ab{w}_{11},\hfill \\ {\dot{w}}_{13}=(c-w_{15})w_{11}+w_{14}{w}_{12}-w_{13},\hfill \\ {\dot{w}}_{14}=(c-w_{15})w_{12}-w_{13}{w}_{12}-w_{14},\hfill \\ {\dot{w}}_{15}=-d{w}_{15}+w_{11}{w}_{13}+w_{12}{w}_{14},\hfill \end{array}$$

(2)

where $w_{11},w_{12},w_{13},w_{14}$, and $w_{15}$ are real state variables.

Based on the model (2), the fractional-order detuned laser model can be written as

$$\begin{array}{c}{}^{C}D^{\sigma }{w}_{11}=a(w_{13}-w_{11})-ab{w}_{12},\hfill \\ {}^{C}D^{\sigma }{w}_{12}=a(w_{14}-w_{12})+ab{w}_{11},\hfill \\ {}^{C}D^{\sigma }{w}_{13}=(c-w_{15})w_{11}+w_{14}{w}_{12}-w_{13},\hfill \\ {}^{C}D^{\sigma }{w}_{14}=(c-w_{15})w_{12}-w_{13}{w}_{12}-w_{14},\hfill \\ {}^{C}D^{\sigma }{w}_{15}=-d{w}_{15}+w_{11}{w}_{13}+w_{12}{w}_{14},\hfill \end{array}$$

(3)

where ${}^{C}D^{\sigma }$ stands for the Caputo fractional derivative $(0<\sigma \le 1)$ [1], $w_{1j}\in \mathbf{R}$, $j=1,2,\dots ,5$, and $a,b,c$, and d are the real parameters of model (3).

In this paper, we focus on what we call the distributed-order hyperchaotic detuned (DOHD) laser model, given as follows:

$$\begin{array}{c}{D}^{\psi \left(\sigma \right)}{w}_{11}=a(w_{13}-w_{11})-ab{w}_{12},\hfill \\ D^{\psi \left(\sigma \right)}{w}_{12}=a(w_{14}-w_{12})+ab{w}_{11},\hfill \\ D^{\psi \left(\sigma \right)}{w}_{13}=(c-w_{15})w_{11}+w_{14}{w}_{12}-w_{13},\hfill \\ D^{\psi \left(\sigma \right)}{w}_{14}=(c-w_{15})w_{12}-w_{13}{w}_{12}-w_{14},\hfill \\ D^{\psi \left(\sigma \right)}{w}_{15}=-d{w}_{15}+w_{11}{w}_{13}+w_{12}{w}_{14},\hfill \end{array}$$

(4)

Extreme multistability and multistability phenomena have recently become very important in the study of chaotic models. Indeed, multistability frequently appears in nonlinear dynamical systems and denotes the presence of multiple attractors for the same set of model parameters [18]. Additionally, this phenomenon is often referred to as extreme multistability when an infinite number of attractors coexist for the same set of model parameters [19]. An enhanced two stable node-foci example of Chua’s circuit was investigated and the model’s multistability was examined in [20]. In [21], coexisting chaotic attractors, as well as periodic and point attractors, were studied in a new 4D smooth chaotic model. Chen [22] discovered many kinds of coexisting behaviors, such as coexisting chaotic and periodic attractors, chaotic attractors and singular degenerate heteroclinic cycles, different kinds of periodic attractors, as well as periodic attractors and singular degenerate heteroclinic cycles. Moreover, the phenomenon of extreme multistability, with an infinite number of hidden attractors, was investigated in a novel memristive hyperchaotic model in [23]. Mengxin et al. [24] also observed the phenomenon of extreme multistability in a complex simplified Lorenz model with integer-order derivatives. Finally, a logarithmic memcapacitor model was comprehensively investigated with coexisting attractors and multistable coexisting oscillations in [25].

The synchronization of hyperchaotic (or chaotic) models is an essential branch of nonlinear dynamics research. It has been thoroughly studied in a number of areas, such as circuit implementation [12], neural networks [26], color image encryption [10], and secure communications [9]. Many types of synchronization, including complete synchronization [3], projective synchronization [26], adaptive synchronization [12], and the generalization of combination synchronization [10] were investigated for DO models.

In this article, we present the dynamics and numerical solutions of the DOHD laser model (4) for the first time. The coexistence of several attractors with the same parameter set but different initial conditions is investigated, while we also study the dual combination synchronization (DCS) for integer and DO hyperchaotic models. Other types of synchronization can also be studied, as particular cases of the suggested DCS phenomenon, as noted in the literature. Here, using the tracking control technique [27], we present schemes for the DCS with four drive and two response integer and distributed-order models, respectively. To derive analytical formulas for control functions, we formulate and prove a new theorem. A particular case is provided to demonstrate how well the numerical and analytical results agree with each other. To this end, here, we applied the modified Predictor–Corrector approach [3] to obtain our numerical results.

The format of this article is as follows. A preliminary introduction and an application of the Caputo fractional derivative to our model are given in Section 2 and Section 3, respectively. Next, the dynamical properties and Lyapunov exponents (LEs) of the proposed model (4) are calculated in Section 4. Section 5 contains the numerical simulations of the multistability phenomenon for a model with various coexisting attractors. A scheme to achieve the DCS using the tracking control technique is investigated in Section 6. Furthermore, a particular case is provided to demonstrate the validity of the generated analytical control functions. Our overall conclusions are described in the final section.

2. Application of the Caputo Fractional Derivative to the Model (3)

In this Section, we use the classical form of the Caputo derivative, as stated in Equation (3) of Section 3, and present the results on their chaotic behavior in Figure 1 and Figure 2 (see below). The reader is advised to inspect these figures, in connection with their corresponding data, described in the subsection that follows, and compare them with the results of the DO derivative presented in later sections of the paper.

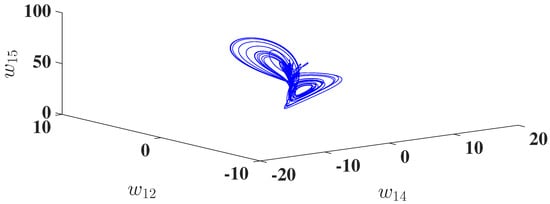
Figure 1. Chaotic attractors for the fractional order detuned laser model (3) for $(a,b,c,d,\sigma )=(10,0.001,41.3,1.2,0.99)$, $(w_{14},w_{12},w_{15})$ space.

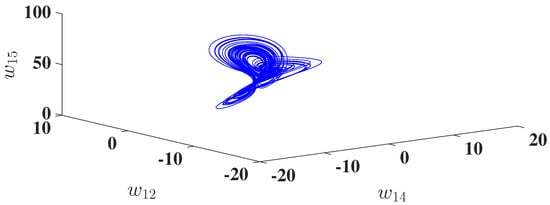
Figure 2. Chaotic attractors for the fractional order detuned laser model (3) for $(a,b,c,d,\sigma )=(10,0.001,41.3,1.2,1)$, $(w_{14},w_{12},w_{15})$ space.

2.1. Numerical Solutions of the Fractional-Order Detuned Laser Model (3)

The numerical solutions of the fractional-order detuned laser model (3) are computed applying the Predictor–Corrector technique [28]. We calculated the LEs by a modified technique of the well–known Wolf algorithm [29] implemented using a MATLAB R2016a software program. This model has five LEs ${\mathsf{\Gamma }}_i,i=1,\dots ,5$. The signs of these LEs give a useful characterization of the dynamics of this model’s solutions [10]. For the following cases, we determined the LEs for an observation time 1000, sampling size 0.001 and the initial conditions ${(w_{11},w_{12},w_{13},w_{14},w_{15})}^T\left(0\right)={(2,1,5,3,4)}^T$, where T denotes the transpose.

2.1.1. Solutions That Approach Fixed Points

For model (3), if we choose $(a,b,c,d,\sigma )=(10,0.001,41.3,1.2,0.92)$, we obtain the following values of the LEs: ${\mathsf{\Gamma }}_1=-0.0001$, ${\mathsf{\Gamma }}_2=-1.3139$, ${\mathsf{\Gamma }}_3=-1.3185$, ${\mathsf{\Gamma }}_4=-16.0130$ and ${\mathsf{\Gamma }}_5=-16.0115$. These imply that the solution of model (3) approaches a stable fixed point in the 5-dimensional space and indeed we find numerically that it does. The same holds true for $\sigma =0.95,0.96$.

2.1.2. Solutions That Approach a Chaotic Attractor

It is important, however, to note that for $(a,b,c,d)=(10,0.001,41.3,1.2)$ and $\sigma =0.97,0.98,0.99$, the Caputo derivative model (3) continues to have a chaotic attractor, as in the case $\sigma =1$, see, e.g., Figure 1 and Figure 2. This is very interesting, as one might have expected that for all $\sigma <1$ values, the dynamics would lead to a stable fixed point.

2.1.3. The Difference Between Caputo and DO Dynamics

We emphasize that the DO derivative studied here extends the property of the dynamics, beyond the Caputo derivative, by integrating over all $\sigma$. Thus, as we describe below, it leads not only to stable fixed points but also to chaotic and hyperchaotic attractors.

3. Preliminaries

In this section, we provide definitions, lemmas, and a theorem [1,3,30] for our analysis of the DO derivative, which constitute the fundamental ideas of the paper.

Definition 1 

([1]). For any $r\in {\mathbb{N}}^{+},(r-1<\sigma \le r).$ For the function $w\left(t\right)$, the Caputo fractional derivative is defined as follows:

$${}^{C}D^{\sigma }w\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(r-\sigma )}}{\int }_0^t{\displaystyle \frac{w^{\left(r\right)}\left(u\right)}{{(t-u)}^{\sigma -r+1}}}du.$$

(5)

Definition 2 

([30]). The distributed derivative of any continuous function $w\left(t\right)$ is

$$D^{\psi \left(\sigma \right)}w\left(t\right)={\int }_{r-1}^r\psi {\left(\sigma \right)}^C{D}^{\sigma }w\left(t\right)d\sigma \approx \sum _{j=1}^m\psi {\left({\sigma }_j\right)}^C{D}^{{\sigma }_j}w\left(t\right)\mathsf{\Delta }{\nu }_j,$$

(6)

where $r-1<\sigma \le r$, $0={\nu }_0<{\nu }_1<\dots {\nu }_m=1,\mathsf{\Delta }{\nu }_j={\nu }_j-{\nu }_{j-1}={\displaystyle \frac{1}{m}},{\sigma }_j={\displaystyle \frac{{\nu }_j+{\nu }_{j-1}}{2}}={\displaystyle \frac{2j-1}{2m}},j=1,2,\dots ,m,m\in \mathbb{N}$.

Theorem 1 

([3]). Assume that a dynamical system with DO on several terms of our fractional-order model is given by

$${\Sigma }_{j=1}^m\psi {\left({\sigma }_j\right)}^C{D}^{{\sigma }_j}w\left(t\right)\mathsf{\Delta }{\nu }_j=JF\left(w\left(t\right)\right)+f\left(w\left(t\right)\right),$$

(7)

where $w\in {\mathbb{R}}^n$ and let $\xi \left({\displaystyle \frac{{\delta }_{i-1}}{{\delta }_i}}\right)$ represent the eigenvalues of ${\displaystyle \frac{{\delta }_{i-1}}{{\delta }_i}}$, if

1. 

$\underset{\parallel w\left(t\right)\parallel \to 0}{lim}{\displaystyle \frac{\parallel f\left(w\right(t\left)\right)\parallel }{\parallel w\left(t\right)\parallel }}=0;$

2. 

$|arg\left({\xi }_k(-{\displaystyle \frac{{\delta }_{i-1}}{{\delta }_i}})\right)|>{\displaystyle \frac{\pi {\lambda }_i}{2}},k=1,2,3,\dots ,n;i=1,2,3,\dots ,m.$

where f contains the nonlinear terms of our model, J is the $m\times m$ constant matrix, ${\delta }_m\in {\mathbb{R}}^{n\times n}$ so that ${\delta }_0=-J,{\delta }_j=I\mathsf{\Delta }{\nu }_j\psi \left({\sigma }_j\right),j=1,\dots ,m$, ${\lambda }_m={\sigma }_m-{\sigma }_{m-1}$, I is the $(m\times m)$ identity matrix, and $(m+1)$ is the number of steps for $\sigma \in [0,1)$. It follows that (7) has a zero solution that is asymptotically stable.

Lemma 1 

([31]). Assume that a Lyapunov function $V(t,w(t\left)\right)$ exists that satisfies

$$r_1{\parallel w\parallel }^a\le V(t,w\left(t\right))\le r_2{\parallel w\parallel }^{ab},$$

(8)

$$D^{\psi \left(\sigma \right)}V(t,w\left(t\right))\le -r_3{\parallel w\parallel }^{ab},$$

(9)

where $a,b,r_i>0,i=1,2,3$ and $\sigma \in (0,1]$. Thus, $\overline{w}=0$ is Mittag–Leffler stable, where $\overline{w}$ is a FP for the DO model (7). If these assumptions hold globally on ${\mathbb{R}}^n$, then $\overline{w}$ is globally Mittag–Leffler stable.

Lemma 2 

([31]). Let $w\left(t\right)\in {\mathbb{R}}^n$ be a differentiable function, hence

$${\displaystyle \frac{1}{2}}{D}^{\psi \left(\sigma \right)}{w}^T\left(t\right)w\left(t\right)\le w^T\left(t\right)D^{\psi \left(\sigma \right)}w\left(t\right),$$

(10)

where T denotes the transpose operation.

4. Analysis of the DOHD Laser Model (4)

In this section, we examine the dissipation, invariance, FPs, stability, and coexistence properties of a hyperchaotic attractor of the DOHD laser model (4).

4.1. Invariance and Dissipation

Under the transformation $(w_{11},w_{12},w_{13},w_{14},w_{15})\to (-w_{11},-w_{12},-w_{13},-w_{14},w_{15})$, the model (4) is symmetric, and $w_{15}$ is the axis of rotational symmetry. The divergence of (4) is as follows:

$$\nabla ·F=\sum _{i,j=1}^5{\displaystyle \frac{\partial \dot{w_{ij}}}{\partial w_{ij}}}=-(2a+d+2).$$

Consequently, we can conclude that our model (4) is dissipative when $2a+d+2>0$.

4.2. Fixed Points and Their Stability

First, the FPs of model (4) can be obtained as follows:

$$\begin{array}{c}a(w_{13}-w_{11})-ab{w}_{12}=0,\hfill \\ a(w_{14}-w_{12})+ab{w}_{11}=0,\hfill \\ (c-w_{15})w_{11}+w_{14}{w}_{12}-w_{13}=0,\hfill \\ (c-w_{15})w_{12}-w_{13}{w}_{12}-w_{14}=0,\hfill \\ -d{w}_{15}+w_{11}{w}_{13}+w_{12}{w}_{14}=0.\hfill \end{array}$$

(11)

One solution of (4) is clearly $F_0=(0,0,0,0,0)$, which is the trivial FP, while we also obtain a circle of nontrivial FPs $F_{\theta }$ as follows:

$$\begin{gathered} w_{11}=rcos\theta ,w_{12}=rsin\theta ,w_{13}=rcos\theta +brsin\theta ,w_{14}=rsin\theta -brcos\theta , \\ {w}_{15}=(c-1-b^2), (w_{11}^2+w_{12}^2=r^2), \end{gathered}$$

where $r=\sqrt{d(c-1-b^2)}$ and $\theta \in [0,2\pi ]$. So, model (4) has the circle of FPs: $F_{\theta }=(rcos\theta ,rsin\theta ,rcos\theta +brsin\theta ,rsin\theta -brcos\theta ,(c-1-b^2))$.

For model (4), we analyze the stability of $F_0=(0,0,0,0,0)$ by applying Theorem 1. The first condition of Theorem 1 can be tested using the following steps:

$$\begin{array}{cc}\hfill \underset{\parallel w\left(t\right)\parallel \to 0}{lim}{\displaystyle \frac{\parallel f\left(w\right(t\left)\right)\parallel }{\parallel w\left(t\right)\parallel }}& =\underset{\parallel w\left(t\right)\parallel \to 0}{lim}{\displaystyle \frac{\sqrt{{(-w_{15}{w}_{11})}^2+{(-w_{15}{w}_{12})}^2+{\left(w_{11}{w}_{13}\right)}^2+{\left(w_{12}{w}_{14}\right)}^2}}{\parallel w\left(t\right)\parallel }}\hfill \\ & =\underset{\parallel w\left(t\right)\parallel \to 0}{lim}{\displaystyle \frac{\sqrt{w_{15}^2(w_{11}^2+w_{12}^2)+w_{11}^2{w}_{13}^2+w_{12}^2{w}_{14}^2}}{\parallel w\left(t\right)\parallel }}\hfill \\ & \le \underset{\parallel w\left(t\right)\parallel \to 0}{lim}{\displaystyle \frac{{3\parallel w\left(t\right)\parallel }^4}{\parallel w\left(t\right)\parallel }}=\underset{\parallel w\left(t\right)\parallel \to 0}{lim}3{\parallel w\left(t\right)\parallel }^3=0,\hfill \end{array}$$

(12)

where $w={(w_{11},w_{12},w_{13},w_{14},w_{15})}^T$.

We test a particular case by examining the second requirement of Theorem 1, as the stability cannot be known in general. The form of trivial FPs is $F_0={(0,0,0,0,0)}^T$. Taking $m=30,\psi \left(\sigma \right)={\displaystyle \frac{{\sigma }^2}{300{(1-\sigma )}^2}},k=1$ and $\mathsf{\Delta }{\nu }_1={\displaystyle \frac{1}{m}}$, we find

$$-{\displaystyle \frac{{\delta }_0}{{\delta }_1}}=3.19193\times {10}^8\left(\begin{array}{ccccc}-a& -ab& a& 0& 0\\ ab& -a& 0& a& 0\\ c& 0& -1& b& 0\\ 0& c& -b& -1& 0\\ 0& 0& 0& 0& -d\end{array}\right),$$

(13)

where ${\delta }_0=-J$, ${\delta }_1={\displaystyle \frac{1}{30}}I\psi \left({\displaystyle \frac{1}{60}}\right)$, I is a $(5\times 5)$ identity matrix and J is the matrix of the linear part of model (4). The equivalent characteristic polynomial is

$$p\left(\xi \right)=-\left[(d+\xi )\left(-2a\left(a{b}^{2}c-2b\xi +\xi (-1+c-\xi )(1+\xi )\right)+(2ab+2\xi )(2b+2(1+\xi ))+2a\left(2b+2(1-c+\xi )\right)\right)\right],$$

(14)

this indicates that each point on this circle is stable if $|arg\left({\xi }_i\right)|>{\displaystyle \frac{\alpha \pi }{2}}$, $i=1,\dots ,5$; else, it is a circle of unstable FPs.

4.3. Numerical Solutions of the DOHD Laser Model (4)

Utilizing the improved Predictor–Corrector technique [3], the numerical solutions for the DOHD laser model (4) are established. Our technique for calculating the LEs involves modifying the Wolf algorithm [29]. Clearly, there are five LEs for this model, ${\mathsf{\Gamma }}_i,i=1,\dots ,5$ and its solutions to this model are characterized by the signs of LEs [10]. Selecting ${(a,b,c,d)}^T={(10,0.001,41.3,1.2)}^T$ and the initial conditions ${(w_{11},w_{12},w_{13},w_{14},w_{15})}^T\left(0\right)={(2,1,5,3,4)}^T$, where the LEs of the model (4) are calculated, for an observation time 30,000 and sampling size 0.001, ${\mathsf{\Gamma }}_1=1.836,{\mathsf{\Gamma }}_2=0.002627,{\mathsf{\Gamma }}_3=-0.003746,{\mathsf{\Gamma }}_4=-24.1569$, and ${\mathsf{\Gamma }}_5=-28.9801$, see Figure 3. This indicates, as shown in Figure 4, that this model has a hyperchaotic attractor. We study the dynamics of the DOHD Laser model (4) using another approach, which entails the bifurcation diagrams. In Figure 5, we plotted these diagrams for the parameters ${(a,b,c,d)}^T={(10,0.001,41.3,1.2)}^T$ and the initial conditions ${(w_{11},w_{12},w_{13},w_{14},w_{15})}^T\left(0\right)={(2,1,5,3,4)}^T$.

Figure 3. LEs of the DOHD laser model (4), (a) ${\mathsf{\Gamma }}_1$ versus t, (b) ${\mathsf{\Gamma }}_2$ versus t, (c) ${\mathsf{\Gamma }}_3$, ${\mathsf{\Gamma }}_4$, and ${\mathsf{\Gamma }}_5$ versus t.

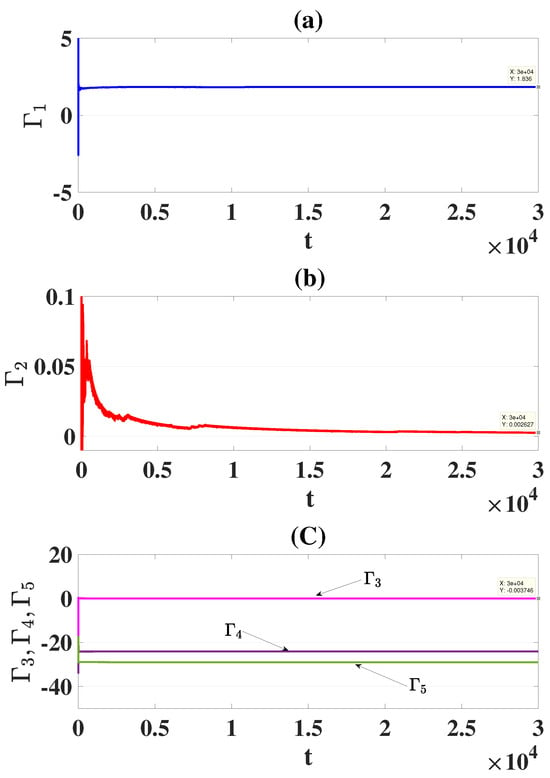
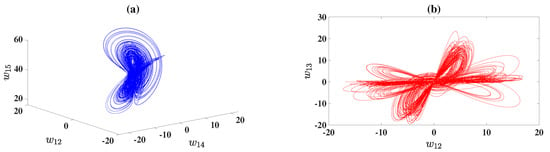
Figure 4. Hyperchaotic attractors for the DOHD laser model (4) for $(a,b,c,d)=(10,0.001,41.3,1.2)$, (a) $(w_{14},w_{12},w_{15})$ space, and (b) $(w_{12},w_{13})$ space.

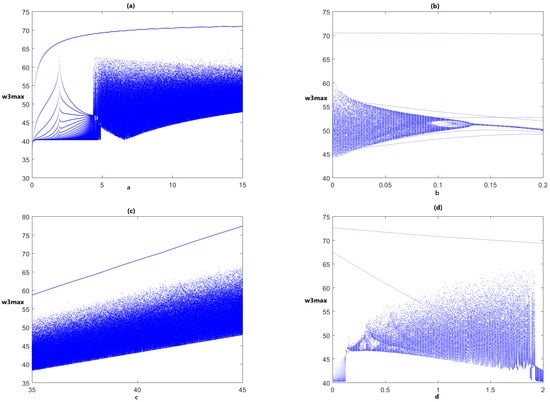
Figure 5. Bifurcation diagrams of the DOHD Laser model (4), (a) $(a,w_{13})$ space, (b) $(b,w_{13})$ space, (c) $(c,w_{13})$ space, and (d) $(d,w_{13})$ space.

5. Coexisting Attractors of the DOHD Laser Model (4)

In this section, we discuss the coexistence of more than one attractors, under various initial conditions, for the same sets of parameters, a phenomenon known as multistability. Model (4) has many coexisting attractors for the various ranges of initial conditions.

5.1. Chaotic and Hyperchaotic Attractors

This subsection deals with generating many coexisting multiple attractors of model (4) by various ranges of initial conditions and fixing the parameters $a,b,c$, and d. We calculated the LEs for model (4) with various ranges of initial conditions and the same sets of parameters for the following cases:

5.1.1. Fix $a=10$, $b=0.001$, $c=41.3$, $d=1.2$, ${(w_{12},w_{13},w_{14},w_{15})}^T\left(0\right)={(1,5,3,4)}^T$ and Vary $w_{11}\left(0\right)$

We determined the LEs for the initial condition of $w_{11}\left(0\right)\in [-4,4)$ of model (4) as seen in Figure 6. This model has a hyperchaotic attractor for $w_{11}\left(0\right)\in [-4,-0.1)$ and $w_{11}\left(0\right)\in [1.9,2.5)$ and it has chaotic attractors for $w_{11}\left(0\right)\in [-0.1,1.9)$ and $w_{11}\left(0\right)\in [2.5,4)$.

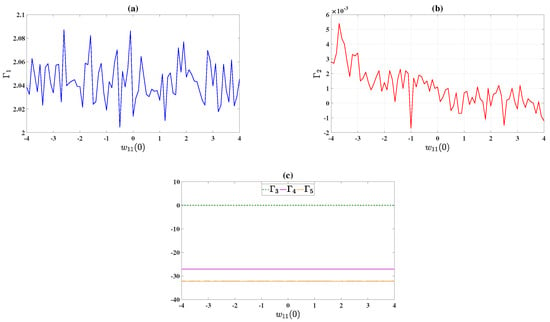
Figure 6. LEs of model (4) for $(a,b,c,d)=(10,0.001,41.3,1.2)$, (a) ${\mathsf{\Gamma }}_1$ versus $w_{11}\left(0\right)$, (b) ${\mathsf{\Gamma }}_2$ versus $w_{11}\left(0\right)$, (c) ${\mathsf{\Gamma }}_3,{\mathsf{\Gamma }}_4$ and ${\mathsf{\Gamma }}_5$ versus $w_{11}\left(0\right)$.

For $(a,b,c,d)=(10,0.001,41.3,1.2)$ and the initial condition $(w_{11},w_{12},w_{13},w_{14},$$w_{15}{)}^T\left(0\right)={(-3.7,1,5,3,4)}^T$, the solutions of (4) converge to a hyperchaotic attractor ${\mathsf{\Omega }}_1$. The corresponding LEs of this hyperchaotic attractors are

$${\mathsf{\Gamma }}_1=1.8206,{\mathsf{\Gamma }}_2=0.0093,{\mathsf{\Gamma }}_3=-0.0095,{\mathsf{\Gamma }}_4=-24.1597 \mathrm{and} {\mathsf{\Gamma }}_5=-28.9637.$$

When $(a,b,c,d)=(10,0.001,41.3,1.2)$ and the initial condition ${(w_{11},w_{12},w_{13},w_{14},w_{15})}^T$$\left(0\right)={(3.7,1,5,3,4)}^T$, the solution of the model (4) goes to a chaotic attractor ${\mathsf{\Omega }}_2$. Also, the related LEs of this chaotic attractor are

$${\mathsf{\Gamma }}_1=1.8436,{\mathsf{\Gamma }}_2=-0.0027,{\mathsf{\Gamma }}_3=-0.0007,{\mathsf{\Gamma }}_4=-24.1530 \mathrm{and} {\mathsf{\Gamma }}_5=-28.9886.$$

The phase space of ${\mathsf{\Omega }}_1$ and ${\mathsf{\Omega }}_2$ are seen in Figure 7.

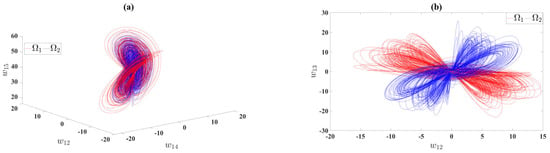
Figure 7. Different coexisting attractors of model (4) for $(a,b,c,d)=(10,0.001,41.3,1.2)$ and different initial conditions ${\mathsf{\Omega }}_1$ and ${\mathsf{\Omega }}_2$ on (a) $(w_{14},w_{12},w_{15})$ space and (b) $(w_{12},w_{13})$ space.

5.1.2. Fix $a=10$, $b=0.001$, $c=41.3$, $d=1.2$, ${(w_{11},w_{13},w_{14},w_{15})}^T\left(0\right)={(2,5,3,4)}^T$ and Vary $w_{12}\left(0\right)$

By computing the LEs for model (4) for the initial condition of $w_{12}\left(0\right)\in [0,1.8)$, we conclude that our model has a hyperchaotic attractor for $w_{12}\left(0\right)\in [0.5,1.8)$ and for $w_{12}\left(0\right)\in [0,0.5)$ it has a chaotic attractor.

5.1.3. Fix $a=10$, $b=0.001$, $c=41.3$, $d=1.2$, ${(w_{11},w_{12},w_{14},w_{15})}^T\left(0\right)={(2,1,3,4)}^T$ and Vary $w_{13}\left(0\right)$

For the initial condition of $w_{13}\left(0\right)\in [3.6,6)$, model (4) has a hyperchaotic attractor for $w_{13}\left(0\right)\in [4.6,6)$ and for $w_{13}\left(0\right)\in [3.6,4.6)$ it has chaotic attractors.

5.1.4. Fix $a=10$, $b=0.001$, $c=41.3$, $d=1.2$, ${(w_{11},w_{12},w_{13},w_{15})}^T\left(0\right)={(2,1,5,4)}^T$ and Vary $w_{14}\left(0\right)$

As we did before, we concluded that for $w_{14}\left(0\right)\in [1.7,3.4)$, model (4) has a hyperchaotic attractor for $w_{14}\left(0\right)\in [2.1,3.4)$ and it has chaotic attractors for $w_{14}\left(0\right)\in [1.7,2.1)$.

5.1.5. Fix $a=10$, $b=0.001$, $c=41.3$, $d=1.2$, ${(w_{11},w_{12},w_{13},w_{14})}^T\left(0\right)={(2,1,5,3)}^T$ and Vary $w_{15}\left(0\right)$

Under the initial condition $w_{15}\left(0\right)\in [2,5)$, our model (4) has a hyperchaotic attractor for $w_{15}\left(0\right)\in [3.3,5)$ and it has chaotic attractors for $w_{15}\left(0\right)\in [2,3.3)$.

5.2. Solution That Approaches Fixed Points

In a similar way as we did above, we evaluated the LEs for the following case:

$$\mathrm{Fix} a=5.7,b=0.01,c=2.3,d=30.6 \mathrm{and} \mathrm{Vary} \mathrm{the} \mathrm{Initial} \mathrm{Conditions}$$

The solution of model (4) approaches FPs for any values of initial conditions. For example, if we choose $a=5.7$, $b=0.01$, $c=2.3$, $d=30.6$ and ${(w_{11},w_{12},w_{13},w_{14},w_{15})}^T\left(0\right)={(-2,0.5,3.1,-2.6,-0.7)}^T\left(0\right)$, we compute the LEs, which are ${\mathsf{\Gamma }}_1=-0.0004$, ${\mathsf{\Gamma }}_2=-9.0303$, ${\mathsf{\Gamma }}_3=-9.0424$, ${\mathsf{\Gamma }}_4=-15.4003$ and ${\mathsf{\Gamma }}_5=-53.4817$. This means that our solution approaches FPs at these initial conditions. We added nine initial conditions starting at some distance “circularly” around the fixed point and plotted the resulting orbits to show that they all approach the fixed point as shown in Figure 8.

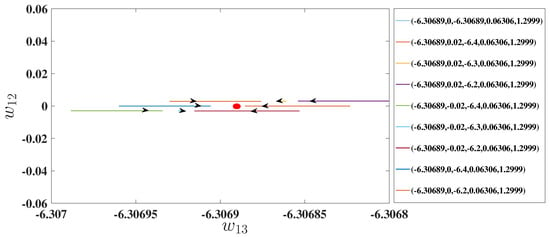
Figure 8. Solutions that approach an FP of the DOHD laser model (4) for $(a,b,c,d)=(5.7,0.01,2.3,30.6)$ and nine different initial conditions $(w_{13},w_{12})$ spacea.

6. A Scheme for DCS Between Integer and Distributed-Order Hyperchaotic Models

The DCS of n-dimensional hyperchaotic integer-order and DO dynamical systems with four drive and two response models are introduced in this part. For the drive models, we need one pair of two integer-order hyperchaotic models, and for the response models, we need another pair of DO hyperchaotic models.

Let the drive models be

$$\begin{array}{c}{\dot{u}}_1=f_1\left(u_1\right),\hfill \\ {\dot{u}}_2=f_2\left(u_2\right),\hfill \end{array}$$

(15)

and

$$\begin{array}{c}{\dot{v}}_1=g_1\left(v_1\right),\hfill \\ {\dot{v}}_2=g_2\left(v_2\right),\hfill \end{array}$$

(16)

where the state vectors of drive models (15) and (16) are $u_1=diag(u_{11},u_{12},\dots ,u_{1n})\in {\mathbf{R}}^{n\times n}$, $u_2=diag(u_{21},u_{22},\dots ,u_{2n})\in {\mathbf{R}}^{n\times n}$, $v_1=diag(v_{11},v_{12},\dots ,v_{1n})\in {\mathbf{R}}^{n\times n}$, $v_2=diag(v_{21},v_{22},\dots ,v_{2n})\in {\mathbf{R}}^{n\times n}$ and the four continuous vector functions $f_1=diag(f_{11},f_{12},\dots ,f_{1n})\in {\mathbf{R}}^{n\times n}$, $f_2=diag(f_{21},f_{22},\dots ,f_{2n})\in {\mathbf{R}}^{n\times n}$, $g_1=diag(g_{11},g_{12},\dots ,g_{1n})\in {\mathbf{R}}^{n\times n}$, $g_2=diag(g_{21},g_{22},\dots ,g_{2n})\in {\mathbf{R}}^{n\times n}$.

Models (15) and (16) can be expressed as

$$\dot{\mathbf{u}}=\mathbf{f}\left(\mathbf{u}\right),$$

(17)

and

$$\dot{\mathbf{v}}=\mathbf{g}\left(\mathbf{v}\right),$$

(18)

where $\mathbf{u}=diag(u_{11},u_{12},\dots ,u_{1n},u_{21},u_{22},\dots ,u_{2n})$, $\mathbf{v}=diag(v_{11},v_{12},\dots ,v_{1n},v_{21},v_{22},\dots ,v_{2n})$, $\mathbf{f}=diag(f_{11},f_{12},\dots ,f_{1n},f_{21},f_{22},\dots ,f_{2n})$, and $\mathbf{g}=diag(g_{11},g_{12},\dots ,g_{1n},g_{21},g_{22},\dots ,g_{2n})$.

These are the equivalent of one pair of two response models, as follows:

$$\begin{array}{c}{D}^{\psi \left(\sigma \right)}{w}_1=h_1\left(w_1\right)+k_1,\hfill \\ D^{\psi \left(\sigma \right)}{w}_2=h_2\left(w_2\right)+k_2,\hfill \end{array}$$

(19)

where $w_1=diag(w_{11},w_{12},\dots ,w_{1n})\in {\mathbf{R}}^{\mathbf{n}\times \mathbf{n}}$, $w_2=diag(w_{21},w_{22},\dots ,w_{2n})\in {\mathbf{R}}^{\mathbf{n}\times \mathbf{n}}$ is the state vectors of the response models (19), $h_1=diag(h_{11},h_{12},\dots ,h_{1n})\in {\mathbf{R}}^{\mathbf{n}\times \mathbf{n}}$ and $h_2=diag(h_{21},h_{22},\dots ,h_{2n})\in {\mathbf{R}}^{\mathbf{n}\times \mathbf{n}}$ are continuous vector functions and $k_1=diag(k_{11},k_{12},\dots ,k_{1n})\in {\mathbf{R}}^{\mathbf{n}\times \mathbf{n}}$, $k_2=diag(k_{21},k_{22},\dots ,k_{2n})\in {\mathbf{R}}^{\mathbf{n}\times \mathbf{n}}$ are two control functions of the response models (19).

Models (19) can be expressed in vector form as:

$$D^{\psi \left(\sigma \right)}\mathbf{w}=\mathbf{h}\left(\mathbf{w}\right)+\mathbf{k},$$

(20)

where, $\mathbf{w}=diag(w_{11},w_{12},\dots ,w_{1n},w_{21},w_{22},\dots ,w_{2n})$, $\mathbf{h}=diag(h_{11},h_{12},\dots ,h_{1n},h_{21},h_{22},\dots ,h_{2n})$ and $\mathbf{k}=diag(k_{11},k_{12},\dots ,k_{1n},k_{21},k_{22},\dots ,k_{2n})$.

Definition 3. 

Given that three non-zero constant diagonal matrices $T,R$, and S in ${\mathbf{R}}^{\mathbf{2}\mathbf{n}\times \mathbf{2}\mathbf{n}}$ exist,

$$\underset{t\to \infty }{lim}\parallel e\parallel =\underset{t\to \infty }{lim}\parallel T\mathit{u}+R\mathit{v}-S\mathit{w}\parallel =0,$$

(21)

then the drive models (17) and (18) are said to be in DCS with the response models (20), where the synchronization error is $e\in {\mathbf{R}}^{\mathbf{2}\mathbf{n}\times \mathbf{2}\mathbf{n}}$, while the matrix norm is $\parallel ·\parallel$.

Remark 1. 

Additional synchronization kinds, such as projective [32] and modified projective [33], may be considered as particular cases of (21).

Assume the following for the control function ${\rm Y}(\mathbf{u},\mathbf{v},\mathbf{w})$:

$${\rm Y}(\mathbf{u},\mathbf{v},\mathbf{w})=S\mathbf{w}=\alpha (\mathbf{u},\mathbf{v})+\gamma (\mathbf{u},\mathbf{v},\mathbf{w}),$$

(22)

with the compensation control $\alpha (\mathbf{u},\mathbf{v})\in {\mathbf{R}}^{\mathbf{2}\mathbf{n}}$ described as

$$\alpha (\mathbf{u},\mathbf{v})=D^{\psi \left(\sigma \right)}(T\mathbf{u}+R\mathbf{v})-T\mathbf{h}\left(\mathbf{u}\right)-R\mathbf{h}\left(\mathbf{v}\right).$$

(23)

The vector of the control function $\gamma (\mathbf{u},\mathbf{v},\mathbf{w})$ will be defined as follows below.

Theorem 2. 

The drive models (17) and (18) and response model (20) may perform the DCS, if the control function vector is constructed as follows:

$$\gamma (\mathit{u},\mathit{v},\mathit{w})=T\mathit{h}\left(\mathit{u}\right)+R\mathit{h}\left(\mathit{v}\right)-S\mathit{h}\left(\mathit{w}\right)+Ke,$$

(24)

where a positive-definite diagonal gain matrix $K=diag(k_{11},k_{12},\dots ,k_{1n},k_{21},k_{22},\dots ,k_{2n})\in {\mathbf{R}}^{\mathbf{n}\times \mathbf{n}}$ and $\gamma =diag({\gamma }_{11},{\gamma }_{12},...,{\gamma }_{1n},{\gamma }_{21},{\gamma }_{22},...,{\gamma }_{2n})\in {\mathbf{R}}^{\mathbf{2}\mathbf{n}}\times {\mathbf{R}}^{\mathbf{2}\mathbf{n}}$.

Proof. 

Multiplying Equation (20) by S gives

$$S{D}^{\psi \left(\sigma \right)}\mathbf{w}=S\mathbf{h}\left(\mathbf{w}\right)+S\mathbf{k},$$

(25)

which implies that

$$D^{\psi \left(\sigma \right)}\left(S\mathbf{w}\right)=S\mathbf{h}\left(\mathbf{w}\right)+\alpha (\mathbf{u},\mathbf{v})+\gamma (\mathbf{u},\mathbf{v},\mathbf{w}).$$

(26)

Suppose now that the compensation control has the form

$$\alpha (\mathbf{u},\mathbf{v})=D^{\psi \left(\sigma \right)}(T\mathbf{u}+R\mathbf{v})-T\mathbf{h}\left(\mathbf{u}\right)-R\mathbf{h}\left(\mathbf{v}\right),$$

(27)

and hence that model (26) becomes

$$D^{\psi \left(\sigma \right)}e=T\mathbf{h}\left(\mathbf{u}\right)+R\mathbf{h}\left(\mathbf{v}\right)-S\mathbf{h}\left(\mathbf{w}\right)-\gamma (\mathbf{u},\mathbf{v},\mathbf{w}).$$

(28)

Assume now that

$$\gamma (\mathbf{u},\mathbf{v},\mathbf{w})=T\mathbf{h}\left(\mathbf{u}\right)+R\mathbf{h}\left(\mathbf{v}\right)-S\mathbf{h}\left(\mathbf{w}\right)+Ke,$$

(29)

The result of substituting Equation (29) into Equation (28) gives

$$D^{\psi \left(\sigma \right)}e=-Ke.$$

(30)

If K is chosen so that Theorem 2 is satisfied, then $e\left(t\right)⟶0$ as $t⟶\infty$. So, DCS among one response model (21) and two drive models (17) and (18) can be performed. □

A Special Case

Using four integer-order and two DO detuned laser models as drive and response models, respectively, the control functions (29) are calculated numerically as an example to achieve the DCS. The four drive models are

$$\begin{array}{c}{\dot{u}}_{j1}=a_{j1}(u_{j3}-u_{j1})-a_{j1}{b}_{j1}{u}_{j2},\hfill \\ {\dot{u}}_{j2}=a_{j1}(u_{j4}-u_{j2})+a_{j1}{b}_{j1}{u}_{j1},\hfill \\ {\dot{u}}_{j3}=(c_{j1}-u_{j5})u_{j1}+u_{j4}{u}_{j2}-u_{j3},\hfill \\ {\dot{u}}_{j4}=(c_{j1}-u_{j5})u_{j2}-u_{j3}{u}_{j2}-u_{j4},\hfill \\ {\dot{u}}_{j5}=-d_{j1}{u}_{j5}+u_{j1}{u}_{j3}+u_{j2}{u}_{j4},\hfill \end{array}$$

(31)

and

$$\begin{array}{c}{\dot{v}}_{j1}=a_{j2}(v_{j3}-v_{j1})-a_{j2}{b}_{j2}{v}_{j2},\hfill \\ {\dot{v}}_{j2}=a_{j2}(v_{j4}-v_{j2})+a_{j2}{b}_{j2}{v}_{j1},\hfill \\ {\dot{v}}_{j3}=(c_{j2}-v_{j5})v_{j1}+v_{j4}{v}_{j2}-v_{j3},\hfill \\ {\dot{v}}_{j4}=(c_{j2}-v_{j5})v_{j2}-v_{j3}{v}_{j2}-v_{j4},\hfill \\ {\dot{v}}_{j5}=-d_{j2}{v}_{j5}+v_{j1}{v}_{j3}+v_{j2}{v}_{j4},\hfill \end{array}$$

(32)

the two associated response models are

$$\begin{array}{c}{D}^{\psi \left(\sigma \right)}{w}_{j1}=a_{j3}(w_{j3}-w_{j1})-a_{j3}{b}_{j3}{w}_{j2}+k_{j1},\hfill \\ D^{\psi \left(\sigma \right)}{w}_{j2}=a_{j3}(w_{j4}-w_{j2})+a_{j3}{b}_{j3}{w}_{j1}+k_{j2},\hfill \\ D^{\psi \left(\sigma \right)}{w}_{j3}=(c_{j3}-w_{j5})w_{j1}+w_{j4}{w}_{j2}-w_{j3}+k_{j3},\hfill \\ D^{\psi \left(\sigma \right)}{w}_{j4}=(c_{j3}-w_{j5})w_{j2}-w_{j3}{w}_{j2}-w_{j4}+k_{j4},\hfill \\ D^{\psi \left(\sigma \right)}{w}_{j5}=-d_{j3}{w}_{j5}+w_{j1}{w}_{j3}+w_{j2}{w}_{j4}+k_{j5},\hfill \end{array}$$

(33)

where the control functions of the response models (33) are $\mathbf{k}=diag(k_{11},k_{12},k_{13},k_{14},k_{15},k_{21},k_{22}$, $k_{23},k_{24},k_{25})$ and $j=1,2$.

We now choose $T=diag(1,-2,4,1,-3,-1,4,2,6,-5)$, $R=diag(4,1,-5,1,4,2,5,3,6,-1)$, $S=diag(3,-5,1,6,-1,2,4,1,5,-3)$, and $K=diag(k_{11},k_{12},k_{13},k_{14},k_{15},k_{21},k_{22},k_{23},k_{24},g_{25})$. In a similar manner to other choices of T, R, S, and K can be studied.

Using Theorem 2, we may now generate the control function matrix as

$$\gamma =diag({\gamma }_{11},{\gamma }_{12},{\gamma }_{13},{\gamma }_{14},{\gamma }_{15},{\gamma }_{21},{\gamma }_{22},{\gamma }_{23},{\gamma }_{24},{\gamma }_{25}),$$

(34)

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\gamma }_{11}=& a_{11}(u_{13}-u_{11})-a_{11}{b}_{11}{u}_{12}+4a_{12}(v_{13}-v_{11})-4a_{12}{b}_{12}{v}_{12}-3a_{13}(w_{13}-w_{11})+3a_{13}{b}_{13}{w}_{12}\hfill \\ \hfill +& k_{11}{e}_{11},\hfill \\ \hfill {\gamma }_{12}=& -2a_{11}(u_{14}-u_{12})-2a_{11}{b}_{11}{u}_{11}+a_{12}(v_{14}-v_{12})+a_{12}{b}_{12}{v}_{11}+5a_{13}(w_{14}-w_{12})+5a_{13}{b}_{13}{w}_{11}\hfill \\ \hfill +& k_{12}{e}_{12},\hfill \\ \hfill {\gamma }_{13}=& 4(c_{11}-u_{15})u_{11}+4u_{14}{u}_{12}-4u_{13}-5(c_{12}-v_{15})v_{11}-5v_{14}{v}_{12}+5v_{13}-(c_{13}-w_{15})w_{11}-w_{14}{w}_{12}+w_{13}\hfill \\ \hfill +& k_{13}{e}_{13},\hfill \\ \hfill {\gamma }_{14}=& (c_{11}-u_{15})u_{12}-u_{13}{u}_{12}-u_{14}+(c_{12}-v_{15})v_{12}-v_{13}{v}_{12}-v_{14}-6(c_{13}-w_{15})w_{12}+6w_{13}{w}_{12}+6w_{14}\hfill \\ \hfill +& k_{14}{e}_{14},\hfill \\ \hfill {\gamma }_{15}=& 3d_{11}{u}_{15}-3u_{11}{u}_{13}-3u_{12}{u}_{14}-4d_{12}{v}_{15}+4v_{11}{v}_{13}+4v_{12}{v}_{14}-d_{13}{w}_{15}+w_{11}{w}_{13}+w_{12}{w}_{14}\hfill \\ \hfill +& k_{15}{e}_{15},\hfill \\ \hfill {\gamma }_{21}=& -a_{21}(u_{23}-u_{21})+a_{21}{b}_{21}{u}_{22}+2a_{22}(v_{23}-v_{21})-2a_{22}{b}_{22}{v}_{22}-2a_{23}(w_{23}-w_{21})+2a_{23}{b}_{23}{w}_{22}\hfill \\ \hfill +& k_{21}{e}_{21},\hfill \\ \hfill {\gamma }_{22}=& 4a_{21}(u_{24}-u_{22})+4a_{21}{b}_{21}{u}_{21}+5a_{22}(v_{24}-v_{22})+5a_{22}{b}_{22}{v}_{21}-4a_{23}(w_{24}-w_{22})-4a_{23}{b}_{23}{w}_{21}\hfill \\ \hfill +& k_{22}{e}_{22},\hfill \\ \hfill {\gamma }_{23}=& 2(c_{21}-u_{25})u_{21}+2u_{24}{u}_{22}-2u_{23}+3(c_{22}-v_{25})v_{21}+3v_{24}{v}_{22}-3v_{23}-(c_{23}-w_{25})w_{21}-w_{24}{w}_{22}+w_{23}\hfill \\ \hfill +& k_{23}{e}_{23},\hfill \\ \hfill {\gamma }_{24}=& 6(c_{21}-u_{25})u_{22}-6u_{23}{u}_{22}-6u_{24}+6(c_{22}-v_{25})v_{22}-6v_{23}{v}_{22}-6v_{24}-5(c_{23}-w_{25})w_{22}+5w_{23}{w}_{22}+5w_{24}\hfill \\ \hfill +& k_{24}{e}_{24},\hfill \\ \hfill {\gamma }_{25}=& 5d_{21}{u}_{25}-5u_{21}{u}_{23}-5u_{22}{u}_{24}+d_{22}{v}_{25}-v_{21}{v}_{23}-v_{22}{v}_{24}-3d_{23}{w}_{25}+3w_{21}{w}_{23}+3w_{22}{w}_{24}\hfill \\ \hfill +& k_{25}{e}_{25},\hfill \end{array}\end{array}$$

Equation (24) yields the error model (30) as

$$\begin{array}{c}{D}^{\psi \left(\sigma \right)}{e}_{11}=-k_{11}{e}_{11},\hfill \\ D^{\psi \left(\sigma \right)}{e}_{12}=-k_{12}{e}_{12},\hfill \\ D^{\psi \left(\sigma \right)}{e}_{13}=-k_{13}{e}_{13},\hfill \\ D^{\psi \left(\sigma \right)}{e}_{14}=-k_{14}{e}_{14},\hfill \\ D^{\psi \left(\sigma \right)}{e}_{15}=-k_{15}{e}_{15},\hfill \\ D^{\psi \left(\sigma \right)}{e}_{21}=-k_{21}{e}_{21},\hfill \\ D^{\psi \left(\sigma \right)}{e}_{22}=-k_{22}{e}_{22},\hfill \\ D^{\psi \left(\sigma \right)}{e}_{23}=-k_{23}{e}_{23},\hfill \\ D^{\psi \left(\sigma \right)}{e}_{24}=-k_{24}{e}_{24},\hfill \\ D^{\psi \left(\sigma \right)}{e}_{25}=-k_{25}{e}_{25},\hfill \end{array}$$

(35)

where

$$\begin{array}{ccc}\hfill e_{11}& =& u_{11}+4v_{11}-3w_{11},\hfill \\ \hfill e_{12}& =& -2u_{12}+v_{12}+5w_{12},\hfill \\ \hfill e_{13}& =& 4u_{13}-5v_{13}+w_{13},\hfill \\ \hfill e_{14}& =& u_{14}+v_{14}-6w_{14},\hfill \\ \hfill e_{15}& =& -3u_{15}+4v_{15}+w_{15},\hfill \\ \hfill e_{21}& =& -u_{21}+2v_{21}-2w_{21},\hfill \\ \hfill e_{22}& =& 4u_{22}+5v_{22}-4w_{22},\hfill \\ \hfill e_{23}& =& 2u_{23}+3v_{23}-w_{23},\hfill \\ \hfill e_{24}& =& 6u_{24}+6v_{24}-5w_{24},\hfill \\ \hfill e_{25}& =& -5u_{25}-v_{25}+3w_{25}.\hfill \end{array}$$

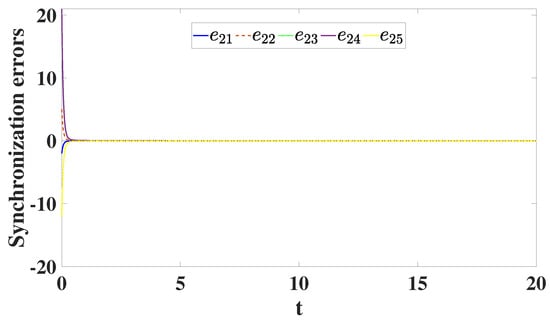
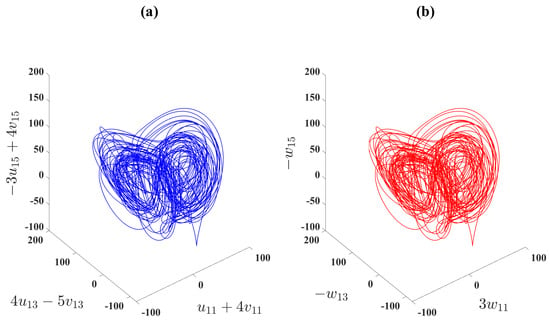
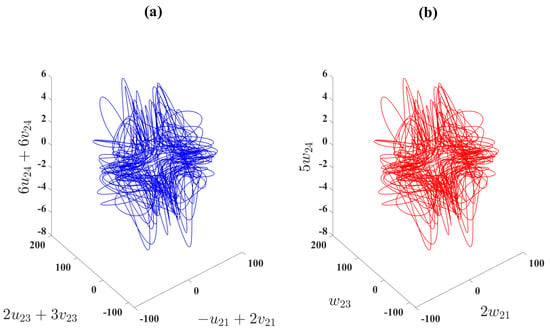
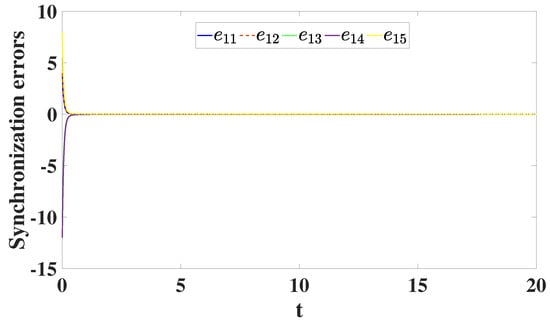
In order to achieve the DCS between the four drive models (31) and (32) and the two response models (33), numerical solutions are performed using the control functions (34). The initial conditions of the drive models (31) and (32) and the response models (33) are, respectively, $diag(u_{11},u_{12},u_{13},u_{14},u_{15})\left(0\right)=diag(2,-2,20,3,-12),$$diag(u_{21},u_{22},u_{23},u_{24},u_{25})\left(0\right)=diag(-2,4,10,18,-20)$, $diag(v_{11},v_{12},v_{13},v_{14},v_{15})\left(0\right)=diag(8,1,-25,3,16),diag(v_{21},v_{22},v_{23},v_{24},v_{25})\left(0\right)=diag(4,5,15,18,-4)$, $diag(w_{11},w_{12},$$w_{13},w_{14},w_{15})\left(0\right)=diag(6,-5,5,18,-4)$, and $diag(w_{21},w_{22},w_{23},w_{24},w_{25})\left(0\right)=diag(4,4,$$5,15,-12)$. Selecting $a_{11}=a_{12}=a_{13}=a_{21}=a_{22}=a_{23}=10$, $b_{11}=b_{12}=b_{13}=b_{21}=b_{22}=b_{23}=0.001$, $c_{11}=c_{12}=c_{13}=c_{21}=c_{22}=c_{23}=41.3$ and $d_{11}=d_{12}=d_{13}=d_{21}=d_{22}=d_{23}=1.2$, the results of DCS of models (31)–(33) are depicted in Figure 9, Figure 10, Figure 11 and Figure 12. The three dimensional projection in the first two drive models of (31) and (32) and the first one response model of (33) are plotted in Figure 9a $(u_{11}+4v_{11},4u_{13}-5v_{13},-3u_{15}+4v_{15})$, and Figure 9b $(3w_{11},-w_{13},-w_{15})$. In addition, the three dimensional projection in the second two drive models of (31) and (32) and second response model of (33) are indicated in Figure 10a $(-u_{21}+2v_{21},2u_{23}+3v_{23},6u_{24}+6v_{24})$ and Figure 10b $(2w_{21},w_{23},5w_{24})$. This shows that the DCS is performed as suggested by Theorem 2. As shown in Figure 11 and Figure 12, on the other hand, the synchronization errors e converge to zero very rapidly as $t\to \infty$.

Figure 9. DCS of (a) the first two drive models of (31) and (32) in $(u_{11}+4v_{11},4u_{13}-5v_{13},-3u_{15}+4v_{15})$ space and (b) the first response model of (33) in $(3w_{11},-w_{13},-w_{15})$ space.

Figure 10. DCS of (a) the second two drive models of (31) and (32) in $(-u_{21}+2v_{21},2u_{23}+3v_{23},6u_{24}+6v_{24})$ space and (b) the second response model of (33) in $(2w_{21},w_{23},5w_{24})$ space.

Figure 11. Synchronization errors for the first two drive models of (31) and (32) and the first one response model of (33) versus t, (solution of the model (35) for $(k_{11},k_{12},k_{13},k_{14},k_{15})=(7,7,7,7,7)$).

Figure 12. Synchronization errors for the second two drive models of (31) and (32) and the second one response model of (33) versus t, (solution of the model (35) for $(k_{21},k_{22},k_{23},k_{24},k_{25})=(7,7,7,7,7)$).

7. Conclusions

We have examined the dynamical properties of the proposed DOHD laser model (4), including dissipation and invariance and studied its FPs and the coexistence of a hyperchaotic attractor. We have shown that this model has a hyperchaotic attractor and a circle of FPs. The observation of multiple coexisting behaviors demonstrates that this hyperchaotic model has multistability, with (i) chaotic and hyperchaotic attractors and (ii) solutions that approach the FP as seen in Figure 6, Figure 7 and Figure 8, respectively. In the domain where our mode (4) has solutions that approach FPs, we find that choosing different initial conditions does not affect the type of solutions in the corresponding intervals. We also obtained solutions that approach FPs for all different choices of initial conditions. Other choices of our initial conditions in different intervals can be similarly studied. We introduced the Definition 3 of DCS for two DO response models and four integer-order drive models. Remark 1 states that this definition is considered a generalization of those found in the literature. Furthermore, we introduced a scheme to achieve DCS. The formula for the analytical control function to achieve DCS is obtained by Theorem 2. Examples are provided to illustrate the great agreement among the numerical and analytical results, see Figure 9, Figure 10, Figure 11 and Figure 12. With respect to the Caputo derivative, the outcomes are largely consistent with those of the DO method, except when $\sigma$ is very close to 1 from below. In that case, the system still tends to a chaotic attractor. For all other values of $\sigma$, both the Caputo and DO approaches lead to a rapid convergence to the fixed point. We are currently in the process of extending the investigation of our models (3) and (4) by including time delay. We also intend to study the phenomenon of desynchronization in these models. Our findings will be presented in future publications, focusing on topics such as Cryptography and using different approaches, such as the employment neuralnetworks.