Analytical Solutions of Time-Fractional Navier–Stokes Equations Employing Homotopy Perturbation–Laplace Transform Method

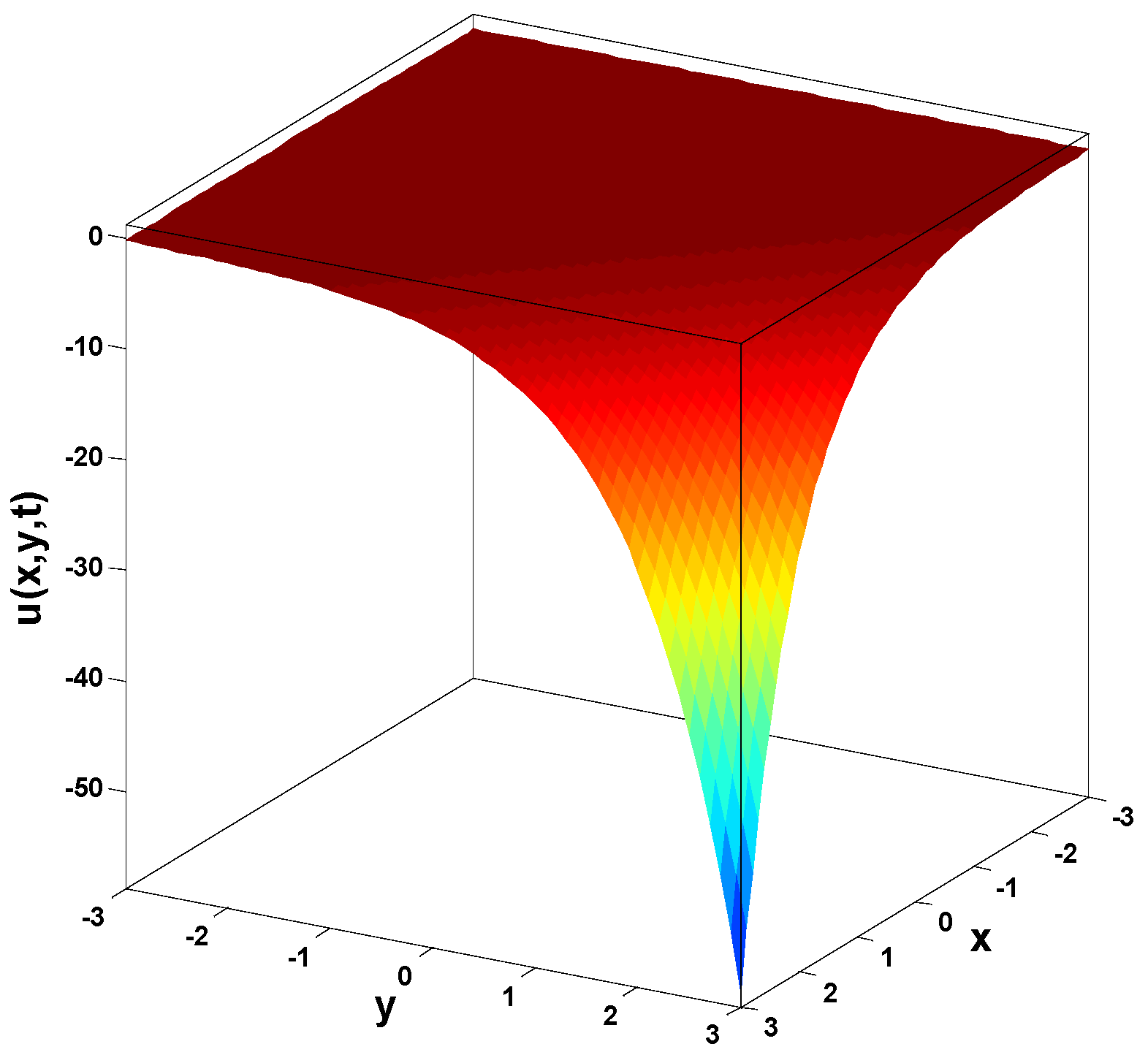
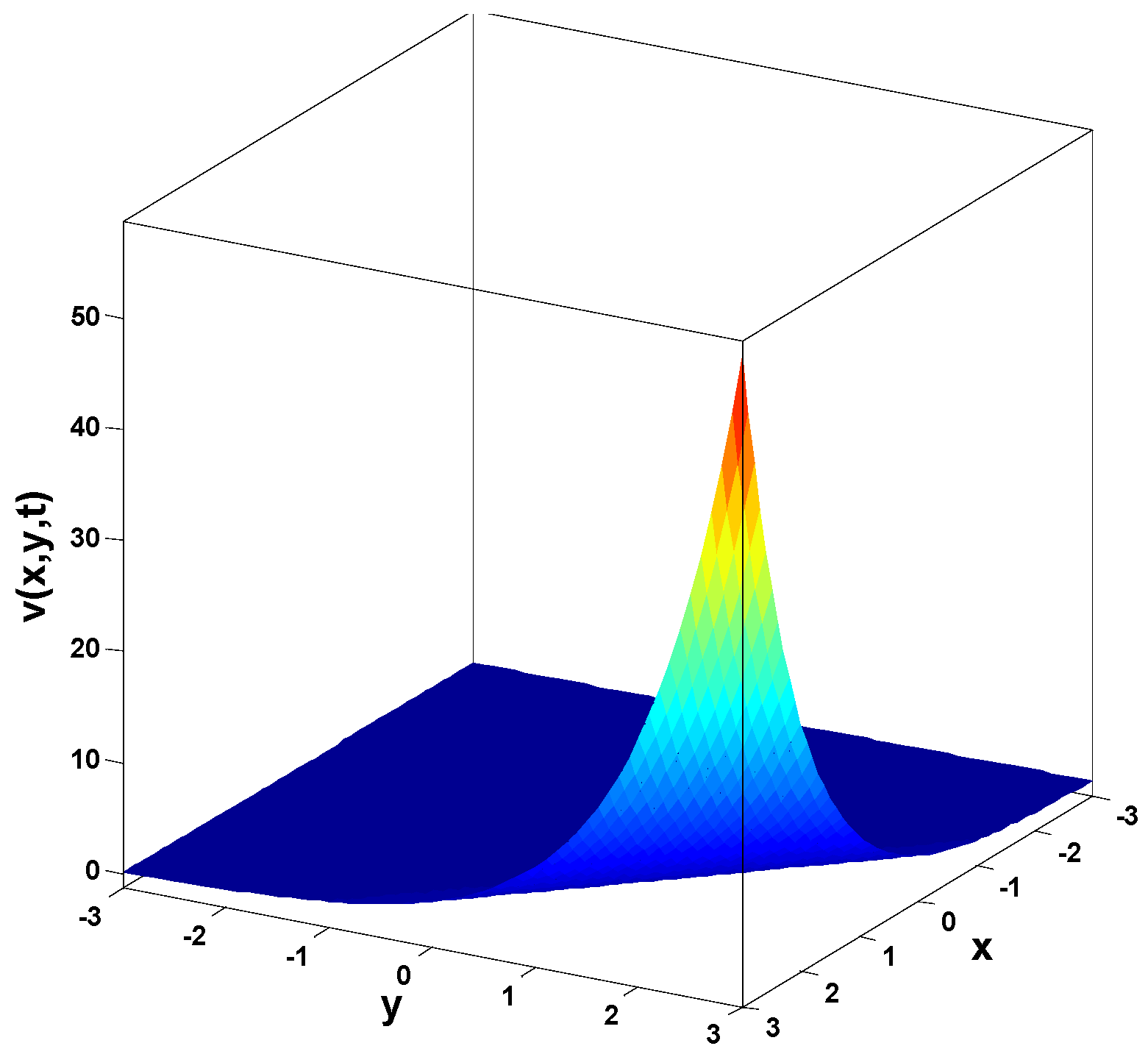
Abstract

The aim of this article is to introduce analytical and approximate techniques to obtain the solution of time-fractional Navier–Stokes equations. This proposed technique consists is coupling the homotopy perturbation method (HPM) and Laplace transform (LT). The time-fractional derivative used is the Caputo–Hadamard fractional derivative (CHFD). The effectiveness of this method is demonstrated and validated through two test problems. The results show that the proposed method is robust, efficient, and easy to implement for both linear and nonlinear problems in science and engineering. Additionally, its computational efficiency requires less computation compared to other schemes.

1. Introduction

A significant area of practical mathematics is fractional calculus (FC), which studies integral and differential operators with non-integral powers. In addition, as a consequence of its proven broad variety of applications in rheology, viscoelasticity, electrochemistry, electromagnetism, fluid dynamics, etc., fractional calculus has gained popularity; for further information, refer to West et al.’s monographs [1], Oldham and Spanier [2], Miller and Ross [3], Kilbas and Srivastava [4], Podlubny [5], Klafter and Lim [6], Baleanu and Machado [7], Goldfain [8], as they provide some foundational works on various facets of fractional calculus. Additionally, the method for solving differential equations of arbitrary real order is outlined, along with applications of these methods across various fields. Nevertheless, numerous analytical and approximate techniques have recently been developed to solve fractional differential equations [9,10]. Moreover, there are many methods used, including the Adomian decomposition method (ADM) [11,12,13], variational iteration method (VIM) [14], homotopy perturbation method (HPM) [15,16,17,18], differential transform method (DTM) [19,20], and several other methods. Most importantly, the homotopy perturbation method, originally developed by Chinese researcher J.H. He in 1998, has proven to be the most significant among all the methods mentioned above, as it directly addresses the problem without the need for any kind of transformation and linearization. Moreover, the proposed method does not need the problem to be discriminated against to obtain numerical results; we can evaluate the approximate solution by using the $n$-term approximation, solved with the aid of well-known transforms, such as Laplace, Elzaki, and Sumudu. El-Shahed and Salem [21] used the Laplace transform (LT), finite Hankel transforms (FHT), and Fourier sine transforms to solve the traditional Navier–Stokes equation. Likewise, Kumar et al.’s analytical solution of a nonlinear fractional NS equation [22] used the HPM and LT algorithms in conjunction. Above and beyond, Birajdar [23] and Momani et al. [24] used the ADM, by using the homotopy analysis approach, to solve the fractional Navier–Stokes equation, whilst Sunil Kumar et al. [25] solved the same equation by combining LT with FHT, and then Chaurasia and Kumar [26] obtained the analytical answer of the fractional Navier–Stokes equation using the ADM and LT technique. In order to obtain an approximate analytical solution for the time-fractional order multi-dimensional Navier–Stokes equation, Dhiman and Chauhan [27] employed the fractional reduced differential transformation technique (FRDTM). The residual power series (RPS) approach was employed by Jaber and Ahmad [28] to solve the two-dimensional nonlinear time-fractional Navier–Stokes equation. Nevertheless, numerical approximations, for a class of Navier–Stokes equations with time-fractional derivatives, were proposed by Zhang and Wang [29] and H Eltayeb, IBachar, SMesloub [30] applied the Sumudu-generalized Laplace transform decomposition method (DGLTDM), which combines Sumudu-generalized Laplace transform and the decomposition method. In addition, Prakash et al. [31] proposed the q-homotopy analysis transform method (q-HATM). Mahmood et al. [32] used the Laplace Adomian decomposition method (LADM), which stands for a combination of the Laplace transform and ADM is used for the analytical solution of the system of time fractional Navier–Stokes equation. The present paper gives an approximate solution for the proposed problem of the time-fractional Navier–Stokes equation by using the homogony perturbation–Laplace transform method (HP–LTM) under Caputo–Hadamard memory. For more important works, we refer the reader to the works [33,34] related to the fractional calculus, [35,36,37,38,39] for fractional Navier–Stokes equation and [40,41] for the Caputo–Hadamard fractional differential equations.

The paper is organized as follows: Section 2 discusses some fundamental aspects of Caputo–Hadamard fractional derivatives in relation to the stated issues. Section 3 and Section 4 contain the Laplace transform and the expanded version of the HP–LTM, respectively. Section 5 contains convergence analysis and error estimation. In Section 6, we present the approximate analytic solutions of two test problems involving the time-fractional order Navier–Stokes equation with Caputo–Hadamard memory to confirm the efficacy and precision of the suggested approach. Lastly, a conclusion is provided in Section 7.

2. Preliminaries and Definitions

In this section, we provide the necessary definitions, properties, and lemmas of FC theory which will be used throughout this work [3,4,33,34,40,41].

Definition 1

([33]). Let $\left(0<a\le b\le \infty \right)$ represent a finite or infinite interval on the positive half-axis ${\mathbb{R}}^{+}$. The left-sided and right-sided Hadamard fractional integrals of order $\alpha , \left(\alpha \in \mathbb{R}, \alpha >0\right),$ are defined by the following:

$$I_{a+}^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_a^t{\left(lnt-ln\xi \right)}^{\alpha -1}{\displaystyle \frac{f\left(\xi \right)}{\xi }}d\xi ={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_a^t{\left(ln{\displaystyle \frac{t}{\xi }}\right)}^{\alpha -1}f\left(\xi \right){\displaystyle \frac{d\xi }{\xi }},$$

(1)

$$I_{b-}^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_t^b{\left(lnt-ln\xi \right)}^{\alpha -1}{\displaystyle \frac{f\left(\xi \right)}{\xi }}d\xi ={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_t^b{\left(ln{\displaystyle \frac{t}{\xi }}\right)}^{\alpha -1}f\left(\xi \right){\displaystyle \frac{d\xi }{\xi }},$$

(2)

respectively, if the integrals exist.

The left-sided and right-sided Hadamard fractional derivatives of order $\alpha$, with $(\alpha \in \mathbb{R}, \alpha >0, n=\left[\alpha \right]+1)$, are defined by the following:

$${}^H\mathbb{D}_{a+}^{\alpha }f\left(t\right)={\left(t{\displaystyle \frac{d}{dt}}\right)}^n{I}_{a+}^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(n-\alpha \right)}}{\left(t{\displaystyle \frac{d}{dt}}\right)}^n{\int }_a^t{\left(ln {\displaystyle \frac{t}{\xi }}\right)}^{n-\alpha -1}f\left(\xi \right){\displaystyle \frac{d\xi }{\xi }},$$

$${}^H\mathbb{D}_{b-}^{\alpha }f\left(t\right)={\left(-t{\displaystyle \frac{d}{dt}}\right)}^n{I}_{b-}^{\alpha }f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(n-\alpha \right)}}{\left(-t{\displaystyle \frac{d}{dt}}\right)}^n{\int }_t^b{\left(ln {\displaystyle \frac{\xi }{t}}\right)}^{n-\alpha -1}{\left(t{\displaystyle \frac{d}{dt}}\right)}^{n}f\left(\xi \right){\displaystyle \frac{d\xi }{\xi }},$$

respectively, where $\Gamma \left(.\right)$ represents the Gamma function.

$$\Gamma \left(\alpha \right)={\int }_0^{+\infty }{t}^{\alpha -1}{e}^{-t}dt.$$

Remark 1.

The number $\alpha$ can be taken as a complex number with a positive real part in the previous definitions.

Caputo–Hadamard Fractional Derivatives

We introduce the Caputo adaptation of the left-sided and right-sided Hadamard fractional derivatives, respectively, as follows:

Theorem 1.

([33,34]). Let $\left(0<a<b<\infty \right), (\alpha >0, n=\left[\alpha \right]+1).$ If $f\in {AC}_{\delta }^n\left(\left[a,b\right]\right)$, where

$$A{C}_{\delta }^n\left(\left[a,b\right]\right)=\left\{g:\left[a,b\right]\to \mathbb{C}:{ \delta }^{n-1}g\left(x\right)\in AC\left[a,b\right], \delta =x{\displaystyle \frac{d}{dx}}\right\},$$

(3)

and $AC[a,b]$: be the spaces of absolutely continuous functions on $[a, b]$.

Then ${}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }f\left(t\right), {}^{\mathit{CH}}\mathbb{D}_{b-}^{\alpha }f\left(t\right)$ exist everywhere on $\left[a,b\right]$ and Caputo-type Hadamard fractional derivatives are defined by the following:

$${}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }f\left(t\right)=I_{a+}^{\alpha }{\left(t{\displaystyle \frac{d}{dt}}\right)}^{n}f\left(t\right)={\displaystyle \frac{1}{\Gamma \left(n-\alpha \right)}}{\int }_a^t{\left(ln {\displaystyle \frac{t}{\xi }}\right)}^{n-\alpha -1}{\left(t{\displaystyle \frac{d}{dt}}\right)}^{n}f\left(\xi \right){\displaystyle \frac{d\xi }{\xi }},$$

(4)

$${}^{\mathit{CH}}\mathbb{D}_{b-}^{\alpha }f\left(t\right)=I_{b-}^{\alpha }{\left(-t{\displaystyle \frac{d}{dt}}\right)}^{n}f\left(t\right)={\displaystyle \frac{{\left(-1\right)}^n}{\Gamma \left(n-\alpha \right)}}{\int }_t^b{\left(ln {\displaystyle \frac{\xi }{t}}\right)}^{n-\alpha -1}{\left(t{\displaystyle \frac{d}{dt}}\right)}^{n}f\left(\xi \right){\displaystyle \frac{d\xi }{\xi }}.$$

(5)

Lemma 1

([33]). Let $f\in C\left(\left[a,b\right]\right)$, $\alpha \in \mathbb{R},\alpha >0, n=\left[\alpha \right]+1$ if, then

$${}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }{I}_{a+}^{\alpha }f\left(t\right)=f\left(t\right),{}^{\mathit{CH}}\mathbb{D}_{b-}^{\alpha }{I}_{b-}^{\alpha }f\left(t\right)=f\left(t\right).$$

(6)

Lemma 2

([33]). Let $f\in {AC}^n\left(\left[a,b\right]\right)$, and $\alpha \in \mathbb{R},\alpha >0, n=\left[\alpha \right]+1$. Then

$$I_{a+}^{\alpha }{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }f\left(t\right)=f\left(t\right)-{\sum }_{k=0}^{n-1}{\displaystyle \frac{{\delta }^{k}f\left(a\right)}{k!}}{\left(ln{\displaystyle \frac{t}{a}}\right)}^k,$$

(7)

$$I_{b-}^{\alpha }{}^{\mathit{CH}}\mathbb{D}_{b-}^{\alpha }f\left(t\right)=f\left(t\right)-{\sum }_{k=0}^{n-1}{\displaystyle \frac{{\delta }^{k}f\left(b\right)}{k!}}{\left(ln{\displaystyle \frac{b}{t}}\right)}^k.$$

(8)

Definition 2.

A two-parameter Mittag–Leffler function ${{\rm E}}_{\alpha ,\beta }\left(t\right),$ is defined by the following series:

$${{\rm E}}_{\alpha ,\beta }\left(t\right)={\sum }_{k=0}^{\infty }{\displaystyle \frac{t^k}{\Gamma \left(\alpha k+\beta \right)}}, \alpha ,\beta ,t\in \mathbb{R},with \alpha ,\beta >0.$$

(9)

If $\beta =1$, we have the one-parameter Mittag–Leffler function:

$${{\rm E}}_{\alpha }\left(t\right)={{\rm E}}_{\alpha ,1}\left(t\right)={\sum }_{k=0}^{\infty }{\displaystyle \frac{t^k}{\Gamma \left(\alpha k+1\right)}}.$$

3. The Amended Laplace Transforms

Definition 3

([40]). The amended Laplace transform of a given function $f$ with $t\in (a,\infty ) (a>0)$ is defined by the following:

$$G\left(s\right)=\mathcal{L}\left[f\left(t\right),s\right]={\int }_a^{+\infty }{e}^{-ln{\displaystyle \frac{s}{a}}ln{\displaystyle \frac{t}{a}}}f\left(t\right){\displaystyle \frac{dt}{t}}, 0\ne s\in \mathbb{C}.$$

(10)

The inverse amended Laplace transform is given by the following:

$$f\left(t\right)={\mathcal{L}}^{-1}\left[G\left(s\right)\right]={\displaystyle \frac{1}{2\pi i}}{\int }_{c-i\infty }^{c+i\infty }{e}^{-ln{\displaystyle \frac{s}{a}}ln{\displaystyle \frac{t}{a}}}G\left(s\right){\displaystyle \frac{ds}{s}}, c=\mathfrak{R}\left(s\right), t\in \left(a,\infty \right), a>0$$

(11)

At this point, we take the principal value branch in the logarithmic function $ln{\displaystyle \frac{s}{a}}$ since the variable $s$ is a complex number.

The amended Laplace transform of a function $f$ defined on $[a,\infty ) (a>0)$, exists. If the function $f$ is $\delta$-exponential order, i.e.,

(i)

$f$ is continuous or piecewise continuous on every finite subinterval of $[a,\infty )$,

(ii)

There exist a positive constant $M>0$ and $\sigma >0$ a such that for a given large $T>a$,

$$\left|f\left(t\right)\right|\le M{t}^{ln{\displaystyle \frac{\sigma }{a}}}, \mathrm{for} T>a, \mathrm{With} \Re \left(\mathrm{s}\right)>\sigma .$$

In the sense of $\delta$-derivative, it follows from the amended Laplace transform the following:

$$\mathcal{L}\left\{\left({\delta }^{n}f\left(t\right),s \right)\right\}={\left(ln{\displaystyle \frac{s}{a}}\right)}^{\alpha }\left\{\mathcal{L}(f\left(t\right),s)\right\}-{\sum }_{k=0}^{n-1}{\left(ln{\displaystyle \frac{s}{a}}\right)}^{n-k-1}{\delta }^{n}f\left(a\right), n\in \mathbb{N}.$$

In addition, by applying the Laplace transform on both sides of Equation (4), we find that Laplace transform of the Caputo–Hadamard fractional derivative is given by the following:

Theorem 2

([40]). Let $f\in {AC}_{\delta }^{n-1}\left[a,t\right),$ such that ${\delta }^{i}f, i=\mathrm{0,1},2,\dots ,n-1$ are $\delta$-exponential order. Then, the amended Laplace transform of ${}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }f$ exists and

$$\mathcal{L}\left\{\left({}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }f\left(t\right),s\right)\right\}={\left(ln{\displaystyle \frac{s}{a}}\right)}^{\alpha }\left\{\mathcal{L}(f\left(t\right),s)\right\}-{\sum }_{k=0}^{n-1}{\left(ln{\displaystyle \frac{s}{a}}\right)}^{\alpha -k-1}{\delta }^{k}f\left(a\right).$$

(12)

Definition 4

([40]). Supposes that functions $f$ and $g$ are defined on $\left[a,+\infty \right), \left(a>0\right).$

The integral ${\int }_a^{t}f\left(a{\displaystyle \frac{t}{\xi }}\right)g\left(\xi \right){\displaystyle \frac{d\xi }{\xi }}$ is called the convolution of $f$ and $g$, that is

$$(f\ast g)\left(t\right)={\int }_a^{t}f\left(a{\displaystyle \frac{t}{\xi }}\right)g\left(\xi \right){\displaystyle \frac{d\xi }{\xi }}.$$

(13)

Lemma 3

(Convolution property). If $\mathcal{L}\left[f\left(t\right),s\right]=F\left(s\right)$ and $\mathcal{L}\left[g\left(t\right),s\right]=G\left(s\right),$

$$\mathcal{L}\left\{\left(f\ast g\right)\left(t\right),s\right\}=\mathcal{L}\left[f\left(t\right),s\right]\mathcal{L}\left[g\left(t\right),s\right]=F\left(s\right)G\left(s\right).$$

(14)

or equivalently,

$${\mathcal{L}}^{-1}\left\{F\left(s\right)G\left(s\right),t\right\}=(f\ast g)\left(t\right).$$

Lemma 4.

• $\mathcal{L}\left\{1,s\right\}={\displaystyle \frac{1}{ln\frac{s}{a}}}, s>0.$
• $\mathcal{L}\left\{{\left(ln{\displaystyle \frac{t}{a}}\right)}^{\beta },s\right\}={\displaystyle \frac{\Gamma \left(\beta \right)}{({ln\frac{s}{a})}^{\beta }}}, \beta >0, s>0.$

4. Homotopy Perturbation–Laplace Transform Method (HP–LTM)

For elucidation purpose of the HP–LTM concept, we examine a fractional order nonlinear non-homogeneous partial differential equation with an initial condition (IC), as presented hereunder:

$${}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }f\left(x,y,z,t\right)+Rf\left(x,y,z,t\right)+Nf\left(x,y,z,t\right)=g\left(x,y,z,t\right), n<\alpha \le n+1,$$

(15)

$$f\left(x,y,z,0\right)=h\left(x, y, z\right),$$

(16)

where ${}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }f$ is the time fractional derivative of $f$ in Caputo–Hadamard sense, R, N are the linear and nonlinear differential operators and $g$ is the source term. At this moment, by taking LT on both sides of Equation (15), we have the following:

$$\mathcal{L}\left\{{}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }f\left(x,y,z,t\right)+Rf\left(x,y,z,t\right)+Nf\left(x,y,z,t\right)\right\}=\mathcal{L}\left\{g\left(x,y,z,t\right)\right\},$$

(17)

$$\mathcal{L}\left\{{}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }f\left(x,y,z,t\right)\right\}=\mathcal{L}\left\{-Rf\left(x,y,z,t\right)-Nf\left(x,y,z,t\right)\right\}+\mathcal{L}\left\{g\left(x,y,z,t\right)\right\},$$

(18)

Now, using the property (12) of the amended Laplace transform for the fractional derivative

$$\begin{gathered} \mathcal{L}\left\{{}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }f\left(x,y,z,t\right)\right\}={\left(ln{\displaystyle \frac{s}{a}}\right)}^{\alpha }\left\{\mathcal{L}\left\{f\left(x,y,z,t\right)\right\}\right\}-\sum _{k=0}^{n-1}{\left(\left(ln{\displaystyle \frac{s}{a}}\right)\right)}^{\alpha -k-1}{\delta }^{k}f\left(a\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =\mathcal{L}\left\{-Rf\left(x,y,z,t\right)-Nf\left(x,y,z,t\right)\right\}+\mathcal{L}\left\{g\left(x,y,z,t\right)\right\}, \end{gathered}$$

(19)

on simplifying of Equation (19), we have the following:

$$\mathcal{L}\left\{f\left(x,y,z,t\right)\right\}={\sum }_{k=0}^{n-1}{\left(ln{\displaystyle \frac{s}{a}}\right)}^{-k-1}{\delta }^{k}f\left(a\right)+{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{g\left(x,y,z,t\right)\right\}-\mathcal{L}\left\{Rf\left(x,y,z,t\right)+Nf\left(x,y,z,t\right)\right\}\right\}.$$

(20)

Operating the inverse Laplace transform on both sides in Equation (20), we obtain the following:

$$f\left(x,y,z,t\right)=G\left(x,y,z,t\right)-{\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{Rf\left(x,y,z,t\right)+Nf\left(x,y,z,t\right)\right\}\right\}\right].$$

(21)

where $G\left(x,y,z,t\right)$ denotes the term arising from the initial condition and source term.

Through the application of the HPM to Equation (21), we obtain the following:

$$f\left(x,y,z,t\right)=G\left(x,y,z,t\right)-p\left({\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{Rf\left(x,y,z,t\right)+Nf\left(x,y,z,t\right)\right\}\right\}\right]\right).$$

(22)

The homotopy parameter p is employed to expand the solution as follows:

$$f\left(x,y,z,t\right)={\sum }_{n=0}^{\infty }{p}^n{f}_n\left(x,y,z,t\right),$$

(23)

The nonlinear term is decomposed in the following manner:

$$Nf\left(x,y,z,t\right)={\sum }_{n=0}^{\infty }{p}^n{H}_n\left(f\right),$$

(24)

where ${ H}_n\left(f\right)$ is He’s polynomials and is given by the following:

$$H_n\left(f_0,f_1,f_2,\dots f_n\right)={\displaystyle \frac{1}{n!}}{\displaystyle \frac{\partial }{\partial p^n}}\left[N{\sum }_{n=0}^{\infty }{p}^n{f}_n\right].$$

(25)

Through substituting Equations (23) and (24) in Equation (22), we obtain the following:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{n=0 }^{\infty }}{p}^n{f}_n\left(x,y,z,t\right)& =G\left(x,y,z,t\right)\hfill \\ & -p\left({\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{R{\sum }_{n=0}^{\infty }{p}^n{f}_n(x,y,z,t)+N{\sum }_{n=0}^{\infty }{p}^n{H}_n\left(f\right)\right\}\right\}\right]\right).\hfill \end{array}$$

(26)

Possibly, the following equations may be derived by comparing the coefficients of equal powers of p from both sides:

$$p^0:f_0\left(x,y,z,t\right)=G\left(x,y,z,t\right).$$

(27)

$$\begin{gathered} p^1:f_1\left(x,y,z,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{R{f}_0\left(x,y,z,t\right)+H_0\left(f\right)\right\}\right\}\right]. \\ {p}^2:f_2\left(x,y,z,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{R{f}_1\left(x,y,z,t\right)+H_1\left(f\right)\right\}\right\}\right]. \end{gathered}$$

(28)

$⋮.$

Finally, we find the solution $f_n\left(x,y,z,t\right)$ in this manner, which can be written as follows:

$$f\left(x,y,z,t\right)=f_0\left(x,y,z,t\right)+f_1\left(x,y,z,t\right)+f_2\left(x,y,z,t\right){+f}_3\left(x,y,z,t\right)+\cdots$$

(29)

which represents the analytical solution of problem (15) with initial condition (16).

5. Convergence Analysis and Error Estimation

In fact, converging the HPM towards a solution for the fractional NS equation, as well as estimating $\mathrm{C}$ the errors of HPM, are established through the two theorems hereunder. Consider $\Omega \in {\mathbb{R}}^{\mathrm{n}}$ as an opened and bounded domain, and let T be a positive constant with $0<T\le \infty .$ For illustration purposes of the HPM technique, let us consider the fractional NS equation for any $(x,y,z,t)\in \Omega \times \left[0,T\right]$.

Theorem 3

([39]). Let $f_n(x,y,z,t)$ be the function in a Banach space $C\left(\Omega \times \left[0,T\right]\right)$ defined by Equation (29) for any $n\in \mathbb{N}$. The infinite series $\sum _{k=0}^{\infty }{f}_k\left(x,y,z,t\right)$ converges to the solution $f$ of Equation (15) if there exists a constant $0<\mu <1$ such that $f_n(x,y,z,t)\le \mu f_{n-1}(x,y,z,t)$ for all $n\in \mathbb{N}$. Define that ${\left\{S_n\right\}}_{n=0}^{\infty }$ is the sequence of the partial sums of the series $\sum _{k=0}^{\infty }{f}_k\left(x,y,z,t\right)$.

Thus, ${\left\{S_n\right\}}_{n=0}^{\infty }$ is a Cauchy sequence in $C\left(\left[0,T\right],\mathbb{R}\right)$; consequently, the solution $\sum _{k=0}^{\infty }{f}_k(x,y,z,t)$ converge to $f$.

Subsequently, we present the theorem for truncating an imprecise solution as follows:

Theorem 4

([39]). The maximum absolute error of the series solution, defined in Equation (29), is estimated as follows:

$$\left|f(x,y,z,t)-\sum _{k=0}^{\infty }{f}_k(x,y,z,t)\right|\le \left({\displaystyle \frac{{\mu }^{m+1}}{1-\mu }}\right)‖f_0‖.$$

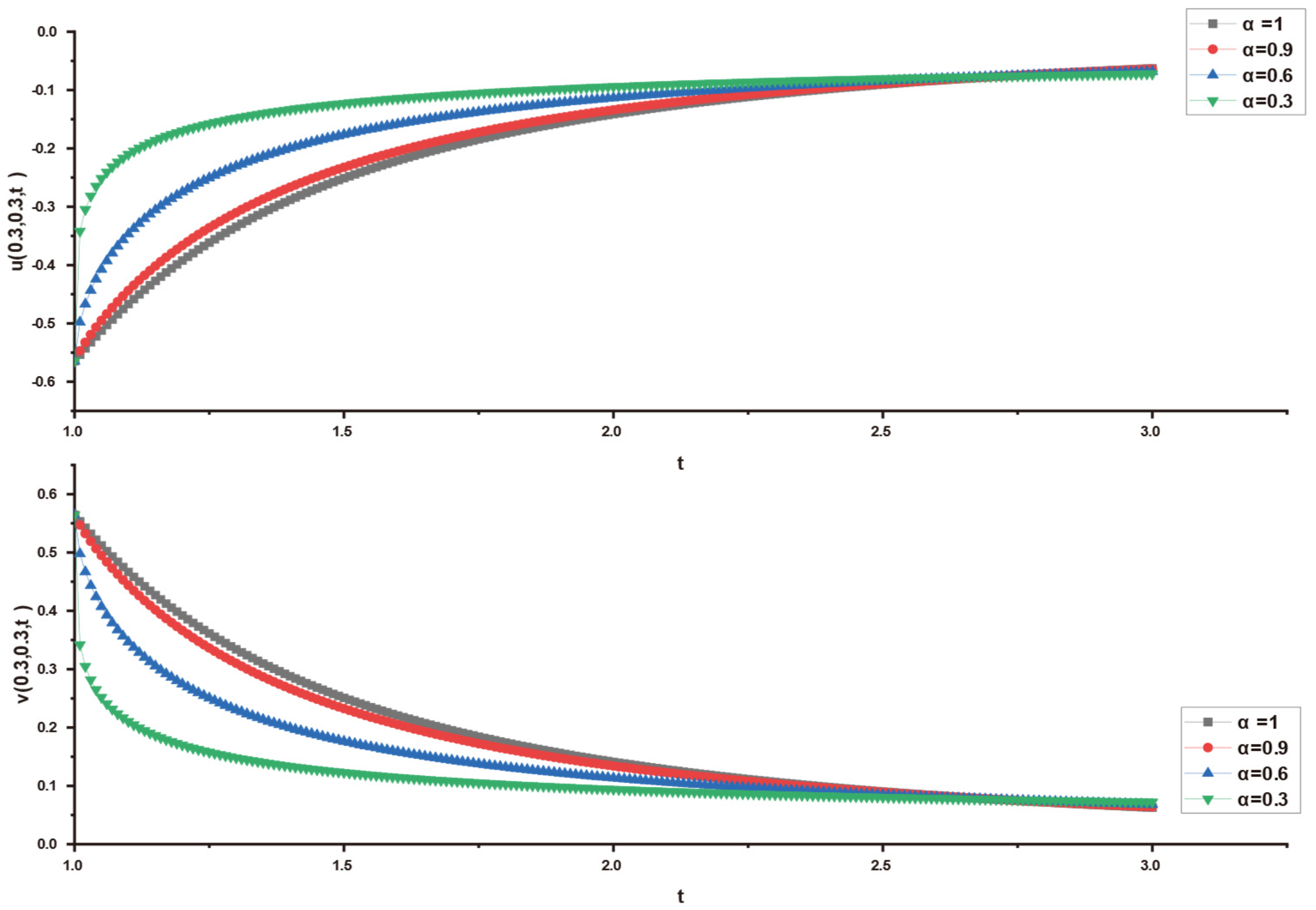
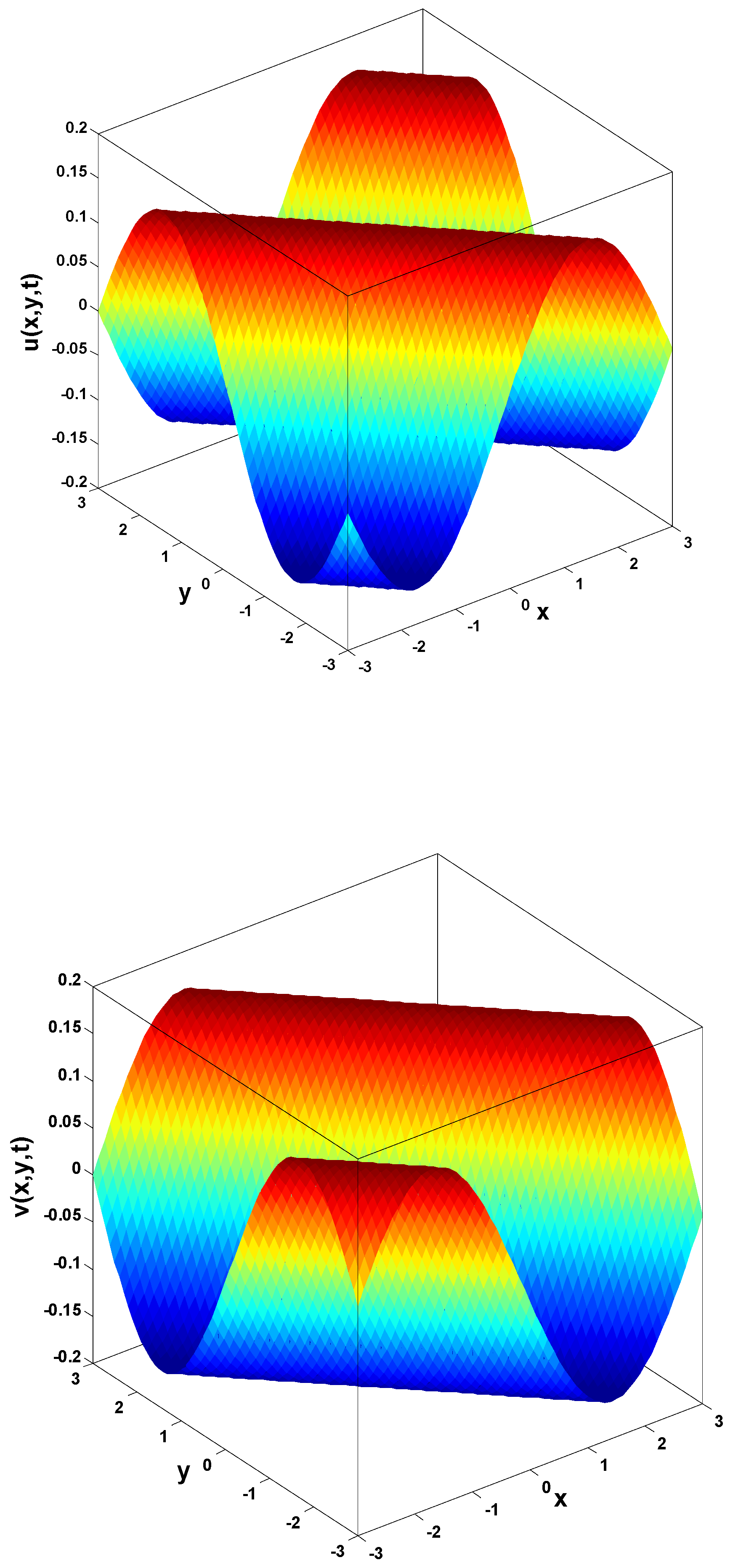
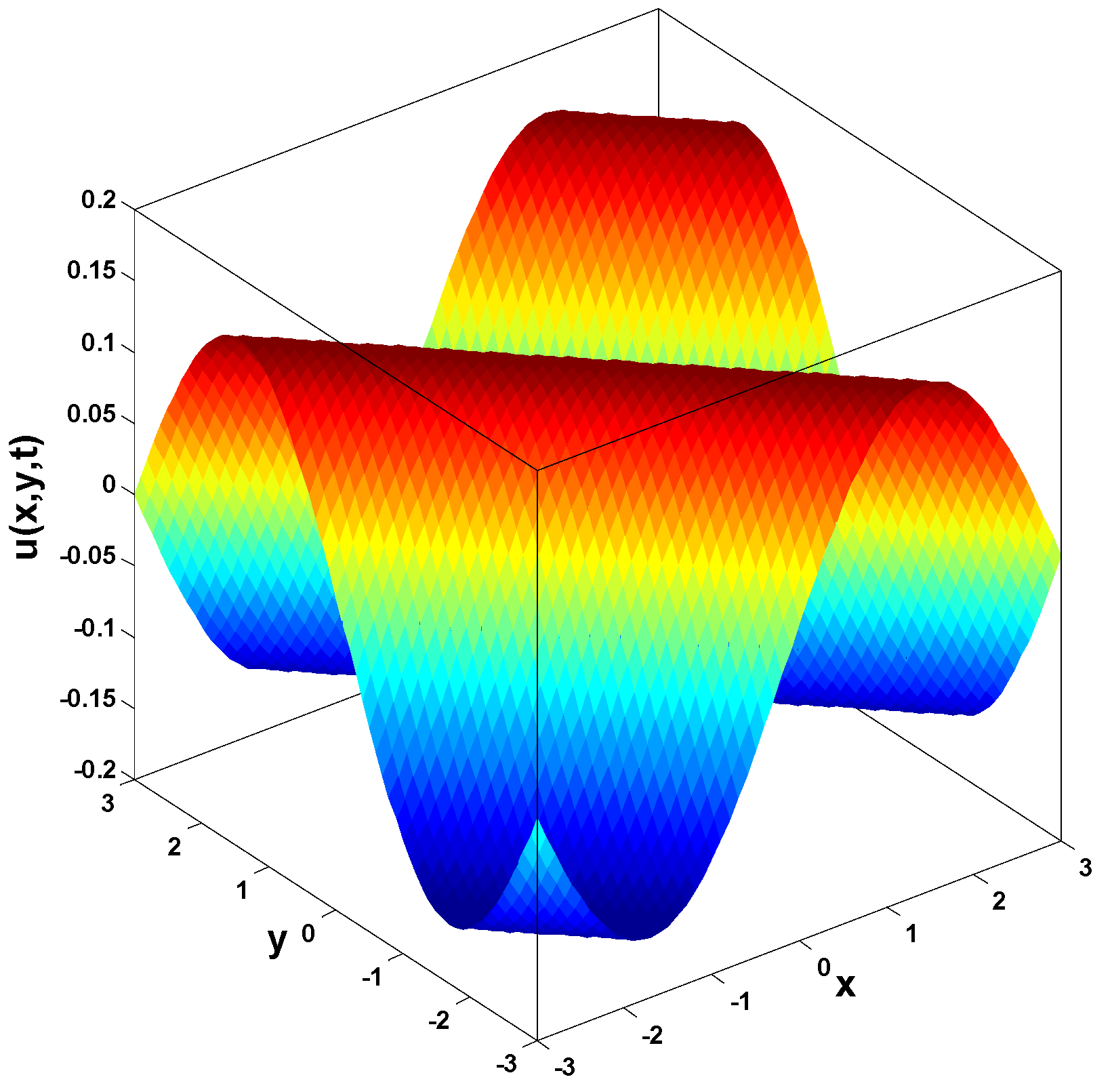
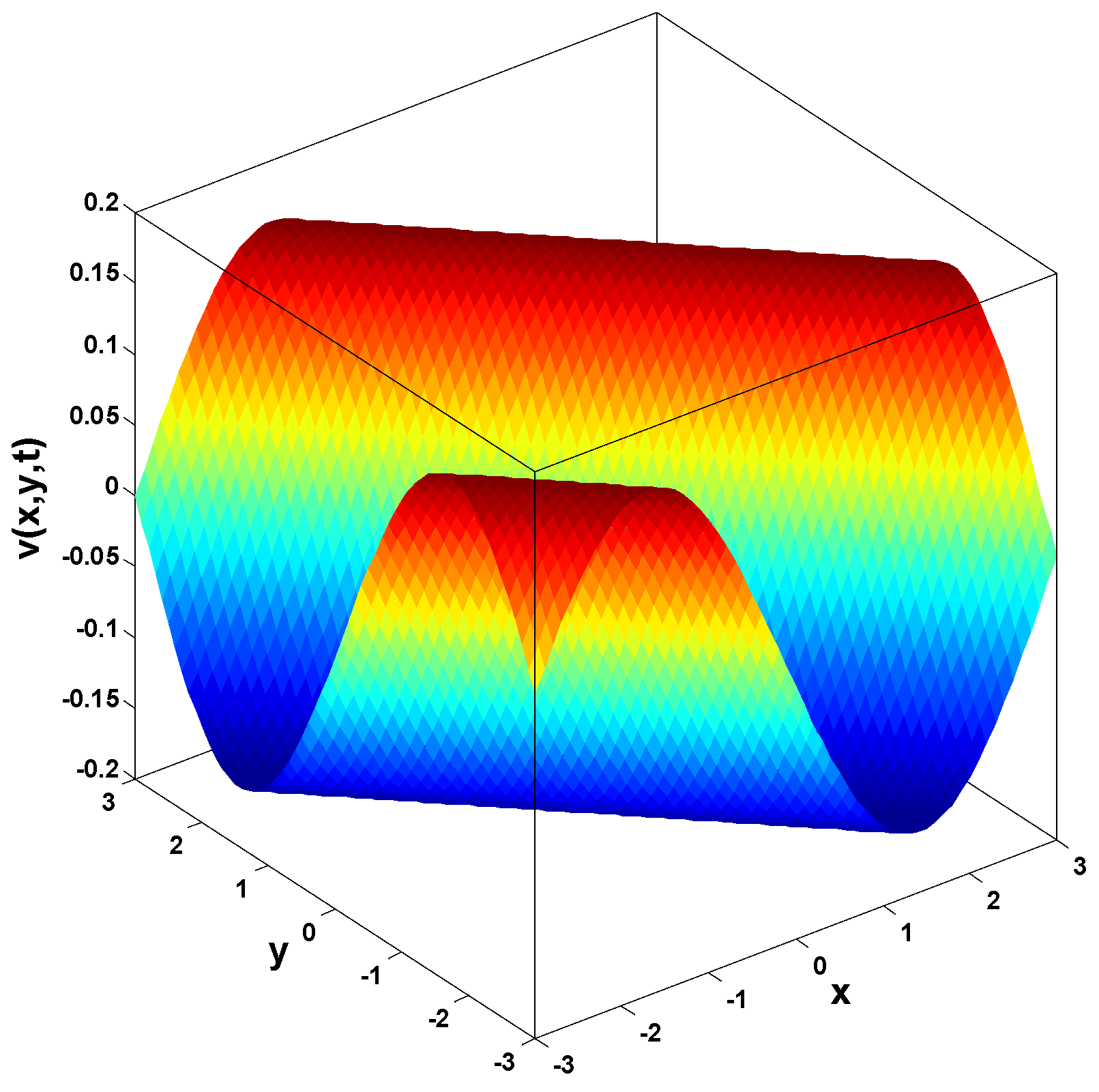
6. Application of HP–LTM on NS Equation

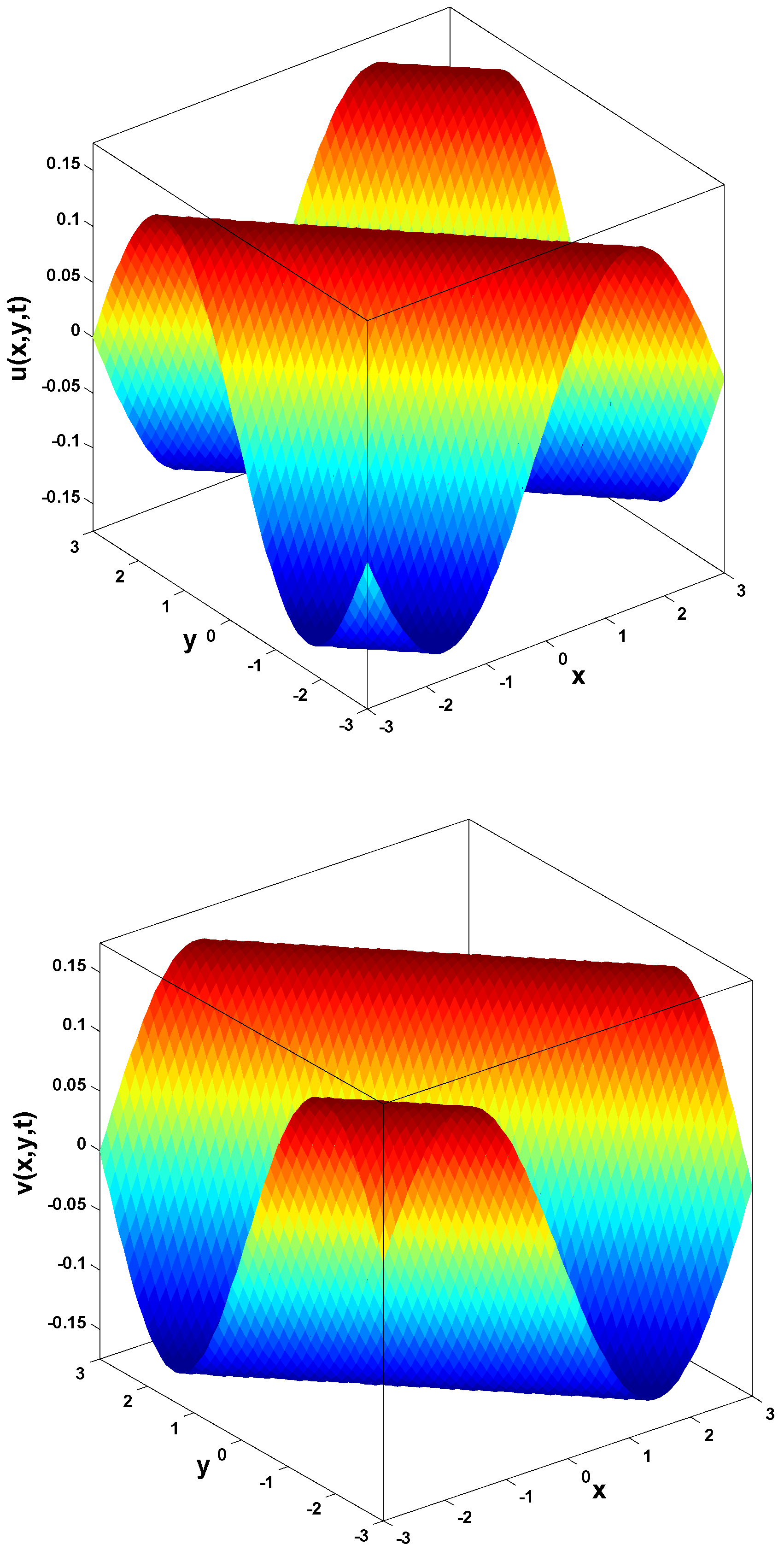
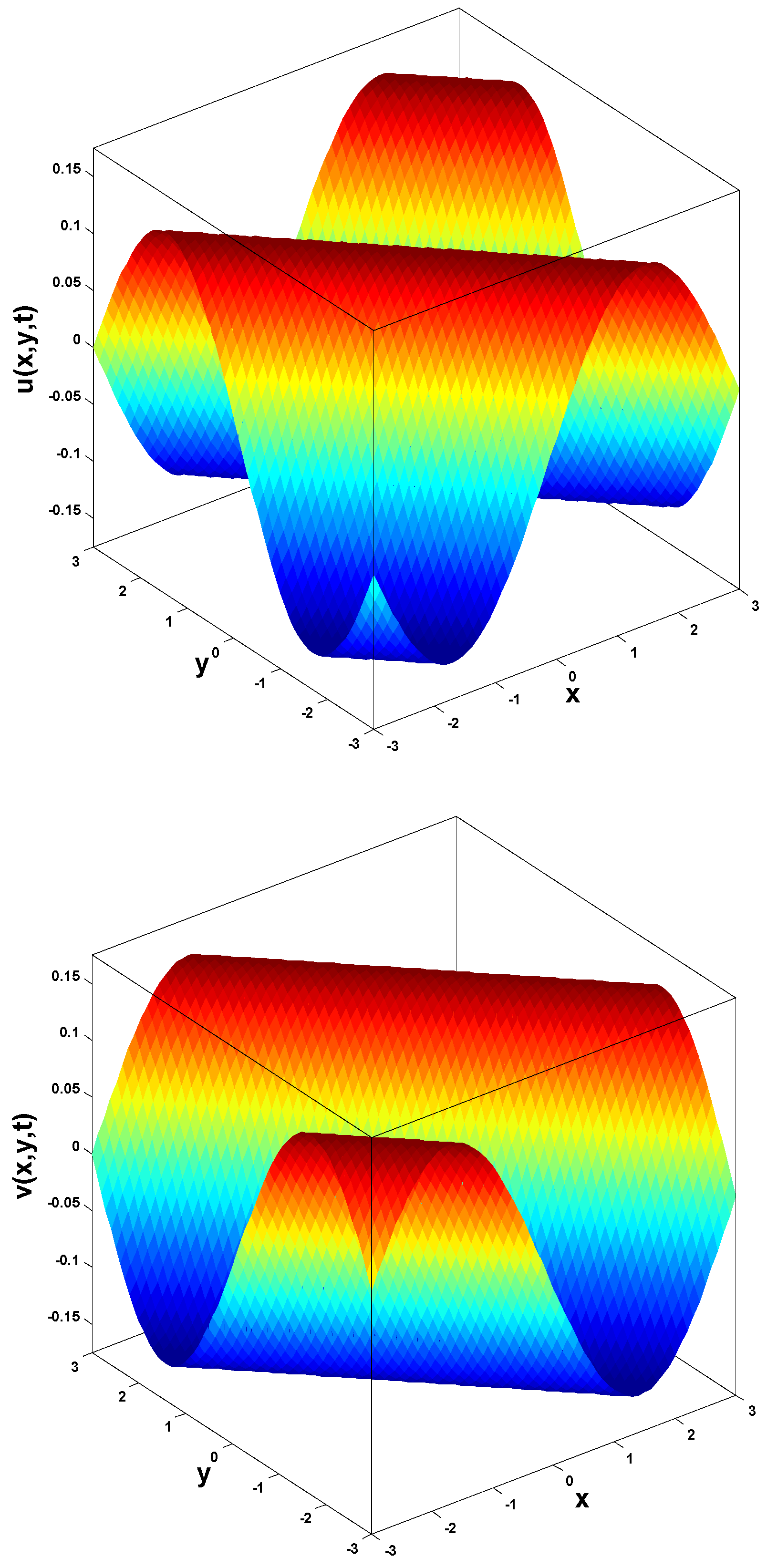
In this section, we apply the homotopy perturbation–Laplace transform method (HP–LTM) to solve time-fractional Navier–Stokes equation. The time-fractional NS equation with constant density $\rho$ and kinematic viscosity $v={\displaystyle \frac{\eta }{\rho }}$ is given as follows:

$$\begin{gathered} {}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }U\left(x,y,z,t\right)+\left(U\left(x,y,z,t\right).\mathsf{\nabla }\right)U\left(x,y,z,t\right)={\rho }_0{\mathsf{\nabla }}^{2}U\left(x,y,z,t\right)-{\displaystyle \frac{1}{\rho }}\mathsf{\nabla }P, \\ \mathsf{\nabla } U\left(x,y,z,t\right)=0, on \Omega \times \left(0,T\right) \\ U\left(x,y,z,0\right)=h\left(x,y,z\right), on \Omega \end{gathered}$$

(30)

here, U represents the velocity vector, P stands for pressure, ${\rho }_0={\displaystyle \frac{\eta }{\rho }}$ denotes the kinematic viscosity where η represents dynamic viscosity and $\rho$ is density. Additionally, the first component ${}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }U\left(x,y,z,t\right)$ denotes the local acceleration, reflecting velocity changes over time at a fixed point in the flow as particles pass. Further, the second part $\left(U\left(x,y,z,t\right).\mathsf{\nabla }\right)U\left(x,y,z,t\right)$ signifies convective acceleration, indicating velocity changes in space as particles move within the flow field over infinitesimal time intervals. In addition, ${\displaystyle \frac{1}{\rho }}\mathsf{\nabla }P$ represents the pressure term, suggesting fluid flow in the direction of the steepest pressure change. As for ${\rho }_0{\mathsf{\nabla }}^{2}U\left(x,y,z,t\right)$, it is the viscous term, illustrating frictional forces due to viscosity acting on fluid particles as they flow with velocity U. Both pressure and viscous forces act on the surface of fluid particles and are classified as external forces. In closing, $\mathrm{\Omega }=\left(-\mathrm{3,3}\right)\times \left(-\mathrm{3,3}\right)$ defines the domain with boundary $\partial \mathrm{\Omega }$ [35].

Formulation of Equation (30) in Cartesian coordinates following on $x,y$ and z is written as follows:

$$\begin{gathered} {}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }U\left(x,y,z,t\right)+U{\displaystyle \frac{\partial U}{\partial x}}+V{\displaystyle \frac{\partial U}{\partial y}}+W{\displaystyle \frac{\partial U}{\partial z}}=-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial P}{\partial x}}+{\rho }_0\left({\displaystyle \frac{{\partial }^{2}U}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial y}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial z}^2}}\right), \\ {}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }V\left(x,y,z,t\right)+U{\displaystyle \frac{\partial V}{\partial x}}+V{\displaystyle \frac{\partial V}{\partial y}}+W{\displaystyle \frac{\partial V}{\partial z}}=-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial P}{\partial y}}+{\rho }_0\left({\displaystyle \frac{{\partial }^{2}V}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial y}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial z}^2}}\right), \\ {}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }W\left(x,y,z,t\right)+U{\displaystyle \frac{\partial W}{\partial x}}+V{\displaystyle \frac{\partial W}{\partial y}}+W{\displaystyle \frac{\partial W}{\partial z}}=-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial P}{\partial z}}+{\rho }_0\left({\displaystyle \frac{{\partial }^{2}W}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}W}{{\partial y}^2}}+{\displaystyle \frac{{\partial }^{2}W}{{\partial z}^2}}\right). \end{gathered}$$

(31)

Applications: Time-Fractional Navier–Stokes Equations

If p is known, then all the values of $g_1=-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial P}{\partial x}},g_2={\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial P}{\partial y}}$ and $g_3=-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial P}{\partial z}}$ can be determined.

Application 1.

From Equation (31), 2D Navier–Stokes equations of fractional order with $g_1$ = −$g_2$ may be written as follows:

$$\begin{gathered} {}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }U\left(x,y,t\right)+U{\displaystyle \frac{\partial U}{\partial x}}+V{\displaystyle \frac{\partial U}{\partial y}}=+g_1+{\rho }_0\left({\displaystyle \frac{{\partial }^{2}U}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial y}^2}}\right) , \\ {}_t{}^{\mathit{CH}}\mathbb{D}_{a+}^{\alpha }V\left(x,y,t\right)+U{\displaystyle \frac{\partial V}{\partial x}}+V{\displaystyle \frac{\partial V}{\partial y}}=-g_2+{\rho }_0\left({\displaystyle \frac{{\partial }^{2}V}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial y}^2}}\right) , \\ {\displaystyle \frac{\partial U}{\partial x}}\left(x,y,t\right)+{\displaystyle \frac{\partial V}{\partial y}}\left(x,y,t\right)=0, \end{gathered}$$

(32)

with IC [36] $U\left(x,y,0\right)=-sin\left(x+y\right), V\left(x,y,0\right)=sin\left(x+y\right).$

By application of LT on both sides of Equation (32), we obtain the following:

$$\mathcal{L}\left\{U\left(x,y,t\right)\right\}=-{\displaystyle \frac{1}{\left(ln\frac{s}{a}\right)}}sin\left(x+y\right)+{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}U}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial y}^2}}\right)+g_1-U{\displaystyle \frac{\partial U}{\partial x}}-V{\displaystyle \frac{\partial U}{\partial y}}\right\}\right\},$$

(33)

$$\mathcal{L}\left\{V\left(x,y,t\right)\right\}={\displaystyle \frac{1}{\left(ln\frac{s}{a}\right)}}sin\left(x+y\right)+{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}V}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial y}^2}}\right)-g_2-U{\displaystyle \frac{\partial V}{\partial x}}-V{\displaystyle \frac{\partial V}{\partial y}}\right\}\right\}.$$

(34)

The inverse Laplace transform of Equations (33) and (34) implies that

$$U\left(x,y,t\right)=-sin\left(x+y\right)+{\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}U}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial y}^2}}\right)+g_1-U{\displaystyle \frac{\partial U}{\partial x}}-V{\displaystyle \frac{\partial U}{\partial y}}\right\}\right\}\right],$$

(35)

$$V\left(x,y,t\right)=sin\left(x+y\right)+{\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}V}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial y}^2}}\right)-g_2-U{\displaystyle \frac{\partial V}{\partial x}}-V{\displaystyle \frac{\partial V}{\partial y}}\right\}\right\}\right],$$

(36)

by simplification of Equations (35) and (36), we obtain the following:

$$U\left(x,y,t\right)=-sin\left(x+y\right)+g_1{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}+{\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}U}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial y}^2}}\right)-U{\displaystyle \frac{\partial U}{\partial x}}-V{\displaystyle \frac{\partial U}{\partial y}}\right\}\right\}\right],$$

(37)

$$V\left(x,y,t\right)=sin\left(x+y\right)-g_2{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}+{\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}V}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial y}^2}}\right)-U{\displaystyle \frac{\partial V}{\partial x}}-V{\displaystyle \frac{\partial V}{\partial y}}\right\}\right\}\right].$$

(38)

Now, through employing the homotopy perturbation method, we obtain the following:

$${\sum }_{n=0}^{\infty }{p}^n{U}_n\left(x,y,t\right)=-\sin \left(x+y\right)+g_1{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}+p\left({\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{N\sum _{n=0}^{\infty }{p}^n{H}_n\left(U\right)\right\}\right\}\right]\right),$$

(39)

$${\sum }_{n=0}^{\infty }{p}^n{V}_n\left(x,y,t\right)=\mathit{sin}(x+y)-g_2{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}+p\left({\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{N\sum _{n=0}^{\infty }{p}^n{H}_n\left(V\right)\right\}\right\}\right]\right),$$

(40)

where $H_n\left(U\right)$ and $H_n\left(V\right)$ represent He’s polynomials, denoting the nonlinear terms.

$$\left\{\begin{array}{c}{H}_n\left(U\right)={\rho }_0\left({\displaystyle \frac{{\partial }^{2}U}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial y}^2}}\right)-U{\displaystyle \frac{\partial U}{\partial x}}-V{\displaystyle \frac{\partial U}{\partial y}},\\ H_n\left(V\right)={\rho }_0\left({\displaystyle \frac{{\partial }^{2}V}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial y}^2}}\right)-U{\displaystyle \frac{\partial V}{\partial x}}-V{\displaystyle \frac{\partial V}{\partial y}},\end{array}\right.$$

(41)

where

$$\left\{\begin{array}{c}U=U_0+p{U}_1+p^2{U}_2+p^3{U}_3+\cdots ,\\ V=V_0+p{V}_1+p^2{V}_2+p^3{V}_3+\cdots , \end{array}\right.$$

(42)

the first few components of He’s polynomials are provided as follows:

$$\left\{\begin{array}{c}{H}_0\left(U\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{U}_0}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{U}_0}{{\partial y}^2}}\right)-U_0{\displaystyle \frac{\partial U_0}{\partial x}}-V_0{\displaystyle \frac{\partial U_0}{\partial y}},\\ H_0\left(V\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{V}_0}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{V}_0}{{\partial y}^2}}\right)-U_0{\displaystyle \frac{\partial V_0}{\partial x}}-V_0{\displaystyle \frac{\partial V_0}{\partial y}},\end{array}\right.$$

(43)

$$\left\{\begin{array}{c}{H}_1\left(U\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{U}_1}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{U}_1}{{\partial y}^2}}\right)-U_0{\displaystyle \frac{\partial U_1}{\partial x}}-V_0{\displaystyle \frac{\partial U_1}{\partial y}}-U_1{\displaystyle \frac{\partial U_0}{\partial x}}-V_1{\displaystyle \frac{\partial U_0}{\partial y}},\\ H_1\left(V\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{V}_1}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{V}_1}{{\partial y}^2}}\right)-U_0{\displaystyle \frac{\partial V_1}{\partial x}}-V_0{\displaystyle \frac{\partial V_1}{\partial y}}-U_1{\displaystyle \frac{\partial V_0}{\partial x}}-V_1{\displaystyle \frac{\partial V_0}{\partial y}},\end{array}\right.$$

(44)

$$\left\{\begin{array}{c}{H}_2\left(U\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{U}_2}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{U}_2}{{\partial y}^2}}\right)-\cdots ,\\ H_2\left(V\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{V}_2}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{V}_2}{{\partial y}^2}}\right)-\cdots ,\end{array}\right.$$

(45)

$⋮.$

Equating the coefficients of like powers of p in Equations (39) and (40), we obtain the following results:

$$p^0:\left\{\begin{array}{c}{U}_0\left(x,y,t\right)=-\mathit{sin}(x+y)+g_1{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}},\\ V_0\left(x,y,t\right)=\mathit{sin}(x+y)-g_2{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}},\end{array}\right.$$

(46)

$$p^1:\left\{\begin{array}{c}{U}_1\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_0\left(U\right)\right\}\right\}\right]=2{\rho }_{0}sin\left(x+y\right){\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}},\\ V_1\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_0\left(V\right)\right\}\right\}\right]=-2{\rho }_{0}sin\left(x+y\right){\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}},\end{array}\right.$$

(47)

$$p^2:\left\{\begin{array}{c}{U}_2\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_1\left(U\right)\right\}\right\}\right]=-4{{\rho }_0}^{2}sin\left(x+y\right){\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{2\alpha }}{\Gamma \left(2\alpha +1\right)}},\\ V_2\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_1\left(V\right)\right\}\right\}\right]=4{{\rho }_0}^{2}sin\left(x+y\right){\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{2\alpha }}{\Gamma \left(2\alpha +1\right)}},\end{array}\right.$$

(48)

$$p^3:\left\{\begin{array}{c}{U}_3\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_2\left(U\right)\right\}\right\}\right]=8{{\rho }_0}^{3}sin\left(x+y\right){\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{3\alpha }}{\Gamma \left(3\alpha +1\right)}},\\ V_3\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_2\left(V\right)\right\}\right\}\right]=-8{{\rho }_0}^{3}sin\left(x+y\right){\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{3\alpha }}{\Gamma \left(3\alpha +1\right)}},\end{array}\right.$$

(49)

$⋮$.

Thus, the solutions $\mathrm{U}\left(\mathrm{x},\mathrm{y},\mathrm{t}\right)$ and $\mathrm{V}\left(\mathrm{x},\mathrm{y},\mathrm{t}\right)$ are written in the following form:

$$\begin{array}{cc}\hfill U\left(x,y,t\right)& =U_0\left(x,y,t\right)+U_1\left(x,y,t\right)+U_2\left(x,y,t\right)+U_3\left(x,y,t\right)+\cdots \hfill \\ & =-\mathit{sin}(x+y)e^{-{2\rho }_0{\left(ln{\displaystyle \frac{t}{a}}\right)}^{\alpha }}+g_1{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}},\hfill \end{array}$$

$$\begin{array}{cc}\hfill V\left(x,y,t\right)& =V_0\left(x,y,t\right)+V_1\left(x,y,t\right)+V_2\left(x,y,t\right)+V_3\left(x,y,t\right)+\cdots \hfill \\ & =\mathit{sin}(x+y)e^{-{2\rho }_0{\left(ln{\displaystyle \frac{t}{a}}\right)}^{\alpha }}-g_2{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}.\hfill \end{array}$$

(50)

Finally, we work on writing infinite sums in terms of the Mittag–Leffler function, Equation (9) is as follows:

$$\begin{gathered} U\left(x,y,t\right)=-\mathit{sin}\left(x+y\right){{\rm E}}_{\alpha ,1}\left(-{2\rho }_0{\left(\mathit{ln}{\displaystyle \frac{t}{a}}\right)}^{\alpha }\right)+g_1{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}, \\ V\left(x,y,t\right)=\mathit{sin}\left(x+y\right){{\rm E}}_{\alpha ,1}\left(-{2\rho }_0{\left(\mathit{ln}{\displaystyle \frac{t}{a}}\right)}^{\alpha }\right)-g_2{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}. \end{gathered}$$

(51)

Additionally, $g_1=g_2=0$ and $a$ = 1, Equation (51) reduce to the following:

$$\begin{gathered} U\left(x,y,t\right)=-sin\left(x+y\right)e^{-{2\rho }_0{\left(lnt\right)}^{\alpha }}, \\ V\left(x,y,t\right)=sin\left(x+y\right)e^{-{2\rho }_0{\left(lnt\right)}^{\alpha }}. \end{gathered}$$

(52)

As consequence, these solutions of Equation (52) are in agreement with the solutions found by Oliveira et al. using homotopy analysis method (HAM) [37], This solution is in good agreement with the solutions found by [36] using homotopy perturbation Elzaki transform(HPETM) and are in agreement with the solutions found by Singh and Kumar using fractional reduced differential transformation method (FRDTM) [38] and also are in agreement with the solutions found by Eltayeb et al. applying double Sumudu generalized Laplace transform decomposition method (DGLTDM) [30].

The plots of Equation (51) are depicted in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 for different values of $\alpha =1, 0.9, 0.6, 0.3$, ${\rho }_0$ = 1, t = 2.5, $a=1$, and $g_1=g_2=0$.

Figure 1. Plots solution application 1 with $a=1, {\rho }_0=1, y=0.3, t=2.5, g_1=g_2=0, \alpha =1, 0.9, 0.6, 0.3$.

Figure 2. Plots solution application 1 with $a=1, {\rho }_0=1, x=y=0.3,{ g}_1=g_2=0, \alpha =1, 0.9, 0.6, 0.3$.

Figure 3. Plots solution application 1 with $a=1, { \rho }_0=1, t=2.5, \alpha =1$.

Figure 4. Plots solution application 1 with $a=1, { \rho }_0=1, t=2.5, \alpha =0.9$.

Figure 5. Plots solution application 1 with $a=1, { \rho }_0=1, t=2.5, \alpha =0.6$.

Figure 6. Plots solution application 1 with $a=1, { \rho }_0=1, t=2.5, \alpha =0.3$.

The exact solution of classical NS equation for the velocity [30,36,38]:

$$\left\{\begin{array}{c}U\left(x,y,t\right)=-sin\left(x+y\right)e^{-{\rho }_{0}t},\\ V\left(x,y,t\right)=sin\left(x+y\right)e^{-2{\rho }_{0}t}.\end{array}\right.$$

Application 2.

From Equation (31), 2D Navier–Stokes equations of fractional order with $g_1$ = −$g_2$ and with IC [36] $U\left(x,y,0\right)=-e^{x+y}, V\left(x,y,0\right)=e^{x+y}.$

By application of LT on both sides of Equation (32), we obtain the following:

$$\mathcal{L}\left\{U\left(x,y,t\right)\right\}=-{\displaystyle \frac{1}{\left(ln\frac{s}{a}\right)}}{e}^{x+y}+{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}U}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial y}^2}}\right)+g_1-U{\displaystyle \frac{\partial U}{\partial x}}-V{\displaystyle \frac{\partial U}{\partial y}}\right\}\right\},$$

(53)

$$\mathcal{L}\left\{V\left(x,y,t\right)\right\}={\displaystyle \frac{1}{\left(ln\frac{s}{a}\right)}}{e}^{x+y}+{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}V}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial y}^2}}\right)-g_2-U{\displaystyle \frac{\partial V}{\partial x}}-V{\displaystyle \frac{\partial V}{\partial y}}\right\}\right\}.$$

(54)

The inverse Laplace transform of Equations (53) and (54) implies the following:

$$U\left(x,y,t\right)=-e^{x+y}+{\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}U}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial y}^2}}\right)+g_1-U{\displaystyle \frac{\partial U}{\partial x}}-V{\displaystyle \frac{\partial U}{\partial y}}\right\}\right\}\right],$$

(55)

$$V\left(x,y,t\right)=e^{x+y}+{\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}V}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial y}^2}}\right)-g_2-U{\displaystyle \frac{\partial V}{\partial x}}-V{\displaystyle \frac{\partial V}{\partial y}}\right\}\right\}\right].$$

(56)

By simplification of Equations (55) and (56), we obtain the following:

$$U\left(x,y,t\right)=-e^{x+y}+g_1{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}+{\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}U}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial y}^2}}\right)-U{\displaystyle \frac{\partial U}{\partial x}}-V{\displaystyle \frac{\partial U}{\partial y}}\right\}\right\}\right],$$

(57)

$$V\left(x,y,t\right)=e^{x+y}-g_2{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}+{\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{{\rho }_0\left({\displaystyle \frac{{\partial }^{2}V}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial y}^2}}\right)-U{\displaystyle \frac{\partial V}{\partial x}}-V{\displaystyle \frac{\partial V}{\partial y}}\right\}\right\}\right].$$

(58)

Now, through applying the homotopy perturbation method, we obtain the following:

$${\sum }_{n=0}^{\infty }{p}^n{U}_n\left(x,y,t\right)=-e^{x+y}+g_1{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}+p\left({\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{N{\sum }_{n=0}^{\infty }{p}^n{H}_n\left(U\right)\right\}\right\}\right]\right),$$

(59)

$${\sum }_{n=0}^{\infty }{p}^n{V}_n\left(x,y,t\right)=e^{x+y}-g_2{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}+p\left({\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{N{\sum }_{n=0}^{\infty }{p}^n{H}_n\left(V\right)\right\}\right\}\right]\right),$$

(60)

where $H_n\left(U\right)$ and $H_n\left(V\right)$ are He’s polynomials which signify the nonlinear terms.

$$\begin{gathered} H_n\left(U\right)={\rho }_0\left({\displaystyle \frac{{\partial }^{2}U}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}U}{{\partial y}^2}}\right)-U{\displaystyle \frac{\partial U}{\partial x}}-V{\displaystyle \frac{\partial U}{\partial y}}=0, \\ {H}_n\left(V\right)={\rho }_0\left({\displaystyle \frac{{\partial }^{2}V}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^{2}V}{{\partial y}^2}}\right)-U{\displaystyle \frac{\partial V}{\partial x}}-V{\displaystyle \frac{\partial V}{\partial y}}=0, \end{gathered}$$

(61)

where

$$U=U_0+p{U}_1+p^2{U}_2+p^3{U}_3+\cdots ,V=V_0+p{V}_1+p^2{V}_2+p^3{V}_3+\cdots .$$

(62)

The first few components of He’s polynomials are given as follows:

$$\left\{\begin{array}{c}{H}_0\left(U\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{U}_0}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{U}_0}{{\partial y}^2}}\right)-U_0{\displaystyle \frac{\partial U_0}{\partial x}}-V_0{\displaystyle \frac{\partial U_0}{\partial y}},\\ H_0\left(V\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{V}_0}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{V}_0}{{\partial y}^2}}\right)-U_0{\displaystyle \frac{\partial V_0}{\partial x}}-V_0{\displaystyle \frac{\partial V_0}{\partial y}},\end{array}\right.$$

(63)

$$\left\{\begin{array}{c}{H}_1\left(U\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{U}_1}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{U}_1}{{\partial y}^2}}\right)-U_0{\displaystyle \frac{\partial U_1}{\partial x}}-V_0{\displaystyle \frac{\partial U_1}{\partial y}}-U_1{\displaystyle \frac{\partial U_0}{\partial x}}-V_1{\displaystyle \frac{\partial U_0}{\partial y}},\\ H_1\left(V\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{V}_1}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{V}_1}{{\partial y}^2}}\right)-U_0{\displaystyle \frac{\partial V_1}{\partial x}}-V_0{\displaystyle \frac{\partial V_1}{\partial y}}-U_1{\displaystyle \frac{\partial V_0}{\partial x}}-V_1{\displaystyle \frac{\partial V_0}{\partial y}},\end{array}\right.$$

(64)

$$\left\{\begin{array}{c}{H}_2\left(U\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{U}_2}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{U}_2}{{\partial y}^2}}\right)-\cdots ,\\ H_2\left(V\right)={\rho }_0\left({\displaystyle \frac{{\partial }^2{V}_2}{{\partial x}^2}}+{\displaystyle \frac{{\partial }^2{V}_2}{{\partial y}^2}}\right)-\cdots ,\end{array}\right.$$

(65)

$⋮.$

Equating the coefficients of like powers of p in Equations (39) and (40), we obtain the following results:

$$p^0:\left\{\begin{array}{c}{U}_0\left(x,y,t\right)=-e^{x+y}+g_1{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}},\\ V_0\left(x,y,t\right)=e^{x+y}-g_2{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}},\end{array}\right.$$

(66)

$$p^1:\left\{\begin{array}{c}{U}_1\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_0\left(U\right)\right\}\right\}\right]=2{\rho }_0{e}^{x+y}{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}},\\ V_1\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_0\left(V\right)\right\}\right\}\right]=-2{\rho }_0{e}^{x+y}{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}},\end{array}\right.$$

(67)

$$p^2:\left\{\begin{array}{c}{U}_2\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_1\left(U\right)\right\}\right\}\right]=-4{{\rho }_0}^2{e}^{x+y}{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{2\alpha }}{\Gamma \left(2\alpha +1\right)}},\\ V_2\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_1\left(V\right)\right\}\right\}\right]=4{{\rho }_0}^2{e}^{x+y}{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{2\alpha }}{\Gamma \left(2\alpha +1\right)}},\end{array}\right.$$

(68)

$$p^3:\left\{\begin{array}{c}{U}_3\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_2\left(U\right)\right\}\right\}\right]=8{{\rho }_0}^3{e}^{x+y}{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{3\alpha }}{\Gamma \left(3\alpha +1\right)}},\\ V_3\left(x,y,t\right)={\mathcal{L}}^{-1}\left[{\displaystyle \frac{1}{{\left(ln\frac{s}{a}\right)}^{\alpha }}}\left\{\mathcal{L}\left\{H_2\left(V\right)\right\}\right\}\right]=-8{{\rho }_0}^3{e}^{x+y}{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{3\alpha }}{\Gamma \left(3\alpha +1\right)}},\end{array}\right.$$

(69)

$⋮.$

As a consequence, the solutions u$\left(x,y,t\right)$ and v$\left(x,y,t\right)$ are written in the following form:

$$\begin{array}{cc}\hfill U\left(x,y,t\right)& =U_0\left(x,y,t\right)+U_1\left(x,y,t\right)+U_2\left(x,y,t\right)+U_3\left(x,y,t\right)+\cdots \hfill \\ & =-e^{x+y}{e}^{-{2\rho }_0{\left(ln{\displaystyle \frac{t}{a}}\right)}^{\alpha }}+g_1{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}},\hfill \end{array}$$

$$\begin{array}{cc}\hfill V\left(x,y,t\right)& =V_0\left(x,y,t\right)+V_1\left(x,y,t\right)+V_2\left(x,y,t\right)+V_3\left(x,y,t\right)+\cdots \hfill \\ & =e^{x+y}{e}^{-{2\rho }_0{\left(ln{\displaystyle \frac{t}{a}}\right)}^{\alpha }}-g_2{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}.\hfill \end{array}$$

(70)

Finally, we endeavour to write infinite sums in terms of the Mittag–Leffler function, Equation (9) is as follows:

$$\begin{gathered} U\left(x,y,t\right)=-e^{x+y}{{\rm E}}_{\alpha ,1}\left(-{2\rho }_0{\left(\mathit{ln}{\displaystyle \frac{t}{a}}\right)}^{\alpha }\right)+g_1{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}, \\ V\left(x,y,t\right)=e^{x+y}{{\rm E}}_{\alpha ,1}\left(-{2\rho }_0{\left(\mathit{ln}{\displaystyle \frac{t}{a}}\right)}^{\alpha }\right)-g_2{\displaystyle \frac{{\left(ln\frac{t}{a}\right)}^{\alpha }}{\Gamma \left(\alpha +1\right)}}. \end{gathered}$$

(71)

For ${a=1, g}_1$ = $g_2=$ 0, Equation (71) reduce to:

$$\begin{gathered} U\left(x,y,t\right)=-e^{x+y}{e}^{-{2\rho }_0{\left(lnt\right)}^{\alpha }}, \\ V\left(x,y,t\right)=e^{x+y}{e}^{-{2\rho }_0{\left(lnt\right)}^{\alpha }}. \end{gathered}$$

(72)

Nonetheless, this solution (71) to Equations (53) and (54) using (HP–LTM) and operator the Hadamard fractional derivative is considered an approximate solution, for different values of α = 1, 0.9, 0.6, 0.3, ${\rho }_0$ = 1, t = 2.5, $a=1$,$g_1$ = $g_2$= 0 shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, This solution is in good agreement with the solutions found by [36] using homotopy perturbation Elzaki transform(HPETM) and are in agreement with the solutions found by Singh and Kumar using Fractional Reduced Differential Transformation Method (FRDTM) [38].

Figure 7. Plots solution application 2 with $a=1, {\rho }_0=1, y=0.3$, $t=2.5, g_1=g_2=0, \alpha =1, 0.9, 0.6, 0.3$.

Figure 8. Plots solution application 1 with $a=1, {\rho }_0=1, x=y=0.3, g_1=g_2=0, \alpha =1, 0.9, 0.6, 0.3$.

Figure 9. Plots solution application 2 with $a=1, {\rho }_0=1, t=2.5, g_1=g_2=0, \alpha =1$.

Figure 10. Plots solution application 2 with $a=1, {\rho }_0=1, t=2.5, g_1=g_2=0, \alpha =0.9$.

Figure 11. Plots solution application 2 with $a=1,{ \rho }_0=1,t=2.5,{ g}_1=g_2=0,\alpha =0.6$.

Figure 12. Plots solution application 2 with $a=1,{\rho }_0=1,t=2.5,g_1=g_2=0,\alpha =0.3$.

The exact solution of classical NS equation for the velocity [36,38], is as follows:

$$\left\{\begin{array}{c}U\left(x,y,t\right)=-exp\left(x+y\right)e^{-{2\rho }_{0}t},\\ V\left(x,y,t\right)=exp\left(x+y\right)e^{-{2\rho }_{0}t}.\end{array}\right.$$

7. Conclusions

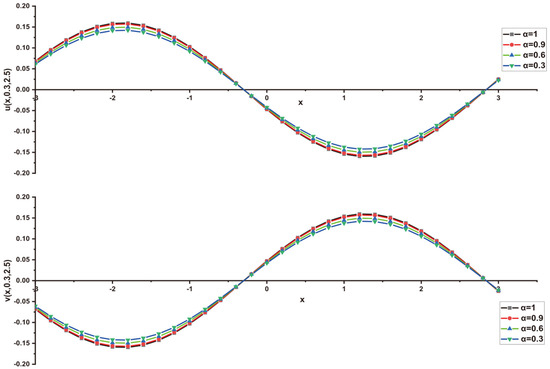
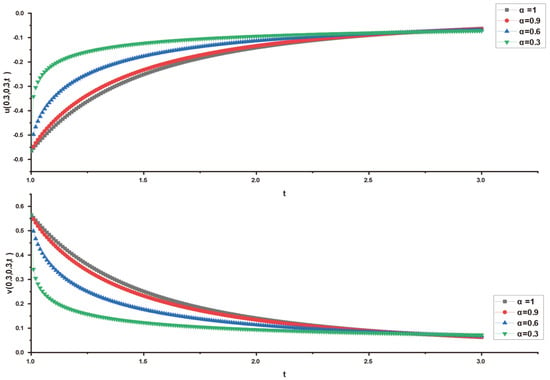
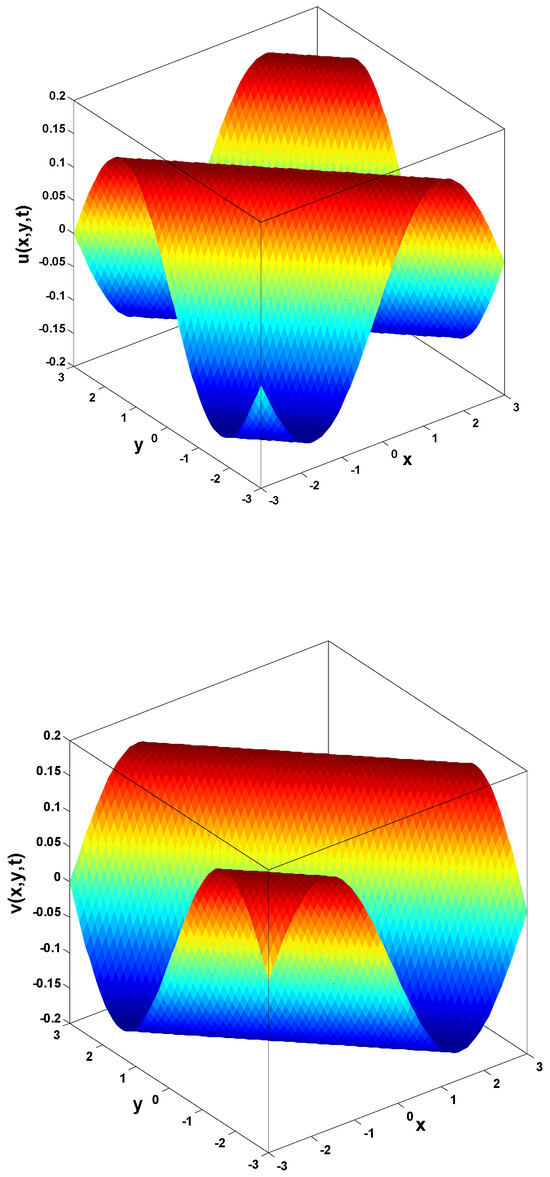
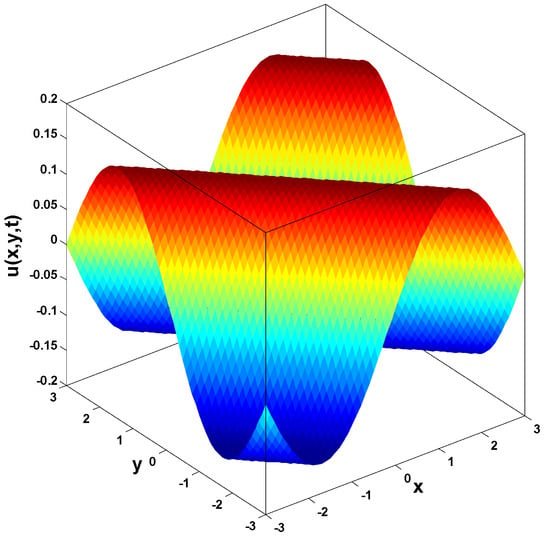
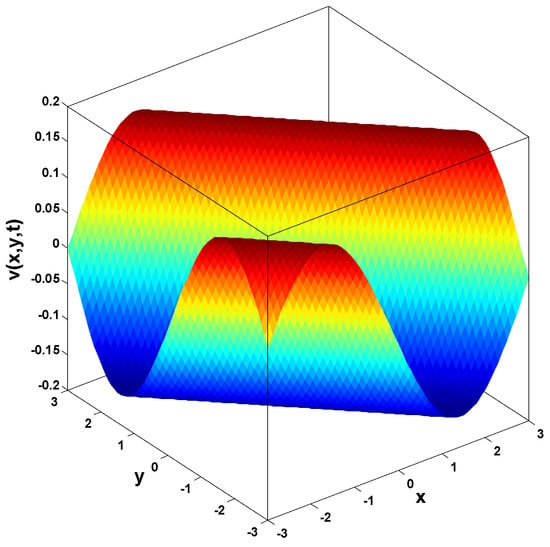
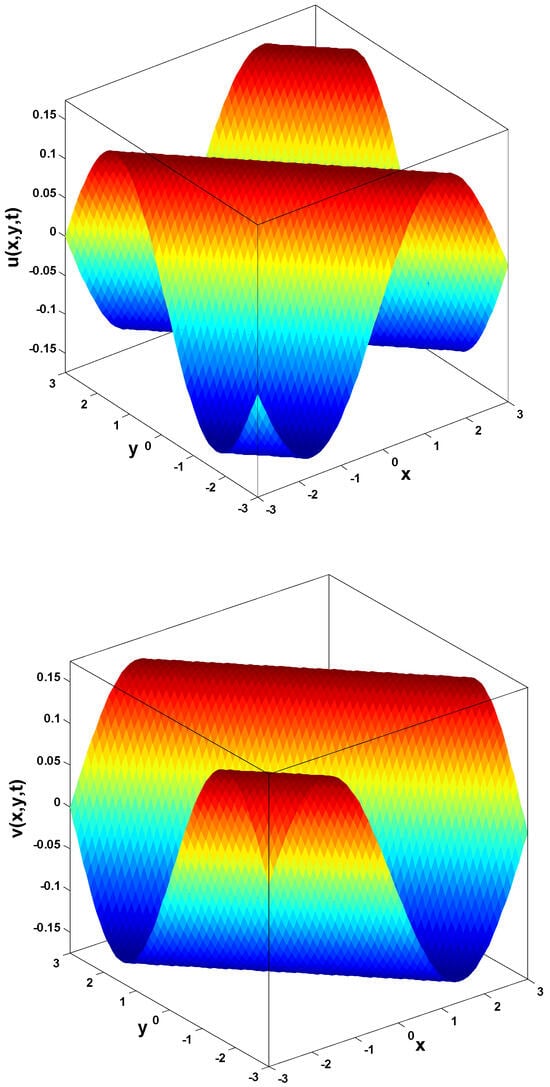
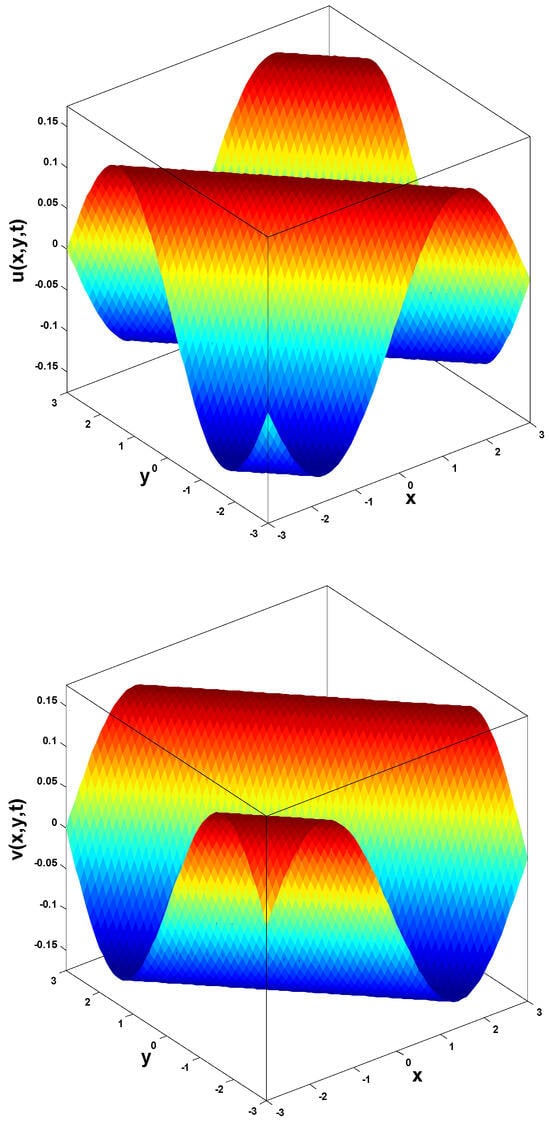
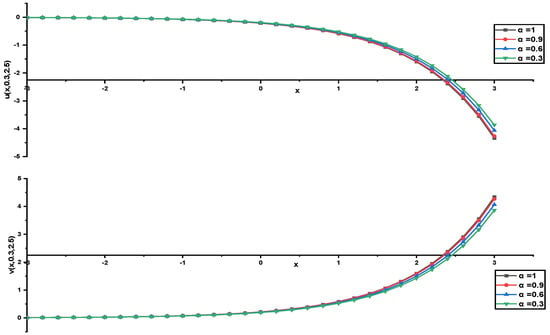
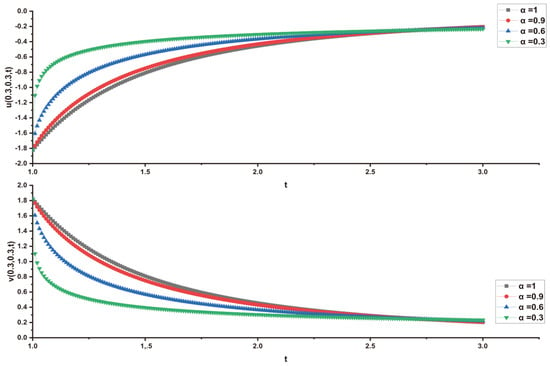
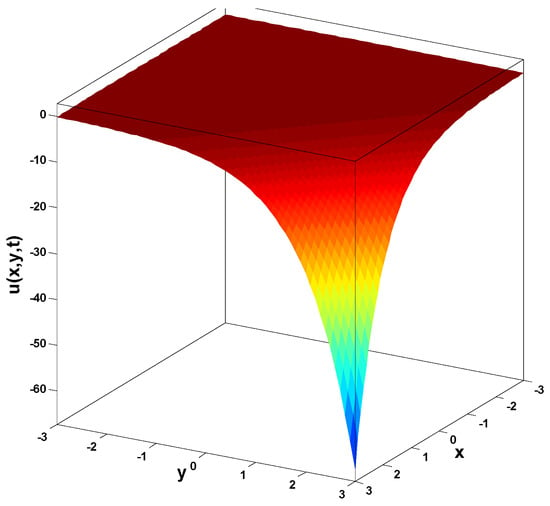
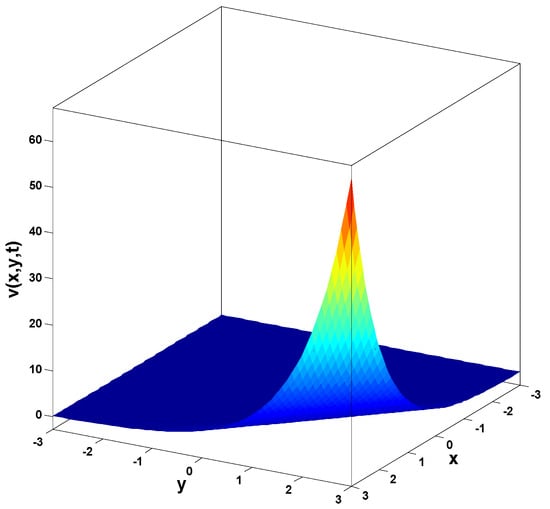
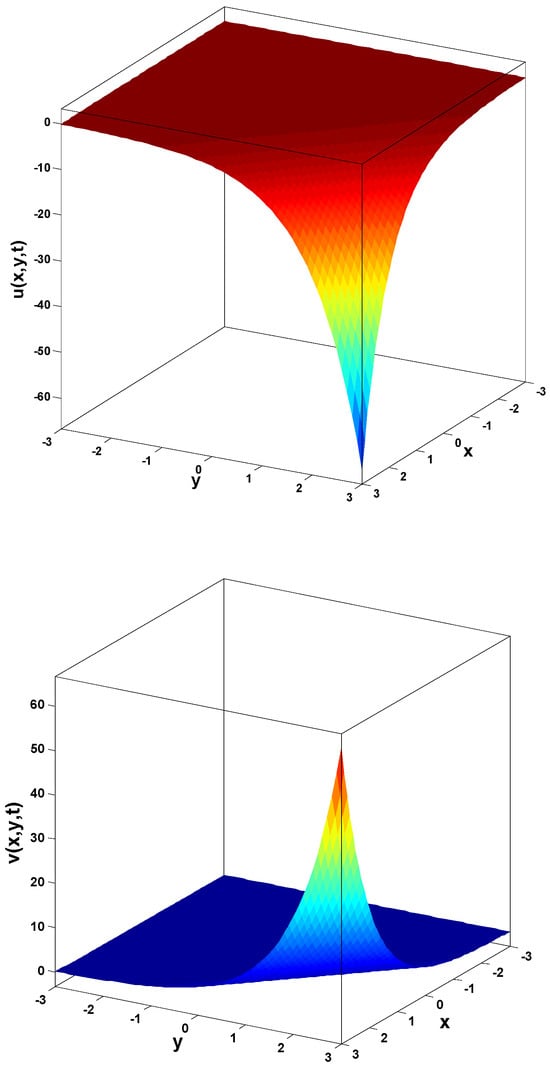
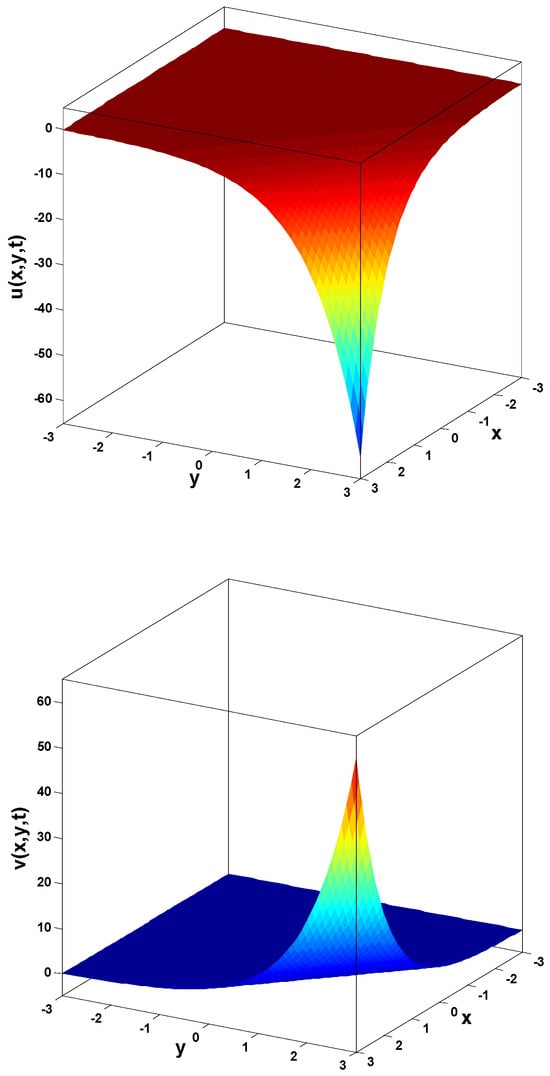
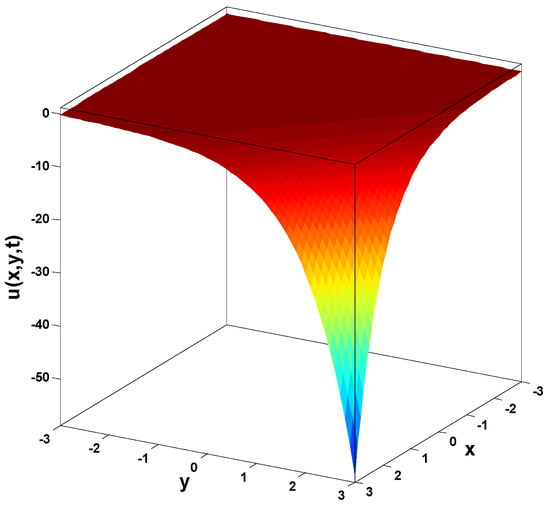
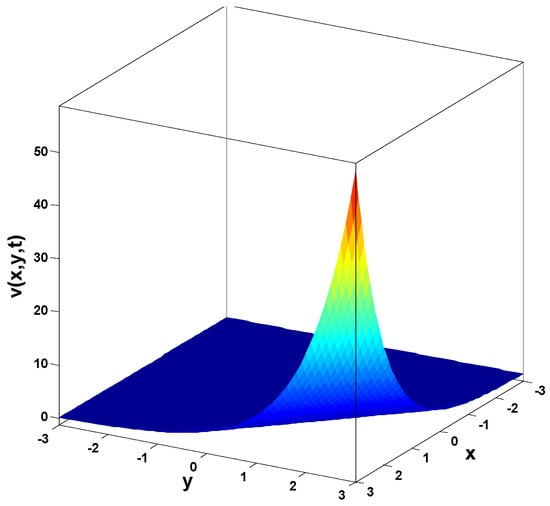
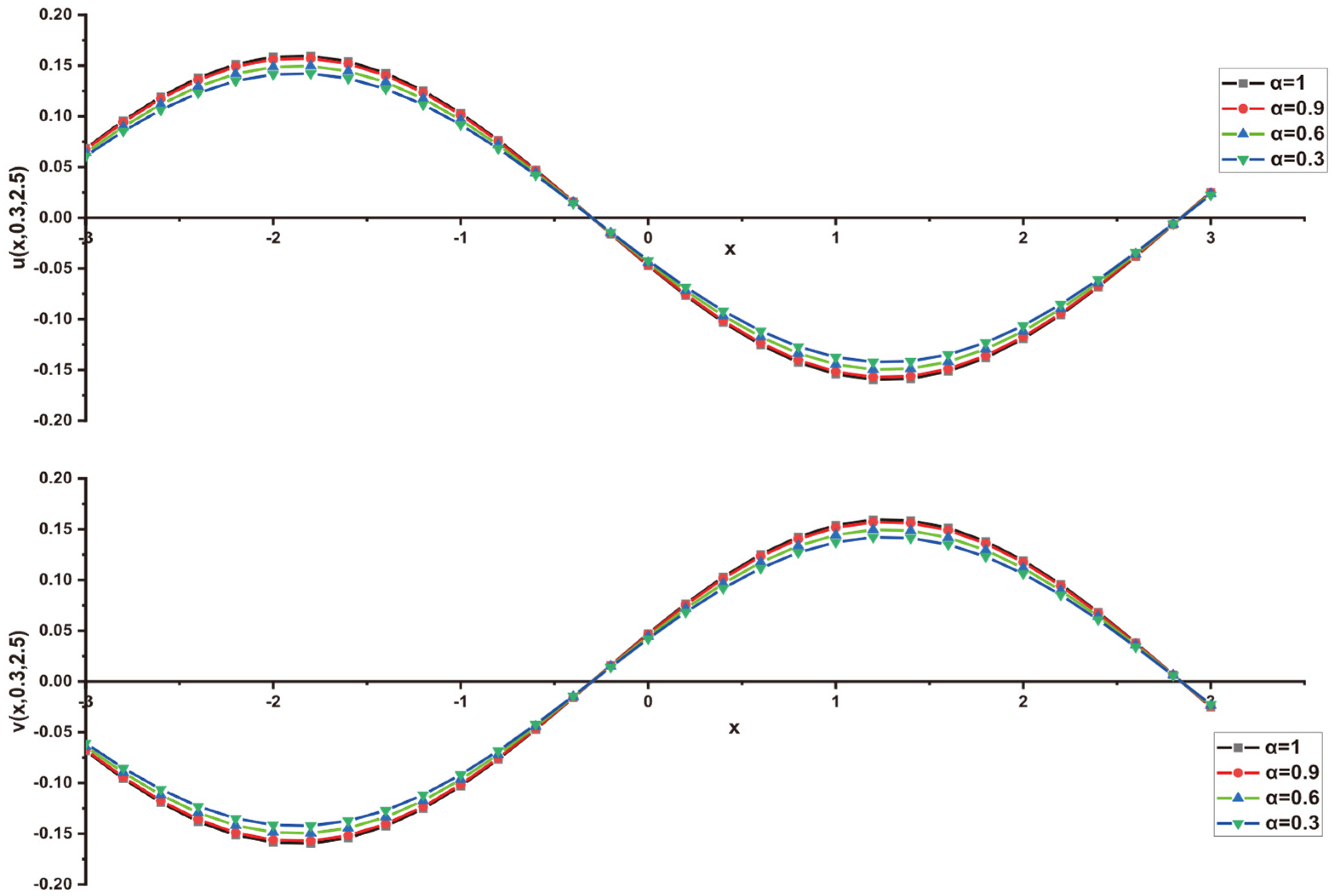
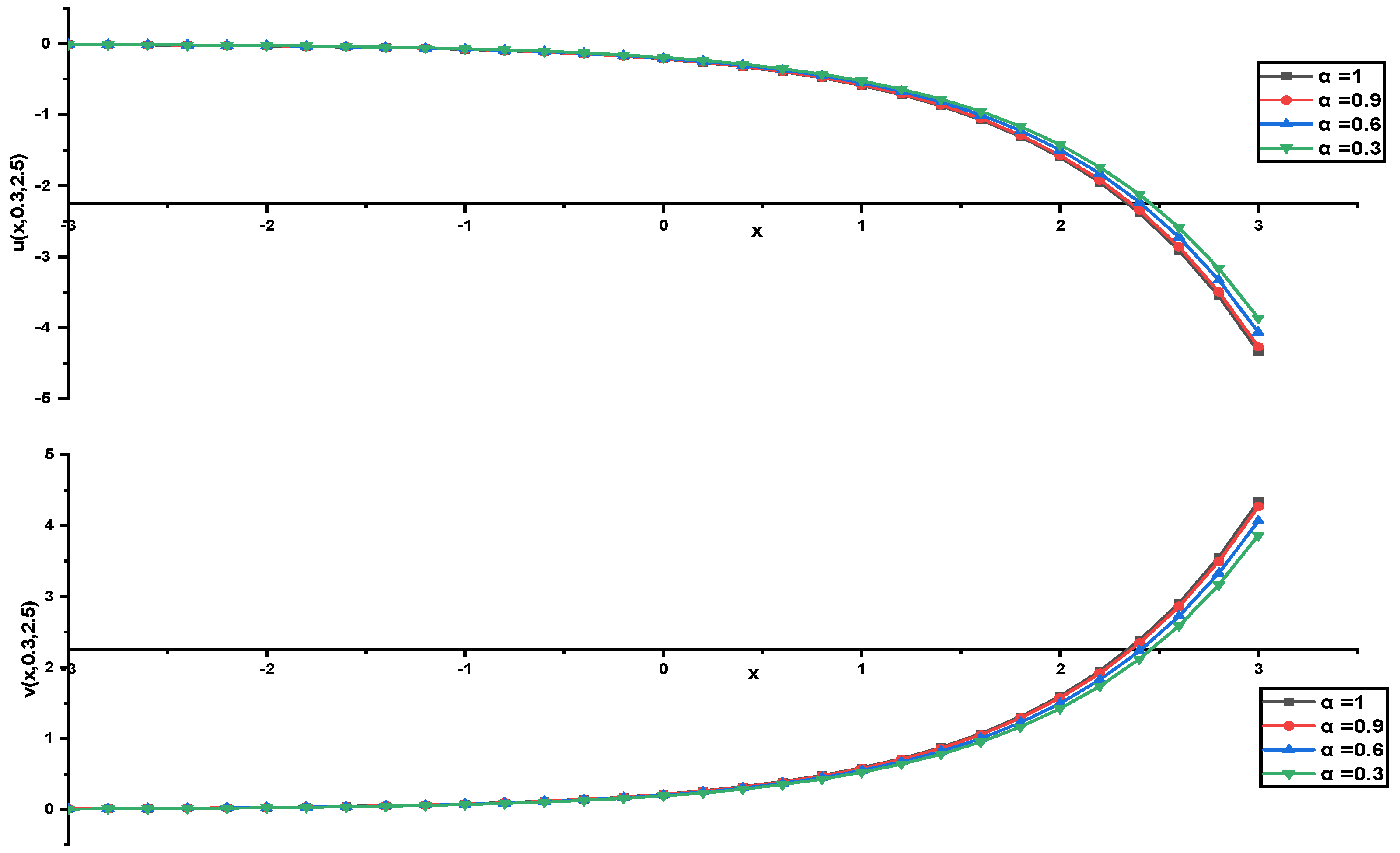
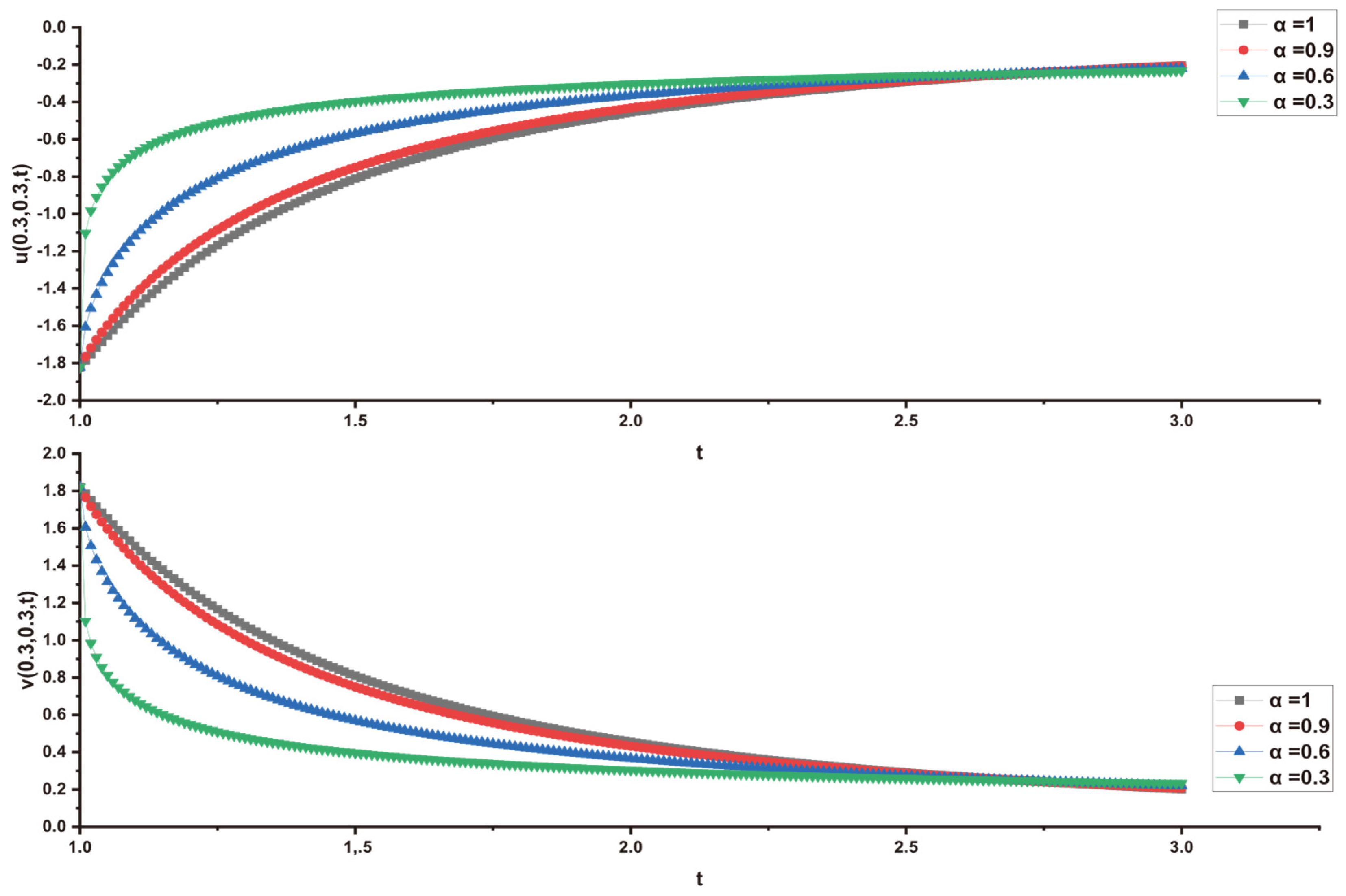
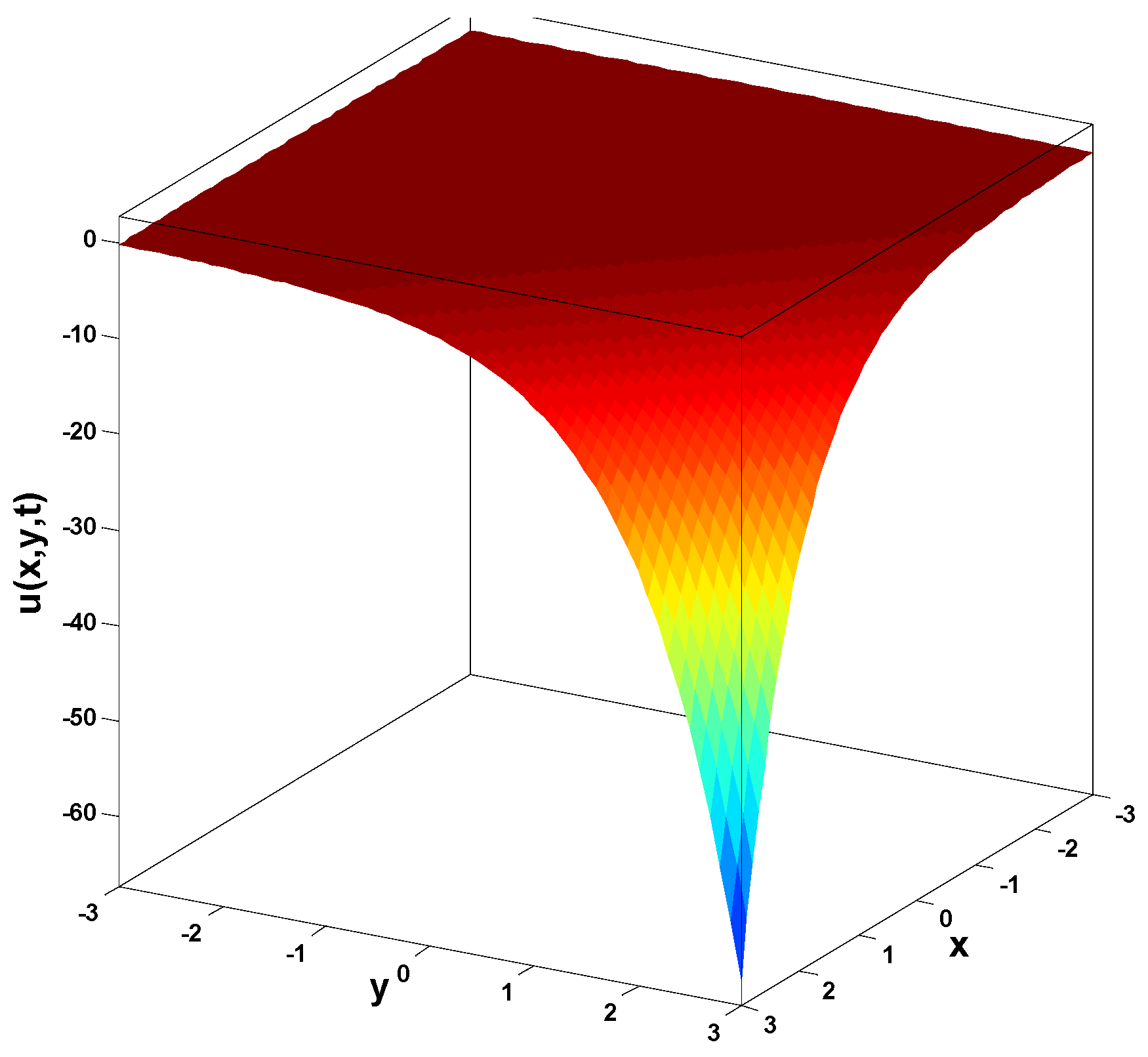
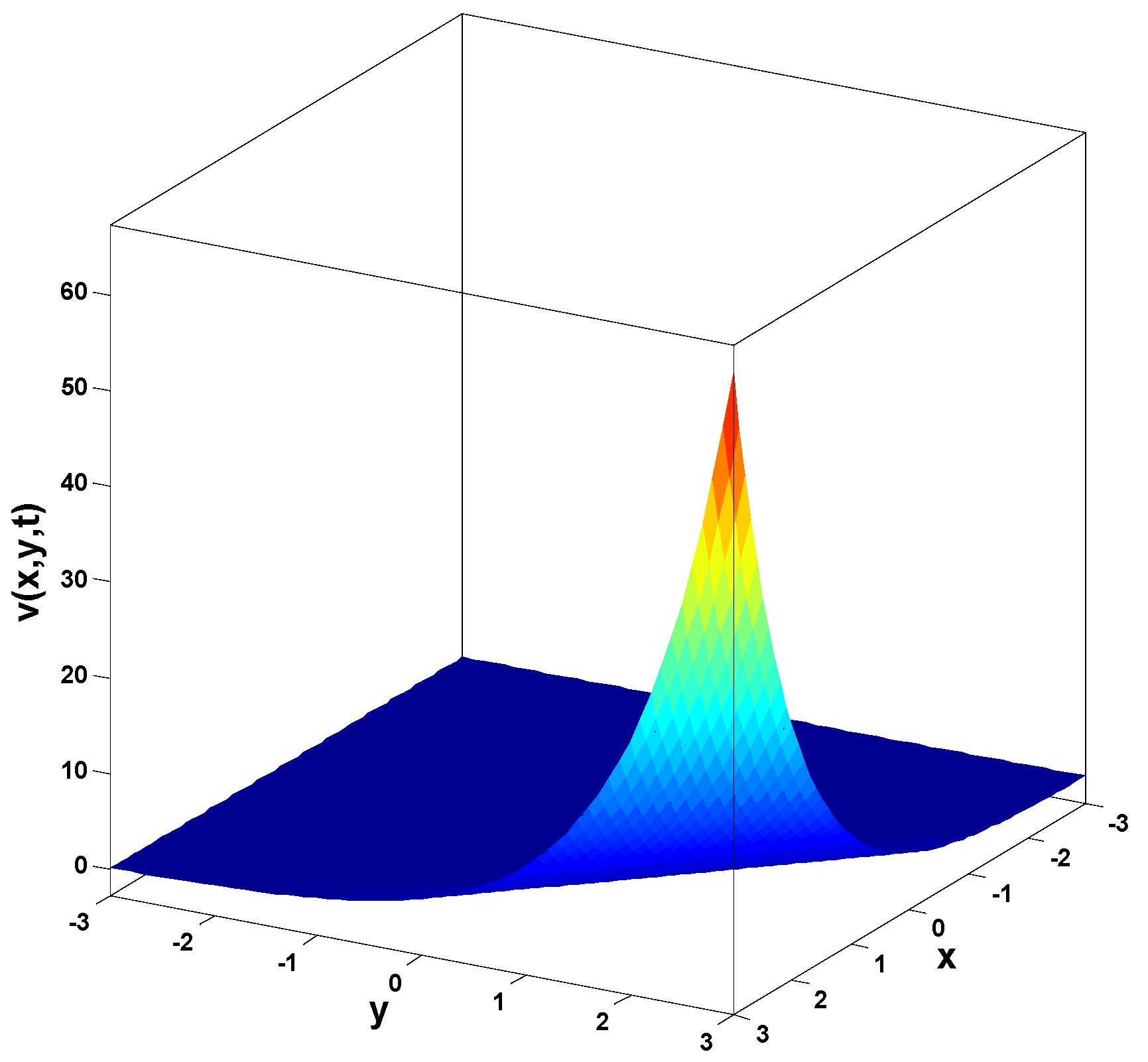
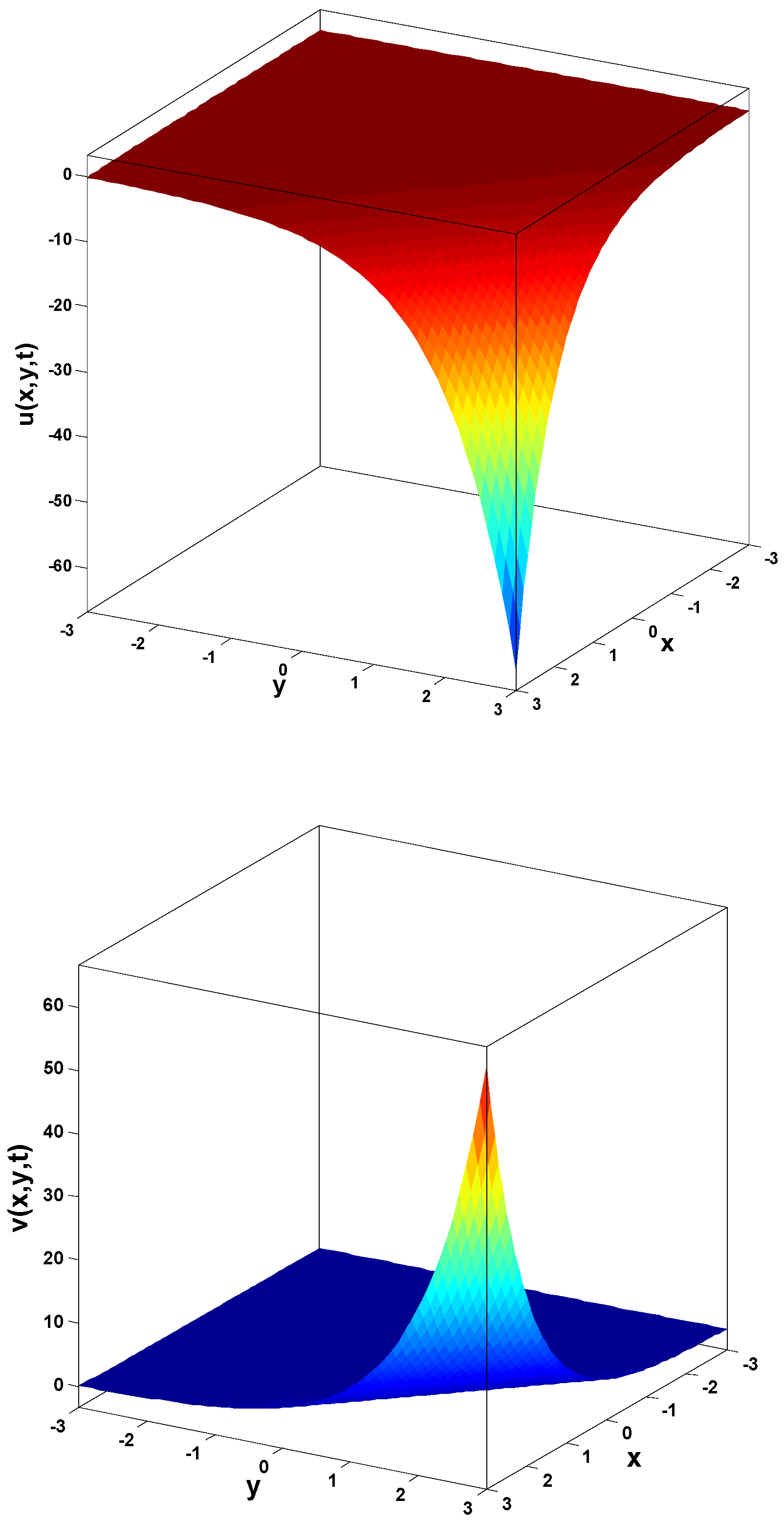
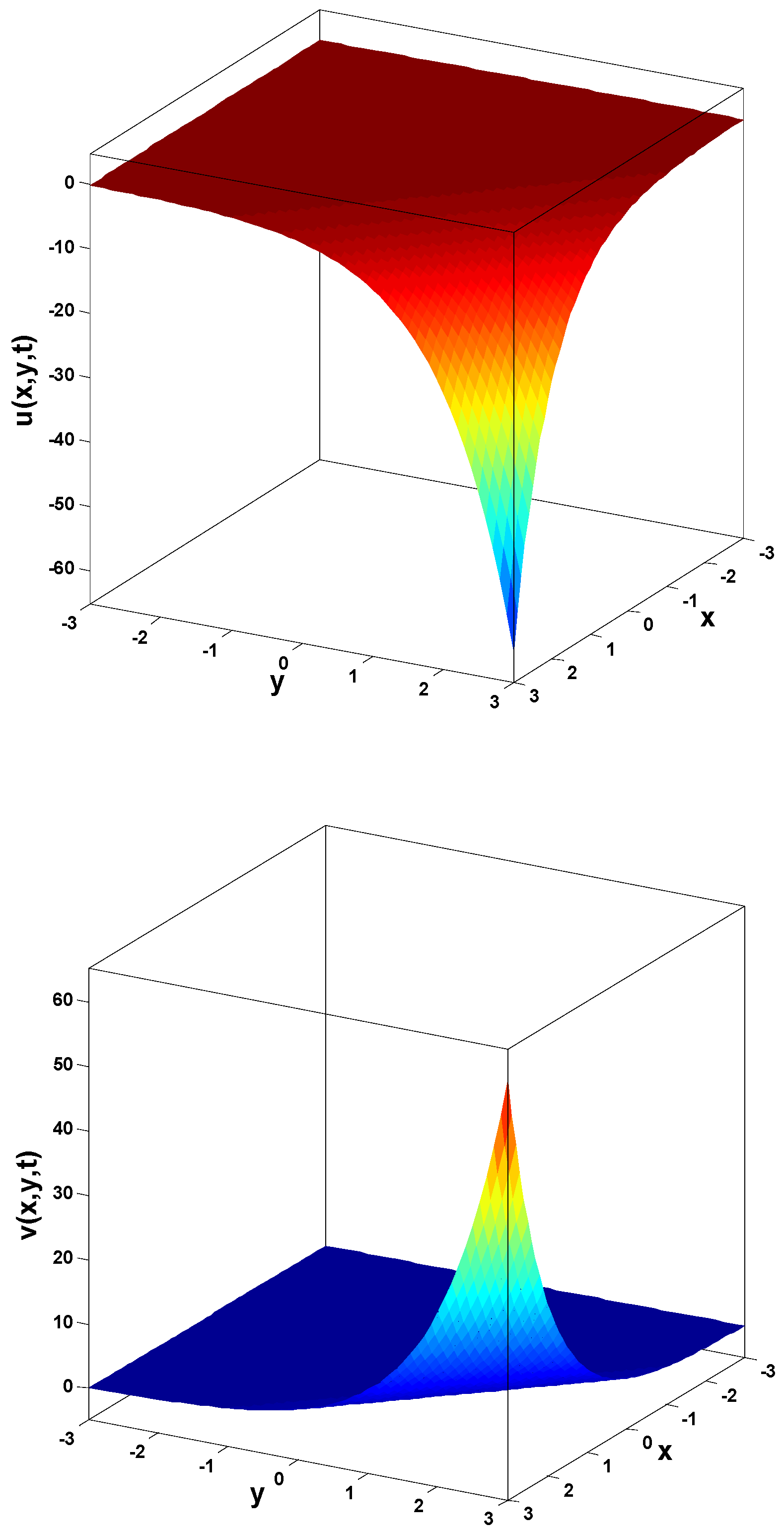
In this research, a numerical simulation of the fractional-time Navier–Stokes equations was performed using the homotopy perturbation–Laplace transform technique (HP–LTM), with the Caputo–Hadamard fractional derivative. The solutions are obtained in the form of a power series expressed by the Mittag–Leffler function. Two test problems are implemented for verification purposes and to demonstrate the effectiveness of the approach. The proposed solutions are approximated without discretization, transformation, perturbation, or constraint conditions, and they agree well with HPETM [36], HAM [37], and FRDTM [38]. The proposed approach also demonstrates a relatively modest computational cost compared to ADM polynomials and other methods, efficiently finding both analytical and approximate solutions in a robust manner.

We hope this work represents a step towards expanding the use of the HP–LTM to solve linear and nonlinear fractional mathematical physics problems significantly and will be addressed in more detail in future works.