Split-Step Galerkin FE Method for Two-Dimensional Space-Fractional CNLS

Abstract

In this paper, we study a split-step Galerkin finite element (FE) method for the two-dimensional Riesz space-fractional coupled nonlinear Schrödinger equations (CNLSs). The proposed method adopts a second-order split-step technique to handle the nonlinearity and FE approximation to discretize the fractional derivatives in space, which avoids iteration at each time layer. The analysis of mass conservative and convergent properties for this split-step FE scheme is performed. To test its capability, some numerical tests and the simulation of the double solitons intersection and plane wave are carried out. The results and comparisons with the algorithm combined with Newton’s iteration illustrate its effectiveness and advantages in computational efficiency.

1. Introduction

The nonlinear Schrödinger equation (NLS) was raised by Feynman and Hibbs from the path integral over the Brownian paths [1], which presents an effective model for describing the quantum state of physical systems. The space-fractional NLS was generated by Laskin via extending the Feynman path integral to a novel path integral over the Lévy quantum mechanical paths, which opens a new perspective for quantum mechanics and can characterize many new phenomena absent from the classical NLS [2,3]. The fractional NLS plays an important role in mathematical physics and it is ubiquitous in various fields as diverse as quantum optics, water wave dynamics [4], beam propagation inside crystals, the study of Boson–Einstein condensation, and the continuum limit with long-range lattice interaction [5]. The space-fractional NLS on 2D domains appears as follows:

$$\begin{array}{cc}\hfill & i{\partial }_{t}u-\gamma {(-{\Delta }_x)}^{\alpha /2}u-\gamma {(-{\Delta }_y)}^{\beta /2}u+\lambda {\left|u\right|}^{2}u=0,0<t\le T,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill & u(x,y,0)=u_0(x,y),(x,y)\in {\mathbf{R}}^2,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & u(x,y,t)=0,(x,y;t)\in {\mathbf{R}}^2\setminus \Omega \times (0,T],\hfill \end{array}$$

(3)

with $i^2=-1$ and real numbers $\gamma >0$, $\lambda$, $1<\alpha ,\beta \le 2$, $\Omega =[a,b]\times [c,d]$, and $-{(-{\Delta }_x)}^{\alpha /2}u$ is the Riesz fractional derivative with respect to x [6]:

$$\begin{array}{cc}\hfill & -{(-{\Delta }_x)}^{\alpha /2}u(x,y,t):=-\frac{1}{2cos(\alpha \pi /2)}{[}^{RL}{D}_{a^{+}}^{\alpha }u(x,y,t){+}^{RL}{D}_{b^{-}}^{\alpha }u(x,y,t)]\hfill \end{array}$$

with ${\text{}}^{RL}{D}_{a^{+}}^{\alpha }u(x,y,t)$ and ${\text{}}^{RL}{D}_{b^{-}}^{\alpha }u(x,y,t)$ being the $\alpha$-th left- and right-hand Riemann–Liouville derivatives of x, respectively, and $-{(-{\Delta }_y)}^{\beta /2}$ is similarly defined. The fractional NLS happens to be the classical cubic NLS when $\alpha =2$, which is necessary to characterize the evolution of nonrelativistic systems and can provide a detailed description of the true nature of the microscopic events in a probabilistic sense.

The space-fractional NLS and CNLS have been of great interest over recent years. However, due to their nonlocal fractional operators involved in space, solving them numerically appears extremely challenging, so the existent algorithms still remain limited for high-dimensional problems. There are many research works devoted to studying the 1D space-fractional NLS, but fewer works investigate the numerical approaches for the high-dimensional space-fractional NLS/CNLS. Amore et al. derived a simple collocation method based on little Sinc functions for the quantum mechanical equation involving the fractional Laplacian [7]. Herzallaha and Gepreel developed an adomian decomposition method to solve the time–space-fractional NLS [8]. In [9,10,11], several second-order finite difference (FD) methods have been established for the 1D single and coupled space-fractional NLS, where the mass and energy conservation properties are rigorously discussed. The Fourier spectral method was first proposed by Klein et al. to study the finite time blow-up, the stability of nonlinear ground states and the long-time behavior of solutions in classical or semiclassical settings [12]. Such a spectral method was further investigated by Duo and Zhang for the 1D space-fractional NLS in a semiclassical regime with the split step, Crank–Nicolson and relaxation schemes being used in time [13]. In [14,15,16], the linearized Galerkin FE schemes for the space-fractional NLS and CNLS on 1D domains were developed. In [17], we proposed an implicit FE scheme to solve the 1D time–space-fractional equations of NLS type and further extended this scheme to the 2D situation. Li et al. gave a fast linearized conservative FE scheme for the 1D strongly space-fractional CNLS [18]. Fan and Qi proposed an efficient FE method for the 2D time–space-fractional NLS [19]. In [20], Aboelenen constructed a high-order nodal discontinuous Galerkin FE method for the 1D space-fractional problem of NLS type.

Aside from the difficulty in designing the algorithm to approximate the fractional derivatives in high dimensions, another main concern about the construction of numerical schemes for the fractional NLS and CNLS is how to efficiently discretize the nonlinear terms. A wealth of experience has shown that the split-step method is one of the important approaches to solve high-dimensional nonlinear problems, which is linearized and can reduce the computational cost and memory requirement. A few works have been devoted to this area. Wang and Huang developed a split-step conservative ADI FD method for the 2D space-fractional NLS [21], which solves the problem without any iteration by splitting the governing equation into linear and nonlinear subparts. Along the same line, a high-order split-step FD method for the 1D space-fractional CNLS was proposed in [22]. Recently, Wang et al. considered the semiclassical linear space-fractional Schrödinger equation by a Lie–Trotter operator splitting spectral method [23]. In [24], Aboelenen proposed a split-step Fourier pseudo-spectral scheme for the 1D space-fractional CNLS. Wang et al. developed a split-step spectral Galerkin scheme for 2D space-fractional NLS [25].

In this work, we consider the 2D space-fractional CNLS

$$\begin{array}{cc}\hfill & i{\partial }_{t}u-\gamma {(-{\Delta }_x)}^{\alpha /2}u-\gamma {(-{\Delta }_y)}^{\beta /2}u+{\lambda \left(\right|u|}^2+{\rho \left|v\right|}^2)u=0,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & i{\partial }_{t}v-\gamma {(-{\Delta }_x)}^{\alpha /2}v-\gamma {(-{\Delta }_y)}^{\beta /2}v+{\lambda \left(\rho \right|u|}^2+{\left|v\right|}^2)v=0,0<t\le T,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & u(x,y,0)=u_0(x,y),v(x,y,0)=v_0(x,y),(x,y)\in {\mathbf{R}}^2,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & u(x,y,t)=0,v(x,y,t)=0,(x,y;t)\in {\mathbf{R}}^2\setminus \Omega \times (0,T],\hfill \end{array}$$

(7)

with the real numbers $\gamma >0$, $\lambda$, $\rho$ and $1<\alpha ,\beta \le 2$. When $\rho =0$, the above problem degenerates to the single fractional NLS, which preserves

$$\begin{array}{c}\mathrm{mass}:Q\left(t\right)={\int }_{{\mathbf{R}}^2}{\left|u(x,y,t)\right|}^{2}d\Omega =Q\left(0\right),\\ \mathrm{energy}:E\left(t\right)=\gamma {\int }_{{\mathbf{R}}^2}{u}^{*}{(-{\Delta }_x)}^{\alpha /2}u+u^{*}{(-{\Delta }_y)}^{\beta /2}ud\Omega -\frac{\lambda }{2}{\int }_{{\mathbf{R}}^2}{\left|u\right|}^{4}d\Omega =E\left(0\right),\end{array}$$

along with the time evolution [21], where $u^{*}$ is the conjugate of u.

Although the spectral Galerkin method based on orthogonal polynomials is a kind of high-accuracy technique, it has a strict limit on computational domains, which are usually multiplicative rectangular regions. Besides, it requires high regularity for the model problem. The FE method is a high-performing and commonly used algorithm for complex domain problems with unstructured meshes in scientific and engineering computing, which can achieve high accuracy with lower regularity, but due to the nonlocality of fractional derivative operators, seldom works have been reported on this method for the high-dimensional space-fractional NLS and CNLS. Inspired by this, we try to establish an efficient split-step Galerkin FE scheme for the 2D space-fractional CNLS (4)–(7). The mass conservation property is proved and the convergence is also analyzed. The proposed method is utilized to simulate these problems on unstructured meshes, and no internal iteration is required at each time layer, thereby greatly reducing the computational complexity.

The outline is as follows. In Section 2, some preliminaries are introduced, and in Section 3, the variational formulation is derived. In Section 4, we engage in a detailed derivative course of the split-step FE scheme for Equations (4)–(7) and further analyze its mass conservation property and error estimates. In Section 5, a numerical study on the dynamics of NLS and CNLS involving fractional derivatives is conducted, and a short conclusion is made lastly.

2. Preliminaries

We recall some auxiliary definitions and results about the fractional derivatives. If $f\left(x\right)$ is smooth enough, the $\mu$-th left-hand Riemann–Liouville derivative is defined by

$${\text{}}^{RL}{D}_{a^{+}}^{\mu }f\left(x\right)=\frac{1}{\Gamma (n-\mu )}\frac{d^n}{d{x}^n}{\int }_a^x\frac{f\left(\omega \right)d\omega }{{(x-\omega )}^{\mu -n+1}},x>a,$$

and $\mu$-th right-hand Riemann–Liouville derivative is defined by

$${\text{}}^{RL}{D}_{b^{-}}^{\mu }f\left(x\right)=\frac{{(-1)}^n}{\Gamma (n-\mu )}\frac{d^n}{d{x}^n}{\int }_x^b\frac{f\left(\omega \right)d\omega }{{(\omega -x)}^{\mu -n+1}},x<b,$$

where $n-1<\mu \le n$, $n\in {\mathbf{Z}}^{+}$ and $\Gamma \left(z\right)={\int }_0^{+\infty }exp(-t)t^{z-1}dt$.

Another commonly used fractional derivative is called the Riesz derivative:

$$\frac{{\partial }^{\mu }f\left(x\right)}{{\partial \left|x\right|}^{\mu }}=-\frac{1}{2cos(\mu \pi /2)}\left[{\text{}}^{RL}{D}_{a^{+}}^{\mu }f\left(x\right)+{\text{}}^{RL}{D}_{b^{-}}^{\mu }f\left(x\right)\right],a<x<b,$$

and similarly, we can define the fractional derivatives with regard to y.

Meanwhile, letting $\Omega =[a,b]\times [c,d]$, ${\left|\right|u\left|\right|}_{L^2\left({\mathbf{R}}^2\right)}={(u,u)}_{L^2\left({\mathbf{R}}^2\right)}^{1/2}$ and ${(u,v)}_{L^2\left({\mathbf{R}}^2\right)}={\int }_{{\mathbf{R}}^2}uvdxdy$, we denote $\left|\right|·{\left|\right|}_{L^2(\Omega )}$ by $\left|\right|·{\left|\right|}_{0,\Omega }$, $\left|\right|·{\left|\right|}_{H^s(\Omega )}$ by $\left|\right|·{\left|\right|}_{s,\Omega }$ and ${(·,·)}_{L^2(\Omega )}$, ${(·,·)}_{L^2\left({\mathbf{R}}^2\right)}$ by $(·,·)$ with $s>0$. For a real-valued $u(x,y)$ on $\Omega$, we define the following fractional derivative spaces [26,27]:

Definition 1.

Letting $\mu >0$, we define the left seminorm

$${\left|u\right|}_{J_L^{\mu }(\Omega )}={\left(\left|\right|{\text{}}^{RL}{D}_{a^{+}}^{\mu }{u(x,y)\left|\right|}_{0,\Omega }^2+\left|\right|{\text{}}^{RL}{D}_{c^{+}}^{\mu }u(x,y){\left|\right|}_{0,\Omega }^2\right)}^{1/2},$$

and left norm

$${\left|\right|u\left|\right|}_{J_L^{\mu }(\Omega )}={\left({\left|\right|u\left|\right|}_{0,\Omega }^2+{\left|u\right|}_{J_L^{\mu }(\Omega )}^2\right)}^{1/2},$$

and let $J_L^{\mu }(\Omega )$ be the closure of $C^{\infty }(\Omega )$ with respect to $\left|\right|·{\left|\right|}_{J_L^{\mu }(\Omega )}$.

Definition 2.

Letting $\mu >0$, we define the right seminorm

$${\left|u\right|}_{J_R^{\mu }(\Omega )}={\left(\left|\right|{\text{}}^{RL}{D}_{b^{-}}^{\mu }{u(x,y)\left|\right|}_{0,\Omega }^2+\left|\right|{\text{}}^{RL}{D}_{d^{-}}^{\mu }u(x,y){\left|\right|}_{0,\Omega }^2\right)}^{1/2},$$

and right norm

$${\left|\right|u\left|\right|}_{J_R^{\mu }(\Omega )}={\left({\left|\right|u\left|\right|}_{0,\Omega }^2+{\left|u\right|}_{J_R^{\mu }(\Omega )}^2\right)}^{1/2},$$

and let $J_R^{\mu }(\Omega )$ be the closure of $C^{\infty }(\Omega )$ with respect to $\left|\right|·{\left|\right|}_{J_R^{\mu }(\Omega )}$.

Definition 3.

Letting $\mu >0$ and $\mathcal{F}\left(u\right)$ be the Fourier transform of u defined in Ω, i.e.,

$$\mathcal{F}\left(u\right)={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }u(x,y)exp(-i{\omega }_{1}x-i{\omega }_{2}y)dxdy,$$

we define the seminorm

$${\left|u\right|}_{\mu ,\Omega }={\left|\right|\left|\mathit{\omega }\right|}^{\mu }\mathcal{F}\left(\tilde{u}\right){\left|\right|}_{0,\Omega },$$

and norm

$${\left|\right|u\left|\right|}_{\mu ,\Omega }={\left({\left|\right|u\left|\right|}_{0,\Omega }^2+{\left|u\right|}_{\mu ,\Omega }^2\right)}^{1/2},$$

and denote the closure of $C^{\infty }(\Omega )$ with respect to $\left|\right|·{\left|\right|}_{\mu ,\Omega }$ by $H^{\mu }(\Omega )$, where $\omega =({\omega }_1,{\omega }_2)$ and $\tilde{u}$ is the extension of u by zero outside of Ω.

Similar to $J_L^{\mu }(\Omega )$, $J_R^{\mu }(\Omega )$ and $H^{\mu }(\Omega )$, we define $J_{L,0}^{\mu }(\Omega )$, $J_{R,0}^{\mu }(\Omega )$ and $H_0^{\mu }(\Omega )$ by the closures of $C_0^{\infty }(\Omega )$ with respect to $\left|\right|·{\left|\right|}_{J_L^{\mu }(\Omega )}$, $\left|\right|·{\left|\right|}_{J_R^{\mu }(\Omega )}$ and $\left|\right|·{\left|\right|}_{\mu ,\Omega }$, respectively. If $\mu \ne n-1/2$, $n\in {\mathbf{Z}}^{+}$, $J_{L,0}^{\mu }(\Omega )$, $J_{R,0}^{\mu }(\Omega )$ and $H_0^{\mu }(\Omega )$ are equivalent with the equivalent seminorms and norms, i.e.,

$$C_1{\left|\right|u\left|\right|}_{\mu ,\Omega }\le max\left\{{\left|\right|u\left|\right|}_{J_L^{\mu }(\Omega )}{,\left|\right|u\left|\right|}_{J_R^{\mu }(\Omega )}\right\}\le C_2{\left|\right|u\left|\right|}_{\mu ,\Omega },$$

where $\mu >0$ and $C_1$ and $C_2$ are two positive constants independent of u.

Lemma 1.

Letting $\mu >0$, we have the below identities in the $L^2$-nrom sense:

$$\begin{array}{cc}\hfill & ({\text{}}^{RL}{D}_{a^{+}}^{\mu }u,{\text{}}^{RL}{D}_{b^{-}}^{\mu }u)+({\text{}}^{RL}{D}_{b^{-}}^{\mu }u,{\text{}}^{RL}{D}_{a^{+}}^{\mu }u)=2cos\left(\mu \pi \right)\left|\right|{\text{}}^{RL}{D}_{a^{+}}^{\mu }\tilde{u}{\left|\right|}_{0,{\mathbf{R}}^2}^2,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & ({\text{}}^{RL}{D}_{c^{+}}^{\mu }u,{\text{}}^{RL}{D}_{d^{-}}^{\mu }u)+({\text{}}^{RL}{D}_{d^{-}}^{\mu }u,{\text{}}^{RL}{D}_{c^{+}}^{\mu }u)=2cos\left(\mu \pi \right)\left|\right|{\text{}}^{RL}{D}_{c^{+}}^{\mu }\tilde{u}{\left|\right|}_{0,{\mathbf{R}}^2}^2.\hfill \end{array}$$

(9)

Proof. 

Firstly, according to [27], we have

$$\begin{array}{c}\hfill \mathcal{F}\left({\text{}}^{RL}{D}_{a^{+}}^{\mu }u\right)={\left(i{\omega }_1\right)}^{\mu }\widehat{u}\left(\mathit{\omega }\right),\mathcal{F}\left({\text{}}^{RL}{D}_{b^{-}}^{\mu }u\right)={(-i{\omega }_1)}^{\mu }\widehat{u}\left(\mathit{\omega }\right),\end{array}$$

with $\widehat{u}\left(\mathit{\omega }\right)=\mathcal{F}\left(u\right)$. Then, from

$$\begin{array}{c}\hfill \overline{{\left(i{\omega }_1\right)}^{\mu }}=\left\{\begin{array}{cc}exp(-i\pi \mu )\overline{{(-i{\omega }_1)}^{\mu }},\hfill & \mathrm{for}{\omega }_1\ge 0,\hfill \\ exp\left(i\pi \mu \right)\overline{{(-i{\omega }_1)}^{\mu }},\hfill & \mathrm{for}{\omega }_1<0,\hfill \end{array}\right.\end{array}$$

and the property of Fourier transform, it follows that

$$\begin{array}{cc}\hfill & ({\text{}}^{RL}{D}_{a^{+}}^{\mu }u,{\text{}}^{RL}{D}_{b^{-}}^{\mu }u)=\left({\left(i{\omega }_1\right)}^{\mu }\widehat{u},{(-i{\omega }_1)}^{\mu }\widehat{u}\right)\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }\left({\int }_{-\infty }^0{\left(i{\omega }_1\right)}^{\mu }\widehat{u}\overline{{(-i{\omega }_1)}^{\mu }\widehat{u}}d{\omega }_1+{\int }_0^{\infty }{\left(i{\omega }_1\right)}^{\mu }\widehat{u}\overline{{(-i{\omega }_1)}^{\mu }\widehat{u}}d{\omega }_1\right)d{\omega }_2\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }({\int }_{-\infty }^0{\left(i{\omega }_1\right)}^{\mu }\widehat{u}exp(-i\pi \mu )\overline{{\left(i{\omega }_1\right)}^{\mu }\widehat{u}}d{\omega }_1\hfill \\ \hfill & +{\int }_0^{\infty }{\left(i{\omega }_1\right)}^{\mu }\widehat{u}exp\left(i\pi \mu \right)\overline{{\left(i{\omega }_1\right)}^{\mu }\widehat{u}}d{\omega }_1)d{\omega }_2\hfill \\ \hfill & =cos\left(\pi \mu \right){\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\left(i{\omega }_1\right)}^{\mu }\widehat{u}\overline{{\left(i{\omega }_1\right)}^{\mu }\widehat{u}}d{\omega }_{1}d{\omega }_2\hfill \\ \hfill & +isin\left(\pi \mu \right)\left\{{\int }_{-\infty }^{\infty }\left({\int }_0^{\infty }|{\left(i{\omega }_1\right)}^{\mu }\widehat{u}{|}^{2}d{\omega }_1-{\int }_{-\infty }^0{\left|{\left(i{\omega }_1\right)}^{\mu }\widehat{u}\right|}^{2}d{\omega }_1\right)d{\omega }_2\right\},\hfill \end{array}$$

and the similar result

$$\begin{array}{cc}\hfill & ({\text{}}^{RL}{D}_{b^{-}}^{\mu }u,{\text{}}^{RL}{D}_{a^{+}}^{\mu }u)=\left((-i{\omega }_1)\widehat{u},\left(i{\omega }_1\right)\widehat{u}\right)\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }\left({\int }_{-\infty }^0(-i{\omega }_1)\widehat{u}\overline{\left(i{\omega }_1\right)\widehat{u}}d{\omega }_1+{\int }_0^{\infty }(-i{\omega }_1)\widehat{u}\overline{\left(i{\omega }_1\right)\widehat{u}}d{\omega }_1\right)d{\omega }_2\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }({\int }_{-\infty }^0{(-i{\omega }_1)}^{\mu }\widehat{u}exp\left(i\pi \mu \right)\overline{{(-i{\omega }_1)}^{\mu }\widehat{u}}d{\omega }_1\hfill \\ \hfill & +{\int }_0^{\infty }{(-i{\omega }_1)}^{\mu }\widehat{u}exp(-i\pi \mu )\overline{{(-i{\omega }_1)}^{\mu }\widehat{u}}d{\omega }_1)d{\omega }_2\hfill \\ \hfill & =cos\left(\pi \mu \right){\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{(-i{\omega }_1)}^{\mu }\widehat{u}\overline{{(-i{\omega }_1)}^{\mu }\widehat{u}}d{\omega }_{1}d{\omega }_2\hfill \\ \hfill & +isin\left(\pi \mu \right)\left\{{\int }_{-\infty }^{\infty }\left({\int }_{-\infty }^0|{(-i{\omega }_1)}^{\mu }\widehat{u}{|}^{2}d{\omega }_1-{\int }_0^{\infty }{\left|{(-i{\omega }_1)}^{\mu }\widehat{u}\right|}^{2}d{\omega }_1\right)d{\omega }_2\right\}.\hfill \end{array}$$

Consequently, we come to Equation (8) by summing these equations together, and Equation (9) can be easily deduced in the same way as above. □

Moreover, for any $u\in H_0^{\mu }(\Omega )$, we have ${\left|\right|u\left|\right|}_{0,\Omega }\le C{\left|u\right|}_{\mu ,\Omega }$, and for $0<s<\mu$, $\mu \ne n-1/2$, $n\in {\mathbf{Z}}^{+}$, there holds ${\left|u\right|}_{s,\Omega }\le C{\left|u\right|}_{\mu ,\Omega }$, which are the well-known fractional Poincaré–Friedrichs inequalities, where C is a positive constant independent of u. For any $u\in J_{L,0}^{\mu }(\Omega )$ or $J_{R,0}^{\mu }(\Omega )$ and $0<s<\mu$, the similar inequalities can be validated, such as ${\left|\right|u\left|\right|}_{0,\Omega }\le C{\left|u\right|}_{J_L^{\mu }(\Omega )}$, ${\left|u\right|}_{J_L^s(\Omega )}\le C{\left|u\right|}_{J_L^{\mu }(\Omega )}$.

3. Variational Formulation

To derive the weak problem, we define the energy norm

$$\begin{array}{c}{\left|\psi \right|}_{EN}={\left(|({\text{}}^{RL}{D}_{a^{+}}^{\alpha /2}\psi ,{\text{}}^{RL}{D}_{b^{-}}^{\alpha /2}\psi )|+|({\text{}}^{RL}{D}_{c^{+}}^{\beta /2}\psi ,{\text{}}^{RL}{D}_{d^{-}}^{\beta /2}\psi )|\right)}^{1/2},\\ \left|\right|\left|\psi \right|\left|\right|={\left({\left|\right|\psi \left|\right|}_{0,\Omega }^2+{\left|\psi \right|}_{EN}^2\right)}^{1/2}\end{array}$$

and introduce a family of regular triangular subdivisions ${\mathcal{T}}_h={\left\{K_i\right\}}_{i=1}^{m_h}$ of $\Omega$ with the meshsize h. Also, for $\phi ,\psi \in J_{L,0}^{\alpha }(\Omega )$ or $J_{R,0}^{\alpha }(\Omega )$, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ({\text{}}^{RL}{D}_{a^{+}}^{\alpha }\phi ,\psi )& =({\text{}}^{RL}{D}_{a^{+}}^{\alpha /2}\phi ,{\text{}}^{RL}{D}_{b^{-}}^{\alpha /2}\psi ),\hfill \\ \hfill ({\text{}}^{RL}{D}_{b^{-}}^{\alpha }\phi ,\psi )& =({\text{}}^{RL}{D}_{b^{-}}^{\alpha /2}\phi ,{\text{}}^{RL}{D}_{a^{+}}^{\alpha /2}\psi ),\hfill \end{array}\end{array}$$

(10)

and the analogous results hold for ${\text{}}^{RL}{D}_{c^{+}}^{\beta }\phi$, ${\text{}}^{RL}{D}_{d^{-}}^{\beta }\phi$ [26].

Rewrite u and v in Equations (4)–(7) by their real and imaginary parts, i.e., $u=u_1+i{u}_2$, $v=v_1+i{v}_2$, and introduce the symmetric bilinear form:

$$\begin{array}{cc}\hfill {\mathcal{A}}_h(\phi ,\psi )& =\frac{1}{2cos(\alpha \pi /2)}\left\{({\text{}}^{RL}{D}_{a^{+}}^{\alpha /2}\phi ,{\text{}}^{RL}{D}_{b^{-}}^{\alpha /2}\psi )+({\text{}}^{RL}{D}_{b^{-}}^{\alpha /2}\phi ,{\text{}}^{RL}{D}_{a^{+}}^{\alpha /2}\psi )\right\}\hfill \\ \hfill & +\frac{1}{2cos(\beta \pi /2)}\left\{({\text{}}^{RL}{D}_{c^{+}}^{\beta /2}\phi ,{\text{}}^{RL}{D}_{d^{-}}^{\beta /2}\psi )+({\text{}}^{RL}{D}_{d^{-}}^{\beta /2}\phi ,{\text{}}^{RL}{D}_{c^{+}}^{\beta /2}\psi )\right\},\hfill \end{array}$$

which satisfies the coercivity and continuity properties:

$${\mathcal{A}}_h(\psi ,\psi )\ge C\left|\right|\left|\psi \right|\left|\right|,{\mathcal{A}}_h(\phi ,\psi )\le C\left|\right|\left|\phi \right|\left|\right|·\left|\right|\left|\psi \right|\left|\right|.$$

Using the property (10) and splitting u and v, the weak problem can be defined as follows: find $u,v\in L^2(0,T;V)\cap C^0(0,T;L^2(\Omega ))$ to fulfill

$$\begin{array}{c}\hfill ({\partial }_t{u}_1,{\chi }_u^1)-\gamma {\mathcal{A}}_h(u_2,{\chi }_u^1)+\lambda \left(\right(|u_1{|}^2+|u_2{|}^2+\rho |v_1{|}^2+\rho |v_2{|}^2)u_2,{\chi }_u^1)=0,\end{array}$$

(11)

$$\begin{array}{c}\hfill ({\partial }_t{u}_2,{\chi }_u^2)+\gamma {\mathcal{A}}_h(u_1,{\chi }_u^2)-\lambda \left(\right(|u_1{|}^2+|u_2{|}^2+\rho |v_1{|}^2+\rho |v_2{|}^2)u_1,{\chi }_u^2)=0,\end{array}$$

(12)

$$\begin{array}{c}\hfill ({\partial }_t{v}_1,{\chi }_v^1)-\gamma {\mathcal{A}}_h(v_2,{\chi }_v^1)+\lambda \left(\right(\rho |u_1{|}^2+\rho |u_2{|}^2+|v_1{|}^2+|v_2{|}^2)v_2,{\chi }_v^1)=0,\end{array}$$

(13)

$$\begin{array}{c}\hfill ({\partial }_t{v}_2,{\chi }_v^2)+\gamma {\mathcal{A}}_h(v_1,{\chi }_v^2)-\lambda \left(\right(\rho |u_1{|}^2+\rho |u_2{|}^2+|v_1{|}^2+|v_2{|}^2)v_1,{\chi }_v^2)=0,\end{array}$$

(14)

with ${\chi }_u^1,{\chi }_u^2,{\chi }_v^1,{\chi }_v^2\in V$ and $V=H_0^{\alpha /2}(\Omega )\cap H_0^{\beta /2}(\Omega )$, subjected to

$$\begin{array}{cc}\hfill & u_1(x,y,0)=\mathrm{Re}{u}_0(x,y),u_2(x,y,0)=\mathrm{Im}{u}_0(x,y),(x,y)\in \Omega ,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & v_1(x,y,0)=\mathrm{Re}{v}_0(x,y),v_2(x,y,0)=\mathrm{Im}{v}_0(x,y),(x,y)\in \Omega ,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & u_1(x,y,t)=0,u_2(x,y,t)=0,(x,y;t)\in {\mathbf{R}}^2\setminus \Omega \times (0,T],\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & v_1(x,y,t)=0,v_2(x,y,t)=0,(x,y;t)\in {\mathbf{R}}^2\setminus \Omega \times (0,T].\hfill \end{array}$$

(18)

Denoting the set of polynomials of degree not greater than $m-1$ on element K by $P_{m-1}\left(K\right)$, we define the FE subspace $X_h$ on ${\mathcal{T}}_h$ as follows:

$$X_h:=\{\psi \in V:\psi {|}_E\in P_{m-1}\left(K\right),\forall K\in {\mathcal{T}}_h\}.$$

Then, the semidiscrete FE scheme is defined as follows: find $u_{1,h},u_{2,h},v_{1,h},v_{2,h}\in X_h$, such that

$$\begin{array}{c}\hfill ({\partial }_t{u}_{1,h},{\chi }_u^1)-\gamma {\mathcal{A}}_h(u_{2,h},{\chi }_u^1)+\lambda \left(\right(|u_{1,h}{|}^2+|u_{2,h}{|}^2+\rho |v_{1,h}{|}^2+\rho |v_{2,h}{|}^2)u_{2,h},{\chi }_u^1)=0,\end{array}$$

(19)

$$\begin{array}{c}\hfill ({\partial }_t{u}_{2,h},{\chi }_u^2)+\gamma {\mathcal{A}}_h(u_{1,h},{\chi }_u^2)-\lambda \left(\right(|u_{1,h}{|}^2+|u_{2,h}{|}^2+\rho |v_{1,h}{|}^2+\rho |v_{2,h}{|}^2)u_{1,h},{\chi }_u^2)=0,\end{array}$$

(20)

$$\begin{array}{c}\hfill ({\partial }_t{v}_{1,h},{\chi }_v^1)-\gamma {\mathcal{A}}_h(v_{2,h},{\chi }_v^1)+\lambda \left(\right(\rho |u_{1,h}{|}^2+\rho |u_{2,h}{|}^2+|v_{1,h}{|}^2+|v_{2,h}{|}^2)v_{2,h},{\chi }_v^1)=0,\end{array}$$

(21)

$$\begin{array}{c}\hfill ({\partial }_t{v}_{2,h},{\chi }_v^2)+\gamma {\mathcal{A}}_h(v_{1,h},{\chi }_v^2)-\lambda \left(\right(\rho |u_{1,h}{|}^2+\rho |u_{2,h}{|}^2+|v_{1,h}{|}^2+|v_{2,h}{|}^2)v_{1,h},{\chi }_v^2)=0,\end{array}$$

(22)

with ${\chi }_u^1,{\chi }_u^2,{\chi }_v^1,{\chi }_v^2\in X_h$ subjected to

$$\begin{array}{cc}\hfill & u_{1,h}(x,y,0)=u_{1,h}^0(x,y),u_{2,h}(x,y,0)=u_{2,h}^0(x,y),(x,y)\in \Omega ,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & v_{1,h}(x,y,0)=v_{1,h}^0(x,y),v_{2,h}(x,y,0)=v_{2,h}^0(x,y),(x,y)\in \Omega ,\hfill \end{array}$$

(24)

where $u_{1,h}^0(x,y)$, $u_{2,h}^0(x,y)$, $v_{1,h}^0(x,y)$ and $v_{2,h}^0(x,y)$ are the appropriate approximations of $\mathrm{Re}{u}_0(x,y)$, $\mathrm{Im}{u}_0(x,y)$, $\mathrm{Re}{v}_0(x,y)$ and $\mathrm{Im}{v}_0(x,y)$, respectively.

The semidiscrete FE scheme (19)–(24) preserves the mass, i.e., $\left|\right|u_{1,h}\left(t\right){\left|\right|}_{0,\Omega }^2+$$\left|\right|u_{2,h}{\left(t\right)\left|\right|}_{0,\Omega }^2=\left|\right|u_{1,h}^0{\left|\right|}_{0,\Omega }^2+\left|\right|u_{2,h}^0{\left|\right|}_{0,\Omega }^2$ and $\left|\right|v_{1,h}{\left(t\right)\left|\right|}_{0,\Omega }^2+\left|\right|v_{2,h}{\left(t\right)\left|\right|}_{0,\Omega }^2=\left|\right|v_{1,h}^0{\left|\right|}_{0,\Omega }^2+\left|\right|v_{2,h}^0{\left|\right|}_{0,\Omega }^2$. By taking ${\chi }_u^1=u_{1,h}\left(t\right)$ and ${\chi }_u^2=u_{2,h}\left(t\right)$, the sum of Equations (19)–(20) and the symmetry of bilinear form give the conservation property of u, and the result with respect to v followed by a similar procedure.

4. Fully Discrete Split-Step FE Method

Letting $N\in {\mathbf{Z}}^{+}$, we define $t_n=n\tau$ on $[0,T]$ with $\tau =T/N$, $n=0,1,2,\dots ,N$. In what follows, we propose a fully discrete split-step Galerkin FE scheme for Equations (4)–(7) and analyze its discrete conversation property and error estimate.

4.1. Discretization in Time

The idea of the split-step method is to solve the nonlinear problem by splitting the considered equation into linear and nonlinear parts [28,29,30], which is a popular technique in nonlinear dynamics. If the classical NLS is given by $i{\partial }_{t}u=\mathcal{L}u+\mathcal{N}u$ with $\mathcal{L}$, $\mathcal{N}$ being the linear and nonlinear operators, then by separation of variables, we obtain

$$u\left(t\right)=e^{-i\mathcal{L}\tau -i\mathcal{N}\tau }u(t-\tau )=e^{-i\mathcal{N}\tau /2}{e}^{-i\mathcal{L}\tau }{e}^{-i\mathcal{N}\tau /2}u(t-\tau ).$$

Then, the second-order Strang split-step scheme is reported as follows:

$$u^{1,*}=e^{-i\mathcal{N}\tau /2}u\left(t_{n-1}\right),u^{2,*}=e^{-i\mathcal{L}\tau }{u}^{1,*},u\left(t_n\right)=e^{-i\mathcal{N}u\tau /2}{u}^{2,*},$$

from $t=t_{n-1}$ to $t_n$, where $u^{1,*}$ and $u\left(t_n\right)$ are integrated exactly from $i{u}_t=\mathcal{N}u$.

Inspired by this, we consider the coupled system of space-fractional CNLS:

$$\begin{array}{cc}\hfill {\partial }_t{u}_1+\gamma \mathcal{L}{u}_2+\lambda \overline{\mathcal{N}}\left(t\right)u_2& =0,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\partial }_t{u}_2-\gamma \mathcal{L}{u}_1-\lambda \overline{\mathcal{N}}\left(t\right)u_1& =0,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\partial }_t{v}_1+\gamma \mathcal{L}{v}_2+\lambda \tilde{\mathcal{N}}\left(t\right)v_2& =0,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill {\partial }_t{v}_2-\gamma \mathcal{L}{v}_1-\lambda \tilde{\mathcal{N}}\left(t\right)v_1& =0,t\in (t_{n-1},t_n],\hfill \end{array}$$

(28)

with $\overline{\mathcal{N}}\left(t\right)$ and $\tilde{\mathcal{N}}\left(t\right)$ being the nonlinear terms, i.e.,

$$\begin{array}{cc}\hfill \overline{\mathcal{N}}\left(t\right)& =|u_1{\left(t\right)|}^2+|u_2{\left(t\right)|}^2+\rho |v_1{\left(t\right)|}^2+\rho {\left|v_2\left(t\right)\right|}^2,\hfill \\ \hfill \tilde{\mathcal{N}}\left(t\right)& =\rho |u_1{\left(t\right)|}^2+\rho |u_2{\left(t\right)|}^2+|v_1{\left(t\right)|}^2+{\left|v_2\left(t\right)\right|}^2.\hfill \end{array}$$

Take the inner product sequentially with $u_1\left(t\right)$, $u_2\left(t\right)$, $v_1\left(t\right)$ and $v_2\left(t\right)$ in the above equations; then, the sums of Equations (25)–(28) give

$$\begin{array}{cc}\hfill |u_1{\left(t\right)|}^2+{\left|u_2\left(t\right)\right|}^2& =|u_1\left(t_{n-1}\right){|}^2+{\left|u_2\left(t_{n-1}\right)\right|}^2,\hfill \\ \hfill |v_1{\left(t\right)|}^2+{\left|v_2\left(t\right)\right|}^2& =|v_1\left(t_{n-1}\right){|}^2+{\left|v_2\left(t_{n-1}\right)\right|}^2,t\in (t_{n-1},t_n],\hfill \end{array}$$

which implies that $\overline{\mathcal{N}}\left(t\right)$, $\tilde{\mathcal{N}}\left(t\right)$ are invariant in time, i.e., $\overline{\mathcal{N}}\left(t\right)=\overline{\mathcal{N}}\left(t_{n-1}\right)$, $\tilde{\mathcal{N}}\left(t\right)=\tilde{\mathcal{N}}\left(t_{n-1}\right)$. Meanwhile, we split the coupled system (25)–(28) into the subproblems:

•

Nonlinear subproblem:

$$\begin{array}{cc}\hfill {\partial }_t{u}_1+\lambda \overline{\mathcal{N}}\left(t\right)u_2& =0,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {\partial }_t{u}_2-\lambda \overline{\mathcal{N}}\left(t\right)u_1& =0,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill {\partial }_t{v}_1+\lambda \tilde{\mathcal{N}}\left(t\right)v_2& =0,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill {\partial }_t{v}_2-\lambda \tilde{\mathcal{N}}\left(t\right)v_1& =0,t\in (t_{n-1},t_n],\hfill \end{array}$$

(32)

•

Linear subproblem:

$$\begin{array}{cc}\hfill {\partial }_t{u}_1+\gamma \mathcal{L}{u}_2& =0,\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill {\partial }_t{u}_2-\gamma \mathcal{L}{u}_1& =0,\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill {\partial }_t{v}_1+\gamma \mathcal{L}{v}_2& =0,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill {\partial }_t{v}_2-\gamma \mathcal{L}{v}_1& =0,t\in (t_{n-1},t_n],\hfill \end{array}$$

(36)

then, to solve Equations (25)–(28), one can solve the linear subproblem firstly, followed by solving the nonlinear subproblem. Next, we are devoted to finding the analytic solutions to the nonlinear Equations (29)–(32). To this end, consider Equations (29) and (30) and separate $u_1\left(t\right)$ from Equation (30), i.e., $u_1\left(t\right)=\frac{1}{\lambda \overline{\mathcal{N}}\left(t\right)}\frac{\partial u_2\left(t\right)}{\partial t}$. Using the property $\overline{\mathcal{N}}\left(t\right)=\overline{\mathcal{N}}\left(t_{n-1}\right)$ and substituting it into Equation (29) yields

$$\frac{{\partial }^2{u}_2\left(t\right)}{\partial t^2}+{\lambda }^2{\overline{\mathcal{N}}}^2\left(t_{n-1}\right)u_2\left(t\right)=0,$$

(37)

with the characteristic equation $r^2+{\lambda }^2{\overline{\mathcal{N}}}^2\left(t_{n-1}\right)=0$. Due to $\Delta =-4{\lambda }^2{\overline{\mathcal{N}}}^2\left(t_{n-1}\right)<0$, we have

$$u_2\left(t\right)=C_{3}cos\left[\lambda \overline{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right]+C_{4}sin\left[\lambda \overline{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right],$$

(38)

where $C_3$, $C_4\in \mathbf{R}$. Since $u_2{\left(t\right)|}_{t=t_{n-1}}=u_2\left(t_{n-1}\right)$, it is easy to obtain $C_3=u_2\left(t_{n-1}\right)$. Taking the derivative of both sides on Equation (38) with respect to t at $t=t_{n-1}$, there exists

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\partial u_2\left(t\right)}{\partial t}{|}_{t=t_{n-1}}& =C_4\lambda \overline{\mathcal{N}}\left(t_{n-1}\right)cos\left[\lambda \overline{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right]{|}_{t=t_{n-1}}\hfill \\ \hfill & =C_4\lambda \overline{\mathcal{N}}\left(t_{n-1}\right).\hfill \end{array}\end{array}$$

(39)

Then, we obtain $C_4=u_1\left(t_{n-1}\right)$ by comparing Equation (30) with Equation (39), which yields

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill u_2\left(t\right)& =cos\left[\lambda \overline{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right]u_2\left(t_{n-1}\right)\hfill \\ \hfill & +sin\left[\lambda \overline{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right]u_1\left(t_{n-1}\right),\hfill \end{array}\end{array}$$

(40)

and substituting it into Equation (30), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill u_1\left(t\right)& =cos\left[\lambda \overline{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right]u_1\left(t_{n-1}\right)\hfill \\ \hfill & -sin\left[\lambda \overline{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right]u_2\left(t_{n-1}\right).\hfill \end{array}\end{array}$$

(41)

Doing a similar process as above for Equations (31) and (32), it is not difficult to prove

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill v_1\left(t\right)& =cos\left[\lambda \tilde{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right]v_1\left(t_{n-1}\right)\hfill \\ \hfill & -sin\left[\lambda \tilde{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right]v_2\left(t_{n-1}\right),\hfill \end{array}\end{array}$$

(42)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill v_2\left(t\right)& =cos\left[\lambda \tilde{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right]v_2\left(t_{n-1}\right)\hfill \\ \hfill & +sin\left[\lambda \tilde{\mathcal{N}}\left(t_{n-1}\right)(t-t_{n-1})\right]v_1\left(t_{n-1}\right).\hfill \end{array}\end{array}$$

(43)

Thus, based on $u_1\left(t\right)$, $u_2\left(t\right)$, $v_1\left(t\right)$ and $v_2\left(t\right)$, the above coupled nonlinear system can be solved in splitting steps, i.e., we firstly solve Equations (33)–(36) and then take the solutions as initial values for Equations (29)–(32), where the solutions are integrated exactly in physical space.

4.2. Crank–Nicolson FE Scheme

As the solutions to Equations (29)–(32) have been found, we now focus on the linear subproblem and propose a fully discrete Crank–Nicolson FE scheme for it. Let

$$\begin{array}{c}\hfill {\nabla }_t{u}^n=\frac{u^n-u^{n-1}}{\tau },{\overline{u}}^{n-\frac{1}{2}}=\frac{u^n+u^{n-1}}{2},\end{array}$$

with $u^n=u\left(t_n\right)$. Applying the Crank–Nicolson scheme in time, the fully discrete FE scheme reads as follows: find $U_{1,h}^n,U_{2,h}^n,V_{1,h}^n,V_{2,h}^n\in X_h$, such that

$$\begin{array}{cc}\hfill ({\nabla }_t{U}_{1,h}^n,{\chi }_U^1)-\gamma {\mathcal{A}}_h({\overline{U}}_{2,h}^{n-\frac{1}{2}},{\chi }_U^1)& =0,\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill ({\nabla }_t{U}_{2,h}^n,{\chi }_U^2)+\gamma {\mathcal{A}}_h({\overline{U}}_{1,h}^{n-\frac{1}{2}},{\chi }_U^2)& =0,\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill ({\nabla }_t{V}_{1,h}^n,{\chi }_V^1)-\gamma {\mathcal{A}}_h({\overline{V}}_{2,h}^{n-\frac{1}{2}},{\chi }_V^1)& =0,\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill ({\nabla }_t{V}_{2,h}^n,{\chi }_V^2)+\gamma {\mathcal{A}}_h({\overline{V}}_{1,h}^{n-\frac{1}{2}},{\chi }_V^2)& =0,\hfill \end{array}$$

(47)

with ${\chi }_U^1,{\chi }_U^2,{\chi }_V^1,{\chi }_V^2\in X_h$ subjected to

$$\begin{array}{cc}\hfill U_{1,h}^0& =u_{1,h}^0(x,y),U_{2,h}^0=u_{2,h}^0(x,y),(x,y)\in \Omega ,\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill V_{1,h}^0& =v_{1,h}^0(x,y),V_{2,h}^0=v_{2,h}^0(x,y),(x,y)\in \Omega ,\hfill \end{array}$$

(49)

where $u_{1,h}^0(x,y)$, $u_{2,h}^0(x,y)$, $v_{1,h}^0(x,y)$ and $v_{2,h}^0(x,y)$ are the appropriate approximations of $\mathrm{Re}{u}_0(x,y)$, $\mathrm{Im}{u}_0(x,y)$, $\mathrm{Re}{v}_0(x,y)$ and $\mathrm{Im}{v}_0(x,y)$, respectively.

To obtain the error bound, we introduce a general constant C that can be different on different occasions and the fractional orthogonal projection operator ${\Pi }_h:V\mapsto X_h$ [31]:

$$\Lambda (\psi -{\Pi }_h\psi ,{\chi }_h)=0,\forall {\chi }_h\in X_h,$$

which has the approximate property $\left|\right|\psi -{\Pi }_h{\psi \left|\right|}_{0,\Omega }\le C{h}^m{\left|\right|\psi \left|\right|}_{m,\Omega }$.

Theorem 1.

The solutions obtained by the Crank–Nicolson FE scheme (44)–(49) satisfy

$$Q_{U,h}^n=Q_{U,h}^0,Q_{V,h}^n=Q_{V,h}^0,n\ge 1,$$

where $Q_{U,h}^n=\left|\right|U_{1,h}^n{\left|\right|}_{0,\Omega }^2+\left|\right|U_{2,h}^n{\left|\right|}_{0,\Omega }^2$ and $Q_{V,h}^n=\left|\right|V_{1,h}^n{\left|\right|}_{0,\Omega }^2+\left|\right|V_{2,h}^n{\left|\right|}_{0,\Omega }^2$.

Proof. 

We mainly focus on $Q_{U,h}^n=Q_{U,h}^0$, and the result related to v can be analogously derived. Choosing ${\chi }_U^1={\overline{U}}_{1,h}^{n-\frac{1}{2}}$ in Equation (44), there exists

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ({\nabla }_t{U}_{1,h}^n,{\overline{U}}_{1,h}^{n-\frac{1}{2}})& -\gamma {\mathcal{A}}_h({\overline{U}}_{2,h}^{n-\frac{1}{2}},{\overline{U}}_{1,h}^{n-\frac{1}{2}})\hfill \\ \hfill & =\frac{\left|\right|U_{1,h}^n{\left|\right|}_{0,\Omega }^2-\left|\right|U_{1,h}^{n-1}{\left|\right|}_{0,\Omega }^2}{2\tau }-\gamma {\mathcal{A}}_h({\overline{U}}_{2,h}^{n-\frac{1}{2}},{\overline{U}}_{1,h}^{n-\frac{1}{2}})\hfill \end{array}\end{array}$$

(50)

and choosing ${\chi }_U^2={\overline{U}}_{2,h}^{n-\frac{1}{2}}$ in Equation (45) reaches to

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ({\nabla }_t{U}_{2,h}^n,{\overline{U}}_{2,h}^{n-\frac{1}{2}})& +\gamma {\mathcal{A}}_h({\overline{U}}_{1,h}^{n-\frac{1}{2}},{\overline{U}}_{2,h}^{n-\frac{1}{2}})\hfill \\ \hfill & =\frac{\left|\right|U_{2,h}^n{\left|\right|}_{0,\Omega }^2-\left|\right|U_{2,h}^{n-1}{\left|\right|}_{0,\Omega }^2}{2\tau }+\gamma {\mathcal{A}}_h({\overline{U}}_{1,h}^{n-\frac{1}{2}},{\overline{U}}_{2,h}^{n-\frac{1}{2}}).\hfill \end{array}\end{array}$$

(51)

By virtue of the symmetry of ${\mathcal{A}}_h(·,·)$, adding Equation (50) to Equation (51) leads to

$$\begin{array}{cc}\hfill ({\nabla }_t{U}_{1,h}^n,{\overline{U}}_{1,h}^{n-\frac{1}{2}})+({\nabla }_t{U}_{2,h}^n,{\overline{U}}_{2,h}^{n-\frac{1}{2}})& =\frac{\left|\right|U_{1,h}^n{\left|\right|}_{0,\Omega }^2-\left|\right|U_{1,h}^{n-1}{\left|\right|}_{0,\Omega }^2}{2\tau }+\frac{\left|\right|U_{2,h}^n{\left|\right|}_{0,\Omega }^2-\left|\right|U_{2,h}^{n-1}{\left|\right|}_{0,\Omega }^2}{2\tau }\hfill \\ \hfill & =\frac{Q_{U,h}^n-Q_{U,h}^{n-1}}{2\tau }=0,\hfill \end{array}$$

and therefore, $Q_{U,h}^n=Q_{U,h}^{n-1}=\cdots =Q_{U,h}^0$. Similarly, choosing ${\chi }_V^1={\overline{V}}_{1,h}^{n-\frac{1}{2}}$, ${\chi }_V^2={\overline{V}}_{2,h}^{n-\frac{1}{2}}$ in Equations (46) and (47), $Q_{V,h}^n=Q_{V,h}^0$ is obtained. This completes the proof. □

Lemma 2

(Discrete Gronwall inequality [32]). If the non-negative numbers $a_l$, $b_l$, $c_l$, ${\gamma }_l$ ( $l\ge 0$), τ and H satisfy

$$a_n+\tau \sum _{l=0}^n{b}_l\le \tau \sum _{l=0}^n{\gamma }_l{a}_l+\tau \sum _{l=0}^n{c}_l+H,n\ge 0,$$

 and supposing that $\tau {\gamma }_l<1$ and ${\sigma }_l={(1-\tau {\gamma }_l)}^{-1}$, one obtains

$$a_n+\tau \sum _{l=0}^n{b}_l\le exp\left(\tau \sum _{l=0}^n{\sigma }_l{\gamma }_l\right)\left[\tau \sum _{l=0}^n{c}_l+H\right].$$

In the sequel, we analyze the error estimate of the Crank–Nicolson FE scheme (44)–(49). For this purpose, we define the complex-valued fractional derivative spaces: $H_0^{\mu ,\mathbf{C}}(\Omega )=H_0^{\mu }(\Omega )+i{H}_0^{\mu }(\Omega )$, equipped with the complex norm

$$\begin{array}{c}\hfill {\left|u\right|}_{\mu ,\Omega }={\left({\left|\right|\left|\mathit{\omega }\right|}^{\mu }\mathcal{F}\left(Re\left(\tilde{u}\right)\right){\left|\right|}_{0,{\mathbf{R}}^2}^2+{\left|\right|\left|\mathit{\omega }\right|}^{\mu }\mathcal{F}\left(Im\left(\tilde{u}\right)\right){\left|\right|}_{0,{\mathbf{R}}^2}^2\right)}^{1/2}\end{array}$$

with $\mu >0$. Let u and v be the exact solutions of Equations (4)–(7) with their real and imaginary parts being $u_1$, $u_2$ and $v_1$, $v_2$, respectively. Also, letting $U_{1,h}^n$, $U_{2,h}^n$ and $V_{1,h}^n$, $V_{2,h}^n$ be the solutions at $t_n$ obtained by the above scheme and denoting $u_h^0=u_{1,h}^0+i{u}_{2,h}^0$, $v_h^0=v_{1,h}^0+i{v}_{2,h}^0$ and $U_h^n=U_{1,h}^n+i{U}_{2,h}^n$, we define

$$\left|\right|e_u^n{\left|\right|}_{0,\Omega }=\left|\right|U_h^n-u^n{\left|\right|}_{0,\Omega }=\sqrt{\left|\right|U_{1,h}^n-u_1^n{\left|\right|}_{0,\Omega }^2+\left|\right|U_{2,h}^n-u_2^n{\left|\right|}_{0,\Omega }^2},$$

and the similar norm $\left|\right|e_v^n{\left|\right|}_{0,\Omega }$ by $v_1^n$, $v_2^n$ and $V_{1,h}^n$, $V_{2,h}^n$, $n=1,2,\dots ,N$.

Theorem 2.

Assume ${\partial }_{t}u$, ${\partial }_{t}v\in L^2(0,T;H^m(\Omega ))$, ${\partial }_t^{2}u$, ${\partial }_t^{2}v\in L^2(0,T;V)$, ${\partial }_t^{3}u$, ${\partial }_t^{3}v\in L^2(0,T;$$L^2(\Omega ))$ and $\delta =max\{\alpha ,\beta \}$; then, for the Crank–Nicolson FE scheme (44)–(49), we have

$$\begin{array}{cc}\hfill \left|\right|e_u^n{\left|\right|}_{0,\Omega }^2& \le C{\displaystyle \{}\left|\right|u_0-u_h^0{\left|\right|}_{0,\Omega }^2+h^{2m}\left|\right|u_0{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & +{\tau }^4{\int }_0^T\left|\right|{\partial }_t^3{u\left|\right|}_{0,\Omega }^{2}dt+h^{2m}{\int }_0^T\left|\right|{\partial }_t{u\left|\right|}_{m,\Omega }^{2}dt+{\tau }^4{\int }_0^T\left|\right|{\partial }_t^{2}u{\left|\right|}_{\delta ,\Omega }^{2}dt\},\hfill \\ \hfill \left|\right|e_v^n{\left|\right|}_{0,\Omega }^2& \le C{\displaystyle \{}\left|\right|v_0-v_h^0{\left|\right|}_{0,\Omega }^2+h^{2m}\left|\right|v_0{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & +{\tau }^4{\int }_0^T\left|\right|{\partial }_t^3{v\left|\right|}_{0,\Omega }^{2}dt+h^{2m}{\int }_0^T\left|\right|{\partial }_t{v\left|\right|}_{m,\Omega }^{2}dt+{\tau }^4{\int }_0^T\left|\right|{\partial }_t^{2}v{\left|\right|}_{\delta ,\Omega }^{2}dt\},\hfill \end{array}$$

where C is a constant independent of τ and h and $n=1,2,\dots ,N$.

Proof. 

Since the scheme is decoupled, we only prove the error bound of $\left|\right|e_u^n{\left|\right|}_{0,\Omega }^2$, and the result for $\left|\right|e_v^n{\left|\right|}_{0,\Omega }^2$ follows similarly. Letting ${\theta }_{u_1}^n=U_{1,h}^n-{\Pi }_h{u}_1^n$, ${\xi }_{u_1}^n={\Pi }_h{u}_1^n-u_1^n$, ${\theta }_{u_2}^n=U_{2,h}^n-{\Pi }_h{u}_2^n$ and ${\xi }_{u_2}^n={\Pi }_h{u}_2^n-u_2^n$, write

$$e_{u_1}^n=U_{1,h}^n-u_1^n={\theta }_{u_1}^n+{\xi }_{u_1}^n,e_{u_2}^n=U_{2,h}^n-u_2^n={\theta }_{u_2}^n+{\xi }_{u_2}^n.$$

By virtue of the approximate property of ${\Pi }_h$, we know that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left|\right|{\xi }_u^n{\left|\right|}_{0,\Omega }^2:& =\left|\right|{\xi }_{u_1}^n{\left|\right|}_{0,\Omega }^2+\left|\right|{\xi }_{u_2}^n{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & =\left|\right|{\Pi }_h{u}_1^n-u_1^n{\left|\right|}_{0,\Omega }^2+\left|\right|{\Pi }_h{u}_2^n-u_2^n{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & \le C{h}^{2m}\left|\right|u_1\left(t_n\right){\left|\right|}_{m,\Omega }^2+C{h}^{2m}\left|\right|u_2\left(t_n\right){\left|\right|}_{m,\Omega }^2\hfill \\ \hfill & \le C{h}^{2m}\left|\right|u\left(t_n\right){\left|\right|}_{m,\Omega }^2\hfill \\ \hfill & \le C{h}^{2m}\left\{\left|\right|u_0{\left|\right|}_{0,\Omega }^2+{\int }_0^T\left|\right|{\partial }_{t}u{\left|\right|}_{m,\Omega }^{2}dt\right\},\hfill \end{array}\end{array}$$

(52)

then we only have to evaluate $\left|\right|{\theta }_{u_1}^n{\left|\right|}_{0,\Omega }^2$, $\left|\right|{\theta }_{u_2}^n{\left|\right|}_{0,\Omega }^2$. Let $t=t_{n-\frac{1}{2}}$, and for $\left|\right|{\theta }_{u_1}^n{\left|\right|}_{0,\Omega }^2$, we have

$$\begin{array}{cc}\hfill ({\nabla }_t{\theta }_{u_1}^n,{\chi }_U^1)-\gamma {\mathcal{A}}_h({\overline{\theta }}_{u_2}^{n-\frac{1}{2}},{\chi }_U^1)& =({\nabla }_t{U}_{1,h}^n,{\chi }_U^1)-({\nabla }_t{\Pi }_h{u}_1^n,{\chi }_U^1)\hfill \\ \hfill & -\gamma {\mathcal{A}}_h({\overline{U}}_{2,h}^{n-\frac{1}{2}},{\chi }_U^1)+\gamma {\mathcal{A}}_h({\Pi }_h{\overline{u}}_2^{n-\frac{1}{2}},{\chi }_U^1).\hfill \end{array}$$

Using the definition of ${\Pi }_h$ and Equations (33) and (44), there exists

$$\begin{array}{cc}\hfill ({\nabla }_t{\theta }_{u_1}^n,{\chi }_U^1)-\gamma {\mathcal{A}}_h({\overline{\theta }}_{u_2}^{n-\frac{1}{2}},{\chi }_U^1)& =-({\nabla }_t{\Pi }_h{u}_1^n,{\chi }_U^1)+\gamma {\mathcal{A}}_h({\Pi }_h{\overline{u}}_2^{n-\frac{1}{2}},{\chi }_U^1)\hfill \\ \hfill & =({\partial }_t{u}_1^{n-\frac{1}{2}},{\chi }_U^1)-({\nabla }_t{\Pi }_h{u}_1^n,{\chi }_U^1)\hfill \\ \hfill & -\gamma {\mathcal{A}}_h(u_2^{n-\frac{1}{2}},{\chi }_U^1)+\gamma {\mathcal{A}}_h({\Pi }_h{\overline{u}}_2^{n-\frac{1}{2}},{\chi }_U^1)\hfill \\ \hfill & =\left((I_h-{\Pi }_h){\nabla }_t{u}_1^n,{\chi }_U^1\right)+({\partial }_t{u}_1^{n-\frac{1}{2}}-{\nabla }_t{u}_1^n,{\chi }_U^1)\hfill \\ \hfill & -\gamma {\mathcal{A}}_h(u_2^{n-\frac{1}{2}}-{\overline{u}}_2^{n-\frac{1}{2}},{\chi }_U^1)+\gamma {\mathcal{A}}_h({\Pi }_h{\overline{u}}_2^{n-\frac{1}{2}}-{\overline{u}}_2^{n-\frac{1}{2}},{\chi }_U^1),\hfill \\ \hfill & =\left((I_h-{\Pi }_h){\nabla }_t{u}_1^n,{\chi }_U^1\right)+({\partial }_t{u}_1^{n-\frac{1}{2}}-{\nabla }_t{u}_1^n,{\chi }_U^1)\hfill \\ \hfill & -\gamma {\mathcal{A}}_h(u_2^{n-\frac{1}{2}}-{\overline{u}}_2^{n-\frac{1}{2}},{\chi }_U^1),\hfill \end{array}$$

(53)

where $I_h$ is the identity operator.

Similarly, for the term $\left|\right|{\theta }_{u_2}^n{\left|\right|}_{0,\Omega }^2$, using Equations (34) and (45), we derive

$$\begin{array}{cc}\hfill ({\nabla }_t{\theta }_{u_2}^n,{\chi }_U^2)+\gamma {\mathcal{A}}_h({\overline{\theta }}_{u_1}^{n-\frac{1}{2}},{\chi }_U^2)& =-({\nabla }_t{\Pi }_h{u}_2^n,{\chi }_U^2)-\gamma {\mathcal{A}}_h({\Pi }_h{\overline{u}}_1^{n-\frac{1}{2}},{\chi }_U^2)\hfill \\ \hfill & =({\partial }_t{u}_2^{n-\frac{1}{2}},{\chi }_U^2)-({\nabla }_t{\Pi }_h{u}_2^n,{\chi }_U^2)\hfill \\ \hfill & +\gamma {\mathcal{A}}_h(u_1^{n-\frac{1}{2}},{\chi }_U^2)-\gamma {\mathcal{A}}_h({\Pi }_h{\overline{u}}_1^{n-\frac{1}{2}},{\chi }_U^2)\hfill \\ \hfill & =\left((I_h-{\Pi }_h){\nabla }_t{u}_2^n,{\chi }_U^2\right)+({\partial }_t{u}_2^{n-\frac{1}{2}}-{\nabla }_t{u}_2^n,{\chi }_U^2)\hfill \\ \hfill & +\gamma {\mathcal{A}}_h(u_1^{n-\frac{1}{2}}-{\overline{u}}_1^{n-\frac{1}{2}},{\chi }_U^2).\hfill \end{array}$$

(54)

Choosing ${\chi }_U^1={\overline{\theta }}_{u_1}^{n-\frac{1}{2}}$, ${\chi }_U^2={\overline{\theta }}_{u_2}^{n-\frac{1}{2}}$ in Equations (53) and (54), using the symmetry of ${\mathcal{A}}_h(·,·)$ and adding them together, we obtain

$$\begin{array}{cc}\hfill ({\nabla }_t{\theta }_{u_1}^n,{\overline{\theta }}_{u_1}^{n-\frac{1}{2}})+({\nabla }_t{\theta }_{u_2}^n,{\overline{\theta }}_{u_2}^{n-\frac{1}{2}})& =\left((I_h-{\Pi }_h){\nabla }_t{u}_1^n,{\overline{\theta }}_{u_1}^{n-\frac{1}{2}}\right)+({\partial }_t{u}_1^{n-\frac{1}{2}}-{\nabla }_t{u}_1^n,{\overline{\theta }}_{u_1}^{n-\frac{1}{2}})\hfill \\ \hfill & -\gamma {\mathcal{A}}_h(u_2^{n-\frac{1}{2}}-{\overline{u}}_2^{n-\frac{1}{2}},{\overline{\theta }}_{u_1}^{n-\frac{1}{2}})+\left((I_h-{\Pi }_h){\nabla }_t{u}_2^n,{\overline{\theta }}_{u_2}^{n-\frac{1}{2}}\right)\hfill \\ \hfill & +({\partial }_t{u}_2^{n-\frac{1}{2}}-{\nabla }_t{u}_2^n,{\overline{\theta }}_{u_2}^{n-\frac{1}{2}})+\gamma {\mathcal{A}}_h(u_1^{n-\frac{1}{2}}-{\overline{u}}_1^{n-\frac{1}{2}},{\overline{\theta }}_{u_2}^{n-\frac{1}{2}}).\hfill \end{array}$$

Substituting

$$({\nabla }_t{\theta }_{u_k}^n,{\overline{\theta }}_{u_k}^{n-\frac{1}{2}})=\frac{\left|\right|{\theta }_{u_k}^n{\left|\right|}_{0,\Omega }^2-\left|\right|{\theta }_{u_k}^{n-1}{\left|\right|}_{0,\Omega }^2}{2\tau },k=1,2,$$

into the above equation, we further obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\left|\right|{\Theta }_u^n{\left|\right|}_{0,\Omega }^2-\left|\right|{\Theta }_u^{n-1}{\left|\right|}_{0,\Omega }^2}{2\tau }& =({\omega }_{u_1}^{1,n},{\overline{\theta }}_{u_1}^{n-\frac{1}{2}})+({\omega }_{u_1}^{2,n},{\overline{\theta }}_{u_1}^{n-\frac{1}{2}})-\gamma {\mathcal{A}}_h({\omega }_{u_2}^{3,n},{\overline{\theta }}_{u_1}^{n-\frac{1}{2}})\hfill \\ \hfill & +({\omega }_{u_2}^{1,n},{\overline{\theta }}_{u_2}^{n-\frac{1}{2}})+({\omega }_{u_2}^{2,n},{\overline{\theta }}_{u_2}^{n-\frac{1}{2}})+\gamma {\mathcal{A}}_h({\omega }_{u_1}^{3,n},{\overline{\theta }}_{u_2}^{n-\frac{1}{2}}),\hfill \end{array}\end{array}$$

(55)

where

$$\begin{array}{cc}\hfill \left|\right|{\Theta }_u^n{\left|\right|}_{0,\Omega }^2& =\left|\right|{\theta }_{u_1}^n{\left|\right|}_{0,\Omega }^2+\left|\right|{\theta }_{u_2}^n{\left|\right|}_{0,\Omega }^2,{\omega }_{u_k}^{1,n}=(I_h-{\Pi }_h){\nabla }_t{u}_k^n,\hfill \\ \hfill {\omega }_{u_k}^{2,n}& ={\partial }_t{u}_k^{n-\frac{1}{2}}-{\nabla }_t{u}_k^n,{\omega }_{u_k}^{3,n}=u_k^{n-\frac{1}{2}}-{\overline{u}}_k^{n-\frac{1}{2}}.\hfill \end{array}$$

Then, by Young’s inequality, we have

$$\begin{array}{cc}\hfill ({\omega }_{u_k}^{1,n},{\overline{\theta }}_{u_k}^{n-\frac{1}{2}})+({\omega }_{u_k}^{2,n},{\overline{\theta }}_{u_k}^{n-\frac{1}{2}})& \le \left|\right|{\omega }_{u_k}^{1,n}{\left|\right|}_{0,\Omega }\left|\right|{\overline{\theta }}_{u_k}^{n-\frac{1}{2}}{\left|\right|}_{0,\Omega }+\left|\right|{\omega }_{u_k}^{2,n}{\left|\right|}_{0,\Omega }\left|\right|{\overline{\theta }}_{u_k}^{n-\frac{1}{2}}{\left|\right|}_{0,\Omega }\hfill \\ \hfill & \le \left|\right|{\omega }_{u_k}^{1,n}{\left|\right|}_{0,\Omega }^2+\left|\right|{\omega }_{u_k}^{2,n}{\left|\right|}_{0,\Omega }^2+\left|\right|{\overline{\theta }}_{u_k}^{n-\frac{1}{2}}{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & \le \left|\right|{\omega }_{u_k}^{1,n}{\left|\right|}_{0,\Omega }^2+\left|\right|{\omega }_{u_k}^{2,n}{\left|\right|}_{0,\Omega }^2+\left|\right|{\theta }_{u_k}^n{\left|\right|}_{0,\Omega }^2+\left|\right|{\theta }_{u_k}^{n-1}{\left|\right|}_{0,\Omega }^2,\hfill \end{array}$$

(56)

and by the variational principle (10), there holds

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{A}}_h({\omega }_{u_k}^{3,n},{\overline{\theta }}_{u_j}^{n-\frac{1}{2}})& =\left(-(-{\Delta }_x^{\alpha /2}){\omega }_{u_k}^{3,n},{\overline{\theta }}_{u_j}^{n-\frac{1}{2}}\right)+\left(-(-{\Delta }_y^{\beta /2}){\omega }_{u_k}^{3,n},{\overline{\theta }}_{u_j}^{n-\frac{1}{2}}\right)\hfill \\ \hfill & \le \left|\right|-(-{\Delta }_x^{\alpha /2}){\omega }_{u_k}^{3,n}{\left|\right|}_{0,\Omega }^2+\left|\right|-(-{\Delta }_y^{\beta /2}){\omega }_{u_k}^{3,n}{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & +\left|\right|{\theta }_{u_j}^n{\left|\right|}_{0,\Omega }^2+\left|\right|{\theta }_{u_j}^{n-1}{\left|\right|}_{0,\Omega }^2,\hfill \end{array}\end{array}$$

(57)

where $k,j=1,2$, but $k\ne j$. Substituting (56) and (57) into Equation (55) and summing it from $l=1$ to n, we obtain

$$\begin{array}{cc}\hfill \left|\right|{\Theta }_u^n{\left|\right|}_{0,\Omega }^2-\left|\right|{\Theta }_u^0{\left|\right|}_{0,\Omega }^2& \le 4(\gamma +1)\tau \sum _{l=0}^n\left|\right|{\Theta }_u^l{\left|\right|}_{0,\Omega }^2+2\tau \sum _{l=1}^n\left|\right|{\omega }_{u_1}^{1,l}{\left|\right|}_{0,\Omega }^2+2\tau \sum _{l=1}^n\left|\right|{\omega }_{u_2}^{1,l}{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & +2\tau \sum _{l=1}^n\left|\right|{\omega }_{u_1}^{2,l}{\left|\right|}_{0,\Omega }^2+2\tau \sum _{l=1}^n\left|\right|{\omega }_{u_2}^{2,l}{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & +2\gamma \tau \sum _{l=1}^n\left(\left|\right|-(-{\Delta }_x^{\alpha /2}){\omega }_{u_1}^{3,l}{\left|\right|}_{0,\Omega }^2+\left|\right|-(-{\Delta }_x^{\alpha /2}){\omega }_{u_2}^{3,l}{\left|\right|}_{0,\Omega }^2\right)\hfill \\ \hfill & +2\gamma \tau \sum _{l=1}^n\left(\left|\right|-(-{\Delta }_y^{\beta /2}){\omega }_{u_1}^{3,l}{\left|\right|}_{0,\Omega }^2+\left|\right|-(-{\Delta }_y^{\beta /2}){\omega }_{u_2}^{3,l}{\left|\right|}_{0,\Omega }^2\right).\hfill \end{array}$$

(58)

Next, we estimate each term on the right side of the above inequality item by item. Firstly, from the approximate property of ${\Pi }_h$, it follows that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left|\right|{\Theta }_u^0{\left|\right|}_{0,\Omega }^2& =\left|\right|u_h^0-{\Pi }_h{u}_0{\left|\right|}_{0,\Omega }^2\le 2\left|\right|u_0-{\Pi }_h{u}_0{\left|\right|}_{0,\Omega }^2+2\left|\right|u_0-u_h^0{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & \le 2\left|\right|u_0-u_h^0{\left|\right|}_{0,\Omega }^2+C{h}^{2m}\left|\right|u_0{\left|\right|}_{0,\Omega }^2.\hfill \end{array}\end{array}$$

(59)

Secondly, using Taylor expansions, we have the upper bounds for the terms

$$\begin{array}{cc}\hfill \tau \sum _{l=1}^n\left|\right|{\omega }_{u_1}^{1,l}{\left|\right|}_{0,\Omega }^2+\tau \sum _{l=1}^n\left|\right|{\omega }_{u_2}^{1,l}{\left|\right|}_{0,\Omega }^2& =\tau \sum _{l=1}^n\left|\right|(I_h-{\Pi }_h){\nabla }_t{u}_1^l{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & +\tau \sum _{l=1}^n\left|\right|(I_h-{\Pi }_h){\nabla }_t{u}_2^l{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & \le C{h}^{2m}\sum _{l=1}^n{\int }_{t_{l-1}}^{t_l}\left|\right|{\partial }_t{u}_1{\left|\right|}_{m,\Omega }^{2}dt\hfill \\ \hfill & +C{h}^{2m}\sum _{l=1}^n{\int }_{t_{l-1}}^{t_l}\left|\right|{\partial }_t{u}_2{\left|\right|}_{m,\Omega }^{2}dt\hfill \\ \hfill & \le C{h}^{2m}{\int }_0^T\left|\right|{\partial }_{t}u{\left|\right|}_{m,\Omega }^{2}dt,\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill \tau \sum _{l=1}^n\left|\right|{\omega }_{u_1}^{2,l}{\left|\right|}_{0,\Omega }^2+\tau \sum _{l=1}^n\left|\right|{\omega }_{u_2}^{2,l}{\left|\right|}_{0,\Omega }^2& =\tau \sum _{l=1}^n\left|\right|{\partial }_t{u}_1^{l-\frac{1}{2}}-{\nabla }_t{u}_1^l{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & +\tau \sum _{l=1}^n\left|\right|{\partial }_t{u}_2^{l-\frac{1}{2}}-{\nabla }_t{u}_2^l{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & \le C{\tau }^4\sum _{l=1}^n{\int }_{t_{l-1}}^{t_l}\left|\right|{\partial }_t^3{u}_1{\left|\right|}_{0,\Omega }^{2}dt\hfill \\ \hfill & +C{\tau }^4\sum _{l=1}^n{\int }_{t_{l-1}}^{t_l}\left|\right|{\partial }_t^3{u}_2{\left|\right|}_{0,\Omega }^{2}dt\hfill \\ \hfill & \le C{\tau }^4{\int }_0^T\left|\right|{\partial }_t^{3}u{\left|\right|}_{0,\Omega }^{2}dt.\hfill \end{array}$$

(61)

Meanwhile, by the equivalency of fractional norms, there is no doubt that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \tau \sum _{l=1}^n\left(\right||-(-{\Delta }_x^{\alpha /2}){\omega }_{u_k}^{3,l}{\left|\right|}_{0,\Omega }^2& =\tau \sum _{l=1}^n\left(\right||-(-{\Delta }_x^{\alpha /2})(u_k^{l-\frac{1}{2}}-{\overline{u}}_k^{l-\frac{1}{2}}){\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & \le C{\tau }^4\sum _{l=1}^n{\int }_{t_{l-1}}^{t_l}\left|\right|-(-{\Delta }_x^{\alpha /2}){\partial }_t^2{u}_k{\left|\right|}_{0,\Omega }^{2}dt\hfill \\ \hfill & \le C{\tau }^4\sum _{l=1}^n{\int }_{t_{l-1}}^{t_l}\left|\right|{\partial }_t^2{u}_k{\left|\right|}_{\alpha ,\Omega }^{2}dt,\hfill \end{array}\end{array}$$

(62)

which yields

$$\begin{array}{c}\hfill \tau \sum _{l=1}^n\left(\left|\right|-(-{\Delta }_x^{\alpha /2}){\omega }_{u_1}^{3,l}{\left|\right|}_{0,\Omega }^2+\left|\right|-(-{\Delta }_x^{\alpha /2}){\omega }_{u_2}^{3,l}{\left|\right|}_{0,\Omega }^2\right)\le C{\tau }^4{\int }_0^T\left|\right|{\partial }_t^{2}u{\left|\right|}_{\alpha ,\Omega }^{2}dt,\end{array}$$

(63)

and in the same fashion, we can prove

$$\begin{array}{c}\hfill \tau \sum _{l=1}^n\left(\left|\right|-(-{\Delta }_y^{\beta /2}){\omega }_{u_1}^{3,l}{\left|\right|}_{0,\Omega }^2+\left|\right|-(-{\Delta }_y^{\beta /2}){\omega }_{u_2}^{3,l}{\left|\right|}_{0,\Omega }^2\right)\le C{\tau }^4{\int }_0^T\left|\right|{\partial }_t^{2}u{\left|\right|}_{\beta ,\Omega }^{2}dt.\end{array}$$

(64)

Combining (60)–(64) with (58), we obtain

$$\begin{array}{cc}\hfill \left|\right|{\Theta }_u^n{\left|\right|}_{0,\Omega }^2& \le 4(\gamma +1)\tau \sum _{l=0}^n\left|\right|{\Theta }_u^l{\left|\right|}_{0,\Omega }^2+\left|\right|{\Theta }_u^0{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & +C\left\{h^{2m}{\int }_0^T\left|\right|{\partial }_t{u\left|\right|}_{m,\Omega }^{2}dt+{\tau }^4{\int }_0^T\left|\right|{\partial }_t^3{u\left|\right|}_{0,\Omega }^{2}dt+{\tau }^4{\int }_0^T\left|\right|{\partial }_t^{2}u{\left|\right|}_{\delta ,\Omega }^{2}dt\right\}.\hfill \end{array}$$

(65)

From the discrete Gronwall inequality and (59), it follows that

$$\begin{array}{cc}\hfill \left|\right|{\Theta }_u^n{\left|\right|}_{0,\Omega }^2& \le C\{||u_0-u_h^0{\left|\right|}_{0,\Omega }^2+h^{2m}\left|\right|u_0{\left|\right|}_{0,\Omega }^2+h^{2m}{\int }_0^T\left|\right|{\partial }_{t}u{\left|\right|}_{m,\Omega }^{2}dt\hfill \\ \hfill & +{\tau }^4{\int }_0^T\left|\right|{\partial }_t^3{u\left|\right|}_{0,\Omega }^{2}dt+{\tau }^4{\int }_0^T\left|\right|{\partial }_t^{2}u{\left|\right|}_{\delta ,\Omega }^{2}dt\},\hfill \end{array}$$

with a sufficiently small $\tau$. By using (52), we finally obtain

$$\begin{array}{cc}\hfill \left|\right|e_u^n{\left|\right|}_{0,\Omega }^2& \le 2\left\{\left|\right|{\xi }_u^n{\left|\right|}_{0,\Omega }^2+\left|\right|{\Theta }_u^n{\left|\right|}_{0,\Omega }^2\right\}\hfill \\ \hfill & \le C{h}^{2m}\left\{\left|\right|u_0{\left|\right|}_{0,\Omega }^2+{\int }_0^T\left|\right|{\partial }_{t}u{\left|\right|}_{m,\Omega }^{2}dt\right\}+2\left|\right|{\Theta }_u^n{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & \le C{\displaystyle \{}\left|\right|u_0-u_h^0{\left|\right|}_{0,\Omega }^2+h^{2m}\left|\right|u_0{\left|\right|}_{0,\Omega }^2\hfill \\ \hfill & +{\tau }^4{\int }_0^T\left|\right|{\partial }_t^3{u\left|\right|}_{0,\Omega }^{2}dt+h^{2m}{\int }_0^T\left|\right|{\partial }_t{u\left|\right|}_{m,\Omega }^{2}dt+{\tau }^4{\int }_0^T\left|\right|{\partial }_t^{2}u{\left|\right|}_{\delta ,\Omega }^{2}dt\}.\hfill \end{array}$$

The upper bound of $\left|\right|e_v^n{\left|\right|}_{0,\Omega }^2$ can be similarly established. This completes the proof. □

4.3. Split-Step FE Scheme

According to the idea of the split-step method, the space-fractional CNLS can be split by solving the subproblems (29)–(32) and (33)–(36). Then, combining with the split step via the second-order Strang splitting technique and using the analytical solutions (40)–(43), the split-step FE scheme can be established by the following three steps:

•

Step 1:

$$\begin{array}{cc}\hfill U_{1,h}^{*,1}& =cos\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]U_{1,h}^{n-1}-sin\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]U_{2,h}^{n-1},\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill U_{2,h}^{*,1}& =cos\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]U_{2,h}^{n-1}+sin\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]U_{1,h}^{n-1},\hfill \end{array}$$

(67)

$$\begin{array}{cc}\hfill V_{1,h}^{*,1}& =cos\left[\lambda {\tilde{\mathcal{N}}}^{n-1}\tau /2\right]V_{1,h}^{n-1}-sin\left[\lambda {\tilde{\mathcal{N}}}^{n-1}\tau /2\right]V_{2,h}^{n-1},\hfill \end{array}$$

(68)

$$\begin{array}{cc}\hfill V_{2,h}^{*,1}& =cos\left[\lambda {\tilde{\mathcal{N}}}^{n-1}\tau /2\right]V_{2,h}^{n-1}+sin\left[\lambda {\tilde{\mathcal{N}}}^{n-1}\tau /2\right]V_{1,h}^{n-1},\hfill \end{array}$$

(69)

•

Step 2:

$$\begin{array}{cc}\hfill \left(\frac{U_{1,h}^{*,2}-U_{1,h}^{*,1}}{\tau },{\chi }_U^1\right)-\gamma {\mathcal{A}}_h\left(\frac{U_{2,h}^{*,1}+U_{2,h}^{*,2}}{2},{\chi }_U^1\right)& =0,\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill \left(\frac{U_{2,h}^{*,2}-U_{2,h}^{*,1}}{\tau },{\chi }_U^2\right)+\gamma {\mathcal{A}}_h\left(\frac{U_{1,h}^{*,1}+U_{1,h}^{*,2}}{2},{\chi }_U^2\right)& =0,\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill \left(\frac{V_{1,h}^{*,2}-V_{1,h}^{*,1}}{\tau },{\chi }_V^1\right)-\gamma {\mathcal{A}}_h\left(\frac{V_{2,h}^{*,1}+V_{2,h}^{*,2}}{2},{\chi }_V^1\right)& =0,\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill \left(\frac{V_{2,h}^{*,2}-V_{2,h}^{*,1}}{\tau },{\chi }_V^2\right)+\gamma {\mathcal{A}}_h\left(\frac{V_{1,h}^{*,1}+V_{1,h}^{*,2}}{2},{\chi }_V^2\right)& =0,\hfill \end{array}$$

(73)

•

Step 3:

$$\begin{array}{cc}\hfill U_{1,h}^n& =cos\left[\lambda {\overline{\mathcal{N}}}^{*,2}\tau /2\right]U_{1,h}^{*,2}-sin\left[\lambda {\overline{\mathcal{N}}}^{*,2}\tau /2\right]U_{2,h}^{*,2},\hfill \end{array}$$

(74)

$$\begin{array}{cc}\hfill U_{2,h}^n& =cos\left[\lambda {\overline{\mathcal{N}}}^{*,2}\tau /2\right]U_{2,h}^{*,2}+sin\left[\lambda {\overline{\mathcal{N}}}^{*,2}\tau /2\right]U_{1,h}^{*,2},\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill V_{1,h}^n& =cos\left[\lambda {\tilde{\mathcal{N}}}^{*,2}\tau /2\right]V_{1,h}^{*,2}-sin\left[\lambda {\tilde{\mathcal{N}}}^{*,2}\tau /2\right]V_{2,h}^{*,2},\hfill \end{array}$$

(76)

$$\begin{array}{cc}\hfill V_{2,h}^n& =cos\left[\lambda {\tilde{\mathcal{N}}}^{*,2}\tau /2\right]V_{2,h}^{*,2}+sin\left[\lambda {\tilde{\mathcal{N}}}^{*,2}\tau /2\right]V_{1,h}^{*,2},\hfill \end{array}$$

(77)

with ${\chi }_U^1$, ${\chi }_U^2$, ${\chi }_V^1$, ${\chi }_V^2\in X_h$ subjected to

$$\begin{array}{cc}\hfill & U_{1,h}^0=u_{1,h}^0(x,y),U_{2,h}^0=u_{2,h}^0(x,y),(x,y)\in \Omega ,\hfill \end{array}$$

(78)

$$\begin{array}{cc}\hfill & V_{1,h}^0=v_{1,h}^0(x,y),V_{2,h}^0=v_{2,h}^0(x,y),(x,y)\in \Omega ,\hfill \end{array}$$

(79)

where

$$\begin{array}{c}{\overline{\mathcal{N}}}^n=|U_{1,h}^n{|}^2+|U_{2,h}^n{|}^2+\rho |V_{1,h}^n{|}^2+\rho {\left|V_{2,h}^n\right|}^2,\\ {\tilde{\mathcal{N}}}^n=\rho |U_{1,h}^n{|}^2+\rho |U_{2,h}^n{|}^2+|V_{1,h}^n{|}^2+{\left|V_{2,h}^n\right|}^2,\\ {\overline{\mathcal{N}}}^{*,2}=|U_{1,h}^{*,2}{|}^2+|U_{2,h}^{*,2}{|}^2+\rho |V_{1,h}^{*,2}{|}^2+\rho {\left|V_{2,h}^{*,2}\right|}^2,\\ {\tilde{\mathcal{N}}}^{*,2}=\rho |U_{1,h}^{*,2}{|}^2+\rho |U_{2,h}^{*,2}{|}^2+|V_{1,h}^{*,2}{|}^2+{\left|V_{2,h}^{*,2}\right|}^2,\end{array}$$

and $u_{1,h}^0(x,y)$, $u_{2,h}^0(x,y)$, $v_{1,h}^0(x,y)$ and $v_{2,h}^0(x,y)$ are also the appropriate approximations of $\mathrm{Re}{u}_0(x,y)$, $\mathrm{Im}{u}_0(x,y)$, $\mathrm{Re}{v}_0(x,y)$ and $\mathrm{Im}{v}_0(x,y)$, respectively.

Theorem 3.

The solutions obtained by the split-step FE scheme (66)–(79) satisfy

$$Q_{U,h}^n=Q_{U,h}^0,Q_{V,h}^n=Q_{V,h}^0,n\ge 1,$$

where $Q_{U,h}^n=\left|\right|U_{1,h}^n{\left|\right|}_{0,\Omega }^2+\left|\right|U_{2,h}^n{\left|\right|}_{0,\Omega }^2$ and $Q_{V,h}^n=\left|\right|V_{1,h}^n{\left|\right|}_{0,\Omega }^2+\left|\right|V_{2,h}^n{\left|\right|}_{0,\Omega }^2$.

Proof. 

We only prove that $Q_{U,h}^n=Q_{U,h}^0$ and $Q_{V,h}^n=Q_{V,h}^0$ can be analogously obtained. Using the properties of the triangular function, we have

$$\begin{array}{cc}\hfill |U_{1,h}^{*,1}{|}^2+{\left|U_{2,h}^{*,1}\right|}^2& ={\left(cos\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]U_{1,h}^{n-1}-sin\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]U_{2,h}^{n-1}\right)}^2\hfill \\ \hfill & +{\left(cos\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]U_{2,h}^{n-1}+sin\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]U_{1,h}^{n-1}\right)}^2\hfill \\ \hfill & =\left({cos}^2\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]+{sin}^2\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]\right){\left|U_{1,h}^{n-1}\right|}^2\hfill \\ \hfill & +\left({cos}^2\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]+{sin}^2\left[\lambda {\overline{\mathcal{N}}}^{n-1}\tau /2\right]\right){\left|U_{2,h}^{n-1}\right|}^2\hfill \\ \hfill & =|U_{1,h}^{n-1}{|}^2+{\left|U_{2,h}^{n-1}\right|}^2\hfill \end{array}$$

and $\left|\right|U_{1,h}^n{\left|\right|}_{0,\Omega }^2+\left|\right|U_{2,h}^n{\left|\right|}_{0,\Omega }^2=\left|\right|U_{1,h}^{*,2}{\left|\right|}_{0,\Omega }^2+\left|\right|U_{2,h}^{*,2}{\left|\right|}_{0,\Omega }^2$. Noting the argument in Theorem 1, we obtain $|U_{1,h}^{*,2}{|}^2+|U_{2,h}^{*,2}{|}^2=|U_{1,h}^{*,1}{|}^2+{\left|U_{2,h}^{*,1}\right|}^2$ and thus $Q_{U,h}^n=Q_{U,h}^{n-1}=\cdots =Q_{U,h}^0$. This completes the proof. □

Theorem 4.

If we let $u_{1,h}^0={\Pi }_h\mathrm{Re}{u}_0(x,y)$, $u_{2,h}^0={\Pi }_h\mathrm{Im}{u}_0(x,y)$, $v_{1,h}^0={\Pi }_h\mathrm{Re}{v}_0(x,y)$ and $v_{2,h}^0={\Pi }_h\mathrm{Im}{v}_0(x,y)$, then for the split-step FE scheme (66)–(79), there holds

$$\begin{array}{c}\hfill \left|\right|e_u^n{\left|\right|}_{0,\Omega }^2+\left|\right|e_v^n{\left|\right|}_{0,\Omega }^2\le C({\tau }^4+h^{2m}),\end{array}$$

where C is a constant independent of τ and h and $n=1,2,\dots ,N$.

Proof. 

One can easily find this result by combining the property of the standard second-order Strang split-step technique and Theorem 2, and hence the details are omitted. □

Remark 1.

The present split-step FE scheme together with its theoretical results are applicable to α, $\beta >2$ because Lemma 1 and Equation (10) also hold in this case. The only issue required to be addressed is the generation of the stiffness matrix, but the algorithm is similar to the case of $0<\alpha$ and $\beta \le 2$.

5. Numerical Experiments

In this section, three numerical examples are provided to illustrate the computational accuracy and conservation property of the proposed split-step FE method. The uniform unstructured triangular meshes are utilized in all the tests and the algorithm to assemble the stiffness matrices, which is a difficult issue that we addressed in [31]. The codes are tested on the numerical simulation of the double solitons intersection and plane wave. All the tests are carried out by using linear interpolation, i.e., $m=2$, and run by MATLAB R2015b on a PC with Windows 7 Ultimate SP1, AMD Athlon(tm) II $\times 2$ 250 3.00 GHz Processor and 8 GB DDR3 1600MHz RAM. According to the foregoing theoretical analysis, we anticipate the second-order convergent rates both in time and space.

5.1. One-Dimensional Problem

Example 1.

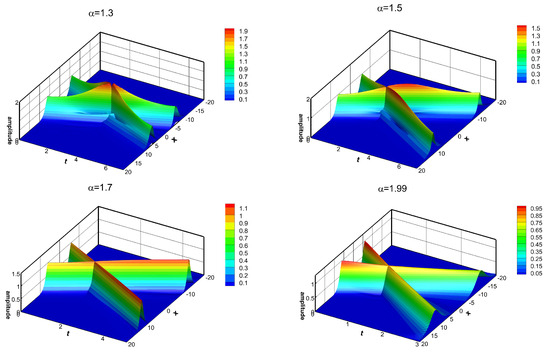
We simulate the intersection of double solitons governed by the following 1D coupled space-fractional CNLS:

$$\begin{array}{cc}\hfill i{\partial }_{t}u-{(-{\Delta }_x)}^{\alpha /2}u+{\lambda \left(\right|u|}^2+{\rho \left|v\right|}^2)u& =0,\hfill \\ \hfill i{\partial }_{t}v-{(-{\Delta }_x)}^{\alpha /2}v+{\lambda \left(\rho \right|u|}^2+{\left|v\right|}^2)v& =0,0<t\le T,\hfill \end{array}$$

with the initial wave functions [33]:

$$\begin{array}{cc}\hfill & u(x,0)=\sqrt{2{\sigma }_1}\mathit{sech}(\sqrt{2{\vartheta }_1}x+x_0)exp\left(i{\upsilon }_{1}x\right),\hfill \\ \hfill & v(x,0)=\sqrt{2{\sigma }_2}\mathit{sech}(\sqrt{2{\vartheta }_2}x-x_0)exp\left(i{\upsilon }_{2}x\right),x\in \mathbf{R},\hfill \end{array}$$

where $\sqrt{2{\sigma }_k}$ is the amplitude and ${\upsilon }_k$ is the propagation velocity with $k=1,2$.

When $\left|x\right|$ tends to infinity, the solitons can be negligible; then, we truncate the problem on $\Omega =[-\ell ,\ell ]$ by taking a large enough ℓ and imposing the homogeneous boundary conditions as follows:

$$\begin{array}{c}\hfill u(x,t)=0,v(x,t)=0,(x;t)\in \mathbf{R}\setminus \Omega \times (0,T].\end{array}$$

 In particular, the above problem is an integrable Manakov model if we take $\alpha =2$ and $\rho =1$, which describes an elastic collision without any reflection, transmission, trapping and the new solitary wave created by the intersection of two solitons.

Letting  $\ell =20$, $\lambda =\rho =1$ and  ${\sigma }_k={\vartheta }_k=1/2$, we simulate the dynamics of the double solitons intersection with $x_0=6$ and study the potential impact brought by fractional derivatives to double solitons collision. For this purpose, letting the velocity of both moving solitons be opposite but with equivalent size, i.e., ${\upsilon }_1=-{\upsilon }_2$, we take  $\tau =$ 2.0  × 10⁻² and  $h=0.05$ and present the evolution of solitons over time for  $\alpha =1.3$,  $1.5$,  $1.7$ and  $1.99$ with  ${\upsilon }_1=3$ and  ${\upsilon }_2=-3$ in Figure 1. As we observed, as  $\alpha$ becomes smaller, the propagation velocity of solitons will be slower, which means that the time of the solitons collision will be delayed if  $\alpha$ is assigned a small number. Meanwhile, the shape of the solitons changes with  $\alpha$, including both the width and amplitude. More specifically, the smaller the  $\alpha$ is, the higher the amplitude of solitons would be, and the variation trend of width seems to be the opposite. In addition, this phenomenon is more evident when they collide with each other. The reason for this phenomenon may be that   $\alpha$ and $\beta$ can affect the diffusion rate of microscopic particles in Lévy processes. 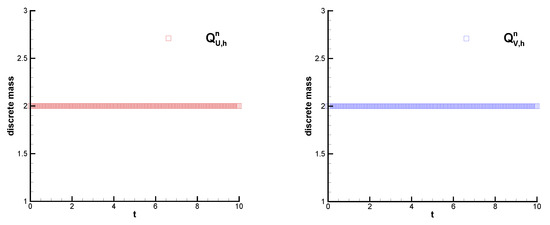Resetting $\tau =$ 5.0  × 10⁻² and $h=0.1$, we compute the conservation quantities   $Q_{U,h}^n$ and  $Q_{V,h}^n$ and present their variation versus time for  $\alpha =1.2$ in Figure 2. Besides, we report the values of  $Q_{U,h}^n$ and  $Q_{V,h}^n$ at different times for  $\alpha =1.2$,  $1.6$ and  $1.8$ in Table 1. From these figures and table, it is observed that our split-step FE scheme preserves  $Q_{U,h}^n$ and  $Q_{V,h}^n$ and can be applied to long-time simulation in practice.

Figure 1. Interaction of double solitons with different $\alpha$.

Figure 2. The variation in conservation quantities $Q_{U,h}^n$ and $Q_{V,h}^n$ for $\alpha =1.2$.

Table 1. The values of $Q_{U,h}^n$ and $Q_{V,h}^n$ at different time.

		$\mathit{\alpha }=1.2$	$\mathit{\alpha }=1.6$	$\mathit{\alpha }=1.8$
	$t=0$	1.999999999998474	1.999999999998474	1.999999999998474
	$t=2$	2.000000000386479	1.999999999998581	1.999999999998507
$Q_{U,h}^n$	$t=4$	2.000000002291670	2.000000000000949	2.000000000225318
	$t=6$	2.000000000786256	2.000000009781684	2.000789620154900
	$t=8$	2.000000005975913	2.000181449524869	2.000000085658504
	$t=10$	2.000000012622097	2.000002000716171	2.000000061847427
	$t=0$	1.999999999998475	1.999999999998475	1.999999999998475
	$t=2$	2.000000000386490	1.999999999998548	1.999999999998647
$Q_{V,h}^n$	$t=4$	2.000000002291678	2.000000000000807	2.000000000225574
	$t=6$	2.000000000786264	2.000000009781226	2.000789620155215
	$t=8$	2.000000005975903	2.000181449524379	2.000000085658829
	$t=10$	2.000000012622083	2.000002000715644	2.000000061847727

In order to obtain more insight about computational efficiency, we use the pure Crank–Nicolson FE scheme to discretize the above space-fractional CNLS and run the algorithm with a Newton’s iteration loop to obtain the solutions at each time layer. We compare the computational time of the pure Crank–Nicolson FE and split-step FE methods with a different   $\tau$ and h, where the Newton’s iteration algorithm is terminated by reaching a solution with the tolerant error 1.0 × 10⁻¹². Letting  $\alpha =1.8$ and  $\ell =10$, we compute the solutions at  $t=1$ by using both methods and report the used CPU times in Table 2. From this table, we easily observe that the CPU times of our method are markedly less than those of the Crank–Nicolson FE scheme with Newton’s iteration, which implies that the proposed split-step FE method is more efficient than iteration algorithms.

Table 2. The CPU times of split-step FE method and Crank–Nicolson FE method with Newton’s iteration.

$\mathit{\tau }$, h	Algorithm	CPU Time (s)
$0.01$, $0.1$	Split-step FE method	7.14
	Newton method	38.18
$0.002$, $0.05$	Split-step FE method	191.90
	Newton method	1508.97
$0.00125$, $0.04$	Split-step FE method	522.12
	Newton method	3635.59

5.2. Two-Dimensional Problems

Example 2.

We consider the 2D space-fractional problem of CNLS type:

$$\begin{array}{cc}\hfill & i{\partial }_{t}u-\gamma {(-{\Delta }_x)}^{\alpha /2}u-\gamma {(-{\Delta }_y)}^{\beta /2}u+{\lambda \left(\right|u|}^2+{\rho \left|v\right|}^2)u=R_1(x,y,t),\hfill \\ \hfill & i{\partial }_{t}v-\gamma {(-{\Delta }_x)}^{\alpha /2}v-\gamma {(-{\Delta }_y)}^{\beta /2}v+{\lambda \left(\rho \right|u|}^2+{\left|v\right|}^2)v=R_2(x,y,t),0<t\le T,\hfill \end{array}$$

 on the domain $\Omega ={[0,1]}^2$, where the right-side terms are as follows:

$$\begin{array}{cc}\hfill R_1(x,y,t)& =30t^2{\chi }_1^2{\chi }_2^2+1000\lambda t^9{\chi }_1^6{\chi }_2^6+10\lambda \rho t^7{\chi }_1^8{\chi }_2^8\hfill \\ \hfill & +\frac{10\gamma t^3{\chi }_2^2\left(G(\alpha ,x)+G(\alpha ,1-x)\right)}{cos(\alpha \pi /2)}+\frac{10\gamma t^3{\chi }_1^2\left(G(\beta ,y)+G(\beta ,1-y)\right)}{cos(\beta \pi /2)},\hfill \\ \hfill R_2(x,y,t)& =\left(iexp\left(it\right)t^2+2exp\left(it\right)t\right){\chi }_1^3{\chi }_2^3+\lambda t^6{\chi }_1^9{\chi }_2^{9}exp\left(it\right)+100\lambda \rho t^8{\chi }_1^7{\chi }_2^{7}exp\left(it\right)\hfill \\ \hfill & +\frac{\gamma t^{2}exp\left(it\right){\chi }_2^3\left(H(\alpha ,x)+H(\alpha ,1-x)\right)}{cos(\alpha \pi /2)}+\frac{\gamma t^{2}exp\left(it\right){\chi }_1^3\left(H(\beta ,y)+H(\beta ,1-y)\right)}{cos(\beta \pi /2)},\hfill \end{array}$$

with ${\chi }_1=x(1-x)$, ${\chi }_2=y(1-y)$ and the functions

$$\begin{array}{cc}\hfill G(s,\delta )& =\frac{{\delta }^{2-s}}{\Gamma (3-s)}-\frac{6{\delta }^{3-s}}{\Gamma (4-s)}+\frac{12{\delta }^{4-s}}{\Gamma (5-s)},\hfill \\ \hfill H(s,\delta )& =\frac{48{\delta }^{3-s}}{\Gamma (4-s)}-\frac{288{\delta }^{4-s}}{\Gamma (5-s)}+\frac{720{\delta }^{5-s}}{\Gamma (6-s)}-\frac{720{\delta }^{6-s}}{\Gamma (7-s)}.\hfill \end{array}$$

It can be validated that the analytical solutions are

$$\begin{array}{cc}\hfill & u(x,y,t)=10t^3{x}^2{(1-x)}^2{y}^2{(1-y)}^2,\hfill \\ \hfill & v(x,y,t)=t^2{x}^3{(1-x)}^3{y}^3{(1-y)}^{3}exp\left(it\right),(x,y;t)\in {\mathbf{R}}^2\setminus \Omega \times (0,T].\hfill \end{array}$$

In this test, we evaluate the convergent accuracy of the Crank–Nicolson FE and split-step FE methods. On the one hand, we take $\gamma =1$ and  $\lambda =0$, and then the problem degenerates into a coupled linear problem and the Crank–Nicolson FE scheme is applied. We compute the mean square errors  $\left|\right|e_u^n{\left|\right|}_{0,\Omega }$ and  $\left|\right|e_v^n{\left|\right|}_{0,\Omega }$ at  $t=1$ with different  $\tau$ by using  $h=\tau$, and the numerical results for  $\alpha =1.7$ and  $\beta =1.8$ are documented in Table 3. Next, taking  $\tau =$  1.0 × 10 ⁻³, we compute the errors at  $t=1$  with a different h and document the numerical results in Table 4, where in order to verify the accuracy, we calculate the temporal convergent order by 

$$Orde{r}_{time}={log}_2\left(\frac{\left|\right|e({\tau }_1,h){\left|\right|}_{0,\Omega }}{\left|\right|e({\tau }_2,h){\left|\right|}_{0,\Omega }}\right)/{log}_2\left(\frac{{\tau }_1}{{\tau }_2}\right),$$

 and the spatial convergent order by 

$$Orde{r}_{space}={log}_2\left(\frac{\left|\right|e(\tau ,h_1){\left|\right|}_{0,\Omega }}{\left|\right|e(\tau ,h_2){\left|\right|}_{0,\Omega }}\right)/{log}_2\left(\frac{h_1}{h_2}\right),$$

with  $\left|\right|e({\tau }_i,h_j){\left|\right|}_{0,\Omega }$ being the error computed by using the time and space meshsizes  ${\tau }_i$ and  $h_j$.

Table 3. The errors and order $Orde{r}_{time}$ of Crank–Nicolson FE scheme for $\alpha =1.7$ and $\beta =1.8$.

$\mathit{\tau }$	$\left|\right|{\mathit{e}}_{\mathit{u}}^{\mathit{n}}{\left|\right|}_{0,\mathbf{\Omega }}$	${\mathit{Order}}_{\mathit{time}}$	$\left|\right|{\mathit{e}}_{\mathit{v}}^{\mathit{n}}{\left|\right|}_{0,\mathbf{\Omega }}$	${\mathit{Order}}_{\mathit{time}}$
1/8	1.26746 $\times {10}^{-3}$	-	6.93411 $\times {10}^{-6}$	-
1/16	3.16521 $\times {10}^{-4}$	2.00	1.75065 $\times {10}^{-6}$	1.99
1/24	1.42515 $\times {10}^{-4}$	1.97	7.87270 $\times {10}^{-7}$	1.97

Table 4. The errors and order $Orde{r}_{space}$ of Crank–Nicolson FE scheme for $\alpha =1.7$ and $\beta =1.8$.

h	$\left|\right|{\mathit{e}}_{\mathit{u}}^{\mathit{n}}{\left|\right|}_{0,\mathbf{\Omega }}$	${\mathit{Order}}_{\mathit{space}}$	$\left|\right|{\mathit{e}}_{\mathit{v}}^{\mathit{n}}{\left|\right|}_{0,\mathbf{\Omega }}$	${\mathit{Order}}_{\mathit{space}}$
0.127599	2.10951 $\times {10}^{-3}$	-	1.42094 $\times {10}^{-5}$	-
0.059989	5.21634 $\times {10}^{-4}$	1.85	3.48642 $\times {10}^{-6}$	1.86
0.030385	1.42805 $\times {10}^{-4}$	1.90	8.96400 $\times {10}^{-7}$	2.00

On the other hand, we take  $\gamma =\lambda =1$ and  $\rho =2$ and apply the split-step FE scheme to treat this nonlinear coupled system. We test the codes as above and document the corresponding results at  $t=1$ for  $\alpha =1.8$ and  $\alpha =1.9$, which are in Table 5 and Table 6, respectively. We easily observe from the tables that the convergent order of two FE schemes are almost two both in time and space, which demonstrates that the proposed FE schemes are convergent with theoretical accuracy.

Table 5. The errors and order $Orde{r}_{time}$ of split-step FE scheme for $\alpha =1.8$ and $\beta =1.9$.

$\mathit{\tau }$	$\left|\right|{\mathit{e}}_{\mathit{u}}^{\mathit{n}}{\left|\right|}_{0,\mathbf{\Omega }}$	${\mathit{Order}}_{\mathit{time}}$	$\left|\right|{\mathit{e}}_{\mathit{v}}^{\mathit{n}}{\left|\right|}_{0,\mathbf{\Omega }}$	${\mathit{Order}}_{\mathit{time}}$
1/8	1.31299 $\times {10}^{-3}$	-	7.20499 $\times {10}^{-6}$	-
1/16	3.28346 $\times {10}^{-4}$	2.00	1.82686 $\times {10}^{-6}$	1.98
1/24	1.45658 $\times {10}^{-4}$	2.00	8.08489 $\times {10}^{-7}$	2.01

Table 6. The errors and order $Orde{r}_{space}$ of split-step FE scheme for $\alpha =1.8$ and $\beta =1.9$.

h	$\left|\right|{\mathit{e}}_{\mathit{u}}^{\mathit{n}}{\left|\right|}_{0,\mathbf{\Omega }}$	${\mathit{Order}}_{\mathit{space}}$	$\left|\right|{\mathit{e}}_{\mathit{v}}^{\mathit{n}}{\left|\right|}_{0,\mathbf{\Omega }}$	${\mathit{Order}}_{\mathit{space}}$
0.127599	2.09283 $\times {10}^{-3}$	-	1.42088 $\times {10}^{-5}$	-
0.059989	5.07955 $\times {10}^{-4}$	1.88	3.43539 $\times {10}^{-6}$	1.88
0.030385	1.34423 $\times {10}^{-4}$	1.95	8.56923 $\times {10}^{-7}$	2.04

Example 3.

Letting $\rho =0$, we simulate the dynamic of plane wave governed by

$$\begin{array}{c}\hfill i{\partial }_{t}u-\gamma {(-{\Delta }_x)}^{\alpha /2}u-\gamma {(-{\Delta }_y)}^{\beta /2}u+\lambda {\left|u\right|}^{2}u=0,\end{array}$$

with the initial wave function

$$\begin{array}{cc}\hfill & u(x,y,0)=\frac{2}{\sqrt{\pi }}exp(-x^2-y^2),(x,y)\in {\mathbf{R}}^2.\hfill \end{array}$$

When $\left|x\right|$ and $\left|y\right|$ tend to infinity, the initial wave exponentially decays to zero, and if Ω is large enough, then the height of the wave is nearly zero outside of Ω; thus, we suggest the homogeneous boundary condition imposed as

$$\begin{array}{c}\hfill u(x,y,t)=0,(x,y;t)\in {\mathbf{R}}^2\setminus \Omega \times (0,T].\end{array}$$

The main purpose of this test is to evaluate the actual performance of the proposed split-step FE scheme in practice, and we conduct the numerical simulation divided into three steps. Firstly, the evolution of the wave over time will be simulated. On a finer unstructured triangular mesh, the initial wave is plotted, which is given in Figure 3 (right). We easily see that its amplitude is nearly one. Letting $\gamma =1$,   $\tau =0.01$,   $h\approx 0.12287$  and   $\Omega ={[-5,5]}^2$, we use the split-step FE scheme to handle this problem. The used unstructured triangular mesh is given in Figure 3 (left), and the profiles of the approximate wave at the time  $t=0.1$, 0.4, 0.7 and 1 for  $\alpha =\beta =1.2$ are plotted in Figure 4. The comparison of the approximate waves at  $t=0.3$ for different  $\alpha$ and  $\beta$ are presented in Figure 5. From these figures, we observe that the wave travels with its size and height being continuously variable. More precisely, the plane wave is centered at origin coordinates with the height being one at   $t=0$, and as time goes on, the modulus of the wave solution becomes smaller and the wave gets fatter and fatter. The physical shape of the waves can obviously be affected by the fractional derivatives, and a bigger   $\alpha$  and   $\beta$ would lead to a faster rate of decay of plane waves. As compared to the classical ones, the wave governed by the fractional model possesses a narrower width and larger amplitude, and such an impact would grow as   $\alpha$  and   $\beta$ become small. Letting   $\alpha =1.3$ and   $\beta =1.9$, Figure 6 (left) shows the contour of an approximate wave. We observe that the decay speed of the wave solution along the x-axis is smaller than that of the y-axis. On the contrary, reletting   $\alpha =1.9$ and   $\beta =1.3$, the exact opposite result is observed in Figure 6 (right), which further confirms that   $\alpha$ and   $\beta$ can affect the decay speed of the wave solution and a large fractional power would lead to a fast decay velocity. What caused this phenomenon? The most intuitive explanation is that the value of fractional exponents   $\alpha$ and   $\beta$ have an impact on the diffusion behavior of particles. More precisely, as   $\alpha$ and   $\beta$ increase toward two, the diffusion occurs faster, and conversely, the diffusion occurs slowly if   $\alpha$ and   $\beta$ are small. As to why this occurred, it may be related to how the value of   $\alpha$ and   $\beta$ determines how a particular "non-Gaussian" probability distribution of particle displacements becomes in Lévy flights.

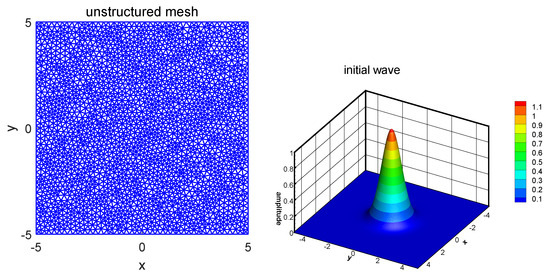
Figure 3. Unstructured triangular mesh and initial plane wave.

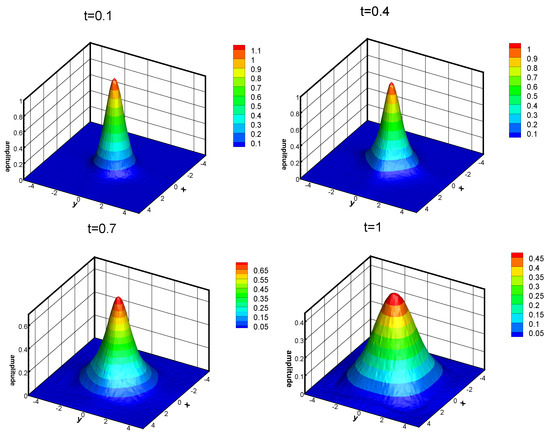
Figure 4. Profiles of wave solution at different time for $\alpha =\beta =1.2$.

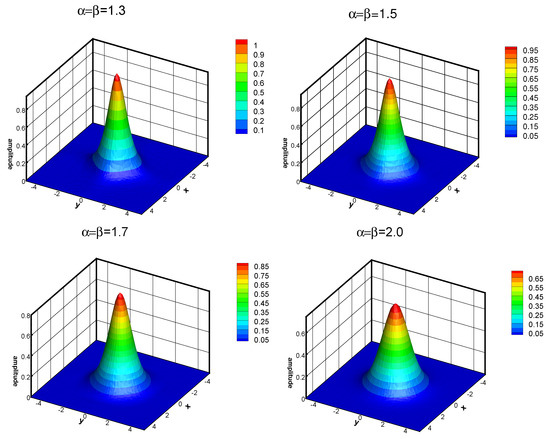
Figure 5. Profiles of wave solution for different $\alpha$ and $\beta$ at $t=0.3$.

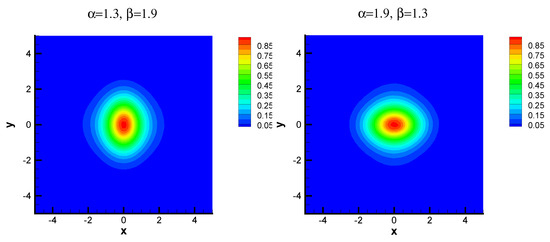
Figure 6. Contour plots of wave solution with $\alpha \ne \beta$.

Secondly, we show that the mass conservation property is maintained by both Crank–Nicolson FE and split-step FE schemes. Taking   $\lambda =0$,$\alpha =\beta =1.1$ and   $\Omega ={[-10,10]}^2$, we use the Crank–Nicolson FE scheme to solve this problem based on the meshsizes   $\tau =0.05$ and   $h=0.5$ and exhibit how the conservation quantity   $Q_{U,h}^n$ changes over time in Figure 7 (left). Furthermore, retaking   $\lambda =1$, we use the split-step FE scheme to solve this problem and present the variation tendency of the value of   $Q_{U,h}^n$ versus time in Figure 7 (right). The computational results in the above figures illustrate that both two FE schemes preserve   $Q_{U,h}^n$.

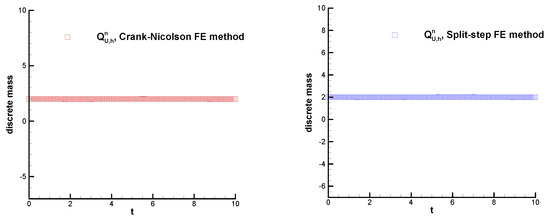
Figure 7. The variation in conservation quantity $Q_{U,h}^n$ for $\alpha =\beta =1.1$.

Finally, as we did before, we use the pure Crank–Nicolson FE scheme with Newton’s iteration to discretize the above problem with   $\lambda =1$ and compare the time cost of the Crank–Nicolson FE and split-step FE schemes, where the tolerant error is also chosen to be 1.0 × 10 ⁻¹². Letting   $\alpha =\beta =1.8$ and   $\Omega ={[-5,5]}^2$, we compute the solutions at   $t=0.5$ by both methods and report the used CPU times in Table 7. It is easy to observe that the CPU times of our method are much less than those of the pure Crank–Nicolson FE scheme, which demonstrates that the proposed split-step FE method is very competitive in an actual numerical simulation.

Table 7. The CPU times of split-step FE method and Crank–Nicolson FE method with Newton’s iteration.

$\mathit{\tau }$, h	Algorithm	CPU Time (s)
$0.001$, $0.24165$	Split-step FE method	504.14
	Newton method	1179.60
$0.0005$, $0.16144$	Split-step FE method	4005.10
	Newton method	15,233.46

6. Conclusions

The high-dimensional space-fractional CNLS is a coupled nonlinear system, and its main difficulty comes from the nonlocality of fractional derivatives. This paper considered a split-step Galerkin FE scheme for the 2D space-fractional CNLS, and the proposed method is particularly adequate for solving this type of equation. The designed split-step FE scheme avoids solving nonlinear algebraic equations and can effectively reduce computational burden in practice. We also studied its mass conservation property in a discrete sense and unconditional convergence. The algorithm was evaluated by a constructive numerical test and the simulation of a double solitons collision and plane wave on unstructured meshes. The numerical outcomes and comparison with the pure Crank–Nicolson FE method with Newton’s iteration have illustrated its superiority and capacity.

The fractional NLS extends the application scope of classical NLS, and it tremendously enriches the connotation of quantum mechanics. The nonlocal convolution structure in fractional derivatives brings forward a great challenge in numerical simulation. Hence, an efficient numerical technique like our method can not only help to study the inner mechanisms of a microscopic quantum system but also play a certain role in increasing the popularity of fractional NLS/CNLS, and this would indirectly promote the upgrading of technological products. For example, we can study how a light beam travels in a fractional diffraction system in a numerical sense to provide a reference for the production of highly sensitive optical switches, optical devices, beam splitters, etc. Moreover, it is worth mentioning that artificial neural networks have also recently emerged as a promising alternative to simulate the systems involving fractional calculus [34,35,36,37]. As a kind of artificial intelligence algorithm, they have many advantages, such as strong fault tolerance and robustness for all quantitative applications and sensibility to spatial dimensions. We believe that they can be extended to simulate the high-dimensional space-fractional CNLS as well and would possess strong competitiveness as compared to the existing methods for our algorithm. We will consider this interesting topic in the future.