An Iterative Method for the Approximation of Common Fixed Points of Two Mappings: Application to Fractal Functions

Abstract

This paper proposes an iterative algorithm for the search for common fixed points of two mappings. The properties of approximation and convergence of the method are analyzed in the context of Banach spaces. In particular, this article provides sufficient conditions for the strong convergence of the sequence generated by the iterative scheme to a common fixed point of two operators. The method is illustrated with some examples of application. The procedure is used to approach a common solution of two Fredholm integral equations of the second kind. In the second part of the article, the existence of a fractal function coming from two different Read–Bajraktarević operators is proved. Afterwards, a study of the approximation of fixed points of a fractal convolution of operators is performed, in the framework of Lebesgue or Bochner spaces.

1. Introduction

In this paper, we address the approximation of a common fixed point of a finite number of mappings through an iterative method, and its applications to the study of fractal functions involving two different operators. From a practical point of view, the problem of finding common fixed points of two mappings appears in mathematical applications such as convex optimization (see, for instance, [1]).

Das and Debata [2] extended the classical iteration proposed by Ishikawa [3] to find a critical point of a single operator, acting on a normed space, to the case of the approximation of a common fixed point of two maps S and T. The iterative scheme is the following:

$$\begin{array}{cc}\hfill y_n& \hfill =(1-{\alpha }_n)x_n+{\alpha }_{n}S{x}_n,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill x_{n+1}& \hfill =(1-{\beta }_n)x_n+{\beta }_{n}T{y}_n,\hfill \end{array}$$

(2)

for ${\alpha }_n,{\beta }_n\in [0,1].$ They considered quasi-nonexpansive maps defined on uniformly convex Banach spaces. Takahashi and Tamura [4] studied the same method in the nonexpansive case on a strictly convex Banach space. Khan and Takahashi [5] generalized the procedure to deal with asymptotically nonexpansive operators.

In reference [6], Yadav proposed a variant of the iteration considered by Sahu [7] for a single map, in order to include two different mappings. The recurrence is given by the following steps:

$$\begin{array}{cc}\hfill y_n& \hfill =(1-{\beta }_n)T{x}_n+{\beta }_{n}S{x}_n,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill x_{n+1}& \hfill =T{y}_n,\hfill \end{array}$$

(4)

for ${\beta }_n\in [0,1].$ This method was called Y-iteration by the author. He gave sufficient conditions on the space and the maps S and T in order to obtain weak and strong convergences of the sequence $\left(x_n\right)$ to a common fixed point of both mappings, and presented some examples of the application of the algorithm.

The single operator case proves that not all the fixed point approximation methods are useful for all kind of mappings. The convergence of each procedure depends on the underlying space and the properties of the map involved. Thus, it is desirable to have a variety of algorithms to focus a given problem. We propose a different iterative method for the search for common fixed points of a finite family of quasi-nonexpansive mappings, based on an algorithm defined in [8].

One of the first results of common fixed point existence of a family of operators is due to Browder [9]:

Theorem 1.

Let X be a uniformly convex Banach space, and $C\subseteq X$ be nonempty, bounded, closed and convex. If $\left\{U_{\lambda }\right\}$ is a commuting family of nonexpansive mappings $U_{\lambda }:C\to C,$ then the set $\left\{U_{\lambda }\right\}$ has a common fixed point.

The proof of this theorem is based on the well-known fixed point result of the same author for nonexpansive mappings on uniformly convex Banach spaces [9]. Theorem 1 is an extension of of the Markov–Kakutani Theorem [10,11]. It is also a generalization of the Theorem of De Marr [12], where C is assumed to be compact.

Afterwards, a great number of researchers expanded this result. For instance, R.E. Bruck [13] considered this problem in a Banach space X and $C\subseteq X$ satisfying some fixed point conditions, given in the following definition.

Definition 1.

Let X be a Banach space; a subset $C\subseteq X$ has the fixed point property for nonexpansive mappings if every nonexpansive map $f:C\to C$ has a fixed point. C has the conditional fixed point property for nonexpansive mappings if every nonexpansive mapping $f:C\to C$ satisfies either that f has no fixed points or that f has a fixed point in every nonempty bounded, closed and convex f-invariant subset ofC.

Example 1.

If X is a uniformly convex Banach space, any subset C that is nonempty, bounded, closed and convex has the fixed point property for nonexpansive mappings.

$C=X$, where X is a uniformly convex Banach space, has the conditional fixed point property for nonexpansive mappings.

Both are consequences of Browder’s Theorem on the existence of fixed points (Theorem 1 of reference [9]).

Bruck’s Theorem [13] states that if X is a real or complex Banach space and $C\subseteq X$ has the fixed point property and the conditional fixed point property for nonexpansive mappings, and C is either weakly compact or bounded and separable, then any commuting family of nonexpansive self-mappings of C has a common fixed point. This is a generalization of Browder’s common fixed point Theorem 1.

The existence of common fixed points of two maps was then historically linked to their commutativity. There was a conjecture stating that if two maps $f,g:[0,1]\to [0,1]$ are continuous and commute, they need to have a common fixed point. This hypothesis was refuted by Boyce [14] and Huneke [15]. However, the fact is true if some additional conditions are added on the underlying space X and the maps, as seen in Browder’s Thereom.

It is clear that commutativity and continuity are not necessary conditions for the existence of common fixed points, and current research on the topic tries to remove both conditions (see, for instance, [16,17]). A discussion and bibliography on this subject can be found in reference [18].

We avoid in this article the problem of the existence of common fixed points (except in the definition of fractal functions of Section 5), and focus on their search in case of existence. We give sufficient conditions on the space and the maps for the strong convergence of a new procedure to approximate a common fixed point of the mappings S and T (Section 2 and Section 3). Through two examples, the algorithm is illustrated in the cases of the approximation of a commom fixed point of two real maps and the search for a common solution of two integral equations of Fredholm type (Section 4).

In a subsequent section we give conditions for the existence of a common fractal function coming from two different Read–Bajraktarević operators (Section 5). Finally, we consider an application to the approximation of fixed points of the fractal convolution of two operators by means of the algorithm proposed (Section 6).

2. An Algorithm for the Approximation of Common Fixed Points of Quasi-Nonexpansive Operators

In this section, we propose an algorithm for the approximation of a common fixed point of two mappings. We start with a normed space X and two operators $S,T:C\to C$, where $C\subseteq X$ is nonempty, closed and convex. The algorithm to find a simultaneous critical point of S and T is given by the following iterative scheme:

$$\begin{array}{cc}\hfill z_n& \hfill =(1-{\gamma }_n)x_n+{\gamma }_{n}S{x}_n,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill y_n& \hfill =(1-{\beta }_n)x_n+{\beta }_n{z}_n,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill x_{n+1}& \hfill =(1-{\alpha }_n)y_n+{\alpha }_{n}T{y}_n,\hfill \end{array}$$

(7)

where ${\alpha }_n,{\beta }_n,{\gamma }_n\in [0,1]$ for $n\in \mathbb{N},$ and $x_0\in C.$ This method will be called common N-iteration, and it generalizes the N-iteration proposed in [8] for a single map. Throughout the paper, $F_S$ and $F_T$ will denote the set of fixed points of S and T, respectively. We propose the following definitions.

Definition 2.

A sequence $\left(x_n\right)\subseteq C$ has the common limit existence property (CLE) with respect to S and T if ${lim}_{n\to \infty }\left|\right|x_n-x^{*}\left|\right|=l\in \mathbb{R}$ for any $x^{*}\in F_S\cap F_T$, provided that $F_S\cap F_T\ne \varnothing .$

Remark 1.

This definition can be generalized to a finite number of mappings ( $T_1,T_2,\dots ,T_m$).

Definition 3.

A sequence $\left(x_n\right)\subseteq C$ has the approximate fixed point property (AF) with respect to S if ${lim}_{n\to \infty }\left|\right|x_n-S{x}_n\left|\right|=0.$

Definition 4.

Let X be a normed space. A map $U:C\subseteq X\to X$ is quasi-nonexpansive if $F_U\ne \varnothing$ and

$$\left|\right|Ux-x^{*}\left|\right|\le \left|\right|x-x^{*}\left|\right|,$$

(8)

for any $x\in C$ and $x^{*}\in F_U.$

Proposition 1.

Let X be a normed space and $C\subseteq X$ be nonempty, closed and convex. Let $S,T:C\to C$ be two quasi-nonexpansive operators such that $F_S\cap F_T\ne \varnothing$. The common N-iteration has the CLE property; that is to say, for $\left(x_n\right)$ defined as in (5), (6) and (7), ${lim}_{n\to \infty }\left|\right|x_n-x^{*}\left|\right|=l\in \mathbb{R}$ for any $x^{*}\in F_S\cap F_T$ and any $x_0\in C.$

Proof. 

Let $x^{*}\in F_S\cap F_T$ and $x_0\in C.$ According to (5),

$$\left|\right|z_n-x^{*}\left|\right|\le (1-{\gamma }_n)\left|\right|x_n-x^{*}\left|\right|+{\gamma }_n\left|\right|S{x}_n-x^{*}\left|\right|\le \left|\right|x_n-x^{*}\left|\right|.$$

(9)

In the same way, using (6),

$$\left|\right|y_n-x^{*}\left|\right|\le (1-{\beta }_n)\left|\right|y_n-x^{*}\left|\right|+{\beta }_n\left|\right|z_n-x^{*}\left|\right|\le \left|\right|x_n-x^{*}\left|\right|.$$

(10)

Finally,

$$\left|\right|x_{n+1}-x^{*}\left|\right|\le (1-{\alpha }_n)\left|\right|y_n-x^{*}\left|\right|+{\alpha }_n\left|\right|T{y}_n-x^{*}\left|\right|\le \left|\right|y_n-x^{*}\left|\right|\le \left|\right|x_n-x^{*}\left|\right|.$$

(11)

Consequently, the sequence $\left(\right||x_n-x^{*}|\left|\right)$ is non-increasing and bounded and thus ${lim}_{n\to \infty }\left|\right|x_n-x^{*}\left|\right|=l$ exists and it is real. □

The next lemma can be consulted in reference [19].

Lemma 1.

Let X be a uniformly convex Banach space, and let a sequence $\left({\lambda }_n\right)\subseteq X$ be such that there exist $p,q\in \mathbb{R}$ satisfying the condition $0<p\le {\lambda }_n\le q<1$ for all $n\in \mathbb{N}.$ Let $\left(x_n\right)$, $\left(y_n\right)$ be sequences of X such that ${lim\; sup}_{n\to \infty }\left|\right|x_n\left|\right|\le r$, ${lim\; sup}_{n\to \infty }\left|\right|y_n\left|\right|\le r$, and ${lim\; sup}_{n\to \infty }\left|\right|{\lambda }_n{x}_n+(1-{\lambda }_n)y_n\left|\right|=r$ for some $r\ge 0.$ Then, ${lim}_{n\to \infty }\left|\right|x_n-y_n\left|\right|=0.$

Theorem 2.

Let X be a uniformly convex Banach space and $C\subseteq X$ be nonempty, closed and convex. If $S,T:C\to C$ are two quasi-nonexpansive operators such that $F_S\cap F_T\ne \varnothing$ and $0<inf{\gamma }_n\le sup{\gamma }_n<1,$$0<inf{\alpha }_n\le sup{\alpha }_n<1,$ then

• The sequences $\left(x_n\right)$, $\left(y_n\right)$ and $\left(z_n\right)$ defined in (5), (6) and (7) have the CLE property.
• $\left(x_n\right)$ has the AF property with respect to S and $\left(y_n\right)$ has the AF property with respect to T.

Proof. 

Let $x^{*}\in F_S\cap F_T.$ By the previous proposition, $l:={lim}_{n\to \infty }\left|\right|x_n-x^{*}\left|\right|$ exists and it is real. According to (10),

$$\underset{n\to \infty }{lim\; sup}\left|\right|y_n-x^{*}\left|\right|\le l,$$

(12)

and

$$\underset{n\to \infty }{lim\; sup}\left|\right|T{y}_n-x^{*}\left|\right|\le \underset{n\to \infty }{lim\; sup}\left|\right|y_n-x^{*}\left|\right|\le l.$$

(13)

Using Lemma 1 and the following equality

$$l=\underset{n\to \infty }{lim}\left|\right|x_{n+1}-x^{*}\left|\right|=\underset{n\to \infty }{lim}\left|\right|(1-{\alpha }_n)(y_n-x^{*})+{\alpha }_n(T{y}_n-x^{*})\left|\right|$$

we have that

$$\underset{n\to \infty }{lim}\left|\right|y_n-T{y}_n\left|\right|=0.$$

Hence, $\left(y_n\right)$ has the AF property with respect to T. Again, by the third step of the algorithm,

$$\left|\right|x_{n+1}-x^{*}\left|\right|\le \left|\right|y_n-x^{*}\left|\right|+{\alpha }_n\left|\right|T{y}_n-y_n\left|\right|.$$

Then,

$$l\le \underset{n\to \infty }{lim\; inf}\left|\right|y_n-x^{*}\left|\right|.$$

(14)

By (12) and (14), $l={lim}_{n\to \infty }\left|\right|y_n-x^{*}\left|\right|.$ Let us consider now that

$$\left|\right|y_n-x^{*}\left|\right|\le (1-{\beta }_n)\left|\right|x_n-x^{*}\left|\right|+{\beta }_n\left|\right|z_n-x^{*}\left|\right|,$$

$$\left|\right|y_n-x^{*}\left|\right|-\left|\right|x_n-x^{*}\left|\right|\le {\beta }_n\left(\right||z_n-x^{*}\left|\right|-\left|\right|x_n-x^{*}\left|\right|)\le \left|\right|z_n-x^{*}\left|\right|-\left|\right|x_n-x^{*}\left|\right|.$$

Then,

$$\left|\right|y_n-x^{*}\left|\right|\le \left|\right|z_n-x^{*}\left|\right|.$$

Consequently,

$$l=\underset{n\to \infty }{lim}\left|\right|y_n-x^{*}\left|\right|\le \underset{n\to \infty }{lim\; inf}\left|\right|z_n-x^{*}\left|\right|.$$

By (9), ${lim\; sup}_{n\to \infty }\left|\right|z_n-x^{*}\left|\right|\le l$ and hence $l={lim}_{n\to \infty }\left|\right|z_n-x^{*}\left|\right|.$ Consequently, the sequences $\left(x_n\right)$, $\left(y_n\right)$ and $\left(z_n\right)$ have the CLE property, with the same limit:

$$\underset{n\to \infty }{lim}\left|\right|x_n-x^{*}\left|\right|=\underset{n\to \infty }{lim}\left|\right|y_n-x^{*}\left|\right|=\underset{n\to \infty }{lim}\left|\right|z_n-x^{*}\left|\right|,$$

for $x^{*}\in F_S\cap F_T.$ The quasi-nonexpansiveness of S implies that

$$\underset{n\to \infty }{lim\; sup}\left|\right|S{x}_n-x^{*}\left|\right|\le l.$$

The equality

$$l=\underset{n\to \infty }{lim}\left|\right|z_n-x^{*}\left|\right|=\underset{n\to \infty }{lim}\left|\right|(1-{\gamma }_n)(x_n-x^{*})+{\gamma }_n(S{x}_n-x^{*})\left|\right|,$$

along with the inequality ${lim\; sup}_{n\to \infty }\left|\right|S{x}_n-x^{*}\left|\right|\le l$ imply, by Lemma 1, that

$$\underset{n\to \infty }{lim}\left|\right|x_n-S{x}_n\left|\right|=0,$$

and $\left(x_n\right)$ has the AF property with respect to $S.$ □

According to Proposition 1 and Theorem 2, the approximation properties of the common N-iteration are true also for the two-step common N-iteration, given by the following recurrence:

$$\begin{array}{cc}\hfill y_n& =(1-{\gamma }_n)x_n+{\gamma }_{n}S{x}_n,\end{array}$$

(15)

$$\begin{array}{cc}\hfill x_{n+1}& =(1-{\alpha }_n)y_n+{\alpha }_{n}T{y}_n.\end{array}$$

(16)

where $0<inf{\gamma }_n\le sup{\gamma }_n<1$ and $0<inf{\alpha }_n\le sup{\alpha }_n<1$ (taking ${\beta }_n=1$ for all n in (6)).

This iterative scheme can be generalized to a finite number of operators with common fixed points, in order to provide the following m-step common fixed point N-algorithm for the mappings $T_1,T_2,\dots ,T_m:C\to C$ such that ${\cap }_{i=1}^m{F}_{T_i}\ne \varnothing$:

$$\begin{array}{cc}\hfill x_n^1& =(1-c_n^1)x_n+c_n^1{T}_1{x}_n,\end{array}$$

(17)

$$\begin{array}{cc}\hfill x_n^2& =(1-c_n^2)x_n^1+c_n^2{T}_2{x}_n^1,\end{array}$$

(18)

$$\begin{array}{cc}\hfill \dots & \dots \end{array}$$

(19)

$$\begin{array}{cc}\hfill x_n^i& =(1-c_n^i)x_n^{i-1}+c_n^i{T}_i{x}_n^{i-1},\end{array}$$

(20)

$$\begin{array}{cc}\hfill \dots & \dots \end{array}$$

(21)

$$\begin{array}{cc}\hfill x_{n+1}=x_n^m& =(1-c_n^m)x_n^{m-1}+c_n^m{T}_m{x}_n^{m-1},\end{array}$$

(22)

where $0<{inf}_n{c}_n^i\le {sup}_n{c}_n^i<1$ for all $n\ge 1$, $i=1,\dots ,m,$ and $x_0\in C.$

3. Convergence Theorems for the Common N-Iteration

Throughout this section, we will assume a normed space X, $C\subseteq X,$$C\ne \varnothing ,$ and $S,T:C\to C,$ such that $F_S\cap F_T\ne \varnothing .$ We will consider the common N-iteration given by (5), (6) and (7) with the conditions for ${\alpha }_n$ and ${\gamma }_n$ given in Theorem 2.

Remark 2.

The notation $Id$ will represent the identity operator.

Theorem 3.

Let X be a uniformly convex Banach space and $C\subseteq X$ be compact and convex. If $S,T:C\to C$ are quasi-nonexpansive and closed, then the common N-iteration described converges strongly to a common fixed point of S and $T$.

Proof. 

Since C is compact, the sequence $\left(y_n\right)$ of the iteration has a convergent subsequence. Let ${lim}_{j\to \infty }{y}_{n_j}=\overline{x}\in C.$ Since $\left(y_n\right)$ has the AF property with respect to T, then $\left|\right|y_{n_j}-T{y}_{n_j}\left|\right|$ tends to zero. Since $Id-T$ is closed, then $0=(Id-T)\overline{x}$, and $\overline{x}\in F_T.$

According to the third step of the algorithm,

$$\left|\right|x_{n_j+1}-\overline{x}\left|\right|=\left|\right|(1-{\alpha }_{n_j})(y_{n_j}-\overline{x})+{\alpha }_{n_j}(T{y}_{n_j}-\overline{x})\left|\right|\le \left|\right|y_{n_j}-\overline{x}\left|\right|\to 0.$$

Consequently, ${lim}_{j\to \infty }{x}_{n_j+1}=\overline{x}$.

Since $Id-S$ is closed and $\left(x_n\right)$ has the AF property with respect to S, then $0=(Id-S)\overline{x},$ and $\overline{x}\in F_S\cap F_T.$ The CLE property of $\left(x_n\right)$ implies that ${lim}_{n\to \infty }\left|\right|x_n-\overline{x}\left|\right|=0.$ □

Corollary 1.

Let X be a uniformly convex Banach space, and let $C\subseteq X$ be compact andconvex. If $S,T:C\to C$ are nonexpansive, then the common N-iteration described converges strongly to a common fixed point of S and $T.$

Proof. 

A nonexpansive mapping with a fixed point is quasi-nonexpansive and continuous, and we have the hypotheses of Theorem 3. □

Definition 5.

Let X be a normed space. A mapping $T:X\to X$, such that there exists $B\ge 0$ satisfying for any $f,g\in X$ the following inequality

$$\left|\right|Tf-Tg\left|\right|\le \left|\right|f-g\left|\right|+Bmin\left\{\right||f-Tf||,||g-Tg|\left|\right\},$$

(23)

is a nonexpansive partial contractivity.

For $B=0$, we have a nonexpansive mapping.

Corollary 2.

Let X be a uniformly convex Banach space, and let $C\subseteq X$ be compact andconvex. If $S,T:C\to C$ are closed nonexpansive partial contractivities, then the common N-iteration described converges strongly to a common fixed point of S and $T.$

Proof. 

A nonexpansive partial contractivity with a fixed point is quasi-nonexpansive, and we are in the conditions of Theorem 3. □

Definition 6.

Let X be a normed space, and $C\subseteq X$. A map $T:C\to X$ is demicompact if a bounded sequence $\left(x_n\right)\subseteq C$, such that $(T{x}_n-x_n)$ is convergent, has a convergent subsequence. If a sequence $\left(x_n\right)\subseteq C$, such that $(T{x}_n-x_n)$ is convergent to zero, has a convergent subsequence $\left(x_{n_j}\right)$, then T is demicompact at zero.

Remark 3.

According to this definition, if T is demicompact at zero, $\left(x_n\right)$ is bounded and it has the AF property with respect to T, then there exists a convergent subsequence $\left(x_{n_j}\right).$

Proposition 2.

Let X be a uniformly convex Banach space, and let $C\subseteq X$ be closed andconvex. If $S,T:C\to C$ are quasi-nonexpansive and closed, and T is demicompact at zero, then the common N-iteration described converges strongly to a common fixed point of S and $T.$

Proof. 

The CLE property of $\left(y_n\right)$ implies that the sequence $\left(y_n\right)$ is bounded. The AF property of $\left(y_n\right)$ with respect to T implies that $\left|\right|y_n-T{y}_n\left|\right|$ tends to zero. As T is demicompact, there is a convergent subsequence $\left(y_{m_k}\right)$. Let $x^{*}:={lim}_{n\to \infty }{y}_{m_k}$. Then, $(Id-T)y_{m_k}\to 0.$ Since T is closed, then $0=(Id-T)x^{*}$, and $x^{*}\in F_T.$

Regarding $\left(x_n\right)$, according to the last step of the algorithm,

$$\left|\right|x_{m_k+1}-x^{*}\left|\right|=\left|\right|(1-{\alpha }_{m_k})(y_{m_k}-x^{*})+{\alpha }_{m_k}(T{y}_{m_k}-x^{*})\left|\right|\le \left|\right|y_{m_k}-x^{*}\left|\right|\to 0.$$

As $(Id-S)x_{m_k+1}$ tends to zero due to the AF property of $\left(x_n\right)$ and $Id-S$ is closed, then $0=(Id-S)x^{*}$ and $x^{*}\in F_S\cap F_T.$

The CLE property of $\left(x_n\right)$ implies that the common N-iteration converges strongly to $x^{*}$ for any $x_0\in C.$ □

Corollary 3.

Let X be a uniformly convex Banach space, and let $C\subseteq X$ be closed and convex. If $S,T:C\to C$ are nonexpansive and T is demicompact at zero, then the common N-iteration described converges strongly to a common fixed point of S and $T.$

Corollary 4.

Let X be a uniformly convex Banach space, and let $C\subseteq X$ be closed andconvex. If $S,T:C\to C$ are closed nonexpansive partial contractivities and T is demicompact at zero, then the common N-iteration described converges strongly to a common fixed point of S and $T.$

Definition 7.

Let $X,Y$ be Banach spaces. Then, $S:X\to Y$ is demiclosed (at $z\in Y$) if $y_n\rightharpoonup y$ and $S{y}_n\to z$ imply that $Sy=z.$

Remark 4.

The symbol ⇀ denotes the weak convergence of a sequence.

The following demiclosedness principle for nonexpansive mappings can be consulted in reference [20], Theorem 10.4:

Theorem 4.

Let X be a uniformly convex Banach space, C a nonempty, closed and convex subset of X and $T:C\to X$ a nonexpansive mapping. Then, $Id-T$ is demiclosed on C.

Definition 8.

Let $X,Y$ be Banach spaces. Then, $S:X\to Y$ is completely continuous if $x_n\rightharpoonup x$ implies that $S{x}_n\to Sx.$

Remark 5.

A completely continuous mapping is demiclosed.

Proposition 3.

Let X be a uniformly convex Banach space, and let $C\subseteq X$ be bounded, closed and convex. If $S,T:C\to C$ are nonexpansive and T is completely continuous, then the common N-iteration described converges strongly to a common fixed point of S and $T.$

Proof. 

Since C is bounded, closed and convex in a uniformly convex space, there exists a weakly convergent subsequence $\left(y_{n_j}\right)$ of $\left(y_n\right)$. That is to say, $y_{n_j}\rightharpoonup \overline{x}.$ The AF property of $\left(y_n\right)$ with respect to T implies that $\left|\right|y_{n_j}-T{y}_{n_j}\left|\right|$ tends to zero. According to Theorem 4, $Id-T$ is demiclosed and this implies that $0=(Id-T)\overline{x}$, that is to say, $\overline{x}\in F_T.$

Since T is completely continuous, ${lim}_{j\to \infty }T{y}_{n_j}=T\overline{x}=\overline{x}$. Then,

$$y_{n_j}=(y_{n_j}-T{y}_{n_j})+T{y}_{n_j}\to \overline{x}.$$

$$\left|\right|x_{n_j+1}-\overline{x}\left|\right|\le \left|\right|(1-{\alpha }_{n_j})(y_{n_j}-\overline{x})+{\alpha }_{n_j}(S{y}_{n_j}-\overline{x})\left|\right|\le \left|\right|y_{n_j}-\overline{x}\left|\right|\to 0.$$

Since $\left((Id-S)x_{n_j+1}\right)$ tends to zero due to the AF property of $\left(x_n\right)$ with respect to S, and $Id-S$ is continuous, then $0=(Id-S)\overline{x}$ and $\overline{x}\in F_S\cap F_T.$

The CLE property of $\left(x_n\right)$ implies its convergence to $\overline{x}.$ □

Remark 6.

All the results obtained in this section are applicable to the case $S=T$, and the usual N-algorithm for a single map defined in reference [8].

4. Some Applications of the Common N-Iteration

In this section, we present two examples of the application of the common N-iteration.

4.1. Approximation of a Common Fixed Point of Two Mappings

The maps $S,T:[0,1]\to [0,1]$ given by $S\left(x\right)={\left(\sqrt{1-x^{2/3}}\right)}^3$ and $T\left(x\right)=x$ have a common fixed point at $x^{*}\simeq 0.353553.$ The common N-iteration with all the scalars equal to $1/2$ has been used to approach this point. Namely, we have computed the successive values of $x_n$ by means of the iterative scheme:

$$z_n={\displaystyle \frac{x_n+S{x}_n}{2}},$$

$$y_n={\displaystyle \frac{x_n+z_n}{2}},$$

$$x_{n+1}={\displaystyle \frac{y_n+T{y}_n}{2}}.$$

The abscissas $x_0=0.1$ and $x_0=1$ have been chosen as starting points of two performances of the algorithm. The subsequent errors, computed as $|x_n-x^{*}|,$ are collected in Table 1. The left part gathers the errors for $x_0=0.1$ and the right part displays the case $x_0=1.$

Table 1. Approximation errors of the first values given by the N-algorithm for a common fixed point of two maps starting at $x_0=0.1$ (left) and $x_0=1$ (right).

Iteration	Error	Iteration	Error
0	0.25355	0	0.64645
1	0.10482	1	0.39645
2	0.04951	2	0.22717
3	0.02415	3	0.12388
4	0.01193	4	0.06521
5	0.00593	5	0.03355
6	0.00296	6	0.01703
7	0.00148	7	0.00858
8	0.00074	8	0.00431
9	0.00037	9	0.00216
10	0.00018	10	0.00108

4.2. Search for a Common Solution of Two Fredholm Integral Equations of the Second Kind

Let us consider the following integral equations of Fredholm type:

$$f\left(x\right)=h\left(x\right)+{\int }_a^{b}K(x,y)f\left(y\right)dy,$$

$$g\left(x\right)=h^{\prime }\left(x\right)+{\int }_a^b{K}^{\prime }(x,y)g\left(y\right)dy,$$

where we look for a common solution in ${\mathcal{L}}^2\left([a,b]\right)$. This problem is equivalent to the search for a common fixed point of the operators $S,T:{\mathcal{L}}^2\left([a,b]\right)\to {\mathcal{L}}^2\left([a,b]\right)$ defined as

$$Su\left(x\right)=h\left(x\right)+{\int }_a^{b}K(x,y)u\left(y\right)dy,$$

$$Tu\left(x\right)=h^{\prime }\left(x\right)+{\int }_a^b{K}^{\prime }(x,y)u\left(y\right)dy.$$

It is well known that if K and $K^{\prime }$ are such that $K,K^{\prime }\in {\mathcal{L}}^2(I\times I)$, where $I=[a,b]$, then the operators S and T are linear and compact and consequently demicompact. They are nonexpansive if

$${\int }_{I\times I}\left|K(x,y)\right|dxdy\le 1,$$

$${\int }_{I\times I}\left|K^{\prime }(x,y)\right|dxdy\le 1.$$

The following integral equations:

$$f\left(x\right)=(e^x-1)+{\int }_0^{1}yf\left(y\right)dy,$$

$$f\left(x\right)=(e^x+1-e)+{\int }_0^{1}f\left(y\right)dy.$$

have a common exact solution at $f\left(x\right)=e^x.$ Let us apply the two-step common N-algorithm ( ${\beta }_n=0$), and let us choose ${\alpha }_n={\gamma }_n=1/2$ for all $n\ge 1.$ Thus, the N-iteration is given by the following scheme:

$$g_n\left(x\right)=\left(f_n\left(x\right)+(e^x-1)+{\int }_0^{1}y{f}_n\left(y\right)dy\right)/2,$$

$$f_{n+1}\left(x\right)=\left(g_n\left(x\right)+(e^x+1-e)+{\int }_0^1{g}_n\left(y\right)dy\right)/2.$$

Let the starting function be $f_0\left(x\right)=x.$ The error of every approximation is computed as

$$Er{r}_n={\left({\int }_0^1{|f_n\left(x\right)-f\left(x\right)|}^{2}dx\right)}^{1/2},$$

where $f\left(x\right)$ is the exact solution. Table 2 collects the errors from the first to the twentieth iteration. Figure 1 represents the exact common solution (in yellow) along with the first, fourth, seventh and tenth approximations, respectively (in blue).

Table 2. Errors of the first twenty approximations given by the two-step N-algorithm for a common solution of two Fredholm integral equations.

Iteration	Error	Iteration	Error
1	0.94392	11	0.05539
2	0.71417	12	0.04041
3	0.53734	13	0.03031
4	0.40345	14	0.02273
5	0.30270	15	0.01705
6	0.22705	16	0.01279
7	0.17030	17	0.00960
8	0.12772	18	0.00719
9	0.09579	19	0.00539
10	0.07184	20	0.00405

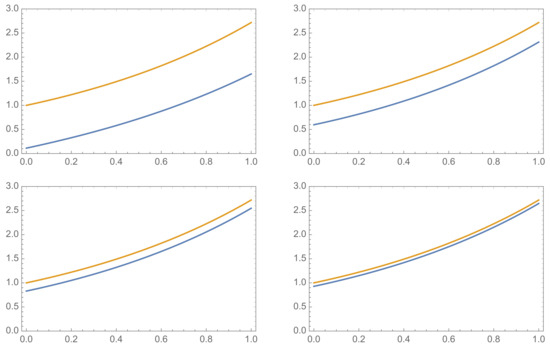
Figure 1. From upper left to bottom right, exact solution (yellow) along with the first, fourth, seventh and tenth approximations ( $f_1,$$f_4,$$f_7,$$f_{10}$) (blue).

5. Fractal Functions as Common Fixed Points of Two Different Operators

In this section, we find a fractal function as a common fixed point of two different Read–Bajraktarević operators.

According to the formalism of these mappings, we consider a compact real interval $I=[a,b]$, and a partition of it $\Delta :a=t_0<t_1<t_2\dots <t_M=b.$ Let us consider $I_m=[t_{m-1},t_m)$, for $m=1,2,\dots M-1$ and $I_M=[t_{M-1},t_M]$ and define $L_m:I\to I_m$ such that $L_m\left(t\right)=a_{m}t+b_m$ and

$$L_m\left(t_0\right)=t_{m-1},L_m\left(t_M\right)=t_m.$$

(24)

Let $S_m,T_m$ be mappings on the space ${\mathcal{L}}^p\left(I\right)$, that is to say, $S_m,T_m:{\mathcal{L}}^p\left(I\right)\to {\mathcal{L}}^p\left(I\right),$, and let us assume that $1<p<\infty .$ Let us define the operators of Read–Bajraktarević type $S,T:{\mathcal{L}}^p\left(I\right)\to {\mathcal{L}}^p\left(I\right)$ given by

$$Sf\left(t\right)=S_m\left(f\right)\circ L_m^{-1}\left(t\right),$$

(25)

$$Tf\left(t\right)=T_m\left(f\right)\circ L_m^{-1}\left(t\right),$$

(26)

for $t\in I_m.$ The next result gives sufficient conditions for the existence of a fractal function as a common fixed point of S and T. Let $\left|\right|·{\left|\right|}_p$ denote the norm of the space ${\mathcal{L}}^p\left(I\right)$ for $1<p<\infty .$

Theorem 5.

Let the operators $S_m,T_m$ meet the following conditions for $m=1,2,\dots ,M$:

1. 

There exists $R>0$ satisfying $\left|\right|S_{m}f{\left|\right|}_p\le R$ and $\left|\right|T_{m}f{\left|\right|}_p\le R$ for any $f\in {\mathcal{L}}^p\left(I\right)$ such that ${\left|\right|f\left|\right|}_p\le R.$

2. 

$S_m$ and $T_m$ are nonexpansive.

3. 

$T_m\left({\sum }_{i=1}^M{\kappa }_{I_i}(·)S_i\left(f\right)\circ L_i^{-1}(·)\right)=S_m\left({\sum }_{i=1}^M{\kappa }_{I_i}(·)T_i\left(f\right)\circ L_i^{-1}(·)\right),$ where ${\kappa }_{I_i}$ is the indicator map of $I_i$ or, equivalently, $S_m\left(T_{j}f\circ L_j^{-1}(·)\right)=T_m\left(S_{j}f\circ L_j^{-1}(·)\right)$ where $L_j^{-1}:I_j\to I,$ for $j=1,\dots ,M.$

Then, the operators S and T defined in (25) and (26) commute, they are nonexpansive and there exists a fractal function $\overline{f}\in {\mathcal{L}}^p\left(I\right)$ such that $\overline{f}$ is a common fixed point of S and T. This function can be approached using the common N-iteration of the maps S and T whenever $0<inf{\alpha }_n\le sup{\alpha }_n<1$ and $0<inf{\gamma }_n\le sup{\gamma }_n<1.$

Proof. 

The Hypothesis (1) of the theorem enables the restriction of the domain and codomain of the operators S and T to the closed ball with a center in the null function $f_0$ and radius $R,$$\overline{B}(f_0,R)\subseteq {\mathcal{L}}^p\left(I\right)$ since

$${\left|\right|Sf\left|\right|}_p\le R,$$

$${\left|\right|Tf\left|\right|}_p\le R,$$

for $f\in \overline{B}(f_0,R).$ Thus, S and T can be defined from and onto the bounded, closed and convex subset $\overline{B}(f_0,R)$ of the uniformly convex Banach space ${\mathcal{L}}^p\left(I\right)$. It is easy to check that S and T are nonexpansive, since

$$\left|\right|Sf-S{f}^{\prime }{\left|\right|}_p\le {\left(\sum _{m=1}^M{a}_m\right)}^{1/p}\left|\right|S_{m}f-S_m{f}^{\prime }{\left|\right|}_p\le \left|\right|f-f^{\prime }{\left|\right|}_p,$$

$$\left|\right|Tf-T{f}^{\prime }{\left|\right|}_p\le {\left(\sum _{m=1}^M{a}_m\right)}^{1/p}\left|\right|T_{m}f-T_m{f}^{\prime }{\left|\right|}_p\le \left|\right|f-f^{\prime }{\left|\right|}_p,$$

and ${\sum }_{m=1}^M{a}_m=1$ due to conditions (24). Moreover,

$$(T\circ S)f\left(L_{m}t\right)=T\left(Sf\right)\left(L_{m}t\right)=T_m\left(Sf\right)\left(t\right),$$

and

$$(S\circ T)f\left(L_{m}t\right)=S\left(Tf\right)\left(L_{m}t\right)=S_m\left(Tf\right)\left(t\right),$$

where

$$T_m\left(Sf\right)=T_m\left(\sum _{i=1}^M{\kappa }_{I_i}(·)S_i\left(f\right)\circ L_i^{-1}(·)\right)=T_m\left(S_{j}f\circ L_j^{-1}(·)\right)$$

and

$$S_m\left(Tf\right)=S_m\left(\sum _{i=1}^M{\kappa }_{I_i}(·)T_i\left(f\right)\circ L_i^{-1}(·)\right)=S_m\left(T_{j}f\circ L_j^{-1}(·)\right)$$

where $L_j^{-1}:I_j\to I.$ The last two equations are equal due to the Hypothesis (3) of the theorem, and, consequently, $S\circ T=T\circ S.$ Then, we have the hypotheses of Browder’s Theorem 1 for $C=\overline{B}(f_0,R)$, and S and T have a common fixed point $\overline{f}\in \overline{B}(f_0,R)\subseteq {\mathcal{L}}^p\left(I\right).$ □

Example 2.

The operators defined as $S_{m}f=c_{m}f$, $T_{m}f=c_m^{\prime }f$ for $c_m,c_m^{\prime }\in \mathbb{R},$$|c_m|,|c_m^{\prime }|\le 1,$ and $c_m{c}_j^{\prime }=c_m^{\prime }{c}_j$ for $m,j=1,2,\dots ,M,$ satisfy the hypotheses required.

6. Fixed Points of the Fractal Convolution of Several Types of Operators

In this section, we consider a special type of operators defined in (26),

$$Tf\left(t\right)=T_m\left(f\right)\circ L_m^{-1}\left(t\right),$$

(27)

for $t\in I_m$ and

$$T_{m}f\left(t\right)=u\circ L_m\left(t\right)+k_m(f\left(t\right)-v\left(t\right)),$$

where $u,v\in {\mathcal{L}}^p\left(I\right)$ and $k_m\in \mathbb{R}$ are constant and such that $|k_m|<1$ for $m=1,2,\dots ,M.$ In this case, the operator T is a contraction since

$$\left|\right|Tf-T{f}^{\prime }{\left|\right|}_p\le k\left|\right|f-f^{\prime }{\left|\right|}_p,$$

for any $f,f^{\prime }\in {\mathcal{L}}^p\left(I\right)$ and $k=max\left\{\right|k_m\left|\right\}<1.$ Then, T has a fixed point, usually denoted as $u^{\alpha }$, called $\alpha$-fractal function in previous papers (see, for instance, [21] for the two-dimensional case). In other articles (see, for instance, [22]), $u^{\alpha }$ has been considered as the result of a binary internal operation in ${\mathcal{L}}^p\left(I\right),$, that is to say,

$$u^{\alpha }=u\ast v.$$

The operation ∗ has been called “fractal convolution”. This operation has useful properties such as idempotency, namely, $u\ast u=u$ for any $u\in {\mathcal{L}}^p\left(I\right).$ Other features of the fractal convolution can be consulted in reference [22]. From this background, we have also defined a fractal convolution between operators on the same space defined, for $V,W:{\mathcal{L}}^p\left(I\right)\to {\mathcal{L}}^p\left(I\right)$, as

$$(V\ast W)f=\left(Vf\right)\ast \left(Wf\right),$$

for $f\in {\mathcal{L}}^p\left(I\right).$

The fractal convolution of operators also has the property of idempotency, that is to say,

$$V\ast V=V.$$

A straightforward consequence of this characteristic is that, if $F_V$ and $F_W$ are the sets of fixed points of V and $W,$ respectively, then

$$(F_V\cap F_W)\subseteq F_{V\ast W}.$$

Namely, a common fixed point of V and W is a fixed point of $V\ast W.$

In the following, we assume that V and W are such that $F_V\cap F_W\ne \varnothing ,$ and $V,W:C\to C,$ where $C\subseteq {\mathcal{L}}^p\left(I\right)$ or $C\subseteq {\mathcal{B}}^p\left(I\right),$ where ${\mathcal{B}}^p\left(I\right)$ denotes the Bochner space of p-integrable maps $f:I\to B$, with B being a uniformly convex Banach space.

Let us consider $C\ne \varnothing$ and $1<p<\infty .$ For the common N-iteration algorithm, we will assume the following conditions on the scalars: $0<inf{\alpha }_n\le sup{\alpha }_n<1$ and $0<inf{\gamma }_n\le sup{\gamma }_n<1.$

The results obtained in previous sections for the common fixed points of two mappings and their approximation are applicable to the search for fixed points of $V\ast W.$ A summary of these results, applied to $V\ast W$, is the following:

• If C is compact and convex and $V,W$ are quasi-nonexpansive and closed, then the common N-iteration converges strongly to a fixed point of $V\ast W.$
• If C is compact and convex and $V,W$ are nonexpansive, then the common N-iteration converges strongly to a fixed point of $V\ast W.$
• If C is compact and convex and $V,W$ are closed nonexpansive partial contractivities, then the common N-iteration converges strongly to a fixed point of $V\ast W.$
• If C is closed and convex, $V,W$ are quasi-nonexpansive and closed and W is demicompact at zero, then the common N-iteration converges strongly to a fixed point of $V\ast W.$
• If C is closed and convex, $V,W$ are nonexpansive and W is demicompact at zero, then the common N-iteration converges strongly to a fixed point of $V\ast W.$
• If C is closed and convex, $V,W$ are closed nonexpansive partial contractivities and W is demicompact at zero, then the common N-iteration converges strongly to a fixed point of $V\ast W.$
• If C is bounded, closed and convex, $V,W$ are nonexpansive and W is completely continuous, then the common N-iteration converges strongly to a fixed point of $V\ast W.$

7. Conclusions

This article presents an iterative method to find common fixed points of two maps $S,T:C\to C,$ where C is a nonempty, closed and convex subset of a normed space X. The recurrence is called common N-iteration, and it is given by the recurrence:

$$\begin{array}{cc}\hfill z_n& \hfill =(1-{\gamma }_n)x_n+{\gamma }_{n}S{x}_n,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill y_n& \hfill =(1-{\beta }_n)x_n+{\beta }_n{z}_n,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill x_{n+1}& \hfill =(1-{\alpha }_n)y_n+{\alpha }_{n}T{y}_n.\hfill \end{array}$$

(30)

for ${\alpha }_n,{\beta }_n,{\gamma }_n\in [0,1]$ and $x_0\in C.$

It has been proved that $\left(x_n\right)$, $\left(y_n\right)$ and $\left(z_n\right)$ have the CLE property, $\left(x_n\right)$ has the AF property with respect to S, and $\left(y_n\right)$ has the AF property with respect to T. This article provides sufficient conditions on X, C and the maps S and T for the strong convergence of the algorithm to a common fixed point of S and T, in case of existence.

The procedure has been applied to the approximation of a common fixed point of two maps defined in the interval $[0,1]$ and a common solution of two Fredholm integral equations of the second kind.

This paper has proved the existence of a fractal function that is a common fixed point of two different nonexpansive Read–Bajraktarević operators defined on ${\mathcal{L}}^p\left(I\right)$ or ${\mathcal{B}}^p\left(I\right).$ In the last section, the article gives sufficient conditions for the convergence of the algorithm to a fixed point of a fractal convolution of operators $V\ast W$, where $V,W:{\mathcal{L}}^p\left(I\right)\to {\mathcal{L}}^p\left(I\right)$ or $V,W:{\mathcal{B}}^p\left(I\right)\to {\mathcal{B}}^p\left(I\right).$ In both cases, the range of values of p is $1<p<\infty .$