Topological Degree for Operators of Class (S)₊ with Set-Valued Perturbations and Its New Applications

Abstract

We investigate the topological degree for generalized monotone operators of class ${\left(S\right)}_{+}$ with compact set-valued perturbations. It is assumed that perturbations can be represented as the composition of a continuous single-valued mapping and an upper semicontinuous set-valued mapping with aspheric values. This allows us to extend the standard degree theory for convex-valued operators to set-valued mappings whose values can have complex geometry. Several theoretical aspects concerning the definition and main properties of the topological degree for such set-valued mappings are discussed. In particular, it is shown that the introduced degree has the homotopy invariance property and can be used as a convenient tool in checking the existence of solutions to corresponding operator inclusions. To illustrate the applicability of our approach to studying models of real processes, we consider an optimal feedback control problem for the steady-state internal flow of a generalized Newtonian fluid in a 3D (or 2D) bounded domain with a Lipschitz boundary. By using the proposed topological degree method, we prove the solvability of this problem in the weak formulation.

1. Introduction

Fixed point theory is a very important and emerging scientific branch, which lies at the intersection of pure and applied mathematics [1,2,3,4,5,6,7,8]. It provides effective methods for solving numerous complex (both linear and nonlinear) problems arising in diverse fields such as physics, chemistry, biology, engineering, game theory, and mathematical economics. An interesting deep connection has been discovered between fixed point theory and fractal geometry [9,10,11,12,13,14,15,16,17]. In particular, fractals, which are intuitively understood as highly irregular sets with fractional dimension and self-similarity properties, can be realized as fixed points of special operators on the space of compact subsets of a metric-type space. Using the formalism of iterated function systems, one can provide a way of constructing such operators and a scheme for the approximation of their fixed points [18,19,20], as well as obtain sharp results on the Hausdorff dimension in terms of fractal structures [21].

A natural generalization of the fixed point problem is the coincidence problem. Recall that for given nonempty sets X, Y and mappings $\varphi ,\psi :X\to Y$, a point $x\in X$ satisfying the equality $\varphi \left(x\right)=\psi \left(x\right)$ is said to be a coincidence point of the mappings $\varphi$ and $\psi$ in the set X. Clearly, if $\varphi$ (or $\psi$) is a one-to-one operator, then finding a coincidence point is reduced to finding a fixed point of the mapping ${\varphi }^{-1}\circ \psi$ (or ${\psi }^{-1}\circ \varphi$, respectively). However, in applications, it is very often needed to deal with mappings that are not bijective. Interesting results from the coincidence theory (the study of coincidence points) can be found in the works [22,23,24,25,26,27,28,29].

The further development of this theory is related to the consideration of the case where one of the mappings in a pair $(\varphi ,\psi )$ is set-valued. For the sake of being definite, let the single-valued mapping $\psi :X\to Y$ be replaced by a set-valued mapping $\Psi :X⊸Y$. The passing from the equation $\varphi \left(x\right)=\psi \left(x\right)$ to the inclusion $\varphi \left(x\right)\in \Psi \left(x\right)$ produces significant difficulties in handling the corresponding “set-valued” coincidence problem. To overcome these difficulties, various coincidence point principles were developed by introducing and applying the topological degree for different classes of set-valued perturbations of single-valued operators [30,31,32,33,34,35,36,37,38]. The proposed approaches and abstract results are successfully used to solve complex problems arising in various real-world applications (see, for example, [39,40,41]).

The present paper continues and extends the results of the PhD thesis [37] of the first author, in which a variant of the topological degree theory for set-valued perturbations of monotone-like operators between a reflexive Banach space and its dual has been proposed. Our aim is to discuss the definition, some properties and new applications of the topological degree for set-valued mappings that can be represented in the form $T-\Phi$, where T is a single-valued ${\left(S\right)}_{+}$-operator [42,43,44], while $\Phi$ is a compact set-valued operator with not necessarily convex values. More precisely, unlike conventional approaches that require the convexity values property for the definition of topological degree [25,45,46,47], we use set-valued operators with aspheric values. This allows us to consider set-valued mappings with values having complex geometry, in particular, with values that are fractal-type contractible sets. We present the construction of the degree mapping, which is based on the principle of continuous single-valued approximations [26,47] and essentially uses the monotonicity arguments that are appropriate for ${\left(S\right)}_{+}$-operators [48]. It is shown that the introduced topological degree can be used as a tool for checking the existence of a solution to the inclusion $T\left(x\right)\in \Phi \left(x\right)$.

The remainder of this paper is organized as follows. The next section is entirely devoted to the necessary preliminaries. In Section 3, we construct the topological degree for ${\left(S\right)}_{+}$-operators with compact set-valued perturbations (Definition 13) and show that this degree is well defined. Section 4 is devoted to studying the main properties of the introduced degree (Theorems 1–3) and obtaining sufficient conditions for the existence of solutions to the inclusion $T\left(x\right)\in \Phi \left(x\right)$ (Theorem 4). Finally, in Section 5, we apply our abstract results to the analysis of the solvability of an optimal control problem for a model of incompressible fluid dynamics with shear-dependent viscosity (Theorem 6).

2. Preliminaries

This section provides the notions and statements that will be needed to obtain our main results.

2.1. Topological Degree for Operators of Class ${\left(S\right)}_{+}$

Let X be a real reflexive Banach space. $X^{*}$ denotes its dual space.

For any $x\in X$ and $\ell \in X^{*}$, by ${⟨\ell ,x⟩}_{X^{*}\times X}$ we denote the value of the functional ℓ on the element x. For brevity, we will sometimes write $⟨\ell ,x⟩$ instead of ${⟨\ell ,x⟩}_{X^{*}\times X}$ when it is clear from the context that a duality pairing is meant.

The symbol → (⇀, resp.) denotes strong (weak, resp.) convergence.

Let $\mathcal{D}$ be an arbitrary open set in X and let $\overline{\mathcal{D}}$ be its closure.

Definition 1. 

An operator $A:\overline{\mathcal{D}}\to X^{*}$ is called strong-to-weak continuous (or demicontinuous) on $\overline{\mathcal{D}}$, if, for any sequence ${\left\{u_n\right\}}_{n=1}^{\infty }\subset \overline{\mathcal{D}}$ and $u_0\in \overline{\mathcal{D}}$, from $u_n\to u_0$ in X it follows that $A\left(u_n\right)\rightharpoonup A\left(u_0\right)$ in $X^{*}$ as $n\to \infty$.

Definition 2. 

An operator $B:\overline{\mathcal{D}}\to X^{*}$ is called weak-to-strong continuous (or completely continuous) on $\overline{\mathcal{D}}$, if, for any sequence ${\left\{u_n\right\}}_{n=1}^{\infty }\subset \overline{\mathcal{D}}$ and $u_0\in \overline{\mathcal{D}}$, from $u_n\rightharpoonup u_0$ in X it follows that $B\left(u_n\right)\to B\left(u_0\right)$ in $X^{*}$ as $n\to \infty$.

Definition 3. 

An operator $M:\overline{\mathcal{D}}\to X^{*}$ is called monotone if the following inequality holds:

$$⟨M\left(u\right)-M\left(v\right),u-v⟩\ge 0,\forall u,v\in \overline{\mathcal{D}}.$$

Moreover, if there exists a positive constant c such that

$$⟨M\left(u\right)-M\left(v\right),u-v⟩\ge c{\parallel u-v\parallel }_X^2,\forall u,v\in \overline{\mathcal{D}},$$

then the operator M is said to be strongly monotone.

The monotonicity property, in conjunction with some other conditions, makes it possible to obtain existence theorems for solutions to operator equations and these theorems have applications to various boundary value problems of partial differential equations, to differential equations in Banach spaces, and to integral equations [48,49,50].

Let us recall the definitions of three frequently used classes of generalized monotone mappings in Banach spaces (see [48]).

Definition 4. 

Let $T_1,T_2,T_3:\overline{\mathcal{D}}\to X^{*}$ be operators.

• An operator $T_1$ is said to be pseudo-monotone if it is bounded and if, for any sequence ${\left\{u_n\right\}}_{n=1}^{\infty }\subset \overline{\mathcal{D}}$, from $u_n\rightharpoonup u_0$ in X and

  $$\underset{n\to \infty }{lim\; sup}⟨T_1\left(u_n\right),u_n-u_0⟩\le 0$$

  it follows that

  $$\underset{n\to \infty }{lim\; inf}⟨T_1\left(u_n\right),u_n-x⟩\ge ⟨T_1\left(u_0\right),u_0-x⟩,\forall x\in X.$$
• We say that an operator $T_2$ satisfies the condition ${\alpha }_0\left(\mathcal{F}\right)$, where $\mathcal{F}$ is a subset $\overline{\mathcal{D}}$, if, for any sequence ${\left\{u_n\right\}}_{n=1}^{\infty }\subset \mathcal{F}$, from $u_n\rightharpoonup u_0$ in X, $T_2\left(u_n\right)\rightharpoonup 0$ in $X^{*}$, and

  $$\underset{n\to \infty }{lim\; sup}⟨T_2\left(u_n\right),u_n-u_0⟩\le 0$$

  it follows that $u_n\to u_0$ in X as $n\to \infty$.
• We say that the operator $T_3$ satisfies the condition ${\left(S\right)}_{+}$ if, for any sequence ${\left\{u_n\right\}}_{n=1}^{\infty }\subset \overline{\mathcal{D}}$, from $u_n\rightharpoonup u_0$ in X and

  $$\underset{n\to \infty }{lim\; sup}⟨T_3\left(u_n\right),u_n-u_0⟩\le 0$$

  it follows that $u_n\to u_0$ in X as $n\to \infty$.

Mappings that satisfy the condition ${\left(S\right)}_{+}$ are sometimes called ${\left(S\right)}_{+}$-operators or operators of class ${\left(S\right)}_{+}$.

The following proposition gives an important example of ${\left(S\right)}_{+}$-operators.

Proposition 1. 

Suppose that

• $M_1:\overline{\mathcal{D}}\to X^{*}$ is a strongly monotone operator;
• $M_2:\overline{\mathcal{D}}\to X^{*}$ is a monotone operator;
• $B:\overline{\mathcal{D}}\to X^{*}$ is a weak-to-strong continuous operator.

Then the operator $T:=M_1+M_2+B$ is an ${\left(S\right)}_{+}$-operator.

The proof of this statement can be found in [40].

Skrypnik has developed the theory of topological degree for operators satisfying the condition ${\left(S\right)}_{+}$ (or the condition ${\alpha }_0$) and has considered its applications to the study of nonlinear elliptic boundary value problems [48].

Here, we give a scheme of the construction of the topological degree for ${\left(S\right)}_{+}$-operators.

By $\mathcal{F}\left(X\right)$ denote the set of all finite-dimensional subspaces of X. Let $\mathrm{E}\in \mathcal{F}\left(X\right)$ and ${\mathcal{D}}_{\mathrm{E}}:=\mathcal{D}\cap \mathrm{E}$. We introduce the projection ${\pi }_{\mathrm{E}}:X^{*}\to \mathrm{E}$ by

$${\pi }_{\mathrm{E}}\left(h\right):=\sum _{i=1}^m⟨h,v_i⟩v_i,\forall h\in X^{*},$$

(1)

where $v_1,\cdots ,v_m$ is a basis of the space $\mathrm{E}$.

Lemma 1. 

Let $T:\overline{\mathcal{D}}\to X^{*}$ be an operator such the following two conditions hold:

• T is strong-to-weak continuous and satisfies the condition ${\left(S\right)}_{+};$
• $T\left(x\right)\ne 0$ for any $x\in \partial \mathcal{D}$, where $\partial \mathcal{D}$ denotes the boundary of the set $\mathcal{D}$.

Then there exists a subspace ${\mathrm{E}}_0\in \mathcal{F}\left(X\right)$ such that, for any $\mathrm{E}\in \mathcal{F}\left(X\right)$ satisfying the containment ${\mathrm{E}}_0\subset \mathrm{E}$, we have

$$({\pi }_{\mathrm{E}}\circ T)\left(x\right)\ne 0,\forall x\in \partial {\mathcal{D}}_{\mathrm{E}},$$

and

$$deg({\pi }_{\mathrm{E}}\circ T,{\overline{\mathcal{D}}}_{\mathrm{E}},0)=deg({\pi }_{{\mathrm{E}}_0}\circ T,{\overline{\mathcal{D}}}_{{\mathrm{E}}_0},0),$$

where“deg”denotes the topological degree for a finite-dimensional mapping (Brouwer’s degree [51]).

Consider the triplet $(T,\overline{\mathcal{D}},0)$, where $0\in X^{*}$. Taking into account Lemma 1, one can define the topological degree of this triplet as follows

$$\mathrm{Deg}(T,\overline{\mathcal{D}},0):=deg({\pi }_{{\mathrm{E}}_0}\circ T,{\overline{\mathcal{D}}}_{{\mathrm{E}}_0},0).$$

The numerical characteristic $\mathrm{Deg}(T,\overline{\mathcal{D}},0)$ introduced in this way is well defined and has all the natural properties of the Brouwer degree. In particular, the following existence result holds.

Proposition 2. 

Suppose a strong-to-weak continuous operator $T:\overline{\mathcal{D}}\to X^{*}$ satisfies the condition ${\left(S\right)}_{+}$ and $T\left(x\right)\ne 0$ for any $x\in \partial \mathcal{D}$. Moreover, suppose that

$$\mathrm{Deg}(T,\overline{\mathcal{D}},0)\ne 0.$$

Then the equation $T\left(x\right)=0$ has at least one solution in the domain $\mathcal{D}$.

2.2. Set-Valued Mappings of C-ASV-Type

Let us give the definition of one class of set-valued mappings, denoted by C-ASV. First, we recall some concepts and facts (see [26,52]).

Let $\mathcal{X}$, ${\mathcal{X}}^{\prime }$, and $\mathcal{Y}$ be metric spaces.

Definition 5. 

A set-valued mapping $\Sigma :\mathcal{X}⊸\mathcal{Y}$ is called compact-set-valued if the $\Sigma \left(x\right)$ is compact in $\mathcal{Y}$ for all $x\in \mathcal{X}$.

Below, we will consider only compact-set-valued mappings.

Definition 6. 

A nonempty compact set $\mathcal{M}$ in $\mathcal{X}$ is called aspheric if, for any $\epsilon >0$, there exists a number δ, $0<\delta <\epsilon$, such that, for each $n\in \mathbb{N}\cup \left\{0\right\}$, any continuous mapping $\xi :{\mathcal{S}}^n\to O_{\delta }\left(\mathcal{M}\right)$ can be extended to a continuous mapping $\tilde{\xi }:{\mathcal{B}}^{n+1}\to O_{\epsilon }\left(\mathcal{M}\right)$, where

$$\begin{array}{cc}\hfill {\mathcal{S}}^n& :=\left\{\overrightarrow{r}\in {\mathbb{R}}^{n+1}:{\parallel \overrightarrow{r}\parallel }_{{\mathbb{R}}^{n+1}}=1\right\},\hfill \\ \hfill {\mathcal{B}}^{n+1}& :=\left\{\overrightarrow{r}\in {\mathbb{R}}^{n+1}:{\parallel \overrightarrow{r}\parallel }_{{\mathbb{R}}^{n+1}}\le 1\right\},\hfill \\ \hfill O_{\epsilon }\left(\mathcal{M}\right)& :=\left\{x\in \mathcal{X}:\mathrm{dist}(x,\mathcal{M})<\epsilon \right\}.\hfill \end{array}$$

Three examples of aspheric sets in ${\mathbb{R}}^2$ are given in Figure 1.

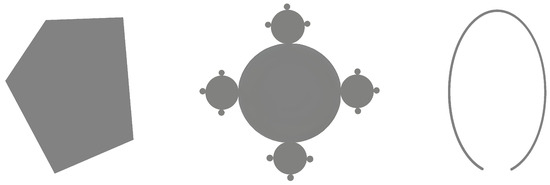
Figure 1. Examples of aspheric sets: one convex non-smooth set and two non-convex smooth sets.

Definition 7. 

A set-valued mapping $\Sigma :\mathcal{X}⊸\mathcal{Y}$ is called ASV-mapping if $\Sigma \left(x\right)$ is an aspheric set for any $x\in \mathcal{X}$.

Of course, the initialism ASV stands for “Aspheric-Set-Valued”.

If $\Sigma :\mathcal{X}⊸\mathcal{Y}$ is an upper semicontinuous ASV-mapping, we write $\Sigma \in \mathrm{ASV}(\mathcal{X},\mathcal{Y})$. By $C-\mathrm{A}\mathrm{S}\mathrm{V}(\mathcal{X},{\mathcal{X}}^{\prime })$ denote the set of all set-valued mappings $\Phi :\mathcal{X}⊸{\mathcal{X}}^{\prime }$ representable in the form $\Phi =\psi \circ \Sigma$, where $\Sigma \in \mathrm{ASV}(\mathcal{X},\mathcal{Y})$ and $\psi :\mathcal{Y}\to {\mathcal{X}}^{\prime }$ is a continuous single-valued mapping.

In order to demonstrate how wide the C-ASV-class of set-valued mappings is, we recall the following definitions and statements (see [26,53] for details).

Definition 8. 

A metric space $\mathcal{Y}$ is said to be an ANR-space (absolute neighborhood retract) if, for any closed subset $\mathcal{B}$ of any metric space $\mathcal{X}$ and any continuous mapping $f:\mathcal{B}\to \mathcal{Y}$, there exist a neighborhood U of the set $\mathcal{B}$ in $\mathcal{X}$ and a continuous extension $\tilde{f}:U\to \mathcal{Y}$ of the mapping f.

Definition 9. 

A topological space $\mathcal{T}$ is said to be locally contractible at a point $x_0\in \mathcal{T}$ if any neighborhood U of $x_0$ contains a neighborhood $U_0$ contractible to a point with respect to U.

Definition 10. 

A space is said to be locally contractible if this space is locally contractible at each of its points.

Proposition 3. 

A finite-dimensional compact set is an ANR-space if and only if it is locally contractible.

Definition 11. 

A compact nonempty set is said to be an $R_{\delta }$-set if it can be expressed as the intersection of a decreasing sequence of compact contractible sets.

Proposition 4. 

Suppose $\mathcal{Y}$ is an ANR-space and $\Sigma :\mathcal{X}⊸\mathcal{Y}$ is an upper semicontinuous set-valued mapping. Then $\Sigma \in \mathrm{ASV}(\mathcal{X},\mathcal{Y})$ if at least one of the following conditions hold:

• $\Sigma \left(x\right)$ is a convex set, for any $x\in \mathcal{X};$
• $\Sigma \left(x\right)$ is a contractible set, for any $x\in \mathcal{X};$
• $\Sigma \left(x\right)$ is a $R_{\delta }$-set, for any $x\in \mathcal{X}$.

2.3. Continuous Single-Valued Approximations of Set-Valued Mappings

Let $\mathcal{X}$ and $\mathcal{Y}$ be metric spaces and let $\Sigma :\mathcal{X}⊸\mathcal{Y}$ be a set-valued mapping.

Definition 12. 

For a positive number ε, a continuous single-valued mapping ${\sigma }_{\epsilon }:\mathcal{X}\to \mathcal{Y}$ is called an ε-approximation of the set-valued mapping Σ if, for any element $x\in \mathcal{X}$, there exists an element $x^{\prime }\in O_{\epsilon }\left(x\right)$ such that ${\sigma }_{\epsilon }\left(x\right)\in O_{\epsilon }(\Sigma \left(x^{\prime }\right))$.

By $\mathrm{appr}(\Sigma ,\epsilon )$ we denote the set of all $\epsilon$-approximations of the set-valued mapping $\Sigma$.

In the next two lemmas, we summarize some important properties of $\epsilon$-approximations (see [26] for details).

Lemma 2. 

Let $\Sigma :\mathcal{X}⊸\mathcal{Y}$ be an upper semicontinuous set-valued mapping. Then the following statements hold.

(i)

For any compact subset ${\mathcal{X}}_0$ of $\mathcal{X}$ and for any positive number ε, there exists a positive number δ such that

$${\sigma \in \mathrm{appr}(\Sigma ,\delta )⟹\sigma |}_{{\mathcal{X}}_0}\in \mathrm{appr}(\Sigma {|}_{{\mathcal{X}}_0},\epsilon ).$$

(ii)

Suppose $\mathcal{X}$ is a compact set and $\psi :\mathcal{Y}\to {\mathcal{X}}^{\prime }$ is a continuous mapping. Then, for any $\epsilon >0$, there exists $\delta >0$ such that

$$\sigma \in \mathrm{appr}(\Sigma ,\delta )⟹\psi \circ \sigma \in \mathrm{appr}(\psi \circ \Sigma ,\epsilon ).$$

(iii)

Suppose $\mathcal{X}$ is a compact set and ${\Sigma }_{*}:\mathcal{X}\times [0,1]⊸\mathcal{Y}$ is an upper semicontinuous set-valued mapping. Then, for any $\lambda \in [0,1]$ and $\epsilon >0$, there exists $\delta >0$ such that

$${\sigma }_{*}\in \mathrm{appr}({\Sigma }_{*},\delta )⟹{\sigma }_{*}(·,\lambda )\in \mathrm{appr}({\Sigma }_{*}(·,\lambda ),\epsilon ).$$

Let $f:\mathcal{X}\to {\mathcal{X}}^{\prime }$ be a single-valued mapping and let $\Lambda :\mathcal{X}⊸{\mathcal{X}}^{\prime }$ be a set-valued mapping. By $\mathrm{Coin}(f,\Lambda )$ we denote the solutions set for the inclusion $f\left(x\right)\in \Lambda \left(x\right)$, that is,

$$\mathrm{Coin}(f,\Lambda ):=\left\{x\in \mathcal{X}:f\left(x\right)\in \Lambda \left(x\right)\right\}.$$

Lemma 3. 

Suppose $f:\mathcal{X}\to {\mathcal{X}}^{\prime }$ and $\psi :\mathcal{Y}\to {\mathcal{X}}^{\prime }$ are continuous mappings and $\Sigma :\mathcal{X}⊸\mathcal{Y}$ is an upper semicontinuous set-valued mapping. Let ${\mathcal{X}}_0$ be a compact subset of $\mathcal{X}$ such that

$${\mathcal{X}}_0\cap \mathrm{Coin}(f,\psi \circ \Sigma )=\varnothing .$$

If $\epsilon >0$ is sufficiently small and the inclusion ${\sigma }_{\epsilon }\in \mathrm{appr}(\Sigma ,\epsilon )$ holds, then

$${\mathcal{X}}_0\cap \mathrm{Coin}(f,\psi \circ {\sigma }_{\epsilon })=\varnothing .$$

In the paper [54], the following approximability properties of ASV-mappings have been established.

Proposition 5. 

Suppose $\mathcal{X}$ is a compact ANR-space, $\Sigma \in \mathrm{ASV}(\mathcal{X},\mathcal{Y})$, then

(i)

the set-valued mapping Σ is approximable, that is, for any $\epsilon >0$ there exists ${\sigma }_{\epsilon }\in \mathrm{appr}(\Sigma ,\epsilon );$

(ii)

for any $\epsilon >0$, there exists ${\delta }_0>0$ such that, for any δ$(0<\delta <{\delta }_0)$ and any δ-approximations ${\sigma }_{\delta }$, ${\sigma }_{\delta }^{\prime }\in \mathrm{appr}(\Sigma ,\delta )$, there exists a continuous mapping $\tilde{\sigma }:\mathcal{X}\times [0,1]\to \mathcal{Y}$ satisfying the following properties:

1)

$\tilde{\sigma }(·,0)={\sigma }_{\delta }$ and $\tilde{\sigma }(·,1)={\sigma }_{\delta }^{\prime };$

2)

$\tilde{\sigma }(·,\lambda )\in \mathrm{appr}(\Sigma ,\epsilon )$ for any $\lambda \in [0,1]$.

2.4. Leray–Schauder Lemma

Lemma 4 

(see [55]). Let $\mathcal{D}$ be a bounded open subset of ${\mathbb{R}}^n$ such that

$${\mathcal{D}}^{\prime }:=\mathcal{D}\cap \left\{x:x_n=0\right\}\ne \varnothing .$$

Suppose that $\omega :\overline{\mathcal{D}}\to {\mathbb{R}}^n$ is a continuous mapping such that

$$\begin{array}{c}{\omega }_n(x_1,\cdots ,x_n)\equiv x_n,\forall (x_1,\cdots ,x_n)\in \mathcal{D},\\ \omega \left(x\right)\ne 0,\forall x\in \partial \mathcal{D}.\end{array}$$

Then

$$deg(\omega ,\overline{\mathcal{D}},0)=deg({\omega }^{\prime },{\overline{\mathcal{D}}}^{\prime },0),$$

where the mapping ${\omega }^{\prime }:{\overline{\mathcal{D}}}^{\prime }\to {\mathbb{R}}^{n-1}$ is defined by

$${\omega }^{\prime }(x_1,\cdots ,x_{n-1}):=\left({\omega }_1(x_1,\cdots ,x_{n-1},0),\cdots ,{\omega }_{n-1}(x_1,\cdots ,x_{n-1},0)\right).$$

3. Topological Degree for ${\left(S\right)}_{+}$-Operators with Set-Valued Perturbations

3.1. Construction of Topological Degree

Let X be a real separable reflexive Banach space and let $\mathcal{Y}$ be a metric space. Suppose $\mathcal{U}$ is a bounded open subset of X such that for any $\mathrm{E}\in \mathcal{F}\left(X\right)$, the set $\overline{\mathcal{U}\cap \mathrm{E}}$ is locally contractible.

We will construct the topological degree of a set-valued mapping $T-\Phi :\overline{\mathcal{U}}⊸X^{*}$ that satisfies the following four conditions:

(H.1)

the single-valued mapping $T:\overline{\mathcal{U}}\to X^{*}$ is strong-to-weak continuous and satisfies the condition ${\left(S\right)}_{+};$

(H.2)

the set-valued mapping $\Phi =\psi \circ \Sigma :\overline{\mathcal{U}}⊸X^{*}$ belongs to the class $C-\mathrm{A}\mathrm{S}\mathrm{V}(\overline{\mathcal{U}},X^{*})$;

(H.3)

the set $\Phi \left(\overline{\mathcal{U}}\right)$ is relatively compact in $X^{*}$;

(H.4)

the equality $\mathrm{Coin}(T,\Phi )\cap \partial \mathcal{U}=\varnothing$ holds.

Let $\mathrm{E}$ be a finite-dimensional subspace of X with a basis $v_1,\cdots ,v_m$ and let ${\pi }_{\mathrm{E}}$ be the mapping defined in (1).

For an arbitrary subset $\mathcal{S}$ of X, by ${\mathcal{S}}_{\mathrm{E}}$ we denote the intersection $\mathcal{S}\cap \mathrm{E}$.

Let us consider the three mappings:

$${\pi }_{\mathrm{E}}\circ T:{\overline{\mathcal{U}}}_{\mathrm{E}}\to \mathrm{E},{\pi }_{\mathrm{E}}\circ \psi :\mathcal{Y}\to \mathrm{E},{\pi }_{\mathrm{E}}\circ \Phi :{\overline{\mathcal{U}}}_{\mathrm{E}}⊸\mathrm{E}.$$

The following statement is true.

Lemma 5. 

Suppose conditions(H.1) and (H.3)hold and $\mathcal{V}$ is a subset of $\overline{\mathcal{U}}$ such that

(i)

the set $\mathcal{V}$ is closed;

(ii)

the equality $\mathrm{Coin}(T,\Phi )\cap \mathcal{V}=\varnothing$ holds.

Then there exists a space ${\mathrm{E}}_0\in \mathcal{F}\left(X\right)$ such that

$$\mathrm{E}\in \mathcal{F}\left(X\right) and \mathrm{E}\supset {\mathrm{E}}_0⟹\mathrm{Coin}({\pi }_{\mathrm{E}}\circ T,{\pi }_{\mathrm{E}}\circ \Phi )\cap {\mathcal{V}}_{\mathrm{E}}=\varnothing .$$

(2)

Proof. 

Following [37], we introduce the set $\mathfrak{A}(\mathrm{E},{\mathrm{E}}_0)$ by

$$\begin{array}{cc}\hfill \mathfrak{A}(\mathrm{E},{\mathrm{E}}_0):=\{x\in {\mathcal{V}}_{\mathrm{E}}:& \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} \mathrm{e}\mathrm{x}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{s} y\in \Phi \left(x\right) \mathrm{s}\mathrm{u}\mathrm{c}\mathrm{h} \mathrm{t}\mathrm{h}\mathrm{a}\mathrm{t} ⟨T\left(x\right)-y,x⟩\le 0\hfill \\ \hfill & \mathrm{a}\mathrm{n}\mathrm{d} ⟨T\left(x\right)-y,v⟩=0, \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{n}\mathrm{y} v\in {\mathrm{E}}_0\}.\hfill \end{array}$$

First, we show there exists a subspace ${\mathrm{E}}_0\in \mathcal{F}\left(X\right)$ such that

$$\mathrm{E}\in \mathcal{F}\left(X\right) \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{E}\supset {\mathrm{E}}_0⟹\mathfrak{A}(\mathrm{E},{\mathrm{E}}_0)=\varnothing .$$

(3)

Assume the converse, that is, for any subspace $\mathrm{E}\in \mathcal{F}\left(X\right)$, there exists a subspace ${\mathrm{E}}_1\in \mathcal{F}\left(X\right)$ such that

$${\mathrm{E}}_1\supset \mathrm{E}\mathrm{a}\mathrm{n}\mathrm{d}\mathfrak{A}({\mathrm{E}}_1,\mathrm{E})\ne \varnothing .$$

Let

$${\mathfrak{R}}_{\mathrm{E}}:=\bigcup _{{\mathrm{E}}^{\prime }\supset \mathrm{E}}\mathfrak{A}({\mathrm{E}}^{\prime },\mathrm{E}), \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} {\mathrm{E}}^{\prime }\in \mathcal{F}\left(X\right).$$

By ${\overline{\mathfrak{R}}}_{\mathrm{E}}^{\left(\mathrm{weak}\right)}$ we denote the weak closure of ${\mathfrak{R}}_{\mathrm{E}}$. We claim that the following system

$$\left\{{\overline{\mathfrak{R}}}_{\mathrm{E}}^{\left(\mathrm{weak}\right)}:\mathrm{E}\in \mathcal{F}\left(X\right)\right\}$$

(4)

is centered.

Let ${\overline{\mathfrak{R}}}_{{\mathrm{E}}_1}^{\left(\mathrm{weak}\right)},\cdots ,{\overline{\mathfrak{R}}}_{{\mathrm{E}}_p}^{\left(\mathrm{weak}\right)}$ be an arbitrary finite subsystem of this system. By $\mathcal{L}({\mathrm{E}}_1,\cdots ,{\mathrm{E}}_p)$ we denote the linear hull of ${\mathrm{E}}_1,\cdots ,{\mathrm{E}}_p$. By our assumption, there exists $\tilde{\mathrm{E}}\in \mathcal{F}\left(X\right)$ such that

$$\mathfrak{A}(\tilde{\mathrm{E}},\mathcal{L}({\mathrm{E}}_1,\cdots ,{\mathrm{E}}_p))\ne \varnothing .$$

Note that

$$\mathfrak{A}(\tilde{\mathrm{E}},\mathcal{L}({\mathrm{E}}_1,\cdots ,{\mathrm{E}}_p))\subset \mathfrak{A}(\tilde{\mathrm{E}},{\mathrm{E}}_j)\subset {\mathfrak{R}}_{{\mathrm{E}}_j}\subset {\overline{\mathfrak{R}}}_{{\mathrm{E}}_j}^{\left(\mathrm{weak}\right)},j=1,\cdots ,p,$$

and hence

$$\bigcap _{j=1}^p{\overline{\mathfrak{R}}}_{{\mathrm{E}}_j}^{\left(\mathrm{weak}\right)}\ne \varnothing ,$$

which means that system (4) is centered.

Since the space X is reflexive and system (4) is centered, there exists an element $u_0$ such that

$$u_0\in \bigcap _{\mathrm{E}\in \mathcal{F}\left(X\right)}{\overline{\mathfrak{R}}}_{\mathrm{E}}^{\left(\mathrm{weak}\right)}.$$

Let us show that $u_0\in \mathcal{V}$ and $T\left(u_0\right)\in \Phi \left(u_0\right)$.

Consider $\mathrm{E}\in \mathcal{F}\left(X\right)$ such that $u_0\in \mathrm{E}$. Taking into account the inclusion $u_0\in {\overline{\mathfrak{R}}}_{\mathrm{E}}^{\left(\mathrm{weak}\right)}$, we see that there exist sequences ${\left\{u_n\right\}}_{n=1}^{\infty }$ and ${\left\{y_n\right\}}_{n=1}^{\infty }$ such that

$$u_n\in \mathfrak{A}({\mathrm{E}}_n,\mathrm{E}),{\mathrm{E}}_n\in \mathcal{F}\left(X\right),{\mathrm{E}}_n\supset \mathrm{E},\forall n\in \mathbb{N},$$

$$u_n\rightharpoonup u_0 \mathrm{i}\mathrm{n} X \mathrm{a}\mathrm{s} n\to \infty ,$$

$$y_n\in \Phi \left(u_n\right)\subset \Phi \left(\overline{\mathcal{U}}\right),\forall n\in \mathbb{N},$$

$$⟨T\left(u_n\right)-y_n,u_n⟩\le 0,⟨T\left(u_n\right)-y_n,u_0⟩=0,\forall n\in \mathbb{N},$$

(5)

$$⟨T\left(u_n\right)-y_n,w⟩=0,\forall n\in \mathbb{N},w\in \mathrm{E}.$$

(6)

Moreover, since the set $\Phi \left(\overline{\mathcal{U}}\right)$ is relatively compact, we can assume without loss of generality that

$$y_n\to y_0 \mathrm{i}\mathrm{n} X^{*} \mathrm{a}\mathrm{s} n\to \infty ,$$

for some $y_0\in X^{*}$.

Note that the following representation of $⟨T\left(u_n\right),u_n-u_0⟩$ holds:

$$\begin{array}{cc}\hfill ⟨T\left(u_n\right),u_n-u_0⟩& =⟨T\left(u_n\right)-y_n,u_n-u_0⟩\hfill \\ \hfill & +⟨y_n-y_0,u_n-u_0⟩+⟨y_0,u_n-u_0⟩,\forall n\in \mathbb{N}.\hfill \end{array}$$

(7)

Clearly, the second and third terms in the right-hand side of equality (7) converge to zero.

From (5) it follows that

$$⟨T\left(u_n\right)-y_n,u_n-u_0⟩\le 0,\forall n\in \mathbb{N},$$

whence

$$\underset{n\to \infty }{lim\; sup}⟨T\left(u_n\right),u_n-u_0⟩\le 0.$$

(8)

Since the operator T satisfies the condition ${\left(S\right)}_{+}$, inequality (8) and the inclusion

$$u_n\in {\mathcal{V}}_{{\mathrm{E}}_n}\subset \overline{\mathcal{U}},\forall n\in \mathbb{N},$$

holds, and $u_n\rightharpoonup u_0$ in X as $n\to \infty$, so we have $u_n\to u_0$ in X as $n\to \infty$. Therefore, recalling that the set $\mathcal{V}$ is closed, we obtain the inclusion $u_0\in \mathcal{V}$.

Moreover, from the conditions

$$\begin{array}{c}{u}_n\to u_0 \mathrm{i}\mathrm{n} X \mathrm{a}\mathrm{s} n\to \infty ,\\ y_n\in \Phi \left(u_n\right),\forall n\in \mathbb{N},\\ y_n\to y_0 \mathrm{i}\mathrm{n} X^{*} \mathrm{a}\mathrm{s} n\to \infty ,\end{array}$$

and the upper semicontinuity of the set-valued mapping $\Phi$, it follows that $y_0\in \Phi \left(u_0\right)$.

Further, we pass the limit $n\to \infty$ in equality (6); this gives

$$⟨T\left(u_0\right)-y_0,w⟩=0,\forall w\in \mathrm{E}.$$

(9)

Therefore, for any space $\mathrm{E}\in \mathcal{F}\left(X\right)$ such that $u_0\in \mathrm{E}$, there exists $y_0\in \Phi \left(u_0\right)$ satisfying equality (9).

In view of the space in which X is separable, there exists a countable set $\mathcal{Q}$ such that $\mathcal{Q}\subset X$ and $\mathcal{Q}$ is dense in X. For the sake of being definite, let $\mathcal{Q}={\left\{x_i\right\}}_{i=1}^{\infty }$.

Consider the sequence of spaces ${\left\{{\mathrm{F}}_i\right\}}_{i=1}^{\infty }$, where

$${\mathrm{F}}_k:=\mathrm{span}\{u_0,x_1,\cdots ,x_k\},\forall k\in \mathbb{N}.$$

From the above reasoning, it follows that, for any ${\mathrm{F}}_k\in \mathcal{F}\left(X\right)$, there exists $f_k\in \Phi \left(u_0\right)$ such that

$$⟨T\left(u_0\right)-f_k,w⟩=0,\forall w\in {\mathrm{F}}_k.$$

(10)

Without loss of generality, it can be assumed that

$$f_k\to f_0\in \Phi \left(u_0\right) \mathrm{i}\mathrm{n} X^{*} \mathrm{a}\mathrm{a}\mathrm{s} k\to \infty$$

(11)

because the set $\Phi \left(u_0\right)$ is compact.

Let us show that $T\left(u_0\right)=f_0$. Fix arbitrary $x\in X$ and $\epsilon >0$. Suppose C is a constant such that

$$\begin{array}{cc}\hfill \parallel T\left(u_0\right){\parallel }_{X^{*}}& <C,\hfill \\ \hfill \parallel f_k{\parallel }_{X^{*}}& <C,\forall k\in \mathbb{N}.\hfill \end{array}$$

(12)

Because the set $\mathcal{Q}$ is dense in X, there exists an element $x_m\in \mathcal{Q}$ such that

$$\parallel x-x_m{\parallel }_X<{\displaystyle \frac{\epsilon }{4C}}.$$

(13)

Let us take a sufficiently large integer k such that $k\ge m$ and

$$\left|⟨f_k-f_0,x⟩\right|<{\displaystyle \frac{\epsilon }{4}}.$$

(14)

This is possible since the element x is fixed and convergence (11) holds.

We observe that $x_m\in {\mathrm{F}}_m\subset {\mathrm{F}}_k$. Therefore, from equality (10), it follows that

$$⟨T\left(u_0\right)-f_k,x_m⟩=0.$$

(15)

Using relations (12)–(15), we derive

$$\begin{array}{cc}\hfill & \left|⟨T\left(u_0\right)-f_0,x⟩\right|\hfill \\ \hfill & =|⟨T\left(u_0\right)-f_k,x_m⟩+⟨T\left(u_0\right)-f_k,x-x_m⟩+⟨f_k-f_0,x⟩|\hfill \\ \hfill & \le \left|⟨T\left(u_0\right)-f_k,x_m⟩\right|+\left|⟨T\left(u_0\right)-f_k,x-x_m⟩\right|+\left|⟨f_k-f_0,x⟩\right|\hfill \\ \hfill & \le \parallel T\left(u_0\right){\parallel }_{X^{*}}\parallel x-x_m{\parallel }_X+\parallel f_k{\parallel }_{X^{*}}{\parallel x-x_m\parallel }_X+\left|⟨f_k-f_0,x⟩\right|\hfill \\ \hfill & \le C(\epsilon /4C)+C(\epsilon /4C)+\epsilon /4\hfill \\ \hfill & =3\epsilon /4<\epsilon ,\hfill \end{array}$$

whence,

$$⟨T\left(u_0\right)-f_0,x⟩=0,$$

(16)

since $\epsilon$ was taken arbitrarily.

Moreover, taking into account that x is an arbitrary element from the space X, we deduce from equality (16) the relation $T\left(u_0\right)=f_0\in \Phi \left(u_0\right),$ and hence, $u_0\in \mathrm{Coin}(T,\Phi )$. Combining this with $u_0\in \mathcal{V}$, we obtain

$$u_0\in \mathrm{Coin}(T,\Phi )\cap \mathcal{V},$$

which contradicts condition (ii).

Thus, we have proved the existence of a subspace ${\mathrm{E}}_0\in \mathcal{F}\left(X\right)$ such that implication (3) holds for any $\mathrm{E}\in \mathcal{F}\left(X\right)$.

Now we will show that the subspace ${\mathrm{E}}_0$ satisfies implication (2). Assume the converse. Then there exists a subspace ${\mathrm{E}}_1\in \mathcal{F}\left(X\right)$ such that

$${\mathrm{E}}_1\supset {\mathrm{E}}_0 \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{Coin}({\pi }_{{\mathrm{E}}_1}\circ T,{\pi }_{{\mathrm{E}}_1}\circ \Phi )\cap {\mathcal{V}}_{{\mathrm{E}}_1}\ne \varnothing .$$

Let $u_1$ be an element satisfying

$$u_1\in \mathrm{Coin}({\pi }_{{\mathrm{E}}_1}\circ T,{\pi }_{{\mathrm{E}}_1}\circ \Phi )\cap {\mathcal{V}}_{{\mathrm{E}}_1}.$$

We show that $u_1\in \mathfrak{A}({\mathrm{E}}_1,{\mathrm{E}}_0)$. Due to the inclusion

$$u_1\in \mathrm{Coin}({\pi }_{{\mathrm{E}}_1}\circ T,{\pi }_{{\mathrm{E}}_1}\circ \Phi ),$$

there exists $y_1\in \Phi \left(u_1\right)$ such that

$$({\pi }_{{\mathrm{E}}_1}\circ T)\left(u_1\right)={\pi }_{{\mathrm{E}}_1}\left(y_1\right).$$

(17)

Let $v_1,\cdots ,v_{m_1}$ be a basis of $\mathrm{E}\in \mathcal{F}\left(X\right)$. Then equality (17) is equivalent to

$$⟨T\left(u_1\right)-y_1,v_i⟩=0,i=1,\cdots ,m_1.$$

(18)

Since $u_1\in {\mathrm{E}}_1$, we have the representation

$$u_1=\sum _{i=1}^{m_1}{\zeta }_i{v}_i,$$

(19)

where ${\zeta }_1$, ..., ${\zeta }_{m_1}$ are some real numbers.

Using equality (18) and representation (19), we obtain

$$⟨T\left(u_1\right)-y_1,u_1⟩=\sum _{i=1}^{m_1}{\zeta }_i⟨T\left(u_1\right)-y_1,v_i⟩=0.$$

Similarly, we derive

$$⟨T\left(u_1\right)-y_1,v⟩=0,\forall v\in {\mathrm{E}}_0.$$

Thus, we have established $u_1\in \mathfrak{A}({\mathrm{E}}_1,{\mathrm{E}}_0)$. On the other hand, for the subspaces ${\mathrm{E}}_0$ and ${\mathrm{E}}_1$, we have $\mathfrak{A}({\mathrm{E}}_1,{\mathrm{E}}_0)=\varnothing$. This contradiction proves Lemma 5. □

Now we can return to constructing the topological degree of the set-valued mapping $T-\Phi$. Note that for the set $\mathcal{V}=\partial \mathcal{U}$ conditions (i) and (ii) of Lemma 5 hold. Let us fix a subspace ${\mathrm{E}}_0\in \mathcal{F}\left(X\right)$ such that

$$\mathrm{Coin}({\pi }_{{\mathrm{E}}_0}\circ T,{\pi }_{{\mathrm{E}}_0}\circ \Phi )\cap \partial {\mathcal{U}}_{{\mathrm{E}}_0}=\varnothing .$$

(20)

From our assumptions on the geometrical properties of $\mathcal{U}$, it follows that the set ${\overline{\mathcal{U}}}_{{\mathrm{E}}_0}=\overline{\mathcal{U}\cap {\mathrm{E}}_0}$ is locally contractible. Therefore, applying Proposition 3, we see that ${\overline{\mathcal{U}}}_{{\mathrm{E}}_0}$ is a compact ANR-space. Thus, for ${\Sigma |}_{{\overline{\mathcal{U}}}_{{\mathrm{E}}_0}}$, all the conditions of Proposition 5 hold. This implies that, for any $\epsilon >0$, there exists a continuous $\epsilon$-approximation ${\sigma }_{\epsilon }\in \mathrm{appr}(\Sigma {|}_{{\overline{\mathcal{U}}}_{{\mathrm{E}}_0}},\epsilon )$.

From equality (20) and Lemma 3 it follows that there exists ${\epsilon }_0>0$ such that, for any $\epsilon \in (0,{\epsilon }_0]$, we have

$$\left({\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon }\right)\left(x\right)\ne 0,\forall x\in \partial {\mathcal{U}}_{{\mathrm{E}}_0}.$$

(21)

Moreover, applying Proposition 5 (ii), we deduce that there exists ${\delta }_0\in (0,{\epsilon }_0)$ such that, for any $\epsilon \in (0,{\delta }_0)$ and ${\sigma }_{\epsilon },{\sigma }_{\epsilon }^{\prime }\in \mathrm{appr}(\Sigma {|}_{{\overline{\mathcal{U}}}_{{\mathrm{E}}_0}},\epsilon )$, there exists a continuous mapping $\tilde{\sigma }:{\overline{\mathcal{U}}}_{{\mathrm{E}}_0}\times [0,1]\to \mathcal{Y}$ satisfying the following conditions:

$$\begin{array}{c}\tilde{\sigma }(·,0)={\sigma }_{\epsilon },\tilde{\sigma }(·,1)={\sigma }_{\epsilon }^{\prime },\end{array}$$

(22)

$$\begin{array}{c}\tilde{\sigma }(·,t)\in \mathrm{appr}(\Sigma {|}_{{\overline{\mathcal{U}}}_{{\mathrm{E}}_0}},{\epsilon }_0),\forall t\in [0,1].\end{array}$$

(23)

Fix $\epsilon \in (0,{\delta }_0)$. Assuming that conditions (H.1)–(H.4) hold, we give the next definition.

Definition 13. 

The topological degree of a set-valued mapping $T-\Phi :\overline{\mathcal{U}}⊸X^{*}$ with respect to $\overline{\mathcal{U}}$ and $0\in X^{*}$ is defined by the equality

$$\mathrm{Deg}(T-\Phi ,\overline{\mathcal{U}},0)=deg({\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{{\mathrm{E}}_0},0),$$

where $deg({\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{{\mathrm{E}}_0},0)$ denotes the Brouwer degree of the mapping

$${\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon }:{\overline{\mathcal{U}}}_{{\mathrm{E}}_0}\to {\mathrm{E}}_0$$

with respect to ${\overline{\mathcal{U}}}_{{\mathrm{E}}_0}$ and $0\in {\mathrm{E}}_0$.

3.2. Well-Definedness of Topological Degree

Let us show that the topological degree $\mathrm{Deg}(T-\Phi ,\overline{\mathcal{U}},0)$ is well defined, that is, its value depends neither on the choice of an $\epsilon$-approximation ${\sigma }_{\epsilon }$ nor on the choice of a subspace ${\mathrm{E}}_0$.

Step 1. First, we establish the independence of $\mathrm{Deg}(T-\Phi ,\overline{\mathcal{U}},0)$ from the choice of an $\epsilon$-approximation. More precisely, it is necessary to prove that, for any $\epsilon \in (0,{\delta }_0)$ and ${\sigma }_{\epsilon },{\sigma }_{\epsilon }^{\prime }\in \mathrm{appr}(\Sigma {|}_{{\overline{\mathcal{U}}}_{{\mathrm{E}}_0}},\epsilon )$, the following equality holds:

$$deg({\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{{\mathrm{E}}_0},0)=deg({\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon }^{\prime },{\overline{\mathcal{U}}}_{{\mathrm{E}}_0},0).$$

(24)

From relations (21) and (23) it follows that

$$({\pi }_{{\mathrm{E}}_0}\circ T)\left(x\right)-({\pi }_{{\mathrm{E}}_0}\circ \psi \circ \tilde{\sigma })(x,t)\ne 0,\forall (x,t)\in \partial {\mathcal{U}}_{{\mathrm{E}}_0}\times [0,1],$$

which together with (22) yield that the mappings

$${\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon }:{\overline{\mathcal{U}}}_{{\mathrm{E}}_0}\to {\mathrm{E}}_0\mathrm{a}\mathrm{n}\mathrm{d}{\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon }^{\prime }:{\overline{\mathcal{U}}}_{{\mathrm{E}}_0}\to {\mathrm{E}}_0$$

are homotopic. Therefore, in view of the homotopy invariance property of the Brouwer degree, we arrive at equality (24).

Step 2. Now we will show the independence of $\mathrm{Deg}(T-\Phi ,\overline{\mathcal{U}},0)$ from the choice of a subspace ${\mathrm{E}}_0$.

Let us fix $\mathrm{E}\in \mathcal{F}\left(X\right)$ such that $\mathrm{E}\supset {\mathrm{E}}_0$ and prove that the following equality is valid:

$$deg({\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{{\mathrm{E}}_0},0)=deg({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}},0),$$

(25)

where ${\sigma }_{\epsilon }\in \mathrm{appr}(\Sigma {|}_{{\overline{\mathcal{U}}}_{\mathrm{E}}},\epsilon )$.

Let us choose a basis of $\mathrm{E}\in \mathcal{F}\left(X\right)$ in the form $v_1,\cdots ,v_m,w_1,\cdots ,w_k$, where $v_1,\cdots ,v_m$ is a basis of ${\mathrm{E}}_0\in \mathcal{F}\left(X\right)$, and consider the three finite-dimensional mappings:

$$\left({\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon }\right)\left(x\right):=\sum _{i=1}^m⟨T\left(x\right),v_i⟩v_i-\sum _{i=1}^m⟨(\psi \circ {\sigma }_{\epsilon })\left(x\right),v_i⟩v_i,$$

$$\begin{array}{cc}\hfill \left({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon }\right)\left(x\right)& :=\sum _{i=1}^m⟨T\left(x\right),v_i⟩v_i-\sum _{i=1}^m⟨(\psi \circ {\sigma }_{\epsilon })\left(x\right),v_i⟩v_i\hfill \\ \hfill & +\sum _{i=1}^k⟨T\left(x\right),w_i⟩w_i-\sum _{i=1}^k⟨(\psi \circ {\sigma }_{\epsilon })\left(x\right),w_i⟩w_i,\hfill \end{array}$$

$$R_{\epsilon ,\mathrm{E}}\left(x\right):=\sum _{i=1}^m⟨T\left(x\right),v_i⟩v_i-\sum _{i=1}^m⟨(\psi \circ {\sigma }_{\epsilon })\left(x\right),v_i⟩v_i+\sum _{i=1}^k⟨p_i,x⟩w_i,$$

where ${\sigma }_{\epsilon }\in \mathrm{appr}(\Sigma {|}_{{\overline{\mathcal{U}}}_{\mathrm{E}}},\epsilon )$ and $p_i$ is an element from the space $X^{*}$ such that

$$\begin{array}{cc}\hfill & ⟨p_i,w_j⟩={\delta }_{ij},i=1,\cdots ,k,j=1,\cdots ,k,\hfill \\ \hfill & ⟨p_i,v_j⟩=0,i=1,\cdots ,k,j=1,\cdots ,m,\hfill \end{array}$$

and ${\delta }_{ij}$ is the Kronecker delta.

In view of Lemma 4, we have

$$deg({\pi }_{{\mathrm{E}}_0}\circ T-{\pi }_{{\mathrm{E}}_0}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{{\mathrm{E}}_0},0)=deg(R_{\epsilon ,\mathrm{E}},{\overline{\mathcal{U}}}_{\mathrm{E}},0).$$

(26)

Moreover, we will show that if $\epsilon >0$ is small enough, then

$$deg({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}},0)=deg(R_{\epsilon ,\mathrm{E}},{\overline{\mathcal{U}}}_{\mathrm{E}},0).$$

(27)

Due to the homotopy invariance property of the Brouwer degree, it is sufficient to prove the next lemma.

Lemma 6. 

There exists ${\epsilon }_0>0$ such that, for any ${\sigma }_{\epsilon }\in \mathrm{appr}(\Sigma {|}_{{\overline{\mathcal{U}}}_{\mathrm{E}}},\epsilon )$ with $0<\epsilon <{\epsilon }_0$, the following relation is true:

$$t\left({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon }\right)\left(x\right)+(1-t)R_{\epsilon ,\mathrm{E}}\left(x\right)\ne 0,\forall (x,t)\in \partial {\mathcal{U}}_{\mathrm{E}}\times [0,1].$$

Proof. 

Assume the converse. Then there exist sequences ${\left\{{\epsilon }_n\right\}}_{n=1}^{\infty }\subset (0,\infty )$, ${\left\{t_n\right\}}_{n=1}^{\infty }\subset [0,1]$, and ${\left\{x_n\right\}}_{n=1}^{\infty }\subset \partial {\mathcal{U}}_{\mathrm{E}}$ such that ${\epsilon }_n\to 0$ as $n\to \infty$ and

$$t_n\left({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{{\epsilon }_n}\right)\left(x_n\right)+(1-t_n)R_{{\epsilon }_n,\mathrm{E}}\left(x_n\right)=0,$$

(28)

for some ${\sigma }_{{\epsilon }_n}\in \mathrm{appr}(\Sigma {|}_{{\overline{\mathcal{U}}}_{\mathrm{E}}},{\epsilon }_n)$.

Equality (28) is equivalent to the two following relations:

$$\begin{array}{c}⟨(T-\psi \circ {\sigma }_{{\epsilon }_n})\left(x_n\right),v_i⟩=0,i=1,\cdots ,m,\end{array}$$

(29)

$$\begin{array}{c}{t}_n⟨(T-\psi \circ {\sigma }_{{\epsilon }_n})\left(x_n\right),w_i⟩+(1-t_n)⟨p_i,x_n⟩=0,i=1,\cdots ,k.\end{array}$$

(30)

Without loss of generality, it can be assumed that

$$\begin{array}{c}{x}_n\to x_{*}\in \partial {\mathcal{U}}_{\mathrm{E}} \mathrm{i}\mathrm{n} X \mathrm{a}\mathrm{s} n\to \infty ,\\ t_n\to t_{*}\in [0,1] \mathrm{a}\mathrm{s} n\to \infty ,\\ (\psi \circ {\sigma }_{{\epsilon }_n})\left(x_n\right)\to y_{*}\in (\psi \circ \Sigma )\left(x_{*}\right) \mathrm{i}\mathrm{n} X^{*} \mathrm{a}\mathrm{s} n\to \infty ,\end{array}$$

Further, we pass to the limit $n\to \infty$ in equalities (29) and (30); this gives

$$\begin{array}{c}⟨T\left(x_{*}\right)-y_{*},v_i⟩=0,i=1,\cdots ,m,\end{array}$$

(31)

$$\begin{array}{c}{t}_{*}⟨T\left(x_{*}\right)-y_{*},w_i⟩+(1-t_{*})⟨p_i,x_{*}⟩=0,i=1,\cdots ,k.\end{array}$$

(32)

We claim that, in the last equality, $t_{*}\ne 0$. Assume the converse. Then

$$⟨p_j,x_{*}⟩=0,j=0,\cdots ,k.$$

Since $x_{*}\in \partial {\mathcal{U}}_{\mathrm{E}}\subset \mathrm{E},$ we have the representation

$$x_{*}=\sum _{i=1}^m{a}_i{v}_i+\sum _{i=1}^k{b}_i{w}_i$$

(33)

with some $a_i,b_i\in \mathbb{R}$. Applying the functional $p_j\in X^{*}$ to both sides of equality (33), we obtain

$$⟨p_j,x_{*}⟩=b_j$$

(34)

Recalling that $⟨p_j,x_{*}⟩=0$, we arrive at the equality $b_j=0$. Therefore,

$$x_{*}=\sum _{i=1}^m{a}_i{v}_i\in {\mathrm{E}}_0,$$

and hence $x_{*}\in \partial {\mathcal{U}}_{{\mathrm{E}}_0}.$

Moreover, from the definition of the mapping ${\pi }_{{\mathrm{E}}_0}\circ T$ and equality (31), it follows that

$$\begin{array}{cc}\hfill ({\pi }_{{\mathrm{E}}_0}\circ T)\left(x_{*}\right)& =\sum _{i=1}^m⟨T\left(x_{*}\right),v_i⟩v_i\hfill \\ \hfill & =\sum _{i=1}^m⟨y_{*},v_i⟩v_i\hfill \\ \hfill & ={\pi }_{{\mathrm{E}}_0}\left(y_{*}\right)\in ({\pi }_{{\mathrm{E}}_0}\circ \Phi )\left(x_{*}\right).\hfill \end{array}$$

This means that

$$x_{*}\in \mathrm{Coin}({\pi }_{{\mathrm{E}}_0}\circ T,{\pi }_{{\mathrm{E}}_0}\circ \Phi ),$$

whence, taking into account inclusion $x_{*}\in \partial {\mathcal{U}}_{{\mathrm{E}}_0}$, we deduce

$$x_{*}\in \mathrm{Coin}({\pi }_{{\mathrm{E}}_0}\circ T,{\pi }_{{\mathrm{E}}_0}\circ \Phi )\cap \partial {\mathcal{U}}_{{\mathrm{E}}_0},$$

which contradicts equality (20). Thus, we have established that $t_{*}\ne 0$.

Further, let us estimate the value of $⟨T\left(x_{*}\right)-y_{*},x_{*}⟩$. Using relations (31)–(34), we derive

$$\begin{array}{cc}\hfill ⟨T\left(x_{*}\right)-y_{*},x_{*}⟩& =⟨T\left(x_{*}\right)-y_{*},\sum _{i=1}^m{a}_i{v}_i⟩+⟨T\left(x_{*}\right)-y_{*},\sum _{j=1}^k{b}_j{w}_j⟩\hfill \\ \hfill & =\sum _{j=1}^k{b}_j⟨T\left(x_{*}\right)-y_{*},w_j⟩\hfill \\ \hfill & =-{\displaystyle \frac{(1-t_{*})}{t_{*}}}\sum _{j=1}^k{b}_j⟨p_j,x_{*}⟩\hfill \\ \hfill & =-{\displaystyle \frac{(1-t_{*})}{t_{*}}}\sum _{j=1}^k{b}_j^2\le 0.\hfill \end{array}$$

Similarly, it can be shown that

$$⟨T\left(x_{*}\right)-y_{*},v⟩=0,\forall v\in {\mathrm{E}}_0.$$

From the relations established above, it follows that $x_{*}\in \mathfrak{A}(\mathrm{E},{\mathrm{E}}_0)$. On the other hand, in the framework of the proof of Lemma 5, we have shown that $\mathfrak{A}(\mathrm{E},{\mathrm{E}}_0)=\varnothing$. This contradiction proves Lemma 6. □

Combining (26) and (27), we obtain the required equality (25).

Thus, we have established that the introduced characteristic $\mathrm{Deg}(T-\Phi ,\overline{\mathcal{U}},0)$ is well defined.

Remark 1. 

The topological degree for mappings of class ${\left(S\right)}_{+}$ with maximal monotone perturbations has been developed in [32,35].

4. Properties of Topological Degree for ${\left(\mathbf{S}\right)}_{+}$-Operators with Set-Valued Perturbations

In this section, following [37], we show that the constructed characteristic possesses natural properties of a topological degree.

Theorem 1 

(Additivity property). Let ${\mathcal{U}}^{\prime }$ and ${\mathcal{U}}^{\prime \prime }$ be disjoint open subsets of $\mathcal{U}$ such that

• the equality $\mathrm{Coin}(T,\Phi )\cap \left(\overline{\mathcal{U}}\setminus ({\mathcal{U}}^{\prime }\cup {\mathcal{U}}^{\prime \prime })\right)=\varnothing$ holds;
• the sets $\overline{{\mathcal{U}}^{\prime }\cap \mathrm{E}}$ and $\overline{{\mathcal{U}}^{\prime \prime }\cap \mathrm{E}}$ are local contractible, for any $\mathrm{E}\in \mathcal{F}\left(X\right)$.

Then

$$\mathrm{Deg}(T-\Phi ,\overline{\mathcal{U}},0)=\mathrm{Deg}(T-\Phi ,{\overline{\mathcal{U}}}^{\prime },0)+\mathrm{Deg}(T-\Phi ,{\overline{\mathcal{U}}}^{\prime \prime },0).$$

(35)

Proof. 

Note that the set $\mathcal{V}=\overline{\mathcal{U}}\setminus \left({\mathcal{U}}^{\prime }\cup {\mathcal{U}}^{\prime \prime }\right)$ satisfies the conditions of Lemma 5. Hence, there exists a subspace ${\mathrm{E}}_0\in \mathcal{F}\left(X\right)$ such that

$$\mathrm{E}\in \mathcal{F}\left(X\right) \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{E}\supset {\mathrm{E}}_0⟹\mathrm{Coin}({\pi }_{\mathrm{E}}\circ T,{\pi }_{\mathrm{E}}\circ \Phi )\cap \left({\overline{\mathcal{U}}}_{\mathrm{E}}\setminus ({\mathcal{U}}_{\mathrm{E}}^{\prime }\cup {\mathcal{U}}_{\mathrm{E}}^{\prime \prime })\right)=\varnothing ,$$

(36)

where ${\mathcal{U}}_{\mathrm{E}}^{\prime }$ and ${\mathcal{U}}_{\mathrm{E}}^{\prime \prime }$ stand for ${\mathcal{U}}^{\prime }\cap \mathrm{E}$ and ${\mathcal{U}}^{\prime \prime }\cap \mathrm{E}$, respectively.

Due to Proposition 5, there exists ${\sigma }_{\epsilon }\in \mathrm{appr}(\Sigma {|}_{{\overline{\mathcal{U}}}_{\mathrm{E}}},\epsilon )$, for any $\epsilon >0$.

From equality (36) and Lemma 3 it follows that if $\epsilon >0$ is small enough, then

$$({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon })\left(x\right)\ne 0,\forall x\in {\overline{\mathcal{U}}}_{\mathrm{E}}\setminus \left({\mathcal{U}}_{\mathrm{E}}^{\prime }\cup {\mathcal{U}}_{\mathrm{E}}^{\prime \prime }\right).$$

Taking into account the additivity property of the Brouwer degree, we obtain

$$\begin{array}{cc}\hfill & deg({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}},0)\hfill \\ \hfill & =deg({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}}^{\prime },0)+deg({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}}^{\prime \prime },0).\hfill \end{array}$$

(37)

On the other hand, according to Definition 13, we have

$$\begin{array}{cc}\hfill & \mathrm{Deg}(T-\Phi ,\overline{\mathcal{U}},0)=deg({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}},0),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & \mathrm{Deg}(T-\Phi ,{\overline{\mathcal{U}}}^{\prime },0)=deg({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}}^{\prime },0),\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & \mathrm{Deg}(T-\Phi ,{\overline{\mathcal{U}}}^{\prime \prime },0)=deg({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}}^{\prime \prime },0).\hfill \end{array}$$

(40)

Combining equalities (37)–(40), we arrive at relation (35). Thus, Theorem 1 is proved. □

Now, we will discuss the property of homotopy invariance of the constructed topological degree. Consider operators $T_i:\overline{\mathcal{U}}\to X^{*}$ and ${\Phi }_i={\psi }_i\circ {\Sigma }_i:\overline{\mathcal{U}}⊸X^{*}$, where $i=0,1$, satisfying conditions (H.1)–(H.3) with

$$T:=T_i,\Phi :={\Phi }_i,\psi :={\psi }_i,\Sigma :={\Sigma }_i.$$

Definition 14. 

The set-valued mappings $T_0-{\Phi }_0$ and $T_1-{\Phi }_1$ are homotopic with respect to the set $\mathcal{U}$ if the following four conditions hold:

• There exists a strong-to-weak continuous mapping $\tilde{T}:\overline{\mathcal{U}}\times [0,1]\to X^{*}$ such that

  $$\tilde{T}(·,0)=T_0,\tilde{T}(·,1)=T_1,$$
  and, for any sequences ${\left\{x_n\right\}}_{n=1}^{\infty }\subset \partial \mathcal{U}$ and ${\left\{t_n\right\}}_{n=1}^{\infty }\subset [0,1]$, from $x_n\rightharpoonup x_0$ in X and

  $$\underset{n\to \infty }{lim\; sup}⟨\tilde{T}(x_n,t_n),x_n-x_0⟩\le 0$$
  it follows that $x_n\to x_0$ in X as $n\to \infty$.
• There exist a set-valued mapping $\tilde{\Sigma }\in \mathrm{ASV}(\overline{\mathcal{U}}\times [0,1],\mathcal{Y})$ and a continuous single-valued mapping $\tilde{\psi }:\mathcal{Y}\times [0,1]\to X^{*}$ such that

  $$\begin{array}{c}\tilde{\Sigma }(·,0)={\Sigma }_0,\tilde{\Sigma }(·,1)={\Sigma }_1,\\ \tilde{\psi }(·,0)={\psi }_0,\tilde{\psi }(·,1)={\psi }_1.\end{array}$$
• For the set-valued mapping $\tilde{\Phi }:\overline{\mathcal{U}}\times [0,1]⊸X^{*}$ defined by

  $$\tilde{\Phi }(x,t):=\tilde{\psi }(\tilde{\Sigma }(x,t),t),\forall (x,t)\in \overline{\mathcal{U}}\times [0,1],$$
  the set $\tilde{\Phi }(\overline{\mathcal{U}}\times [0,1])$ is relatively compact in $X^{*}$.
• The intersection of the sets $\mathcal{U}\times [0,1]$ and $\mathrm{Coin}(\tilde{T},\tilde{\Phi })$, where

  $$\mathrm{Coin}(\tilde{T},\tilde{\Phi }):=\left\{(x,t)\in \overline{\mathcal{U}}\times [0,1]:\tilde{T}(x,t)\in \tilde{\Phi }(x,t)\right\},$$
  is the empty set.

Theorem 2 

(Invariance under homotopy). If the set-valued mappings $T_0-{\Phi }_0$ and $T_1-{\Phi }_1$ are homotopic with respect to the set $\mathcal{U}$, then

$$\mathrm{Deg}(T_0-{\Phi }_0,\overline{\mathcal{U}},0)=\mathrm{Deg}(T_1-{\Phi }_1,\overline{\mathcal{U}},0).$$

Proof. 

Taking into account the last condition in Definition 14, by the same arguments as in Lemma 5, one can prove the existence of a subspace ${\mathrm{E}}_0\in \mathcal{F}\left(X\right)$ such that

$$\mathrm{E}\in \mathcal{F}\left(X\right) \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{E}\supset {\mathrm{E}}_0⟹\mathrm{Coin}({\pi }_{\mathrm{E}}\circ \tilde{T},{\pi }_{\mathrm{E}}\circ \tilde{\Phi })\cap \left(\partial {\mathcal{U}}_{\mathrm{E}}\times [0,1]\right)=\varnothing .$$

(41)

For the set-valued mapping $\tilde{\Sigma }{|}_{{\overline{\mathcal{U}}}_{\mathrm{E}}\times [0,1]}$, all the conditions of Proposition 5. Therefore, there exists ${\tilde{\sigma }}_{\epsilon }\in \mathrm{appr}(\tilde{\Sigma }{|}_{{\overline{\mathcal{U}}}_{\mathrm{E}}\times [0,1]},\epsilon )$, for any $\epsilon >0$.

Let ${\sigma }_{i\epsilon }:={\tilde{\sigma }}_{\epsilon }(·,i)$, where $i=0,1$. Clearly, if $\epsilon >0$ is small enough, then the mapping ${\sigma }_{i\epsilon }$ can be used as a continuous approximation of the set-valued mapping ${\Sigma }_i{|}_{{\overline{\mathcal{U}}}_{\mathrm{E}}}$ (see Lemma 2 (iii)) to calculate $\mathrm{Deg}(T_i-{\Phi }_i,\overline{\mathcal{U}},0)$. Namely, we have

$$\mathrm{Deg}(T_i-{\Phi }_i,\overline{\mathcal{U}},0)=deg({\pi }_{\mathrm{E}}\circ T_i-{\pi }_{\mathrm{E}}\circ {\psi }_i\circ {\sigma }_{i\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}},0),i=0,1.$$

Therefore, to prove Theorem 2, it is sufficient to establish the following equality

$$deg({\pi }_{\mathrm{E}}\circ T_0-{\pi }_{\mathrm{E}}\circ {\psi }_0\circ {\sigma }_{0\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}},0)=deg({\pi }_{\mathrm{E}}\circ T_1-{\pi }_{\mathrm{E}}\circ {\psi }_1\circ {\sigma }_{1\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}},0).$$

(42)

Let us use a one-parameter family of mappings ${\{{\tilde{H}}_t:{\overline{\mathcal{U}}}_{\mathrm{E}}\to X^{*}\}}_{t\in [0,1]}$ defined by

$${\tilde{H}}_t\left(x\right):=\tilde{T}(x,t)-\tilde{\psi }({\tilde{\sigma }}_{\epsilon }(x,t),t),\forall (x,t)\in {\overline{\mathcal{U}}}_{\mathrm{E}}\times [0,1].$$

Clearly, we have

$${\tilde{H}}_i\left(x\right)=T_i\left(x\right)-({\psi }_i\circ {\sigma }_{i\epsilon })\left(x\right),i=0,1.$$

(43)

Moreover, from equality (41) and Lemma 3 it follows that

$$\mathrm{Coin}({\pi }_{\mathrm{E}}\circ \tilde{T},{\pi }_{\mathrm{E}}\circ \tilde{\psi }\circ {\tilde{\sigma }}_{\epsilon })\cap \left(\partial {\overline{\mathcal{U}}}_{\mathrm{E}}\times [0,1]\right)=\varnothing ,$$

and hence,

$$({\pi }_{\mathrm{E}}\circ {\tilde{H}}_t)\left(x\right)\ne 0,\forall x\in \partial {\overline{\mathcal{U}}}_{\mathrm{E}},t\in [0,1].$$

Therefore, by the homotopy invariance property of the Brouwer degree, we obtain

$$deg({\pi }_{\mathrm{E}}\circ {\tilde{H}}_0,{\overline{\mathcal{U}}}_{\mathrm{E}},0)=deg({\pi }_{\mathrm{E}}\circ {\tilde{H}}_1,{\overline{\mathcal{U}}}_{\mathrm{E}},0).$$

(44)

Combining relations (43) and (44), we arrive at equality (42). This completes the proof of Theorem 2. □

One of the most important properties of the introduced degree is formulated in the following theorem.

Theorem 3 

(Zero degree). If conditions (H.1)–(H.3) hold and $\mathrm{Coin}(T,\Phi )=\varnothing$, then

$$\mathrm{Deg}(T-\Phi ,\overline{\mathcal{U}},0)=0.$$

Proof. 

For the set $\mathcal{V}=\overline{\mathcal{U}}$, all the conditions of Lemma 5 are valid. Therefore, there exists a subspace ${\mathrm{E}}_0\in \mathcal{F}\left(X\right)$ such that

$$\mathrm{E}\in \mathcal{F}\left(X\right) \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{E}\supset {\mathrm{E}}_0⟹\mathrm{Coin}({\pi }_{\mathrm{E}}\circ T,{\pi }_{\mathrm{E}}\circ \Phi )\cap {\overline{\mathcal{U}}}_{\mathrm{E}}=\varnothing .$$

(45)

In view of Proposition 5, there exists ${\sigma }_{\epsilon }\in \mathrm{appr}(\Sigma {|}_{{\overline{\mathcal{U}}}_{\mathrm{E}}},\epsilon )$, for any $\epsilon >0$.

From equality (45) and Lemma 3 it follows that if $\epsilon >0$ is small enough, then

$$\left({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon }\right)\left(x\right)\ne 0,\forall x\in {\overline{\mathcal{U}}}_{\mathrm{E}},$$

whence, by the properties of the Brouwer degree and Definition 13, we obtain

$$\mathrm{Deg}(T-\Phi ,\overline{\mathcal{U}},0)=deg({\pi }_{\mathrm{E}}\circ T-{\pi }_{\mathrm{E}}\circ \psi \circ {\sigma }_{\epsilon },{\overline{\mathcal{U}}}_{\mathrm{E}},0)=0.$$

Thus, Theorem 3 is proved. □

As a direct consequence, we obtain the following coincidence principle.

Theorem 4 

(Existence solution property). Suppose that conditions (H.1)–(H.4) hold and

$$\mathrm{Deg}(T-\Phi ,\overline{\mathcal{U}},0)\ne 0.$$

Then the coincidence set $\mathrm{Coin}(T,\Phi )$ is nonempty; that is, the inclusion $T\left(x\right)\in \Phi \left(x\right)$ has at least one solution in the set $\mathcal{U}$.

The last theorem shows that our degree theory can be used as a tool for checking the existence of solutions to operator inclusions. Moreover, arguing as in [40], one can establish the compactness of the coincidence set.

Theorem 5 

(Compactness property). Under the conditions of Theorem 4, the coincidence set $\mathrm{Coin}(T,\Phi )$ is compact.

5. Application: Optimal Feedback Control for Generalized Navier–Stokes System

In this section, we apply the obtained results to studying the solvability of an optimal feedback control problem for generalized stationary Navier–Stokes equations in the weak formulation.

5.1. Statement of Optimal Control Problem

Consider the following optimal control problem for the model describing the steady flow of an incompressible generalized Newtonian fluid with shear-dependent viscosity:

$$\left\{\begin{array}{cc}(\overrightarrow{v}·\nabla )\overrightarrow{v}-\mathrm{div}\mathbb{S}+\nabla p=\overrightarrow{f}+\overrightarrow{u}\hfill & \mathrm{i}\mathrm{n} \Omega ,\hfill \\ \nabla ·\overrightarrow{v}=0\hfill & \mathrm{i}\mathrm{n} \Omega ,\hfill \\ \mathbb{S}={\eta }_0\mathbb{D}\left(\overrightarrow{v}\right)+\eta \left(\right|\mathbb{D}\left(\overrightarrow{v}\right)\left|\right)\mathbb{D}\left(\overrightarrow{v}\right)\hfill & \mathrm{i}\mathrm{n} \Omega ,\hfill \\ \overrightarrow{v}=\overrightarrow{0}\hfill & \mathrm{o}\mathrm{n} \Gamma ,\hfill \\ \overrightarrow{u}\in \Sigma \left(\overrightarrow{v}\right),\hfill \\ J=J\left(\overrightarrow{v}\right)\to min,\hfill \end{array}\right.$$

(46)

where

• $\Omega$ is a bounded Lipschitz domain in ${\mathbb{R}}^d$, $d=2$ or 3, representing the flow region;
• $\Gamma$ denotes the boundary of the domain $\Omega$;
• $\overrightarrow{v}=\overrightarrow{v}\left(\overrightarrow{x}\right)$ is the velocity vector;
• $\mathbb{S}={\left({\mathrm{S}}_{ij}\left(\overrightarrow{x}\right)\right)}_{i,j=1}^d$ is the stress tensor deviator;
• $p=p\left(\overrightarrow{x}\right)$ is the pressure;
• $\overrightarrow{f}=\overrightarrow{f}\left(\overrightarrow{x}\right)$ is the given external body force;
• $\overrightarrow{u}=\overrightarrow{u}\left(\overrightarrow{x}\right)$ is the control vector function;
• the operators ∇ and “div” are the gradient and the divergence, respectively,

  $$\nabla :=\left({\displaystyle \frac{\partial }{\partial x_1}},\cdots ,{\displaystyle \frac{\partial }{\partial x_d}}\right),\mathrm{div}\mathbb{S}:=\left(\sum _{i=1}^d{\displaystyle \frac{\partial {\mathrm{S}}_{i1}}{\partial x_i}},\cdots ,\sum _{i=1}^d{\displaystyle \frac{\partial {\mathrm{S}}_{id}}{\partial x_i}}\right);$$
• $\mathbb{D}\left(\overrightarrow{v}\right)$ denotes the rate-of-strain tensor,

  $$\mathbb{D}\left(\overrightarrow{v}\right):={\displaystyle \frac{1}{2}}\left(\nabla \overrightarrow{v}+{(\nabla \overrightarrow{v})}^{\top }\right);$$
• ${\eta }_0$ is the “Newtonian” viscosity, ${\eta }_0>0$;
• $\eta =\eta \left(\right|\mathbb{D}\left(\overrightarrow{v}\right)\left|\right)$ is the “non-Newtonian” viscosity, $\eta \left(\right|\mathbb{D}\left(\overrightarrow{v}\right)\left|\right)\ge 0$;
• $\Sigma =\Sigma \left(\overrightarrow{v}\right)$ is the feedback control function (set-valued operator);
• $J=J\left(\overrightarrow{v}\right)$ is the cost functional (real-valued function).

A feature of optimal control problem (46) is that values of the functional J are independent of $\overrightarrow{u}$. A control with such a cost functional is referred to as rigid [56].

Note that, in the particular case $\eta \equiv 0$, the first three equations in (46) reduce to the incompressible stationary Navier–Stokes system describing the steady motion of fluids with constant viscosity.

5.2. Function Spaces and Assumptions on Model Data

First, we introduce some notation and the function spaces used.

For $s\in [1,\infty )$ and $k\in \mathbb{N}$, by $L^s(\Omega )$ and $H^k(\Omega )$ we denote the Lebesgue and Sobolev spaces, respectively. The definitions and detailed descriptions of the properties of these spaces can be found in the monographs [57,58].

Let

$$\begin{array}{cc}\hfill L^s{(\Omega )}^d& :=\underset{d\mathrm{times}}{\underbrace{L^s(\Omega )\times \cdots \times L^s(\Omega )}},\hfill \\ \hfill H^k{(\Omega )}^d& :=\underset{d\mathrm{times}}{\underbrace{H^k(\Omega )\times \cdots \times H^k(\Omega )}}.\hfill \end{array}$$

Furthermore, we introduce the three spaces:

$$\begin{array}{cc}\hfill \mathfrak{D}{(\Omega )}^d& :=\left\{\overrightarrow{\varphi }:\Omega \to {\mathbb{R}}^d:\overrightarrow{\varphi }\in C^{\infty }{(\Omega )}^d,\mathrm{supp}\overrightarrow{\varphi }\subset \Omega \right\},\hfill \\ \hfill {\mathfrak{D}}_{\mathrm{sol}}{(\Omega )}^d& :=\left\{\overrightarrow{\varphi }\in \mathfrak{D}{(\Omega )}^d:\nabla ·\overrightarrow{\varphi }=0\right\},\hfill \\ \hfill V(\Omega )& \mathrm{i}\mathrm{s} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{c}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{e}\mathrm{t} {\mathfrak{D}}_{\mathrm{sol}}{(\Omega )}^d \mathrm{i}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{e} H^1{(\Omega )}^d.\hfill \end{array}$$

Note that $V(\Omega )$ is a Hilbert space and, for $d=2,3$, the embedding $V(\Omega )\hookrightarrow L^4{(\Omega )}^d$ is compact.

For any matrices $\mathbb{A}={\left({\mathrm{A}}_{ij}\right)}_{i,j=1}^d$ and $\mathbb{B}={\left({\mathrm{B}}_{ij}\right)}_{i,j=1}^d$, by $\mathbb{A}:\mathbb{B}$ and $\left|\mathbb{A}\right|$ we denote their scalar product and the Euclidean norm of $\mathbb{A}$, respectively:

$$\mathbb{A}:\mathbb{B}:=\sum _{i=1}^d{\mathrm{A}}_{ij}{\mathrm{B}}_{ij},\left|\mathbb{A}\right|:={(\mathbb{A}:\mathbb{A})}^{1/2}.$$

Suppose that

(A.1)

the vector function $\overrightarrow{f}:\Omega \to {\mathbb{R}}^d$ belongs to the space $L^2{(\Omega )}^d$;

(A.2)

the function $\eta :{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$, where ${\mathbb{R}}_{+}:=[0,\infty )$, is continuous and bounded;

(A.3)

the inequality

$$\left(\eta \right(\left|\mathbb{X}\right|)\mathbb{X}-\eta (\left|\mathbb{Y}\right|\left)\mathbb{Y}\right):(\mathbb{X}-\mathbb{Y})\ge 0$$

holds for any symmetric $d\times d$-matrices $\mathbb{X}$ and $\mathbb{Y}$;

(A.4)

the set-valued mapping $\Sigma :V(\Omega )⊸L^2{(\Omega )}^d$ is upper-semicontinuous;

(A.5)

for any vector function $\overrightarrow{v}\in V(\Omega )$, the set $\Sigma \left(\overrightarrow{v}\right)$ is aspheric in the space $L^2{(\Omega )}^d$;

(A.6)

for any bounded set $\mathcal{B}\subset V(\Omega )$, the set $\Sigma \left(\mathcal{B}\right)$ is relatively compact in the space $L^2{(\Omega )}^d$;

(A.7)

the set-valued mapping $\Sigma$ is globally bounded; that is, there exists a constant $q_{max}$ such that, for any vector function $\overrightarrow{v}\in V(\Omega )$, we have

$$\underset{q\in \Sigma \left(\overrightarrow{v}\right)}{sup}{\parallel q\parallel }_{L^2{(\Omega )}^d}\le q_{max};$$

(A.8)

the functional $J:V(\Omega )\to \mathbb{R}$ is lower semicontinuous.

Note that condition (A.3), which is imposed for the viscosity function $\eta$, holds when the function $\tilde{\eta }:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$, $\tilde{\eta }\left(\tau \right):=\eta \left(\tau \right)\tau$ is non-decreasing. Indeed, using the Cauchy–Schwarz inequality $|\mathbb{X}:\mathbb{Y}|\le \left|\mathbb{X}\right|\left|\mathbb{Y}\right|$, we obtain

$$\begin{array}{cc}\hfill & \left\{\eta \left(\right|\mathbb{X}\left|\right)\mathbb{X}-\eta \left(\right|\mathbb{Y}\left|\right)\mathbb{Y}\right\}:\left(\mathbb{X}-\mathbb{Y}\right)\hfill \\ \hfill & ={\eta \left(\right|\mathbb{X}\left|\right)\left|\mathbb{X}\right|}^2-\eta \left(\right|\mathbb{X}\left|\right)\mathbb{X}:\mathbb{Y}-\eta \left(\right|\mathbb{Y}\left|\right)\mathbb{Y}:\mathbb{X}+{\eta \left(\right|\mathbb{Y}\left|\right)\left|\mathbb{Y}\right|}^2\hfill \\ \hfill & \ge {\eta \left(\right|\mathbb{X}\left|\right)\left|\mathbb{X}\right|}^2-\eta \left(\right|\mathbb{X}\left|\right)\left|\mathbb{X}\right|\left|\mathbb{Y}\right|-\eta \left(\right|\mathbb{Y}\left|\right)\left|\mathbb{Y}\right|\left|\mathbb{X}\right|+{\eta \left(\right|\mathbb{Y}\left|\right)\left|\mathbb{Y}\right|}^2\hfill \\ \hfill & =\left\{\eta \left(\right|\mathbb{X}\left|\right)\left|\mathbb{X}\right|-\eta \left(\right|\mathbb{Y}\left|\right)\left|\mathbb{Y}\right|\right\}\left(\left|\mathbb{X}\right|-\left|\mathbb{Y}\right|\right)\hfill \\ \hfill & =\left\{\tilde{\eta }\left(\right|\mathbb{X}\left|\right)-\tilde{\eta }\left(\right|\mathbb{Y}\left|\right)\right\}\left(\left|\mathbb{X}\right|-\left|\mathbb{Y}\right|\right)\ge 0,\hfill \end{array}$$

for any $d\times d$-matrices $\mathbb{X}$ and $\mathbb{Y}$.

Recall that materials whose viscosity increases with the rate of shear strain are called dilatant [59] (also termed shear-thickening [60,61]). As examples of dilatant fluids, we can mention highly concentrated suspensions: starch paste, a suspension of river sand, etc.

Typical examples of the cost functional J are

$$\begin{array}{cc}\hfill & J=J_1\left(\overrightarrow{v}\right):=\underset{\Omega }{\int }{|\overrightarrow{v}-{\overrightarrow{v}}_{*}|}^2\mathrm{d}\overrightarrow{x},\hfill \\ \hfill & J=J_2\left(\overrightarrow{v}\right):=\underset{\Omega }{\int }{\left|\mathbb{D}\left(\overrightarrow{v}\right)\right|}^2\mathrm{d}\overrightarrow{x},\hfill \\ \hfill & J=J_3\left(\overrightarrow{v}\right):=\underset{\Omega }{\int }{\left|\mathbb{W}\left(\overrightarrow{v}\right)\right|}^2\mathrm{d}\overrightarrow{x},\hfill \end{array}$$

where ${\overrightarrow{v}}_{*}:\Omega \to {\mathbb{R}}^d$ is a given vector function representing the desired velocity distribution in the flow region $\Omega$ and $\mathbb{W}\left(\overrightarrow{v}\right)$ denotes the spin tensor, $\mathbb{W}\left(\overrightarrow{v}\right):=\left(\nabla \overrightarrow{v}-{(\nabla \overrightarrow{v})}^{\top }\right)/2$. It is easy to see that each of these functionals satisfies condition (A.8).

5.3. Weak Formulation of Optimal Control Problem and Existence Theorem

Definition 15. 

We will say that a vector function $\overrightarrow{v}\in V(\Omega )$ is an admissible weak solution of problem (46) if

$$\begin{array}{c}-\sum _{k=1}^d\underset{\Omega }{\int }{v}_k\overrightarrow{v}·{\displaystyle \frac{\partial \overrightarrow{w}}{\partial x_k}}\mathrm{d}\overrightarrow{x}+{\eta }_0\underset{\Omega }{\int }\mathbb{D}\left(\overrightarrow{v}\right):\mathbb{D}\left(\overrightarrow{w}\right)\mathrm{d}\overrightarrow{x}+\underset{\Omega }{\int }\eta \left(\right|\mathbb{D}\left(\overrightarrow{v}\right)\left|\right)\mathbb{D}\left(\overrightarrow{v}\right):\mathbb{D}\left(\overrightarrow{w}\right)\mathrm{d}\overrightarrow{x}\\ =\underset{\Omega }{\int }\overrightarrow{u}·\overrightarrow{w}\mathrm{d}\overrightarrow{x}+\underset{\Omega }{\int }\overrightarrow{f}·\overrightarrow{w}\mathrm{d}\overrightarrow{x},\forall \overrightarrow{w}\in V(\Omega ),\end{array}$$

for some vector function $\overrightarrow{u}\in \Sigma \left(\overrightarrow{v}\right)$.

By ${\mathfrak{M}}_{\mathrm{ad}}$ we denote the set of all admissible weak solutions of (46).

Definition 16. 

We will say that a vector function ${\overrightarrow{v}}_{*}\in V(\Omega )$ is an optimal weak solution of problem (46) if this vector function belongs to the set ${\mathfrak{M}}_{\mathrm{ad}}$ and the following equality holds:

$$J\left({\overrightarrow{v}}_{*}\right)=\underset{\overrightarrow{v}\in {\mathfrak{M}}_{\mathrm{ad}}}{inf}J\left(\overrightarrow{v}\right).$$

Let us introduce the operators $\psi$, T, and $\Phi$ by the following formulae:

$$\begin{array}{cc}\hfill & \psi :L^2(\Omega )\to V^{*}(\Omega ),\hfill \\ \hfill & {⟨\psi \left(\overrightarrow{u}\right),\overrightarrow{w}⟩}_{V^{*}(\Omega )\times V(\Omega )}:=\underset{\Omega }{\int }\overrightarrow{u}·\overrightarrow{w}\mathrm{d}\overrightarrow{x},\forall \overrightarrow{u}\in L^2{(\Omega )}^d,\overrightarrow{w}\in V(\Omega ),\hfill \\ \hfill & T:V(\Omega )\to V^{*}(\Omega ),\hfill \\ \hfill & {⟨T\left(\overrightarrow{v}\right),\overrightarrow{w}⟩}_{V^{*}(\Omega )\times V(\Omega )}:=-\sum _{k=1}^d\underset{\Omega }{\int }{v}_k\overrightarrow{v}·{\displaystyle \frac{\partial \overrightarrow{w}}{\partial x_k}}\mathrm{d}\overrightarrow{x}+{\eta }_0\underset{\Omega }{\int }\mathbb{D}\left(\overrightarrow{v}\right):\mathbb{D}\left(\overrightarrow{w}\right)\mathrm{d}\overrightarrow{x}\hfill \\ \hfill & +\underset{\Omega }{\int }\eta \left(\right|\mathbb{D}\left(\overrightarrow{v}\right)\left|\right)\mathbb{D}\left(\overrightarrow{v}\right):\mathbb{D}\left(\overrightarrow{w}\right)\mathrm{d}\overrightarrow{x}-\underset{\Omega }{\int }\overrightarrow{f}·\overrightarrow{w}\mathrm{d}\overrightarrow{x},\forall \overrightarrow{v},\overrightarrow{w}\in V(\Omega ),\hfill \end{array}$$

and

$$\Phi :V(\Omega )\to V^{*}(\Omega ),\Phi :=\psi \circ \Sigma .$$

Clearly, the problem of finding an admissible weak solution of (46) is equivalent to the inclusion $T\left(\overrightarrow{v}\right)\in \Phi \left(\overrightarrow{v}\right).$

Using Proposition 1 and condition (A.3), one can show that the operator T is of class ${\left(S\right)}_{+}$. Moreover, due to conditions (A.4) and (A.5), the set-valued mapping $\Phi$ belongs to the class $C-\mathrm{A}\mathrm{S}\mathrm{V}$.

Taking into account conditions (A.1)–(A.8), by Theorems 4 and 5, we establish the following result.

Theorem 6 

(Existence of optimal weak solutions). Under conditions(A.1)–(A.8), problem (46) has at least one optimal weak solution in the sense of Definition 16.

Remark 2. 

The proposed approach can also be applied to the investigation of various control problems arising in other models for fluid flows [62,63,64,65,66], as well as in heat and mass transfer models [67,68,69,70,71].

6. Conclusions

This article develops the topological degree method for studying the operator inclusions of the form $T\left(x\right)\in \Phi \left(x\right)$, where T is a single-valued ${\left(S\right)}_{+}$-operator and $\Phi$ is a compact set-valued operator. Using the topological degree of $T-\Phi$, we have established sufficient conditions for the solvability of the inclusion $T\left(x\right)\in \Phi \left(x\right)$. This result is an important generalization of the known results from fixed point theory for set-valued mappings. A feature of our approach is that it successfully combines very different techniques such as the monotonicity method and the principle of continuous single-valued approximation of set-valued mappings. Moreover, unlike conventional approaches used in topological degree theory for set-valued operators, we do not require the convexity condition of values of $\Phi$. This extends a range of possible applications. In particular, we give an example illustrating how the introduced topological degree can be used in the analysis of the solvability of a strongly nonlinear system of partial differential equations and inclusions describing feedback control with complex geometry of admissible controls sets. A natural extension of this work includes analyzing topological characteristics of monotone-type single-valued operators with non-compact (for example, T-condensing) set-valued perturbations and their real-world applications.