A Novel Scheme of the ARA Transform for Solving Systems of Partial Fractional Differential Equations

Abstract

In this article, a new analytical scheme of the ARA transform is introduced to solve systems of fractional partial differential equations. The principle of the proposed technique is based on combining the ARA transform with the residual power series method to create an approximate series solution for a system of partial differential equations of fractional order on the form of a rapid convergent series. To illustrate the effectiveness, accuracy, and validity of the suggested technique, an Attractive physical system, the fractional neutron diffusion equation with one delayed neutrons group, is discussed and solved. Two different neutron flux initial conditions are presented numerically to clarify various cases in order to ensure the theoretical results. The necessary Mathematica codes are run using vital nuclear reactor cross-section data, and the results for various values of time are tabulated and graphically represented.

1. Introduction

Fractional calculus is a parallel area of calculus that cannot be viewed as an expanded form of integer order. In many areas, fractional order systems are preferable to integer order systems because they may explain phenomena that are related to memory and affected by inherited traits [1,2,3,4,5,6,7,8]. Many definitions of the derivative and integral of fractional order have been created since the seventeenth century, when fractional calculus first appeared. The definitions of fractional operators that are most significant are Caputo and Riemann-Liouville definitions [9,10,11,12]. The fractional derivative and fractional integral have just been given new definitions, the Atangana–Baleanu definition and the conformable fractional derivative definition are the two most significant ones [13,14,15,16]. By creating fractional models, many researchers have used them. Nevertheless, Caputo’s definition is still considered to be acceptable and desirable by the majority of scholars.

There have been numerous contributions made to the research area for solving systems of fractional partial differential equations (FPDEs). Finding analytical solutions for systems of FPDEs can occasionally involve complicated calculations, so analytical and numerical techniques have been created and improved to obtain solutions of linear and nonlinear systems of FPDEs [17,18,19,20,21].

The KdV-Burgers equations [22], the nonlinear Schrodinger equations [23], the neutron diffusion equations [24] are just a few examples of fractional order differential equations for which the residual power series technique (RPST) has proven to be successful and accurate in creating approximate series solutions. Moreover, many systems of linear and nonlinear equations that have appeared in a variety of engineering and science domains have been solved analytically using RPST [25,26,27]. Without linearization, perturbation, or discretization, the RPST is a powerful technique for creating power series solutions of differential equations. RPST does not need comparing the coefficients of the related terms, in contrast to the standard power series approach. By using a series of equations with one or more variables, this technique calculates the power series coefficients. On the other hand, many powerful methods for solving differential equations have been presented [28,29,30,31].

The ARA residual power series technique (ARA-RPST) is used in this investigation, which was first published in [32], to create analytical and approximate solutions for the linear and nonlinear systems of FPDEs. This method combines the ARA transform [33,34] and RPST.

One of the most interesting physics problems that are expressed through partial differential equations is the neutron diffusion equations with delayed neutrons system (NDEDNS) of the form [35,36,37,38]:

$$\begin{gathered} \frac{1}{v_u}{z}_t\left(x,t\right)=D{z}_{xx}\left(x,t\right)+\left(\mathsf{\gamma }{\sum }_f-{\sum }_a\right)z\left(x,t\right)+\lambda u(x,t), \\ {u}_t\left(x,t\right)=\beta \mathsf{\gamma }{\sum }_{f}z\left(x,t\right)-\lambda u(x,t), \end{gathered}$$

(1)

with initial conditions:

$$z\left(x,0\right)=z_0\left(x\right),u\left(x,0\right)=\frac{\beta \mathsf{\gamma }{\sum }_f}{\lambda }{z}_0\left(x\right),$$

(2)

where $z\left(x,t\right)$ is the neutron flux, $u\left(x,t\right)$ is the delayed neutron density, $v_u$ is neutron velocity, ${\sum }_a$ is the macroscopic absorption cross-section, $D$ is the neutron diffusion coefficient and β, λ, and γ are the fraction of the delayed fission neutrons, the radioactive decay constant, and the average number of neutrons produced per fission, respectively.

The coupled fractional neutron diffusion equations with delayed neutrons with one group of delayed neutrons were solved by Adomian decomposition method (ADM) to get an analytical approximation solution [35]. Furthermore, an exact solution in the case of one-dimensional neutron diffusion kinetic equation with one delayed precursor concentration in Cartesian geometry was studied in [36].

In this article, we are interested in implementing the ARA-RPST to find the approximate series solution of one group of neutron diffusion equations when delayed neutrons are averaged by one group of delayed neutrons [35]:

$$\begin{gathered} \frac{1}{v_u}{\mathfrak{D}}_t^{\alpha }z\left(x,t\right)=D{z}_{xx}\left(x,t\right)+\left(\gamma {\sum }_f-{\sum }_a\right)z\left(x,t\right)+\lambda u\left(x,t\right), \\ {\mathfrak{D}}_t^{\alpha }u\left(x,t\right)=\beta \gamma {\sum }_{f}z\left(x,t\right)-\lambda u(x,t), \end{gathered}$$

(3)

$0<\alpha <1,$ with the initial conditions

$$z\left(x,0\right)=z_0\left(x\right),u\left(x,0\right)=\frac{\beta \mathsf{\gamma }{\sum }_f}{\lambda }{z}_0\left(x\right).$$

(4)

To achieve our goal, we operate the ARA transform on the equations in (3) and then we formulate the new system’s solution as a series expansion, with the expansion coefficients coming from the idea of the limit at infinity. After that, we apply the ARA transform inverse on the obtained solution to transform it to the original space. When compared to the residual power series approach, ARA-RPST requires fewer calculations to obtain the coefficients because instead of using a fractional derivation such as in RPST, it depends on the concept of the limit. The current method is speedy, uses little computer memory. Additionally, the power series coefficients are computed using a set of equations involving more than one variable, indicating that the present method has a rapid convergence.

The format of this study is as follows: Definitions, concepts, and properties related to the ARA transform and fractional derivatives are covered in further detail in the next section. In Section 3, we formulate series solutions for fractional neutron diffusion equations with one delayed neutrons group using the ARA-RPST. The current methodology has been applied to investigate a number of fractional equations, as shown in Section 4. Finally, the conclusion section includes a summary of our findings.

2. Fundamental Concepts and Properties

This section includes the definition of the Caputo fractional operator. Additionally, some theorems and properties pertaining to the ARA-RPST are provided.

Definition 1.

For $n$ to be the smallest integer that exceeds $\alpha$, the Caputo fractional derivatives of order $\alpha >0$ is given by

$${\mathfrak{D}}_{\mathrm{t}}^{\alpha }z\left(x,t\right)=J_t^{n-\alpha }{\mathfrak{D}}_t^{n}z\left(x,t\right), n-1<\alpha <n, n\in \mathbb{N},x\in I, t>0,$$

where $I$ is an interval and $J_t^{\beta }$ isthe time-fractional Riemann–Liouville integral operator of order $\alpha >0$, defined as

$$J_t^{\beta }z\left(x,t\right)=\left\{\begin{array}{c}\frac{1}{\Gamma \left(\beta \right)}\underset{0}{\overset{t}{\int }}{\left(t-\tau \right)}^{\beta -1}z\left(x,\tau \right)d\tau , \beta >0, t>\tau \ge 0\\ \hfill z\left(x,t\right), \beta =0.\hfill \end{array}\right.$$

Definition 2

([33]). The ARA transform of order $m$of the continuous function $z(x,t)$ on $I\times \left[0,\infty \right.)$ for the variable $t$, is given by

$${\mathcal{A}}_m\left[z\left(x,t\right)\right](s)=s\underset{0}{\overset{\mathrm{\infty }}{\int }}{t}^{m-1}{e}^{-st}z\left(x,t\right)dt,s>0.$$

For  $m=1,$  The ARA transform  ${\mathcal{A}}_1$  is defined as

$${\mathcal{A}}_1\left[z\left(x,t\right)\right](s)=s\underset{0}{\overset{\mathrm{\infty }}{\int }}{e}^{-st}z\left(x,t\right)dt.$$

For  $m=2,$  The ARA transform  ${\mathcal{A}}_2$  is defined as

$${\mathcal{A}}_2\left[z\left(x,t\right)\right](s)=s\underset{0}{\overset{\mathrm{\infty }}{\int }}\mathrm{t}{e}^{-st}z\left(x,t\right)dt.$$

Definition 3

([32]). The ARA transform inverse is defined as

$$z\left(x,t\right)={\mathcal{A}}_{m+1}^{-1}\left[{\mathcal{A}}_{m+1}\left[z\left(x,t\right)\right]\right]=\frac{{\left(-1\right)}^m}{2\pi i}\underset{c-i\infty }{\overset{c+i\infty }{\int }}{e}^{st}\left((-{1)}^m\left(\frac{1}{s\mathsf{\Gamma }\left(m-1\right)}\underset{0}{\overset{s}{\int }}{\left(s-w\right)}^{m-1}{\mathcal{A}}_{m+1}\left[z\left(x,t\right)\right](w)dw+\sum _{k=0}^{m-1}\frac{s^k}{k!}\frac{{\partial }^{k}Z\left(x,0\right)}{\partial s^k}\right)\right)ds,$$

where

$$Z\left(x,s\right)=\underset{0}{\overset{\infty }{\int }}{e}^{-st}z\left(x,t\right)dt,$$

is  $(m-1)$  times differentiable.

The following lemma contains some of the ARA transform properties that are essential to our investigation.

Lemma 1

([32,33,34]). Let $z(x,t)$and $u(x,t)$ be continuous functions. Then

• ${\mathcal{A}}_m\left[p z\left(x,t\right)+q u\left(x,t\right)\right]\left(s\right)=p {\mathcal{A}}_m\left[z\left(x,t\right)\right]\left(s\right)+{q \mathcal{A}}_m\left[u\left(x,t\right)\right]\left(s\right),$ where $p$ and $q$ are nonzero constants.
• $\underset{s\to \mathrm{\infty }}{\lim }s{\mathcal{A}}_2\left[u\left(x,t\right)\right](s)=u\left(x,0\right),x\in I,s>0.$
• ${\mathcal{A}}_2\left[{\mathfrak{D}}_t^{\alpha }u\left(x,t\right)\right]\left(s\right)=s^{\alpha }{\mathcal{A}}_2\left[u\left(x,t\right)\right]\left(s\right)-\alpha s^{\alpha -1}{\mathcal{A}}_1\left[u\left(x,t\right)\right]\left(s\right)+\left(\alpha -1\right)s^{\alpha -1}u\left(x,0\right),s>0,0<\alpha \le 1.$
• ${\mathcal{A}}_1\left[{\mathfrak{D}}_t^{n\alpha }u\left(x,t\right)\right]\left(s\right)=s^{n\alpha }{\mathcal{A}}_1\left[u\left(x,t\right)\right]\left(s\right)-\sum _{k=0}^{n-1}{s}^{\left(n-k\right)\alpha }{\mathfrak{D}}_t^{k\alpha }u\left(x,0\right),$ where ${\mathfrak{D}}_t^{n\alpha }=\underset{n-times}{\underbrace{{\mathfrak{D}}_t^{\alpha }{\mathfrak{D}}_t^{\alpha }\cdots {\mathfrak{D}}_t^{\alpha }}}$
• ${\mathcal{A}}_2\left[t^{\alpha }\right](s)=\frac{\mathsf{\Gamma }(\alpha +2)}{s^{\alpha +1}},sb>0,\alpha >0.$

The reader can refer [32,33,34] for further details about the ARA transform.

Theorem 1

([32]). Suppose that the ARA transform ${\mathcal{A}}_2$ of the continuous function $z(x,t)$ for the variable $t$ exists and has the fractional expansion

$${\mathcal{A}}_2\left[z\left(x,t\right)\right]\left(s\right)={\sum }_{n=0}^{\infty }\frac{h_n\left(x\right)}{s^{n\alpha +1}}, x\in I, s>0, 0<\alpha \le 1.Then$$

(5)

$$h_n\left(x\right)=\left(n\alpha +1\right){\mathfrak{D}}_t^{n\alpha }z\left(x,0\right).$$

(6)

Remark 1

([32]).

• The jth truncated series of the fractional expansion (5) is given by

  $${\mathcal{A}}_2{\left[z\left(x,t\right)\right]}_j\left(s\right)=\sum _{n=0}^j\frac{h_n\left(x\right)}{s^{n\alpha +1}}.$$

  (7)
• If  ${\mathcal{A}}_2\left[z\left(x,t\right)\right]\left(s\right)$  has the fractional expansion (5), then  ${\mathcal{A}}_1\left[z\left(x,t\right)\right]\left(s\right)$  can be expressed as

  $${\mathcal{A}}_1\left[z\left(x,t\right)\right](s)=\sum _{n=0}^{\infty }\frac{h_n\left(x\right)}{{\left(n\alpha +1\right)s}^{n{\alpha }^{\prime }}}$$

  (8)

  and the jth truncated series is given by

  $${\mathcal{A}}_1{\left[z\left(x,t\right)\right]}_j(s)=\sum _{n=0}^j\frac{h_n\left(x\right)}{{\left(n\alpha +1\right)s}^{n\alpha }}.$$

  (9)
• The ARA transform invers of order two  ${\mathcal{A}}_2^{-1}$  of the fractional expansion (5) is defined as

  $$z(x,t)={\mathcal{A}}_2^{-1}\left[\sum _{n=0}^{\infty }\frac{h_n\left(x\right)}{s^{n\alpha +1}}\right]\left(t\right)=\sum _{n=0}^{\infty }\frac{{\mathfrak{D}}_t^{n\alpha }z(x,0)}{\Gamma (n\alpha +1)}{t}^{n\alpha }.$$

  (10)

The convergence conditions of the expansion shown in Theorem 1 for ${\mathcal{A}}_2\left[z\left(x,t\right)\right]\left(s\right)$ are included in the following theorem, which is based on the relationship between ${\mathcal{A}}_1\left[z\left(x,t\right)\right]\left(s\right)$ and ${\mathcal{A}}_2\left[z\left(x,t\right)\right]\left(s\right)$ and the properties of Taylor’s series.

Theorem 2.

Assume that $z(x,t)$ is continuous on $I\times [0,\mu ]$ where the ARA transform for the variable $t$exists. Let${\mathcal{A}}_1\left[z\left(x,t\right)\right]\left(r\right)$has the expansion

$${\mathcal{A}}_1\left[z\left(x,t\right)\right]\left(s\right)=\sum _{n=0}^{\infty }\frac{D_t^{n\alpha }z\left(x,0\right)}{s^{n\alpha }}.$$

If  $\left|{\mathcal{A}}_1\left[{\mathfrak{D}}_t^{\left(n+1\right)\alpha }z\left(x,t\right)\right]\right|\le K$  on  $0<s\le b$, then  $R_n(x,s)$  satisfies

$$\left|R_n(x,s)\right|\le \frac{K\left(x\right)}{s^{\left(n+1\right)\alpha }}, x\in I, 0<s\le b.$$

Proof. 

Assume that ${\mathcal{A}}_1\left[{\mathfrak{D}}_t^{m\alpha }z\left(x,t\right)\right]\left(s\right)$ exists on $0<s\le b$ for $m=0,\dots ,n.$ The definition of the remainder implies

$$R_n(x,s)={\mathcal{A}}_1\left[z\left(x,t\right)\right]\left(s\right)-\sum _{m=0}^n\frac{{\mathfrak{D}}_t^{m\alpha }z\left(x,0\right)}{s^{m\alpha }}.$$

Multiplying the previous equation by $s^{\left(n+1\right)\alpha }$, part (4) of Lemma 1 yields that

$$s^{\left(n+1\right)\alpha }{R}_n(x,s)=s^{\left(n+1\right)\alpha }{\mathcal{A}}_1\left[z\left(x,t\right)\right]\left(s\right)-{\displaystyle {\sum }_{m=0}^n}\frac{{\mathfrak{D}}_t^{m\alpha }z\left(x,0\right)}{s^{m\alpha }}{s}^{\left(n+1\right)\alpha }={\mathcal{A}}_1\left[{\mathfrak{D}}_t^{(n+1)\alpha }z\left(x,t\right)\right]\left(s\right).$$

Thus,

$$\left|s^{\left(n+1\right)\alpha }{R}_n(x,s)\right|=\left|{\mathcal{A}}_1\left[{\mathfrak{D}}_t^{(n+1)\alpha }z\left(x,t\right)\right]\left(s\right)\right|\le K.$$

This yields that

$$\left|R_n(x,s)\right|\le \frac{K}{s^{\left(n+1\right)\alpha }},0<s\le b.$$

□

3. Formulating Series Solutions of Fractional Neutron Diffusion Equations with One Delayed Neutrons Group

The main goal of the current section is to construct a series solution to the fractional neutron diffusion equations with one delayed neutrons group using the ARA-RPST. It should be noted that the ARA transform is ineffective at solving nonlinear equations unless the power series method is applied. Thus, nonlinear FPDEs can be solved using this strategy. The core idea behind the ARA-RPST is to use the power series approach to solve the given FPDEs in the ARA space; nevertheless, this approach needs an appropriate expansion that shows the solutions in their final form. In addition, we carefully apply a novel method to calculate the expansion coefficients in this section.

Now, the algorithm of the ARA-RPST is demonstrated to solve the fractional NDEDNS of the form:

$$\begin{gathered} \frac{1}{v_u}{\mathfrak{D}}_t^{\alpha }z\left(x,t\right)=D{z}_{xx}\left(x,t\right)+\left(\gamma {{\displaystyle \sum }}_f-{{\displaystyle \sum }}_a\right)z\left(x,t\right)+\lambda u(x,t), \\ {\mathfrak{D}}_t^{\alpha }u\left(x,t\right)=\beta \gamma {{\displaystyle \sum }}_{f}z\left(x,t\right)-\lambda u(x,t), \end{gathered}$$

(11)

with the initial conditions

$$z\left(x,0\right)=z_0\left(x\right), u\left(x,0\right)=\frac{\beta \gamma {{\displaystyle \sum }}_f}{\lambda }{z}_0\left(x\right),$$

(12)

Replacing $B=\beta \gamma {\sum }_f$ and $\sum =\gamma {\sum }_f-{\sum }_a,$ the coupled equations in (11) can be written as

$$\begin{gathered} {\mathfrak{D}}_t^{\alpha }z\left(x,t\right)=v_{u}D{z}_{xx}\left(x,t\right)+v_u{\displaystyle \sum }z\left(x,t\right)+v_u\lambda u(x,t), \\ {\mathfrak{D}}_t^{\alpha }u\left(x,t\right)=Bz\left(x,t\right)-\lambda u(x,t), \end{gathered}$$

(13)

with the initial conditions

$$z\left(x,0\right)=z_0\left(x\right), u\left(x,0\right)=\frac{B}{\lambda }{z}_0\left(x\right).$$

(14)

To get the ARA-RPS solution (ARA-RPSS) of the coupled equations in (13), we operate the ARA transform ${\mathcal{A}}_2$ on the coupled equations to obtain

$$\begin{gathered} \begin{array}{ll}{\mathcal{A}}_2\left[{\mathfrak{D}}_t^{\alpha }z\left(x,t\right)\right](s)& \\ & =v_{u}D{\mathcal{A}}_2\left[z_{xx}\left(x,t\right)\right](s)+v_u\sum {\mathcal{A}}_2\left[z\left(x,t\right)\right](s)\\ & +v_u\lambda {\mathcal{A}}_2\left[u\left(x,t\right)\right](s),\end{array} \\ {\mathcal{A}}_2\left[{\mathfrak{D}}_t^{\alpha }u\left(x,t\right)\right]\left(s\right)=B{\mathcal{A}}_2\left[z\left(x,t\right)\right]\left(s\right)-\lambda {\mathcal{A}}_2\left[u\left(x,t\right)\right]\left(s\right). \end{gathered}$$

(15)

Lemma 1 part (3) yields that

$$\begin{gathered} \begin{array}{ll}{s}^{\alpha }{\mathcal{A}}_2\left[z\left(x,t\right)\right](s)& -\alpha s^{\alpha -1}{\mathcal{A}}_1\left[z\left(x,t\right)\right](s)+\left(\alpha -1\right)s^{\alpha -1}z\left(x,0\right)\\ & =v_{u}D{\partial }_{xx}{\mathcal{A}}_2\left[z\left(x,t\right)\right](s)+v_u\sum {\mathcal{A}}_2\left[z\left(x,t\right)\right](s)\\ & +v_u\lambda {\mathcal{A}}_2\left[u\left(x,t\right)\right](s),\end{array} \\ {s}^{\alpha }{\mathcal{A}}_2\left[u\left(x,t\right)\right]\left(s\right)-\alpha s^{\alpha -1}{\mathcal{A}}_1\left[u\left(x,t\right)\right]\left(s\right)+\left(\alpha -1\right)s^{\alpha -1}u\left(x,0\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=B{\mathcal{A}}_2\left[z\left(x,t\right)\right]\left(s\right)-\lambda {\mathcal{A}}_2\left[u\left(x,t\right)\right]\left(s\right). \end{gathered}$$

(16)

So, the Equations in (16) can be expressed after using the given initial conditions on the form

$$\begin{array}{l}\begin{array}{ll}{\mathcal{A}}_2\left[z\left(x,t\right)\right](s)-& \frac{\alpha }{s}{\mathcal{A}}_1\left[z\left(x,t\right)\right](s)+\frac{\left(\alpha -1\right)}{s}{z}_0\left(x\right)\\ & =\frac{v_{u}D}{s^{\alpha }}{\partial }_{xx}{\mathcal{A}}_2\left[z\left(x,t\right)\right](s)+\frac{v_u\sum }{s^{\alpha }}{\mathcal{A}}_2\left[z\left(x,t\right)\right](s)\\ & +\frac{v_u\lambda }{s^{\alpha }}{\mathcal{A}}_2\left[u\left(x,t\right)\right](s),\end{array}\\ \begin{array}{ll}{\mathcal{A}}_2\left[u\left(x,t\right)\right](s)-\frac{\alpha }{s}{\mathcal{A}}_1\left[u\left(x,t\right)\right]& (s)+\frac{\left(\alpha -1\right)}{s}\frac{B}{\lambda }{z}_0\left(x\right)=\frac{B}{s^{\alpha }}{\mathcal{A}}_2\left[z\left(x,t\right)\right](s)-\\ & \frac{\lambda }{s^{\alpha }}{\mathcal{A}}_2\left[u\left(x,t\right)\right](s)\end{array}\end{array}$$

(17)

Regarding to the ARA-RPST, we assume the ARA-RPSSs of the coupled equations in (17) have the following series representations:

$$\begin{gathered} {\mathcal{A}}_1\left[z\left(x,t\right)\right]\left(s\right)=\sum _{n=0}^{\mathrm{\infty }}\frac{h_n\left(x\right)}{\left(n\alpha +1\right)s^{n\alpha }},{\mathcal{A}}_2\left[z\left(x,t\right)\right]\left(s\right)=\sum _{n=0}^{\mathrm{\infty }}\frac{h_n\left(x\right)}{s^{n\alpha +1}}, \\ {\mathcal{A}}_1\left[u\left(x,t\right)\right]\left(s\right)=\sum _{n=0}^{\mathrm{\infty }}\frac{{\mathcal{\ell }}_n\left(x\right)}{\left(n\alpha +1\right)s^{n\alpha }},{\mathcal{A}}_2\left[u\left(x,t\right)\right](s)=\sum _{n=0}^{\mathrm{\infty }}\frac{{\mathcal{\ell }}_n\left(x\right)}{s^{n\alpha +1}} \end{gathered}$$

(18)

Using the fact that $\underset{s\to \infty }{\lim }s{\mathcal{A}}_2\left[z\left(x,t\right)\right]\left(s\right)=z\left(x,0\right),\underset{s\to \infty }{\lim }s{\mathcal{A}}_2\left[u\left(x,t\right)\right]\left(s\right)=u\left(x,0\right)$ and the given initial conditions, we obtain that $h_0\left(x\right)=z_0\left(x\right),{\mathcal{\ell }}_0\left(x\right)=\frac{B}{\lambda }{z}_0\left(x\right)$ and so the jth ARA-RPSSs of the coupled equations in (17) have the form:

$$\begin{gathered} {\mathcal{A}}_1{\left[z\left(x,t\right)\right]}_j\left(s\right)=z_0\left(x\right)+\sum _{n=1}^j\frac{h_n\left(x\right)}{\left(n\alpha +1\right)s^{n\alpha }}, \\ {\mathcal{A}}_2{\left[z\left(x,t\right)\right]}_j\left(s\right)=\frac{z_0\left(x\right)}{s}+\sum _{n=1}^j\frac{h_n\left(x\right)}{s^{n\alpha +1}}, \\ {\mathcal{A}}_1{\left[u\left(x,t\right)\right]}_j\left(s\right)=\frac{B}{\lambda }{z}_0\left(x\right)+\sum _{n=1}^j\frac{{\mathcal{\ell }}_n\left(x\right)}{\left(n\alpha +1\right)s^{n\alpha }}, \\ {\mathcal{A}}_2{\left[u\left(x,t\right)\right]}_j\left(s\right)=\frac{B{z}_0\left(x\right)}{\lambda s}+\sum _{n=1}^j\frac{{\mathcal{\ell }}_n\left(x\right)}{s^{n\alpha +1}}. \end{gathered}$$

(19)

Next, in order to determine the series’ unknown coefficients, the ARA-residual functions (ARA-RFs) of the Equations in (17) are defined as

$$\begin{gathered} {\mathcal{A}}_2{Res}_z\left(x,s\right)={\mathcal{A}}_2\left[z\left(x,t\right)\right](s)-\frac{\alpha }{s}{\mathcal{A}}_1\left[z\left(x,t\right)\right](s)+\frac{\left(\alpha -1\right)}{s}{z}_0\left(x\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{v_{u}D}{s^{\alpha }}{\partial }_{xx}{\mathcal{A}}_2\left[z\left(x,t\right)\right](s)-\frac{v_u\sum }{s^{\alpha }}{\mathcal{A}}_2\left[z\left(x,t\right)\right](s) \\ -\frac{v_u\lambda }{s^{\alpha }}{\mathcal{A}}_2\left[u\left(x,t\right)\right](s),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \\ {{\mathcal{A}}_2{Res}_u\left(x,s\right)=\mathcal{A}}_2\left[u\left(x,t\right)\right](s)-\frac{\alpha }{s}{\mathcal{A}}_1\left[u\left(x,t\right)\right](s)+\frac{\left(\alpha -1\right)}{s}\frac{B}{\lambda }{z}_0\left(x\right)- \\ \frac{B}{s^{\alpha }}{\mathcal{A}}_2\left[z\left(x,t\right)\right](s)+\frac{\lambda }{s^{\alpha }}{\mathcal{A}}_2\left[u\left(x,t\right)\right](s) \end{gathered}$$

(20)

The jth ARA-RFs are given by

$$\begin{gathered} {\mathcal{A}}_2{Res}_z{\left(x,s\right)}_j={\mathcal{A}}_2{\left[z\left(x,t\right)\right]}_j(s)-\frac{\alpha }{s}{\mathcal{A}}_1{\left[z\left(x,t\right)\right]}_j(s)+\frac{\left(\alpha -1\right)}{s}{z}_0\left(x\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{v_{u}D}{s^{\alpha }}{\partial }_{xx}{\mathcal{A}}_2{\left[z\left(x,t\right)\right]}_j(s)-\frac{v_u\sum }{s^{\alpha }}{\mathcal{A}}_2{\left[z\left(x,t\right)\right]}_j(s) \\ \hspace{1em}-\frac{v_u\lambda }{s^{\alpha }}{\mathcal{A}}_2{\left[u\left(x,t\right)\right]}_j(s),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \\ {{\mathcal{A}}_2{Res}_u{\left(x,s\right)}_j=\mathcal{A}}_2{\left[u\left(x,t\right)\right]}_j\left(s\right)-\frac{\alpha }{s}{\mathcal{A}}_1{\left[u\left(x,t\right)\right]}_j\left(s\right)+\frac{\left(\alpha -1\right)}{s}\frac{B}{\lambda }{z}_0\left(x\right) \\ -\frac{B}{s^{\alpha }}{\mathcal{A}}_2{\left[z\left(x,t\right)\right]}_j(s)+\frac{\lambda }{s^{\alpha }}{\mathcal{A}}_2{\left[u\left(x,t\right)\right]}_j(s) \end{gathered}$$

(21)

To get the ARA-RPSSs, we need the following facts.

• ${\mathcal{A}}_2{Res}_z{\left(x,s\right)}_j=0,$
• $\underset{j\to \mathrm{\infty }}{\lim }{\mathcal{A}}_2{Res}_z{\left(x,s\right)}_j={\mathcal{A}}_2{Res}_z\left(x,s\right),$
• $\underset{s\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}s{\mathcal{A}}_2{Res}_z\left(x,s\right)=0$ and $\underset{s\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}s{\mathcal{A}}_2{Res}_z{\left(x,s\right)}_j=0,$
• $\underset{s\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}{s}^{j\alpha +1}{\mathcal{A}}_2{Res}_z\left(x,s\right)=\underset{s\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}{s}^{j\alpha +1}{\mathcal{A}}_2{Res}_z{\left(x,s\right)}_j=0,$

for $0<\alpha <1,x\in I,s>0,j=1,2,\dots .$

To find $h_1\left(x\right)$ and ${\mathcal{\ell }}_1\left(x\right)$ of the series expansions (19), we substitute ${\mathcal{A}}_1{\left[z\left(x,t\right)\right]}_1\left(s\right),{\mathcal{A}}_1{\left[u\left(x,t\right)\right]}_1\left(s\right)$, ${\mathcal{A}}_2{\left[z\left(x,t\right)\right]}_1\left(s\right)$ and ${\mathcal{A}}_2{\left[u\left(x,t\right)\right]}_1\left(s\right)$ into the first ARA-RFs ${\mathcal{A}}_2{Res}_z{\left(x,s\right)}_1$ and ${\mathcal{A}}_2{Res}_u{\left(x,s\right)}_1,$ to get

$$\begin{gathered} {\mathcal{A}}_2{Res}_z{\left(x,s\right)}_1=\frac{z_0\left(x\right)}{s}+\frac{h_1\left(x\right)}{s^{\alpha +1}}-\frac{\alpha }{s}\left(z_0\left(x\right)+\frac{h_1\left(x\right)}{\left(\alpha +1\right)s^{\alpha }}\right)+\frac{\left(\alpha -1\right)}{s}{z}_0\left(x\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{v_{u}D}{s^{\alpha }}{\partial }_{xx}\left(\frac{z_0\left(x\right)}{s}+\frac{h_1\left(x\right)}{s^{\alpha +1}}\right)-\frac{v_u\sum }{s^{\alpha }}\left(\frac{z_0\left(x\right)}{s}+\frac{h_1\left(x\right)}{s^{\alpha +1}}\right) \\ -\frac{v_u\lambda }{s^{\alpha }}\left(\frac{B{z}_0\left(x\right)}{s\lambda }+\frac{{\mathcal{\ell }}_1\left(x\right)}{s^{\alpha +1}}\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \\ {\mathcal{A}}_2{Res}_u{\left(x,s\right)}_1=\frac{B{z}_0\left(x\right)}{s\lambda }+\frac{{\mathcal{\ell }}_1\left(x\right)}{s^{\alpha +1}}-\frac{\alpha }{s}\left(\frac{B}{\lambda }{z}_0\left(x\right)+\frac{{\mathcal{\ell }}_1\left(x\right)}{\left(\alpha +1\right)s^{\alpha }}\right)+\frac{\left(\alpha -1\right)B}{s\lambda }{z}_0\left(x\right) \\ -\frac{B}{s^{\alpha }}\left(\frac{z_0\left(x\right)}{s}+\frac{h_1\left(x\right)}{s^{\alpha +1}}\right)+\frac{\lambda }{s^{\alpha }}\left(\frac{B{z}_0\left(x\right)}{s\lambda }+\frac{{\mathcal{\ell }}_1\left(x\right)}{s^{\alpha +1}}\right). \end{gathered}$$

(22)

Which is equivalent to

$$\begin{gathered} {\mathcal{A}}_2{Res}_z{\left(x,s\right)}_1=\frac{1}{s^{\alpha +1}}\left(h_1\left(x\right)-\frac{\alpha }{\alpha +1}{h}_1\left(x\right)-v_{u}D{z}_0^{″}\left(x\right)-v_u\sum z_0\left(x\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-v_{u}B{z}_0\left(x\right)\right)+\frac{1}{s^{2\alpha +1}}\left(-v_{u}D{h}_1^{″}\left(x\right)-v_u\sum h_1\left(x\right)-v_u\lambda {\mathcal{\ell }}_1\left(x\right)\right), \\ {\mathcal{A}}_2{Res}_u{\left(x,s\right)}_1=\frac{1}{s^{\alpha +1}}\left({\mathcal{\ell }}_1\left(x\right)-\frac{\alpha }{\alpha +1}{l}_1\left(x\right)\right)+\frac{1}{s^{2\alpha +1}}\left(-{Bh}_1\left(x\right)+\lambda {\mathcal{\ell }}_1\left(x\right)\right). \end{gathered}$$

(23)

By taking the limit as $s\to \mathrm{\infty }$ after multiplying equations in (23) by $s^{\alpha +1}$, the facts $\underset{s\to \mathrm{\infty }}{\lim }\left(s^{\alpha +1}{\mathcal{A}}_2{Res}_z{\left(x,s\right)}_1\right)=0$ and $\underset{s\to \mathrm{\infty }}{\lim }\left(s^{\alpha +1}{\mathcal{A}}_2{Res}_u{\left(x,s\right)}_1\right)=0$ yield that

$$\begin{gathered} h_1\left(x\right)=\left(\alpha +1\right)\left(v_{u}D{z}_0^{″}\left(x\right)+v_u\sum z_0\left(x\right)+v_{u}B{z}_0\left(x\right)\right), \\ {l}_1\left(x\right)=0. \end{gathered}$$

(24)

Similarly, the coefficients of $h_2\left(x\right)$ and ${\mathcal{\ell }}_2\left(x\right)$ in the expansions (19) can be determined by substituting ${\mathcal{A}}_1{\left[z\left(x,t\right)\right]}_2\left(s\right),{\mathcal{A}}_1{\left[u\left(x,t\right)\right]}_2\left(s\right)$, ${\mathcal{A}}_2{\left[z\left(x,t\right)\right]}_2\left(s\right)$ and ${\mathcal{A}}_2{\left[u\left(x,t\right)\right]}_2\left(s\right)$ into the second ARA-RFs ${\mathcal{A}}_2{Res}_z{\left(x,s\right)}_2$ and ${\mathcal{A}}_2{Res}_u{\left(x,s\right)}_2,$ to get

$$\begin{array}{l}\begin{array}{ll}{\mathcal{A}}_2{Res}_z{\left(x,s\right)}_2=& \frac{z_0\left(x\right)}{s}+\frac{h_1\left(x\right)}{s^{\alpha +1}}+\frac{h_2\left(x\right)}{s^{2\alpha +1}}-\frac{\alpha }{s}\left(z_0\left(x\right)+\frac{h_1\left(x\right)}{\left(\alpha +1\right)s^{\alpha }}+\frac{h_2\left(x\right)}{\left(2\alpha +1\right)s^{2\alpha }}\right)\\ & +\frac{\left(\alpha -1\right)}{s}{z}_0\left(x\right)-\frac{v_{u}D}{s^{\alpha }}{\partial }_{xx}\left(\frac{z_0\left(x\right)}{s}+\frac{h_1\left(x\right)}{s^{\alpha +1}}+\frac{h_2\left(x\right)}{s^{2\alpha +1}}\right)\\ & -\frac{v_u\sum }{s^{\alpha }}\left(\frac{z_0\left(x\right)}{s}+\frac{h_1\left(x\right)}{s^{\alpha +1}}+\frac{h_2\left(x\right)}{s^{2\alpha +1}}\right)\\ & -\frac{v_u\lambda }{s^{\alpha }}\left(\frac{B{z}_0\left(x\right)}{s\lambda }+\frac{{\mathcal{\ell }}_1\left(x\right)}{s^{\alpha +1}}+\frac{{\mathcal{\ell }}_2\left(x\right)}{s^{2\alpha +1}}\right),\end{array}\\ \begin{array}{ll}{\mathcal{A}}_2{Res}_u{\left(x,s\right)}_2=& \frac{B{z}_0\left(x\right)}{s\lambda }+\frac{{\mathcal{\ell }}_1\left(x\right)}{s^{\alpha +1}}+\frac{{\mathcal{\ell }}_2\left(x\right)}{s^{2\alpha +1}}\\ & -\frac{\alpha }{s}\left(\frac{B}{\lambda }{z}_0\left(x\right)+\frac{{\mathcal{\ell }}_1\left(x\right)}{\left(\alpha +1\right)s^{\alpha }}+\frac{{\mathcal{\ell }}_2\left(x\right)}{\left(2\alpha +1\right)s^{2\alpha }}\right)+\frac{\left(\alpha -1\right)}{s}\frac{B}{\lambda }{z}_0\left(x\right)\\ \hfill -\frac{B}{s^{\alpha }}(z_0\left(x\right)& +\frac{h_1\left(x\right)}{\left(\alpha +1\right)s^{\alpha }}+\frac{h_2\left(x\right)}{\left(2\alpha +1\right)s^{2\alpha }})+\frac{\lambda }{s^{\alpha }}\left(\frac{B{z}_0\left(x\right)}{s\lambda }+\frac{{\mathcal{l}}_1\left(x\right)}{s^{\alpha +1}}+\frac{{\mathcal{l}}_2\left(x\right)}{s^{2\alpha +1}}\right).\end{array}\end{array}$$

(25)

Then, taking the limit as $s\to \mathrm{\infty }$ after multiplying the obtained equations by $s^{2\alpha +1}$ to get

$$\begin{gathered} h_2\left(x\right)=\left(2\alpha +1\right)\left(v_{u}D{h}_1^{″}\left(x\right)+v_u\sum h_1\left(x\right)\right), \\ {l}_2\left(x\right)=\left(2\alpha +1\right)B{h}_1\left(x\right). \end{gathered}$$

(26)

Again, substitute the third truncated expansions ${\mathcal{A}}_1{\left[z\left(x,t\right)\right]}_3\left(s\right),{\mathcal{A}}_1{\left[u\left(x,t\right)\right]}_3\left(s\right)$, ${\mathcal{A}}_2{\left[z\left(x,t\right)\right]}_3\left(s\right)$ and ${\mathcal{A}}_2{\left[u\left(x,t\right)\right]}_3\left(s\right)$ into the third ARA-RFs ${\mathcal{A}}_2{Res}_z{\left(x,s\right)}_3$ and ${\mathcal{A}}_2{Res}_u{\left(x,s\right)}_3,$ then we multiply the obtained equations by $s^{3\alpha +1}$ and evaluating the limit as $s\to \mathrm{\infty }$ to obtain

$$\begin{gathered} h_3\left(x\right)=\left(3\alpha +1\right)\left(v_{u}D{h}_2^{″}\left(x\right)+v_u\sum h_2\left(x\right)+v_u\lambda l_2\left(x\right)\right), \\ {l}_3\left(x\right)=\left(3\alpha +1\right)\left(B{h}_2\left(x\right)-\lambda l_2\left(x\right)\right). \end{gathered}$$

(27)

If we keep acting the same way, the coefficients $h_n\left(x\right)$, ${\mathcal{\ell }}_n\left(x\right)$ for $n\ge 1$ can be obtained by the following recurrence relations with considering $h_0\left(x\right)=z_0\left(x\right),{\mathcal{\ell }}_0\left(x\right)=\frac{B}{\lambda }{z}_0\left(x\right)$.

$$\begin{gathered} h_n\left(x\right)=\left(n\alpha +1\right)\left(v_{u}D{h}_{n-1}^{″}\left(x\right)+v_u\sum h_{n-1}\left(x\right)+v_u\lambda l_{n-1}\left(x\right)\right), \\ {\mathcal{\ell }}_n\left(x\right)=\left(n\alpha +1\right)\left(B{h}_{n-1}\left(x\right)-\lambda {\mathcal{\ell }}_{n-1}\left(x\right)\right), \end{gathered}$$

(28)

Consequently, the series solutions of the coupled equations in (17) are

$$\begin{gathered} {\mathcal{A}}_2\left[z\left(x,t\right)\right]\left(s\right)=\frac{z_0\left(x\right)}{s}+\sum _{n=1}^{\mathrm{\infty }}\frac{h_n\left(x\right)}{s^{n\alpha +1}},\hspace{1em}\hspace{1em}x\in I,\hspace{1em}\hspace{1em}s>\delta \ge 0, \\ {\mathcal{A}}_2\left[u\left(x,t\right)\right]\left(s\right)=\frac{B}{\lambda s}{z}_0\left(x\right)+\sum _{n=1}^{\mathrm{\infty }}\frac{{\mathcal{\ell }}_n\left(x\right)}{s^{n\alpha +1}},\hspace{1em}\hspace{1em}x\in I,\hspace{1em}\hspace{1em}s>\delta \ge 0. \end{gathered}$$

(29)

Consequently, by applying the ARA transform inverse to the obtained solution in (29) to return it to its original space, the series solution of the fractional neutron diffusion equations (11) can be achieved.

$$\begin{gathered} z\left(x,t\right)=z_0\left(x\right)+\sum _{n=1}^{\mathrm{\infty }}\frac{h_n\left(x\right)t^{n\alpha }}{\Gamma \left(n\alpha +1\right)},t\ge 0,x\in I. \\ u\left(x,t\right)=\frac{B}{\lambda }{z}_0\left(x\right)+\sum _{k=3}^{\infty }\frac{{\mathcal{\ell }}_n\left(x\right)t^{n\alpha }}{\Gamma \left(n\alpha +1\right)},t\ge 0,x\in I, \end{gathered}$$

(30)

where

$$\begin{gathered} h_n\left(x\right)=\left(n\alpha +1\right)\left(v_{u}D{h}_{n-1}^{″}\left(x\right)+v_u\sum h_{n-1}\left(x\right)+v_u\lambda l_{n-1}\left(x\right)\right), \\ {\mathcal{\ell }}_n\left(x\right)=\left(n\alpha +1\right)\left(B{h}_{n-1}\left(x\right)-\lambda {\mathcal{\ell }}_{n-1}\left(x\right)\right),\hspace{1em}\hspace{1em}n=\mathrm{1,2},3,\dots \\ {h}_0\left(x\right)=z_0\left(x\right),{\mathcal{\ell }}_0\left(x\right)=\frac{B}{\lambda }{z}_0\left(x\right) \end{gathered}$$

(31)

4. Numerical Results

In order to validate the driving theories using ARA-RPST, we succeeded in solving NDEDNS. After that, the solutions were validated using the numerical values of the next nuclear reactor cross-section [35].

In this section, we consider $v_u=\mathrm{220,000} \mathrm{c}\mathrm{m}/\mathrm{s},$ $D=0.356,B=0.000735 {\mathrm{c}\mathrm{m}}^{-1},\lambda =0.08 {\mathrm{s}}^{-1},\Sigma =0.005 {\mathrm{c}\mathrm{m}}^{-1}$.

Numerical results at different values of $\alpha$ are shown in Table 1. We compare our technique to another existing numerical approach, for $\alpha =0.1,\alpha =0.3$ and $\alpha =0.5$. Comparisons are made between the approximate solutions produced by ADM [35] and the approximate solutions produced by ARA-RPST.

Table 1. Numerical results of neutron flux at different values of $\alpha ,z_0\left(x\right)=1$.

$\mathit{t}\left(\mathbf{s}\right)$	$\mathit{\alpha }=0.1$		$\mathit{\alpha }=0.3$		$\mathit{\alpha }=0.5$
	ARA-RPST	ADM	ARA-RPST	ADM	ARA-RPST	ADM
0.0001	$1.07571\times {10}^8$	$1.04535\times {10}^8$	$4.05001\times {10}^5$	$3.58370\times {10}^5$	1302.5	1137.4
0.00039	$1.61768\times {10}^8$	$1.59662\times {10}^8$	$1.37130\times {10}^6$	$1.22266\times {10}^6$	9415.6	8236.4
0.00068	$1.91108\times {10}^8$	$1.89937\times {10}^8$	$2.25808\times {10}^6$	$2.02159\times {10}^6$	21,346.4	18,694.4
0.00097	$2.12584\times {10}^8$	$2.12264\times {10}^8$	$3.10591\times {10}^6$	$2.78898\times {10}^6$	36,086.6	31,632.6
0.00126	$2.29927\times {10}^8$	$2.30390\times {10}^8$	$3.92798\times {10}^6$	$3.53571\times {10}^6$	53,165.1	46,640.0
0.00155	$2.44660\times {10}^8$	$2.45852\times {10}^8$	$4.73090\times {10}^6$	$4.26719\times {10}^6$	72,290.4	63,462.9
0.00184	$2.57571\times {10}^8$	$2.59449\times {10}^8$	$5.51864\times {10}^6$	$4.98668\times {10}^6$	93,259.2	81,923.8
0.00213	$2.69125\times {10}^8$	$2.71652\times {10}^8$	$6.29385\times {10}^6$	$5.69632\times {10}^6$	115,919.1	101,889.9
0.00242	$2.79625\times {10}^8$	$2.82770\times {10}^8$	$7.05841\times {10}^6$	$6.39764\times {10}^6$	140,150.0	123,256.5
0.00271	$2.89277\times {10}^8$	$2.93014\times {10}^8$	$7.81373\times {10}^6$	$7.09176\times {10}^6$	165,854.5	145,938.8
0.003	$2.98231\times {10}^8$	$3.02536\times {10}^8$	$8.56090\times {10}^6$	$7.77958\times {10}^6$	192,951.2	169,865.8

Figure 1 shows the neutron fluxe $z(x,t)$ with the initial condition $z_0\left(x\right)=1$ and Figure 2 shows the neutron fluxe $z(x,t)$ with the initial condition $z_0\left(x\right)=x^2.$

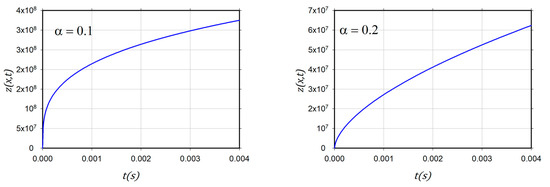
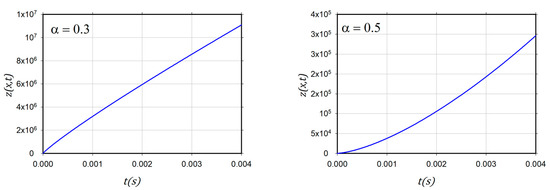
Figure 1. 2D graphs of neutron flux $z(x,t)$ for α = 0.1, 0.2, 0.3, 0.5. and $\alpha ,z_0\left(x\right)=1$.

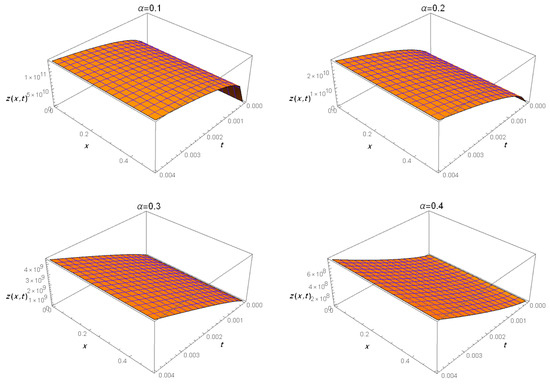
Figure 2. 3D graphs of neutron flux $z(x,t)$ for α = 0.1, 0.2, 0.3, 0.4 and $z_0\left(x\right)=1$.

The introduced figures of the neutron fluxes for various values of $\alpha$ in case $z\left(x,0\right)=1$ and case $z\left(x,0\right)=x^2$ demonstrate that the results matched those of the ADM [35].

Finally, as can be seen from the tables and figures, the ARA-RPST gives us more details regarding the neutron flux in non-Gaussian diffusion for a variety of chosen times.

5. Conclusions

The ARA-RPST is introduced to construct a fractional series solution of NDEDNS. Two different nuclear physics numerical case studies have validated the theoretical presentation of the method, and additionally, the results are validated when they are compared with the ADM. It should be mentioned that the suggested technique is envisaged to be used in research on many nuclear reactor theories and other scientific phenomena.