Abstract
In this article, a new analytical scheme of the ARA transform is introduced to solve systems of fractional partial differential equations. The principle of the proposed technique is based on combining the ARA transform with the residual power series method to create an approximate series solution for a system of partial differential equations of fractional order on the form of a rapid convergent series. To illustrate the effectiveness, accuracy, and validity of the suggested technique, an Attractive physical system, the fractional neutron diffusion equation with one delayed neutrons group, is discussed and solved. Two different neutron flux initial conditions are presented numerically to clarify various cases in order to ensure the theoretical results. The necessary Mathematica codes are run using vital nuclear reactor cross-section data, and the results for various values of time are tabulated and graphically represented.
1. Introduction
Fractional calculus is a parallel area of calculus that cannot be viewed as an expanded form of integer order. In many areas, fractional order systems are preferable to integer order systems because they may explain phenomena that are related to memory and affected by inherited traits [1,2,3,4,5,6,7,8]. Many definitions of the derivative and integral of fractional order have been created since the seventeenth century, when fractional calculus first appeared. The definitions of fractional operators that are most significant are Caputo and Riemann-Liouville definitions [9,10,11,12]. The fractional derivative and fractional integral have just been given new definitions, the Atangana–Baleanu definition and the conformable fractional derivative definition are the two most significant ones [13,14,15,16]. By creating fractional models, many researchers have used them. Nevertheless, Caputo’s definition is still considered to be acceptable and desirable by the majority of scholars.
There have been numerous contributions made to the research area for solving systems of fractional partial differential equations (FPDEs). Finding analytical solutions for systems of FPDEs can occasionally involve complicated calculations, so analytical and numerical techniques have been created and improved to obtain solutions of linear and nonlinear systems of FPDEs [17,18,19,20,21].
The KdV-Burgers equations [22], the nonlinear Schrodinger equations [23], the neutron diffusion equations [24] are just a few examples of fractional order differential equations for which the residual power series technique (RPST) has proven to be successful and accurate in creating approximate series solutions. Moreover, many systems of linear and nonlinear equations that have appeared in a variety of engineering and science domains have been solved analytically using RPST [25,26,27]. Without linearization, perturbation, or discretization, the RPST is a powerful technique for creating power series solutions of differential equations. RPST does not need comparing the coefficients of the related terms, in contrast to the standard power series approach. By using a series of equations with one or more variables, this technique calculates the power series coefficients. On the other hand, many powerful methods for solving differential equations have been presented [28,29,30,31].
The ARA residual power series technique (ARA-RPST) is used in this investigation, which was first published in [32], to create analytical and approximate solutions for the linear and nonlinear systems of FPDEs. This method combines the ARA transform [33,34] and RPST.
One of the most interesting physics problems that are expressed through partial differential equations is the neutron diffusion equations with delayed neutrons system (NDEDNS) of the form [35,36,37,38]:
with initial conditions:
where is the neutron flux, is the delayed neutron density, is neutron velocity, is the macroscopic absorption cross-section, is the neutron diffusion coefficient and β, λ, and γ are the fraction of the delayed fission neutrons, the radioactive decay constant, and the average number of neutrons produced per fission, respectively.
The coupled fractional neutron diffusion equations with delayed neutrons with one group of delayed neutrons were solved by Adomian decomposition method (ADM) to get an analytical approximation solution [35]. Furthermore, an exact solution in the case of one-dimensional neutron diffusion kinetic equation with one delayed precursor concentration in Cartesian geometry was studied in [36].
In this article, we are interested in implementing the ARA-RPST to find the approximate series solution of one group of neutron diffusion equations when delayed neutrons are averaged by one group of delayed neutrons [35]:
with the initial conditions
To achieve our goal, we operate the ARA transform on the equations in (3) and then we formulate the new system’s solution as a series expansion, with the expansion coefficients coming from the idea of the limit at infinity. After that, we apply the ARA transform inverse on the obtained solution to transform it to the original space. When compared to the residual power series approach, ARA-RPST requires fewer calculations to obtain the coefficients because instead of using a fractional derivation such as in RPST, it depends on the concept of the limit. The current method is speedy, uses little computer memory. Additionally, the power series coefficients are computed using a set of equations involving more than one variable, indicating that the present method has a rapid convergence.
The format of this study is as follows: Definitions, concepts, and properties related to the ARA transform and fractional derivatives are covered in further detail in the next section. In Section 3, we formulate series solutions for fractional neutron diffusion equations with one delayed neutrons group using the ARA-RPST. The current methodology has been applied to investigate a number of fractional equations, as shown in Section 4. Finally, the conclusion section includes a summary of our findings.
2. Fundamental Concepts and Properties
This section includes the definition of the Caputo fractional operator. Additionally, some theorems and properties pertaining to the ARA-RPST are provided.
Definition 1.
For to be the smallest integer that exceeds , the Caputo fractional derivatives of order is given by
where is an interval and isthe time-fractional Riemann–Liouville integral operator of order , defined as
Definition 2
([33]). The ARA transform of order of the continuous function on for the variable , is given by
For
The ARA transform
is defined as
For
The ARA transform
is defined as
Definition 3
([32]). The ARA transform inverse is defined as
where
is
times differentiable.
The following lemma contains some of the ARA transform properties that are essential to our investigation.
Lemma 1
([32,33,34]). Let and be continuous functions. Then
- where and are nonzero constants.
- where
The reader can refer [32,33,34] for further details about the ARA transform.
Theorem 1
([32]). Suppose that the ARA transform of the continuous function for the variable exists and has the fractional expansion
Remark 1
([32]).
- The jth truncated series of the fractional expansion (5) is given by
- If has the fractional expansion (5), then can be expressed asand the jth truncated series is given by
- The ARA transform invers of order two of the fractional expansion (5) is defined as
The convergence conditions of the expansion shown in Theorem 1 for are included in the following theorem, which is based on the relationship between and and the properties of Taylor’s series.
Theorem 2.
Assume that is continuous on where the ARA transform for the variable exists. Lethas the expansion
If
on
, then
satisfies
Proof.
Assume that
exists on for The definition of the remainder implies
Multiplying the previous equation by , part (4) of Lemma 1 yields that
Thus,
This yields that
□
3. Formulating Series Solutions of Fractional Neutron Diffusion Equations with One Delayed Neutrons Group
The main goal of the current section is to construct a series solution to the fractional neutron diffusion equations with one delayed neutrons group using the ARA-RPST. It should be noted that the ARA transform is ineffective at solving nonlinear equations unless the power series method is applied. Thus, nonlinear FPDEs can be solved using this strategy. The core idea behind the ARA-RPST is to use the power series approach to solve the given FPDEs in the ARA space; nevertheless, this approach needs an appropriate expansion that shows the solutions in their final form. In addition, we carefully apply a novel method to calculate the expansion coefficients in this section.
Now, the algorithm of the ARA-RPST is demonstrated to solve the fractional NDEDNS of the form:
with the initial conditions
Replacing and the coupled equations in (11) can be written as
with the initial conditions
To get the ARA-RPS solution (ARA-RPSS) of the coupled equations in (13), we operate the ARA transform on the coupled equations to obtain
Lemma 1 part (3) yields that
So, the Equations in (16) can be expressed after using the given initial conditions on the form
Regarding to the ARA-RPST, we assume the ARA-RPSSs of the coupled equations in (17) have the following series representations:
Using the fact that and the given initial conditions, we obtain that and so the jth ARA-RPSSs of the coupled equations in (17) have the form:
Next, in order to determine the series’ unknown coefficients, the ARA-residual functions (ARA-RFs) of the Equations in (17) are defined as
The jth ARA-RFs are given by
To get the ARA-RPSSs, we need the following facts.
- and
for
To find and of the series expansions (19), we substitute , and into the first ARA-RFs and to get
Which is equivalent to
By taking the limit as after multiplying equations in (23) by , the facts and yield that
Similarly, the coefficients of and in the expansions (19) can be determined by substituting , and into the second ARA-RFs and to get
Then, taking the limit as after multiplying the obtained equations by to get
Again, substitute the third truncated expansions , and into the third ARA-RFs and then we multiply the obtained equations by and evaluating the limit as to obtain
If we keep acting the same way, the coefficients , for can be obtained by the following recurrence relations with considering .
Consequently, the series solutions of the coupled equations in (17) are
Consequently, by applying the ARA transform inverse to the obtained solution in (29) to return it to its original space, the series solution of the fractional neutron diffusion equations (11) can be achieved.
where
4. Numerical Results
In order to validate the driving theories using ARA-RPST, we succeeded in solving NDEDNS. After that, the solutions were validated using the numerical values of the next nuclear reactor cross-section [35].
In this section, we consider .
Numerical results at different values of are shown in Table 1. We compare our technique to another existing numerical approach, for and . Comparisons are made between the approximate solutions produced by ADM [35] and the approximate solutions produced by ARA-RPST.

Table 1.
Numerical results of neutron flux at different values of .
Figure 1 shows the neutron fluxe with the initial condition and Figure 2 shows the neutron fluxe with the initial condition
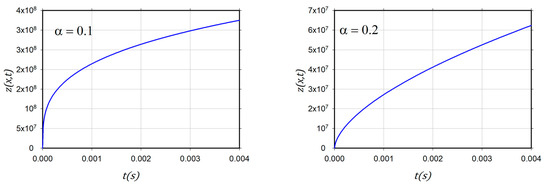
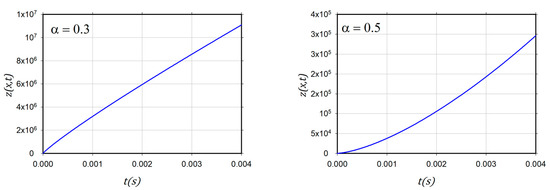
Figure 1.
2D graphs of neutron flux for α = 0.1, 0.2, 0.3, 0.5. and .
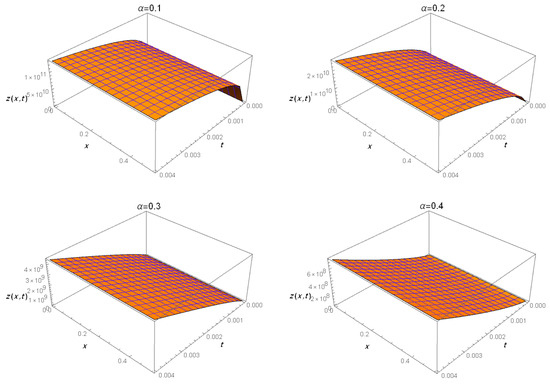
Figure 2.
3D graphs of neutron flux for α = 0.1, 0.2, 0.3, 0.4 and .
The introduced figures of the neutron fluxes for various values of in case and case demonstrate that the results matched those of the ADM [35].
Finally, as can be seen from the tables and figures, the ARA-RPST gives us more details regarding the neutron flux in non-Gaussian diffusion for a variety of chosen times.
5. Conclusions
The ARA-RPST is introduced to construct a fractional series solution of NDEDNS. Two different nuclear physics numerical case studies have validated the theoretical presentation of the method, and additionally, the results are validated when they are compared with the ADM. It should be mentioned that the suggested technique is envisaged to be used in research on many nuclear reactor theories and other scientific phenomena.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The author thanks the editor and referees for their insightful criticism, which helped to improve the paper’s final version.
Conflicts of Interest
The author declares no conflict of interest.
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Du, M.; Wang, Z.; Hu, H. Measuring memory with the order of fractional derivative. Sci. Rep. 2013, 3, 3431. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Cifani, S.; Jakobsen, E.R. Entropy solution theory for fractional degenerate convection–diffusion equations. Ann. De L’institut Henri Poincaré C 2011, 28, 413–441. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.Q. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Khandaqji, M.; Burqan, A. Results on sequential conformable fractional derivatives with applications. J. Comput. Anal. Appl. 2021, 29, 1115–1125. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Almeida, R.; Tavares, D.; Torres, D. The Variable-Order Fractional Calculus of Variations; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Khalil, R.; Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- El-Ajou, A. A modification to the conformable fractional calculus with some applications. Alex. Eng. J. 2020, 59, 2239–2249. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Thermal Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Hasan, S.; El-Ajou, A.; Hadid, S.; Al-Smadi, M.; Momani, S. Atangana-Baleanu fractional framework of reproducing kernel technique in solving fractional population dynamics system. Chaos Solitons Fractals 2020, 133, 109624. [Google Scholar] [CrossRef]
- Burqan, A.; El-Ajou, A.; Saadeh, R.; Al-Smadi, M. A new efficient technique using Laplace transforms and smooth expansions to construct a series solution to the time-fractional Navier-Stokes equations. Alex. Eng. J. 2022, 61, 1069–1077. [Google Scholar] [CrossRef]
- Jafari, H.; Seifi, S. Solving a system of nonlinear fractional partial differential equations using homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1962–1969. [Google Scholar] [CrossRef]
- Jafari, H.; Khalique, C.M.; Nazari, M. Application of the Laplace decomposition method for solving linear and nonlinear fractional diffusion–wave equations. Appl. Math. Lett. 2011, 24, 1799–1805. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The variational iteration method for solving linear and nonlinear systems of PDEs. Comput. Math. Appl. 2007, 54, 895–902. [Google Scholar] [CrossRef]
- Jafari, H.; Nazari, M.; Baleanu, D.; Khalique, C.M. A new approach for solving a system of fractional partial differential equations. Comput. Math. Appl. 2013, 66, 838–843. [Google Scholar] [CrossRef]
- El-Ajou, A.; Al-Zhour, Z.; Oqielat, M.A.; Momani, S.; Hayat, T. Series solutions of nonlinear conformable fractional KdV-Burgers equation with some applications. Eur. Phys. J. Plus 2019, 134, 402. [Google Scholar] [CrossRef]
- Moa’ath, N.O.; El-Ajou, A.; Al-Zhour, Z.; Alkhasawneh, R.; Alrabaiah, H. Series solutions for nonlinear time-fractional Schrödinger equations: Comparisons between conformable and Caputo derivatives. Alex. Eng. J. 2020, 59, 2101–2114. [Google Scholar]
- Shqair, M.; El-Ajou, A.; Nairat, M. Analytical solution for multi-energy groups of neutron diffusion equations by a residual power series method. Mathematics 2019, 7, 633. [Google Scholar] [CrossRef]
- El-Ajou, A.; Moa’ath, N.O.; Al-Zhour, Z.; Momani, S. A class of linear non-homogenous higher order matrix fractional differential equations: Analytical solutions and new technique. Fract. Calc. Appl. Anal. 2020, 23, 356–377. [Google Scholar] [CrossRef]
- El-Ajou, A.; Arqub, O.A.; Zhour, Z.A.; Momani, S. New results on fractional power series: Theories and applications. Entropy 2013, 15, 5305–5323. [Google Scholar] [CrossRef]
- Alquran, M. Analytical solution of time-fractional two-component evolutionary system of order 2 by residual power series method. J. Appl. Anal. Comput. 2015, 5, 589–599. [Google Scholar] [CrossRef]
- Yang, J.J.; Tian, S.F. Riemann–Hilbert problem and dynamics of soliton solutions of the fifth-order nonlinear Schrödinger equation. Appl. Math. Lett. 2022, 128, 107904. [Google Scholar] [CrossRef]
- Liu, Y.H.; Guo, R.; Li, X.L. Rogue wave solutions and modulation instability for the mixed nonlinear Schrödinger equation. Appl. Math. Lett. 2021, 121, 107450. [Google Scholar] [CrossRef]
- Dong, L.; Huang, C.; Qi, W. Nonlocal solitons in fractional dimensions. Opt. Lett. 2019, 44, 4917–4920. [Google Scholar] [CrossRef] [PubMed]
- Qazza, A.; Burqan, A.; Saadeh, R.; Khalil, R. Applications on Double ARA–Sumudu Transform in Solving Fractional Partial Differential Equations. Symmetry 2022, 14, 1817. [Google Scholar] [CrossRef]
- Burqan, A.; Saadeh, R.; Qazza, A. A novel numerical approach in solving fractional neutral pantograph equations via the ARA integral transform. Symmetry 2021, 14, 50. [Google Scholar] [CrossRef]
- Saadeh, R.; Qazza, A.; Burqan, A. A new integral transform: ARA transform and its properties and applications. Symmetry 2020, 12, 925. [Google Scholar] [CrossRef]
- Qazza, A.; Burqan, A.; Saadeh, R. A new attractive method in solving families of fractional differential equations by a new transform. Mathematics 2021, 9, 3039. [Google Scholar] [CrossRef]
- Sardar, T.; Saha Ray, S.; Bera, R.K.; Biswas, B.B.; Das, S. The solution of coupled fractional neutron diffusion equations with delayed neutrons. Int. J. Nucl. Energy Sci. Technol. 2010, 5, 105–113. [Google Scholar] [CrossRef]
- Khaled, S.M. Exact solution of the one-dimensional neutron diffusion kinetic equation with one delayed precursor concentration in Cartesian geometry. AIMS Math. 2022, 7, 12364–12373. [Google Scholar] [CrossRef]
- Almenas, K.; Lee, R.; Almenas, K.; Lee, R. Neutron Diffusion—Basic Concepts. In Nuclear Engineering: An Introduction; Springer: Berlin/Heidelberg, Germany, 1992; pp. 83–118. [Google Scholar]
- Palma, D.A.; Martinez, A.S.; Gonçalves, A.C. Analytical solution of point kinetics equations for linear reactivity variation during the start-up of a nuclear reactor. Ann. Nucl. Energy 2009, 36, 1469–1471. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).