A New Technique for Solving a Nonlinear Integro-Differential Equation with Fractional Order in Complex Space

Abstract

This work aims to explore the solution of a nonlinear fractional integro-differential equation in the complex domain through the utilization of both analytical and numerical approaches. The demonstration of the existence and uniqueness of a solution is established under certain appropriate conditions with the use of Banach fixed point theorems. To date, no research effort has been undertaken to look into the solution of this integro equation, particularly due to its fractional order specification within the complex plane. The validation of the proposed methodology was performed by utilizing a novel strategy that involves implementing the Rationalized Haar wavelet numerical method with the application of the Bernoulli polynomial technique. The primary reason for choosing the proposed technique lies in its ability to transform the solution of the given nonlinear fractional integro-differential equation into a representation that corresponds to a linear system of algebraic equations. Furthermore, we conduct a comparative analysis between the outcomes obtained from the suggested method and those derived from the rationalized Haar wavelet method without employing any shared mathematical methodologies. In order to evaluate the precision and effectiveness of the proposed method, a series of numerical examples have been developed.

1. Introduction

Complex functions are extensively employed in broad scientific fields such as physics, quantum mechanics, electromagnetic engineering, biological processes, chemistry, the field of economics, control theory, mathematics, AC voltage analysis, AC circuit calculations, indicate analysis, fluid dynamics, improper integrals, alternating current and resistance, radio wave transmission, cell phone technology, fractals, and statistics [1,2]. In the last thirty years, there has been considerable focus on the topic of fractional calculus. This field of research allows for the investigation of integration and differentiation beyond the limitations of whole number orders. Fractional calculus is extensively used in both pure and applied fields of study, such as physical science, chemical science, the aerodynamics and electrostatics of complex mediums, viscosity, thermal transmission, electrical mechanics, and controlling theory, which is a big part of why this is happening. The subject of fractional calculus can be regarded as both ancient and contemporary. The field of mathematics was initially shaped by the conjectures put forth by influential thinkers such as Leibniz and Euler. Subsequently, prominent mathematicians, including Laplace, Fourier, Abel, Liouville, Riemann, and Holmgren, further contributed to its development.

Most research publications concentrate on examining the presence of unique solutions to equations involving various types of differential and integral equations in either one or several dimensions. The Banach fixed point principle, formulated by the renowned Polish mathematician Stefan Banach in 1922, is a potent and significant methodology. Recently, many academics have investigated the presence, distinctiveness, and reliability of fractional nonlinear differential and integro-differential equations (ND/IDEqs). These theorems provide a fundamental theoretical basis for a wide range of applications. In references [3,4], the authors establish the existence of a solution by utilizing fixed point theorems to solve a non-homogeneous fractional integro-differential equation in a dual Banach space. Additionally, study [5] provides the necessary cases to examine the originality of solutions to an FDEq by utilizing Banach’s contraction mapping principle. Reference [6] demonstrates the uniqueness theorem for solutions to Nabla FDEqs with non-Lipschitz nonlinearities. This result cannot be obtained using the currently accessible discrete fractional Gronwall inequality. The study utilized the semi-group approach to examine the accuracy of solutions in Banach space FDEqs of the heat type [7].

In recent times, there has been a significant amount of attention directed towards the utilization of wavelet methods for solving integral equations, as initially proposed by Beylkin, G. in 1991 [8]. Subsequently, other studies have been conducted to explore the applicability of this approach to addressing various forms of integral equations. The application of the Haar wavelet method is explored in [9] for the solution of various types of linear integral equations, including Fredholm, Volterra, integro-differential, and weakly singular integral equations. Additionally, the eigenvalue problem is addressed. In [10], the rational Haar wavelet is used to solve nonlinear Volterra integro-differential equations and nonlinear Fredholm integro-differential equations. Moreover, the wavelet technique is employed to calculate the solution of a complex plane NVHIEq and a mixed VFHIEq of the second type. Several additional investigations, including those referenced as [11,12,13,14,15,16,17,18,19,20], have also examined comparable subjects.

The goal of this study, which builds on previous research, is to look into how to solve the nonlinear fractional integro-differential equation (NFIDEq) in complex space. Both analytical and numerical approaches are employed to solve the following equation:

$$D_t^{\alpha } \left(u (s, t) - k (s, t)\right)={\displaystyle \underset{0}{\overset{1}{\int }}u \left(s, t, \theta , u (\theta , t)\right) d\theta },$$

(1)

with initial conditions

$$u(s,0)=h_1(s), u(0,t)=h_2(t).$$

where $u(s,t)=\zeta (s,t)+i \eta (s,t),$ is an unknown complex function with $(s,t)\in \left[0, 1\right]\times \left[0, 1\right]$ such that $u\in E \left(\left[0, 1\right]\times \left[0, 1\right] , C\right),$ and $\zeta , \eta : \left[0, 1\right]\times \left[0, 1\right] \stackrel{ }{\to } {ℝ}^2, D_t^{\alpha }$ is a Caputo fractional derivative with order $0 < \alpha < 1.$ Also, $k{(s, t)=k}_1{ (s, t)+i k}_2 (s, t),$ is a known complex function such that

$$k_j(s,t): \left[0, 1\right]\times \left[0, 1\right] \stackrel{ }{\to } {ℝ}^2, j=1, 2.$$

This study looks at an area of fractional calculus that has not been looked at as much. It gives a qualitative analysis of how to solve the NFIDEq from a previous study. The analysis entails an examination of the presence and originality of the solution. Additionally, a novel numerical approach is proposed that combines the rationalized Haar wavelet method (RHM) with the Bernoulli polynomial method. For the first time, this method is used to solve a fractional problem whose parameters are specified in the complex plane. The method proposed uses a power series to obtain an approximate solution that converges rapidly and features a number of terms that can be computed conveniently. The methodology exhibits computational efficiency, rendering the technique readily implementable on a computer system.

The structure of this paper is as follows: Section 2 covers the essential ideas. In Section 3, we present enough conditions to establish both the existence and uniqueness of solutions for Equation (1). The numerical solution to the given issue is obtained using the rational Haar wavelet RH approach and a newly developed method in Section 4. In Section 5, we provide numerical examples to demonstrate the correctness and efficiency of the proposed method. These examples relate to the topics discussed in Section 4 and showcase the method’s accuracy. Additionally, we calculate the absolute errors of the problem. Finally, in Section 6, a conclusion is presented.

2. Basic Concepts

To facilitate progress, this paper presents a set of fundamental concepts and theorems that will be utilized in subsequent sections.

Definition 1

([21]). The Riemann–Liouville fractional integral operator of order $\gamma > 0$ is as follows:

$$I_x^{\gamma } u(x)=\frac{1}{\Gamma (\gamma )} {\displaystyle \underset{0}{\overset{x}{\int }}{(x - s)}^{\gamma -1} }u(s) ds , u > 0.$$

in which $\Gamma (.)$ is the Gamma function.

Proposition 1

([22]). The $(R-L)$ fractional integral operator $I^{\gamma }$ and the fractional derivative of Caputo sense $D^{\gamma }$ possess certain characteristics, such as the following:

• $D^{\gamma }{ I}^{\gamma } \tau \left(\xi )=\tau \right(\xi ),$
• $I^{\gamma } D^{\gamma } \tau (\xi )=\tau (\xi )-{\displaystyle \sum _{a=0}^{n-1}\frac{{\tau }^{(a)} \left(0\right)}{a!}} {\xi }^a,$
• $\left(D^{\alpha } I^{\gamma } \tau \right)(\xi {)=(I}^{\gamma -\alpha } \tau ) (\xi ) ,$ for $\gamma > \alpha$.

Theorem 1

([23]). There is exactly one fixed point for any contraction mapping on a Banach space.

Definition 2

([24]). If ${\rm E}\subseteq ℂ$ is an open set and ${\rm E} : u \stackrel{ }{\to } ℂ$ is a $C^{\prime }$ function, then ${\rm E}\left(Z\right)=e (x+i y) :=\tilde{e}(x, y)=\rho (x, y)+i \nu (x, y).$ where $\rho$ and $\nu$ are real valued functions.

Definition 3

([25]). The following equation can be used to describe Bernoulli polynomials of order:

$$B_r (\omega )={\displaystyle \sum _{i=0}^r\left(\begin{array}{c}r\\ i\end{array}\right)} B_{r-d} {\omega }^i , \omega \in \left[0, 1\right].$$

in which $B_i=B_i(0), i=0, 1, 2, \dots r,$ are Bernoulli numbers.

Definition 4

([26]). For $n \in \mathrm{N},$ we have degenerate Bernoulli polynomials of complex variables defined as

$$B_{n,\lambda } (x, y)={\displaystyle \sum _{k=0}^{\left[\frac{n-1}{2}\right]}}{\displaystyle \sum _{\ell =2k+1}^n\left(\begin{array}{c}n\\ \ell \end{array}\right)} {\lambda }^{\ell -2k+1}{ S}^{\left(1\right)} {\beta }_{{}_{n-1,\lambda }} (x),$$

where $S^{(1)}$ is a Stirling number of the first kind.

Definition 5

([12]). The rationalized Haar wavelet functions $h_n\left(\mathrm{t}\right)$ for $n={ 2}^{\mathrm{j}}+\mathrm{k}, \mathrm{j}=0, 1, \dots$, and $k=0, 1, \dots \stackrel{j}{2} - 1,$ are defined by $h_n \left(\mathrm{t}\right) ={ \mathrm{H} (2}^{\mathrm{j}} \mathrm{t} - \mathrm{k})$, $\forall t\in \left[0,1\right)$, where $H(t)=\{\begin{array}{cc}1& 0<t\le \frac{1}{2},\\ -1& \frac{1}{2}<t<1\\ 0& Otherwise.\end{array},$.

3. Existence and Uniqueness Solution

Before starting to study the existence and uniqueness of solutions for Equation (1), we will apply the (R-L) integral operator for both sides of Equation (1).

$$u (s, t) - k (s, t) - {\displaystyle \sum _{a=0}^{\infty }\frac{u^{(a)}{ (0, t)+k}^{(a)} (0, t)}{t!}}=h_1(s)+h_2(t)+I_t^{\alpha } \left({\displaystyle \underset{0}{\overset{1}{\int }}(s, t, \theta , u (\theta , t) d\theta }\right).$$

Using Definition 1 and Proposition 1, the previous form can simply be written as:

$$\begin{array}{c}u (s, t)=k (s, t)+h_1(s)+h_2(t)+ \frac{1}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}\tilde{U} \left(s, t, \theta , \mu , u (\theta , \mu )\right) d\theta d\mu }\\ +{\displaystyle \sum _{a=0}^{\infty }\frac{u^{(a)}{ (0, t)+k}^{(a)} (0, t)}{t!}}.\end{array}$$

(2)

where $\tilde{U}\left(s, t, \theta , \mu , u (\theta , \mu )\right)={\left(t-\mu \right)}^{\alpha -1}U\left(s,\theta , \mu , u (\theta , \mu )\right)$.

Then, Equation (1) transforms into a two-dimensional nonlinear mixed integral equation in complex $E \left(\left[0, 1\right]\times \left[0, 1\right], C\right)$.

Now, assume that the following conditions are satisfied:

A₁. Consider that we have two continuous functions,

$$f(\theta , \mu ) , g (\theta , \mu ) : E \left(\left[0, 1\right]\times \left[0, 1\right]\right) \stackrel{ }{\to } {ℝ}^2$$

such that

$$\tilde{U} \left(s, t, \theta , \mu , u (\theta , \mu )\right){=U}_1\left(s, t, \theta , \mu , f (\theta , \mu )\right)+{i U}_2\left(s, t, \theta , \mu , g (\theta , \mu )\right)$$

A₂. The function $U_{{}_1} : E \left({\left[0, 1\right]}^4\times C{\left[0, 1\right]}^2, {ℝ}^2\right)$ satisfies Lipschitz’s condition in the fifth variable as

$$\left|U_1 \left(s, t, \theta , \mu {, f}_1 (\theta , \mu )\right){ - U}_1\left(s, t, \theta , \mu {, f}_2 (\theta , \mu )\right)\right| \le r_1 \left|f_1(\theta , \mu ) - f_2(\theta , \mu )\right| ,{ r}_1 \ge 0 .$$

A₃. The function $U_{{}_2} : E \left({\left[0, 1\right]}^4\times C{\left[0, 1\right]}^2, {ℝ}^2\right)$ satisfies Lipschitz’s condition in the fifth variable as

$$\left|U_2 \left(s, t, \theta , \mu {, g}_1 (\theta , \mu )\right){ - U}_2\left(s, t, \theta , \mu {, g}_2 (\theta , \mu )\right)\right| \le { r}_2 \left|g_1(\theta , \mu ) - g_2(\theta , \mu )\right| ,{ r}_2 \ge 0.$$

A₄. d is a non-negative number such that

$$d=max \left\{r_{{}_1}{ , r}_{{}_2}\right\} < \frac{1}{2}.$$

Theorem 2.

Under conditions $A_1{,A}_2$ and $A_3.$ The integral operator $\Xi \in \left(C{[0,1]}^2, {\Vert .\Vert }_{\infty }\right)$, such that

$$\begin{array}{c}\Xi u(s, t)=k (s, t)+h_1(s)+h_2(t)+\frac{1}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}\tilde{U} \left(s, t, \theta , \mu , u (\theta , \mu )\right) d\theta d\mu }\\ +{\displaystyle \sum _{a=0}^{\infty }}\frac{u_{}^{(a)}(0,t)+k_{}^{(a)}(0,t)}{t!} ,\end{array}$$

(3)

is well defined.

Proof. 

From Condition $(A_1),$ we have

$$\begin{array}{c}\left|\Xi u (s, t)\right| \le \left|k (s, t)\right|+\left|h_1(s)+h_2(t)\right|+\frac{1}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}\left|U \left(s, t, \theta , \mu , u (\theta , \mu )\right)\right| d\theta d\mu },\\ \le \left|k (s, t)\right|+\left|h_1(s)+h_2(t)\right|+\frac{1}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}\left|U_1 \left(s, t, \theta , \mu , f (\theta , \mu )\right)\right| d\theta d\mu }\\ +\frac{i}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}\left|U_2 \left(s, t, \theta , \mu , g (\theta , \mu )\right)\right| d\theta d\mu },\\ \left|\Xi u (s, t)\right| \le \left|k(s, t)\right|+\left|h_1(s)+h_2(t)\right|{+b}_1 {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}\left|f (\theta , \mu )\right| d\theta d\mu }\\ +\frac{{i b}_2}{\Gamma \left(\alpha \right)} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}\left|g (\theta , \mu )\right| d\theta d\mu }.\end{array}$$

So,

$$Sup \left|\Xi u (s, t)\right| \le {\Vert k (s, t)\Vert }_{\infty }+{\Vert h_1(s)\Vert }_{\infty }+{\Vert h_2(t)\Vert }_{\infty }{+b}_1 {\Vert f (\theta , t)\Vert }_{\infty }{+b}_2 {\Vert g(\theta , t)\Vert }_{\infty }.$$

Then, the operator $\Xi$ is well defined, and, in this way, we can look for solutions of integral Equation (2) in $E \left(\left[0, 1\right]\times \left[0, 1\right], ℂ\right)$. □

Theorem 3.

Suppose that conditions $(A_2)$ and $(A_3),$ are achieved. Therefore, Equation (2) has a unique solution in $E \left(\left[0, 1\right]\times \left[0, 1\right], ℂ\right)$.

Proof. 

According to Theorem 1, and using the triangle inequality, we have

$$\begin{array}{c}\left|\Xi u_1 (s, t) - \Xi u_2 (s, t)\right| \le \frac{1}{\Gamma (\alpha )} |{\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}({\tilde{U}}_1 \left(s, t, \theta , \mu {, u}_1 (\theta , \mu )\right) }\\ {-\tilde{U}}_2 \left(s, t, \theta , \mu {, u}_2 (\theta , \mu )\right)) d\theta d\mu |+{\displaystyle \sum _{a=0}^{\infty }}\frac{ 1 }{t!} \left|u_1^{(a)} (0, t) - u_2^{(a)} (0, t)\right| .\\ \le \frac{1}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}|U_1 \left(s, t, \theta , \mu {, u}_1 (\theta , \mu )\right) }-U_2 \left(s, t, \theta , \mu {, f}_2 (\theta , \mu )\right)| d\theta d\mu \\ +\frac{i}{\Gamma (\alpha )}{\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}}\left|U_1 \left((s, t, \theta , \mu {, g}_1 (\theta , \mu )\right) - U_2 \left((s, t, \theta , \mu {, g}_2 (\theta , \mu )\right)\right| d\theta d\mu \\ +{\displaystyle \sum _{a=0}^{\infty }}\frac{ 1 }{t!} \left|u_1^{(a)} (0, t) - u_2^{(a)} (0, t)\right| .\end{array}$$

Using conditions $(A_2)$ and $(A_3),$ we obtain

$$\begin{array}{c}\left|\Xi u_1 (s, t) - \Xi u_2 (s, t)\right| \le { r}_1 {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}\left|f_1 \left(\theta , \mu ){ - f}_2 (\theta , \mu )\right)\right| d\theta d\mu }+\\ { r}_2 {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}\left|g_1 \left(\theta , \mu ){ - g}_2 (\theta , \mu )\right)\right| d\theta d\mu },\\ \le { r}_1 \Vert f_1 \left(x, t){ - f}_2 (x, t)\right)\Vert {+r}_2 \Vert g_1 \left(x, t){ - g}_2 (x, t)\right)\Vert .\end{array}$$

Now, define $\stackrel{*}{x} (\theta , \mu {)=f}_1 (\theta , \mu {)+i g}_1 (\theta , \mu ),$

$$\stackrel{*}{y} (\theta , \mu {)=f}_2 (\theta , \mu {)+i g}_2 (\theta , \mu ).$$

Using the triangle inequality, we obtain

$$\left|\Xi u_1 (s, t) - \Xi u_2 (s, t)\right| \le 2d \Vert \stackrel{*}{x} (s, t) - \stackrel{*}{y} (s, t)\Vert .$$

Successively, for $n \in \mathbb{N}$, we obtain

$${\Vert {\Xi }_{}^n{u}_1 - {\Xi }_{}^n{u}_2\Vert }_{\infty } \le { (2 d)}^n {\Vert \stackrel{*}{x} - \stackrel{*}{y}\Vert }_{\infty },$$

as $n \stackrel{ }{\to } \infty$ and according to condition $(A_4)$, the geometric sequence ${\left\{2d\right\}}^n$ is convergent, and hence $\Xi$ is a contraction mapping where

$${{\displaystyle \sum _{n=1}^{\infty } \Vert {\Xi }_{u_{{}_1}}^n - {\Xi }_{u_{{}_2}}^n\Vert }}_{\infty } < \infty .$$

And so, Equation (2) has a unique fixed point, according to the Banach fixed point theorem. □

4. Computational Approaches for Solving the NFIDEq (1)

4.1. Rationalized Haar Wavelet Method

Haar wavelets are the most basic wavelets among several types of wavelets. The step functions comprise an orthogonal and complete collection of functions that represent discredited and piecewise constant functions [10]. According to Definition 5, we can expand any function $f(x) \in ℂ [0, 1]$ with RH functions as

$$f(x) \simeq {\displaystyle \sum _{n=0}^{\infty }{a}_n{ h}_n \left(x\right)},$$

where

$$a_n{=2}^r {\displaystyle \underset{0}{\overset{1}{\int }}{f\left(y\right) h}_n \left(y\right) \mathrm{dy}}{=2}^r{ < f, h}_i{ > h}_i.$$

Also, the series ${\displaystyle \sum _r^{} 2^r{ < f, h}_i{ > h}_i, } r=1, 2, \dots , i$ converges uniformly to f.

Furthermore, for any function $f(x,y),$ we can approximate RH functions as follows:

$$f(x,y) \simeq {\displaystyle \sum _{q=0}^{m-1}}{\displaystyle \sum _{r=0}^{m-1}{f}_{qr}{ h}_{\mathrm{qr}} (x,y)},$$

(4)

where

$$h_{\mathrm{qr}}{ (x,y)=h}_q{ \left(x\right) h}_r \left(y\right),$$

(5)

and $f_{qr}$ are given by

$$f_{\mathrm{qr}}=\frac{{< f (x, y), h}_{\mathrm{qr}} (x, y) >}{{< h}_{\mathrm{qr}}{ (x, y), h}_{\mathrm{qr}} (x, y) >}.$$

(6)

Numerical Solution for Solving NFIDEq Using RH Method:

We will define a sequence of complex functions, denoted by $u_{{}_N} (s,t)$, obtained recursively by using interpolation and the RH basis on Equation (2) as

$$\begin{array}{c}{u}_N (s, t)=k_N (s, t)+h_{1,N}(s)+h_{2,N}(t)+\frac{1}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}{\tilde{U}}_1 \left(s, t, \theta , \mu {, u}_{N-1} (\theta , \mu )\right) d\theta d\mu }\\ +{\displaystyle \sum _{a=0}^{\infty }}{\displaystyle \sum _{N=1}^a\frac{u_N^{(a)}{ (0, t)+k}_N^{\left(a\right)} (0, t)}{t !}},\\ =k_N (s, t)+h_{1,N}(s)+h_{2,N}(t)+\frac{1}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}{U}_1 \left(s, t, \theta , \mu {, u}_{N-1} (\theta , \mu )\right) d\theta d\mu }+\\ \frac{i}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}{U}_{{}_2} \left(s, t, \theta , \mu {, u}_{{}_{N-1}} (\theta , \mu )\right) d\theta d\mu }+{\displaystyle \sum _{a=0}^{\infty }}{\displaystyle \sum _{N=1}^a\frac{u_N^{(a)}{ (0, t)+k}_N^{\left(a\right)} (0, t)}{t !}}.\end{array}$$

Assume that

$$\begin{array}{c}{A}_{N-1}(s,t,\theta ,\mu )=u_1(s,t,\theta ,\mu ,{ u}_{N-1} (\theta ,\mu )),\\ B_{N-1}(s,t,\theta ,\mu )=u_2(s,t,\theta ,\mu ,{ u}_{N-1} (\theta ,\mu )).\end{array}$$

Then, we have

$$\begin{array}{c}{u}_N (s, t)=k_N (s, t)+h_{1,N}(s)+h_{2,N}(t)+\frac{1}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}{A}_{N-1} \left(s, t, \theta , \mu \right) d\theta d\mu }\\ +\frac{i}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}}{\displaystyle \underset{0}{\overset{1}{\int }}{B}_{N-1} \left(s, t, \theta , \mu \right) d\theta d\mu }+{\displaystyle \sum _{a=0}^{\infty }}{\displaystyle \sum _{N=1}^a\frac{u_N^{(a)}{ (0, t) - k}_N^{\left(a\right)} (0, t)}{t !}}.\end{array}$$

(7)

Through the use of Equations (4)–(6), Equation (7) is transformed into

$$\begin{array}{c}{u}_N (s, t) \simeq k_N (s, t)+h_{1,N}(s)+h_{2,N}(t)+\frac{1}{\Gamma (\alpha )} {\displaystyle \sum _{q=0}^N}{\displaystyle \sum _{r=0}^N}{\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N{C}^{(1)}}{h}_{qr}{ (s, t) h}_{\ell m} (\theta , \mu )\\ +\frac{i}{\Gamma (\alpha )} {\displaystyle \sum _{q=0}^N}{\displaystyle \sum _{r=0}^N}{\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N{C}^{(2)}}{h}_{qr}{ (s, t) h}_{\ell m} (\theta , \mu )+{\displaystyle \sum _{a=0}^{\infty }}{\displaystyle \sum _{N=1}^a\frac{u_N^{(a)}{ (0, t)+k}_N^{\left(a\right)} (0, t)}{t !}},\end{array}$$

(8)

and C⁽¹⁾ and C⁽²⁾ are coefficients which are given by

$$C^{\left(1\right)}=\frac{{< A}_{{}_{N-1}} (s, t, \theta , \mu {), h}_{\mathrm{qr}}{ (s, t) h}_{\ell m} (\theta , \mu ) >}{{< h}_{\mathrm{qr}}{ (s, t), h}_{\mathrm{qr}}{ (s, t) > < h}_{\ell m} (\theta , \mu {), h}_{\ell m} (\theta , \mu ) >},$$

(9)

$$C^{\left(2\right)}=\frac{{< B}_{{}_{N-1}} (s, t, \theta , \mu {), h}_{\mathrm{qr}}{ (s, t) h}_{\ell m} (\theta , \mu ) >}{{< h}_{\mathrm{qr}}{ (s, t), h}_{\mathrm{qr}}{ (s, t) > < h}_{\ell m} (\theta , \mu {), h}_{\ell m} (\theta , \mu ) >}.$$

(10)

4.2. New Technique for Solving the NFIDEq (1)

In this subsection, we will combine a Bernoulli approach method with the RH method for solving NFIDEq (1).

4.2.1. Bernoulli Polynomial Approximation

Using Definition 3, we can approximate the solution of $g(x,t)$ using the truncated Bernoulli series.

$$g (x, t)={\displaystyle \sum _{u=0}^N}{\displaystyle \sum _{v=0}^N}\underset{}{g_{u,v}} \underset{u}{\beta }\left(x\right) \underset{v}{\beta }\left(t\right),$$

(11)

where the coefficients $\underset{}{g_{u,v}}$ were extracted as

$$\underset{}{g_{u,v}}=\frac{1}{u! v!} {\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{{\partial }^{u+v} g (x, t)}{\partial { x}^u \partial { t}^v} dx dt}}.$$

(12)

Lemma 1.

Consider the approximation of the fractional derivative of the complex function $Z(s,t)$ using the Bernoulli polynomials

$$D_t^{\gamma } Z (s, t)={\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N}\underset{\ell ,m}{Z} \underset{n}{\beta }(s, t), 0 < \gamma \le 1.$$

(13)

where $\underset{n}{\beta }(s, t)$ are Bernoulli polynomials of complex variables. Then, we have

$$Z (s, t)={\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N}\underset{\ell ,m}{Z} \underset{n,\lambda }{Q}(s, t)+{\displaystyle \sum _{b=0}^{\infty }\frac{Z_{(x,0)}^{(b)}{ t}^b}{b!}}$$

where $Q_{n,\lambda } (s, t)=Z (s, t)={\displaystyle \sum _{k=0}^{\left[\frac{n-1}{2}\right]}}{\displaystyle \sum _{r=0}^n}{\lambda }^{1-2k}{ (-1)}^k{ S}^{\left(1\right)} {\beta }_{n-1} \left(s\right) {\displaystyle \underset{0}{\overset{t}{\int }}\frac{x^{2k+1}}{{(x-s)}^{1-\alpha }}} dx$.

Proof. 

According to Definition 4, Bernoulli polynomials of complex functions in two variables are

$${\beta }_{n,\lambda } (s, t)={\displaystyle \sum _k^{\left[\frac{n-1}{2}\right]}}{\displaystyle \sum _r^n\left(\begin{array}{c}n\\ r\end{array}\right) }{\lambda }^{1-2k}{ (-1)}^k{ S}^{\left(1\right)} {\beta }_{n-1,\lambda }{ \left(s\right) t}^{2k+1},$$

where $S^{\left(1\right)}$ are Stirling numbers of the first kind, $\lambda \in ℝ$.

Apply $I_t^{\gamma }$ on both sides of formula (5), and, using Equation (4), we obtain

$$Z (s, t) - {\displaystyle \sum _{b=0}^{n-1}\frac{Z_{(s,0)}^{(b)}{ t}^b}{b!}}=I_t^{\gamma } \left[{\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N}\underset{\ell ,m}{Z} \underset{n}{\beta }(s, t)\right]$$

with the aid of formula (6), we have

$$Z (s, t) - {\displaystyle \sum _{b=0}^{n-1}\frac{Z_{}^{(b)}(s,0){ t}^b}{b!}}=I_t^{\gamma } \left[{\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N}\underset{\ell ,m}{Z}\left\{{\displaystyle \sum _k^{\left[\frac{n-1}{2}\right]}}{\displaystyle \sum _r^n\left(\begin{array}{c}n\\ r\end{array}\right) }{\lambda }^{1-2k}{ (-1)}^k{ S}^{\left(1\right)} {\beta }_{n-1,}{ \left(s\right) t}^{2k+1}\right\}\right].$$

So,

$$Z (s, t) - {\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N}\underset{\ell ,m}{Z} {\displaystyle \sum _{k=0}^{\left[\frac{n-1}{2}\right]}}{\displaystyle \sum _{r=0}^n\left(\begin{array}{c}n\\ r\end{array}\right) }{\lambda }^{1-2k}{ (-1)}^k{ S}^{\left(1\right)} {\beta }_{n-1} \left(S\right) {\displaystyle \underset{0}{\overset{t}{\int }}\frac{x^{2k+1}}{{(x-s)}^{1-\gamma }}} dx.$$

Then,

$$Z (s, t)={\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N}\underset{\ell ,m}{Z} Q_{n,\lambda } (s, t)+{\displaystyle \sum _{b=0}^{n-1} }\frac{Z_{(s,0)}^{(b)} t^b}{b!}.$$

where

$$Q_{n,\lambda } (s, t)={\displaystyle \sum _{k=0}^{\left[\frac{n-1}{2}\right]}}{\displaystyle \sum _{r=0}^n\left(\begin{array}{c}n\\ r\end{array}\right) }{\lambda }^{1-2k}{ (-1)}^k{ S}^{\left(1\right)} {\beta }_{n-1} \left(S\right) {\displaystyle \underset{0}{\overset{t}{\int }}\frac{x^{2k+1}}{{(x-s)}^{1-\alpha }}} dx.$$

 □

4.2.2. The Proposed Technique (B—RH Method) for Solving NFIDEq (1)

By employing Bernoulli polynomials and RH functions, we can transform the NFIDEq into a set of algebraic equations. This is achieved by expanding the pertinent approximate solution into a linear combination of the Bernoulli and RH bases, as demonstrated below.

According to Lemma 1, we can obtain an approximation of the L.H.S of Equation (1) as

$$D_t^{\alpha } \left(u (s, t) - k (s, t)\right)={\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N\left(\underset{\ell ,m}{u} - \underset{\ell ,m}{k}\right)} Q_{n,\lambda } (s, t)+{\displaystyle \sum _{b=0}^{n-1} }\frac{u_{}^{(a)}(s,0) - k_{}^{(a)}(s,0)}{a!}{ t}^a$$

(14)

We use the RH method to approximate the R.H.S of Equation (1) as

$${\displaystyle \underset{0}{\overset{1}{\int }}u (s, t, \theta ,u(\theta , t)} d\theta ={\displaystyle \underset{0}{\overset{1}{\int }}{u}_1 (s, t, \theta ,u_{N-1}(\theta , t)} d\theta +i {\displaystyle \underset{0}{\overset{1}{\int }}{u}_2 (s, t, \theta ,u_{N-1}(\theta , t)} dx\theta$$

(15)

Assume ${\Lambda }_{N-1} (s, t, \theta ){=u}_1 \left(s, t, \theta ,{ u}_{N-1} (\theta , t)\right),$

$${\Phi }_{N-1} (s, t, \theta ){=u}_2 \left(s, t, \theta ,{ u}_{N-1} (\theta , t)\right).$$

Then, Equation (15) will be

$${\displaystyle \underset{0}{\overset{1}{\int }}u (s, t, \theta ,u(\theta , t)} d\theta ={\displaystyle \underset{0}{\overset{1}{\int }}{\Lambda }_{N-1} (s, t, \theta )} d\theta +i {\displaystyle \underset{0}{\overset{1}{\int }}{\Phi }_{N-1} (s, t, \theta )} d\theta .$$

(16)

Using Equations (4)–(6), Equation (16) transforms into

$$\begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}u (s, t, \theta ,u(\theta , t)} d\theta =\\ {\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N}{\displaystyle \sum _{q=0}^N}{E}^{(1)}{ h}_{\ell .m}{(s, t) h}_q\left(\theta )+i {\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N}{\displaystyle \sum _{q=0}^N}{E}^{(2)}{ h}_{\ell .m}{(s, t) h}_q\right(\theta ).\end{array}$$

(17)

where $E^{(1)}$ and $E^{(2)}$ are coefficients determined by

$$E^{\left(1\right)}=\frac{< {\Lambda }_{{}_{N-1}} (s, t, \theta {), h}_{{}_{\ell m}}{ (s, t) h}_q (\theta ) >}{{< h}_{{}_{\ell m}}{ (s, t), h}_{{}_{\ell m}}{ (s, t) > < h}_q (\theta {), h}_q (\theta ) >},$$

(18)

$$E^{\left(2\right)}=\frac{< {\Phi }_{{}_{N-1}} (s, t, \theta {), h}_{{}_{\ell m}}{ (s, t) h}_q (\theta ) >}{{< h}_{{}_{\ell m}}{ (s, t), h}_{{}_{\ell m}}{ (s, t) > < h}_q (\theta {), h}_q (\theta ) >}.$$

(19)

Thus, according to the results in Equations (14) and (17), the numerical approach of Equation (1) will be

$$\begin{array}{l}{\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N\left(\underset{\ell ,m}{u} - \underset{\ell ,m}{k}\right)} Q_{n,\lambda } (s, t)={\displaystyle \sum _{\ell =0}^N}{\displaystyle \sum _{m=0}^N}{\displaystyle \sum _{q=0}^N \left(E^{(1)}+i{ E}^{\left(2\right)}\right)} h_{\ell m} (s, t) h_q (\theta ) \\ +{\displaystyle \sum _{a=0}^{N-1} \frac{u^{(a)}{ (s, 0) - k}^{\left(a\right)} (s, 0)}{a !}}{ t}^a.\end{array}$$

(20)

Theorem 4.

For some fixed constants ${\lambda }_1 , {\lambda }_2 , \dots , {\lambda }_j > 0$, $j \ge 1$, we have ${\Vert { u - u}_N\Vert }_{\infty } \le {\Vert { u}_0{ - u}_0\Vert }_{\infty } {\displaystyle \sum _{k=N}^{\infty }}{d}^k+{\displaystyle \sum _{k=1}^N}{d}^{N-k}{\lambda }_k.$

Proof. 

Using Equations (3) and (16), we have

$$\begin{array}{c}{\Vert \Xi u_{N-1}{ - u}_N\Vert }_{\infty } \le \frac{1}{\Gamma (\alpha )} \Vert {\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{1}{\int }}\left(A_{N-1} (s, t, \theta , \mu ) - {\Lambda }_{N-1} (s, t, \theta )\right)}} d\theta d\mu \\ +\frac{i}{\Gamma (\alpha )} {\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{1}{\int }}\left(B_{N-1} (s, t, \theta , \mu ) - {\Phi }_{N-1} (s, t, \theta )\right)}}\Vert d\theta d\mu ,\\ \le \frac{1}{\Gamma (\alpha )} \Vert {\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{1}{\int }}\left(A_{N-1} (s, t, \theta , \mu ) - {\Lambda }_{N-1} (s, t, \theta )\right)}} d\theta d\mu \Vert ,\\ +\frac{i}{\Gamma (\alpha )} \Vert {\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{0}{\overset{1}{\int }}\left(B_{N-1} (s, t, \theta , \mu ) - {\Phi }_{N-1} (s, t, \theta )\right)}} d\theta d\mu \Vert ,\\ \le \frac{1}{\Gamma (\alpha )} \Vert A_{N-1} - {\Lambda }_{N-1}\Vert +\frac{1}{\Gamma (\alpha )} \Vert B_{N-1} - {\Phi }_{N-1}\Vert \end{array}$$

Set $\Delta (s, t, \theta , \mu )=A_{N-1} - {\Lambda }_{N-1}$.

If we use the interpolation property for the variables

$$\begin{array}{c}{S}_{\ell }=\frac{1}{2^{N_1}+1}+\frac{x_1}{2^{N_1}} , \ell =2^{N_1}+x_1 , \ell \ge 1\\ t_m=\frac{1}{2^{N_2}+1}+\frac{x_2}{2^{N_2}} , m=2^{N_2}+x_2 , m \ge 1\\ {\theta }_n=\frac{1}{2^{N_3}+1}+\frac{x_3}{2^{N_3}} , n=2^{N_3}+x_3 , n \ge 1\\ {\mu }_q=\frac{1}{2^{N_4}+1}+\frac{x_4}{2^{N_4}} , q=2^{N_4}+x_4 , q \ge 1\end{array}$$

in which $N_1 , N_2 , N_3 , N_4 \ge 1,$ then we have

$$\begin{array}{c}{\Vert A_{N-1} - {\Lambda }_{N-1}\Vert }_{\infty }=\\ \Vert \Delta { (s}_{\ell }{, t}_m, {\theta }_n, {\mu }_q)+\frac{\partial \Delta \left(\zeta , t, \theta , \mu \right)}{\partial S}(\zeta - s_1)+\frac{\partial \Delta \left(s, \tau , \theta , \mu \right)}{\partial t} (\tau { - t}_m) +\\ \frac{\partial \Delta \left(s, t, \beta , {\theta }_{}\right)}{\partial \theta } (\beta - {\theta }_n)+{\frac{\partial \Delta \left(s, t, \theta , \upsilon \right)}{\partial \mu } (\upsilon - {\mu }_q) \Vert }_{\infty },\\ =\Vert \Delta { (s}_{\ell }{, t}_m, {\theta }_n, {\mu }_q)+{\Delta }_s^{}(\zeta , t, \theta , \mu ) +{\Delta }_t^{}\left(s, \tau , \theta , \mu )+\Delta \theta \right(s, t, \beta , \mu )+\\ {{\Delta }_{\mu }(s, t, \theta , \upsilon ) \Vert }_{\infty }\cdot Sup \left\{{\Vert \zeta { - S}_{\ell }\Vert }_{\infty } . {\Vert \tau { - t}_m\Vert }_{\infty } . {\Vert \beta - {\theta }_n\Vert }_{\infty } . {\Vert \upsilon - {\mu }_q\Vert }_{\infty }\right\},\\ \le \frac{3}{2^N} {\Vert \Delta { (s}_{\ell }{, t}_m, {\theta }_n, {\mu }_q)+{\Delta }_s^{}\left(\zeta , t, \theta , \mu )+{\Delta }_{\theta }\right(\zeta , t, \beta , \mu )+{\Delta }_{\mu }{}_{}(s, t, \theta , \upsilon ) \Vert }_{\infty }.\\ \le \frac{4{ E}_{N-1}}{2^{N-1}}.\end{array}$$

where $E_{N-1}=Sup \left\{{\Vert \frac{\partial {\Delta }_{N-1}}{\partial S}\Vert }_{\infty } . {\Vert \frac{\partial {\Delta }_{N-1}}{\partial t}\Vert }_{\infty } . {\Vert \frac{\partial {\Delta }_{N-1}}{\partial \theta }\Vert }_{\infty } . {\Vert \frac{\partial {\Delta }_{N-1}}{\partial \mu }\Vert }_{\infty }\right\}$.

Similarly, for $B_{N-1}$, we have

$$\Vert \Xi u_{N-1} - u_N\Vert \le \frac{8 E_{N-1}}{2^{N-1}}.$$

Choose ${\lambda }_1 , {\lambda }_2 ,\dots , {\lambda }_j > 0$, with $\frac{8 E_{j-1}}{2^{j-1}} < {\lambda }_j$, for $j=1,2,\dots ,N$.

Then, we possess,

$$\Vert \Xi u_{N-1} - u_N\Vert <{\lambda }_N, \mathrm{for} N \ge 1.$$

(21)

Using the triangle inequality, we obtain

$$\Vert u - u_N\Vert \le \Vert u - {\Xi }^N{u}_0\Vert +{\displaystyle \sum _{k=N}^{\infty }{d}^k} {\Vert \Xi u_{k-1} - u_k\Vert }_{\infty } .$$

(22)

According to Equations (21) and (22), we obtain

$$\Vert u - u_N\Vert \le \Vert \Xi u_0 - u_0\Vert {\displaystyle \sum _{k=N}^{\infty }{d}^k}+{\displaystyle \sum _{k=1}^N{d}^{N-k}} {\lambda }_k .$$

(23)

 □

Lemma 2.

The proposed method has a rate of convergence of order $O{ (N}^2{\left(2d\right)}^N).$

Proof. 

According to Equation (23), since d < 1, the series ${\displaystyle \sum _{N=1}^{\infty } d^N},$ converges to $\frac{d^k}{1-d}$.

If we set $d=\frac{1}{2} - \frac{1}{2^{n+1}} < \frac{1}{2}$, for $n\in N$, then Equation (23) will be

$$\begin{array}{ll}\Vert u - u_N\Vert & \le {\Vert \Xi u_0 - u_0\Vert }_{\infty } \frac{d^k}{1-d}+{\displaystyle \sum _{k=1}^N{\left(\frac{1}{2} - \frac{1}{2^{n+1}}\right)}^{N-k}} . \frac{8E_{j-1} }{2^{j-1}},\\ & ={\Vert \Xi u_0 - u_0\Vert }_{\infty } \frac{d^k}{1-d}+16 {\left(\frac{1}{2} - \frac{1}{2^{n+1}}\right)}^n {\displaystyle \sum _{k=1}^N{\left(\frac{1}{2} - \frac{1}{2^{n+1}}\right)}^{-k}} . \frac{E_{j-1} }{2^j}.\end{array}$$

(24)

Moreover, the sequence $E_{j-1}$ is uniformly bounded for any $\forall j\in N$. Thus, for every $j \le N$, $\exists N < \infty$ set $\left|E_{j-1}\right| \le N$. Thus, Equation (24) obtains

$$\begin{array}{ll}\Vert u - u_N\Vert & \le {\Vert \Xi u_0 - u_0\Vert }_{\infty } \frac{d^k}{1-d}{+16 \left(d\right)}^N . {\displaystyle \sum _{k=1}^N{\left(\frac{1}{2} - \frac{1}{2^{n+1}}\right)}^{-k}} \frac{N }{2^j},\\ & ={\Vert \Xi u_0 - u_0\Vert }_{\infty } \frac{d^k}{1-d}{+16 N \left(d\right)}^N . {\displaystyle \sum _{j=1}^N\left(1+\frac{1}{2^j-1}\right)} \frac{N }{2^j},\end{array}$$

(25)

For any $j \in N , \left(1+\frac{1}{2^j-1}\right) < 2$, then

$${\Vert u - u_N\Vert }_{\infty } \le {\Vert \Xi u_0 - u_0\Vert }_{\infty } \frac{d^k}{1-d}{+16 N\left(d\right)}^N . {\displaystyle \sum _{j=1}^N{2}^j}\le {\Vert \Xi u_0 - u_0\Vert }_{\infty } \frac{d^k}{1-d}{+16 N \left(d\right)}^N . N 2^N.$$

(26)

For $d < \frac{1}{2}$ and letting $N \stackrel{ }{\to } \infty$, we obtain

${\Vert u - u_N\Vert }_{\infty } \le { 16 N}^2{ \left(2d\right)}^N.$ So, we can see that the rate of convergence reaches order $O{ (N}^2{(2d)}^N).$ □

5. Numerical Problems

Example 1.

Consider the following NFIDEq

$$D_t^{0.7} \left(u (s, t) - k (s, t)\right)={\displaystyle \underset{0}{\overset{1}{\int }}\frac{\cos \left(u\left(\theta ,t\right)\right)}{\left(s+1\right)\left(t+2\right)}d\theta }.$$

(27)

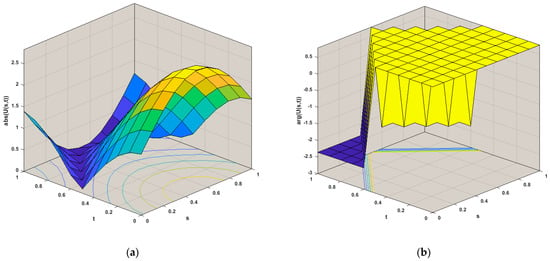
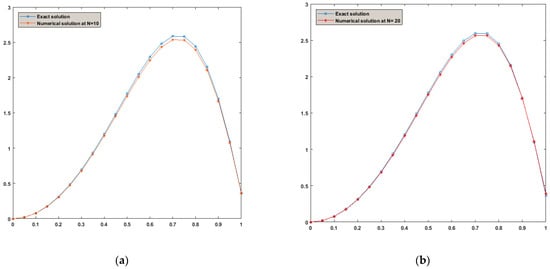
where $k(s,{ t)=s}^2+t^2,$ is the known function selected so that the exact solution of Example 1 will be $u(s,t)=\left(sin3s+cos3t\right)+i\left(sin3s+cos3t\right),$ and the approximate solutions of $u_N(s, t)$ are shown in spreading $s,t\in \left[0,1\right]$ as $x,t=0.1:0.1:1.$ Based on the RH method and the proposed technique, the B-RH method, the numerical solutions and the absolute errors of Example 1 are displayed in Table 1 for two values of N by taking $N=10$, and $N=20$. The average run time is 0.7341 s. Additionally, in Figure 1 and Figure 2, and by taking $N=20$, we represent the numerical solution $u_N(s, t)$ of Example 1 with the aid of its magnitude $abs\left(u(s,t)\right),$ and the argument $\arg \left(u(s,t)\right)$ using the B-RH method.

Table 1. Represents abs. errors for approximate solutions for Equation (27).

$({\mathit{s}}_{\mathit{i}},{\mathit{t}}_{\mathit{i}})$	For N = 10		For N = 20
	HR Method	The Proposed Method	HR Method	The Proposed Method
(0.1, 0.1)	7.87 × 10−9	9.69 × 10−10	1.14 × 10−10	2.44 × 10−11
(0.2, 0.2)	8.47 × 10−10	5.18 × 10−11	7.29 × 10−11	4.25 × 10−12
(0.3, 0.3)	2.41 × 10−10	1.64 × 10−10	3.17 × 10−10	9.36 × 10−13
(0.4, 0.4)	7.57 × 10−9	4.02 × 10−9	4.09 × 10−10	6.08 × 10−12
(0.5, 0.5)	1.07 × 10−9	3.47 × 10−10	8.14 × 10−10	1.17 × 10−12
(0.6, 0.6)	7.14 × 10−11	7.64 × 10−11	7.06 × 10−12	1.49 × 10−11
(0.7, 0.7)	5.09 × 10−11	1.17 × 10−12	5.87 × 10−10	3.04 × 10−10
(0.8, 0.8)	9.22 × 10−9	3.77 × 10−12	2.19 × 10−11	2.91 × 10−12
(0.9, 0.9)	4.72 × 10−10	7.97 × 10−11	1.36 × 10−11	8.07 × 10−13
(1, 1)	1.39 × 10−11	2.04 × 10−12	7.19 × 10−11	9.75 × 10−13

Figure 1. Numerical solutions for Equation (27) with the aid of its magnitude $abs\left(u(s,t)\right)$ in (a) and the argument $\arg \left(u(s,t)\right)$ in (b), using the B-RH method by choosing $N=20$.

Figure 2. The variance between the numerical and exact solutions for Equation (27) at $N=10$ in (a) and $N=20$ in (b).

Example 2.

Consider the following NFIDEq

$$D_t^{0.3} \left(u (s, t) - k (s, t)\right)={\displaystyle \underset{0}{\overset{1}{\int }}\left(s+t\right)u^2\left(\theta ,t\right)d\theta }.$$

(28)

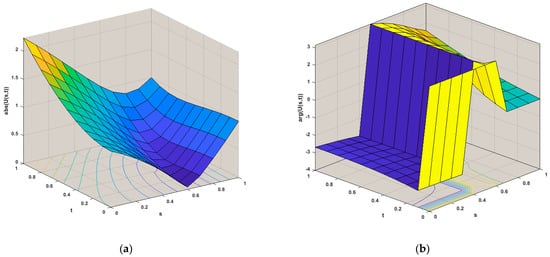
where $k(s,{ t)=s}^{}-t^2+i\left(t^3-s\right),$ is the known function selected so that the exact solution of Example 2 will be $u(s,t)={\left(s+it\right)}^2+\left(s-it\right)-1,$ and the approximate solutions of $u_N(s, t)$ are shown in spreading $s,t\in \left[0,1\right]$ as $x,t=0.1:0.1:1.$ Based on the RH method and the proposed technique, the B-RH method, the numerical solutions and the absolute errors of Example 2 are displayed in Table 2 for $N=15$, and $N=25$. The average run time is 0.9820 s. Additionally, in Figure 3, and by taking $N=25$, we represent the numerical solution $u_N(s, t)$ of Example 2 with the aid of its magnitude $abs\left(u(s,t)\right),$ and the argument $\arg \left(u(s,t)\right)$ using the B-RH method.

Table 2. Represents abs. errors for approximate solutions for Equation (28).

$({\mathit{s}}_{\mathit{i}},{\mathit{t}}_{\mathit{i}})$	For N = 15		For N = 25
	HR Method	The Proposed Method (B-HR)	HR Method	The Proposed Method (B-HR)
(0.1, 0.1)	1.14 × 10−10	2.87 × 10−11	7.27 × 10−11	9.05 × 10−11
(0.2, 0.2)	3.26 × 10−9	4.66 × 10−11	9.06 × 10−10	4.57 × 10−12
(0.3, 0.3)	7.75 × 10−10	9.19 × 10−10	7.11 × 10−9	6.33 × 10−12
(0.4, 0.4)	5.22 × 10−11	6.07 × 10−12	1.75 × 10−10	7.17 × 10−13
(0.5, 0.5)	3.09 × 10−9	1.75 × 10−11	9.67 × 10−11	3.98 × 10−12
(0.6, 0.6)	9.77 × 10−11	1.09 × 10−12	4.27 × 10−11	7.39 × 10−13
(0.7, 0.7)	4.19 × 10−10	3.66 × 10−11	1.67 × 10−10	9.07 × 10−13
(0.8, 0.8)	7.37 × 10−11	2.73 × 10−11	7.18 × 10−11	5.75 × 10−14
(0.9, 0.9)	1.75 × 10−11	8.97 × 10−12	1.06 × 10−11	1.36 × 10−14
(1, 1)	7.77 × 10−11	4.01 × 10−12	9.87 × 10−11	6.01 × 10−13

Figure 3. Numerical solutions for Equation (28) with the aid of its magnitude $abs\left(u(s,t)\right)$ in (a), and the argument $\arg \left(u(s,t)\right)$ in (b), using the B-RH method by choosing $N=25$.

To compare the findings, the variation between exact answers and approximate solutions for different values of N is calculated based on Example 1. The results are presented in Table 1 and Figure 1 and Figure 2. Based on the absolute errors, the following observations were made:

$N=10$	HR Method		B-HR Method
	$(s,t)$	abs. Error	$(s,t)$	abs. Error
Largest abs. error	(0.5, 0.5)	1.07 × 10−9	(0.3, 0.3)	1.64 × 10−10
Least abs. error	(0.6, 0.6)	7.14 × 10−11	(0.8, 0.8)	3.77 × 10−12

$N=20$	HR Method		B-HR Method
	$(s,t)$	abs. Error	$(s,t)$	abs. Error
Largest abs. error	(0.1, 0.1)	1.14 × 10−10	(0.7, 0.7)	3.04 × 10−10
Least abs. error	(0.6, 0.6)	7.06 × 10−12	(1, 1)	9.75 × 10−13

Example 2 demonstrates the disparity between exact answers and approximate solutions for various values of N. This discrepancy is illustrated in Table 2 as well as Figure 3 and Figure 4. The following results were obtained:

$N=15$	HR Method		B-HR Method
	$(s,t)$	abs. Error	$(s,t)$	abs. Error
Largest abs. error	(0.5, 0.5)	3.9 × 10−9	(0.3, 0.3)	9.19 × 10−10
Least abs. error	(0.6, 0.6)	9.77 × 10−11	(0.9, 0.9)	8.97 × 10−12
$N=25,$	HR method		B-HR method
	$(s,t)$	abs. error	$(s,t)$	abs. error
Largest abs. error	(0.3, 0.3)	7.11 × 10−9	(0.1, 0.1)	9.05 × 10−11
Least abs. error	(1, 1)	9.87 × 10−11	(0.8, 0.8)	5.75 × 10−14

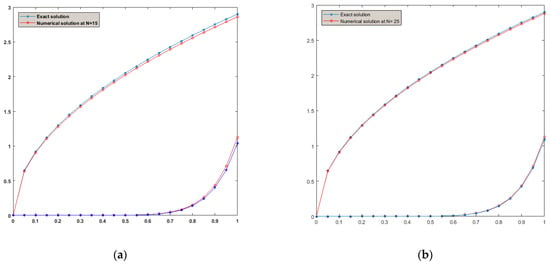
Figure 4. The variance between the numerical and exact solutions for Equation (28) at $N=15$ in (a) and $N=25$ in (b).

6. Conclusions

We know that the solution of the NFIDEq is generally complicated, especially if the unknown function is complex. Therefore, authors frequently strive to acquire an approximate solution. The RH technique is a highly efficient and effective approach for solving Equation (1). This research employs a novel strategy that utilizes the Bernoulli polynomial method to construct the RH method. We present the theoretical results of the suggested method with the results of the RH method in Section 4. Additionally, in Section 5, we provide two instances of numerical computations utilizing Matlab R2022b. These computations serve as the conclusive step in validating the theoretical investigation. The provided examples demonstrate the contrasts between precise solutions and numerical solutions for different values of N. Additionally, Table 1 and Table 2 display the absolute errors in each example. Figure 3 and Figure 4 demonstrate a significant convergence between the exact and numerical answers, particularly in the data pertaining to the B-HR approach. This convergence appears explicitly at times in the range $t=0.6\sim 1,$ especially in Figure 2b and Figure 4b, more than the solutions at times in the range $t=0.1\sim 0.5,$ in Figure 2a and Figure 4a. Based on the findings, we can conclude that when we take a bigger value of N and increase the time to reach at $t\to 1$. The B-HR method yields higher accuracy in numerical solutions compared with the HR method. Therefore, we can infer that the B-HR method is particularly efficient in determining precise numerical solutions and considerably reduces computation time while maintaining accuracy. This can be observed by comparing the numerical solutions and exact answers in the provided examples.

7. Future Work

We would like to solve the linear system of Fredholm integro-differential equations as a disease model based on the proposed approach and compare the results with other numerical methods.