Numerical Approximation of the Fractional Rayleigh–Stokes Problem Arising in a Generalised Maxwell Fluid

Abstract

This paper presents a numerical technique to approximate the Rayleigh–Stokes model for a generalised Maxwell fluid formulated in the Riemann–Liouville sense. The proposed method consists of two stages. First, the time discretization of the problem is accomplished by using the finite difference. Second, the space discretization is obtained by means of the predictor–corrector method. The unconditional stability result and convergence analysis are analysed theoretically. Numerical examples are provided to verify the feasibility and accuracy of the proposed method.

1. Introduction

Fractional calculus (FC) generalises the classical integer-order calculus [1,2]. In the last decade, FC has received considerable attention in a variety of scientific areas [3,4,5,6]. In most cases, it is difficult to compute an explicit solution to fractional differential equations, which has attracted researchers to look for accurate and efficient numerical approaches for solving these Equations [7,8,9,10,11,12,13,14].

FC has successfully described viscoelastic fluid constitutive relations [15,16,17]. One usually starts the process of modelling viscoelastic fluids via fractional derivatives by modifying a traditional differential equation. This generalisation involves using the Riemann–Liouville (R–L) fractional derivative operator instead of the standard time derivative. Shen et al. [18] derived the Rayleigh–Stokes Equation (RSE) for a generalised fluid of the second grade flowing within a heated edge and over a heated flat plate. The analytic solutions for the temperature and velocity fields were obtained via the fractional Laplace and the Fourier sine transforms. Mainardi [19] provided a comprehensive review of the relationship between FC and viscoelastic models, linear viscoelasticity, and wave propagation. Qi and Xu [20] studied an unsteady flow of fractional Maxwell fluid in a channel. Xue and Nie [21] addressed the RSE to a heated generalised fluid of the second grade with fractional derivative flows inside a porous half-space.

In this paper, we investigate the numerical solution for the time fractional Rayleigh–Stokes Equation (TFRSE) including the time fractional derivative

$$\begin{array}{cc}\hfill \frac{\partial v(x,y,t)}{\partial t}& ={}_0{D}_t^{1-\gamma }\left[k_1\frac{{\partial }^{2}v(x,y,t)}{\partial x^2}+k_2\frac{{\partial }^{2}v(x,y,t)}{\partial y^2}\right]\hfill \\ \hfill & +k_3\frac{{\partial }^{2}v(x,y,t)}{\partial x^2}+k_4\frac{{\partial }^{2}v(x,y,t)}{\partial y^2}+f(x,y,t),\hfill \end{array}$$

(1)

with initial and boundary conditions (abbreviated as IC and BCs, respectively):

$$\begin{array}{ll}v(x,y,0)\hfill & =\varphi (x,y),0\le x,y\le L,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill v(x,0,t)& ={\phi }_1(x,t),v(x,L,t)={\phi }_2(x,t),0\le t\le T,0\le x\le L,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill v(0,y,t)& ={\psi }_1(y,t),v(L,y,t)={\psi }_2(y,t),0\le t\le T,0\le y\le L,\hfill \end{array}$$

(4)

where $v(x,y,t)$ represent the velocity field, the coefficients $k_1$, $k_2,$$k_3$ and $k_4$ are positive constants, $0<\gamma <1$, $f(x,y,t)$ is a source term, functions $\varphi$, ${\phi }_1$, ${\phi }_2$, ${\psi }_1$ and ${\psi }_2$ are prescribed and ${}_0{D}_t^{1-\gamma }v(x,y,t)$ is the R–L fractional differential derivative of order $1-\gamma$ denoted by

$${}_0{D}_t^{1-\gamma }v(x,y,t)=\frac{1}{\Gamma (\gamma )}\frac{\partial }{\partial t}\underset{0}{\overset{t}{\int }}\frac{v(x,y,\eta )}{{(t-\eta )}^{1-\gamma }}\mathrm{d}\eta .$$

(5)

Some numerical techniques have been used to approximate the TFRSE Equation (1). Chen et al. [22] formulated an implicit finite difference (FD) algorithm. Wu [23] presented an implicit numerical approximation scheme. Jiang and Lin [24] proposed a numerical technique based on the method of reproducing kernel. Mohebbi et al. [25] adopted the compact FD method (CFDM) and radial basis function (RBF) meshless method (RMM). Zaky [26] and Shivanian et al. [27] used the Legendre–Tau and the meshless singular boundary methods, respectively. Hafez et al. [28] applied the Jacobi Spectral Galerkin method for the distributed TFRSE. Safari and HongGuang [29] adopted the improved dual reciprocity and singular boundary schemes for the TFRSE, while Golbabai et al. [30] proposed the local meshless RBF. Khan et al. [31] developed the high-order compact scheme, whereas Naz et al. [32] advanced a modified implicit scheme for the TFRSE.

This paper introduces a numerical method for the TFRSE and is organized as follows. Section 2 describes an algorithm to approximate the time fractional derivative of the TFRSE Equation (1). Section 3 accomplishes the space discretization with the help of the predictor–corrector method. Section 4 studies the unconditional stability result and convergence analysis of the proposed strategy by using Fourier analysis. Section 5 reports the numerical examples of the TFRSE and verifies the efficiency of the proposed scheme. Finally, Section 6 provides a concise conclusion.

2. The Time Discretization

Let us define $t_k=k\tau ,$ where $\tau =\frac{T}{N}$ represents the time step size for $k=0,1,2,\dots ,N.$ We suppose that the solution $u(x,y,t)$ has a continuous partial derivative $\frac{\partial u(x,y,t)}{\partial t}$ for $t\ge 0$, and that the R–L fractional derivative ${}_0{D}_t^{1-\gamma }u(x,y,t)$ can be evaluated using the Grünwald–Letnikov (G–L) formulation [33], described as

$${}_0{D}_t^{1-\gamma }u(x,y,t)=\frac{1}{{\tau }^{1-\gamma }}\sum _{j=0}^{[t/\tau ]}{\lambda }_j^{(1-\gamma )}u(x,y,t-j\tau )+\mathcal{O}\left({\tau }^q\right),0<\gamma <1,0<q<1,$$

(6)

so that ${\lambda }_j^{(1-\gamma )}$ correspond to the coefficients of the generating function

$$\lambda (z,1-\gamma )=\sum _{j=0}^{\infty }{\lambda }_j^{(1-\gamma )}{z}^j,$$

where the coefficients ${\lambda }_0^{(1-\gamma )}=1$ and ${\displaystyle {\lambda }_j^{(1-\gamma )}={(-1)}^j\left(\genfrac{}{}{0pt}{}{1-\gamma }{j}\right)}$ are the normalized G–L weights. The coefficients can be obtained recursively as:

$${\lambda }_0^{(1-\gamma )}=1,{\lambda }_j^{(1-\gamma )}=\left(1-\frac{2-\gamma }{j}\right){\lambda }_{j-1}^{(1-\gamma )},j\ge 1.$$

The ${\lambda }_j^{1-\gamma }$ have some useful properties, as given by Lemma 1 ([33]).

Lemma 1.

The coefficients ${\lambda }_j^{1-\gamma }$ introduced in Equation (6) satisfy

• ${\lambda }_j^{(1-\gamma )}<0,j=1,2,\dots .$
• ${\displaystyle \sum _{j=0}^{\infty }}{\lambda }_j^{(1-\gamma )}=0,\forall n\in \mathbb{N},-{\displaystyle \sum _{j=0}^n}{\lambda }_j^{(1-\gamma )}<1\mathrm{and}$${\displaystyle \sum _{j=0}^{n-1}}{\lambda }_j^{(1-\gamma )}>0.$
• ${\displaystyle \sum _{j=n}^{\infty }}{\lambda }_j^{(1-\gamma )}\ge {\displaystyle \frac{1}{n^{1-\gamma }\mathrm{\Gamma }\left(\gamma \right)}}·$

Let us consider the following notations:

$${\left[{}_0{D}_t^{1-\gamma }v(x,y,t)\right]}_{t=t_k}={\tau }^{\gamma -1}\sum _{l=0}^k{\lambda }_{l}v(x,y,t_{k-l})+\mathcal{O}\left(\tau \right),$$

(7)

$$\frac{\partial v(x_{},y_{},t_k)}{\partial t}=\frac{v(x_{},y_{},t_k)-v(x_{},y_{},t_{k-1})}{\tau }+\mathcal{O}\left(\tau \right).$$

(8)

Now, we can formulate the semi-time discretization scheme for Equation (1) by means of the aforementioned relations

$$\begin{array}{cc}\hfill \frac{v(x_{},y_{},t_k)-v(x_{},y_{},t_{k-1})}{\tau }& ={\tau }^{\gamma -1}\sum _{l=0}^k{\lambda }_l\left(k_1\frac{{\partial }^{2}v(x_{},y_{},t_{k-l})}{\partial x^2}+k_2\frac{{\partial }^{2}v(x_{},y_{},t_{k-l})}{\partial y^2}\right)\hfill \\ & +\left(k_3\frac{{\partial }^{2}v(x_{},y_{},t_{k-l})}{\partial x^2}+k_4\frac{{\partial }^{2}v(x_{},y_{},t_{k-l})}{\partial y^2}\right)+f(x_{},y_{},t_k).\hfill \end{array}$$

(9)

3. The Space Discretization

Let $\mathrm{\Omega }=\left\{(x_i,y_j)\right|1\le i\le M_1,1\le j\le M_2\}$ with $x_i=i{h}_x,y_j=j{h}_y$, so that $h_x=\frac{L}{M_1}$, $h_y=\frac{L}{M_2}$ represent the space steps in the x and y directions, respectively, and also $M_1$ and $M_2$ denote the total number of space steps in the x and y directions, respectively. Discretizing Equation (1) at the above grid points $(x_i,x_j,t_k)$ and by using

$$\frac{{\partial }^{2}v(x_i,y_j,t_k)}{\partial x^2}=\frac{{\delta }_x^{2}v(x_i,y_j,t_k)}{h_x^2}+\mathcal{O}\left(h_x^2\right),$$

(10)

$$\frac{{\partial }^{2}v(x_i,y_j,t_k)}{\partial y^2}=\frac{{\delta }_y^{2}v(x_i,y_j,t_k)}{h_y^2}+\mathcal{O}\left(h_y^2\right),$$

(11)

where

$${\delta }_x^{2}v(x_i,y_j,t_k)=v(x_{i-1},y_j,t_k)-2v(x_i,y_j,t_k)+v(x_{i+1},y_j,t_k),$$

$${\delta }_y^{2}v(x_i,y_j,t_k)=v(x_i,y_{j-1},t_k)-2v(x_i,y_j,t_k)+v(x_i,y_{j+1},t_k),$$

we obtain the following corrector formula as

$$\begin{array}{cc}\hfill v_{i,j}^k=& \frac{1}{\tau }[v_{i,j}^{k-1}+{\mu }_1\sum _{l=1}^k{\lambda }_l{\delta }_x^2{v}_{i,j}^{k-l}+{\mu }_2\sum _{l=1}^k{\lambda }_l{\delta }_y^2{v}_{i,j}^{k-l}+({\mu }_1+{\mu }_3)(v_{i+1,j}^k+v_{i-1,j}^k)\hfill \\ \hfill +& ({\mu }_2+{\mu }_4)(v_{i,j+1}^k+v_{i,j-1}^k)+\tau f_{i,j}^k],\hfill \end{array}$$

(12)

$$1\le i\le K_1-1,1\le j\le K_2-1,1\le k\le N.$$

such that

$$\tau =1+2({\mu }_1+{\mu }_2+{\mu }_3+{\mu }_4),$$

$$\begin{array}{c}\hfill {\mu }_1=k_1\frac{{\tau }^{\gamma }}{h_x^2},{\mu }_2=k_2\frac{{\tau }^{\gamma }}{h_y^2},{\mu }_3=k_3\frac{\tau }{h_x^2},{\mu }_4=k_4\frac{\tau }{h_y^2},\end{array}$$

(13)

with $f_{i,j}^k$ representing the value of function f at $(x_i,y_j,t_k).$ The truncation error [22] is obtained as

$$\begin{array}{c}\hfill R=\mathcal{O}(h_x^2+h_y^2){\tau }^{\gamma }\sum _{l=0}^k{\lambda }_l+\mathcal{O}(\tau h_x^2+\tau h_y^2+{\tau }^2),\end{array}$$

(14)

and the predictor formula is denoted by

$$\begin{array}{cc}\hfill v_{i,j}^k& =v_{i,j}^{k-1}-ϵv_{i,j}^{k-1},\hfill \end{array}$$

(15)

$$1\le i\le K_1-1,1\le j\le K_2-1,1\le k\le N,$$

with the IC and BCs

$$\begin{array}{cc}\hfill & v_{i,j}^0=\varphi (x_i,y_j),i=0,1,\dots ,K_1,j=0,1,\dots ,K_2,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & v_{i,0}^k={\phi }_1(x_i,t_k),v_{i,K_2}^k={\phi }_2(x_i,t_k),i=1,2,\dots ,K_1-1,k=1,2,\dots ,N,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & v_{0,j}^k={\psi }_1(y_j,t_k),v_{K_1,j}^k={\psi }_2(y_j,t_k),j=1,2,\dots ,K_2-1,k=1,2,\dots ,N,\hfill \end{array}$$

(18)

respectively. We can adopt the following iterative procedure to approximate Equation (1) with Equations (2)–(4).

P: Predict some value ${\left[v_{i,j}^k\right]}^0$ for $v_{i,j}^k$ with

$$\begin{array}{cc}\hfill {\left[v_{i,j}^k\right]}^0& =v_{i,j}^{k-1}-ϵv_{i,j}^{k-1}\hfill \end{array}$$

$$1\le i\le K_1-1,1\le j\le K_2-1,1\le k\le N,$$

where $ϵ$ is a very small number.

E: Evaluate the implicit part in Equation (12) with ${\left[v_{i,j}^k\right]}^0$.

C: Correct ${\left[v_{i,j}^k\right]}^0$ to obtain a new ${\left[v_{i,j}^k\right]}^1$ for $v_{i,j}^k$ with

$$\begin{array}{cc}\hfill {\left[v_{i,j}^k\right]}^1=& \frac{1}{\tau }[v_{i,j}^{k-1}+{\mu }_1\sum _{l=1}^k{\lambda }_l{\delta }_x^2{v}_{i,j}^{k-l}+{\mu }_2\sum _{l=1}^k{\lambda }_l{\delta }_y^2{v}_{i,j}^{k-l}+({\mu }_1+{\mu }_3)({\left[v_{i+1,j}^k\right]}^0+{\left[v_{i-1,j}^k\right]}^0)\hfill \\ \hfill +& ({\mu }_2+{\mu }_4)({\left[v_{i,j+1}^k\right]}^0+{\left[v_{i,j-1}^k\right]}^0)+\tau f_{i,j}^k],\hfill \end{array}$$

$$1\le i\le K_1-1,1\le j\le K_2-1,1\le k\le N.$$

E: Evaluate the implicit part in Equation (12) with ${\left[v_{i,j}^k\right]}^1$.

C: Correct ${\left[v_{i,j}^k\right]}^1$ with

$$\begin{array}{cc}\hfill {\left[v_{i,j}^k\right]}^2=& \frac{1}{\tau }[v_{i,j}^{k-1}+{\mu }_1\sum _{l=1}^k{\lambda }_l{\delta }_x^2{v}_{i,j}^{k-l}+{\mu }_2\sum _{l=1}^k{\lambda }_l{\delta }_y^2{v}_{i,j}^{k-l}+({\mu }_1+{\mu }_3)({\left[v_{i+1,j}^k\right]}^1+{\left[v_{i-1,j}^k\right]}^1)\hfill \\ \hfill +& ({\mu }_2+{\mu }_4)({\left[v_{i,j+1}^k\right]}^1+{\left[v_{i,j-1}^k\right]}^1)+\tau f_{i,j}^k],\hfill \end{array}$$

$$1\le i\le K_1-1,1\le j\le K_2-1,1\le k\le N.$$

⋮

The sequence of operations

PECECECEC…

determines $v_{i,j}^k$ for a sequence of values as

$${\left[v_{i,j}^k\right]}^0,{\left[v_{i,j}^k\right]}^1,{\left[v_{i,j}^k\right]}^2,\dots$$

An appropriate stop condition is

$$|{\left[v_{i,j}^k\right]}^{n+1}-{\left[v_{i,j}^k\right]}^n|<\epsilon ,n=0,1,2,\dots$$

where n is the number of iterations. Hence, the relation Equation (12) can be rewritten in following form:

$$\left\{\begin{array}{c}{\left[v_{i,j}^k\right]}^P=v_{i,j}^{k-1}-ϵv_{i,j}^{k-1}\hfill \\ \begin{array}{cc}\hfill {\left[v_{i,j}^k\right]}^C=& \frac{1}{\tau }[v_{i,j}^{k-1}+{\mu }_1\sum _{l=1}^k{\lambda }_l{\delta }_x^2{v}_{i,j}^{k-l}+{\mu }_2\sum _{l=1}^k{\lambda }_l{\delta }_y^2{v}_{i,j}^{k-l}+({\mu }_1+{\mu }_3)({\left[v_{i+1,j}^k\right]}^P+{\left[v_{i-1,j}^k\right]}^P)\hfill \\ \hfill & +({\mu }_2+{\mu }_4)({\left[v_{i,j+1}^k\right]}^P-{\left[v_{i,j-1}^k\right]}^P)+\tau f_{i,j}^k],\hfill \end{array}\hfill \end{array}\right.$$

(19)

$$1\le i\le K_1-1,1\le j\le K_2-1,1\le k\le N,$$

with the IC and BCs Equations (16)–(18).

4. Theoretical Analysis of the Proposed Method

4.1. Stability Analysis

We now examine the stability of the proposed method Equation (19) by using Fourier analysis. Let $v_{i,j}^k$ and ${\overline{v}}_{i,j}^k$ be the exact and the approximated solutions for ${\left[v_{i,j}^k\right]}^C$ in Equation (19). Then, the error can be defined as:

$$E_{i,j}^k=v_{i,j}^k-{\overline{v}}_{i,j}^k.$$

We can obtain for corrector formula

$$\begin{array}{cc}\hfill E_{i,j}^k=& \frac{1}{\tau }[E_{i,j}^{k-1}+{\mu }_1\sum _{l=1}^k{\lambda }_l{\delta }_x^2{E}_{i,j}^{k-l}+{\mu }_2\sum _{l=1}^k{\lambda }_l{\delta }_y^2{E}_{i,j}^{k-l}+({\mu }_1+{\mu }_3)(E_{i+1,j}^k+E_{i-1,j}^k)\hfill \\ \hfill & +({\mu }_2+{\mu }_4)(E_{i,j+1}^k+E_{i,j-1}^k)].\hfill \end{array}$$

(20)

Let us introduce the following function:

$$E^k(x,y)=\left\{\begin{array}{cc}{E}_{i,j}^k\hfill & (x,y)\in {\Omega }_1,\hfill \\ 0\hfill & (x,y)\in {\Omega }_2,\hfill \end{array}\right.$$

such that

$${\Omega }_1=\left\{(x,y)|x_{i-\frac{1}{2}}<x\le x_{i+\frac{1}{2}},y_{j-\frac{1}{2}}<y\le y_{j+\frac{1}{2}}\right\},$$

$${\Omega }_2=\left\{(x,y)|0\le x\le \frac{h_x}{2}\mathrm{or}L-\frac{h_x}{2}<x\le Lor0\le y\le \frac{h_y}{2}orL-\frac{h_y}{2}<y\le L\right\}.$$

Then, $E^k(x,y)$ can be approximated by using the Fourier series as

$$E^k(x,y)=\sum _{l_1=-\infty }^{+\infty }\sum _{l_2=-\infty }^{+\infty }{\zeta }_k(l_1,l_2)e^{2\pi I\frac{(l_{1}x+l_{2}y)}{L}}1\le k\le N,$$

where

$${\zeta }_k(l_1,l_2)=\frac{1}{L^2}\underset{0}{\overset{L}{\int }}\underset{0}{\overset{L}{\int }}{E}^k(x,y)e^{-2\pi I\frac{l_{1}x+l_{2}y}{L}}\mathrm{d}x\mathrm{d}y,I=\sqrt{-1}.$$

Applying Parseval equality for $k=0,1,\dots ,N$

$$\begin{array}{cc}\hfill \left|\right|E^k{\left|\right|}_2& ={\left[\sum _{i=1}^{K_1-1}\sum _{j=1}^{K_2-1}{h}_x{h}_y{\left|E_{i,j}^k\right|}^2\right]}^{\frac{1}{2}}={\left[\sum _{l_1=-\infty }^{\infty }\sum _{l_2=-\infty }^{\infty }{\left|{\zeta }_k(l_1,l_2)\right|}^2\right]}^{\frac{1}{2}}.\hfill \end{array}$$

(21)

Suppose that the difference Equation (20) has the following solution

$$\begin{array}{cc}\hfill E_{i,j}^k& ={\zeta }_k{e}^{I({\sigma }_{1}i{h}_x+{\sigma }_{2}j{h}_y)},\hfill \end{array}$$

(22)

where ${\sigma }_1=\frac{2\pi l_1}{L}$ and ${\sigma }_2=\frac{2\pi l_2}{L}·$ Substituting Equation (22) into Equation (20) and simplifying leads to

$$\begin{array}{c}\hfill {\zeta }_k=\frac{1}{\tau }\left[{\zeta }_{k-1}-\psi \sum _{l=1}^k{\lambda }_l{\zeta }_{k-l}+\varphi {\zeta }_k\right],\end{array}$$

(23)

such that

$$\begin{array}{cc}\hfill & \psi =4{\mu }_1{sin}^2\frac{{\sigma }_1{h}_x}{2}+4{\mu }_2{sin}^2\frac{{\sigma }_2{h}_y}{2},\hfill \\ \hfill & \varphi =2({\mu }_1+{\mu }_3)(1-2{sin}^2\frac{{\sigma }_1{h}_x}{2})+2({\mu }_2+{\mu }_4)(1-2{sin}^2\frac{{\sigma }_2{h}_y}{2}).\hfill \end{array}$$

Now, we investigate the stability of the method Equation (19).

Theorem 1.

The predictor–corrector method Equation (19) is stable if and only if $\varphi \ge 0$.

Proof. 

The proof will be obtained by using mathematical induction. For $k=1$, we get

$$\begin{array}{cc}\hfill |{\zeta }_1|=& \frac{1}{\tau }|\left[1-\psi (\gamma -1)+\varphi \right]\left|\right|{\zeta }_0|\le \frac{1}{\tau }\left[1-\psi \left|\right(\gamma -1\left)\right|+\varphi \right]|{\zeta }_0|\le |{\zeta }_0|.\hfill \end{array}$$

(24)

Assume that

$$|{\zeta }_k|\le |{\zeta }_0|,k=1,2,\dots ,N-1.$$

(25)

Then, by using [Lemma 2 in [25]], we arrive at

$$\begin{array}{cc}\hfill |{\zeta }_k|& =\left|\frac{1}{\tau }\left[{\zeta }_{k-1}-\psi \sum _{l=1}^k{\lambda }_l{\zeta }_{k-l}+\varphi {\zeta }_k\right]\right|,\hfill \\ \hfill & \le \frac{1}{\tau }\left[1-\psi \left|\sum _{l=1}^k{\lambda }_l\right|+\varphi \right]\left|{\zeta }_0\right|,\hfill \\ \hfill & =\frac{1}{\tau }\left[1+\psi \sum _{l=1}^k{\lambda }_l+\varphi \right]\left|{\zeta }_0\right|,\hfill \\ \hfill & \le \frac{1}{\tau }(1-\psi +\varphi )\left|{\zeta }_0\right|,\hfill \\ \hfill & \le |{\zeta }_0|.\hfill \end{array}$$

Using the Parseval equality Equation (21), the error in the solution of the difference Equation (23) satisfies

$$\left|\right|E^k{\left|\right|}_2\le \left|\right|E^0{\left|\right|}_2,k=1,2,\dots ,N.$$

The proof of the theorem is completed. □

4.2. Convergence Analysis

Let us define the truncation error in the proposed method to satisfy the following form

$$\begin{array}{cc}\hfill R_{i,j}^k=& v(x_i,y_j,t_k)-v(x_i,y_j,t_{k-1})-{\mu }_1\sum _{l=0}^k{\lambda }_l{\delta }_x^{2}v(x_i,y_j,t_{k-l})-{\mu }_2\sum _{l=0}^k{\lambda }_l{\delta }_y^{2}v(x_i,y_j,t_{k-l})\hfill \\ \hfill -& {\mu }_3{\delta }_x^{2}v(x_i,y_j,t_k)-{\mu }_4{\delta }_x^{2}v(x_i,y_j,t_k)-\tau f(x_i,y_j,t_k),\hfill \end{array}$$

(26)

$$1\le i\le K_1-1,1\le j\le K_2-1,1\le k\le N.$$

From Lemma 3 in [25], we have

$$R_{i,j}^k=\mathcal{O}(\tau h_x^2+\tau h_y^2+{\tau }^2),$$

or

$$\begin{array}{c}\hfill |R_{i,j}^k|\le C_1(\tau h_x^2+\tau h_y^2+{\tau }^2).\end{array}$$

(27)

$$1\le i\le K_1-1,1\le j\le K_2-1,1\le k\le N,$$

where ${\mathrm{C}}_1\in {\mathbb{R}}^{+}$. Subtracting Equation (12) from Equation (26), we get

$$\begin{array}{cc}\hfill e_{i,j}^k=& \frac{1}{\tau }[e_{i,j}^{k-1}+{\mu }_1\sum _{l=1}^k{\lambda }_l{\delta }_x^2{e}_{i,j}^{k-l}+{\mu }_2\sum _{l=1}^k{\lambda }_l{\delta }_y^2{e}_{i,j}^{k-l}+({\mu }_1+{\mu }_3)(e_{i+1,j}^k+e_{i-1,j}^k)\hfill \\ \hfill & +({\mu }_2+{\mu }_4)(e_{i,j+1}^k+e_{i,j-1}^k)+R_{i,j}^k],\hfill \end{array}$$

(28)

where $e_{i,j}^k=v(x_i,y_j,t_k)-v_{i,j}^k,$ and

$$e_{0,j}^k=e_{K_1,j}^k=0,e_{i,0}^k=e_{i,K_2}^k=0,e_{i,j}^0=0,$$

$$1\le i\le K_1,1\le j\le K_2,1\le k\le N.$$

Let us consider the following two functions:

$$e^k(x,y)=\left\{\begin{array}{cc}{e}_{i,j}^k,\hfill & (x,y)\in {\Omega }_1,\hfill \\ 0,\hfill & (x,y)\in {\Omega }_2,\hfill \end{array}\right.$$

and

$$R^k(x,y)=\left\{\begin{array}{cc}{R}_{i,j}^k,\hfill & (x,y)\in {\Omega }_1,\hfill \\ 0,\hfill & (x,y)\in {\Omega }_2.\hfill \end{array}\right.$$

Then, $e_{i,j}^k$ and $R_{i,j}^k$ can by approximated by the Fourier series

$$\begin{array}{cc}\hfill & e^k(x,y)=\sum _{l_1=-\infty }^{+\infty }\sum _{l_2=-\infty }^{+\infty }{\alpha }_k(l_1,l_2)e^{2\pi I\frac{(l_{1}x+l_{2}y)}{L}}0\le k\le N,\hfill \\ \hfill & R^k(x,y)=\sum _{l_1=-\infty }^{+\infty }\sum _{l_2=-\infty }^{+\infty }{\beta }_k(l_1,l_2)e^{2\pi I\frac{(l_{1}x+l_{2}y)}{L}}0\le k\le N,\hfill \end{array}$$

in which

$${\alpha }_k(l_1,l_2)=\frac{1}{L^2}{\int }_0^L\underset{0}{\overset{L}{\int }}{e}^k(x,y)e^{-2\pi I\frac{l_{1}x+l_{2}y}{L}}\mathrm{d}\mathrm{x}\mathrm{d}y$$

and

$${\beta }_k(l_1,l_2)=\frac{1}{L^2}\underset{0}{\overset{L}{\int }}\underset{0}{\overset{L}{\int }}{R}^k(x,y)e^{-2\pi I\frac{l_{1}x+l_{2}y}{L}}\mathrm{d}\mathrm{x}\mathrm{d}y.$$

Moreover, we can obtain the values of $\left|\right|e^k{\left|\right|}_2$ and $\left|\right|R^k{\left|\right|}_2$ for $k=0,1,\dots ,N$ as

$$\begin{array}{cc}\hfill \left|\right|e^k{\left|\right|}_2& ={\left[\sum _{i=1}^{K_1-1}\sum _{j=1}^{K_2-1}{h}_x{h}_y{\left|e_{i,j}^k\right|}^2\right]}^{\frac{1}{2}}={\left[\sum _{l_1=-\infty }^{\infty }\sum _{l_2=-\infty }^{\infty }{\left|{\alpha }_k(l_1,l_2)\right|}^2\right]}^{\frac{1}{2}},\hfill \end{array}$$

(29)

and

$$\begin{array}{cc}\hfill \left|\right|R^k{\left|\right|}_2& ={\left[\sum _{i=1}^{K_1-1}\sum _{j=1}^{K_2-1}{h}_x{h}_y{\left|R_{i,j}^k\right|}^2\right]}^{\frac{1}{2}}={\left[\sum _{l_1=-\infty }^{\infty }\sum _{l_2=-\infty }^{\infty }{\left|{\beta }_k(l_1,l_2)\right|}^2\right]}^{\frac{1}{2}}.\hfill \end{array}$$

(30)

Suppose that $e_{i,j}^k$ and $R_{i,j}^k$ have the following form

$$\begin{array}{c}\hfill e_{i,j}^k={\alpha }_k{e}^{I({\sigma }_{1}i{h}_x+{\sigma }_{2}j{h}_y)},R_{i,j}^k={\beta }_k{e}^{I({\sigma }_{1}i{h}_x+{\sigma }_{2}j{h}_y)},\end{array}$$

(31)

where

$${\sigma }_1=\frac{2\pi l_1}{L},{\sigma }_2=\frac{2\pi l_2}{L}·$$

Substituting Equation (31) into Equation (28) gives

$$\begin{array}{c}\hfill {\alpha }_k=\frac{1}{\tau }\left[{\alpha }_{k-1}-\psi \sum _{l=1}^k{\lambda }_l{\alpha }_{k-l}+\varphi {\alpha }_k+{\beta }_k\right],\end{array}$$

(32)

where $\tau ,\psi$ and $\varphi$ are as defined before. By virtue of the relations Equations (27) and (30), we get

$$\begin{array}{cc}\hfill \left|\right|R^k{\left|\right|}_2& \le \sqrt{K_1{h}_x}\sqrt{K_2{h}_y}{C}_1(\tau h_x^2+\tau h_y^2+{\tau }^2),\hfill \\ \hfill & =C_{1}L(\tau h_x^2+\tau h_y^2+{\tau }^2).\hfill \end{array}$$

(33)

Based on [22], it holds that

$$\begin{array}{c}\hfill |{\beta }_k|\equiv |{\beta }_k(l_1,l_2)|\le C_2|{\beta }_1|\equiv C_2\left|{\beta }_1(l_1,l_2)\right|k=1,2,\dots ,N,\end{array}$$

(34)

where $C_2\in {\mathbb{R}}^{+}$.

Proposition 1.

Let ${\alpha }_k$ denote the solutions of Equation (32). Then, we have

$$|{\alpha }_k|\le C_{2}k\left|{\beta }_1\right|,1\le k\le N,$$

where $C_2\in {\mathbb{R}}^{+}$.

Proof. 

The principle of mathematical induction is applied by considering $e^0=0$, which leads to

$${\alpha }_0\equiv {\alpha }_0(l_1,l_2)=0.$$

For $k=1$, we obtain

$$|{\alpha }_1|\le |\frac{1}{\tau }\left|\right|{\beta }_1|\le |{\beta }_1|\le C_2\left|{\beta }_1\right|.$$

Let us assume that

$$|{\alpha }_n|\le n{C}_2\left|{\beta }_1\right|1\le n\le k-1.$$

Then, based on Lemma in [25], we can conclude that

$$\begin{array}{cc}\hfill |{\alpha }_k|& \le \frac{1}{\tau }[(k-1)-\psi (k-1)\sum _{l=1}^k|{\lambda }_l|+\varphi (k-1)+1]C_2\left|{\beta }_1\right|,\hfill \\ \hfill & \le \frac{1}{\tau }[k-\psi (k-1)+\varphi (k-1)]C_2\left|{\beta }_1\right|,\hfill \\ \hfill & \le k{C}_2\left|{\beta }_1\right|,\hfill \end{array}$$

which completes the proof. □

Theorem 2.

The predictor–corrector method Equation (19) is convergent with the order $\mathcal{O}(h_x^2+h_y^2+\tau ).$

Proof. 

By considering Proposition 1 and using relations Equations (32) and (33), we can obtain

$$\left|\right|e^k{\left|\right|}_2\le k{C}_2\left|\right|R^1{\left|\right|}_2\le k{C}_1{C}_{2}L(\tau h_x^2+\tau h_y^2+\tau ),$$

and noticing that $k\tau \le T,$ then

$$\left|\right|e^k{\left|\right|}_2\le C(h_x^2+h_y^2+\tau ),$$

in which

$$C=C_1{C}_{2}TL,$$

and this completes the proof. □

5. Results and Discussion

This section presents two numerical examples for illustrating the stability and accuracy of the proposed method with several values of $h_x,h_y,\tau$ and $\gamma$. For this aim, we compute the following maximum-norm error $L_{\infty }$:

$$L_{\infty }=\underset{1\le j\le N-1}{max}|v({\mathbf{x}}_j,T)-V({\mathbf{x}}_j,T)|,$$

where v and V are the approximate and exact solutions, respectively. In addition, we evaluate the computational order in the time direction for the proposed method as:

$$C_{\tau }=\frac{log\left(\frac{E_1}{E_2}\right)}{log\left(\frac{{\tau }_1}{{\tau }_2}\right)},$$

where $E_1$ and $E_2$ represent the errors corresponding to time step with sizes ${\tau }_1$ and ${\tau }_2$, respectively.

Example 1.

Let us consider the following TFRSE:

$$\begin{array}{cc}\hfill & \frac{\partial v(x,y,t)}{\partial t}={}_0{D}_t^{1-\gamma }\left(\frac{{\partial }^{2}v(x,y,t)}{\partial x^2}+\frac{{\partial }^{2}v(x,y,t)}{\partial y^2}\right)\hfill \\ \hfill & +\frac{{\partial }^{2}v(x,y,t)}{\partial x^2}+\frac{{\partial }^{2}v(x,y,t)}{\partial y^2}+f(x,y,t),(x,y)\in \mathrm{\Omega }={[0,1]}^2.\hfill \end{array}$$

The IC and BCs as well as $f(x,y,t)$ are determined from an exact solution $v(x,y,t)=exp(x+y)t^{1+\gamma }.$

The proposed method is implemented for solving this problem when the total time $T=1$ with various values of $h_x,h_y,\tau$ and $\gamma$. Table 1 presents the maximum absolute errors $L_{\infty }$, time convergence orders $C_{\tau }$ and execution times (in seconds) for $h_x=h_y=\frac{1}{8}$, $\gamma \in \{0.55,0.85\}$ and various values of $\tau$. We see that the obtained computational orders $C_{\tau }$ in time direction are close to the theoretical convergence rate, that is, $\mathcal{O}\left(\tau \right).$ Table 2 lists the maximum absolute errors $L_{\infty }$ in the solution for $\gamma \in \{0.5,0.75\}$, and several values of $h_x=h_y$ and $\tau .$ Table 3 compares the maximum absolute errors $L_{\infty }$ in the solution with those resulting from the method described in [25] for $h_x=h_y=\frac{1}{16}$, $\gamma =0.15$ and various values of $\tau .$ Table 4 makes the comparison of $L_{\infty }$ errors in the solution with those resulting from the method in [25] for different values of $h_x=h_y$, $\gamma =0.2$, and $\tau .$ Table 5 compares the maximum absolute errors $L_{\infty }$ in the solution and execution times (in seconds) with those obtained with other schemes [22,25] for $h_x=h_y=\frac{1}{4}$, $\tau =\frac{1}{900}$ and different values of $\gamma$. Figure 1 shows the approximate solution and the associated computational error $L_{\infty }$ of the proposed method with $\gamma =0.85$, $K_1=K_2=16$, and $N=256$.

Table 1. The maximum absolute errors $L_{\infty }$, time convergence orders $C_{\tau }$ and execution times (in seconds) of Example 1 for $h_x=h_y=\frac{1}{8}$ and $\gamma \in \{0.55,0.85\}$ and different values of $\tau$.

$\mathit{\tau }$	$\mathit{\gamma }=0.55$	$\mathit{\gamma }=0.85$
	$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$	${\mathit{C}}_{\mathit{\tau }}$	CPU Time (s)	$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$	${\mathit{C}}_{\mathit{\tau }}$	CPU Time (s)
1/8	65	$6.3090\times {10}^{-3}$	−	$0.1285$	47	$9.3000\times {10}^{-3}$	−	$0.1689$
1/10	63	$5.3982\times {10}^{-3}$	$0.69871$	$0.1493$	47	$8.9975\times {10}^{-3}$	$0.14819$	$0.1093$
1/16	65	$3.7302\times {10}^{-3}$	$0.78639$	$0.1558$	48	$4.8582\times {10}^{-3}$	$1.31122$	$1.7073$
1/40	66	$1.6951\times {10}^{-3}$	$0.86077$	$0.5390$	44	$2.3980\times {10}^{-3}$	$0.77053$	$0.6569$
1/64	64	$1.1170\times {10}^{-3}$	$0.88743$	$6.5077$	40	$1.5138\times {10}^{-3}$	$0.97874$	$1.3609$
1/128	70	$5.6189\times {10}^{-4}$	$0.99127$	$11.508$	32	$7.6491\times {10}^{-4}$	$0.98481$	$2.1372$

Table 2. The maximum absolute errors $L_{\infty }$ in the solution of Example 1 for $\gamma \in \{0.5,0.75\}$, and different values of $h_x=h_y$ and $\tau$.

${\mathit{h}}_{\mathit{x}}$	$\mathit{\tau }$	$\mathit{\gamma }=0.5$		$\mathit{\gamma }=0.75$
		$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$	$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$
1/4	1/4	8	$7.9397\times {10}^{-3}$	7	$1.6266\times {10}^{-2}$
1/10	1/64	117	$1.2258\times {10}^{-3}$	80	$1.5186\times {10}^{-3}$
1/16	1/128	419	$6.7026\times {10}^{-5}$	200	$7.8371\times {10}^{-4}$
1/8	1/210	387	$9.6004\times {10}^{-4}$	40	$8.2789\times {10}^{-4}$

Table 3. The maximum absolute errors $L_{\infty }$ of Example 1 for $h_x=h_y=\frac{1}{16}$, $\gamma =0.15$ and different values of $\tau$.

$\mathit{\tau }$	Proposed Method		RMM [25]	CFDM [25]
	$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$	${\mathit{L}}_{\mathit{\infty }}$	${\mathit{L}}_{\mathit{\infty }}$
1/10	672	$4.7049\times {10}^{-3}$	$6.8422\times {10}^{-3}$	$4.3318\times {10}^{-3}$
1/20	775	$2.4089\times {10}^{-3}$	$4.9548\times {10}^{-3}$	$2.2982\times {10}^{-3}$
1/30	791	$1.6230\times {10}^{-3}$	$3.3632\times {10}^{-3}$	$1.5709\times {10}^{-3}$

Table 4. The maximum absolute errors $L_{\infty }$ and execution times (in seconds) of Example 1 for $\gamma =0.2$, and different values of $h_x=h_y$ and $\tau$.

${\mathit{h}}_{\mathit{x}}$	$\mathit{\tau }$	Proposed Method		CFDM [25]
		n	${\mathit{L}}_{\mathit{\infty }}$	CPU Time (s)	${\mathit{L}}_{\mathit{\infty }}$	CPU Time (s)
1/4	1/50	13	$8.8037\times {10}^{-4}$	$0.8212$	$9.6999\times {10}^{-4}$	$0.0470$
1/8	1/128	116	$2.0750\times {10}^{-4}$	$0.9606$	$3.8649\times {10}^{-4}$	$0.5000$
1/18	1/28	900	$1.7396\times {10}^{-3}$	$6.3644$	$1.7554\times {10}^{-3}$	$0.0460$

Table 5. The maximum absolute errors $L_{\infty }$ of Example 1 for $h_x=h_y=\frac{1}{4}$ and $\tau =\frac{1}{900}$ and different values of $\gamma$.

$\mathit{\gamma }$	Proposed Method		RMM [25]	CFDM [25]
	$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$	${\mathit{L}}_{\mathit{\infty }}$	${\mathit{L}}_{\mathit{\infty }}$
$0.7$	5	$8.3469\times {10}^{-4}$	$5.8055\times {10}^{-4}$	$1.8231\times {10}^{-3}$
$0.8$	4	$7.0423\times {10}^{-4}$	$7.3493\times {10}^{-4}$	$1.8250\times {10}^{-3}$
$0.9$	4	$9.8265\times {10}^{-4}$	$9.0422\times {10}^{-4}$	$1.8265\times {10}^{-3}$

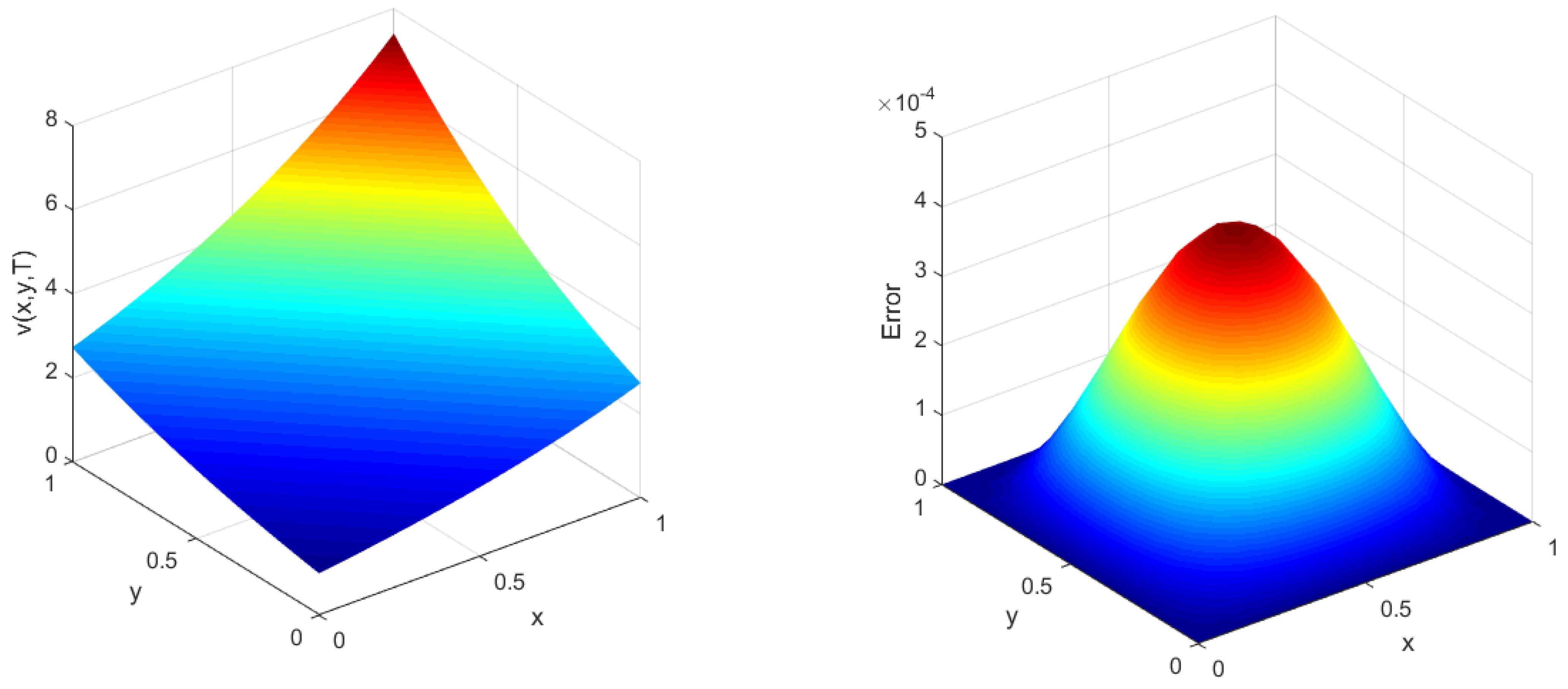
Figure 1. Approximate solution $v(x,y,T)$ and the associated computational error $L_{\infty }$ of the proposed method with $\gamma =0.85$ and $K_1=K_2=16$ and $N=256,n=263$ (left and right panels, respectively).

Example 2.

Consider the following TFRSE:

$$\begin{array}{cc}\hfill \frac{\partial v(x,y,t)}{\partial t}& ={}_0{D}_t^{1-\gamma }\left(\frac{{\partial }^{2}v(x,y,t)}{\partial x^2}+\frac{{\partial }^{2}v(x,y,t)}{\partial y^2}\right)\hfill \\ \hfill & +\frac{{\partial }^{2}v(x,y,t)}{\partial x^2}+\frac{{\partial }^{2}v(x,y,t)}{\partial y^2}+f(x,y,t),(x,y)\in \mathrm{\Omega }={[0,1]}^2.\hfill \end{array}$$

The IC and BCs as well as source term $f(x,y,t)$ are achieved from an exact solution $v(x,y,t)=exp(x+y)t^2.$

The proposed method is adopted for solving this problem when the total time $T=1$ with various values of $h_x,h_y,\tau$ and $\gamma$. Table 6 reports the maximum absolute errors $L_{\infty }$ and time convergence orders $C_{\tau }$ for $h_x=h_y=\frac{1}{8}$, $\gamma \in \{0.65,0.95\}$ and various values of $\tau .$ As shown in Table 6, the computational orders $C_{\tau }$ agree with the theoretical convergence order. Table 7 compares the maximum absolute errors $L_{\infty }$ in the solution for $\gamma \in \{0.35,0.75\}$ and several values of $h_x=h_y$ and $\tau .$ Table 8 lists the maximum absolute errors $L_{\infty }$ in the solution for $\gamma =0.2$ and several values of $h_x=h_y$ and $\tau .$ Table 9 makes the comparison of the maximum absolute errors $L_{\infty }$ in the solution and execution times (in seconds) with those obtained with other schemes [22,25] for $h_x=h_y=\frac{1}{4}$ and $\tau =\frac{1}{256}$ and various values of $\gamma$. Figure 2 depicts the approximate solution and the associated computational error $L_{\infty }$ of proposed method with $\gamma =0.95$, $K_1=K_2=16$, and $N=256$.

Table 6. The maximum absolute errors $L_{\infty }$ and time convergence orders $C_{\tau }$ of Example 2 for $h_x=h_y=\frac{1}{8}$, $\gamma \in \{0.65,0.95\}$ and different values of $\tau$.

$\mathbf{\tau }$	$\mathit{\gamma }=0.55$	$\mathit{\gamma }=0.85$
	$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$	${\mathit{C}}_{\mathit{\tau }}$	$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$	${\mathit{C}}_{\mathit{\tau }}$
1/10	54	$6.7051\times {10}^{-3}$	-	117	$9.9156\times {10}^{-3}$	−
1/40	57	$1.5503\times {10}^{-3}$	$1.0563$	34	$8.5430\times {10}^{-3}$	$0.1075$
1/90	52	$6.9213\times {10}^{-4}$	$0.9944$	31	$1.0942\times {10}^{-3}$	$2.5342$
1/190	45	$3.3634\times {10}^{-4}$	$0.9658$	22	$5.1960\times {10}^{-4}$	$0.9967$
1/1200	21	$7.7520\times {10}^{-5}$	$0.7963$	25	$8.3012\times {10}^{-5}$	$0.9951$

Table 7. The maximum absolute errors $L_{\infty }$ of Example 2 for $\gamma \in \{0.35,0.75\}$ and different values of $h_x=h_y$ and $\tau$.

${\mathit{h}}_{\mathit{x}}$	$\mathit{\tau }$	$\mathit{\gamma }=0.35$		$\mathit{\gamma }=0.75$
		$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$	$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$
1/4	1/8	160	$9.9757\times {10}^{-3}$	8	$8.0374\times {10}^{-3}$
1/8	1/8	151	$3.8090\times {10}^{-3}$	73	$7.0374\times {10}^{-3}$
1/16	1/8	486	$4.4059\times {10}^{-3}$	290	$3.0374\times {10}^{-3}$
1/8	1/64	88	$3.1647\times {10}^{-4}$	46	$1.1573\times {10}^{-3}$
1/12	1/64	283	$3.1281\times {10}^{-4}$	116	$1.1583\times {10}^{-3}$
1/4	1/12	11	$7.5942\times {10}^{-4}$	7	$4.8539\times {10}^{-4}$
1/15	1/128	947	$1.6066\times {10}^{-5}$	160	$1.8297\times {10}^{-4}$
1/8	1/30	95	$6.4711\times {10}^{-4}$	51	$2.4751\times {10}^{-3}$
1/60	1/16	740	$1.9589\times {10}^{-3}$	243	$2.8112\times {10}^{-3}$

Table 8. The maximum absolute errors $L_{\infty }$ of Example 2 for $\gamma =0.2$, and several values of $h_x=h_y$ and $\tau$.

${\mathit{h}}_{\mathit{x}}$	$\mathit{\tau }$	Proposed Method		Implicit Method [25]
		$\mathit{n}$	${\mathit{L}}_{\mathit{\infty }}$	${\mathit{L}}_{\mathit{\infty }}$
1/4	1/50	9	$7.0500\times {10}^{-4}$	$2.0154\times {10}^{-3}$
1/8	1/128	84	$8.8460\times {10}^{-5}$	$1.3776\times {10}^{-4}$
1/16	1/32	55	$2.0142\times {10}^{-3}$	$2.1391\times {10}^{-3}$

Table 9. The maximum absolute errors $L_{\infty }$ and execution times (in seconds) of Example 2 for $h_x=h_y=\frac{1}{4}$ and $\tau =\frac{1}{256}$ and different values of $\gamma$.

$\mathit{\gamma }$	Proposed Method			Implicit Method [25]
	n	${\mathit{L}}_{\mathit{\infty }}$	CPU Time (s)	${\mathit{L}}_{\mathit{\infty }}$	CPU Time (s)
$0.18$	8	$9.2879\times {10}^{-4}$	$1.4274$	$3.2350\times {10}^{-3}$	$0.5373$
$0.35$	6	$4.9674\times {10}^{-4}$	$1.5169$	$3.2306\times {10}^{-3}$	$0.5397$
$0.70$	3	$7.8135\times {10}^{-4}$	$1.5070$	$3.2302\times {10}^{-3}$	$0.5719$
$0.80$	4	$2.3660\times {10}^{-3}$	$1.4007$	$3.2368\times {10}^{-3}$	$0.5651$
$0.90$	3	$3.0465\times {10}^{-3}$	$1.3906$	$3.2457\times {10}^{-3}$	$0.5102$

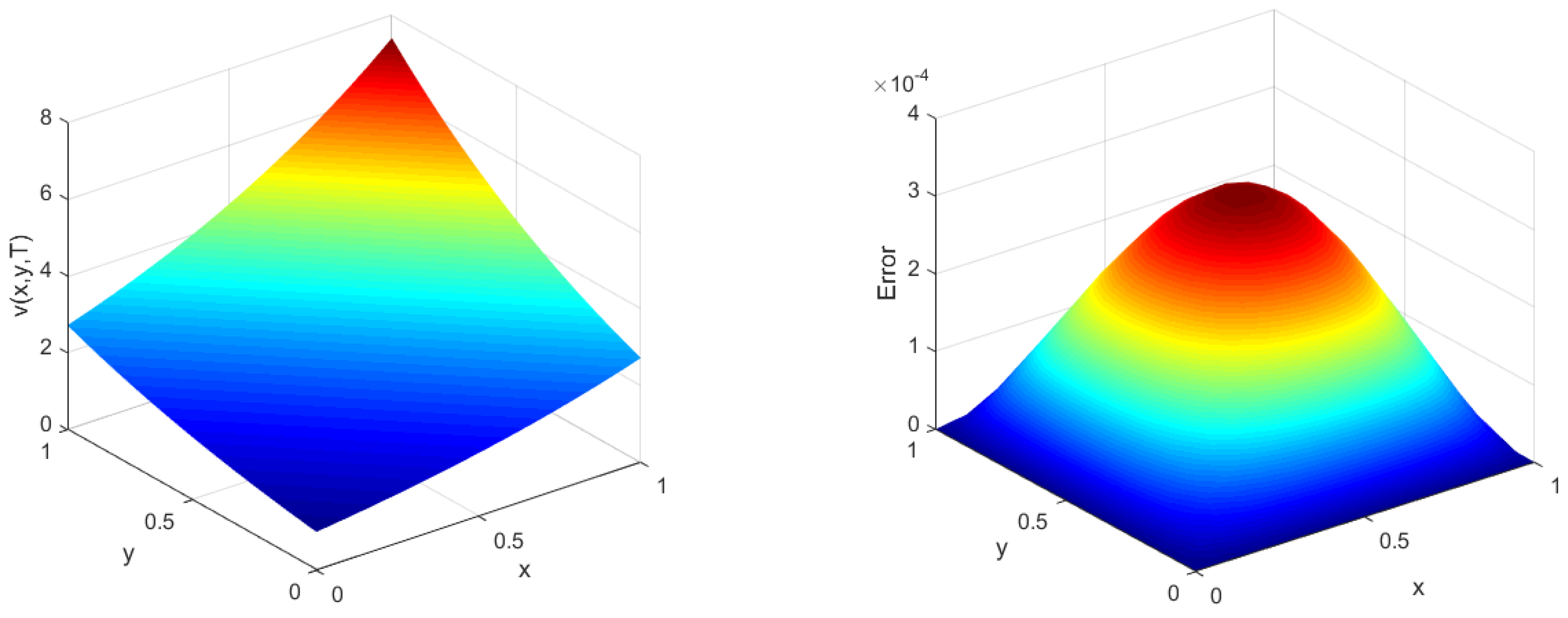
Figure 2. Approximate solution $v(x,y,T)$ and the associated computational error $L_{\infty }$ of the proposed method with $\gamma =0.95$ and $K_1=K_2=16$ and $N=256,n=263$ (left and right panels, respectively).

6. Concluding Remarks

We adopted the predictor–corrector method for approximating the TFRSE. First, the time discretization of the problem was accomplished by using the finite difference. Second, the space discretization was obtained with the help of the predictor–corrector method. The convergence and unconditional stability properties of the approach were discussed theoretically. Numerical experiments compared the results obtained with the proposed method and those produced using existing alternative schemes. The superiority of the new approach was thus verified and illustrated.