Lower and Upper Bounds of Fractional Metric Dimension of Connected Networks

Abstract

The distance centric parameter in the theory of networks called by metric dimension plays a vital role in encountering the distance-related problems for the monitoring of the large-scale networks in the various fields of chemistry and computer science such as navigation, image processing, pattern recognition, integer programming, optimal transportation models and drugs discovery. In particular, it is used to find the locations of robots with respect to shortest distance among the destinations, minimum consumption of time, lesser number of the utilized nodes, and to characterize the chemical compounds, having unique presentations in molecular networks. After the arrival of its weighted version, known as fractional metric dimension, the rectification of distance-related problems in the aforementioned fields has revived to a great extent. In this article, we compute fractional as well as local fractional metric dimensions of web-related networks called by subdivided QCL, 2-faced web, 3-faced web, and antiprism web networks. Moreover, we analyse their final results using 2D and 3D plots.

1. Introduction

The rising sun of each day arrives with a bunch of advancements related to the arena of information and technology, cheminformatics, and medicines. These advancements raised disciplines such as artificial intelligence, drug discovery, and image processing. Besides many concepts, metric dimensions of networks have a stake in their emergence. Such as in robotics, distance intervenes when we have to allocate robots to different sites known as landmarks without loss of economical operation cost and employing fewer robots. This objective is achieved by turning this whole situation into a graph-theoretic model and allowing metric dimension to give an appropriate picturesque model. Topics such as these have been covered in [1,2,3].

The domains of chemistry, which include chemical bonding, drug discovery, and development of diagnostic kits for different diseases are incomplete without the notion of distance centric dimensions. With the help of graph-theoretic picturesque imagery of chemical compounds along with metric dimensions, people from the chemical and medical fraternity can develop drugs, chemical compounds, and testing kits having higher accuracy and parsimony with ease. For further insight into this topic, we refer to [4,5,6].

In a network $\mathbb{G}$, the path with the shortest distance between two distinct vertices s and t is denoted by $d(s,t)$. Consider $\mathbb{W}=\{w_1,w_2,w_3,\cdots ,w_k\}\subseteq V(\mathbb{G})$ and a vertex $s\in V(\mathbb{G})$ the metric form of s regarding $\mathbb{W}$ is an ordered k-tuple $r(s|\mathbb{W})=(d(s,w_1),d(s,w_2),d(s,w_3),\cdots ,d(s,w_k))$. The set $\mathbb{W}$, having a unique metric form with respect to s in $\mathbb{G}$, is called the resolving set. The metric basis of $\mathbb{G}$ determined by the resolving set having the least number of elements and its cardinality represents its metric dimension (MD).

After Slater [2,7], Harary and Melter [8] have discovered by themselves the notions of resolving sets and MDs of networks, many researchers have incorporated the same for various network types. These findings can be found in [3,4,9,10]. Chartrand et al. employed the MD for solving the integer programming problem (IPP) [4]. Afterwards, Currie et al. laid the foundation of fractional metric dimension (FMD) with its aid, and evaluated the IPP acquiring results with high precision [11]. It was Arumugam and Mathew who formally defined the FMD by bringing into light its undercover features [12]. Afterwards, researchers have stormed with the results of FMD of networks, which are the resultants of various graph operations such as comb, corona, Cartesian, hierarchical, and lexicographic products, see [13,14,15,16]. Similarly, the FMDs of the generalized Jahangir network, metal organic networks, rotationally symmetric and planar networks, tetrahedral diamond and grid-like networks can be found in [17,18,19,20,21]. Moreover, for improved lower bound of FMD and bounds of FMD of convex polytopes, see [22].

Aisyah et al. (2019) founded the local fractional metric dimension (LFMD) and obtained it for corona product of two networks [23]. The results regarding the sharp bounds of LFMD of connected networks and prism related networks can be found in [24,25]. In this article, we calculate the upper bounds of FMD as well as LFMD of web-related networks called by subdivided divided QCL, 2-faced web, 3-faced web, and antiprism web networks. These networks bear rotational symmetry and planarity, which will help in designing information and chemical structures. The upper extremal values of FMD and LFMD are analyzed numerically as well as graphically. The flow of the article is as follows: Section 1 is the introduction, Section 2 discussed the preliminaries and construction of networks under consideration and Section 3 deals with the local as well as pairwise resolving neighborhood sets of the networks titled above. In Section 4, the evaluation of the FMDs as well as the LFMDs of ${\mathbb{SQ}}_m$, ${\mathbb{WB}}_m^1$, ${\mathbb{WB}}_m^2$, ${\mathbb{WB}}_m^3$ and ${\mathbb{AWB}}_m$ is done. Section 5, ends the article with the conclusions and future directions.

2. Preliminaries

For any node $f\in V(\mathbb{G})$ and $\{s,t\}\subseteq V(\mathbb{G})$ then f is said to resolve the pair $\{s,t\}$ if $d(s,f)\ne d(t,f)$. The set comprising of all such nodes is called the resolving neighborhood set (RNs). The RNs of $\{s,t\}$ is denoted by $R\{s,t\}=\{f\in V(\mathbb{G})|d(s,f)\ne d(t,f)\}$. For $\mathbb{G}(V(\mathbb{G}),E(\mathbb{G}))$ that is connected and having v as its order, a resolving function (RF) $\mu :V(\mathbb{G})\to [0,1]$ of $\mathbb{G}$ is a function fulfilling the condition $\mu (R\{s,t\})\ge 1$∀$\{s,t\}\in V(\mathbb{G})$, where $\mu (R\{s,t\})={\displaystyle \sum _{f\in R\{s,t\}}}\mu (f)$. An RF $\mu$ of $\mathbb{G}$ is known as the minimal resolving function (MRF) if ∃ some function $\gamma :V(\mathbb{G})\to [0,1]$ where $\gamma \le \mu$ and $\mu (f)\ne \gamma (f)$ for some $f\in V(\mathbb{G})$, which is not the RF of $\mathbb{G}$. For $\mathbb{G}$, the FMD is denoted by $fdim(\mathbb{G})$ is given by $fdim(\mathbb{G})=min\{|\mu |:\mu$ is the MRF of $\mathbb{G}\}$, where $|\mu |={\displaystyle \sum _{f\in V(\mathbb{G})}}\mu (f)$. For more details, see [12]. The resolving function is called the local resolving function (LRF) if $\eta (R\{st\})\ge 1$. Similarly, FMD will become LFMD if we only consider the pair of adjacent vertices only, denoted by $lfdim(\mathbb{G})$ [23]. We are sharing the following results, without which our article is incomplete.

Theorem 1 

([25]). Suppose that $\mathbb{G}(V(\mathbb{G}),E(\mathbb{G}))$ is a connected network. If $|LR(st)\cap X|\ge \alpha$, ∀$st\in E(\mathbb{G})$, then

$$1\le lfdim(\mathbb{G})\le \frac{|X|}{\beta },$$

where $\beta =min\{|LR(st)|:st\in E(\mathbb{G})\}$, $X=\cup \{LR(st):|LR(st)|=\beta \}$ and $2\le \beta \le |V(\mathbb{G})|$.

Theorem 2 

([21]). Suppose that $\mathbb{G}(V(\mathbb{G}),E(\mathbb{G}))$ is the connected network and $R\{s,t\}$ is the resolving neighborhood set for $\{s,t\}$ in $\mathbb{G}$. If $\beta =min\{|R\{s,t\}|\}$, $X=\cup \left\{R\right\{s,t\}:|R\{s,t\}|=\beta \}$ and $|R\{s,t\}\cap X|\ge \beta$ then

$$1\le fdim(\mathbb{G})\le \frac{|X|}{\beta },$$

where $2\le \beta \le |V(\mathbb{G})|$.

Theorem 3 

([25]). Suppose that $\mathbb{G}$ is the connected network,

(a) 

If $\mathbb{G}$ is bipartite then $lfdim(\mathbb{G})=1$,

(b) 

If $lfdim(\mathbb{G})=1$ then either $\mathbb{G}$ is either bipartite or it bears a distinct odd cycle of minimum length.

Construction of Web-Related Networks

This section is dedicated to the construction of the networks under consideration.

As defined in [19], for $m\ge$ a quadrangular circular ladder (QCL) ${\mathbb{Q}}_m^1$ is a cubic network that is the network obtained after the Cartesian product of $P_2\times C_m$. A subdivided QCL denoted by ${\mathbb{SQ}}_m$ is formed after applying the subdivision operation on QCL by adding vertex $x_s$ between vertices $v_s$ and $v_{s+1}$, $y_s$ between vertices $v_s$ and $w_s$ and $z_s$ between vertices $w_s$ and $w_{s+1}$. It can be seen that subdivided QCL is a bipartite network. The sets $V({\mathbb{SQ}}_m)$ and $E({\mathbb{SQ}}_m)$ are given by: $V({\mathbb{SQ}}_m)=\{v_j^r|1\le j\le s\}\cup \{w_j|1\le j\le s\}\cup \{w_j|1\le j\le s\}\cup \{x_j|1\le j\le s\}\cup \{y_j|1\le j\le s\}\cup \{z_j|1\le j\le s\}$ and $E({\mathbb{SQ}}_m)=\{x_s{v}_{s+1}|1\le s\le m\wedge v_{m+1}=v_1\}\cup \{x_s{v}_s|1\le s\le m\}\cup \{w_s{y}_s|1\le s\le m\}\cup \{v_s{y}_s|1\le s\le m\}\cup \{w_s{z}_s|1\le s\le m\}\cup \{w_s{z}_{s-1}|1\le s\le m\wedge z_0=z_m\}$ respectively. The subdivided QCL is shown in Figure 1.

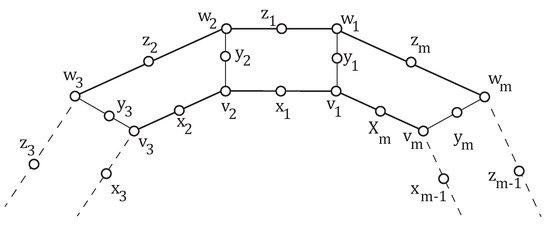
Figure 1. ${\mathbb{SQ}}_m$.

The 2-faced web network ${\mathbb{WB}}_m^1$ is formed by joining vertices $z_s$ to the vertices $y_s$ of 2-faced QCL as defined in [19]. Its order is $3m$ and size is $4m$. Its $V({\mathbb{WB}}_m^1)$ and $E({\mathbb{WB}}_m^1)$ are given as follows:

$V({\mathbb{WB}}_m^1)=\{x_j|1\le j\le s\}\cup \{y_j|1\le j\le s\}\cup \{z_j|1\le j\le s\}$ and $E({\mathbb{WB}}_m^1)=\{x_s{y}_{s+1}|1\le s\le m\}\cup \{y_s{z}_s|1\le s\le m\}\cup \{x_s{y}_{s+1}|1\le s\le m\wedge y_{s+1}=y_1\}$ respectively. The Figure 2 illustrates ${\mathbb{WB}}_m^1$.

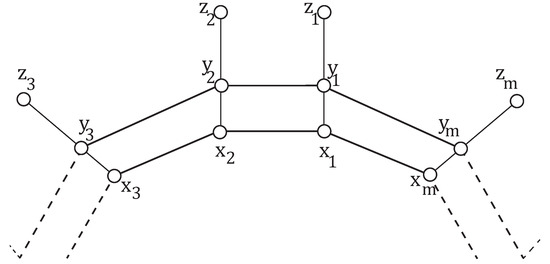
Figure 2. The 2-faced web network ${\mathbb{WB}}_m^1$.

It is clear from Figure 2 that ${\mathbb{WB}}_m^1$ is a bipartite network.

The 3-faced web networks ${\mathbb{WB}}_m^2$ and ${\mathbb{WB}}_m^3$ are formed by joining vertices $z_s$ to the vertices $y_s$ of 3-faced QCLs ${\mathbb{Q}}_m^2$ and ${\mathbb{Q}}_m^3$ as defined in [19]. Their order is $3m$ and size is $5m$. The sets $V({\mathbb{WB}}_m^2)$, $E({\mathbb{WB}}_m^2)$,$V({\mathbb{WB}}_m^3)$ and $E({\mathbb{WB}}_m^3)$ are given as follows:

• $V({\mathbb{WB}}_m^2)=\{x_j^r|1\le j\le s\}\cup \{y_j^r|1\le j\le s\}\cup \{z_j^r|1\le j\le s\}$,
• $E({\mathbb{WB}}_m^2)=\{x_s{y}_{s+1}|1\le s\le m\}\cup \{y_s{z}_s|1\le s\le m\}\cup \{x_s{y}_{s+1}|1\le s\le m\wedge y_{s+1}=y_1\}\cup \{x_s{y}_{s-1}|1\le s\le m\wedge y_0=y_m\}$,
• $V({\mathbb{WB}}_m^3)=\{x_j^r|1\le j\le s\}\cup \{y_j^r|1\le j\le s\}\cup \{z_j^r|1\le j\le s\}$, and
• $E({\mathbb{WB}}_m^3)=\{x_s{y}_{s+1}|1\le s\le m\}\cup \{y_s{z}_s|1\le s\le m\}\cup \{x_s{y}_{s+1}|1\le s\le m\wedge y_{s+1}=y_1\}\cup \{x_s{y}_{s+1}|1\le s\le m\wedge y_{m+1}=y_1\}$ respectively.

The Figure 3 illustrates (a) ${\mathbb{WB}}_m^2$ and (b) ${\mathbb{WB}}_m^3$.

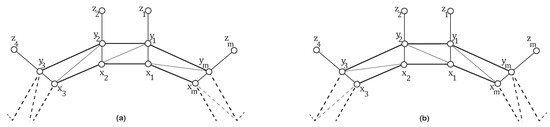
Figure 3. Possible 3-faced web networks (a) ${\mathbb{WB}}_m^2$ (b) ${\mathbb{WB}}_m^3$ (right).

From Figure 3 we can see that ${\mathbb{WB}}_m^2\cong {\mathbb{WB}}_m^3$.

An Antiprism web network ${\mathbb{AWB}}_m$ is formed by joining vertices $z_s$ to vertex $y_s$ of Antiprism ${\mathbb{A}}_m$. Its order is $3m$ and size is $4m$. Its sets $V({\mathbb{AWB}}_m)$ and $E({\mathbb{AWB}}_m)$ are given by: $V({\mathbb{AWB}}_m)=\{x_j^r|1\le j\le s\}\cup \{y_j^r|1\le j\le s\}\cup \{z_j^r|1\le j\le s\}$, and $E({\mathbb{AWB}}_m)=\{x_s{y}_s|1\le s\le m\}\cup \{y_s{z}_s|1\le s\le m\}\cup \{x_s{y}_{s-1}|1\le s\le m\wedge y_0=y_m\}\cup \{x_s{y}_{s-1}|1\le s\le m\wedge y_0=y_m\}\cup \{x_s{x}_{s+1}|1\le s\le m\wedge x_{m+1}=y_1\}\cup \{y_s{y}_{s+1}|1\le s\le m\wedge y_{m+1}=y_1\}$ respectively.

The Figure 4 illustrates ${\mathbb{AWB}}_m$.

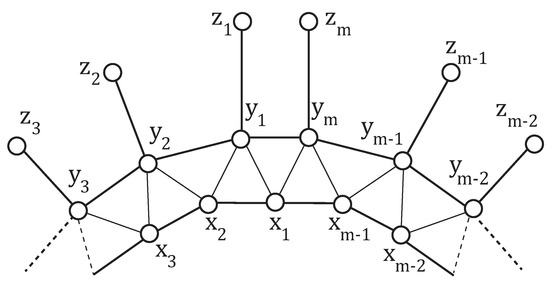
Figure 4. Antiprism Web Network ${\mathbb{AWB}}_m$.

3. RNs of Web-Related Networks

The present section concerns with the local as well as pairwise RNs of the networks under consideration.

3.1. RNs of Subdivided QCL

Lemma 1. 

Let $\mathbb{G}\cong {\mathbb{SQ}}_m$ be a subdivided QCL, for any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$ then:

(a) 

For $1\le s\le m$, $|R_s|=|R\{x_s,y_s\}|=\frac{5m}{2}+1$ and $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=5m$ and

(b) 

For $1\le y\le 7$, $|R_s|\le |{\overline{R}}_y|$ and $|{\overline{R}}_y\cap {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$, for each RNs ${\overline{R}}_y$ other than $R_s$ of $\mathbb{G}$.

Proof. 

The RN having a fewer number of elements in $\mathbb{G}$ is

$R_s=R\{x_s,y_s\}=V({\mathbb{SQ}}_m)-\{v_j|j\equiv s,s-1,\cdots ,s-\frac{m}{2}+1(mod$$m)\}\cup \{w_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{x_j|j\equiv s-1,s-2,\cdots ,s-\frac{m}{2}(mod$$m)\}\cup \{y_j|j\equiv s-1,s-2,s-3,\cdots ,s-\frac{m}{2}+1(mod$$m)\}\cup \{z_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}-1(mod$$m)\}$.

Hence, $|R_l|=2(n-1)$ for $1\le l\le 3$, ${\displaystyle \bigcup _{s=1}^m}{R}_s=V({\mathbb{SQ}}_m)$ and $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=5m$.

(b) For the proof of required RNs, the following variables will be needed:

• $1\le s\le m$
• $t\ge 1$ and $t\equiv 1(mod$ $2)$
• $p\ge 3$ and $p\equiv 1(mod$ $2)$
• $r\ge 2$ and $r\equiv 0(mod$ $2)$

${\overline{R}}_y$ for $1\le y\le 27$ other than $R_s$ are

• ${\overline{R}}_1=R\{v_s,v_{s+p}\}=V({\mathbb{SQ}}_m)-\{x_j|j\equiv s+\frac{p-1}{2},s+\frac{m+p-1}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{p-1}{2},s+\frac{m+p-1}{2}(mod$$m)\}={\overline{R}}_2=R\{y_s,y_{s+p}\}={\overline{R}}_3=R\{w_s,w_{s+p}\}={\overline{R}}_4=R\{z_s,z_{s+r}\}$,
• ${\overline{R}}_5=R\{x_s,x_{s+p}\}=V({\mathbb{SQ}}_m)-\{v_j|j\equiv s+\frac{p+1}{2},s+\frac{m+p+1}{2}(mod$$m)\}\cup \{w_j|j\equiv s+\frac{p+1}{2},s+\frac{m+p+1}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{p+1}{2},s+\frac{m+p+1}{2}(mod$$m)\}={\overline{R}}_6=R\{y_s,y_{s+r}\}={\overline{R}}_7=R\{w_s,w_{s+r}\}={\overline{R}}_8=R\{z_s,z_{s+p}\}$,
• ${\overline{R}}_9=R\{v_s,w_{s+p}\}=V(\mathbb{SQ})-\{y_j|1\le j\le m\}$,
• ${\overline{R}}_{10}=R\{x_s,y_{s+1}\}=V({\mathbb{SQ}}_m)-\{v_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{w_j|j\equiv s,s-1,\cdots ,s-\frac{m}{2}+1(mod$$m)\}\cup \{x_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{y_j|j\equiv s+2,s+3,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{z_j|j\equiv s-1,s-2,\cdots ,s-\frac{m}{2}+1(mod$$m)\}$,
• ${\overline{R}}_{11}=R\{y_s,z_s\}=V({\mathbb{SQ}}_m)-\{w_j|j\equiv s,s-1,s-2,\cdots ,s-\frac{m}{2}+1(mod$$m)\}\cup \{x_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}-1(mod$$m)\}\cup \{y_j|j\equiv s-1,s-2,\cdots ,s-\frac{m}{2}+1(mod$$m)\}\cup \{z_j|j\equiv s-1,s-2,\cdots ,s-\frac{m}{2}+1(mod$$m)\}$,
• ${\overline{R}}_{12}=R\{v_s,w_{s+1}\}=V({\mathbb{SQ}}_m)-\{v_j|j\equiv s+1,s+2,\cdots ,s-\frac{m}{2}(mod$$m)\}\cup \{w_j|j\equiv s,s-1,\cdots ,s-\frac{m}{2}+1(mod$$m)\}\cup \{z_j|j\equiv s-1,s-2,\cdots ,s-\frac{m}{2}+1(mod$$m)\}$,
• ${\overline{R}}_{13}=R\{v_s,w_{s+p}\}=V({\mathbb{SQ}}_m)-\{v_j|j\equiv s+\frac{p+1}{2},s+fracm+p+12(mod$$m)\}\cup \{w_j|j\equiv s+\frac{p-1}{2},s+\frac{m+p-1}{2}(mod$$m)\}$,
• ${\overline{R}}_{14}=R\{v_s,w_{s+r}\}=V({\mathbb{SQ}}_m)-\{x_j|j\equiv s+\frac{s}{2},s+fracm2(mod$$m)\}\cup \{y_j|j\equiv s+\frac{s}{2},s+\frac{m+r}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{s-2}{2},s+\frac{m+r}{2}(mod$$m)\}$,
• ${\overline{R}}_{15}=R\{x_s,y_{s+r}\}=V({\mathbb{SQ}}_m)-\{v_j|j\equiv s+\frac{m+r}{2}(mod$$m)\}\cup \{x_j|j\equiv s+\frac{s}{2},s+fracm2(mod$$m)\}\cup \{y_j|j\equiv s+\frac{m+r}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{s-2}{2}(mod$$m)\}$,
• ${\overline{R}}_{16}=R\{x_s,y_{s+p}\}=V({\mathbb{SQ}}_m)-\{v_j|j\equiv s+\frac{p+1}{2}(mod$$m)\}\cup \{x_j|j\equiv s+\frac{n+p+1}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{p+1}{2}(mod$$m)\}$,
• ${\overline{R}}_{17}=R\{x_s,z_{s+1}\}=V({\mathbb{SQ}}_m)-\{v_j|j\equiv s+2,s+3,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{x_j|j\equiv s+2,s+3,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{w_j|j\equiv s,s-1(mod$$m)\}\cup \{y_j|j\equiv s+\frac{n+2}{2}(mod$$m)\}\cup \{z_j|j\equiv s-1,s-2(mod$$m)\}$,
• ${\overline{R}}_{18}=R\{x_s,z_{s+p}\}=V({\mathbb{SQ}}_m)-\{x_j|j\equiv s+\frac{p+1}{2},s+\frac{p+n-1}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{p+1}{2},s+\frac{p+n+1}{2}(mod$$m)\}$,
• ${\overline{R}}_{19}=R\{x_s,z_{s+r}\}=V({\mathbb{SQ}}_m)-\{w_j|j\equiv s+\frac{s}{2}(mod$$m)\}\cup \{v_j|j\equiv s+\frac{s+2}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{s-2}{2}(mod$$m)\}$,
• ${\overline{R}}_{20}=R\{y_s,z_{s+p}\}=V({\mathbb{SQ}}_m)-\{v_j|j\equiv s+\frac{p+1}{2}(mod$$m)\}\cup \{x_j|j\equiv s+\frac{p+1}{2},s+\frac{p+m+1}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{p+m+1}{2}(mod$$m)\}$,
• ${\overline{R}}_{21}=R\{y_s,z_{s+r}\}=V({\mathbb{SQ}}_m)-\{w_j|j\equiv s+\frac{s}{2}(mod$$m)\}\cup \{x_j|j\equiv s+\frac{s}{2},s+\frac{m+r}{2}(mod$$m)\}$,
• ${\overline{R}}_{22}=R\{v_s,y_{s+p}\}={\overline{R}}_{23}=R\{v_s,y_{s+r}\}={\overline{R}}_{24}=R\{v_s,x_{s+p}\}={\overline{R}}_{25}=R\{v_s,x_{s+r}\}={\overline{R}}_{26}=R\{v_s,z_{s+p}\}={\overline{R}}_{27}=R\{v_s,z_{s+r}\}=V({\mathbb{SQ}}_m)$.

Their cardinalities can be summarized in Table 1. □

Table 1. RNs ${\overline{R}}_y$ for $1\le y\le 27$.

RNs	Cardinalities
${\overline{R}}_1$,${\overline{R}}_2$,${\overline{R}}_3$,${\overline{R}}_4$	$5m-4$
${\overline{R}}_5$,${\overline{R}}_6$,${\overline{R}}_7$,${\overline{R}}_8$,${\overline{R}}_{14}$	$5m-6$
${\overline{R}}_9$	$4m$
${\overline{R}}_{10}$	$\frac{5m}{2}+2$
${\overline{R}}_{11}$	$\frac{5m}{2}+1$
${\overline{R}}_{12}$	$\frac{7m}{2}+3$
${\overline{R}}_{13},{\overline{R}}_{18}$	$5m-4$
${\overline{R}}_{15}$	$5(m-1)$
${\overline{R}}_{16},{\overline{R}}_{17},{\overline{R}}_{19},{\overline{R}}_{20},{\overline{R}}_{21}$	$5m-3$
${\overline{R}}_{22},{\overline{R}}_{23},{\overline{R}}_{24},{\overline{R}}_{25},{\overline{R}}_{26},{\overline{R}}_{27}$	$5m$

Table 1 shows that $|R_s|\le |{\overline{R}}_y|$ and $|{\overline{R}}_y\cup {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$.

3.2. RNs of 2-Faced Web Network

Lemma 2. 

Let $\mathbb{G}\cong {\mathbb{WB}}_m^1$ be a 2-faced subdivided web network, for any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$ then:

(a) 

For $1\le s\le m$, $|R_s|=|R\{x_s,z_s\}|=n+1$ and $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and

(b) 

For $1\le y\le 7$, $|R_s|\le |{\overline{R}}_y|$ and $|{\overline{R}}_y\cap {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$, for each RN set ${\overline{R}}_y$ other than $R_s$ of $\mathbb{G}$.

Proof. 

The RN bearing fewer number of elements in $\mathbb{G}$ is

$R_s=R\{y_s,z_s\}=V({\mathbb{WB}}_m^1)-\{y_j|1\le s\le m\}\cup \{z_j|j\equiv s+1,s+2,\cdots ,s+n-1(mod$$m)\}$.

Thus, $|R_s|=2(n-1)$ for $1\le l\le 3$, ${\displaystyle \bigcup _{s=1}^m}{R}_s=V({\mathbb{SQ}}_m)$ and $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$.

(b) For the proof of required RNs, the following variables will be needed:

• $1\le s\le m$
• $t\ge 1$ and $t\equiv 1(mod$ $2)$
• $p\ge 3$ and $p\equiv 1(mod$ $2)$
• $r\ge 2$ and $r\equiv 0(mod$ $2)$

RNs ${\overline{R}}_y$ for $1\le y\le 12$ other than $|R_s|$ are as under:

• ${\overline{R}}_1=R\{x_s,x_{s+t}\}={\overline{R}}_2=R\{x_s,z_{s+t}\}={\overline{R}}_3=R\{y_s,y_{s+t}\}={\overline{R}}_4=R\{z_s,z_{s+t}\}={\overline{R}}_5=R\{x_s,y_s\}={\overline{R}}_6=R\{x_s,z_{s+t}\}={\overline{R}}_7=R\{x_s,z_{s+t}\}={\overline{R}}_8=R\{y_s,z_{s+r}\}=V({\mathbb{WB}}_m^1)$,
• ${\overline{R}}_9=R\{x_s,y_{s+1}\}=V({\mathbb{WB}}_m^1)-\{x_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{y_j|j\equiv s,s-1,s-2,\cdots ,s-\frac{m}{2}+1(mod$$m)\}\cup \{z_j|j\equiv s,s-1,s-2,\cdots ,s-\frac{m}{2}+1(mod$$m)\}$,
• ${\overline{R}}_{10}=R\{x_s,z_{s+1}\}=V({\mathbb{WB}}_m^1)-\{x_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{y_j|j\equiv s,s-1,s-2,\cdots ,s-\frac{m}{2}+1(mod$$m)\}\cup \{z_j|j\equiv s,s-1,s-2,\cdots ,s-\frac{m}{2}+1(mod$$m)\}$,
• ${\overline{R}}_{11}=R\{x_s,z_{s+2}\}=V({\mathbb{WB}}_m^1)-\{x_j|j\equiv s+2,s+3,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{m+r}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{m+r}{2}(mod$$m)\}$,
• ${\overline{R}}_{12}=R\{y_s,z_{s+p}\}=V({\mathbb{WB}}_m^1)-\{x_j|j\equiv s+\frac{p+1}{2},s+\frac{m+p+1}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{p+1}{2},s+\frac{m+p+1}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{p+1}{2},s+\frac{m+p+1}{2}(mod$$m)\}$.

Whereas, their cardinalities are listed in Table 2. □

Table 2. RNs ${\overline{R}}_y$ for $1\le y\le 12$.

RNs	Cardinalities
${\overline{R}}_1$,${\overline{R}}_2$,${\overline{R}}_3$,${\overline{R}}_4$,${\overline{R}}_5$,${\overline{R}}_6$,${\overline{R}}_7$,${\overline{R}}_8$	$3m$
${\overline{R}}_9,{\overline{R}}_{10}$	$\frac{3m}{2}$
${\overline{R}}_{11}$	$\frac{3m}{2}+3$
${\overline{R}}_{12}$	$3(m-2)$

Table 2 shows that $|R_s|\le |{\overline{R}}_y|$ and $|{\overline{R}}_y\cup {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$.

3.3. RNs of 3-Faced Web Network

Lemma 3. 

Let $\mathbb{G}\cong {\mathbb{WB}}_m^2$ be a 3-faced subdivided web network, for any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$ then:

(a) For $1\le s\le m$, $|R_s|=|R\{x_s,y_{s-1}\}|=\frac{3m}{2}+1$ and $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and

(b) For $1\le y\le 7$, $|R_s|\le |{\overline{R}}_y|$ and $|{\overline{R}}_y\cap {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$, for each RN set ${\overline{R}}_y$ different from $R_s$ of $\mathbb{G}$.

Proof. 

The RN having a fewer number of elements in $\mathbb{G}$ is $R_s=R\{x_s,y_{s-1}\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s,s-1,s-2,\cdots ,s-\frac{m}{2}+1(mod$ $m)\}\cup \{y_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$ $m)\}\cup \{z_j|j\equiv s+2,s+3,\cdots ,s+\frac{m}{2}(mod$ $m)\}$.

Therefore, $|R_s|=\frac{3m}{2}+1$ for $1\le s\le m$, ${\displaystyle \bigcup _{s=1}^m}{R}_s=V({\mathbb{WB}}_m^2)$ and $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$.

(b) For the proof of required RNs, the following variables will be needed:

• $1\le s\le m$
• $t\ge 1$ and $t\equiv 1(mod$ $2)$
• $p\ge 3$ and $p\equiv 1(mod$ $2)$
• $r\ge 2$ and $r\equiv 0(mod$ $2)$

RNs ${\overline{R}}_y$ for $1\le y\le 12$ other than $|R_s|$ are given as follows:

• ${\overline{R}}_1=R\{y_s,z_s\}=V({\mathbb{WB}}_m^2)$,
• ${\overline{R}}_2=R\{x_s,x_{s+p}\}=V({\mathbb{WB}}_m^2)-\{y_j|j\equiv s+\frac{p-1}{2},s+\frac{m+p-1}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{p-1}{2},s+\frac{m+p-1}{2}(mod$$m)\}={\overline{R}}_3=R\{z_s,z_{s+r}\}$,
• ${\overline{R}}_4=R\{y_s,y_{s+p}\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s+\frac{p+1}{2},s+\frac{m+p+1}{2}(mod$$m)\}=R\{z_s,z_{s+p}\}={\overline{R}}_5=R\{x_s,x_{s+r}\}={\overline{R}}_6=R\{z_s,z_{s+p}\}$,
• ${\overline{R}}_7=R\{x_s,y_{s+t}\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s+\frac{t+1}{2},s+\frac{m+t+1}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{p-1}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{p-1}{2}(mod$$m)\}$,
• ${\overline{R}}_8=R\{x_s,y_{s+r}\}=R\{x_s,z_{s+p}\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s+\frac{m+r}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{m+r}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{m+r}{2}(mod$$m)\}$,
• ${\overline{R}}_9=R\{x_s,z_s\}=V({\mathbb{WB}}_m^2)-\{y_j|j\equiv s,s+1,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{z_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}$,
• ${\overline{R}}_{10}=R\{x_s,z_{s+1}\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s+2,s+3,\cdots ,s+\frac{m}{2}(mod$$m)\}$,
• ${\overline{R}}_{11}=R\{y_s,z_{s+1}\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s+2,s+3,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{y_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{z_j|j\equiv s+2,s+3,\cdots ,s+\frac{m-2}{2}(mod$$m)\}$,
• ${\overline{R}}_{12}=R\{y_s,z_{s+p}\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s+\frac{m+p+1}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{m+p+1}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{m+p+1}{2}(mod$$m)\}$,
• ${\overline{R}}_{13}=R\{y_s,z_{s+r}\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s+\frac{s+2}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{s}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{s}{2}(mod$$m)\}$.

□

The cardinalities of the aforementioned RNs have been summarized in Table 3.

Table 3. RNs ${\overline{R}}_y$ for $1\le y\le 12$.

RNs	Cardinalities
${\overline{R}}_1$	$3m$
${\overline{R}}_2$, ${\overline{R}}_3$,${\overline{R}}_4$,${\overline{R}}_5$,${\overline{R}}_6$	$\frac{3m}{2}$
${\overline{R}}_7$, ${\overline{R}}_{11}$	$\frac{3m}{2}+3$
${\overline{R}}_8$	$3(m-2)$
${\overline{R}}_9$	$2m$
${\overline{R}}_{10}$	$\frac{3m}{2}$
${\overline{R}}_{12}$	$3(m-1)$
${\overline{R}}_{13}$	$3m-3$

Table 3 shows that $|R_s|\le |{\overline{R}}_y|$ and $|{\overline{R}}_y\cup {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$.

Lemma 4. 

Let $\mathbb{G}\cong {\mathbb{WB}}_m^2$ be a 3-faced subdivided web network, for any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$ then:

(a) 

For $1\le s\le m$, $|LRs|=|LR\{x_s,y_{s-1}\}|=\frac{3m}{2}+1$ and $|{\displaystyle \bigcup _{s=1}^m}LRs|=3m$ an

(b) 

For $1\le y\le 7$, $|LRs|\le |{\overline{LR}}_y|$ and $|{\overline{LR}}_y\cap {\displaystyle \bigcup _{s=1}^m}LRr|\ge |LRs|$, for each RN set ${\overline{LR}}_y$ different from $R_s$ of $\mathbb{G}$.

Proof. 

For proof, see Lemma 3(a).

(b) The required LRNs ${\overline{LR}}_y$ for $1\le y\le 12$ are as follows:

• ${\overline{LR}}_1=LR\{x_s,y_s\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}$,
• ${\overline{LR}}_2=LR\{x_s,x_{s+1}\}=V({\mathbb{WB}}_m^2)-\{y_j|j\equiv s,s+\frac{m}{2}(mod$$m)\}\cup \{z_j|j\equiv s,s+\frac{m}{2}(mod$$m)\}$,
• ${\overline{LR}}_3=LR\{y_s,y_{s+1}\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s+1,s+\frac{m+2}{2}(mod$$m)\}$,
• ${\overline{LR}}_4=LR\{x_s,y_{s+t}\}=V({\mathbb{WB}}_m^2)-\{x_j|j\equiv s+\frac{t+1}{2},s+\frac{m+t+1}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{p-1}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{p-1}{2}(mod$$m)\}$,
• ${\overline{LR}}_5=LR\{x_s,y_s\}=V({\mathbb{WB}}_m^2)$.

□

The cardinalities of the aforementioned RNs have been summarized in Table 4.

Table 4. RNs ${\overline{LR}}_y$ for $1\le y\le 5$.

RNs	Cardinalities
${\overline{LR}}_1$	$\frac{3m}{2}$
${\overline{LR}}_2$	$3m-4$
${\overline{LR}}_3$	$3m-2$
${\overline{LR}}_4$	$\frac{3m}{2}+3$
${\overline{LR}}_5$	$3m$

Table 4 shows that $|LRs|\le |{\overline{LR}}_y|$ and $|{\overline{LR}}_y\cup {\displaystyle \bigcup _{s=1}^m}LRs|\ge |LRs|$.

3.4. RNs of Antiprism Web Network

Lemma 5. 

Let $\mathbb{G}\cong {\mathbb{AWB}}_m$ be an antiprism web network, for any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$ then:

(a) 

For $1\le s\le m$, $|R_s|=|R\{x_s,y_s\}|=\frac{3m}{2}$ and $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and

(b) 

For $1\le y\le 7$, $|R_s|\le |{\overline{R}}_y|$ and $|{\overline{R}}_y\cap {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$, for each RN set ${\overline{R}}_y$ of $\mathbb{G}$ different from $R_s$.

Proof. 

The RN having fewer number of elements in $\mathbb{G}$ is $R_s=R\{x_s,y_s\}=V({\mathbb{AWB}}_m)-\{x_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$ $m)\}\cup \{y_j|j\equiv s-1,s-2,\cdots ,s-\frac{m}{2}(mod$ $m)\}\cup \{z_j|j\equiv s-1,s-2,\cdots ,s-\frac{m}{2}(mod$ $m)\}$.

Consequently, $|R_s|=\frac{3m}{2}+1$ for $1\le s\le m$, ${\displaystyle \bigcup _{s=1}^m}{R}_s=V({\mathbb{AWB}}_m)$ and $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$.

(b) For the proof of required RNs, the following variables will be needed:

• $1\le s\le m$
• $t\ge 1$ and $t\equiv 1(mod$ $2)$
• $p\ge 3$ and $p\equiv 1(mod$ $2)$
• $r\ge 2$ and $r\equiv 0(mod$ $2)$

${\overline{R}}_y$ for $1\le y\le 14$ other than $|R_s|$ are given by:

• ${\overline{R}}_1=R\{x_s,x_{s+t}\}=V({\mathbb{AWB}}_m)-\{y_j|j\equiv s+\frac{t-1}{2},s+\frac{m+t-1}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{p-1}{2},s+\frac{m+p-1}{2}(mod$$m)\}={\overline{R}}_2=R\{z_s,z_{s+r}\}$,
• ${\overline{R}}_3=R\{y_s,y_{s+t}\}=V({\mathbb{AWB}}_m)-\{x_j|j\equiv s+\frac{t+1}{2},s+\frac{m+t+1}{2}(mod$$m)\}={\overline{R}}_4=R\{z_s,z_{s+t}\}={\overline{R}}_5=R\{x_s,x_{s+r}\}={\overline{R}}_6=R\{x_s,x_{s+r}\}$,
• ${\overline{R}}_7=R\{x_s,y_{s+t}\}=V({\mathbb{AWB}}_m)-\{x_j|j\equiv s+\frac{t+1}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{t-1}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{t-1}{2}(mod$$m)\}$,
• ${\overline{R}}_8=R\{x_s,y_{s+r}\}=V({\mathbb{AWB}}_m)-\{x_j|j\equiv s+\frac{m+r}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{m+r}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{m+r}{2}(mod$$m)\}$,
• ${\overline{R}}_9=R\{x_s,z_s\}=V({\mathbb{AWB}}_m)-\{y_j|j\equiv s,s+1,\cdots ,s+\frac{m}{2}-1(mod$$m)\}\cup \{z_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}$,
• ${\overline{R}}_{11}=R\{x_s,z_{s+p}\}=V({\mathbb{AWB}}_m)-\{x_j|j\equiv s+\frac{m+p+1}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{m+p+1}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{m+p+1}{2}(mod$$m)\}$,
• ${\overline{R}}_{12}=R\{x_s,z_{s+r}\}=V({\mathbb{AWB}}_m)-\{x_j|j\equiv s+\frac{s+2}{2}(mod$$m)\}\cup \{y_j|j\equiv s+\frac{s}{2}(mod$$m)\}\cup \{z_j|j\equiv s+\frac{s}{2}(mod$$m)\}$,
• ${\overline{R}}_{13}=R\{x_s,y_{s-1}\}=V({\mathbb{AWB}}_m)-\{x_j|j\equiv s-1,s-2,\cdots ,s-\frac{m}{2}(mod$$m)\}\cup \{y_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{z_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}$,
• ${\overline{R}}_{14}=R\{y_s,z_s\}=V({\mathbb{AWB}}_m)$.

The cardinalities of the aforementioned RNs have been summarized in Table 5. □

Table 5. RNs ${\overline{R}}_y$ for $1\le y\le 14$.

RNs	Cardinalities
${\overline{R}}_1$,${\overline{R}}_2$	$3m-4$
${\overline{R}}_3$,${\overline{R}}_4$,${\overline{R}}_5$,${\overline{R}}_6$	$3m-2$
${\overline{R}}_7,{\overline{R}}_8$, ${\overline{R}}_{11},{\overline{R}}_{12}$	$3(m-1)$
${\overline{R}}_9$	$2n$
${\overline{R}}_{13}$	$\frac{3m}{2}$
${\overline{R}}_{14}$	$3m$

Table 5 shows that $|R_s|\le |{\overline{R}}_y|$ and $|{\overline{R}}_y\cup {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$.

Lemma 6. 

Let $\mathbb{G}\cong {\mathbb{AWB}}_m$ be an antiprism web network, for any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$ then:

(a)

For $1\le s\le m$, $|L{R}_s|=|LR\{x_s,y_s\}|=\frac{3m}{2}$ and $|{\displaystyle \bigcup _{s=1}^m}L{R}_s|=3m$ and

(b)

For $1\le y\le 7$, $|L{R}_s|\le |{\overline{R}}_y|$ and $|{\overline{LR}}_y\cap {\displaystyle \bigcup _{s=1}^m}L{R}_s|\ge |L{R}_s|$, for each RN set ${\overline{LR}}_y$ of $\mathbb{G}$ different from $L{R}_s$.

Proof. 

For proof see Lemma 5(a).

(b) The required LRNs ${\overline{LR}}_y$ for $1\le y\le 12$ are given as follows:

• ${\overline{LR}}_1=R\{x_s,x_{s+1}\}=V({\mathbb{AWB}}_m)-\{y_j|j\equiv s,s+\frac{m}{2}(mod$$m)\}\cup \{z_j|j\equiv s,s+\frac{m}{2}(mod$$m)\}$,
• ${\overline{LR}}_2=R\{y_s,y_{s+1}\}=V({\mathbb{AWB}}_m)-\{x_j|j\equiv s+1,s+\frac{m+2}{2}(mod$$m)\}$,
• ${\overline{LR}}_3=R\{x_s,y_{s-1}\}=V({\mathbb{AWB}}_m)-\{x_j|j\equiv s-1,s-2,\cdots ,s-\frac{m}{2}(mod$$m)\}\cup \{y_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}\cup \{z_j|j\equiv s+1,s+2,\cdots ,s+\frac{m}{2}(mod$$m)\}$,
• ${\overline{LR}}_4=R\{y_s,z_s\}=V({\mathbb{AWB}}_m)$.

The cardinalities of the aforementioned RNs has been summarized in Table 6. □

Table 6. RNs ${\overline{LR}}_y$ for $1\le y\le 14$.

RNs	Cardinalities
${\overline{LR}}_1$	$3m-4$
${\overline{LR}}_2$	$3m-2$
${\overline{LR}}_3$	$\frac{3m}{2}$
${\overline{LR}}_4$	$3m$

Table 6 shows that $|L{R}_s|\le |{\overline{LR}}_y|$ and $|{\overline{LR}}_y\cup {\displaystyle \bigcup _{s=1}^m}L{R}_s|\ge |L{R}_s|$.

4. FMD and LFMD of Web-Related Networks

This section covers the results regarding the FMD and LFMD of the networks under consideration.

4.1. FMD and LFMD of Subdivided QCL

Theorem 4. 

Suppose that $\mathbb{G}\cong {\mathbb{SB}}_m$ be subdivided QCL network, taking any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$, then $1\le fdim(\mathbb{G})\le \frac{3}{2}$.

Proof. Case I: 

For $m=6$.

By making use of symmetry, the RNs are tabulated as below:

Table 7 is exhibiting the RNs with the least cardinality of 17. Whereas RNs with maximum cardinality has been shown by Table 8, Table 9, Table 10, Table 11, Table 12, Table 13 and Table 14, respectively. Hence ${\displaystyle \bigcup _{s=1}^9}{R}_l=V(\mathbb{G})$, $|{\displaystyle \bigcup _{s=1}^9}{R}_s|=30$ and $|{\overline{R}}_y\cap {\displaystyle \bigcup _{s=1}^9}{R}_s|\ge |R_s|$, where $1\le y\le 70$. Now, we are defining a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that $\mu (v_k)=\mu (w_k)=\mu (x_k)=\mu (y_k)=\mu (z_k)=\frac{1}{17}$. We can see that $R_s$ for $1\le r\le 9$ of $V(\mathbb{G})$ are intersecting in a pairwise manner, showing non-cyclic behavior with ${\displaystyle \bigcap _{s=1}^{12}}{R}_s=\varphi$, so, by Theorem 3, we arrive at $1\le fdim(\mathbb{G})\le {\displaystyle \sum _{s=1}^{32}}\frac{1}{17}=\frac{30}{17}$.

Table 7. RNs $R_s$ for $1\le s\le 9$.

RNs	Elements
$R\{x_1,y_1\}$	$V({\mathbb{SQ}}_6)-\{v_1,v_5,v_6\}\cup \{w_2,w_3,w_4\}\cup \{x_3,x_4,x_5\}\cup \{y_3,y_4\}\cup \{z_2,z_3\}$
$R\{x_2,y_2\}$	$V({\mathbb{SQ}}_6)-\{v_1,v_2,v_6\}\cup \{w_3,w_4,w_5\}\cup \{x_4,x_5,x_6\}\cup \{y_4,y_5\}\cup \{z_3,z_4\}$
$R\{x_3,y_3\}$	$V({\mathbb{SQ}}_6)-\{v_1,v_2,v_3\}\cup \{w_4,w_5,w_6\}\cup \{x_1,x_5,x_6\}\cup \{y_5,y_6\}\cup \{z_4,z_5\}$
$R\{x_1,y_2\}$	$V({\mathbb{SQ}}_6)-\{v_2,v_3,v_4\}\cup \{w_1,w_5,w_6\}\cup \{x_2,x_3,x_4\}\cup \{y_3,y_4\}\cup \{z_5,z_6\}$
$R\{x_2,y_3\}$	$V({\mathbb{SQ}}_6)-\{v_3,v_4,v_5\}\cup \{w_1,w_2,w_6\}\cup \{x_3,x_4,x_5\}\cup \{y_4,y_5\}\cup \{z_1,z_6\}$
$R\{x_3,y_4\}$	$V({\mathbb{SQ}}_6)-\{v_4,v_5,v_6\}\cup \{w_1,w_2,w_3\}\cup \{x_4,x_5,x_6\}\cup \{y_5,y_6\}\cup \{z_1,z_2\}$
$R\{y_1,z_1\}$	$V({\mathbb{SQ}}_6)-\{v_2,v_3,v_4\}\cup \{w_1,w_5,w_6\}\cup \{x_2,x_3,x_4\}\cup \{y_5,y_6\}\cup \{z_5,z_6\}$
$R\{y_2,z_2\}$	$V({\mathbb{SQ}}_6)-\{v_3,v_4,v_5\}\cup \{w_1,w_2,w_6\}\cup \{x_3,x_4,x_5\}\cup \{y_1,y_6\}\cup \{z_1,z_6\}$
$R\{y_3,z_3\}$	$V({\mathbb{SQ}}_6)-\{v_1,v_2,v_3\}\cup \{w_4,w_5,w_6\}\cup \{x_1,x_5,x_6\}\cup \{y_1,y_2\}\cup \{z_1,z_2\}$

Table 8. RNs $\overline{R_y}$ for $1\le y\le 3$.

RNs	Elements
$R\{x_1,z_2\}$	$V({\mathbb{SQ}}_6)-\{v_3,v_4\}\cup \{x_3,x_4\}\cup \{w_1,w_6\}\cup \left\{y_5\right\}\cup \{z_5,z_6\}$
$R\{x_2,z_3\}$	$V({\mathbb{SQ}}_6)-\{v_4,v_5\}\cup \{x_4,x_5\}\cup \{w_1,w_2\}\cup \left\{y_6\right\}\cup \{z_1,z_6\}$
$R\{x_3,z_4\}$	$V({\mathbb{SQ}}_6)-\{v_5,v_6\}\cup \{x_5,x_6\}\cup \{w_2,w_3\}\cup \left\{y_1\right\}\cup \{z_1,z_2\}$

Table 9. RNs $\overline{R_y}$ for $4\le y\le 6$.

RNs	Elements
$R\{v_1,w_2\}$	$V({\mathbb{SQ}}_6)-\{v_2,v_3,v_4\}\cup \{w_1,w_5,w_6\}\cup \{z_4,z_5\}$
$R\{v_2,w_3\}$	$V({\mathbb{SQ}}_6)-\{v_3,v_4,v_5\}\cup \{w_1,w_2,w_6\}\cup \{z_5,z_6\}$
$R\{v_3,w_4\}$	$V({\mathbb{SQ}}_6)-\{v_4,v_5,v_6\}\cup \{w_1,w_2,w_3\}\cup \{z_1,z_6\}$

Table 10. RNs $\overline{R_y}$ for $7\le y\le 9$ and $p=3$.

RNs	Elements
$R\{v_s,w_{s+p}\}$	$V(\mathbb{SQ})-\{y_j|1\le j\le m\}$

Table 11. RNs $\overline{R_y}$ for $10\le y\le 17$.

RNs	Elements	Equality
$R\{x_1,x_2\}$	$V({\mathbb{SQ}}_6)-\{v_2,v_5\}\cup \{w_2,w_5\}\cup \{y_2,y_5\}$	$R\{z_1,z_2\}$, $R\{x_3,x_6\}$
$R\{x_2,x_3\}$	$V({\mathbb{SQ}}_6)-\{v_3,v_6\}\cup \{w_3,w_6\}\cup \{y_3,y_6\}$	$R\{z_2,z_3\}$, $R\{x_1,x_4\}$
$R\{v_3,v_4\}$	$V({\mathbb{SQ}}_6)-\{v_1,v_4\}\cup \{w_1,w_4\}\cup \{y_1,y_4\}$	$R\{z_3,z_4\}$, $R\{x_2,x_5\}$

Table 12. RNs $\overline{R_y}$ for $18\le y\le 44$.

RNs	Elements	Equality
$R\{v_1,w_4\}$	$V({\mathbb{SQ}}_6)-\{v_3,v_6\}\cup \{w_1,w_4\}$
$R\{v_2,w_3\}$	$V({\mathbb{SQ}}_6)-\{v_1,v_4\}\cup \{w_2,w_5\}$
$R\{v_3,w_4\}$	$V({\mathbb{SQ}}_6)-\{v_2,v_5\}\cup \{w_3,w_6\}$
$R\{v_1,w_3\}$	$V({\mathbb{SQ}}_6)-\{v_3,v_6\}\cup \{w_1,w_4\}$
$R\{v_2,w_4\}$	$V({\mathbb{SQ}}_6)-\{v_1,v_4\}\cup \{w_2,w_5\}$
$R\{v_3,w_5\}$	$V({\mathbb{SQ}}_6)-\{v_2,v_5\}\cup \{w_3,w_6\}$
$R\{x_1,z_4\}$	$V({\mathbb{SQ}}_6)-\{x_3,x_5\}\cup \{y_3,y_5\}$
$R\{x_2,z_5\}$	$V({\mathbb{SQ}}_6)-\{x_4,x_6\}\cup \{y_4,y_6\}$
$R\{x_3,z_6\}$	$V({\mathbb{SQ}}_6)-\{x_1,x_5\}\cup \{y_1,y_5\}$
$R\{x_1,z_4\}$	$V({\mathbb{SQ}}_6)-\{w_3,w_5\}\cup \{x_3,x_5\}$
$R\{x_2,z_5\}$	$V({\mathbb{SQ}}_6)-\{w_4,w_6\}\cup \{x_4,x_6\}$
$R\{x_3,z_6\}$	$V({\mathbb{SQ}}_6)-\{w_1,w_5\}\cup \{x_1,x_5\}$
$R\{x_1,y_3\}$	$V({\mathbb{SQ}}_6)-\left\{v_3\right\}\cup \left\{x_6\right\}\cup \left\{y_1\right\}\cup \left\{z_4\right\}$
$R\{x_2,y_4\}$	$V({\mathbb{SQ}}_6)-\left\{v_4\right\}\cup \left\{x_1\right\}\cup \left\{y_2\right\}\cup \left\{z_5\right\}$
$R\{x_3,y_5\}$	$V({\mathbb{SQ}}_6)-\left\{v_5\right\}\cup \left\{x_2\right\}\cup \left\{y_3\right\}\cup \left\{z_6\right\}$
$R\{y_1,z_4\}$	$V({\mathbb{SQ}}_6)-\left\{v_3\right\}\cup \{x_3,x_6\}\cup \left\{y_6\right\}$
$R\{y_2,z_5\}$	$V({\mathbb{SQ}}_6)-\left\{v_4\right\}\cup \{x_1,x_4\}\cup \left\{y_1\right\}$
$R\{y_3,z_6\}$	$V({\mathbb{SQ}}_6)-\left\{v_5\right\}\cup \{x_2,x_5\}\cup \left\{y_2\right\}$
$R\{x_1,y_3\}$	$V({\mathbb{SQ}}_6)-\left\{v_3\right\}\cup \left\{x_6\right\}\cup \left\{y_1\right\}\cup \left\{z_4\right\}$
$R\{x_2,y_4\}$	$V({\mathbb{SQ}}_6)-\left\{v_4\right\}\cup \left\{x_1\right\}\cup \left\{y_2\right\}\cup \left\{z_5\right\}$
$R\{x_3,y_5\}$	$V({\mathbb{SQ}}_6)-\left\{v_5\right\}\cup \left\{x_2\right\}\cup \left\{y_3\right\}\cup \left\{z_6\right\}$
$R\{v_1,v_2\}$	$V({\mathbb{SQ}}_6)-\{x_1,x_4\}\cup \{z_1,z_4\}$	$R\{y_1,y_2\}$, $R\{v_3,v_6\}$
$R\{v_2,v_3\}$	$V({\mathbb{SQ}}_6)-\{x_2,x_5\}\cup \{z_2,z_5\}$	$R\{y_2,y_3\}$, $R\{v_1,v_4\}$
$R\{v_3,v_4\}$	$V({\mathbb{SQ}}_6)-\{x_3,x_6\}\cup \{z_3,z_6\}$	$R\{y_3,y_6\}$, $R\{v_2,v_5\}$

Table 13. RNs $\overline{R_y}$ for $45\le y\le 52$.

RNs	Elements
$R\{x_1,y_4\}$	$V({\mathbb{SQ}}_6)-\left\{v_3\right\}\cup \left\{x_6\right\}\cup \left\{y_3\right\}$
$R\{x_2,y_5\}$	$V({\mathbb{SQ}}_6)-\left\{v_4\right\}\cup \left\{x_1\right\}\cup \left\{y_4\right\}$
$R\{x_3,y_6\}$	$V({\mathbb{SQ}}_6)-\left\{v_5\right\}\cup \left\{x_2\right\}\cup \left\{y_5\right\}$
$R\{x_1,z_3\}$	$V({\mathbb{SQ}}_6)-\left\{w_2\right\}\cup \left\{v_3\right\}\cup \left\{z_1\right\}$
$R\{x_2,z_4\}$	$V({\mathbb{SQ}}_6)-\left\{w_3\right\}\cup \left\{v_4\right\}\cup \left\{z_2\right\}$
$R\{x_3,z_5\}$	$V({\mathbb{SQ}}_6)-\left\{w_4\right\}\cup \left\{v_5\right\}\cup \left\{z_3\right\}$
$R\{y_1,z_3\}$	$V({\mathbb{SQ}}_6)-\left\{w_2\right\}\cup \{x_2,x_5\}$
$R\{y_2,z_4\}$	$V({\mathbb{SQ}}_6)-\left\{w_3\right\}\cup \{x_3,x_6\}$
$R\{y_3,z_5\}$	$V({\mathbb{SQ}}_6)-\left\{w_4\right\}\cup \{x_1,x_4\}$

Table 14. RNs ${\overline{R}}_y$ for $53\le y\le 70$.

RNs	RNs	Elements
$R\{v_s,y_{s+p}\}$	$R\{v_s,y_{s+r}\}$	$V({\mathbb{SQ}}_m)$
$R\{v_s,x_{s+p}\}$	$R\{v_s,x_{s+r}\}$	$V({\mathbb{SQ}}_m)$
$R\{v_s,z_{s+p}\}$	$R\{v_s,z_{s+r}\}$	$V({\mathbb{SQ}}_m)$

Case II: For any $m\ge 6$:

As we can see from Lemma 1 the RN with the least cardinality of $\frac{5m}{2}+2$ is $R_s=R\{x_s,y_s\}$, $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=5m$ and $|R\{s,t\}\cap {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$∀$\{s,t\}\in V(\mathbb{G})$. Suppose that $\sigma =|{\displaystyle \bigcup _{s=1}^m}{R}_s|=5m$ and $\kappa =|R_s|=\frac{5m}{2}+2$. Then we define a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that

$\mu (v)=\left\{\begin{array}{cc}\frac{1}{\beta }\hfill & \mathrm{for}a\in {\displaystyle \bigcup _{s=1}^m}{R}_s,\hfill \\ 0\hfill & \mathrm{for}a\in V(\mathbb{G})-{\displaystyle \bigcup _{s=1}^m}{R}_s\hfill \end{array}\right.$

We can see that $\mu$ is a RF for $\mathbb{G}$ with $m\ge 6$ because $\mu (R\{s,t\})\ge 1$∀$s,t\in V(\mathbb{G})$. On contrary, assume that there exists a different RF $\gamma$, such that $\gamma (u)\le \mu (u)$, for some $u\in V(\mathbb{G})$ $\gamma (u)\ne \mu (u)$. Consequently, $\gamma (R\{s,t\})<1$, where $R\{s,t\}$ is an RN of $\mathbb{G}$ having the least cardinality $\beta$. This shows that $\gamma$ is not an RF. Thus, $\mu$ is a MRF that acquires minimum $|\mu |$ for $\mathbb{G}$. Also, all the $R_s$ are intersecting in pairwise manner, holding non-cyclic behavior with ${\displaystyle \bigcap _{s=1}^m}{R}_s=\varphi$, thus by Theorem 3, assigning $\frac{1}{\beta }$ to the vertices of $\mathbb{G}$ in ${\displaystyle \bigcup _{s=1}^m}{R}_s$ and evaluating the summation of all the weights, we get: $1\le fdim(\mathbb{G})\le {\displaystyle \sum _{l=1}^{\sigma }}\frac{1}{\beta }=\frac{10m}{5m+4}.$ □

Theorem 5. 

Suppose that $\mathbb{G}\cong {\mathbb{SB}}_m$ is a subdivided QCL network, taking any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$, then $ldim(\mathbb{G})=1$.

Proof. 

Since $\mathbb{G}$ is a bipartite network, therefore by Theorem 2,

$$ldim(\mathbb{G})=1.$$

□

4.2. FMD and LFMD of 2-Faced Web Network

Theorem 6. 

Suppose that $\mathbb{G}\cong {\mathbb{WB}}_m^1$ is a 2-faced web network, taking any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$, then $1\le fdim(\mathbb{G})\le \frac{3m}{m+1}$.

Proof. Case I: 

For $m=6$.

By making use of symmetry, the RNs are tabulated as below:

Table 15 exhibits the RNs with the least cardinality of 7. Whereas RNs with maximum cardinality has been shown by Table 16, Table 17, Table 18, Table 19 and Table 20 respectively. Thus ${\displaystyle \bigcup _{s=1}^3}{R}_s=V(\mathbb{G})$. It is observed that $|{\displaystyle \bigcup _{s=1}^3}{R}_s|=18$ and $|{\overline{R}}_y\cap {\displaystyle \bigcup _{s=1}^9}{R}_s|\ge |R_s|$, where $1\le y\le 30$. Now, we are defining a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that $\mu (x_k)=\mu (y_k)=\mu (z_k)=\frac{1}{7}$. It can be seen that $R_s$ for $1\le r\le 9$ of $V(\mathbb{G})$ intersecting in pairwise manner, showing non-cyclic behavior with ${\displaystyle \bigcap _{s=1}^3}{R}_s=\varphi$, therefore, by Theorem 3, we have $1\le fdim(\mathbb{G})\le {\displaystyle \sum _{s=1}^{18}}\frac{1}{7}=\frac{18}{7}$.

Table 15. RNs $R_s$ for $1\le s\le 3$.

RNs	Elements
$R\{x_1,z_1\}$	$V({\mathbb{WB}}_6^1)-\{y_j|1\le j\le 6\}\cup \{z_2,z_3,z_4,z_5,z_6\}$
$R\{x_2,z_2\}$	$V({\mathbb{WB}}_6^1)-\{y_j|1\le j\le 6\}\cup \{z_1,z_3,z_4,z_5,z_6\}$
$R\{x_3,z_3\}$	$V({\mathbb{WB}}_6^1)-\{y_j|1\le j\le 6\}\cup \{z_1,z_2,z_4,z_5,z_6\}$

Table 16. RNs $\overline{R_y}$ for $1\le y\le 6$.

RNs	Elements
$R\{x_1,y_2\}$	$V({\mathbb{WB}}_6^1)-\{x_2,x_3,x_4\}\cup \{y_1,y_5,y_6\}\cup \{z_1,z_5,z_6\}$
$R\{x_2,y_3\}$	$V({\mathbb{WB}}_6^1)-\{x_3,x_4,x_5\}\cup \{y_1,y_2,y_6\}\cup \{z_1,z_2,z_6\}$
$R\{x_3,y_4\}$	$V({\mathbb{WB}}_6^1)-\{x_4,x_5,x_6\}\cup \{y_1,y_2,y_3\}\cup \{z_1,z_2,z_3\}$
$R\{x_1,z_2\}$	$V({\mathbb{WB}}_6^1)-\{x_2,x_3,x_4\}\cup \{y_1,y_2,y_3\}\cup \{z_1,z_2,z_3\}$
$R\{x_2,z_3\}$	$V({\mathbb{WB}}_6^1)-\{x_3,x_4,x_5\}\cup \{y_2,y_3,y_4\}\cup \{z_2,z_3,z_4\}$
$R\{x_3,z_4\}$	$V({\mathbb{WB}}_6^1)-\{x_4,x_5,x_6\}\cup \{y_3,y_4,y_5\}\cup \{z_3,z_4,z_5\}$

Table 17. RNs $\overline{R_y}$ for $7\le y\le 9$.

RNs	Elements
$R\{y_1,z_4\}$	$V({\mathbb{WB}}_6^1)-\{x_3,x_5\}\cup \{y_3,y_5\}\cup \{z_3,z_5\}$
$R\{y_2,z_5\}$	$V({\mathbb{WB}}_6^1)-\{x_4,x_6\}\cup \{y_4,y_6\}\cup \{z_4,z_6\}$
$R\{y_3,z_6\}$	$V({\mathbb{WB}}_6^1)-\{x_1,x_5\}\cup \{y_1,y_5\}\cup \{z_1,z_5\}$

Table 18. RNs $\overline{R_y}$ for $10\le y\le 12$.

RNs	Elements
$R\{x_1,z_3\}$	$V({\mathbb{WB}}_6^1)-\{x_3,x_4\}\cup \left\{y_5\right\}\cup \left\{z_5\right\}$
$R\{x_2,z_4\}$	$V({\mathbb{WB}}_6^1)-\{x_4,x_5\}\cup \left\{y_6\right\}\cup \left\{z_6\right\}$
$R\{y_3,z_5\}$	$V({\mathbb{WB}}_6^1)-\{x_5,x_6\}\cup \left\{y_1\right\}\cup \left\{z_1\right\}$

Table 19. RNs $\overline{R_y}$ for $13\le y\le 20$.

RNs	Elements	Equality
$R\{x_1,x_2\}$	$V({\mathbb{WB}}_6^1)-\{v_2,v_5\}\cup \{w_2,w_5\}\cup \{y_2,y_5\}$	$R\{z_1,z_2\}$, $R\{x_3,x_6\}$
$R\{x_2,x_3\}$	$V({\mathbb{WB}}_6^1)-\{v_3,v_6\}\cup \{w_3,w_6\}\cup \{y_3,y_6\}$	$R\{z_2,z_3\}$, $R\{x_1,x_4\}$
$R\{v_3,v_4\}$	$V({\mathbb{WB}}_6^1)-\{v_1,v_4\}\cup \{w_1,w_4\}\cup \{y_1,y_4\}$	$R\{z_3,z_4\}$, $R\{x_2,x_5\}$

Table 20. RNs $\overline{R_y}$ for $21\le y\le 30$.

RNs	Elements	Equality
$R\{x_s,x_{s+t}\}$	$R\{z_s,z_{s+t}\}$	$V({\mathbb{WB}}_m^1)$
$R\{x_s,z_{s+t}\}$	$R\{x_s,y_s\}$	$V({\mathbb{WB}}_m^1)$
$R\{y_s,y_{s+t}\}$	$R\{y_s,z_s\}$	$V({\mathbb{WB}}_m^1)$
$R\{x_s,z_{s+t}\}$	$R\{x_s,z_{s+t}\}$	$V({\mathbb{WB}}_m^1)$
$R\{y_s,z_{s+r}\}$		$V({\mathbb{WB}}_m^1)$

□

Case II: For any $m\ge 6$: As we can see from Lemma 3.2.1 the RN with the least cardinality of $m+1$ is $R_s=R\{x_s,z_s\}$, $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and $|R\{s,t\}\cap {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$∀$\{s,t\}\in V(\mathbb{G})$. Suppose that $\sigma =|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and $\beta =|R_s|=n+1$. Then, we define a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that

$\mu (v)=\left\{\begin{array}{cc}\frac{1}{\beta }\hfill & \mathrm{for}a\in {\displaystyle \bigcup _{s=1}^m}{R}_s,\hfill \\ 0\hfill & \mathrm{for}a\in V(\mathbb{G})-{\displaystyle \bigcup _{s=1}^m}{R}_s\hfill \end{array}\right.$

It is observed that $\mu$ is a RF for $\mathbb{G}$ with $m\ge 6$ because $\mu (R\{s,t\})\ge 1$∀$s,t\in V(\mathbb{G})$. Assume on the contrary that ∃ a different RF $\gamma$, such that $\gamma (u)\le \mu (u)$, for some $u\in V(\mathbb{G})$ $\gamma (u)\ne \mu (u)$. Consequently, $\gamma (R\{s,t\})<1$, where $R\{s,t\}$ is an RN of $\mathbb{G}$ having the least cardinality $\beta$. This shows that $\gamma$ is not a RF a contradiction. Hence, $\mu$ is a MRF that attains minimum $|\mu |$ for $\mathbb{G}$. Also, all the $R_s$ are intersecting in pairwise manner, exhibiting non-cyclic behaviour with ${\displaystyle \bigcap _{s=1}^m}{R}_s=\varphi$, thus by Theorem 3, assigning $\frac{1}{\beta }$ to the vertices of $\mathbb{G}$ in ${\displaystyle \bigcup _{s=1}^m}{R}_s$ and evaluating the summation of all the weights, we get: $1\le fdim(\mathbb{G})\le {\displaystyle \sum _{l=1}^{\sigma }}\frac{1}{\beta }=\frac{3m}{m+1}.$

Theorem 7. 

Suppose that $\mathbb{G}\cong {\mathbb{WB}}_m^1$ is a 2-faced web network network, taking any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$, then $ldim(\mathbb{G})=1$.

Proof. 

Since $\mathbb{G}$ is a bipartite network, therefore by Theorem 2,

$$ldim(\mathbb{G})=1.$$

□

4.3. FMD and LFMD of 3-Faced Web Network

Theorem 8. 

Suppose that $\mathbb{G}\cong {\mathbb{WB}}_m^2$ is a 3-faced web network network, taking any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$, then $1\le fdim(\mathbb{G})\le 2$.

Proof. Case I: 

For $m=6$. By making use of symmetry, the RNs are tabulated as below:

Table 21 is exhibiting the RNs with the least cardinality of 9. Whereas RNs with maximum cardinality has been shown by Table 22, Table 23, Table 24, Table 25, Table 26 and Table 27, respectively. Thus ${\displaystyle \bigcup _{s=1}^3}{R}_s=V(\mathbb{G})$. It is observed that $|{\displaystyle \bigcup _{s=1}^3}{R}_s|=18$ and $|{\overline{R}}_y\cap {\displaystyle \bigcup _{s=1}^3}{R}_s|\ge |R_s|$, where $1\le y\le 27$. Now, we are defining a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that $\mu (x_k)=\mu (y_k)=\mu (z_k)=\frac{1}{7}$. We have seen that $R_s$ for $1\le r\le 3$ of $V(\mathbb{G})$ intersecting in pairwise manner, holding non-cyclic behavior with ${\displaystyle \bigcap _{s=1}^3}{R}_s=\varphi$, therefore, by Theorem 3, we have $1\le fdim(\mathbb{G})\le {\displaystyle \sum _{s=1}^{18}}\frac{1}{9}=2$.

Table 21. RNs $R_s$ for $1\le s\le 3$.

RNs	Elements
$R\{x_2,y_1\}$	$V({\mathbb{WB}}_m^2)-\{x_1,x_5,x_6\}\cup \{y_2,y_3,y_4\}\cup \{z_2,z_3,z_4\}$
$R\{x_3,y_2\}$	$V({\mathbb{WB}}_m^2)-\{x_1,x_2,x_6\}\cup \{y_3,y_4,y_5\}\cup \{z_3,z_4,z_5\}$
$R\{x_4,y_3\}$	$V({\mathbb{WB}}_m^2)-\{x_1,x_2,x_3\}\cup \{y_4,y_5,y_6\}\cup \{z_4,z_5,z_6\}$

Table 22. RNs ${\overline{R}}_y$ for $1\le y\le 3$.

RNs	Elements
$R\{y_1,z_2\}$	$V({\mathbb{WB}}_6^2)-\{x_3,x_4\}\cup \{y_2,y_3,y_4\}\cup \{z_3,z_4,z_5\}$
$R\{y_2,z_3\}$	$V({\mathbb{WB}}_6^2)-\{x_4,x_5\}\cup \{y_3,y_4,y_5\}\cup \{z_4,z_5,z_6\}$
$R\{y_3,z_4\}$	$V({\mathbb{WB}}_6^2)-\{x_5,x_6\}\cup \{y_4,y_5,y_6\}\cup \{z_1,z_5,z_6\}$

Table 23. RNs ${\overline{R}}_y$ for $4\le y\le 6$.

RNs	Elements
$R\{x_1,z_1\}$	$V({\mathbb{WB}}_6^2)-\{y_1,y_2,y_3,y_4\}\cup \{z_2,z_3,z_4\}$
$R\{x_2,z_2\}$	$V({\mathbb{WB}}_6^2)-\{y_2,y_3,y_4,y_5\}\cup \{z_3,z_4,z_5\}$
$R\{x_3,z_3\}$	$V({\mathbb{WB}}_6^2)-\{y_3,y_4,y_5,y_6\}\cup \{z_4,z_5,z_6\}$

Table 24. RNs ${\overline{R}}_y$ for $7\le y\le 12$.

RNs	Elements
$R\{x_1,y_2\}$	$V({\mathbb{WB}}_6^2)-\{x_2,x_5\}\cup \left\{y_1\right\}\cup \left\{z_1\right\}$
$R\{x_2,y_3\}$	$V({\mathbb{WB}}_6^2)-\{x_3,x_6\}\cup \left\{y_2\right\}\cup \left\{z_2\right\}$
$R\{x_3,y_4\}$	$V({\mathbb{WB}}_6^2)-\{x_1,x_4\}\cup \left\{y_3\right\}\cup \left\{z_3\right\}$
$R\{x_1,x_2\}$	$V({\mathbb{WB}}_6^2)-\{y_1,y_4\}\cup \{z_1,z_4\}$
$R\{x_2,x_3\}$	$V({\mathbb{WB}}_6^2)-\{y_2,y_5\}\cup \{z_2,z_5\}$
$R\{x_3,x_4\}$	$V({\mathbb{WB}}_6^2)-\{y_3,y_6\}\cup \{z_3,z_6\}$

Table 25. RNs ${\overline{R}}_y$ for $13\le y\le 21$.

RNs	Elements	Equality
$R\{x_1,y_3\}$	$V({\mathbb{WB}}_6^2)-\left\{x_5\right\}\cup \left\{y_5\right\}\cup \left\{z_5\right\}$
$R\{y_1,z_4\}$	$V({\mathbb{WB}}_6^2)-\left\{x_6\right\}\cup \left\{y_6\right\}\cup \left\{z_6\right\}$	$R\{x_2,y_4\}$
$R\{x_2,y_4\}$	$V({\mathbb{WB}}_6^2)-\left\{x_1\right\}\cup \left\{y_1\right\}\cup \left\{z_1\right\}$	$R\{x_3,y_5\}$
$R\{x_3,y_5\}$	$V({\mathbb{WB}}_6^2)-\left\{x_2\right\}\cup \left\{y_2\right\}\cup \left\{z_2\right\}$
$R\{y_1,z_3\}$	$V({\mathbb{WB}}_6^2)-\left\{x_3\right\}\cup \left\{y_2\right\}\cup \left\{z_2\right\}$
$R\{x_2,y_4\}$	$V({\mathbb{WB}}_6^2)-\left\{x_4\right\}\cup \left\{y_3\right\}\cup \left\{z_3\right\}$
$R\{x_3,y_5\}$	$V({\mathbb{WB}}_6^2)-\left\{x_5\right\}\cup \left\{y_4\right\}\cup \left\{z_4\right\}$

Table 26. RNs ${\overline{R}}_y$ for $22\le y\le 25$.

RNs	Elements
$R\{y_1,y_2\}$	$V({\mathbb{WB}}_6^2)\cup \{x_2,x_5\}$
$R\{y_2,y_3\}$	$V({\mathbb{WB}}_6^2)\cup \{x_3,x_6\}$
$R\{y_3,y_4\}$	$V({\mathbb{WB}}_6^2)\cup \{x_1,x_4\}$

Table 27. RNs ${\overline{R}}_y$ for $25\le y\le 27$.

RNs	Elements
$R\{y_s,z_s\}$	$V({\mathbb{WB}}_m^2)$

□

Case II: For any $m\ge 6$:

As we can see from Lemma 3. the RN with the least cardinality of $\frac{3m}{2}$ is $R_s=R\{x_s,y_{s-1}\}$, $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and $|R\{s,t\}\cap {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$∀$\{s,t\}\in V(\mathbb{G})$. Suppose that $\alpha =|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and $\beta =|R_s|=\frac{3m}{2}$. Then we define a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that

$\mu (v)=\left\{\begin{array}{cc}\frac{1}{\beta }\hfill & \mathrm{for}a\in {\displaystyle \bigcup _{s=1}^m}{R}_s,\hfill \\ 0\hfill & \mathrm{for}a\in V(\mathbb{G})-{\displaystyle \bigcup _{s=1}^m}{R}_s\hfill \end{array}\right.$

It is observed that $\mu$ is a RF for $\mathbb{G}$ with $m\ge 6$ because $\mu (R\{s,t\})\ge 1$∀$s,t\in V(\mathbb{G})$. Assume on the contrary that there exists a different RF $\gamma$, such that $\gamma (u)\le \mu (u)$, for some $u\in V(\mathbb{G})$ $\gamma (u)\ne \mu (u)$. Consequently, $\gamma (R\{s,t\})<1$, where $R\{s,t\}$ is an RN of $\mathbb{G}$ having the least cardinality $\beta$. This shows that $\gamma$ is not a RF contradiction. Consequently, $\mu$ is a MRF that attains minimum $|\mu |$ for $\mathbb{G}$. Also, all the $R_s$ are intersecting in a pairwise manner, representing non-cyclic pattern with ${\displaystyle \bigcap _{s=1}^m}{R}_s=\varphi$, thus by Theorem 3, assigning $\frac{1}{\beta }$ to the vertices of $\mathbb{G}$ in ${\displaystyle \bigcup _{s=1}^m}{R}_s$ and evaluating the summation of all the weights, we get: $1\le fdim(\mathbb{G})\le {\displaystyle \sum _{l=1}^{\alpha }}\frac{1}{\beta }=2.$

Corollary 1. 

Suppose that $\mathbb{G}\cong {\mathbb{WB}}_m^3$ is a 3-faced web network network, taking any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$, then $1\le fdim(\mathbb{G})\le 2$.

Proof. 

The above statement is true as ${\mathbb{WB}}_m^2\equiv {\mathbb{WB}}_m^3$. □

Theorem 9. 

Suppose that $\mathbb{G}\cong {\mathbb{WB}}_m^2$ is a 3-faced web network network, taking any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$, then $1\le lfdim(\mathbb{G})\le 2$.

Proof. Case I: 

For $m=6$.

By making use of symmetry, the LRNs are tabulated as below:

Table 28 is exhibiting the LRNs with the least cardinality of 9. Whereas LRNs with maximum cardinality has been shown by Table 29, Table 30 and Table 31 respectively. Thus ${\displaystyle \bigcup _{s=1}^3}{R}_s=V(\mathbb{G})$. It is observed that $|{\displaystyle \bigcup _{s=1}^3}{R}_s|=18$ and $|{\overline{LR}}_y\cap {\displaystyle \bigcup _{s=1}^3}{R}_s|\ge |R_s|$, where $1\le y\le 9$. Now, we are defining a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that $\mu (x_k)=\mu (y_k)=\mu (z_k)=\frac{1}{9}$. It is observed that $R_s$ for $1\le r\le 3$ of $V(\mathbb{G})$ intersecting in pairwise manner, representing non-cyclic pattern with ${\displaystyle \bigcap _{s=1}^3}{R}_s=\varphi$, therefore, by Theorem 1, we have $1\le lfdim(\mathbb{G})\le {\displaystyle \sum _{s=1}^{18}}\frac{1}{9}=2$.

Table 28. RNs $R_s$ for $1\le s\le 3$.

LRNs	Elements
$LR\{x_2,y_1\}$	$V({\mathbb{WB}}_m^2)-\{x_1,x_5,x_6\}\cup \{y_2,y_3,y_4\}\cup \{z_2,z_3,z_4\}$
$LR\{x_3,y_2\}$	$V({\mathbb{WB}}_m^2)-\{x_1,x_2,x_6\}\cup \{y_3,y_4,y_5\}\cup \{z_3,z_4,z_5\}$
$LR\{x_4,y_3\}$	$V({\mathbb{WB}}_m^2)-\{x_1,x_2,x_3\}\cup \{y_4,y_5,y_6\}\cup \{z_4,z_5,z_6\}$

Table 29. LRNs ${\overline{LR}}_y$ for $1\le y\le 3$.

LRNs	Elements
$LR\{x_1,x_2\}$	$V({\mathbb{WB}}_6^2)-\{y_1,y_4\}\cup \{z_1,z_4\}$
$LR\{x_2,x_3\}$	$V({\mathbb{WB}}_6^2)-\{y_2,y_5\}\cup \{z_2,z_5\}$
$LR\{x_3,x_4\}$	$V({\mathbb{WB}}_6^2)-\{y_3,y_6\}\cup \{z_3,z_6\}$

Table 30. LRNs ${\overline{LR}}_y$ for $4\le y\le 6$.

LRNs	Elements
$LR\{y_1,y_2\}$	$V({\mathbb{WB}}_6^2)\cup \{x_2,x_5\}$
$LR\{y_2,y_3\}$	$V({\mathbb{WB}}_6^2)\cup \{x_3,x_6\}$
$LR\{y_3,y_4\}$	$V({\mathbb{WB}}_6^2)\cup \{x_1,x_4\}$

Table 31. LRNs ${\overline{LR}}_y$ for $7\le y\le 9$.

LRNs	Elements
$LR\{y_s,z_s\}$	$V({\mathbb{WB}}_m^2)$

□

Case II: For any $m\ge 6$:

As we can see from Lemma 4 the LRN with the least cardinality of $\frac{3m}{2}$ is $R_s=LR\{x_s,y_{s-1}\}$, $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and $|LR\left\{st\right\}\cap {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$∀$\{s,t\}\in V(\mathbb{G})$. Suppose that $\alpha =|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and $\beta =|R_s|=\frac{3m}{2}$. Then we define a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that

$\mu (v)=\left\{\begin{array}{cc}\frac{1}{\beta }\hfill & \mathrm{for}a\in {\displaystyle \bigcup _{s=1}^m}{R}_s,\hfill \\ 0\hfill & \mathrm{for}a\in V(\mathbb{G})-{\displaystyle \bigcup _{s=1}^m}{R}_s\hfill \end{array}\right.$

It is observed that $\mu$ is a LRF for $\mathbb{G}$ with $m\ge 6$ because $\mu (LR\{st\})\ge 1$∀$s,t\in V(\mathbb{G})$. On the contrary, suppose that there exists a different LRF $\gamma$, such that $\gamma (u)\le \mu (u)$, for some $u\in V(\mathbb{G})$ $\gamma (u)\ne \mu (u)$. Consequently, $\gamma (LR\{st\})<1$, where $LR\left\{st\right\}$ is an RN of $\mathbb{G}$ having the least cardinality $\beta$. This shows that $\gamma$ is not a LRF a contradiction. Therefore, $\mu$ is a MRF that attains minimum $|\mu |$ for $\mathbb{G}$. Also, all the $R_s$ intersecting in pairwise manner, show non-cyclic behavior with ${\displaystyle \bigcap _{s=1}^m}{R}_s=\varphi$, thus by Theorem 1, assigning $\frac{1}{\beta }$ to the vertices of $\mathbb{G}$ in ${\displaystyle \bigcup _{s=1}^m}{R}_s$ and evaluating the summation of all the weights, we get: $1\le lfdim(\mathbb{G})\le {\displaystyle \sum _{l=1}^{\alpha }}\frac{1}{\beta }=2.$

4.4. FMD and LFMD of Antiprism Web Network

Theorem 4.4.1: 

Suppose that $\mathbb{G}\cong {\mathbb{AWB}}_m$ is the antiprism web network network, taking any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$, then $1\le fdim(\mathbb{G})\le 2$.

Proof. Case I: 

For $m=6$.

By making use of symmetry, the RNs are tabulated as below:

Table 32 is exhibiting the RNs with the least cardinality of 9. Whereas RNs with maximum cardinality has been shown by Table 33, Table 34, Table 35, Table 36 and Table 37 respectively. Thus ${\displaystyle \bigcup _{s=1}^6}{R}_s=V(\mathbb{G})$. It is observed that $|{\displaystyle \bigcup _{s=1}^6}{R}_s|=18$ and $|{\overline{R}}_y\cap {\displaystyle \bigcup _{s=1}^6}{R}_s|\ge |R_s|$, where $1\le y\le 26$. Now, we are defining a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that $\mu (x_k)=\mu (y_k)=\mu (z_k)=\frac{1}{7}$. It is observed that $R_s$ for $1\le r\le 3$ of $V(\mathbb{G})$ intersecting in pairwise manner, holding non-cyclic behavior with ${\displaystyle \bigcap _{s=1}^3}{R}_s=\varphi$, therefore, by Theorem 3, we have $1\le fdim(\mathbb{G})\le {\displaystyle \sum _{s=1}^{18}}\frac{1}{9}=2$.

Table 32. RNs $R_s$ for $1\le s\le 6$.

RNs	Elements
$R\{x_1,y_1\}$	$V({\mathbb{AWB}}_m)-\{x_2,x_3,x_4\}\cup \{y_4,y_5,y_6\}\cup \{z_4,z_5,z_6\}$
$R\{x_2,y_2\}$	$V({\mathbb{AWB}}_m)-\{x_3,x_4,x_5\}\cup \{y_1,y_5,y_6\}\cup \{z_1,z_5,z_6\}$
$R\{x_3,y_3\}$	$V({\mathbb{AWB}}_m)-\{x_4,x_5,x_6\}\cup \{y_1,y_2,y_6\}\cup \{z_1,z_2,z_6\}$
$R\{x_2,y_1\}$	$V({\mathbb{AWB}}_m)-\{x_1,x_5,x_6\}\cup \{y_2,y_3,y_4\}\cup \{z_2,z_3,z_4\}$
$R\{x_3,y_2\}$	$V({\mathbb{AWB}}_m)-\{x_1,x_2,x_6\}\cup \{y_3,y_4,y_5\}\cup \{z_3,z_4,z_5\}$
$R\{x_4,y_3\}$	$V({\mathbb{AWB}}_m)-\{x_1,x_2,x_3\}\cup \{y_4,y_5,y_6\}\cup \{z_4,z_5,z_6\}$

Table 33. RNs ${\overline{R}}_y$ for $1\le y\le 3$.

RNs	Elements
$R\{x_1,z_1\}$	$V({\mathbb{AWB}}_6)-\{y_1,y_2,y_3\}\cup \{z_2,z_3,z_4\}$
$R\{x_2,z_2\}$	$V({\mathbb{AWB}}_6)-\{y_2,y_3,y_4\}\cup \{z_3,z_4,z_5\}$
$R\{x_3,z_3\}$	$V({\mathbb{AWB}}_6)-\{y_3,y_4,y_5\}\cup \{z_4,z_5,z_6\}$

Table 34. RNs ${\overline{R}}_y$ for $4\le y\le 14$.

RNs	Elements	Equality
$R\{x_1,y_2\}$	$V({\mathbb{AWB}}_6)-\left\{x_2\right\}\cup \left\{y_1\right\}\cup \left\{z_1\right\}$
$R\{x_2,y_3\}$	$V({\mathbb{AWB}}_6)-\left\{x_3\right\}\cup \left\{y_2\right\}\cup \left\{z_2\right\}$	$R\{x_1,z_3\}$
$R\{x_2,y_3\}$	$V({\mathbb{AWB}}_6)-\left\{x_4\right\}\cup \left\{y_3\right\}\cup \left\{z_3\right\}$	$R\{x_2,z_4\}$
$R\{x_1,y_3\}$	$V({\mathbb{AWB}}_6)-\left\{x_5\right\}\cup \left\{y_5\right\}\cup \left\{z_5\right\}$	$R\{x_3,y_5\}$
$R\{x_2,y_4\}$	$V({\mathbb{AWB}}_6)-\left\{x_6\right\}\cup \left\{y_6\right\}\cup \left\{z_6\right\}$	$R\{x_1,z_4\}$
$R\{x_3,y_5\}$	$V({\mathbb{AWB}}_6)-\left\{x_1\right\}\cup \left\{y_1\right\}\cup \left\{z_1\right\}$	$R\{x_2,z_5\}$

Table 35. RNs ${\overline{R}}_y$ for $15\le y\le 17$.

RNs	Elements	Equality
$R\{x_1,x_2\}$	$V({\mathbb{AWB}}_6)-\{y_1,y_4\}\cup \{z_1,z_4\}$	$R\{z_1,z_3\}$
$R\{x_2,x_3\}$	$V({\mathbb{AWB}}_6)-\{y_2,y_5\}\cup \{z_2,z_5\}$	$R\{z_2,z_4\}$
$R\{x_2,x_3\}$	$V({\mathbb{AWB}}_6)-\{y_3,y_6\}\cup \{z_3,z_6\}$	$R\{z_3,z_5\}$

Table 36. RNs ${\overline{LR}}_y$ for $18\le y\le 20$.

RNs	Elements	Equality
$R\{y_1,y_2\}$	$V({\mathbb{AWB}}_6)-\{x_2,x_5\}$	$R\{z_1,z_3\}$
$R\{y_2,y_3\}$	$V({\mathbb{AWB}}_6)-\{x_3,x_6\}$	$R\{z_2,z_4\}$
$R\{y_2,y_3\}$	$V({\mathbb{AWB}}_6)-\{x_1,x_4\}$	$R\{z_3,z_5\}$

Table 37. RNs ${\overline{R}}_y$ for $21\le y\le 26$.

RNs	Elements
$LR\{y_s,z_s\}$	$V({\mathbb{AWB}}_6)$

□

Case II: For any $m\ge 6$:

As we can see from Lemma 5. the RN with the least cardinality of $\frac{3m}{2}$ is $R_s=R\{x_s,y_s\}$, $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and $|R\{s,t\}\cap {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$∀$\{s,t\}\in V(\mathbb{G})$. Suppose that $\alpha =|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and $\beta =|R_s|=\frac{3m}{2}$. Then we define a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that

$\mu (v)=\left\{\begin{array}{cc}\frac{1}{\beta }\hfill & \mathrm{for}a\in {\displaystyle \bigcup _{s=1}^m}{R}_s,\hfill \\ 0\hfill & \mathrm{for}a\in V(\mathbb{G})-{\displaystyle \bigcup _{s=1}^m}{R}_s\hfill \end{array}\right.$

It is observed that $\mu$ is a RF for $\mathbb{G}$ with $m\ge 6$ because $\mu (R\{s,t\})\ge 1$∀$s,t\in V(\mathbb{G})$. Assume on the contrary that there exists a different RF $\gamma$, such that $\gamma (u)\le \mu (u)$, for some $u\in V(\mathbb{G})$ $\gamma (u)\ne \mu (u)$. Consequently, $\gamma (R\{s,t\})<1$, where $R\{s,t\}$ is an RN of $\mathbb{G}$ having the least cardinality $\beta$. This shows that $\gamma$ is not a RF contradiction. Hence, $\mu$ is a MRF that attains minimum $|\mu |$ for $\mathbb{G}$. Also, all the $R_s$ intersecting in pairwise manner, representing non-cyclic behavior with ${\displaystyle \bigcap _{s=1}^m}{R}_s=\varphi$, thus by Theorem 3, assigning $\frac{1}{\beta }$ to the vertices of $\mathbb{G}$ in ${\displaystyle \bigcup _{s=1}^m}{R}_s$ and evaluating the summation of all the weights, we get: $1\le fdim(\mathbb{G})\le {\displaystyle \sum _{l=1}^{\alpha }}\frac{1}{\beta }=2.$

Theorem 10. 

Suppose that $\mathbb{G}\cong {\mathbb{AWB}}_m$ is a antiprism web network, taking any non-zero positive number $m\ge 6$ and $m\equiv 0(mod$ $2)$, then $1\le ldim(\mathbb{G})\le 2$.

Proof. Case I: 

For $m=6$.

By making use of symmetry, the LRNs are tabulated as below:

Table 38 is exhibiting the LRNs with the least cardinality of 9. Whereas LRNs with maximum cardinality has been shown by Table 39, Table 40 and Table 41 respectively. Thus ${\displaystyle \bigcup _{s=1}^3}{R}_s=V(\mathbb{G})$. It is observed that $|{\displaystyle \bigcup _{s=1}^3}{R}_s|=18$ and $|{\overline{LR}}_y\cap {\displaystyle \bigcup _{s=1}^3}{R}_s|\ge |R_s|$, where $1\le y\le 9$. Now, we are defining a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that $\mu (v_k^j)=\frac{1}{9}$. It is observed that $R_s$ for $1\le r\le 3$ of $V(\mathbb{G})$ are intersecting in a pairwise manner, showing non-cyclic behavior with ${\displaystyle \bigcap _{s=1}^3}{R}_s=\varphi$, therefore, by Theorem 1, we have $1\le lfdim(\mathbb{G})\le {\displaystyle \sum _{s=1}^{18}}\frac{1}{9}=2$.

Table 38. LRNs $R_s$ for $1\le s\le 6$.

LRNs	Elements
$LR\{x_1,y_1\}$	$V({\mathbb{AWB}}_m)-\{x_2,x_3,x_4\}\cup \{y_4,y_5,y_6\}\cup \{z_4,z_5,z_6\}$
$LR\{x_2,y_2\}$	$V({\mathbb{AWB}}_m)-\{x_3,x_4,x_5\}\cup \{y_1,y_5,y_6\}\cup \{z_1,z_5,z_6\}$
$LR\{x_3,y_3\}$	$V({\mathbb{AWB}}_m)-\{x_4,x_5,x_6\}\cup \{y_1,y_2,y_6\}\cup \{z_1,z_2,z_6\}$
$LR\{x_2,y_1\}$	$V({\mathbb{AWB}}_m)-\{x_1,x_5,x_6\}\cup \{y_2,y_3,y_4\}\cup \{z_2,z_3,z_4\}$
$LR\{x_3,y_2\}$	$V({\mathbb{AWB}}_m)-\{x_1,x_2,x_6\}\cup \{y_3,y_4,y_5\}\cup \{z_3,z_4,z_5\}$
$LR\{x_4,y_3\}$	$V({\mathbb{AWB}}_m)-\{x_1,x_2,x_3\}\cup \{y_4,y_5,y_6\}\cup \{z_4,z_5,z_6\}$

Table 39. LRNs ${\overline{R}}_y$ for $1\le y\le 3$.

LRNs	Elements
$LR\{x_1,x_2\}$	$V({\mathbb{AWB}}_6)-\{y_1,y_4\}\cup \{z_1,z_4\}$
$LR\{x_2,x_3\}$	$V({\mathbb{AWB}}_6)-\{y_2,y_5\}\cup \{z_2,z_5\}$
$LR\{x_3,x_4\}$	$V({\mathbb{AWB}}_6)-\{y_3,y_6\}\cup \{z_3,z_6\}$

Table 40. LRNs ${\overline{R}}_y$ for $1\le y\le 3$.

LRNs	Elements
$LR\{y_1,y_2\}$	$V({\mathbb{AWB}}_6)-\{x_2,x_5\}$
$LR\{y_2,y_3\}$	$V({\mathbb{AWB}}_6)-\{x_3,x_6\}$
$LR\{y_2,y_3\}$	$V({\mathbb{AWB}}_6)-\{x_1,x_4\}$

Table 41. LRNs ${\overline{R}}_y$ for $1\le y\le 3$.

LRNs	Elements
$LLR\{y_s,z_s\}$	$V({\mathbb{AWB}}_6)$

□

Case II: For any $m\ge 6$:

As we can see from Lemma 6. the LRN with the least cardinality of $\frac{3m}{2}$ is $R_s=LR\{x_s,y_{s-1}\}$, $|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and $|LR\left\{st\right\}\cap {\displaystyle \bigcup _{s=1}^m}{R}_s|\ge |R_s|$∀$\{s,t\}\in V(\mathbb{G})$. Suppose that $\alpha =|{\displaystyle \bigcup _{s=1}^m}{R}_s|=3m$ and $\beta =|R_s|=\frac{3m}{2}$. Then we define a mapping $\mu :V(\mathbb{G})\to [0,1]$ such that

$\mu (v)=\left\{\begin{array}{cc}\frac{1}{\beta }\hfill & \mathrm{for}a\in {\displaystyle \bigcup _{s=1}^m}{R}_s,\hfill \\ 0\hfill & \mathrm{for}a\in V(\mathbb{G})-{\displaystyle \bigcup _{s=1}^m}{R}_s\hfill \end{array}\right.$

It is observed that $\mu$ is a LRF for $\mathbb{G}$ with $m\ge 6$ because $\mu (LR\{st\})\ge 1$∀$s,t\in V(\mathbb{G})$. Assume on the contrary that there exists a different LRF $\gamma$, such that $\gamma (u)\le \mu (u)$, for some $u\in V(\mathbb{G})$ $\gamma (u)\ne \mu (u)$. Consequently, $\gamma (LR\{st\})<1$, where $LR\left\{st\right\}$ is an RN of $\mathbb{G}$ having the least cardinality $\beta$. This shows that $\gamma$ is not a LRF a contradiction. Therefore, $\mu$ is a MRF that attains minimum $|\mu |$ for $\mathbb{G}$. Also, all the $R_s$ are intersecting in pairwise manner, holding non-cyclic behavior with ${\displaystyle \bigcap _{s=1}^m}{R}_s=\varphi$, thus by Theorem 1, assigning $\frac{1}{\beta }$ to the vertices of $\mathbb{G}$ in ${\displaystyle \bigcup _{s=1}^m}{R}_s$ and evaluating the summation of all the weights, we get: $1\le lfdim(\mathbb{G})\le {\displaystyle \sum _{l=1}^{\alpha }}\frac{1}{\beta }=2.$

5. Conclusions

In this article, we have:

• Found the FMD and LFMD of networks called by subdivided QCL, 2-faced web, 3-faced web, and antiprism web networks;
• Since subdivided QCL and 2-faced web networks are bipartite in nature, both thus have $lfdim$ as unity;
• The 3-faced web and antiprism web networks have FMD and LFMD in the interval $[1,2]$;
• The summary of obtained results are shown in Table 42.
  Table 42. Summarized Numerical Results.

  $\mathbb{G}$	$\mathit{fdim}$	$\mathit{lfdim}$	$\underset{\mathit{fdim}\to \mathit{\infty }}{lim}$	$\underset{\mathit{lfdim}\to \mathit{\infty }}{lim}$	Remarks
  ${\mathbb{SQ}}_m$	$[1,\frac{3}{2}]$	1	$3/2$	1	Bounded and Constant
  ${\mathbb{WB}}_m^1$	$[1,\frac{3m}{m+1}]$	1	3	1	Bounded and Constant
  ${\mathbb{WB}}_m^2$	$[1,2]$	$[1,2]$	2	2	Bounded and Constant
  ${\mathbb{WB}}_m^3$	$[1,2]$	$[1,2]$	2	2	Bounded and Constant
  ${\mathbb{AWB}}_m$	$[1,2]$	$[1,2]$	2	2	Bounded and Constant

• The graphical analysis of obtained results at ∞ is shown in Figure 5.
  

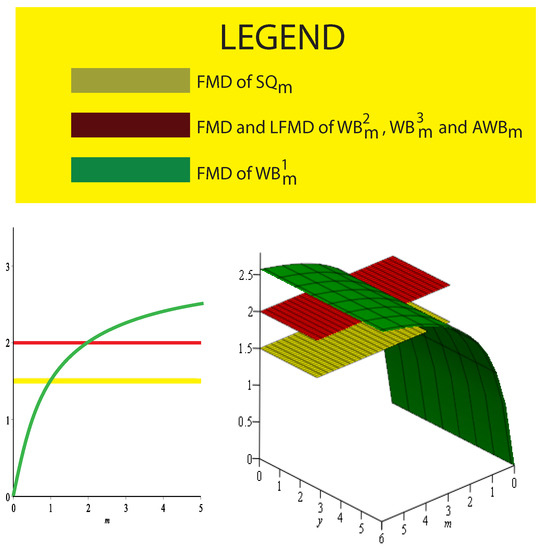  Figure 5. Graphical analysis, 2D (left) and 3D (right).
• The networks under consideration bear rotational symmetry and planarity as well. Moreover, they are non-regular and vertex transitive networks with the attachment of a pendent edge that they can use to help solve the problems related to designing a fire exit plan, computer network, or in chemical strata.
• These results strengthen and prove the tautology of Theorem 1, Theorems 2 and 3 proved in [21,25].
• However, finding the distance-based fractional dimensions of families of networks other than web-related ones is still an open problem.