Monotone Iterative Method for ψ-Caputo Fractional Differential Equation with Nonlinear Boundary Conditions

Abstract

The main contribution of this paper is to prove the existence of extremal solutions for a novel class of $\mathsf{\psi }$-Caputo fractional differential equation with nonlinear boundary conditions. For this purpose, we utilize the well-known monotone iterative technique together with the method of upper and lower solutions. Finally, we provide an example along with graphical representations to confirm the validity of our main results.

1. Introduction

In the mathematical modeling of real life phenomena, the study of fractional differential equations has gained notable importance among interested researchers. It is realized that the use of fractional calculus methods is quite prominent in modeling various processes. The main reason for the widespread use (applications) of fractional operators is the fact that, unlike “integer” operators, these operators possess non-local behavior which enables us to trace the past effects of the involved phenomena [1,2,3,4,5]. Based on some classical approaches, such as Riemann-Liouville, Caputo, and Hadamard fractional operators, there are many new definitions which have attempted to provide a general platform that includes these classical operators [6,7,8]. For the sake of consolidating these different definitions under one single fractional operator, the $\mathsf{\psi }$-fractional operator has been introduced [9,10]. The main feature of the the $\mathsf{\psi }$-fractional operator is that the function in its integral kernel an be adapted to accommodate other definitions when replacing it by specific functions. Other significant features include non-local behavior and the semigroup property which are clearly preserved. It has been recognized that these types of operators have been successfully used to describe and model many real life phenomena; therefore, several related research works have been produced [11,12,13]. Along with the recent developments in fractional differential equations, researchers have contributed many research studies that discus the solutions’ behavior in terms of different types of fractional differential equations [14,15,16,17,18,19,20,21,22,23,24,25,26,27].

There are different types of fractional differential equations involving different fractional operators, which are associated with the various types of initial and boundary conditions that have been investigated by many researchers in various research works [28,29,30]. By exploring the literature, one can figure out that the existence of solutions has been the main target of investigations. In order to prove this, researchers often utilize some fixed point hypothesis along with certain mathematical inequalities. To the best of our observations, the monotone iterative technique combined with the method of upper and lower solutions has not been used to study the existence of solutions for $\mathsf{\psi }$-Caputo fractional differential equation with nonlinear boundary conditions. For more expository details on monotone iterative method, the readers can consult some interesting research works [31,32,33,34,35].

Oriented by the above discussion, we study the following $\mathsf{\psi }$-Caputo fractional differential equation (CpFDE) with nonlinear boundary conditions:

$$\left\{\begin{array}{c}{{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right)\mathfrak{z}\left(\vartheta \right)=\mathbb{F}\left(\vartheta ,\mathfrak{z}\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\left(\vartheta \right)\right),\hfill \\ \mathbb{H}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(b\right)\right)=0,\mathbb{G}(\mathfrak{z}\left(a\right),\mathfrak{z}\left(b\right))=0,\hfill \end{array}\right.$$

(1)

for $\vartheta \in \mathrm{\Omega }:= [a,b]$, where ${{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}$ and ${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}$ denote the $\mathsf{\psi }$-Caputo fractional derivatives of order $\tau$ and $\lambda$, respectively, such that $\tau$, $\lambda \in (0,1]$, $\sigma >0$, $\mathbb{F}\in C(\mathrm{\Omega }\times {\mathbb{R}}^2,\mathbb{R})$, $\mathbb{G}$, $\mathbb{H}\in C({\mathbb{R}}^2,\mathbb{R})$. It is worth mentioning here that, unlike the above mentioned relevant works, the CpFDE (1) is subject to nonlinear boundary conditions. The above equation is the deterministic fractional differential equation, therefore, a fractional differential equation with its deterministic solution is only considered in this work without the involvement of any random processes.

The remaining part of the paper is organized as follows: In Section 2, we present some definitions and lemmas that will be used to prove our results. In Section 3, we prove our main results, which conveys the existence of extremal solutions for CpFDE (1). For this purpose, we use the monotone iterative method together with the technique of upper and lower solutions. In Section 4, we apply our results by providing an example and illustrate the solutions of behavior graphically.

2. Relevant Preliminaries

In the current section, we state some basic concepts of fractional calculus that are related to our work. Let $\mathrm{\Omega }=[a,b]$, $0\le a<b<\infty$ be a finite interval and $\mathsf{\psi }:\mathrm{\Omega }\to \mathbb{R}$ be an increasing differentiable function such that ${\mathsf{\psi }}^{\prime }\left(\vartheta \right)\ne 0$, for all $\vartheta \in \mathrm{\Omega }$.

Definition 1

([9]). The Riemann–Lebesgue (RL) fractional integral of order $\tau >0$ for an integrable function $\mathfrak{z}:\mathrm{\Omega }\to \mathbb{R}$ with respect to $\mathsf{\psi }$ is described by the following:

$${\mathbb{I}}_{a^{+}}^{\tau ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)=\frac{1}{\mathrm{\Gamma }\left(\tau \right)}{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right){\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right)\right)}^{\tau -1}\mathfrak{z}\left(\eta \right)\mathrm{d}\eta ,$$

(2)

where $\mathrm{\Gamma }\left(\tau \right)={\int }_0^{+\infty }{\vartheta }^{\tau -1}{e}^{-\vartheta }\mathrm{d}\vartheta$, $\tau >0$ is the Gamma function.

Definition 2

([9]). Let $\mathsf{\psi }$, $\mathfrak{z}$$\in C^n(\mathrm{\Omega },\mathbb{R})$. The RL fractional derivative of a function $\mathfrak{z}$ of order $n-1<\tau <n$ with respect to $\mathsf{\psi }$ is given by the following:

$$\begin{array}{cc}\hfill {\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)& ={\left(\frac{D_{\vartheta }}{{\mathsf{\psi }}^{\prime }\left(\vartheta \right)}\right)}^n{\mathbb{I}}_{a^{+}}^{n-\tau ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)\hfill \\ \hfill & =\frac{1}{\mathrm{\Gamma }(n-\tau )}{\left(\frac{D_{\vartheta }}{{\mathsf{\psi }}^{\prime }\left(\vartheta \right)}\right)}^n{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right){\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right)\right)}^{n-\tau -1}\mathfrak{z}\left(\eta \right)\mathrm{d}\eta ,\hfill \end{array}$$

where $n=\left[\tau \right]+1$, $n\in \mathbb{N}$ and $D_{\vartheta }=\frac{\mathrm{d}}{\mathrm{d}\vartheta }$.

Definition 3

([9]). Let $\mathsf{\psi }$, $\mathfrak{z}\in C^n(\mathrm{\Omega },\mathbb{R})$. The Caputo fractional derivative of $\mathfrak{z}$ of order $n-1<\tau <n$ with respect to $\mathsf{\psi }$ is defined by the following

$${{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)={\mathbb{I}}_{a^{+}}^{n-\tau ;\mathsf{\psi }}{\mathfrak{z}}_{\mathsf{\psi }}^{\left[n\right]}\left(\vartheta \right),$$

where $n=\left[\tau \right]+1$ for $\tau \notin \mathbb{N}$, $n=\tau$ for $\tau \in \mathbb{N}$ and ${\mathfrak{z}}_{\mathsf{\psi }}^{\left[n\right]}\left(\vartheta \right)={\left(\frac{D_{\vartheta }}{{\mathsf{\psi }}^{\prime }\left(\vartheta \right)}\right)}^n\mathfrak{z}\left(\vartheta \right)$. From the definition, it is clear that the following is the case.

$${{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)=\left\{\begin{array}{cc}{\displaystyle {\int }_a^{\vartheta }\frac{{\mathsf{\psi }}^{\prime }\left(\eta \right){\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right)\right)}^{n-\tau -1}}{\mathrm{\Gamma }(n-\tau )}{\mathfrak{z}}_{\mathsf{\psi }}^{\left[n\right]}\left(\eta \right)\mathrm{d}\eta ,}\hfill & \tau \notin \mathbb{N},\hfill \\ {\displaystyle {\mathfrak{z}}_{\mathsf{\psi }}^{\left[n\right]}\left(\vartheta \right),}\hfill & \tau \in \mathbb{N}.\hfill \end{array}\right.$$

(3)

Some basic properties of the $\mathsf{\psi }$-fractional operators are listed in the following Lemma.

Lemma 1

([9]). Let τ, $\lambda >0$, and $\mathfrak{z}\in C(\mathrm{\Omega },\mathbb{R})$. Then for each $\vartheta \in \mathrm{\Omega }$, we have the following.

•  ${{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}{\mathbb{I}}_{a^{+}}^{\tau ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)=\mathfrak{z}\left(\vartheta \right)$,
•  ${\mathbb{I}}_{a^{+}}^{\tau ;\mathsf{\psi }}{{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)=\mathfrak{z}\left(\vartheta \right)-\mathfrak{z}\left(a\right)$ for $0<\tau \le 1$,
•  ${\mathbb{I}}_{a^{+}}^{\tau ;\mathsf{\psi }}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda -1}=\frac{\mathrm{\Gamma }\left(\lambda \right)}{\mathrm{\Gamma }(\lambda +\tau )}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda +\tau -1}$,
•  ${{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda -1}=\frac{\mathrm{\Gamma }\left(\lambda \right)}{\mathrm{\Gamma }(\lambda -\tau )}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda -\tau -1}$,
•  ${{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^k=0$, for all $k\in \{0,\dots ,n-1\}$, $n\ge 1$.

Definition 4

([36]). The Mittag–Leffler functions (MLFs) of one and two parameters are given by:

$${\mathbb{E}}_{\nu }\left(\varpi \right)=\sum _{k=0}^{\infty }\frac{{\varpi }^k}{\mathrm{\Gamma }(\nu k+1)},(\varpi \in \mathbb{R},\nu >0),$$

(4)

and

$${\mathbb{E}}_{\nu ,\lambda }\left(\varpi \right)=\sum _{k=0}^{\infty }\frac{{\varpi }^k}{\mathrm{\Gamma }(\nu k+\lambda )},(\nu ,\lambda >0,\varpi \in \mathbb{R}),$$

(5)

respectively. It is obvious that ${\mathbb{E}}_{1,1}\left(\varpi \right)={\mathbb{E}}_1\left(\varpi \right)=e^{\varpi }$.

We denote the set $\mathbb{X}$ by the following.

$$\mathbb{X}=C^{\lambda }\left(\mathrm{\Omega }\right)=\left\{x:{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}x\left(\xi \right)\in C\left(\mathrm{\Omega }\right)\right\}.$$

Equipped with the norm, we have the following:

$${\parallel x\parallel }_{\mathbb{X}}={\parallel x\parallel }_{\infty }+{∥{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}x∥}_{\infty },$$

where ${\parallel x\parallel }_{\infty }={max}_{\xi \in \mathrm{\Omega }}\left|x\right(\xi \left)\right|$ and one can conclude that $(\mathbb{X},\parallel ·{\parallel }_{\mathbb{X}})$ is a Banach space.

Lemma 2.

For a given $\ell \in C(\mathrm{\Omega },\mathbb{R})$, $\lambda ,\tau \in (0,1]$ and $\sigma >0$, the linear fractional initial value problem is as follows:

$$\left\{\begin{array}{c}{{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right)\mathfrak{z}\left(\vartheta \right)=\ell \left(\vartheta \right),\hfill \\ {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(a\right)={\mathfrak{z}}_{\lambda },\mathfrak{z}\left(a\right)={\mathfrak{z}}_a,\hfill \end{array}\right.$$

(6)

for $\vartheta \in \mathrm{\Omega }$ is equivalent to the following Volterra integral equation.

$$\mathfrak{z}\left(\vartheta \right)={\mathfrak{z}}_a+\frac{{\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a}{\mathrm{\Gamma }(\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }+\sigma {\mathbb{I}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)+{\mathbb{I}}_{a^{+}}^{\tau +\lambda ;\mathsf{\psi }}\ell \left(\vartheta \right).$$

(7)

Moreover, the explicit solution of the Volterra integral Equation (7) can be represented by the following.

$$\begin{array}{cc}\hfill \mathfrak{z}\left(\vartheta \right)=& {\mathfrak{z}}_a+{\mathfrak{z}}_{\lambda }{\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right)\right)}^{\lambda }{\mathbb{E}}_{\lambda ,\lambda +1}\left(\sigma {\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right)\right)}^{\lambda }\right)\hfill \\ \hfill & +{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right){\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right)\right)}^{\lambda +\tau -1}\hfill \\ \hfill & \times {\mathbb{E}}_{\lambda ,\lambda +\tau }\left(\sigma {\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right)\right)}^{\lambda }\right)\ell \left(\eta \right)\mathrm{d}\eta .\hfill \end{array}$$

(8)

Proof. 

Applying the $\mathsf{\psi }$-Riemann-Liouville fractional integral of order $\tau$ to both sides of (6) and by using Lemma 1, we obtain the following.

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)={\mathfrak{z}}_{\lambda }+\sigma (\mathfrak{z}\left(\vartheta \right)-{\mathfrak{z}}_a)+{\mathbb{I}}_{a^{+}}^{\tau ;\mathsf{\psi }}\ell \left(\vartheta \right).$$

(9)

Hence, we have the following.

$$\mathfrak{z}\left(\vartheta \right)={\mathfrak{z}}_a+\frac{{\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a}{\mathrm{\Gamma }(\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }+\sigma {\mathbb{I}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)+{\mathbb{I}}_{a^{+}}^{\tau +\lambda ;\mathsf{\psi }}\ell \left(\vartheta \right).$$

(10)

The converse can be proven by direct computation. Now, we apply the method of successive approximations in order to prove that the integral Equation (7) can be expressed by the following.

$$\begin{array}{cc}\hfill \mathfrak{z}\left(\vartheta \right)=& {\mathfrak{z}}_a+{\mathfrak{z}}_{\lambda }{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }{\mathbb{E}}_{\lambda ,\lambda +1}\left(\sigma {(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }\right)\hfill \\ \hfill & +{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right){(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{\lambda +\tau -1}\hfill \\ \hfill & \times {\mathbb{E}}_{\lambda ,\lambda +\tau }\left(\sigma {(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{\lambda }\right)\ell \left(\eta \right)\mathrm{d}\eta .\hfill \end{array}$$

For this, we set the following.

$$\left\{\begin{array}{c}{\displaystyle {\mathfrak{z}}_0\left(\vartheta \right)={\mathfrak{z}}_a+\frac{{\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a}{\mathrm{\Gamma }(\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda },}\hfill \\ {\displaystyle {\mathfrak{z}}_m\left(\vartheta \right)={\mathfrak{z}}_0\left(\vartheta \right)+\sigma {\mathbb{I}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_{m-1}\left(\vartheta \right)+{\mathbb{I}}_{a^{+}}^{\tau +\lambda ;\mathsf{\psi }}\ell \left(\vartheta \right).}\hfill \end{array}\right.$$

(11)

It follows from Equation (11) and Lemma 1 that the following is the case.

$$\begin{array}{cc}\hfill {\mathfrak{z}}_1\left(\vartheta \right)& ={\mathfrak{z}}_0\left(\vartheta \right)+\sigma {\mathbb{I}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right)+{\mathbb{I}}_{a^{+}}^{\lambda +\tau ;\mathsf{\psi }}\ell \left(\vartheta \right)\hfill \\ \hfill & {\displaystyle ={\mathfrak{z}}_a+\frac{{\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a}{\mathrm{\Gamma }(\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }+\sigma \frac{{\mathfrak{z}}_a}{\mathrm{\Gamma }(\lambda +1)}{\left[\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right)\right]}^{\lambda }}\hfill \\ \hfill & +\sigma \frac{{\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a}{\mathrm{\Gamma }(2\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{2\lambda }+{\mathbb{I}}_{a^{+}}^{\lambda +\tau ;\mathsf{\psi }}\ell \left(\vartheta \right).\hfill \end{array}$$

(12)

Similarly, Equations (11) and (12) and Lemma 1 yield the following.

$$\begin{array}{cc}\hfill {\mathfrak{z}}_2\left(\vartheta \right)& ={\mathfrak{z}}_0\left(\vartheta \right)+\sigma {\mathbb{I}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(\vartheta \right)+{\mathbb{I}}_{a^{+}}^{\lambda +\tau ;\mathsf{\psi }}\ell \left(\vartheta \right)\hfill \\ \hfill & ={\mathfrak{z}}_a+\frac{{\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a}{\mathrm{\Gamma }(\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }\hfill \\ \hfill & +\sigma {\mathbb{I}}_{a^{+}}^{\lambda ;\mathsf{\psi }}({\mathfrak{z}}_a+\frac{{\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a}{\mathrm{\Gamma }(\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }\hfill \\ \hfill & +\sigma \frac{{\mathfrak{z}}_a}{\mathrm{\Gamma }(\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }+\sigma \frac{{\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a}{\mathrm{\Gamma }(2\lambda +1)}(\mathsf{\psi }\left(\vartheta \right)\hfill \\ \hfill & {-\mathsf{\psi }\left(a\right))}^{2\lambda }+{\mathbb{I}}_{a^{+}}^{\lambda +\tau ;\mathsf{\psi }}\ell \left(\vartheta \right))+{\mathbb{I}}_{a^{+}}^{\lambda +\tau ;\mathsf{\psi }}\ell \left(\vartheta \right)\hfill \\ \hfill & ={\mathfrak{z}}_a+\sum _{k=0}^2\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{k\lambda }\hfill \\ \hfill & +({\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a)\sum _{k=0}^2\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\mathsf{\psi }\left(a\right))}^{k\lambda +\lambda }\hfill \\ \hfill & +\sigma {\mathbb{I}}_{a^{+}}^{2\lambda +\tau ;\mathsf{\psi }}\ell \left(\vartheta \right)+I_{a^{+}}^{\lambda +\tau ;\mathsf{\psi }}\ell \left(\vartheta \right)\hfill \\ \hfill & ={\mathfrak{z}}_a+\sum _{k=0}^2\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{k\lambda }\hfill \\ \hfill & +({\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a)\sum _{k=0}^2\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{k\lambda +\lambda }\hfill \\ \hfill & +{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right)\sum _{k=1}^2\frac{{\sigma }^{k-1}{\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right)\right)}^{k\lambda +\tau -1}}{\mathrm{\Gamma }(k\lambda +\tau )}\ell \left(\eta \right)\mathrm{d}\eta .\hfill \end{array}$$

In continuing this process, we derive the following relation.

$$\begin{array}{cc}\hfill {\mathfrak{z}}_m\left(\vartheta \right)& ={\mathfrak{z}}_a+\sum _{k=0}^m\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{k\lambda }\hfill \\ \hfill & +({\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a)\sum _{k=0}^m\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{k\lambda +\lambda }\hfill \\ \hfill & +{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right)\sum _{k=1}^m\frac{{\sigma }^{k-1}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{k\lambda +\tau -1}}{\mathrm{\Gamma }(k\lambda +\tau )}\ell \left(\eta \right)\mathrm{d}\eta \hfill \\ \hfill & ={\mathfrak{z}}_a+\sum _{k=0}^m\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{k\lambda }\hfill \\ \hfill & +\frac{({\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a)}{\sigma }\sum _{k=1}^m\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{k\lambda }\hfill \\ \hfill & +{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right){(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{\lambda +\tau -1}\sum _{k=1}^m\frac{{\sigma }^{k-1}{\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right)\right)}^{k\lambda -\lambda }}{\mathrm{\Gamma }(k\lambda +\tau )}\ell \left(\eta \right)\mathrm{d}\eta .\hfill \end{array}$$

Taking the limit as $m\to \infty$, we obtain the following explicit solution $\mathfrak{z}\left(\vartheta \right)$ of the integral Equation (7).

$$\begin{array}{cc}\hfill \mathfrak{z}\left(\vartheta \right)& ={\mathfrak{z}}_a+\sum _{k=0}^{\infty }\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{k\lambda }\hfill \\ \hfill & +\frac{({\mathfrak{z}}_{\lambda }-\sigma {\mathfrak{z}}_a)}{\sigma }\sum _{k=1}^{\infty }\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{k\lambda }\hfill \\ \hfill & +{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right){(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{\lambda +\tau -1}\sum _{k=0}^{\infty }\frac{{\sigma }^k{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{k\lambda }}{\mathrm{\Gamma }(k\lambda +\lambda +\tau )}\ell \left(\eta \right)\mathrm{d}\eta \hfill \\ \hfill & ={\mathfrak{z}}_a+\frac{{\mathfrak{z}}_{\lambda }}{\sigma }\sum _{k=1}^{\infty }\frac{{\sigma }^k}{\mathrm{\Gamma }(k\lambda +1)}{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{k\lambda }\hfill \\ \hfill & +{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right){(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{\lambda +\tau -1}{\mathbb{E}}_{\lambda ,\lambda +\tau }\left(\sigma {(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{\lambda }\right)\ell \left(\eta \right)\mathrm{d}\eta \hfill \\ \hfill & ={\mathfrak{z}}_a+{\mathfrak{z}}_{\lambda }{(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }{\mathbb{E}}_{\lambda ,\lambda +1}\left(\sigma {(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }\right)\hfill \\ \hfill & +{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right){(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{\lambda +\tau -1}{\mathbb{E}}_{\lambda ,\lambda +\tau }\left(\sigma {(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{\lambda }\right)\ell \left(\eta \right)\mathrm{d}\eta .\hfill \end{array}$$

Then, the proof is completed. □

Lemma 3

(Comparison Result). Let λ, $\tau \in (0,1]$, and $\sigma >0$. If $\Delta \in C(\mathrm{\Omega },\mathbb{R})$ fulfills the following inequalities:

$$\left\{\begin{array}{cc}{{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right)\Delta \left(\vartheta \right)\ge 0,\hfill & \vartheta \in (a,b],\hfill \\ \Delta \left(a\right)\ge 0,{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\Delta \left(a\right)\ge 0,\hfill \end{array}\right.$$

then $\Delta \left(\vartheta \right)\ge 0$ and ${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\Delta \left(\vartheta \right)\ge 0$ for all $\vartheta \in \mathrm{\Omega }$.

Proof. 

Since ${\mathbb{E}}_{{\rho }_1,{\rho }_2}\left(x\right)\ge 0$ for ${\rho }_1\in (0,1]$, ${\rho }_2\ge {\rho }_1$, $x\in \mathbb{R}$, we allow the following:

$$\ell \left(\vartheta \right)={{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right)\Delta \left(\vartheta \right)\ge 0,$$

$\Delta \left(a\right)={\mathfrak{z}}_a\ge 0$ and ${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\Delta \left(a\right)={\mathfrak{z}}_{\lambda }\ge 0$ in Lemma 2. Then, it follows by Equations (8) and (9) that the conclusion of Lemma 3 holds. □

Let $(\mathcal{X},\mathcal{T})$ be a topological Hausdorff space and $g_1,g_2:\mathcal{X}\to \mathbb{R}$ be a lower semi-continuous function and an upper semi-continuous function, respectively. This means that for every $r\in \mathbb{R}$, the subsets of the following:

$$\left\{g_1>r\right\}:= \left\{x\in \mathcal{X}:g_1\left(x\right)>r\right\},\left\{g_2<r\right\}:= \left\{x\in \mathcal{X}:g_2\left(x\right)<r\right\},$$

are open in $\mathcal{X}$. Suppose that $g_1\left(x\right)\le g_2\left(x\right)$ for all $x\in \mathcal{X}$ and we allow the interval $[g_1,g_2]$ consist of those upper or lower semi-continuous functions $h:\mathcal{X}\to \mathbb{R}$ such that $g_1\left(x\right)\le h\left(x\right)\le g_2\left(x\right)$ for all $x\in \mathcal{X}$. Let $\mathrm{\Omega }:[g_1,g_2]\to [g_1,g_2]$ be a monotone mapping in the sense that $g_1\le h_1\le h_2\le g_2$ implies $g_1\le \mathrm{\Omega }\left(h_1\right)\le \mathrm{\Omega }\left(h_2\right)\le g_2$. In addition, suppose that the sequence ${\left\{\mathrm{\Omega }\left(h_n\right)\right\}}_{n\in \mathbb{N}}\subset [g_1,g_2]$ consist of lower semi-continuous functions that increase pointwise to $\mathrm{\Omega }\left(h\right)$ whenever the sequence ${\left\{h_n\right\}}_{n\in \mathbb{N}}\subset [g_1,g_2]$ consist of lower semi-continuous functions that increase pointwise to h. A similar assumption is made when the sequence ${\left\{h_n\right\}}_{n\in \mathbb{N}}\subset [g_1,g_2]$ consist of upper semi-continuous functions, which decreases pointwise to $h\in [g_1,g_2]$. In particular, assume that $\mathrm{\Omega }\left(h\right)$ is lower semi-continuous whenever h is lower semi-continuous and that $\mathrm{\Omega }\left(h\right)$ is upper semi-continuous whenever h is so. Then for every $n\in \mathbb{N}$, we have the following.

$$g_1\le {\mathrm{\Omega }}^n\left(g_1\right)\le {\mathrm{\Omega }}^{n+1}\left(g_1\right)\le {\mathrm{\Omega }}^{n+1}\left(g_2\right)\le {\mathrm{\Omega }}^n\left(g_2\right)\le g_2.$$

Substitute ${\omega }_1={sup}_{n\in \mathbb{N}}{\mathrm{\Omega }}^n\left(g_1\right)$ and ${\omega }_2={sup}_{n\in \mathbb{N}}{\mathrm{\Omega }}^n\left(g_2\right)$. Then, ${\omega }_1$ and ${\omega }_2$ belong to the interval $[g_1,g_2]$, the function ${\omega }_1$ is lower semi-continuous, the function ${\omega }_2$ is upper semi-continuous, and the equalities $\mathrm{\Omega }\left({\omega }_1\right)={\omega }_1$ and $\mathrm{\Omega }\left({\omega }_2\right)={\omega }_2$ are valid. If the monotone mapping $\mathrm{\Omega }$ has at most one fixed point, then ${\omega }_1={\omega }_2=\mathrm{\Omega }\left({\omega }_1\right)=\mathrm{\Omega }\left({\omega }_2\right)$ is a continuous function. When the mapping $\mathrm{\Omega }:[g_1,g_2]\to [g_1,g_2]$ does not posses this sequential continuity property, then one needs a more subtle version of the Tarski–Knaster fixed point theorem. More precisely, define the functions $h_{prefix}$ and $h_{postfix}$, respectively, by the following:

$$h_{\mathrm{prefix}}=inf \left\{h\in [g_1,g_2]\mathrm{\Omega }\left(h\right)\le h,h\mathrm{is}\mathrm{upper}\mathrm{semi-continuous}\right\},$$

and the following.

$$h_{\mathrm{postfix}}=sup \left\{h\in [g_1,g_2]\mathrm{\Omega }\left(h\right)\ge h,h\mathrm{is}\mathrm{lower}\mathrm{semi-continuous}\right\}.$$

Then, we obtain the following.

$$\mathrm{\Omega }\left(h_{\mathrm{prefix}}\right)=h_{\mathrm{prefix}}\le \underset{n\in \mathbb{N}}{inf}{\mathrm{\Omega }}^n\left(g_2\right),\mathrm{\Omega }\left(h_{\mathrm{postfix}}\right)=h_{\mathrm{postfix}}\ge \underset{n\in \mathbb{N}}{sup}{\mathrm{\Omega }}^n\left(g_1\right).$$

Moreover, the function $h_{\mathrm{prefix}}$ is upper semi-continuous and the function $h_{\mathrm{postfix}}$ is lower semi-continuous. Consequently, if $\mathrm{\Omega }$ has at most one fixed point, then

$$\mathrm{\Omega }\left(h_{\mathrm{prefix}}\right)=h_{\mathrm{prefix}}=\mathrm{\Omega }\left(h_{\mathrm{postfix}}\right)=h_{\mathrm{postfix}},$$

and, therefore, this unique fixed point is a continuous function.

3. Main Results

In this section, we prove the existence of extremal solutions for problem (1). Before proceeding, we provide the definitions of lower and upper solutions of the problem (1).

Definition 5.

A function ${\mathfrak{z}}_0\in \mathbb{X}$ is called a lower solution of (1), if it satisfies the following:

$$\left\{\begin{array}{c}{{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right){\mathfrak{z}}_0\left(\vartheta \right)\le \mathbb{F}\left(\vartheta ,{\mathfrak{z}}_0\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right)\right),\hfill \\ \mathbb{H}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(b\right)\right)\le 0,\mathbb{G}\left({\mathfrak{z}}_0\left(a\right),{\mathfrak{z}}_0\left(b\right)\right)\le 0,\hfill \end{array}\right.$$

for $\vartheta \in \mathrm{\Omega }$.

Definition 6.

A function ${\tilde{\mathfrak{z}}}_0\in \mathbb{X}$ is called an upper solution of (1), if it satisfies the following:

$$\left\{\begin{array}{c}{{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right){\tilde{\mathfrak{z}}}_0\left(\vartheta \right)\ge \mathbb{F}\left(\vartheta ,{\tilde{\mathfrak{z}}}_0\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(\vartheta \right)\right),\hfill \\ \mathbb{H}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(b\right)\right)\ge 0,\mathbb{G}\left({\tilde{\mathfrak{z}}}_0\left(a\right),{\tilde{\mathfrak{z}}}_0\left(b\right)\right)\ge 0,\hfill \end{array}\right.$$

for each $\vartheta \in \mathrm{\Omega }$.

Theorem 1.

Let $\mathbb{F}:\mathrm{\Omega }\times {\mathbb{R}}^2\to \mathbb{R}$ be a continuous function such that the following assumptions hold:

(H1) 

There exist ${\mathfrak{z}}_0$ and ${\tilde{\mathfrak{z}}}_0$ as lower and upper solutions of (1) in $\mathbb{X}$, respectively, with ${\mathfrak{z}}_0\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_0\left(\vartheta \right)$ and;

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(\vartheta \right),\vartheta \in \mathrm{\Omega }.$$

(H2) 

$\mathbb{F}$ satisfies the following condition:

$$\mathbb{F}(\vartheta ,y\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}y\left(\vartheta \right))\le \mathbb{F}(\vartheta ,\mathfrak{z}\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)),$$

for $y_0\left(\vartheta \right)\le y\left(\vartheta \right)\le \mathfrak{z}\left(\vartheta \right)\le {\mathfrak{z}}_0\left(\vartheta \right)$ and the following:

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{y}_0\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}y\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right),$$

for each $\vartheta \in \mathrm{\Omega }$.

(H3) 

There exist constants $c>0$ and $d\ge 0$, such that for ${\mathfrak{z}}_0\left(a\right)\le {\xi }_1\le {\xi }_2\le {\tilde{\mathfrak{z}}}_0\left(a\right)$ and ${\mathfrak{z}}_0\left(b\right)\le {\zeta }_1\le {\zeta }_2\le {\tilde{\mathfrak{z}}}_0\left(b\right)$,

$$\mathbb{G}({\xi }_2,{\zeta }_2)-\mathbb{G}({\xi }_1,{\zeta }_1)\le c({\xi }_2-{\xi }_1)-d({\zeta }_2-{\zeta }_1).$$

(H4) 

There exist constants $e>0$ and $f\ge 0$, such that for the following:

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(a\right)\le {\xi }_1\le {\xi }_2\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(a\right),$$

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(b\right)\le {\zeta }_1\le {\zeta }_2\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(b\right),$$

and the following obtains.

$$\mathbb{H}({\xi }_2,{\zeta }_2)-\mathbb{H}({\xi }_1,{\zeta }_1)\le e({\xi }_2-{\xi }_1)-f({\zeta }_2-{\zeta }_1).$$

Then, there exist monotone iterative sequences $\left\{{\mathfrak{z}}_n\right\}$ and $\left\{{\tilde{\mathfrak{z}}}_n\right\}$,which converge uniformly on Ω to the extremal solutions of (1) in the sector $[{\mathfrak{z}}_0,{\tilde{\mathfrak{z}}}_0]$, where

$$\left[{\mathfrak{z}}_0,{\tilde{\mathfrak{z}}}_0\right]=\left\{\mathfrak{z}\in \mathbb{X}:{\mathfrak{z}}_0\left(\vartheta \right)\le \mathfrak{z}\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_0\left(\vartheta \right),\vartheta \in \mathrm{\Omega }\right\}.$$

Proof. 

For any ${\mathfrak{z}}_0,{\tilde{\mathfrak{z}}}_0\in \mathbb{X}$, we define the following:

$$\left\{\begin{array}{cc}{{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right){\mathfrak{z}}_{n+1}\left(\vartheta \right)=\mathbb{F}\left(\vartheta ,{\mathfrak{z}}_n\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(\vartheta \right)\right),\hfill & \vartheta \in \mathrm{\Omega },\hfill \\ {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_{n+1}\left(a\right)={{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(a\right)-\frac{1}{e}\mathbb{H}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(b\right)\right),\hfill & \\ {\mathfrak{z}}_{n+1}\left(a\right)={\mathfrak{z}}_n\left(a\right)-\frac{1}{c}\mathbb{G}\left({\mathfrak{z}}_n\left(a\right),{\mathfrak{z}}_n\left(b\right)\right),\hfill \end{array}\right.$$

(13)

and the following as well.

$$\left\{\begin{array}{cc}{{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right){\tilde{\mathfrak{z}}}_{n+1}\left(\vartheta \right)=\mathbb{F}\left(\vartheta ,{\tilde{\mathfrak{z}}}_n\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(\vartheta \right)\right),\hfill & \vartheta \in \mathrm{\Omega },\hfill \\ {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_{n+1}\left(a\right)={{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(a\right)-\frac{1}{e}\mathbb{H}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(b\right)\right),\hfill & \\ {\tilde{\mathfrak{z}}}_{n+1}\left(a\right)={\tilde{\mathfrak{z}}}_n\left(a\right)-\frac{1}{c}\mathbb{G}\left({\tilde{\mathfrak{z}}}_n\left(a\right),{\tilde{\mathfrak{z}}}_n\left(b\right)\right).\hfill \end{array}\right.$$

(14)

By Lemma 2, we know that (13) and (14) have unique solutions in $\mathbb{X}$ that are the following.

$$\begin{array}{cc}\hfill {\mathfrak{z}}_{n+1}\left(\vartheta \right)& ={\mathfrak{z}}_n\left(a\right)-\frac{1}{c}\mathbb{G}\left({\mathfrak{z}}_n\left(a\right),{\mathfrak{z}}_n\left(b\right)\right)\hfill \\ \hfill & +\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(a\right)-\frac{1}{e}\mathbb{H}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(b\right)\right)\right)\hfill \\ \hfill & \times {(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }{\mathbb{E}}_{\lambda ,\lambda +1}\left(\sigma {(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }\right)\hfill \\ \hfill & +{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right){\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right)\right)}^{\lambda +\tau -1}\hfill \\ \hfill & \times {\mathbb{E}}_{\lambda ,\lambda +\tau }\left(\sigma {\left(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right)\right)}^{\lambda }\right)\mathbb{F}\left(\eta ,{\mathfrak{z}}_n\left(\eta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(\eta \right)\right)\mathrm{d}\eta ,\hfill \\ \hfill {\tilde{\mathfrak{z}}}_{n+1}\left(\vartheta \right)& ={\tilde{\mathfrak{z}}}_n\left(a\right)-\frac{1}{c}\mathbb{G}\left({\tilde{\mathfrak{z}}}_n\left(a\right),{\tilde{\mathfrak{z}}}_n\left(b\right)\right)\hfill \\ \hfill & +\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(a\right)-\frac{1}{e}\mathbb{H}({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(b\right))\right)\hfill \\ \hfill & \times {(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }{\mathbb{E}}_{\lambda ,\lambda +1}\left(\sigma {(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(a\right))}^{\lambda }\right)\hfill \\ \hfill & +{\int }_a^{\vartheta }{\mathsf{\psi }}^{\prime }\left(\eta \right){(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{\lambda +\tau -1}\hfill \\ \hfill & \times {\mathbb{E}}_{\lambda ,\lambda +\tau }\left(\sigma {(\mathsf{\psi }\left(\vartheta \right)-\mathsf{\psi }\left(\eta \right))}^{\lambda }\right)\mathbb{F}\left(\eta ,{\tilde{\mathfrak{z}}}_n\left(\eta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(\eta \right)\right)\mathrm{d}\eta .\hfill \end{array}$$

First, we show that the sequences ${\mathfrak{z}}_n\left(\vartheta \right)$ and ${\tilde{\mathfrak{z}}}_n\left(\vartheta \right)(n\ge 1)$ are lower and upper solutions of (1), respectively, and ${\mathfrak{z}}_n\left(\vartheta \right)$ and ${\tilde{\mathfrak{z}}}_n\left(\vartheta \right)(n\ge 1)$ satisfy the following relations:

$${\mathfrak{z}}_0\left(\vartheta \right)\le {\mathfrak{z}}_1\left(\vartheta \right)\le \cdots \le {\mathfrak{z}}_n\left(\vartheta \right)\le \cdots \le {\tilde{\mathfrak{z}}}_n\left(\vartheta \right)\le \cdots \le {\tilde{\mathfrak{z}}}_1\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_0\left(\vartheta \right),$$

(15)

for $\vartheta \in \mathrm{\Omega }$ and the following is the case:

$$\begin{array}{cc}\hfill {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right)& \le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(\vartheta \right)\le \cdots \le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(\vartheta \right)\le \cdots \le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(\vartheta \right)\le \cdots \hfill \\ \hfill & \le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_1\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(\vartheta \right),\hfill \end{array}$$

(16)

for $\vartheta \in \mathrm{\Omega }$, respectively. Now, we show that ${\mathfrak{z}}_0\left(\vartheta \right)\le {\mathfrak{z}}_1\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_1\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_0\left(\vartheta \right)$, for $\vartheta \in \mathrm{\Omega }$ and

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_1\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(\vartheta \right),$$

for each $\vartheta \in \mathrm{\Omega }$. For this end, set $\Delta \left(\vartheta \right)={\mathfrak{z}}_1\left(\vartheta \right)-{\mathfrak{z}}_0\left(\vartheta \right)$. From (13) and Definition 5, we obtain the following.

$$\begin{array}{cc}\hfill {{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right)\Delta \left(\vartheta \right)& ={{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right){\mathfrak{z}}_1\left(\vartheta \right)-{{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right){\mathfrak{z}}_0\left(\vartheta \right)\hfill \\ \hfill & =\mathbb{F}\left(\vartheta ,{\mathfrak{z}}_0\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right)\right)-{{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right){\mathfrak{z}}_0\left(\vartheta \right)\ge 0.\hfill \end{array}$$

Again, this is because the following is the case.

$$\left\{\begin{array}{c}\Delta \left(a\right)=-\frac{1}{c}\mathbb{G}({\mathfrak{z}}_0\left(a\right),{\mathfrak{z}}_0\left(b\right))\ge 0,\hfill \\ {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\Delta \left(a\right)=-\frac{1}{e}\mathbb{H}({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(b\right))\ge 0.\hfill \end{array}\right.$$

Invoking Lemma 3, we obtain $\Delta \left(\vartheta \right)\ge 0$ and ${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\Delta \left(\vartheta \right)\ge 0$ for $\vartheta \in \mathrm{\Omega }$. Thus, ${\mathfrak{z}}_0\left(\vartheta \right)\le {\mathfrak{z}}_1\left(\vartheta \right)$ and the following is the case:

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(\vartheta \right),$$

$\vartheta \in \mathrm{\Omega }$. In a similar manner, we can find that ${\tilde{\mathfrak{z}}}_1\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_0\left(\vartheta \right)$ and the following:

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_1\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(\vartheta \right),$$

$\vartheta \in \mathrm{\Omega }$. Now, let $\Delta \left(\vartheta \right)={\tilde{\mathfrak{z}}}_1\left(\vartheta \right)-{\mathfrak{z}}_1\left(\vartheta \right)$. Using (13) and (14) together with assumptions (H${}_1$)–(H${}_3$) we obtain the following.

$${{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right)\Delta \left(\vartheta \right)=\mathbb{F}\left(\vartheta ,{\tilde{\mathfrak{z}}}_0\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(\vartheta \right)\right)-\mathbb{F}\left(\vartheta ,{\mathfrak{z}}_0\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right)\right)\ge 0.$$

Notice the following inequalities:

$$\begin{array}{cc}\hfill \Delta \left(a\right)& ={\tilde{\mathfrak{z}}}_0\left(a\right)-{\mathfrak{z}}_0\left(a\right)-\frac{1}{c}\left[\mathbb{G}\left({\tilde{\mathfrak{z}}}_0\left(a\right),{\tilde{\mathfrak{z}}}_0\left(b\right)\right)-\mathbb{G}\left({\mathfrak{z}}_0\left(a\right),{\mathfrak{z}}_0\left(b\right)\right)\right]\hfill \\ \hfill & \ge \frac{d}{c}\left({\tilde{\mathfrak{z}}}_0\left(b\right)-{\mathfrak{z}}_0\left(b\right)\right)\ge 0,\hfill \end{array}$$

and the following is the case.

$$\begin{array}{cc}\hfill {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\Delta \left(a\right)& ={{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(a\right)-{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(a\right)\hfill \\ \hfill & -\frac{1}{e}\left[\mathbb{H}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(b\right)\right)-\mathbb{H}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(b\right)\right)\right]\hfill \\ \hfill & \ge \frac{f}{e}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(b\right)-{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(b\right)\right)\ge 0.\hfill \end{array}$$

According to Lemma 3, we obtain ${\mathfrak{z}}_1\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_1\left(\vartheta \right)$ and

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_1\left(\vartheta \right),$$

$\vartheta \in \mathrm{\Omega }$. Next, we show that the functions ${\mathfrak{z}}_1\left(\vartheta \right),{\tilde{\mathfrak{z}}}_1\left(\vartheta \right)$ are a lower and an upper solution of the equation in (1), respectively. Since ${\mathfrak{z}}_0$ and ${\tilde{\mathfrak{z}}}_0$ are lower and upper solutions of (1), by (H${}_2$) and (H${}_3$), it follows that the following is the case:

$$\begin{array}{cc}\hfill {{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right){\mathfrak{z}}_1\left(\vartheta \right)& =\mathbb{F}\left(\vartheta ,{\mathfrak{z}}_0\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right)\right)\le \mathbb{F}\left(\vartheta ,{\mathfrak{z}}_1\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(\vartheta \right)\right)\hfill \\ \hfill \mathbb{G}({\mathfrak{z}}_1\left(a\right),{\mathfrak{z}}_1\left(b\right))& \le \mathbb{G}({\mathfrak{z}}_0\left(a\right),{\mathfrak{z}}_0\left(b\right))+c\left({\mathfrak{z}}_1\left(a\right)-{\mathfrak{z}}_0\left(a\right)\right)-d({\mathfrak{z}}_1\left(b\right)-{\mathfrak{z}}_0\left(b\right))\hfill \\ \hfill & =-d({\mathfrak{z}}_1\left(b\right)-{\mathfrak{z}}_0\left(b\right))\le 0,\hfill \end{array}$$

and the following obtains.

$$\begin{array}{cc}\hfill \mathbb{H}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(b\right)\right)& \le \mathbb{H}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(a\right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(b\right)\right)\hfill \\ \hfill & +e\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(a\right)-{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(a\right)\right)\hfill \\ \hfill & -f({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(b\right)-{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(b\right))\hfill \\ \hfill & =-f({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_1\left(b\right)-{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(b\right))\le 0.\hfill \end{array}$$

Therefore, ${\mathfrak{z}}_1\left(\vartheta \right)$ is a lower solution of (1). Analogously, it can be obtained that ${\tilde{\mathfrak{z}}}_1\left(\vartheta \right)$ is an upper solution of (1). By the above arguments and mathematical induction, we can show that the sequences ${\mathfrak{z}}_n\left(\vartheta \right),{\tilde{\mathfrak{z}}}_n\left(\vartheta \right)$, $(n\ge 1)$ are lower and upper solutions of (1), respectively, and the relations (15) and (16) are true. On the contrary, by employing the earlier arguments, together with Ascoli–Arzela’s Theorem, we can show that the following:

$$\parallel {\mathfrak{z}}_n-{\mathfrak{z}}^{*}{\parallel }_{\mathbb{X}}\to 0,{\parallel {\tilde{\mathfrak{z}}}_n-{\tilde{\mathfrak{z}}}^{*}\parallel }_{\mathbb{X}}\to 0,$$

when $n\to \infty$. Finally, it remains to show that ${\mathfrak{z}}^{*}$ and ${\tilde{\mathfrak{z}}}^{*}$ are extremal solutions of (1) in $[{\mathfrak{z}}_0,{\tilde{\mathfrak{z}}}_0]$. To conduct this, let $\mathfrak{z}\in [{\mathfrak{z}}_0,{\tilde{\mathfrak{z}}}_0]$ be any solution of (1). Suppose for some $n\in {\mathbb{N}}^{*}$ that the following is the case:

$${\mathfrak{z}}_n\left(\vartheta \right)\le \mathfrak{z}\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_n\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(\vartheta \right),$$

(17)

for $\vartheta \in \mathrm{\Omega }$. Setting $\Delta \left(\vartheta \right)=\mathfrak{z}\left(\vartheta \right)-{\mathfrak{z}}_{n+1}\left(\vartheta \right)$. It follows that the following obtains.

$${{}^c\mathbb{D}}_{a^{+}}^{\tau ;\mathsf{\psi }}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}-\sigma \right)\Delta \left(\vartheta \right)=\mathbb{F}\left(\vartheta ,\mathfrak{z}\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)\right)-\mathbb{F}\left(\vartheta ,{\mathfrak{z}}_n\left(\vartheta \right),{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(\vartheta \right)\right)\ge 0.$$

Notice the inequalities in the following:

$$\begin{array}{cc}\hfill {\mathfrak{z}}_{n+1}\left(a\right)& ={\mathfrak{z}}_n\left(a\right)+\frac{1}{c}\left[\mathbb{G}(\mathfrak{z}\left(a\right),\mathfrak{z}\left(b\right))-\mathbb{G}({\mathfrak{z}}_n\left(a\right),{\mathfrak{z}}_n\left(b\right))\right]\hfill \\ \hfill & \le \mathfrak{z}\left(a\right)-\frac{d}{c}\left(\mathfrak{z}\left(b\right)-{\mathfrak{z}}_n\left(b\right)\right)\hfill \\ \hfill & \le \mathfrak{z}\left(a\right),\hfill \end{array}$$

and the following.

$$\begin{array}{cc}\hfill {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_{n+1}\left(a\right)& ={{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(a\right)+\frac{1}{e}\left[\mathbb{H}\left(\mathfrak{z}\left(a\right),\mathfrak{z}\mathfrak{z}\left(b\right)\right)-\mathbb{H}\left({\mathfrak{z}}_n\left(a\right),\mathfrak{z}{\mathfrak{z}}_n\left(b\right)\right)\right]\hfill \\ \hfill & \le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(a\right)-\frac{f}{e}\left({{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(b\right)-{{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(b\right)\right)\hfill \\ \hfill & \le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(a\right).\hfill \end{array}$$

By Lemma 3, we obtain $\Delta \left(\vartheta \right)\ge 0$, $\vartheta \in \mathrm{\Omega }$, which implies ${\mathfrak{z}}_{n+1}\left(\vartheta \right)\le \mathfrak{z}\left(\vartheta \right)$ and the following:

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_{n+1}\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right),$$

for almost all $\vartheta \in \mathrm{\Omega }$.

By using the same method, we can show that $\mathfrak{z}\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_{n+1}\left(\vartheta \right)$ and

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_{n+1}\left(\vartheta \right),$$

for each $\vartheta \in \mathrm{\Omega }$. Hence, ${\mathfrak{z}}_{n+1}\left(\vartheta \right)\le \mathfrak{z}\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_{n+1}\left(\vartheta \right)$, for $\vartheta \in \mathrm{\Omega }$, and the following is the case:

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_{n+1}\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_{n+1}\left(\vartheta \right),$$

for $\vartheta \in \mathrm{\Omega }$. Therefore, (17) holds on $\mathrm{\Omega }$ for all $n\in \mathbb{N}$. Taking the limit as $n\to \infty$ on both sides of (17), we obtain ${\mathfrak{z}}^{*}\left(\vartheta \right)\le \mathfrak{z}\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}^{*}\left(\vartheta \right)$ and the following:

$${{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}^{*}\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)\le {{}^c\mathbb{D}}_{a^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}^{*}\left(\vartheta \right),$$

for each $\vartheta \in \mathrm{\Omega }$. This means that ${\mathfrak{z}}^{*}$, ${\tilde{\mathfrak{z}}}^{*}$ are the extremal solutions of (1) in $[{\mathfrak{z}}_0,{\tilde{\mathfrak{z}}}_0]$. Thus, the proof of Theorem 1 is complete. □

4. Illustration

The theoretical outcomes are verified by a particular example with specific values. All the experiments are carried out in MATLAB Ver. 8.5.0.197613 (R2015a) on a computer equipped with a CPU AMD Athlon(tm) II X2 245 at 2.90 GHz running under the operating system Windows 7.

Example 1.

Consider problem (1) with the following.

$$\tau =\lambda =0.5, \sigma =\frac{\sqrt{\pi }}{2},a=0, b=1, \mathsf{\psi }\left(\vartheta \right)=\vartheta .$$

(18)

In order to illustrate Theorem 1, we take the following:

$$\begin{array}{cc}\hfill \mathbb{F}\left(\vartheta ,\mathfrak{z}\left(\vartheta \right),{{}^c\mathbb{D}}_{0^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)\right)& =(1-\sqrt{\vartheta })\hfill \\ \hfill & \times exp\left(\mathfrak{z}\left(\vartheta \right)+{{}^c\mathbb{D}}_{0^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(\vartheta \right)-\frac{2}{\sqrt{\pi }}-2\right),\hfill \end{array}$$

(19)

for $\vartheta \in [0,1]$ and obtain.

$$\begin{array}{c}\mathbb{H}\left({{}^c\mathbb{D}}_{0^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(0\right),{{}^c\mathbb{D}}_{0^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(1\right)\right)={{}^c\mathbb{D}}_{0^{+}}^{\lambda ;\mathsf{\psi }}\mathfrak{z}\left(0\right),\hfill \\ \mathbb{G}\left(\mathfrak{z}\left(0\right),\mathfrak{z}\left(1\right)\right)=\mathfrak{z}\left(0\right)-1.\hfill \end{array}$$

(20)

Obviously, $\mathbb{F}$, $\mathbb{G}$ and $\mathbb{H}$ are continuous. In addition, we can easily verify that ${\mathfrak{z}}_0\left(\vartheta \right)=1$ and ${\tilde{\mathfrak{z}}}_0\left(\vartheta \right)=1+\vartheta$ are lower and upper solutions of (1), respectively. Moreover, we can obtain ${\mathfrak{z}}_0\left(\vartheta \right)\le {\tilde{\mathfrak{z}}}_0\left(\vartheta \right)$ and the following:

$${{}^c\mathbb{D}}_{0^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_0\left(\vartheta \right)\le {{}^c\mathbb{D}}_{0^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_0\left(\vartheta \right),$$

for all $\vartheta \in [0,1]$. On the other hand, one can observe that the assumptions(H2)–(H4) of Theorem 1 are fulfilled. So, An application of Theorem 1 shows that the problem (1) with the data (18) and (19) has extremal solutions in $[{\mathfrak{z}}_0,{\tilde{\mathfrak{z}}}_0]$, which can be approximated by the following iterative sequences:

$$\begin{array}{cc}\hfill {\mathfrak{z}}_{n+1}\left(\vartheta \right)& =1+{\int }_0^{\vartheta }{\mathbb{E}}_{0.5}\left(\frac{\sqrt{\pi (\vartheta -\eta )}}{2}\right)(1-\sqrt{\eta })\hfill \\ \hfill & \times exp\left({\mathfrak{z}}_n\left(\eta \right)+{{}^c\mathbb{D}}_{0^{+}}^{\lambda ;\mathsf{\psi }}{\mathfrak{z}}_n\left(\eta \right)-\frac{2}{\sqrt{\pi }}-2\right)\mathrm{d}\eta ,\hfill \end{array}$$

(21)

with ${\mathfrak{z}}_0\left(\vartheta \right)=1$ and the following:

$$\begin{array}{cc}\hfill {\tilde{\mathfrak{z}}}_{n+1}\left(\vartheta \right)& =1+{\int }_0^{\vartheta }{\mathbb{E}}_{0.5}\left(\frac{\sqrt{\pi (\vartheta -\eta )}}{2}\right)(1-\sqrt{\eta })\hfill \\ \hfill & \times exp\left({\tilde{\mathfrak{z}}}_n\left(\eta \right)+{{}^c\mathbb{D}}_{0^{+}}^{\lambda ;\mathsf{\psi }}{\tilde{\mathfrak{z}}}_n\left(\eta \right)-\frac{2}{\sqrt{\pi }}-2\right)\mathrm{d}\eta ,\hfill \end{array}$$

(22)

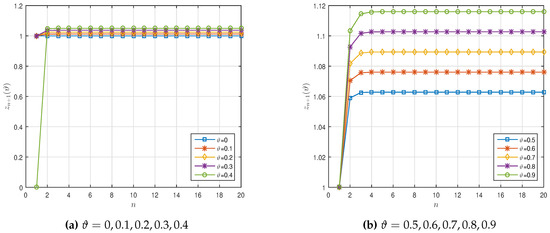
with ${\tilde{\mathfrak{z}}}_0\left(\vartheta \right)=1+\vartheta$. Table 1 and Table 2 show the numerical results of the iterative sequences of ${\mathfrak{z}}_{n+1}\left(\vartheta \right)$ for $\vartheta =0,0.1,0.2,0.3,0.4$ and $0.5,0.6,0.7,0.8,0.9,$ respectively. We plot these results in Figure 1a,b.

Table 1. Numerical results of ${\mathfrak{z}}_{n+1}\left(\vartheta \right)$ for $n=1,2,\dots ,20$ and $\vartheta =0$, $0.1$, $0.2$, $0.3$, $0.4$ by using (21) in Example 1.

n	$\mathit{\vartheta }$
	0	0.1	0.2	0.3	0.4
1	$1.000000$	$1.000000$	$1.000000$	$1.000000$	$1.000000$
2	$1.000000$	$1.011901$	$1.023786$	$1.035626$	$1.047386$
3	$1.000000$	$1.012044$	$1.024359$	$1.036918$	$1.049685$
4	$1.000000$	$1.012045$	$1.024373$	$1.036966$	$1.049799$
5	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
6	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
7	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
8	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
9	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
10	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
11	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
12	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
13	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
14	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
15	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
16	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
17	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
18	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
19	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$
20	$1.000000$	$1.012045$	$1.024373$	$1.036968$	$1.049805$

Table 2. Numerical results of ${\mathfrak{z}}_{n+1}\left(\vartheta \right)$ for $n=1,2,\cdots ,20$ and $\vartheta =0.5$, $0.6$, $0.7$, $0.8$, $0.9$ by using (21) in Example 1.

n	$\mathit{\vartheta }$
	0.5	0.6	0.7	0.8	0.9
1	$1.000000$	$1.000000$	$1.000000$	$1.000000$	$1.000000$
2	$1.059021$	$1.070482$	$1.081716$	$1.092662$	$1.103258$
3	$1.062609$	$1.075629$	$1.088674$	$1.101659$	$1.114490$
4	$1.062834$	$1.076019$	$1.089293$	$1.102578$	$1.115784$
5	$1.062848$	$1.076049$	$1.089348$	$1.102672$	$1.115933$
6	$1.062849$	$1.076051$	$1.089353$	$1.102682$	$1.115951$
7	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
8	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
9	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
10	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
11	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
12	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
13	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
14	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
15	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
16	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
17	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
18	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
19	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$
20	$1.062849$	$1.076051$	$1.089353$	$1.102683$	$1.115953$

Figure 1. Graphical representation of ${\mathfrak{z}}_{n+1}\left(\vartheta \right)$ in Example 1.

Table 3 and Table 4 show the numerical results of the iterative sequences of ${\tilde{\mathfrak{z}}}_{n+1}\left(\vartheta \right)$ for $\vartheta =0$, $0.1,0.2,0.3,0.4$ and $0.5,0.6,0.7,0.8,0.9$, respectively. We plot these results in Figure 2a,b.

Table 3. Numerical results of ${\tilde{\mathfrak{z}}}_{n+1}\left(\vartheta \right)$ for $n=1,2,\cdots ,20$ and $\vartheta =0$, $0.1$, $0.2$, $0.3$, $0.4$ by using (22) in Example 1.

n	$\mathit{\vartheta }$
	0	0.1	0.2	0.3	0.4
1	$1.000000$	$1.100000$	$1.200000$	$1.300000$	$1.400000$
2	$1.000000$	$1.018793$	$1.048121$	$1.089222$	$1.144311$
3	$1.000000$	$1.017327$	$1.041341$	$1.072265$	$1.111752$
4	$1.000000$	$1.017302$	$1.041061$	$1.071050$	$1.108172$
5	$1.000000$	$1.017301$	$1.041050$	$1.070964$	$1.107785$
6	$1.000000$	$1.017301$	$1.041049$	$1.070958$	$1.107743$
7	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107739$
8	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
9	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
10	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
11	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
12	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
13	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
14	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
15	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
16	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
17	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
18	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
19	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$
20	$1.000000$	$1.017301$	$1.041049$	$1.070957$	$1.107738$

Table 4. Numerical results of ${\tilde{\mathfrak{z}}}_{n+1}\left(\vartheta \right)$ for $n=1,2,\cdots ,20$ and $\vartheta =0.5$, $0.6$, $0.7$, $0.8$, $0.9$, 1 by using (22) in Example 1.

n	$\mathit{\vartheta }$
	0.5	0.6	0.7	0.8	0.9	1.0
1	$1.500000$	$1.600000$	$1.700000$	$1.800000$	$1.900000$	$2.000000$
2	$1.216106$	$1.307784$	$1.422976$	$1.565785$	$1.740782$	$1.953002$
3	$1.162695$	$1.229793$	$1.320631$	$1.447644$	$1.631747$	$1.909249$
4	$1.154233$	$1.212553$	$1.289440$	$1.397764$	$1.566487$	$1.870324$
5	$1.152934$	$1.208920$	$1.280551$	$1.378410$	$1.530698$	$1.837098$
6	$1.152735$	$1.208162$	$1.278068$	$1.371156$	$1.512041$	$1.809741$
7	$1.152705$	$1.208004$	$1.277379$	$1.368474$	$1.502577$	$1.787890$
8	$1.152700$	$1.207972$	$1.277187$	$1.367487$	$1.497842$	$1.770860$
9	$1.152699$	$1.207965$	$1.277134$	$1.367124$	$1.495491$	$1.757843$
10	$1.152699$	$1.207963$	$1.277120$	$1.366991$	$1.494327$	$1.748043$
11	$1.152699$	$1.207963$	$1.277116$	$1.366942$	$1.493752$	$1.740747$
12	$1.152699$	$1.207963$	$1.277115$	$1.366925$	$1.493469$	$1.735363$
13	$1.152699$	$1.207963$	$1.277114$	$1.366918$	$1.493329$	$1.731414$
14	$1.152699$	$1.207963$	$1.277114$	$1.366916$	$1.493260$	$1.728532$
15	$1.152699$	$1.207963$	$1.277114$	$1.366915$	$1.493225$	$1.726435$
16	$1.152699$	$1.207963$	$1.277114$	$1.366914$	$1.493209$	$1.724913$
17	$1.152699$	$1.207963$	$1.277114$	$1.366914$	$1.493200$	$1.723811$
18	$1.152699$	$1.207963$	$1.277114$	$1.366914$	$1.493196$	$1.723013$
19	$1.152699$	$1.207963$	$1.277114$	$1.366914$	$1.493194$	$1.722437$
20	$1.152699$	$1.207963$	$1.277114$	$1.366914$	$1.493193$	$1.722021$

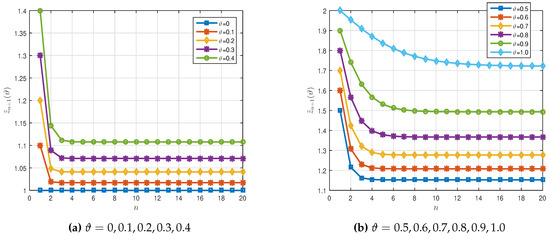
Figure 2. Graphical representation of ${\tilde{\mathfrak{z}}}_{n+1}\left(\vartheta \right)$ in Example 1.

5. Conclusions

This paper is devoted to the study of a new type of $\mathsf{\psi }$-Caputo fractional differential equation. The addressed problem is considered in the framework of nonlinear boundary value conditions. Our work is different from the existing results in the literature, which are basically based on fixed point approaches. However, we have proved our main results with the help of monotone iterative techniques along with the method of upper and lower solutions. It is observed that these methods are closely related to the Tarski–Knaster theorem and that, essentially speaking, also results in fixed point results. The main results have been verified and demonstrated by an example with explicit numerical values.