Abstract
A Practical Byzantine Fault Tolerance (PBFT) is a consensus algorithm deployed in a consortium blockchain that connects a group of related participants. This type of blockchain suits the implementation of the Building Information Modeling (BIM) information exchange with few participants. However, when much more participants are involved in the BIM information exchange, the PBFT algorithm, which inherently requires intensive communications among participating nodes, has limitations in terms of scalability and performance. The proposed solution for a multi-layer BFT hypothesizes that multi-layer BFT reduces communication complexity. However, having more layers will introduce more latency. Therefore, in this paper, Double-Layer Byzantine Fault Tolerance (DLBFT) is proposed to improve the blockchain scalability and performance of BIM information exchange. This study shows a double-layer network structure of nodes that can be built with each node on the first layer, which connects and forms a group with several nodes on the second layer. This network runs the Byzantine Fault Tolerance algorithm to reach a consensus. Instead of having one node send messages to all the nodes in the peer-to-peer network, one node only sends messages to a limited number of nodes on Layer 1 and up to three nodes in each corresponding group in Layer 2 in a hierarchical network. The DLBFT algorithm has been shown to reduce the required number of messages exchanged among nodes by 84% and the time to reach a consensus by 70%, thus improving blockchain scalability. Further research is required if more than one party is involved in multi-BIM projects.
1. Introduction
Various improvements have been made in the blockchain compared to that previously offered by Bitcoin [1,2], such as the use of smart contracts in the blockchain. This usage takes the blockchain back to the domain of database replication protocols, particulary the state machine replication. It has a protocol called Practical Byzantine Fault Tolerance (PBFT).
PBFT has various characteristics, i.e., (1) fault tolerance, (2) absolute consensus finality, (3) the existence of a peer node known by its corresponding nodes, and (4) a high consistency. The explanations of these characteristics are as follows: (1) Fault-tolerance: The protocol reaches consensus despite (n − 1)/3 nodes out of total of n replicas being malicious/faulty simultaneously [3]. If the number of faulty nodes is lower than this threshold, the system will not be affected or crash as a safety element [4]; (2) Absolute consensus finality mandates how any transaction is immediately determined once it is included in a valid block and added to the blockchain [5,6]. Consensus finality is defined as if a correct node p adds block b to its copy of the blockchain before adding block b’, then no correct node q adds block b’ before b to its copy of the blockchain; (3) The protocol requires the whole sets of its peer nodes that participate in a consensus to be understood by their corresponding node. This requirement for known identities might be required for meeting legal and compliance requirements; (4) A higher consistency involves small-scale node numbers [4,7,8,9,10]. PBFT is also a relatively fast and efficient consensus algorithm since it does not require a computing challenge compared to proof-of-work (PoW). It also does not require a round of selection as proof-of-stake (PoS) [11].
With these four characteristics, PBFT is suitable for the permissioned/consortium blockchain system with a high-speed network and a small number of nodes [12]. PBFT has been shown to be practical [4,13] and has good characteristics, such as a high efficiency [14]; high throughput [2,15,16]; low complexity; low computational power [4]; low latency; and low energy consumption [4,8,9]. PBFT offers a universal solution for distributed systems [10,17,18,19,20,21,22]. These benefits have been shown not only in prototypes [2,23,24,25] but also in practical systems [2,26].
A consortium blockchain is suited for the Building Information Modeling (BIM) information exchange [27], as depicted in Figure 1. This is because: (1) It involves multiple parties who do not trust each other but know each other; (2) It has the same goal of completing the project; (3) It has a higher throughput compared to the public blockchain [2,28]; (4) It allows varying levels of function and permissions; and (5) It addresses the cybersecurity aspect by having BIM information in a tampered-proof blockchain [29]. Thus, this BIM information exchange can be implemented in a consortium blockchain with the PBFT algorithm.
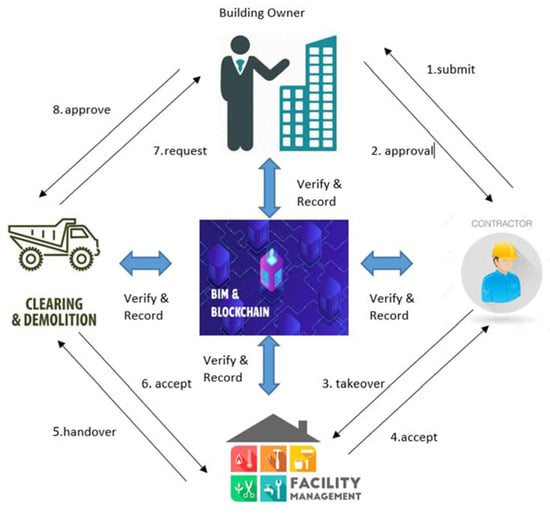
Figure 1.
BIM workflow and participants [27].
Since the PBFT algorithm determines the number of running nodes in the entire network [2,8,13,14,15,30,31], it does not work well in the consortium blockchain system with many nodes [2,12,14]. In a peer-to-peer (P2P) network, nodes join or exit the network continually; thus, the number of nodes does not always continue to be fixed. Due to the uncertain consumption of the network message because of an unknown number of nodes in the entire network, the PBFT algorithm has a limited usability in P2P networks with many nodes [16]. The performance of the system decreases greatly when the number of nodes exceeds a threshold [15,32]. Moreover, with the increasing number of nodes participating in the PBFT algorithm, the system becomes safer, but the delay will be longer [16,31,33]. With an increasing number of participating nodes, the number of consensus messages that are transmitted through the network becomes large, which may lead to congestion and network unavailability [16]. Thus, the main limitation of the PBFT protocol is scalability regarding the number of consensus participants due to the high degree of complexity in exchanging messages [30,34]. The PBFT-based blockchain hardly scales up to 100 nodes.
There are many PBFT variants, such as Dynamic BFT [35], Istanbul BFT [36,37], Tendermint [38], QBFT [39], Democratic BFT [40], T-BFT [6] and R-PBFT [41], but since they run in a peer-to-peer network, they tend to have high communication complexities since each node transmits messages to all the nodes in the network. This results in limitations in terms of scalability.
This can be addressed via multi-layer BFT, as shown in the research of Li et al. on a multi-layer BFT algorithm based on MATLAB [28]. However, more layers will produce more latency to reach a consensus. This could be ineffective for a complex situation such as the BIM information exchange. Thus, in this research, we proposed to reduce communication complexity using a Double-Layer Byzantine Fault Tolerance (DLBFT) algorithm that runs on a two-layer network. The network is divided into groups of four nodes. Each group consists of one node in Layer 1 and three other nodes in Layer 2. The BFT algorithm is run within nodes on Layer 1 and within groups. Thus, communication is limited among Layer 1 nodes and groups; it reduces the overall communication complexity. As a result, this algorithm has the potential to improve scalability by a horizontal expansion, which promotes the overall performance of the system by increasing the number of nodes.
Therefore, the main contribution of this study is to propose the DLBFT algorithm that runs on a consortium blockchain for BIM information exchange. This algorithm reduces communication complexity—by reducing the number of messages exchanged—and the time to complete the algorithm. Thus, it improves the blockchain scalability and performance of BIM information exchange. The remainder of this paper is organized as follows: Section 2: Theory and Related Components; Section 3: Methodology; Section 4: Implementation and Experiment; Section 5: Results; Section 6: Discussion; and Section 7: Conclusions.
2. Background and Related Work
In this section, the following components will be discussed: (1) background and (2) related work. In the background: BIM, blockchain technology, PBFT consensus algorithm, scalability, tree-based architecture, and hierarchical network will be discussed. In related work: PBFT consensus protocols, and hierarchical BFT consensus algorithms will be explained.
2.1. Background
2.1.1. BIM (Building Information Modeling)
BIM digitally represents a facility’s characteristics, e.g., physical and functional. BIM creates a common knowledge information resource that forms a reliable platform for decision making during the building lifecycle; it spans the process from the first conception to demolition [27,42,43]. BIM is a cutting-edge digital transformation in the Architectural Engineering and Construction (AEC) industry. It strengthens trust and collaboration, and it simplifies the exchange of data.
BIM is used in the process of designing, building, operating, maintaining, and demolishing highly sophisticated buildings. It allows design and construction teams to work more efficiently and capture data during the processes to benefit operations and maintenance activities by using facility management. The data that are captured include building structure and materials and mechanical and electrical designs and components.
However, the rate of digital transformation in the AEC industry is one of the slowest [44] due to several contributing factors. One of them is a lack of a collaborative framework. The integration of a blockchain in BIM can uplift the hurdle in the industry’s digital transformation and accelerate a new technological uptake. The implementation of a blockchain for BIM also addresses current issues such as data ownership, non-repudiation, confidentiality, traceability, provenance tracking, and change tracing. Thus, integrating the blockchain in a BIM setting will also facilitate the recording of all the transactions [29].
Theoretically, when implementing a blockchain in the construction industry, it is important to determine the: (1) Blockchain type; (2) Suitable consensus mechanism; (3) Project information repository; and (4) Cybersecurity aspects. The advent of BIM in the AEC industry provides a new opportunity to solidify and incorporate all related building data into a single common digital model. This holds for financial, temporal, and geometric aspects as well as for compliance checking, modeling, and collaborative plug-in tools. By applying BIM in every stage of the building lifecycle, it is feasible to simulate real-time on-site conditions and examine a single or a whole set of variables.
Blockchain-based BIM information exchange that involves only a few participants is sufficient to be executed on single-layer PBFT (Figure 1). However, for a model with an increasing number of participants, another PBFT variant is needed. This could be executed on a double-layer network structure, which could offer improved scalability.
2.1.2. Blockchain Technology
One of the emerging methods in the BIM workflow is a blockchain that has been widely recognized as a reliable, decentralized, transparent, and relatively secure database [29]. The blockchain can record all transactions and it is able to utilize a solid cryptography, storage, asset sharing, and transfer, and its data can access audit trails in an immutable, secure, chronological, and resilient peer-to-peer network. It has many advantages for individuals, firms, clients, industry, and society at large, and it is creating a change in workflow dynamics and the existing culture [29].
The blockchain is based on a distributed general ledger and a shared database that stores data not only in one location or those that are owned solely by one entity. Due to decentralized control, data in shared databases are not easy to be tampered with, stolen, or altered [45].
Based on network types, the blockchain can be categorized as follows: (1) A public blockchain where any nodes can join the blockchain. The public blockchain is completely distributed; anyone can join or exit the system. The system operates with untrusted and unknown nodes; (2) A private blockchain is a shared ledger that is authorized by a predetermined group of nodes. This system requires the initiation or authorization of nodes that want to join the system and that are responsible for maintaining a consensus. The private blockchain is suited for closed systems and semi-closed systems. A closed system is a system that consists of all trusted nodes; (3) A consortium blockchain is a semi-closed system that consists of several parties that have the same goals. The consortium blockchain is partially centralized, and the consensus process is permission, meaning it runs among a set of known and predetermined nodes [46]. This blockchain type is a hybrid between public and private blockchains, as shown in Figure 2 [6,47,48]. It ensures secure interactions among a group of enterprises that share a common goal but do not fully trust each other [9]. It also restricts the actors that can contribute to the system state consensus. A restricted set of users solely have the right to authorize transactions and may also restrict access to authorized actors who can create smart contracts. This type of blockchain can execute a complex application more efficiently than a PoW-based blockchain [32]. There may be a conflict among different enterprises and some nodes can become malicious nodes, so it is better to use a Byzantine consensus algorithm called PBFT in this scenario [12].
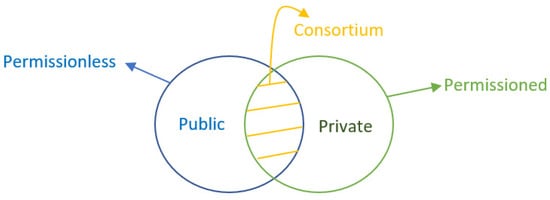
Figure 2.
Blockchain types.
Based on the types of access permission, a blockchain can be classified into: (1) A permissionless blockchain, where any node can join the network; and (2) A permissioned blockchain, where access to the network is controlled by a preselected set of nodes and the participants are authenticated.
2.1.3. PBFT Consensus Algorithm
PBFT is one of the consensus algorithms, which are the main components of blockchain technology [49]. It describes the rules that must be followed to reach a consensus, governs the proper functioning of a distributed system, and solves data synchronization between nodes [16]. It also ensures a consistent view among peers [50].
PBFT is a state machine replication protocol [3]. Each replica maintains service states and implements service operations. The service is replicated against different nodes in a distributed system [3,28,29,51,52]. The PBFT algorithm is presented in Algorithm 1.
| Algorithm 1. Practical Byzantine Fault Tolerance (PBFT) [3]. |
|
In addition to the primary node, there is another type of node called a replica or backup. There are two requirements on the replica that must be met: (1) The replica must be deterministic (the execution of an operation under a certain state and with a certain set of arguments that produce the same result); and (2) The replicas must start in the same state.
Under normal operating conditions, a Primary node (P0) accepts client requests (M) and initiates a three-phase protocol, e.g., pre-prepare, prepare, and commit, to multicast requests to replicas/nodes. Figure 3 shows the operation of the PBFT algorithm under normal conditions where there is no primary fault or damaged. Replica 0 is Primary, Replica 3 is a faulty node, and C is Client.
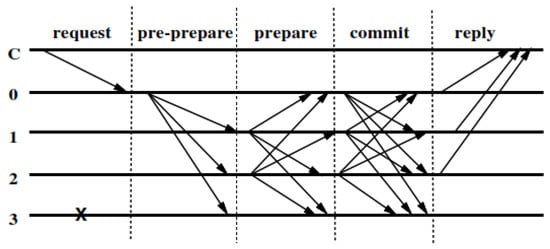
Figure 3.
PBFT consensus algorithm [3].
In the pre-prepare stage, the primary node simultaneously sends a message to each destination node. The pre-prepare and prepare stages are used to sort requests sent in the same view even though the primary is in a faulty condition. The prepare and commit stages are used to ensure that the committed requests are in a sequential condition. To accomplish consensus results, the overall number of messages that must be sent in the network is [15]
as shown in Table 1.
n + (n − 1) + (n − 1) × (n − 1) + n × (n − 1) + n = O (2n2),

Table 1.
Communication complexity of single-layer network structure
When the number of nodes reaches 100, the total number of messages reaches 20,000; this places a great strain on the communication network. The performance of the PBFT protocol decreases dramatically when there is a number of nodes that surpasses a certain amount due to the complexity of communications [8]. Broadcasting a request in the PBFT algorithm wastes a lot of the network’s resources [15].
2.1.4. Scalability
The objective of blockchain scalability is to have a high throughput indicated by processing a high number of transactions per second without sacrificing decentralization and security [53,54]. Indeed, the throughput can easily be increased in exchange of losing the key characteristic of the blockchain, i.e., decentralization [53,54,55].
PBFT has a low scalability, which is defined as the ability to support an increasing number of nodes in the blockchain network [16]. Due to the frequency of inter-node communications, it cannot be applied to large-scale blockchain systems [15,18,28,34,56,57].
Scalability, which is divided into a horizontal and vertical expansion, as shown in Figure 4, is very important for distributed systems [58]. A horizontal expansion indicates an increasing number of machines/nodes, which promotes the overall performance of the system. One barrier to its use though lies in the limitations of multimachine management. A vertical expansion indicates an increasing overall performance of the system by improving the performance of a single machine. However, there is an upper bound to a single machine/node performance. In distributed systems, such as a blockchain, horizontal expansions are generally adopted to improve system performance and usually consist of inexpensive and efficient nodes.

Figure 4.
(a) Scalability by horizontal expansion, and (b) scalability by vertical expansion.
2.1.5. Tree-Based Architecture
PBFT that runs on one P2P network is called a single-layer PBFT (Figure 5), which has a high communication complexity. One example of this is dBFT [59].
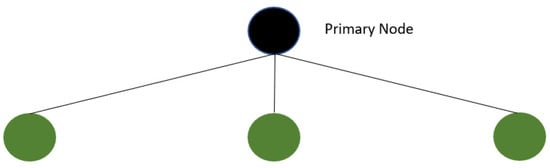
Figure 5.
Single-layer PBFT.
In a small P2P group, mutual cast can be used to maximize the overall throughput during a broadcast session. However, in a situation where the P2P group is large, mutual cast has a high communication complexity. Mutual cast can be made scalable by having a collaborative P2P tree-based architecture. It consists of two main components: (1) Clustering or peer grouping; and (2) Hierarchical tree-based content distribution [60]. A tree-based architecture has other advantages, such as easy maintenance, a reduced end-to-end delivery time, and low resource consumption [60].
In tree-based architecture, the participating peers are formed into a single tree, which consists of the source node and interior or leaf nodes. The tree root is located at the source node. At the same time, the other participating peers are categorized into interior or leaf nodes. At the first level, the source peer transmits the data to the requesting peers, then these peers transmit the data to the requesting peers located a level below the tree structure, and so on, until the leaf peers are reached. This tree structure perhaps has the most effective distribution structure in terms of delay optimization and bandwidth [61]. However, it has an inherent disadvantage in that a relatively small number of interior nodes carry out the burden of forwarding multicast messages [60].
2.1.6. Hierarchical Network
A new alternative emerges from the hierarchical clustering/network in which peers are organized into clusters, and these clusters form a tree topology, as outlined earlier. This new topology can provide an efficient transmission in several ways: (1) It increases transmission robustness; and (2) It cuts down the upload bandwidth usage and peer communication tension [60].
In this hierarchical network structure, clusters are elementary units involving one source peer and a few requesting peers. The root (source) node is located at the first level. Peers in the system are arranged into small clusters to ensure that the root cluster is formed by the peers closest to the root node in the distribution tree. In the intermediate cluster, peers—with a longer time proximity to the source peer—form a group, while from the source peer, the time proximity of leaf or child clusters is the longest. The number of peers in these clusters needs to be constant and small [60]. The choice of a proximity metric depends on the desired qualities of the resulting overlay (e.g., low delay, high bandwidth, low network utilization). In practice, these metrics can be translated into, for example: (1) Round-trip time (minimum of a series of pings); (2) Bandwidth measurement (using the packet pair technique); and (3) The number of IP routing hops (measured using traceroute) or some combination [62]. In the same cluster, communication among peers is bidirectional.
2.2. Related Work
2.2.1. PBFT Consensus Protocols
Table 2 shows PBFT-variant algorithms’ comparison. Most of them run on a peer-to-peer network topology with high communication complexities of at least O(n2).

Table 2.
PBFT-variant algorithms’ comparison.
2.2.2. Hierarchical BFT Consensus Algorithms
There are various hierarchical structure-based algorithms, as described in Table 3. The hierarchical group topology in Steward for a wide-area network reduces the number of messages and communication rounds compared to the flat topology in BFT [64,65]. In a star topology, such as HotStuff [66], due to its centralized control, it is inherently non-scalable [65]. However, in a tree topology, the number of messages exchanged is reduced; there is a tendency to increase latency for each consensus round [65]. Thus, a two-level tree structure called Double-Layer BFT (DLBFT) is introduced for the blockchain to limit this tendency and to reduce the number of messages exchanged.

Table 3.
Comparison of hierarchical structure.
3. Methodology
In order to improve blockchain scalability, there are two important factors to consider, i.e., network structure and blockchain protocol. Thus, the most potential approach is using a double-layer network structure, while for blockchain, there are several solutions to scale it, which can be classified into two categories: (1) An on-chain solution, which is the modification of the blockchain protocols, e.g., sharding and block increase; and (2) An off-chain, denoting solutions that are built on blockchain protocols, such as processing certain transactions outside the blockchain and only recording significant transactions [53].
In our hierarchical structure, the source of new second-level clusters are peers from the first clusters. Thus, peer P1 in Cluster 1 forwards messages and acts as a source peer-to-peer in Cluster 2 (which consists of peers P4, P5, and P6) simultaneously. There is a child cluster of peer P1 [60]. Peers P2 and P3 can also extend their own clusters. Because there are only two layers, there is no intermediate layer. Several peers are organized into groups. Each group has a unique group id. Each group must have one or more super peers with special characteristics and responsibilities. Each group operates autonomously from the other groups [67] (Figure 6).
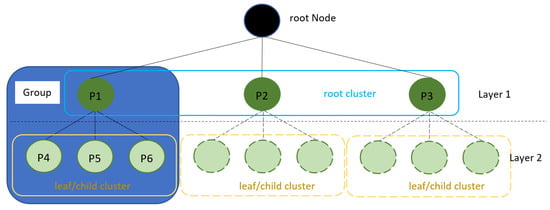
Figure 6.
Hierarchical network.
A hierarchical organization has an advantage over a single-level organization. Using super peers as more reliable peers at the top level provides a high stability. Super peers are expected to be the most stable and powerful group nodes. Therefore, super peers should monitor the peers that join a group and present “good characteristics” [67].
Intuitively, to reduce the communication complexity and the cost of communication, a horizontal expansion can be formed by a hierarchical Double-Layer PBFT (DLBFT) with a sub-consensus, which can be performed per group. With this model, for example, if there are three groups, there will be three sub-consensuses. The consensus is defined as (n + 1) sub-consensuses, which, in this example, is equal to four.
This DLBFT system model is initially proposed to provide a brief analysis of communication complexity based on a particular case [4]. However, there are still many challenges that need to be addressed before this idea can be applied in a real system. One of them is that the complexity analysis cannot be applied to generic situations as it is developed under the premise that there is an equal number of nodes in each group [68].
In this paper, DLBFT is proposed to: (1) Decrease the number of messages exchanged as a proxy for blockchain scalability by reorganizing network structure and by restraining communication within layers and groups; and (2) Reduce communication time compared to PBFT. In DLBFT, total number of messages exchanged is shown in Table 4.

Table 4.
Communication complexity of double-layer network structure.
4. Implementation and Experiment
A hierarchical tree two-layer structure in DLBFT is proposed in this study (Figure 7) and was run on a local computer running Ubuntu 18.04 with 32 GB RAM and 2.60 GHz. The information in this structure defined each node in Layer 1 as the head node. Then, four nodes in Layer 1 were formed. These nodes consist of one primary node and three head nodes, which are also called super peers and act as the source of message broadcasts for the corresponding nodes in Layer 2. Each group consists of one head node in Layer 1 and three other nodes in Layer 2. Each node in each group is interconnected. To form a double-layered network structure, a minimum of one primary node and three head nodes in Layer 1 and nine nodes in Layer 2 that form three groups is required. Adding more nodes, depicted as “…” in the network, can be achieved by forming more groups that consist of head nodes in Layer 1 and nodes in Layer 2 (Figure 7).
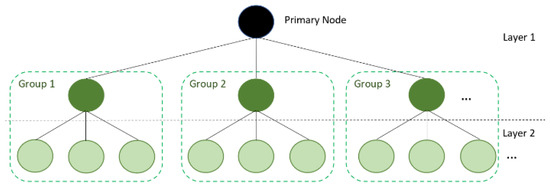
Figure 7.
DLBFT structure for the study.
The messages will be broadcasted from the primary node to the head nodes in Layer 1. Then, each head node will broadcast messages to other nodes in the corresponding group. In each group, each node in Layer 2 receives broadcast messages from its corresponding head node in Layer 1 and sends messages to other neighboring nodes.
The components of BIM information exchange with the two algorithms, PBFT and DLBFT, are depicted in Figure 8.
Figure 8.
Experimental components.
In this research, the DLBFT structure is extensible to 153 nodes, consisting of 39 nodes in Layer 1 and up to 114 nodes in Layer 2 (Figure 9), and its configuration (Table 5). Layer 1 consists of 1 primary node and 38 Layer 1 nodes from 38 groups; thus, there are 39 nodes in total in Layer 1. Both the PBFT algorithm on a single-layer node structure and the DLBFT algorithm on a double-layer node structure were extended to the abovementioned number of nodes. The evaluation of the results was conducted in relation to the number of messages exchanged among the nodes as a proxy for scalability and the time to complete the algorithm. The total number of nodes in this research is 153 nodes, taking into account the performance of the blockchain degrades when the P2P nodes reach 100 [28].
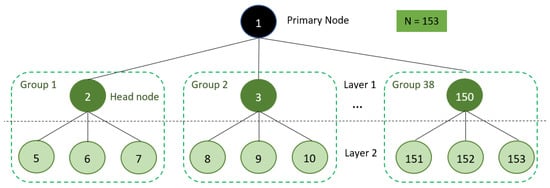
Figure 9.
Primary node and head nodes in double-layer network structure.

Table 5.
Configuration of double-layer network structure.
The phases in DLBFT are a modified from the single-layer PBFT protocol, consisting of PrePrepare1, Prepare1, Commit1, and Reply1 phases in Layer 1 and Pre-Prepare2, Commit2, and Reply2 phases in each group (Figure 10).
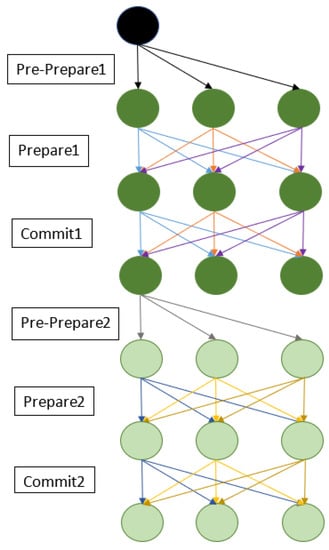
Figure 10.
Double-layer BFT messages.
The communication protocol is as follows: the primary node sends Pre-Prepare messages to all the nodes in Layer 1. Then, each node in Layer 1, including the Primary node, will send Prepare messages to all the nodes in Layer 1. Subsequently, each node in Layer 1 sends a Commit message to all the nodes in Layer 1. Afterwards, each node in Layer 1, except the Primary node, sends Pre-Prepare messages to all the nodes in the corresponding group in Layer 2. For example, a node in Group1 Layer 1 will send Pre-Prepare messages to all the nodes in Group1 Layer 2. Then, all the nodes in Group 1 send Prepare and Commit messages within the group. At last, all the nodes in Group1 Layer 2 send Reply messages to the nodes in Group1 Layer1. All the other groups, e.g., Group2, Group3, and Group4, as shown in Figure 10, show the exchange of messages among the nodes in Layer 1 and Layer 2. Then, all the nodes in Layer 1, except the Primary node, will send Reply messages to the Primary Node. This DLBFT algorithm can be extended to as many groups of four nodes, as shown in Algorithm 2.
| Algorithm 2. Double-layer Byzantine Fault Tolerance (DLBFT). |
|
5. Experiment Results
For the PBFT algorithm, the number of messages exchanged is 364 for a peer-to-peer single-layer node structure with 13 nodes, increasing to 47,124 messages for 153 nodes, whereas for the DLBFT algorithm, the number of exchanged messages starts at 157—for a double-layer network structure with 13 nodes—and increases to 4602 messages for 153 nodes (Figure 11).
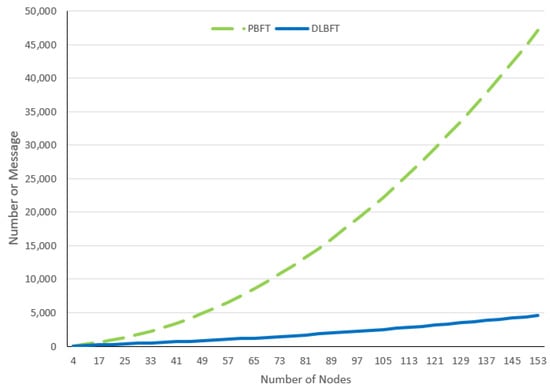
Figure 11.
The number of messages exchanged in PBFT vs. DLBFT.
Based on the experiments, the difference in the number of messages exchanged in PBFT and DLBFT is measured and shown in Table 6. DLBFT has a smaller number of messages exchanged compared to PBFT; the difference is 56.87% for 13 nodes and up to 90.23% for 153 nodes, with an average of 84.28%.

Table 6.
The difference in the number of messages exchanged in PBFT and DLBFT.
The time to complete PBFT is 0.068 s for 13 nodes and 2.2 s for 153 nodes, while for the DLBFT algorithm, it is 0.0428 s for 13 nodes and 0.3730 s for 153 nodes (Figure 12). Using the DLBFT algorithm, the time to complete the algorithm was reduced by 30.65 % for 13 nodes and by 83.05% for 153 nodes. The average reduction was 69.20% compared to PBFT.
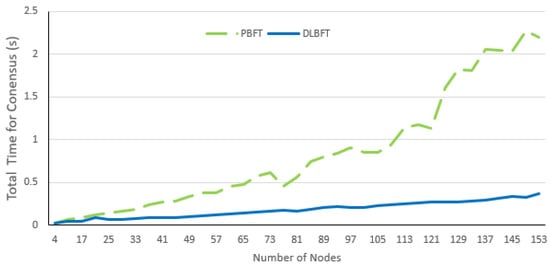
Figure 12.
Time to complete PBFT vs. DLBFT.
In addition, the number of messages exchanged in Layer 1 is higher than in Layer 2 (Figure 13). This is because each group in Layer 2 consists of only 4 nodes, whereby Layer 1 consists of up to 39 nodes.
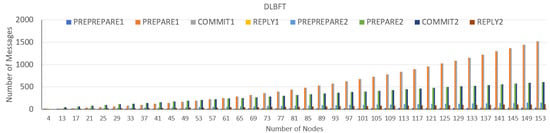
Figure 13.
DLBFT algorithm running on double-layer structure node.
6. Discussion
The scalability and time to complete the algorithm was improved because the DLBFT algorithm, which runs on a double-layer hierarchical network, required a much smaller number of messages to be exchanged; in contrast, the PBFT algorithm, which ran a peer-to-peer network, involved a more intensive communication among the nodes. This research also reported a fluctuation in the time needed to complete the algorithm in PBFT, which could be caused by the network connection speed.
In addition, the increased rate of messages exchanged in the PBFT algorithm tended to be exponential, confirming that there was a high number of messages exchanged, while DLFBT tended to be linear. The higher the number of participating nodes in the network, the more significant the difference in the number of messages exchanged between the two algorithms. In this study, the threshold was shown after more than 100 nodes [15,28,56]. The mean time to consensus for n = 100 is more than 5.3 times that for n = 4 [28,56]. Theoretically, it has internode communication C ≈ 1.9 Z4/3 compared to the traditional PBFT system of O(Z2) [4]. For this study, the communication complexity is approximately 3.5 n7/5.
There was a difference in the number of messages exchanged in each layer of DLBFT. The number of exchanged messages in Layer 1 increased rapidly as the number of participating nodes increased, which mimics the PBFT algorithm on a peer-to-peer network. The number of exchanged messages in each group tended to increase linearly because each group consisted of four nodes. This is the minimum number of nodes required to run the BFT-variant algorithms since they can accommodate 1/3 of faulty nodes [29,48].
As the number of participating nodes increased, the percentage difference in the number of messages exchanged between PBFT and DLFBT increased from 57% (for 13 nodes) to 90% (for 153 nodes). Thus, the rate to complete the DLBFT algorithm was also reduced from 31% (for 13 nodes) to 83% (for 153 nodes) compared to the PBFT algorithm. In addition, there was a fluctuation in the completion time in broadcasting the messages due to the network speed.
The main contribution of this study is the improvement of the blockchain scalability and the amount of time taken to complete the algorithm by using DLBFT. This could be beneficial for information exchange in BIM that includes a higher number of participating nodes in a consortium blockchain.
However, there are several challenges in this model, which brings limitations to this study. First, the performance degrades when the number of nodes in Layer 1 reaches 100, similar to the PBFT algorithm. Second, this study does not discuss the packet sizes used for node messaging. Third, this research only involves four fixed parties: building owner, contractor, facility management, and clearing and demolition in a BIM project. Fourth, this research assumes that only one party can be involved in one specific BIM project. Further research can be addressed to cater for the possibilities of the involvement of this one party in several BIM projects. Several research suggestions for the future, among others, are: (1) To study different approaches to cater for more than 100 groups in the network to prevent performance degradation; (2) To analyze optimum packet sizes for node messaging; (3) To examine the network effect of having more than four parties involved in one BIM project; and finally (4) To explore one party involvement in several BIM projects.
7. Conclusions
In this study, a hierarchical tree structure using a double-layer network structure is constructed as DLBFT. The result shows that the number of messages exchanged among nodes in DLBFT is reduced with an increasing number of participating nodes with an average of 84.28%. The increase rate of the number of messages exchanged is linear without any node threshold. The total time to complete the DLBFT algorithm is reduced with an increasing number of nodes, with an average of 69.20% in comparison to PBFT. In addition, the number of messages exchanged in each group that consists of Layer 1 and Layer 2 is smaller than in Layer 1 in DLBFT.
The contribution of this experiment is that DLBFT can decrease the number of messages exchanged as a proxy for scalability and time to complete the algorithm compared to PBFT, which runs on a peer-to-peer network. A low number of messages exchanged among the nodes in this algorithm can prevent network congestion and unavailability. DLBFT can also improve node scalability by allowing more participating nodes, which is more suitable for information exchange in BIM. Further research is required, among others, to explore the expansion of one party being involved in multi-BIM projects.
Author Contributions
Conceptualization, W.N.S. and R.F.S.; methodology, W.N.S.; software, W.N.S.; validation, W.N.S. and R.F.S.; formal analysis, W.N.S.; resources, W.N.S. and R.F.S.; data curation, W.N.S.; writing—original draft preparation, W.N.S.; writing—review and editing, R.F.S.; visualization, W.N.S.; supervision, R.F.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors thank the Ministry of Education, Culture, Research, and Technology of the Republic of Indonesia for financial support for this research under the PTUPT Grant number NKB-289/UN2.RST/HKP.05.00/2021.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank Habib Yajam for facilitating the foundation of blockchain framework.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bonneau, J.; Miller, A.; Clark, J.; Narayanan, A.; Kroll, J.A.; Felten, E.W. Sok: Research perspectives and challenges for bitcoin and cryptocurrencies. In 2015 IEEE Symposium on Security and Privacy; IEEE: New York, NY, USA, 2015; pp. 104–121. [Google Scholar]
- Vukolić, M. The quest for scalable blockchain fabric: Proof-of-work vs. BFT replication. In International Workshop on Open Problems in Network Security; Springer: Berlin/Heidelberg, Germany, 2015; pp. 112–125. [Google Scholar]
- Castro, M.; Liskov, B. Practical Byzantine fault tolerance. In Proceedings of the Third Symposium on Operating Systems Design and Implementation (OSDI’99), New Orleans, LA, USA, 22–25 February 1999; USENIX: Berkeley, CA, USA, 1999; Volume 99, pp. 173–186. [Google Scholar]
- Feng, C.; Li, W.; Yang, B.; Sun, Y.; Zhang, L. A Low Communication Complexity Double-layer PBFT Consensus. Wirel. Blockchain Princ. Technol. Appl. 2021, 73–92. [Google Scholar] [CrossRef]
- Min, Y.-A. The Modification of pBFT Algorithm to Increase Network Operations Efficiency in Private Blockchains. Appl. Sci. 2021, 11, 6313. [Google Scholar] [CrossRef]
- Gao, S.; Yu, T.; Zhu, J.; Cai, W. T-PBFT: An EigenTrust-based practical Byzantine fault tolerance consensus algorithm. China Commun. 2019, 16, 111–123. [Google Scholar] [CrossRef]
- Wang, X.; WeiLi, J.; Chai, J. The research on the incentive method of consortium blockchain based on practical byzantine fault tolerant. In Proceedings of the 2018 11th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 8–9 December 2018; IEEE: New York, NY, USA, 2018; Volume 2, pp. 154–156. [Google Scholar]
- Wang, Y.; Cai, S.S.; Lin, T.C.; Chen, F.Z.; Wang, T.; Gao, S.Z.; Zhou, S.C. Study of blockchains’s consensus mechanism based on credit. IEEE Access 2019, 7, 10224–10231. [Google Scholar] [CrossRef]
- Perera, S.; Nanayakkara, S.; Rodrigo, M.; Senaratne, S.; Weinand, R. Blockchain technology: Is it hype or real in the construction industry? J. Ind. Inf. Integr. 2020, 17, 100125. [Google Scholar] [CrossRef]
- Zhang, J.; Rong, Y.; Cao, J.; Rong, C.; Bian, J.; Wu, W. DBFT: A Byzantine Fault Tolerance Protocol with Graceful Performance Degradation. IEEE Trans. Dependable Secur. Comput. 2021, 19, 3387–3400. [Google Scholar] [CrossRef]
- Chiu, W.-Y.; Meng, W. EdgeTC-a PBFT blockchain-based ETC scheme for smart cities. Peer-Peer Netw. Appl. 2021, 14, 2874–2886. [Google Scholar] [CrossRef]
- Mingxiao, D.; Xiaofeng, M.; Zhe, Z.; Xiangwei, W.; Qijun, C. A review on consensus algorithm of blockchain. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; IEEE: New York, NY, USA, 2017; pp. 2567–2572. [Google Scholar]
- Castro, M.; Liskov, B. Practical Byzantine fault tolerance and proactive recovery. ACM Trans. Comput. Syst. (TOCS) 2002, 20, 398–461. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, N.; Lou, W.; Hou, Y.T. A survey of distributed consensus protocols for blockchain networks. IEEE Commun. Surv. Tutor. 2020, 22, 1432–1465. [Google Scholar] [CrossRef]
- Yu, G.; Wu, B.; Niu, X. Improved Blockchain Consensus Mechanism Based on PBFT Algorithm. In Proceedings of the 2020 2nd International Conference on Advances in Computer Technology, Information Science and Communications (CTISC), Suzhou, China, 10–12 July 2020; IEEE: New York, NY, USA, 2020; pp. 14–21. [Google Scholar]
- Wu, Y.; Song, P.; Wang, F. Hybrid consensus algorithm optimization: A mathematical method based on POS and PBFT and its application in blockchain. Math. Probl. Eng. 2020, 2020, 7270624. [Google Scholar] [CrossRef]
- Group, H.W.P.W. An Introduction to Hyperledger. Ed. 2018. Available online: https://www.hyperledger.org/wp-content/uploads/2018/07/HL_Whitepaper_IntroductiontoHyperledger.pdf (accessed on 4 October 2019).
- Lao, L.; Dai, X.; Xiao, B.; Guo, S. G-PBFT: A location-based and scalable consensus protocol for IOT-Blockchain applications. In Proceedings of the 2020 IEEE International Parallel and Distributed Processing Symposium (IPDPS), New Orleans, LA, USA, 18–22 May 2020; IEEE: New York, NY, USA, 2020; pp. 664–673. [Google Scholar]
- Androulaki, E.; Barger, A.; Bortnikov, V.; Cachin, C.; Christidis, K.; De Caro, A.; Yellick, J. Hyperledger fabric: A distributed operating system for permissioned blockchains. In Proceedings of the Thirteenth EuroSys Conference, Porto, Portugal, 23–26 April 2018; pp. 1–15. [Google Scholar]
- Feng, L.; Zhang, H.; Chen, Y.; Lou, L. Scalable dynamic multi-agent practical byzantine fault-tolerant consensus in permissioned blockchain. Appl. Sci. 2018, 8, 1919. [Google Scholar] [CrossRef]
- Seo, J.; Ko, D.; Kim, S.; Park, S. A Coordination Technique for Improving Scalability of Byzantine Fault-Tolerant Consensus. Appl. Sci. 2020, 10, 7609. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, J.; Peng, Z.; Bui, V.C.; Chen, S.; Ding, Y.; Xiang, Y. Security Analysis on dBFT protocol of NEO. In Proceedings of the International Conference on Financial Cryptography and Data Security, Kota Kinabalu, Malaysia, 10–14 February 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 20–31. [Google Scholar]
- Guerraoui, R.; Knežević, N.; Quéma, V.; Vukolić, M. The next 700 BFT protocols. In Proceedings of the 5th European Conference on Computer Systems, Passau, Germany, 14–16 November 2010; pp. 363–376. [Google Scholar]
- Clement, A.; Wong, E.L.; Alvisi, L.; Dahlin, M.; Marchetti, M. Making Byzantine Fault Tolerant Systems Tolerate Byzantine Faults. In Proceedings of the 6th USENIX Symposium on Networked Systems Design and Implementation (NSDI ’09), Boston, MA, USA, 22–24 April 2009; USENIX: Berkeley, CA, USA, 2009; Volume 9, pp. 153–168. [Google Scholar]
- Kotla, R.; Alvisi, L.; Dahlin, M.; Clement, A.; Wong, E. Zyzzyva: Speculative byzantine fault tolerance. ACM Trans. Comput. Syst. (TOCS) 2010, 27, 1–39. [Google Scholar] [CrossRef]
- Bessani, A.; Sousa, J.; Alchieri, E.E. State machine replication for the masses with BFT-SMART. In Proceedings of the 2014 44th Annual IEEE/IFIP International Conference on Dependable Systems and Networks, Atlanta, GA, USA, 23–26 June 2014; IEEE: New York, NY, USA, 2014; pp. 355–362. [Google Scholar]
- Suliyanti, W.N.; Sari, R.F. Blockchain-Based Implementation of Building Information Modeling Information Using Hyperledger Composer. Sustainability 2021, 13, 321. [Google Scholar] [CrossRef]
- Li, W.; Feng, C.; Zhang, L.; Xu, H.; Cao, B.; Imran, M.A. A Scalable Multi-layer PBFT Consensus for Blockchain. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 1146–1160. [Google Scholar] [CrossRef]
- Nawari, N.O.; Ravindran, S. Blockchain technologies in BIM workflow environment. In Computing in Civil Engineering 2019: Visualization, Information Modeling, and Simulation; American Society of Civil Engineers Reston: Reston, VA, USA, 2019; pp. 343–352. [Google Scholar]
- Amoussou-Guenou, Y.; Del Pozzo, A.; Potop-Butucaru, M.; Tucci-Piergiovanni, S. Dissecting tendermint. In Proceedings of the International Conference on Networked Systems, Munich, Germany, 18–21 March 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 166–182. [Google Scholar]
- Cachin, C.; Schubert, S.; Vukolić, M. Non-determinism in byzantine fault-tolerant replication. arXiv 2016, arXiv:1603.07351. [Google Scholar]
- Dinh, T.T.A.; Wang, J.; Chen, G.; Liu, R.; Ooi, B.C.; Tan, K.-L. Blockbench: A framework for analyzing private blockchains. In Proceedings of the 2017 ACM International Conference on Management of Data, Chicago, IL, USA, 14–19 May 2017; pp. 1085–1100. [Google Scholar]
- Yuan, Y.; Ni, X.; Zeng, S.; Wang, F. Blockchain consensus algorithms: The state of the art and future trends. Acta Autom. Sin. 2018, 44, 2011–2022. [Google Scholar]
- Rebello, G.A.F.; Camilo, G.F.; Guimaraes, L.; de Souza, L.A.C.; Duarte, O. Security and Performance Analysis of Quorum-based Blockchain Consensus Protocols. In Proceedings of the 2022 6th Cyber Security in Networking Conference (CSNet), Rio de Janeiro, Brazil, 24–26 October 2022. [Google Scholar]
- Hao, X.; Yu, L.; Zhiqiang, L.; Zhen, L.; Dawu, G. Dynamic practical byzantine fault tolerance. In Proceedings of the 2018 IEEE Conference on Communications and Network Security (CNS), Beijing, China, 30 May–1 June 2018; IEEE: New York, NY, USA, 2018; pp. 1–8. [Google Scholar]
- Moniz, H. The Istanbul BFT consensus algorithm. arXiv 2020, arXiv:2002.03613. [Google Scholar]
- Saltini, R.; Hyland-Wood, D. Correctness analysis of IBFT. arXiv 2019, arXiv:1901.07160. [Google Scholar]
- Buchman, E.; Kwon, J.; Milosevic, Z. The latest gossip on BFT consensus. arXiv 2018, arXiv:1807.04938. [Google Scholar]
- Fan, C.; Lin, C.; Khazaei, H.; Musilek, P. Performance Analysis of Hyperledger Besu in Private Blockchain. In Proceedings of the 2022 IEEE International Conference on Decentralized Applications and Infrastructures (DAPPS), Online, 15–18 August 2022; IEEE: New York, NY, USA, 2022; pp. 64–73. [Google Scholar]
- Crain, T.; Gramoli, V.; Larrea, M.; Raynal, M. Dbft: Efficient leaderless byzantine consensus and its application to blockchains. In Proceedings of the 2018 IEEE 17th International Symposium on Network Computing and Applications (NCA), Cambridge, MA, USA, 1–3 November 2018; IEEE: New York, NY, USA, 2018; pp. 1–8. [Google Scholar]
- Liu, S.; Wang, X.; Hui, L.; Wu, W. Blockchain-Based Decentralized Federated Learning Method in Edge Computing Environment. Appl. Sci. 2023, 13, 1677. [Google Scholar] [CrossRef]
- Nwodo, M.; Anumba, C.; Asadi, S. BIM-based life cycle assessment and costing of buildings: Current trends and opportunities. Comput. Civ. Eng. 2017, 2017, 51–59. [Google Scholar]
- Abanda, F.H.; Vidalakis, C.; Oti, A.H.; Tah, J.H. A critical analysis of Building Information Modelling systems used in construction projects. Adv. Eng. Softw. 2015, 90, 183–201. [Google Scholar] [CrossRef]
- Belle, I. The architecture, engineering and construction industry and blockchain technology. Digit. Cult. 2017, 2017, 279–284. [Google Scholar]
- Suliyanti, W.N.; Sari, R.F. Evaluation of Hash Rate-based Double-Spending based on Proof-of-Work Blockchain. In Proceedings of the 10th International Conference on Information and Communication Technology Convergence, ICTC 2019, Jeju Island, Republic of Korea, 16–18 October 2019; IEEE: New York, NY, USA, 2019; pp. 169–174. [Google Scholar]
- Douceur, J.R. The sybil attack. In Proceedings of the International Workshop on Peer-to-Peer Systems, Cambridge, MA, USA, 7–8 March 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 251–260. [Google Scholar]
- Buterin, V. On Public and Private Blockchains. In Ethereum Foundation Blog, 2015 Ed. Available online: https://blog.ethereum.org/2015/08/07/on-public-and-private-blockchains (accessed on 28 January 2020).
- Zheng, Z.; Xie, S.; Dai, H.; Chen, X.; Wang, H. An overview of blockchain technology: Architecture, consensus, and future trends. In Proceedings of the 2017 IEEE International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; IEEE: New York, NY, USA, 2017; pp. 557–564. [Google Scholar]
- Chen, J.; Zhang, X.; Shangguan, P. Improved PBFT Algorithm Based on Reputation and Voting Mechanism. J. Phys. Conf. Ser. 2020, 1486, 032023. [Google Scholar] [CrossRef]
- Saad, M.; Spaulding, J.; Njilla, L.; Kamhoua, C.; Shetty, S.; Nyang, D.H.; Mohaisen, D. Exploring the attack surface of blockchain: A comprehensive survey. IEEE Commun. Surv. Tutor. 2020, 22, 1977–2008. [Google Scholar] [CrossRef]
- Lamport, L. Time, clocks, and the ordering of events in a distributed system. In Concurrency: The Works of Leslie Lamport; ACM: New York City, NY, USA, 2019; pp. 179–196. [Google Scholar]
- Chen, Z.; Gul, O.M.; Kantarci, B. Practical Byzantine Fault Tolerance-based Robustness for Mobile Crowdsensing. In Distributed Ledger Technologies: Research and Practice; ACM: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Hafid, A.; Hafid, A.S.; Samih, M. New Mathematical Model to Analyze Security of Sharding-Based Blockchain Protocols. IEEE Access 2019, 7, 185447–185457. [Google Scholar] [CrossRef]
- Kim, S.; Kwon, Y.; Cho, S. A survey of scalability solutions on blockchain. In Proceedings of the 2018 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 17–19 October 2018; IEEE: New York, NY, USA, 2018; pp. 1204–1207. [Google Scholar]
- Buterin, V. Notes on Scalable Blockchain Protocols. Available online: https://github.com/vbuterin/scalability_paper/blob/master/scalability.pdf (accessed on 1 February 2020).
- Sukhwani, H.; Martínez, J.M.; Chang, X.; Trivedi, K.S.; Rindos, A. Performance modeling of PBFT consensus process for permissioned blockchain network (hyperledger fabric). In Proceedings of the 2017 IEEE 36th Symposium on Reliable Distributed Systems (SRDS), Hong Kong, China, 26–29 September 2017; IEEE: New York, NY, USA, 2017; pp. 253–255. [Google Scholar]
- Zheng, K.; Liu, Y.; Dai, C.; Duan, Y.; Huang, X. Model checking PBFT consensus mechanism in healthcare blockchain network. In Proceedings of the 2018 9th International Conference on Information Technology in Medicine and Education (ITME), Hangzhou, China, 19–21 October 2018; IEEE: New York, NY, USA, 2018; pp. 877–881. [Google Scholar]
- Xu, F.; Yang, G.-W.; Ju, D.-P. Design of distributed storage system on peer-to-peer structure. J. Softw. 2004, 15, 268–277. [Google Scholar]
- Coelho, I.M.; Coelho, V.N.; Araujo, R.P.; Qiang, W.Y.; Rhodes, B.D. Challenges of PBFT-Inspired Consensus for Blockchain and Enhancements over Neo dBFT. Future Internet 2020, 12, 129. [Google Scholar] [CrossRef]
- Hasimoto-Beltran, R.; Lopez-Fuentes, F.A.; Vera-Lopez, M. Hierarchical P2P architecture for efficient content distribution. Peer-Peer Netw. Appl. 2019, 12, 724–739. [Google Scholar] [CrossRef]
- Wang, F.; Xiong, Y.; Liu, J. mTreebone: A hybrid tree/mesh overlay for application-layer live video multicast. In Proceedings of the 27th International Conference on Distributed Computing Systems (ICDCS’07), Toronto, ON, Canada, 25–29 June 2007; IEEE: New York, NY, USA, 2007; p. 49. [Google Scholar]
- Castro, M.; Druschel, P.; Hu, Y.C.; Rowstron, A. Exploiting NETWORK Proximity in Peer-to-Peer Overlay Networks. 2002. Available online: https://www.microsoft.com/en-us/research/publication/exploiting-network-proximity-peer-peer-overlay-networks/ (accessed on 22 July 2021).
- Chen, Y.; Li, M.; Zhu, X.; Fang, K.; Ren, Q.; Guo, T.; Chen, X.; Li, C.; Zou, Z.; Deng, Y. An improved algorithm for practical byzantine fault tolerance to large-scale consortium chain. Inf. Process. Manag. 2022, 59, 102884. [Google Scholar] [CrossRef]
- Amir, Y.; Danilov, C.; Dolev, D.; Kirsch, J.; Lane, J.; Nita-Rotaru, C.; Olsen, J.; Zage, D. Steward: Scaling byzantine fault-tolerant replication to wide area networks. IEEE Trans. Dependable Secur. Comput. 2008, 7, 80–93. [Google Scholar] [CrossRef]
- Neiheiser, R.; Matos, M.; Rodrigues, L. Kauri: Scalable bft consensus with pipelined tree-based dissemination and aggregation. In Proceedings of the ACM SIGOPS 28th Symposium on Operating Systems Principles, Virtual, 26–29 October 2021; pp. 35–48. [Google Scholar]
- Yin, M.; Malkhi, D.; Reiter, M.K.; Gueta, G.G.; Abraham, I. Hotstuff: Bft consensus with linearity and responsiveness. In Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing, Toronto, ON, Canada, 29 July–2 August 2019; pp. 347–356. [Google Scholar]
- Garces-Erice, L.; Biersack, E.W.; Ross, K.W.; Felber, P.A.; Urvoy-Keller, G. Hierarchical peer-to-peer systems. Parallel Process. Lett. 2003, 13, 643–657. [Google Scholar] [CrossRef]
- Lv, W.; Zhou, X.; Yuan, Z. Design of tree topology based Byzantine fault tolerance system. J. Commun. 2017, 38, 139. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).