Renewed Interest in Spectroscopy of the Lightest Doubly-Odd N = Z Nuclei

Abstract

The existing experimental data for the $\gamma$ decay of the stable $N=Z$ doubly-odd nuclei and the $\beta$ decay of the corresponding isospin multiplets is reviewed. The structure of the lightest nuclei with masses $A\le 14$ is used to test and constrain ab initio nuclear theories. Most of the data were obtained in the second half of the last century and, in some cases, lack the needed precision for comparison with theoretical calculations. Recent spectroscopic studies in the lightest doubly-odd N = Z nuclei are discussed, as well as open problems related to the understanding of their structures and ideas for future experiments.

1. Introduction

The theoretical description of light nuclei is a subject of ab initio calculations in a challenging attempt to understand their structures from first principles. For a recent review, see Ref. [1] and the references therein. In many cases, the calculations successfully reproduce physics quantities, such as binding energies, rms charge radii, nuclear magnetic dipole and electric quadrupole moments, level schemes, and transition rates.

There are only four stable $N=Z$ doubly-odd nuclei, the deuteron ($N=Z=1$), ${}^6$Li ($N=Z=3$), ${}^{10}$B ($N=Z=5$), and ${}^{14}$N ($N=Z=7$), which are called self-conjugate nuclei. Since the deuteron, ${}^2$H, does not have excited states, here, we limit ourselves to ${}^6$Li, ${}^{10}$B, and ${}^{14}$N. The experimental observables of interest in these nuclei are the energies of the excited states; the spin parity, $J^{\pi }$, and isospin, T; assignments of the ground and excited states; the half-lives, $t_{1/2}$, of bound and resonance states; and their total, $\Gamma$, and partial, ${\Gamma }_i$, decay widths, where $i=\gamma$ stays for $\gamma$ decay and $i=\alpha$− for $\alpha$ decay. Experimental studies related to their structure were carried out in the 1960s to 1980s, being some of the first nuclear systems to be addressed. The evaluated experimental data for the $A=6$, $A=10$, and $A=14$ mass chains are available in Refs. [2,3,4], respectively. However, with the advances in ab initio many-body theories, there is renewed interest in the structures of these nuclei. The reason is that, in the pioneering studies, the experimental techniques were in their infancy, and many subtle structural effects remained unexplored. In this paper, we discuss the recent spectroscopic studies in the lightest doubly-odd $N=Z$ nuclei, as well as open problems related to the understanding of their structures and ideas for the next experiments.

The structures of these nuclei in terms of the shell model are described with the lowest-lying orbits, having in ground state the nucleons in the $1s1p$ shell and populating excited states across the shell gap in the $2s1d-2p1f$ shell. The modern description of these nuclei is based on two-nucleon (NN) and three-nucleon (3N) interactions derived from chiral effective field theories (EFT). The strong interaction is sufficiently small to allow perturbative expansions at high energies but large in the low-energy domain relevant for nuclear structure and dynamics. This makes the description of the lightest nuclei possible at the quantum chromodynamics (QCD) level and thus serves as a testing ground for different effective interactions that are consistent with the QCD symmetries.

Isospin quantum number and isospin mixing: Traditionally, the lightest doubly-odd $N=Z$ nuclei and their isobars are the foundations for studies of the isospin effects in nuclei. The isospin quantum number, T, was introduced by Heisenberg to describe the two different charge states of the nucleon [5]. The projection of T on the z-axis, $T_z$, in the isospin space takes a value $+\frac{1}{2}$ for the neutron and $-\frac{1}{2}$ for the proton. Two couplings, anti-symmetric, $T=0$, and symmetric, $T=1$, are possible in proton–neutron (pn) pair correlations, and both channels play an important role in nuclear structure studies.

The appearance of the $T=0$ pn pair is peculiar to $N=Z$ doubly-odd nuclei. Unlike the $T=1$ pair, the $T=0$ pn pair has intrinsic spin $S=1$, similar to the deuteron, and, therefore, it provides different J states in the low-energy region because of angular momentum coupling. Experimentally, it is known that many $T=0$ states coexist along with the $T=1$, $J^{\pi }=0^{+}$ state in the low-energy spectra of these nuclei. Moreover, a high J state with $T=0$ comes down to the ground state in many $N=Z$ doubly-odd nuclei in the light mass region. For example, the ground state (gs) of ${}^{10}$B is the $J^{\pi }=3^{+}$ state, for which the importance of three-nucleon forces is discussed in the no-core shell model calculations [6,7].

Competition between $T=0$ and $T=1$ pn pairs has been attracting great interest and was proposed to describe the level ordering of $T=1$, $J^{\pi }=0^{+}$ and $T=0$, $J^{\pi }=1^{+}$ states in $N=Z$ doubly-odd nuclei and neighboring nuclei. Thus, in these nuclei, in addition to the well-known spin-parity selection rules for $\gamma$-ray transitions, additional isospin selection rules come into action, e.g., for $\Delta T=0$ transitions, $E1$ transitions are forbidden and $M1$ transitions are strongly suppressed and are much weaker than their counterparts, which involve $\Delta T=1$ isospin change transitions. Isospin is an approximate quantum number, and spectroscopic studies in light doubly-odd nuclei are a tool for the study of isospin-mixing effects. Experimental evidence for isospin symmetry breaking are isospin-forbidden processes, which are due to isospin mixing, e.g., the observation of isospin-forbidden Fermi $\beta$ decay, the existence of $E1$ transitions in $N=Z$ nuclei, the strength of the $\Delta T=0$, $M1$ transitions or the isospin-forbidden nucleon emission. Isospin violation appears also in the violation of the isobaric multiplet mass equation (IMME) [8] and by isospin-forbidden transitions in direct reactions. Data about the observed isospin-forbidden dipole decays in light nuclei are summarized in Ref. [9]. Isospin mixing was studied in direct reactions and was reported for all nuclei of interest, i.e., ${}^6$Li [10], ${}^{10}$B [11] and ${}^{14}$N [12].

Isobaric analog states (IAS) and isospin multiplets: IAS are observed in neighboring nuclei. For example, for the $A=10$ mass chain, ${}^{10}$Be, ${}^{10}$B, and ${}^{10}$C may be regarded as consisting of a ${}^8$Be core plus two nucleons. Therefore, certain energy levels in these nuclei should be similar. Thus, the $J^{\pi }=0_1^{+}$, $T=1$ IAS is at similar energies compared to the $T=1$, $J^{\pi }=0^{+}$ states, which are the gs in ${}^{10}$Be and ${}^{10}$C. Similar isospin triplets are observed for the $A=6$ and $A=14$ mass chains. Studies of the decay of the IAS in mass triplets provide information about the isospin symmetry breaking, as recently done for the $A=10$ mass chain [13], where the rate of the $T=1$, $J^{\pi }=2^{+}$ to $T=1$, $J^{\pi }=0^{+}$ transition in ${}^{10}$B ($T=1$, $T_z=0$) is compared to the analog transitions in ${}^{10}$Be ($T=1$, $T_z=-1$) and ${}^{10}$C ($T=1$, $T_z=+1$) and provides constraints on ab initio calculations using realistic nuclear forces.

In a recent review, the current data for the $\beta$ and $\gamma$ decays from the IAS in a $T=1$, $T=3/2$, and $T=2$ multiplets were discussed from the point of view of recoil effects and weak magnetism [14]. For example, the decay of the $T=1$ IAS to a common $T=0$ daughter state makes it possible to extract the weak magnetism form factors of the $\beta$ transitions. Here, we summarize the data related to the self-conjugate nuclei of interest.

Clustering effects: In the light-mass $N=Z$ region, $\alpha$ clustering is another important feature, which brings rich structures together with the pn correlations. These states are described in the framework of the antisymmetrized molecular dynamics (AMD) models [15,16]. For a recent review, see Ref. [17]. The method was applied to ${}^{10}$B and describes the coexistence of $T=0$ and $T=1$ states in low-energy spectra. Strong $M1$, $0_1^{+}\to 1_1^{+}$, and $E2$, $1_2^{+}\to 1_1^{+}$ transitions are understood by the spin excitation of the pn pair and the rotation of a deformed core, respectively [18].

The $\alpha$ clusters in light nuclei are considered to be weakly bound with the other nucleons and form a spatially localized subsystem. Therefore, intrinsic excitations of the $\alpha$ cluster are expected. The excitation of the giant dipole resonance (GDR) of the $\alpha$ cluster provides distinct experimental evidence for clustering in atomic nuclei.

Total and partial widths and branching ratios: A quick check of the existing data for ${}^6$Li [2], ${}^{10}$B [3], and ${}^{14}$N [4] shows that, in many cases, the widths of the levels and the $\gamma$-ray to $\alpha$-particle branching ratios are reported with large uncertainties. Therefore, experiments should aim at the precise and accurate determination of the width of the states of interest through $\gamma$-ray to $\alpha$-particle branching ratio measurements. Recently, some precise measurements became available, e.g., for ${}^6$Li [19], where a direct measurement of the decay width of the excited $T=1$, $J^{\pi }=0^{+}$ state was done. This measurement was used to extract the transition rate to the $T=0$, $J^{\pi }=1^{+}$ ground state, which was compared to the results of ab initio calculations based on chiral effective field theory, which takes into account contributions to the magnetic dipole operator beyond leading order.

Clearly, further precise measurements are needed in the light nuclei. In this paper, we discuss the results of the most recent experiments, address the prospective experimental techniques and point out some of the open problems in these nuclei.

2. Level Schemes and Open Problems

2.1. Experimental Data about ${}^6$Li

The nucleus ${}^6$Li is one of the simplest many-body systems, having three protons and three neutrons. Evaluated data and references related to ${}^6$Li are to be found in Ref. [2]. A partial level scheme of ${}^6$Li, revealing the levels below the neutron separation energy, is shown in Figure 1. There are in total three excited states below the proton separation threshold and two more states above the proton separation energy. A number of resonance states have been reported, too. Except for the highest lying $1_2^{+}$ state, $\gamma$-ray transitions are reported between the excited states and the ground state. The energies of the $\gamma$-rays and the energies of excited states, which are given in the text and Figure 1, are taken from the evaluated nuclear structure data file (ENSDF) [2]. In some cases, these values differ from each other.

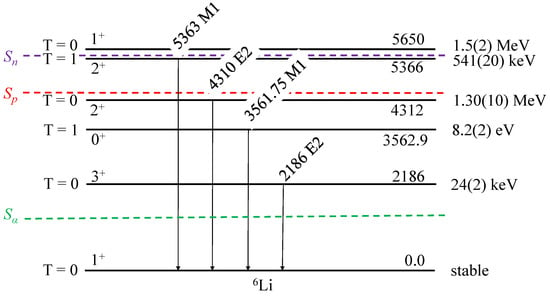
Figure 1. Partial level scheme of the ${}^6$Li. The energies and the multipolarities of the observed $\gamma$-ray transitions are indicated above the arrows. $S_{\alpha }$, $S_p$ and $S_n$ indicate the $\alpha$, proton and neutron separation energies, correspondingly. On the left-hand side of the figure are indicated the isospin and spin-parity assignments of the level; on the right-hand side are their total decay widths from Ref. [2].

In terms of the shell model, the gs of ${}^6$Li is described as having two protons and two valence neutrons occupying the 1s shell and one valence proton and one valence neutron in the 1p shell. Isospin $T=0$ and spin parity $J^{\pi }=1^{+}$ are assigned to the ground state. The first excited state is a $T=0$, $J^{\pi }=3^{+}$ state, and the second one is a $T=1$, $J^{\pi }=0^{+}$ IAS. Only a few $\gamma$-ray transitions have been observed in ${}^6$Li, as indicated in the level scheme in Figure 1. No branching ratios of the $\gamma$-rays, as well as no $\alpha$-branching ratios, have been reported. Gamma-ray spectroscopic studies in the heavier $N=Z$ nuclei, e.g., ${}^{10}$B, report a number of weak transitions between states with similar structures. It is interesting to study the $\gamma$ decay of IAS in ${}^6$Li in more detail and find out whether such weak transitions can be observed.

No data about the $\alpha$ decay widths, ${\Gamma }_{\alpha }$, in ${}^6$Li have been reported. The existence of $\alpha$-decay resonances can be measured in a photo-disintegration experiment with a quasi-monochromatic $\gamma$-ray beam, as recently done for ${}^7$Li [20].

Isospin mixing, i.e., the impurities of the isospin quantum number, in ${}^6$Li was studied by Bray et al. [10]. They populated the 5163.9-keV, $J^{\pi }=2^{+}$, $T=0$ state in the ${}^7$Li(${}^3$He,$\alpha$)${}^6$Li reaction and measured the disintegration of ${}^6$Li into an $\alpha$ particle and deuteron. The experiment imposed an upper limit for the $\alpha$-decay branch of < 10${}^{-2}$, resulting in an upper limit for the isospin-mixing coefficient of $\alpha \le 8·{10}^3$.

The ${}^6$Li nucleus can be understood as a ${}^4$He core and a pn pair coupled to it. Experimentally, two resonance components of the GDR are observed in ${}^6$Li, a low-energy component at ∼12 MeV and a high-energy component at ∼28 MeV. Note that in ${}^4$He, the isovector giant dipole resonance (IVGDR) is located at $E_{GDR}$(${}^4$He) = 26 MeV. Splitted dipole resonances were reported in ($p,p^{\prime }$), (${}^3$He,t) and (${}^7$Li,${}^7$Be) reactions on ${}^{6,7}$Li and were commonly excited in the $A=6$ (${}^6$Li, ${}^6$Be, ${}^6$He) and $A=7$ (${}^7$Li, ${}^7$Be, ${}^7$He) nuclei [21].

In a recent photoneutron experiment, the splitting of the GDR in ${}^6$Li was confirmed [22]. The GDR was studied via the ${}^6$Li($\gamma$,$xn$) reactions using quasi-monochromatic $\gamma$-rays in the energy range $E_{\gamma }=4.9–53.6$ MeV. The $\gamma$-beams were generated in the Compton backscattering of relativistic electrons at the NewSUBARU storage ring at the SPring-8 laboratory in Japan.

Recently, direct measurement of the decay width, ${\Gamma }_{\gamma }$, of the $T=1$, $0^{+}$ IAS was performed using the newly developed relative self-absorption technique [19]. Prior to this experiment, the ENSDF value ${\Gamma }_{\gamma }=8.19\left(17\right)$ eV, and, correspondingly, a value for the isovector dipole transition probability $B\left(M1\right)=15.65\left(32\right)$ ${\mu }_N$, was reported [2]. These values were based on an evaluation using the most precise last measurements, neglecting approximately ten other measurements, which either scattered or had too large uncertainties [4]. However, two of these three measurements were done in (e,$e^{\prime }$) scattering experiments [23,24]. In such an experiment, the extracted $B\left(M1\right)$ is model dependent and is obtained from the measured form factor $\mid F\left(q\right){\mid }^2$, where q is the transferred momentum. In the experiment of Friman-Gayer et al., a value of ${\Gamma }_{\gamma }(0_1^{+}\to 1_1^{+})=8.17{{(}_{-013}^{+0.14})}_{stat}{{(}_{-0.11}^{+0.10})}_{syst}$ eV was reported [19], in line with the previous evaluated value, which corresponds to a transition probability $B(M1;0^{+}\to 1^{+})=15.61{{(}_{-0.25}^{+0.27})}_{stat}{{(}_{-0.21}^{+0.19})}_{syst}{\mu }_N^2$.

The $0_{1,T=1}^{+}\to 1_{1,T=0}^{+}$ transition in ${}^6$Li is the electromagnetic (EM) analog transition to the ${}^6$He $\beta$ decay (see Figure 2). The $\beta$ decay of ${}^6$He is remarkably simple. Except for a small branch of ∼10${}^{-6}$ [25], it proceeds exclusively to the ground state of ${}^6$Li; see Figure 2. However, early work on the ${}^6$He half-life yielded controversial results [26,27,28,29,30], reporting values around 807 ms [26,27] and below 800 ms [28,29,30]. Recently, intense ${}^6$He sources were built [31,32], which enabled high-precision measurements of the ${}^6$He half-life [31,33]. The experiments yielded consistent values, i.e., $t_{1/2}=806.89\pm 0.{11}_{stat}{{(}_{-0.19}^{+0.23})}_{syst}$ ms [33] and $t_{1/2}=807.25\pm 0.{16}_{stat}\pm 0.{11}_{syst}$ ms [31], improving the precision by a factor of six. This allowed us to extract the value, which was reported, e.g., as $ft=803.{04}_{-0.23}^{+0.26}$, resulting in a Gamow–Teller matrix element for the ${}^6$He $\beta$ decay of $\left|M\right(GT\left)\right|=2.1645\left(43\right)$ [33].

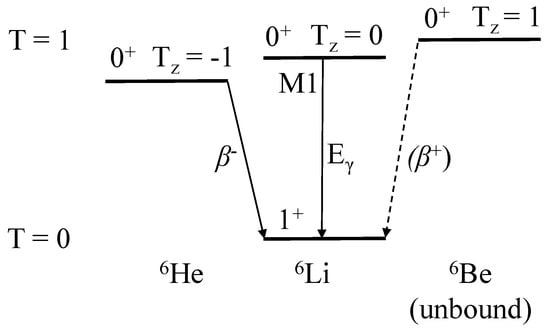
Figure 2. The $T=1$ isospin triplet for the $A=6$ nuclei. The isospin projection and the spin-parity assignments of the levels are indicated, as well as their decay to the common $T=0$ state in ${}^6$Li.

The new measurements of IAS ${\Gamma }_{\gamma }$ in ${}^6$Li and the $t_{1/2}$ of ${}^6$He make a comprehensive test of electroweak interactions possible for the $A=6$ multiplet. The idea is that the weak magnetism form factor, b, mixes with the dominant axial-vector strength in a Gamow–Teller transition. The conserved-vector-current (CVC) hypothesis [34,35] states that the vector current, $V_{\mu }$, from $\beta$ decay forms an isospin triplet with the electromagnetic current, $J_{\mu }^{EM}$,

$$V_{\mu }=\mp [{\tau }^{\pm },J_{\mu }^{EM}],$$

(1)

where ${\tau }^{\pm }$ is the isospin ladder operator. In the case of a $\beta$ decay where $\Delta T=1$, the CVC hypothesis results in a relation of the weak magnetism form factor [36], b, to the isovector part of the decay width, ${\Gamma }_{\gamma }$, of the corresponding analog $M1$ $\gamma$ transition,

$$b^2=6\eta \frac{{\Gamma }_{\gamma }{M}^2}{\alpha E_{\gamma }^3},$$

(2)

where M is the average mass of the mother and daughter nucleus, $\alpha$ is the fine structure constant, $E_{\gamma }$ is the $\gamma$-ray energy and $\eta$ is equal to unity in the case that the final state is the same for the $\beta$ and $\gamma$ decay, and $\eta =(2J_i+1)/(2J_f+1)$ when the initial (i) and final (f) states of the $\gamma$-ray transition are reversed relative to the $\beta$ decay; $J_i$ and $J_f$ are the spins of the states, correspondingly.

The evidence of a weak magnetism component is the observation of a term, $(1+C_0+C_{1}E+C_{-1}/E)$, which multiplies the $\beta$-energy spectrum; here, E is the total energy of the $\beta$ particle and the coefficients $C_i$ depend on the weak magnetism factor, and the Gamow–Teller strength is

$$C_1=\frac{2}{3M}\left(5+\frac{2b}{g_{A}M\left(GT\right)}\right)$$

(3)

$$C_{-1}=\frac{2m_e^2}{3M}\left(1+\frac{b}{g_{A}M\left(GT\right)}\right),$$

(4)

where M is the mass of the recoiling nucleus, $m_e$ is the electron mass and $g_A$ is the nucleon axial weak coupling constant.

At present, the uncertainty of the $C_i$ coefficients is dominated by the experimental uncertainty of the IAS $\gamma$-decay width in ${}^6$Li, and possible tensor form factor terms are neglected. The $\beta$-energy spectra have been measured in several neutral or ion trap-based experiments. For a recent review, see Ref. [37]. It should be noted that a weak magnetism component was observed in the shape of the Gamow–Teller $\beta$-decay spectra in ${}^{12}$B and ${}^{12}$N [38]. The physics picture for the $A=6$ mass chain might be more complicated, since the IAS in ${}^6$He and ${}^6$Li is suggested to have a halo structure [39,40].

2.2. Experimental Data about ${}^{10}$B

The nucleus ${}^{10}$B has five protons and five neutrons. Evaluated data and references related to ${}^{10}$B can be found in Ref. [3]. A partial level scheme is shown in Figure 3. The levels of ${}^{10}$B are particle bound below $\alpha$-particle separation energy $S_{\alpha }$ = 4.4461 keV. The proton and neutron separation energies are also indicated in Figure 3. There are in total four excited states below the $\alpha$-separation energy, six more excited states below the proton separation energy, four more states below the neutron separation energy and one more state above the neutron separation energy. Gamma-decay transitions were observed for all these states, as well as for a few resonance states. In terms of the shell model, the gs of ${}^{10}$B can be described as having two protons and two neutrons in the $1s$ shell and three valence protons and three valence neutrons in the $1p$ shell. This results in a more complicated level scheme compared to ${}^6$Li. The energies of the $\gamma$ rays and the energies of excited states, which are given in the text, Table 1 and Table 2 and Figure 2, are taken from the evaluated data file [3]. In some cases, these values differ.

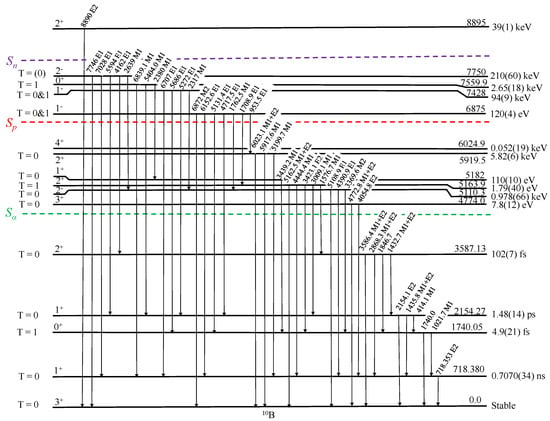
Figure 3. Partial level scheme of the ${}^{10}$B. The notations are the same as defined in Figure 1. For the levels below $S_{\alpha }$, the half-life is indicated, while, for those above $S_{\alpha }$, the total decay width is shown.

Table 1. Branching ratios for the bound states in ${}^{10}$B were reported in different experiments. The values are in percentages. In the first three columns, the energies of the initial, $E_i$, and final, $E_f$, levels, and the energies of the $\gamma$-ray transitions, $E_{\gamma }$, in keV, are indicated.

${\mathit{E}}_{\mathit{i}}$ (keV)	${\mathit{E}}_{\mathit{f}}$ (keV)	${\mathit{E}}_{\mathit{\gamma }}$ (keV)	Ref. [41]	Ref. [42]	Ref. [43]	Ref. [44]	Ref. [45]	Ref. [46]	Ref. [47]
1740.05	0.0	1740.0	-	-	-	<0.2	<0.5	<0.5	-
	718.380	1021.7	-	100	-	100	100	100	-
2154	0.0	2154.1	-	16	27(7)	24	17.5(20)	20.2(14)	17.5(4)
	718.380	1435.8	-	29	26(6)	23	26.3(20)	28.6(20)	24.8(5)
	1740.05	414.1	-	55	47(5)	53	56.2(20)	51.2(31)	57.7(6)
3587	0.0	3586.4	21(5)	-	18	12	16.6(20)	24.2(17)	16.7(3)
	718.380	2868.3	58(11)	-	54	76	68.1(20)	63.8(19)	66.0(5)
	1740.05	1846.7	-	-	10(5)	<0.3	<5	<1	<1
	2154.27	1432.7	21(5)	-	18	12	15.4(20)	12.0(9)	17.3(3)

Table 2. Branching ratios for the 5163.9-keV unbound state in ${}^{10}$B were reported in different experiments. The notations are the same as in Table 1.

${\mathit{E}}_{\mathit{i}}$ (keV)	${\mathit{E}}_{\mathit{f}}$ (keV)	${\mathit{E}}_{\mathit{\gamma }}$ (keV)	Ref. [48]	Ref. [49]	Ref. [50]	Ref. [51]	Ref. [52]	Ref. [47]
5163.9	0.0	5162.5	5(1)	7	-	4.4(4)	-	7.3(5)
	718.380	4444.4	24(3)	27	-	22.4(6)	-	55.5(16)
	1740.05	3423.1	2(1)	-	<0.5	0.7(2)	<0.6	0.16(4)
	2154.27	3009.1	69(5)	57	-	64.8(9)	-	31.7(12)
	3587.13	1576.7	-	9(2)	4.5(10)	7.7(3)	-	5.3(5)

The gs of ${}^{10}$B is the $T=0$, $J^{\pi }=3^{+}$ state, the first excited state is the 718.380-keV $T=0$, $J^{\pi }=1^{+}$ state and the second excited state is the 1740.05-keV, $T=1$, $J^{\pi }=0^{+}$ IAS. The half-life of the IAS state is known with large uncertainty $t_{1/2}(0^{+},T=1)=4.9\left(21\right)$ fs, and it would be interesting for it to be measured with higher precision, as done recently for ${}^6$Li [19].

The $\gamma$ decay of the partically bound states in ${}^{10}$B was measured in a number of experiments [41,42,43,44,45,46,47]. The results are summarized in Table 1 and demonstrate a considerable spread between the different measurements. The $\gamma$-decay data for the unbound 5163.9-keV, $T=1$, $J^{\pi }=2^{+}$ state are summarized in Table 2 [47,48,49,50,51,52]. Most of the reported measurements have uncertainties between ∼10% and ∼25%, which necessitates new, precise measurements of the reported weak branches, especially such as the reported uncertain ($M3$) transition between the IAS and the gs, the reported $E2$ transition between the 3587.13-keV state and the IAS, and the $E2$ transition between the 5163.9-keV level and the IAS (see Table 1 and Table 2).

The $T=1$, $J^{\pi }=2^{+}$, 5163.9-keV level appears as a triplet with the $T=0$, $J^{\pi }=2^{-}$, 5110.3-keV and the $T=0$, $J^{\pi }=1^{+}$, 5182-keV levels in the decay of the particle-unbound levels of ${}^{10}$B. Even if all the levels are above the $\alpha$ decay threshold, because of the isospin conservation, $\alpha$ decay is isospin-forbidden for the 5163.9-keV level. Therefore, there is competition between $\alpha$ and $\gamma$ decay, while the 5110.3-keV and 5182-keV levels decay by almost 100% $\alpha$ emission.

In this section, we focus on the $\gamma$-decay branching ratios and, especially, on the reported weak transitions. The 1740.0-keV ($M3$) transition has been established in $(\pi ,{\pi }^{\prime })$ [53], $(e,e^{\prime }d)$ [54] and $(e,e^{\prime })$ [55,56,57] experiments, which aimed at understanding the gs structure. The 1846.7-keV $E2$ transition is between $2_{1,T=0}^{+}\to 0_{1,T=1}^{+}$ states. Both transitions are very weak since isospin change is involved and it is not likely that they are collectively enhanced. As demonstrated in Table 1, there is no firm evidence for the 1740.0-keV and 1846.7-keV $\gamma$-ray transitions. The 3423.1-keV, $2_{2,T=1}^{+}\to 1_{0,T=1}^{+}$, $\gamma$-ray transition has been measured in several experiments (see Table 2). Recently, McCutchan et al. placed a limit of 0.16(4)% on this $\gamma$-ray branch by using the ${}^{10}$B(p,$p^{\prime }\gamma$)${}^{10}$B reaction [47]. This work reports so far the most precise result related to the weak $\gamma$-ray branches in ${}^{10}$B.

Electron scattering experiments from ${}^{10}$B were performed to determine the transverse form factor, $F_{M3}\left(q\right)$, of the 1740.05-keV level in the momentum transfer range of $q=0.61$ to $1.81$ fm${}^{-1}$ [55]. The experimental form factor was described by the generalized Helm model [58], which yielded the ground state radiative width as ${\Gamma }_{\gamma }=1.05\left(25\right)$·${10}^{-7}$ eV, which corresponds to a transition probability $B(M3;1^{+}\to 0^{+})=6.0\left(14\right)e^2$fm${}^6$. The multipolarity of the transition was reported as pure $M3$, although a note was added that this transition could be $E2$ or a mixture of both. Hicks et al. studied the form factor of the same level in the higher momentum transfer range of 2.0 to 3.9 fm${}^{-1}$ to determine the radial shape of the 1$p_{3/2}$ single-particle wave function [56]. Detailed calculations on the effects of core polarization of $(e,e^{\prime })$ reactions were done for transitions between $1p$-shell states [59]. A high-resolution measurement of the electron-scattering transverse form factor of the 1740.0-keV $M3$ transition has been performed in the momentum transfer range $q=0.481$ to $2.581$ fm${}^{-1}$ [57]. The obtained results were explained by expanding the shell model basis space to $2\hslash \omega$, including core polarization. However, the structure of the $J^{\pi }=3^{+},T=0$ gs still poses questions and needs to be addressed via ab initio calculations.

Recently, in an attempt to obtain a better understanding of isospin effects and charge symmetry breaking in the $A=10$ nuclei, several experiments were performed. The first precise measurements using the Doppler shift attenuation method (DSAM) of the half-lives of electromagnetic transitions in ${}^{10}$Be and ${}^{10}$C were carried out [60,61]. The partial $\gamma$-decay branch of the ($J^{\pi }=2^{+},T=1,5163.9$ keV) → ($J^{\pi }=0^{+},T=1,1740.05$ keV) isoscalar transition was measured as 0.16(4)% [47]. Further, the $\alpha$-decay branching ratio for the 5163.9-keV, $J^{\pi }=2^{+},T=1$ was addressed [13]. Previously, this branching ratio was reported as <$0.20$ [62], $0.13\pm 0.04$ [63], $0.27\pm 0.15$ [44]. The new measurement yielded a value ${\Gamma }_{\alpha }/\Gamma =0.144\left(27\right)$. Finally, by combining the two results, the $B\left(E2\right)$ of the isoscalar transition was determined as $B\left(E2\right)=7.0\pm 2.2$ e${}^2$fm${}^2$ [13].

The isospin impurity of the 6875-keV, $J^{\pi }=1^{-}$, $T=0$ state in ${}^{10}$B was studied in the ${}^9$Be($p,\gamma$)${}^{10}$B reaction [64]. The transitions from the 6875-keV resonance level to the first three excited states of ${}^{10}$B are all $E1$ transitions. According to the isospin selection rule, although $E1$ transitions that have $\Delta T=0$ are prohibited, the transitions from the 6875-keV resonance level of ${}^{10}$B to the first and third excited levels were established. The observation of such an isospin-forbidden decay mode indicates isospin-symmetry breaking and the presence of isospin mixing in the 6875-keV state as a $T=1$ impurity admixture [65]. The 7428-keV state was suggested as an isospin-mixed pair state to the 6875-keV state. The isospin-mixing coefficients were derived in Ref. [11]. The idea is that the two states mix, which makes it possible to observe isospin-forbidden transitions. The wave functions of these two states can be expressed as

$$\begin{array}{c}\hfill |6875>=\alpha |1^{-},T=0>+\beta |1^{-},T=1>\\ \hfill |7428>=-\beta |1^{-},T=0>+\alpha |1^{-},T=1>\end{array}$$

(5)

where ${\alpha }^2+{\beta }^2=1$. The isospin impurity, ${\alpha }^2$, can be estimated from the ratio of the $E1$ transition strength of the isospin-forbidden transitions to the 718.380- and 2154-keV states and the allowed transitions to the 1740.05-keV, IAS state as

$${\alpha }^2\left(T^{\prime }\right)\sim \frac{{\left|B(E1;6875\to 718.380)\right|}^2}{{\left|B(E1;6875\to IAS)\right|}^2}vs.\frac{{\left|B(E1;6875\to 2154)\right|}^2}{{\left|B(E1;6875\to IAS)\right|}^2}$$

(6)

where $T^{\prime }$ is the intensity of admixed isospin in the 6875-keV state. The isospin impurity coefficient in the 6875-keV state was obtained as ${\alpha }^2=0.17$ and ${\alpha }^2=0.14$, respectively, by using the first and second parts of Equation (6).

Recently, the $\gamma$-decay transitions in ${}^{10}$B were measured in a ($p,p$${}^{\prime }$$\gamma$) experiment [66] at the Horia Hulubei National Institute for R&D in Physics and Nuclear Engineering (IFIN-HH). A hybrid array of HPGe detectors and large-volume LaBr${}_3$:Ce and CeBr${}_3$ detectors placed in anti-Compton shields was used. Details of the experimental setup can be found in Ref. [67]. Such a setup makes it possible to detect weak transitions with MeV energies and study branching ratios at a level ≥ 10${}^{-5}$.

Interesting nuclear structure studies in ${}^{10}$B are related to the nature of the $T=1$, $J^{\pi }=0^{+}$, 1740.05-keV, and $J^{\pi }=2^{+}$, 5163.9-keV states. These states are the isobaric analogs to the $0^{+}$ gs and $2^{+}$ excited states in the neighboring $T=1$ nuclei ${}^{10}$Be and ${}^{10}$C. In a cluster picture, these states can be described as consisting of two $\alpha$-particles and a pn, nn or pp pair as valence nucleons coupled to them. The positive low-lying spectrum of ${}^{10}$Be contains several rotational bands, such as ground and excited state bands, up to their 4${}^{+}$ state [3,68,69,70]. These bands are understood as being built on a molecular state consisting of two $\alpha$ clusters, resembling an ${}^8$Be core, plus two valence neutrons in molecular orbitals. There are two types of orbits, $\sigma$ and $\pi$. The $\sigma$ molecular orbital originates from the overlap orbitals of the valence particles in a head-to-head direction along the inter-nuclear axis, while the $\pi$ molecular orbitals occur in a parallel direction. The valence neutrons can be placed either in a $\sigma$ orbital (positive parity around the equator of the molecular state) or in a $\pi$ (negative parity, with lobes extending along the axis of the molecular state). Thus, the gs band in ${}^{10}$Be has a low moment of inertia (weakly deformed) with two neutrons in $\sigma$ orbitals, while the excited band built on the 6.2-MeV state has a high moment of inertia (strongly deformed) due to the neutrons extending far past the ends of the molecular state, in $\pi$ orbitals. On the other hand, the negative parity bands have one neutron in a $\sigma$ orbital and one in a $\pi$ orbital [71]. Isobaric analogs of the 6.18, 7.54 and 10.15-MeV states in ${}^{10}$Be would correspond to rotational bands with a high moment of inertia in ${}^{10}$B and ${}^{10}$C [68,72,73]. In the ${}^{10}$B case, the cluster structure consists again of two $\alpha$ particles, but now with a proton and a neutron in the molecular orbitals. The relation of the highly deformed rotational band in ${}^{10}$Be at 7.54 MeV to the $J^{\pi }=2^{+}$, $T=1$ state at 8895 keV in ${}^{10}$B is discussed in Ref. [74]. A $T=1$ state is obtained through ${}^{11}$B(${}^3$He,$\alpha$)${}^{10}$B reaction at 11.3-MeV excitation energy, which is a possible candidate for the $4^{+}$ state of this rotation band [75].

The $M1$, $0_{1,T=1}^{+}\to 1_{1,T=0}^{+}$ transition in ${}^{10}$B is an analog to the GT $\beta$-decay transition from the gs in ${}^{10}$C to the 718.380-keV, $J^{\pi }=1^{+}$, $T=0$ state in ${}^{10}$B as shown in Figure 4. It is a 98.500(20)% branch of the gs $\beta$ decay of ${}^{10}$C. The $\beta$ decay of the $J^{\pi }=0^{+}$, $T=1$ gs in ${}^{10}$C to the 1740.05-keV, $J^{\pi }=0^{+}$, $T=1$ state in ${}^{10}$B is a super-allowed Fermi transition. Its weight in the $\beta$-decay branching ratio of the ${}^{10}$C gs is 1.4601(19)% [3]. In a recent experiment, the value of this branch was reported to be 1.4638(50) [76]. For the determination of the experimental $ft$ value, the half-life, the $Q_{EC}$ value and the branching ratio are needed. Recently, high-precision half-life measurements of ${}^{10}$C were performed. Two experimental techniques, $\gamma$-ray photopeak, and $\beta$-decay counting, were utilized, yielding consistent results for the half-life, $t_{1/2}=19.2969\left(74\right)$ s and $t_{1/2}=19.3009\left(17\right)$ s, respectively [77]. The super-allowed Fermi $\beta$ decay of ${}^{10}$C will be discussed further in Section 2.3. The $B\left(GT\right)$ matrix element, which was extracted from the experimental data, agrees with theoretical calculations [14].

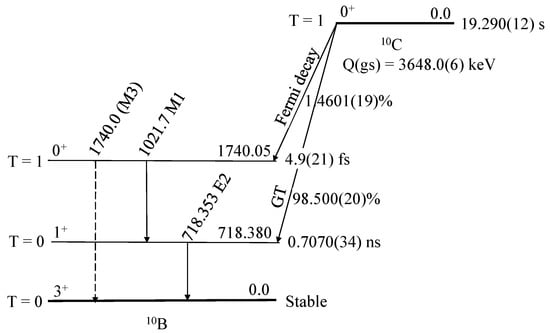
Figure 4. The $\beta$ decay of ${}^{10}$C to the excited states of ${}^{10}$B.

Ab initio no-core shell model (NCSM) calculations using four different realistic NN interactions have been reported in a recent theoretical study of ${}^{10-14}$B isotopes [78]. Among the applied relativistic NN interactions, inside-outside Yukawa (INOY) interaction provided a quite reasonable description of the gs energies, excitation spectra, and electromagnetic properties, e.g., magnetic moments and $M1$ transitions of boron isotopes. However, this interaction was not successful in the description of nuclear radii and hence density. Recent studies show that non-local 3N interactions should be included in the calculations to obtain the correct description of the nuclear binding and nuclear size.

2.3. Experimental Data about ${}^{14}$N

The nucleus ${}^{14}$N has seven protons and seven neutrons, being the heaviest stable doubly-odd self-conjugate nucleus. Evaluated data and references related to ${}^{14}$N can be found in Ref. [4]. A partial level scheme revealing the levels for which $\gamma$-ray transitions were observed is shown in Figure 5. The gs of ${}^{14}$N is the $T=0$, $J^{\pi }=1^{+}$ state and the first excited state is the 2312.8-keV, $T=1$, $J^{\pi }=0^{+}$ IAS. Again, as in the case of ${}^7$Li and ${}^{10}$B, the experimental data for ${}^{14}$N are known with rather large uncertainties, and the values of the reported branching ratios spread considerably. There are several weak branches—for example, the ones that are reported with an upper limit between 4915.1-keV and 3948.10-keV states and between 4915.1-keV and 2312.798-keV states.

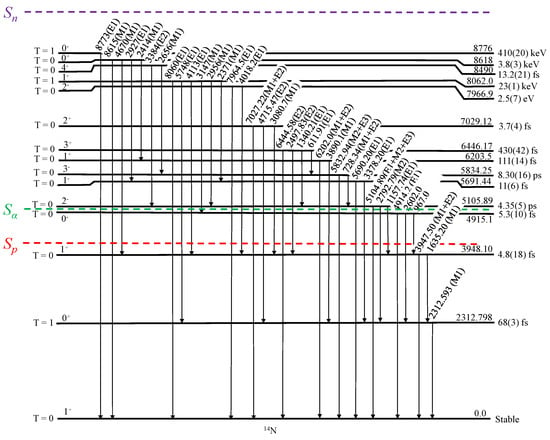
Figure 5. Partial level scheme of the ${}^{14}$N. The notations are the same as indicated in Figure 1.

Excited states in ${}^{14}$N were studied in a number of experiments. In most of the cases, the ${}^{13}$C($p,\gamma$) reaction was used [79,80,81,82,83,84], but also the ${}^9$Be(${}^7$Li,$2n\gamma$) [85], the ${}^{12}$C(${}^3$He,p) [86], and the ${}^{13}$C($p,n$) reactions [87] were explored.

In terms of the shell model, the gs of ${}^{14}$N can be described as having two protons and two neutrons in the $1s$ shell and one proton hole and one neutron hole in the $1p$ shell. Compared to ${}^7$Li and ${}^{10}$B, the level scheme of ${}^{14}$N is much more complicated since a larger number of excitations across the shell gap in the $2s1d-2p1f$ shell are possible. The levels in ${}^{14}$N are particle-bound below the $\alpha$-separation energy, $S_{\alpha }$. A shell model description of the excited states in ${}^{14}$N can be found in Ref. [88].

Several nuclear structure features of ${}^{14}$N have attracted experimental interest: the $\gamma$ decay in ${}^{14}$N, studies of isospin mixing in isospin-forbidden reactions, parity mixing of the $0^{+}/0^{-}$, $T=1$, states at ∼8 MeV, measurements of the radiative width of the IAS, studies of the Gamow–Teller $\beta$ decay of ${}^{14}$O and the super-allowed Fermi $\beta$ decay of ${}^{14}$O to the IAS in ${}^{14}$N. Most of these experiments were carried out in the 1960s–1980s, and some of them need to be repeated with better precision.

Isospin non-conservation in ${}^{14}$N was studied in isospin-forbidden reactions, such as ($d,\alpha$) [89], ($d,d^{\prime }$) [90,91,92] and (${}^6$Li,$\alpha$) [93]. The 2312.8-keV, $T=1, J^{\pi }=0^{+}$ IAS should not be excited in such reactions. In the experiments, the excitation of the IAS was compared to the excitation of the 3948.1-keV, $T=0,J^{\pi }=1^{+}$ excited state, and the reaction cross-section ratio was established. Two isospin-mixing reaction mechanisms have been considered, i.e., two-step processes involving isospin-mixed intermediate states in the reaction channel, or the involvement of resonances in the compound nucleus. In the case of ($d,d^{\prime }$) scattering, the reported isospin-mixing factor takes values in the range of 1–3% for energies of the incident deuterons in the interval 6–10 MeV [90] and decreases to 0.5% for energies in the interval 10–18 MeV [91,92]. For the ${}^{12}$C(${}^6$Li,$\alpha$)${}^{14}$N reaction, the isospin-forbidden cross-section was measured in the energy range 3.2–8.0 MeV and was found to be 1–2% [93]. The ${}^{16}$O($d,\alpha$)${}^{14}$N reaction was studied in the energy region of 14–18 MeV, in an attempt to understand the dominant reaction mechanisms. Two resonances were observed in the excitation function of the reaction at deuteron energies $E_d$ = 14.4 and 15.0 MeV, which were understood as compound-nucleus resonances, involving selected states in the compound nucleus. Renan et al. studied the $\gamma$ decay of the 5691.4-keV and 8062-keV, 1${}^{-}$ states in ${}^{14}$N and derived the isospin-mixing coefficients [12]. The $\gamma$ decay of a pair of $T=0$ and $T=1, J^{\pi }=1^{-}$ states was first discussed in Ref. [94]. The idea is that the two states mix, which makes it possible to observe isospin-forbidden transitions.

The isospin impurity, ${\alpha }^2$, was estimated from the ratio of the $E1$ transition strength as

$$\frac{{\left|B(E1;8062\to IAS)\right|}^2}{{\left|B(E1;8062\to gs)\right|}^2}vs.\frac{{\left|B(E1;5691.4\to gs)\right|}^2}{{\left|B(E1;8062\to gs)\right|}^2}=\frac{{\alpha }^2}{1-{\alpha }^2}$$

(7)

It is necessary to know the $\gamma$-decay widths, ${\Gamma }_{{\gamma }_i}$, of the two states and their branching ratios. The isospin-mixing coefficient for the 8062-keV transition ${\alpha }^2\left(8062\right)=0.046$ was obtained by comparing the B(E1) strength for the isospin-forbidden ($J^{\pi }=1^{-}$, $T=1$)→ ($J^{\pi }=0^{+},T=1$; IAS) transition, with that of the isospin-mixing coefficient reported as ${\alpha }^2\left(5691.4\right)=0.09$. These results were compared to shell model calculations [95].

Studies of parity mixing in ${}^{14}$N were described by Adelberger et al. [96]. Parity mixing for the $J^{\pi }=0_2^{+}$($E_i=8618$ keV)/$J^{\pi }=0_2^{-}$($E_i$ = 8776 keV), $T=1$ doublet can probe the isoscalar component of the parity non-conserving (PNC) NN interaction, which is the only example of a flavor-conserving hadronic weak interaction. The weak matrix element between the $0^{+}/0^{-}$ levels, $⟨H_{weak}⟩=0.38\pm 0.28$ eV, was determined by measuring the analyzing power for the $J^{\pi }=0^{+}$${}^{13}$C($\overrightarrow{p},p$) resonance at $E_p=1.16$ MeV [97]. A study of the PNC effect in ${}^{14}$N was considered to have several advantages compared to the other cases, i.e., small spacing between the levels of the doublet, which is quite isolated, i.e., the nearest $J=0$ state lies approximately 3 MeV away, and the favorable ratio of the radiative widths, as both levels are $T=1$ states, which results in isoscalar parity mixing [96,97]. The levels were believed to have a quite simple structure, e.g., the $J^{\pi }=0^{+},T=1$ state to have a $1p^{-2}(2\hslash \omega )$ configuration and the $J^{\pi }=0^{-},T=1$ state − a $2s_{1/2}$ nucleon coupled to the $A=13$ gs. In the experiment, the excitation energies, $E_i$, the radiative widths, ${\Gamma }_{{\gamma }_i}$, and the $\gamma$ decay branching ratios for the $0^{+}/0^{-}$ doublet states were measured with much better precision compared to the values reported previously. A $5\sigma$ discrepancy in the $H_{weak}$ value with the model predictions was found. The authors concluded that this questions the shell-model calculations. The reason might be that the system is unbound, which was taken into account in Ref. [98]. However, more sophisticated calculations involving ab initio models are needed in this case.

The lifetime of the $J^{\pi }=0_1^{+}$, $T=1$ IAS was measured in Doppler shift attenuation (DSAM) experiments [99], or in nuclear resonance fluorescence (NRF) experiments [100], which reported a lifetime of ${\tau }_{\mathrm{DSAM}}=105\left(15\right)$ fs and ${\tau }_{\mathrm{NRF}}=106\left(10\right)$ fs. The half-life reported in ENSDF is $t_{1/2-\left(\mathrm{ENSDF}\right)}=68\left(3\right)$, which corresponds to a lifetime ${\tau }_{\mathrm{ENSDF}}=98\left(4\right)$ fs. It would be interesting to measure this value with better precision, using, e.g., the relative self-absorption technique [19].

The $\beta$ decay from the $0^{+}$, $T=1$ gs of ${}^{14}$C to the $1^{+}$, $T=1$ gs of ${}^{14}$N is a Gamow–Teller (GT) transition. Out of more than 700 nuclei that decay through a GT transition, ${}^{14}$C has the highest log$ft$ value, log$ft$ = 9.225(2) [14]; hence, its decay is the most strongly hindered. The GT transition between the $0^{+}$, $T=1$ gs of ${}^{14}$O and the $1^{+}$, $T=1$ gs of ${}^{14}$N also has a higher than average log$ft$ value, log$ft$ = 7.309(7) [14]. Explaining the unusually long half-life of ${}^{14}$C is a challenge in nuclear theory, but it also triggered new experiments to understand the $\beta$ decay of the $A=14$ multiplet. In 1954, it was suggested that tensor forces might play a role in shell-model interactions and may play a role in ${}^{14}$C $\beta$ decay [101].

The GT strength distributions to excited states in ${}^{14}$C and ${}^{14}$O were studied in (d,${}^2$He) and (${}^3$He,${}^3$H) charge-exchange reactions on ${}^{14}$N with high resolution [102]. The experiments tested the underlying structure of the ${}^{14}$N gs wave function and demonstrated the fragmentation of the GT strength over several $J^{\pi }=2^{+}$ final states. These results confirm the D-wave nature of the two-hole pair of the $J^{\pi }=1^{+}$ gs of ${}^{14}$N. In a recent experiment, the (d,${}^2$He) charge-exchange reactions were used in inverse kinematics. The GT transition strength between ${}^{14}$O and ${}^{14}$N was extracted up to an excitation energy of 22 MeV [103]. The microscopic origins of the anomalously suppressed $\beta$ decay of ${}^{14}$C were studied using the ab initio no-core shell model with the Hamiltonian from the chiral effective field theory, including 3N interactions. It was demonstrated that the 3N force reduced the contributions from the NN interactions by an order of magnitude [104].

Nuclear $\beta$ decay involves weak transitions between up, u, and down, d, quarks, and one consequence is that the decay rates are proportional to the $|V_{ud}{|}^2$ term of the Cabibbo–Kobayashi–Maskawa (CKM) matrix. The value of $V_{ud}$ is most accurately determined from the analysis of the measured rates for super-allowed Fermi $\beta$ decays, i.e., for $0^{+}\to 0^{+}$ transitions between nuclear IAS. The 2020 analysis of the world data yielded a result $V_{ud}$ = 0.97373 ± 0.00031 [105].

Furthermore, super-allowed Fermi $\beta$ decay provides a highly sensitive test of the CVC hypothesis [34,35] and sets limits on the existence of scalar currents. According to it, the weak vector coupling constant, $G_V$, is not renormalized in the nuclear medium. As a result, the experimental $ft$-value for super-allowed Fermi $\beta$ decay should be the same independent of the nucleus, except for some small radiative and isospin-mixing corrections. Hence, the corrected $Ft$-value should be the same for all super-allowed Fermi $\beta$ decays:

$$Ft=ft(1+{\delta }_r^{\prime })(1+{\delta }_{NS}+{\delta }_c)=\frac{K}{2{\left(G_V\right)}^2(1+\Delta )},$$

(8)

where K is constant, $K/\hslash c=8120.2787\left(11\right)·{10}^{-10}$ GeV${}^{-4}·$s, $\Delta$ is the transition-independent radiative correction, ${\delta }_r^{\prime }$ and ${\delta }_{NS}$ are transition-dependent radiative corrections and ${\delta }_c$ is the transition-dependent isospin-mixing correction. The value of $G_V$ derived from the super-allowed Fermi $\beta$ decay data is used to test the unitarity of the CKM matrix.

The largest deviation of $Ft$ from constancy in the data occurs for the supper-allowed Fermi $\beta$ decays of ${}^{10}$C →${}^{10}$B and ${}^{14}$O →${}^{14}$N [105]. In the last few years, new measurements were presented of the ${}^{14}$O half-life [106], $\beta$ decay branching ratio [107] and $Q_{E}C$ value [108], as well as the ${}^{10}$C half-life [77], $Q_{EC}$ value [109], which reduced uncertainties on the $Ft$ values for the low-Z parents.

Low-Z, super-allowed Fermi $\beta$-emitters, such as ${}^{14}$O, are particularly significant in setting limits on the existence of scalar currents. In the case of scalar interaction, an additional term inversely proportional to $Q_{EC}$ would be present in Equation (8). As the $Q_{EC}$ values are smaller for lower-Z isotopes, they would be most sensitive to the presence of a scalar current, showing the largest deviation in $Ft$ from a constant value. This issue was discussed in Refs. [77,108], and there is the deviation of the $Ft$ value for ${}^{10}$C above the average $Ft$ line. Hardy and Towner set a limit for the Fierz interference term, $b_F=-2C_S/C_V$, which is the ratio of the weak scalar to vector coefficients, $|b_F|\le 0.0033$ with 90% confidence [105].

In a series of experiments, the dissociation of ${}^{14}$N of a primary momentum of 2.9 $A·$GeV to different channels, including the $3\alpha$ Hoyle state, was studied; see Ref. [110] and the references therein. The primary beam was interacting with the emulsion nuclei and the reaction tracks were analyzed. Similarly to the dissociation of ${}^{10}$B to $2\alpha$ states [111] (see Section 2.2), the contribution of ${}^8$Be and ${}^9$B to the ${}^{14}$N dissociation was determined. The fraction of the ${}^{14}$N →${}^8$Be+X →$3\alpha$+X channel, involving the production of an intermediate ${}^8$Be nucleus, was reported to be approximately 25% [112]. In addition, a new specific feature that was identified in these experiments was Hoyle state decay in the dissociation ${}^{14}$N →$3\alpha$ + X [110].

3. Summary and Outlook

The spectroscopic studies of the $N=Z$ doubly-odd self-conjugate nuclei provide information about a variety of physics phenomena, starting with fundamental interactions and encompassing subtle details of the nuclear structures and reaction mechanisms.

Studies of fundamental interactions are related to precise studies of Gamow–Teller and super-allowed Fermi $\beta$ decays, which are related to the test of the CVC hypothesis, e.g., the existence of weak magnetism or scalar-to-vector coupling. The $Ft$ values of the super-allowed Fermi $\beta$-decay transitions provide a stringent test for the unitarity of the CKM matrix; two of the 21 transitions that have a complete set of data to obtain the world average $Ft$ value are the ${}^{10}$C →${}^{10}$B and ${}^{14}$O →${}^{14}$N $0_{gs}^{+}$→$0_{IAS}^{+}$ decays. Data related to these decays are among the most precise measurements obtained in recent experiments with state-of-art techniques. $Ft$ values, which are obtained in these studies, require a better understanding of the nuclear structure. One such problem is the anomalously hindered GT $\beta$ decay of ${}^{14}$C, which involves the structures of the mother and daughter nuclei and the role of the tensor forces. The precise description of the super-allowed Fermi $\beta$ decays is related to the understanding of the structure of the $J^{\pi }=0_1^{+}$, $T=0$ IAS in ${}^{10}$B and ${}^{14}$N, such that structure corrections are accurately calculated.

Isospin is an approximate quantum number that is best manifested in light nuclei. Naturally, studies of isospin non-conservation were carried out for light $N=Z$ nuclei. The spectroscopic data for the odd-odd self-conjugate nuclei were collected mostly approximately 40 to 60 years ago and have large uncertainties for the $\gamma$-decay branching ratios and the $\alpha$-decay widths. In some cases, e.g., for ${}^{10}$B, new, more precise experimental information was obtained in the search for a better understanding of isospin mixing. However, the data for the $\gamma$-ray branching ratios also, in this case, suffer from ambiguities. It may be timely to revisit these nuclei and obtain more precise data.

Another aspect of interest is related to molecular cluster structures in these nuclei. Different experimental techniques have been applied to several such excitations. However, this topic remains largely unexplored.

In conclusion, spectroscopic studies in light doubly-odd $N=Z$ nuclei clearly provide new opportunities for exciting nuclear structure research.