1. Introduction
Today there is no consensus on a theoretical model that allows, within the framework of a single scenario, to describe the phase diagram of the high-
cuprates, including the HTSC mechanism itself, pseudogap phase, strange metal phase, a variety of static and dynamic fluctuations, etc. In our opinion we miss several fundamental points: The strong but specific electron-lattice effects, inapplicability of the Bardeen–Cooper–Schrieffer (BCS) paradigm which implies a search for a “superconducting glue” for the
-momentum pairing of metallic quasiparticles, and inherent intrinsic electronic phase separation in cuprates. Recent precision measurements of various physical characteristics on thousands of cuprate samples [
1] indicate “insurmountable” discrepancies with ideas based on the canonical BCS approach and rather support local pairing mechanism for HTSC cuprates.
Recently, Pelc et al. [
2] have introduced a phenomenological model wherein two electronic subsystems coexist within the unit cell: Itinerant and localized holes, with the
p holes introduced via doping always being itinerant while pairing is associated with the localized holes. Their minimalistic phenomenological model based on the localization/itineracy interplay and intrinsic electronic inhomogeneity captures key unconventional experimental results for the normal and superconducting state behavior at a quantitative level. The success and simplicity of the model greatly demystify the cuprate phase diagram and unambiguously point to a local superconducting pairing mechanism rather than to BCS. In fact, they argue that the Fermi liquid subsystem in cuprates is responsible for the normal state with angle-resolved photoemission spectra (ARPES), magnetic quantum oscillations, and Fermi arcs, but not for the unconventional superconducting state. According to the authors, their model is “comparable to well-known phenomenological approaches in science, such as the Standard Model of particle physics, the Landau theory of phase transitions, and models of population growth”. However, the authors could not elucidate the nature of local pairing to be a central point of the cuprate puzzle.
A large variety of different theoretical models has been designed to account for exotic electronic properties of cuprates and to shed light on their interplay with unconventional superconductivity. A common feature of model approaches to the description of the electronic structure of cuprates is the selection of a limited set of Cu and O atomic states, which automatically limits the possibilities of a quantitative and, in some cases, qualitative description. Many theoretical approaches, such as a familiar
t–
J model [
3], effective two-band Hubbard model [
4], recent Spin–Fermion–Hubbard model [
5,
6], to the high-T
cuprates are based on variations or approximations of the three-band
p–
d effective model proposed by Emery [
7] and Varma et al. [
8] in 1987. However, despite more than three decades that have passed since the discovery of the HTSC, the most important questions remain unanswered to date.
Earlier, we started to develop a minimal “unparticle” model for the CuO
planes with the “on-site” Hilbert space of the CuO
plaquettes to be a main element of the crystal and electron structure of high-T
cuprates, reduced to states formed by only three effective valence centers [CuO
]
(nominally Cu
, respectively), forming a “well isolated” charge triplet [
9,
10,
11]. The very possibility of considering these centers on equal footing is predetermined by the strong effects of electron-lattice relaxation in cuprates [
12,
13]. The centers are characterized by different conventional spin: S = 1/2 for “bare”, or “parent” [CuO
]
center and S = 0 for “electron” and “hole” centers ([CuO
]
- and [CuO
]
-centers, respectively) and different orbital symmetry:
for the ground states of the [CuO
]
center,
for the electron center, and the Zhang–Rice (ZR)
or more complicated low-lying non-ZR states for the hole center. Electrons of many-electron atomic species with strong p-d covalence and strong intra-center correlations cannot be described within any conventional (quasi) particle approach that addresses the [CuO
]
centers within the on-site hole representation
, n = 0, 1, 2, respectively. Instead of conventional quasiparticle
-momentum description, we make use of a real space on-site “unparticle” S = 1 pseudospin formalism to describe the charge triplets and introduce an effective spin-pseudospin Hamiltonian that takes into account both local and nonlocal correlations, single and two-particle transport, as well as the Heisenberg spin exchange interaction. We perform the analysis of the ground state and
T-
n phase diagrams of the model Hamiltonian by means of a site-dependent variational approach in the grand canonical ensemble within effective field approximation, which treats the on-site quantum fluctuations exactly and all the intersite interactions within the mean-field approximation (MFA) typical for spin-magnetic systems. Within two-sublattice approximation and
-couplings we arrive at several MFA, or Néel-like phases in CuO
planes with a single nonzero local-order parameter: Antiferromagnetic insulator (AFMI), charge order (CO), glueless
d-wave Bose superfluid phase (BS), and unusual metallic phase (FL).
2. S = 1 Pseudospin Formalism
To describe the diagonal and off-diagonal, or quantum local charge order we start with a simplified
charge triplet model that implies a full neglect of spin and orbital degrees of freedom [
9,
10,
11]. Three charge states of the CuO
plaquette: A bare center
= [CuO
]
, a hole center
= [CuO
]
, and an electron center
= [CuO
]
are assigned to three components of the S = 1 pseudospin triplet with the pseudospin projections
, respectively.
The S = 1 spin algebra includes the eight independent nontrivial pseudospin operators, the three dipole and five quadrupole operators:
The two pseudospin raising/lowering operators
and
change the pseudospin projection by
, with slightly different properties. In lieu of
and
operators one may use two novel operators:
which do realize transformations [CuO
]
↔ [CuO
]
and [CuO
]
↔ [CuO
]
, respectively. Strictly speaking, we should extend the on-site Hilbert space to a spin-pseudospin quartet
:
and
, where
, and instead of spinless operators
and
, we introduce operators
and
, which transform both on-site charge (pseudospin) and spin states as follows:
These Fermi-like operators obeying the anticommutation permutation rules are actually operators of creation/annihilation of an electron/hole in the many-particle atomic state of the parent [CuO] center. Expansion of a charge triplet to a spin-charge (spin-pseudospin) quartet automatically “turns on” the spin operator of the parent [CuO] center.
The spin-pseudospin quartet differs from the quartet of quasiparticle states of the effective one-band model of CuO
-planes [
14]:
where
is a “vacuum” state with no holes (electron center [CuO
]
) and
is the
-hole creation operator with spin projection
. This difference is associated with three fundamental features of charge centers [CuO
]
:
(i) The electronic [CuO
]
and hole [CuO
]
centers in the parent cuprate are actually small polarons with an active
breathing mode of local displacements [
15]. The Cu-O bond length in the electron/hole center is about 0.1 Å longer/shorter than in the parent [CuO
]
center;
(ii) Multielectron configurations of charge centers are not described within the framework of simplified quasiparticle models (see, for example, Ref. [
16]), and the perturbation theory must take into account the lattice (vibrational) degree of freedom;
(iii) Taking into account the effects of electron-lattice relaxation in cuprates can lead to a significant “reduction” in the energy scale characteristic of a spin-charge quartet from several eV (see, for example, Ref. [
14]) to several tenths of eV [
9,
10,
11,
16].
The two “spinless” Bose-like pseudospin raising/lowering operators
/
(
=
), change the pseudospin projection by
, respectively. In other words, these operators can be associated with creation/annihilation of an on-site hole pair, or composite on-site “ZR boson”, with a kinematic constraint
= 0, that underlines its “hard-core” nature. For the Bose creation/annihilation operators
=
/
=
, we arrive at Fermi-like on-site and Bose-like inter-site permutation relations on the space with the on-site
states:
The on-site anticommutation relation can be rewritten as follows:
Simplified, the local on-site composite hole boson in our theory is a pair of holes coupled by local correlations both with each other and with the “core”, that is, the electronic center [CuO] (nominally Cu). In fact, such a local boson exists only as an indivisible part of the ZR hole center [CuO] (nominally Cu). We emphasize that namely this effective on-site composite hole boson is a supercarrier both in the hole and electron-doped cuprates.
It should be noted that the effective “quasiparticle” wave function of the on-site ZR boson has the tetragonal
-, more precisely,
-symmetry and formally coincides with the two-particle wave function of the Zhang–Rice singlet. The function has a maximum along the Cu–O bond direction and nodes on the nodal [110] directions in the Brillouin zone. It might be called an extended, anisotropic, or, more precisely, “nodal”
s-wave. The boson-like pseudospin raising/lowering operators
define a complex superconducting local order parameter [
9]:
It is worth noting that there is a one-to-one correspondence between all the independent 15 on-site spin-pseudospin operators:
and the 15 independent on-site Hubbard
-operators:
acting in the Hilbert space of the quartet
,
,
[
14]:
It means that the algebra of the spin-pseudospin operators coincides with that of Hubbard -operators, however, the spin-pseudospin formalism, which allows one to use the well-known methods of spin algebra and the analysis of spin-magnetic systems, is more physically clear and intuitive than the formal method of -operators.
3. Effective Spin-Pseudospin Hamiltonian
As for conventional spin-magnetic systems, we can integrate out the high-energy degrees of freedom, and after projecting onto the Hilbert basis of well-isolated charge triplet we have chosen, to arrive at the effective spin-pseudospin Hamiltonian obeying the spin and pseudospin kinematic rules. This approach is absolutely analogous to the typical approach for spin magnets with the ground state spin S, when, using perturbation theory, we take into account the contribution of high-lying states and construct the effective Hamiltonian of one- and two-ion anisotropy, isotropic exchange, etc. in terms of the ground state spin multiplets.
Hereafter, we consider the effective Hamiltonian of the CuO
planes in the model cuprate under the assumption of a “frozen” lattice. Within such an approach, strong electron-lattice effects are taken into account implicitly through the effective renormalization of correlation parameters and transfer integrals [
17].
The effective S = 1 pseudospin Hamiltonian, which does commute with the
z-component of the total pseudospin
, thus conserving the total charge of the system can be written to be a sum of potential and kinetic energies:
where:
with a charge density constraint:
, where
n is the deviation from a half-filling. The first on-site term in
describes the effects of a bare pseudospin splitting, or the local energy of
centers and relates with the on-site density-density interactions,
=
U/2,
U being the local correlation parameter, or pair binding energy for the on-site composite boson. The second term may be related to a pseudo-magnetic field ‖
Z with
being the hole chemical potential. The third term in
describes the inter-site density-density interactions, or nonlocal correlations. Kinetic energy
is a sum of one-particle and two-particle transfer contributions. In terms of
and
operators the Hamiltonian
reads as follows:
All the three terms here suppose a clear physical interpretation. The first
-type term describes one-particle transfer processes, that is a rather conventional motion of the hole[CuO
]
-centers in the lattice formed by parent [CuO
]
-centers (
p-type carriers, respectively) while the second
-type term also describes a one-particle transfer process, that is a motion of the electron [CuO
]
-centers in the lattice formed by parent [CuO
]
-centers (
n-type carriers). The third
(
) term in
defines a very different one-particle transfer process: [CuO
]
+ [CuO
]
↔ [CuO
]
+ [CuO
]
, [CuO
]
+ [CuO
]
, that is the
local disproportionation/recombination, or the
electron-hole pair creation/annihilation. It is this interaction that is responsible for the appearance of carrier sign uncertainty and violation of the “classical” Fermi-particle behavior. Interestingly, the term can be related with a local pairing as the hole [CuO
]
-center can be addressed to be a hole pair (=composite hole boson) localized on the electron [CuO
]
-center. Hamiltonian
:
describes the two-particle (local composite boson) inter-site transfer that is the motion of the hole center in the lattice formed by the electron centers, or the exchange reaction: [CuO
]
+ [CuO
]
↔ [CuO
]
+ [CuO
]
. In other words,
is the transfer integral for the local composite boson. Depending on the sign of
, this interaction will stabilize the superconducting uniform
- (
) or nonuniform
- (
) phase.
Conventional Heisenberg spin exchange Cu
–Cu
coupling should be transformed as follows:
where operator
takes into account the on-site spin density
.
The inclusion of spin exchange in the effective spin-pseudospin Hamiltonian requires additional comment. Indeed, disregarding the effects of electron-lattice relaxation, it is the PN-type charge transfer [CuO] + [CuO]→ [CuO] + [CuO] through the 2 eV optical charge transfer gap that contributes to the spin exchange with an exchange integral on the order of 0.1 eV. However, the “unrelaxed” centers [CuO] and [CuO] have the high-energy configuration of the parent center [CuO]. After taking into account the electron-lattice relaxation, we arrive at new “relaxed” centers [CuO] and [CuO] with a new local configuration and much lower energy, the optical gap is reduced to a thermal (adiabatic) gap with a much smaller value. The relaxed charge states are included in the “well-isolated” triplet, so that the spin exchange, as a result of taking into account the contribution of high-lying states, is included in the effective Hamiltonian.
Making use of the “Cartesian” form of pseudospin operators:
with hermitian operators
,
, and
one can rewrite the spin-pseudospin Hamiltonian in symbolic “vector” form as follows:
where we added interaction with an external magnetic field
and limited ourselves to the interaction of the nearest neighbors,
,
,
,
.
We emphasize once again that the correlation parameters and transfer integrals in (
5) are effective model parameters assumed to include all the possible renormalizations and contributions like those coming from the strong electron-lattice coupling. This primarily concerns the parameters of local and nonlocal correlations, the “screened” value of which will substantially depend on the electron/hole doping
n.
It is worth noting that neglecting nonlocal correlations, that is, for
= 0, the spin-pseudospin Hamiltonian of our model (
5) is formally equivalent to the sum of the Hamiltonians (7.8) and (7.15) from Plakida’s book [
14], written in terms of
- operators, but obtained within the framework of a rather controversial microscopic model (
, …). Strangely, the standard BCS approach assumes that the contribution of the transfer of hole pairs is neglected, although the corresponding transfer term of the
(
) type always accompanies the typical Heisenberg exchange term.
4. Effective-Field Approximation for the Doped Cuprates
Simple effective-field (EF) or mean-field theory is as always a good starting point to provide physically clear a semi-quantitative description of strongly correlated systems. Making use of local order parameters without switching to the momentum -representation is a typical way to describe “classical” phases for spin magnetic systems, such as the simple Néel order.
Hereafter, we perform the analysis of the ground state and
T-
n phase diagrams of the model Hamiltonian (
11) by means of a site-dependent variational approach (VA) in the grand canonical ensemble within effective-field approximation, which treats the on-site correlation term exactly and all the intersite interactions within the MFA typical for spin-magnetic systems [
18].
We start with assuming the existence of two interpenetrating lattices (
A and
B), restricting the analysis to the two-sublattice solutions for the single nonzero local order parameter phases. In such a case, we introduce 14 parameters of an uniform and 14 parameters of a non-uniform, or staggered order, as follows:
where
are local order parameters
for
sublattice. The corresponding parameters of uniform and staggered order will be denoted below as
n,
,
,
,
and
, respectively (
n is a doping level).
One basic problem with the local
and
operators and their handling within on-site real-space formalism is their fermionic character. For the first time, the local mean values of fermionic operators similar
and
have been introduced by Caron and Pratt [
19] to describe the Hubbard model in the real coordinate space. At variance with Bose-systems, the ground state for kinetic energy in electronic systems is composed, due to the Pauli exclusion principle, of states with different momenta
forming the Fermi sea. The problem with local centers is that these only have a limited number of eigenstates and thus seem to be unable to yield any energy bands. However, all of the band states may be easily generated, if to take into account the phase uncertainty of the mean values such as
and make use of self-consistency relations reflecting the appropriate Bloch symmetry for the wave vector chosen [
20]. As C. Gros [
21] has shown, the correct ground state energy for non-interacting electrons can be recovered by averaging all of the possible boundary conditions, a method called the “boundary integration technique”.
The resulting Hamiltonian can be rewritten as a sum of one-site Hamiltonians as follows:
where
, the upper (lower) sign corresponds to
A (
B) sublattice,
=
,
,
,
,
, and
=
,
,
,
,
(
) are uniform and staggered molecular fields, respectively. Using the partition function:
where
, we obtain the expressions for the charge density
n and other order parameters as follows:
The variational approach that will be employed is based on the Bogolyubov inequality for the grand potential
:
where
is the Hamiltonian under study (
11),
is the trial Hamiltonian (
13) which depends on the variational order parameters and can be exactly solved, the thermal average is taken over the ensemble defined by
. We estimate the free energy of the system per one site,
, as follows:
By minimizing the free energy, we get a system of site-dependent self-consistent VA equations to determine the values of the order parameters:
5. EF Phase Diagrams
Let us assume that the model cuprate described by Hamiltonian (
13) can be found only in homogeneous phase states with a long-range order determined by a single nonzero (vector) local order parameter (“monophases”): CO (
), AFMI (
), BS (
), and two types of metallic FL (
phases. It is worth noting the specificity of the two metallic FL phases, which in our model represent a mixture of
P- and
N-phases due to the
(
) contribution to the single-particle transport Hamiltonian
, which leads to “strange” properties of the Fermi-type metal phases of cuprates with a specific coexistence of hole and electron carriers, characteristic of both hole- and electron-doped systems. It is interesting that in this somewhat naive model, it is possible to obtain relatively simple transcendental equations for the “critical” temperatures
,
,
, and
that determine the stability boundaries of certain homogeneous phases with one or another long-range order or corresponding second-order phase transition lines [
22].
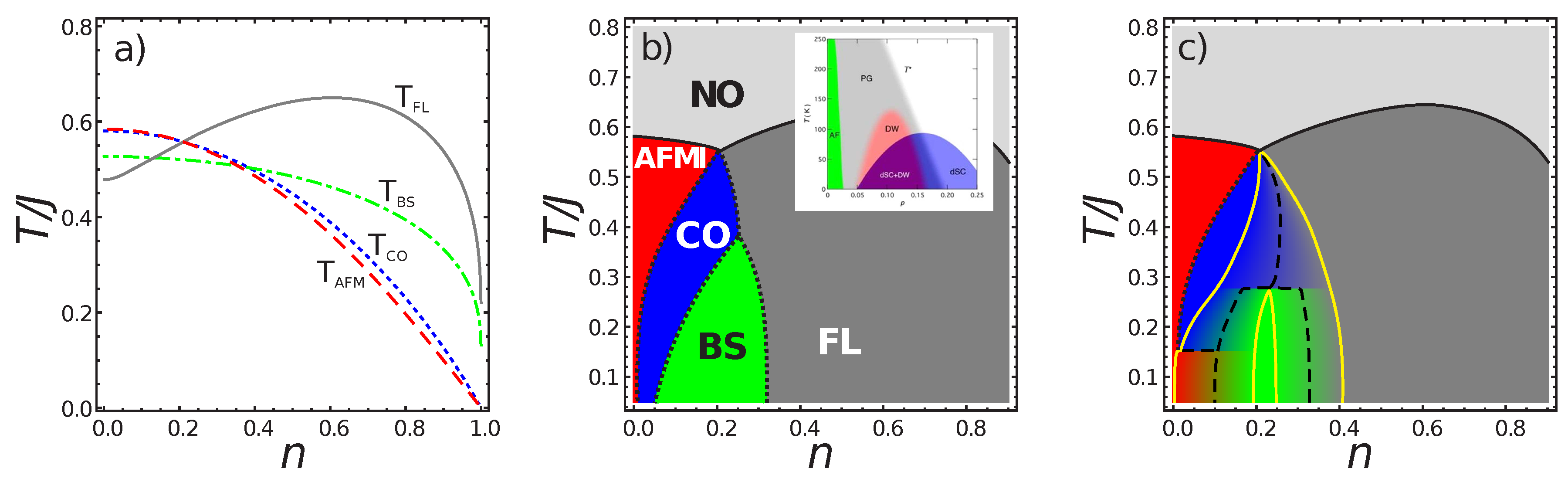
Making use of Exp. (
15), we numerically estimated the free energies of different phases and have built a
T-
n phase diagram. In
Figure 1, we present model phase diagrams of a cuprate calculated given quite arbitrarily-chosen parameters of the model Hamiltonian (
11) as
= 0.20,
V = 0.35,
=
= 0.46,
= 0.05, and
= 0.65 (all in units of the exchange integral
J).
Figure 1a shows the doping dependence of the “critical” temperatures
,
,
, and
. The NO-AFMI-CO-BS-FL phase diagram is shown in
Figure 1b, where the regions of the minimum free energy of the phases are highlighted in different colors. Given this set of parameters, the lines of phase transitions NO-AFMI, NO-FL are lines of second-order transitions, while the lines of phase transitions AFMI-CO, CO-BS, CO-FL, and BS-FL turn out to be lines of first-order phase transitions.
Comparison with the phase diagram typical of doped cuprates (see inset in
Figure 1b) shows that the “MFA portrait”, obtained under extremely simplifying assumptions, can reproduce quite well some principal features of the real phase diagram. However, a somewhat naive assumption of only homogeneous single-order parameter phases may not be validated if the full multi-parameter thermodynamic field space is considered. For instance, the free energy minimum under the assumption of a single nonzero superconducting order parameter (
) will be just a saddle point, if the nonzero charge order parameter (
) is also “turned on”, which, it would seem, should lead to the appearance of a homogeneous supersolid phase with the on-site CO-BS mixing. However, despite the much more complicated Hamiltonian, the situation turns out to be absolutely similar to that implemented in the “negative-
U” or hard-core boson model or a lattice model of a superconductor with pair hopping and on-site correlation term [
18] where, instead of forming homogeneous phases with the on-site mixing of local order parameters, the system can find it thermodynamically more convenient to phase separately into subsystems with different volume fractions that can be readily found by adapting what is known as a Maxwell construction [
18,
24]. As a consequence, as a result of the numerical implementation of the Maxwell construction for the same parameters as above, phase separation can be realized in the region of coexistence of phases separated by a first-order phase transition line. This works for phases AFMI-FL, AFMI-BS, CO-BS, CO-FL, and BS-FL, but not for AFMI-CO. Generally speaking, in the latter case this means the possibility of the formation of a homogeneous mixed phase, such as spin-charge density wave, although the effects typical for the region of the phase coexistence will most likely be observed. Results of the Maxwell construction for our model cuprate presented in
Figure 1c show the significant transformation of the “naive” phase diagram in
Figure 1b with phase separation (PS) taken into account.
A transition between a homogeneous phase and the PS state can be symbolically named as a “third-order” transition with the concentration difference as the order parameter [
18]. At this transition, a size of one domain in the PS state decreases continuously to zero at the transition temperature.
First- and second-order transitions in
Figure 1b,c are denoted by dotted and solid lines, respectively, black-dashed curves point to fifty-fifty volume fraction for two adjacent phases, while yellow curves indicate “third order” transition that delineate areas with 100% volume fraction. It is worth noting that at “third order” transitions, the specific heat exhibits a finite jump as at the second order transitions [
18].
As we see the inclusion of the PS states into consideration, substantially modifies the phase diagrams of the models assuming only homogeneous phases. In the PS states, the system breaks into coexisting static or dynamic domains/grains of two different phases with varying volume fraction and shape. Hole carrier density in metallic FL phase and in metallic domains in PS phase is
, however, taking into account a diminishing volume fraction of metallic phase with decreasing doping we arrive at effective carrier density demonstrating the smooth crossover from
to
p across optimal doping [
25]. The zero resistivity transition in the phase separated state arises only when the Josephson coupling between BS domains is of the order of the thermal energy and phase locking takes place along the percolating BS system. This implies a two-step superconducting transition with the formation of the isolated BS domains without phase coherence and than by Josephson coupling with phase locking at lower temperatures.
There is now considerable evidence that the tendency toward phase separation or intrinsic electronic inhomogeneity is a universal feature of doped cuprates (see, e.g., Refs. [
26,
27] and references therein). Despite these evidences, the majority of the theoretical approaches are based on the assumption of homogeneous phases.
It should be noted that the PS model does predict several temperatures of the “third order” PS transitions limiting the PS phases, that is delineating areas with 100% volume fraction, and the temperatures of the percolation transitions, which can manifest itself in the peculiarities of the temperature behavior for different physical quantities [
28]. All the phases AFMI, CO, and BS are separated from the 100% coherent metallic Fermi liquid phase by the “third order” phase transition line
, which is believed to be responsible for the onset of the pseudogap phenomena as a main candidate for the upper “pseudogap” temperature. The PS phenomenon immediately implies an opportunity to observe as a minimum two energy pseudogaps for superconducting cuprates, related to antiferromagnetic and charge fluctuations for underdoped and overdoped compositions, respectively. In general, the enigmatic pseudogap phase in doped cuprates seems to be an inhomogeneous system of static and dynamic fluctuations, to be a precursor for long-range orderings, both for the CDW and dBS phases.
As we see the EF approach, realized under extremely simplifying assumptions, is able to reproduce essential features of the phase diagram for doped cuprates, however, for an adequate description of real phase diagrams in the framework of the EF theory, it is necessary to take into account a number of additional vital effects. First of all, this concerns the real inclusion of electron-lattice polarization effects, long-range inter-site (nonlocal) correlations, and inhomogeneous potential in cuprates with nonisovalent substitution. As a result, we must increase the number of possible phase states, first of all, by introducing new commensurate or incommensurate spin-charge modes, or spin-charge density waves like stripes, and also take into account the screening effect of local and nonlocal correlations. The latter effect can be accurately described only with a rigorous consideration of the electron-lattice polarization effects. Experimental data point to a dramatically enhanced screening of Coulomb interactions in cuprates under doping [
29,
30]. In addition, all the “effective” transfer integrals
and
will depend on the doping level through the effects of “vibronic” reduction. Furthermore, our version of the effective field model assumed the use of the simplest version of the Caron–Pratt method [
19] for the “real-space” description of one-particle transport, which seemingly leads to an overestimation of the contribution of one-particle kinetic energy. A specific feature of doped cuprates with nonisovalent substitution is the presence of centers of an inhomogeneous electric field, which are the nucleation centers for nanoscopic regions of condensed charge fluctuations, providing an efficient screening of the impurity Coulomb potential. Inhomogeneous potential will largely destroy long-range order and lead to strong spatial fluctuations of the effective energy parameters and critical temperatures [
2].
Despite the advantages of the simple EF-MFA approach realized above, a detailed meaningful comparison with an ever-expanding set of experimental data unavoidably requires the inclusion of novel effects about the mean field. First it concerns the effects of low-dimensionality and nonlocal quantum fluctuations. Obviously, the effective field theory cannot provide an adequate quantitative, and in some cases, possibly even a qualitative, description of low-dimensional 2D systems. The 2D systems, in particular, the S = 1 pseudo (spin) system is prone to a creation of different topological structures, which form topologically-protected inhomogeneous distributions of the eight local S = 1 pseudospin-order parameters [
11]. Puzzlingly, these unconventional structures can be characterized by a variety of unusual properties, in particular, filamentary superfluidity in antiphase domain walls of the CO phase and unusual skyrmions. The main limitation of mean field theory is the neglect of correlations between spins or pseudospins i.e., the effective replacement of nonlocal correlators such as
by a simple product of local-order parameters
. The MFA describes a long-range order of local-order parameters, however, it cannot describe its precursor, that is short-range fluctuations which are of principal importance near the critical temperatures. One of the advantages of the EF-MFA variant used by us is the exact quantum-mechanical description of local correlations, however, the classical nature of the molecular fields leads to fundamental problems in the description of the ground state which are characteristic even of the simplest quantum antiferromagnets. Indeed, the true ground state of the S = 1/2 antiferromagnet (given even number of spins) is a quantum superposition of all possible states with full spin S = 0 and zero value of the local-order parameter:
= 0. The Néel state is just a classic “component” of this “hidden” quantum state, so-called “physical” ground state. The Néel phases start to form at high temperatures in the nonordered phase, when thermal fluctuations and fluctuating non-uniform fields destroy the quantum states, while the Néel-type domains become increasingly extended and stable with a decreasing temperature, leaving no real chance of the formation of a true quantum ground state in the low-temperature limit. The contribution of purely quantum states is manifested in a significant decrease in the value of the local order parameter in the Néel “portrait” as compared with the nominally maximum value of
s. It should be noted that all the phases with the long-range order we address above, AFMI, CO, and BS, are Néel-like, that is these are characterized by a nonzero local order parameters. As in quantum magnets, the existence of the “MFA-hidden” quantum state in HTSC cuprates leads to a significant suppression of the magnitude of the local-order parameters for CDW and superconducting (BS) phases [
1,
31]. Thus, the EF-MFA phase diagram we are considering “hides” the existence of a true quantum ground state, a “quantum background”, such as the Anderson’s RVB (resonating valence bond) phase [
32], formed by a system of EH dimers [
33].