Optimal Placement and Capacity of BESS and PV in EV Integrated Distribution Systems: The Tenth Feeder of Phitsanulok Substation Case Study

Abstract

Installing a battery energy storage system (BESS) and renewable energy sources can significantly improve distribution network performance in several aspects, especially in electric vehicle (EV)-integrated systems because of high load demands. With the high costs of the BESS and PV, optimal placement and capacity of them must be carefully considered. This work proposes a solution for determining the optimal placement and capacity of a BESS and photovoltaic (PV) in a distribution system by considering EV penetrations. The objective function is to reduce system costs, comprising installation, replacement, and operation and maintenance costs of the BESS and PV. The replacement cost is considered over 20 years, and the maintenance and operation costs incurred in the distribution system include transmission line loss, voltage regulation, and peak demand costs. To solve the problem, two metaheuristic algorithms consisting of particle swarm optimization (PSO) and the African vulture optimization algorithm (AVOA) are utilized. The tenth feeder of Phitsanulok substation 1 (PLA10), Thailand, which is a 91-bus distribution network, is tested to evaluate the performance of the proposed approach. The results obtained from the considered algorithms are compared based on distribution system performance enhancement, payback period, and statistical analysis. It is found from the simulation results that the installation of the BESS and PV could significantly minimize system cost, improve the voltage profile, reduce transmission line loss, and decrease peak demand. The voltage deviation could be reduced by 86%, line loss was reduced by 0.78 MW, and peak demand could be decreased by 5.706 MW compared to the case without BESS and PV installations.

1. Introduction

Currently, energy consumption is continuously rising because of economic expansion and developments in industrial technology, causing electricity to play a key role in boosting economies and raising the living standard in various countries [1,2,3]. In addition, the production and utilization of electric vehicles (EVs) and renewable energy, especially in photovoltaic (PV) industries, have increased, which will notably affect both the economy and the electricity production system in the future [4,5,6,7,8]. The growing number of EVs will require more electric vehicle charging stations, and the usage of PV, which will become common in daily life, will be integrated into electricity distribution systems, leading to risks in managing power systems from the perspective of the voltage profile and total harmonic distortion (THD) [9,10]. Therefore, to accommodate the increasing electricity demand from EVs and the growth of energy consumption, PV will be integrated into the distribution system, and energy storage systems (ESSs) will also be installed to preserve energy from PV and the grid during times of low electricity demand and provide the energy back into the system during times of peak demand.

Various types of ESS technology have been studied to be efficiently installed in distribution systems selected based on a number of variables, including cost, energy capacity, efficiency, and reliability, with a primary focus on safety in operation [11]. Additionally, suitable ESSs to be installed in distribution networks should have a moderate discharge time frame (minutes to hours) since this discharge time frame can meet the daily load demands immediately, and battery energy storage systems (BESSs) mostly reach this time frame [12]. Moreover, by installing BESSs in distribution networks, the placement and capacity of the BESS must be considered as they are crucial factors in improving the efficiency and reliability of the distribution systems and reduce system costs. Due to the high price of the BESS, oversized BESSs may incur excessive investment costs with longer payback periods, and inappropriate BESS placement can incur large amounts of energy losses. With the optimal placement and capacity of the BESS, the remaining energy from DGs after being provided to the loads can be efficiently stored in the installed BESS with low power loss in the transmission lines, and the amount of stored energy is also appropriate to provide energy back to the system during high peak periods, resulting in peak shaving and voltage deviation reductions. So, the optimal placement and capacity of the BESS must be efficiently found to obtain the best feasible investment costs together with high system performance enhancement.

Many approaches have been introduced to find the optimal BESS location and sizing in distribution networks, and the optimal location and sizing of distribution generators (DGs) are also included in some literature. A novel algorithm called the artificial hummingbird algorithm (AHA) was introduced in [13] to find the best position and size of DGs based on biomass in radial systems, aiming to reduce losses and improve voltage deviation. The results indicated that the distribution system efficiency was improved in terms of reductions in power loss and voltage deviation. In [14], the best location and BESS sizing connected to renewable energy sources (RESs) were presented to find the minimum system cost in the IEEE 33-bus system. The genetic algorithm (GA) and particle swarm optimization (PSO) were used, and the results showed that PSO was more effective in cost reduction than GA. The best possible DG position and size in the 118-bus system of IEEE and the practical system in Egypt identified using a modified forensic-based investigation (mFBI) were introduced in [15]. The optimization problem has been considered a multi-objective function where the objective functions consist of minimizing energy loss, voltage deviation, and operation cost while maximizing voltage stability, and they demonstrated that mFBI outperformed various methods in the literature and generated better results according to the objective values. In [16], the GA and the greedy algorithm were applied to find the optimal position and size of a BESS connected to EVs and DGs to reduce installation, operation, and maintenance (O&M) costs in a rural 22-bus distribution network. In [17], the best feasible BESS installation combined with PV and wind turbine (WT) in the IEEE 33-bus distribution network was proposed, adopting the interior point method to control operations in conjunction with a distribution management system (DMS) and energy management system (EMS) aiming to decrease system expenses. It was found that BESS could enhance the performance of the system, as investigated through voltage deviation examination, power loss reduction, and peak demand decrease. In [18], a stand-alone microgrid system with 17 buses connected to residential loads and EVs was used to assess the best position and sizing of DGs and the BESS by applying teaching–learning-based optimization (TLBO), resulting in reduced power losses and improved voltage quality. The best BESS sizing and position in a radial distribution system were determined using the hierarchical planning mode and natural aggregation algorithm (NAA) in order to manage voltage and lower life cycle costs (LCC) [19]. The optimal installation of BESS utilizing a fuzzy method to forecast the ambiguity of load profiles and employing tabu search (TS) and simulated annealing (SA) to determine the DG capacity, battery quantity, BESS power, and BESS size and location was proposed in [20]. The results showed that the presented methods could reduce purchased electricity costs from the grid and minimize power losses in the distribution system. As mentioned in previous works, it can be observed that various approaches have been introduced to find the optimal location and sizing of a BESS in distribution networks to minimize total system expenses comprising installation, replacement, power loss, voltage deviation, and peak demand costs. However, only some of these costs have been considered in each work, and most of these works applied traditional algorithms to solve the problems.

To fully and efficiently reduce system costs and improve distribution network performance, some studies have proposed approaches to find the optimal position and capacity of BESS in distribution networks by considering the total system costs, and some of them employed newly proposed algorithms to achieve efficient objective values. In [21], the best possible BESS installation alongside DGs and EVs was proposed, applying multi-objective PSO (MOPSO) and Monte Carlo simulation (MCS) to search for the optimal LCC, including initial investment costs (ICs), maintenance costs (MCs), and replacement costs (RCs). The outcomes indicated that installing the BESS in the distribution system reduced the total LCC. The optimal approach for Interline-PV (I-PV) systems under varying EV loads, focusing on reducing power losses and improving voltage profiles, was proposed in [22]. Three optimization algorithms were employed to specify the best solution strategies, and it was found that I-PV enhanced voltage profiles, reduced power losses, and was able to be adapted to practical problems. However, this work only evaluated the installation of I-PV, which included the installation of PV and a BESS at the same location, without considering the costs of installing the BESS and the optimal PV location. In [23], the best feasible BESS position and size in a DG-connected distribution system using GA, PSO, and the salp swarm algorithm (SSA) were proposed to reduce system expenses consisting of power loss, voltage fluctuation, and peak power expenses in the IEEE 33- and 69-bus systems. It revealed that system costs, power loss, and peak demand could be reduced and voltage stability could be improved. However, only the O&M costs of the system were computed in this research without considering installation and battery replacement costs. The best feasible placement and sizing of BESS in the IEEE 33- and 69-bus distribution networks connected to PV and EVs were presented in [24] to decrease the system expenses, consisting of installation, replacement, and O&M costs of the BESS, and the distribution network performance was improved in terms of transmission loss, the voltage deviation index (VDI), and peak power reductions. Three algorithms consisting of PSO, the African vulture optimization algorithm (AVOA), and SSA were applied to solve this problem and compared the aspects of the system cost, distribution system efficiency improvement, payback period, and statistical results, and the results in both systems showed that PSO gave the best objective values and AVOA provided the fastest payback period. A detailed summary of the previous work conducted in the optimal placement and capacity of the BESS is provided in Table 1.

Table 1. Summary of the previous works conducted in the optimal placement and capacity of the BESS.

Refs	Objective Functions	Total System Costs	DGs	Test Systems	Algorithms
[13]	minimizing losses and voltage deviation	x	biomass	IEEE 33-, 69-, 119-bus system	AHA
[14]	minimizing voltage regulation cost, power loss cost, and peak demand cost	x	PV, WT	IEEE 33-bus system	GA, PSO
[15]	minimizing energy loss, voltage deviation, operation cost while maximizing voltage stability	x	PV, WT	Egypt system	mFBI
[16]	minimizing investment and O&M costs	✓	PV	rural 22-bus network	GA, greedy algorithm
[17]	minimizing battery costs and system costs due to system losses, peak demand, and voltage regulation.	✓	PV, WT	IEEE 33-bus system	interior point method
[18]	minimizing power losses and improving voltage quality	x	PV, WT,	17-bus stand-alone microgrid	TLBO
[19]	minimizing investment cost, operation cost, maintenance cost, and residual value	x	PV	IEEE 15-, 69-bus system	NAA
[20]	minimizing operation cost and reliability cost	x	N/A	modified 21-node system	TS, SA
[21]	minimizing life cycle cost including initial, maintenance, and replacement costs	✓	PV, WT	a house in Sanandaj	MOPSO, MCS
[22]	minimizing power losses and improving voltage quality	x	PV	IEEE 33-bus system system	COA, PSO, GWO
[23]	minimizing reduce system costs consisting of power loss, voltage deviation, and peak demand costs	x	PV, WT	IEEE 33-, 69-bus system	GA, PSO, SSA
[24]	minimizing system costs consisting of installation, replacement, and O&M costs	✓	PV	IEEE 33-, 69-bus system	PSO, SSA, AVOA

Although some research studies have investigated the optimal position and capacity of BESS, most of them have not evaluated installation and battery replacement costs [22,23]. In [24], the installation and battery replacement costs were included; however, the location and size of PV have not been optimally placed, and only IEEE systems were tested. Moreover, it was found in [24] that PSO and AVOA were high-performance algorithms to solve the problem of the optimal position and sizing of BESSs in distribution systems connected to PV and EVs. Therefore, the optimal placement and capacity of the BESS and PV in distribution networks considering EV penetrations are proposed in this work. The objective functions considered to be minimized are system costs including installation, replacement, and O&M costs of the BESS and the installation cost of PV, and the network performance is aimed to be improved in aspects of line loss, voltage deviation, and peak demand reductions by the BESS installation. A practical system, namely the tenth feeder of Phitsanulok substation 1 (PLA10), Thailand, which is a 91-bus distribution system, is used to evaluate the performance of the approach. The conventional efficient algorithm, which is PSO, as well as the new efficient algorithm, which is AVOA, are utilized to determine the optimal solutions.

The main contributions of this work are as follows:

• The optimal placement and capacity of the BESS and PV in the PLA10 distribution system considering EV penetrations are investigated in this work by considering the overall system costs including installation, replacement, and operational and maintenance costs as the objective functions to be minimized.
• The distribution system performance is improved by reducing line losses, minimizing peak demand, and enhancing the voltage profile after the installation of the BESS and PV.
• Two optimization algorithms including PSO and AVOA are employed to find the optimal solutions, and their simulation results, statistical analysis, and payback period are compared.

The rest of the paper is divided as follows. Section 2 introduces input data models of the BESS and EV charging stations in the distribution network. The problem formulation of the optimal placement and capacity of the BESS and PV in the distribution network is provided in Section 3. In Section 4, the methodology of this work is presented. Section 5 shows the simulation results and discussions. Finally, the conclusion of this work is presented in Section 6.

2. Input Data Models

This section presents the modeling of the BESS and EV charging stations in the distribution network.

2.1. Battery Energy Storage Systems (BESSs) in a Distribution System

An electrochemical BESS is employed in this paper since it has an appropriate discharge time and the ability to quickly respond to daily loads [12,25,26,27]. The simulation of the BESS is explained below.

2.1.1. BESS Simulation

A Li-ion battery has been selected as the BESS of this work due to its various advantages, including over 90% efficiency, high energy density (90–190 Wh/kg), high life cycle, and reasonable cost. Although Li-ion has some disadvantages such as the need for a protection circuit, degradation at high temperatures and high voltage, and the impossibility of rapid charge at freezing temperatures when compared to other BESSs, Li-ion can still overcome other BESSs for this work because of its various advantages and suitability for distribution systems. However, the temperature, number of BESS operation cycles, and depth of discharge (DOD) are some of the factors that can impact the life cycle of a Li-ion battery. So, extended service life of the BESS is achieved by controlling heat dissipation at the ideal temperature, which is between 15 and 35 degrees Celsius, preventing frequent charging and discharging, and maintaining operation at the recommended DOD of a Li-ion, which is 80% of the total capacity [28,29].

The BESS simulation considers charging and discharging the BESS for the same amount of time each day, or 24 h [14,17,23]. The period is divided evenly into one hour, thirty minutes, and fifteen minutes to accommodate the battery’s charging and discharging rates of 24, 48, or 96, respectively. The charging and discharging rates over any period are calculated using the given equation.

$$C_{iT}=\left[\begin{array}{l}{E}_B(1)\\ \hspace{1em}⋮\\ E_B(m)\end{array}\right]$$

(1)

where C_iT is the charging and discharging rates in the considered duration E_B(t) is the energy in the BESS (MWh) at time t = 1, 2, 3, …, m.

To calculate the energy in the BESS, the Fourier series is applied using the Fourier coefficient vector (C_iF), produced by the optimization operation since the energy in the BESS represented in finely dispersed periodic patterns can be found by using the Fourier series. The periodic pattern is separated into sinusoidal components in the time domain using the Fourier series, which allows for a comprehensive analysis of the BESS energy [30]. In this method, the process uses the Fourier transform to forecast the energy (E_B) in the BESS hourly, starting at random with sixteen values of the Fourier coefficient. Then, the state of energy (SOE) is represented for the whole period considered by using the Fourier series. The energy in the BESS is calculated using the given equations [17,30].

$$C_{iF}=\left[\begin{array}{l}{a}_1,b_1\\ \hspace{1em}⋮\\ a_n,b_n\end{array}\right]$$

(2)

$$E_B(t)=a_0+a_1\cos \left(\frac{2\pi t}{T}\right)+b_1\sin \left(\frac{2\pi t}{T}\right)+\dots +a_n\cos \left(\frac{2\pi nt}{T}\right)+b_n\sin \left(\frac{2\pi nt}{T}\right)$$

(3)

where a₀, a_n, b_n, n, t, and T denote the constant Fourier coefficient, Fourier cosine coefficient, Fourier sine coefficient, number of Fourier coefficients, which is set to 8, time, and total period, respectively. Additionally, a_n and b_n are optimization variables in this problem.

By substituting C_iF from Equation (2) into Equation (3), the BESS energy, E_B(t), can be found. According to Equation (3), a₀ is not required because it has no effect on the BESS charging and discharging processes and the energy cost coefficient. Thus, following an optimization process, it may be adjusted to guarantee that the BESS power curve does not fall below the minimal amount necessary to meet the DOD criteria. The changes in energy in the BESS at two continuous times can be calculated using Equation (4), and it is used to determine the BESS power as in Equation (5) and Equation (6). The BESS power is utilized to present the state of the BESS. The BESS power is positive when it is in a charging state, signifying the addition of energy to the BESS. On the other hand, the BESS power is negative when it is in the discharging stage, signifying the release of energy from the BESS.

$$\Delta E_B=E_B(t)-E_B(t-1)$$

(4)

$$P_B(t)=\Delta E_B/\left(\Delta t\times {\eta }_c\right),P_B(t)>0$$

(5)

$$P_B(t)=\left(\Delta E_B\times {\eta }_d\right)/\Delta t,P_B(t)<0$$

(6)

where $\Delta E_B$ indicates the changes in energy in the BESS at two continuous times, ${\eta }_c$, ${\eta }_d$, P_B, and $\Delta t$ are the charging efficiency of the BESS, discharging efficiency of the BESS, BESS power, and sampling interval time, respectively, ${\eta }_c$ = ${\eta }_d$ = $\sqrt{{\eta }_{bat}}$, and ${\eta }_{bat}$ is the cycle efficiency of BESS, which is set to 0.9.

2.1.2. BESS Simulation

Power and energy capacities should be considered to find the optimal BESS capacity in order to reduce overall costs and maintain the reliability and quality of a distribution system. The number of cycles and the SOC, which are two main factors affecting the BESS life, should also be considered [11]. The efficiency of the BESS life cycle can be increased by reducing daily SOC fluctuations via improved charging and discharging cycles in the BESS. Thus, the BESS size can be formulated as given in Equation (7). The daily cycle and lifespan of the BESS are evaluated as Equations (8) and (9), respectively.

$$Battery\hspace{0.17em}size(\mathrm{kWh})=\frac{\left|E_B^{\max }-E_B^{\min }\right|}{DO{D}_{\max }}$$

(7)

where E_B^max and E_B^min are the maximum and minimum energies of the BESS, respectively, and DOD_max is the maximum DOD, which is equal to 0.8 in this work.

$$Cycles=\frac{1}{2}\left(\frac{{\displaystyle {\sum }_{t=1}^T{E}_B(t)-E_B(t-1)}}{DO{D}_{\max }\times Battery\hspace{0.17em}size}\right)$$

(8)

$$Q(\mathrm{years})=\frac{CyclesLife}{Cycles\times D}$$

(9)

where Cycles indicate the daily cycle of the BESS, D is operation days, which is equal to 285 days, CyclesLife is the nominal life cycle of the Li-ion battery, which is 3000 cycles, and Q represents the lifespan of the BESS in years.

2.2. Charging Station for EV Modeling

To find the best possible location and sizing of the BESS and PV in the distribution network connected to EV charging stations, the charging stations are considered EV penetrations. To add the EV penetration into the systems, it can be assumed that the BESS and grid feed power to the EVs according to the penetration load while increasing the EV demand on all buses through the use of an AC/DC converter or charging port. [22,31]. Additional active and reactive loads of EVs are calculated using the presented equations.

$$P_{ev(n)}^0={\lambda }_{ev}\times P_{L(n)}^0$$

(10)

$$Q_{ev(n)}^0=P_{ev(n)}^0\times \tan ({\phi }_{n(c)})$$

(11)

where P⁰_ev(n) and Q⁰_ev(n) are additional active and reactive loads by the EV penetrations at the n^th bus, ${\lambda }_{ev}$ is a scale factor that shows how much of an EV load there is in relation to the real power demand at each location, P⁰_L(n) is the nominal real load power at the n^th bus, and ${\phi }_{n(c)}$ is the AC/DC converter power factor.

The total active and reactive load powers of the EV penetration at each placement are then formulated using the provided equations.

$$P_{d(n)}^t=P_{L(n)}^0\times {\left(\frac{V_{(n)}^t}{V_{(n)}^0}\right)}^{\alpha }+\left\{P_{ev(n)}^0\times {\left(\frac{V_{(n)}^t}{V_{(n)}^0}\right)}^{{\alpha }_{ev}}\right\}$$

(12)

$$Q_{d(n)}^t=Q_{L(n)}^0\times {\left(\frac{V_{(n)}^t}{V_{(n)}^0}\right)}^{\beta }+\left\{Q_{ev(n)}^0\times {\left(\frac{V_{(n)}^t}{V_{(n)}^0}\right)}^{{\beta }_{ev}}\right\}$$

(13)

where P^t_d(n) and Q^t_d(n) are the total active and reactive power loads integrating the EV penetration at the n^th bus, respectively, Q⁰_L(n) is the nominal reactive load power at bus n, V^t_(n) and V⁰_(n) indicate the time and initial nominal voltages, respectively, $\alpha$ and $\beta$ are active and reactive power exponents of the load demand, respectively, which are both equal to 0, and ${\alpha }_{ev}$ and ${\beta }_{ev}$ are the active and reactive power exponents of the EV load demand, respectively, which are equal to 2.59 and 4.06, respectively [31].

3. Problem Formulation

The optimal position and sizing of the BESS and PV in the distribution network integrated with EV charging stations in this research are proposed to minimize the system costs comprising the installation, replacement, and operation and maintenance costs of the BESS and installation cost of the PV. The system costs are set to be the minimized objective function subject to technical constraints. So, this section defines the objective function and constraints of this work.

3.1. Objective Function

The system costs are considered the objective function to minimize the costs of the BESS installation, which are the investment cost, replacement cost, and operation and maintenance costs and the cost of the PV installation [18,19,23]. The objective function is determined using the equations below.

$$f(C_{iF})=\min \left(C_{system}\right)$$

(14)

$$C_{system}=C_I+C_R+C_{O\&M}+C_{pv}$$

(15)

$$C_I=N_{bat}\times {\gamma }_I$$

(16)

$$C_R=N_{bat}\times {\gamma }_I\times \frac{t_{year}}{Q(years)}$$

(17)

$$C_{O\&M}=C_{VR}+C_{loss}+C_p$$

(18)

$$C_{VR}=\left({\displaystyle {\sum }_{t=1}^T{\displaystyle {\sum }_{i=1}^{N_{bus}}\left|V_i-V_{ref}\right|}}\right)\times {\gamma }_{VR}$$

(19)

$$C_{loss}=\left({\displaystyle {\sum }_{t=1}^T{\displaystyle {\sum }_{i=1}^{N_{br}}\left|P_L\right|}}\right)\times {\gamma }_{loss}$$

(20)

$$C_p=P_{\max }\times \Delta t\times {\gamma }_p$$

(21)

$$C_{pv}=N_{pv}\times {\gamma }_{pv}$$

(22)

where C_system, C_I, C_R, C_O&M, and C_PV are the system costs, BESS investment cost, BESS replacement cost, BESS operation and maintenance costs, and PV installation cost, respectively; C_VR, C_loss, and C_p are the costs of voltage regulation, line loss, and peak demand, respectively; N_bat, N_pv, t_year, V_i, V_ref, P_L, and P_max are the BESS size (kWh), PV size (kW), study duration (set to 20 years), voltage at the i^th bus (p.u.), reference voltage, which is 1 p.u., real loss in each line, and maximum power demand, respectively; N_bus, N_br, ${\gamma }_I$, ${\gamma }_{VR}$, ${\gamma }_{loss}$, ${\gamma }_p$, and ${\gamma }_{pv}$ are the total number of buses, total number of branches, rate of the BESS installation cost (equal to 100 $/kWh), rate of the voltage regulation cost (equal to 0.142 $/p.u.), rate of the transmission loss cost (equal to 0.284 $/kWh), rate of the maximum energy demand cost (equal to 200 $/kWh/year), and rate of the PV installation cost (equal to 2000 $/kW), respectively.

When integrating the BESS into the distribution system, THD can occur when the power from the BESS is transmitted through the power conversion system (PCS). The THD can cause the voltage and current waveforms to be distorted resulting in low-quality transmitted power. However, most of the present distribution systems normally contain high-efficiency filters in the PCS, which can significantly relieve THD. So, by integrating the BESS into distribution systems, THD is assumed to be ignored in this work.

3.2. Constraints

The considered objective function must be subjected to technical constraints while solving the optimization problem. The equality and inequality constraints of this work are presented below.

3.2.1. Equality Constraints

The system power balance in the distribution system is controlled as presented in the given equation.

$$P_{grid}(t)=P_D(t)-P_{pv}(t)\pm P_B(t)+P_L(t)$$

(23)

where P_grid(t), P_D(t), P_pv(t), P_B(t), and P_L(t) are the power of the grid, power of the load demand, power of the PV, power of the BESS, and power of the transmission loss at time t, respectively.

3.2.2. Inequality Constraints

The voltages of all buses must be within the range of the limits, which is considered ±10% of the reference voltage as shown in the following Equation.

$$V_{\min }\le V_i^t\le V_{\max }$$

(24)

where V_min and V_max indicate the minimum and maximum voltages of each bus, which are 0.9 and 1.1, respectively, and V_i^t is the voltage at bus i at time t.

The BESS power and energy are also restricted to keep it safe while charging and discharging. These constraints are represented by the provided equations.

$$P_B^{\min }\le P_{cha}^t,P_{dis}^t\le P_B^{\max }$$

(25)

$$E_B^{\min }\le E_B^t\le E_B^{\max }$$

(26)

where P_B^min and P_B^max denote the minimum and maximum powers of the BESS, respectively, P^t_cha and P^t_dis are the charging and discharging of the BESS at time t, and E_B^min and E_B^max are the minimum and maximum energies of the BESS, respectively.

4. Methodology

To solve the optimization problem in this work, metaheuristic algorithms, namely PSO and AVOA, are applied to provide the optimal location and sizing of the BESS and PV in the distribution network. Moreover, these algorithms are compared using the distribution system efficiency evaluation in aspects of VDI, line losses, and peak demand enhancement. The methodology used in this work is explained below.

4.1. Particle Swarm Optimization (PSO)

PSO was introduced by Kennedy and Eberhart in 1995 to determine the optimal solution to an optimization problem. Despite being a traditional approach, PSO has shown the potential to outperform recently proposed optimization algorithms in various studies [23,32,33]. Moreover, PSO was considered a high-performance algorithm in solving the problem of finding the placement and location of the BESS in distribution networks as presented in [24]. A key idea of PSO came from imitating a flock of birds foraging for food. Each bird in the flock would follow the bird that is currently closest to the best food source [34]. Every particle in the PSO, which is each bird in the flock, represents a potential solution, and the best solution can be searched for using the PSO process. The process of PSO can be explained by updating the velocity and position of each particle using the equations below.

$$v_i^{k+1}=w^k\times v_i^k+c_1{r}_1(p_{best,i}^k-x_i^k)+c_2{r}_2(g_{best}^k-x_i^k)$$

(27)

$$x_i^{k+1}=x_i^k+v_i^{k+1}$$

(28)

where v_i^k+1 and v_i^k denote the velocity of particle i at iterations k + 1 and k, respectively, w^k is the inertia weight at iteration k, c₁ and c₂ are positive constant values, r₁ and r₂ refer to random values between 0 and 1, p^k_best,i and g^k_best are the best position of the particle i (personal best) and the best position of the entire particle (global best) at iteration k, respectively, and the positions of particle i at iterations k and k + 1 are indicated by x_i^k and x_i^k+1, respectively. w^k can be calculated using the following equation.

$$w^k=w_{\max }-(\frac{w_{\max }-w_{\min }}{ite{r}_{\max }}\times k)$$

(29)

where w_max and w_min are the maximum and minimum inertia weights set to 0.9 and 0.4, respectively, and iter_max is the maximum iteration.

4.2. African Vulture Optimization Algorithm (AVOA)

African vultures, which normally migrate in groups to search for food and settle down where the food source is, which refers to the optimal solution, served as the model for the new metaheuristic algorithm called AVOA. The initial locations of the vultures in the search space are randomly sampled to start the AVOA, and the equation below is used to determine the best two vultures.

$$R(i)=\left\{\begin{array}{l}BestVultur{e}_1 if p_i=L_1\\ BestVultur{e}_2 if p_i=L_2\end{array}\right.$$

(30)

$$p_i=\frac{F_i}{{\displaystyle {\sum }_{i=1}^n{F}_i}}$$

(31)

where R(i) denotes one of the best vultures chosen, p_i indicates the probability of selecting the best solution, the indicators determined before the searching process are represented by L₁ and L₂ where the values are between 0 and 1 and the summation of them must equal 1, and n is the number of vulture groups. Then, the starvation rates of both vultures can be found using the provided equations.

$$F=\left(2\times ran{d}_1+1\right)\times z\times \left(1-\frac{iter}{ite{r}_{\max }}\right)+t$$

(32)

$$t=h\times \left({\sin }^w\left(\frac{\pi }{2}\times \frac{iter}{ite{r}_{\max }}\right)+\cos \left(\frac{\pi }{2}\times \frac{iter}{ite{r}_{\max }}\right)-1\right)$$

(33)

where F is the starvation rate of the vultures, rand₁ refers to a random value between 0 and 1, z is a number randomly generated between −1 and 1, which is regenerated in each iteration, t is a parameter used to enhance the searching operation, h indicates a number randomly chosen between −2 and 2, and the exploration and exploitation phases can be balanced by using w [35]. If a number generated by z is less than 0 ([−1, 0)), the vultures are starved, and if a number generated by z is more than 0 ([0, 1]), the vultures are satiated. The starvation rate of the vultures can be described as shown below.

If the F of the vultures is equal to or less than 1, the vultures are satiated. Then, at random distances from one of the two groups, the vultures explore for food by updating the position as shown in the given equations.

$$D(i)=\left|X\times R(i)-P(i)\right|$$

(34)

$$P(i+1)=R(i)-D(i)\times F$$

(35)

$$P(i+1)=R(i)-F+ran{d}_2\times \left(\left(ub-lb\right)\times ran{d}_{3}lb\right)$$

(36)

where D(i) is adopted to update the best vulture positions in two groups, X is the movement of vultures that randomly move to protect food from others, P(i) and P(i + 1) are the vectors of the vulture position at iterations i and i + 1, rand₂ and rand₃ are numbers randomly generated between 0 and 1, and ub and lb are the variable upper and lower bounds, respectively.

When F is equal to or more than 0.5 and less than 1, violent arguments break out among vultures, and hostile vultures do not share their food. Weaker vultures obtain food scraps from stronger vultures. So, the vultures update their positions in this situation using the presented equations.

$$d(t)=R(i)-P(i)$$

(37)

$$P(i+1)=D(i)\times \left(F+ran{d}_4\right)-d(t)$$

(38)

$$S_1=R(i)\times \left(\frac{ran{d}_5\times P(i)}{2\pi }\right)\times \cos (P(i))$$

(39)

$$S_2=R(i)\times \left(\frac{ran{d}_6\times P(i)}{2\pi }\right)\times \sin (P(i))$$

(40)

$$P(i+1)=R(i)-(S_1+S_2)$$

(41)

where d(t) denotes the distance of the vulture from one of the best vultures in the two groups, S₁ and S₂ are spiral equations obtained between all vultures and one of the best vultures in the two groups, and rand₄, rand₅, and rand₆ are numbers randomly generated between 0 and 1.

Conflicts occur among vultures if F is less than 0.5 because it is assumed that there are a greater number of vultures than food sources. Usually, all vultures tend to fly to the same place where the food is. Thus, the vulture position is updated using the equations shown below.

$$A_1=BestVultur{e}_1(i)-\frac{BestVultur{e}_1(i)\times P(i)}{BestVultur{e}_1(i)-P{(i)}^2}\times F$$

(42)

$$A_2=BestVultur{e}_2(i)-\frac{BestVultur{e}_2(i)\times P(i)}{BestVultur{e}_2(i)-P{(i)}^2}\times F$$

(43)

$$P(i+1)=\frac{A_1+A_2}{2}$$

(44)

$$P(i+1)=R(i)-\left|d(t)\right|\times F\times Levy(d)$$

(45)

where A₁ and A₂ are rivalries for food that might lead to an accumulation of different vulture species in one food supply, the best vultures of the first and second groups at iteration i are represented by BestVulture₁(i) and BestVulture₂(i), respectively, and Levy(d) indicates a Levy flight employed to boost the randomness of AVOA and is calculated using the presented equation.

$$Levy(d)=0.01\times \frac{u\times \sigma }{{\left|v\right|}^{\frac{1}{\beta }}},\sigma ={\left(\frac{\Gamma (1+\beta )\times \sin (\frac{\pi \beta }{2})}{\Gamma (1+2\beta )\times \beta \times 2(\frac{\beta -1}{2})}\right)}^{\frac{1}{\beta }}$$

(46)

4.3. System Efficiency Evaluation

After the installation of the BESS and PV, the efficiency of the distribution network is investigated regarding different aspects by referring to the objective function in terms of VDI, transmission losses, and peak demand.

4.3.1. Voltage Deviation Index (VDI)

The efficiency of the distribution network is evaluated using the VDI to examine the voltage profile improvement after the BESS and PV installations. The percentage of VDI is found by the difference between the reference voltage and the actual voltage for each period as the presented equation.

$$\begin{array}{l}\%VD{I}_i={\max }_T\frac{\left|V_{ref}-V_i\right|}{V_{ref}}\times 100,\\ \%VDI={\displaystyle \sum _{i=1}^{N_{bus}}\%VD{I}_i}\end{array}$$

(47)

where %VDI_i is the maximum percentage of VDI at bus i for each period T, V_ref and V_i are the voltage values of the reference bus and bus i, respectively, %VDI is the total percentage of the VDI in the system, and N_bus is the number of buses.

4.3.2. Transmission Losses

After installing the BESS and PV, the distribution network’s efficiency is also assessed and compared using transmission losses, which are calculated using the following equation and comprise active power, reactive power, and apparent power losses.

$$\begin{array}{l}{P}_{loss}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _l^{N_{br}}{P}_L^t,}}\\ Q_{loss}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _l^{N_{br}}{Q}_L^t,}}\\ S_{loss}=\sqrt{{P_{loss}}^2+{Q_{loss}}^2}\end{array}$$

(48)

where P_loss, Q_loss, and S_loss indicate the active power, reactive power, and apparent power losses, respectively, for each period T, and the active and reactive power losses of line l at each time t are represented by P^t_L and Q^t_L, respectively.

4.3.3. Peak Demand

Peak demand is evaluated after the installation of the BESS and PV specified by peak shaving. The peak demand, which considers a duration of 24 h in this work, is the maximum active power consumption under the consideration period.

4.4. Implementation

The placement and sizing of the BESS and PV in the distribution network considering EV penetrations are optimized by employing two metaheuristic algorithms comprising PSO and AVOA. The optimization process of the proposed approach is illustrated by the flowchart in Figure 1.

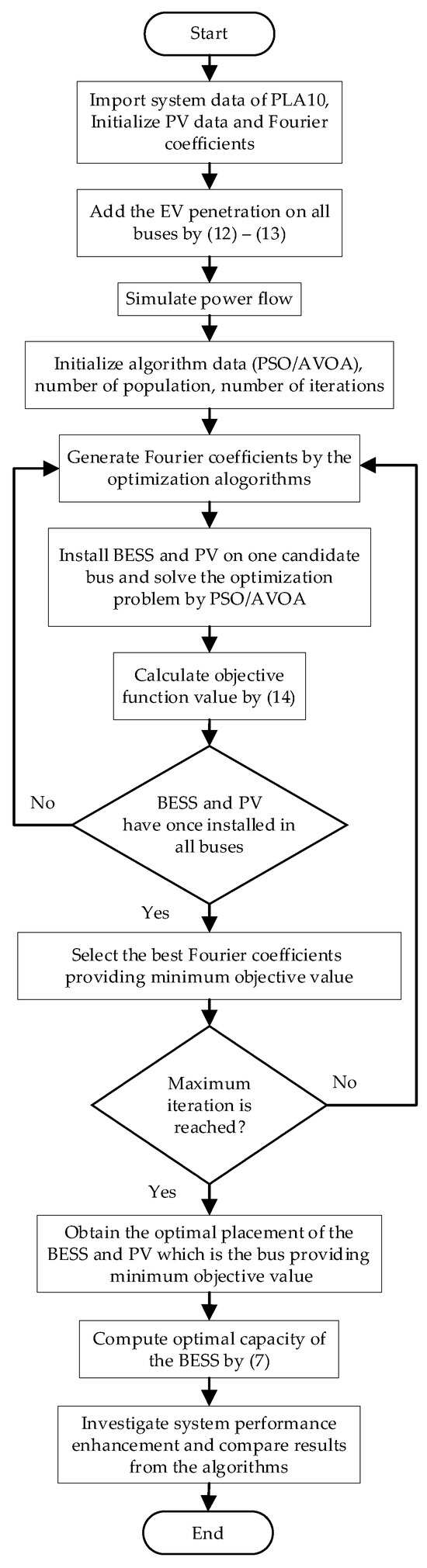
Figure 1. Optimization process of the proposed approach.

5. Simulation Results

The optimal placement and sizing of the BESS and PV were simulated in the practical distribution network by considering EV penetrations. The two algorithms, which are PSO and AVOA, were used to generate the solutions to the optimization problem with minimum system costs. The process was operated in MATLAB 2021a, and MATPOWER 7.1 was adopted to simulate the power flow [36]. The population number and maximum iterations of the metaheuristic algorithms were set to 60 and 250, respectively. The input system data and simulation results are presented and discussed in the following subsections.

5.1. Input System Data

The practical distribution network investigated in this study is the tenth feeder of Phitsanulok substation 1 (PLA10), Thailand, which is a 91-bus distribution network. At present, the Provincial Electricity Authority of Thailand is planning to install BESSs in several substations due to the increasing load demands, renewable energy sources, and EVs. Phitsanulok is an important economic zone of the upper central region of Thailand (the capital city of Thailand is in the central region), and there will be more investment in this area in the future. So, by installing a BESS and PV in Phitsanulok Substation, the growing load demands and EV demands will be able to be fully supported, and the system performance will be significantly enhanced in the future. The single-line diagram of PLA10 is shown in Figure 2, and the system data including load demand at each bus and transmission line data are given in Table A1 in Appendix A. The base power is 1 MVA, the base voltage is 22 kV, and the maximum load demand of the system is 9045.40 kW. The 24-h load demand and PV generation are presented in p.u. as shown in Table 2. The load demand and EV penetration at 20%, 40%, and 60% of the PLA10 distribution network within a day are illustrated in Figure 3.

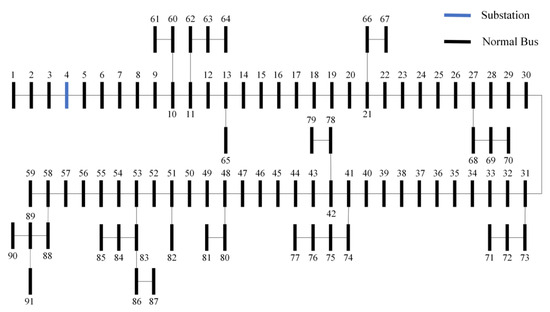
Figure 2. Single-line diagram of the PLA10 distribution network.

Table 2. Hourly load demand and PV generation within a day.

Hr.	Load (p.u.)	PVp (p.u.)	Hr.	Load (p.u.)	PVp (p.u.)
1	0.366	0.000	13	0.923	0.987
2	0.353	0.000	14	0.964	0.916
3	0.335	0.000	15	0.985	0.729
4	0.315	0.000	16	1.000	0.427
5	0.314	0.000	17	0.817	0.179
6	0.295	0.000	18	0.739	0.014
7	0.292	0.072	19	0.770	0.000
8	0.342	0.325	20	0.748	0.000
9	0.404	0.608	21	0.592	0.000
10	0.485	0.820	22	0.363	0.000
11	0.736	0.950	23	0.323	0.000
12	0.902	1.000	24	0.306	0.000

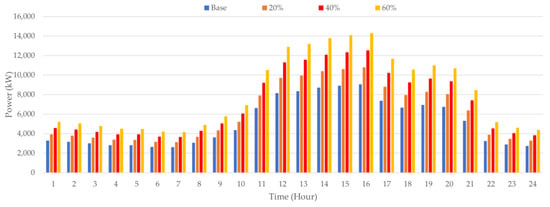
Figure 3. Hourly load demand and EV penetration at 20%, 40%, and 60% of the PLA10 distribution network.

5.2. Results and Discussion

The optimal position and sizing of the BESS and PV were generated by the considered algorithms in the PLA10 distribution network. After the installation of the BESS and PV, the effectiveness of each algorithm is examined in terms of the minimal system costs, which include the costs of the PV installation and operation and maintenance as well as the investment and replacement costs. Furthermore, the performance improvement of the distribution network generated by PSO and AVOA is compared before and after BESS and PV installation in aspects of the VDI, line loss, and peak demand. The simulation results of this system are presented as follows:

5.2.1. Optimal Placement and Capacity of the BESS and PV

To find the most feasible placement and capacity of the BESS and PV, the generated Fourier coefficients of the algorithms were used to calculate the SOE of the BESS in a day. The SOE depending on the load demand at each EV penetration throughout the day is illustrated in Figure 4. The optimal placement and capacity of the BESS and PV, power and lifetime of the BESS, and system costs are presented in Table 3.

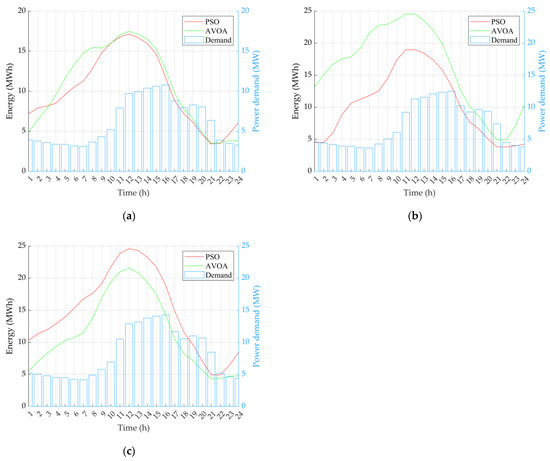
Figure 4. Stage of Energy (SOE) of the BESS generated by each algorithm and power demand in the PLA10 distribution system: (a) at ${\lambda }_{ev}$ 20%; (b) at ${\lambda }_{ev}$ 40%; (c) at ${\lambda }_{ev}$ 60%.

Table 3. Optimal placement and capacity of the BESS and PV generated by each algorithm at each considered EV penetration.

Algorithm	${\mathit{\lambda }}_{\mathit{e}\mathit{v}}$	BESS Placement	BESS Size (MWh)	PV Placement	PV Size (kW)	Power of BESS (MW)	Lifetime of BESS	System Costs ($)
PSO	20%	41	17.1415	51	2356.65	2.8215	8.824658	40,208,157.04
	40%	41	18.9705	51	2544.36	3.1765	8.824658	47,213,163.04
	60%	41	24.5914	51	3913.34	3.8928	8.824658	54,148,223.67
AVOA	20%	41	17.4733	51	2598.12	2.8497	8.784056	40,283,138.35
	40%	31	24.5594	82	2460.39	3.6452	8.824658	47,234,023.75
	60%	41	19.7769	50	3689.10	3.4387	8.824658	54,435,077.17

From Figure 4, it can be noted from all EV penetrations that the BESS was in the charging state when the demand was low from 1 a.m. to around noon. Even though the demand started to become higher from 9 a.m. to noon, the BESS could still be in a charging state because of the energy generated from PV. The BESS then started to be in a discharging state in the afternoon until around 9 p.m. due to very high load demand. In Table 3, it is observed that the optimal placements of the BESS installation obtained by PSO were at the 41st bus at all considered EV penetrations and by AVOA at the 41st, 31st, and 41st buses at 20%, 40%, and 60% EV penetrations, respectively. By considering the objective function value, PSO could provide better system costs than those of AVOA for all EV penetrations. So, by considering the results provided by PSO, the optimal placement was the 41st bus, which is the location of New Ice Factory, Ban Krang Subdistrict, Mueang Phitsanulok District, Phitsanulok. This place was observed and found to be suitable and has space to install the BESS. Furthermore, the optimal locations of the PV obtained by PSO were at the 51st bus at all EV penetrations. Unfortunately, the actual area survey found that this place cannot invest in PV installation since a university is located on this bus. However, the PV can be installed on a nearby bus, which is the 52nd bus, because there are areas that have not yet been developed. In addition, the largest BESS size obtained by PSO was 24.5914 MWh at 60% of EV penetrations, followed by AVOA, which was 24.5594 MWh at 40% of EV penetrations.

5.2.2. System Performance Improvement Comparison

The performance improvement of PLA10 was evaluated in different terms by referring to the objective function in terms of the VDI, transmission line losses, and peak demand before and after the installation of the BESS and PV by each algorithm as shown in Table 4, where the base case was the case without a BESS.

Table 4. Comparison of distribution system performance improvements before and after the BESS and PV installations.

Algorithm	${\mathit{\lambda }}_{\mathit{e}\mathit{v}}$	VDI (%)	Real Power Loss (MW)	Reactive Power Loss (MVAr)	Apparent Power Loss (MVA)	Peak Demand (MW)
Base	20%	256.99	1.515	3.256	3.591	10.786
	40%	298.12	2.045	4.397	4.849	12.535
	60%	339.84	2.661	5.722	6.31	14.293
PSO	20%	199.77	1.126	2.434	2.682	6.882
	40%	233.55	1.546	3.341	3.681	8.171
	60%	253.81	1.881	4.064	4.478	8.587
AVOA	20%	197.60	1.125	2.432	2.679	6.749
	40%	242.57	1.570	3.398	3.743	7.749
	60%	261.65	1.921	4.153	4.575	9.143

It is observed from Table 4 that after the BESS and PV installations in the PLA10 distribution system, both algorithms provided reductions in the VDI, line losses, and peak demand for all EV penetrations. Moreover, it was found that AVOA was more efficient than PSO at 20% of EV penetration for VDI, losses, and peak demand reductions, but PSO generated better reductions of those terms than AVOA at 40% and 60% of EV penetrations except for the peak demand at 40% of EV penetration. The VDI could be reduced the most compared to the base case by around 59.39%, 64.57%, and 86.03% for 20%, 40%, and 60% of EV penetrations, respectively. The biggest decrease in real power loss compared to the base case reached approximately 0.39, 0.499, and 0.78 MW for 20%, 40%, and 60% of EV penetrations, respectively. For the highest peak demand reductions at 20%, 40%, and 60% of EV penetrations, they dropped around 4.037, 4.786, and 5.706 MW, respectively. So, the system performance could be significantly improved after the BESS and PV installations, especially in the high EV penetration case.

The 24-h voltage profiles at the weakest bus, which is the 91st bus, for 20%, 40%, and 60% of EV penetrations obtained by PSO and AVOA are presented in Figure 5 to show the improvement voltage profiles before and after the BESS and PV installations.

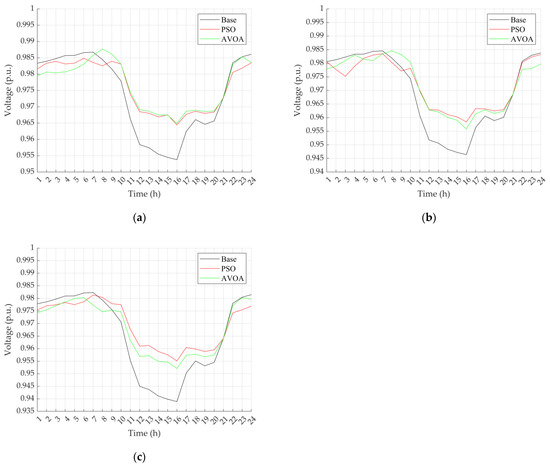
Figure 5. Voltage profile at the 91st bus in the PLA10 distribution system: (a) at ${\lambda }_{ev}$ 20%; (b) at ${\lambda }_{ev}$ 40%; (c) at ${\lambda }_{ev}$ 60%.

In Figure 5, it is noticeable that the voltage before the BESS and PV installations in the base case at 4.00 p.m. was at the lowest value because this period has the highest demand. However, the all-day voltage profile could be enhanced by installing the BESS and PV regardless of the increase in EV penetrations.

The 24-h real line losses in the PLA10 before and after installing the BESS for 20%, 40%, and 60% of EV penetrations provided by PSO and AVOA are plotted in Figure 6.

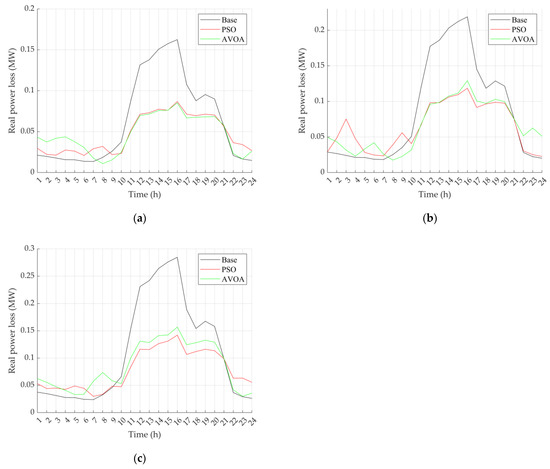
Figure 6. Real power loss in the PLA10 distribution system: (a) at ${\lambda }_{ev}$ 20%; (b) at ${\lambda }_{ev}$ 40%; (c) at ${\lambda }_{ev}$ 60%.

It can be seen in Figure 6 that the BESS was charging to reserve power to reduce the peak power during the peak period, resulting in the transmission line loss increasing, which was more than the base case in some periods from around 1.00 a.m. to 10.00 a.m. and 9.00 p.m. to 12.00 a.m. However, there was a noticeable drop in transmission loss between 10.00 a.m. and 9.00 p.m. because the BESS discharged power to assist in supplying the network’s demand, as evident in Table 4. So, the installation of the BESS and PV enhanced the 24-h transmission line loss when compared to the base case.

Finally, the peak demands in the PLA10 for 20%, 40%, and 60% of EV penetrations before and after installing the BESS and PV by PSO and AVOA are plotted in Figure 7.

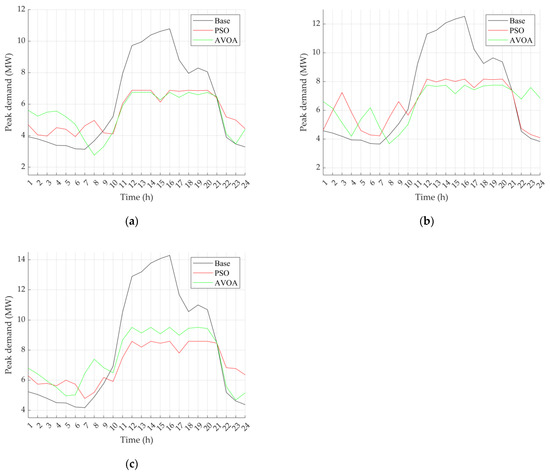
Figure 7. Peak demand in the PLA10 distribution system: (a) at ${\lambda }_{ev}$ 20%; (b) at ${\lambda }_{ev}$ 40%; (c) at ${\lambda }_{ev}$ 60%.

It can be observed from Figure 7 that the peak demand was at 4.00 p.m. for the base case. It is also evident that, following the BESS installation, there were times between 1:00 a.m. and 10:00 a.m. and 9.00 p.m. and 12:00 a.m. when the peak demand exceeded that of the base case because the BESS was charging in order to store energy to lower the peak demand during the highest peak period. Thus, as shown in Table 4, the peak demand was greatly reduced from 10:00 a.m. to 9.00 p.m. following the installation of the BESS, resulting in a 24-h peak demand decrease.

5.2.3. Statistical Analysis and Algorithm Performance Comparison

The statistical results of the considered algorithms are investigated, and the performance of the algorithms is compared. The statistical results and operation times of each algorithm for 20%, 40%, and 60% of EV penetrations are given in Table 5, and the convergence curves of PSO and AVOA for solving the system costs for 20%, 40%, and 60% of EV penetrations are potted in Figure 8.

Table 5. Statistical results of each algorithm in the PLA10 distribution system.

Algorithm	${\mathit{\lambda }}_{\mathit{e}\mathit{v}}$	Best	Worst	Mean	Median	Std.
PSO	20%	40,208,157.04	40,476,376.40	40,369,678.50	40,397,090.20	99,605.69
	40%	47,213,163.04	47,313,442.33	47,254,287.65	47,236,257.59	42,878.09
	60%	54,148,223.67	54,333,070.57	54,229,925.23	54,208,481.46	76,971.73
AVOA	20%	40,2831,38.35	40,814,701.71	40,487,523.12	40,466,871.68	198,660.95
	40%	47,234,023.75	47,750,305.34	47,464,793.62	47,410,051.78	214,296.01
	60%	54,435,077.17	55,431,002.91	54,761,252.60	54,599,970.51	347,863.18

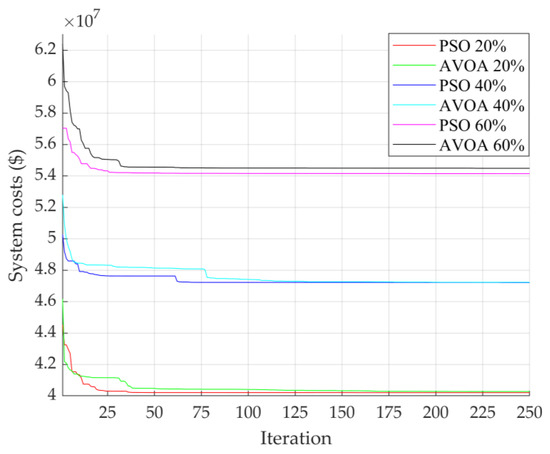
Figure 8. Convergence curves of each algorithm in the PLA10 distribution system at ${\lambda }_{ev}$ 20%, 40%, and 60%.

It can be seen from Table 5 that PSO provided the best results in terms of the best value, worst value, mean, median, and standard deviation. From Figure 8, it is noted that the convergence curves generated by both algorithms were very close to each other where both PSO and AVOA took turns converging faster towards the optimal solution.

For investment considerations, the calculation of the break-even point involved dividing the costs of installing BESS and PV by the difference between the system’s operation and maintenance costs before and following the BESS and PV installations as presented in Table 6.

Table 6. Break-even point of each algorithm.

Algorithm	${\mathit{\lambda }}_{\mathit{e}\mathit{v}}$	System Costs ($)	Operation and Maintenance Costs for 1 Day ($)	Payback (Years)
Base	20%	-	6345.0331	-
	40%	-	7454.8843	-
	60%	-	8594.2133	-
PSO	20%	40,208,157.04	4095.3141	7.8274
	40%	47,213,163.04	4921.6504	7.5551
	60%	54,148,223.67	5245.0794	8.4142
AVOA	20%	40,2831,38.35	4022.0764	8.1893
	40%	47,234,023.75	4697.4262	7.3293
	60%	54,435,077.17	5561.2344	8.4512

Table 6 shows that the optimal installation of the BESS and PV generated by PSO provided a faster payback period than that of AVOA. However, AVOA provided the quickest payback time at 40% of EV penetration because AVOA has a larger BESS size than that of PSO resulting in a bigger reduction in the peak demand, which affects the costs. However, the break-even point is found based on the same behavior of using BESS and PV every day for a period of 20 years, which may change according to usage behavior.

6. Conclusions

This paper proposed an approach to find the optimal placement and capacity of the BESS and PV while minimizing system costs and enhancing the performance of the distribution system integrated with EVs. The system costs, which are the main objective functions, consisting of installation, replacement, transmission loss, voltage regulation, and peak demand costs, are minimized while satisfying the considered constraints. The metaheuristic algorithms consisting of PSO and AVOA were applied to solve the problem, and the PLA10 distribution network in Thailand was tested. The simulation results showed that the optimal placement and capacity of BESS and PV in PLA10 considering several levels of EV penetrations could be obtained by both algorithms while PSO could provide lower overall system costs than AVOA. The optimal placement of the BESS for the PLA10 was at the 41st bus, which was observed to be suitable for installing the BESS, while the optimal PV location was at the 51st bus, which was found to be inappropriate for installing the PV, but it can be installed at a nearby bus. For the system performance investigation, it is revealed in most cases of EV penetrations that PSO generated better VDI improvement and real loss reductions while AVOA achieved superior peak demand reductions. The VDI could be reduced, at most, by 86.03%, real power loss decreased the most by 0.78 MW, and the largest peak demand reduction reached 5.706 MW compared to those of the case without installing a BESS and PV. It is found that the system performance could be significantly improved after BESS and PV installations, especially in the case of high EV penetration. In the statistical analysis and algorithm performance comparison, PSO obtained the best statistical values including best value, worst value, mean, median, and standard deviation, and PSO also converged to the optimal solutions faster and had a faster payback period than those of AVOA. So, to find the optimal placement and capacity of the BESS and PV in this tested system, PSO should be adopted to provide efficient solutions. However, this work provided the optimal placement and capacity of the BESS and PV in the practical system simulation, so the real location of the system is required to be observed to determine whether the BESS and PV can really be installed. In the future, the optimal placement and capacity of the BESS and PV from this work will be considered for installation in the real PLA10 distribution network in order to improve system efficiency with minimum investment costs. Moreover, the TOU pricing method can be applied, and the energy from the BESS sold back to the grid can be considered in order to more optimally store and consume the energy, resulting in a faster payback period. In addition, the effect of the EV state of charge on the energy demand can be also studied in order to further interpret the BESS behaviors.