Experiment-Based Determination of Optimal Parameters in Constant Temperature–Constant Voltage Charging Technique for Lithium-Ion Batteries Using Taguchi Method
Abstract
1. Introduction
- (1)
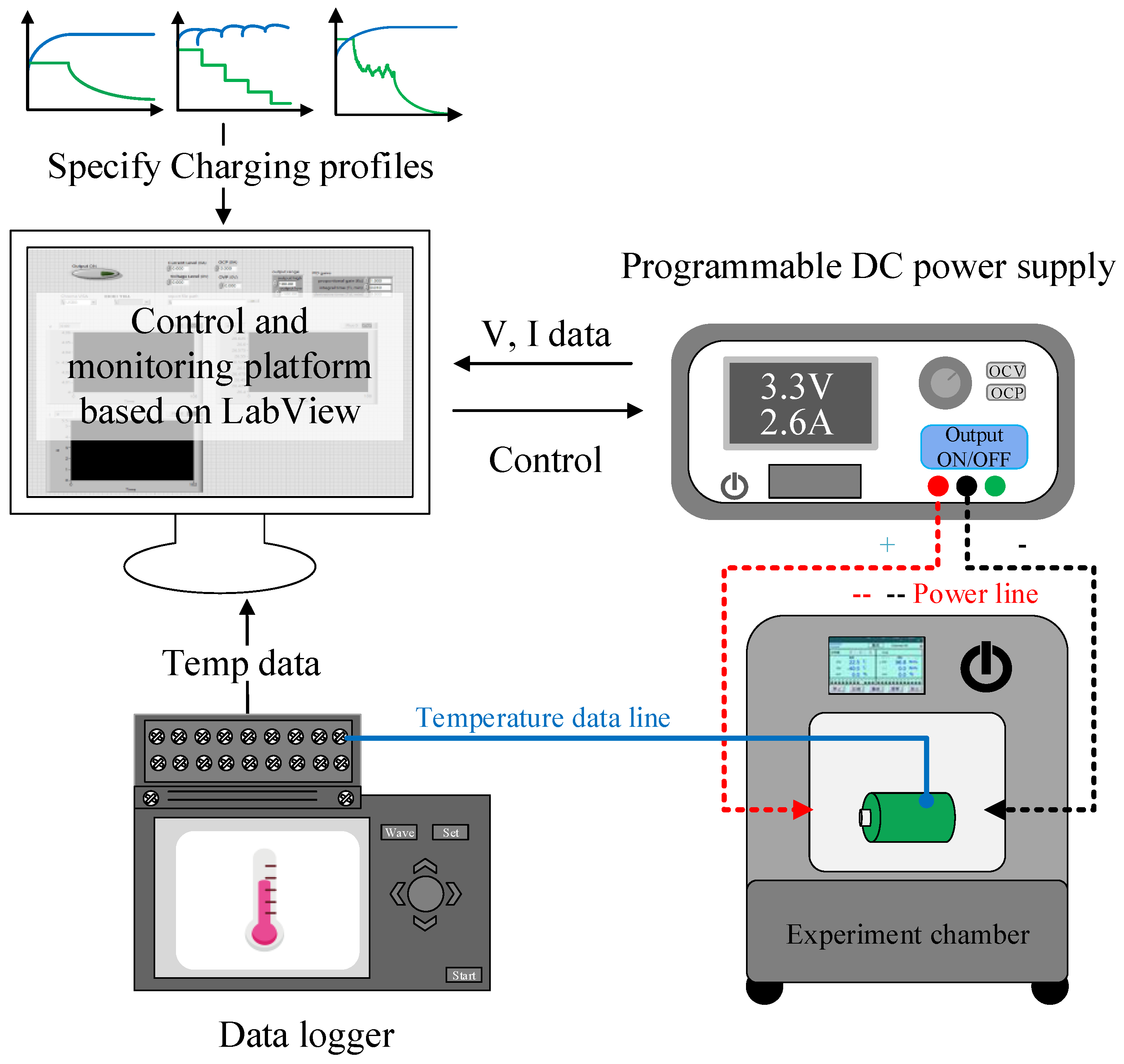
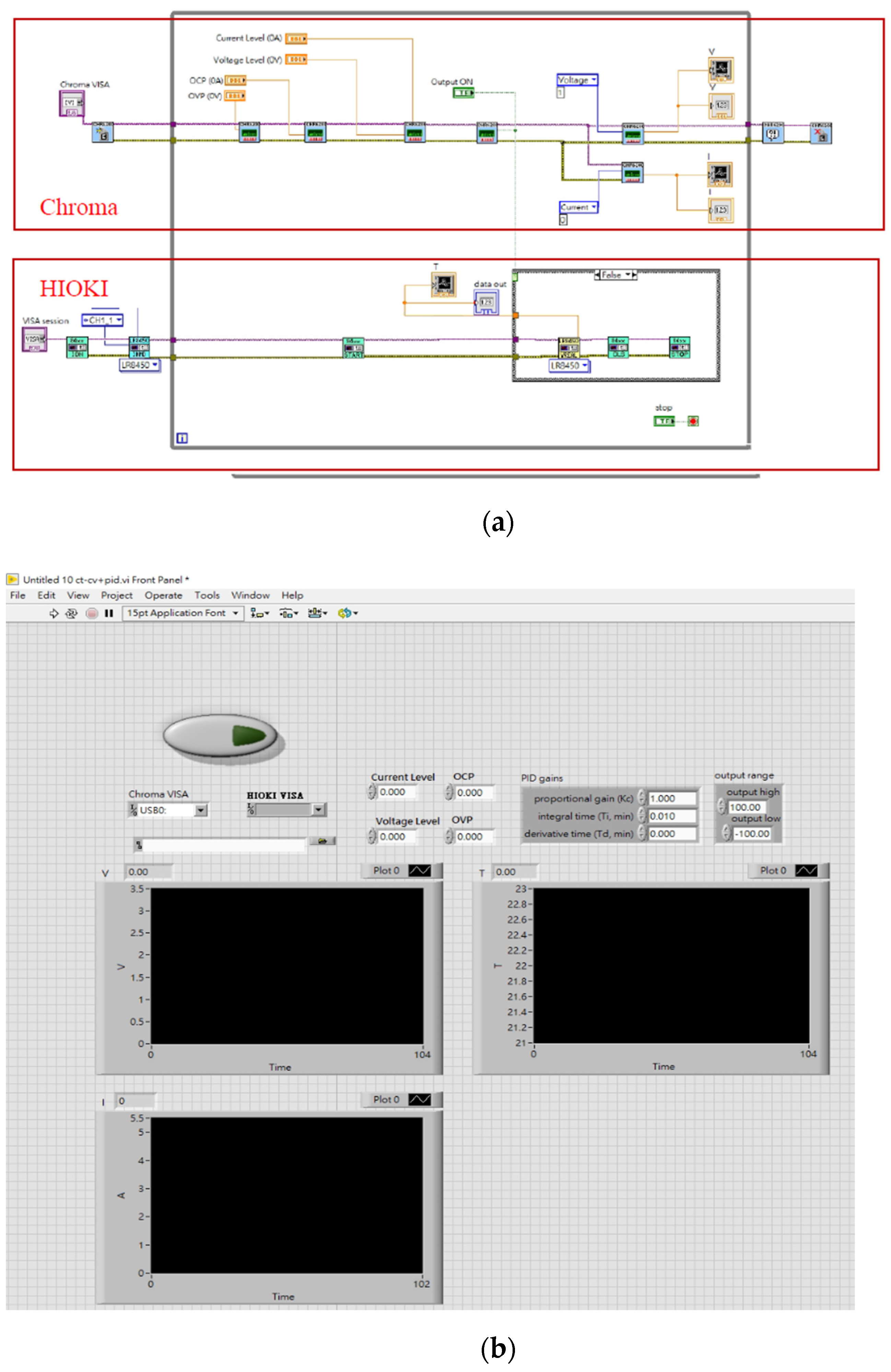
- Development of a charging test platform: A charging test platform is developed based on LabVIEW software version 2018, enabling easy setting of the charging parameters and monitoring of the charging process;
- (2)
- Investigation of the CT-CV charging method: Three trial cases of CT-CV methods are implemented by enumeration to exhibit the effect of key parameters on the charging performance at the initial stage;
- (3)
- Demonstration of the application of the Taguchi method on CT-CV optimization: The Taguchi method is used to find the optimal configurations of the CT-CV method. The results show that the optimized CT-CV method is able to maintain similar temperature rise and charging efficiency and achieve shorter charging time;
- (4)
- Comprehensive comparisons and discussion of the investigated charging methods: The results of the charging performances are revealed and discussed. This provides a clear overview when designing a CT-CV method.
2. Experimental Setup and Investigated Charging Strategies
2.1. Experimental Setup
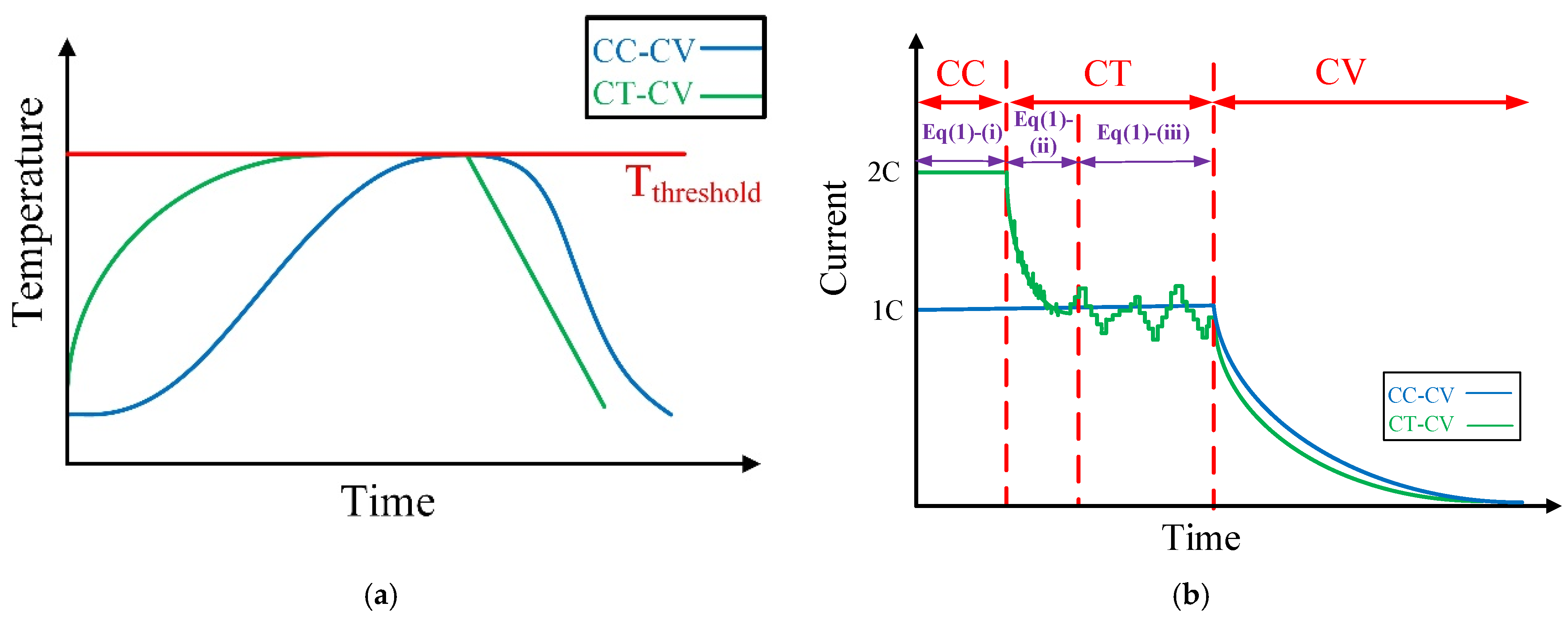
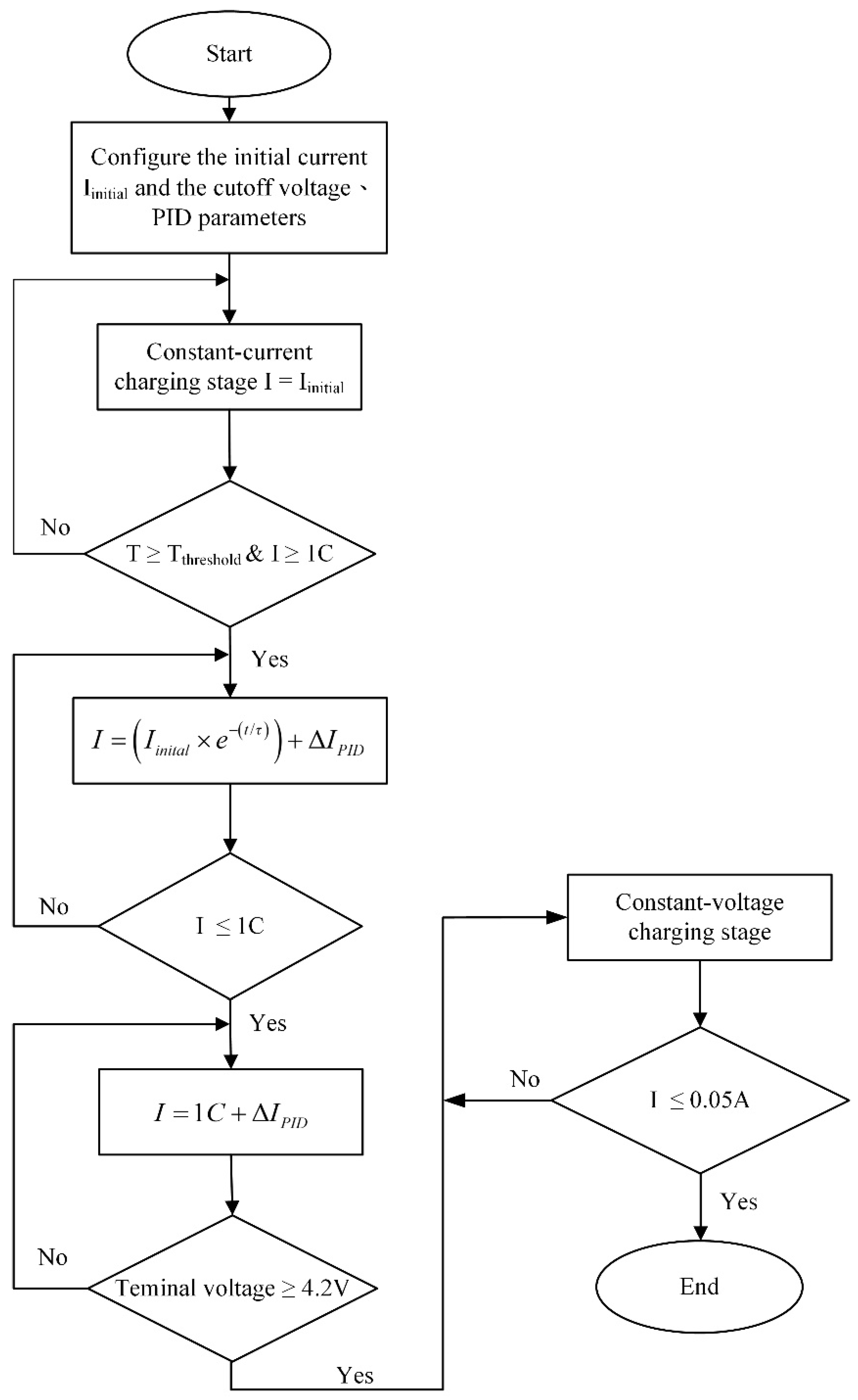
2.2. CT-CV Charging Strategies
2.3. Enumeration of the Configuration of CT-CV Charging Methods
3. Optimized CT-CV Charging Strategy Based on Taguchi Method
3.1. Experiment Design Using Taguchi Method
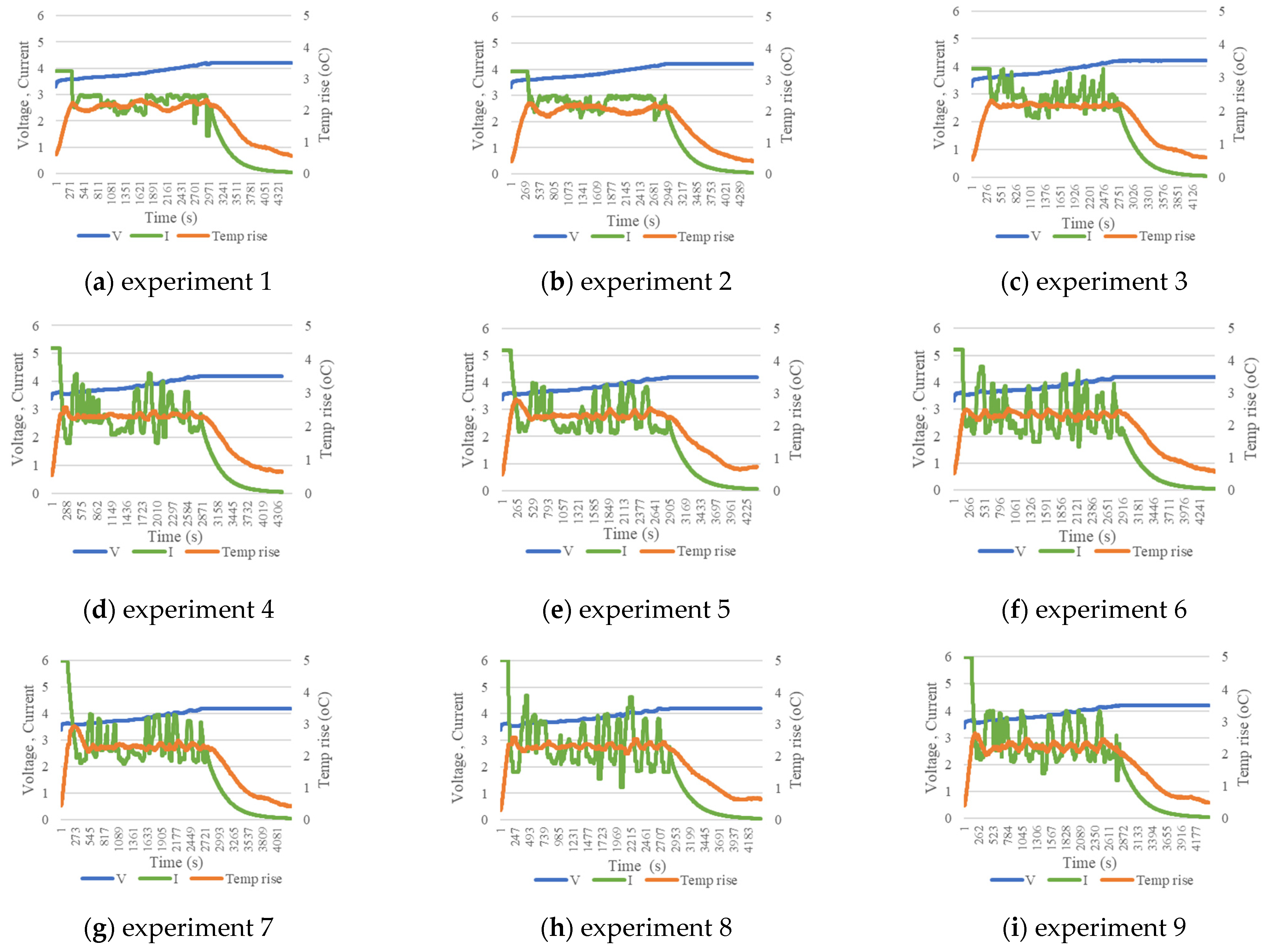
3.2. Experimental Results from the Orthogonal Array
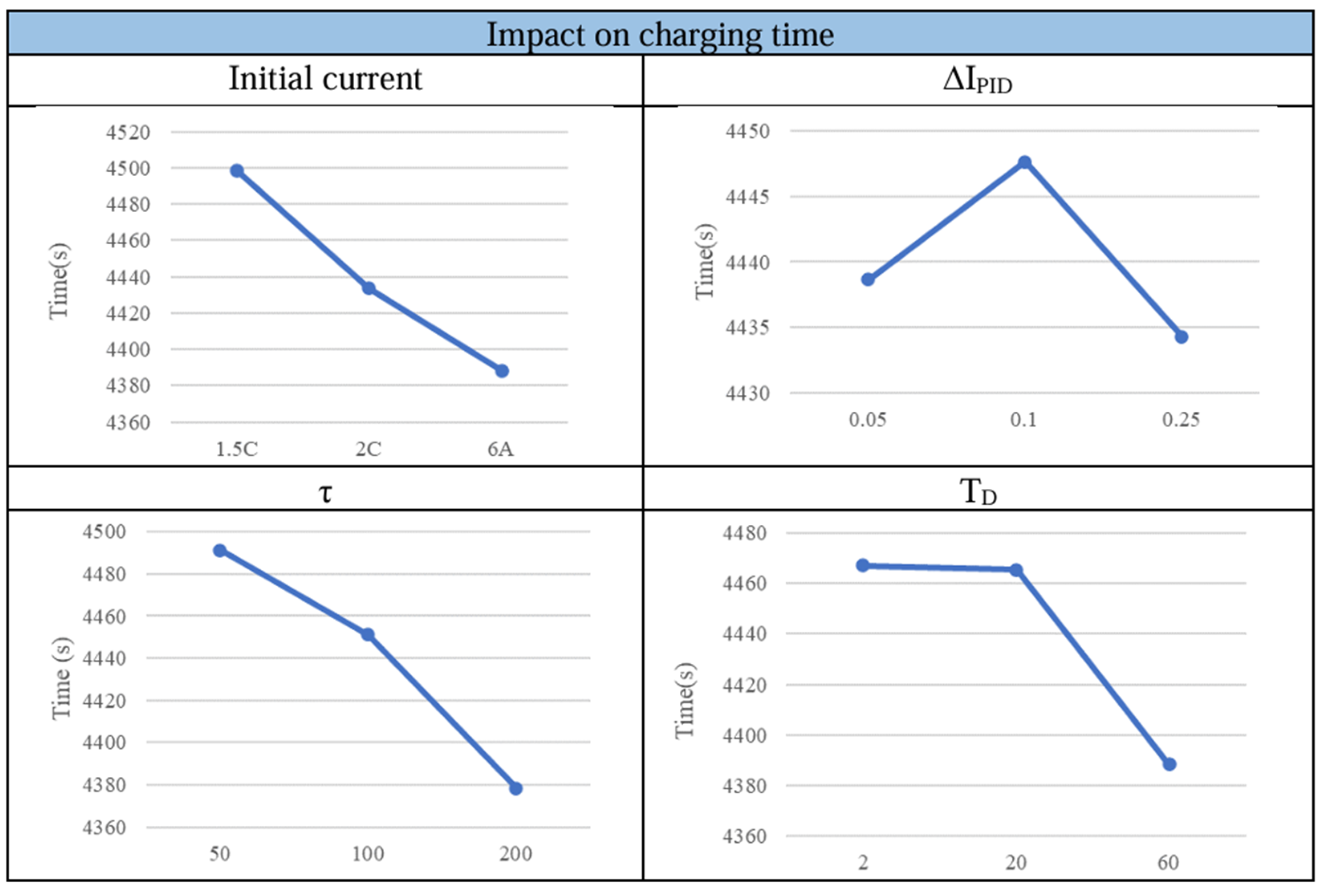
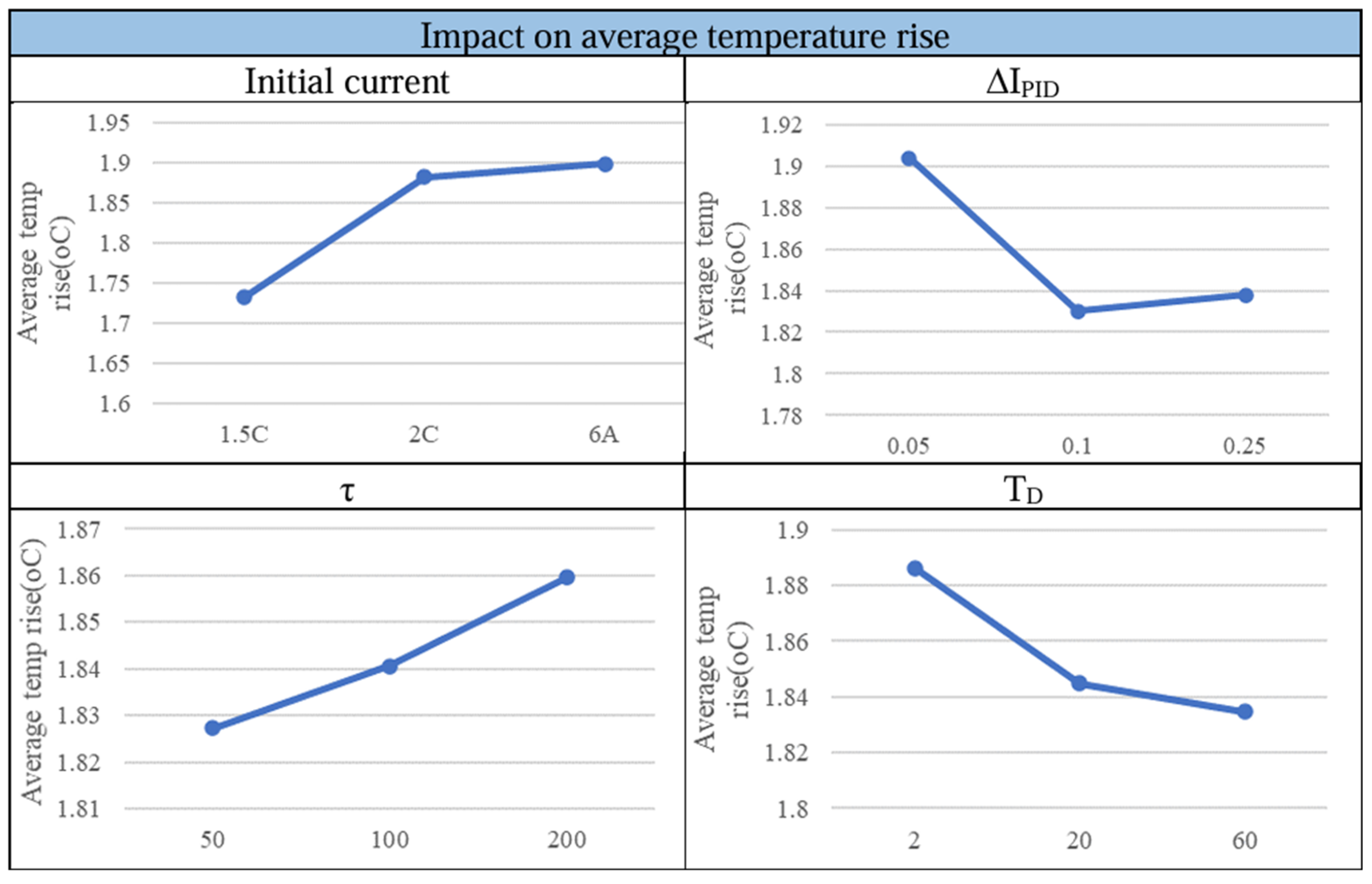
3.3. Analysis of the Key Control Factors Based on Taguchi Method
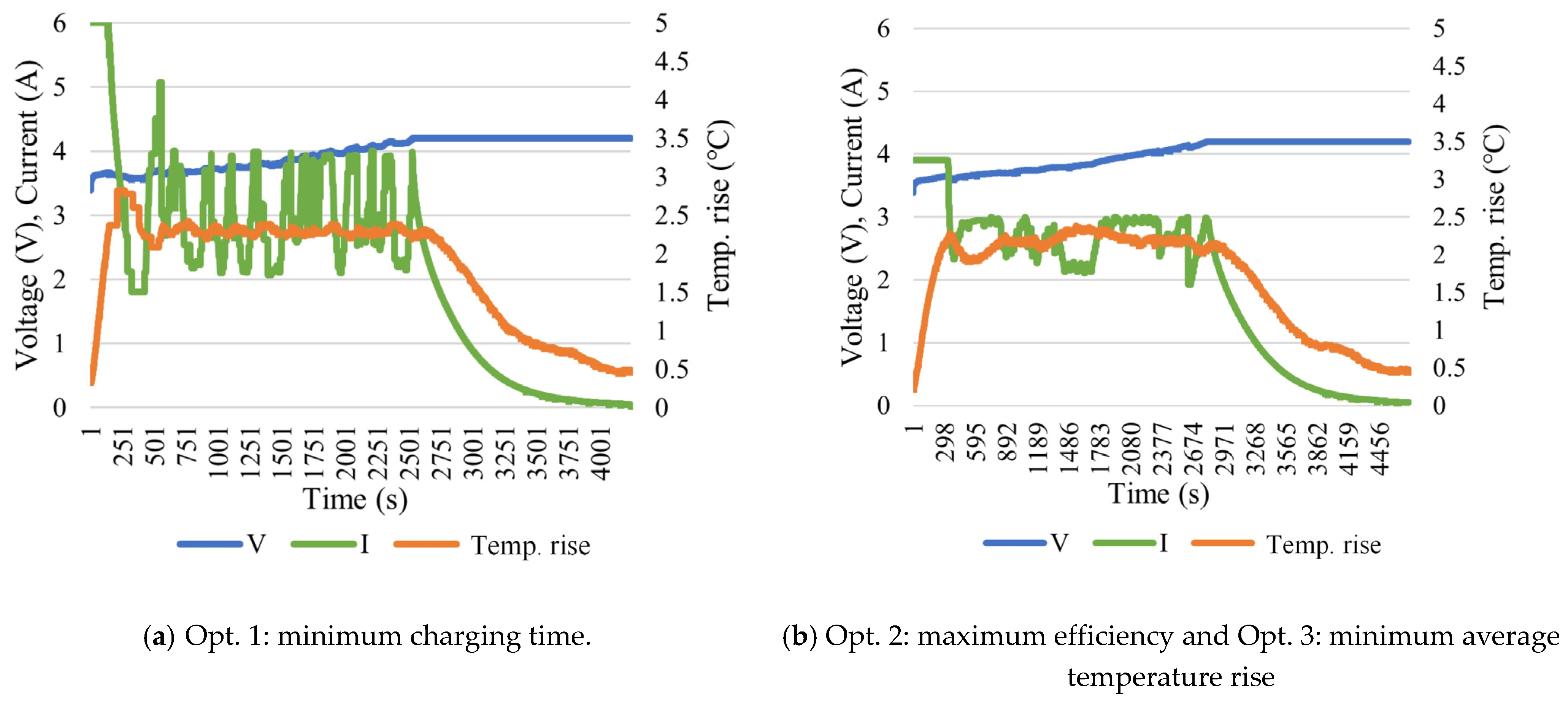
4. Comprehensive Comparison and Discussion of the Investigated Charging Methods
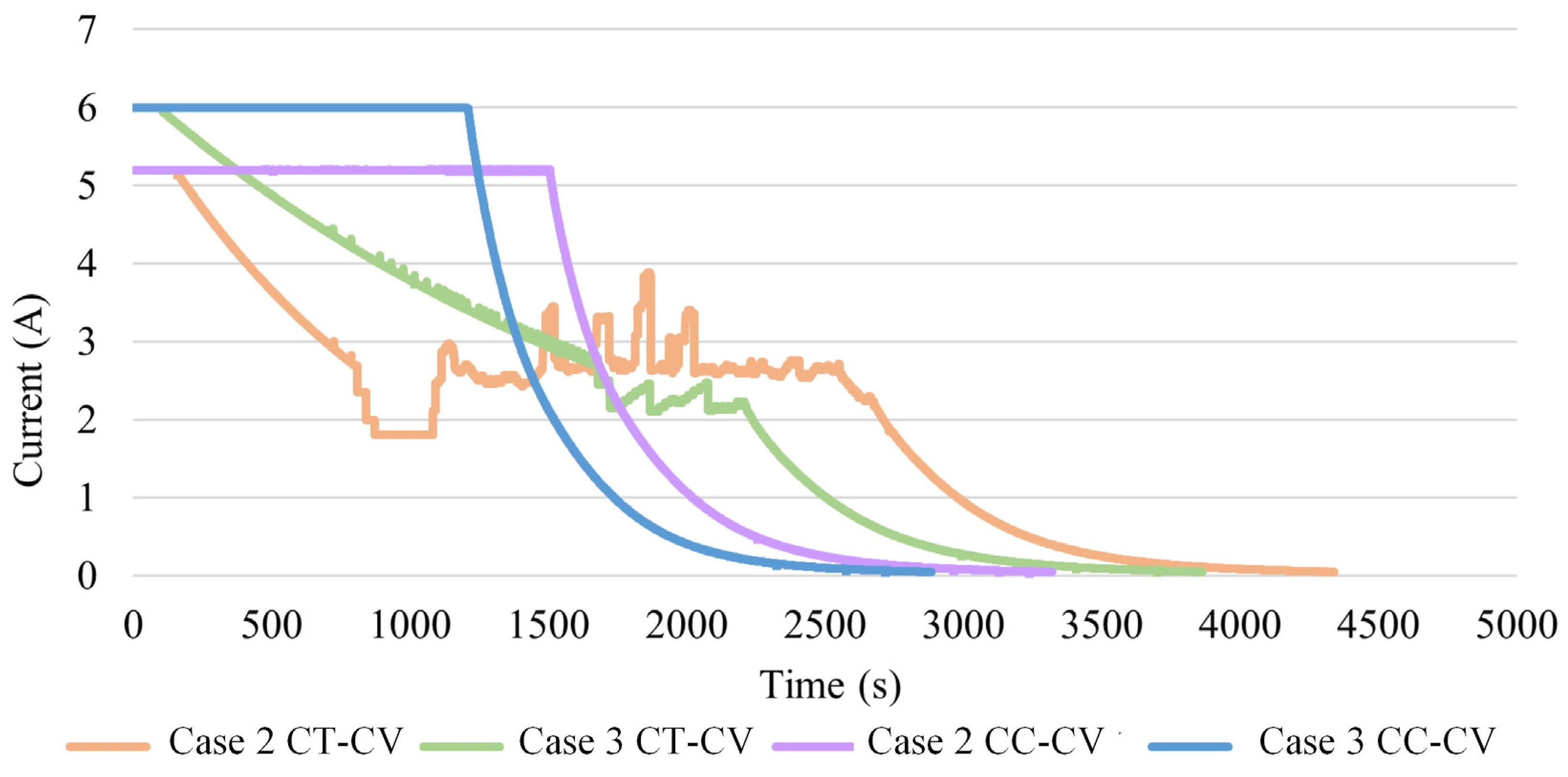
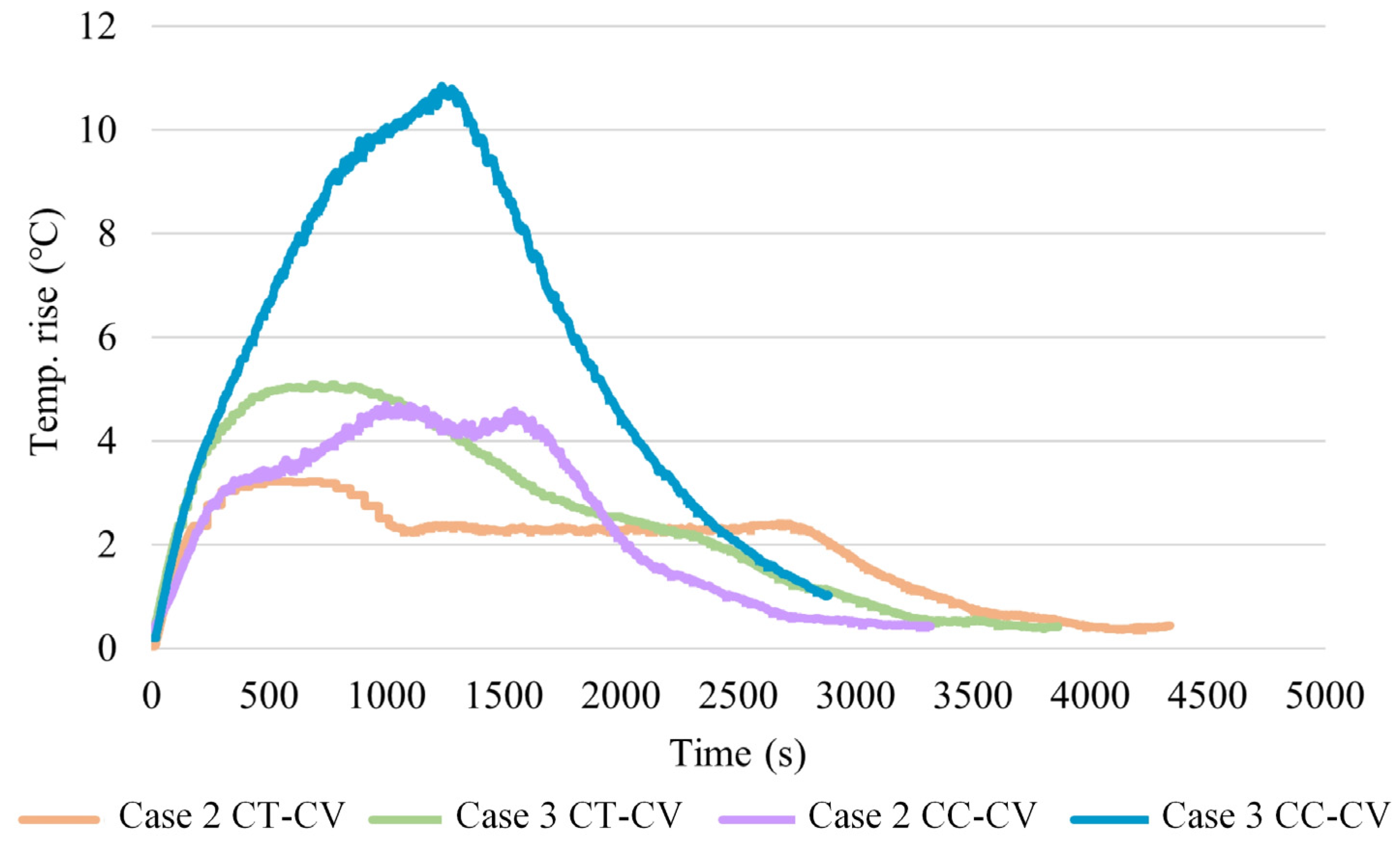
4.1. Comparison between CC-CV and CT-CV Methods
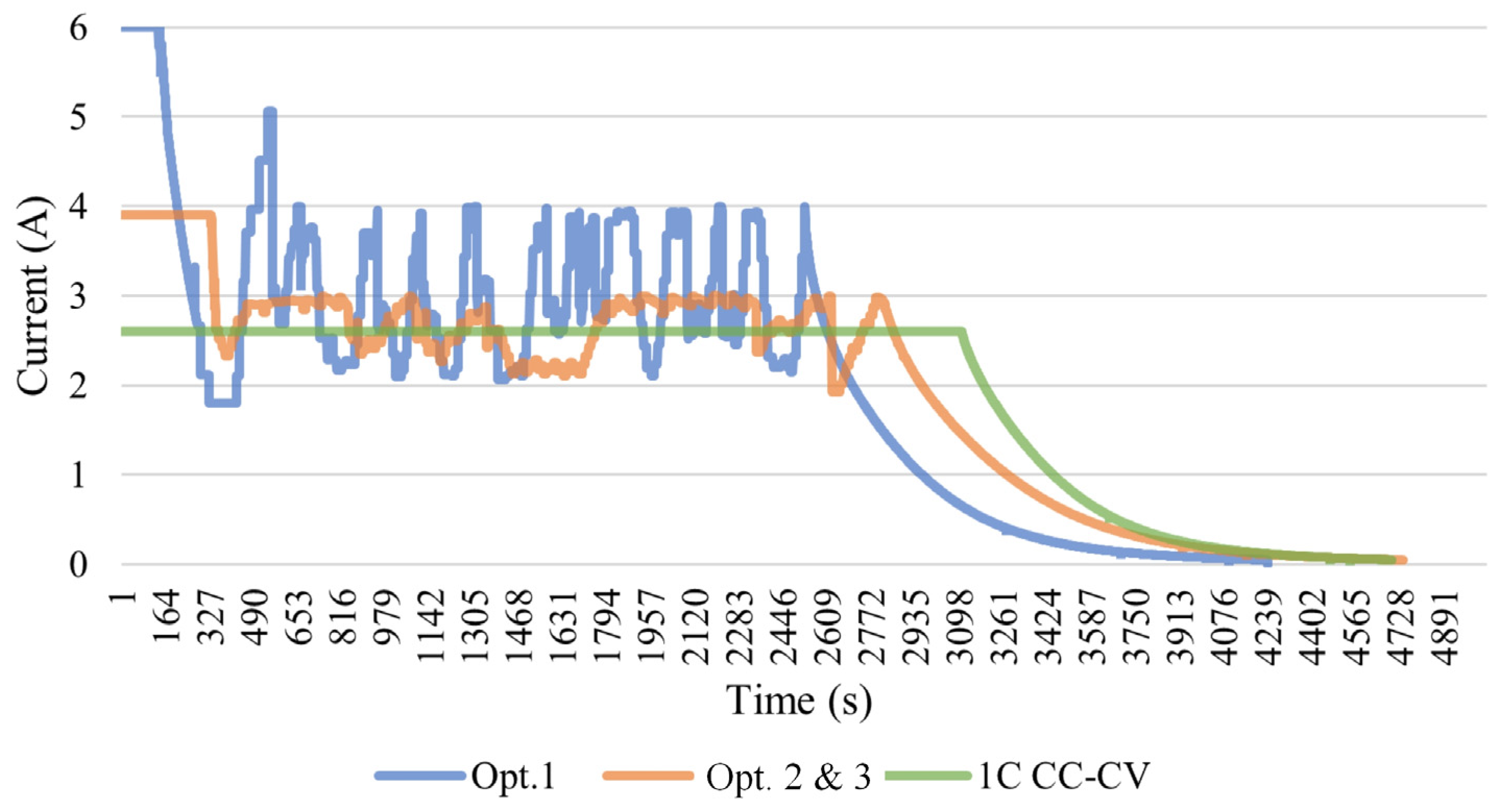
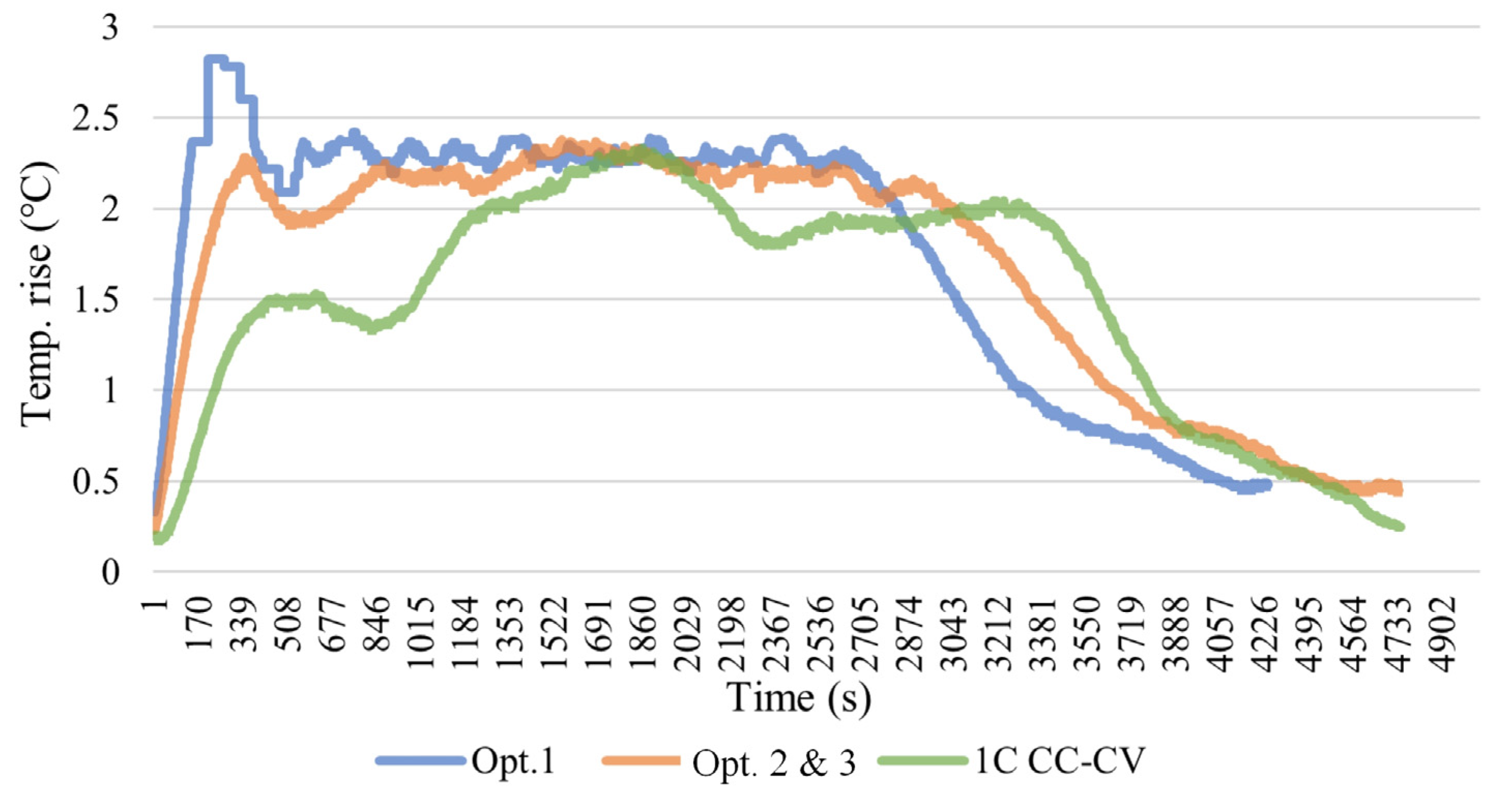
4.2. Comparison between CC-CV and Optimized CT-CV Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jeudy-Hugo, S.; Re, L.L.; Falduto, C. Understanding Countries’ Net-Zero Emissions Targets; OECD Publishing: Paris, France, 2021. [Google Scholar]
- Raugei, M.; Peluso, A.; Leccisi, E.; Fthenakis, V. Life-Cycle Carbon Emissions and Energy Implications of High Penetration of Photovoltaics and Electric Vehicles in California. Energies 2021, 14, 5165. [Google Scholar] [CrossRef]
- Armenta-Deu, C.; Coulaud, T. Control Unit for Battery Charge Management in Electric Vehicles (EVs). Future Transp. 2024, 4, 429–449. [Google Scholar] [CrossRef]
- Xie, Y.; Song, Z.; Yue, H.; Fan, Y.; Yu, M.; Li, H.; Zhang, Y. A Self-Adaptive Multistage Constant Current Fast-Charging Strategy for Lithium-Ion Batteries Integrating Cooling Strategy. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 95–106. [Google Scholar] [CrossRef]
- Shen, W.; Vo, T.T.; Kapoor, A. Charging algorithms of lithium-ion batteries: An overview. In Proceedings of the 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 1567–1572. [Google Scholar] [CrossRef]
- Gonzalez-Saenz, J.; Becerra, V. Determining Fast Battery Charging Profiles Using an Equivalent Circuit Model and a Direct Optimal Control Approach. Energies 2024, 17, 1470. [Google Scholar] [CrossRef]
- Gonzalez-Saenz, J.; Becerra, V. Determination of Fast Battery-Charging Profiles Using an Electrochemical Model and a Direct Optimal Control Approach. Batteries 2024, 10, 2. [Google Scholar] [CrossRef]
- Wang, B.; Min, H.; Sun, W.; Yu, Y. Research on Optimal Charging of Power Lithium-Ion Batteries in Wide Temperature Range Based on Variable Weighting Factors. Energies 2021, 14, 1776. [Google Scholar] [CrossRef]
- Wang, S.-C.; Zhang, Z.-Y. Research on Optimum Charging Current Profile with Multi-Stage Constant Current Based on Bio-Inspired Optimization Algorithms for Lithium-Ion Batteries. Energies 2023, 16, 7641. [Google Scholar] [CrossRef]
- Patnaik, L.; Praneeth, A.V.J.S.; Williamson, S.S. A Closed-Loop Constant-Temperature Constant-Voltage Charging Technique to Reduce Charge Time of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2019, 66, 1059–1067. [Google Scholar] [CrossRef]
- Hans, M.R.; Kalbhage, S.Y.; Nigam, M.K.; Patel, B. Performance Analysis of the Lithium-Ion Batteries using CT-CV Charging Technique. In Proceedings of the 2021 IEEE Mysore Sub Section International Conference (MysuruCon), Hassan, India, 24–25 October 2021; pp. 572–5770. [Google Scholar]
- Chen, G.-J.; Liu, C.-L.; Liu, Y.-H.; Wang, J.-J. Implementation of Constant Temperature–Constant Voltage Charging Method with Energy Loss Minimization for Lithium-Ion Batteries. Electronics 2024, 13, 645. [Google Scholar] [CrossRef]
- Zheng, D.; Wang, H.; An, J.; Chen, J.; Pan, H.; Chen, L. Real-Time Estimation of Battery State of Charge with Metabolic Grey Model and LabVIEW Platform. IEEE Access 2018, 6, 13170–13180. [Google Scholar] [CrossRef]
- Jiménez-Romero, F.J.; González-Jiménez, J.R.; García-Torres, F.; Caballero, Á.; Lara-Raya, F.R. A novel testing equipment based on Arduino and LabVIEW for electrochemical performance studies on experimental cells: Evaluation in lithium-sulfur technology. Measurement 2024, 224, 113922. [Google Scholar] [CrossRef]
- Molicel INR-18650-P26A Lithium Ion Battery Specification. Available online: https://www.molicel.com/wp-content/uploads/INR18650P26A-V2-80087.pdf (accessed on 15 April 2024).
- Kaleem, A.; Khalil, I.U.; Aslam, S.; Ullah, N.; Al Otaibi, S.; Algethami, M. Feedback PID Controller-Based Closed-Loop Fast Charging of Lithium-Ion Batteries Using Constant-Temperature–Constant-Voltage Method. Electronics 2021, 10, 2872. [Google Scholar] [CrossRef]
- Amanor-Boadu, J.M.; Guiseppi-Elie, A.; Sánchez-Sinencio, E. Search for Optimal Pulse Charging Parameters for Li-Ion Polymer Batteries Using Taguchi Orthogonal Arrays. IEEE Trans. Ind. Electron. 2018, 65, 8982–8992. [Google Scholar] [CrossRef]
- Lee, C.-H.; Wang, X.-J.; Lin, K.-Y.; Jiang, J.-A. Experiment-Based Determination of the Optimized Current Level to Achieve Multiple Constant Current Charging for Lithium-Ion Batteries. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2648–2657. [Google Scholar] [CrossRef]
- Lee, C.-H.; Hsu, C.-Y.; Hsu, S.-H.; Jiang, J.-A. Effect of Weighting Strategies on Taguchi-Based Optimization of the Four-Stage Constant Current Charge Pattern. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2704–2714. [Google Scholar] [CrossRef]
- Jiang, L.; Li, Y.; Huang, Y.; Yu, J.; Qiao, X.; Wang, Y.; Huang, C.; Cao, Y. Optimization of multi-stage constant current charging pattern based on Taguchi method for Li-Ion battery. Appl. Energy 2020, 259, 114148. [Google Scholar] [CrossRef]




| MOLICEL INR-18650-P26A Li-Ion Battery | ||
|---|---|---|
| Capacity | Typical | 2600 mAh |
| Cell Voltage | Nominal | 3.6 V |
| Charge | 4.2 V | |
| Discharge | 2.5 V | |
| Charge Current | Standard | 2.6 A |
| Maximum | 6.0 A | |
| Charge Time | Standard | 1.5 h |
| Discharge Current | Maximum | 35 A |
| Ambient Temperature | Charge | 0~60 °C |
| Discharge | −40~60 °C | |
| Energy Density | Volumetric | 535 Wh/L |
| Gravimetric | 190 Wh/kg | |
| Exp. | Case 1 | Case 2 | Case 3 | |
|---|---|---|---|---|
| Initial current Iinitial | 1.5 C (3.9 A) | 2 C (5.2 A) | Imax (6 A) | |
| Time constant τ | 200 s | 1000 s | 2000 s | |
| PID | KP | 0.25 | ||
| KI | 0.02 | |||
| KD | 1 | |||
| Max. ∆IPID | ±0.25 A | |||
| Case 1 CT-CV | Case 2 CT-CV | Case 3 CT-CV | |
|---|---|---|---|
| Maximum temp. rise (°C) | 2.5 | 3.22 | 5.09 |
| Average temp. rise (°C) | 1.8 | 1.9 | 2.58 |
| Charge capacity (mAh) | 2526.27 | 2523.28 | 2533.77 |
| Discharge capacity (mAh) | 2515.12 | 2514.20 | 2503.38 |
| Efficiency (%) | 99.6 | 99.6 | 98.8 |
| Charging time (s) | 4668 | 4342 | 3863 |
| Level | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Factors | Initial current Iinitial | 1.5 C (3.9 A) | 2 C (5.2 A) | Imax (6 A) |
| Time constant τ | 50 s | 100 s | 200 s | |
| Delayed time TD | 2 s | 20 s | 60 s | |
| Limit of ΔIPID | 0.05 A | 0.1 A | 0.25 A | |
| Experiment | Initial Current Iinitial (A) | Limit of ΔIPID (A) | τ (s) | TD (s) |
|---|---|---|---|---|
| 1 | 1.5 C (3.9 A) | 0.05 | 50 | 2 |
| 2 | 1.5 C (3.9 A) | 0.1 | 100 | 20 |
| 3 | 1.5 C (3.9 A) | 0.25 | 200 | 60 |
| 4 | 2 C (5.2 A) | 0.05 | 100 | 60 |
| 5 | 2 C (5.2 A) | 0.1 | 200 | 2 |
| 6 | 2 C (5.2 A) | 0.25 | 50 | 20 |
| 7 | Imax (6 A) | 0.05 | 200 | 20 |
| 8 | Imax (6 A) | 0.1 | 50 | 60 |
| 9 | Imax (6 A) | 0.25 | 100 | 2 |
| Control Factors | Evaluation Metrics | |||||||
|---|---|---|---|---|---|---|---|---|
| Initial Current Iinitial (A) | Limit of ΔIPID (A) | τ (s) | TD (s) | Charging Time (s) | Charging Efficiency (%) | Max. Temp. Rise (°C) | Avg. Temp. Rise (°C) | |
| 1 | 1.5 C (3.9 A) | 0.05 | 50 | 2 | 4575 | 99.71 | 2.35 | 1.72 |
| 2 | 1.5 C (3.9 A) | 0.1 | 100 | 20 | 4542 | 99.86 | 2.26 | 1.74 |
| 3 | 1.5 C (3.9 A) | 0.25 | 200 | 60 | 4379 | 99.68 | 2.31 | 1.77 |
| 4 | 2 C (5.2 A) | 0.05 | 100 | 60 | 4391 | 99.55 | 2.56 | 1.88 |
| 5 | 2 C (5.2 A) | 0.1 | 200 | 2 | 4406 | 99.45 | 2.8 | 1.89 |
| 6 | 2 C (5.2 A) | 0.25 | 50 | 20 | 4504 | 99.70 | 2.57 | 1.87 |
| 7 | Imax (6 A) | 0.05 | 200 | 20 | 4350 | 99.26 | 2.95 | 1.91 |
| 8 | Imax (6 A) | 0.1 | 50 | 60 | 4395 | 99.61 | 2.58 | 1.88 |
| 9 | Imax (6 A) | 0.25 | 100 | 2 | 4420 | 99.43 | 2.64 | 1.90 |
| Iinitial (A) | ∆IPID (A) | τ (s) | TD (s) | Evaluation Indicators | |||
|---|---|---|---|---|---|---|---|
| Charging Time (s) | Charging Efficiency (%) | Average Temperature Rise (°C) | |||||
| Opt. 1 minimum charging time | Imax (6 A) | 0.25 | 200 | 60 | 4241 | 99.47 | 1.90 |
| Opt. 2 maximum efficiency | 1.5 C (3.9 A) | 0.1 | 50 | 60 | 4739 | 99.89 | 1.67 |
| Opt. 3 minimum average temperature rise | |||||||
| CC-CV | CT-CV | Optimized CT-CV | ||||||
|---|---|---|---|---|---|---|---|---|
| Charging method | Case 1 | Case 2 | Case 3 | Case 1 | Case 2 | Case 3 | Opt. 1 CT-CV | Opt. 2 CT-CV |
| Constant/initial current | 1 C (2.6 A) | 2 C (5.2 A) | Imax (6 A) | 1.5 C (3.9 A) | 2 C (5.2 A) | Imax (6 A) | Imax (6 A) | 1.5 C (3.9 A) |
| Maximum temperature rise (°C) | 2.33 | 4.69 | 10.84 | 2.5 | 3.22 | 5.09 | 2.82 | 2.30 |
| Average temperature rise (°C) | 1.5 | 2.49 | 5.79 | 1.8 | 1.9 | 2.58 | 1.90 | 1.67 |
| Charging efficiency (%) | 99.85 | 99.7 | 97.3 | 99.6 | 99.6 | 98.8 | 99.47 | 99.89 |
| Charging time (s) | 4747 | 3321 | 2886 | 4668 | 4342 | 3863 | 4241 | 4739 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.-S.; Lin, S.-F.; Ho, K.-C. Experiment-Based Determination of Optimal Parameters in Constant Temperature–Constant Voltage Charging Technique for Lithium-Ion Batteries Using Taguchi Method. Batteries 2024, 10, 211. https://doi.org/10.3390/batteries10060211
Cheng Y-S, Lin S-F, Ho K-C. Experiment-Based Determination of Optimal Parameters in Constant Temperature–Constant Voltage Charging Technique for Lithium-Ion Batteries Using Taguchi Method. Batteries. 2024; 10(6):211. https://doi.org/10.3390/batteries10060211
Chicago/Turabian StyleCheng, Yu-Shan, Su-Fen Lin, and Kun-Che Ho. 2024. "Experiment-Based Determination of Optimal Parameters in Constant Temperature–Constant Voltage Charging Technique for Lithium-Ion Batteries Using Taguchi Method" Batteries 10, no. 6: 211. https://doi.org/10.3390/batteries10060211
APA StyleCheng, Y.-S., Lin, S.-F., & Ho, K.-C. (2024). Experiment-Based Determination of Optimal Parameters in Constant Temperature–Constant Voltage Charging Technique for Lithium-Ion Batteries Using Taguchi Method. Batteries, 10(6), 211. https://doi.org/10.3390/batteries10060211







