Abstract
In this article, the structural, elastic, electronic, and magnetic characteristics of both regular and inverse Heusler alloys, Sc2TiAl and Sc2TiSi, were investigated using a full-potential, linearized augmented plane-wave (FP-LAPW) method, within the density functional theory. The optimized structural parameters were determined from the minimization of the total energy versus the volume of the unit cell. The band structure and DOS calculations were performed within the generalized gradient approximation (GGA) and modified Becke–Johnson approaches (mBJ-GGA), employed in the Wien2K code. The density of states (DOS) and band structure (BS) indicate the metallic nature of the regular structure of the two compounds. The total spin magnetic moments for the two compounds were consistent with the previous theoretical results. We calculated the elastic properties: bulk moduli, , Poisson’s ratio, , shear modulus, S, Young’s modulus (Y), and the B/s ratio. Additionally, we used Blackman’s diagram and Every’s diagram to compare the elastic properties of the studied compounds, whereas Pugh’s and Poisson’s ratios were used in the analysis of the relationship between interatomic bonding type and physical properties. Mechanically, we found that the regular and inverse full-Heusler compounds Sc2TiAl and Sc2TiSi were stable. The results agree with previous studies, providing a road map for possible uses in electronic devices.
1. Introduction
The discovery of Heusler compounds has been greatly applied in spintronics, shape memory, thermoelectrics, and a tremendous domain of functionalities. Changing elements afforded Heusler alloys multiple functionalities, which led to a broad range of interest [1,2,3,4,5,6,7,8].
Heusler alloys could be categorized into four groups: (i) Full Heusler alloys (FHAs), with the chemical formula X2YZ, crystallize in the regular Heusler (L21)(225) crystal structure with the prototype AlCu2Mn, when the valence number of Y is less than that of X. (ii) The inverse Heusler (Xa)(216), which has the same chemical formula as full Heusler, but it crystallizes in the C1b type with prototype CuHg2Ti, where the valence number of Y is greater than that of X. (iii) Half-Heusler alloys (HHAs) have the chemical formula XYZ, crystalline in the C1b structure, as an inverse Heusler with one X missing. (iv) Quaternary Heusler alloys (QHAs) have the chemical formula XX′YZ, crystalline in the LiMgPdSn (Y-type). In all categories, X, X′, and Y are transition metals, while Z is the main-group element.
Heusler compounds and other half-metallic compounds have been the subject of several previous studies utilizing a variety of computational and experimental techniques. In 2019, Han et al. [9] performed a study on 171 scandium-based full Heusler compounds. They found that the L21-type structure (regular structure) is more stable than the Xa structure (inverse structure) since the energy difference between the two structures (E = EXA − EL21) is greater than zero. This means that the L21-type structure is more likely to be synthesized. They also calculated the band structure of Sc2TiAl and Sc2TiSi alloys using the first-principle calculations. The calculated electronic structures of the L21-type structure and the Xa structure of Sc2TiAl and Sc2TiSi are ferromagnetic.
Full Heusler compounds are intermetallic compounds that have the composition X2YZ, where X and Y are transition metals and Z is a main-group element. These compounds have attracted significant attention due to their interesting electronic, magnetic, and thermoelectric properties. Among the various types of full Heusler compounds, metallic full Heusler compounds have attracted significant attention due to their high electrical conductivity, which makes them suitable for electronic applications [10,11,12,13,14].
Several studies have explored the properties and potential applications of metallic full Heusler compounds. Graf et al. [15] discussed the simple rules for understanding the crystal structure of Heusler compounds. Felser and Hirohata [16] highlighted the potential of Heusler compounds for spintronics and related applications. Nayak et al. [17] provided a comprehensive review of computational and experimental studies on half-metallic Heusler compounds, including Mn2PtGa. These studies demonstrate the growing interest in metallic full Heusler compounds and the potential they hold for various applications [15,16,17].
A review on the recent development and future perspectives has been conducted by Elphick et al. [18]. Wu et al. investigated the mechanical properties of various Co2-based Heusler compounds by calculating their elastic constants using a full-potential all-electron method [19].
Recently, Yahya et al. computationally investigated the structural, electronic, and elastic properties of Co2CrAl and Cr2MnSb Heusler alloys. The results revealed that both compounds have half-metallic characters [20]. In 2020, Abu Baker et al. [21] used the FP-LAPW approach to explore the structural, electronic, magnetic, and elastic properties of the regular Co2TiSn and inverse Co2TiSn full Heusler alloys. The inverse Zr2RhGa and regular Co2TiSn have lattice parameters of 6.619 Å and 6.094 Å, respectively. Additionally, it was discovered that these compounds have total magnetic moments of 1.9786 and 1.99 , respectively. Furthermore, the indirect energy gaps for these compounds are 0.482 eV and 0.573 eV, respectively. They are also mechanically stable. On the other hand, Alrahamneh et al. calculated the thermoelectric properties for Zr2RhGa and Zr2RhIn compounds, and they found that both compounds exhibit half-metallic behavior and are unsuitable for thermoelectric applications [5].
In 2021, Yotong Li et al. [22] screened the half-metallic X2Y (Al/Si) full Heusler alloys based on first-principle calculations. There are 26 stable alloys, out of which 24 are magnetic and 10 are half-metallic. For alloys with magnetism, DOS were calculated by applying the GGA. The (Ag/Cu/Mg)2Y(Al/Si) alloys were found to be unstable, while (Mn/Co)2Y(Al/Si) alloys are always stable. X2Cr(Al/Si) alloys are stable, while X2Nb(Al/Si) alloys are always unstable. The (Co/Mn)2YZ alloys always exhibit magnetism and half-metallicity. Moreover, they predicted that (Mn/Co)2Y(Al/Si) alloys can be considered as candidates for spintronic devices and serve as a valuable reference for future experimental work.
The main purpose of this work is to investigate and predict the structural, magnetic, electronic, and elastic properties of Sc2TiAl and Sc2TiSi in the cubic phase for possible spintronic applications. Spintronics reveals a possible high capacity for next-generation information technology [23]. To determine if our compounds are suitable for spintronics, we have studied various properties using the FP-LAPW method.
The motivation of the present study is to examine the mechanical properties of the compounds and analyze their stability by investigating their behavior. Considering the limited availability of theoretical and experimental data on this topic, it is crucial to validate the findings reported in [9].
This work is divided into four sections. The first section has provided an introduction that highlighted the importance of Heusler alloys and a literature review about Sc2TiAl and Sc2TiSi specifically, and Heusler alloys generally, in addition to outlining the main purpose of this work. The second section describes the computational method used. The third section presents the results obtained by referring to other results available in the literature review; therefore, all the results obtained are systematically compared. The last section is a conclusion, that summarizes the physical properties of the regular and inverse Sc2TiAl and Sc2TiSi compounds.
2. Computational Method
In this work, the density functional theory (DFT) calculations were carried out using the full-potential, linearized augmented plane-wave (FP-LAPW) technique, as implemented in the WIEN2k package [24]. The generalized gradient approximation, parameterized by Perdew, Burke, and Ernzerhof (GGA-PBE) [25], was used to calculate the structural parameters, namely the lattice parameters and the bulk modulus. The GGA-PBE method depends on the local gradient of the electronic density, in addition to the value of the density, providing a more accurate description of variations in the electron–electron interactions. The GGA-PBE functional calculations mostly underestimate the energy bandgap values; therefore, a modified Becke–Johnson (mBJ-GGA) functional [26,27] might be used to enhance the energy bandgap values. For Sc2TiAl, the muffin-tin (MT) radii of Sc, Ti, and Al atoms are 2.50, 2.50, and 2.39 a.u., respectively, whereas, for Sc2TiSi, Sc, Ti, and Si atoms are 2.45, 2.45, and 2.14 a.u., respectively. To obtain a self-consistency for Sc2TiAl and Sc2TiSi, 1240 special k-points in the irreducible Brillion zone (IBZ) were used with a grid equivalent to 50,000 k-points in the full BZ [28]. Furthermore, the expansions of the wave functions were set to inside the MT spheres and the number of plane waves was restricted by . The self-consistent calculations were considered to converge only when the calculated total energy of the crystal converged to less than 0.01 mRy. Finally, using the second-order derivative within the IRelast formalism [29], the elastic constants were calculated.
3. Results
3.1. Structural Properties
To calculate the optimized structural properties: lattice constant (a), bulk modulus (B), its pressure derivative (B′), and minimum energy, , the total energy (in Ry) versus volume (in a.u3) graphs were fitted using Murnaghan’s equation of state (EOS), which is given by [30,31]:
where pressure, , and bulk modulus, .
The regular Heusler Sc2TiAl and Sc2TiSi compounds have the space group Fm-3m L21 (225), while the inverse Heusler Sc2TiAl and Sc2TiSi compounds have the space group F-43m Xa (216) [1]. Figure 1 shows the crystal structures of the full Heusler Sc2TiAl and Sc2TiSi compounds.
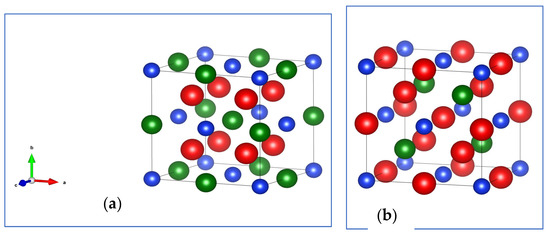
Figure 1.
Crystal structures of Sc2TiAl and Sc2TiSi in (a) regular Heusler (L21) and (b) inverse Heusler (Xa) (Red: Sc, Green: Ti, Blue: Al/Si).
In the optimized volume calculation, an estimated value of the lattice parameter was used for each compound, and the total energy versus the volume of Sc2TiAl and Sc2TiSi alloys is shown in Figure 2 and Figure 3. Figure 2 indicates that the regular Sc2TiAl has a minimum energy, , lower than the inverse Sc2TiAl, indicating that the regular structure of Sc2TiAl is more mechanically stable than the inverse structure. Similarly, Figure 3 demonstrates that the regular Sc2TiSi has a minimum energy, , lower than the inverse Sc2TiSi implying that the regular structure of Sc2TiSi is more mechanically stable than the inverse structure.
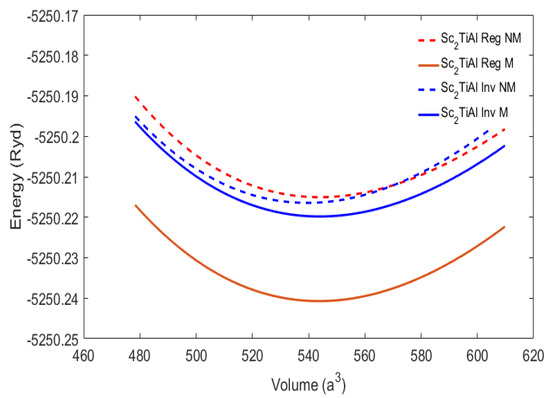
Figure 2.
The total energy (Ry) versus volume (a.u3) of non-magnetic, regular, and inverse Sc2TiAl Heusler.
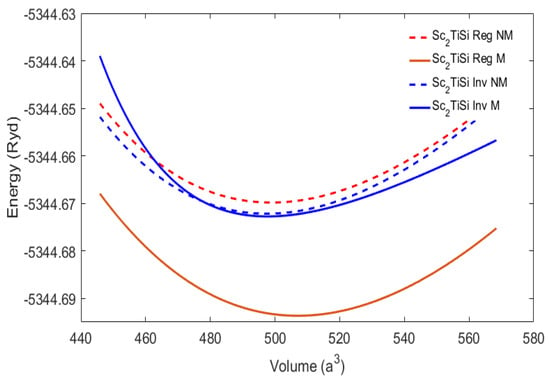
Figure 3.
The total energy (Ry) versus volume (a.u3) of non-magnetic, regular, and inverse Sc2TiSi Heusler.
The calculated structural parameters of the regular and the inverse Sc2TiAl and Sc2TiSi are listed in Table 1. The table demonstrates that the present calculated lattice constants are compatible with the previous theoretical results for both the regular and inverse Heusler structures of Sc2TiAl and Sc2TiSi [9].

Table 1.
The obtained lattice constant (a), bulk modulus (B), pressure derivative of the bulk modulus (B’), minimum energy (E0), and formation energy (Ef) for the regular and inverse Heusler of both Sc2TiAl and Sc2TiSi.
3.2. Formation Energy
In this section, we show how to calculate the formation energy of the Sc2TiX (X = Si and Al) compounds in both regular and inverse structures. The formation energy (Ef) is defined as the difference between the total energy of a compound and the energy of its components, and is given by the following formula [32]:
Here, represents the total energy of the Sc2TiX compound in the structure being studied, while and represent the energy of scandium and titanium in hexagonal structures, respectively. Additionally, represents the energy for aluminum (face-centered cubic) and silicon (diamond structure). The calculated values of Ef are listed in Table 1.
The formation energy indicates the stability of the compound and the extent of its natural formation [5]. A negative value means that the compound could be naturally formed. Based on Table 1, we observe that the formation energy of Sc2TiAl and Sc2TiSi compounds are negative in both regular and inverse structures, with the regular structure being the most stable for both systems. This is because the formation energy is less than that of the inverse structure. As the formation energy decreases, the stability of the compound increases. Therefore, we can conclude that the Sc2TiX compounds exist in nature in the regular structure.
3.3. Magnetic Properties
The total and atom-resolved spin magnetic moments for the regular and inverse Heusler compounds Sc2TiAl and Sc2TiSi were calculated, and the results were compared with those of other theoretical works, as shown in Table 2. As indicated in Table 2, we concluded that the computed total spin magnetic moment (MMtot) of the regular and inverse Heusler compounds Sc2TiAl and Sc2TiSi is reasonably comparable to the findings of prior theoretical studies [9].

Table 2.
Total, atom-resolved, and interstitial spin magnetic moments for inverse and regular Sc2TiAl and Sc2TiSi.
The MMtot for the regular Sc2TiAl was 2.72 , while it was 2.07 for the inverse Sc2TiAl. The MMtot in the inverse structure is lower than that in the normal structure due to the low contribution of the Ti atom in the inverse case, whereas its contribution was higher in the normal case. Therefore, it can be noted from the results produced here that the regular and inverse Sc2TiAl compound’s computed MMtot values are close to the prior theoretical findings [9].
Table 2 shows the results for the regular and inverse Heusler Sc2TiSi compounds. The main contribution in the MMtot was due to the high contribution of the Ti atom in the regular case, while its contribution was lower by 34% in the inverse case, which caused the MMtot to be lower (MMtot = 2.204 ) in the inverse case compared to the case of regular Heusler Sc2TiSi (MMtot = 2.808 ). It was noticed that the atoms that occupied the Z position in X2YZ or XYXZ structures for both molecules Sc2TiAl and Sc2TiSi did not significantly contribute to the MMtot. The non-integral total magnetic moment of both compounds confirmed their metallic nature and was consistent with the results of their band structures and DOS. Based on the magnetic results, our studied compounds are unlikely to be half-metallic.
3.4. Electronic Structure
In this section, we investigated both the partial and total density of states (PDOS, TDOS) and the band structure (BS) for both Sc2TiAl and Sc2TiSi alloys. Since the regular L21 cubic structure is the ground state, we will focus on the regular L21 electronic structure. The analysis of the BS for regular Heusler structures of Sc2TiAl and Sc2TiSi showed that they exhibited metallic behavior for both spin-up and spin-down within the GGA-PBE and mBJ-GGA methods, with zero-energy gaps, as shown in Figure 4.
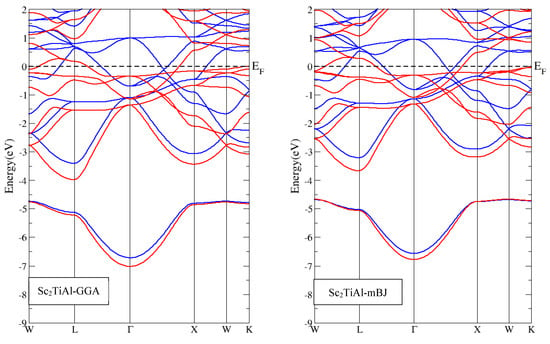
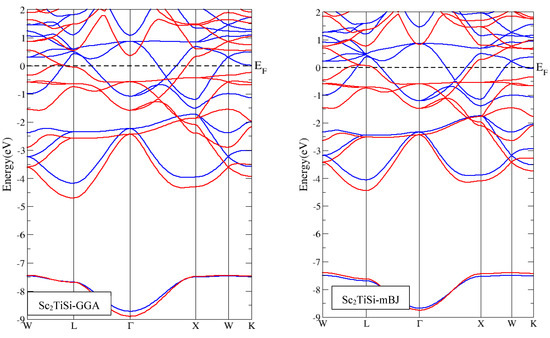
Figure 4.
Calculated band structure for regular Sc2TiAl and Sc2TiSi using GGA and mBJ (blue lines for spin-up, red lines for spin-down).
Figure 5 and Figure 6 show the TDOS and PDOS for the spin-up and spin-down of regular Sc2TiAl and Sc2TiSi Heusler alloys. These figures also show the metallic behavior for both alloys.
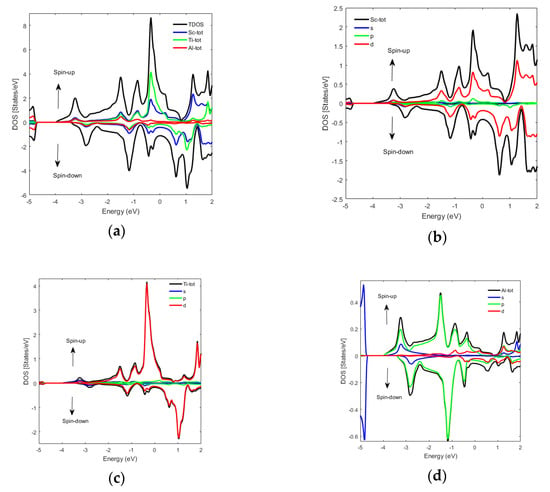
Figure 5.
(a) TDOS for regular Sc2TiAl, and PDOS for the (b) Sc atom, (c) Ti atom, and the (d) Al atom.
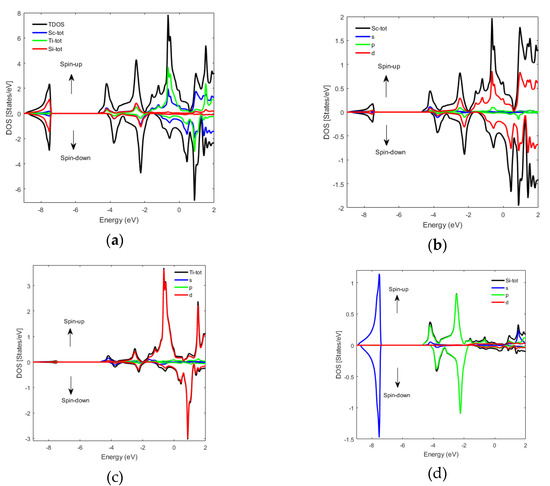
Figure 6.
(a) TDOS for regular Sc2TiSi, and PDOS for the (b) Sc atom, (c) Ti atom, and the (d) Si atom.
In the spin-up regular Sc2TiAl (Figure 5), the main contributions to the valence band (VB) and conduction band come from the Sc-d state, the Ti-d state, and both the s- and p-states of Al. The main contributions come from the Ti atom, then the Sc atom, and then a small contribution from the Al atom in this compound. In addition, the main contributions to the conduction band come from the Sc-d state, the Ti-d state, and the s- and p-states of Al, with the main contributions coming from the Sc atom, then the Ti atom, and then a small contribution from the Al atom in this compound. In spin-down of regular Sc2TiAl (Figure 5), the main contributions to the valence band come from the Sc-d state, the Ti-d state, and the s- and p-states of Al, with the main contributions coming from the Sc atom, then a small contribution from the Al atom, and then the Ti atom in this compound. The main contributions to the conduction band come from the Sc-d state, the Ti-d state, and the s- and p-states of Al, with the main contributions coming from the Sc atom, then the Ti atom, and then a small contribution from the Al atom in this compound.
In the spin-up and spin-down states of regular Sc2TiSi (Figure 6), the Sc-d and Ti-d states, as well as the s- and p-states of Si, make the main contributions to the valence and conduction bands.
3.5. Elastic Properties
In this study, we investigated the bulk modulus (B), shear modulus (S), elastic constants (Cij), Bugh ratio (B/S), Poisson’s ratio (ν), Young’s modulus (Y), and the anisotropic factor (A) for the regular and inverse Heusler alloys Sc2TiAl and Sc2TiSi. To investigate the stability, we computed three symmetry elements, ,, and , for cubic bulk alloys. The Born–Huang criteria of mechanical stability are as follows [33,34,35]:
where the bulk C44-shear, and the tetragonal shear moduli, , must be positive [19]. The third criterion is known as the spinodal pressure, , while the last criterion is used to define an additional elastic constant, called the tetragonal shear modulus:
Tetragonal stability is achieved when the hydrostatic pressure becomes .
The Cauchy pressure for cubic crystals is given by the relation [19]:
Based on the investigated compounds and the mechanical stability conditions mentioned above, both the regular and inverse structures of Sc2TiAl and Sc2TiSi were stable (see Table 3).

Table 3.
Elastic constants (), bulk modulus (B), and anisotropic factor (A) of Sc2TiAl and Sc2TiSi.
Afterwards, the ductile behavior and the type of chemical bonds were investigated. We found that compounds with a Pugh ratio of and were ductile, while others were brittle [36,37,38,39]. The Voigt shear modulus,, the Reuss shear modulus,, the Hill shear modulus,, and the bulk modulus, B, were calculated using the following equations [40,41,42]:
The nature of bonding is indicated by the value. Compounds with covalent bonds have a value smaller than 0.25, while for compounds with ionic bonds, the value is between 0.25 and 0.5 [34,35,36]. According to Table 4, the regular and inverse Heusler compounds Sc2TiAl and Sc2TiSi are ductile, and they have dominant ionic bonds.
or

Table 4.
Shear modulus (), ratio, Voigt Poisson’s ratio (), and Young’s modulus () of Sc2TiAl and Sc2TiSi.
The third and fourth criterions in Equation (1) restrict the range of Poisson’s ratio to .
Young modulus (Y) (the ratio between stress and strain) is given by the following:
The anisotropic factor is given by:
The cubic elastic anisotropy or the Zener ratio can be used as physical quantities to describe the structural stability of a material. Materials with large Zener ratios tend to deviate from cubic structures. Materials with negative Zener ratios are mechanically unstable since they violate at least one of the stability criteria [19].
The hardness of materials is measured by the B and S moduli [43], while the stiffness of materials is measured by Young’s modulus (Y). In addition, the elastic anisotropy, A, is a parameter used to measure the degree of anisotropy of the materials [44]. The elastic anisotropy (A) equals one for an isotropic alloy, while any value other than one indicates elastic anisotropy [45]. The inverse and regular Heusler Sc2TiAl and Sc2TiSi compounds exhibit elastic anisotropy, as shown in Table 3.
Table 3 shows that both Sc2TiAl and Sc2TiSi, in both regular and inverse structures, satisfy the stability conditions and are considered mechanically stable with elastic anisotropy. Table 4 shows that the regular and inverse structures of Sc2TiSi are ductile, as and . However, the regular structure of Sc2TiAl is brittle ( and ), while the inverse structure is ductile ( and ).
Blackman’s and Every’s diagrams are used due to their efficiency in comparing the elastic properties of cubic materials. These diagrams correlate dimensionless quantities that are related to ratios of different moduli. Figure 7 summarizes the results of this study in such diagrams. Blackman’s diagram compares to , while Every’s diagram is more complicated. It compares as a function of . Materials with s3 = 0 are isotropic, and the two quantities, s2 and s3, are related to the elastic waves. Since c44 > 0, then F44 > 0, whereas F12 is restricted to −0.5 < F12 < 1. These are the restrictions for Blackman’s diagram, and all values within these ranges are allowed. In Every’s diagram, the values for stability are restricted to fall into the triangle with (s2, s3), equal to (−0.5, −1)–(1, 0)–(1, 1.5), as shown in Figure 7. It is noticed that the studied compounds in this study were below the isotropy line, where s3 = 0 [19].
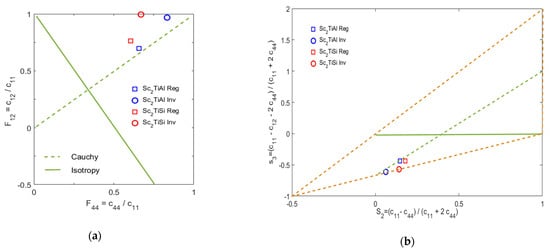
Figure 7.
(a) Blackman’s and (b) Every’s diagrams. The full green line refers to the isotropic case, where Ae = 1, and the dashed green line refers to the case where Cauchy pressure = 0. In Every’s diagram, the stability triangle is marked by dashed brown lines.
From both diagrams, it can be noticed that the studied compounds were close to the Cauchy line, where ps = 0. Additionally, all the studied compounds were in the region where the anisotropy index is positive [19].
Pettiford proposed a criterion that suggests that when Cauchy pressure is positive, it indicates that the compound has metallic bonding, whereas negative Cauchy pressure indicates covalent bonding in the compound. According to Pugh’s criterion, materials are brittle when k 1.75, where k = B/S, and materials are ductile when k 1.75. Figure 8 shows a plot of the Cauchy pressure as a function of Pugh’s ratio, with the two criteria depicted as horizontal and vertical lines.
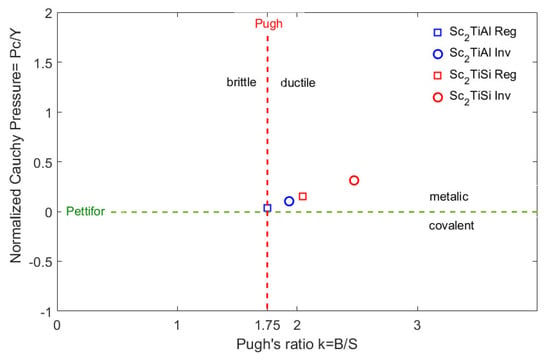
Figure 8.
Ductile–brittle diagram for the studied compounds. The horizontal dashed line corresponds to the metallic-covalent criteria of Pettiford, and the vertical dashed line corresponds to the brittleness–ductile criteria of Pugh.
All studied compounds were classified as ductile and metallic materials, except the regular compound of Sc2TiAl (k = 1.7), which lay slightly to the left of the vertical line between brittle and ductile. Therefore, it was considered a brittle compound.
4. Conclusions
This article scrutinized the structural, magnetic, electronic, and elastic properties of both Sc2TiAl and Sc2TiSi. The results were as follows: According to the electronic properties, both regular Heusler Sc2TiAl and Sc2TiSi compounds are metals with zero-energy bandgaps in both GGA-PBE and mBJ methods. As for the magnetic properties, both Sc2TiAl and Sc2TiSi alloys are ferromagnetic compounds with a total magnetic moment of 2.86, 2.09, 2.97, and 2.54 , respectively. Additionally, the elastic properties of these compounds emphasized that both regular and inverse Sc2TiAl and regular Sc2TiSi are mechanically stable. The B/S ratios showed that both regular and inverse Heusler Sc2TiAl and Sc2TiSi compounds have ductile natures. Moreover, the Poisson’s ratio values indicated that both Sc2TiAl and Sc2TiSi alloys have ionic bonds. Finally, both Sc2TiAl and Sc2TiSi compounds exhibited elastic anisotropy.
Author Contributions
Conceptualization, M.S.A.-J.; project administration, M.S.A.-J.; supervision, M.S.A.-J. and M.F.; investigation, K.M.A.-M., M.S.A.-J., D.D., A.A.M. and R.K.; data curation, K.M.A.-M., M.F., D.D. and A.A.M.; formal analysis, K.M.A.-M., M.F., A.A.M. and R.K.; methodology, K.M.A.-M., M.F., M.S.A.-J., D.D., A.A.M. and S.M.A.; software, K.M.A.-M., M.F., D.D., S.M.A. and A.A.M.; writing—original draft, K.M.A.-M. and M.F.; visualization, M.S.A.-J. and R.K.; writing—review and editing, M.S.A.-J., A.A.M., S.M.A. and R.K.; validation, M.S.A.-J., A.A.M., S.M.A. and R.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- Paudel, R.; Zhu, J. Investigation of half-metallicity and magnetism of (Ni/Pd/Ru) ZrTiAl quaternary Heusler alloys for spintronic applications. Phys. Condens. Matter 2019, 557, 45–51. [Google Scholar] [CrossRef]
- Azar, S.; Mousa, A.; Khalifeh, J. Structural, electronic and magnetic properties of Ti1+xFeSb Heusler alloys. Intermetallics 2017, 85, 197–205. [Google Scholar] [CrossRef]
- Berrahal, M.; Bentouuaf, A.; Rached, H.; Mebsout, R.; Aissa, B. Investigation of Ruthenium based Full-Heusler compound for thermic, spintronic and thermoelectric applications: DFT computation. Mater. Sci. Semicond. Process. 2021, 134, 106047. [Google Scholar] [CrossRef]
- Patel, P.; Pandaya, J.; Shinde, S.; Gupta, S.; Narayan, S. Investigation of Full-Heusler compound Mn2MgGe for magnetism, spintronics and thermoelectric applications: DFT study. Comput. Condens. Matter 2020, 23, e00472. [Google Scholar] [CrossRef]
- Alrahamneh, M.; Mousa, A.; Khalifeh, J. First principles study of the structural, electronic, magnetic and thermoelectric properties of Zr2RhAl. Phys. Condens. Matter 2019, 552, 227–235. [Google Scholar] [CrossRef]
- Remil, G.; Zitouni, A.; Bouadjemi, B.; Houari, M.; Abbad, A.; Benstaali, W.; Cherid, S.; Matougui, M.; Lantri, T.; Bentata, S. A potential full Heusler thermoelectric material CO2ZrZ (Z=Al, Si, Ga and Sn) in low temperature: An Ab-initio investigation. Solid State Commun. 2021, 336, 114422. [Google Scholar] [CrossRef]
- Srivastava, V.; Kaur, N.; Khenata, R.; Dar, S. Investigation of the electronic, magnetic, elastic, thermodynamic and thermoelectric properties of Mn2CoCr Heusler compound A DFT-based simulation. J. Magn. Magn. Mater. 2020, 513, 167107. [Google Scholar] [CrossRef]
- Mushtaq, M.; Khalid, S.; Atif Sattar, M.; Khenata, R.; Seddik, T.; Ahmad Dar, S.; Muhammad, I.; Bin Omran, S. Electronic band structure, phase stability, magnetic and thermoelectric characteristics of the quaternary Heusler alloys CoCuZrAs and CoRhMoAl: Insights from DFT computations. Inorg. Chem. Commun. 2021, 124, 108384. [Google Scholar] [CrossRef]
- Han, Y.; Chen, Z.; Kuang, M.; Liu, Z.; Wang, X.; Wang, X. 171 Scandium-based full Heusler compounds: A comprehensive study of competition between XA and L21 atomic ordering. Results Phys. 2019, 12, 435–446. [Google Scholar] [CrossRef]
- Wang, C.; Casper, F.; Gasi, T.; Ksenofontov, V.; Balke, B.; Fecher, G.H.; Felser, C.; Hwu, Y.; Lee, J. Structural and magnetic properties of Fe2CoGa Heusler nanoparticles. J. Phys. Appl. Phys. 2012, 45, 295001. [Google Scholar] [CrossRef]
- Shan, R.; Ouardi, S.; Fecher, G.H.; Gao, L.; Kellock, A.; Gloskovskii, A.; ViolBarbosa, C.E.; Ikenaga, E.; Felser, C.; Parkin, S.S.P. A p-type Heusler compound: Growth, structure, and properties of epitaxial thin NiYBi films on MgO(100). Appl. Phys. Lett. 2012, 101, 212102. [Google Scholar] [CrossRef]
- Galanakis, I.; Şaşıoğlu, E. High TC half-metallic fully-compensated ferrimagnetic Heusler compounds. Appl. Phys. Lett. 2011, 99, 052509. [Google Scholar] [CrossRef]
- Nayak, A.K.; Shekhar, C.; Winterlik, J.; Gupta, A.; Felser, C. Mn2PtIn: A tetragonal Heusler compound with exchange bias behavior. Appl. Phys. Lett. 2012, 100, 152404. [Google Scholar] [CrossRef]
- Wei, X.P.; Hu, X.R.; Liu, B.; Lei, Y.; Deng, H.; Yang, M.K.; Deng, J.B. Electronic structure and magnetism in full-Heusler compound Mn2ZnGe. J. Magn. Magn. Mater. 2011, 323, 1606. [Google Scholar] [CrossRef]
- Graf, T.; Felser, C.; Parkin, S.S. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Felser, C.; Hirohata, A. Heusler Alloys Properties, Growth, Applications. In Springer Series in Materials Science; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978-3-319-21449-8. [Google Scholar]
- Nayak, A.K.; Nicklas, M.; Chadov, S.; Shekhar, C.; Skourski, Y.; Winterlik, J.; Felser, C. Large zero-field cooled exchange-bias in bulk Mn2PtGa. Phys. Rev. Lett. 2013, 110, 127204. [Google Scholar] [CrossRef]
- Elphick, K.; Frost, W.; Samiepour, M.; Kubota, T.; Takanashi, K.; Sukegawa, H.; Mitani, S.; Hirohata, A. Heusler alloys for spintronic devices: Review on recent development and future perspectives. Sci. Technol. Adv. Mater. 2021, 22, 235. [Google Scholar] [CrossRef]
- Wu, S.-C.; Fecher, G.H.; Naghavi, S.S.; Felser, C. Elastic properties and stability of Heusler compounds: Cubic Co2YZ compounds with L21 structure. J. Appl. Phys. 2019, 125, 082523. [Google Scholar] [CrossRef]
- Yahya, S.J.; Abu-Jafar, M.S.; Al Azar, S.; Mousa, A.A.; Khenata, R.; Abu-Baker, D.; Farout, M. The Structural, Electronic, Magnetic and Elastic Properties of Full-Heusler Co2CrAl and Cr2MnSb: An Ab Initio Study. Crystals 2022, 12, 1580. [Google Scholar] [CrossRef]
- Abu Baker, D.N.; Abu-Jafar, M.S.; Mousa, A.; Jaradat, R.; Ilaiwi, K.; Khenata, R. Structural, magnetic, electronic and elastic properties of half-metallic ferromagnetism full-Heusler alloys: Regular- Co2TiSn and inverse- Zr2RhGa using FP-LAPW method. Mater. Chem. Phys. 2020, 240, 122122. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J.; Paudel, R.; Huang, J.; Zhou, F. Screen the half metallic X2Y (Al/Si) full Heusler alloys based on the first principle calculations. Comput. Mater. Sci. 2021, 193, 110391. [Google Scholar] [CrossRef]
- Oudrane, D.; Bourachid, I.; Bouafia, H.; Abidri, B.; Rached, D. Computational insights in predicting structural, mechanical, electronic, magnetic and optical properties of EuAlO3 cubic Perovskite using FP-LAPW. Comput. Condens. Matter 2021, 26, e00537. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.H.; Marks, L.D. WIEN2k: An APW+lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Becke, A.; Johnson, E. A simple effective potential for exchange. J. Chem. Phys. 2006, 124, 221101. [Google Scholar] [CrossRef] [PubMed]
- Tran, F.; Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef] [PubMed]
- Blaha, P.; Schwarz, K.; Medsen, G.K.H.; Kvasnicka, D.; Luitz, J. WIEN2k, An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties; Vienna University Technology: Vienna, Austria, 2001; Available online: https://www.scirp.org/(S(i43dyn45teexjx455qlt3d2q))/reference/ReferencesPapers.aspx?ReferenceID=1880359 (accessed on 5 January 2023).
- IRelast Package is Provided by M. Jamal as Part of the Commercial Code WIEN2K. 2014. Available online: http://www.wien2k.at/ (accessed on 5 January 2023).
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. U.S.A. 1944, 30, 244. [Google Scholar] [CrossRef]
- Tyuterev, V.G.; Vast, N. Murnaghan’s equation of state for the electronic ground state energy. Comput. Mater. Sci. 2006, 38, 350. [Google Scholar] [CrossRef]
- Mousa, A.; Hamad, B.; Khalifeh, J. Structure, electronic and elastic properties of the NbRu shape memory alloys. Eur. Phys. J. 2009, 72, 575–581. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices. Am. J. Phys. 1956, 23, 474. [Google Scholar] [CrossRef]
- Gupta, Y.; Sinha, M.; Verma, S. Exploring the structural, elastic, lattice dynamical stability and thermoelectric properties of semiconducting novel quaternary Heusler alloy LiScPdPb. J. Solid State Chem. 2021, 304, 122601. [Google Scholar] [CrossRef]
- Abu-Jafar, M.; Dayton-Oxland, R.; Jaradat, R.; Mousa, A.; Khenata, R. Structural, electronic, mechanical and elastic properties of Scandium Chalcogenides by first-principles calculations. Phase 2020, 93, 773. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823. [Google Scholar] [CrossRef]
- Abu-Jafar, M.; Leonhardi, v.; Jaradat, R.; Mousa, A.; Al-Qaisi, S.; Mahmoud, N.; Bassalat, A.; Khenata, R.; Bouhemadou, A. Structural, electronic, mechanical, and dynamical properties of scandium carbide. Results Phys. 2021, 21, 103804. [Google Scholar] [CrossRef]
- Cheriet, A.; Khenchoul, S.; Aissani, L.; Lagoun, B.; Zaabat, M.; Alhussein, A. First-principles calculations to investigate structural, magnetic, electronic and elastic properties of full-Heusler alloys Co2MB (M=V, Mn). Solid State Commun. 2021, 337, 114426. [Google Scholar] [CrossRef]
- Abada, A.; Marbouh, N.; Bentayeb, A. First-principles calculations to investigate structural, elastic, electronic and magnetic properties of novel d half metallic half Heusler alloys XSrB (X=Be, Mg). Intermetallics 2022, 140, 107392. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die Beziehung Zwischen den Beiden Elasticitätsconstanten Isotroper Körper; Wiley Online Library: San Marcos, CA, USA, 1889; p. 38. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Math Phys. 1929, 9, 49. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. 1952, 65, 349. [Google Scholar] [CrossRef]
- Teter, D.M. Computational alchemy: The search for new superhard materials. MRS Bull. 1998, 23, 22. [Google Scholar] [CrossRef]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, USA, 1948. [Google Scholar] [CrossRef]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).