Abstract
The main objective of this work is to analyze and compare the numerical solutions of an unsteady separated stagnation point flow due to a Riga plate using copper–alumina/water and graphene–alumina/water hybrid nanofluids. The Riga plate generates electro-magnetohydrodynamics (EMHD) which is expected to delay the boundary layer separation. The flow and energy equations are mathematically developed based on the boundary layer assumptions. These equations are then simplified with the aid of the similarity variables. The numerical results are generated by the bvp4c function and then presented in graphs and tables. The limitation of this model is the use of a Riga plate as the testing surface and water as the base fluid. The results may differ if another wall surfaces or base fluids are considered. Another limitation is the Takabi and Salehi’s correlation of hybrid nanofluid is used for the computational part. The findings reveal that dual solutions exist where the first solution is stable using the validation from stability analysis. Graphene–alumina/water has the maximum skin friction coefficient while copper–alumina/water has the maximum thermal coefficient for larger acceleration parameter. Besides, the single nanofluids (copper–water, graphene–water and alumina–water) are also tested and compared with the hybrid nanofluids. Surprisingly, graphene–water has the maximum skin friction coefficient while alumina–water has the maximum heat transfer rate. The findings are only conclusive and limited to the comparison between graphene–alumina and copper–alumina with water base fluid. The result may differ if another base fluid is used. Hence, future study is necessary to investigate the thermal progress of these hybrid nanofluids.
1. Introduction
Over the course of many decades, the amount of research that has been carried out to improve the thermal efficiency of industrial equipment has steadily increased. A variety of active and passive techniques have been developed by researchers to improve the thermal performance of a system. One of the most well-known techniques is by employing the smart heat transfer fluid known as nanofluid. Nanofluid is produced by dispersing a small amount of nanosized particles either metallic or non-metallic (e.g., copper, alumina, silver, magnetite, cobalt ferrite) into a carrier fluid like water, oil, ethylene glycol, etc. (see Choi and Eastman [1]). Multiple investigations have shown that even at low concentrations, nanoparticles possess special features in terms of thermal performance, particularly enhancements in thermal conductivity [2]. The special properties of nanofluid have been scrutinized comprehensively by Yu et al. [3], Yu and Xie [4], Das et al. [5], and Ali and Salam [6].
After the development of nanofluid, recently, researchers have found another new heat transfer fluid which considers two different kinds of nanoparticles. The thermal conductivity of hybrid nanofluid is higher than that of conventional nanofluid, enabling it to be useful in a wide range of thermal transmission applications like heat pipes, solar collectors and heat exchangers [7,8,9,10,11]. On the other hand, far more research must be carried out on hybrid nanofluid in order to make the most of its unique qualities. In this context, a significant amount of experimental research pertaining to hybrid nanofluids has been carried out. For instance, Suresh et al. [12] experimented a laminar convective heat transfer and pressure drop properties of hybrid nanofluid via a heated circular tube. Their findings presented that the hybrid nanofluid creates a higher Nusselt number compared to the regular base fluid. Madhesh and Kalaiselvam [13] also stated that the heat transfer rate was found to be maximum for hybrid nanofluid in their experimental study. Additionally, the heat transfer of hybrid nanofluid has been proven to enhance when the concentration of nanoparticles is maximized accordingly (see Alawi et al. [14]).
The Riga plate was one of the most notable breakthroughs for overcoming weak fluid conductivity (see Gailitis and Lielausus [15]). This device is an electromagnetic actuator that is made up of alternating pairs of electrodes and magnets. It is used to generate an electromagnetic field that produced the Lorentz force to regulate the fluid flow. Besides, the Riga plate can be used to minimize surface friction and prevent turbulence formation [16]. Upon reviewing the literature, the flow of nanofluid over a Riga plate has been previously carried out by Hayat et al. [17]. Ayub et al. [18] examine the magnetic slip flow of a viscous nanofluid across a Riga plate. Ramzan et al. [19] then also considered the heated Riga plate towards the radiative Williamson nanofluid with the combination of a chemical reaction. Due to the concern towards the heat transfer advancement, hybrid nanofluid has also been considered by the researchers to interrogate its properties when the flow is configured over a Riga plate. Zari et al. [20] analyzed the radiative Hiemenz flow of copper–alumina/water nanofluid towards an EMHD Riga plate. Some of the recent works are contributed by Abbas et al. [21], Khashi’ie et al. [22,23,24], Zainal et al. [25], Wahid et al. [26], Tabassum et al. [27], Shatnawi et al. [28], Siddique et al. [29], Kumar [30] and Asogwa et al. [31].
The stagnation point flow occurs when an inviscid and outer flow impinges on a solid surface (fixed or moving) with a certain strain rate. This flow phenomenon is seen to be steady if the strain rate remains the same throughout time, whereas the unsteady flow is supposed to be the opposite of steady flow. When it comes to engineering processes, steady flow is preferred since it makes operations much easier to control. Engineers also find it easier to predict the outcomes of such processes. However, real-world experience demonstrates that even in the ideal scenario of fluid flow, undesired unstable effects may still manifest themselves in close proximity to a device. These undesirable consequences might be the result of self-inflicted motions of the body or non-uniformities in the fluid. Both of these possibilities are possible. The unsteady separated stagnation point (USSP) flow in a two-dimensional system due to an impermeable surface has been studied by Ma and Hui [32]. Then, Dholey and Gupta [33,34] improved the flow problem by considering the transpiration effect. Lok and Pop [35] considered the similar problem by considering the stretched/shrunk surface. Later, Dholey [36,37,38] inserted magnetohydrodynamic (MHD) effect towards the USSP flow problem, while Roşca et al. [39], Renuka et al. [40], Khashi’ie et al. [41], and Zainal et al. [42] integrated it with the hybrid nanofluid model.
Upon a thorough exploration of the relevant literature, it is found that only limited studies have been conducted regarding the USSP flow of a hybrid nanofluid driven by a Riga plate. Thus, it is interesting and important to investigate such problems as it can be useful for future guidance in the area of fluid dynamics. In this study, we provide the formulation of the model together with the numerical solutions under a possible specific configuration. The governing mathematical equations of the flow model are simplified using the relevant similarity transformations, and then are solved using bvp4c (Matlab). In addition, stability analysis is provided so that the features of the numerical solutions may be investigated. Using the control parameters that were taken into consideration, this research might give insight and guidance that could be used to correctly regulate the flow mechanism of a hybrid nanofluid.
2. Mathematical Formulation
The unsteady separated stagnation point flow of two hybrid nanofluids (copper–alumina/water and graphene–alumina/water) as depicted in Figure 1 are analyzed subjected to a moving plate with few physical assumptions as stated below:
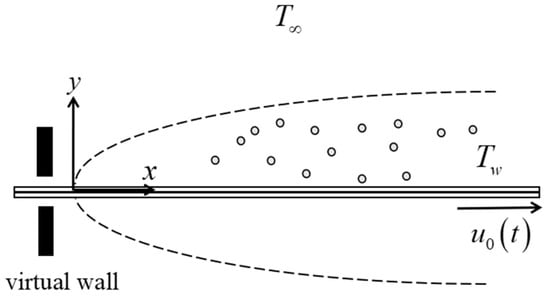
Figure 1.
Illustration of the physical model.
- The term in the mathematical model is used to represent the electro-magnetohydrodynamics effect from the Riga plate where and ; is the electrodes’ current density, is a constant, is the reference time (constant), is the width of magnets and electrodes, is the unsteadiness accelerating/decelerating parameter, is the time and is the plate’s displacement.
- The velocity of free stream flow which align with the plate is ; is the acceleration parameter. Meanwhile, the velocity of the moving plate is
- The terms and respectively stand for surface and ambient temperatures.
- The sedimentation and aggregation effects are omitted by considering that the nanofluids are stable.
The modelling equations subjected to the above stated model are (see Dholey [36] and Khashi’ie et al. [43])
The similarity transformation which is useful to simplify the complex model is [36,43]
The transformed equations (ODEs) and reduced boundary conditions (BCs) are obtained upon the substitution of similarity transformation which is useful to simplify the similarity transformation which useful to simplify the Equation (5) into Equations (2)–(4).
From Equations (6) and (7), is the width parameter, is the EMHD parameter and is the Prandtl number. The properties for the nanoparticles and water base fluid are listed in Table 1. Meanwhile, the correlations of hybrid nanofluid’s properties are shown in Table 2 (see Takabi and Salehi [44]).

Table 1.
Physical properties.

Table 2.
General correlations of hybrid nanofluids.
The similarity transformation method as presented in Equation (5) is the common method for the nondimensionalization process of the boundary layer equations so that it can be easily solved using the bvp4c solver or other numerical approaches. From the similarity technique, the boundary layer and energy equations are transformed into a set of ordinary differential equations which are simpler to solve. However, depending on the physical situations and restrictions, similarity technique is not suitable. Hence, a few methods have been introduced to solve the original model in partial differential equations, for example method of local non-similarity (LNS) as introduced by Sparrow and Yu [45] and also discussed by Hussain and Sheremet [46]. Meanwhile, Kumar et al. [47] used the Laplace and Hankel transformations to analyze the general solution of two dimensional incompressible and axisymmetric fluid flow through porous media. The combination of Laplace transform with eigenvalue technique was also adopted by Abbas [48] for the solution of thermoelastic diffusion in an infinite medium with a spherical cavity.
3. Stability Analysis
The stability analysis is performed upon the observation of multiple solutions. The transformation with the inclusion of time variable is introduced as follows [49]:
By substituting Equation (9) into Equations (2)–(4), the reduced equations are
The reduced equations and condition in Equations (10)–(12) are then tested using eigenvalue approach for any possible disturbance. The perturbation equations are [50]:
By substituting Equation (13) into Equations (10)–(12), the linearized set of eigenvalue equations are obtained with the consideration of a relaxing boundary condition as suggested by Harris et al. [51].
For the successful smallest eigenvalues, is substituted with .
4. Results and Discussion
The numerical computation is fully conducted using the bvp4c application in the Matlab software by first reducing Equations (6)–(8) into the coded equation. The results are displayed for the variations of (a) skin friction coefficient, (b) heat transfer/thermal rate, (c) velocity, and (d) temperature of the tested working fluids (copper–alumina/water and graphene–alumina/water). Besides, the results are portrayed to highlight the effects of pertinent parameters like EMHD parameter and acceleration parameter towards the unsteadiness parameter with fixed volumetric nanoparticle’s concentration , Prandtl number and width parameter . Table 3 shows the comparison of numerical values with previous results for the validation purpose. The present value (1.5394731) is consistent with the other values yet shows the accuracy of the present model. Meanwhile, Table 4 presents the smallest eigenvalues by solving the Equations (14)–(16) using the bvp4c application. Positive values of denote that the solution is stable. Another way to check if the stability analysis is correct by observing the trend of where as

Table 3.
Validation when and with previous findings.

Table 4.
Smallest eigenvalue for the stability analysis of the graphene–alumina/water when and .
The USSP flow of the working fluids usually can produce dual solutions based on the unsteadiness strength. The unsteadiness parameter measures three cases: accelerating case for , decelerating case for and steady state case when . Dual solutions normally appear when by virtue of the boundary layer thickening from the instability of the vortices. These dual solutions are available up to a critical value or the end point of the boundary layer solutions as demonstrated in Figure 2, Figure 3 and Figure 4. Another subject of interest for the USSP flow is the separation value between AFS-attached flow solution and RFS-reverse flow solution . Usually, the AFS is only possible up to a certain value of the unsteadiness parameter and it is possible when . However, the priority of this work is to observe the flow and thermal characteristics of the nanofluids when high magnitude of negative is considered.
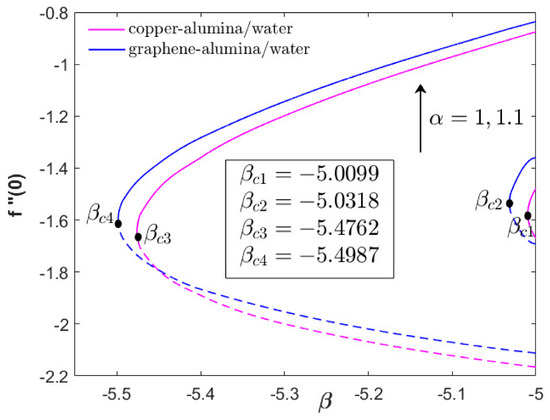
Figure 2.
for various hybrid nanofluids and (acceleration parameter) when and .
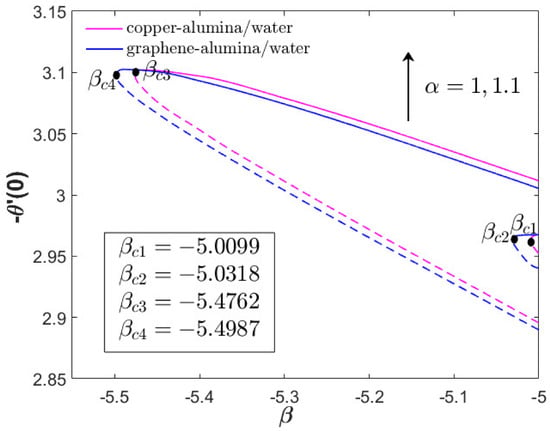
Figure 3.
for various hybrid nanofluids and (acceleration parameter) when and .
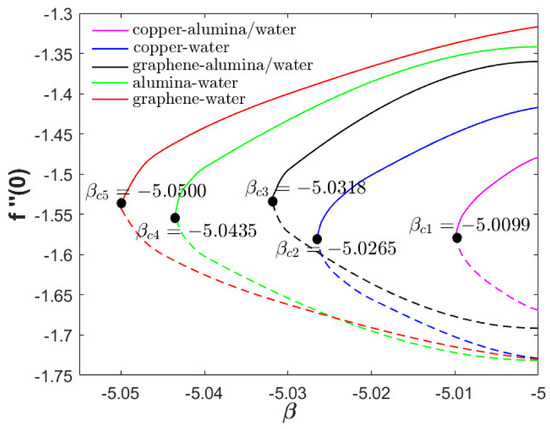
Figure 4.
for various working fluids when and .
Figure 2 and Figure 3 compare and of the copper–alumina/water and graphene–alumina water hybrid nanofluids when (basic Hiemenz flow) and . In Figure 2, the negative values of for both hybrid nanofluids within the range of unsteadiness parameter implies that the solutions are reverse flow solutions (RFS). Few studies have highlighted the observation of attached flow solution (AFS) when and . However, no AFS is seen in Figure 2 due to the high magnitude of unsteadiness decelerating parameter which tends to weaken the vortices of the fluid flow (see). In addition, as the decelerating parameter increases , the value of slightly decreases for both hybrid nanofluids which shows the retardation of the fluid flow. However, upon the increment of the acceleration parameter , the value of significantly increases due the role of the acceleration parameter in stabilizing the vortices and enhancing the flow progress. From Figure 2, it is obvious that the graphene–alumina/water has higher skin friction and critical value than the copper–alumina/water which indicates that the combination of graphene and alumina nanoparticles is progressive in assisting the fluid movement and delaying the boundary layer separation. Moreover, from Figure 3, the heat transfer coefficient of the copper–alumina/water is moderately greater than the graphene–alumina/water within a certain range of the decelerating parameter. However, the graphene–alumina/water is still the best option for the heat transfer fluid as we can see that the value of is the greatest when considering maximum decelerating parameter .
Figure 4 and Figure 5 compares the distributions of and for different working nanofluids (hybrid and single) namely copper–alumina/water, graphene–alumina/water, copper–water, graphene–water and alumina–water. The graphene–water (nanofluid) has the maximum skin friction coefficient and critical value followed by alumina–water (nanofluid), graphene–alumina/water (hybrid nanofluid), copper–water (nanofluid) and copper–alumina/water (hybrid nanofluid) as depicted in Figure 4. Surprisingly, in Figure 5, the nanofluids have greater thermal rate than the hybrid nanofluids such that alumina–water > graphene–water > copper–water > graphene–alumina/water > copper–alumina/water. This outcome is supported by the experimental findings by Ahammed et al. [53] such that the graphene–water nanofluid augmented the heat transfer coefficient for the heat exchanger application up to 88.62% followed by graphene–alumina/water hybrid nanofluid (63.13%) and alumina–water nanofluid (31.89%), respectively.
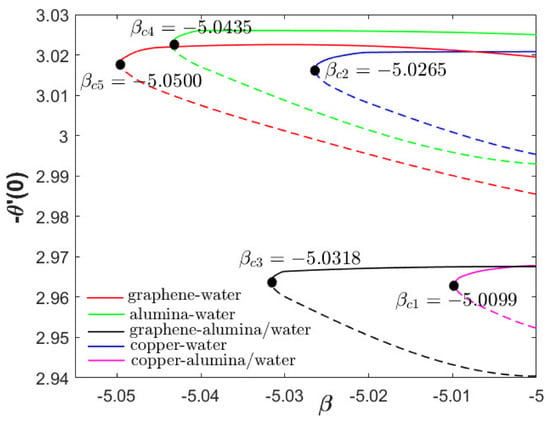
Figure 5.
for various working fluids when and .
Figure 6, Figure 7, Figure 8 and Figure 9 present the velocity and temperature of the graphene–alumina water hybrid nanofluid with different testing parameters (unsteadiness decelerating parameter, EMHD parameter and width parameter). All the profiles comply with the boundary condition (8), hence fulfill the validation criteria of the pertinent model. Similar to the previous figures, Figure 6, Figure 7, Figure 8 and Figure 9 also portray the potential second solution. Previous studies have shown that the USSP flow could produce two solutions with the first solution as the real one. In Figure 6, the first/physical solution for the velocity profile decreases as the decelerating parameter enhances which contradicts the second solution. Meanwhile, both solutions for the temperature profile reduces with the increment of . Physically, the addition of leads to higher resistance in fluid movement and consequently, reduces the velocity profile. In Figure 7, the temperature profile also depreciates due to the active heat transport from the hot fluid to the cool ambient. The effect of EMHD parameter (generated from the Riga plate) on the flow and thermal profiles is displayed in Figure 8 and Figure 9. The velocity of the hybrid nanofluid enhances while the temperature profile lessens with the increment of . The EMHD effect physically can assist the fluid movement by reducing the wall drag which, consequently, accelerates the fluid velocity whilst delays the separation of laminar flow. Meanwhile, the reduction in the temperature profile is consistent with the active process of the heat transfer transmission.
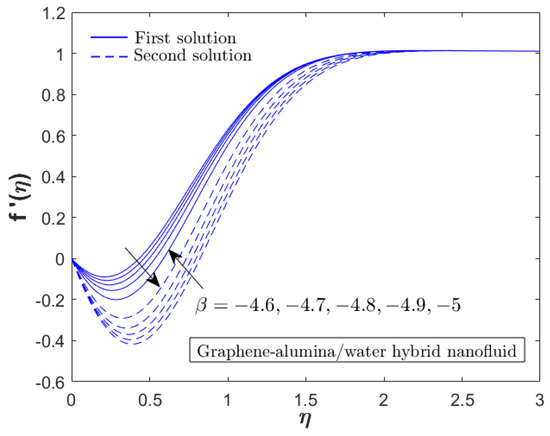
Figure 6.
Velocity profile for various (decelerating parameter) when and .
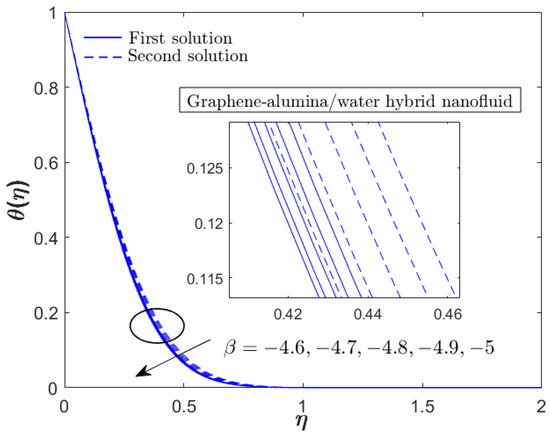
Figure 7.
Temperature profile for various (decelerating parameter) when and .
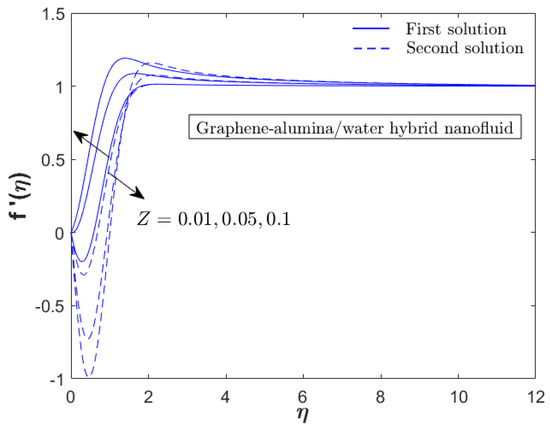
Figure 8.
Velocity profile for various (EMHD parameter) when and .
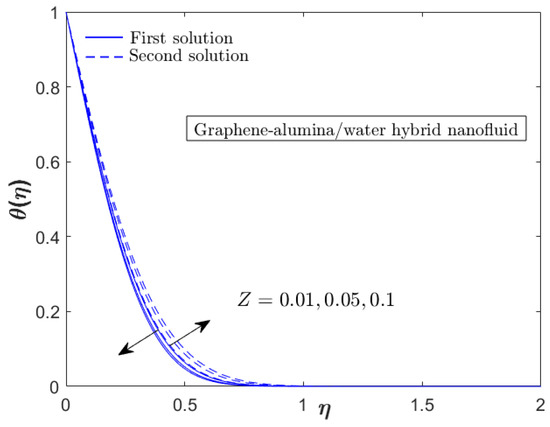
Figure 9.
Temperature profile for various (EMHD parameter) when and .
5. Conclusions
The USSP flow of hybrid nanofluids (copper–alumina/water and graphene–alumina/water) subjected to an EMHD Riga plate is numerically studied. The mathematical model is developed based on few physical and boundary layer assumptions. Similarity transformation is used to reduce the complex model into a set of simpler differential equations which then solved using the bvp4c solver. The main highlight is to analyze and compare the flow and thermal progresses of hybrid nanofluids. The conclusions of the present work are as follows:
- The acceleration parameter enhances the skin friction and heat transfer coefficients for both hybrid nanofluids. However, the graphene–alumina/water has the maximum skin friction coefficient while copper–alumina/water has the maximum thermal coefficient for larger acceleration parameter.
- Upon the comparison of the hybrid and single nanofluids, the graphene–water has the maximum skin friction coefficient while alumina–water has the maximum heat transfer rate followed by graphene–water and copper–water nanofluids. This implies that the single nanofluids are a progressive heat transfer fluid and better than hybrid nanofluids for the case of unsteadiness decelerating flow.
- The increment of the decelerating parameter depreciates the velocity profile while the EMHD parameter accelerates the fluid velocity.
- Both decelerating and EMHD parameters reduce the temperature profile of the hybrid nanofluid by actively transmitting the fluid particle heat.
However, the findings are only conclusive and limited to the comparison between graphene–alumina and copper–alumina with water base fluid. The results may differ if another base fluid is used. Hence, future study is necessary to investigate the thermal progress of these hybrid nanofluids. The recommendations for future study are as follows:
- The researchers can consider oil base fluid like ethylene glycol or combination of water and ethylene glycol.
- The researchers can consider magnetized hybrid nanofluid like magnetite–cobalt ferrite which actively operated under the magnetic field (EMHD) environment.
- The researchers can apply statistical data analysis like response surface methodology (RSM) and sensitivity analysis in investigating the significance of the physical parameters in this physical situation.
Author Contributions
Formulation of mathematical model and methodology, N.S.K., N.M.A. and I.P.; model validation, N.S.K. and N.M.A.; writing, N.S.K. and N.S.W.; review and editing, N.S.K., N.M.A. and N.S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We acknowledge the supports from Universiti Putra Malaysia, Universiti Teknikal Malaysia Melaka (FRGS/1/2021/STG06/UTEM/03/1) and Ministry of Higher Education (Malaysia).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. ASME Fluids Eng. Div. 1995, 231, 99–106. [Google Scholar]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously Increased Effective Thermal Conductivities of Ethylene Glycol-Based Nanofluids Containing Copper Nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Yu, W.; France, D.M.; Routbort, J.L.; Choi, S.U.S. Review and Comparison of Nanofluid Thermal Conductivity and Heat Transfer Enhancements. Heat Transf. Eng. 2008, 29, 432–460. [Google Scholar] [CrossRef]
- Yu, W.; Xie, H. A Review on Nanofluids: Preparation, Stability Mechanisms, and Applications. J. Nanomater. 2012, 2012, 1–17. [Google Scholar] [CrossRef]
- Das, S.K.; Choi, S.U.S.; Patel, H.E. Heat Transfer in Nanofluids—A Review. Heat Transf. Eng. 2006, 27, 3–19. [Google Scholar] [CrossRef]
- Ali, A.R.I.; Salam, B. A Review on Nanofluid: Preparation, Stability, Thermophysical Properties, Heat Transfer Characteristics and Application. SN Appl. Sci. 2020, 2, 1636. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Adamu, I.M.; Jamil, M.M.; Kefayati, G.H.R.; Mamat, R.; Najafi, G. Recent Progress on Hybrid Nanofluids in Heat Transfer Applications: A Comprehensive Review. Int. Commun. Heat Mass Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Hybrid Nanofluids for Heat Transfer Applications–A State-of-the-Art Review. Int. J. Heat Mass Transf. 2018, 125, 82–103. [Google Scholar] [CrossRef]
- Jamil, F.; Ali, H.M. Applications of Hybrid Nanofluids in Different Fields. In Hybrid Nanofluids for Convection Heat Transfer; Elsevier: Amsterdam, The Netherlands, 2020; pp. 215–254. [Google Scholar]
- Kshirsagar, D.P.; Venkatesh, M.A. A Review on Hybrid Nanofluids for Engineering Applications. Mater. Today Proc. 2021, 44, 744–755. [Google Scholar] [CrossRef]
- Vallejo, J.P.; Prado, J.I.; Lugo, L. Hybrid or Mono Nanofluids for Convective Heat Transfer Applications. A Critical Review of Experimental Research. Appl. Therm. Eng. 2022, 203, 117926. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Effect of Al2O3–Cu/Water Hybrid Nanofluid in Heat Transfer. Exp. Therm. Fluid Sci. 2012, 38, 54–60. [Google Scholar] [CrossRef]
- Madhesh, D.; Kalaiselvam, S. Experimental Analysis of Hybrid Nanofluid as a Coolant. Procedia Eng. 2014, 97, 1667–1675. [Google Scholar] [CrossRef]
- Alawi, O.A.; Kamar, H.M.; Hussein, O.A.; Mallah, A.R.; Mohammed, H.A.; Khiadani, M.; Roomi, A.B.; Kazi, S.N.; Yaseen, Z.M. Effects of Binary Hybrid Nanofluid on Heat Transfer and Fluid Flow in a Triangular-Corrugated Channel: An Experimental and Numerical Study. Powder Tech. 2022, 395, 267–279. [Google Scholar] [CrossRef]
- Gailitis, A.; Lielausus, O. On a Possibility to Reduce the Hydrodynamic Resistance of a Plate in an Electrolyte. Appl. Magnetohydrodyn. 1961, 12, 143–146. [Google Scholar]
- Ganesh, N.V.; Al-Mdallal, Q.M.; Al Fahel, S.; Dadoa, S. Riga–Plate Flow of γ Al2O3-Water/Ethylene Glycol with Effective Prandtl Number Impacts. Heliyon 2019, 5, e01651. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, T.; Ayub, M.; Farooq, M.; Alsaedi, A. Flow of Nanofluid Due to Convectively Heated Riga Plate with Variable Thickness. J. Mol. Liq. 2016, 222, 854–862. [Google Scholar] [CrossRef]
- Ayub, M.; Abbas, T.; Bhatti, M.M. Inspiration of Slip Effects on Electromagnetohydrodynamics (EMHD) Nanofluid Flow through a Horizontal Riga Plate. Eur. Phys. J. Plus 2016, 131, 193. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. Radiative Williamson Nanofluid Flow over a Convectively Heated Riga Plate with Chemical Reaction-A Numerical Approach. Chin. J. Phys. 2017, 55, 1663–1673. [Google Scholar] [CrossRef]
- Zari, I.; Ali, F.; Khan, T.S.; Shafiq, A. Radiative Hiemenz flow towards a stretching Riga plate in hybrid nanofluid. Int. Comm. Heat Mass Transf. 2022, 139, 106492. [Google Scholar] [CrossRef]
- Abbas, N.; Nadeem, S.; Malik, M.Y. Theoretical Study of Micropolar Hybrid Nanofluid over Riga Channel with Slip Conditions. Phys. A 2020, 551, 124083. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Waini, I.; Kasim, A.R.M.; Zainal, N.A.; Arifin, N.M.; Pop, I. Thermal Progress of a Non-Newtonian Hybrid Nanofluid Flow on a Permeable Riga Plate with Temporal Stability Analysis. Chin. J. Phys. 2022, 77, 279–290. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Waini, I.; Arifin, N.M.; Pop, I. Dual solutions of unsteady two-dimensional electro-magneto-hydrodynamics (EMHD) axisymmetric stagnation-point flow of a hybrid nanofluid past a radially stretching/shrinking Riga surface with radiation effect. Int. J. Numer. Methods Heat Fluid Flow 2022, 33, 333–350. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Zokri, S.M.; Kasim, A.R.M.; Waini, I.; Zainal, N.A. Insight into hybrid nanofluid induced by a Riga plate: Investigation on second grade fluid model. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady Stagnation Point Flow Past a Permeable Stretching/Shrinking Riga Plate in Al2O3-Cu/H2O Hybrid Nanofluid with Thermal Radiation. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 2640–2658. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.M.; Khashi’ie, N.S.; Pop, I.; Bachok, N.; Hafidzuddin, M.E.H. Hybrid Nanofluid Stagnation Point Flow Past a Slip Shrinking Riga Plate. Chin. J. Phys. 2022, 78, 180–193. [Google Scholar] [CrossRef]
- Tabassum, R.; Al-Zubaidi, A.; Rana, S.; Mehmood, R.; Saleem, S. Slanting transport of hybrid (MWCNTs-SWCNTs/H2O) nanofluid upon a Riga plate with temperature dependent viscosity and thermal jump condition. Int. Comm. Heat Mass Transf. 2022, 135, 106165. [Google Scholar] [CrossRef]
- Shatnawi, T.A.; Abbas, N.; Shatanawi, W. Mathematical Analysis of Unsteady Stagnation Point Flow of Radiative Casson Hybrid Nanofluid Flow over a Vertical Riga Sheet. Mathematics 2022, 10, 3573. [Google Scholar] [CrossRef]
- Siddique, I.; Khan, Y.; Nadeem, M.; Awrejcewicz, J.; Bilal, M. Significance of heat transfer for second-grade fuzzy hybrid nanofluid flow over a stretching/shrinking Riga wedge. AIMS Math. 2023, 8, 295–316. [Google Scholar] [CrossRef]
- Kumar, L. Cu–Al2O3/engine oil Williamson hybrid nanofluid flow over a stretching/shrinking Riga plate with viscous dissipation and radiation effect. Heat Transf. 2022, 51, 2279–2305. [Google Scholar] [CrossRef]
- Asogwa, K.K.; Mebarek-Oudina, F.; Animasaun, I.L. Comparative investigation of water-based Al2O3 nanoparticles through water-based CuO nanoparticles over an exponentially accelerated radiative Riga plate surface via heat transport. Arab. J. Sci. Eng. 2022, 47, 8721–8738. [Google Scholar] [CrossRef]
- Ma, P.K.H.; Hui, W.H. Similarity Solutions of the Two-Dimensional Unsteady Boundary-Layer Equations. J. Fluid Mech. 1990, 216, 537–559. [Google Scholar] [CrossRef]
- Dholey, S.; Gupta, A.S. Unsteady Separated Stagnation-Point Flow of an Incompressible Viscous Fluid on the Surface of a Moving Porous Plate. Phys. Fluids 2013, 25, 023601. [Google Scholar] [CrossRef]
- Dholey, S. Unsteady Separated Stagnation-Point Flow over a Permeable Surface. Z. Angew. Math. Phys. 2019, 70, 10. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Pop, I. Stretching or Shrinking Sheet Problem for Unsteady Separated Stagnation-Point Flow. Meccanica 2014, 49, 1479–1492. [Google Scholar] [CrossRef]
- Dholey, S. Magnetohydrodynamic Unsteady Separated Stagnation-Point Flow of a Viscous Fluid over a Moving Plate. Z. Angew. Math. Mech. 2016, 96, 707–720. [Google Scholar] [CrossRef]
- Dholey, S. An Unsteady Separated Stagnation-Point Flow Towards a Rigid Flat Plate. J. Fluids Eng. 2019, 141, 021202. [Google Scholar] [CrossRef]
- Dholey, S. Unsteady Separated Stagnation-Point Flows and Heat Transfer over a Plane Surface Moving Normal to the Flow Impingement. Int. J. Therm. Sci. 2021, 163, 106688. [Google Scholar] [CrossRef]
- Roşca, N.C.; Roşca, A.V.; Pop, I. Unsteady Separated Stagnation-Point Flow and Heat Transfer Past a Stretching/Shrinking Sheet in a Copper-Water Nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 2588–2605. [Google Scholar] [CrossRef]
- Renuka, A.; Muthtamilselvan, M.; Al-Mdallal, Q.M.; Doh, D.H.; Abdalla, B. Unsteady Separated Stagnation Point Flow of Nanofluid Past a Moving Flat Surface in the Presence of Buongiorno’s Model. J. Appl. Comp. Mech. 2021, 7, 1283–1290. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Wahid, N.S.; Arifin, N.M.; Pop, I. Magnetohydrodynamics Unsteady Separated Stagnation-point (USSP) Flow of a Hybrid Nanofluid on a Moving Plate. Z Angew. Math. Mech. 2022, 102, e202100410. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Magnetic Impact on the Unsteady Separated Stagnation-Point Flow of Hybrid Nanofluid with Viscous Dissipation and Joule Heating. Mathematics 2022, 10, 2356. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Waini, I.; Wahid, N.S.; Arifin, N.M.; Pop, I. Unsteady separated stagnation point flow due to an EMHD Riga plate with heat generation in hybrid nanofluid. Chin. J. Phys. 2022, 81, 181–192. [Google Scholar] [CrossRef]
- Takabi, B.; Salehi, S. Augmentation of the Heat Transfer Performance of a Sinusoidal Corrugated Enclosure by Employing Hybrid Nanofluid. Adv. Mech. Eng. 2015, 6, 147059. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Yu, H.S. Local non-similarity thermal boundary-layer solutions. J. Heat Transf. 1971, 93, 328–334. [Google Scholar] [CrossRef]
- Hussain, M.; Sheremet, M. Convection analysis of the radiative nanofluid flow through porous media over a stretching surface with inclined magnetic field. Int. Commun. Heat Mass Transf. 2023, 140, 106559. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, S.; Gourla, M.G. Axi-symmetric deformation due to various sources in saturated porous media with incompressible fluid. J. Solid Mech. 2013, 5, 74–91. [Google Scholar]
- Abbas, I.A. Eigenvalue approach on fractional order theory of thermoelastic diffusion problem for an infinite elastic medium with a spherical cavity. Appl. Math. Model. 2015, 39, 6196–6206. [Google Scholar] [CrossRef]
- Merkin, J.H. On Dual Solutions Occurring in Mixed Convection in a Porous Medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The Effect of Transpiration on Self-Similar Boundary Layer Flow over Moving Surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed Convection Boundary-Layer Flow Near the Stagnation Point on a Vertical Surface in a Porous Medium: Brinkman Model with Slip. Transp. Porous Med. 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Ahmad, R.; Mustafa, M.; Turkyilmazoglu, M. Buoyancy effects on nanofluid flow past a convectively heated vertical Riga-plate: A numerical study. Int. J. Heat Mass Transf. 2017, 111, 827–835. [Google Scholar] [CrossRef]
- Ahammed, N.; Asirvatham, L.G.; Wongwises, S. Entropy generation analysis of graphene–alumina hybrid nanofluid in multiport minichannel heat exchanger coupled with thermoelectric cooler. Int. J. Heat Mass Transf. 2016, 103, 1084–1097. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).