Abstract
The transport of deformable particles (TDPs) through porous media has been of considerable interest due to the multiple applications found in industrial and medical processes. The adequate design of these applications has been mainly achieved through experimental efforts, since TDPs through porous media are challenging to model because of the mechanical blockage of the pore throat due to size exclusion, deformation in order to pass through the pore throat under the driven pressure, and breakage under strong extrusion. In this work, based on the diffusivity equation and considering the TDP as a complex fluid whose viscosity and density depend on the local pressure, a simple but accurate theoretical model is proposed to describe the pressure behavior under steady- and unsteady-state flow conditions. Assuming a linear pressure dependence of the viscosity and density of the TDPs, valid for moderate pressure changes, the solution of the mathematical model yields a quantitative correlation between the pressure evolution and the parameters compressibility, viscosity coefficient, elastic modulus, particle size, and friction factor. The predictions of the model agree with experiments and allow the understanding of transport of deformable particles through a porous media.
1. Introduction
The transport of deformable particles (TDPs) in porous media is important in many biological and industrial processes, such as enhanced oil recovery (EOR), filtration, and microfluidic applications [1,2,3]. For example, injecting deformable particles of gel as an EOR method in oil reservoirs makes it possible to block off water from areas of high conductivity and diversify the flow towards non-swept areas to increase the oil recovery factor [4]. In another application, hydrogel particles have also been used to repair porous bone tissue, given their ability to reach and provide drugs to the areas of interest [5]. The transport of deformable particles through a porous medium, unlike flow with suspended solid particles, favors particle deformation in order to pass across pore throats and their re-migration under high-pressure gradients. As the flow of deformable particles moves through a porous medium, there may be processes such as shearing of the gel particles, mechanical blocking of the pore throat due to size exclusion, deformation in order to pass through the pore throat under the driven pressure, and breakage under strong extrusion [6,7,8,9,10].
Many displacement experiments have been carried out in porous media to evaluate the effect of different properties, such as particle size, storage modulus, salinity, compressibility, and resistance factor (RF). The RF is the differential pressure ratio developed in the porous medium during the flow of deformable particles compared to water, and it is an important parameter that assesses the feasibility of placement [7,8,9,11,12,13]. However, given the complex characteristics of the transport of deformable particles, theoretical modeling has been developed to a lesser extent.
Wang et al. [14] presented a numerical model that considered the deformable particles as a continuous phase fluid through the porous medium. In their analysis, many correlations were required to adequately represent phenomena such as deformation, trapping and release, effective viscosity, and permeability change due to pore plugging. Liu et al. [15] proposed a kinetic equation for the plugging, bridging, deposition, and deforming of elastic microparticles in order to pass through pores based on the size exclusion theory, which describes the pressure gradient in an unsteady-state flow when a suspension of deformable particles in water flows through a porous medium. The model fits the experimental data well, but it requires many parameters that are difficult to measure experimentally, and they must be determined by history matching. This study did not consider the effect on the pressure gradient under steady-state flow conditions to define the resistance factor. Wang et al. [16] presented a model that included both preformed particle gel (PPG) plugging and restarting behaviors using log-normal and normal distribution functions to calculate the PPG plugging probability, and a power law equation was used to calculate the PPG restarting rate. Wang’s model matches favorably with several laboratory experiments, but due to the large number of parameters involved, a more practical and global model is necessary for field application. Zhou et al. [17] demonstrated a simulation method for transport of preformed particle gel (PPG) through porous media, which combined various techniques such as a lattice Boltzmann method for fluid flow, discrete element method for particle interaction, and immersed moving boundary method for the solid–fluid interaction. The method was validated by matching of the placement, plugging, and deformation of PPG between numerical simulations and microscopic visualization experiments. Wang et al. [9] developed a theoretical model to determine the threshold pressure necessary for deformable particles to pass through pore throats as a function of elastic modulus, Poisson´s ratio, the diameter ratio of particle to throat, and friction coefficient. They found that when the ratio of the particle diameter to the throat is greater than or equal to three, the particle can break apart. Imqam et al. [18] reported that preformed particle gel displacement through unconsolidated sandstone presents different scenarios: low gel particle retention and pass; high gel particle retention and pass; high gel particle retention, breaking, and pass; and gel particle accumulation and plug. In that work, they proposed an empirical power law model for the resistance factor dependence on the injection rate. However, it is impossible to extrapolate the parameters fitted to the resistance factor model regarding gel properties to generalize them to different conditions. Li et al. [10] developed a capillary bundle model and analyzed the influence of other preformed particle gel flow parameters on the pressure gradients. This model works well for steady-state flow, but no results have been presented for cases where the gel moves under unsteady flow. Farasat et al. [19] proposed a modification to Darcy’s law to represent the displacement of deformable particles through a porous medium. They considered that effective viscosity was affected by the resistance factor, while trapping modified the particle concentration. The model accurately represents the pressure behavior while the particles move through a porous medium, but it requires knowing in advance both the resistance factor and the concentration of particles as a function of the injection flow rate. Recently, and based on the lattice Boltzmann method, Coelho et al. [20] performed 2D numerical simulations to investigate the behavior of droplets when passing through a porous medium. They found that at high flow rates, the droplets and the surrounding fluid behaved as a single fluid. However, at low velocity, the droplets blocked several pores, and as a result increased the flow velocity in the others. This occurred until the pressure difference over the pores was large enough to allow a droplet to deform and then flow through them. Although this study clarifies how droplets would be transported through a two-dimensional porous medium, it is not obvious in 3D that flexible particles show similar behavior and therefore limits the application of the proposed model. Chen et al. [21] performed experiments and developed a theory on the migration process and the prediction of flow resistance of elastic particles in porous media. Based on Hertz contact theory, which is used to calculate the stress at the contact surface of two contact and extrusion elastomers, they proposed a model that described the strength necessary for plugging and release through porous media. However, several experimental tests are necessary to adjust the parameters.
To the best of our knowledge, there is no report in the literature of a simple theoretical model able to predict the pressure gradients of the transport of deformable particles in porous media under unsteady- and steady-state conditions. Such a model would allow us to reduce the number of experiments needed to characterize flow behavior and improve the understanding of the phenomena that occur in the porous medium, and could be easily implemented in numerical simulators devoted to modeling the injection of PPG.
We derived a simple semi-analytical model to predict the pressure behavior of the transport of deformable particles as a function of particle size, permeability, porosity, compressibility, and viscoelastic properties (viscosity coefficient, elastic modulus, and friction factor) under unsteady- and steady-state conditions. Our approaches to the viscosity and density have a phenomenological basis, although the final mathematical model is based on first principles (momentum and mass balance). The mathematical model also allows identification of the stages of accumulation, displacement, and stabilization of deformable particles as they move through a porous medium. We verified the accuracy of the model predictions, and the results follow the trends of laboratory experiments from two groups of researchers [9,18]. The modeling of the flow of deformable particles in porous media indicates that it is still an open problem and of wide interest for engineering applications.
2. Modeling TDPs as a Time Pressure-Dependent Complex Fluid
In this section, the theoretical foundations of the proposed model for unsteady and steady flow conditions are presented. The deformable particles are assumed to be a complex fluid with a strong dependence of viscosity and density on pressure. The viscous mechanism of transport of gel particles is akin to polymer flooding. Therefore, a viscosity–pressure model for polymers can be used to calculate the viscosity. Thus, for the pressure dependence of the viscosity μ, a linear law is proposed:
where is the gauge fluid pressure, is the viscosity at the reference zero pressure, and is a parameter often referred to as the viscosity–pressure-dependence coefficient. Equation (1) is a linear law known as Barus’s law [22], and it has been used in a wide range of applications where fluid viscosity is affected by local sudden changes in pressure, such as those occurring for polymers in the extrusion process.
The deformable particles are compressed at the pore throats until they reach a pressure to pass through them, affecting the local density as the particle front is propagated. In this case, a linear equation of state relating the density to pressure is proposed:
where is the density at zero pressure and is the constant isothermal compressibility. Note that Equation (1) describes a fluid with dilatant-type rheological properties, while Equation (2) describes a pressure linear approximation of density for slightly compressible fluids. For the purposes of this study, we found that linear approximations were enough to estimate the viscosity and density of deformable particles, as demonstrated below in Section 3, where good agreement between theoretical and experimental results are met.
2.1. Unsteady TDP Case
Generally, the continuity equation for the fluid flowing into a porous medium reads:
where and are the fluid volumetric velocity and the porosity, respectively. In turn, the velocity can be obtained through Darcy’s law:
where is the permeability of the porous medium.
By combining Equations (3) and (4) and substituting the pressure-dependent density and viscosity properties (Equations (1) and (2)), the transport equation is written as:
For one-dimensional flow, Equation (5) simplifies to:
with:
Imqam et al. [18], Wang et al. [9], and Zhou et al. [17] showed that the front of deformable particles advanced with constant velocity through the porous medium with a characteristic pressure profile. Therefore, to solve Equation (6), the following change of variable for the traveling waveform is proposed:
where is the velocity at which the particle front propagates. Thus, Equation (6) becomes:
Integrating Equation (9), the following equation is obtained:
where and are constants of integration. Wang et al. [9] and Li et al. [10] showed that particles required a pressure threshold to pass through a restriction such as a pore throat. This pressure is the same as that required by the particle front to move through the porous medium in an unsteady state. Then, if we assume that the particle front () moves with constant pressure (, and that far from there (), the pressure is zero (), then and . Therefore, Equation (10) becomes:
Equation (11) allows the monitoring of pressure over time as the particle front is positioned and transported through the porous medium. Also, if it is considered that the average pressure needed by the particle front to propagate in the porous medium is equal to the pressure required by a particle to enter a pore throat of equivalent radius , then can be determined by [9]:
where is the friction coefficient, is the elastic modulus, is Poisson’s ratio, and is the average particle’s radius. The equivalent average radius of the pore throat can be calculated from the Kozeny–Carman relationship:
Hence, the equation describing the implicit relationship between inlet pressure and is the following:
Equation (14) can be used to calculate the injection pressure of a solution of deformable particles into a porous medium under different propagation scenarios.
The curves plotted in Figure 1 show on the one hand, the influence of the diffusivity coefficient on the pressure evolution. Note that in Figure 1, the x-axis refers to the dimensionless time, . On the y-axis, the dimensionless pressure is used. These dimensionless variables are introduced to facilitate the comparison of solutions with different parameters. According to Equation (7), the diffusivity coefficient quantitatively compares the effect of compaction and permeability. If the particles clump together and/or if the permeability is relatively small , then the inlet pressure increases rapidly. Otherwise, if the permeability increases and/or the particles remain separated from each other , then the inlet pressure increases slowly.
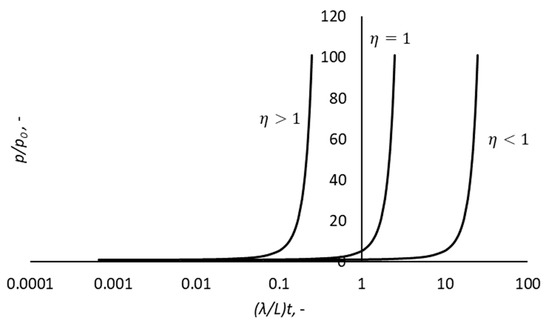
Figure 1.
Effect of the diffusivity parameter η on the pressure behavior over time. Pressure and time are non-dimensions with and , respectively. is the length of the porous medium. In these cases, .
On the other hand, the curves plotted in Figure 2 show the influence of parameters and on the inlet pressure. If the viscous properties exceed those of compaction , the pressure required to transport the fluid increases considerably in a short time. However, if compaction properties predominate over the viscous properties , then part of the energy provided by the fluid injection compacts the fluid instead of moving it forward, as stipulated in Equation (9), since the parameter directly impacts the diffusivity coefficient. This phenomenon explains the longer time required to increase the inlet pressure in Figure 2.
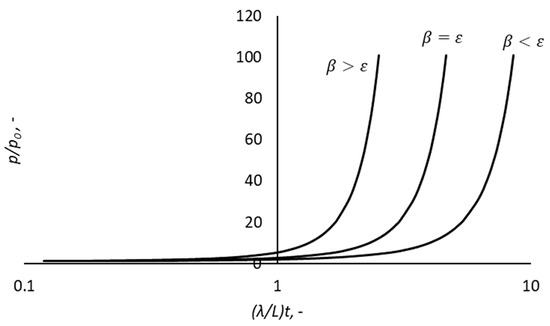
Figure 2.
Effect of and parameters on the pressure behavior over time during the transport of deformable particles. Pressure and time are dimensionless with and , respectively. is the length of the porous medium. In these cases, .
2.2. Steady TDP Case
In the case of a steady-state flow , Equation (6) becomes:
This implies that:
Now, introducing Darcy-type condition, i.e.,
where is the volumetric flow rate, and using the linear approaches (1) and (2), we can write Equation (16) as:
The following step requires the integration from to , that is:
and finally, we obtain:
where is the length of the porous medium, is the permeability, and is the cross-section area of the porous medium. Solving for , Equation (20) allows calculation of the resistance factor (RF) in terms of few parameters. Note that in Equation (20), if:
then the classical Darcy equation for porous media is recovered. Also, Equation (20) allows computation of the pressure profile along the entire porous medium once the deformable particles have passed through it. In other words, the steady-state solution calculates the operative established pressure.
Finally, we recognize that the strengths of both developed models (11) and (20) are limited by the validity of the linear approximations employed for the viscosity and density pressure dependence. Future research involves the implementation of equations of state and more robust rheological models, although looking for a balanced compromise between simplicity and accuracy of the resulting equations, which facilitates its potential applications.
3. Application of the Model on Preformed Particle Gel (PPG) Flowing Through a Porous Medium
This section shows the fit of the proposed model with experimental data reported in the literature over the transport of deformable particles through the porous medium, both under unsteady and steady flow conditions. In these experiments, an aqueous solution of preformed gel particles is prepared at a given concentration and then injected through a porous medium at a constant flow rate. During the process, the pressure is recorded at different points along the porous medium to monitor the pressure developed in the experiments analyzed in this work. In the inlet where the PPG is injected, two different scenarios can appear: (i) the PPG easily enters the porous medium, or (ii) PPG requires additional forces to compress and can eventually enter the void spaces. This phenomenon is explained below in the following sections.
3.1. Unsteady-State TDP Case
The proposed theoretical model was used to analyze data from the literature on pressure behavior developed during the transport of preformed particle gel (PPG) in porous media under an unsteady-state flow condition. The model was fitted to the experimental data of Imqam et al. [18] and Wang et al. [9]. These researchers reported sufficient measured properties used by the model, which are collected in Table 1 along with the fitting parameters employed in the theoretical model.

Table 1.
Properties and parameters used to fit proposed theoretical model to published data.
In tests A and B of Imqam’s experiments, a solution of deformable particles with concentration of 0.2% was injected at 2 mL/min flow rate through a horizontal sand pack with porosity of 0.39 and permeability of 2.62 × 10−11 and 6.54 × 10−11 m2, respectively. The pressure was recorded at four points located along the sand pack. Tests C and D performed by Wang et al. [9] are like those presented by Imqam et al. [18]. In these tests, a solution with a concentration of 0.1% of deformable particles was injected at a flow rate of 1 mL/min into porous media with similar porosity and permeability. Unlike Imqam’s experiments, Wang et al. [9] modified the radii of the particles involved in the displacements: 130.0 μm in test C and 268.5 μm in test D. The analysis of the apparent viscosity under constant flow conditions for the different sections of the sand pack shows a linear dependence on the average pressure, as considered in Equation (1). In Figure 3, we show that the apparent fluid viscosity is more sensitive to pressure in Imqam’s experiments compared to Wang’s results. This behavior is because particles with lower elastic moduli have a rapid response to the stress developed by the fluid within the porous medium.
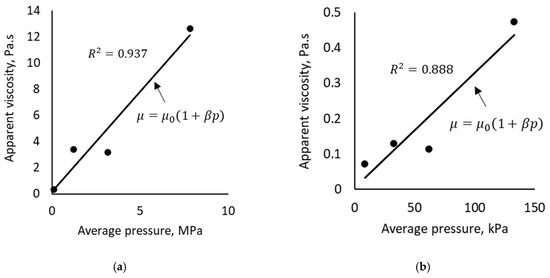
Figure 3.
PPG apparent viscosity as a function of average pressure for different sections of the unconsolidated sand pack. Parameters obtained from experimental data. (a) Imqam’s experiment: Pa∙s and Pa−1; (b) Wang’s experiment: Pa∙s and Pa−1.
In Figure 4, we present experimental data and the fitted model for PPG flowing through a porous medium under unsteady-state flow conditions. In that figure, PPG injection pore volume is a way to measure the elapsed time in experiments, which is computed as:
injection pore volume = (volumetric flow rate) × (time)/(total pore volume of porous medium).
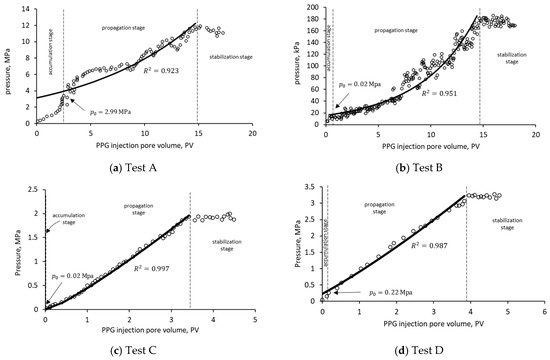
Figure 4.
PPG inlet pressure behavior and fitting model on unconsolidated sand pack. The circles indicate experimental data for tests A and B from Imqam et al. [18] and tests C and D from Wang et al. [9].
Note from Table 1 that the proposed model uses the same fitting properties for porosity, viscosity, density, elastic modulus, Poisson’s modulus, and particle radius because these properties are intrinsic to the considered complex fluid. The pressure behavior indicates that the particle front moves slowly through a porous medium because several pore volumes were injected to observe a pressure increase at the recording points. In this case, the compaction of the particles plays a vital role in the propagation through the porous medium.
The results in Figure 4 help to identify three stages in all cases. In the first stage, the pressure rapidly increases due to the stress required for the PPG to pass through the pore throats. The particles accumulate at the entrance, creating a PPG layer whose thickness rises until it reaches the threshold pressure, , to enter the porous medium. The threshold pressure becomes relevant, since it predicts the pressure required for the gel to enter and move within the porous medium. This parameter depends on the properties of the particle, i.e., elastic modulus, Poisson’s ratio, the diameter of the particle, and friction coefficient (Equation (12)), all of which can be measured experimentally, except the friction factor , a parameter that should be adjusted. The friction factor is affected by the permeability and roughness of the porous medium, and its dependence on fluid flow physics deserves further research. However, the influence of this parameter can be observed in the data from Imqam et al. [18], where they found that PPG entered and moved easily with residual oil in the porous medium. In that scenario, the oil worked as a lubricant, decreasing the friction factor and therefore the threshold pressure . Imqam et al. [18] demonstrated that in the presence of oil, the required threshold pressure is = 0.61 MPa, while in the absence of oil, higher entry pressure is needed, around 17 MPa at the inlet.
In the second stage, the pressure behavior indicates propagation of the deformed particles through the porous medium. The particles are no longer deformed, because there is no change in the data trend. In the third stage, the pressure stabilizes because a steady state has been reached inside the porous medium.
The fitted viscosity coefficient to the experimental data of Figure 4 showed a weak dependence on pressure compared to the isothermal compressibility coefficient . Once the flow of deformable particles entered the porous medium, the viscoelastic properties were no longer strongly influenced by the restrictions imposed by the size of throats of pores or therefore by the local pressure. However, the isothermal compressibility increased because the particles clumped together and moved following the sequence, as they were placed at the entrance of the porous medium [23].
It is quite interesting to note that if the approximation of the PPG density is considered in terms of the particle concentration , the fluid density , and the particle density [24], then we have:
Therefore, from Equations (2) and (22) and considering that the initial density is the same as the density of the fluid solution, the PPG increases its particle concentration through the porous medium as a function of the pressure and the isothermal compressibility factor, i.e.,
In the case shown in Figure 4a, for example, if the initial PPG concentration was 800 ppm with threshold pressure of = 2.99 MPa at the inlet, and assuming = 1.1 × 103 kg/m3 and = 1.0 × 103 kg/m3, then a concentration of 117,926 ppm would be needed to propagate the particles through the porous medium. This statement would have to be confirmed experimentally, although there are some results pointing in that direction [6].
It is stressed that the effect of permeability changes is much more important than the change in particle dimensions. The experiments carried out by Imqam et al. [18] showed a drastic decrease in pressure when the permeability was increased using the same injection rate of the preformed particle gel solution. Furthermore, the propagation of the front was even slower as the permeability decreased, as observed in the experimental data and parameter . The data provided by Wang et al. [9] and the proposed model corroborate this observation, because the increase in particle size in the gel solution does not affect the pressure behavior significantly. The experiments of tests C and D can be represented by the same representative parameters of the preformed particle gel solution. In this case, the velocity of the propagation front is identical and the threshold pressure can be inferred according to Equation (12) using the same friction coefficient.
3.2. Steady-State TDP Case
The resistance factor (RF) has been used by researchers to infer PPG’s ability to move through a porous medium. The RF is obtained experimentally in a steady-state condition, and it is calculated as:
where is the PPG injection pressure measured during the gel’s propagation through the porous medium and is the fluid (usually water) injection pressure before PPG placement at the same flow rate. One of the main advantages of the model proposed in this work is that if the parameters involved in the characterization of the PPG are independent of the flow conditions, then it is enough to consider the same parameters (Table 1) and the corresponding model (Equation (24)) to perform the calculation of the resistance factor. To validate this claim, in Figure 5, we depict experimental data reported by Imqam et al. [18], and the corresponding fitted RF model. The resistance factor model was fitted by solving implicitly for the pressure drop in Equation (20) and then comparing it with the pressure predicted by Darcy’s law.
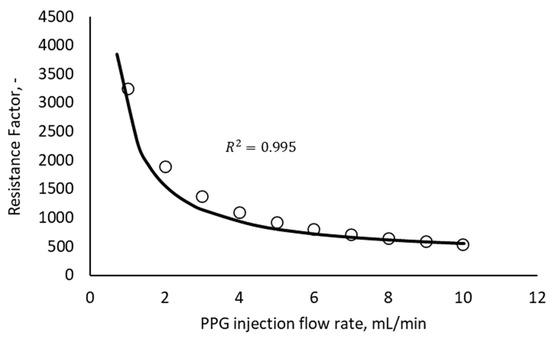
Figure 5.
Resistance factor (Equation (24), continuous line) at different PPG injection rates. Experimental data (circles) from Imqam et al. [18].
4. Conclusions
Based on the diffusivity equation, a simple but accurate mathematical model has been developed to analyze the pressure gradient when a deformable particle solution flows through a porous medium. This model considers the transport of deformable particles as a complex fluid with viscosity and density depending on the local pressure. The model reproduces both experimental unsteady- and steady-state flow conditions considering properties such as compressibility, viscosity coefficient, elastic modulus, particle size, and friction factor. The unsteady-state solution is useful for monitoring the front propagation of particles thorough a porous medium, while the steady-state solution can be used to estimate the pressure profile in operative conditions. The elasticity, friction factor, and ratio between the size of the particle and that of the pore have an important role, since they are associated with the initial stress that the gel requires to be able to enter the porous medium. Finally, the effects of pressure affect the viscosity of TDPs to a lesser extent than its compressibility.
Author Contributions
Conceptualization, V.M.-P. and S.L.-R.; methodology, V.M.-P.; validation, E.F.-U. and C.G.A.-M.; formal analysis, V.M.-P. and S.L.-R.; writing—original draft preparation, E.F.-U.; writing—review and editing, C.G.A.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bai, B.; Liu, Y.; Coste, J.; Li, L. Preformed Particle Gel for Conformance Control: Transport Mechanism Through Porous Media. SPE Reserv. Eval. Eng. 2007, 10, 176–184. [Google Scholar] [CrossRef]
- Lebleu, N.; Roques, C.; Aimar, P.; Causserand, C. Role of the cell-wall structure in the retention of bacteria by microfiltration membranes. J. Membr. Sci. 2009, 326, 178–185. [Google Scholar] [CrossRef]
- Zinchenko, A.; Davis, R. Emulsion flow through a packed bed with multiple drop breakup. J. Fluid Mech. 2013, 725, 611–663. [Google Scholar] [CrossRef]
- Bai, B.; Huang, F.; Liu, Y.; Seright, R.S.; Wang, Y. Case Study of Preformed Particle Gel for in-depth Fluid Diversion. In Proceedings of the SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK, USA, 20–23 April 2008. [Google Scholar] [CrossRef]
- Feng, Y.; Guo, W.; Hu, L.; Yi, X.; Tang, F. Application of Hydrogels as Sustained-Release Drug Carriers in Bone Defect Repair. Polymers 2022, 14, 4906. [Google Scholar] [CrossRef] [PubMed]
- Yao, C.J.; Wang, D.; Wang, J.; Hou, J.; Lei, G.L.; Steenhuis, T.S. Effect of Ionic Strength on the Transport and Retention of Polyacrylamide Microspheres in Reservoir Water Shutoff Treatment. Ind. Eng. Chem. Res. 2017, 56, 8158–8168. [Google Scholar] [CrossRef]
- Goudarzi, A.; Zhang, H.; Varavei, A.; Taksaudon, P.; Hu, Y.P.; Delshad, M.; Bai, B.; Sepehrnoor, K. A Laboratory and Simulation Study of Preformed Particle Gels for Water Conformance Control. Fuel 2015, 140, 502–513. [Google Scholar] [CrossRef]
- Imqam, A.; Bai, B.; Delshad, M. Preformed Particle Gel Propagation Through Super-K Permeability Sand and Its Resistance to Water Flow During Conformance Control. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Nusa Dua, Bali, Indonesia, 20–22 October 2015. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Liu, H.; Zhao, W.; Liu, H.; Yao, C.; Zheng, J.; Shen, Y. Quantification of Transportation of Deformable Gel Particles in Porous Media. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar] [CrossRef]
- Li, S.; Yu, H.H.; Fan, J. Modeling Transport of Soft Particles. Phys. Rev. E 2021, 104, 025112. [Google Scholar] [CrossRef] [PubMed]
- Bai, B.; Li, L.; Liu, Y.; Liu, H.; Wang, Z.; You, C. Preformed Particle Gel for Conformance Control: Factors Affecting its Properties and Applications. SPE Reserv. Eval. Eng. 2007, 10, 415–422. [Google Scholar] [CrossRef]
- Imqam, A.; Goudarzi, A.; Delshad, M.; Bai, B. Development of a Mechanistic Numerical Simulator for Preformed Particle Gel Applications in Non-Crossflow Heterogeneous Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015. [Google Scholar] [CrossRef]
- Imqam, A.; Bai, B. Optimizing the Strength and Size of Preformed Particle Gels for Better Conformance Control Treatment. Fuel 2015, 148, 178–185. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.; Wang, Z.; Xu, J.; Yuan, D. Numerical simulation of preformed particle gel flooding for enhancing oil recovery. J. Pet. Sci. Eng. 2013, 112, 248–257. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, J.; Wang, Q.; Liu, J.; Guo, L.; Yuan, F.; Zhou, K. Flow of Preformed Particle Gel through Porous Media: A Numerical Simulation Study Based on the Size Exclusion Theory. Ind. Eng. Chem. Res. 2017, 56, 2840–2850. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.Q.; Zhang, H.l.; Sepehrnoori, K. Simulation of deformable preformed particle gel propagation in porous media. AIChE J. 2017, 63, 4628–4641. [Google Scholar] [CrossRef]
- Zhou, K.; Hou, J.; Sun, Q.; Guo, L.; Bing, S.; Du, Q.; Yao, C. An efficient LBM-DEM simulation method for suspensions of deformable preformed particle gels. Chem. Eng. Sci. 2017, 167, 288–296. [Google Scholar] [CrossRef]
- Imqam, A.; Bai, B.; Delshad, M. Micro-Particle Gel Transport Performance through Unconsolidated Sandstone and its Blocking to Water Flow During Conformance Control Treatments. Fuel 2018, 231, 479–488. [Google Scholar] [CrossRef]
- Farasat, A.; Younesian-Farid, H.; Sadeghnejad, S. Conformance control study of preformed particle gels (PPGS) in mature waterflooded reservoirs: Numerical and experimental investigations. J. Pet. Sci. Eng. 2021, 203, 108575e108588. [Google Scholar] [CrossRef]
- Coelho, R.C.V.; Silva, D.P.F.; Maschio, A.M.R.; da Gama, M.M.T.; Araújo, N.A.M. Collective transport of droplets through porous media. Phys. Fluids 2023, 35, 013304. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Liu, Z.; Zhang, J.; Trivedi, J.; Li, X. Experimental and theoretical investigation of the migration and plugging of the particle in porous media based on elastic properties. Fuel 2023, 332, 126224. [Google Scholar] [CrossRef]
- Barus, C. Note on the Dependence of Viscosity on Pressure and Temperature. Proc. Am. Acad. Arts Sci. 1891, 27, 13–18. [Google Scholar] [CrossRef]
- O’Connell, M.G.; Lu, N.B.; Browne, C.A.; Datta, S.S. Cooperative Size Sorting of Deformable Particles in Porous Media. Soft Matter 2019, 15, 3620–3626. [Google Scholar] [CrossRef] [PubMed]
- Di Felice, R.; Foscolo, P.U.; Gibilaro, L.G.; Rapagna, S. The Interaction of Particles with a Fluid-Particle Pseudo-Fluid. Chem. Eng. Sci. 1991, 46, 1873–1877. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).