Coaxial Circular Jets—A Review
Abstract
1. Introduction
2. Free Coaxial Circular Jets
2.1. Importance of Different Terms in the Governing Equations
2.2. General Flow Field Characteristics
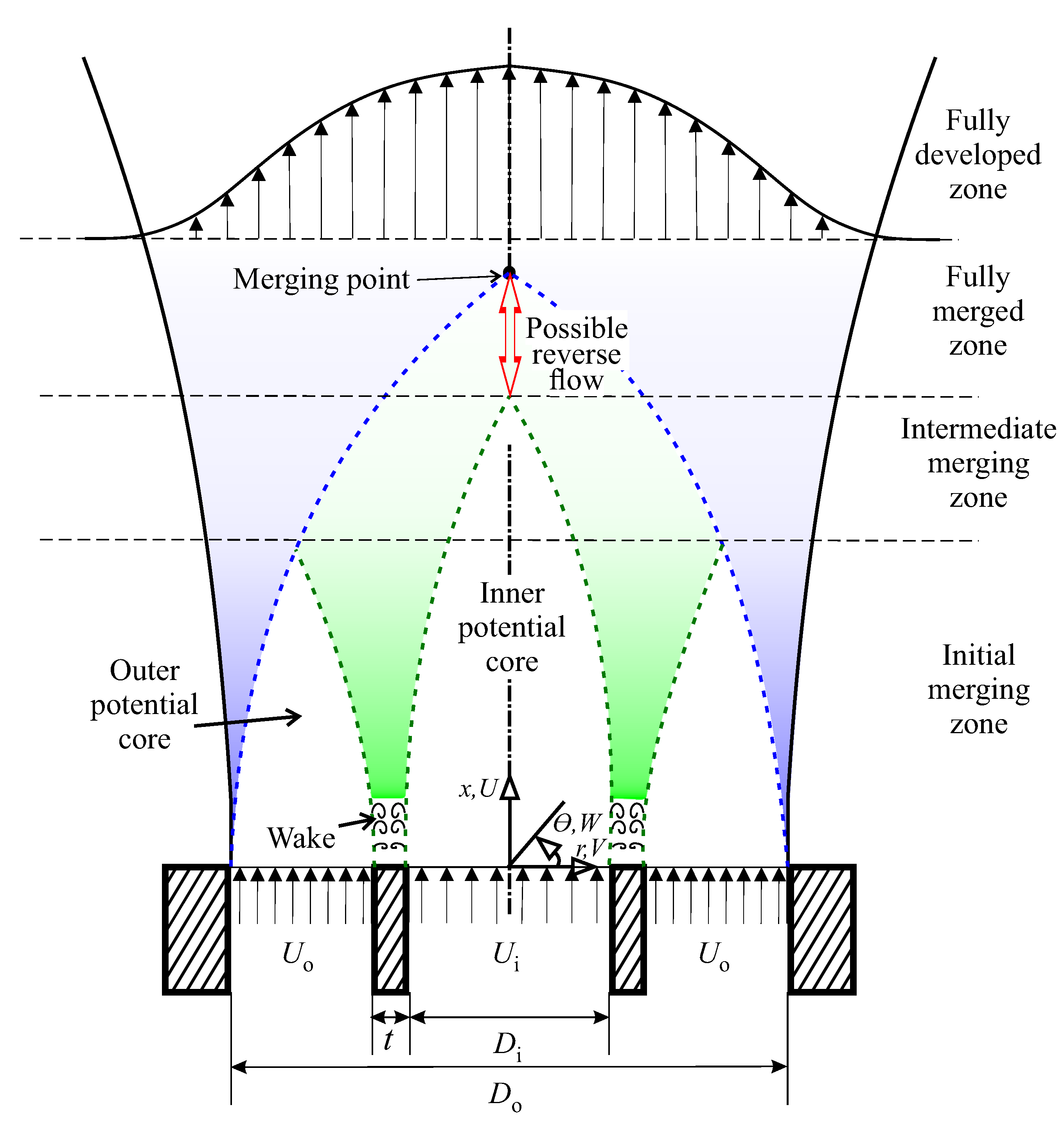
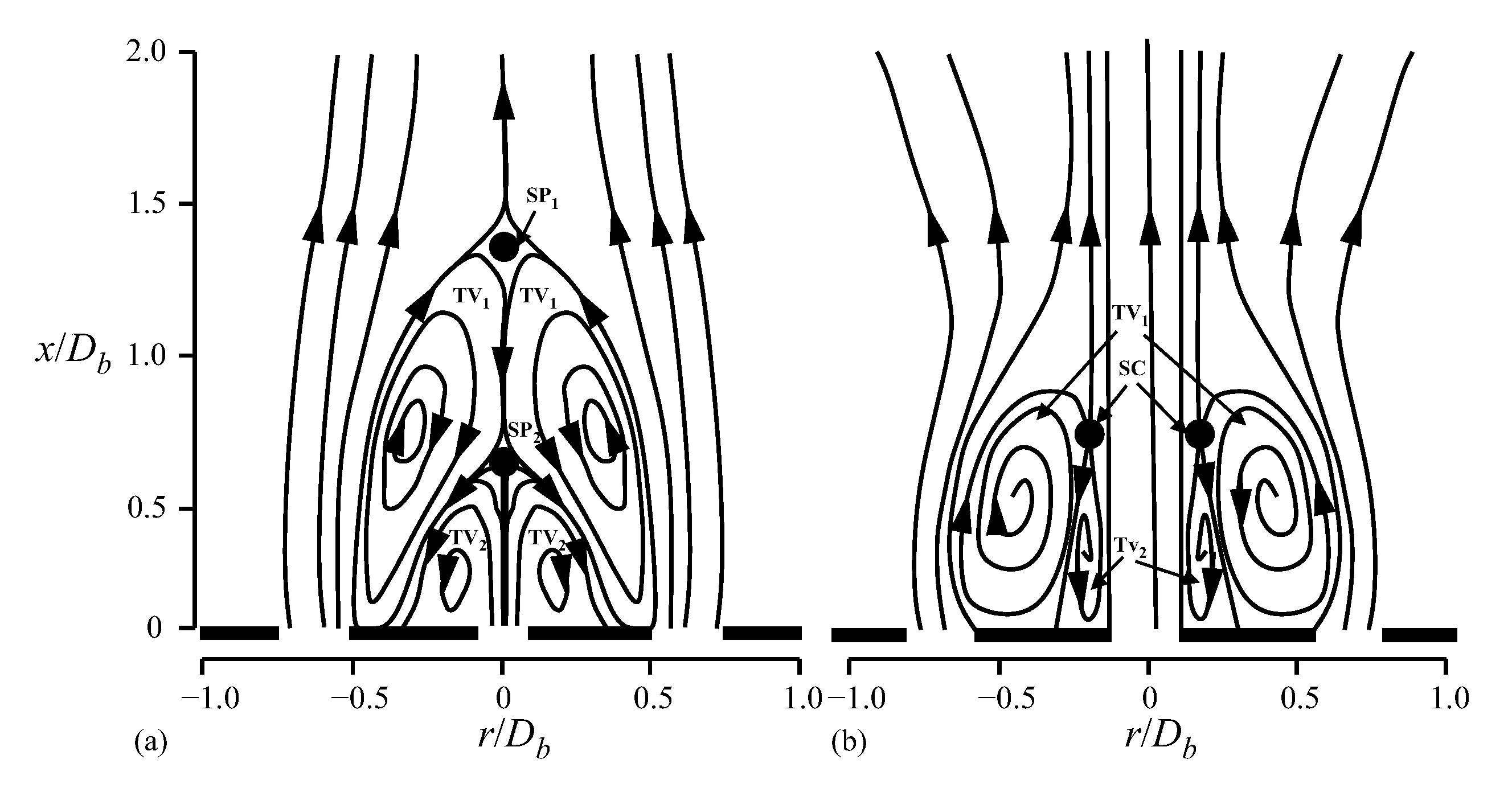
2.2.1. Coaxial Jet Flow Structure
2.2.2. Near-Field Flow and Instability Dynamics
2.3. Discussion
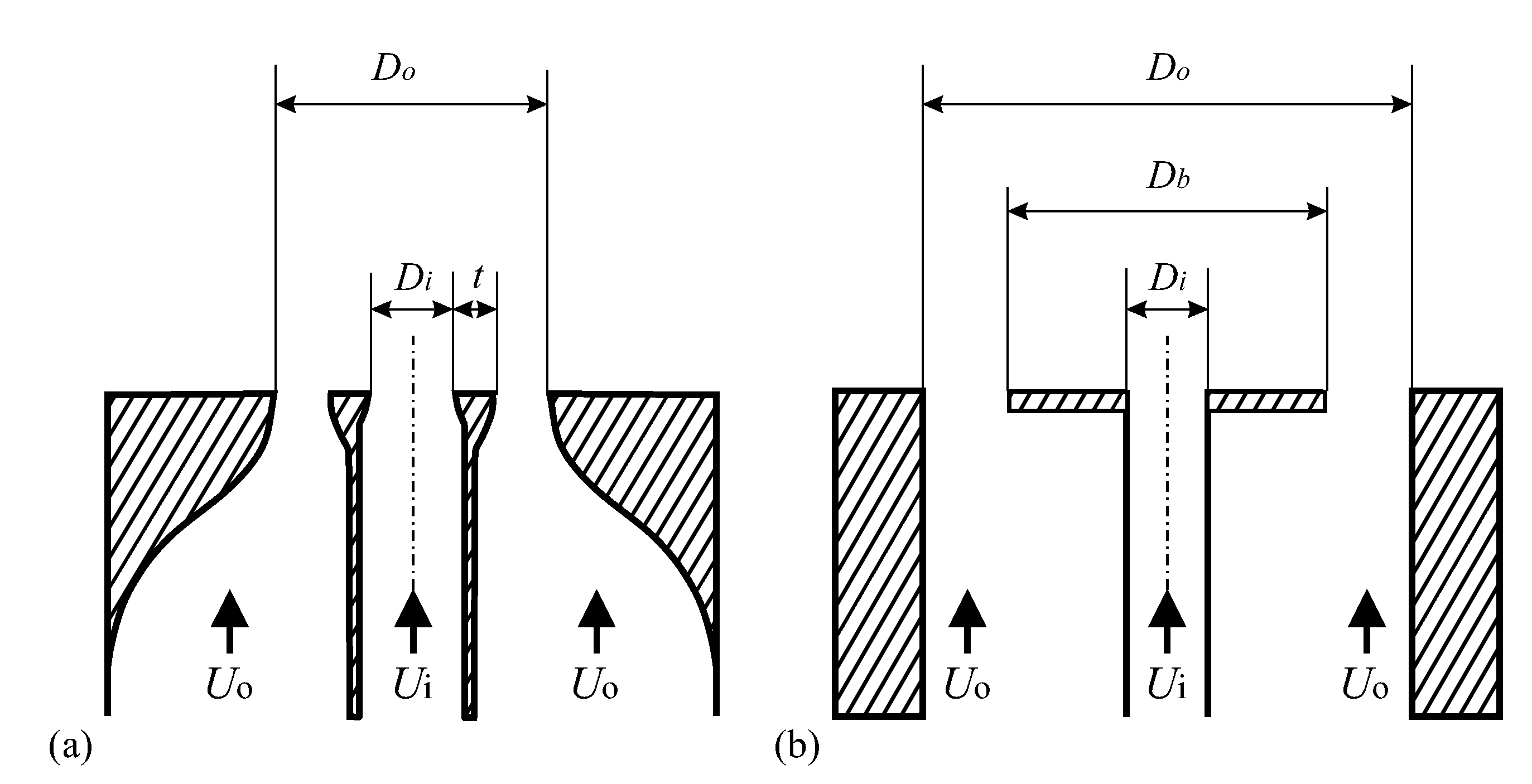
3. Some Remarks on Geometrical Nozzle Modification
4. Coaxial Circular Jets Impinging on a Flat, Smooth Surface
5. Some Practical Applications and Open Questions
5.1. Mass Transfer
5.2. Heat Transfer
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kieffer, S.W.; Sturtevant, B. Laboratory studies of volcanic jets. J. Geophys. Res. Solid Earth 1984, 89, 8253–8268. [Google Scholar] [CrossRef]
- Camci, C.; Herr, F. Forced convection heat transfer enhancement using a self-oscillating impinging planar jet. J. Heat Transf. 2002, 124, 770–782. [Google Scholar] [CrossRef]
- Liu, T.; Sullivan, J. Heat transfer and flow structures in an excited circular impinging jet. Int. J. Heat Mass Transf. 1996, 39, 3695–3706. [Google Scholar] [CrossRef]
- Janetzke, T.; Nitsche, W. Time resolved investigations on flow field and quasi wall shear stress of an impingement configuration with pulsating jets by means of high speed PIV and a surface hot wire array. Int. J. Heat Fluid Flow 2009, 30, 877–885. [Google Scholar] [CrossRef]
- Hofmann, H.M.; Movileanu, D.L.; Kind, M.; Martin, H. Influence of a pulsation on heat transfer and flow structure in submerged impinging jets. Int. J. Heat Mass Transf. 2007, 50, 3638–3648. [Google Scholar] [CrossRef]
- Markal, B.; Aydin, O. Experimental Investigation of Coaxial Impinging Air Jets. Appl. Therm. Eng. 2018. [Google Scholar] [CrossRef]
- Celik, N.; Eren, H. Heat transfer due to impinging co-axial jets and the jets’ fluid flow characteristics. Exp. Therm. Fluid Sci. 2009, 33, 715–727. [Google Scholar] [CrossRef]
- Yule, A.J. Large-scale structure in the mixing layer of a round jet. J. Fluid Mech. 1978, 89, 413–432. [Google Scholar] [CrossRef]
- Geers, L.F.G.; Tummers, M.J.; Hanjalić, K. Experimental investigation of impinging jet arrays. Exp. Fluids 2004, 36, 946–958. [Google Scholar] [CrossRef]
- Banyassady, R.; Piomelli, U. Interaction of inner and outer layers in plane and radial wall jets. J. Turbul. 2015, 16, 460–483. [Google Scholar] [CrossRef]
- Zuckerman, N.; Lior, N. Radial Slot Jet Impingement Flow and Heat Transfer on a Cylindrical Target. J. Thermophys. Heat Transf. 2007, 21, 548–561. [Google Scholar] [CrossRef]
- Hoogendoorn, C. The effect of turbulence on heat transfer at a stagnation point. Int. J. Heat Mass Transf. 1977, 20, 1333–1338. [Google Scholar] [CrossRef]
- Lee, J. The Effect of Nozzle Configuration on Stagnation Region Heat Transfer Enhancement of Axisymmetric Jet Impingement. Int. J. Heat Mass Transf. 2000, 43, 3497–3509. [Google Scholar] [CrossRef]
- Sadr, R.; Klewicki, J.C. An experimental investigation of the near-field flow development in coaxial jets. Phys. Fluids 2003, 15, 1233–1246. [Google Scholar] [CrossRef]
- Dahm, W.J.A.; Frieler, C.E.; Tryggvason, G. Vortex structure and dynamics in the near field of a coaxial jet. J. Fluid Mech. 1992, 241, 371–402. [Google Scholar] [CrossRef]
- Rehab, H.; Villermaux, E.; Hopfinger, E. Flow regimes of large-velocity-ratio coaxial jets. J. Fluid Mech. 1997, 345, 357–381. [Google Scholar] [CrossRef]
- Kwan, A.; Ko, N. Coherent structures in subsonic coaxial jets. J. Sound Vib. 1976, 48, 203–219. [Google Scholar] [CrossRef]
- Violato, D.; Scarano, F. Three-dimensional evolution of flow structures in transitional circular and chevron jets. Phys. Fluids 2011, 23, 124104. [Google Scholar] [CrossRef]
- Raizner, M.; Rinsky, V.; Grossman, G.; van Hout, R. Heat transfer and flow field measurements of a pulsating jet impinging on a flat heated surface. Int. J. Heat Fluid Flow 2019, 77, 278–287. [Google Scholar] [CrossRef]
- Miller, D.R.; Comings, E.W. Static pressure distribution in the free turbulent jet. J. Fluid Mech. 1957, 3, 1–16. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Miller, D.R.; Comings, E.W. Force-momentum fields in a dual-jet flow. J. Fluid Mech. 1960, 7, 237–256. [Google Scholar] [CrossRef]
- Champagne, F.; Wygnanski, I.J. An experimental investigation of coaxial turbulent jets. Int. J. Heat Mass Transf. 1971, 14, 1445–1464. [Google Scholar] [CrossRef]
- Ko, N.; Au, H. Initial region of subsonic coaxial jets of high mean-velocity ratio. J. Fluids Eng. 1981, 103, 335–338. [Google Scholar] [CrossRef]
- Ko, N.; Au, H. Coaxial jets of different mean velocity ratios. J. Sound Vib. 1985, 100, 211–232. [Google Scholar] [CrossRef]
- Ko, N.; Kwan, A. The initial region of subsonic coaxial jets. J. Fluid Mech. 1976, 73, 305–332. [Google Scholar] [CrossRef]
- Au, H.; Ko, N. Coaxial jets of different mean velocity ratios, part 2. J. Sound Vib. 1987, 116, 427–443. [Google Scholar] [CrossRef]
- Villermaux, E.; Rehab, H.; Hopfinger, E.J. Breakup régimes and self-sustained pulsations in coaxial jets. Meccanica 1994, 29, 393–401. [Google Scholar] [CrossRef]
- Wicker, R.B.; Eaton, J.K. Near field of a coaxial jet with and without axial excitation. AIAA J. 1994, 32, 542–546. [Google Scholar] [CrossRef]
- Victorin, K. Untersuchung turbulenter Mischvorgange. Forsch. Geb. Ing. A 1941, 12, 16. [Google Scholar] [CrossRef]
- Ribner, H.S. Field of Flow about a Jet and Effect of Jets on Stability of Jet-Propelled Airplanes; Technical Report; National Aeronautics And Space Admin Langley Research Center: Hampton, VA, USA, 1946. [Google Scholar]
- Deodati, J.B.; Monteath, E.B. An Investigation of the Round Jet in a Moving Air Stream. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1947. [Google Scholar]
- Forstall, W.J.; Shapiro, A. Momentum and Mass Transfer in Coaxial Gas Jets. J. Appl. Mech. 1950, 17, 399–408. [Google Scholar] [CrossRef]
- Squire, H.B.; Trouncer, J. Round Jets in a General Stream; Technical Report; Aeronautical Research Council: London, UK, 1944. [Google Scholar]
- Chigier, N.A.; Beér, J.M. The Flow Region Near the Nozzle in Double Concentric Jets. J. Basic Eng. 1964, 86, 797–804. [Google Scholar] [CrossRef]
- Kwan, S.-H. Noise Mechanisms in the Initial Region of Coaxial Jets. PhD. Thesis, University of Hong Kong, Hong Kong, China, 1975. [Google Scholar]
- Morris, P.J. Turbulence measurements in subsonic and supersonic axisymmetric jets in a parallel stream. AIAA J. 1976, 14, 1468–1475. [Google Scholar] [CrossRef]
- Rajaratnam, N. Developments in Water Science. In Turbulent Jets; Chow, V.T., Ed.; Elsevier: Amsterdam, The Netherlands, 1976; Volume 5. [Google Scholar]
- Bradshaw, P.; Ferriss, D.; Johnson, R. Turbulence in the noise-producing region of a circular jet. J. Fluid Mech. 1964, 19, 591–624. [Google Scholar] [CrossRef]
- Ko, N.; Davies, P. The near field within the potential cone of subsonic cold jets. J. Fluid Mech. 1971, 19, 49–78. [Google Scholar] [CrossRef]
- Buresti, G.; Talamelli, A.; Petagna, P. Experimental characterization of the velocity field of a coaxial jet configuration. Exp. Therm. Fluid Sci. 1994, 9, 135–146. [Google Scholar] [CrossRef]
- Buresti, G.; Petagna, P.; Talamelli, A. Experimental investigation on the turbulent near-field of coaxial jets. Exp. Therm. Fluid Sci. 1998, 17, 18–26. [Google Scholar] [CrossRef]
- Ribeiro, M.; Whitelaw, J. Coaxial jets with and without swirl. J. Fluid Mech. 1980, 96, 769–795. [Google Scholar] [CrossRef]
- Duraõ, D.; Whitelaw, J. Turbulent mixing in the developing region of coaxial jets. J. Fluids Eng. 1973. [Google Scholar] [CrossRef]
- Murugan, S.; Huang, R.F.; Hsu, C.M. Time-averaged flow characteristics and mixing properties of double-concentric jets. Int. J. Heat Fluid Flow 2020, 86, 108707. [Google Scholar] [CrossRef]
- Segalini, A.; Talamelli, A. Experimental analysis of dominant instabilities in coaxial jets. Phys. Fluids 2011, 23, 024103. [Google Scholar] [CrossRef]
- Huang, R.; Lin, C. Flow characteristics and shear-layer vortex shedding of double concentric jets. AIAA J. 1997, 35, 887–892. [Google Scholar] [CrossRef]
- Huang, R.F.; Lin, C.L. Visualized flow patterns of double concentric jets at low annulus velocities. AIAA J. 1994, 32, 1868–1874. [Google Scholar] [CrossRef]
- Markal, B. Experimental investigation of heat transfer characteristics and wall pressure distribution of swirling coaxial confined impinging air jets. Int. J. Heat Mass Transf. 2018, 124, 517–532. [Google Scholar] [CrossRef]
- Afroz, F.; Sharif, M.A.R. Heat Transfer from a Heated Flat Surface Due to Swirling Coaxial Turbulent Jet Impingement. J. Therm. Sci. Eng. Appl. 2020, 1–26. [Google Scholar] [CrossRef]
- Terekhov, V.; Kalinina, S.; Sharov, K. An experimental investigation of flow structure and heat transfer in an impinging annular jet. Int. Commun. Heat Mass Transf. 2016, 79, 89–97. [Google Scholar] [CrossRef]
- Markal, B.; Avci, M.; Aydin, O. Conical coaxial impinging air jets: Angle effect on the heat transfer performance. Heat Mass Transf. 2020, 1–12. [Google Scholar] [CrossRef]
- van Hout, R.; Rinsky, V.; Grobman, Y.G. Experimental study of a round jet impinging on a flat surface: Flow field and vortex characteristics in the wall jet. Int. J. Heat Fluid Flow 2018, 70, 41–58. [Google Scholar] [CrossRef]
- Raizner, M.; Rinsky, V.; Grossman, G.; van Hout, R. Effect of impinging jet pulsation on primary and secondary vortex characteristics. Int. J. Heat Mass Transf. 2020, 151, 119445. [Google Scholar] [CrossRef]
- Garimella, S.V.; Rice, R. Confined and submerged liquid jet impingement heat transfer. J. Heat Transf. 1995, 117, 871–877. [Google Scholar] [CrossRef]
- Hadžiabdić, M.; Hanjalić, K. Vortical structures and heat transfer in a round impinging jet. J. Fluid Mech. 2008, 596, 221–260. [Google Scholar] [CrossRef]
- Celik, N. Effects of the surface roughness on heat transfer of perpendicularly impinging co-axial jet. Heat Mass Transf. 2011, 47, 1209–1217. [Google Scholar] [CrossRef]
- Baughn, J.; Shimizu, S. Heat transfer measurements from a surface with uniform heat flux and an impinging jet. J. Heat Transf. 1989, 111. [Google Scholar] [CrossRef]
- Behnia, M.; Parneix, S.; Durbin, P.A. Prediction of heat transfer in an axisymmetric turbulent jet impinging on a flat plate. Int. J. Heat Mass Transf. 1998, 41, 1845–1855. [Google Scholar] [CrossRef]
- Kataoka, K.; Suguro, M.; Degawa, H.; Maruo, K.; Mihata, I. The effect of surface renewal due to largescale eddies on jet impingement heat transfer. Int. J. Heat Mass Transf. 1987, 30, 559–567. [Google Scholar] [CrossRef]
- Markal, B. The effect of Total flow rate on the cooling performance of swirling coaxial impinging jets. Heat Mass Transf. 2019, 55, 3275–3288. [Google Scholar] [CrossRef]
- Bijarchi, M.A.; Kowsary, F. Inverse optimization design of an impinging co-axial jet in order to achieve heat flux uniformity over the target object. Appl. Therm. Eng. 2018, 132, 128–139. [Google Scholar] [CrossRef]
- Shapiro, M.; Goldenberg, M. Deposition of glass fiber particles from turbulent air flow in a pipe. J. Aerosol Sci. 1993, 24, 65–87. [Google Scholar] [CrossRef]
- Zhang, H.; Ahmadi, G.; Fan, F.G.; McLaughlin, J.B. Ellipsoidal particles transport and deposition in turbulent channel flows. Int. J. Multiph. Flow 2001, 27, 971–1009. [Google Scholar] [CrossRef]
- Voth, G.A.; Soldati, A. Anisotropic particles in turbulence. Annu. Rev. Fluid Mech. 2017, 49, 249–276. [Google Scholar] [CrossRef]
- Sadr, R.; Klewicki, J.C. Flow field characteristics in the near field region of particle-laden coaxial jets. Exp. Fluids 2005, 39, 885–894. [Google Scholar] [CrossRef]
- Fang, C.; Xu, J.; Zhao, H.; Li, W.; Liu, H. Experimental investigation on particle entrainment behaviors near a nozzle in gas–particle coaxial jets. Powder Technol. 2015, 286, 55–63. [Google Scholar] [CrossRef]
- Lin, J.; Shi, X.; Yu, Z. The motion of fibers in an evolving mixing layer. Int. J. Multiph. Flow 2003, 8, 1355–1372. [Google Scholar] [CrossRef]
- Longmire, E.K.; Eaton, J.K. Structure of a particle-laden round jet. J. Fluid Mech. 1992, 236, 217–257. [Google Scholar] [CrossRef]
- Violato, D.; Ianiro, A.; Cardone, G.; Scarano, F. Three-dimensional vortex dynamics and convective heat transfer in circular and chevron impinging jets. Int. J. Heat Fluid Flow 2012, 37, 22–36. [Google Scholar] [CrossRef]
- Mladin, E.; Zumbrunnen, D. Local convective heat transfer to submerged pulsating jets. Int. J. Heat Mass Transf. 1997, 40, 3305–3321. [Google Scholar] [CrossRef]
- Janetzke, T.; Nitsche, W.; Täge, J. Experimental investigations of flow field and heat transfer characteristics due to periodically pulsating impinging air jets. Heat Mass Transf. 2008, 45, 193–206. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B.; Qiu, S.; Poh, H.J.; Mujumdar, A.S. Turbulent impinging jet heat transfer enhancement due to intermittent pulsation. Int. J. Therm. Sci. 2010, 49, 1247–1252. [Google Scholar] [CrossRef]
- Xu, P.; Qiu, S.; Yu, M.; Qiao, X.; Mujumdar, A.S. A study on the heat and mass transfer properties of multiple pulsating impinging jets. Int. Commun. Heat Mass Transf. 2012, 39, 378–382. [Google Scholar] [CrossRef]

 ) [27], (
) [27], ( ) fit (A = 9.9) of [27] for , (
) fit (A = 9.9) of [27] for , ( ) [36], (
) [36], ( ) [37], (
) [37], ( ) [23], = 2.94, (
) [23], = 2.94, ( ) [23], = 1.28, (
) [23], = 1.28, ( ) [38], (
) [38], ( ) [16] (
) [16] ( ) fit (A = 8) of [16] for . The potential inner core length for a simple jet (without annular jet) is for most of the data taken as , except for [23] where it was taken as 7.5.
) fit (A = 8) of [16] for . The potential inner core length for a simple jet (without annular jet) is for most of the data taken as , except for [23] where it was taken as 7.5.
 ) [27], (
) [27], ( ) fit (A = 9.9) of [27] for , (
) fit (A = 9.9) of [27] for , ( ) [36], (
) [36], ( ) [37], (
) [37], ( ) [23], = 2.94, (
) [23], = 2.94, ( ) [23], = 1.28, (
) [23], = 1.28, ( ) [38], (
) [38], ( ) [16] (
) [16] ( ) fit (A = 8) of [16] for . The potential inner core length for a simple jet (without annular jet) is for most of the data taken as , except for [23] where it was taken as 7.5.
) fit (A = 8) of [16] for . The potential inner core length for a simple jet (without annular jet) is for most of the data taken as , except for [23] where it was taken as 7.5.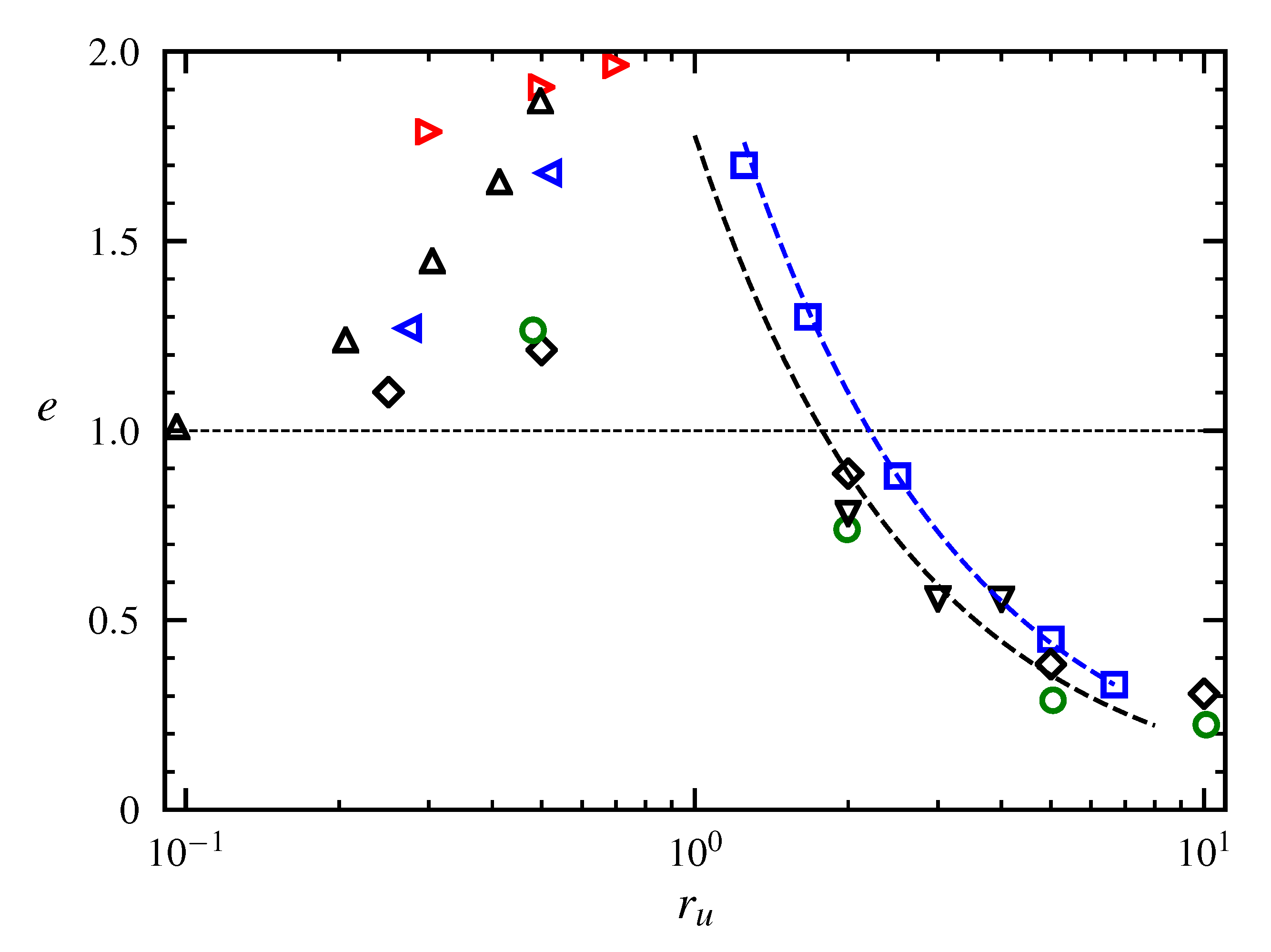
 ) [41,42], (
) [41,42], ( ) [23], (
) [23], ( ) [23], (
) [23], ( ) [15], (
) [15], ( ) [25], (
) [25], ( ) [26], (
) [26], ( ) [16], (▲) [43], (◆) [14], (
) [16], (▲) [43], (◆) [14], ( ) [28], (
) [28], ( ) [29], (
) [29], ( ) [44].
) [44].
 ) [41,42], (
) [41,42], ( ) [23], (
) [23], ( ) [23], (
) [23], ( ) [15], (
) [15], ( ) [25], (
) [25], ( ) [26], (
) [26], ( ) [16], (▲) [43], (◆) [14], (
) [16], (▲) [43], (◆) [14], ( ) [28], (
) [28], ( ) [29], (
) [29], ( ) [44].
) [44].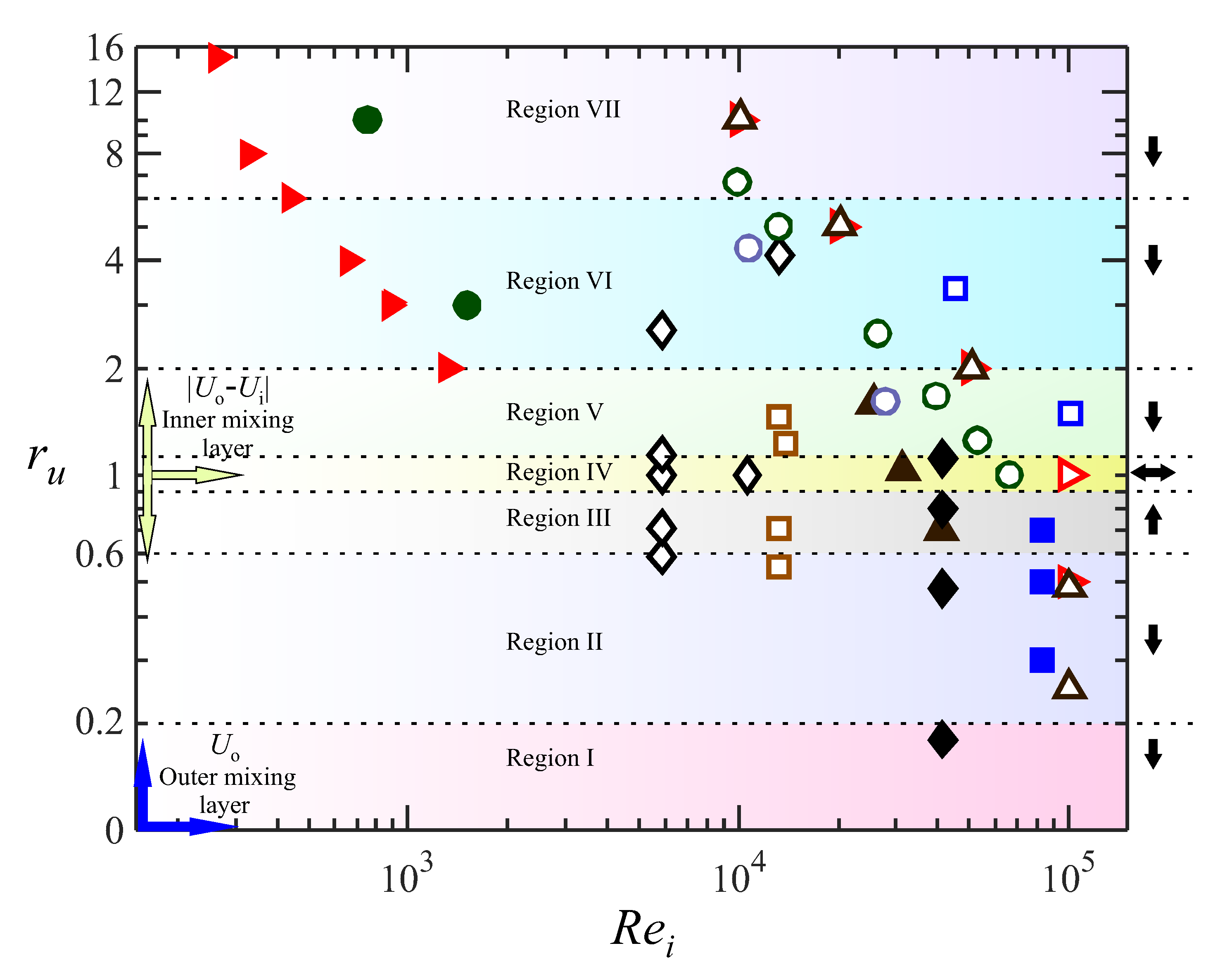

| Ref. (Fluid) | [mm] | [mm] | t [mm] | Profile (I, O) | [m/s] | Re | Re | ||
|---|---|---|---|---|---|---|---|---|---|
| [15] | 0.96 | 53.34 | 76.45 | 1.27 | (TH, TH) | 0.59 | 0.06 | 5847 | 1331 |
| (Water) | 0.71 | 0.08 | 5847 | 1601 | |||||
| 1.0 | 0.11 | 5847 | 2255 | ||||||
| 1.0 | 0.20 | 10,631 | 4100 | ||||||
| 1.14 | 0.13 | 5847 | 2571 | ||||||
| 2.56 | 0.28 | 5847 | 5773 | ||||||
| 4.16 | 1.04 | 13,288 | 21,322 | ||||||
| [14] | 5.04 | 30.0 | 75.0 | 1.50 | (FD, FD) | 0.18 | 0.25 | 41,000 | 10,471 |
| (Water) | 0.48 | 0.67 | 41,000 | 27,924 | |||||
| 0.80 | 1.11 | 41,000 | 46,541 | ||||||
| 1.11 | 1.54 | 41,000 | 64,575 | ||||||
| [23] | 1.28 | 25.4 | 38.35 | - | (TH, TH) | 0.5 | 28.67 | 100,000 | 24,500 |
| (Air) | 0.96 | 57.58 | 100,000 | 49,200 | |||||
| 2.00 | 57.58 | 50,700 | 49,200 | ||||||
| 5.00 | 57.58 | 20,300 | 49,200 | ||||||
| 10.00 | 57.58 | 10,100 | 49,200 | ||||||
| 2.98 | 25.4 | 50.67 | (TH, TH) | 0 | 0 | 100,000 | 0 | ||
| 0.25 | 14.40 | 100,000 | 24,000 | ||||||
| 0.48 | 28.79 | 100,000 | 48,000 | ||||||
| 1.99 | 57.59 | 50,700 | 96,000 | ||||||
| 5.00 | 57.59 | 20,300 | 96,000 | ||||||
| 10.00 | 57.59 | 10,100 | 96,000 | ||||||
| [17] | 2.67 | 21.0 | 41.07 | 0.78 | (TH, TH) | 0.3 | 18.00 | 83,113 | 21,973 |
| [24,25,26,27] | 0.5 | 30.00 | 83,113 | 36,622 | |||||
| (Air) | 0.7 | 42.00 | 83,113 | 51,270 | |||||
| and | 2.73 | 20.0 | 40.0 | 1 | (TH, TH) | 1.00 | 50.00 | 65,963 | 59,366 |
| (Water) | 1.25 | 50.00 | 52,770 | 59,366 | |||||
| 1.66 | 50.00 | 39,577 | 59,366 | ||||||
| 2.50 | 50.00 | 26,385 | 59,366 | ||||||
| 5.00 | 50.00 | 13,193 | 59,367 | ||||||
| 6.67 | 50.00 | 9894 | 59,367 | ||||||
| [28] | 2.09 | 40 | 55 | 2 | (TH, TH) | 3.00 | 1.80 | 1583 | 1306 |
| 10.00 | 3.00 | 791.56 | 2176 | ||||||
| [16] | 1.82 | 20 | 27 | 2 | (TH, TH) | 2.00 | 2.00 | 1319 | 3560 |
| (Water) | 3.00 | 2.00 | 879 | 3560 | |||||
| 4.00 | 2.00 | 659 | 3560 | ||||||
| 6.00 | 2.00 | 439 | 3560 | ||||||
| 8.00 | 2.00 | 329 | 3560 | ||||||
| 15.00 | 2.00 | 263 | 3560 | ||||||
| [29] | 7.72 | 20 | 60 | 1.3 | (TH, TH) | 0.55 | 5.5 | 13,192 | 13,568 |
| (Air) | Sharp | 0.71 | 7.1 | 13,192 | 17,515 | ||||
| 1.23 | 12.3 | 13,192 | 30,344 | ||||||
| 1.45 | 14.5 | 13,192 | 35,771 |
| Regions ( Range) | IVJD & IVJM | Governing | ||
|---|---|---|---|---|
| Region I () | A | Very St | 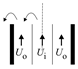 | |
| Region II () | A | St |  | |
| Region III () | We | D | 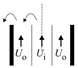 | |
| Region IV () | St | We | 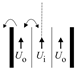 small | |
| Region V () | We | D | 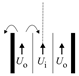 | |
| Region VI () | Ne | D |  | Locking inner and outer jets |
| Region VII () | Ne | D |  | Increased locking inner and outer jets |
| Ref. (Fluid) | [mm] | Profile (I, O) | [m/s] | Re | Re | |||
|---|---|---|---|---|---|---|---|---|
| [35] | 8.50 | (25.0, 97.0, | 0.44 | (TH, TH) | 0.117 | - | ∼ | ∼ |
| (Air) | -, 19.5) | 0.235 | - | ∼ | ∼ | |||
| 1.170 | - | ∼ | ∼ | |||||
| 2.380 | - | ∼ | ∼ | |||||
| ∞ | - | ∼ | ∼ | |||||
| [47,48] | 43.5 | (3.4, 30.0, | 0.44 | (FD, TH) | 0.095 | 0.10 | 235 | 65 |
| (Air) | 20.0, -) | 0.159 | 0.47 | 663 | 310 | |||
| 0.168 | 0.30 | 401 | 197 | |||||
| 0.211 | 0.32 | 340 | 211 | |||||
| 0.270 | 0.30 | 248 | 197 | |||||
| 0.276 | 0.56 | 455 | 369 | |||||
| 0.333 | 0.37 | 248 | 244 | |||||
| 0.394 | 0.43 | 244 | 283 | |||||
| 0.419 | 0.73 | 401 | 494 | |||||
| 43.5 | 3.40 | 0.44 | (FD, TH) | 0.327 | 0.78 | 536 | 515 | |
| 1.101 | 0.78 | 159 | 515 | |||||
| 1.652 | 0.78 | 106 | 515 | |||||
| 2.824 | 0.78 | 62 | 515 | |||||
| 9.551 | 2.34 | 55 | 1545 | |||||
| [41,42] | 2.97 | (76.22, 157.01, | 0.30 | (TH, TH) | 1.49 | 30.00 | 101,056 | 260,003 |
| (Air) | -, 5) | 3.33 | 30.00 | 45,249 | 260,003 | |||
| [45] | 28.0 | (5.0, 40.0, | 0.56 | (FD, FD) | 0.025 | 0.22 | 2897 | 148 |
| (Air) | 30.0, -) | 0.074 | 0.22 | 951 | 148 | |||
| 0.155 | 0.61 | 1281 | 405 | |||||
| 1.017 | 0.61 | 193 | 405 | |||||
| [46] | 2.79 | (50.0, 100.0, | 0.30 | (TH, TH) | 0.2 | 2.09 | 34,500 | 6,210 |
| (Air) | -, 5) | 0.31 | 0.22 | 82,800 | 23,101 | |||
| 1.00 | 0.61 | 13,800 | 12,420 | |||||
| 3.00 | 0.61 | 6,900 | 18,630 | |||||
| 4.5 | 23.19 | 17,000 | 68,850 | |||||
| [43] | 5.98 | (16.1, 44.9, | 0.23 | (FD, FD) | 0.699 | 27.00 | 41,000 | 41,500 |
| (Air) | -, 5.5) | 1.033 | 30.45 | 31,300 | 46,800 | |||
| 1.59 | 38.32 | 25,600 | 58,900 | |||||
| [44] | 5.82 | (16.13, 44.5, | 0.24 | (FD, FD) | 1.61 | 42.75 | 27,800 | 66,400 |
| (Air) | -, 5.46) | 4.34 | 43.94 | 10,700 | 66,400 | |||
| ∞ | 42.75 | 0 | 64,600 |
| Ref. (Fluid) | [mm] | Shape(I, O) | [m/s] | Re | Re | Method | ||
|---|---|---|---|---|---|---|---|---|
| [7] | ∞ | 0, 13.8, - | (FD, | 5000 | HWA | |||
| (Air) | 89.58 | 1.45, 13.8,- | FD) | 5000 | ||||
| 7.16 | 4.83, 13.8, - | 5000 | ||||||
| 2.31 | 7.59, 13.8, - | 5000 | ||||||
| ∞ | 0, 13.8,- | (FD, | 25,000 | |||||
| 89.58 | 1.45, 13.8,- | FD) | 25,000 | |||||
| 7.16 | 4.83, 13.8,- | 25,000 | ||||||
| 2.31 | 7.59, 13.8,- | 25,000 | ||||||
| [57] | ∞ | 0, 8.5, - | (FD, | 10,000 | HWA | |||
| (Air) | FD) | 20,000 | ||||||
| 30,000 | ||||||||
| 3.00 | 4.25, 8.50,- | (FD, | 10,000 | |||||
| FD) | 20,000 | |||||||
| 20,000 | ||||||||
| [6] | 5.25 | 4, 10, 1 | (FD, | 0.06 | 3.79 | 15,747 | 1499 | DM |
| (Air) | FD) | 0.19 | 7.58 | 10,498 | 2999 | |||
| 0.57 | 11.37 | 5249 | 4499 | |||||
| [49] | 0.57 | 4.5, 10,- | (FD, | 0.58 | 36.74 | 18,626 | 43,865 | DM |
| (Air) | swirl) | 1.76 | 73.89 | 12,417 | 87,830 | |||
| 5.29 | 110.83 | 6208 | 131,596 | |||||
| [52] | 5.78 | 3, 14, 12 | (FD, | 0.13 | 8.14 | 12,417 | 1073 | DM |
| (Air) | Cone) | 0.38 | 16.28 | 8278 | 2147 | |||
| 1.16 | 24.41 | 4139 | 3220 | |||||
| [51] | 0, 17.8, - | 0 | 10.1 | 1.2 - | PIV | |||
| (Air) | 30.3 | 3.6 | ||||||
| 9.1, 17.8,- | ∞ | 27.6 | 1.6 - | |||||
| 84.5 | 4.9 | |||||||
| 12, 7, 17.8,- | ∞ | 70.6 | 2.4 - | |||||
| 211.8 | 7.2 | |||||||
| [50] | 7.13 | 4.84, 13.8, - | (swirl) | 1.00 | 10.98 | 3505 | 10,000 | N |
| (Air) | 0.66 | 10.98 | 5258 | 10,000 | ||||
| 1.00 | 27.46 | 8766 | 25,000 | |||||
| 0.66 | 27.46 | 13,150 | 25,000 | |||||
| 1.00 | 54.92 | 17,533 | 50,000 | |||||
| 0.66 | 54.92 | 26,300 | 50,000 |
| Reference (Fluid) | Surface Material | Thickness [mm] | Surface Position | BC | Method | |
|---|---|---|---|---|---|---|
| [7] (Air) | 4–12 | SS | 0.5 | Vertical | CT | TC |
| [57] (Air) | 1–10 | SS | 0.5 | Vertical | CT | TC |
| [6] | 0.5–6.0 | C | 1.5 | 0, 30, 60, 90 | CT | TC |
| (Air) | P-C | 5.0 | 0, 30, 60, 90 | |||
| [49] | 0.5–2.5 | C | 1.5 | 0, 30, 60, 90 | CT | TC |
| (Air) | P-C | 5.0 | 0, 30, 60, 90 | |||
| [52] (Air) | 0.5–6.0 | C | 1 | Horizontal | CT | TC |
| [51] (Air) | 2, 4, 6 | C | 50 | Horizontal | CT | TC |
| [50] (Air) | 0.5–8 | C | 0.5 | Horizontal | CT | N |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Hout, R.; Murugan, S.; Mitra, A.; Cukurel, B. Coaxial Circular Jets—A Review. Fluids 2021, 6, 147. https://doi.org/10.3390/fluids6040147
van Hout R, Murugan S, Mitra A, Cukurel B. Coaxial Circular Jets—A Review. Fluids. 2021; 6(4):147. https://doi.org/10.3390/fluids6040147
Chicago/Turabian Stylevan Hout, René, Sudharson Murugan, Abhijit Mitra, and Beni Cukurel. 2021. "Coaxial Circular Jets—A Review" Fluids 6, no. 4: 147. https://doi.org/10.3390/fluids6040147
APA Stylevan Hout, R., Murugan, S., Mitra, A., & Cukurel, B. (2021). Coaxial Circular Jets—A Review. Fluids, 6(4), 147. https://doi.org/10.3390/fluids6040147







