Numerical Simulation of Propagation and Run-Up of Long Waves in U-Shaped Bays
Abstract
1. Introduction
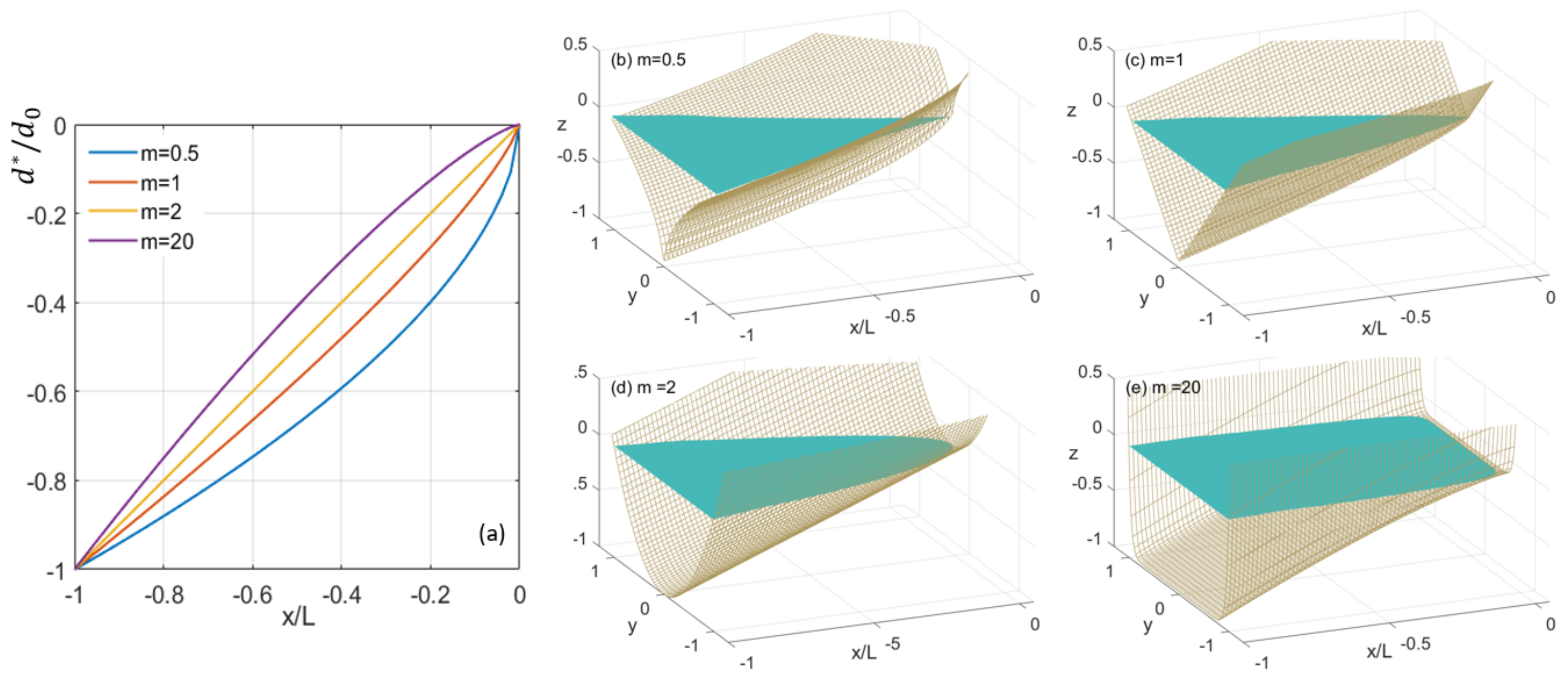
2. Saint-Venant Equations and the MCS Model
Numerical Methods
3. Propagation and Run-Up in Channel
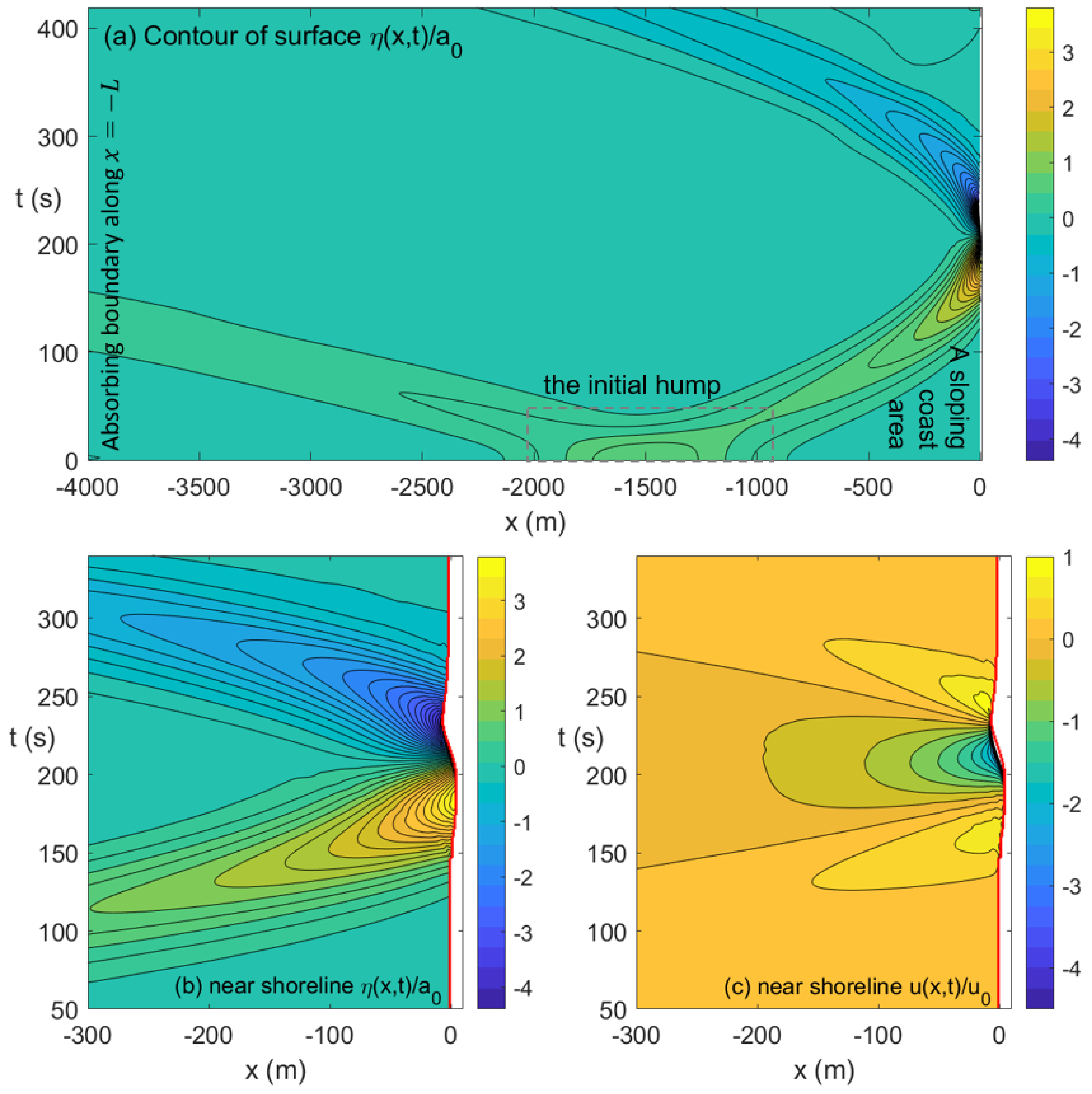
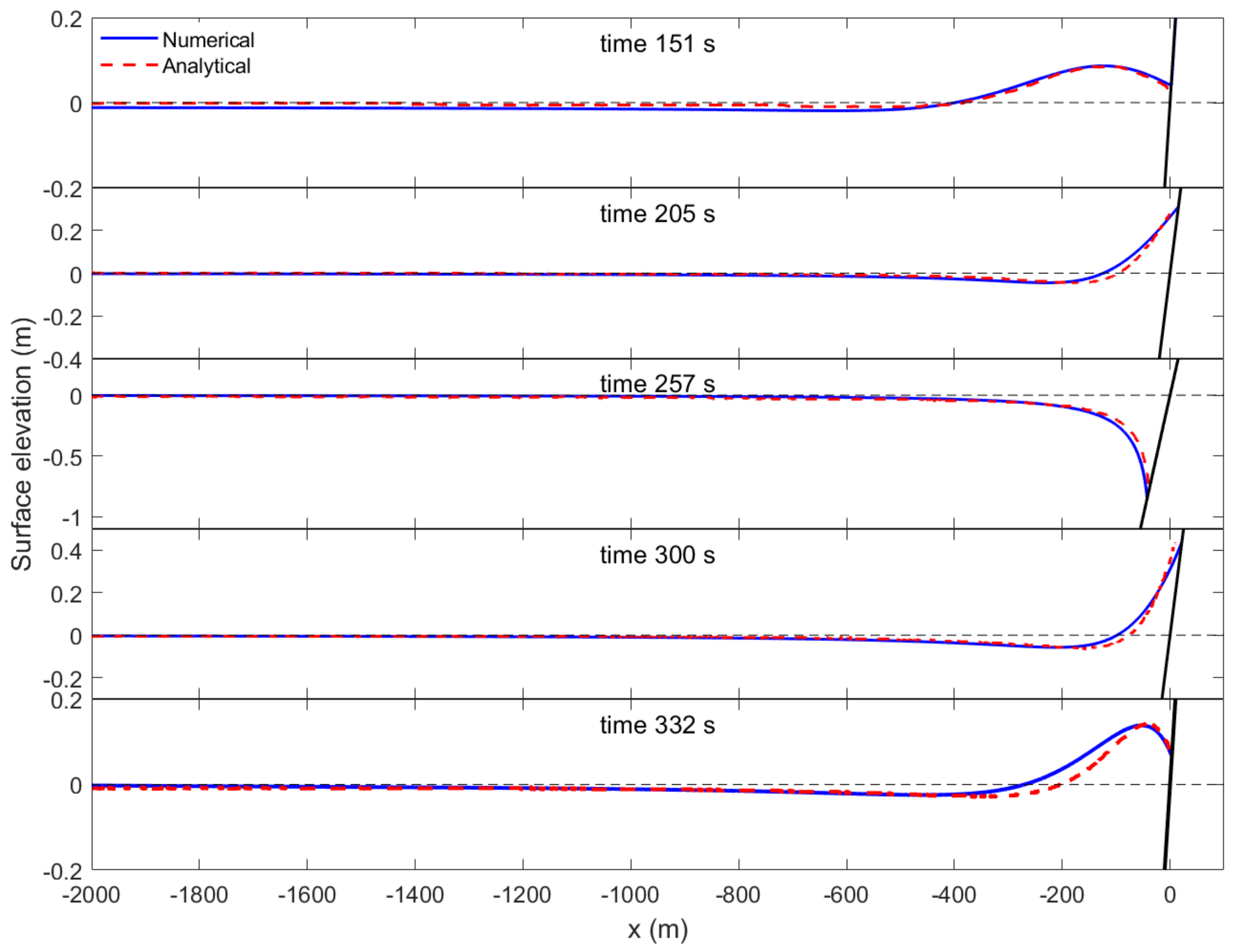
3.1. Simulation of an Initial Hump
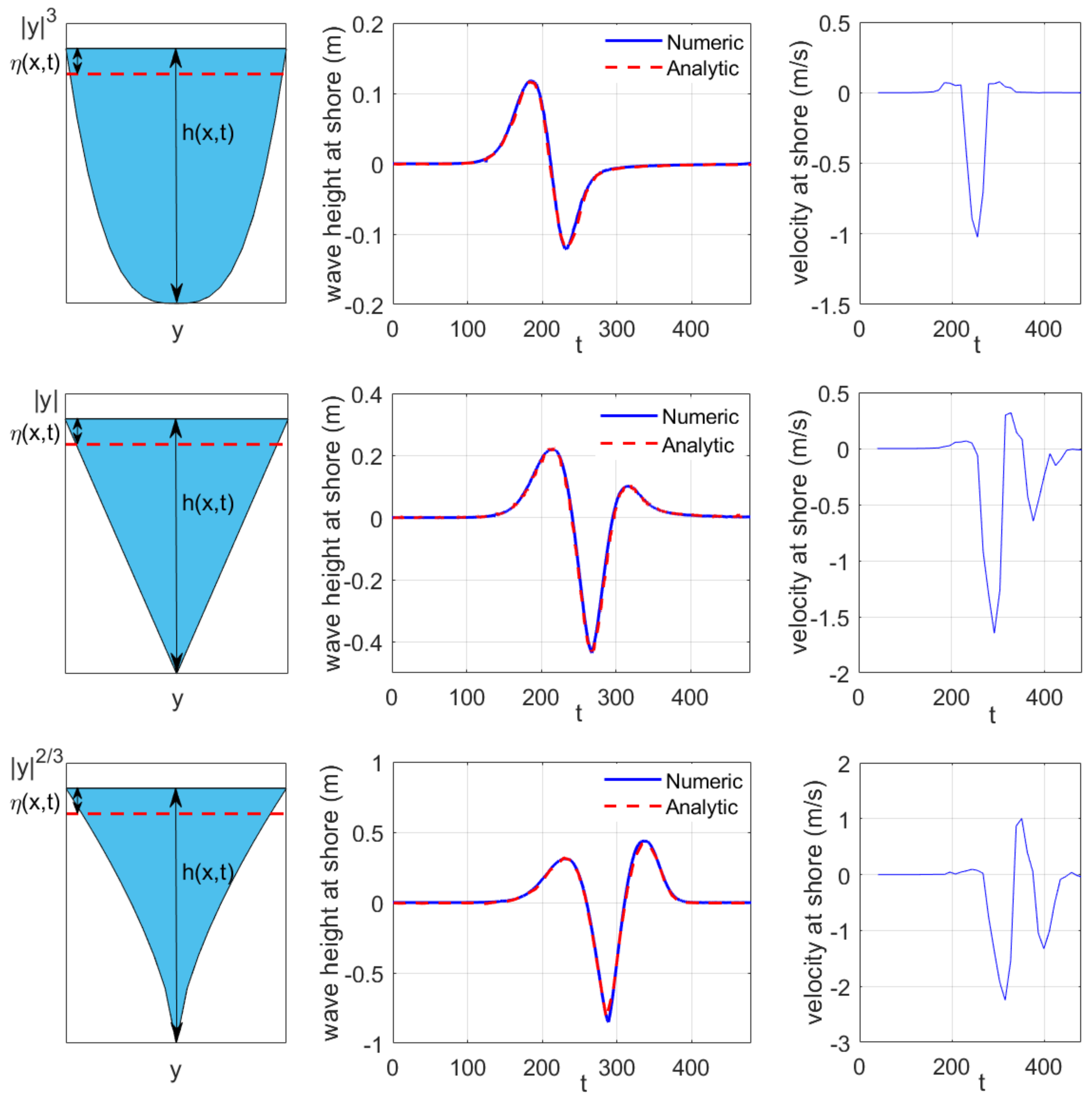
3.2. The Shoreline Dynamics
4. Propagation and Run-Up in Channel
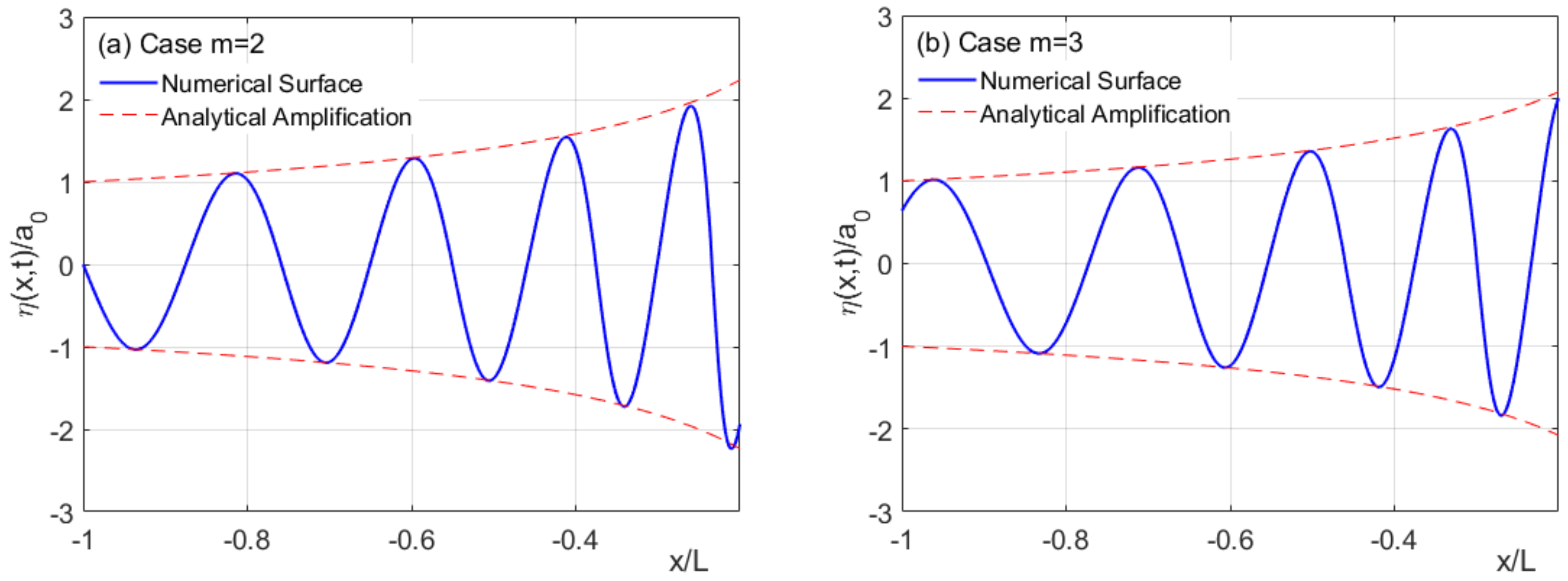
4.1. Shoaling and Run Up of a Monochromatic Wave
4.2. Run Up of a Solitary Hump
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| MCS | Momentum Conserving Staggered-grid |
References
- Bryant, E. Tsunami: The Underrated Hazard; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Frederik, M.C.; Adhitama, R.; Hananto, N.D.; Sahabuddin, S.; Irfan, M.; Moefti, O.; Putra, D.B.; Riyalda, B.F. First results of a bathymetric survey of Palu Bay, Central Sulawesi, Indonesia following the Tsunamigenic Earthquake of 28 September 2018. Pure Appl. Geophys. 2019, 176, 3277–3290. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Troshina, E. Propagation of long waves in straits. Phys. Oceanogr. 1994, 5, 43–48. [Google Scholar] [CrossRef]
- Didenkulova, I.; Pelinovsky, E. Non-dispersive traveling waves in inclined shallow water channels. Phys. Lett. A 2009, 373, 3883–3887. [Google Scholar] [CrossRef]
- Didenkulova, I.; Pelinovsky, E. Nonlinear wave evolution and runup in an inclined channel of a parabolic cross-section. Phys. Fluids 2011, 23, 086602. [Google Scholar] [CrossRef]
- Anderson, D.; Harris, M.; Hartle, H.; Nicolsky, D.; Pelinovsky, E.; Raz, A.; Rybkin, A. Run-up of long waves in piecewise sloping U-shaped bays. Pure Appl. Geophys. 2017, 174, 3185–3207. [Google Scholar] [CrossRef]
- Nesje, A.; Dahl, S.O.; Valen, V.; Øvstedal, J. Quaternary erosion in the Sognefjord drainage basin, western Norway. Geomorphology 1992, 5, 511–520. [Google Scholar] [CrossRef]
- Dartnell, P.; Normark, W.R.; Driscoll, N.W.; Babcock, J.M.; Gardner, J.V.; Kvitek, R.G.; Iampietro, P.J. Multibeam Bathymetry and Selected Perspective Views Offshore SAN Diego, California; Number 2959; US Geological Survey: Reston, VA, USA, 2007.
- Stoker, J. Water Waves; Interscience, Wiley: New York, NY, USA, 1957. [Google Scholar]
- Wu, Y.H.; Tian, J.W. Mathematical analysis of long-wave breaking on open channels with bottom friction. Ocean. Eng. 2000, 27, 187–201. [Google Scholar] [CrossRef]
- Golinko, V.; Osipenko, N.; Pelinovsky, E.; Zahibo, N. Tsunami wave runup on coasts of narrow bays. Int. J. Fluid Mech. Res. 2006, 33, 106–118. [Google Scholar]
- Choi, B.H.; Pelinovsky, E.; Kim, D.; Didenkulova, I.; Woo, S.B. Two-and three-dimensional computation of solitary wave runup on non-plane beach. Nonlinear Process. Geophys. 2008, 15, 489–502. [Google Scholar] [CrossRef]
- Harris, M.; Nicolsky, D.; Pelinovsky, E.; Rybkin, A. Runup of nonlinear long waves in trapezoidal bays: 1-D analytical theory and 2-D numerical computations. Pure Appl. Geophys. 2015, 172, 885–899. [Google Scholar] [CrossRef]
- Garayshin, V.; Harris, M.W.; Nicolsky, D.; Pelinovsky, E.; Rybkin, A. An analytical and numerical study of long wave run-up in U-shaped and V-shaped bays. Appl. Math. Comput. 2016, 279, 187–197. [Google Scholar] [CrossRef]
- Harris, M.; Nicolsky, D.; Pelinovsky, E.; Pender, J.; Rybkin, A. Run-up of nonlinear long waves in U-shaped bays of finite length: Analytical theory and numerical computations. J. Ocean. Eng. Mar. Energy 2016, 2, 113–127. [Google Scholar] [CrossRef]
- Didenkulova, I.; Pelinovsky, E. Runup of tsunami waves in U-shaped bays. Pure Appl. Geophys. 2011, 168, 1239–1249. [Google Scholar] [CrossRef]
- Garayshin, V.V. Tsunami Runup in U and V Shaped Bays. Ph.D. Thesis, University of Alaska Fairbanks, Fairbanks, AK, USA, 2013. [Google Scholar]
- Pudjaprasetya, S.; Magdalena, I. Momentum conservative scheme for dam break and wave run up simulations. East Asian J. Appl. Math. 2014, 4, 152–165. [Google Scholar] [CrossRef]
- Mungkasi, S.; Magdalena, I.; Pudjaprasetya, S.R.; Wiryanto, L.H.; Roberts, S.G. A staggered method for the shallow water equations involving varying channel width and topography. Int. J. Multiscale Comput. Eng. 2018, 16, 3. [Google Scholar] [CrossRef]
- Swastika, P.V.; Pudjaprasetya, S.R.; Wiryanto, L.H.; Hadiarti, R.N. A Momentum-Conserving Scheme for Flow Simulation in 1D Channel with Obstacle and Contraction. Fluids 2021, 6, 26. [Google Scholar] [CrossRef]
- Synolakis, C.E. The runup of solitary waves. J. Fluid Mech. 1987, 185, 523–545. [Google Scholar] [CrossRef]


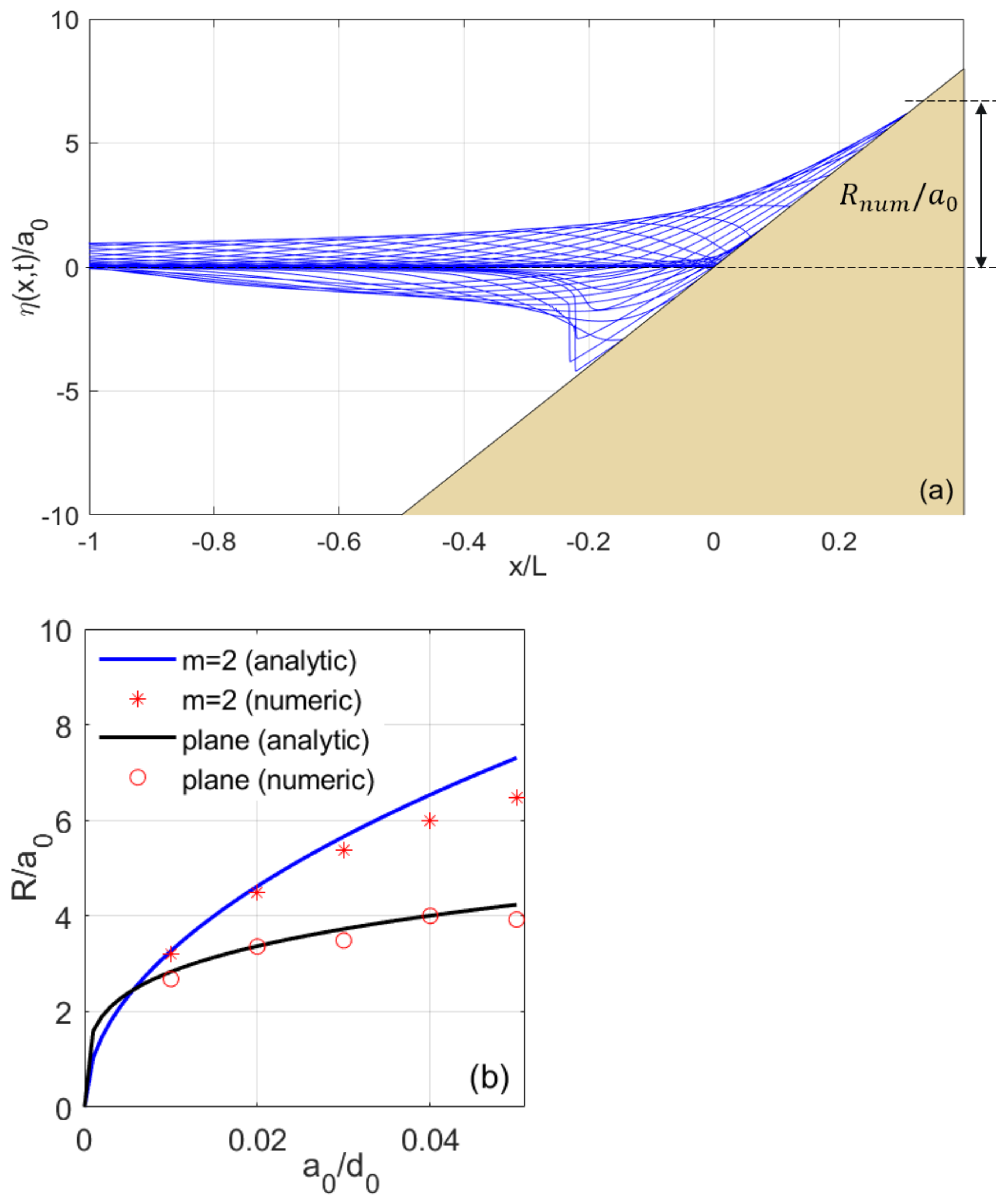
| Amplitude | Parabolic-Bay | Plane Beach | ||
|---|---|---|---|---|
| 0.01 | 3.20 | 3.27 | 2.71 | 2.83 |
| 0.02 | 4.50 | 4.62 | 3.36 | 3.37 |
| 0.03 | 5.40 | 5.66 | 3.78 | 3.73 |
| 0.04 | 6.00 | 6.53 | 4.00 | 4.00 |
| 0.05 | 6.48 | 7.30 | 3.93 | 4.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pudjaprasetya, S.R.; Risriani, V.M.; Iryanto. Numerical Simulation of Propagation and Run-Up of Long Waves in U-Shaped Bays. Fluids 2021, 6, 146. https://doi.org/10.3390/fluids6040146
Pudjaprasetya SR, Risriani VM, Iryanto. Numerical Simulation of Propagation and Run-Up of Long Waves in U-Shaped Bays. Fluids. 2021; 6(4):146. https://doi.org/10.3390/fluids6040146
Chicago/Turabian StylePudjaprasetya, Sri R., Vania M. Risriani, and Iryanto. 2021. "Numerical Simulation of Propagation and Run-Up of Long Waves in U-Shaped Bays" Fluids 6, no. 4: 146. https://doi.org/10.3390/fluids6040146
APA StylePudjaprasetya, S. R., Risriani, V. M., & Iryanto. (2021). Numerical Simulation of Propagation and Run-Up of Long Waves in U-Shaped Bays. Fluids, 6(4), 146. https://doi.org/10.3390/fluids6040146






