Abstract
Electro-osmotic flow, that is, the motion of a polar fluid in microducts induced by an external electric field, is one micro-effect which allows fluid circulation without the use of mechanical pumping. This is of interest in the thermal management of electronic devices, as microchannels with cross sections of almost arbitrary shape can easily be integrated on the chips. It is therefore important to assess how the geometry of the channel influences the heat transfer performance. In this paper, the thermal entry region and the fully developed electro-osmotic flow in a microchannel of rectangular cross section with smoothed corners is investigated for uniform wall temperature. For the fully developed region, correlations for the Poiseuille and Nusselt numbers considering the aspect ratio and nondimensional smoothing radius are given, which can be used for practical design purposes. For thermally developing flow, it is highlighted how smoothing the corners increases the value of the local Nusselt number, with increases up to 18% over sharp corners, but that it also shortens the thermal entry length. It is also found that Joule heating in the fluid may cause a reversal of the heat flux, and that the thermal entry length has a linear dependence on the Reynolds number and the hydraulic diameter and on the logarithm of the nondimensional Joule heating.
1. Introduction
Fundamental research on microchannels has given rise to a vast body of studies ever since the seminal work by Tuckerman and Pease almost four decades ago [1]. Knowledge acquired over the years allowed microchannels to establish themselves as the building blocks of so-called micro-flow devices (MFDs), as can be realized by comparing older reviews on the subject [2,3], to more recent ones [4,5,6], a fact also recognized by the Tuckerman and Pease themselves in a retrospective article published in 2012 [7].
Currently, there is still an amount of research addressing fundamental subjects [8,9,10,11,12,13,14,15,16], but MFDs have now found applications in several fields [17], e.g., micro heat exchangers (MHXs) are employed in air conditioning systems [18] and heat pumping equipment [19]. The use of microjets and two-phase flow as cooling means has been investigated and applied too [20,21,22]. Microchannel heat sinks, a subset of MHXs, have great applicative potential where removal of high heat fluxes is in demand. This makes them particularly interesting for the thermal management of electronic devices, which are steadily growing in compactness and, as a consequence, in power density. Pressure drop across such devices, however, may be significant, especially when liquids are employed as coolants, with the reduction in hydraulic diameter of the ducts quickly leading to viscous heating of the fluid circulated [23] which reverses the direction of the heat flow.
At small scales, however, flow devices can exploit micro-effects such as electro-osmosis, which allows the motion of a liquid relative to a charged surface, induced by an applied external potential gradient across a microchannel [24,25]. If a polar fluid is used in combination with channel walls possessing a net electrical charge, an inhomogeneous charge distribution develops in the liquid, which can be moved by applying electric field over the length of the channel, which acts on the layer of mobile ions close to the walls: the flow which originates is called electro-osmotic (EOF). EOF devices have several advantages: they do not have moving parts, are therefore free of noise and vibrations and no lubrication is needed. Furthermore, liquid reservoirs require tiny volumes, making them ideal for direct connection to the chips. EOFs have been reported to yield experimental Nusselt numbers about larger than pressure-driven flow (PDF) for the same geometry, although Joule heating may become significant when applied voltage between the electrodes increases beyond a certain threshold [26]. Voltage signals sent to electrodes make implementation of EOF devices easier than manufacturing and controlling a micro mechanical pump. Among the drawbacks, the chemical composition at the interface can significantly alter the velocity profiles, which are markedly different from those exhibited by pressure-driven flows, and Joule heating in the fluid may partly or completely offset its cooling action [24]. Electro-osmotic flows in microchannels have been the subject of several fundamental investigations, for a variety of cross sections, ranging from the common circular ducts and parallel plates [27,28], to unusual geometries such as polygonal, elliptical and triangular ducts [29,30,31], as has been the use of electro-osmotic pumps (EOPs) [26,32,33], sometimes with the specific purpose of electronics cooling [26,34,35]. The use of non-Newtonian fluids [36,37] and nanofluids [38] is also a recent field of investigation.
The brief overview above reveals how research on electro-osmotic flow in microchannels has been very active in the recent past, touching on a variety of subjects such as the fluids employed, the electric field magnitude, the presence of the pressure gradient, and the shape of cross section, which can take several forms (circular, trapezoidal, rectangular, etc.) thanks to the current development of micro-fabrication technologies. Optimization of the cross section can lead to improved performance in terms of increased heat transfer and decreased pressure drop and entropy production, and this can be achieved through smoothing of its corners, as demonstrated in [39,40]. Investigation has been extended to pressure-driven flows in microchannels with and without viscous dissipation [41,42,43], and to electro-osmotic flows in the fully developed and constant heat flux and perimeter temperature case [44,45], employing the results to carry out a first-law analysis based on performance evaluation criteria (PEC) [46].
To the best of the Authors’ knowledge, no attempt has been made so far to analyze EOFs in the thermal entry region (the so-called Graetz problem) of a microchannel of rectangular cross section with smoothed corners; therefore, this work aims at filling this gap for the case of uniform temperature of the channel walls, so-called T boundary condition [47]. The fully developed case is also studied in order to provide correlations of practical use for the Poiseuille and Nusselt numbers as a function of both the aspect ratio and the nondimensional radius of curvature, .
The influence of and on the nondimensional thermal entry length is also investigated, as is the dependence of the latter on quantities such as Joule heating, hydraulic diameter, and Reynolds and Peclet numbers. The aim is both to deepen the fundamental understanding of the phenomenon and to gain insights of practical applicability to such devices as heat sinks and micropumps.
The results are also useful for the purpose of conducting optimization studies, e.g., using PEC-type approaches.
2. Mathematical Model
This section reports the nondimensional forms of the governing equations for the electric potential, velocity, and temperature fields and the boundary conditions which are used to solve the problem; the dimensional forms and the normalizing quantities used to obtain them are reported in Appendix A. The equations are written for a Cartesian coordinate system, which has x as the axial coordinate (flow direction), while y and z are the coordinates of the cross section (orthogonal to flow direction), as illustrated in Figure 1.
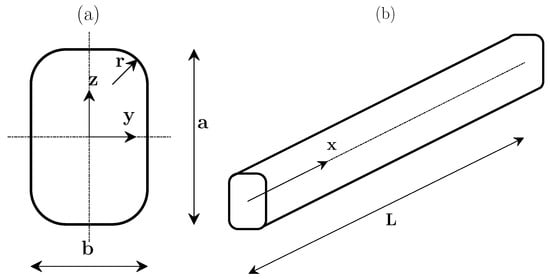
Figure 1.
Channel cross section geometry (a), channel axis (b), and reference Cartesian coordinate system (a,b).
2.1. Electric Potential Field
The nondimensional formulation of the equation governing the electric potential distribution is shown below,
where is the Debye–Hückel parameter (m):
The value of the potential at the Stern plane is used as a boundary condition over the channel wall:
As T-boundary conditions are applied to the temperature field, the nondimensional electric potential , the Debye–Hückel parameter , and the nondimensional Stern potential , Equations (2) and (3) are defined with respect to the imposed wall temperature , which is chosen as the characteristic temperature. Accordingly, variations of and, subsequently, of the inlet temperature of the fluid, , when the temperature drop is fixed, determine the range of values taken by the Debye–Hückel parameter in this work.
2.2. Velocity Field
A steady, hydrodynamically developed laminar flow of a Newtonian, incompressible fluid with uniform thermophysical properties through a microchannel of uniform cross section with rigid, non-porous wall is considered.
Starting from the governing equation and introducing suitable normalising quantities, as reported in Appendix A.2, the component along x axis of Equation (A5) can be written in nondimensional form:
The no-slip boundary condition is imposed through the solid wall, . The only velocity component in the case of fully-developed flow is along the X direction; therefore, equations for the other two velocity components are not shown.
Once the velocity field is computed, the corresponding Poiseuille number can be estimated, details are given in Appendix A.2.
2.3. Temperature Field
The nondimensional temperature distribution is obtained from the solution of the nondimensional energy equation below,
where is the Prandtl number of the fluid, while and are the nondimensional bulk velocity and the Reynolds number,
with the dimensional bulk velocity.
The temperature is imposed (T-boundary conditions) through the channel wall, and a uniform temperature profile is chosen over the inlet section of the channel:
The choice of the boundary conditions imposed to the temperature field through the inlet section will be discussed further in Section 3.
Once the temperature field is computed, the average Nusselt number along channel axis can be estimated, as explained in Appendix A.3.
3. Materials and Methods
3.1. Numerical Modeling
The numerical solution of the governing equations—Equations (1), (4) and (5)—was obtained using the open source software GNU Octave. Additional libraries, provided by Octave Forge, were used: the msh package, which relies on the open source software gmsh, allows to generate triangular and tetrahedral unstructured meshes for Finite Element Method (FEM) or Finite Volume Method (FVM) solvers, and the bim package, which implements both the Finite Volume Scharfetter–Gummel (FVSG) method and the Finite Element Method (FEM), allows to solve Diffusion Advection Reaction (DAV) partial differential equations. The functions bim2a_laplacian, bim2a_reaction, and bim2a_rhs belonging to bim library allow to assemble the finite element discretised operators for solving partial differential equations of the form
on a two-dimensional (2D) unstructured, triangular mesh.
The 2D computational domain, consisting of the channel cross section geometry, is discretized through gmsh software, using a triangular mesh with increased accuracy imposed close to the cross section perimeter, where higher gradients for both the electric potential and the velocity fields are expected. Equation (1) is numerically solved first over the 2D mesh of the channel cross section to compute the electric potential . In order to reduce Equation (1) to the same form of Equation (8), linearization of the reaction term, , is carried out using a first-order Taylor polynomial and the numerical solution of Equation (1) is iterated until convergence of the electric potential field is obtained. Then, the numerical solution of Equation (4), which requires the knowledge of , is computed and the developed velocity field is solved over the channel cross section.
As the energy equation, Equation (5), has the form of a parabolic partial differential equation, the three-dimensional physical problem can be reduced to a 2D mathematical problem. Implementing the weighted scheme for marching over channel axis, Equation (5) is discretized as
where n denotes the integration step along the channel axis. At each step n, Equation (9), which has the same form as Equation (8), is numerically solved over the 2D mesh of the channel cross section through bim library functions.
3.2. Problem Setup
The electro-osmotic flow over a channel of length L with constant cross section is investigated. The geometrical configuration, defined by a rectangular cross section with rounded corners as shown in Figure 1, is characterized by the aspect ratio and the nondimensional smoothing radius . The corresponding hydraulic diameter can be calculated as a function of the length of the longer side, a, and of the nondimensional parameters and :
Taking advantage of the problem symmetry, only one-quarter of the whole channel section is investigated, in order to reduce the computational cost of simulations, and symmetry conditions are imposed through the lines and ,
Dirichlet boundary conditions are imposed along the heated perimeter ,
which correspond to imposed Stern potential, no-slip condition, and prescribed wall temperature respectively. In addition, an inlet temperature profile must be imposed in order to solve the energy equation, Equation (5). As pointed out in [48,49], when a heat source is present, an adiabatic preparation of the fluid (at least over the hydrodynamically developing region) should be provided in order to ensure physical consistency of the boundary conditions at . Yet, under certain flow conditions the increase in the bulk temperature due to Joule heating over the adiabatic section can be neglected if compared to the prescribed temperature difference between wall and inlet. This makes the uniform inlet temperature profile a still consistent approximation. In fact, writing the macroscopic energy balance over the adiabatic section,
and assuming that equals the hydrodynamically developing length, , the increment reduces to
If water at ambient temperature is considered, i.e., , is ensured for , which corresponds to the maximum value of the heat source investigated in this paper.
The Graetz problem for an electro-osmotic flow, which consists of the numerical solution of Equations (1), (4) and (5) with the prescribed boundary conditions, is defined by the following parameters:
- aspect ratio of the channel cross section;
- nondimensional smoothing radius ;
- nondimensional Stern potential ;
- nondimensional parameter , defined by Equation (2), which affects the electric potential field;
- nondimensional electric field , which causes fluid motion;
- nondimensional heat source Q due to Joule heating; and
- reference Peclet number,where is the reference velocity, calculated through Equation (A6).
Note that the reference Peclet number is not fully representative of the flow characteristics. The effective value of the Peclet number,
is verified a posteriori to vary in the range ; this makes the assumption of negligible axial conduction a consistent approximation.
3.3. Grid Independence Analysis
A grid independence analysis (GDA) was also conducted before running several parametric computations. Excluding simulations involving model verification and comparison with literature results, the values of the Debye–Hückel parameter and the nondimensional Stern potential were set to and respectively for most of the parametric computations. As mentioned at the end of Section 2.1, these are determined by the choice of the wall and fluid inlet temperatures; the remaining quantities which compose the Debye–Hückel parameter and the Stern potential have the values of deionized, ultra-filtered water, and are often adopted in the literature [28,30,31,32,33,44,45,50]. The highest values were considered for the GDA, while the channel cross section aspect ratio and the smoothing radius were set to and .
Equations (3), (4) and (A15) were numerically solved for increasing mesh accuracy, which is defined by the imposed grid spacing parameter . Both the Poiseuille and Nusselt numbers of the fully developed flow were computed through Equations (A7) and (A14). Results are listed in Table 1, where the corresponding numbers of mesh nodes and triangular elements are also reported, and are plotted in Figure 2. As a discrepancy of less than 0.35 was observed for reducing from to , a value of was chosen for all the numerical computations. Figure 2 also shows the triangular mesh, generated through the gmsh software, for : it can be noticed that mesh refinement occurs along the heated perimeter, where higher gradients of the electric potential , velocity and developed temperature fields are expected.

Table 1.
Computed Poiseuille number and Nusselt number for different values of mesh accuracy, number of nodes , and number of triangular elements . , , , .
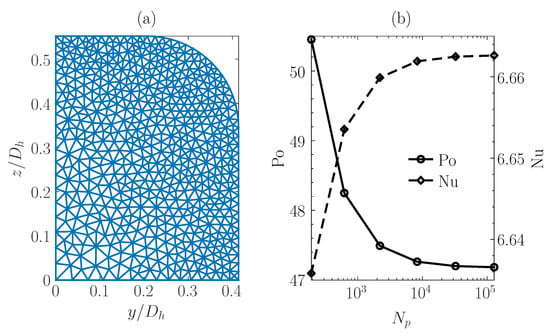
Figure 2.
Triangular mesh for (a). Computed Poiseuille number and Nusselt number for increasing mesh accuracy (b). , , , .
4. Results and Discussion
4.1. Model Validation
Comparison with numerical results in the literature was first conducted in order to check the numerical solution of both the Poisson–Boltzmann equation and the momentum equation, Equations (1) and (4), which were both numerically solved in [45] by means of COMSOL Multiphysics®. Considering the same test case as in [45], and , several geometrical configurations were simulated and the corresponding Poiseuille number computed. As high gradients , due to the high Stern potential, were expected close to the channel wall, the grid spacing parameter was set to , leading to meshes with more than nodes. A good agreement with the numerical results of [45] can be observed in Table 2, with differences below on the computed Poiseuille number always obtained.

Table 2.
Literature vs. computed values of Poiseuille number for different cross-sectional geometries. , .
The electric potential field was also qualitatively verified with the analytical solution, which is available in the limiting case of a cylindrical duct for Stern potential approaching zero. Solving the axisymmetric Poisson–Boltzmann equation under Debye–Hückel linearization, i.e., , gives [51],
where is the nondimensional radial coordinate; and are the first and second kind of modified Bessel functions; and and are constants defined by the boundary conditions imposed.
As a fully developed flow subject to H-boundary condition was investigated in [45], comparison was not possible. However, the developed temperature field under T-boundary condition was quantitatively verified with the analytical solution available for a cylindrical duct. Solving the axisymmetric energy equation for a fully developed flow under T-boundary conditions gives the analytical temperature profile,
where R is the nondimensional radial coordinate.
Both normalized, numerical electric potential profiles for different values of the imposed Stern potential and normalized, analytical electric potential, valid in the limit of approaching zero, are plotted in Figure 3 over the cylindrical cross section: note that the numerical profile approaches the analytical one when low values of are imposed. The numerical velocity profiles for different values of are shown in Figure 3: as mentioned, the higher the value of the Stern potential, the higher the velocity gradient close to the channel wall, resulting in a flow pattern similar to plug flow. The developed temperature profile, which is also shown in Figure 3 and does not depend on the velocity profile, was computed both via the numerical solution of Equation (A15) and as the asymptotic behavior for from the solution of Equation (5). Thus, the numerical temperature profile was quantitatively verified with the analytical solution, Equation (19), computing the mean squared error (MSE) at mesh nodes,
showing perfect agreement.
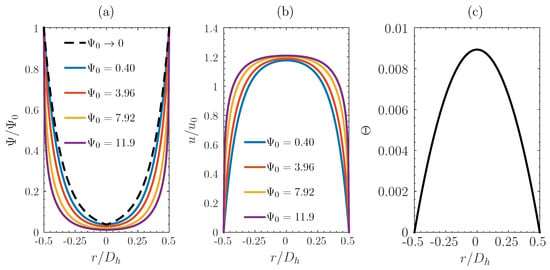
Figure 3.
Computed electric potential for different values of the nondimensional Stern potential and analytical electric potential for approaching zero (a); numerical velocity profile computed for different values of the (b); numerical temperature profile (c). , , , .
The numerical model was also validated with experimental results from the literature. First, the test case of [52] is replicated. Thus, the bulk flow velocity of an EOF is numerically computed and compared with experimental data of [52], where the Authors used nanoparticle image velocimetry technique to measure the mean EOF velocity over 4.9–24.7 m thick channels. The physical properties of a dilute aqueous solution of sodium tetraborate (borax) were chosen according to the method in [52]. The potential required for the boundary condition on the potential field is derived from the experimental values of the mobility factor via the Helmholtz–Smoluchowski formula:
In Figure 4a, numerical results are compared with the experimental data in [52], showing a good agreement for all the concentrations investigated. A small discrepancy is observed at higher values of the electric field, since a linear relationship between bulk velocity and electric field is predicted by the numerical model. However, a linear relationship was also reported according to [26].
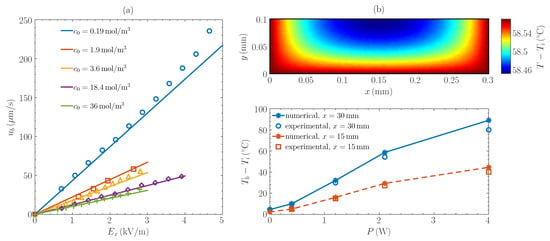
Figure 4.
Numerical bulk velocity (continuous line) versus experimental measurements (markers) of [52] for different borax concentrations and imposed electric fields (a). Numerical versus experimental [26] bulk temperature as a function of heating power at both the middle section and the outlet section of the microchannel (computed, outlet temperature profile for heating power equal to is also shown) (b). Dilute aqueous solution of sodium tetraborate (borax) investigated.
In order to validate the temperature field solution, the experimental setup in [26] was also simulated. In [26], the Authors manufactured and tested a micro-heat sink with the cooling fluid serving both as a heat exchanger and an integrated pump. Twenty parallel microchannels were etched on a silicon substrate and covered by a low thermal conductivity PDMS plate. A heater was attached to the bottom. The borax concentration was set to 0.4 mol/m, different values of the voltage driving the EOF were imposed and heating powers up to 4 W were investigated in [26]. Equations (1), (4) and (5) were therefore numerically solved and the resulting bulk temperature at both the middle section (x = 1.5 cm) and the outlet section (x = 3 cm) compared with the experimental data of [26], for different values of the imposed heating power. The required wall potential was again estimated through Equation (21). Adiabatic conditions were imposed at the channel wall facing the PDMS cover, whilst H1 thermal boundary conditions were applied to the heated perimeter. The required heat flux per unit length was derived from the data supplied in [26]. The electric field was set to . As shown by Figure 4b, numerical temperatures are in good agreement with experimental measurements over the whole heating power range, with a perfect matching observed when the heater is switched off (temperature rise along the channel due solely to Joule heating). The resulting temperature profile through the outlet section is also provided by Figure 4b.
4.2. Fully Developed Flow Solution
After validation, parametric computations were run, in order to investigate the effect of the cross section geometry on the thermal-hydraulic performances of the microchannel. The case of fully developed electro-osmotic flow, defined by Equations (1), (4) and (A15), was first studied. Several values of both the aspect ratio (, , , , , , , , , , 1) and the smoothing radius (, , , , , , , , , , , 1) were investigated, while the nondimensional Debye–Hückel parameter was set to according to [45,50], and the nondimensional Stern potential to , which is roughly half the value analyzed in [45]. Note that the magnitude of both the electric field and the heat heat source Q do not affect the Poiseuille number and the developed Nusselt number. This is because the velocity and the temperature fields are scaled by changing and , but retain the same shape.
The electric potential field , the developed velocity field U and the developed temperature field resulting from a single computation are shown in Figure 5. As pointed out for the cylindrical duct case, significant gradients of both the electric potential and the velocity can be observed close to the cross section wall. The magnitude of both U and linearly depends on the imposed values of and Q. The local Nusselt number was also numerically estimated as
over the heated perimeter of the cross section, . As demonstrated by Figure 6, the highest temperature gradient occurs at the midpoint of the longer side of the rectangular section, whereas smoother slopes are observed close to the rounded corners. Averaging the local Nusselt number along the heated perimeter leads to the mean Nusselt number , which can be computed through Equation (A14).
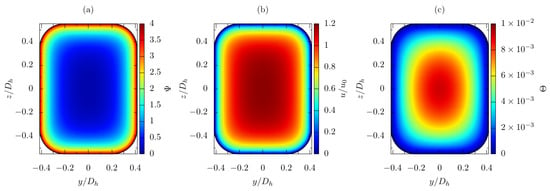
Figure 5.
Electric potential field (a). Developed velocity field (b). Developed temperature field (c). , , , , , .
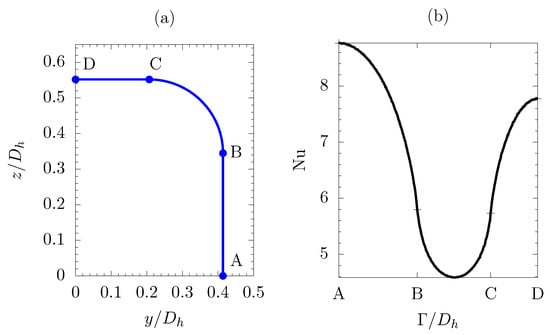
Figure 6.
Cross section geometry (a). Local Nusselt number of the fully developed flow along the heated perimeter (b). , , , .
The results from 110 computations are shown in Figure 7, where the computed Poiseuille and Nusselt numbers are plotted as a function of the channel section geometry, defined by and . The highest values for both and were found at and , whilst the minimum , corresponding to highest efficiency of the micropump, was found for and . Following the approach in [45], the trends of and can be approximated, for a given aspect ratio, via a polynomial correlation as a function of the smoothing radius. However, a single, 3rd-order polynomial correlation taking into account the influence of both and is provided here for and :
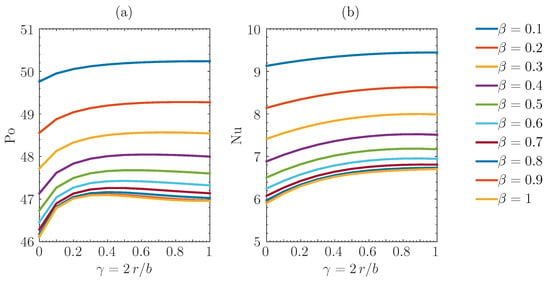
Figure 7.
Poiseuille number as a function of the cross-sectional geometry (a). Nusselt number as a function of the cross-sectional geometry (b). , .
The corresponding fitting coefficients are listed in Table 3. The Root Mean Square Error, also listed in Table 3, demonstrates that an accurate estimate of both and is ensured.

Table 3.
Fitting coefficients of Equations (23) and () for the estimation of the Nusselt and Poiseuille numbers of a fully developed flow and Root Mean Square Error from 110 numerical points.
4.3. Graetz Problem Solution
Finally, the Graetz problem, defined by Equations (1), (4) and (5), was solved, in order to determine the thermal entry length under different operating conditions. The aspect ratio was fixed to and four different, nondimensional radii of curvature, namely, , , , 1 were investigated. The Debye–Hückel parameter and the nondimensional Stern potential were set to and respectively. The nondimensional electric field and the reference Peclet number were and . The effect of changing the heat source due to Joule heating, Q, was investigated: several values ranging between and 10 were simulated and the influence on the thermal entry length assessed. Note that a variation of the heat source Q at fixed , , and , which are the other model input parameters, can be physically obtained varying the reference temperature difference and the electric conductivity (so that is unaffected).
The resulting temperature profile over the channel sections corresponding to , and is shown in Figure 8 for a computation at very high heat generation () and low electric field (). Even if the fully developed temperature profile is reached shortly after the channel entrance because of the high value of Q, important considerations can be made:
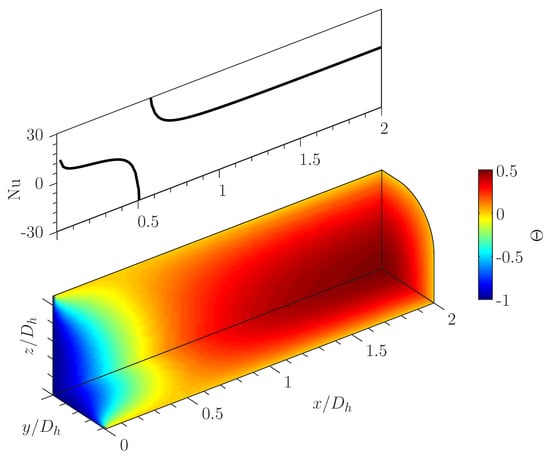
Figure 8.
Temperature field over , , and sections of the channel and average Nusselt number along the channel axis. , , , , , , .
- close to the entry section, the contribution of Joule heating is still negligible and the heat transfer process is mainly driven by conduction and convection, which is the most profitable operating condition for a microchannel heat sink;
- looking at the mean Nusselt number along the channel axis in Figure 8, a vertical asymptote at is observed, corresponding to the change in sign of the fluid bulk temperature;
- for , the heat generation due to Joule heating drives the heat transfer process and the microchannel heat sink is no longer able to dissipate heat from the walls; and
- the thermal entry length is reached at .
Assessing the existence of a change in the direction of heat transfer is obviously important in practical applications, but knowledge of the extension of the thermal entry length is also useful. In fact, if occupies a significant portion of the channel, correlations for the Nusselt number that assume fully developed flow cannot be recommended. Therefore, the rest of the section is devoted to the investigation of .
Results from parametric computations are shown in Figure 9, where the thermal entry length is plotted as a function of the nondimensional source term Q and the smoothing radius . It can be pointed out that decreases for increasing Joule heating following a logarithmic behavior, when the other model input parameters (namely, , , , ) are fixed:
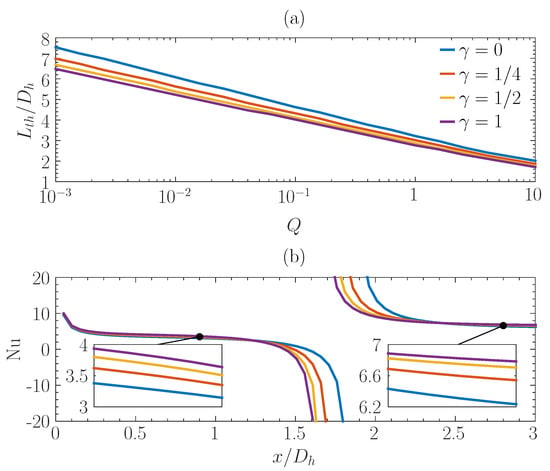
Figure 9.
Thermal entry length as a function of nondimensional heat source, due to Joule heating, and smoothing radius (a); mean Nusselt number along channel axis for different smoothing radii (legend same as subfigure (a) above), (b). , , , , .
The mean Nusselt number along channel axis is also plotted in Figure 9 for different and fixed , showing that
- smoothing the corners shortens the thermal entry length, and, as a consequence, the efficacious channel length (i.e., useful to remove heat from the walls) at high Joule heating, that is for high values of Q;
- heat transfer performance decreases when sharp corners are considered, since lower temperature gradients are observed close to them, meaning that lower Nusselt numbers over the entry region are reached. As an example, in Figure 9 for Nu goes from 3.95 for (maximum smoothing) to 3.38 for (sharp corners);
- small changes in correspond to significant variations of at different values of the smoothing radius .
In order to extend the study to a wider range of practical applications, the analysis is expanded to different hydraulic diameters of the channel cross section. Thus, the nondimensional input parameters of the model are scaled with the hydraulic diameter according to their definitions:
Starting from the set of input parameters investigated and fixing the cross section geometry to and , computations are run at increasing hydraulic diameters. Thus, beginning at , the hydraulic diameter is progressively increased up to 15 , which corresponds to an increase of the nondimensional Debye–Hückel parameter from to . Three different values of the nondimensional heat source, , , and , are chosen. Both the thermal entry length and the Reynolds number, the latter resulting from velocity field solution and depending on the imposed hydraulic diameter as well, are computed. Results are plotted in Figure 10.
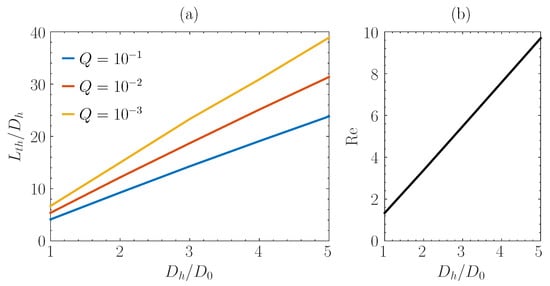
Figure 10.
Thermal entry length as a function of the normalized hydraulic diameter (a); hydraulic diameter versus Reynolds number (b). , , , , , .
The nondimensional thermal entry length linearly depends on the hydraulic diameter, with values up to observed when approaches 5. This trend can be easily explained looking at Equation (5): the advection term is proportional to and , both acting as a scaling parameter for the temperature field evolution along the channel axis, as long as Q is kept constant. On the other hand, this means that weakly depends on the shape of the normalized velocity profile , which tends to plug flow for increasing but does not modify the linear correlation between and . As discussed earlier for Figure 9, the lower the magnitude of heat source term Q, the longer the nondimensional thermal entry region . The dependence of the Reynolds number on is also reported in Figure 10, and is clearly linear. As the magnitude of the dimensional bulk velocity mainly depends on the imposed electric field and the Stern potential but weakly on the hydraulic diameter, as long as , the product of the Prandtl number, which depends on fluid properties, times the Reynolds number is simply proportional to the hydraulic diameter. As a consequence, it can be stated that the nondimensional length of the thermal entry region linearly depends on the normalized hydraulic diameter too.
The influence of wall temperature, which was chosen as the characteristic fluid temperature, was also investigated. Therefore, was varied between 20 and 100 C and three different values were again considered for the nondimensional heating source, , , and . The channel section geometry, the wall potential and the nondimensional electric field were set to , , , and . As the fluid properties depend on temperature, both the Prandtl number and the Reynolds number depend on the imposed , as demonstrated by Figure 11b. On the other hand, a change in the absolute fluid temperature also influences the Debye–Hückel parameter. In fact, in the range investigated, 20–100 C, a deviation of about from the reference value of is observed.
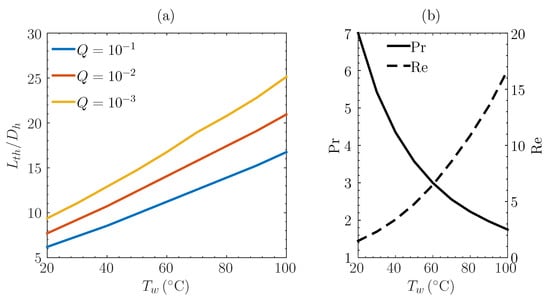
Figure 11.
Thermal entry length as a function of wall temperature (a); variation of Prandtl and Reynolds numbers with the imposed wall temperature (b). , , , .
Figure 11a shows the dependence of the nondimensional thermal entry length on the imposed wall temperature. In accordance with , increases slightly nonlinearly with the imposed temperature : this is readily explained if one considers that the kinematic viscosity in the expressions of the Prandtl and Reynolds numbers cancel out.
5. Conclusions
Although not the main focus of the paper, the fully developed EOF under uniform wall temperature was first investigated for channels with sharp and smoothed corners and rectangular cross sections, after validation with two different experimental works and verification with analytical and numerical cases. The numerical findings highlighted that smoothing increases both the Poiseuille and Nusselt numbers, i.e., friction and heat transfer, respectively. Two correlations which capture simultaneously the influence of the nondimensional aspect ratio and radius of curvature on and were obtained. These are recommended for design purposes, when the flow can be considered as fully developed for most of the channel length. It was also highlighted that neither the magnitude of (nondimensional electric field) nor Q (nondimensional Joule heating) influence the form of the velocity and temperature profiles. Similar results have not been previously reported in the literature, to the best of the Authors’ knowledge.
The Graetz problem under T boundary condition was then investigated, using input parameters representative of practical applications, such as micropumps and micro heat sinks. This subject is even less explored, owing to the experimental difficulties in obtaining temperature distribution in the fluid and at the walls of the channels. Numerical studies also appear to be limited to fully-developed cases and very few are concerned with channels with smoothed corners. The investigation highlighted that high values of Q cause a reversal in the direction of the heat flux, which renders the channel unfit for its purpose. An estimate of the usable channel length under such circumstances was also provided via the solution of the temperature field over the thermal entry region under different operating conditions.
It was then demonstrated that smoothing the corners shortens , which may significantly reduce the usable length of the channel as well, but the Nusselt number in the entry region increases with the radius of curvature. It can therefore be concluded that, when Q is sufficiently low that no heat flux reversal occurs in the channel, smoothing the corners increases the Nusselt number (for the cases investigated an improvement up to around was achieved).
Finally, the thermal entry length was analyzed for different values of the model input parameters. The magnitude of the heat source term and of the variation in hydraulic diameter were investigated, with a wide range of operating conditions covered, and it was found that the nondimensional thermal entry length decreases linearly with the logarithm of Q, while scaling linearly to . The dependence of on the Reynolds and Prandtl numbers was also studied. If the Prandtl number is constant, the thermal entry length is proportional to the Reynolds number; when both vary because of changes in the reference temperature, slightly deviates from proportionality to because of the dependence of thermal diffusivity on temperature, whereas the kinematic viscosity cancels out.
The results presented are crucial for the design of microchannel heat sinks working with an electro-osmotic flow; moreover, knowledge of the Poiseuille number and Nusselt number over the channel length under different operating conditions is required in order to determine, e.g., the best microchannel configuration via a combined first- and second-law-based optimization under typical PEC constraints [40,43,53,54]. In the next future the Authors plan to investigate different geometries, defined by the aspect ratio and the smoothing radius , and the optimal configuration determined for different PECs and different operating conditions (hydraulic diameter , electric double layer thickness , electric potential , source heat power Q, and Stern potential ). Moreover, the effect of axial conduction through the fluid can eventually be accounted for in the numerical model, in order to properly investigate electro-osmotic flows characterized by lower Reynolds numbers and, thus, lower Peclet numbers.
Author Contributions
Conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing—original draft preparation, review and editing, visualization, and supervision, N.S. and M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Specific heat capacity at constant pressure | J·kgK | |
| Reference hydraulic diameter | m | |
| Hydraulic diameter | m | |
| e | Unit electron charge | C |
| E | Electric field component | V·m |
| Electric field | V·m | |
| Nondimensional electric field | - | |
| Current density vector | A·m | |
| Boltzmann Constant | J·K | |
| Debye–Hückel parameter | m | |
| Grid spacing parameter | - | |
| L | Channel length | m |
| Thermal entry length | m | |
| Adiabatic channel length | m | |
| Number of nodes | - | |
| Number of triangular elements | - | |
| Nusselt number | - | |
| Peclet number | - | |
| Prandtl number | - | |
| Joule heating | W·m | |
| Q | Quantity defined by Equation (A11) | - |
| R | Nondimensional radial coordinate | - |
| Reynolds number | - | |
| T | Temperature | K |
| u | Velocity component along the x-axis | m·s |
| Velocity vector | m·s | |
| U | Nondimensional velocity | - |
| x | Axial coordinate | m |
| Nondimensional coordinate vector | - | |
| X | Nondimensional x-coordinate | - |
| Y | Nondimensional y-coordinate | - |
| Ion valence | - | |
| Z | Nondimensional z-coordinate | - |
| Greek letters | ||
| Aspect ratio of the channel | - | |
| Nondimensional smoothing radius | - | |
| Cross-sectional heated perimeter (nondimensional) | - | |
| Nondimensional perimeter | - | |
| Absolute permittivity | F·m | |
| thermal conductivity | W·mK | |
| fluid viscosity | Pa·s | |
| Mobility factor | mVs | |
| Nondimensional cross-sectional area | - | |
| P | Power | W |
| electric potential | V | |
| nondimensional electric potential | - | |
| nondimensional Stern potential | - | |
| Fluid density | kg·m | |
| electric charge density | C·m | |
| electric conductivity | S·m | |
| Nondimensional temperature | K | |
| Stern potential | V | |
| Subscripts | ||
| b | Bulk | |
| i | Inlet | |
| Thermal | ||
| w | Wall | |
| x | Component along the x-direction | |
| ∞ | Fully developed |
Appendix A
This appendix reports the governing equations for the electric potential, velocity, and temperature fields of EOF (i.e., motion of polar fluids through sub-millimeter channels when electric fields are applied across the duct), and the quantities that are introduced to obtain the nondimensional forms reported in Section 2. The interested reader is also referred to the book by Kirby [24], for an extensive treatment of the phenomenon, with the books by Tabeling and Bruus [25,55] offering a more succinct overview. For the purpose of this work, the portion of fluid close to the wall where charge density is non-uniform is treated with the Gouy–Chapman model, in which a net charge at the walls, due to adsorption and ionization, balances a mobile, diffuse charge density; the two regions constitute the electric double layer (EDL), with the potential at the separation plane, the so-called Stern potential, , used as a boundary condition, see in [45] for further details.
Appendix A.1. Electric Potential Field
The governing equation for the electric potential field can be derived from the Maxwell equation, which relates the electric charge distribution to the resulting electric field ,
where is the absolute permittivity of the fluid. Following the work in [45], the electric potential can be analytically obtained from its balance equation,
where is the unit electron charge, is the Boltzmann constant, is the valence of an ion, T is the thermodynamic temperature, and is the electric potential.
Thus, substituting the charge density to Equation (A1) and using the definition of the potential of an electric field, , gives the governing Poisson–Boltzmann equation,
which must be solved in order to find the unknown electric potential . Introducing the following nondimensional quantities,
and further assuming that (i.e., electric potential does not change along channel axis), Equation (A3) becomes Equation (1).
Appendix A.2. Velocity Field
The velocity profile is computed for the conditions stated in Section 2.2. Further, neglecting the pressure gradient along the flow direction and assuming that the only body force acting on the fluid is given by the electric field along the channel axis, , the momentum transport equation gives [45]
Introducing the following quantities,
the nondimensional form, Equation (4), is obtained.
The Poiseuille number is computed from the solution of the nondimensional velocity field, as
where is the nondimensional bulk velocity:
Appendix A.3. Temperature Field
The temperature field is obtained through the solution of the energy equation. Introducing the source term deriving from Joule heating due to the electrical current density flux ,
being the electric conductivity of the fluid, the energy equation gives
Neglecting axial conduction and introducing the following nondimensional quantities,
with and the prescribed inlet temperature and the wall temperature, respectively, Equation (A10) is made nondimensional. From its solution, the Nusselt number, , can be computed as
where is the cross-sectional heated perimeter, is the outward normal direction to , and is the bulk temperature:
After the fully developed flow condition is reached, which means under T-boundary condition, the fully developed Nusselt number can be computed as
Note that the developed temperature field can be either estimated as or via the solution over the 2D channel cross section of the following partial differential equation,
which Equation (5) reduces to for .
References
- Tuckerman, D.; Pease, R. High-Performance Heat Sinking for VLSI. IEEE Electron. Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Schubert, K.; Brandner, J.; Fichtner, M.; Linder, G.; Schygulla, U.; Wenka, A. Microstructure devices for applications in thermal and chemical process engineering. Microscale Thermophys. Eng. 2001, 5, 17–39. [Google Scholar]
- Rostami, A.; Mujumdar, A.; Saniei, N. Flow and heat transfer for gas flowing in microchannels: A review. Heat Mass Transf. Stoffuebertragung 2002, 38, 359–367. [Google Scholar] [CrossRef]
- Venkatesan, S.; Jerald, J.; Asokan, P.; Prabakaran, R. A Comprehensive Review on Microfluidics Technology and its Applications. Lect. Notes Mech. Eng. 2020, 235–245. [Google Scholar] [CrossRef]
- Gilmore, N.; Timchenko, V.; Menictas, C. Microchannel cooling of concentrator photovoltaics: A review. Renew. Sustain. Energy Rev. 2018, 90, 1041–1059. [Google Scholar] [CrossRef]
- Hossan, M.; Dutta, D.; Islam, N.; Dutta, P. Review: Electric field driven pumping in microfluidic device. Electrophoresis 2018, 39, 702–731. [Google Scholar] [CrossRef] [PubMed]
- Tuckerman, D.; Pease, R.; Guo, Z.; Hu, J.; Yildirim, O.; Deane, G.; Wood, L. Microchannel heat transfer: Early history, commercial applications, and emerging opportunities. In Proceedings of the ASME 2011 9th International Conference on Nanochannels, Microchannels, and Minichannels, Edmonton, AB, Canada, 19–22 June 2011; Volume 2, pp. 739–756. [Google Scholar] [CrossRef]
- Kuznetsov, V. Fundamental Issues Related to Flow Boiling and Two-Phase Flow Patterns in Microchannels–Experimental Challenges and Opportunities. Heat Transf. Eng. 2019, 40, 711–724. [Google Scholar] [CrossRef]
- Morini, G.L.; Lorenzini, M.; Colin, S.; Geoffroy, S. Experimental investigation of the compressibility effects on the friction factor of gas flows in microtubes. In Proceedings of the 4th International Conference on Nanochannels, Microchannels and Minichannels, ICNMM2006, Limerick, Ireland, 19–21 June 2006; Volume 47608, pp. 411–418. [Google Scholar]
- Cavazzuti, M.; Corticelli, M.; Karayiannis, T. Compressible Fanno flows in micro-channels: An enhanced quasi-2D numerical model for laminar flows. Therm. Sci. Eng. Prog. 2019, 10, 10–26. [Google Scholar] [CrossRef]
- Cavazzuti, M.; Corticelli, M.; Karayiannis, T. Compressible Fanno flows in micro-channels: An enhanced quasi-2D numerical model for turbulent flows. Int. Commun. Heat Mass Transf. 2020, 111. [Google Scholar] [CrossRef]
- Morini, G.; Yang, Y.; Lorenzini, M. Experimental analysis of gas micro-convection through commercial microtubes. Exp. Heat Transf. 2012, 25, 151–171. [Google Scholar] [CrossRef]
- Cavazzuti, M.; Corticelli, M. Numerical modelling of Fanno flows in micro channels: A quasi-static application to air vents for plastic moulding. Therm. Sci. Eng. Prog. 2017, 2, 43–56. [Google Scholar] [CrossRef]
- Yang, Y.; Chalabi, H.; Lorenzini, M.; Morini, G. The effect on the nusselt number of the nonlinear axial temperature distribution of gas flows through microtubes. Heat Transf. Eng. 2014, 35, 159–170. [Google Scholar] [CrossRef]
- Kockmann, N.; Holvey, C.; Roberge, D. Transitional flow and related transport phenomena in complex microchannels. In Proceedings of the 7th International Conference on Nanochannels, Microchannels, and Minichannels 2009, ICNMM2009, Pohang, Korea, 22–24 June 2009; Volume 43499, pp. 1301–1312. [Google Scholar]
- Lorenzini, M.; Daprá, I.; Scarpi, G. Heat Transfer for a Giesekus Fluid in a Rotating Concentric Annulus. Appl. Therm. Eng. 2017, 122, 118–125. [Google Scholar] [CrossRef]
- Ohadi, M.; Choo, K.; Dessiatoun, S.; Cetegen, E.E. Next Generation Microchannel Heat Exchangers; Springer Briefs in Applied Sciences and Technology; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Y.; Li, M.; Huang, J. A review of development of micro-channel heat exchanger applied in air-conditioning system. Energy Procedia 2012, 14, 148–153. [Google Scholar] [CrossRef]
- Kew, P.; Reay, D. Compact/micro-heat exchangers - Their role in heat pumping equipment. Appl. Therm. Eng. 2011, 31, 594–601. [Google Scholar] [CrossRef][Green Version]
- Henning, T.; Brandner, J.; Schubert, K.; Lorenzini, M.; Morini, G. Low-frequency instabilities in the operation of metallic multi-microchannel evaporators. Heat Transf. Eng. 2007, 28, 834–841. [Google Scholar] [CrossRef]
- Keepaiboon, C.; Dalkilic, A.; Mahian, O.; Ahn, H.; Wongwises, S.; Mondal, P.; Shadloo, M. Two-phase flow boiling in a microfluidic channel at high mass flux. Phys. Fluids 2020, 32. [Google Scholar] [CrossRef]
- Wei, T.W.; Oprins, H.; Fang, L.; Cherman, V.; De Wolf, I.; Beyne, E.; Baelmans, M. Nozzle scaling effects for the thermohydraulic performance of microjet impingement cooling with distributed returns. Appl. Therm. Eng. 2020, 180. [Google Scholar] [CrossRef]
- Morini, G.; Spiga, M. The role of the viscous dissipation in heated microchannels. J. Heat Transf. 2007, 129, 308–318. [Google Scholar] [CrossRef]
- Kirby, B. Micro- and Nanoscale Fluid Mechanics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bruus, H. Theoretical Microfluidics; OUP: Oxford, UK, 2010. [Google Scholar]
- Al-Rjoub, M.F.; Roy, A.K.; Ganguli, S.; Banerjee, R.K. Assessment of an active-cooling micro-channel heat sink device, using electro-osmotic flow. Int. J. Heat Mass Transf. 2011, 54, 4560–4569. [Google Scholar] [CrossRef]
- Rice, C.; Whitehead, R. Electrokinetic flow in a narrow cylindrical capillary. J. Phys. Chem. 1965, 69, 4017–4024. [Google Scholar] [CrossRef]
- Mala, G.; Li, D.; Werner, C.; Jacobasch, H.J.; Ning, Y. Flow characteristics of water through a microchannel between two parallel plates with electrokinetic effects. Int. J. Heat Fluid Flow 1997, 18, 489–496. [Google Scholar] [CrossRef]
- Wang, C.Y.; Chang, C.C. Electro-osmotic flow in polygonal ducts. Electrophoresis 2011, 32, 1268–1272. [Google Scholar] [CrossRef] [PubMed]
- Vocale, P.; Geri, M.; Cattani, L.; Morini, G.; Spiga, M. Electro-osmotic heat transfer in elliptical microchannels under H1 boundary condition. Int. J. Therm. Sci. 2013, 72, 92–101. [Google Scholar] [CrossRef]
- Vocale, P.; Geri, M.; Morini, G.; Spiga, M. Electro-osmotic flows inside triangular microchannels. J. Phys. Conf. Ser. 2014, 501, 012026. [Google Scholar] [CrossRef]
- Geri, M.; Lorenzini, M.; Morini, G. Effects of the Channel Geometry and of the Fluid Composition on the Performance of DC Electro-osmotic Pumps. Int. J. Therm. Sci. 2012, 55, 114–121. [Google Scholar] [CrossRef]
- Morini, G.L.; Lorenzini, M.; Salvigni, S.; Spiga, M. Thermal performance of silicon micro heat-sinks with electrokinetically-driven flows. In Proceedings of the 3rd International Conference on Microchannels and Minichannels, Toronto, ON, Canada, 13–15 June 2005; Volume B, pp. 231–236. [Google Scholar]
- Al-Rjoub, M.; Roy, A.; Ganguli, S.; Banerjee, R. Enhanced electro-osmotic flow pump for micro-scale heat exchangers. In Proceedings of the ASME 2012 3rd International Conference on Micro/Nanoscale Heat and Mass Transfer, MNHMT 2012, Atlanta, GA, USA, 3–6 March 2012; pp. 829–833. [Google Scholar]
- Pramod, K.; Sen, A. Flow and heat transfer analysis of an electro-osmotic flow micropump for chip cooling. J. Electron. Packag. Trans. ASME 2014, 136, 03101201–03201214. [Google Scholar] [CrossRef]
- Shamshiri, M.; Khazaeli, R.; Ashrafizaadeh, M.; Mortazavi, S. Electroviscous and thermal effects on non-Newtonian liquid flows through microchannels. J. Non-Newton. Fluid Mech. 2012, 173–174, 1–12. [Google Scholar] [CrossRef]
- Shit, G.; Mondal, A.; Sinha, A.; Kundu, P. Electro-osmotic flow of power-law fluid and heat transfer in a micro-channel with effects of Joule heating and thermal radiation. Phys. A Stat. Mech. Its Appl. 2016, 462, 1040–1057. [Google Scholar] [CrossRef]
- Al-Rjoub, M.; Roy, A.; Ganguli, S.; Banerjee, R. Enhanced heat transfer in a micro-scale heat exchanger using nano-particle laden electro-osmotic flow. Int. Commun. Heat Mass Transf. 2015, 68, 228–235. [Google Scholar] [CrossRef]
- Ray, S.; Misra, D. Laminar fully developed flow through square and equilateral triangular ducts with rounded corners subjected to H1 and H2 boundary conditions. Int. J. Therm. Sci. 2010, 49, 1763–1775. [Google Scholar] [CrossRef]
- Chakraborty, S.; Ray, S. Performance optimisation of laminar fully developed flow through square ducts with rounded corners. Int. J. Therm. Sci. 2011, 50, 2522–2535. [Google Scholar] [CrossRef]
- Lorenzini, M.; Morini, G. Single-phase, Laminar Forced Convection in Microchannels with Rounded Corners. Heat Transf. Eng. 2011, 32, 1108–1116. [Google Scholar] [CrossRef]
- Lorenzini, M. The Influence of Viscous Dissipation on Thermal Performance of Microchannels with Rounded Corners. La Houille Blanche 2013, 64–71. [Google Scholar] [CrossRef]
- Lorenzini, M.; Suzzi, N. The influence of geometry on the thermal performance of microchannels in laminar flow with viscous dissipation. Heat Trans. Eng. 2016, 37, 1096–1104. [Google Scholar] [CrossRef]
- Lorenzini, M. Electro-osmotic Flow in Rectangular Microchannels: Geometry Optimisation. J. Phys. Conf. Ser. 2017, 923, 1–8. [Google Scholar] [CrossRef]
- Lorenzini, M. Electro-osmotic non-isothermal flow in rectangular channels with smoothed corners. J. Therm. Sci. Eng. Appl. 2020, 19, 100617. [Google Scholar] [CrossRef]
- Webb, R. Principles of Enhanced Heat Transfer; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Shah, R.K.; London, A.K. Laminar Flow Forced Convection in Ducts—A Source Book for Heat Exchanger Analytical Data; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Barletta, A.; Magyari, E. The Graetz-Brinkman problem in a plane-parallel channel with adiabatic-to-isothermal entrance. Int. Commun. Heat Mass 2006, 33, 677–685. [Google Scholar] [CrossRef]
- Suzzi, N.; Lorenzini, M. Viscous heating of a laminar flow in the thermal entrance region of a rectangular channel with rounded corners and uniform wall temperature. Int. J. Therm. Sci. 2019, 145, 106032. [Google Scholar] [CrossRef]
- Morini, G.L.; Lorenzini, M.; Salvigni, S.; Spiga, M. Thermal performance of silicon micro heat-sinks with electrokinetically-driven flows. Int. J. Therm. Sci. 2006, 45, 955–961. [Google Scholar] [CrossRef]
- Jian, Y.; Yang, L.; Liu, Q. Time periodic electro-osmotic flow through amicroannulus. Phys. Fluids 2010, 22, 042001. [Google Scholar] [CrossRef]
- Sadr, R.; Yoda, M.; Zheng, Z.; Conlisk, T. An experimental study of electro-osmotic flow in rectangular microchannels. J. Fluid Mech. 2004, 506, 357–367. [Google Scholar] [CrossRef]
- Zimparov, V. Extended performance evaluation criteria for enhanced heat transfer surfaces: Heat transfer through ducts with constant wall temperature. Int. J. Heat Mass Transf. 2000, 43, 3137–3155. [Google Scholar] [CrossRef]
- Zimparov, V. Extended performance evaluation criteria for enhanced heat transfer surfaces: Heat transfer through ducts with constant heat flux. Int. J. Heat Mass Transf. 2001, 44, 169–180. [Google Scholar] [CrossRef]
- Tabeling, P. Introduction to Microfluidics; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).