Numerical Modelling of Air Pollutant Dispersion in Complex Urban Areas: Investigation of City Parts from Downtowns Hanover and Frankfurt
Abstract
1. Introduction
2. Methodology
2.1. Turbulence Model
2.2. Dispersion Model
2.3. Numerical Procedure
2.4. Validation of the Numerical Model
3. Computational Domain and Boundaries Conditions
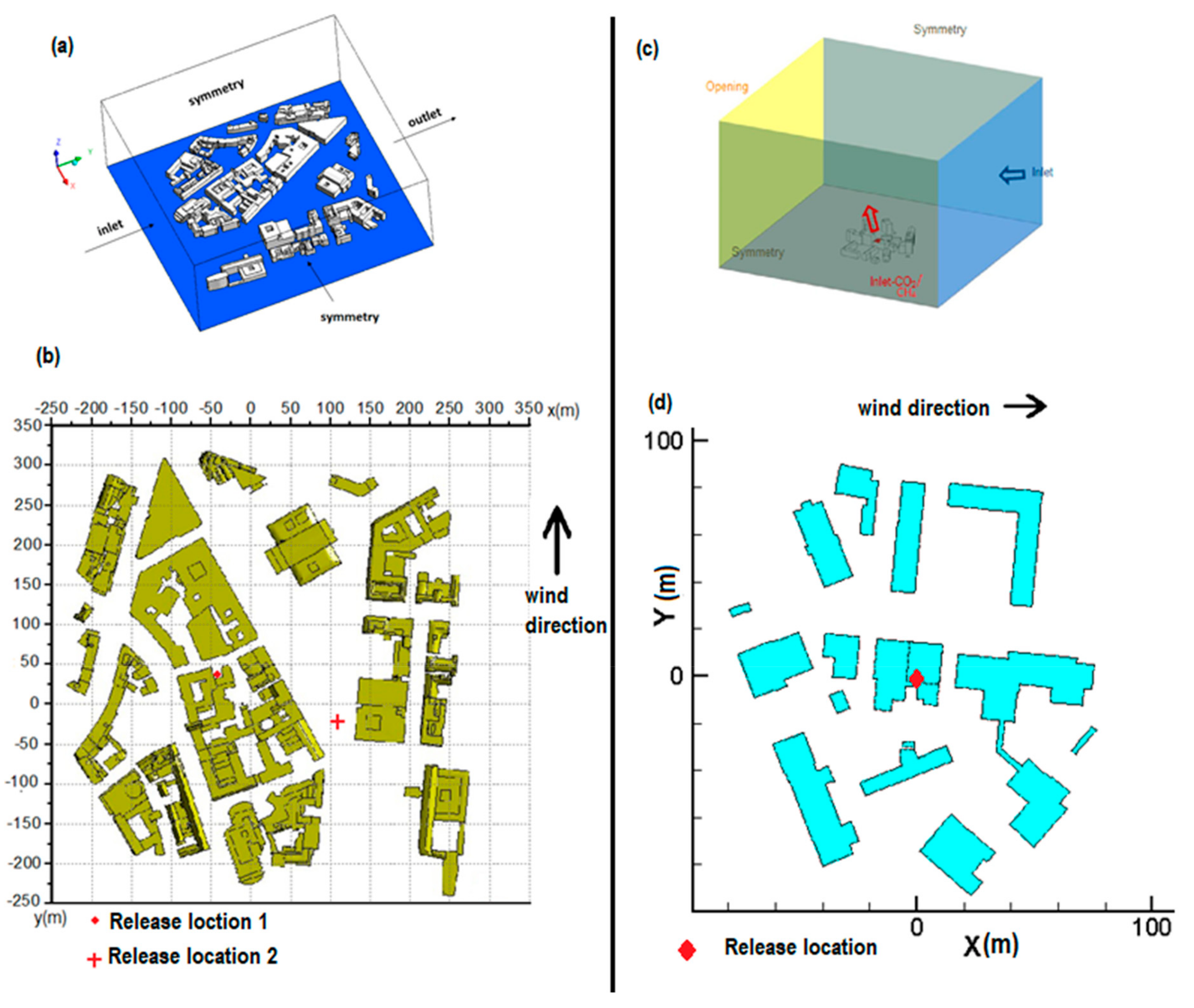
3.1. Geometry and Boundaries Conditions
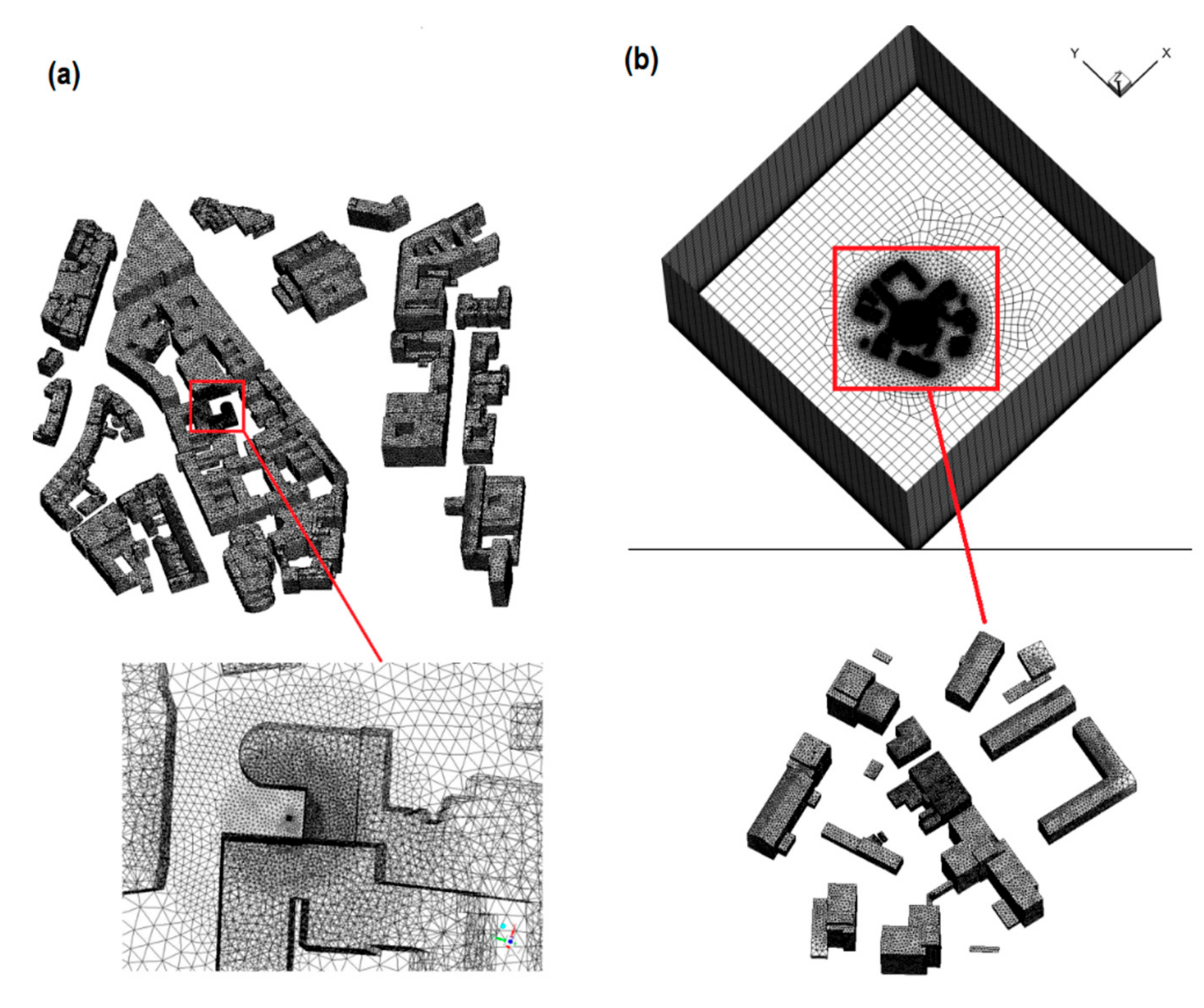
3.2. Computational Grid
4. Results and Discussion
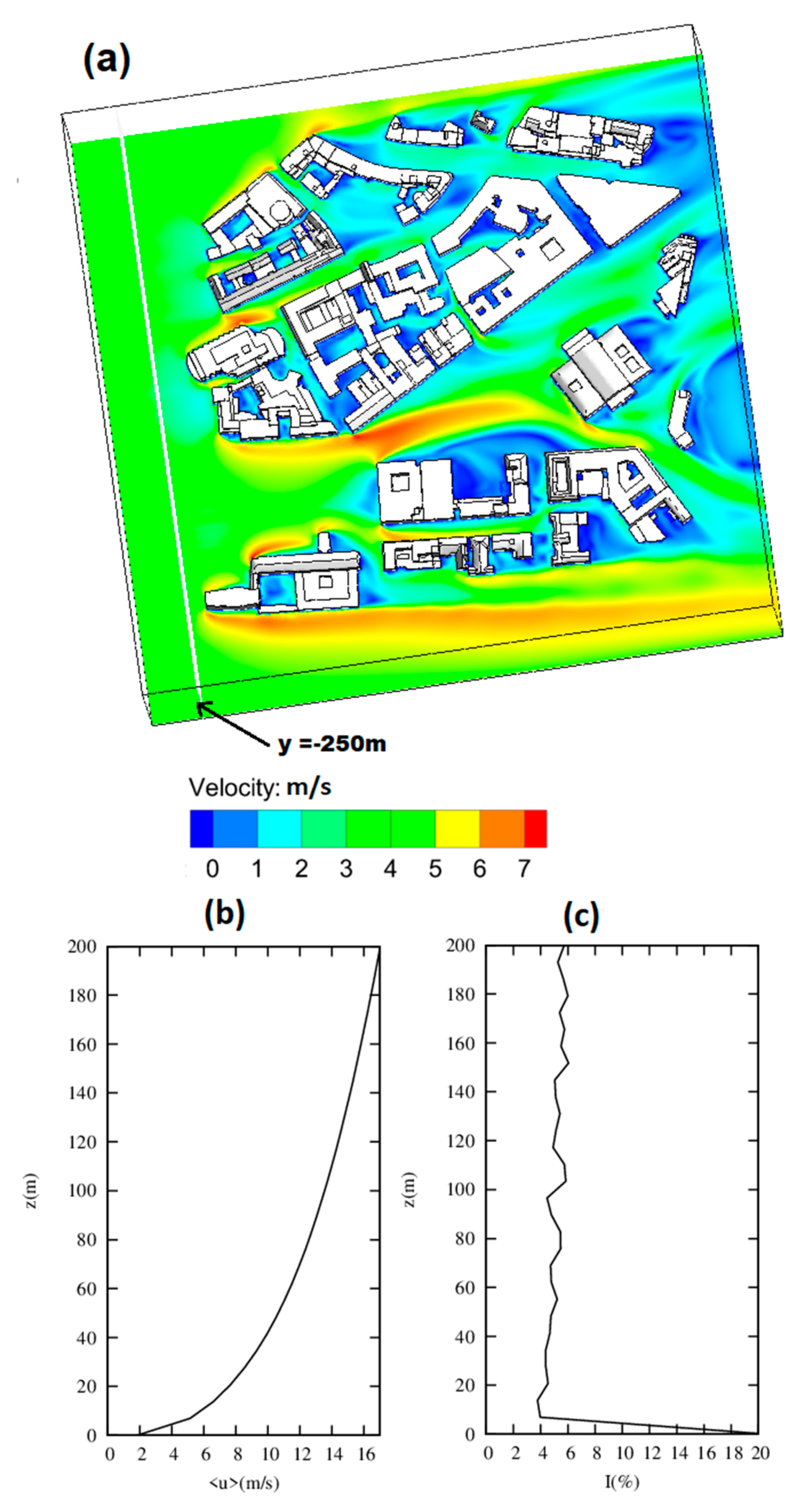
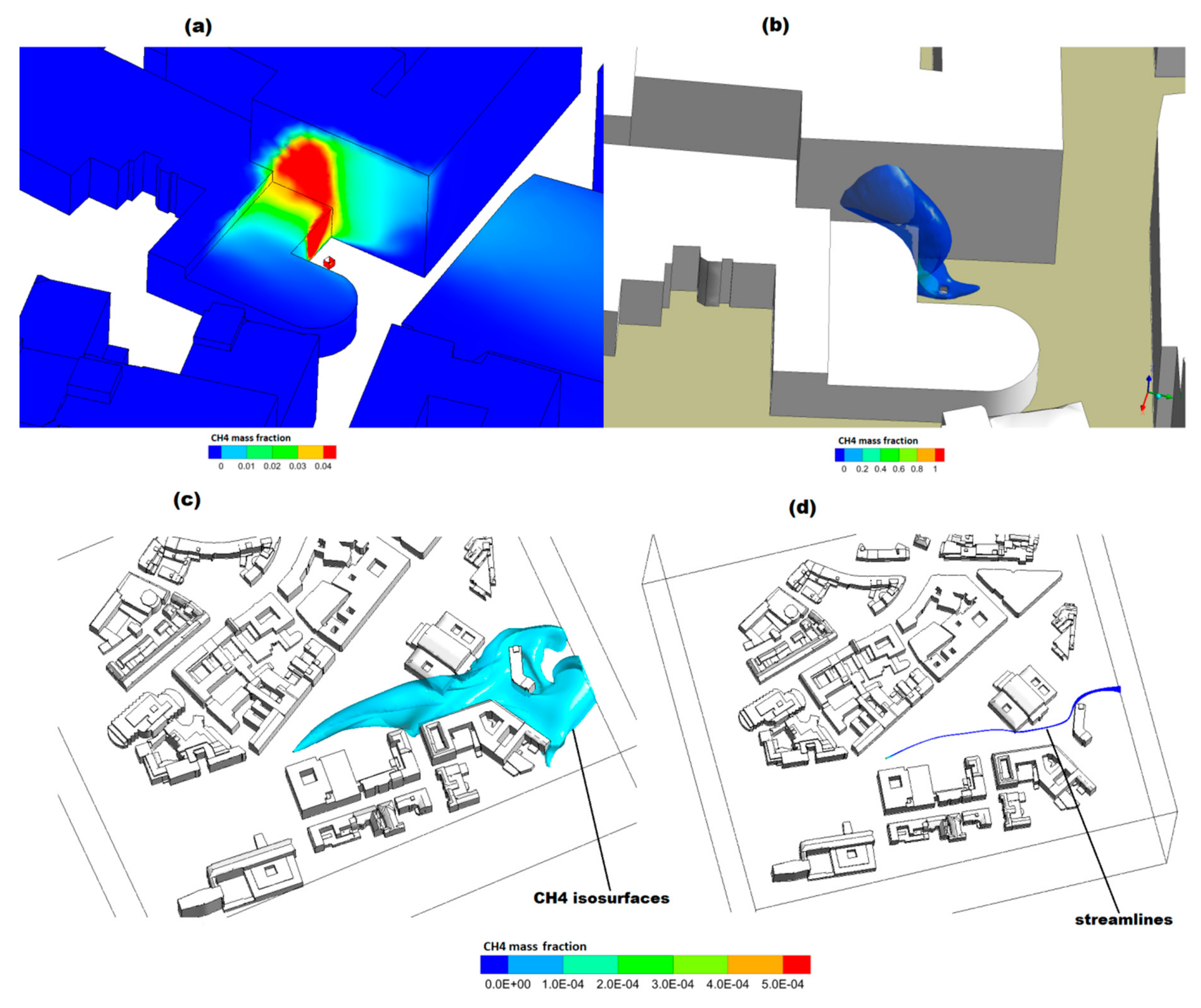
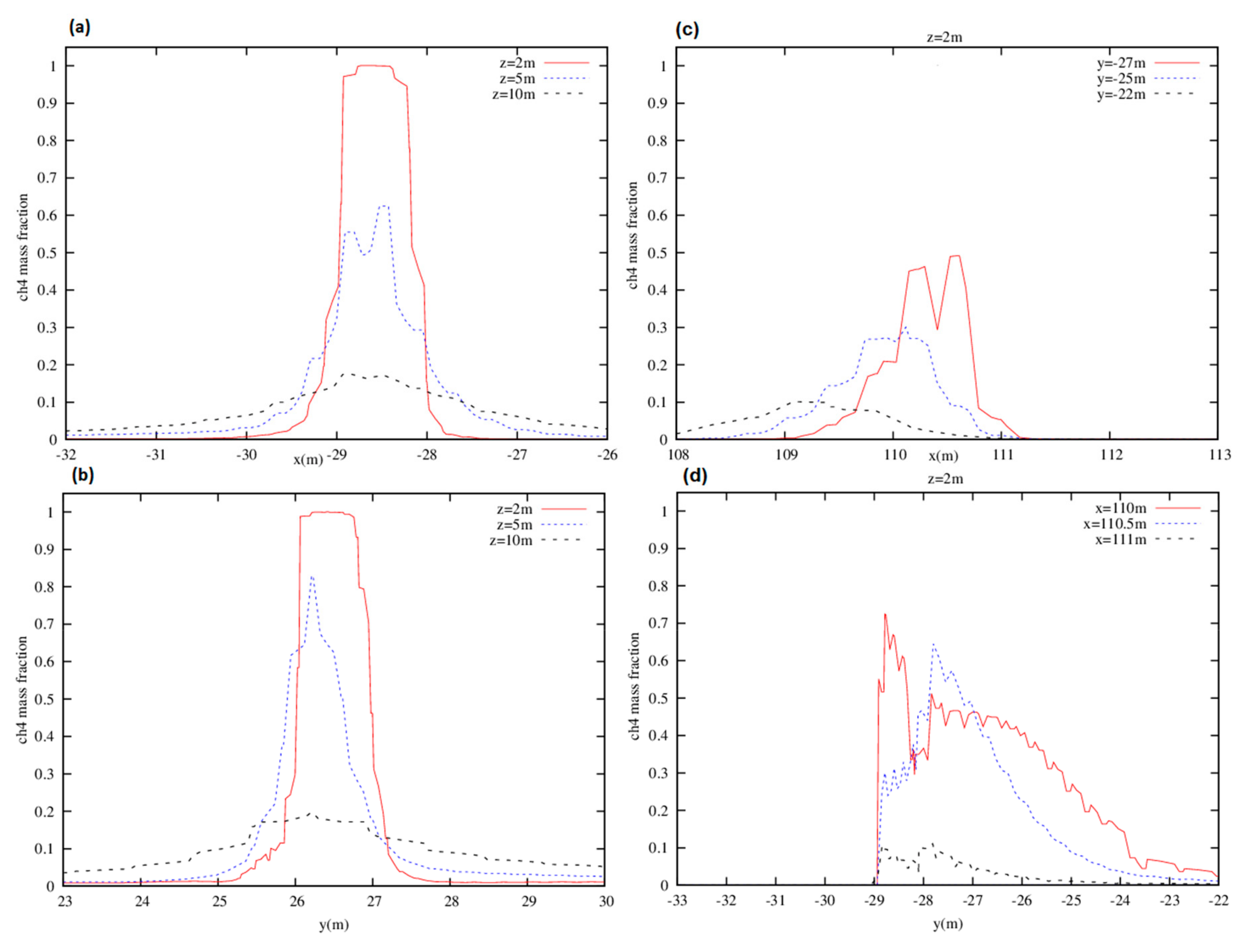
4.1. Hanover City Results
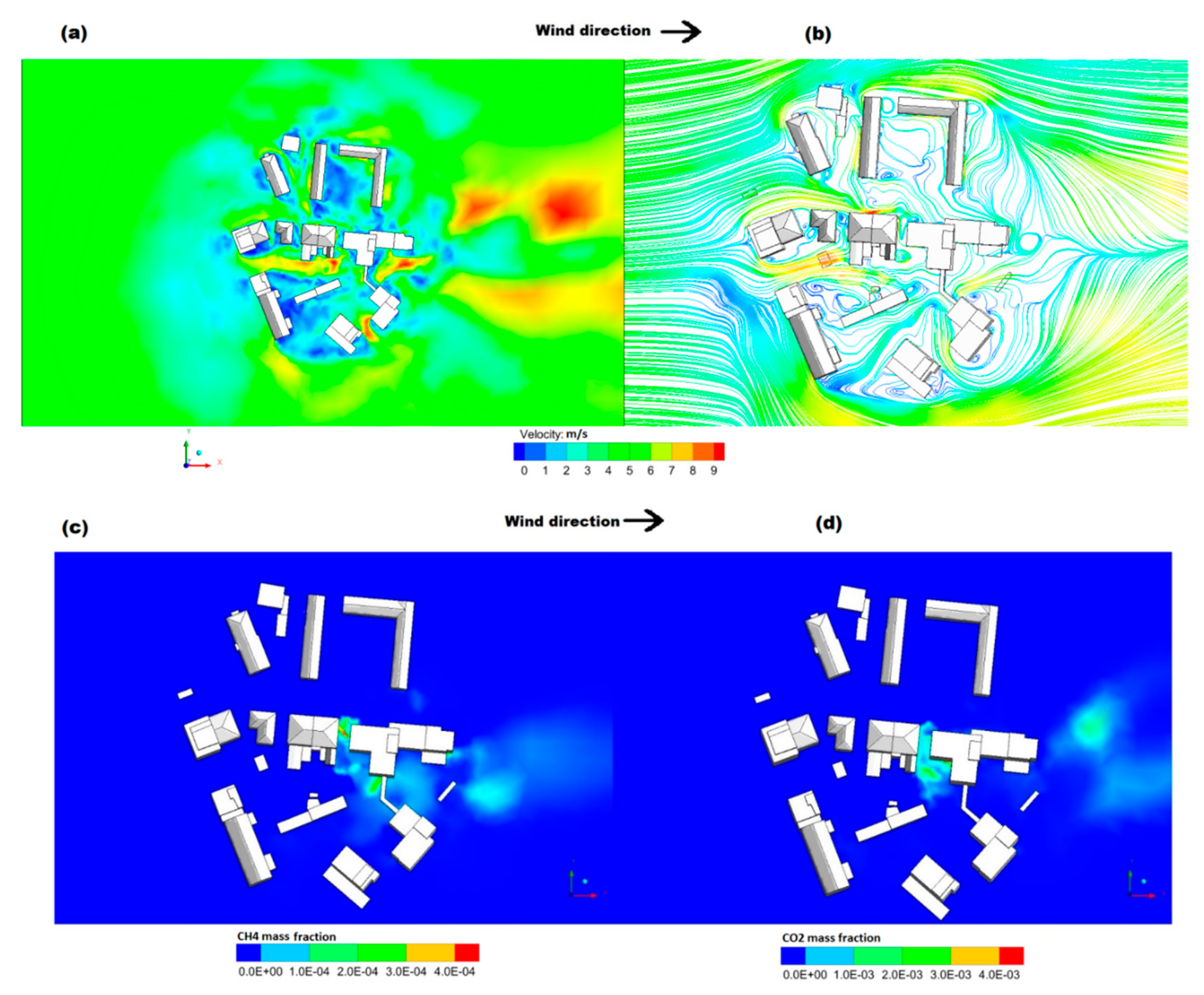
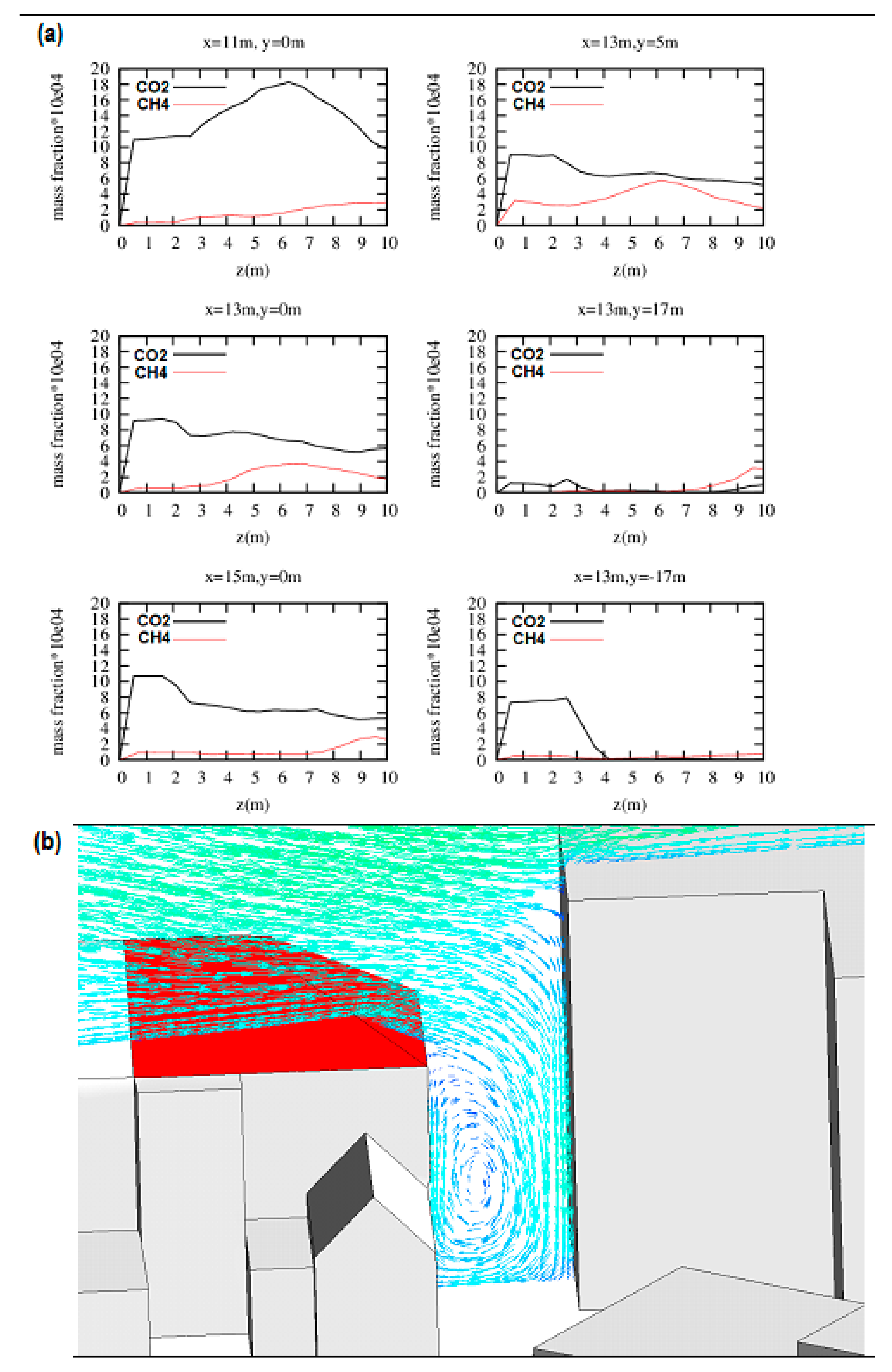
4.2. Frankfurt City Results
5. Conclusions
- (1)
- Smagorinsky LES shows reasonable results of the velocities and turbulence quantities compared to experimental data of generic building configuration. The results agreement is used as validation of the flow model to investigate a larger full-scale 1:1 city geometry.
- (2)
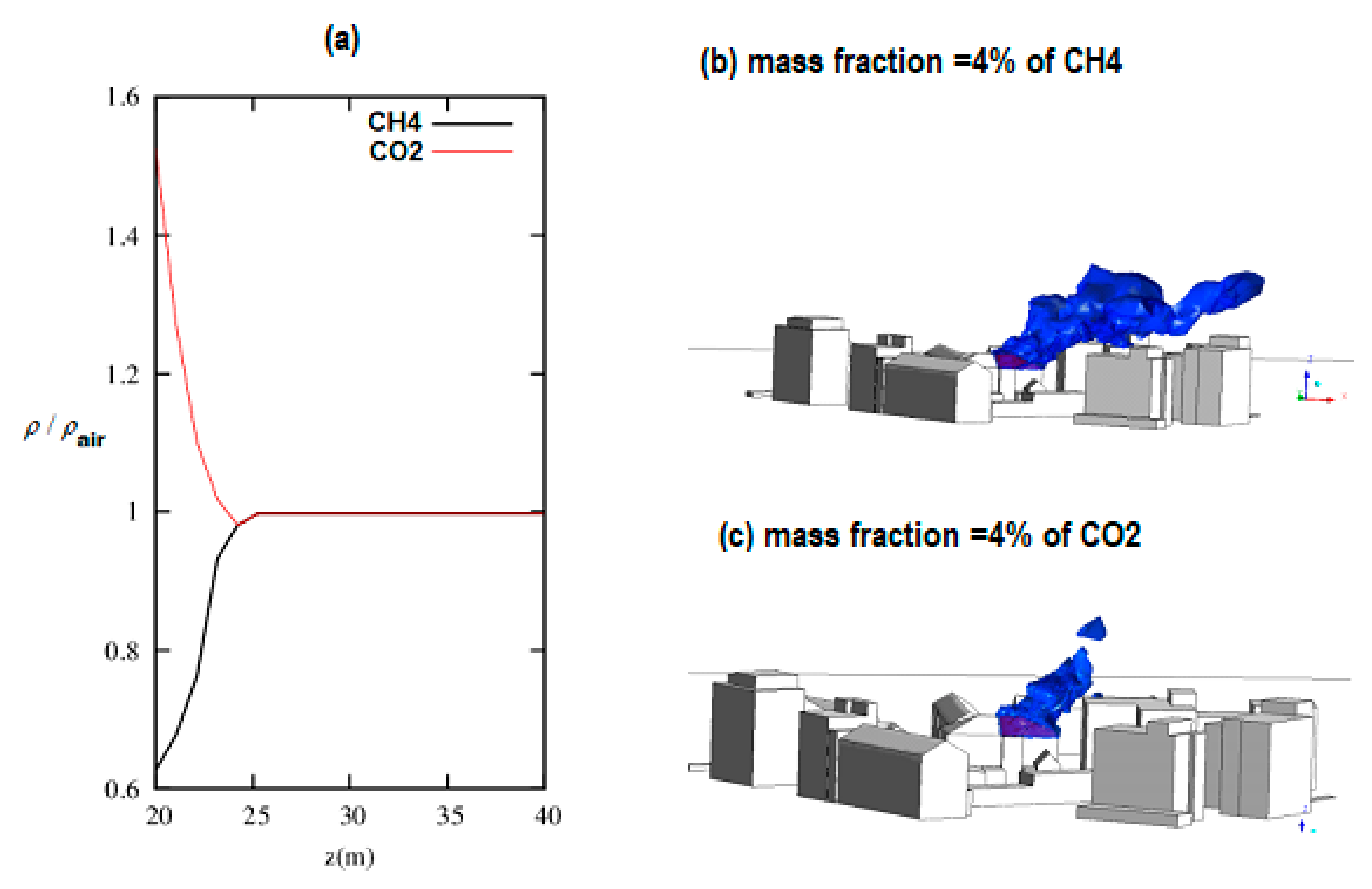
- Methane dispersion is controlled by the air-CH4 density ratio in cases of pollutant injection close to buildings. The buoyancy forces are responsible for the stratification of gases. CH4 species are first transported in the vertical direction then dragged by the carrier phase toward the outlet. The velocity direction of pollutant injection and magnitude, as well as temperature difference between CH4 and ambient air, do not play important roles.
- (3)
- If CH4 is injected far from buildings, i.e., in open area in which carrier phase velocity is important, then the transport of pollutant showed different behavior. CH4 was dragged horizontally much faster than in the vertical direction. It followed the street and kept almost a constant altitude until reaching the outlet.
- (4)
- The main parameter that controls the dispersion in Frankfurt city configuration is the density ratio of CO2 and CH4 to ambient air. Despite the injection of both gases in the vertical direction, only CO2 shows a significant concentration at the ground.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hagler, G.S.; Tang, W. Simulation of rail yard emissions transport to the near-source environment. Atmos. Pollut. Res. 2016, 7, 469–476. [Google Scholar] [CrossRef]
- Hidouri, A.; Gazzah, M.H.; Sassi, M. Numerical investigation of piloted turbulent reacting methane/air jet. Comput. Therm. Sci. Int. J. 2016, 1–12. [Google Scholar] [CrossRef]
- Hidouri, A.; Chrigui, M.; Boushaki, T.; Sadiki, A.; Janicka, J. Large Eddy Simulation of Two Isothermal and Reacting Turbulent Separated Oxy-Fuel Jets. Fuel 2017, 192, 108–120. [Google Scholar] [CrossRef]
- Mouldi, C.; Amsini, S.; Johannes, J. Evaporation and dispersion of N-Heptane droplets within premixed flame. Heat Mass Transf. 2010, 46, 869–880. [Google Scholar] [CrossRef]
- Derome, D.; Kubilay, A.; Defraeye, T.; Blocken, B.; Carmeliet, J. Ten questions concerning modeling of wind-driven rain in the built environment. Build. Environ. 2017, 114, 495–506. [Google Scholar] [CrossRef]
- Vasile, F.S.; Lucian, N.; Bianca, S.; Carol, P. Case studies of methane dispersion patterns and odor strength in vicinity of municipal solid waste landfill of Cluj–Napoca, Romania, using numerical modeling. Atmos. Pollut. Res. 2015, 6, 312–321. [Google Scholar] [CrossRef]
- Tominaga, Y.; Blocken, B. Wind tunnel experiments on cross-ventilation flow of a generic building with contaminant dispersion in unsheltered and sheltered conditions. Build. Environ. 2015, 92, 452–461. [Google Scholar] [CrossRef]
- Jae-Jin, K.; Jong-Jin, B. Effects of inflow turbulence intensity on flow and pollutant dispersion in an urban street canyon. J. Wind Eng. Ind. Aerod. 2003, 91, 309–329. [Google Scholar] [CrossRef]
- Blocken, B. Computational Fluid Dynamics for Urban Physics: Importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef]
- Leitl, B.M.; Kastner-Klein, P.; Rau, M.; Meroney, R.N. Concentration and flow distributions in the vicinity of U-shaped buildings: Wind-tunnel and computational data. J. Wind. Eng. Ind. Aerod. 1997, 67, 745–755. [Google Scholar] [CrossRef]
- Meroney, R.N.; Leitl, B.M.; Rafailidis, S.; Schatzmann, M. Wind-tunnel and numerical modeling of flow and dispersion about several building shapes. J. Wind. Eng. Ind. Aerod. 1999, 81, 333–345. [Google Scholar] [CrossRef]
- Britter, R.E.; Hanna, S.R. Flow and dispersion in urban areas. Ann. Rev. Fluid Mech. 2003, 35, 469–496. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Saathoff, P.; Wang, X. Numerical evaluation of pollutant dispersion in the built environment: Comparisons between models and experiments. J. Wind. Eng. Ind. Aerod. 2008, 96, 1817–1831. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Numerical simulation of dispersion around an isolated cubic building: Comparison of various types of k-e models. Atmos. Environ. 2009, 43, 3200–3210. [Google Scholar] [CrossRef]
- Chun-Ho, L.; Mary, C.B. Large-Eddy simulation of flow and scalar transport in a modeled street canyon. Appl. Metro. 2002, 41, 660–673. [Google Scholar] [CrossRef]
- Baker, J.; Walker, H.L.; Cai, X.M. A study of the dispersion and transport of reactive pollutants in and above street canyons a large eddy simulation. Atmos. Environ. 2004, 38, 6883–6892. [Google Scholar] [CrossRef]
- Xie, Z.T.; Castro, I.P. LES and RANS for turbulent flow over arrays of wall mounted cubes. Flow Turbul. Combust. 2006, 76, 291–312. [Google Scholar] [CrossRef]
- Sada, K.; Sato, A. Numerical calculation of flow and stack-gas concentration fluctuation around a cubical building. Atmos. Environ. 2002, 36, 5527–5534. [Google Scholar] [CrossRef]
- Gu, Z.L.; Jiao, J.Y.; Su, J.W. Large-eddy simulation of the wind field and plume dispersion within different obstacle arrays using a dynamic mixing length subgrid-scale model. Bound. Lay. Meteorol. 2011, 139, 439–455. [Google Scholar] [CrossRef]
- Cheng, W.C.; Chun-Ho, L. Large-Eddy Simulation of Flow and Pollutant Transports in and Above Two-Dimensional Idealized Street Canyons. Bound. Lay. Meteorol. 2011, 139, 411–437. [Google Scholar] [CrossRef]
- Gousseau, P.; Blocken, B.; Van Heijst, G.J.F. Large-eddy simulation of pollutant dispersion around a cubical building: Analysis of the turbulent mass transport mechanism by unsteady concentration and velocity statistics. Environ. Pollut. 2012, 167, 47–57. [Google Scholar] [CrossRef] [PubMed]
- Yoshie, R.; Jiang, G.; Shirasawa, T.; Chung, J. CFD simulations of gas dispersion around high-rise building in non-isothermal boundary layer. J. Wind. Eng. Ind. Aerod. 2011, 99, 279–288. [Google Scholar] [CrossRef]
- Xie, Z.T.; Hayden, P.; Wood, C.R. Large-eddy simulation of approaching-flow stratification on dispersion over arrays of buildings. Atmos. Environ. 2013, 71, 64–74. [Google Scholar] [CrossRef]
- Xue, Y.; Zhai, Z.J. Inverse identification of multiple outdoor pollutant sources with a mobile sensor. Build. Simul. 2017, 10, 255–263. [Google Scholar] [CrossRef]
- Liu, Y.S.; Cui, G.X.; Wang, Z.S.; Zhang, Z.S. Large eddy simulation of wind field and pollutant dispersion in downtown Macao. Atmos. Environ. 2011, 45, 2849–2859. [Google Scholar] [CrossRef]
- Gousseau, P.; Blocken, B.; Stathopoulos, T.; van Heijst, G.J.F. Near-field pollutant dispersion in an actual urban area: Analysis of the mass transport mechanism by high resolution Large Eddy Simulations. Comput. Fluids 2015, 114, 151–162. [Google Scholar] [CrossRef]
- Kubilay, A.; Derome, D.; Blocken, B.; Carmeliet, J. Numerical modeling of turbulent dispersion for wind-driven rain on building facades. Environ. Fluid Mech. 2015, 15, 109–133. [Google Scholar] [CrossRef]
- Van Hooff, T.; Blocken, B. CFD evaluation of natural ventilation of indoor environments by the concentration decay method: CO2 gas dispersion from a semi-enclosed stadium. Build. Environ. 2013, 61, 1–17. [Google Scholar] [CrossRef]
- Amorim, J.H.; Rodrigues, V.; Tavares, R.; Valente, J.; Borrego, C. CFD modelling of the aerodynamic effect of trees on urban air pollution dispersion. Sci. Total Environ. 2013, 461, 541–551. [Google Scholar] [CrossRef]
- Leitl, B.; Schatzmann, M. Cedval at Hamburg University. Available online: http://www.mi.unihamburg.de/cedval (accessed on 17 July 2019).
- Longo, R.; Ferrarotti, M.; Schanchez, C.G.; Deurdi, M.; Parente, A. Advanced turbulence models, boundary conditions and dispersion study for flows around different configurations of ground-mounted buildings. J. Wind. Eng. Ind. Aerod. 2017, 167, 160–182. [Google Scholar] [CrossRef]
- Sadiki, A.; Maltsev, A.; Wegner, B.; Flemming, F.; Kempf, A.; Janicka, J. Unsteady methods (urans and les) for simulation of combustion systems. Int. J. Therm. Sci. 2006, 45, 760–773. [Google Scholar] [CrossRef]
- Tennekes, H. The Logarithmic Wind Profile. J. Atmos. Sci. 1973, 30, 234–238. [Google Scholar] [CrossRef]
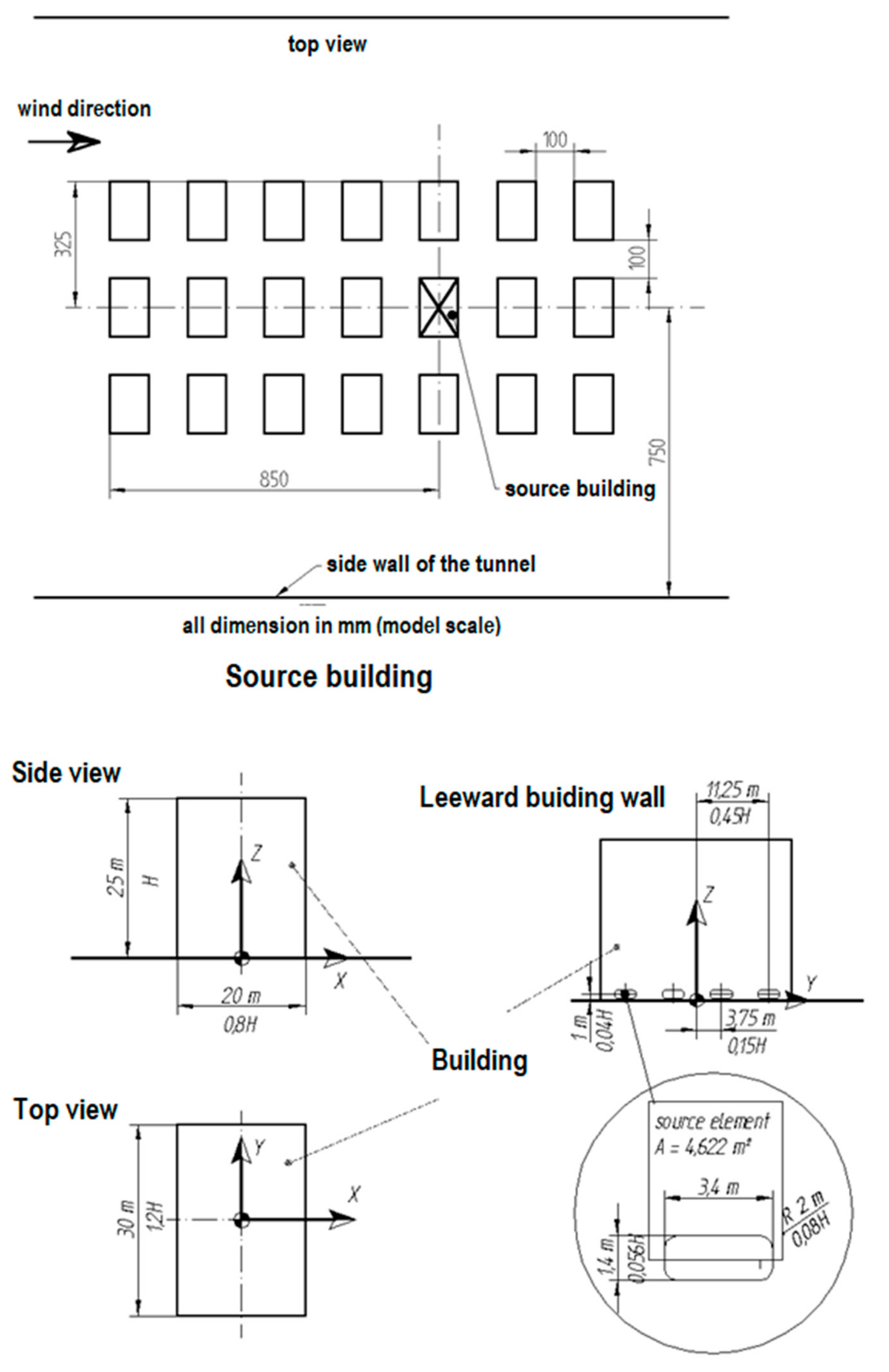
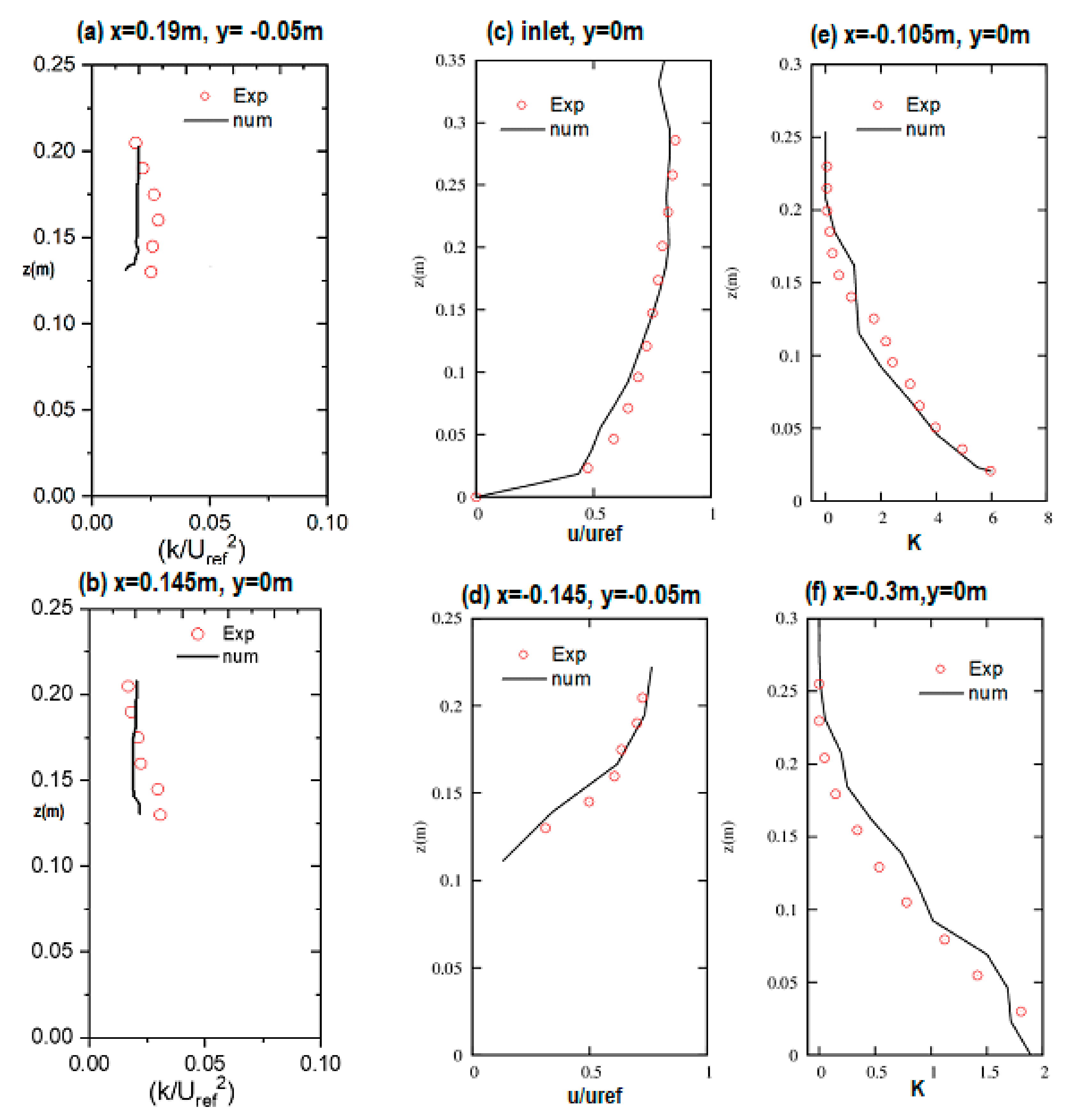
| CEDVAL B1-1 | |||
|---|---|---|---|
| Boundary | Velocity | Temperature | Species |
| Inlet | Profile: Experimental Data | 300 K | air |
| Pollutant source | 0.033 m/s | 300 K | CO2 |
| Outlet | Neuman BC for the pressure | - | - |
| Top | Neuman BC for the pressure | - | - |
| Walls | No slip | - | - |
| Hanover City Case | Frankfurt City Case | |||||
|---|---|---|---|---|---|---|
| Boundary | Velocity | Temperature | Species | Velocity | Temperature | Species |
| Inlet | Profile: Equation (5) | 300 K | air | Profile: Equation (5) | 300 K | air |
| Pollutant source | 8 m/s | 310 K | CH4 | 2 m/s | 310 K | CO2 CH4 |
| Outlet | Neuman BC for the pressure | - | - | Neuman BC for the pressure | - | - |
| Top | Neuman BC for the pressure | - | - | Neuman BC for the pressure | - | - |
| Walls | No slip | - | - | No slip | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Idrissi, M.S.; Ben Salah, N.; Chrigui, M. Numerical Modelling of Air Pollutant Dispersion in Complex Urban Areas: Investigation of City Parts from Downtowns Hanover and Frankfurt. Fluids 2019, 4, 137. https://doi.org/10.3390/fluids4030137
Idrissi MS, Ben Salah N, Chrigui M. Numerical Modelling of Air Pollutant Dispersion in Complex Urban Areas: Investigation of City Parts from Downtowns Hanover and Frankfurt. Fluids. 2019; 4(3):137. https://doi.org/10.3390/fluids4030137
Chicago/Turabian StyleIdrissi, Mohamed Salah, Nabil Ben Salah, and Mouldi Chrigui. 2019. "Numerical Modelling of Air Pollutant Dispersion in Complex Urban Areas: Investigation of City Parts from Downtowns Hanover and Frankfurt" Fluids 4, no. 3: 137. https://doi.org/10.3390/fluids4030137
APA StyleIdrissi, M. S., Ben Salah, N., & Chrigui, M. (2019). Numerical Modelling of Air Pollutant Dispersion in Complex Urban Areas: Investigation of City Parts from Downtowns Hanover and Frankfurt. Fluids, 4(3), 137. https://doi.org/10.3390/fluids4030137





