Artificial Intelligence Computing at the Quantum Level
Abstract
:1. Introduction
1.1. Contributions
- This paper provides foundational concepts about QC and a comprehensive analysis of recent work, investigating the connection between physics and information science and assessing the area’s growth.
- We present flowcharts that summarize the field’s development and/or roadmap, as well as a comparison of common quantum bit technologies and open source development frameworks.
- We explore the field’s current (experimental and theoretical) problems in achieving fully scaled quantum devices. We also provide a summary of past developments as well as a progress report on quantum information science topics of interest.
- We provide a list of topics of interest, together with a high-quality list of reference resources for a more in-depth study of each subject, based on the preferences of the readers.
1.2. Structure
2. Modern Physics and Artificial Intelligence
2.1. Quantum Mechanics
Quantum Theory
2.2. Machine Learning
3. Quantum Information Science
3.1. Quantum Mechanics Postulates, Entanglement, Mixed States and Operations
- Postulate 1: State Space. The state of a quantum system is described by a unit vector that lives in a Hilbert space This state contains all necessary information to characterize the system.
- Postulate 2: Evolution. A closed quantum system undergoes a time evolution . This evolution is described by a unitary transformation that follows the Schrodinger Equation (1).
- Postulate 3: Measurement. Quantum measurements can be expressed using sets of measurement operators In an experiment, m represents the possible measurement outcomes. Upon measuring a state, say , the probability of an m outcome is .
- Postulate 4: Composite Systems. Two or more physical systems can be treated as a composite system. The state space of a composite system is the tensor product space of the states of the component physical systems.
Other Important Properties
- Superposition Linear combination of two states.
- Entanglement When the values of specific qualities of one system are correlated with the values of the corresponding properties of the other system, two quantum systems are said to be entangled.
- Speedup If the quantum algorithm requires fewer queries to solve a problem than the classical approach, the outcome is a quantum speedup [19].
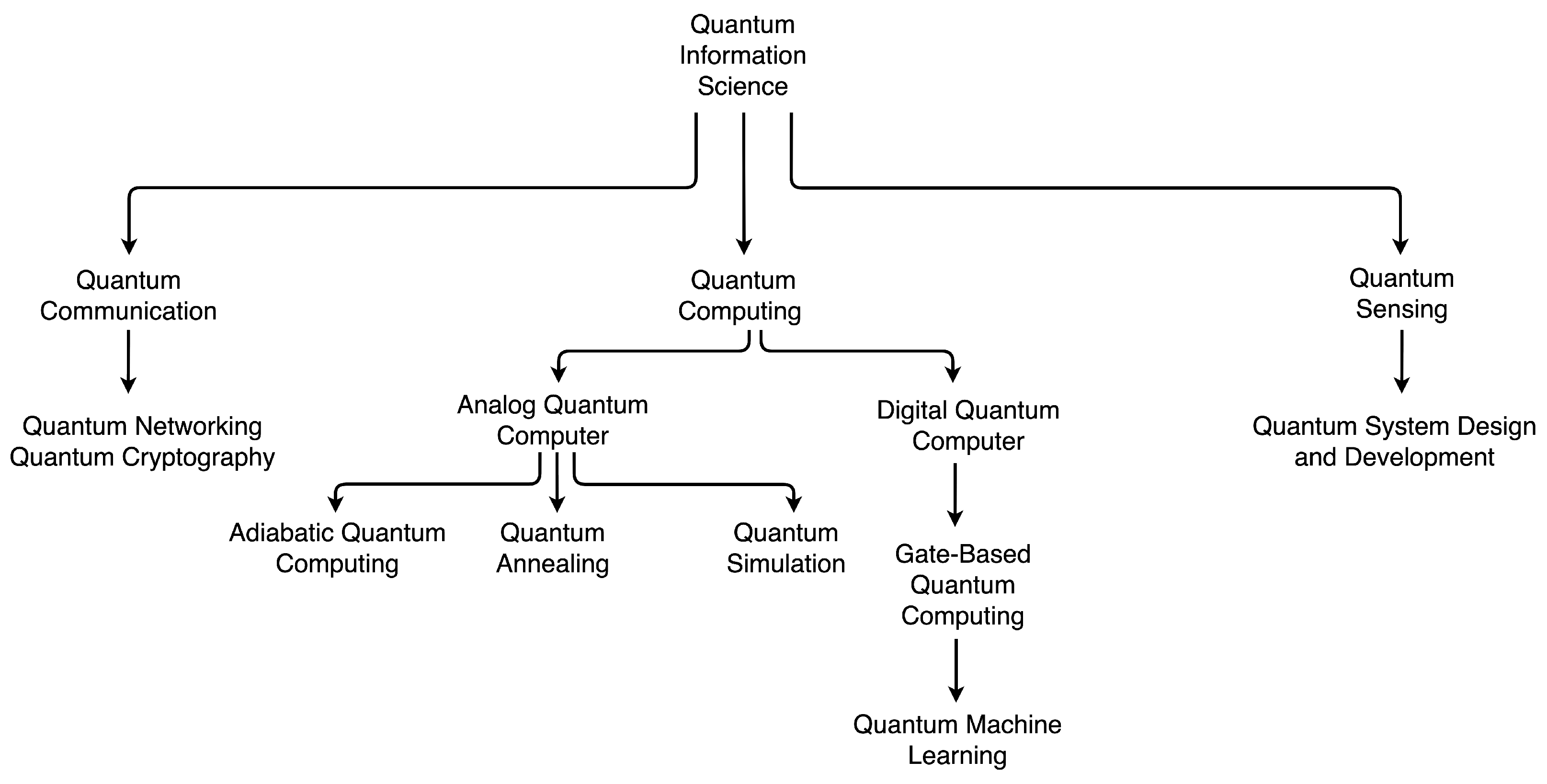
3.2. Quantum Information Science: An Overview
- Adiabatic quantum computing (AQC) is a computational model that employs adiabatic quantum mechanical processes [20].
- Quantum annealing (QA) is a technique for evaluating the minimum of an objective function that is built on AQC concepts but does not meet its stringent requirements [20].
- Quantum simulation (QS) is the use of a controllable quantum system to examine a less controllable or accessible quantum system [21].
- Gate-based quantum computing (GBQC) accepts data and modifies it by a unitary operation, which is expressed as a sequence of gate operations and measurements (i.e., the algorithm) and may be represented by a quantum circuit [22]. Quantum machine learning is the GBQC’s driving force.
3.3. Quantum Computing System
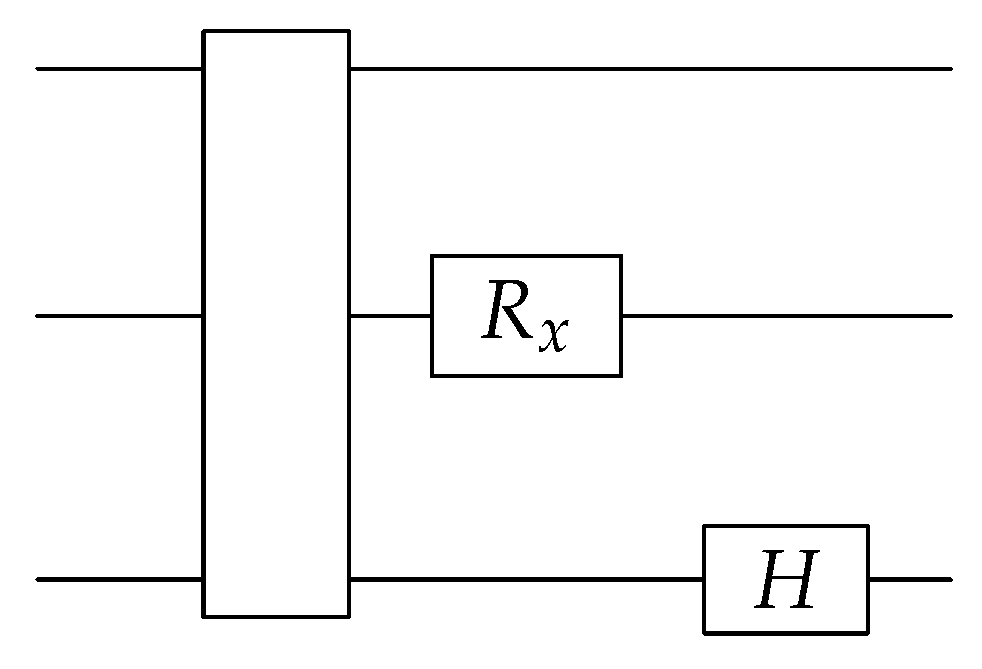
3.4. Q-Gates, Circuits, and Algorithms
3.5. Common Quantum Applications
3.5.1. Information Encoding
- Basis encoding;
- Amplitude encoding;
- Qsample encoding;
- Dynamic encoding.
3.5.2. Quantum Teleportation
- Parties and create an entangled pair.
- applies a CNOT gate with the unknown state .
- applies a Hadamard gate to the first qubit of the result in 2.
- measures the results from 3.
- communicates the measurement results with .
3.5.3. Quantum Cryptography
- No-cloning theorem;
- State collapse when measured;
- Irreversible measurement.
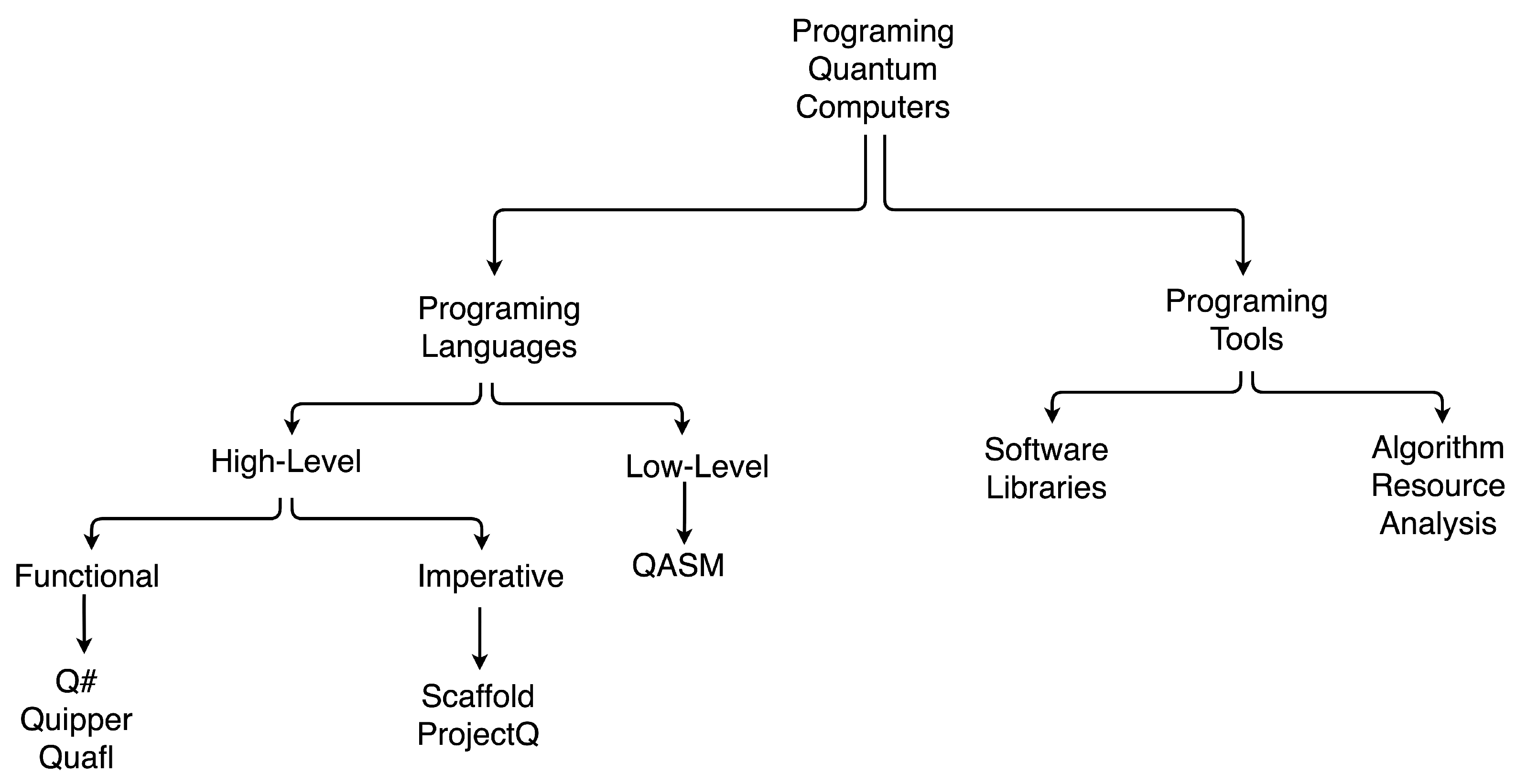
4. Quantum Computing Frameworks
4.1. Comparing Common Types of Quantum Bit Technologies
4.2. Challenges in the Field of Quantum Computation
4.2.1. Experimental Challenges of Quantum Computing: Quantum Computers
- Putting atoms in precise quantum states;
- Manipulating the interactions of the atoms to carry out logical procedures;
- Obtaining the computational output by monitoring the resultant states.
4.2.2. Theoretical Challenges of Quantum Computing: Quantum Simulators
5. Quantum Computing’s Chronology and Origin Sequence
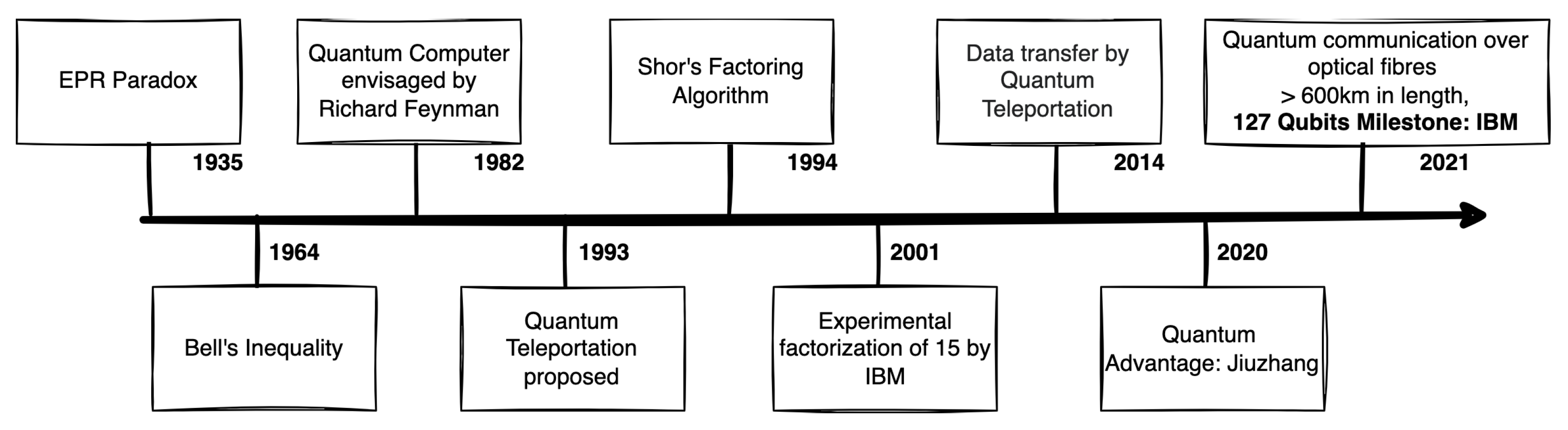
5.1. Quantum Computing Chronology
5.2. From Physics to Quantum Computing
6. Discussion
6.1. State of the Art
6.2. Emerging Quantum Machine Learning Technology
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schuld, M.; Petruccione, F. Supervised Learning with Quantum Computers; Springer: Berlin/Heidelberg, Germany, 2018; Volume 17. [Google Scholar]
- Montanaro, A. Quantum algorithms: An overview. Npj Quantum Inf. 2016, 2, 15023. [Google Scholar] [CrossRef]
- Jordan, S. The Quantum Algorithm Zoo. 2021. Available online: http://math.nist.gov/quantum/zoo/ (accessed on 1 November 2021).
- Marais, A.; Adams, B.; Ringsmuth, A.K.; Ferretti, M.; Gruber, J.M.; Hendrikx, R.; Schuld, M.; Smith, S.L.; Sinayskiy, I.; Krüger, T.P.; et al. The future of quantum biology. J. R. Soc. Interface 2018, 15, 20180640. [Google Scholar] [CrossRef] [Green Version]
- Biamonte, J.; Faccin, M.; De Domenico, M. Complex networks from classical to quantum. Commun. Phys. 2019, 2, 53. [Google Scholar] [CrossRef] [Green Version]
- McMahon, D. Quantum Mechanics Demystified; McGraw-Hill Education: New York, NY, USA, 2013. [Google Scholar]
- Samuel, A.L. Some studies in machine learning using the game of checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Alzubi, J.; Nayyar, A.; Kumar, A. Machine Learning from Theory to Algorithms: An Overview. J. Phys. Conf. Ser. 2018, 1142, 012012. [Google Scholar] [CrossRef]
- Rivas, P. Deep Learning for Beginners: A Beginner’s Guide to Getting Up and Running with Deep Learning from Scratch Using Python; Packt Publishing Ltd.: Birmingham, UK, 2020. [Google Scholar]
- Mehta, P.; Bukov, M.; Wang, C.H.; Day, A.G.; Richardson, C.; Fisher, C.K.; Schwab, D.J. A high-bias, low-variance introduction to machine learning for physicists. Phys. Rep. 2019, 810, 1–124. [Google Scholar] [CrossRef]
- Mahesh, B. Machine Learning Algorithms—A Review. Int. J. Sci. Res. (IJSR) 2020, 9, 381–386. [Google Scholar]
- Bonaccorso, G. Machine Learning Algorithms; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Wittek, P. Quantum Machine Learning: What Quantum Computing Means to Data Mining; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum computation and quantum information. Phys. Today 2001, 54, 60. [Google Scholar]
- McMahon, D. Quantum Computing Explained; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Mermin, N.D. Quantum Computer Science: An Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Kaye, P.; Laflamme, R.; Mosca, M. An Introduction to Quantum Computing; Oxford University Press on Demand: Oxford, UK, 2007. [Google Scholar]
- Grumbling, E.; Horowitz, M. Adiabatic Quantum Computing and Quantum Annealing. In Quantum Computing: Progress and Prospects; The National Academies Press: Washington DC, USA, 2019. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef]
- Grant, E.K.; Humble, T.S. Adiabatic Quantum Computing and Quantum Annealing; Oxford University Press: Oxford, UK, 2020. [Google Scholar] [CrossRef]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153. [Google Scholar] [CrossRef] [Green Version]
- Michielsen, K.; Nocon, M.; Willsch, D.; Jin, F.; Lippert, T.; De Raedt, H. Benchmarking gate-based quantum computers. Comput. Phys. Commun. 2017, 220, 44–55. [Google Scholar] [CrossRef]
- Mosca, M. Quantum algorithms. arXiv 2008, arXiv:0808.0369. [Google Scholar]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef] [Green Version]
- Blatt, R.; Roos, C.F. Quantum simulations with trapped ions. Nat. Phys. 2012, 8, 277–284. [Google Scholar] [CrossRef]
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 2019, 6, 021318. [Google Scholar] [CrossRef]
- Huang, H.L.; Wu, D.; Fan, D.; Zhu, X. Superconducting quantum computing: A review. Sci. China Inf. Sci. 2020, 63, 1–32. [Google Scholar] [CrossRef]
- Kok, P.; Munro, W.J.; Nemoto, K.; Ralph, T.C.; Dowling, J.P.; Milburn, G.J. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 2007, 79, 135. [Google Scholar] [CrossRef] [Green Version]
- Nicolas, A.; Veissier, L.; Giner, L.; Giacobino, E.; Maxein, D.; Laurat, J. A quantum memory for orbital angular momentum photonic qubits. Nat. Photonics 2014, 8, 234–238. [Google Scholar] [CrossRef] [Green Version]
- Weiss, D.S.; Saffman, M. Quantum computing with neutral atoms. Phys. Today 2017, 70, 7–44. [Google Scholar] [CrossRef]
- Havlíček, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chow, J.M.; Gambetta, J.M. Supervised learning with quantum-enhanced feature spaces. Nature 2019, 567, 209–212. [Google Scholar] [CrossRef] [Green Version]
- Schuld, M. Machine Learning in Quantum Spaces; Nature Publishing Group: Berlin, Germany, 2019. [Google Scholar]
- Schuld, M. Quantum machine learning models are kernel methods. arXiv 2021, arXiv:2101.11020. [Google Scholar]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef] [Green Version]
- Bell, J.S. On the einstein podolsky rosen paradox. Phys. Phys. Fiz. 1964, 1, 195. [Google Scholar] [CrossRef] [Green Version]
- Feynman, R.P. Simulating physics with computers. In Feynman and Computation; CRC Press: Boca Raton, FL, USA, 2018; pp. 133–153. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [Green Version]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Vandersypen, L.M.; Steffen, M.; Breyta, G.; Yannoni, C.S.; Sherwood, M.H.; Chuang, I.L. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 2001, 414, 883–887. [Google Scholar] [CrossRef] [Green Version]
- Pfaff, W.; Hensen, B.J.; Bernien, H.; van Dam, S.B.; Blok, M.S.; Taminiau, T.H.; Tiggelman, M.J.; Schouten, R.N.; Markham, M.; Twitchen, D.J.; et al. Unconditional quantum teleportation between distant solid-state quantum bits. Science 2014, 345, 532–535. [Google Scholar] [CrossRef] [Green Version]
- Zhong, H.S.; Wang, H.; Deng, Y.H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [CrossRef]
- Daiss, S.; Langenfeld, S.; Welte, S.; Distante, E.; Thomas, P.; Hartung, L.; Morin, O.; Rempe, G. A quantum-logic gate between distant quantum-network modules. Science 2021, 371, 614–617. [Google Scholar] [CrossRef]
- Ball, P. First quantum computer to pack 100 qubits enters crowded race. Nature 2021, 599, 542. [Google Scholar] [CrossRef]
- Guan, W.; Perdue, G.; Pesah, A.; Schuld, M.; Terashi, K.; Vallecorsa, S.; Vlimant, J.R. Quantum machine learning in high energy physics. Mach. Learn. Sci. Technol. 2021, 2, 011003. [Google Scholar] [CrossRef]
- Vijayasri, I.; Javier, O.-D. Quantum Machine Learning Concepts and Applications. 2020. Available online: https://research.latinxinai.org/workshops/neurips/neurips-2020.html (accessed on 1 November 2021).
- Orduz-Ducuara, J.A. Quantum Machine Learning and Higgs Phenomenology. 2020; in preparation. [Google Scholar]
- Orduz, J.; Iyer, V. Quantum Machine Learning concepts for Physicists. Tecnología Educativa, Revista CONAIC, Mexico City, Mexico, 2021; Volume VIII, pp. 71–75. Número 2, Mayo–Agosto 2021. ISSN 2395-9061. Available online: https://terc.mx/index.php/terc (accessed on 1 November 2021).
- Williams, C.P. Explorations in Quantum Computing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Khanal, B.; Rivas, P.; Orduz, J. Quantum Machine Learning: A Case Study of Grover’s Algorithm. In Proceedings of the 19th International Conference on Scientific Computing (CSC 2021), Las Vegas, NV, USA, 15–17 December 2021. [Google Scholar]
- Jui, T.; Ayoade, O.; Rivas, P.; Orduz, J. Performance Analysis of Quantum Machine Learning Classifiers. In Proceedings of the NeurIPS 2021 Workshop LatinX in AI, Virtual Event, 7 December 2021. [Google Scholar]
- Garg, S.; Ramakrishnan, G. Advances in quantum deep learning: An overview. arXiv 2020, arXiv:2005.04316. [Google Scholar]
- Huang, H.L.; Du, Y.; Gong, M.; Zhao, Y.; Wu, Y.; Wang, C.; Li, S.; Liang, F.; Lin, J.; Xu, Y.; et al. Experimental quantum generative adversarial networks for image generation. Phys. Rev. Appl. 2021, 16, 024051. [Google Scholar] [CrossRef]
- Cong, I.; Choi, S.; Lukin, M.D. Quantum convolutional neural networks. Nat. Phys. 2019, 15, 1273–1278. [Google Scholar] [CrossRef] [Green Version]
- Rivas, P.; Zhao, L.; Orduz, J. Hybrid Quantum Variational Autoencoders for Representation Learning. In Proceedings of the 19th International Conference on Scientific Computing (CSC 2021), Las Vegas, NV, USA, 15–17 December 2021. [Google Scholar]
- Liu, J.; Lim, K.H.; Wood, K.L.; Huang, W.; Guo, C.; Huang, H.L. Hybrid quantum-classical convolutional neural networks. Sci. China Phys. Mech. Astron. 2021, 64, 290311. [Google Scholar] [CrossRef]
- Arunachalam, S.; de Wolf, R. Guest column: A survey of quantum learning theory. ACM Sigact News 2017, 48, 41–67. [Google Scholar] [CrossRef]
- Hogg, T.; Portnov, D. Quantum optimization. Inf. Sci. 2000, 128, 181–197. [Google Scholar] [CrossRef]
- Li, Y.; Tian, M.; Liu, G.; Peng, C.; Jiao, L. Quantum optimization and quantum learning: A survey. IEEE Access 2020, 8, 23568–23593. [Google Scholar] [CrossRef]
- Harrigan, M.P.; Sung, K.J.; Neeley, M.; Satzinger, K.J.; Arute, F.; Arya, K.; Atalaya, J.; Bardin, J.C.; Barends, R.; Boixo, S.; et al. Quantum approximate optimization of non-planar graph problems on a planar superconducting processor. Nat. Phys. 2021, 17, 332–336. [Google Scholar] [CrossRef]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 2015, 56, 172–185. [Google Scholar] [CrossRef] [Green Version]
- Cross, A.W.; DiVincenzo, D.P.; Terhal, B.M. A comparative code study for quantum fault-tolerance. arXiv 2007, arXiv:0711.1556. [Google Scholar] [CrossRef]
- Schumacher, B.; Nielsen, M.A. Quantum data processing and error correction. Phys. Rev. A 1996, 54, 2629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gottesman, D. Theory of fault-tolerant quantum computation. Phys. Rev. A 1998, 57, 127. [Google Scholar] [CrossRef] [Green Version]
- Knill, E.; Laflamme, R.; Viola, L. Theory of quantum error correction for general noise. Phys. Rev. Lett. 2000, 84, 2525. [Google Scholar] [CrossRef] [Green Version]
- Devitt, S.J.; Munro, W.J.; Nemoto, K. Quantum error correction for beginners. Rep. Prog. Phys. 2013, 76, 076001. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, S. Universal quantum simulators. Science 1996, 273, 1073–1078. [Google Scholar] [CrossRef]
- Barreiro, J.T.; Müller, M.; Schindler, P.; Nigg, D.; Monz, T.; Chwalla, M.; Hennrich, M.; Roos, C.F.; Zoller, P.; Blatt, R. An open-system quantum simulator with trapped ions. Nature 2011, 470, 486–491. [Google Scholar] [CrossRef] [Green Version]
- Aspuru-Guzik, A.; Walther, P. Photonic quantum simulators. Nat. Phys. 2012, 8, 285–291. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Chang, M.S.; Korenblit, S.; Islam, R.; Edwards, E.E.; Freericks, J.K.; Lin, G.D.; Duan, L.M.; Monroe, C. Quantum simulation of frustrated Ising spins with trapped ions. Nature 2010, 465, 590–593. [Google Scholar] [CrossRef]
- Shao, C.; Li, Y.; Li, H. Quantum algorithm design: Techniques and applications. J. Syst. Sci. Complex. 2019, 32, 375–452. [Google Scholar] [CrossRef]
- Behrman, E.C.; Steck, J.E.; Kumar, P.; Walsh, K. Quantum algorithm design using dynamic learning. arXiv 2008, arXiv:0808.1558. [Google Scholar] [CrossRef]
- Cafaro, C. Geometric algebra and information geometry for quantum computational software. Phys. A Stat. Mech. Appl. 2017, 470, 154–196. [Google Scholar] [CrossRef] [Green Version]
- Bang, J.; Ryu, J.; Yoo, S.; Pawłowski, M.; Lee, J. A strategy for quantum algorithm design assisted by machine learning. New J. Phys. 2014, 16, 073017. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Lai, Z.Y.; Li, X. Quantum adiabatic algorithm design using reinforcement learning. Phys. Rev. A 2020, 101, 052327. [Google Scholar] [CrossRef]
- Gushanskiy, S.; Polenov, M.; Potapov, V. The methodology of implementation and simulation of quantum algorithms and processes. In Proceedings of the 2017 IEEE 11th International Conference on Application of Information and Communication Technologies (AICT), Moscow, Russia, 20–22 September 2017; pp. 1–5. [Google Scholar]
- Vinci, W.; Albash, T.; Paz-Silva, G.; Hen, I.; Lidar, D.A. Quantum annealing correction with minor embedding. Phys. Rev. A 2015, 92, 042310. [Google Scholar] [CrossRef] [Green Version]
- Tremsin, A.S.; Siegmund, O.H.; Vallerga, J.V.; Hull, J.S.; Abiad, R. Cross-strip readouts for photon counting detectors with high spatial and temporal resolution. IEEE Trans. Nucl. Sci. 2004, 51, 1707–1711. [Google Scholar] [CrossRef] [Green Version]
- Chiesa, A.; Tacchino, F.; Grossi, M.; Santini, P.; Tavernelli, I.; Gerace, D.; Carretta, S. Quantum hardware simulating four-dimensional inelastic neutron scattering. Nat. Phys. 2019, 15, 455–459. [Google Scholar] [CrossRef]
- Mykhailovaa, M.; Soekena, M. Testing Quantum Programs using Q# and Microsoft Quantum Development Kit. In Proceedings of the 2nd Quantum Software and Engineering Workshop (QSET’21), Virtual, 19 October 2021. [Google Scholar]
- Wootton, J.R. Procedural generation using quantum computation. In Proceedings of the International Conference on the Foundations of Digital Games, Bugibba, Malta, 15–18 September 2020; pp. 1–8. [Google Scholar]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [Green Version]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145. [Google Scholar] [CrossRef] [Green Version]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef] [Green Version]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.H.; Brassard, G.; Mermin, N.D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Bessette, F.; Brassard, G.; Salvail, L.; Smolin, J. Experimental quantum cryptography. J. Cryptol. 1992, 5, 3–28. [Google Scholar] [CrossRef]
- Gisin, N.; Thew, R. Quantum communication. Nat. Photonics 2007, 1, 165–171. [Google Scholar] [CrossRef] [Green Version]
- McCaskey, A.; Dumitrescu, E.; Chen, M.; Lyakh, D.; Humble, T. Validating quantum-classical programming models with tensor network simulations. PLoS ONE 2018, 13, e0206704. [Google Scholar] [CrossRef] [Green Version]
- Lanzagorta, M.; Uhlmann, J.K. Hybrid quantum-classical computing with applications to computer graphics. In Proceedings of the ACM SIGGRAPH 2005 Courses, Los Angeles, CA, USA, 31 July–4 August 2005. [Google Scholar]
- Bergholm, V.; Izaac, J.; Schuld, M.; Gogolin, C.; Alam, M.S.; Ahmed, S.; Arrazola, J.M.; Blank, C.; Delgado, A.; Jahangiri, S.; et al. Pennylane: Automatic differentiation of hybrid quantum-classical computations. arXiv 2018, arXiv:1811.04968. [Google Scholar]
- Kop, M. Establishing a Legal-Ethical Framework for Quantum Technology. Yale Law Sch. Yale J. Law Technol. (YJoLT) Rec. 2 March 2021. Available online: https://ssrn.com/abstract=3814422 (accessed on 1 November 2021).
- Perrier, E. Ethical Quantum Computing: A Roadmap. arXiv 2021, arXiv:2102.00759. [Google Scholar]
- Perrier, E. Quantum Fair Machine Learning. arXiv 2021, arXiv:2102.00753. [Google Scholar]






| Quantum Algorithms | |
|---|---|
| Quantum Fourier transform | Amplitude amplification |
| Simon’s algorithm | Grover’s algorithm |
| Shor’s algorithm | Quantum counting |
| Tool | Programming Language | Quantum Computing Paradigm | Framework Description |
|---|---|---|---|
| Cirq | Python | Discrete gate model | A library for creating, manipulating, and optimizing Noisy Intermediate Scale Quantum (NISQ) circuits, which can then be executed on quantum computers and simulators. |
| dwave-system | Python | Quantum annealing | An API for using the D-Wave system as a sampler in the D-Wave Ocean software stack, either directly or via Leap’s cloud-based hybrid solvers. |
| FermiLib | Python | Discrete gate model | An open-source software suite that makes it easier to create and test algorithms for quantum computer simulations of fermionic systems. |
| Qbsolv | C | Quantum annealing | A deconstructing solver that splits a huge quadratic unconstrained binary optimization (QUBO) problem into pieces to obtain a minimal value. |
| QGL.jl | Julia | Discrete gate model | A QGL compiler with a focus on performance. |
| Qiskit.js | JavaScript | Discrete gate model | Quantum Information Science Kit for JavaScript. |
| Qrack | C++ | Discrete gate model | A complete framework for constructing universal virtual quantum processors that is GPU accelerated. |
| Quirk | JavaScript | Discrete gate model | A browser-based quantum circuit simulator with drag-and-drop functionality. A toy for experimenting with and learning about small quantum circuits. |
| Strawberry Fields | Python | Continuous gate model | A Python library for developing, optimizing, and implementing photonic quantum computers. |
| Trapped Ion Qubit | Superconducting Qubit | Photonic Qubit |
|---|---|---|
| To produce qubits, lasers are used to ionize atoms and trap them in electric potentials. The status of the qubits is then measured using an extra laser. | The qubits are created by combining a superconducting resonator with a nonlinear inductor to make an artificial atom. | The squeezed state (light working as qubit) is created by distributing laser light to an array of squeezers (microscopic devices comprised of relatively small ring resonators). |
| Stable qubits can be generated using trapped ion technology, and forming an entangled state is simple. Working with large numbers of qubits in this system is challenging, and implementing a whole quantum algorithm is even more complicated. Decoherence is a difficult problem to solve. | Building and accurately measuring qubits with superconducting technology is simple. These qubits have a nanosecond time scale and a quick decoherence time. Qubits must be cooled to near absolute zero to function, and computation is subject to quantum noise. | Qubits are far more stable in photonic technology and can readily entangle a huge number of photons. It is possible to perform computation at room temperature, but it is less fault-tolerant, and error correction is harder. According to this technique, quantum supremacy is attained. |
| Year | Activity | Reference |
|---|---|---|
| 1935 | EPR Paradox | [34] |
| 1964 | Bell’s Inequality | [35] |
| 1982 | Quantum Computer envisaged by Richard Feynman | [36] |
| 1993 | Quantum Teleportation proposed | [37] |
| 1994 | Shor’s Factoring Algorithm | [38] |
| 2001 | Experimental factorization of 15 by IBM | [39] |
| 2014 | Data transfer by Quantum Teleportation | [40] |
| 2020 | Quantum Advantage: Jiuzhang | [41] |
| 2021 | Quantum communication over optical fibers over 600 km in length | [42] |
| 2021 | 127 Qubits Milestone: IBM | [43] |
| Interesting Reads | Reference |
|---|---|
| Quantum Learning and Optimization | [56,57,58,59] |
| Quantum Machine Learning | [19,32,33,44,54,60] |
| Quantum Fault Tolerance and Error Correction | [61,62,63,64,65] |
| Quantum System Simulation | [21,25,66,67,68,69] |
| Quantum Algorithm Designs | [70,71,72,73,74,75] |
| Quantum Hardware Test Development | [76,77,78,79,80] |
| Quantum Cryptography | [81,82,83,84,85,86,87] |
| Hybrid (Quantum–Classical) Computing | [54,55,88,89,90] |
| Ethical Quantum Computing | [91,92,93] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayoade, O.; Rivas, P.; Orduz, J. Artificial Intelligence Computing at the Quantum Level. Data 2022, 7, 28. https://doi.org/10.3390/data7030028
Ayoade O, Rivas P, Orduz J. Artificial Intelligence Computing at the Quantum Level. Data. 2022; 7(3):28. https://doi.org/10.3390/data7030028
Chicago/Turabian StyleAyoade, Olawale, Pablo Rivas, and Javier Orduz. 2022. "Artificial Intelligence Computing at the Quantum Level" Data 7, no. 3: 28. https://doi.org/10.3390/data7030028
APA StyleAyoade, O., Rivas, P., & Orduz, J. (2022). Artificial Intelligence Computing at the Quantum Level. Data, 7(3), 28. https://doi.org/10.3390/data7030028








