A Fully Unsupervised Deep Learning Framework for Non-Rigid Fundus Image Registration
Abstract
:1. Introduction
- A fully automatic learning strategy that unifies a context-aware CNN, a spatial transformation network and a label-free similarity metric to perform fundus image registration in one-shot without the need for any ground-truth data.
- Once trained, the registration model is capable of aligning fundus images of several classes and databases (e.g., super-resolution, retinal mosaics, and photographs containing anatomical differences).
- The combination of multiple DL networks with image analysis techniques, such as isotropic undecimated wavelet transform and connected component analysis, allowing for the registration of fundus photographs even with low-quality segments and abrupt changes.
2. Related Work
3. Materials and Methods
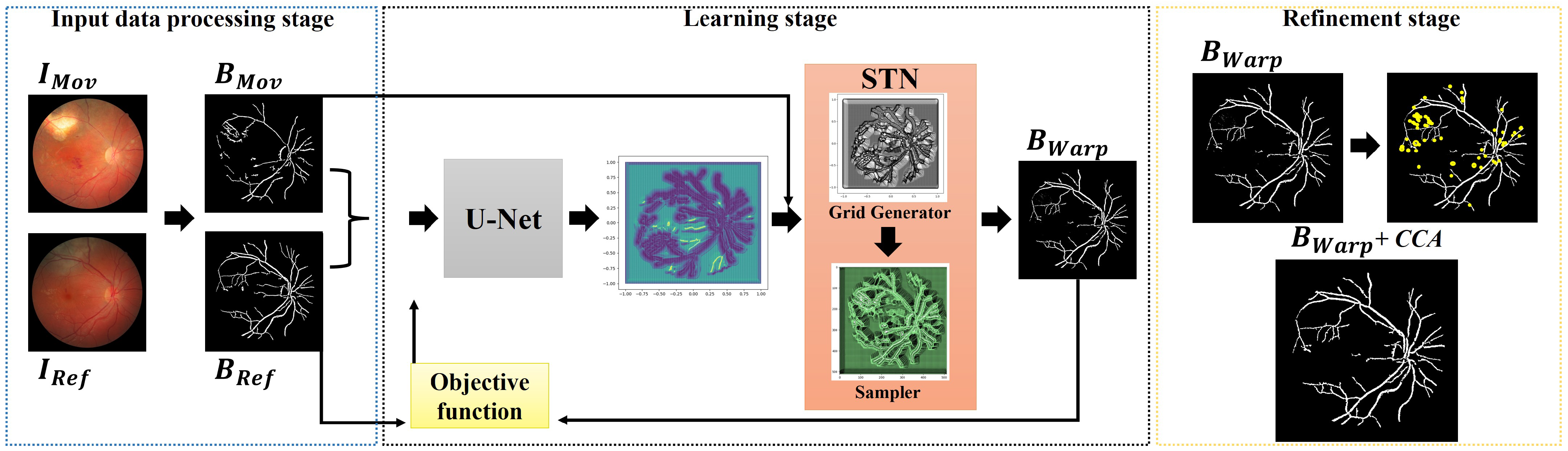
3.1. Overview of the Proposed Approach
3.2. Network Input Preparation
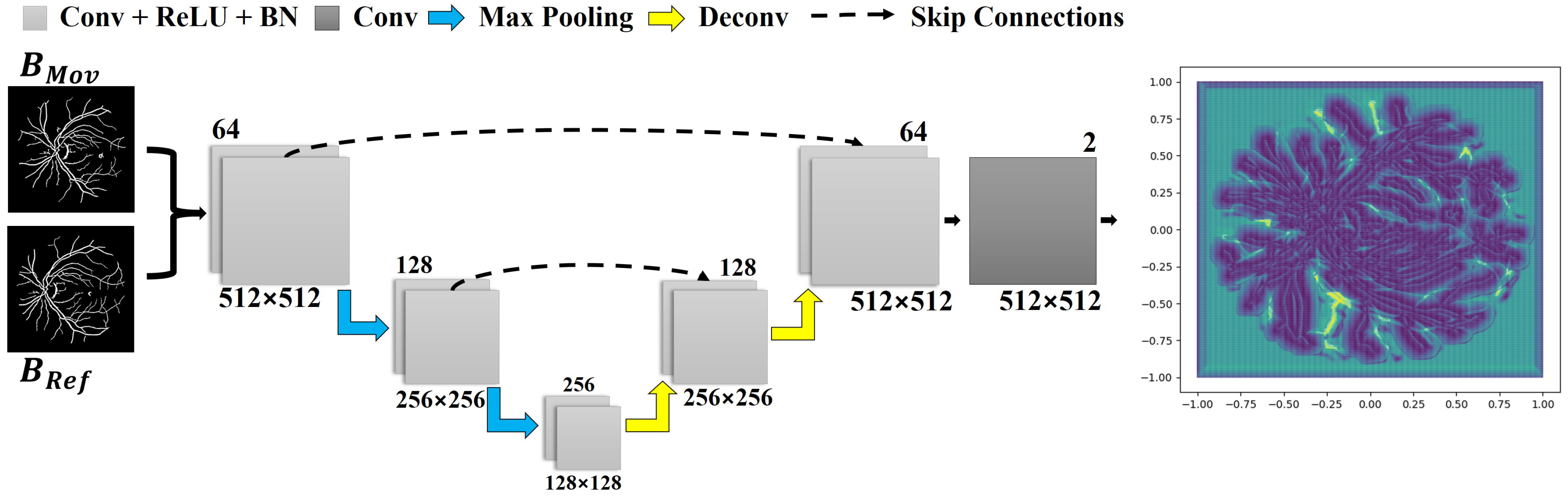
3.3. Learning a Deep Correspondence Grid
3.4. Learning a Spatial Transformation
3.5. Objective Function
3.6. Refinement Process
3.7. Datasets and Assessment Metrics
- FIRE—A full database containing several classes of high-resolution fundus images, as detailed in [49]. This data collection comprises 134 pairs of images, grouped into three categories: A, S, and P. Categories A and S covers 14 and 71 pairs of images, respectively, whose fundus photographs present an estimated overlap of more than 75%. Category A also includes images with anatomical differences. Category P, on the other hand, is formed by image pairs with less than 75% of estimated overlap.
- Image Quality Assessment Dataset (Dataset 1)—this public dataset [50] is composed of 18 pairs of images captured from 18 individuals, where each pair is formed by a poor-quality image (blurred and/or with dark lighting with occlusions), and a high-quality image of the same eye. There are also pairs containing small displacements caused by eye movements during the acquisition process.
- Preventive Eye Exams Dataset: (Dataset 2)—a full database containing 85 pairs of retinal images provided by an ophthalmologist [7]. This data collection gathers real cases of acquisitions such as monitoring diseases, the presence of artifacts, noise, and excessive rotations, i.e., several particular situations typically faced by ophthalmologists and other eye specialists in their routine examinations with real patients.
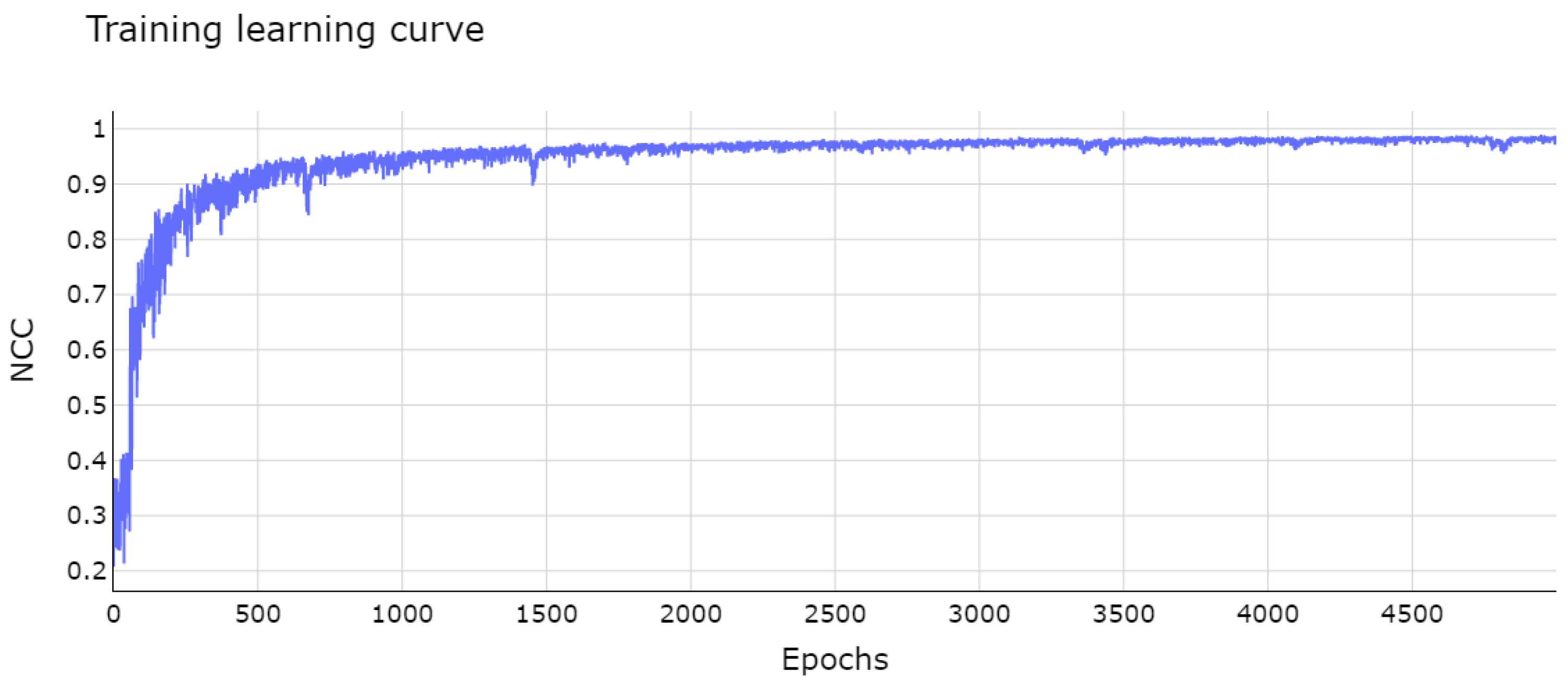
3.8. Implementation Details and Training
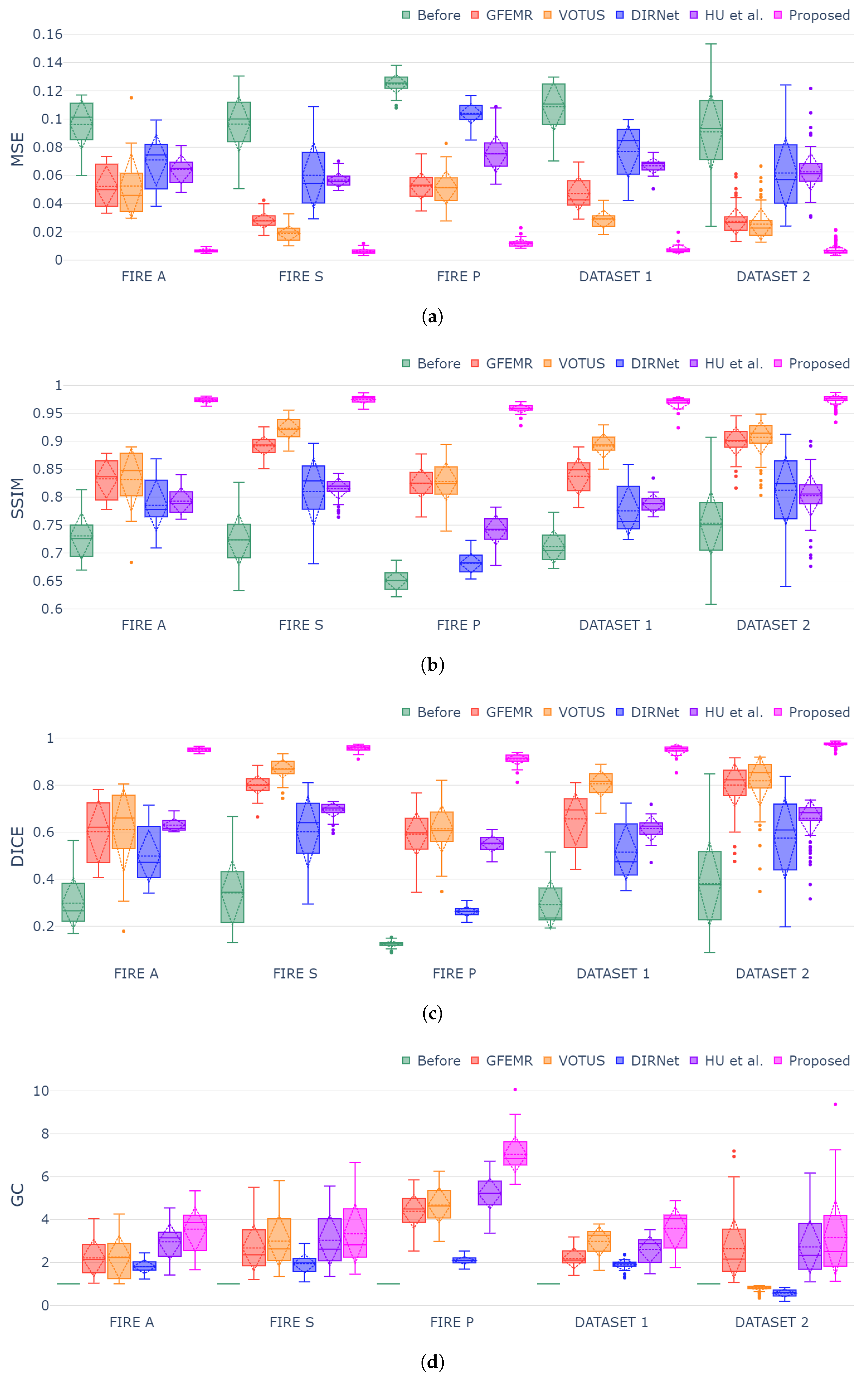
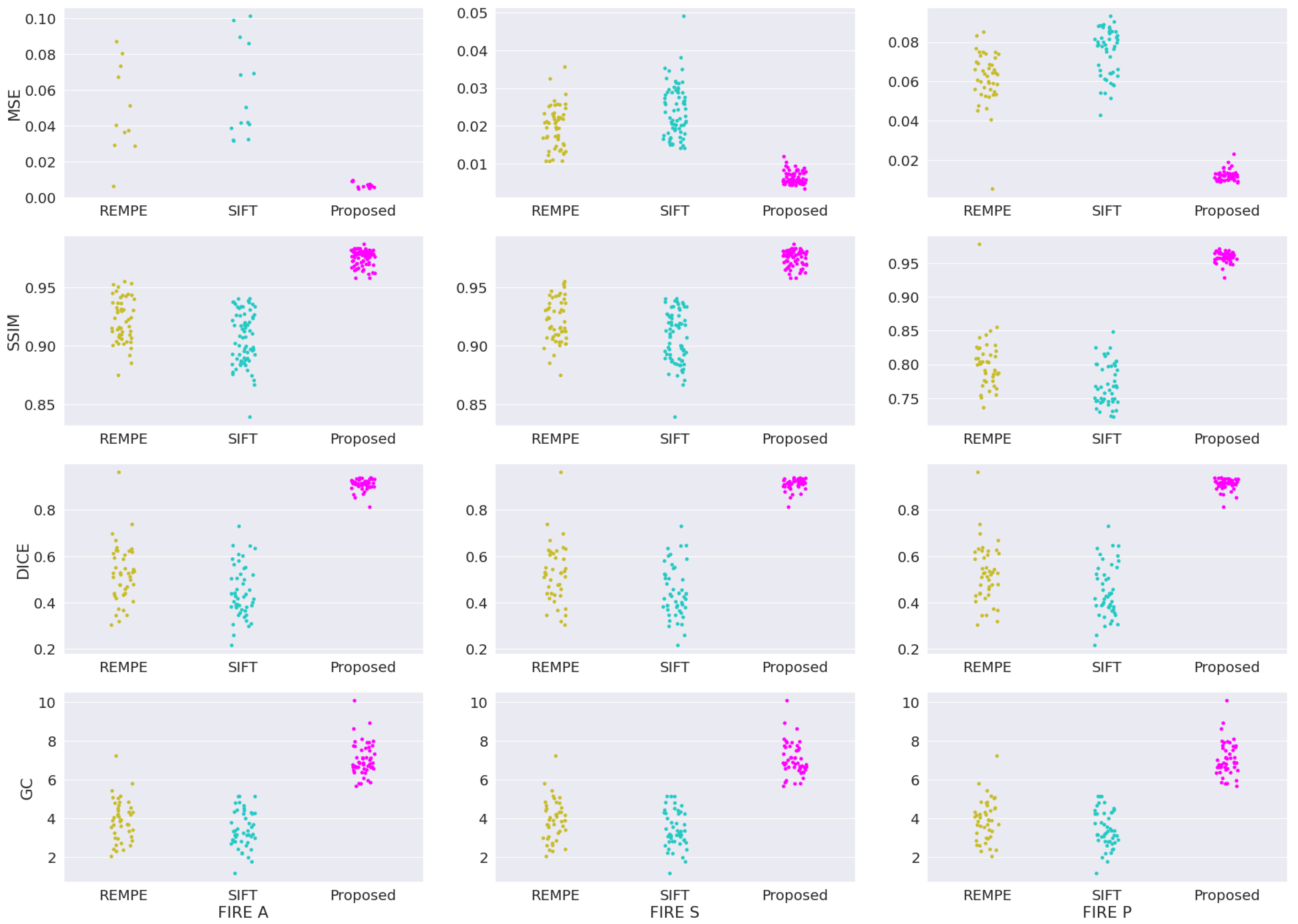
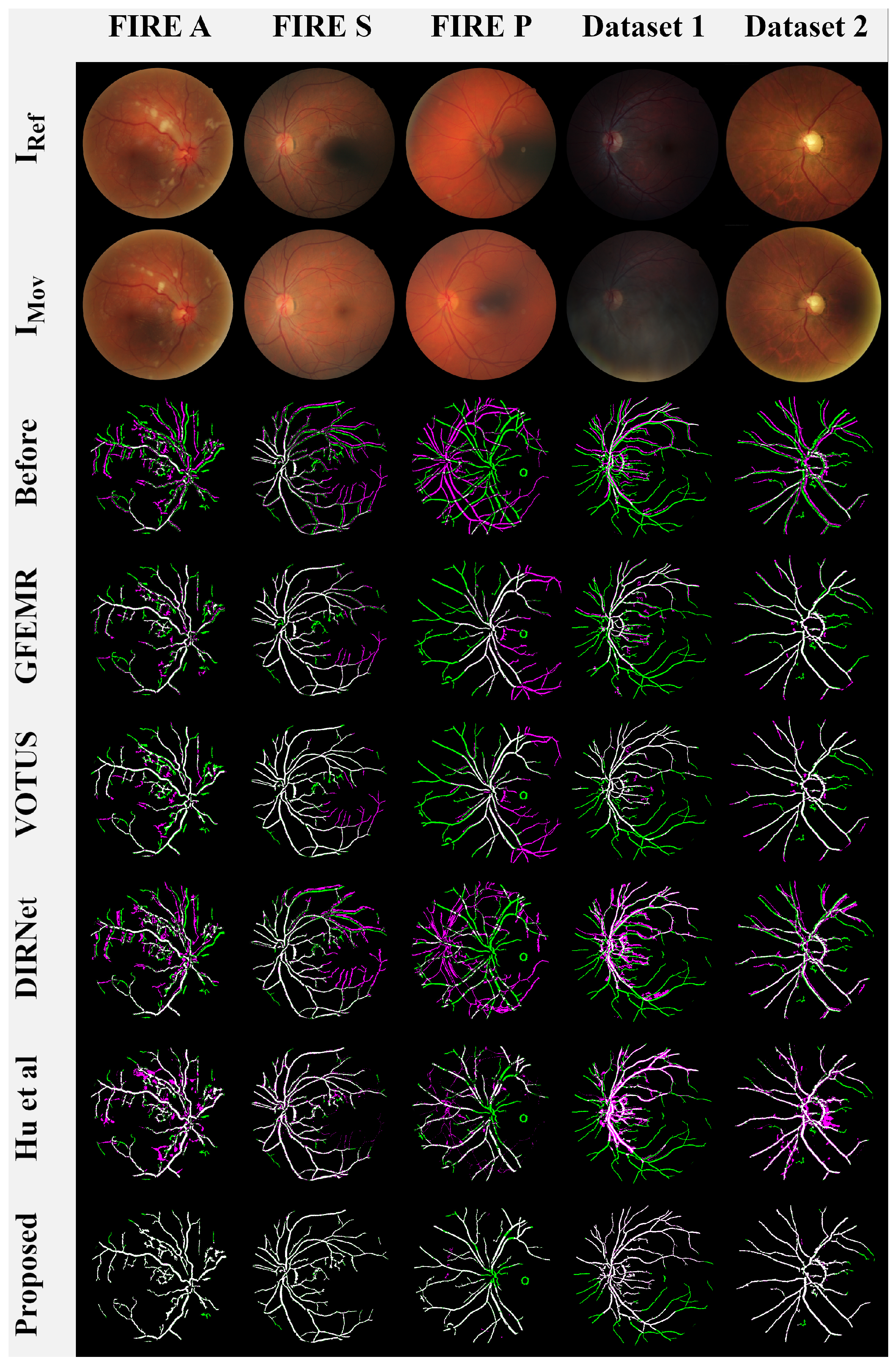
4. Results and Discussion
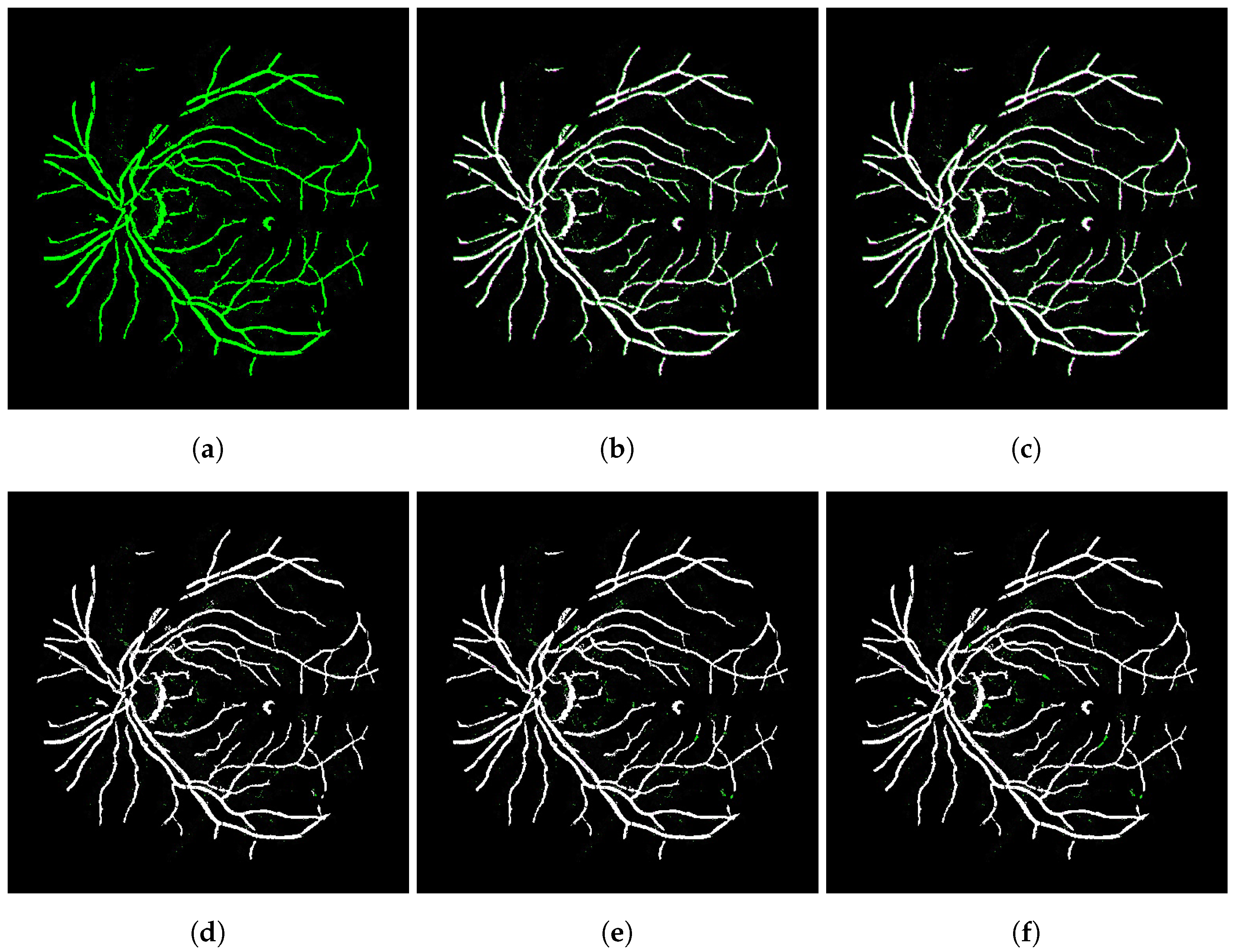
4.1. Ablation Study
4.2. Comparison with Image Registration Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Weinreb, R.N.; Aung, T.; Medeiros, F.A. The pathophysiology and treatment of glaucoma: A review. J. Am. Med. Assoc. (JAMA) 2014, 311, 1901–1911. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, K.M.; Heo, T.Y.; Kim, A.; Kim, J.; Han, K.J.; Yun, J.; Min, J.K. Development of a Fundus Image-Based Deep Learning Diagnostic Tool for Various Retinal Diseases. J. Pers. Med. 2021, 11, 321. [Google Scholar] [CrossRef] [PubMed]
- Shabbir, A.; Rasheed, A.; Shehraz, H.; Saleem, A.; Zafar, B.; Sajid, M.; Ali, N.; Dar, S.H.; Shehryar, T. Detection of glaucoma using retinal fundus images: A comprehensive review. Math. Biosci. Eng. 2021, 18, 2033–2076. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.K.; Xiao, D.; Bhuiyan, A.; Wong, T.Y.; Kanagasingam, Y. Color fundus image registration techniques and applications for automated analysis of diabetic retinopathy progression: A review. Biomed. Signal Process. Control 2019, 47, 288–302. [Google Scholar] [CrossRef]
- Ramli, R.; Hasikin, K.; Idris, M.Y.I.; Karim, N.K.A.; Wahab, A.W.A. Fundus Image Registration Technique Based on Local Feature of Retinal Vessels. Appl. Sci. 2021, 11, 11201. [Google Scholar] [CrossRef]
- Karali, E.; Asvestas, P.; Nikita, K.S.; Matsopoulos, G.K. Comparison of Different Global and Local Automatic Registration Schemes: An Application to Retinal Images. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Saint-Malo, France, 26–29 September 2004; pp. 813–820. [Google Scholar]
- Motta, D.; Casaca, W.; Paiva, A. Vessel Optimal Transport for Automated Alignment of Retinal Fundus Images. IEEE Trans. Image Process. 2019, 28, 6154–6168. [Google Scholar] [CrossRef]
- Dasariraju, S.; Huo, M.; McCalla, S. Detection and classification of immature leukocytes for diagnosis of acute myeloid leukemia using random forest algorithm. Bioengineering 2020, 7, 120. [Google Scholar] [CrossRef]
- Bechelli, S.; Delhommelle, J. Machine Learning and Deep Learning Algorithms for Skin Cancer Classification from Dermoscopic Images. Bioengineering 2022, 9, 97. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.A.; van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [Green Version]
- Haskins, G.; Kruger, U.; Yan, P. Deep learning in medical image registration: A survey. Mach. Vis. Appl. 2020, 31, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Diaz-Pinto, A.; Ravikumar, N.; Frangi, A. Deep learning in medical image registration. Prog. Biomed. Eng. 2020, 3, 012003. [Google Scholar] [CrossRef]
- Pluim, J.P.; Muenzing, S.E.; Eppenhof, K.A.; Murphy, K. The truth is hard to make: Validation of medical image registration. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 2294–2300. [Google Scholar] [CrossRef]
- Punn, N.S.; Agarwal, S. Modality specifc U-Net variants for biomedical image segmentation: A survey. Artif. Intell. Rev. 2022, 3, 1–45. [Google Scholar]
- de Vos, B.D.; Berendsen, F.F.; Viergever, M.A.; Sokooti, H.; Staring, M.; Išgum, I. A deep learning framework for unsupervised affine and deformable image registration. Med. Image Anal. 2019, 52, 128–143. [Google Scholar] [CrossRef] [Green Version]
- Benvenuto, G.A.; Colnago, M.; Casaca, W. Unsupervised Deep Learning Network for Deformable Fundus Image Registration. In Proceedings of the ICASSP 2022—IEEE International Conference on Acoustics, Speech and Signal Processing, Singapore, 22–27 May 2022; pp. 1281–1285. [Google Scholar]
- Oh, K.; Kang, H.M.; Leem, D.; Lee, H.; Seo, K.Y.; Yoon, S. Early detection of diabetic retinopathy based on deep learning and ultra-wide-field fundus images. Sci. Rep. 2021, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Mushtaq, G.; Siddiqui, F. Detection of diabetic retinopathy using deep learning methodology. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Tamil Nadu, India, 4–5 December 2020; Volume 1070, p. 012049. [Google Scholar]
- Ajitha, S.; Akkara, J.D.; Judy, M. Identification of glaucoma from fundus images using deep learning techniques. Indian J. Ophthalmol. 2021, 69, 2702. [Google Scholar] [PubMed]
- Deperlioglu, O.; Kose, U.; Gupta, D.; Khanna, A.; Giampaolo, F.; Fortino, G. Explainable framework for Glaucoma diagnosis by image processing and convolutional neural network synergy: Analysis with doctor evaluation. Future Gener. Comput. Syst. 2022, 129, 152–169. [Google Scholar] [CrossRef]
- Du, R.; Xie, S.; Fang, Y.; Igarashi-Yokoi, T.; Moriyama, M.; Ogata, S.; Tsunoda, T.; Kamatani, T.; Yamamoto, S.; Cheng, C.Y.; et al. Deep learning approach for automated detection of myopic maculopathy and pathologic myopia in fundus images. Ophthalmol. Retin. 2021, 5, 1235–1244. [Google Scholar] [CrossRef] [PubMed]
- Mahapatra, D.; Bozorgtabar, B.; Hewavitharanage, S.; Garnavi, R. Image Super Resolution Using Generative Adversarial Networks and Local Saliency Maps for Retinal Image Analysis. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI, Quebec City, QC, Canada, 11–13 September 2017; Descoteaux, M., Maier-Hein, L., Franz, A., Jannin, P., Collins, D.L., Duchesne, S., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 382–390. [Google Scholar]
- Manakov, I.; Rohm, M.; Kern, C.; Schworm, B.; Kortuem, K.; Tresp, V. Noise as Domain Shift: Denoising Medical Images by Unpaired Image Translation. In Proceedings of the Domain Adaptation and Representation Transfer and Medical Image Learning with Less Labels and Imperfect Data, Shenzhen, China, 13–17 October 2019; Wang, Q., Milletari, F., Nguyen, H.V., Albarqouni, S., Cardoso, M.J., Rieke, N., Xu, Z., Kamnitsas, K., Patel, V., Roysam, B., et al., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 3–10. [Google Scholar]
- Sanchez, Y.D.; Nieto, B.; Padilla, F.D.; Perdomo, O.; Osorio, F.A.G. Segmentation of retinal fluids and hyperreflective foci using deep learning approach in optical coherence tomography scans. Proc. SPIE 2020, 11583, 136–143. [Google Scholar] [CrossRef]
- You, A.; Kim, J.K.; Ryu, I.H.; Yoo, T.K. Application of Generative Adversarial Networks (GAN) for Ophthalmology Image Domains: A Survey. Eye Vis. 2022, 9, 1–19. [Google Scholar] [CrossRef]
- Fu, Y.; Lei, Y.; Wang, T.; Curran, W.J.; Liu, T.; Yang, X. Deep learning in medical image registration: A review. Phys. Med. Biol. 2020, 65, 20TR01. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Kwitt, R.; Styner, M.; Niethammer, M. Fast predictive multimodal image registration. In Proceedings of the 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, Australia, 18–21 April 2017; pp. 858–862. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Yang, J.; Zhang, J.; Nie, D.; Kim, M.; Wang, Q.; Shen, D. Deformable Image Registration Based on Similarity-Steered CNN Regression. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2017, Quebec City, QC, Canada, 11–13 September 2017; Descoteaux, M., Maier-Hein, L., Franz, A., Jannin, P., Collins, D.L., Duchesne, S., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 300–308. [Google Scholar]
- Eppenhof, K.A.J.; Pluim, J.P.W. Pulmonary CT Registration Through Supervised Learning With Convolutional Neural Networks. IEEE Trans. Med. Imaging 2019, 38, 1097–1105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Fan, J.; Cao, X.; Yap, P.T.; Shen, D. BIRNet: Brain image registration using dual-supervised fully convolutional networks. Med. Image Anal. 2019, 54, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Hering, A.; Kuckertz, S.; Heldmann, S.; Heinrich, M.P. Enhancing Label-Driven Deep Deformable Image Registration with Local Distance Metrics for State-of-the-Art Cardiac Motion Tracking. In Bildverarbeitung für die Medizin 2019; Handels, H., Deserno, T.M., Maier, A., Maier-Hein, K.H., Palm, C., Tolxdorff, T., Eds.; Springer: Wiesbaden, Germany, 2019; pp. 309–314. [Google Scholar]
- Hu, Y.; Modat, M.; Gibson, E.; Li, W.; Ghavami, N.; Bonmati, E.; Wang, G.; Bandula, S.; Moore, C.M.; Emberton, M.; et al. Weakly-supervised convolutional neural networks for multimodal image registration. Med. Image Anal. 2018, 49, 1–13. [Google Scholar] [CrossRef]
- Lv, J.; Yang, M.; Zhang, J.; Wang, X. Respiratory motion correction for free-breathing 3D abdominal MRI using CNN-based image registration: A feasibility study. Br. J. Radiol. 2018, 91, 20170788. [Google Scholar] [CrossRef]
- Zhang, J. Inverse-Consistent Deep Networks for Unsupervised Deformable Image Registration. arXiv 2018, arXiv:1809.03443. [Google Scholar]
- Kori, A.; Krishnamurthi, G. Zero Shot Learning for Multi-Modal Real Time Image Registration. arXiv 2019, arXiv:1908.06213. [Google Scholar]
- Wang, C.; Yang, G.; Papanastasiou, G. FIRE: Unsupervised bi-directional inter- and intra-modality registration using deep networks. In Proceedings of the 2021 IEEE 34th International Symposium on Computer-Based Medical Systems (CBMS), Virtual, 7–9 June 2021; pp. 510–514. [Google Scholar] [CrossRef]
- Balakrishnan, G.; Zhao, A.; Sabuncu, M.; Guttag, J.; Dalca, A.V. VoxelMorph: A Learning Framework for Deformable Medical Image Registration. IEEE TMI Trans. Med. Imaging 2019, 38, 1788–1800. [Google Scholar] [CrossRef] [Green Version]
- Mahapatra, D.; Antony, B.; Sedai, S.; Garnavi, R. Deformable Medical Image Registration using Generative Adversarial Networks. In Proceedings of the IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 1449–1453. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; An, C.; Cavichini, M.; Jhingan, M.; Amador-Patarroyo, M.J.; Long, C.P.; Bartsch, D.U.G.; Freeman, W.R.; Nguyen, T.Q. A Segmentation Based Robust Deep Learning Framework for Multimodal Retinal Image Registration. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1369–1373. [Google Scholar] [CrossRef]
- Rivas-Villar, D.; Hervella, Á.S.; Rouco, J.; Novo, J. Color fundus image registration using a learning-based domain-specific landmark detection methodology. Comput. Biol. Med. 2022, 140, 105101. [Google Scholar] [CrossRef]
- Rohé, M.M.; Datar, M.; Heimann, T.; Sermesant, M.; Pennec, X. SVF-Net: Learning Deformable Image Registration Using Shape Matching. In Proceedings of the MICCAI 2017—The 20th International Conference on Medical Image Computing and Computer Assisted Intervention, Quebec City, QC, Canada, 11–13 September 2017; pp. 266–274. [Google Scholar] [CrossRef] [Green Version]
- Bankhead, P.; Scholfield, C.; McGeown, J.; Curtis, T. Fast retinal vessel detection and measurement using wavelets and edge location refinement. PLoS ONE 2012, 7, e32435. [Google Scholar] [CrossRef] [Green Version]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial transformer networks. In Proceedings of the NIPS, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Kaso, A. Computation of the normalized cross-correlation by fast Fourier transform. PLoS ONE 2018, 13, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Hisham, M.; Yaakob, S.N.; Raof, R.; Nazren, A.A.; Wafi, N. Template Matching using Sum of Squared Difference and Normalized Cross Correlation. In Proceedings of the 2015 IEEE Student Conference on Research and Development (SCOReD), Kuala Lumpur, Malaysia, 13–14 December 2015; pp. 100–104. [Google Scholar] [CrossRef]
- Cui, Z.; Qi, W.; Liu, Y. A Fast Image Template Matching Algorithm Based on Normalized Cross Correlation. J. Phys. Conf. Ser. 2020, 1693, 012163. [Google Scholar] [CrossRef]
- He, L.; Ren, X.; Gao, Q.; Zhao, X.; Yao, B.; Chao, Y. The connected-component labeling problem: A review of state-of-the-art algorithms. Pattern Recognit. 2017, 70, 25–43. [Google Scholar] [CrossRef]
- Hernandez-Matas, C.; Zabulis, X.; Triantafyllou, A.; Anyfanti, P.; Douma, S.; Argyros, A. FIRE: Fundus Image Registration Dataset. J. Model. Ophthalmol. 2017, 1, 16–28. [Google Scholar] [CrossRef]
- Köhler, T.; Budai, A.; Kraus, M.F.; Odstrčilik, J.; Michelson, G.; Hornegger, J. Automatic no-reference quality assessment for retinal fundus images using vessel segmentation. In Proceedings of the 26th IEEE International Symposium on Computer-Based Medical Systems, Porto, Portugal, 20–22 June 2013; pp. 95–100. [Google Scholar] [CrossRef] [Green Version]
- Che, T.; Zheng, Y.; Cong, J.; Jiang, Y.; Niu, Y.; Jiao, W.; Zhao, B.; Ding, Y. Deep Group-Wise Registration for Multi-Spectral Images From Fundus Images. IEEE Access 2019, 7, 27650–27661. [Google Scholar] [CrossRef]
- Motta, D.; Casaca, W.; Paiva, A. Fundus Image Transformation Revisited: Towards Determining More Accurate Registrations. In Proceedings of the IEEE International Symposium on Computer-Based Medical Systems (CBMS), Karlstad, Sweden, 18–21 June 2018; pp. 227–232. [Google Scholar]
- Bradski, G. The OpenCV Library. Dr. Dobb’s J. Softw. Tools 2000, 120, 122–125. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Brigato, L.; Iocchi, L. A Close Look at Deep Learning with Small Data. In Proceedings of the IEEE International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 2490–2497. [Google Scholar]
- Wang, J.; Chen, J.; Xu, H.; Zhang, S.; Mei, X.; Huang, J.; Ma, J. Gaussian field estimator with manifold regularization for retinal image registration. Signal Process. 2019, 157, 225–235. [Google Scholar] [CrossRef]
- de Vos, B.; Berendsen, F.; Viergever, M.; Staring, M.; Išgum, I. End-to-end unsupervised deformable image registration with a convolutional neural network. arXiv 2017, arXiv:1704.06065. [Google Scholar]
- Hernandez-Matas, C.; Zabulis, X.; Argyros, A. REMPE: Registration of Retinal Images Through Eye Modelling and Pose Estimation. IEEE J. Biomed. Health Informat. 2020, 24, 3362–3373. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]

| Papers | Ref. | Images Type | Network | Architecture | Transformation |
|---|---|---|---|---|---|
| Yang et al. | [27] | Brain MRI (3D) | Supervised | Encoder + Decoder | Affine + Nonrigid (LDDMM) |
| Cao et al. | [28] | Brain MRI (3D) | Supervised | Network preparation + network learning | Affine + Nonrigid (TPS) |
| Eppenhof and Pluim | [29] | Chest CT (3D) | Supervised | Adapted U-Net | Nonrigid (B-Spline) |
| Fan et al. | [31] | Brain MRI (3D) | Weakly supervised | BIRNet | Nonrigid |
| Hering et al. | [32] | Cardiac MRI (3D) | Weakly supervised | Adapted U-Net | Nonrigid (B-Spline) |
| Hu et al. | [33] | TRUS and prostate MRI (3D) | Weakly supervised | Global Net + Local Net | Affine + Non-rigid |
| Mahapatra et al. | [39] | Retinal FA images + cardiac MRI (2D) | Weakly supervised | GAN | Nonrigid |
| Wang et al. | [40] | Multimodal retinal image | Weakly supervised | Segmentation network + feature detection and description network + outlier rejection network | Affine |
| Rivas-Villar et al. | [41] | Color fundus images | Weakly supervised | U-Net + RANSAC | Similarity transformation |
| Jun et al. | [34] | Abdominal MRI (2D and 3D) | Unsupervised | CNN + STN | Nonrigid (B-Spline) |
| Zhang | [35] | Brain MRI (3D) | Unsupervised | Adapted U-Net + 2 FCN | Nonrigid (B-Spline) |
| Vos et al. | [15] | Cardiac MRI and chest CT (3D) | Unsupervised | CNN Affine + CNN nonrigid | Affine + Nonrigid (B-Spline) |
| Wang et al. | [37] | Brain MRI (2D and 3D) | Unsupervised | Encoder + decoders + transformation networks | Affine + Nonrigid |
| Kori et al. | [36] | Brain MRI (3D) | Unsupervised | VGG-19 + transformation estimator | Affine |
| Balakrishnan et al. | [38] | Brain MRI (3D) | Unsupervised | Adapted U-Net + STN (+ information optional auxiliary) | Nonrigid (linear) |
| Metrics | Methods | FIRE A | FIRE S | FIRE P | Dataset 1 | Dataset 2 |
|---|---|---|---|---|---|---|
| MSE (↓) | Network | 0.0080 (0.0017) | 0.0074 (0.0019) | 0.0143 (0.0026) | 0.0095 (0.0034) | 0.0093 (0.0039) |
| Network + Opening | 0.0287 (0.0030) | 0.0319 (0.0023) | 0.0343 (0.0031) | 0.0324 (0.0037) | 0.0268 (0.0035) | |
| Network + Closing | 0.0284 (0.0029) | 0.0316 (0.0023) | 0.0337 (0.0030) | 0.0321 (0.0035) | 0.0265 (0.0034) | |
| Network + CCA 10 | 0.0068 (0.0015) | 0.0062 (0.0017) | 0.0121 (0.0027) | 0.0079 (0.0034) | 0.0071 (0.0038) | |
| Network + CCA 20 | 0.0068 (0.0014) | 0.0062 (0.0017) | 0.0120 (0.0027) | 0.0079 (0.0035) | 0.0071 (0.0038) | |
| Network + CCA 30 | 0.0069 (0.0015) | 0.0063 (0.0017) | 0.0121 (0.0027) | 0.0080 (0.0035) | 0.0071 (0.0038) | |
| SSIM (↑) | Network | 0.9586 (0.0086) | 0.9638 (0.0104) | 0.9290 (0.0080) | 0.9539 (0.0130) | 0.9572 (0.0162) |
| Network + Opening | 0.8928 (0.0110) | 0.8807 (0.0094) | 0.8773 (0.0107) | 0.8797 (0.0130) | 0.9001 (0.0118) | |
| Network + Closing | 0.8923 (0.0103) | 0.8818 (0.0092) | 0.8752 (0.0104) | 0.8800 (0.0124) | 0.8998 (0.0119) | |
| Network + CCA 10 | 0.9731 (0.0055) | 0.9749 (0.0068) | 0.9575 (0.0076) | 0.9682 (0.0128) | 0.9733 (0.0106) | |
| Network + CCA 20 | 0.9732 (0.0053) | 0.9748 (0.0068) | 0.9585 (0.0075) | 0.9681 (0.0133) | 0.9734 (0.0103) | |
| Network + CCA 30 | 0.9727 (0.0054) | 0.9744 (0.0068) | 0.9580 (0.0073) | 0.9678 (0.0133) | 0.9733 (0.0102) | |
| Dice (↑) | Network | 0.9399 (0.0121) | 0.9484 (0.0143) | 0.8915 (0.0237) | 0.9363 (0.0268) | 0.9295 (0.0425) |
| Network + Opening | 0.7814 (0.0101) | 0.7743 (0.0121) | 0.7367 (0.0173) | 0.7807 (0.0359) | 0.8046 (0.0382) | |
| Network + Closing | 0.7874 (0.0090) | 0.7798 (0.0117) | 0.7465 (0.0171) | 0.7860 (0.0331) | 0.8086 (0.0369) | |
| Network + CCA 10 | 0.9502 (0.0100) | 0.9579 (0.0120) | 0.9103 (0.0238) | 0.9476 (0.0265) | 0.9466 (0.0404) | |
| Network + CCA 20 | 0.9505 (0.0097) | 0.9580 (0.0122) | 0.9109 (0.0238) | 0.9477 (0.0270) | 0.9467 (0.0404) | |
| Network + CCA 30 | 0.9496 (0.0100) | 0.9573 (0.0123) | 0.9097 (0.0236) | 0.9471 (0.0270) | 0.9463 (0.0404) | |
| GC (↑) | Network | 3.4237 (0.9921) | 3.2125 (1.3424) | 6.7499 (0.8029) | 3.4786 (0.9630) | 3.0494 (1.6853) |
| Network + Opening | 2.8025 (0.8065) | 2.5910 (1.0920) | 5.4621 (0.6265) | 2.8544 (0.7680) | 2.6075 (1.4265) | |
| Network + Closing | 2.8733 (0.8394) | 2.6515 (1.1326) | 5.6395 (0.6508) | 2.9203 (0.7960) | 2.6565 (1.4714) | |
| Network + CCA 10 | 3.5511 (1.0343 ) | 3.3379 (1.3973) | 7.0506 (0.8443) | 3.5963 (0.9943) | 3.1755 (1.7625) | |
| Network + CCA 20 | 3.5520 (1.0361) | 3.3378 (1.3965) | 7.0410 (0.8410) | 3.5956 (0.9940) | 3.1716 (1.7571) | |
| Network + CCA 30 | 3.5443 (1.0345) | 3.3321 (1.3920) | 7.0160 (0.8373) | 3.5892 (0.9888) | 3.1672 (1.7517) |
| Metric | Method | Fire A | FIRE S | FIRE P | Dataset 1 | Dataset 2 |
|---|---|---|---|---|---|---|
| MSE | Before | < | 0.0 | 0.0 | < | 0.0 |
| GFEMR | < | 0.0 | 0.0 | < | 0.0 | |
| VOTUS | < | 0.0 | 0.0 | < | 0.0 | |
| DIRNet | < | 0.0 | 0.0 | < | 0.0 | |
| HU et al. | < | 0.0 | 0.0 | < | 0.0 | |
| SSIM | Before | < | 0.0 | 0.0 | < | 0.0 |
| GFEMR | < | 0.0 | 0.0 | < | 0.0 | |
| VOTUS | < | 0.0 | 0.0 | < | 0.0 | |
| DIRNet | < | 0.0 | 0.0 | < | 0.0 | |
| HU et al. | < | 0.0 | 0.0 | < | 0.0 | |
| DICE | Before | < | 0.0 | 0.0 | < | 0.0 |
| GFEMR | < | 0.0 | 0.0 | < | 0.0 | |
| VOTUS | < | 0.0 | 0.0 | < | 0.0 | |
| DIRNet | < | 0.0 | 0.0 | < | 0.0 | |
| HU et al. | < | 0.0 | 0.0 | < | 0.0 | |
| GC | Before | < | 0.0 | 0.0 | < | 0.0 |
| GFEMR | 0.0017 | 0.0028 | 0.0 | 0.0001 | 0.0253 | |
| VOTUS | 0.0058 | 0.1206 | 0.0 | 0.0224 | 0.0 | |
| DIRNet | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| HU et al. | 0.1139 | 0.1994 | 0.0 | 0.0037 | 0.1594 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benvenuto, G.A.; Colnago, M.; Dias, M.A.; Negri, R.G.; Silva, E.A.; Casaca, W. A Fully Unsupervised Deep Learning Framework for Non-Rigid Fundus Image Registration. Bioengineering 2022, 9, 369. https://doi.org/10.3390/bioengineering9080369
Benvenuto GA, Colnago M, Dias MA, Negri RG, Silva EA, Casaca W. A Fully Unsupervised Deep Learning Framework for Non-Rigid Fundus Image Registration. Bioengineering. 2022; 9(8):369. https://doi.org/10.3390/bioengineering9080369
Chicago/Turabian StyleBenvenuto, Giovana A., Marilaine Colnago, Maurício A. Dias, Rogério G. Negri, Erivaldo A. Silva, and Wallace Casaca. 2022. "A Fully Unsupervised Deep Learning Framework for Non-Rigid Fundus Image Registration" Bioengineering 9, no. 8: 369. https://doi.org/10.3390/bioengineering9080369
APA StyleBenvenuto, G. A., Colnago, M., Dias, M. A., Negri, R. G., Silva, E. A., & Casaca, W. (2022). A Fully Unsupervised Deep Learning Framework for Non-Rigid Fundus Image Registration. Bioengineering, 9(8), 369. https://doi.org/10.3390/bioengineering9080369








