Evaluation of Measurement Errors in Rotational Stitching, One-Shot, and Slot-Scanning Full-Length Radiography
Abstract
1. Introduction
2. Materials and Methods
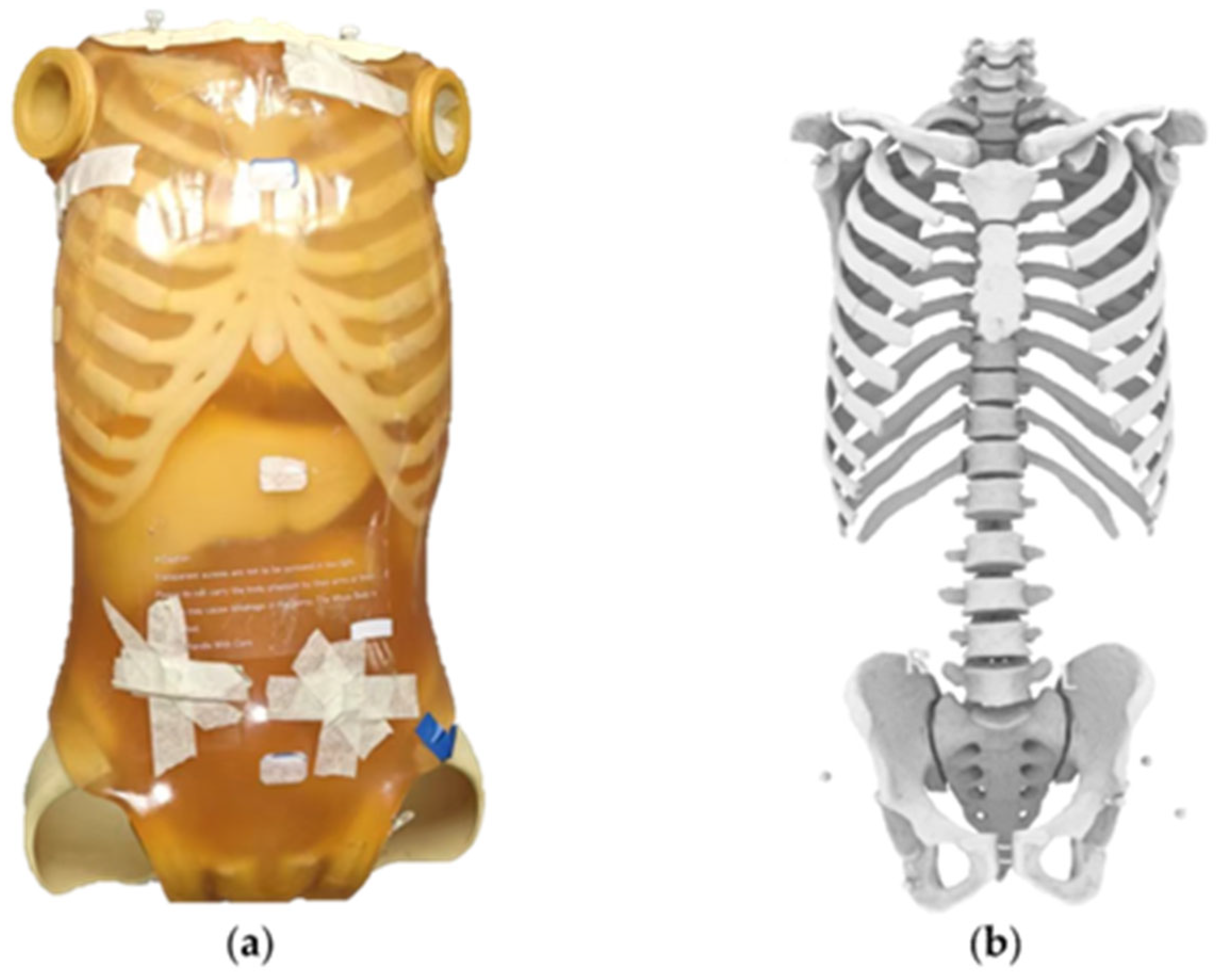
2.1. Phantom Preparation and Reference Standard Establishment
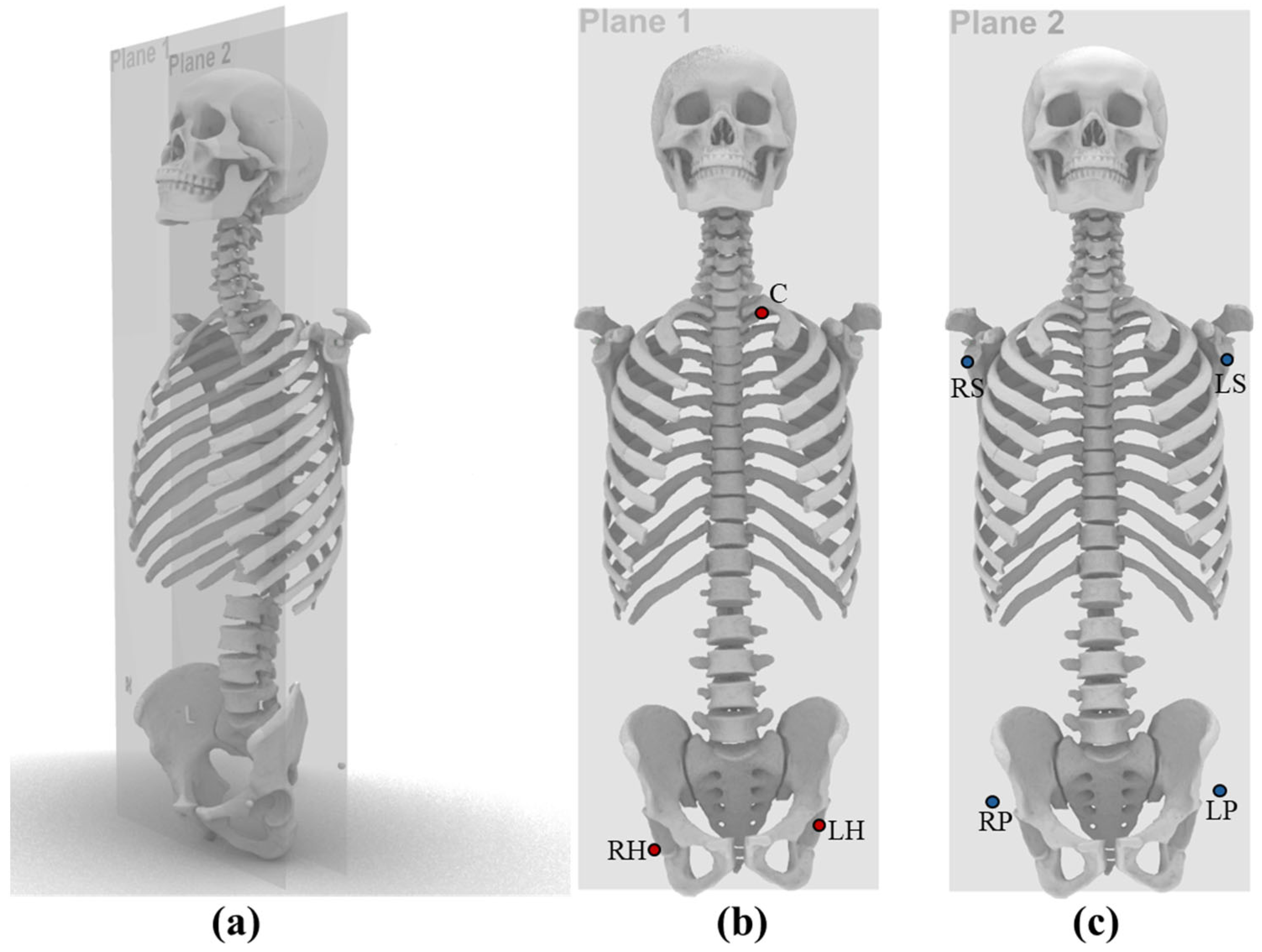
2.2. Fix Markers
2.3. Three-Dimensional Measurement of Anatomical Landmark Distances Using CT
2.4. Two-Dimensional Measurement of Anatomical Landmark Distances on Full-Length Radiographs
2.5. Fitting the Centers of Steel Beads
2.6. Scaling Correction
2.7. Accuracy Comparison
2.8. Statistical Methods
3. Results
3.1. Steel Beads Diameter Measurements
| Markers | Diameter of Steel Beads Measured by Different Systems(mm) | ||||||
|---|---|---|---|---|---|---|---|
| Eagle Eye | EOS | GC85A | UDR780iPro3F | DRX-Compass | DSI-DRP | ||
| Plane 1 | C | 9.69 | 7.92 | 9.14 | 9.93 | 11.92 | 8.67 |
| LH | 9.64 | 7.96 | 9.30 | 10.04 | 11.84 | 8.76 | |
| RH | 9.75 | 8.01 | 9.30 | 10.13 | 11.94 | 8.65 | |
| MEAN | 9.69 | 7.96 | 9.25 | 10.04 | 11.90 | 8.69 | |
| ε | 1.21 | 1.00 | 1.16 | 1.25 | 1.49 | 1.09 | |
| Plane 2 | RP | 9.59 | 7.88 | 8.74 | 9.72 | 11.75 | 8.57 |
| LP | 9.64 | 7.88 | 8.70 | 9.51 | 11.79 | 8.53 | |
| LS | 9.58 | 7.85 | 8.47 | 9.45 | 11.29 | 8.50 | |
| RS | 9.53 | 7.82 | 8.44 | 9.41 | 11.27 | 8.60 | |
| MEAN | 9.58 | 7.86 | 8.58 | 9.52 | 11.53 | 8.55 | |
| ε | 1.20 | 0.98 | 1.07 | 1.19 | 1.44 | 1.07 | |
3.2. Hough Transform Circularity Metric Results
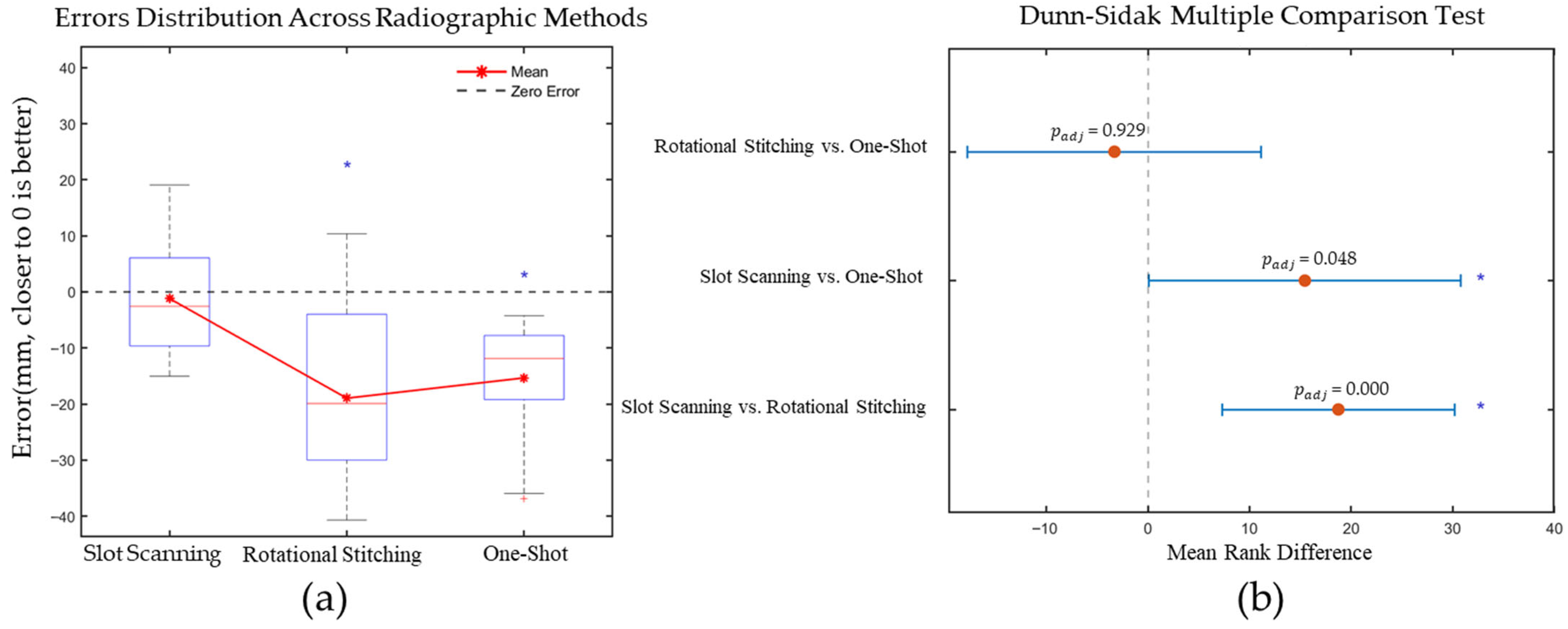
3.3. Distance Error of Different Manufacturers
3.4. Statistical Analysis
3.4.1. Significance of Measurement Errors Across Radiographic Systems
3.4.2. Influence of Imaging Methods on Measurement Error
4. Discussion
4.1. Measurement Accuracy and Systematic Errors Across Rradiographic Systems
4.2. Analysis of Inter-Group Errors
4.2.1. Measurement Errors Attributable to Full-Length Radiography Methods
- Minimization of Geometric Distortion: The extremely narrow collimation produces a quasi-parallel projection at each incremental position, sharply limiting angular ray divergence. By contrast, the one-shot modality deploys a broad cone beam over a large field of view; peripheral rays impinge at steeper angles, generating systematic anisotropic magnification gradients even with a longer SID. Rotational stitching must register and interpolate overlapping segments acquired under slightly varying projection angles; any minor misregistration or interpolation smoothing can propagate into systematic distance bias.
- Systematic Reduction in Scattered Radiation: The slot collimator restricts the irradiated area, reducing scattered radiation by over 80% compared to conventional modalities and significantly enhancing image contrast and edge definition [33].
- Geometric Consistency During Scanning: The fixed geometric relationship and single-axis translation ensure uniform imaging conditions throughout the scanned region. Rotational stitching compounds geometric variability because each partial exposure is acquired at a slightly different source–object–detector geometry along an arcuate or translational path, requiring algorithmic warping and blending that can introduce residual non-linear scaling.
4.2.2. Correction Errors Attributable to Image Protocols and Algorithms
4.3. Analysis of Intra-Group Errors
4.3.1. Difference Between EOS Imaging and Eagle Eye
4.3.2. Difference Between UDR780IPRO3F, GC85A and DRX-Compass
4.4. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SID | Source to Image Distance |
| SOD | Source to Object Distance |
| HTO | High Tibial Osteotomy |
References
- Ichikawa, S.; Muto, H.; Imao, M.; Nonaka, T.; Sakekawa, K.; Sato, Y. Low-Dose Whole-Spine Imaging Using Slot-Scan Digital Radiography: A Phantom Study. BMC Med. Imaging 2023, 23, 17. [Google Scholar] [CrossRef] [PubMed]
- Zampogna, B.; Vasta, S.; Amendola, A.; Uribe-Echevarria Marbach, B.; Gao, Y.; Papalia, R.; Denaro, V. Assessing Lower Limb Alignment: Comparison of Standard Knee Xray vs Long Leg View. Iowa Orthop. J. 2015, 35, 49–54. [Google Scholar]
- Zhang, J.; Yu, Y.; Gao, S.; Hai, Y.; Wu, B.; Su, X.; Wang, Z. The Classification of Coronal Deformity Based on Preoperative Global Coronal Malalignment for Adult Spinal Deformity Is Questionable. BMC Musculoskelet. Disord. 2022, 23, 300. [Google Scholar] [CrossRef] [PubMed]
- Roguski, M.; Benzel, E.C.; Curran, J.N.; Magge, S.N.; Bisson, E.F.; Krishnaney, A.A.; Steinmetz, M.P.; Butler, W.E.; Heary, R.F.; Ghogawala, Z. Postoperative Cervical Sagittal Imbalance Negatively Affects Outcomes Following Surgery for Cervical Spondylotic Myelopathy. Spine 2014, 39, 2070. [Google Scholar] [CrossRef]
- Tang, J.A.; Scheer, J.K.; Deviren, V.; Bess, S.; Hart, R.A.; Lafage, V.; Shaffrey, C.I.; Schwab, F.; Ames, C.P. The Impact of Standing Regional Cervical Sagittal Alignment on Outcomes in Posterior Cervical Fusion Surgery. Neurosurgery 2012, 71, 662–669. [Google Scholar] [CrossRef]
- Renkawitz, T.; Weber, T.; Dullien, S.; Woerner, M.; Dendorfer, S.; Grifka, J.; Weber, M. Leg Length and Offset Differences above 5 Mm after Total Hip Arthroplasty Are Associated with Altered Gait Kinematics. Gait Posture 2016, 49, 196–201. [Google Scholar] [CrossRef]
- Gurney, B. Leg Length Discrepancy. Gait Posture 2002, 15, 195–206. [Google Scholar] [CrossRef]
- Gait Asymmetry in Patients with Limb-Length Inequality: Journal of Pediatric Orthopaedics. Available online: https://journals.lww.com/pedorthopaedics/fulltext/1996/03000/gait_asymmetry_in_patients_with_limb_length.2.aspx (accessed on 6 September 2025).
- Murray, R.; Winkler, P.W.; Shaikh, H.S.; Musahl, V. High Tibial Osteotomy for Varus Deformity of the Knee. JAAOS Glob. Res. Rev. 2021, 5, e21.00141. [Google Scholar] [CrossRef]
- Kfuri, M.; Crist, B.D.; Stannard, J.P. Preoperative Planning and Preservation of the Knee with Complex Osteotomies. Mo. Med. 2022, 119, 144. [Google Scholar]
- Samsudin, S.; Adwan, S.; Arof, H.; Mokhtar, N.; Ibrahim, F. Development of Automated Image Stitching System for Radiographic Images. J. Digit. Imaging 2013, 26, 361–370. [Google Scholar] [CrossRef] [PubMed]
- Naidoo, P.; Botz, B. Evaluation of the Cardiopulmonary Size on Slot-Scanning Full-Spine Radiographs. Imaging 2024, 16, 27–34. [Google Scholar] [CrossRef]
- Xograph Healthcare UK. One Shot—Enhanced Efficiency for Long-Length Radiographic Examinations. Xograph Healthcare UK. Available online: https://www.xograph.com/one-shot/ (accessed on 14 September 2025).
- Bassi, S.; Baldini, S.; Rebuffat, C.; Sarti, R.; Ferretti, F. First Test on Three Stitching Methods with Digital Detectors Used in Radiography. Radiol. Phys. Technol. 2013, 6, 187–196. [Google Scholar] [CrossRef]
- Singh, A.V.; Jungnickel, H.; Leibrock, L.; Tentschert, J.; Reichardt, P.; Katz, A.; Laux, P.; Luch, A. ToF-SIMS 3D Imaging Unveils Important Insights on the Cellular Microenvironment during Biomineralization of Gold Nanostructures. Sci. Rep. 2020, 10, 261. [Google Scholar] [CrossRef] [PubMed]
- Ha, H.-G.; Jung, K.; Lee, S.; Lee, H.; Hong, J. Heterogeneous Stitching of X-ray Images According to Homographic Evaluation. J. Digit. Imaging 2021, 34, 1249. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; He, Y.; Deng, Z.S.; Yan, A. Improvement of Automated Image Stitching System for DR X-ray Images. Comput. Biol. Med. 2016, 71, 108–114. [Google Scholar] [CrossRef]
- 3D and Quantitative Imaging Laboratory. Stitching—A Method for Combining Multiple Two-Dimensional Scans in Medical Imaging. 3D and Quantitative Imaging Laboratory. Available online: https://3dqlab.stanford.edu/stitching/ (accessed on 14 September 2025).
- Shi, L.; Bennett, N.R.; Wang, A.S. Single-Shot Quantitative X-ray Imaging Using a Primary Modulator and Dual-Layer Detector: Simulation and Phantom Studies. Proc. SPIE Int. Soc. Opt. Eng. 2022, 12031, 1203106. [Google Scholar] [CrossRef]
- Elisevich, K.; Cunningham, I.A.; Assis, L. Size Estimation and Magnification Error in Radiographic Imaging: Implications for Classification of Arteriovenous Malformations. AJNR Am. J. Neuroradiol. 1995, 16, 531–538. [Google Scholar]
- Cheng, C.-C.; Ching, Y.-T.; Ko, P.-H.; Hwu, Y. Correction of Center of Rotation and Projection Angle in Synchrotron X-ray Computed Tomography. Sci. Rep. 2018, 8, 9884. [Google Scholar] [CrossRef] [PubMed]
- Takakura, K.; Akasaki, Y.; Kuramoto, T.; Onizuka, Y.; Hattori, A.; Hamai, S.; Tsushima, H.; Kawahara, S.; Nakashima, Y.; Kato, T. Angular Accuracy of Plain Radiographic Measurements in Leg Alignment: Teleoroentgenogram versus Orthoroentgenogram. J. Orthop. Sci. 2022, 27, 642–647. [Google Scholar] [CrossRef] [PubMed]
- Alfuth, M.; Fichter, P.; Knicker, A. Leg Length Discrepancy: A Systematic Review on the Validity and Reliability of Clinical Assessments and Imaging Diagnostics Used in Clinical Practice. PLoS ONE 2021, 16, e0261457. [Google Scholar] [CrossRef]
- Zellner, M.; Tschauner, S.; Weyland, M.S.; Hotz, P.E.; Scheidegger, S.; Kellenberger, C.J. Low-Dose Lung CT: Optimizing Diagnostic Radiation Dose—A Phantom Study. Eur. J. Radiol. Open 2024, 13, 100614. [Google Scholar] [CrossRef]
- Ravenscroft, L.; Baker, L. The Influence of Miscentering on Radiation Dose during Computed Tomography Head Examinations and the Role of Localiser Orientation: A Phantom Study. Radiography 2024, 30, 1517–1523. [Google Scholar] [CrossRef] [PubMed]
- Zahroh, F.; Anam, C.; Sutanto, H.; Irdawati, Y.; Arifin, Z.; Kartikasari, Y. Effect of Silicone Rubber-Lead (SR-Pb) Thickness on Dose Reduction and Image Quality as Gonad Shield. J. Biomed. Phys. Eng. 2020, 10, 699–706. [Google Scholar] [CrossRef] [PubMed]
- Escott, B.G.; Ravi, B.; Weathermon, A.C.; Acharya, J.; Gordon, C.L.; Babyn, P.S.; Kelley, S.P.; Narayanan, U.G. EOS Low-Dose Radiography: A Reliable and Accurate Upright Assessment of Lower-Limb Lengths. J. Bone Jt. surgery. Am. Vol. 2013, 95, e183. [Google Scholar] [CrossRef] [PubMed]
- Sabharwal, S.; Zhao, C.; McKeon, J.; Melaghari, T.; Blacksin, M.; Wenekor, C. Reliability Analysis for Radiographic Measurement of Limb Length Discrepancy: Full-Length Standing Anteroposterior Radiograph versus Scanogram. J. Pediatr. Orthop. 2007, 27, 46–50. [Google Scholar] [CrossRef]
- Park, K.-R.; Lee, J.-H.; Kim, D.-S.; Ryu, H.; Kim, J.; Yon, C.-J.; Lee, S.-W. The Comparison of Lower Extremity Length and Angle between Computed Radiography-Based Teleoroentgenogram and EOS® Imaging System. Diagnostics 2022, 12, 1052. [Google Scholar] [CrossRef]
- Ahrend, M.-D.; Rühle, M.; Springer, F.; Baumgartner, H. Distance from the Magnification Device Contributes to Differences in Lower Leg Length Measured in Patients with TSF Correction. Arch. Orthop. Trauma Surg. 2021, 142, 1511–1522. [Google Scholar] [CrossRef]
- Birkenmaier, C.; Levrard, L.; Melcher, C.; Wegener, B.; Ricke, J.; Holzapfel, B.M.; Baur-Melnyk, A.; Mehrens, D. Distances and Angles in Standing Long-Leg Radiographs: Comparing Conventional Radiography, Digital Radiography, and EOS. Skelet. Radiol. 2024, 53, 1517–1528. [Google Scholar] [CrossRef]
- Illés, T.; Somoskeöy, S. The EOSTM Imaging System and Its Uses in Daily Orthopaedic Practice. Int. Orthop. 2012, 36, 1325. [Google Scholar] [CrossRef]
- Barnes, G.T.; Cleare, H.M.; Brezovich, I.A. Reduction of Scatter in Diagnostic Radiology by Means of a Scanning Multiple Slit Assembly. Radiology 1976, 120, 691–694. [Google Scholar] [CrossRef]
- McKenna, C.; Wade, R.; Faria, R.; Yang, H.; Stirk, L.; Gummerson, N.; Sculpher, M.; Woolacott, N. EOS 2D/3D X-ray Imaging System: A Systematic Review and Economic Evaluation. Health Technol. Assess. 2012, 16, 1–187. [Google Scholar] [CrossRef] [PubMed]



| Systems | Manufactures | Detector Panel Size (mm) | Spatial Resolution (mm) | SID 2/SOD 3 (mm) | Image Size (pixel) | Imaging Principle | Protocal Name |
|---|---|---|---|---|---|---|---|
| Eagle Eye | TAOiMAGE, Shanghai, China | 430 1 | 0.139 | 1230/1500 | 8268 × 3072 | Slot-scanning | FL AP Spine 4 |
| EOS | EOS Imaging, Paris, France | 340 1 | 0.179 | 987/1300 | 5518 × 1896 | Slot-scanning | FL AP Spine 4 |
| GC85A | Samsung Healthcare, Suwon, South Korea | 430 × 430 | 0.14 | 1959/2054 | 8701 × 2928 | Rotational stitching | FL AP Spine 4 |
| UDR780iPro3F | United Image Healthcare, Shanghai, China | 430 × 430 | 0.111 | 1703/1863 | 10,895 × 3258 | Rotational stitching | FL AP Spine 4 |
| DRX-Compass | Carestream Health, Rochester, NY, USA | 430 × 430 | 0.139 | 849/999 | 9792 × 3010 | Rotational stitching | Auto-LLI 5 |
| DSI-DRP | DroidSurg Medical, Shanghai, China | 430 × 1200 | 0.139 | 1900/2100 | 8704 × 3702 | One-shot | SPINE |
| Markers | Hough Transform Circularity Metric of Different Radiographic System | |||||
|---|---|---|---|---|---|---|
| Eagle Eye | EOS Imaging | UDR780iPro3F | GC85A | DRX-Compass | DSI-DRP | |
| RS | 0.68 | 0.60 | 0.61 | 0.63 | 0.48 | 0.54 |
| RP | 0.56 | 0.69 | 0.56 | 0.53 | 0.29 | 0.61 |
| RH | 0.58 | 0.61 | 0.46 | 0.52 | 0.21 | 0.62 |
| LS | 0.57 | 0.60 | 0.52 | 0.61 | 0.50 | 0.59 |
| LP | 0.65 | 0.59 | 0.54 | 0.56 | 0.26 | 0.54 |
| LH | 0.54 | 0.46 | 0.53 | 0.53 | 0.28 | 0.60 |
| C | 0.64 | 0.74 | 0.53 | 0.77 | 0.48 | 0.71 |
| Mean | 0.60 | 0.61 | 0.54 | 0.59 | 0.36 | 0.60 |
| SD | 0.05 | 0.08 | 0.04 | 0.08 | 0.11 | 0.05 |
| Marked Pairs | CT | Error of Full-Length Radiographic Systems | ||||||
|---|---|---|---|---|---|---|---|---|
| Eagle Eye | EOS Imaging | UDR780IPRO3F | GC85A | DRX-Compass | DSI-DRP | |||
| Plane1 | RS-LP | 536.14 | 0.77 | 3.80 | −19.65 | −22.46 | −38.79 | −11.87 |
| LS-RP | 542.83 | −8.81 | −7.76 | −23.63 | −24.54 | −27.10 | −9.65 | |
| RS-RP | 463.26 | −10.42 | −8.56 | −22.00 | −24.06 | −19.89 | −4.48 | |
| LS-RS | 275.69 | −11.03 | −15.02 | −15.58 | −16.94 | −30.94 | −4.24 | |
| LS-LP | 463.30 | 4.29 | 7.49 | −18.66 | −18.54 | −34.79 | −13.61 | |
| LP-RP | 277.23 | 6.08 | 9.92 | −0.54 | −3.17 | −4.84 | −8.86 | |
| Plane2 | C-LH | 543.17 | −12.43 | −9.63 | −40.67 | −33.73 | −2.69 | −35.93 |
| C-RH | 602.95 | −2.70 | −2.41 | −38.59 | −32.18 | −3.69 | −36.86 | |
| LH-RH | 172.42 | 15.97 | 19.08 | −1.88 | −2.39 | 10.37 | −12.42 | |
| MAE | 8.05 | 9.30 | 20.13 | 19.78 | 19.23 | 15.32 | ||
| RMSE | 9.31 | 10.49 | 23.96 | 22.37 | 23.46 | 19.26 | ||
| Bias | −2.03 | −0.34 | −20.13 | −19.78 | −16.93 | −15.32 | ||
| SD | 9.09 | 10.48 | 12.99 | 10.46 | 16.24 | 11.67 | ||
| Radiographic System | Normality p | Distribution | Wilcoxon p | t-Test p |
|---|---|---|---|---|
| Eagle Eye | 0.358 | Normal | 0.570 | 0.545 |
| EOS Imaging | 0.712 | Normal | 0.910 | 0.929 |
| UDR780IPRO3F | 0.420 | Normal | 0.004 | 0.002 |
| GC85A | 0.298 | Normal | 0.004 | 0.001 |
| DRX-Compass | 0.434 | Normal | 0.027 | 0.019 |
| DSI-DRP | 0.008 | Non-normal | 0.004 |
| Full-Length Radiography | Rotational Stitching | One-Shot | Slot-Scanning | |
|---|---|---|---|---|
| Error Source | ||||
| Stitching Errors | Presence of parallax, upper and lower edge distortion | No stitching errors | Distortion and stitching errors decrease as slot width narrows. | |
| Geometric Magnification Errors | Magnification differences lead to inconsistent proportions | Uneven magnification, significant edge geometric distortion | No significant magnification errors | |
| Shooting Angle Errors | Angle deviations between multiple exposures | Non-perpendicular X-ray beam or object tilt causes deformation | No significant angle errors | |
| Motion Artifacts | Patient movement between exposures | Minimal motion artifacts due to single exposure | Line-by-line scanning is easily affected by patient movement | |
| Scattered Radiation | Accumulated scattered radiation from multiple exposures | Large coverage area, significant scattered radiation | Radiation concentrated in the slot area, less scattered radiation | |
| Image Quality | Blurring at stitching areas | Detector resolution may be lower, reducing detail clarity | Affected by slot width and edge quality | |
| System Calibration Errors | Inconsistent parameters across multiple exposures | Detector uniformity and calibration errors | Synchronization issues between slot and detector | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Xia, J.; Wang, C.; Zhu, Z.; Zhang, F.; Tsai, T.-Y.; Zhu, Z.; Yang, K. Evaluation of Measurement Errors in Rotational Stitching, One-Shot, and Slot-Scanning Full-Length Radiography. Bioengineering 2025, 12, 999. https://doi.org/10.3390/bioengineering12090999
Li Z, Xia J, Wang C, Zhu Z, Zhang F, Tsai T-Y, Zhu Z, Yang K. Evaluation of Measurement Errors in Rotational Stitching, One-Shot, and Slot-Scanning Full-Length Radiography. Bioengineering. 2025; 12(9):999. https://doi.org/10.3390/bioengineering12090999
Chicago/Turabian StyleLi, Zhengliang, Jie Xia, Cong Wang, Zhemin Zhu, Fan Zhang, Tsung-Yuan Tsai, Zhenhong Zhu, and Kai Yang. 2025. "Evaluation of Measurement Errors in Rotational Stitching, One-Shot, and Slot-Scanning Full-Length Radiography" Bioengineering 12, no. 9: 999. https://doi.org/10.3390/bioengineering12090999
APA StyleLi, Z., Xia, J., Wang, C., Zhu, Z., Zhang, F., Tsai, T.-Y., Zhu, Z., & Yang, K. (2025). Evaluation of Measurement Errors in Rotational Stitching, One-Shot, and Slot-Scanning Full-Length Radiography. Bioengineering, 12(9), 999. https://doi.org/10.3390/bioengineering12090999









