A Multi-Product and Multi-Period Inventory Planning Model to Optimize the Supply of Medicines in a Pharmacy in Barranquilla, Colombia

Abstract

Background: Supply chains in pharmaceutical industry encounter constant challenges in balancing the availability of medicine with cost efficiency, particularly in developing regions with limited storage capacity, as regulatory constraints increase operational complexity. Methods: This research focuses on developing a multi-product, multi-period inventory planning model designed to optimize the supply process for a pharmacy located in Barranquilla, Colombia. The methodology involves conducting field studies within the pharmaceutical sector, which includes regular visits to pharmacies, interaction with employees, and analysis of historical data collected over a 16-month period. Results: The primary goal is to minimize costs while ensuring that products remain available to customers, considering various internal and external factors. Several scenarios will be examined to evaluate different alternatives for enhancing the supply process. Initial findings suggest that the proposed model could reduce inventory planning costs by approximately 15.78% by classifying antibiotics, which in turn leads to better resource utilization and improved order management. Conclusions: The proposed model minimizes the inventory planning costs associated with antibiotic management, ultimately leading to improved resource utilization and more accurate order management.

1. Introduction

Efficient inventory management is a critical challenge for companies in various sectors, especially for the pharmaceutical sector, where it is essential to maintain a constant flow of medicines available to meet customer demand [1]. Excessive inventory can lead to high storage costs, while insufficient inventory can lead to stockouts and lost sales, affecting both the company and its customers [2,3]. This problem is exacerbated under uncertain demand conditions, where product demand variability can make planning and controlling inventory levels challenging [4].

In this context, the central problem this research addresses is the difficulty of efficiently managing inventories under uncertain demand, which can lead to high costs, stockouts, and loss of profitability.

A case study in a pharmaceutical company aims to evaluate the effectiveness of the proposed model and determine whether it enables improved inventory management under conditions of uncertain demand. The basis of the problem is that in healthcare and pharmaceutical contexts, uncertainty in demand, supply delays, and product perishability can generate severe consequences, from high costs and waste to shortages that compromise patient safety [1,4]. This complexity increases when inventory is managed as a multi-period problem, since decisions in one period directly affect future stock levels, holding costs, and service performance, making dynamic and adaptive models necessary [5,6]. Additionally, the impact of time variations—such as seasonal fluctuations in demand, uncertain lead times, and time-dependent costs caused by inflation, obsolescence, or perishability—further complicates inventory planning [3,7]. These limitations highlight a research gap, underscoring the need for models that extend the inventory planning model into multi-period, time-sensitive, and uncertainty-aware approaches to balance cost efficiency with service reliability [8,9].

The main objective of this research is to develop a multi-product, multi-period inventory planning model that optimizes inventory management in a pharmacy. To achieve this objective, it is necessary to study and analyze each stage of the drug supply process to build a mathematical model. The analysis of this model enables the creation of strategies that offer various benefits, such as reducing storage costs, avoiding stockouts, and improving product availability, thereby contributing to more efficient and profitable inventory management. The study contributes to existing literature by validating a real-world case study using field data. It incorporates scenario-based analysis to account for various operational conditions, highlighting the significance of integrating operational efficiency with service reliability in pharmacy supply chains.

This article is structured as follows: Section 2 incorporates a literature review, which reports on the role played by the pharmaceutical industry. It also presents various models used to optimize its processes and different statistical tools that can be complemented with the models to develop a better study. Section 3 presents the detailed mathematical model for optimizing the pharmacy’s medicine supply. Section 4 presents the corresponding materials and methods for collecting relevant data that may be useful in developing the mathematical model. Section 5 presents the results yielded by the IBM ILOG CPLEX Optimization Studio, Version 22.1.1.0, including the suggested budget capacity, improved planning for orders placed by periods, and the quantity of products needed to order. Section 6 presents the discussion where the results will be analyzed and compared with the decisions made before the study. Finally, Section 7 contains the conclusion of the study.

2. Literature Review

The pharmaceutical industry plays a crucial role in the economic development and social well-being of any community. Healthcare systems aim to provide patients with appropriate care and treatment [1]. To achieve this, the pharmaceutical supply chain within the healthcare system must be effective and efficient.

The medication supply process in healthcare institutions is crucial as it directly impacts service quality, operating costs, and the availability of supplies for patient care. Research shows that many issues in this area stem from supply chain deficiencies [10,11]. The pharmaceutical supply chain has grown increasingly complex, involving multiple stakeholders, including manufacturers, wholesalers, distributors, customers, information service providers, and regulatory agencies [5]. Consequently, any disruption in this supply chain can lead to significant crises [3].

One of the primary challenges in pharmacy services is stock management, which complicates the supply chain [5,7,12,13]. This issue arises from various factors, including demand uncertainty and delivery delays [2]. A major contributing factor is the tendency to maintain high inventory levels, creating a false sense of security regarding the ability to meet customer demand, prevent stockouts, and secure bulk purchase discounts. However, this approach can be problematic as it leads to elevated costs and, if not managed properly, may adversely impact patient health.

Improving the performance of the pharmaceutical industry supply chain is becoming increasingly essential as organizations strive to achieve customer satisfaction at a lower cost. Logistics enables hospitals to maintain a good circulation of pharmaceutical products, reduce stock, minimize waste, and provide more accurate inventory tracking [14]. Given the performance improvements in the supply chain, numerous studies offer relevant recommendations to address the root causes of supply chain issues and pharmaceutical inventory management problems in the healthcare industry [1]. Pharmaceutical supply chain management requires effective inventory control plans and stakeholder alignment.

In this context, the pharmaceutical industry has also sparked the interest of scholars from various disciplines, including chemistry, engineering, and environmental sciences [15], as well as researchers in developing and implementing methodologies to address pharmaceutical supply chain problems. Most researchers focus on optimization model methodologies [16]. Mathematical models are essential for evaluating and identifying key metrics that measure potential outcomes in target transformation situations. They can also be modified to generate effective solutions. A mathematical model of the supply chain should enable an analytical assessment of both its current state and alternative scenarios. It includes examining its structural and behavioral characteristics in response to changes in patient needs, market demands, and resource availability. From a practical perspective, future pharmaceutical supply chain models should be designed to predict and meet patient demand accurately.

A study developed two mathematical models that were considered using real data and simulated scenarios within a pharmacy-hospital context, specifically addressing demand uncertainties [9]. The first model focuses on determining replenishment dates over a specified planning horizon, resulting in cost reductions. In contrast, the second model identifies acceptable expiration dates, which helps the hospital minimize the number of expired medications and optimize inventory levels. Additionally, a simulation model was developed to assess supply chain costs in Colombian hospitals [17]. This model was adapted and validated using real data from the clinic to represent the final cost behavior of medications accurately. The research determined that the final cost of medications varies and is influenced by several factors.

Some models include multimodal transportation to optimize various aspects of pharmaceutical production and distribution, including allocation, ordering, stock management, and transportation [10]. This approach enhances supply chain management, leading to increased patient satisfaction. Additionally, a study has introduced a model and a heuristic method for addressing supply chain issues, which can reduce both the total costs and delivery times of pharmaceutical supplies to hospitals and pharmacies while improving the reliability of the transportation system [18]. Furthermore, due to the rising demand for medications during the pandemic, accurately forecasting drug demand is crucial for minimizing costs, ensuring timely patient service, and preventing drug shortages.

Other studies address the location-inventory problem, with a specific focus on pharmacies. Both studies aim to develop a mathematical model that simultaneously addresses both problems, thereby increasing patient accessibility and improving operational efficiency and patient care [18,19,20,21]. Another research study develops a mathematical optimization model to design a pharmaceutical supply chain that considers drug corruption, considering three key objectives: economic, social, and environmental. A fuzzy programming approach is used to solve the developed model. Numerical evidence from a case study shows that the suggested model is effective and valid.

A period-based dynamic programming model considers stochastic demand [22]. The model is first solved as a mixed-integer linear programming model in Lingo, and then a genetic algorithm (GA) approach is proposed for large-scale problems. This critical study enables managers to make informed decisions about maintaining the optimal quantity of items in their warehouses, thereby utilizing their budgets more efficiently.

A bi-objective mixed integer linear programming model was developed to design a perishable pharmaceutical supply chain network under demand uncertainty, simultaneously minimizing the total network cost and the amount of lost demand [7]. Similarly, a bi-objective mixed-integer linear programming model was constructed to manage a hospital’s pharmaceutical supply chain, aiming to reduce the total cost of obtaining drugs from multiple suppliers and selecting the most appropriate source [23]. Using real-world data, the results obtained from model implementations and sensitivity analysis confirm the efficiency and validity of the suggested mathematical model and solution strategy.

A two-level stochastic mathematical model is proposed for optimizing inventory and allocation over multiple periods in a multi-tier supply chain network [24]. This model addresses uncertainties in demand and incorporates multiple sourcing characteristics, aiming to maximize the total expected profit of the supply chain network. Consequently, this approach enhances the efficiency of the linear approximation of the reorder point policy at the strategic level, leading to robust design solutions in the face of uncertainty.

A proposed multi-layer collaborative pharmaceutical supply chain comprises a central pharmacy and multiple regional pharmacies and hospitals [25]. This system is modeled using a multi-period, multi-product stochastic mathematical approach to minimize drug inventory management costs, including shortages and holding costs. Similarly, a study on a multi-stage Tunisian pharmaceutical supply chain, including a central pharmacy, regional pharmacies, and several hospitals, presents two mathematical models to reduce costs [26]. In the first model, the optimization focuses solely on information sharing between the central and regional pharmacies. The second model expands this information sharing to include all supply chain members. Numerical results from the study demonstrate how information sharing can lead to significant cost savings.

A multi-objective model that simultaneously considers cost minimization, environmental impact minimization, and service level equity maximization was used [27]. The study offers practical insights for optimizing pharmaceutical supply chains by balancing economic efficiency with social responsibility to navigate disruptions and challenges successfully. Additionally, a study developed an innovative simulation and optimization system for pharmacy inventory management, using an empirical allocation approach to model demand [28]. The system was implemented in October 2011 across all Kroger pharmacies in the United States, resulting in increased revenue, reduced inventory, and reduced labor costs for the organization.

One of the most widely used methodologies is the ABC system, which categorizes products based on their economic value or cost impact. Additionally, it is complemented by various approaches, such as lean manufacturing and Kanban, which classify products according to their medical significance or relevance in patient treatment, leading to improved outcomes. The ABC classification method was utilized to assess medication usage within a specific year, while mixed integer linear programming was employed to minimize the cost of managing medication inventory [29]. The study identified 50 types of medications categorized as group A out of 526 medicines in the hospital. Additionally, the study compares the outcomes of two mathematical models: one that takes medication expiration into account and another that does not.

A systematic categorization using ABC and VED analysis was developed for the medications available at a Dermatology Hospital from 2016 to 2020 [30]. The results indicated that Category I medications, the most costly and essential for annual revenue, accounted for only 88% of the total expenses. In contrast, Category II and III medications comprised 5% to 10% and less than 5% of the overall costs, respectively. It is essential to utilize these medications effectively. This analytical method has proven to be a valuable tool for decision-making regarding importing and stockpiling. ABC and VED analyses were conducted in an Indian pharmacy to identify items that required strict management control [31]. The consumption and annual expenditure for each item in the pharmacy during the years 2007 and 2008 were examined. Inventory control techniques were applied, resulting in the following categories: I, II, and III, which showed 4.21%, 22.23%, and 3.56% of the total annual expenditure on medicines, respectively.

Several researchers have implemented the Kanban system, a workflow management method that assists organizations in managing and enhancing work processes, ensuring efficient inventory transportation between cells or facilities, and optimizing inventory management to improve overall workflow efficiency. Some research implemented a Kanban system within a multi-layer pharmaceutical supply chain, presenting how a Kanban system could manage pharmaceutical inventory and enhance information sharing across a multi-tier supply chain [2,3]. Similarly, a study implemented the Kanban system based on ABC analysis to improve inventory management in a supply chain suffering from inadequate inventory practices [32]. The study utilized monthly data collected over a year to conduct the ABC analysis, enabling a thoughtful consideration of the elements to be included in the Kanban system. The results of this analysis indicated an impressive reduction in inventory-related costs of approximately 75%. However, applying this approach in practice is crucial to validate its effectiveness.

The literature review reveals that pharmaceutical supply chains face several challenges, including demand uncertainty, delivery delays, high holding costs, and perishability of products. Many mathematical models have considered cost reductions, reduced waste, and improved service levels. Some studies incorporate ABC and VED classification, lean practices, and Kanban systems to improve inventory control. Then the integration of optimization models with practical tools enhances inventory management, ensuring the availability of medicine, patient satisfaction, and operational efficiency.

3. Problem Definition

A mixed integer programming mathematical model is developed to represent the drug inventory planning problem. The model defines the decision variables, the operating cost minimization objective function, and capacity, budget, and demand constraints.

3.1. Assumptions

The following assumptions are considered in the multi-product and multi-period inventory planning model:

i.

A mixed-integer linear model is formulated to minimize the total costs associated with inventory planning.

ii.

The inventory planning model considers ordering costs and holding costs for each period.

iii.

The demand for each product is deterministic and known.

iv.

The facility has a limited maximum storage capacity, and inventory holding costs are incurred per unit for each period.

v.

The facility must maintain a minimum quantity of products in stock, including both inventory and outstanding orders.

vi.

The facility has a total budget assigned for purchasing products.

vii.

The proposed model contains decision variables, including the order quantity of products for each specified period, a binary variable that indicates whether the facility will place orders during a given period, and the inventory levels of products for each respective period. This framework aims to facilitate more informed decision-making and enhance operational efficiency.

3.2. Notation

3.2.1. Sets

i  products, $i\in \left\{\mathrm{1,2},3\dots I\right\}$

j  periods, $j\in \left\{\mathrm{1,2},3\dots J\right\}$

3.2.2. Parameters

$C_{ij}$   Purchasing cost per unit for the product $i$ during period $j$

$S_j$    Ordering cost during period $j$

$v_{ij}$   Inventory holding cost per unit for the product $i$ during period $j$

$D_{ij}$   Demand for product $i$ during period $j$

C    Total budget available for product purchases

$V_{ij}$   Maximum storage capacity for the product $i$ during period $j$

${lm}_i$ Minimum quantity of the product $i$ at the end of period $j$

3.2.3. Decision Variables

$X_{ij}$   Order Quantity of the product $i$ during period $j$

$Y_j$    Binary decision variable that is 1 if orders are placed in period $j$

$I_{ij}$   Inventory level of the product $i$ at the end of period $j$

3.3. Mathematical Model

The objective function defined in Equation (1) aims to minimize the total costs associated with inventory planning. These costs include the purchase cost of product $i$, ordering costs, and holding costs for each period $j$. Equation (2) presents the inventory balance constraint at the end of each period, considering the initial inventory, the quantities ordered and the demand. Equation (3) specifies that the total purchasing cost must not exceed the available budget $C.$ Equations (4) and (5) detail the constraints imposed by the maximum storage capacity that must be considered when placing orders in period $j$. Equation (6) includes the minimum quantity of products $i$ that must be maintained in stock during each period $j$. Equation (7) contains the non-negative constraint for the variables $X_{ij}$ and $I_{ij}$ and Equation (8) presents the constraint of binary variable for $Y_j$.

$$Z\left(min\right)=\sum _{i=1}^m\sum _{j=1}^n{C}_{ij}{X}_{ij}+\sum _{i=1}^m\sum _{j=1}^n{S}_j{Y}_j+\sum _{i=1}^m\sum _{j=1}^n{v}_{ij}{I}_{ij}$$

(1)

Subject to

$$I_{i,j-1}+X_{ij}-D_{ij}=I_{ij}\forall i=1,\dots m,j=1,\dots ,n,j>1$$

(2)

$$\sum _{i=1}^m\sum _{j=1}^n{C}_{ij}{X}_{ij}\le C$$

(3)

$$\sum _{i=1}^m\sum _{j=1}^n{X}_{ij}\le V_{ij}{Y}_j\forall i=1,\dots m,j=1,\dots ,n$$

(4)

$$I_{ij}+X_{ij}\le V_{ij}\forall i=1,\dots m,j=1,\dots ,n$$

(5)

$$I_{ij}+X_{ij}\ge {lm}_i\forall i=1,\dots m,j=1,\dots ,n$$

(6)

$$X_{ij},I_{ij}\ge 0$$

(7)

$$Y_j\in \left\{\mathrm{0,1}\right\}\forall j=1,\dots n$$

(8)

4. Case Study

The mathematical inventory planning model was validated in a pharmacy in Barranquilla, Colombia, using a dataset collected over 16 months. This data was used to enhance medication inventory planning in healthcare institutions, specifically within the pharmacy department.

Inventory Planning Diagnosis in a Pharmacy in Barranquilla, Colombia

A diagnosis of the current supply and inventory planning conditions at a pharmacy in Barranquilla was conducted. Relevant data, including inventory history, demand, and costs, were collected, and interviews were held with the staff involved. Data analysis tools, specifically Excel, were used to examine the collected information, identify patterns and trends, and pinpoint areas for improvement. One of the statistical methods employed for data analysis was ABC analysis, which categorizes medications based on their importance in terms of value and consumption, enabling prioritized inventory management efforts. Table 1 presents the inventory classification for the antibiotics category using the ABC methodology. A total of 43 types of antibiotics sold at the pharmacy were considered, followed by an analysis of the quantity of products sold. Finally, the ABC inventory classification will be developed using this data to identify the products with the highest sales value over a selected 16-month period.

Table 1. ABC inventory classification.

Products	Demand	Purchasing Cost Per Unit (COP)	Total Cost (COP)	% of Total Cost	% Accumulative Total Cost	% of Product Demand	% Accumulative Product Demand	Type of Product
Azithromycin tablets 500mg, 3 tablets	103	4705	484,600	16.33%	16.33%	17.20%	17.20%	A
Amoxicillin 500 mg, 50 capsules	133	2103	279,672	9.42%	25.75%	22.20%	39.40%	A
Azithromycin 500 mg, 3 tablets	53	5128	271,784	9.16%	34.91%	8.85%	48.25%	A
Azithromycin 500 mg, 3 tablets	49	3909	191,525	6.45%	41.37%	8.18%	56.43%	A
Doxycycline 100 mg, 10 tablets	24	7075	169,794	5.72%	47.09%	4.01%	60.43%	A
Amoxicillin 500 mg, 50 capsules	35	4512	157,932	5.32%	52.41%	5.84%	66.28%	A
Fusidic acid cream 15 g	11	10,804	118,840	4.00%	56.41%	1.84%	68.11%	A
Dicloxacillin 500 mg 50 capsules	20	5007	100,141	3.37%	59.79%	3.34%	71.45%	A
Sulfaplate 1% cream 30 gr	4	22,686	90,744	3.06%	62.85%	0.67%	72.12%	A
Amoxicillin 500 mg 50 capsules	24	3780	90,722	3.06%	65.90%	4.01%	76.13%	A
Fusidic acid cream 15 g	10	8248	82,480	2.78%	68.68%	1.67%	77.80%	A
Trimethoprim sulfa f 160–800 100 tablets	23	3402	78,248	2.64%	71.32%	3.84%	81.64%	A
Azithromycin 500 mg 3 tablets	6	11,400	68,400	2.30%	73.62%	1.00%	82.64%	A
Rifamicin spray 1% 20 mL mk	2	28,867	57,734	1.95%	75.57%	0.33%	82.97%	A
Amoxicillin 250 mg suspension 100 mL	8	7206	57,645	1.94%	77.51%	1.34%	84.31%	A
Erythromycin 500 mg 50 tablets	5	10,462	52,312	1.76%	79.27%	0.83%	85.14%	A
Zidoxtifene 500 mg 3 tablets	5	9849	49,245	1.66%	80.93%	0.83%	85.98%	B
Azithromycin 200 mg suspension 15 mL	4	12,299	49,196	1.66%	82.59%	0.67%	86.64%	B
Ampicillin 1 g 100 tablets	7	6343	44,401	1.50%	84.09%	1.17%	87.81%	B
Plant sulfadiazine 15 gr	6	7187	43,122	1.45%	85.54%	1.00%	88.81%	B
Plant sulfadiazine 30 gr	4	10,655	42,620	1.44%	86.98%	0.67%	89.48%	B
Doxiclor 40 mg 10 tablets	3	13,000	39,000	1.31%	88.29%	0.50%	89.98%	B
Dicloxacillin 500 mg 50 capsules	8	4302	34,412	1.16%	89.45%	1.34%	91.32%	B
Ciprofloxacin 500 mg 300 tablets	10	3235	32,352	1.09%	90.54%	1.67%	92.99%	B
Cefalexin 500 mg 10 capsules	5	5888	29,442	0.99%	91.53%	0.83%	93.82%	B
Amoxicillin 250 mg suspension 100 ml	4	7296	29,182	0.98%	92.52%	0.67%	94.49%	B
Ampicillin 500 mg 100 capsules	5	5541	27,706	0.93%	93.45%	0.83%	95.33%	B
Ciprofloxacin 500 mg 10 tablets	6	4589	27,534	0.93%	94.38%	1.00%	96.33%	B
Sulfaplate 1% cream 60 gr	1	26,282	26,282	0.89%	95.26%	0.17%	96.49%	C
Norfloxacin 400 mg 14 tablets	2	11,455	22,909	0.77%	96.04%	0.33%	96.83%	C
Cefalexin 250 mg suspension 60 mL	3	6955	20,866	0.70%	96.74%	0.50%	97.33%	C
Amoxicillin 250 mg suspension 100 mL	2	7740	15,480	0.52%	97.26%	0.33%	97.66%	C
Azithromycin 500 mg 3 tablets	3	4253	12,760	0.43%	97.69%	0.50%	98.16%	C
Fusidic acid 2% cream 15 gr	1	11,591	11,591	0.39%	98.08%	0.17%	98.33%	C
Cinepride 500 mg 10 tablets	2	5339	10,678	0.36%	98.44%	0.33%	98.66%	C
Levofloxacin 500 mg 7 tablets	1	10,634	10,634	0.36%	98.80%	0.17%	98.83%	C
Cefalexin 250 mg suspension 60 mL	1	8741	8741	0.29%	99.09%	0.17%	99.00%	C
Amoxicillin 250 mg suspension 100 mL	1	8000	8000	0.27%	99.36%	0.17%	99.17%	C
Trimethoprim sulfa 40–200 susp.12	1	5537	5537	0.19%	99.55%	0.17%	99.33%	C
Azithromycin 200 mg suspension 15 mL	1	5000	5000	0.17%	99.72%	0.17%	99.50%	C
Cefalexin 500 mg 20 capsules	1	3712	3712	0.13%	99.84%	0.17%	99.67%	C
Trimethoprim sulfa f 160–800 100 tablets	1	3141	3141	0.11%	99.95%	0.17%	99.83%	C
Trimethoprim sulfa 40–200 susp.60 mL	1	1505	1505	0.05%	100.00%	0.17%	100.00%	C

Figure 1 shows a Pareto chart illustrating the distribution of 43 medicines in the antibiotic category, categorized by their impact on demand and total cumulative cost. The horizontal axis lists the medications, while the vertical axis shows the cumulative percentage, ranging from 0% to 100%. The blue bars represent the first 16 medications, which account for approximately 80% of the total cost and are the most significant economically. The orange bars indicate the following 11 medications, which are highly in demand, although not the most expensive. Finally, the green bars correspond to the last 15 medications, which have a low impact on costs and demand. The curved black line illustrates the cumulative percentage of the total cost, demonstrating the Pareto principle (80/20). This visual representation helps identify key products for strategic decision-making in inventory management and cost control.

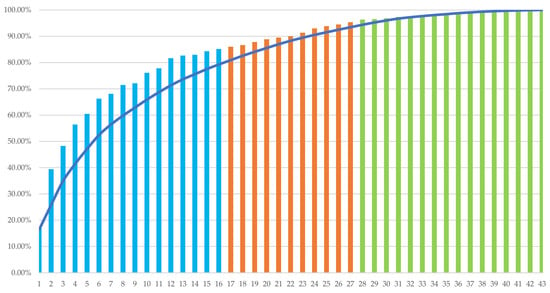
Figure 1. Pareto chart.

The ABC classification is used to select the products categorized in Zone A for further study, as these products are considered more relevant. The unit costs are presented in Table 2, while storage costs are shown in Table 3. Table 4 contains data on the number of units sold in the antibiotics category by the pharmacy over 16 months. Maximum and minimum capacities for each product can be found in Table 5 and Table 6, respectively. These tables provide the necessary data to develop the mathematical model.

Table 2. Purchasing cost per unit for the product i during period j.

Product	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	4705	4705	4705	4705	4705	4705	4940	4940	4940	4940	4940	4940	5187	5446	5719	6005
Amoxicillin 500 mg 50 capsules	2103	2103	2103	2103	2103	2103	2208	2208	2208	2208	2208	2208	2318	2318	2318	2318
Azithromycin 500 mg 3 tablets	5128	5128	5128	5128	5128	5128	5384	5384	5384	5384	5384	5384	5654	5654	5654	5654
Azithromycin 500 mg 3 tablets	3909	3909	3909	3909	3909	3909	4104	4104	4104	4104	4104	4104	4309	4309	4309	4309
Doxycycline 100 mg 10 tablets	7075	7075	7075	7075	7075	7075	7428	7428	7428	7428	7428	7428	7800	7800	7800	7800
Amoxicillin 500 mg 50 capsules	4512	4512	4512	4512	4512	4512	4738	4738	4738	4738	4738	4738	4975	4975	4975	4975
Fusidic acid cream 15 gr gf	10,804	10,804	10,804	10,804	10,804	10,804	11,344	11,344	11,344	11,344	11,344	11,344	11,911	11,911	11,911	11,911
Dicloxacilin 500 mg 50 capsules	5007	5007	5007	5007	5007	5007	5257	5257	5257	5257	5257	5257	5520	5520	5520	5520
Sulfaplate 1% cream 30 gr	22,686	22,686	22,686	22,686	22,686	22,686	23,820	23,820	23,820	23,820	23,820	23,820	25,011	25,011	25,011	25,011
Amoxicillin 500 mg 50 capsules pc	3780	3780	3780	3780	3780	3780	3969	3969	3969	3969	3969	3969	4168	4168	4168	4168
Fusidic acid cream 15 gr	8248	8248	8248	8248	8248	8248	8660	8660	8660	8660	8660	8660	9093	9093	9093	9093
Trimethoprim sulfa f 160–800 100 tablets gf	3402	3402	3402	3402	3402	3402	3572	3572	3572	3572	3572	3572	3751	3751	3751	3751
Azithromycin 500 mg 3 tablets	11,400	11,400	11,400	11,400	11,400	11,400	11,970	11,970	11,970	11,970	11,970	11,970	12,569	12,569	12,569	12,569
Rifamicin spray 1% 20 mL mk	28,867	28,867	28,867	28,867	28,867	28,867	30,310	30,310	30,310	30,310	30,310	30,310	31,826	31,826	31,826	31,826
Amoxicillin 250 mg suspension 100 mL gf	7206	7206	7206	7206	7206	7206	7566	7566	7566	7566	7566	7566	7944	7944	7944	7944
Erythromycin 500 mg 50 tablets gf	10,462	10,462	10,462	10,462	10,462	10,462	10,986	10,986	10,986	10,986	10,986	10,986	11,535	11,535	11,535	11,535

Table 3. Inventory holding cost per unit for the product i during period j.

Product	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	941	941	941	941	941	941	988	988	988	988	988	988	1037	1089	1144	1201
Amoxicillin 500 mg 50 capsules	421	421	421	421	421	421	442	442	442	442	442	442	464	464	464	464
Azithromycin 500 mg 3 tablets	1026	1026	1026	1026	1026	1026	1077	1077	1077	1077	1077	1077	1131	1131	1131	1131
Azithromycin 500 mg 3 tablets	782	782	782	782	782	782	821	821	821	821	821	821	862	862	862	862
Doxycycline 100 mg 10 tablets	1415	1415	1415	1415	1415	1415	1486	1486	1486	1486	1486	1486	1560	1560	1560	1560
Amoxicillin 500 mg 50 capsules	902	902	902	902	902	902	948	948	948	948	948	948	995	995	995	995
Fusidic acid cream 15 gr	2161	2161	2161	2161	2161	2161	2269	2269	2269	2269	2269	2269	2382	2382	2382	2382
Dicloxacillin 500 mg 50 capsules	1001	1001	1001	1001	1001	1001	1051	1051	1051	1051	1051	1051	1104	1104	1104	1104
Sulfaplate 1% cream 30 gr	4537	4537	4537	4537	4537	4537	4764	4764	4764	4764	4764	4764	5002	5002	5002	5002
Amoxicillin 500 mg 50 capsules	756	756	756	756	756	756	794	794	794	794	794	794	834	834	834	834
Fusidic acid cream 15 gr	1650	1650	1650	1650	1650	1650	1732	1732	1732	1732	1732	1732	1819	1819	1819	1819
Trimethoprim sulfa f 160–800 100 tablets	680	680	680	680	680	680	714	714	714	714	714	714	750	750	750	750
Azithromycin 500 mg 3 tablets	2280	2280	2280	2280	2280	2280	2394	2394	2394	2394	2394	2394	2514	2514	2514	2514
Rifamicin spray 1% 20 mL	5773	5773	5773	5773	5773	5773	6062	6062	6062	6062	6062	6062	6365	6365	6365	6365
Amoxicillin 250 mg suspension 100 mL	1441	1441	1441	1441	1441	1441	1513	1513	1513	1513	1513	1513	1589	1589	1589	1589
Erythromycin 500 mg 50 tablets	2092	2092	2092	2092	2092	2092	2197	2197	2197	2197	2197	2197	2307	2307	2307	2307

Table 4. Demand for product i during period j.

Product	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	0	4	0	7	7	15	0	6	14	0	5	5	13	2	0	3
Amoxicillin 500 mg 50 capsules	6	0	0	7	10	14	7	15	6	6	5	4	9	0	0	0
Azithromycin 500 mg 3 tablets	3	13	0	4	6	0	0	0	2	2	0	0	0	0	2	4
Azithromycin 500 mg 3 tablets	0	0	6	1	9	0	0	0	0	4	0	1	4	1	2	3
Doxycycline 100 mg 10 tablets	0	0	3	4	0	2	1	0	0	0	1	1	3	2	0	2
Amoxicillin 500 mg 50 capsules	4	1	3	2	0	0	0	0	0	0	0	0	6	10	6	1
Fusidic acid cream 15 gr	0	0	0	1	0	0	1	0	0	2	0	1	0	0	2	1
Dicloxacillin 500 mg 50 capsules	2	0	1	3	2	1	1	0	1	1	2	3	1	0	0	0
Sulfaplate 1% cream 30 gr	0	0	1	1	0	0	0	0	0	1	0	0	0	1	0	0
Amoxicillin 500 mg 50 capsules	0	5	10	4	0	0	0	0	0	0	0	0	0	0	2	2
Fusidic acid cream 15 gr	2	0	1	0	3	1	1	0	0	0	0	0	0	0	0	0
Trimethoprim sulfa f 160–800 100 tablets	2	0	1	0	3	0	0	1	2	1	4	0	1	1	3	0
Azithromycin 500 mg 3 tablets	2	1	2	2	1	0	0	0	0	0	2	3	0	0	0	1
Rifamicin spray 1% 20 mL	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0
Amoxicillin 250 mg suspension 100 mL	1	1	1	0	0	4	1	0	0	0	0	0	0	0	0	0
Erythromycin 500 mg 50 tablets	0	0	0	0	0	0	0	0	0	0	0	0	0	0	5	0

Table 5. Maximum storage capacity for the product i during period j.

Product	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	33	33	33	33	33	33	33	33	33	33	33	33	33	33	33	33
Amoxicillin 500 mg 50 capsules	37	37	37	37	37	37	37	37	37	37	37	37	37	37	37	37
Azithromycin 500 mg 3 tablets	26	26	26	26	26	26	26	26	26	26	26	26	26	26	26	26
Azithromycin 500 mg 3 tablets	16	16	16	16	16	16	16	16	16	16	16	16	16	16	16	16
Doxycycline 100 mg 10 tablets	9	9	9	9	9	9	9	9	9	9	9	9	9	9	9	9
Amoxicillin 500 mg 50 capsules	30	30	30	30	30	30	30	30	30	30	30	30	30	30	30	30
Fusidic acid cream 15 gr	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4
Dicloxacillin 500 mg 50 capsules	15	15	15	15	15	15	15	15	15	15	15	15	15	15	15	15
Sulfaplate 1% cream 30 gr	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4
Amoxicillin 500 mg 50 capsules	19	19	19	19	19	19	19	19	19	19	19	19	19	19	19	19
Fusidic acid cream 15 gr	7	7	7	7	7	7	7	7	7	7	7	7	7	7	7	7
Trimethoprim sulfa f 160–800 100 tablets	7	7	7	7	7	7	7	7	7	7	7	7	7	7	7	7
Azithromycin 500 mg 3 tablets	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6	6
Rifamicin spray 1% 20 mL	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3
Amoxicillin 250 mg suspension 100 mL	7	7	7	7	7	7	7	7	7	7	7	7	7	7	7	7
Erythromycin 500 mg 50 tablets	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5

Table 6. Minimum quantity of the product i at the end of period j.

Product	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3
Amoxicillin 500 mg 50 capsules	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5	5
Azithromycin 500 mg 3 tablets	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3
Azithromycin 500 mg 3 tablets	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4
Doxycycline 100 mg 10 tablets	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3
Amoxicillin 500 mg 50 capsules	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3
Fusidic acid cream 15 gr	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2
Dicloxacillin 500 mg 50 capsules	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3
Sulfaplate 1% cream 30 gr	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2
Amoxicillin 500 mg 50 capsules	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4	4
Fusidic acid cream 15 gr	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3	3
Trimethoprim sulfa f 160–800 100 tablets	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2
Azithromycin 500 mg 3 tablets	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Rifamicin spray 1% 20 mL	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2
Amoxicillin 250 mg suspension 100 mL	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2
Erythromycin 500 mg 50 tablets	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2	2

5. Results

The proposed mixed integer linear programming model was solved using IBM ILOG CPLEX Optimization Studio V20.1 and executed on an Acer PC with an 11th-generation Intel^® Core™ i5-11400H processor with 2.70 GHz and 24.0 GB of RAM, with a solution time of 0.25 s. An analysis of the results obtained from the software confirms that the strategy is effective in achieving the desired outcome of minimizing the monthly budget capacity. Before implementing the software, the pharmacy’s budget was set at COP 5,000,000. After execution, the software indicates a reduction in monthly budget capacity by approximately 39.58%, bringing the new cost to COP 3,020,533. The budget capacity provided by the software can be attained by following specific strategies, such as determining which months are optimal for placing orders and which months are not advisable. This information is summarized in Table 7. Additionally, Table 8 displays the number of recommended products that can be ordered, while Table 9 provides the inventory levels of products at the end of each period.

Table 7. Orders by periods.

Period	Place Orders	Do Not Place Orders
1		X
2		X
3		X
4		X
5		X
6		X
7		X
8		X
9	X
10		X
11		X
12	X
13		X
14		X
15	X
16	X

Table 8. Order Quantity of products by period.

Product	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	19	0	0	20	0	0	0	2
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	17	0	0	13	0	0	0	0
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	4	0	0	0	0	0	1	3
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	4	0	0	6	0	0	1	2
Doxycycline 100 mg 10 tablets	0	0	0	0	0	0	0	0	1	0	0	6	0	0	0	1
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	0	0	0	16	0	0	3	2
Fusidic acid cream 15 gr	0	0	0	0	0	0	0	0	2	0	0	1	0	0	1	1
Dicloxacillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	4	0	0	4	0	0	0	0
Sulfaplate 1% cream 30 gr	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	2
Fusidic acid cream 15 gr	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Trimethoprim sulfa f 160–800 100 tablets	0	0	0	0	0	0	0	0	7	0	0	2	0	0	2	1
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	2	0	0	3	0	0	0	1
Rifamicin spray 1% 20 mL	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Amoxicillin 250 mg suspension 100 mL	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Erythromycin 500 mg 50 tablets	0	0	0	0	0	0	0	0	0	0	0	0	0	0	2	1

Table 9. Inventory level of products by periods.

Products	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	0	42	38	38	31	24	9	9	3	8	8	3	18	5	3	3	2
Amoxicillin 500 mg 50 capsules	0	58	58	58	51	41	27	20	5	16	10	5	14	5	5	5	5
Azithromycin 500 mg 3 tablets	0	26	13	13	9	3	3	3	3	5	3	3	3	3	3	2	1
Azithromycin 500 mg 3 tablets	0	20	20	14	13	4	4	4	4	8	4	4	9	5	4	3	2
Doxycycline 100 mg 10 tablets	0	13	13	10	6	6	4	3	3	4	4	3	8	5	3	3	2
Amoxicillin 500 mg 50 capsules	0	9	8	5	3	3	3	3	3	3	3	3	19	13	3	0	1
Fusidic acid cream 15 gr	0	4	4	4	3	3	3	2	2	4	2	2	2	2	2	1	1
Dicloxacillin 500 mg 50 capsules	0	11	11	10	7	5	4	3	3	6	5	4	3	3	3	3	3
Sulfaplate 1% cream 30 gr	0	4	4	3	2	2	2	2	2	3	2	2	3	3	2	2	2
Amoxicillin 500 mg 50 capsules	0	23	18	8	4	4	4	4	4	4	4	4	4	4	4	3	3
Fusidic acid cream 15 gr	0	9	9	8	8	5	4	3	3	3	3	3	3	3	3	3	3
Trimethoprim sulfa f 160–800 100 tablets	0	7	7	6	6	3	3	3	2	7	6	2	4	3	2	1	2
Azithromycin 500 mg 3 tablets	0	7	6	4	2	1	1	1	1	3	3	1	1	1	1	1	1
Rifamicin spray 1% 20 mL	0	4	3	2	2	2	2	2	2	2	2	2	2	2	2	2	2
Amoxicillin 250 mg suspension 100 mL	0	9	8	7	7	7	3	2	2	2	2	2	2	2	2	2	2
Erythromycin 500 mg 50 tablets	0	2	2	2	2	2	2	2	2	2	2	2	2	2	2	0	1

The results of the model indicate that the pharmacy should place orders during periods 9, 12, 15, and 16 (see Table 7). The pharmacy does not place orders in periods 1–8, 10–11, and 13–14. Figure 2 illustrates the quantity of products that the pharmacy should order in these specific periods: 9, 12, 15, and 16.

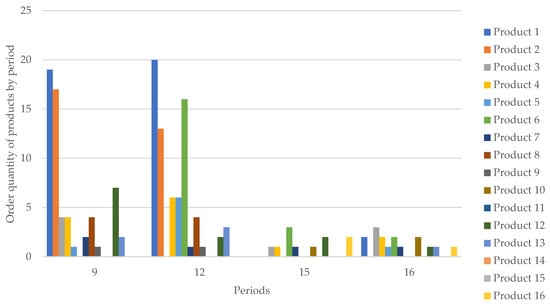
Figure 2. Order quantity of products by period.

6. Discussion

This section presents and analyzes the results obtained from the study, comparing the proposed approach with the one using the developed mathematical model. It focuses on the model’s computational behavior across three different scenarios, where specific parameters were modified to obtain the varying outcomes. Table 10 presents the budgetary capacities for each scenario being compared, along with the objective function for each one.

Table 10. Objective function solutions.

Objective Function	Total Inventory Planning Cost	Variation
Initial solution	COP 3,020,533.00	0%
Scenario 1	COP 3,062,518.00	1.4%
Scenario 2	COP 2,834,295.00	−6.57%
Scenario 3	COP 2,608,870.00	−15.78%

Scenario 1 examines a 15% increase in ordering costs resulting from longer drug delivery times, which are caused by inventory availability issues at pharmaceutical companies and drug distribution centers. The findings indicate that this increase in ordering costs does not affect the decision variables but results in total inventory management costs of COP 3,062,518, representing a 1.4% rise in inventory costs. Table 11 and Table 12 present the optimal results for the order quantity of products over the period and the inventory level of products by period for Scenario 1.

Table 11. Order Quantity of products by period—Scenario 1.

Product	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	19	0	0	20	0	0	0	2
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	17	0	0	13	0	0	0	0
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	4	0	0	0	0	0	1	3
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	4	0	0	6	0	0	1	2
Doxycycline 100 mg 10 tablets	0	0	0	0	0	0	0	0	1	0	0	6	0	0	0	1
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	0	0	0	16	0	0	3	2
Fusidic acid cream 15 gr	0	0	0	0	0	0	0	0	2	0	0	1	0	0	1	1
Dicloxacillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	4	0	0	4	0	0	0	0
Sulfaplate 1% cream 30 gr	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	2
Fusidic acid cream 15 gr	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Trimethoprim sulfa f 160–800 100 tablets	0	0	0	0	0	0	0	0	7	0	0	2	0	0	2	1
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	2	0	0	3	0	0	0	1
Rifamicin spray 1% 20 mL	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Amoxicillin 250 mg suspension 100 mL	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Erythromycin 500 mg 50 tablets	0	0	0	0	0	0	0	0	0	0	0	0	0	0	3	1

Table 12. Inventory level of products by periods—Scenario 1.

Products	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	0	42	38	38	31	24	9	9	3	8	8	3	18	5	3	3	2
Amoxicillin 500 mg 50 capsules	0	58	58	58	51	41	27	20	5	16	10	5	14	5	5	5	5
Azithromycin 500 mg 3 tablets	0	26	13	13	9	3	3	3	3	5	3	3	3	3	3	2	1
Azithromycin 500 mg 3 tablets	0	20	20	14	13	4	4	4	4	8	4	4	9	5	4	3	2
Doxycycline 100 mg 10 tablets	0	13	13	10	6	6	4	3	3	4	4	3	8	5	3	3	2
Amoxicillin 500 mg 50 capsules	0	9	8	5	3	3	3	3	3	3	3	3	19	13	3	0	1
Fusidic acid cream 15 gr	0	4	4	4	3	3	3	2	2	4	2	2	2	2	2	1	1
Dicloxacillin 500 mg 50 capsules	0	11	11	10	7	5	4	3	3	6	5	3	4	3	3	3	3
Sulfaplate 1% cream 30 gr	0	4	4	3	2	2	2	2	2	3	2	2	3	3	2	2	2
Amoxicillin 500 mg 50 capsules	0	23	18	8	4	4	4	4	4	4	4	4	4	4	4	3	3
Fusidic acid cream 15 gr	0	9	9	8	8	5	4	3	3	3	3	3	3	3	3	3	3
Trimethoprim sulfa f 160–800 100 tablets	0	7	7	6	6	3	3	3	2	7	6	2	4	3	2	1	2
Azithromycin 500 mg 3 tablets	0	7	6	4	2	1	1	1	1	3	3	1	1	1	1	1	1
Rifamicin spray 1% 20 mL	0	4	3	2	2	2	2	2	2	2	2	2	2	2	2	2	2
Amoxicillin 250 mg suspension 100 mL	0	9	8	7	7	7	3	2	2	2	2	2	2	2	2	2	2
Erythromycin 500 mg 50 tablets	0	2	2	2	2	2	2	2	2	2	2	2	2	2	2	0	1

Scenario 2 considers a 10% reduction in storage costs resulting from the implementation of the best practices in organization and disposal, as well as a decrease in energy rates in the region, combined with government incentives. The total cost obtained for this scenario is COP 2,834,295, representing a 6.57% reduction from the initial costs. Table 13 and Table 14 present the optimal results for the order quantity of products over the period and the inventory level of products by period for Scenario 1.

Table 13. Order Quantity of products by period—Scenario 2.

Product	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	19	0	0	20	0	0	0	2
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	17	0	0	13	0	0	0	0
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	4	0	0	0	0	0	1	3
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	4	0	0	6	0	0	1	2
Doxycycline 100 mg 10 tablets	0	0	0	0	0	0	0	0	1	0	0	6	0	0	0	1
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	0	0	0	16	0	0	3	2
Fusidic acid cream 15 gr	0	0	0	0	0	0	0	0	2	0	0	1	0	0	1	1
Dicloxacillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	4	0	0	4	0	0	0	0
Sulfaplate 1% cream 30 gr	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	2
Fusidic acid cream 15 gr	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Trimethoprim sulfa f 160–800 100 tablets	0	0	0	0	0	0	0	0	7	0	0	2	0	0	2	1
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	2	0	0	3	0	0	0	1
Rifamicin spray 1% 20 mL	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Amoxicillin 250 mg suspension 100 mL	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Erythromycin 500 mg 50 tablets	0	0	0	0	0	0	0	0	0	0	0	0	0	0	3	1

Table 14. Inventory level of products by periods—Scenario 2.

Products	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	0	42	38	38	31	24	9	9	3	8	8	3	18	5	3	3	2
Amoxicillin 500 mg 50 capsules	0	58	58	58	51	41	27	20	5	16	10	5	14	5	5	5	5
Azithromycin 500 mg 3 tablets	0	26	13	13	9	3	3	3	3	5	3	3	3	3	3	2	1
Azithromycin 500 mg 3 tablets	0	20	20	14	13	4	4	4	4	8	4	4	9	5	4	3	2
Doxycycline 100 mg 10 tablets	0	13	13	10	6	6	4	3	3	4	4	3	8	5	3	3	2
Amoxicillin 500 mg 50 capsules	0	9	8	5	3	3	3	3	3	3	3	3	19	13	3	0	1
Fusidic acid cream 15 gr	0	4	4	4	3	3	3	2	2	4	2	2	2	2	2	1	1
Dicloxacillin 500 mg 50 capsules	0	11	11	10	7	5	4	3	3	6	5	3	4	3	3	3	3
Sulfaplate 1% cream 30 gr	0	4	4	3	2	2	2	2	2	3	2	2	3	3	2	2	2
Amoxicillin 500 mg 50 capsules	0	23	18	8	4	4	4	4	4	4	4	4	4	4	4	3	3
Fusidic acid cream 15 gr	0	9	9	8	8	5	4	3	3	3	3	3	3	3	3	3	3
Trimethoprim sulfa f 160–800 100 tablets	0	7	7	6	6	3	3	3	2	7	6	2	4	3	2	1	2
Azithromycin 500 mg 3 tablets	0	7	6	4	2	1	1	1	1	3	3	1	1	1	1	1	1
Rifamicin spray 1% 20 mL	0	4	3	2	2	2	2	2	2	2	2	2	2	2	2	2	2
Amoxicillin 250 mg suspension 100 mL	0	9	8	7	7	7	3	2	2	2	2	2	2	2	2	2	2
Erythromycin 500 mg 50 tablets	0	2	2	2	2	2	2	2	2	2	2	2	2	2	2	0	1

In Scenario 3, a proposal is made to reduce the minimum batch sizes of medicines by 30% to lower the quantity of products held in inventory. Implementing this scenario results in a total cost of COP 2,608,870, which accounts for 15.78% of the initial total costs. Table 15 and Table 16 present the optimal results for the order quantity of products over the period and the inventory level of products by period for Scenario 1.

Table 15. Order Quantity of products by period—Scenario 3.

Product	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	19	0	0	20	0	0	0	2
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	17	0	0	13	0	0	0	0
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	4	0	0	0	0	0	1	3
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	4	0	0	6	0	0	1	2
Doxycycline 100 mg 10 tablets	0	0	0	0	0	0	0	0	1	0	0	6	0	0	0	1
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	0	0	0	16	0	0	4	2
Fusidic acid cream 15 gr	0	0	0	0	0	0	0	0	2	0	0	1	0	0	1	1
Dicloxacillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	4	0	0	4	0	0	0	0
Sulfaplate 1% cream 30 gr	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0
Amoxicillin 500 mg 50 capsules	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	2
Fusidic acid cream 15 gr	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Trimethoprim sulfa f 160–800 100 tablets	0	0	0	0	0	0	0	0	7	0	0	2	0	0	2	1
Azithromycin 500 mg 3 tablets	0	0	0	0	0	0	0	0	2	0	0	3	0	0	0	1
Rifamicin spray 1% 20 mL	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Amoxicillin 250 mg suspension 100 mL	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
Erythromycin 500 mg 50 tablets	0	0	0	0	0	0	0	0	0	0	0	0	0	0	4	1

Table 16. Inventory level of products by periods—Scenario 3.

Products	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Azithromycin 500 mg 3 tablets	0	41	37	37	30	23	8	8	2	7	7	2	17	4	2	2	1
Amoxicillin 500 mg 50 capsules	0	56	56	56	49	39	25	18	3	14	8	3	12	3	3	3	3
Azithromycin 500 mg 3 tablets	0	25	12	12	8	2	2	2	2	4	2	2	2	2	2	1	0
Azithromycin 500 mg 3 tablets	0	19	19	13	12	3	3	3	3	7	3	3	8	4	3	2	1
Doxycycline 100 mg 10 tablets	0	12	12	9	5	5	3	2	2	3	3	2	7	4	2	2	1
Amoxicillin 500 mg 50 capsules	0	8	7	4	2	2	2	2	2	2	2	2	18	12	2	0	1
Fusidic acid cream 15 gr	0	3	3	3	2	2	2	1	1	3	1	1	1	1	1	0	0
Dicloxacillin 500 mg 50 capsules	0	10	10	9	6	4	3	2	2	5	4	2	3	2	2	2	2
Sulfaplate 1% cream 30 gr	0	3	3	2	1	1	1	1	1	2	1	1	2	2	1	1	1
Amoxicillin 500 mg 50 capsules	0	22	17	7	3	3	3	3	3	3	3	3	3	3	3	2	2
Fusidic acid cream 15 gr	0	8	8	7	7	4	3	2	2	2	2	2	2	2	2	2	2
Trimethoprim sulfa f 160–800 100 tablets	0	6	6	5	5	2	2	2	1	6	5	1	3	2	1	0	1
Azithromycin 500 mg 3 tablets	0	7	6	4	2	1	1	1	1	3	3	1	1	1	1	1	1
Rifamicin spray 1% 20 mL	0	3	2	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Amoxicillin 250 mg suspension 100 mL	0	8	7	6	6	6	2	1	1	1	1	1	1	1	1	1	1
Erythromycin 500 mg 50 tablets	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	1

6.1. Comparison of Total Inventory Planning Cost

A comparative analysis is conducted to evaluate the decision made by the proposed model against the original results and the outcomes of three alternative scenarios. The aim is to identify which result leads to the most significant cost minimization. It is essential to note that the same model is applied across all scenarios. This model is designed to provide flexibility in estimating demand while preventing unnecessary orders. Table 10 presents the budgetary capacities for each scenario being compared, along with the objective function for each one. Additionally, Figure 3 displays a bar chart that illustrates the position of the objective function for each scenario. Among the scenarios, Scenario 3 achieves the most significant cost minimization, with a budgetary capacity result of COP 2,608,870, leading to a variance of −13.6%.

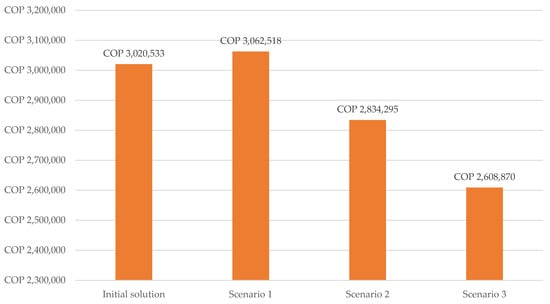
Figure 3. Optimal Solution of the model by scenarios.

Figure 4 illustrates the recommended number of units to order for each medication type during specific periods, based on the current pharmacy situation. It suggests placing orders only in months 9, 12, 14, and 16 to minimize inventory planning costs while maintaining sufficient stock levels, thus avoiding medication shortages. Figure 5, Figure 6 and Figure 7 illustrate the optimal order quantities from the supplier for each medication type across different scenarios. Among the scenarios analyzed, scenario three emerges as the most favorable option based on the values of the objective function. An examination of inventory patterns in previous periods reveals an excess of unsold products. Consequently, reducing the minimum inventory level by 30% could lead to a 15.78% decrease in overall inventory planning costs compared to the initial status of the pharmacy.

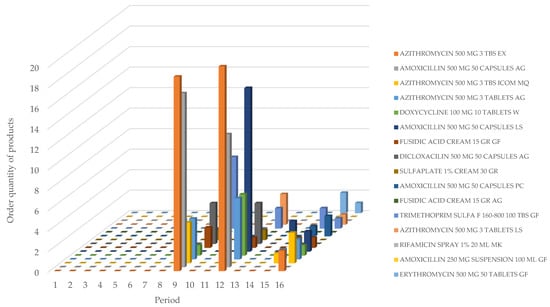
Figure 4. Optimal initial solution of the order quantity of products.

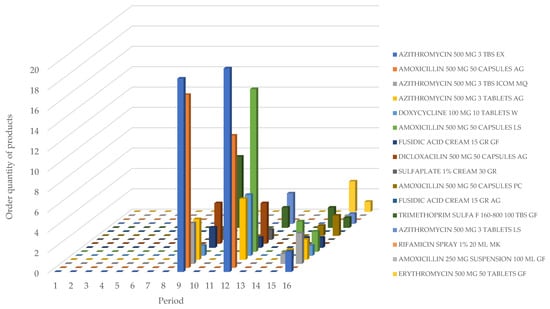
Figure 5. Optimal solution of the order quantity of products by scenario 1.

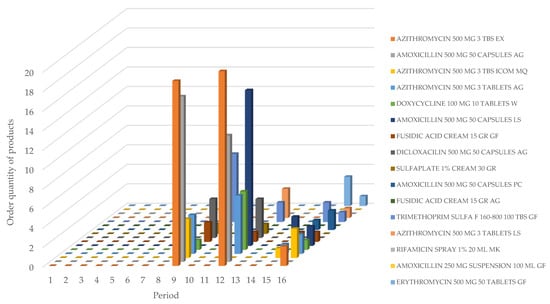
Figure 6. Optimal solution of the order quantity of products by scenario 2.

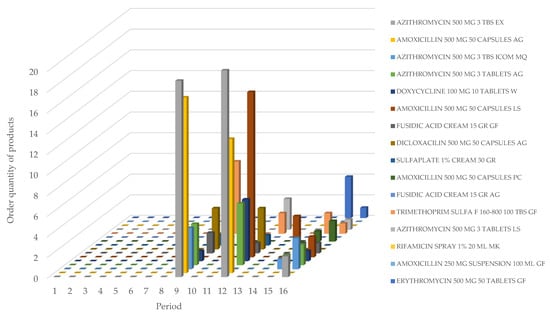
Figure 7. Optimal solution of the order quantity of products by scenario 3.

6.2. Managerial Implications

This study develops and evaluates a multi-product, multi-period inventory planning model for optimizing medicine supply in a pharmacy. The analysis examines three scenarios to assess the impact of changes to operational and cost parameters. In Scenario 1, a 15% increase in ordering costs resulted in a modest 1.4% rise in total inventory costs (COP 3,062,518) without affecting the decision variables. Scenario 2 demonstrated a 10% reduction in storage costs, enabled by best practices and government incentives, yielding a 6.57% cost decrease (COP 2,834,295). Scenario 3 introduced a 30% reduction in minimum batch sizes, resulting in the most significant improvement, with a 15.78% reduction in costs (COP 2,608,870). Comparative analysis with prior studies suggests that storage optimization and reduced lot sizes consistently generate savings across pharmacy contexts [33,34]. In contrast, ordering-cost variations have limited effects unless coupled with demand and lead-time uncertainty [9]. These findings underscore the importance of integrating batch-sizing policies, FEFO-based controls, and uncertainty modeling to strike a balance between cost efficiency and service reliability in pharmaceutical supply chains.

This research highlights the managerial importance of optimizing inventory management, reducing unnecessary costs, and enhancing product availability. The proposed model presents practical insights into how implementing operational policies can lead to cost savings while ensuring a continuous supply of medicine. Managers can use the results to design more efficient procurement strategies, reduce stockouts, and prevent excessive inventory levels that lead to increased waste and costs. The study allows pharmacy managers to anticipate the impact of changes in supply chain parameters and implement policies that balance financial efficiency with service quality, improving profitability and patient satisfaction.

6.3. Limitations of the Study

This study considered the case study of a pharmacy in Barranquilla, Colombia, which may limit the generalizability of the findings to other contexts with different operational, regulatory, or infrastructural conditions. Future research could include some factors such as perishability, expiration dates, or FEFO policies. Additionally, sustainability, collaboration among multiple echelons, or patient service levels should be essential to include in the pharmacy sector.

7. Conclusions

This research developed a mathematical inventory planning model to optimize the supply process of a pharmacy in Barranquilla. The methodology involved studying the pharmaceutical field, observing the supply process, interacting with employees, and using 16 months of historical data to develop the model. The primary objective was to find an optimal method for managing drug inventory, thereby minimizing costs and ensuring product availability to customers. The proposed model aims to minimize inventory planning costs for antibiotic management, resulting in improved resource utilization and more accurate order management.

The model offers strategic insights into the factors that most significantly affect operational efficiency. Scenario analysis revealed that variability in delivery times and supplier reliability are critical variables. Minor improvements in these areas can drive additional profits, whereas significant deterioration could offset some of these benefits.

From a managerial perspective, the research confirms that data-driven decision-making and mathematical models enhance business resilience in the face of market changes, regulatory shifts, or health-related events. Transitioning from empirical methods to an optimized approach not only boosts profitability but also frees up working capital, allowing for investments in value-added initiatives such as loyalty programs and complementary clinical services.

Additionally, the experience gained by staff during the adoption of the model fosters a culture of continuous improvement and encourages the use of analytical tools. However, the study has limitations that deserve consideration in future research. The model assumed a stationary demand and utilized a fixed time horizon. Nevertheless, seasonality and public health events can drastically change consumption patterns. Incorporating advanced forecasting techniques and modules for dynamic replenishment policy review would strengthen the proposal. It would also be beneficial to evaluate integration with multi-echelon inventory systems, as many pharmacies in Barranquilla are part of networks or chains with their distribution centers. Lastly, exploring sustainability indicators, such as minimizing losses due to expiration, would enhance the project’s social and environmental impact.

The developed optimization model provides a robust tool for efficient pharmaceutical inventory management in Barranquilla. The economic benefits achieved, increased operational visibility, and the capability to adapt to various scenarios present compelling reasons for its adoption and expansion. With adjustments aimed at managing uncertainty and multiple supply levels, this solution has the potential to become a reference standard for inventory planning in the local and regional healthcare sector.

Future research should focus on improving pharmaceutical inventory models by considering changing consumer demand, unpredictable lead times, and the perishability of products. Utilizing digital twin simulations and IoT-based monitoring can facilitate real-time decision-making and minimize waste. We should also consider energy efficiency and carbon footprint to make pharmacy operations more environmentally friendly. Expanding the model to include networks that work together and utilizing strategies such as Vendor-Managed Inventory can enhance coordination. Ultimately, converting this model into practical tools will enable healthcare managers and policymakers to make more informed decisions.