Abstract
A computational study is presented in which two strategies of ligand modifications have been explored to invert the relative energy of the metal-to-ligand charge transfer (MLCT) and metal-centered (MC) state in Fe(II)-polypyridyl complexes. Replacing the bipyridines by stronger donors increases the ligand-field strength and pushes the MC state to higher energy, while the use of ligands with a larger conjugation leads to lower MLCT energies.
1. Introduction
Fe(II) polypyridyl complexes have received a great deal of attention because they play a central role in the interpretation of the light induced excited state-spin trapping (LIESST) process [1,2,3]. The mechanism of the photo deactivation has been extensively studied both experimentally and theoretically [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. After light irradiation, the system decays from the singlet metal-to-ligand charge transfer (MLCT) state to the quintet metal-centred (MC) high-spin (HS) state on a femtosecond time scale, making the Fe(II) complexes less useful for applications such as light-harvesting and photocatalysis. On the contrary, Ru(II) complexes have longer excited state lifetimes and do not end up in a metastable MC state. Moreover, these complexes are easily oxidised in the excited state and are therefore much better suited to be used as electron donating complex [25,26,27,28]. The drawback of these systems is the scarcity of Ru, making large scale applications extremely expensive. It is therefore desirable to reproduce the properties of the Ru(II) complexes with the much more abundant Fe. Ligand modification have been proposed and studied to increase the MLCT lifetime in Fe(II) complexes [24,29,30,31,32,33,34,35]. There are basically two strategies to achieve this goal: one is to create a stronger ligand field and push the MC states higher than the MLCT states; another idea is to expand the -conjugation on the ligand, lowering the MLCT states. Both strategies have been explored here using different ligands coordinated to Fe(II). We will show that controlling the relative energy of charge transfer and ligand field states becomes an effective way to influence the excited states dynamics.
Figure 1 sketches the energy levels of the electronic states relevant to the relaxation of the excited state populated after the absorption of a photon by Ru(II)- and Fe(II)-trisbipyridine, which in both cases is the MLCT state. One electron is transferred from a non-bonding metal-d orbital of approximate symmetry to the lowest empty orbital on the ligand. Starting from a delocalised electron in the vertically excited state, it has been shown that the geometry of both complexes relaxes to a situation with the electron localised on one of the three bipyridine ligands. This accompanied by a small increase of the average metal–ligand distance as can be seen in Figure 1 by the displacement of the minimum on the MLCT curve towards larger distance with respect to the LS state. A second process that takes place at a very short time scale is the intersystem crossing (ISC) from MLCT to MLCT. The two states share the same electronic configuration, which makes the energy difference small (formally, just an interatomic exchange integral, typically of the order of 0.1 eV). As there is sizeable spin-orbit coupling between these states, the ISC takes place in less than 100 fs in both complexes.
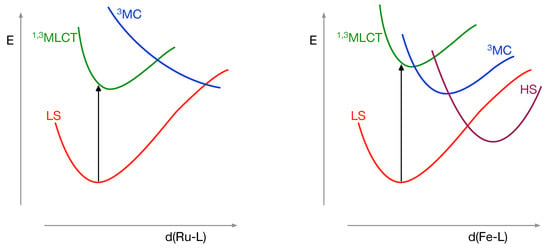
Figure 1.
Schematic representation of the relative energies of the low-spin (LS), high-spin (HS), metal-to-ligand charge-transfer (MLCT) and excited metal-centered (MC) states as function of symmetric expansion of the first coordination sphere in Ru(II)- and Fe(II)-trisbipyridine.
Because of the larger radial extension of the 4d orbitals, the bipyridine ligands exert a much larger ligand field in the Ru(II) complex than in the Fe(II) analogue. For this reason the MC state (with one electron transferred from the non-bonding -like orbital to an antibonding -like orbital) lies at very high energy in the Ru(II) complex. In fact, it only becomes more stable than the MLCT state at Ru-ligand distances that are much longer than the equilibrium distance of the MLCT state and this crossing point will never be reached. Therefore, the system becomes trapped in the MLCT state and has been measured to have a lifetime on the order of s [36,37]. The situation is completely different in Fe(II)-trisbipyridine. The smaller ligand-field lowers all the MC states to such extent that both the MC and MC are close in energy with the MLCT state near the minimum of latter. This favours a fast decay to the metastable HS state (lifetime of ∼650 ps) [38], either directly from MLCT to MC (HS); via the MC state, or a combination of both deactivation paths [12,13,16,20].
From this short outline, it is clear that increasing the -donating character (and hence a larger ligand field) or lowering the energy of the lowest ligand orbital can profoundly change the photophysics of the Fe(II) polypyridyl complexes, ideally reaching the energetic ordering of the Ru complexes, drawn on the left in Figure 1.
2. Enlarging the Conjugation
To investigate the effect of the size of the -system on the MLCT energy we first calculated the lowest unoccupied molecular orbital (LUMO) energy of a series of six ligands similar to bipyridine of increasing size: (a) pyridine, (b) bipyridine, (c) terpyridine, (d) phenantroline, (e) 2-(2-pyridyl)-1,10-phenanathroline, (f) dipyrido-[4,3-b;5,6-b] acridine, depicted in Figure 2. Not unexpected, the smallest ligand (a) gives the highest orbital energy (−0.047 ). The isolated ligands (b), (c) and (d) have very similar orbital energies of −0.071 , −0.070 and −0.072 , respectively. The last two isolated ligands (e) and (f) with the largest system have the lowest energies −0.082 and −0.088 , respectively. Contour plots of these orbitals can be found in the Supporting Information, Figure S1.
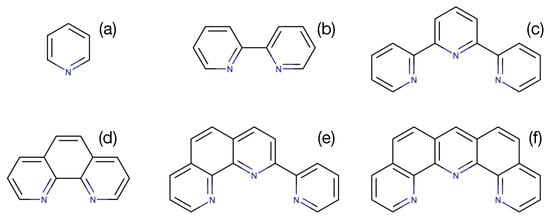
Figure 2.
Six ligands of increasing size used to lower the energy of the MLCT state in Fe(II) complexes. (a) pyridine, (b) bipyridine, (c) terpyridine, (d) phenantroline, (e) 2-(2-pyridyl)-1,10-phenanathroline, (f) dipyrido-[4,3-b;5,6-b] acridine.
With this tendency in mind, we have constructed six complexes with the same Fe(II)N core structure using the ligands of Figure 2 to confirm that a larger -conjugated system indeed leads to a lower MLCT energies. A ball-and-stick representation of the complexes is given in Figure 3 and the vertical excitation energies of the singlet and triplet MLCT and MC states are listed in Table 1.
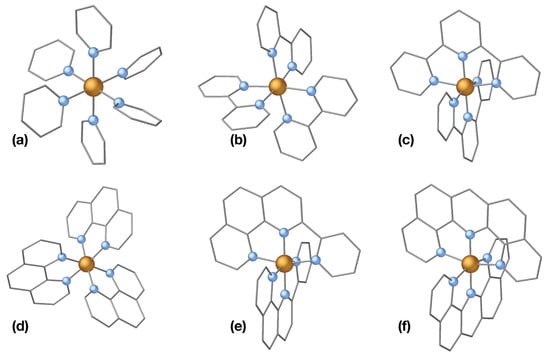
Figure 3.
Six Fe(II) complexes with increasing -conjugation on the ligand. a = [Fe(py)], b = [Fe(bpy)], c = [Fe(terpy)], d = [Fe(phen)], e = [Fe(dipphen)], f = [Fe(acri)]. py = pyridine; bpy = bipyridine; terpy = terpyridine; phen = phenantroline; dipphen = 2-(2-pyridyl)-1,10-phenanathroline; acri = dipyrido-[4,3-b;5,6-b] acridine.

Table 1.
Vertical excitation energies (in eV) of the six Fe(II) complexes with ligands of increasing size.
The influence of the enlargement of the size of the -system on the MLCT states follows approximately the same tendency as the orbital energies. Complex a has the highest MLCT states. The group of complexes with the bidentate bipyridine and phenantroline ligands and the tridentate terpyridine ligand (all three with approximately the same orbital energy for the lowest unoccupied ligand -orbital) have significantly lower MLCT energies and the two complexes with the largest conjugated -system (complexes e and f) have indeed the lowest MLCT transition energies, 0.2 eV lower than in the complexes b, c and d.
Although this in itself is a promising result, we have also to take into account the trend in the MC state as function of the changing ligand. The low relative energy of the MC state in a is in line with the fact that pyridine is a weaker sigma donor than bipyridine, and as a matter of fact, the relative energy of the MC state of 1.11 eV is right in between the relative energy of 1.92 eV calculated for the MC state in [Fe(bpy)] (stronger sigma donor) and the 0.54 eV calculated for [Fe(HO)], a Fe(II) complex with a very weak sigma donating ligand. The relatively high MLCT energy and the low MC transition energy leads to a 1.70 eV gap between these two states, the largest observed in the series.
The vertical MLCT excitation energy of b, c and d is rather close to the MC energy, and becomes degenerate for c. But one should keep in mind that the geometry relaxation of the MC state has a much larger stabilising effect than in the MLCT state (the optimal geometry of the MLCT state is nearly identical to the one of the ground state, while the Fe-ligand distance is significantly larger in the MC state). Therefore, these complexes do not fulfil the requirement of inversion of MLCT and MC states as observed in [Ru(bpy)]. The additional lowering of 0.2 eV of the MLCT energy in e and f is unfortunately accompanied by a similar lowering in the MC excitation energy, which keeps the relative position of the MLCT and MC states similar as in the [Fe(bpy)] reference complex. The lowering of the MC energy is most probably due to the weaker sigma donating character of the ligands of complex e and f.
Hence, the larger -conjugation does lower the MLCT energy but not sufficient to achieve the inversion of the MLCT and MC states required for a long-lived MLCT state.
3. Replacing N by P
Stronger ligand-fields can be created by using stronger -donating ligands. The well-known spectrochemical series indicates that phosphorous ligands are stronger sigma donors than their nitrogen analogs, and hence, replacing N by P could be a possibility to raise the energy of the excited MC states above the MLCT states. An exhaustive search in the Cambridge Structural Database (CSD) revealed 14 different complexes with a FeNP core. Table 2 lists the vertical excitation energies of the MC and MLCT state as a preliminary selection criteria for candidates complexes that might show similar relative energies as [Ru(bpy)]. The complexes are labeled by the acronym that is used in the CSD and results are compared to [Fe(bpy)] and a model complex constructed by replacing all six nitrogens in [Fe(bpy)] by phosphorus. Ball and stick representations of the complexes can be found in the Supporting Information.

Table 2.
Vertical excitation energies for a series of FeNP complexes.
Among the different FeNP systems, MINWOX and JEGRIX have lower MC states and show similar features as the [Fe(bpy)] complex. In the remaining seven examples the MC lies at somewhat higher energy than the MLCT states, but by no means do we reproduce the gap of ∼1 eV calculated for [Ru(bpy)] [47]. Somewhat surprisingly, the complexes which have FeNP and FeNP core structures show again a larger gap between MC and MLCT states, with the MLCT states located at higher energy. Only the model complex obtained by replacing the six N atoms in [Fe(bpy)] by P shows a situation comparable to [Ru(bpy)] with a clearly more stable MLCT state. Looking at the table, we observe that the change in the ordering MLCT/MC that we have achieved is mostly caused by the stabilisation of the MLCT states rather than a destabilisation in the MC states.
Unfortunately, there are no examples of FeP complexes in the literature, and hence, further studying these complexes is not very useful. For further investigation of the FeNP systems that show the higher MC state, the geometry optimisation of the MC state has been done in the case of GIFJAG. However, this complex turns out to be unstable in the triplet state, because the two PPh(Me) ligands dissociate from the complex during the optimisation process. So here we conclude that replacing N with P is not a good strategy to invert the relative stability of the MC and MLCT states in Fe(II) complexes.
4. Replacing Bipyridine by CN
Instead of using P to increase the ligand field, one can also replace one or more N atoms by C. As PPh, CN is also stronger a -donor than bipyridine, and hence, is also a candidate to increase the ligand field strength. In this section we will study the effect of replacing one or two bipyridine ligands by two or four CN groups, leading to the complexes depicted in Figure 4. The excited state dynamics of these complexes have been studied recently with femtosecond resolution by 3p-1s X-ray emission and UV–Visible spectroscopy experiments [29,30,33]. It was found that the complex with two CN ligands displays the same deactivation mechanism as [Fe(bpy)], ending up in the metastable MC state through a double ISC within approximately 100 fs. However, replacing one more bipyridine ligand by another two CN ligands leads to quite a different behaviour. The experimental data indicates a slow decay of the excited state, which was identified as a MLCT state. The lifetime of this MLCT was estimated to be of the order of 20 ps [30].
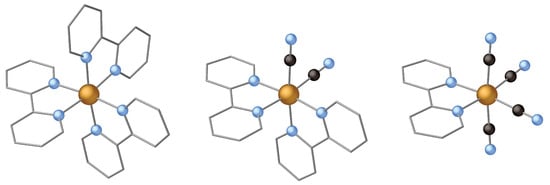
Figure 4.
From left to right: [Fe(bpy)], [Fe(bpy)(CN)] and [Fe(bpy)(CN)]. Large gold spheres represents Fe, blue spheres N, black spheres C and the carbon skeleton of the bipyridine ligand is represented by the grey cylinders. Hydrogens are omitted for clarity.
4.1. Vertical and Adiabatic Energies
At first, we have compared the calculated UV spectrum with the experimental one. To facilitate the comparison we have represented each transition with a gaussian function centred on the calculated transition energy whose height is proportional to the calculated oscillator strength and the width is taken to be 100 nm. The thick lines in Figure 5 represent the calculated data and the thin lines are the experimental results from [29,30]. In both complexes two peaks are observed in the 350–800 nm interval, both dominated by MLCT transitions. The orbitals involved in these MLCT transitions are represented in Figure S6 of the Supporting Information. The MC transitions carry very little intensity and are completely hidden in the high energy peak. Moreover, there is a very intense peak at wave lengths shorter than 350 nm due to inter- and intra ligand – transitions. In the computed spectrum of [Fe(bpy)(CN)], the second MLCT band appears as a shoulder of this ligand–ligand band, which is the reason why the calculated spectrum is sharply rising at 350 nm. The overall agreement between computation and experiment is quite remarkable, both the band maxima and the relative intensities are reproduced in both compounds, implying that the computational scheme applied here is capable of reproducing the lowering of the MLCT energy when bipyridine is replaced by cyanide.
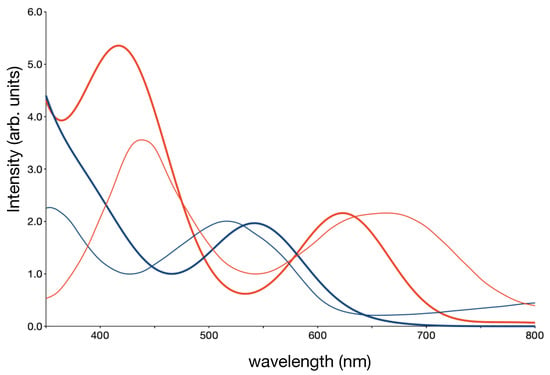
Figure 5.
Calculated (thick lines) and experimental (thin lines) [29,30] UV–Visible spectra for [Fe(bpy)(CN)] in methanol (blue) and [Fe(bpy)(CN)] in dimethyl sulfoxide (red).
The three lowest singlet and triplet MLCT states in [Fe(bpy)(CN)] arise from transitions from the three Fe-3d(-like) orbitals to the lowest empty orbital on the bipyridine ligand. The two lowest singlet MLCT states appear at 1.59 and 1.65 eV but have a very small transition dipole moment. The third one, at 1.99 eV, constitutes the main contribution to the low-lying MLCT band. At somewhat lower energy, 1.29 (2x) and 1.35 eV, we find the three MLCT states, which do not contribute to absorption bands because of these transitions are spin forbidden and even after taking into account spin-orbit coupling the contribution to the absorption spectrum is very small.
In the complex with two bipyridine ligands, there are six low-lying singlet and triplet MLCT states due to excitations from the Fe-3d() orbitals to the two empty orbitals on the bipyridine ligands. The singlets are found in an interval between 1.97 and 2.49 eV with the fifth state at 2.27 eV carrying the largest transition dipole moment. The lowest six triplets span the energy interval between 1.72 and 2.04 eV. Indicating that especially the lowest MLCT state suffers a significant change of the relative energy when bipyridine is replaced with two CN groups. Finally, the energies of the lowest singlet and triplet MLCT in the parent complex [Fe(bpy)] are at still higher energy. The lowest manifold now contains nine states and the span an energy range from 2.20 eV to 2.87 eV for the singlet and 2.09 eV to 2.41 eV for the lowest triplets.
The next point of interest is the relative energy of the lowest MC states. Because of the large on-site exchange integral, the singlet and triplet MC states are much more separated in energy than the MLCT states. There are six low-lying MC states arising from the T and T states of the 3d electronic configuration in a perfect octahedral coordination. This two times threefold degeneracy is of course not present in the here studied complexes, but instead we identify six states as MC between 2.17 eV and 2.80 eV in [Fe(bpy)(CN)] and between 2.45 and 3.23 in [Fe(bpy)(CN)]. The lowest MC states lie at 2.97 eV and 3.45 eV for the complexes with two and one bipyridine ligand, respectively. For the parent compound, the DFT calculation result in vertical excitation energies of 1.87–2.07 eV and 2.31–2.41 eV for the two sets of MC states and 2.78–2.89 eV for the MC state.
When compared to the relative energies of the MLCT and MC states in [Fe(bpy)], it becomes clear that the substitution of bipyridine by CN inverts the relative stability of these states in the Franck-Condon region (vertical excitation). However, for a definite answer one should take into account the geometry relaxation of the triplet states and compare the adiabatic energy differences. As illustrated in Figure 6, the geometry relaxation only has a small effect on the MLCT states, while it significantly lowers the energies of the MC states. We have not been able to optimise the geometry of the latter in [Fe(bpy)(CN)]. The MC lies in an energy range where many other, mostly MLCT states are found and root flipping during the geometry optimization makes it hard (if not impossible) to follow the MC state. A similar problem arises for the MLCT in [Fe(bpy)(CN)], where we have followed the strategy put forward in our earlier studies on [Fe(bpy)] [10]. Given the fact that the electronic configuration of MLCT and MLCT are the same, we have made the approximation that the optimal geometry and vibrational frequencies of the two states are very similar. As the MLCT is the first excited state and well separated from the ground state, it is straightforward to optimise the geometry of this state. The adiabatic MLCT energy is then obtained by performing a single point calculation on the optimised MLCT geometry.
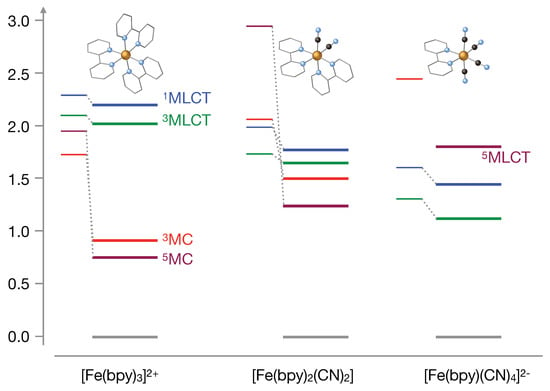
Figure 6.
TPSSh/def2-TZVP vertical and adiabatic excitation energies (in eV) for the [Fe(bpy)(CN)] complexes in dimethyl sulfoxide () and methanol (). The thin lines correspond to vertical excitation energies and the thicker lines to adiabatic energies.
To complete the picture, we have also calculated the relative energies (vertical and adiabatic) of the lowest quintet states. The MLCT states in [Fe(bpy)] were estimated some time ago to lie very high in energy [9] and therefore not relevant for the relaxation process. The vertical excitation energy of the MC state on the other hand is close to the MLCT states and geometry relaxation strongly lowers the energy to convert it into the most stable excited state. [Fe(bpy)(CN)] still shows quite large MLCT energies and the vertical and adiabatic energies of the MC state are significantly higher than in the unsubstituted complex. Replacing a second bipyridine ligand by two CN groups causes a further lowering of the MLCT state, which has become the most stable quintet state now. The MC state is off-scale in Figure 6 and cannot play any role in the excited state dynamics of this complex.
As most important results from the comparison of the adiabatic energies in the three complexes, we observe a clear tendency of increasing MC energy and lower MLCT energies with increasing number of CN ligands. In [Fe(bpy)(CN)] the three states are nearly degenerate, while there is a clear inversion of stability in [Fe(bpy)(CN)]. The calculated adiabatic energies are compatible with the experimental observation of a slow deactivation process in [Fe(bpy)(CN)] with no signs of spin crossover to the MC state. The ordering of the states in [Fe(bpy)(CN)] is similar to the one that is found in [Fe(bpy)] and from this point of view the deactivation path is expected to be the same as in [Fe(bpy)].
4.2. Intersystem Crossing Rates
Having analysed the optimal geometries, vertical and adiabatic excitation energies, we now focus on the description of the photocycle of the two modified complexes. The intersystem crossing rate constants, , were calculated with the VIBES program [48] based on Fermi’s golden rule. The necessary ingredients include: (1) the relative energies of the states involved in the intersystem crossing, (2) a full account of all vibrational wave functions to calculate the vibrational coupling between the different electronic states and (3) estimates of spin-orbit (SO) coupling matrix elements. The first point has been discussed extensively in the previous section, the vibrational modes and the corresponding frequencies were calculated from the optimised geometries used to calculate the adiabatic energy differences and the SO coupling was estimated following the procedure outlined in References [19,20]. The spin-orbit couplings between the relevant electronic states were calculated as the expectation value of the spin-orbit operator using the CASSCF wave functions. This so-called direct estimate of the SO coupling can be improved by taking into account higher order couplings involving other excited states. Direct and effective spin-orbit coupling between the spin states that are possibly involved in the deactivation for both complexes are listed in Table 3. We only list the maximum values. In the case of [Fe(bpy)(CN)], the comparison of the direct and effective interaction shows that the spin-orbit coupling between ligand-field states (GS, MC and MC) is almost not affected by external states, the difference between direct and effective interactions is less than 1 cm. Despite the non-existence of a direct interaction between singlet and quintet when using the standard one-electron spin-orbit operator, a weak effective interaction was observed between the ground state singlet and the MC of 3 cm. Similar small effects are observed for the interaction between MLCT and MC and a moderate increased coupling of 9 cm was observed for the interaction between MLCT and MLCT when external states are considered. In the case of the [Fe(bpy)(CN)] complex, we also observe small changes when comparing direct and effective SO couplings. The SO couplings involving the MC state have not been calculated in this case, because this quintet state lies very high in energy and does not play a role in the deactivation mechanism.

Table 3.
Direct and effective (maximum) spin orbit matrix elements between and .
As reported in Table 4, the calculated lifetime of the MLCT in the decay to the MLCT is around 220 fs in [Fe(bpy)(CN)], somewhat larger than the 30 fs in the parent complex [Fe(bpy)] caused by the reduction in the contribution due to the SO coupling. The maximum value is reduced from 200 [10] to 75 cm, which results in an overall smaller contribution. The second decay path for the MLCT leads to the MC state. The slightly larger energy difference and the larger geometry distortion makes the vibrational term significantly smaller than in the decay to the MLCT, but still the ISC rate is large enough to not exclude this decay path, particularly because Fermi’s golden rule can only be expected to give results within an order of magnitude. As already mentioned in our work on [Fe(bpy)], the internal conversion from MLCT to MC is expected to be at least as fast as the MLCT-MC ISC, and hence, at least a significant population of the MC state will be built up during the decay of the excited state. The MLCT and MC states can undergo intersystem crossings to the MC or fall back to the initial LS state. The direct deactivation of the MLCT to the MC state is highly improbable, while the path for SCO to the quintet state appears viable via the MC state. Whereas the MLCT-LS ISC rate is rather small (although not negligible), the deactivation of the MC to the LS state is extremely fast. Most probably, we are facing here the limits of the application of Fermi’s golden rule. In the first place, the vibrational contribution depends quite dramatically on the adiabatic energy difference as illustrated in Figure S7 of the Supporting Information. Since we are using here DFT adiabatic energies, there is a certain uncertainty in our estimates and an increase of 0.2 eV could easily lead to a decrease of an order of magnitude of .

Table 4.
Intersystem crossing rates () obtained from Fermi’s golden rule for the decay between electronic states of different spin in [Fe(bpy)(CN)]. Adiabatic energies, vibrational and spin-orbit contributions are also listed.
In short, the deactivation of the excited state in [Fe(bpy)(CN)] follows largely the same mechanism as the one that was determined for the parent compound with three bipyridine ligands. The only difference that we have encountered is that the decay to the initial ground state seems more likely in this modified complex.
The situation is quite different when two more CN groups replace another bipyridine. As can be seen in Figure 6, the singlet and triplet MLCT states are the lowest excited states and after the absorption of light to populate the MLCT state, there is only one possible deactivation path. The calculated intersystem crossing rate for the MLCT-MLCT decay is 7.87 × 10, very similar to the one calculated for the complex with two bipyridines. On the other hand, the decay of the MLCT to the ground state is significantly slower ( = 9.4 × 10; t = 106 ps), although we were not able to exactly reproduce the experimental estimate of 20 ps for the lifetime of this state. Again the calculated values show a dependency on the adiabatic energy difference (see Figure S5), and hence, we cannot pretend to be more accurate than an order of magnitude estimate. But the calculations presented here support the general conclusion that replacing bipyridine ligands with stronger -donating groups leads to an increased lifetime of the MLCT state in Fe(II)-polypyridyl complexes.
5. Discussion and Conclusions
Fe(II) and Ru(II) polypyridyl complexes show an inverse ordering the low-lying MC and MLCT states. Generally speaking, the MLCT state is the lowest excited state in the case of Ru, while MC states lie higher and do not play a role in the deactivation. On the contrary, Fe(II) complexes show low-lying MC states, causing very short life times of the MLCT states. To invert this situation, we have explored two different strategies. Larger -systems on the ligands lowers the MLCT relative energy and increasing the -donation pushes the MC states up in energy. In the series of ligands from pyridine to dipyrido-acridine, we indeed observe a lowering of orbital energy of the lowest orbital, which in turn leads to a lower MLCT energy in the complex. However, this lowering is not large enough to cause inversion. The increase of the -donation is most effective when N in the first coordination sphere is replaced by C by changing bipyridine for two CN ligands. Our calculations show that the replacement of one biprydine for two CN groups leads to a near degeneracy of MLCT and MC states but does not lead to a substantially different decay mechanism than the one observed in [Fe(bpy)]. The situation changes completely when another bipyridine is removed from the complex and two more CN ligands coordinate to Fe. The MLCT state is now clearly the lowest excited state and the system becomes trapped for a reasonably long time in this state.
As we observed that for the ligands with the larger -systems both the MLCT and the MC relative energies are lowered by approximately the same amount, an interesting possibility to further improve the excited state properties of the Fe(II) complexes would be the design of a ligand with an equally large system, but with atoms coordinating to Fe that are stronger donors. This would lead to a simultaneous increase of the MC energy and decrease of the MLCT state and further extend the possibility of re-creating the Ru(II) situation in Fe(II) complexes.
From the purely computational point of view, it should be noted that all the energies that we have used in the study of the deactivation are extracted from DFT calculations. In previous studies performed in our group, we relied on multiconfigurational second-order perturbation theory (CASPT2) for the relative energies. In agreement with the findings of Pierloot [49,50], we found in these studies that the DFT optimised geometries are not always the optimal choice for calculating the CASPT2 energies. In general the optimal Fe–ligand distance is significantly shorter in CASPT2 than for most of the DFT functionals. As illustrated in Figure 7, performing CASPT2 calculations with too large Fe-ligand distances can lead to very poor estimates of the vertical excitation energies, and has also a significant effect on the adiabatic energies.
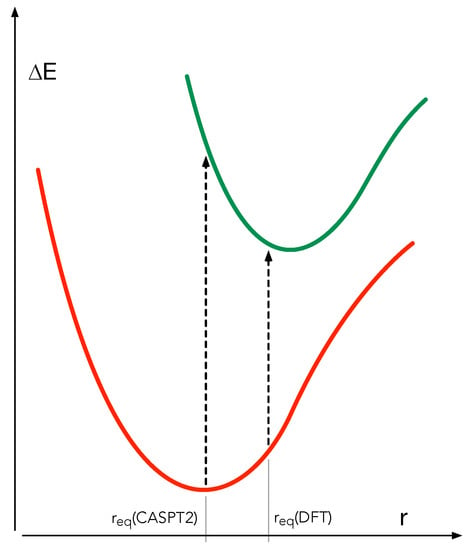
Figure 7.
Schematic CASPT2 energy profiles of two electronic states as function of the Fe-ligand distance r.
Hence, for reliable CASPT2 estimates, one should at least re-optimise the first coordination sphere of the metal, since a full geometry optimisation is far beyond the computational possibilities in all but the smallest model complexes. In our previous applications, this was quite easy since there was only one variable that needed to be optimised, the six Fe–N distances in [Fe(bpy)] are nearly identical in all electronic states (the Jahn-Teller distortion in the T is very weak). Even for two variables [51], it is still possible to follow this partial optimisation strategy. However, for the present complexes, there are three significantly different distances and also the angles can vary independently. Therefore, a partial optimisation becomes simply too complex, which is the reason why we opted for staying at the DFT level, although the energies are slightly less accurate.
Which brings us to the last point of discussion: the uncertainty in the estimate of the intersystem crossing rates. The energy difference is one of the factors that appear in the expression for and, as discussed above, its value depend in some cases rather critically on . There is, however, a more fundamental question about the validity of Fermi’s golden rule to estimate the lifetimes of excited states in ultrafast deactivation processes. One of the underlying assumptions of Fermi’s golden rule is that the non-radiative decay to another electronic state takes place from the equilibrium geometry of the initial state, either from a vibrationally cooled state or from a collection of vibrational states, whose population is conditioned by the Boltzmann distribution. Given the ultrafast decays in the complexes studied here, it might be questioned whether the system has the time to relax its geometry before going through an ISC. For those crossing with the MLCT as initial state, there is certain validity to Fermi’s golden rule as the geometry distortion compared with the LS state is small. The population of the MLCT state by excitation from the LS state does not induces large geometry distortions and the ISC will take place in the Franck-Condon region. However, the MC state has significantly larger Fe–ligand distances and the system needs a certain amount of time to relax. Hence, the calculate with this MC states as initial state might be subject to a larger uncertainty and the 0.11 ps lifetime for the MC to LS ISC should be considered with caution, although it might point at the fact that not all excitation processes lead to SCO ending up in the MC but at occasions the MC return to the initial LS. We have not been able to find any experimental information about the quantum efficiency in [Fe(bpy)(CN)].
6. Computational Information
All DFT calculations were performed with Orca 4.2 [52,53]. Following the conclusions of the study of Kepp and co-workers [54,55,56], we have used the TPSSh functional [57] for geometry optimisations, frequency calculations [58] and vertical excitation energies. The time-dependent calculations were all performed using the Tamm-Dancoff approximation and triplet states were calculated using the ground state singlet as reference. In Figure S8 of the Supporting Information we compare the outcomes of the TD-DFT calculations using the TPSSh functional to those with the CAM-B3LYP functional, often suggested as a good functional to describe charge transfer excitations. The coincidence is almost exact for [Fe(bpy)(CN)], but CAM-B3LYP gives a rather poor description of the excitation energies for the [Fe(bpy)(CN)] complex.
The Kohn-Sham orbitals are expanded in the def2-TZVP basis set [59] and the integral evaluation is accelerated by using the RIJCOSX procedure [60,61], using the standard def2 auxiliary basis set [62]. In those cases where the Hessian was calculated numerically, we increased the grid for numerical integration to “grid6” and “gridx6”.
Solvent effects were included via the conductor-like polarisable continuum model (C-PCM), using the parameters of dimethyl sulfoxide for [Fe(bpy)] and [Fe(bpy)(CN)] and of methanol for [Fe(bpy)(CN)] to reproduce the experimental conditions. The solvent effect is rather small on the optimal geometries as illustrated in Table S9, but cannot be neglected in the calculation of the relative energies, especially for the negatively charged complex.
The compete active space (CAS) calculations to estimate the spin-orbit coupling between the different electronic states were performed with OpenMolcas [63]. An active space of 10 active electrons and 13 active orbitals was used in both complexes. A graphical representation of the active orbitals is given in Figures S3 and S4 of the Supplementary Information. This choice of active space is the standard CAS for transition metal complexes in general [49,50] and has been successfully applied in complexes with spin crossover closely related to the ones treated here [10,64]. Since we are not after highly accurate relative energies, we have used basis sets of moderate size. For all atoms we have used the ANO-RCC basis sets [65,66] with the following contractions: Fe(6s,5p,4d,2f); N and C-atoms in the first coordination sphere (4s,3p1d); other C-atoms (3s,2p) and H(2s). The spin-orbital Hamiltonian is spanned by the lowest 7 singlets, 9 triplets and 6 quintets, whose wave function was obtained three separate state-average CASSCF calculations. Effective spin-orbit couplings have been calculated by the effective Hamiltonian approach outlined in Reference [19].
The intersystem crossing rates were calculated by the time integration of Fermi’s golden rule rewritten in a time-dependent formulation [48]. We used the complete time correlation function and integrated over a time interval of 32 fs using 1024 points, no damping was needed for convergence.
Supplementary Materials
The following are available online at https://www.mdpi.com/2304-6740/8/2/16/s1, Figure S1: Contour plots of the lowest unoccupied ligand orbitals, Figure S2: Atom numbering of [Fe(bpy)(CN)] and [Fe(bpy)(CN)], Figures S3 and S4: Contour plots of the active orbitals of [Fe(bpy)(CN)] and [Fe(bpy)(CN)], Figure S5: Dependence of the vibrational contribution to as function of the adiabatic energy, Tables S1–S4: Cartesian coordinates of the LS, MC, MC and MLCT states of [Fe(bpy)(CN)], Table S5: Selected geometric parameters of the FeNC-core of [Fe(bpy)(CN)], Tables S6 and S7: Cartesian coordinates of the LS and MLCT states of [Fe(bpy)(CN)], Table S8: Selected geometric parameters of the FeNC-core of [Fe(bpy)(CN)], Table S9: Gas-phase and solvent optimised Fe-ligand distances of MLCT state of [Fe(bpy)(CN)].
Author Contributions
Conceptualization, C.d.G.; investigation, J.W. and M.A.; writing–original draft preparation, J.W. and C.d.G.; writing–review and editing, C.d.G., J.W. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support has been provided by the Spanish Administration (CTQ2017-83566-P) and the Generalitat de Catalunya (2017-SGR629).
Conflicts of Interest
The authors declare no conflict of interest.
References
- McGarvey, J.J.; Lawthers, I. Photochemically-induced perturbation of the 1A ⇌5T equilibrium in FeII complexes by pulsed laser irradiation in the metal-to-ligand charge-transfer absorption band. J. Chem. Soc. Chem. Commun. 1982, 906–907. [Google Scholar] [CrossRef]
- Decurtins, S.; Gütlich, P.; Köhler, C.P.; Spiering, H.; Hauser, A. Light-induced excited spin state trapping in a transition-metal complex: The hexa-1-propyltetrazole-iron(II) tetrafluoroborate spin-crossover system. Chem. Phys. Lett. 1984, 105, 1–4. [Google Scholar] [CrossRef]
- Hauser, A. Light-Induced spin-crossover and the high-spin → low-spin relaxation. In Spin Crossover in Transition Metal Compounds II; Topics in Current Chemistry; Gütlich, P., Goodwin, H.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 234, pp. 155–198. [Google Scholar]
- Gawelda, W.; Cannizzo, A.; Pham, V.T.; van Mourik, F.; Bressler, C.; Chergui, M. Ultrafast nonadiabatic dynamics of [FeII(bpy)3]2+ in solution. J. Am. Chem. Soc. 2007, 129, 8199–8206. [Google Scholar] [CrossRef]
- Bressler, C.; Milne, C.; Pham, V.T.; ElNahhas, A.; van der Veen, R.M.; Gawelda, W.; Johnson, S.; Beaud, P.; Grolimund, D.; Kaiser, M.; et al. Femtosecond XANES Study of the Light-Induced Spin Crossover Dynamics in an Iron(II) Complex. Science 2009, 323, 489–492. [Google Scholar] [CrossRef]
- Gawelda, W.; Pham, V.T.; van der Veen, R.M.; Grolimund, D.; Abela, R.; Chergui, M.; Bressler, C. Structural analysis of ultrafast extended X-ray absorption fine structure with subpicometer spatial resolution: Application to spin crossover complexes. J. Chem. Phys. 2009, 130, 124520. [Google Scholar] [CrossRef]
- Cannizzo, A.; Milne, C.J.; Consani, C.; Gawelda, W.; Bressler, C.; van Mourik, F.; Chergui, M. Light-induced spin crossover in Fe(II)-based complexes: The full photocycle unraveled by ultrafast optical and X-ray spectroscopies. Coord. Chem. Rev. 2010, 254, 2677–2686. [Google Scholar] [CrossRef]
- De Graaf, C.; Sousa, C. Study of the Light-Induced Spin Crossover Process of the [FeII(bpy)3]2+ Complex. Chem. Eur. J. 2010, 16, 4550–4556. [Google Scholar] [CrossRef]
- De Graaf, C.; Sousa, C. On the Role of the Metal-to-Ligand Charge Transfer States in the Light-Induced Spin Crossover in FeII(bpy)3. Int. J. Quantum Chem. 2011, 111, 3385–3393. [Google Scholar] [CrossRef]
- Sousa, C.; de Graaf, C.; Rudavskyi, A.; Broer, R.; Tatchen, J.; Etinski, M.; Marian, C.M. Ultrafast deactivation mechanism of the excited singlet in the light-induced spin crossover of [Fe(bpy)3]2+. Chem. Eur. J. 2013, 19, 17541–17551. [Google Scholar] [CrossRef]
- Domingo, A.; Sousa, C.; de Graaf, C. The effect of thermal motion on the electron localization in metal-to-ligand charge transfer excitations in [Fe(bpy)3]2+. Dalton Trans. 2014, 43, 17838–17846. [Google Scholar] [CrossRef]
- Zhang, W.; Alonso-Mori, R.; Bergmann, U.; Bressler, C.; Chollet, M.; Galler, A.; Gawelda, W.; Hadt, R.G.; Hartsock, R.W.; Kroll, T.; et al. Tracking excited-state charge and spin dynamics in iron coordination complexes. Nature 2014, 509, 345–348. [Google Scholar] [CrossRef]
- Auböck, G.; Chergui, M. Sub-50-fs photoinduced spin crossover in [Fe(bpy)3]2+. Nat. Chem. 2015, 7, 629–633. [Google Scholar] [CrossRef]
- Field, R.; Liu, L.C.; Gawelda, W.; Lu, C.; Miller, R.J.D. Spectral Signatures of Ultrafast Spin Crossover in Single Crystal [FeII(bpy)3](PF6)2. Chem. Eur. J. 2016, 22, 5118–5122. [Google Scholar] [CrossRef]
- Zerdane, S.; Wilbraham, L.; Cammarata, M.; Iasco, O.; Rivière, E.; Boillot, M.L.; Ciofini, I.; Collet, E. Comparison of structural dynamics and coherence of d–d and MLCT light-induced spin state trapping. Chem. Sci. 2017, 8, 4978–4986. [Google Scholar] [CrossRef]
- Moguilevski, A.; Wilke, M.; Grell, G.; Bokarev, S.I.; Aziz, S.G.; Engel, N.; Raheem, A.A.; Kühn, O.; Kiyan, I.Y.; Aziz, E.F. Ultrafast spin crossover in [FeII(bpy)3]2+: Revealing two competing mechanisms by extreme ultraviolet photoemission spectroscopy. ChemPhysChem 2017, 18, 465–469. [Google Scholar] [CrossRef]
- Chergui, M.; Collet, E. Photoinduced Structural Dynamics of Molecular Systems Mapped by Time-Resolved X-ray Methods. Chem. Rev. 2017, 117, 11025–11065. [Google Scholar] [CrossRef]
- Collet, E.; Cammarata, M. Disentangling Ultrafast Electronic and Structural Dynamics with X-ray Lasers. Chem. Eur. J. 2018, 24, 15696–15705. [Google Scholar] [CrossRef]
- Sousa, C.; Domingo, A.; de Graaf, C. Effect of Second-Order Spin–Orbit Coupling on the Interaction between Spin States in Spin-Crossover Systems. Chem. Eur. J. 2018, 24, 5146–5152. [Google Scholar] [CrossRef]
- Sousa, C.; Llunell, M.; Domingo, A.; de Graaf, C. Theoretical evidence for the direct 3MLCT-HS deactivation in the light-induced spin crossover of Fe(II)-polypyridyl complexes. Phys. Chem. Chem. Phys. 2018, 20, 2351–2355. [Google Scholar] [CrossRef]
- Xue, S.; Guo, Y.; Rotaru, A.; Müller-Bunz, H.; Morgan, G.G.; Trzop, E.; Collet, E.; Oláh, J.; Garcia, Y. Spin Crossover Behavior in a Homologous Series of Iron(II) Complexes Based on Functionalized Bipyridyl Ligands. Inorg. Chem. 2018, 57, 9880–9891. [Google Scholar] [CrossRef]
- Zerdane, S.; Collet, E.; Dong, X.; Matar, S.F.; Wang, H.F.; Desplanches, C.; Chastanet, G.; Chollet, M.; Glownia, J.M.; Lemke, H.T.; et al. Electronic and Structural Dynamics During the Switching of the Photomagnetic Complex [Fe(L222N5)(CN)2]. Chem. Eur. J. 2018, 24, 5064–5069. [Google Scholar] [CrossRef]
- Zerdane, S.; Cammarata, M.; Iasco, O.; Boillot, M.L.; Collet, E. Photoselective MLCT to d–d pathways for light-induced excited spin state trapping. J. Chem. Phys. 2019, 151, 171101. [Google Scholar] [CrossRef]
- Kjær, K.S.; van Driel, T.B.; Harlang, T.C.B.; Kunnus, K.; Ledbetter, K.; Hartsock, R.W.; Reinhard, M.E.; Koroidov, S.; Li, L.; Laursen, M.G.; et al. Finding Intersections between Electronic Excited State Potential Energy Surfaces with Simultaneous Ultrafast X-ray Scattering and Spectroscopy. Chem. Sci. 2019, 10, 5749–5760. [Google Scholar] [CrossRef]
- Campagna, S.; Puntotiero, F.; Nastasi, F.; Bergamini, G.; Balzani, V. Photochemistry and Photophysics of Coordination Compounds: Ruthenium. In Photochemistry and Photophysics of Coordination Compounds I; Topics in Current Chemistry; Balzani, V., Campagna, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 280, pp. 117–214. [Google Scholar]
- Balzani, V.; Credi, A.; Venturi, M. Photochemical Conversion of Solar Energy. ChemSusChem 2008, 1, 26–58. [Google Scholar] [CrossRef]
- Diamantis, P.; Gonthier, J.F.; Tavernelli, I.; Rothlisberger, U. Study of the Redox Properties of Singlet and Triplet Tris(2,2’-bipyridine)ruthenium(II) ([Ru(bpy)3]2+) in Aqueous Solution by Full Quantum and Mixed Quantum/Classical Molecular Dynamics Simulations. J. Phys. Chem. B 2013, 118, 3950–3959. [Google Scholar] [CrossRef]
- Marchini, M.; Bergamini, G.; Cozzi, P.G.; Ceroni, P.; Balzani, V. Photoredox catalysis: The need to elucidate the photochemical mechanism. Angew. Chem. Int. Ed. 2017, 56, 12820–12821. [Google Scholar] [CrossRef]
- Kjær, K.S.; Zhang, W.; Alonso-Mori, R.; Bergmann, U.; Chollet, M.; Hadt, R.G.; Hartsock, R.W.; Harlang, T.; Kroll, T.; Kubiček, K.; et al. Ligand manipulation of charge transfer excited state relaxation and spin crossover in [Fe(2,2’-bipyridine)2(CN)2]. Struct. Dyn. 2017, 4, 044030. [Google Scholar] [CrossRef]
- Zhang, W.; Kjær, K.S.; Alonso-Mori, R.; Bergmann, U.; Chollet, M.; Fredin, L.A.; Hadt, R.G.; Hartsock, R.W.; Harlang, T.; Kroll, T.; et al. Manipulating charge transfer excited state relaxation and spin crossover in iron coordination complexes with ligand substitution. Chem. Sci. 2017, 8, 515–523. [Google Scholar] [CrossRef]
- Chábera, P.; Liu, Y.; Prakash, O.; Thyrhaug, E.; El Nahhas, A.; Honarfar, A.; Essén, S.; Fredin, L.A.; Harlang, T.C.B.; Kjær, K.S.; et al. A low-spin Fe(III) complex with 100-ps ligand-to-metal charge transfer photoluminescence. Nature 2017, 543, 695–699. [Google Scholar] [CrossRef]
- Chábera, P.; Kjær, K.S.; Prakash, O.; Honarfar, A.; Liu, Y.; Fredin, L.A.; Harlang, T.C.B.; Lidin, S.; Uhlig, J.; Sundström, V.; et al. FeII Hexa N-Heterocyclic Carbene Complex with a 528 ps Metal-to-Ligand Charge-Transfer Excited-State Lifetime. J. Phys. Chem. Lett. 2018, 9, 459–463. [Google Scholar] [CrossRef]
- Kjær, K.S.; Kunnus, K.; Harlang, T.C.B.; van Driel, T.B.; Ledbetter, K.; Hartsock, R.W.; Reinhard, M.E.; Koroidov, S.; Li, L.; Laursen, M.G.; et al. Solvent control of charge transfer excited state relaxation pathways in [Fe(2,2’-bipyridine)(CN)4]2-. Phys. Chem. Chem. Phys. 2018, 20, 4238–4249. [Google Scholar] [CrossRef]
- Kjær, K.S.; Kaul, N.; Chábera, P.; Rosemann, N.W.; Honarfar, A.; Gordivska, O.; Fredin, L.A.; Bergquist, K.E.; Häggström, L.; Ericsson, T.; et al. Luminescence and reactivity of a charge-transfer excited iron complex with nanosecond lifetime. Science 2019, 363, 249–253. [Google Scholar] [CrossRef]
- Tatsuno, H.; Kjær, K.S.; Kunnus, K.; Harlang, T.C.B.; Timm, C.; Guo, M.; Chábera, P.; Fredin, L.A.; Hartsock, R.W.; Reinhard, M.E.; et al. Hot Branching Dynamics in a Light-Harvesting Iron Carbene Complex Revealed by Ultrafast X-ray Emission Spectroscopy. Angew. Chem. Int. Ed. 2020, 59, 364–372. [Google Scholar] [CrossRef]
- Demas, J.N.; Crosby, G.A. Quantum efficiencies on transition metal complexes. II. Charge-transfer luminescence. J. Am. Chem. Soc. 1971, 93, 2841–2847. [Google Scholar]
- Creutz, C.; Chou, M.; Netzel, T.L.; Okumura, M.; Sutin, N. Lifetimes, Spectra, and Quenching of the Excited States of Polypyridine Complexes of Iron(II), Ruthenium(II), and Osmium(II). J. Am. Chem. Soc. 1980, 102, 1309–1319. [Google Scholar] [CrossRef]
- Consani, C.; Premont-Schwarz, M.; ElNahhas, A.; Bressler, C.; van Mourik, F.; Cannizzo, A.; Chergui, M. Vibrational Coherences and Relaxation in the High-Spin State of Aqueous [FeII(bpy)3]2+. Angew. Chem. Int. Ed. 2009, 48, 7184–7187. [Google Scholar] [CrossRef]
- Zell, T.; Langer, R.; Iron, M.A.; Konstantinovski, L.; Shimon, L.J.W.; Diskin-Posner, Y.; Leitus, G.; Balaraman, E.; Ben-David, Y.; Milstein, D. Synthesis, Structures, and Dearomatization by Deprotonation of Iron Complexes Featuring Bipyridine-based PNN Pincer Ligands. Inorg. Chem. 2013, 52, 9636–9649. [Google Scholar] [CrossRef]
- Benito-Garagorri, D.; Becker, E.; Wiedermann, J.; Lackner, W.; Pollak, M.; Mereiter, K.; Kisala, J.; Kirchner, K. Achiral and Chiral Transition Metal Complexes with Modularly Designed Tridentate PNP Pincer-Type Ligands Based on N-Heterocyclic Diamines. Organometallics 2006, 25, 1900–1913. [Google Scholar] [CrossRef]
- Sodano, P.; Simonneaux, G.; Toupet, L. Tertiary phosphine complexes of iron porphyrins: Synthesis, molecular stereochemistry, and crystal structure of bis(dimethylphenylphosphine)-(meso-5,10,15,20 tetraphenylporphyrinato)iron(II). J. Chem. Soc. Dalton Trans. 1988, 10, 2615–2620. [Google Scholar] [CrossRef]
- Belani, R.M.; James, B.R.; Dolphin, D.; Rettig, S.J. Catalytic decarbonylation of aldehydes using iron(II) porphyrin complexes, and the crystal structure of (5,10,15,20-tetraphenylporphinato)bis(tri-n-butylphosphine)iron(II). Can. J. Chem. 1988, 66, 2072–2078. [Google Scholar] [CrossRef]
- Huang, J.S.; Yu, G.A.; Xie, J.; Wong, K.M.; Zhu, N.; Che, C.M. Primary and Secondary Phosphine Complexes of Iron Porphyrins and Ruthenium Phthalocyanine: Synthesis, Structure, and P–H Bond Functionalization. Inorg. Chem. 2008, 47, 9166–9181. [Google Scholar] [CrossRef]
- Mink, L.M.; Polam, J.R.; Christensen, K.A.; Bruck, M.A.; Walker, F.A. Electronic Effects in Transition Metal Porphyrins. 8. The Effect of Porphyrin Substituents, Axial Ligands, “Steric Crowding”, Solvent, and Temperature on the 57Fe Chemical Shifts of a Series of Model Heme Complexes. J. Am. Chem. Soc. 1995, 117, 9329–9339. [Google Scholar] [CrossRef]
- Holzhacker, C.; Calhorda, M.J.; Gil, A.; Deus Carvalho, M.; Ferreira, L.P.; Stöger, B.; Mereiter, K.; Weil, M.; Müller, D.; Weinberger, P.; et al. Six-coordinate high-spin iron(II) complexes with bidentate PN ligands based on 2-aminopyridine—New Fe(II) spin crossover systems. Dalton Trans. 2014, 43, 11152–11164. [Google Scholar] [CrossRef]
- Glatz, M.; Bichler, B.; Mastalir, M.; Stöger, B.; Weil, M.; Mereiter, K.; Pittenauer, E.; Allmaier, G.; Veiros, L.F.; Kirchner, K. Iron(II) complexes featuring κ3- and κ2-bound PNP pincer ligands — The significance of sterics. Dalton Trans. 2015, 44, 281–294. [Google Scholar] [CrossRef]
- Alcover-Fortuny, G.; Wu, J.; Caballol, R.; de Graaf, C. Quantum Chemical Study of the Interligand Electron Transfer in Ru Polypyridyl Complexes. J. Phys. Chem. A 2018, 122, 1114–1123. [Google Scholar] [CrossRef]
- Etinski, M.; Tatchen, J.; Marian, C.M. Time-dependent approaches for the calculation of intersystem crossing rates. J. Chem. Phys. 2011, 134, 154105. [Google Scholar] [CrossRef]
- Pierloot, K.; Vancoillie, S. Relative energy of the high-(5T2g) and low-(1A1g) spin states of [Fe(H2O)6]2+, [Fe(NH3)6]2+, and [Fe(bpy)3]2+: CASPT2 versus density functional theory. J. Chem. Phys. 2006, 125, 124303. [Google Scholar] [CrossRef]
- Pierloot, K.; Vancoillie, S. Relative energy of the high-(5T2g) and low-(1A1g)spin states of the ferrous complexes [Fe(L)NHS4]: CASPT2 versus density functional theory. J. Chem. Phys. 2008, 128, 034104. [Google Scholar] [CrossRef]
- Saureu, S.; de Graaf, C. TD-DFT study of the light-induced spin crossover of Fe(III) complexes. Phys. Chem. Chem. Phys. 2016, 18, 1233–1244. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2018, 8. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F. Orca 4—An ab Initio, DFT and Semiempirical SCF-MO Package; Max-Planck-Institut fur Kohlenforschung: Mulheim, Germany, 2019. [Google Scholar]
- Kepp, K.P. Consistent descriptions of metal–ligand bonds and spin-crossover in inorganic chemistry. Coord. Chem. Rev. 2013, 257, 196–209. [Google Scholar] [CrossRef]
- Kepp, K.P. Theoretical Study of Spin Crossover in 30 Iron Complexes. Inorg. Chem. 2016, 55, 2717–2727. [Google Scholar] [CrossRef]
- Siig, O.S.; Kepp, K.P. Iron(II) and Iron(III) Spin Crossover: Toward an Optimal Density Functional. J. Phys. Chem. A 2018, 122, 4208–4217. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Bykov, D.; Petrenko, T.; Izsak, R.; Kossmann, S.; Becker, U.; Valeev, E.F.; Neese, F. Efficient implementation of the analytic second derivatives of Hartree–Fock and hybrid DFT energies: A detailed analysis of different approximations. Mol. Phys. 2015, 113, 1961–1977. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Izsak, R.; Neese, F. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011, 135, 144105. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Galván, I.F.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef]
- Sousa, C.; Alías, M.; Domingo, A.; de Graaf, C. Deactivation of Excited States in Transition-Metal Complexes: Insight from Computational Chemistry. Chem. Eur. J. 2019, 25, 1152–1164. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.Å.; Veryazov, V.; Widmark, P.O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.Å.; Veryazov, V.; Widmark, P.O. New Relativistic ANO Basis Sets for Transition Metal Atoms. J. Phys. Chem. A 2005, 109, 6575–6579. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).