Abstract
Quantum steering, as a cornerstone of quantum information, is usually used to witness the quantum correlation of bipartite and multi-partite states. Here, we experimentally demonstrate the quantum steering inequality of two-qubit mixed states based on the fine-grained uncertainty relation. Our experimental results show that the steering inequality has potent sensitivity to Werner states and Bell diagonal states. The steering strategy exhibits a strong ability to identify that Werner states are steerable when the decoherence coefficient . Compared to the steering inequality obtained by another stratagem, the steering witness criteria of mixed states based on the fine-grained uncertainty relation demonstrated in our experiment has better precision and accuracy. Moreover, the detection efficiency in our measurement setup is only required to be to close the detection loophole, which means our approach needs less detector efficiency to certificate the steerability of mixed states.
1. Introduction
Quantum nonlocality [1,2,3], as a fundamental feature of quantum theory, divides into quantum entanglement [4,5], quantum steering [6,7,8,9] and Bell nonlocality [10,11,12,13] based on the degree of correlation. A typical application of quantum nonlocality is to witness the type of bipartite and multi-partite states, in which the well-known model is quantum steering inequality. Consider a system where Alice and Bob share a quantum state; they apply a couple of observables to their own sub-systems and then obtain the joint probability distribution. The state is labeled as steerability if the probability cannot be described by any local hidden state (LHS) models. Another way of speaking, the state is steerable if the specific combination of joint probability distribution violates the corresponding quantum steering inequality. In general, if Alice wants to steer Bob, she is allowed to transmit the measurement probability distribution to Bob, while Bob must apply a quantum measurement on the collapsed reduced density matrix. Therefore, the quantum steering strategy permits one of the two parts to carry out the classical measurement, which means one measurement device can be untrusted. Thus, quantum steering is usually connected with the secret key rate in one-sided device-independent quantum key distribution [14,15]. Apart from this, quantum steering shows the advantages to self-test pure entangled states [16,17] and discriminate quantum states [18].
At present, quantum steering inequalities, which are an analog of the Bell-type, have been presented [19,20] and experimentally demonstrated in many systems [21,22,23]. Basically speaking, the observables applied to Alice’s (Bob’s) sub-system are noncommutative in the aforesaid case. It is natural to connect steerability with uncertainty relation. Heisenberg’s uncertainty relation [24], another milestone in the understanding of quantum theory, reveals that two noncommutative observables cannot be accurately measured at the same time. For example, if the position of a particle was able to be measured accurately, the uncertain relation shows that when measuring its momentum, all outcomes would occur with equal probability, which results in uncertainty. Therefore, the uncertainty relation is of paramount significance to explain the double-slit interference of physical particles [25]. Recently, the entropy uncertainty relation in measurement has attracted general attention since it can witness the nonlocality of quantum states [26,27,28,29]. In Ref. [26], Oppenheim J. and Wehner S. show that the uncertainty relation and quantum nonlocality are inextricably and quantitatively linked and obtain the tradeoff relationship between them. Based on this, Pramanik et al. put forward the fine-grained steering (FGS) inequality and discussed the steerability of different quantum states [30].
The experimental demonstration of the FGS inequality of any two-qubit pure entangled states has been realized in Ref. [18]. In this article, we provide experimental evidence of FGS inequality in mixed states via linear optical elements. By comparing to the other stratagem, our approach shows the powerful sensitivity to Werner states and Bell diagonal states, especially to Werner states. Our article is organized as follows. In Section 2, we give a brief introduction of quantum steering based on fine-grained uncertainty relation and present the theoretical violation of two mixed states. Section 3 is the experimental demonstration of the FGS inequality, and we give a comparison between FGS inequality and another steering inequality. In Section 4, we discuss and summarize our results.
2. Fine-Grained Steering Inequality
Consider a system in which Alice and Bob share a quantum state . In the beginning, Alice receives a dichotomic order and applies the corresponding measurement operators to her sub-system, labeled by A. The outcome is defined as . If Alice wants to steer Bob, she is permitted to transmit the measurement probability to Bob, and then Bob must apply a quantum measurement on the collapsed reduced density matrix . By labeling B to Bob’s sub-system and defining the measurement outcome as , we can obtain the joint probability distribution (Figure 1). The joint probability can be written under the LHS model as:
in which is the hidden variable. In a nutshell, Alice can steer Bob if unable to be expanded by any forms of Equation (1). Meanwhile, the state they shared is steerable.
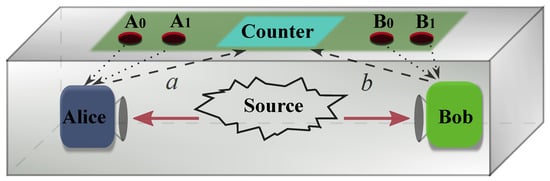
Figure 1.
Schematic diagram for quantum steering. Two spatially separated parties, Alice and Bob, share a quantum state and they want to certify whether it is steerable. Alice performs a set of black-box measurements , while Bob’s performs quantum measurements . The statistics of the outcomes of the measurements are used to verify a violation of the steering inequality.
Here, we give a brief introduction of the fine-grained uncertainty relation. For simplicity, consider the qubit case first. Suppose the dichotomic order , which Alice received is equiprobable, i.e., the probability . When the command is , Alice performs the to the qubit and then obtains the measurement result a, where and are the Pauli matrix. We define that Alice wins the game if she obtains the spin-up outcome, namely the measurement result , regardless of which order she receives. Obviously, the wining probability can be written as:
where is the probability distribution of obtaining a result 0 outcome for the measurement corresponding to the dichotomic order. is the maximum winning probability over all possible strategies, which Alice can choose. Evidently, when the qubit state is the eigenstates of [26]. Similarly, for the measurement outcome 1, the maximum winning probability is the same and occurs for the eigenstates of . This is the well-known fine-grained uncertainty relation, and it can be extended to bipartite systems and tripartite systems [26,27,28].
By introducing the fine-grained uncertainty relation into the LHS model, we can obtain [30]:
where the conditional probability represents the maximum winning probability on Alice’s side in the case of Bob’s side completely unchanged. Since the observables that Alice and Bob choose are random, here we define the two groups of corresponding measurement operators as and , the inequality above becomes:
where and range over all possible maximally incompatible measurements.
Equation (4) is a fine-grained steering criterion satisfied by bipartite states that admit LHS models for the system of Bob. It shows that Alice can steer Bob if it is violated for any combination of outcomes . Here, we consider Alice’s strategy that she obtains no prior knowledge of Bob’s measurement at the beginning. To ensure winning the game, Alice needs to scan all the possible measurement strategies and then maximize the average winning probability in regard to all possible local hidden states. Bob can check whether the state is steerable by calculating the violation of Equation (4) after receiving Alice’s result. The sum of two average winning probability over all possible observables is [30]. In this case, the FGS inequality becomes:
This is the main conclusion of FGS inequality. It clearly shows that Alice can steer Bob when Equation (5) is violated, and the quantum state is steerable.
In the following, we analyze the witness sensitivity of FGS inequality to mixed states. First, we consider that Alice prepares the initial input states as two-qubit Werner states, the forms of the density matrix are give by:
where is the two-qubit maximally entangled pure state, is the identity matrix. Without the loss of generality, we use Equation (6) to represent all classes of Werner states, since the whole Werner states can be translated into Equation (6) via certain unitary operations, which do not change the degree of quantum correlation. In order to steer Bob’s system in a specific basis that is known, Alice needs to choose the observable measurement corresponding to this basis. It is obvious that Equation (5) has four different equivalent forms because . As a demonstration, we define . For simplicity, we specify that Bob’s observable is taken from the set , therefore, the left-hand side of Equation (5) hits the maximum value when Alice applies the same set of observables on her system. The reason is that the Equation (6) states are constructed by introducing completely decoherence in maximally entangled pure state , which violates Equation (5) maximally when Alice and Bob apply the same observables simultaneously [18]. In this case, the left-hand side of Equation (5) obviously becomes:
where the conditional probability distribution . It is easily calculated that the joint probability distribution and [30]. Thus, Equation (6) is shown to be steerable for .
As we know, the quantum concurrence is a strict entanglement criteria, which is defined for a two-qubit mixed state as [31,32]:
where are the eigenvalues in descending order of the Hermitian rotation matrix with . Here, * represents complex conjugation and is the two dimensional Pauli matrix. It is easily calculated that when . Note that Werner states are entangle but not steerable for , so the FGS strategy gives the ultimate tight steering witness bound for Werner states.
Now, we focus on another type of mixed state, Bell diagonal states, where the form can be written as:
where . Note that Bell diagonal states are a linear superposition of the maximally entangled states , according to Ref. [18], for , the maximum value of the left-hand side of Equation (5), is achieved for Alice’s choices when fixing Bob’s measurement observables as . Thus, we can easily calculate that when , Alice should apply the measurement on her subsystem, the corresponding is on her side if . The joint probability distribution , , and . The probabilities of Alice’s measurement result with both observables are . Therefore, we obtain that the left-hand side variables of Equation (5) are all greater than 1.5, except . We can conclude that the FGS inequality has strong sensitivity to certify the steerablity of Bell diagonal states.
3. Experimental Demonstration and Results
In our experiment, and are represented by the horizontal and vertical polarization of a photon, respectively. The experimental setup can be divided into two modules: the state preparation and the measurement module (Figure 2). In the state preparation module, the entangled photon pairs are generated via a type-I spontaneous parametric down-conversion process [33,34] of the pump beam from a semiconductor laser with 400.8 nm on the first platform, P1. The pump beam’s polarization is controlled by a half-wave plate (HWP) , passed through a pair of back-to-back nonlinear -barium-borate (BBO) crystals with two optical axes vertical to each other. By setting the angle of as 22.5°, photon pairs are prepared into . The following couple of -BBO crystals after two mirrors are used to modulate the phase difference between two photon paths. On the basis of P1, the second platform P2 is added to prepare arbitrary Bell diagonal states . Here, we use a couple of quartz crystals of the same length to realize the decoherence parameter p. The optical axis of one quartz crystal is horizontal, and the other is vertical. Different Bell diagonal states are prepared by adjusting the length of quartz crystals. For Werner states, we replace P2 by platform P3. Inspired by Ref. [35], we use the beam splitters (BSs), quartz crystals, and apertures to introduce the decoherence. In the upper path, the photons first go across a 50/50 BS and separate into two ways. The HWP in the transmission way is tilted to compensate the phase of the two-photon states for the generation of . The reflected way has a set of quartz crystals with a sufficient thickness and an HWP with 22.5° to dephase the state into a completely mixed state. The two adjustable apertures in the reflected and transmission ways are used to change the ratio of two states mixed at the output port of the second BS for the generation of an arbitrary Werner state . The optical path difference between the two ways is large enough to lead to incoherent superposition since there is a lack of compensated crystals in a transmission way. In the lower path, the photons directly propagate to the measurement setup.
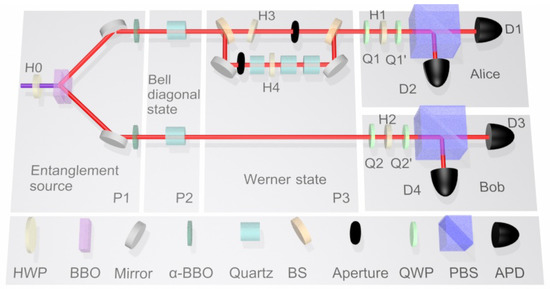
Figure 2.
Experimental setup. The experimental setup can be divided into a state preparation module and measurement module. The maximally polarization-entangled photon pairs are generated via type-I spontaneous parametric down-conversion process on platform P1. On this basis, the platform P2 is used to prepare arbitrary Bell diagonal states and platform P3 is used to prepare arbitrary Werner states . In the measurement setup, the observables Alice and Bob carried out in our whole experiment are realized by a combination of sandwich-type QWP-HWP-QWP sequences and following PBS. All the joint probabilities can be read out from the coincidence between certain APDs. Key to components: HWP, half-wave plate; BBO, -barium-borate crystal; BS, beam splitter; QWP, quarter-wave plate; PBS, polarizing beam splitter; APD, avalanche photodiodes.
In the measurement module, all of the observables Alice and Bob applied in the FGS strategy can be implemented by an HWP, a polarization beam splitter (PBS), and two single-photon avalanche photodiodes (APDs). By rotating the setting angle to = 22.5° and = 22.5°, Alice and Bob carry out measurement , whereas can be realized by a similar setup by removing the two HWPs. The coincidence counting of and represents that Alice and Bob measure the result simultaneously. Thus, the conditional probability distribution can be calculated via dividing by the measurement result in Alice’s side, which is directly read by the coincidence counting summation of and .
For each measurement, we record the clicks for 20 s under a 7 ns time window, and the total coincidence counts are approximately 10,000. The fidelities of Werner states in the experiment are all higher than 0.982, and we show the concurrence with a different decoherence coefficient a, as calculated by the density matrices of the states which are reconstructed through quantum state tomography. In Figure 3a, we show that the experimental values agree well with theoretical concurrence, which tells us the states are entangled when . We then calculate the violation of Equation (5), according to the experimental raw data of conditional probabilities . Figure 3b shows the measurement violation as a linear function of decoherence coefficient a and the experimental values match well with the theoretical ones. At the point , the sum of correlation is , which indicates that the Werner state is steerable when .
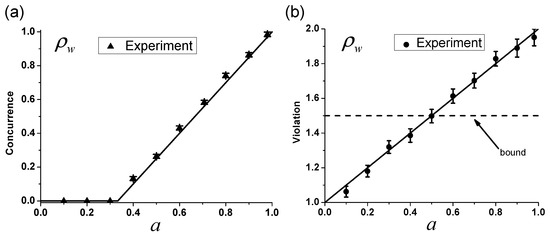
Figure 3.
Experimental results of Werner states. (a) Experimental concurrence as a function of the decoherence coefficient a for different Werner states . The triangle symbols represent the experimental data. Solid line represents the theoretical prediction. Error bars are obtained based on assuming Poisson statistics. (b) Experimental violations of FGS inequality as a function of the state coefficient a. The circular symbols represent the experimental data. Solid line represents the theoretical prediction. Dashed line represents the bounds of violation of FGS inequality. Error bars are due to the statistical uncertainty. The experimental results match well with theoretical predictions.
Unlike Werner states, for Bell diagonal states, the maximum violation of the FGS inequality is achieved when Alice and Bob carry out observables when simultaneously and when . The experimental demonstration is implemented by replacing the state preparation part P3 to P2. In the measurement setup, if we realize the observable , we need add a 45° HWP after the previous HWP . The fidelities of Bell diagonal states are all higher than 0.975. Figure 4a shows the concurrence of the initial states. By scanning p from the range , we find that for any Bell diagonal states in Equation (9), the violations are symmetric with respect to (Figure 4b). At the point , the value of violation means that the state is unsteerable, which agrees well with Figure 4a, which tells us that the concurrence of state is 0, namely, is not entangled, let alone the steerability.
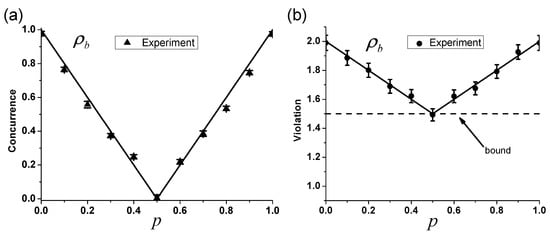
Figure 4.
Experimental results of Bell diagonal states. (a) Experimental concurrence as a function of the parameter p for different Bell diagonal states . The triangle symbols represent the experimental data. Solid line represents the theoretical prediction. Error bars are obtained based on assuming Poisson statistics. (b) Experimental violations of FGS inequality as a function of p. The circular symbols represent the experimental data. Solid lines represent the theoretical prediction. The dashed line represents the bound of violation of FGS inequality. Error bars are due to the statistical uncertainty. The experimental results match well with theoretical predictions.
From the foregoing, the FGS inequality shows the powerful sensitivity to mixed states, especially to Werner states. This is one of the advantages of the steering inequality based on the fine-grained uncertainty relation. As a comparison, we experimentally verify another steering inequality of mixed states, the so-called Cavalcanti-Foster-Fuwa-Wiseman (CFFW) inequality, which is presented by Cavalcanti et al. [19]. In Ref. [19], they derived CFFW inequality for steering, which is an analog of the Clauser–Horne–Shimony–Holt (CHSH) inequality, in that it is necessary and sufficient in the simplest Bell-nonlocality scenario: two parties, two measurements per party and two outcomes per measurement. The CFFW inequality is given by:
Here, the two sets of observables and , which correspondingly applied to Alice’s and Bob’s sub-system are not fixed, but must be two mutually unbiased qubit measurements. The correlations of the form , in which ⊕ is an addition to modulo two and are the respective measurement results of Alice and Bob. A violation of Equation (10) is demonstrating quantum steering.
In order to achieve the maximal violation of CFFW inequality, we scan the whole permitted measurement strategies of Alice and Bob since the observables are unknown but keeping and mutually unbiased. In the experiment, we only need to add certain QWPs in the original measurement setup, namely, a combination of sandwich type QWP-HWP-QWP sequence [36,37,38], and a following PBS to realize the measurement operators. The coincidence counting of the APDs represent the result , simultaneously. Similarly, coincidence counting of APDs represent and , APDs for and , APDs for . As we all know, Werner states consist of different ratios of and a completely mixed state, thus, the observables, which maximally violate the CFFW inequality of Werner states are as the same as and remain unchanged with different decoherence coefficient a.
The symmetry of CFFW inequality is another reason why the observables stay the same. The setting angles of QWP-HWP-QWP are given by {−45°,11.8°,−20.8°}
for , {−45°,21.3°,−3.1°} for , {−45°,34.6°,−25.1°} for and {−45°,1.2°,−41.9°} for . Figure 5 shows the measurement violation of CFFW inequality still varies linearly with parameter a. At the point , the experimental data is , which denotes Werner states are steerable when , based on the CFFW inequality.
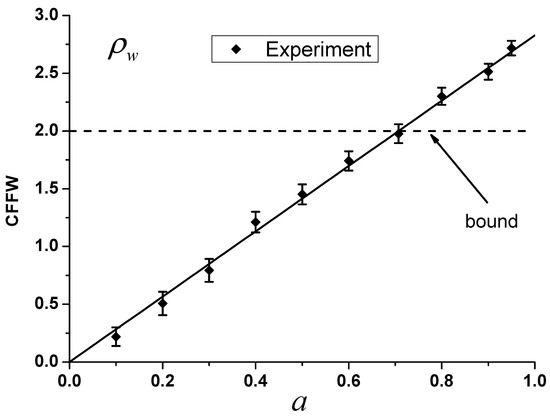
Figure 5.
Experimental violations of CFFW inequality as a function of the state decoherence coefficient a for different Werner states . The diamond symbols represent the experimental data. The solid line represents the theoretical prediction. The dashed line represents the bound of violation of the CFFW inequality. Error bars are due to statistical uncertainty. The experimental results match well with theoretical predictions.
For Bell diagonal states, we also use the sandwich type QWP-HWP-QWP sequence and a PBS to implement the measurement operators. Unlike the Werner state, the setting angles of wave plates change with parameter p. Table 1 gives the whole setting angles of the QWP-HWP-QWP sequence to realize the measurement operators which maximally violate the CFFW inequality of different Bell diagonal states. Figure 6 exhibits the experimental violation data of the CFFW inequality. We conclude that the values are symmetrical about the . When , the point data is , which indicates that the state is unsteerable.

Table 1.
The different setting angles of the sandwich type QWP-HWP-QWP sequence to realize the measurement operators in demonstration of the CFFW inequality.
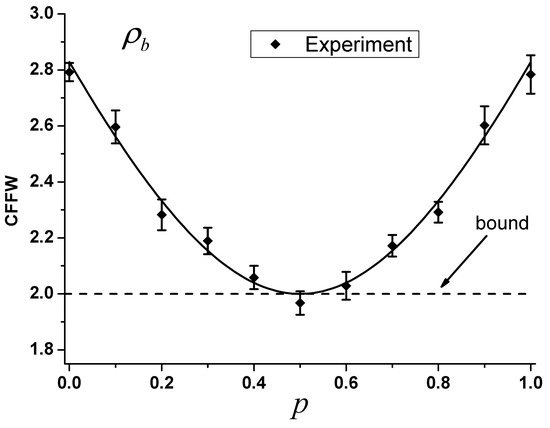
Figure 6.
Experimental violations of the CFFW inequality as a function of the state parameter p for different Bell diagonal states . The diamond symbols represent the experimental data. The solid line represents the theoretical prediction. The dashed line represents the bounds of violation of the CFFW inequality. Error bars are due to the statistical uncertainty. The experimental results match well with theoretical predictions.
Compared to the steering inequality obtained by other stratagems, which identify the steerablity of Werner states when , the inequality based on the fine-grained uncertainty relation has a tighter bound, which means that the steering witness criteria demonstrated in our experiment can obtain better precision and accuracy for Werner states. In addition, the FGS inequality still exhibits the sensitivity to witness the Bell diagonal states. More importantly, the fair sampling condition in steering inequalities needs to be invoked only on the untrusted subsystem [39], the detection efficiency in the measurement setting is required only to be to close the detection loophole [40,41] (the detection efficiency is about in our experiment). Compared to the fully device-independent protocol of an analog of the Bell-CHSH-type steering inequalities, in which the detection efficiency required is up to [42], our approach needs less detector efficiency to certificate the steerablity of mixed states.
4. Discussion and Summary
To summarize, in this article, we have presented an experiment to demonstrate the FGS inequality for different mixed states via linear optical elements. Our experimental proof is on the strength of fact that the steering inequality based on fine-grained uncertainty relations can be used to witness two-qubit mixed states. The experimental results exhibit that FGS inequality has strong sensitivity to Werner states and Bell diagonal states. For Werner states, compared to the steering inequalities obtained by other stratagems, which give the bound , our approach gives the ultimate bound , which has better precision and accuracy. For Bell diagonal states, it still shows the powerful ability to identify whether the class of Bell diagonal states is steerable as well.
It is worth stressing that the approach based on the FGS inequality requires observing joint probabilities only for two pairs of observables and , while for the Bell-CHSH-type steering inequality, to observe joint probabilities requires all four pairs of observables , , , and . Therefore, our approach of steerablity certification requires a lesser number of joint observables. Besides, compared to the fully device-independent protocol for demonstrating the Bell-CHSH-type steering inequality violation, our approach needs less detector efficiency to certificate the steerablity of mixed states, which results in a promising better applicability in practical information processing.
Author Contributions
Z.-H.B. designed the experiments, performed the experiments, analyzed the results, and wrote part of the paper. C.-Y.Y. wrote part of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 12104186), Natural Science Foundation of Jiangsu Province (Grant No. BK20190577), and the Key Laboratory Open Fund of Quantum Information of Chinese Academy of Sciences (Grant No. KQI201).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Bian Z. H. thanks Xue P. for discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LHS | Local hidden state |
| FGS | Fine-grained steering |
| HWP | Half-wave plate |
| BBO | Barium borate |
| QWP | Quarter wave plate |
| BS | Beam splitter |
| PBS | Polarization beamsplitter |
| APD | Avalanche photodiodes |
| CFFW | Cavalcanti-Foster-Fuwa-Wiseman |
| CHSH | Clauser–Horne–Shimony–Holt |
References
- Liang, Y.C.; Curchod, F.J.; Bowles, J.; Gisin, N. Anonymous quantum nonlocality. Phys. Rev. Lett. 2014, 113, 130401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palazuelos, C. Superactivation of quantum nonlocality. Phys. Rev. Lett. 2012, 109, 190401. [Google Scholar] [CrossRef] [Green Version]
- Hirsch, F.; Quintino, M.T.; Bowles, J.; Brunner, N. Genuine hidden quantum nonlocality. Phys. Rev. Lett. 2013, 111, 160402. [Google Scholar] [CrossRef] [Green Version]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef] [Green Version]
- Coffman, V.; Kundu, J.; Wootters, W.K. Distributed entanglement. Phys. Rev. A 2000, 61, 052306. [Google Scholar] [CrossRef] [Green Version]
- Wiseman, H.M.; Jones, S.J.; Doherty, A.C. Steering, entanglement, nonlocality, and the Einstein-Podolsky-Rosen paradox. Phys. Rev. Lett. 2007, 98, 140402. [Google Scholar] [CrossRef] [PubMed]
- Pusey, M.F. Negativity and steering: A stronger Peres conjecture. Phys. Rev. A 2013, 88, 032313. [Google Scholar] [CrossRef] [Green Version]
- Walborn, S.P.; Salles, A.; Gomes, R.M.; Toscano, F.; Ribeiro, P.S. Revealing hidden Einstein-Podolsky-Rosen nonlocality. Phys. Rev. Lett. 2011, 106, 130402. [Google Scholar] [CrossRef] [PubMed]
- Uola, R.; Costa, A.C.; Nguyen, H.C.; Gühne, O. Quantum steering. Rev. Mod. Phys. 2020, 92, 015001. [Google Scholar] [CrossRef] [Green Version]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419–478. [Google Scholar] [CrossRef] [Green Version]
- Das Bhowmik, A.; Parashar, P.; Banik, M. Bell nonlocality and the reality of the quantum wave function. Phys. Rev. A 2021, 104, 022217. [Google Scholar] [CrossRef]
- Temistocles, T.; Rabelo, R.; Cunha, M.T. Measurement compatibility in Bell nonlocality tests. Phys. Rev. A 2019, 99, 042120. [Google Scholar] [CrossRef] [Green Version]
- Patrick, A.; Cabello, A. Bell nonlocality with intensity information only. Phys. Rev. A 2020, 102, 032201. [Google Scholar] [CrossRef]
- Branciard, C.; Cavalcanti, E.G.; Walborn, S.P.; Scarani, V.; Wiseman, H.M. One-sided device-independent quantum key distribution: Security, feasibility, and the connection with steering. Phys. Rev. A 2012, 85, 010301. [Google Scholar] [CrossRef] [Green Version]
- Gheorghiu, A.; Wallden, P.; Kashefi, E. Rigidity of quantum steering and one-sided device-independent verifiable quantum computation. New J. Phys. 2017, 19, 023043. [Google Scholar] [CrossRef]
- Goswami, S.; Bhattacharya, B.; Das, D.; Sasmal, S.; Jebaratnam, C.; Majumdar, A.S. One-sided device-independent self-testing of any pure two-qubit entangled state. Phys. Rev. A 2018, 98, 022311. [Google Scholar] [CrossRef] [Green Version]
- Šupić, I.; Hoban, M.J. Self-testing through EPR-steering. New J. Phys. 2016, 18, 075006. [Google Scholar] [CrossRef] [Green Version]
- Bian, Z.; Majumdar, A.S.; Jebarathinam, C.; Wang, K.; Xiao, L.; Zhan, X.; Zhang, Y.; Xue, P. Experimental demonstration of one-sided device-independent self-testing of any pure two-qubit entangled state. Phys. Rev. A 2020, 101, 020301. [Google Scholar] [CrossRef] [Green Version]
- Cavalcanti, E.G.; Foster, C.J.; Fuwa, M.; Wiseman, H.M. Analog of the Clauser-Horne-Shimony-Holt inequality for steering. J. Opt. Soc. Am. B 2015, 32, A74–A81. [Google Scholar] [CrossRef] [Green Version]
- Roy, A.; Bhattacharya, S.S.; Mukherjee, A.; Banik, M. Optimal quantum violation of Clauser-Horne-Shimony-Holt like steering inequality. J. Phys. A Math. Theor. 2015, 48, 415302. [Google Scholar] [CrossRef] [Green Version]
- Orieux, A.; Kaplan, M.; Venuti, V.; Pramanik, T.; Zaquine, I.; Diamanti, E. Experimental detection of steerability in Bell local states with two measurement settings. J. Opt. 2018, 20, 044006. [Google Scholar] [CrossRef] [Green Version]
- Li, C.M.; Lo, H.P.; Chen, L.Y.; Yabushita, A. Experimental verification of multidimensional quantum steering. Opt. Commun. 2018, 410, 956–960. [Google Scholar] [CrossRef] [Green Version]
- Wollmann, S.; Walk, N.; Bennet, A.J.; Wiseman, H.M.; Pryde, G.J. Observation of genuine one-way Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 2016, 116, 160403. [Google Scholar] [CrossRef] [Green Version]
- Heisenberg, W.V. Paper on the uncertainty principle. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Sánchez-Ruiz, J. Position-momentum entropic uncertainty relation and complementarity in single-slit and double-slit experiments. Phys. Rev. A 1998, 57, 1519. [Google Scholar] [CrossRef] [Green Version]
- Oppenheim, J.; Wehner, S. The uncertainty principle determines the nonlocality of quantum mechanics. Science 2010, 330, 1072–1074. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pramanik, T.; Majumdar, A.S. Fine-grained uncertainty relation and nonlocality of tripartite systems. Phys. Rev. A 2012, 85, 024103. [Google Scholar] [CrossRef] [Green Version]
- Dey, A.; Pramanik, T.; Majumdar, A.S. Fine-grained uncertainty relation and biased nonlocal games in bipartite and tripartite systems. Phys. Rev. A 2013, 87, 012120. [Google Scholar] [CrossRef] [Green Version]
- Costa, A.C.; Uola, R.; Gühne, O. Steering criteria from general entropic uncertainty relations. Phys. Rev. A 2018, 98, 050104. [Google Scholar] [CrossRef] [Green Version]
- Pramanik, T.; Kaplan, M.; Majumdar, A.S. Fine-grained einstein-podolsky-rosen—Steering inequalities. Phys. Rev. A 2014, 90, 050305. [Google Scholar] [CrossRef] [Green Version]
- Wootters, W.K. Entanglement of formation and concurrence. Quantum Inf. Comput. 2001, 1, 27–44. [Google Scholar] [CrossRef]
- Hildebrand, R. Concurrence revisited. J. Math. Phys. 2007, 48, 102108. [Google Scholar] [CrossRef]
- Bian, Z.; Li, J.; Qin, H.; Zhan, X.; Zhang, R.; Sanders, B.C.; Xue, P. Realization of single-qubit positive-operator-valued measurement via a one-dimensional photonic quantum walk. Phys. Rev. Lett. 2015, 114, 203602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bian, Z.H.; Li, J.; Zhan, X.; Twamley, J.; Xue, P. Experimental implementation of a quantum walk on a circle with single photons. Phys. Rev. A 2017, 95, 052338. [Google Scholar] [CrossRef]
- Qi, B.; Hou, Z.; Wang, Y.; Dong, D.; Zhong, H.S.; Li, L.; Xiang, G.Y.; Wiseman, H.M.; Li, C.F.; Guo, G.C. Adaptive quantum state tomography via linear regression estimation: Theory and two-qubit experiment. NPJ Quantum Inf. 2017, 3, 1–7. [Google Scholar] [CrossRef]
- Xue, P.; Zhang, R.; Qin, H.; Zhan, X.; Bian, Z.H.; Li, J.; Sanders, B.C. Experimental quantum-walk revival with a time-dependent coin. Phys. Rev. Lett. 2015, 114, 140502. [Google Scholar] [CrossRef] [Green Version]
- Bian, Z.; Xiao, L.; Wang, K.; Onanga, F.A.; Ruzicka, F.; Yi, W.; Joglekar, Y.N.; Xue, P. Quantum information dynamics in a high-dimensional parity-time-symmetric system. Phys. Rev. A 2020, 102, 030201. [Google Scholar] [CrossRef]
- Bian, Z.; Xiao, L.; Wang, K.; Zhan, X.; Onanga, F.A.; Ruzicka, F.; Yi, W.; Joglekar, Y.N.; Xue, P. Conserved quantities in parity-time symmetric systems. Phys. Rev. Res. 2020, 2, 022039. [Google Scholar] [CrossRef]
- Orsucci, D.; Bancal, J.D.; Sangouard, N.; Sekatski, P. How post-selection affects device-independent claims under the fair sampling assumption. Quantum 2020, 4, 238. [Google Scholar] [CrossRef]
- Passaro, E.; Cavalcanti, D.; Skrzypczyk, P.; Acín, A. Optimal randomness certification in the quantum steering and prepare-and-measure scenarios. New J. Phys. 2015, 17, 113010. [Google Scholar] [CrossRef]
- Sainz, A.B.; Guryanova, Y.; McCutcheon, W.; Skrzypczyk, P. Adjusting inequalities for detection-loophole-free steering experiments. Phys. Rev. A 2016, 94, 032122. [Google Scholar] [CrossRef] [Green Version]
- Garg, A.; Mermin, N.D. Detector inefficiencies in the Einstein-Podolsky-Rosen experiment. Phys. Rev. D 1987, 35, 3831. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).