On the O(1/n) Convergence Rate of the Auxiliary Problem Principle for Separable Convex Programming and Its Application to the Power Systems Multi-Area Economic Dispatch Problem

Abstract

The auxiliary problem principle has been widely applied in power systems to solve the multi-area economic dispatch problem. Although the effectiveness and correctness of the auxiliary problem principle method have been demonstrated in relevant literatures, the aspect connected with accurate estimate of its convergence rate has not yet been established. In this paper, we prove the $O(1/n)$ convergence rate of the auxiliary problem principle method.

1. Introduction

The auxiliary problem principle (APP) [1], originally proposed by G. Cohen in [2], has a wide range of applications in the power systems field [3,4,5,6,7,8]. In fact, the mathematical formulation of multi-area economic dispatch problem can be expressed as follows.

$$min\left\{f\left(x_1\right)+g\left(x_2\right)\left|A{x}_1+B{x}_2\right.=b,x_1\in {\mathsf{\Omega }}_1,x_2\in {\mathsf{\Omega }}_2\right\}$$

(1)

where $f:R^m\to R$ and $g:R^n\to R$ are convex function. ${\mathsf{\Omega }}_1\subseteq R^m$ and ${\mathsf{\Omega }}_2\subseteq R^n$ are closed convex sets. $A\in R^{r\times m}$ and $B\in R^{r\times n}$ are given fixed matrices (not necessarily full rank). $b\in R^r$ is given constant.

For solving (1), the corresponding APP iterative scheme can be expressed as follows.

$$\begin{array}{c}{x}_1^{k+1}=argmin\left\{f\left(x_1\right)+\frac{\beta }{2}{∥A{x}_1∥}^2-\beta ⟨A{x}_1,A{x}_1^k⟩\right.\hfill \\ \left.+⟨-{\lambda }^k+c(A{x}_1^k+B{x}_2^k-b),A{x}_1⟩\left|x_1\in {\mathsf{\Omega }}_1\right.\right\}\hfill \end{array}$$

(2)

$$\begin{array}{c}{x}_2^{k+1}=argmin\left\{g\left(x_2\right)+\frac{\beta }{2}{∥B{x}_2∥}^2-\beta ⟨B{x}_2,B{x}_2^k⟩\right.\hfill \\ \left.+⟨-{\lambda }^k+c(A{x}_1^k+B{x}_2^k-b),B{x}_2⟩\left|x_2\in {\mathsf{\Omega }}_2\right.\right\}\hfill \end{array}$$

(3)

$${\lambda }^{k+1}={\lambda }^k-c\left(A{x}_1^{k+1}+B{x}_2^{k+1}-b\right)$$

(4)

where $\lambda \in R^r$ is the Lagrangian multiplier for the linear constraint $A{x}_1+B{x}_2=0$ and $c>0$ is a given fixed penalty parameter. $⟨·,·⟩$ denotes the inner product, i.e., $⟨x,x⟩=x^{T}x$. The superscript k denotes iteration index. $\beta >2c$ is given fixed auxiliary problem principle parameter [7].

Although the APP iterative scheme is known to be an efficient approach for the convex problem with separable operators [9], the theoretical analysis of its convergence rate has not been established and applied in the literature.

In 2004, Nemirovski gave a proof to show that prox-type method has the $O(1/n)$ convergence rate for variational inequalities with Lipschitz continuous monotone operators, where n denotes the iteration number [10]. Then, for the same problem, the $O(1/n)$ convergence rate of the projection and contraction method was proved in [11]. Inspired by these literatures, taking advantage of the variational inequality approach, the accurate estimate of alternating direction method’s convergence rate has made considerable headway in recent years. To be more exact, in 2012, Bingsheng He’s analysis indicated that the Douglas-Rachford alternating direction method has the $O(1/n)$ convergence rate [12]. After that, in 2014, Yuan Shen and Minghua Xu studied the $O(1/n)$ convergence rate of Ye-Yuan’s modified alternating direction method of multipliers [13].

In this paper, our aim is to investigate the convergence rate of the iterative scheme APP under the framework of variational inequality. In fact, problem (1) is equivalent to solving the following variational inequality (VI) problem: Find $\left(x_1,x_2,\lambda \right)$ such that

$$f\left(x_1^{\prime }\right)-f\left(x_1\right)+\left(x_1^{\prime }-x_1\right)\left(-A^T\lambda \right)\ge 0\forall x_1^{\prime }\in {\mathsf{\Omega }}_1$$

(5)

$$g\left(x_2^{\prime }\right)-g\left(x_2\right)+\left(x_2^{\prime }-x_2\right)\left(-B^T\lambda \right)\ge 0\forall x_2^{\prime }\in {\mathsf{\Omega }}_2$$

(6)

$$\left({\lambda }^{\prime }-\lambda \right)\left(A{x}_1+B{x}_2-b\right)\ge 0\forall {\lambda }^{\prime }\in R^r$$

(7)

Then, the compact form of (5)–(7) can be expressed as follows.

$$\theta \left(u^{\prime }\right)-\theta \left(u\right)+{\left(w^{\prime }-w\right)}^{T}F\left(w\right)\ge 0,\forall w^{\prime }\in W$$

(8)

where

$$u=\left(\begin{array}{c}{x}_1\hfill \\ x_2\hfill \end{array}\right),w=\left(\begin{array}{c}u\hfill \\ \lambda \hfill \end{array}\right),F\left(w\right)=\left(\begin{array}{c}-A^T\lambda \hfill \\ -B^T\lambda \hfill \\ A{x}_1+B{x}_2-b\hfill \end{array}\right)$$

(9)

$$W={\mathsf{\Omega }}_1\times {\mathsf{\Omega }}_2\times R^r,\theta \left(u\right)=f\left(x_1\right)+g\left(x_2\right)$$

(10)

and the mapping $F\left(w\right)$ is monotone.

2. The Convergence Analysis of APP

In this section, we give a convergence analysis of iterative scheme APP under the framework of variational inequality. Meanwhile, the analysis is useful for the accurate estimate of APP’s convergence rate in thr next section. Throughout this paper, we assume the solution set of VI problem (8) is nonempty and denoted by $W^{*}$. $w^{*}$ denotes an arbitrary (but fixed) point in the solution set $W^{*}$.

Lemma 1. 

A single iteration of APP

$$\begin{array}{c}{x}_1^{k+1}=argmin\left\{f\left(x_1\right)+\frac{\beta }{2}{∥A{x}_1∥}^2-\beta ⟨A{x}_1,A{x}_1^k⟩\right.\hfill \\ \left.+⟨-{\lambda }^k+c(A{x}_1^k+B{x}_2^k-b),A{x}_1⟩\left|x_1\in {\mathsf{\Omega }}_1\right.\right\}\hfill \end{array}$$

(11)

$$\begin{array}{c}{x}_2^{k+1}=argmin\left\{g\left(x_2\right)+\frac{\beta }{2}{∥B{x}_2∥}^2-\beta ⟨B{x}_2,B{x}_2^k⟩\right.\hfill \\ \left.+⟨-{\lambda }^k+c(A{x}_1^k+B{x}_2^k-b),B{x}_2⟩\left|x_2\in {\mathsf{\Omega }}_2\right.\right\}\hfill \end{array}$$

(12)

is equivalent to

$$\begin{array}{c}{x}_1^{k+1}=argmin\left\{f\left(x_1\right)+\frac{\beta -c}{2}{∥A{x}_1-A{x}_1^k∥}^2\right.\hfill \\ +\left.\frac{c}{2}{∥A{x}_1+B{x}_2^k-b∥}^2+⟨-{\lambda }^k,A{x}_1⟩\left|x_1\in {\mathsf{\Omega }}_1\right.\right\}\hfill \end{array}$$

(13)

$$\begin{array}{c}{x}_2^{k+1}=argmin\left\{g\left(x_2\right)+\frac{\beta -c}{2}{∥B{x}_2-B{x}_2^k∥}^2\right.\hfill \\ \left.+\frac{c}{2}{∥A{x}_1^k+B{x}_2-b∥}^2+⟨-{\lambda }^k,B{x}_2⟩\left|x_2\in {\mathsf{\Omega }}_2\right.\right\}\hfill \end{array}$$

(14)

Proof of Lemma 1. 

Adding a quadratic term $\frac{\beta }{2}{∥A{x}_1^k∥}^2$ to the objective function (11) without changing its optimization result, then (11) can be expressed as follows.

$$\begin{array}{c}{x}_1^{k+1}=argmin\left\{f\left(x_1\right)+\frac{\beta }{2}{∥A{x}_1-A{x}_1^k∥}^2\right.\hfill \\ +\left.⟨-{\lambda }^k+c(A{x}_1^k+B{x}_2^k-b),A{x}_1⟩\left|x_1\in {\mathsf{\Omega }}_1\right.\right\}\hfill \end{array}$$

(15)

Considering the following equation

$$\begin{array}{c}⟨c(A{x}_1^k+B{x}_2^k-b),A{x}_1⟩=c⟨A{x}_1^k-A{x}_1,A{x}_1⟩+c⟨A{x}_1+B{x}_2^k-b,A{x}_1⟩\hfill \\ =\frac{c}{2}\left({∥A{x}_1+B{x}_2^k-b∥}^2-{∥A{x}_1-A{x}_1^k∥}^2\right)\hfill \\ +\frac{c}{2}\left({∥A{x}_1^k∥}^2-{∥B{x}_2^k-b∥}^2\right)\hfill \end{array}$$

(16)

Then, combing (15) and (16), we obtain

$$\begin{array}{c}{x}_1^{k+1}=argmin\left\{f\left(x_1\right)+\frac{\beta -c}{2}{∥A{x}_1-A{x}_1^k∥}^2+\frac{c}{2}{∥A{x}_1+B{x}_2^k-b∥}^2\right.\hfill \\ \left.+⟨-{\lambda }^k,A{x}_1⟩+\frac{c}{2}\left({∥A{x}_1^k∥}^2-{∥B{x}_2^k-b∥}^2\right)\left|x_1\in {\mathsf{\Omega }}_1\right.\right\}\hfill \end{array}$$

(17)

Removing the constant term $\frac{c}{2}\left({∥A{x}_1^k∥}^2-{∥B{x}_2^k-b∥}^2\right)$, we get

$$\begin{array}{c}{x}_1^{k+1}=argmin\left\{f\left(x_1\right)+\frac{\beta -c}{2}{∥A{x}_1-A{x}_1^k∥}^2+\frac{c}{2}{∥A{x}_1+B{x}_2^k-b∥}^2\right.\hfill \\ \left.+⟨-{\lambda }^k,A{x}_1⟩\left|x_1\in {\mathsf{\Omega }}_1\right.\right\}\hfill \end{array}$$

(18)

Analogously, we have

$$\begin{array}{c}{x}_2^{k+1}=argmin\left\{g\left(x_2\right)+\frac{\beta -c}{2}{∥B{x}_2-B{x}_2^k∥}^2+\frac{c}{2}{∥A{x}_1^k+B{x}_2-b∥}^2\right.\hfill \\ \left.+⟨-{\lambda }^k,B{x}_2⟩\left|x_2\in {\mathsf{\Omega }}_2\right.\right\}\hfill \end{array}$$

(19)

as we wanted to prove. Thus Lemma 1 is proved.   □

Lemma 2. 

Let sequence $\left\{w^k\right\}$ is generated by the iterative scheme APP. We denote ${∥x∥}_M=x^{T}Mx$ and $∥x∥=x^{T}x$, then we get

$${∥w^k-w^{*}∥}_M^2-{∥w^{k+1}-w^{*}∥}_M^2\ge {∥w^k-w^{k+1}∥}_M^2$$

(20)

$$\begin{array}{c}f\left(x_1\right)+g\left(x_2\right)-f\left(x_1^{k+1}\right)-g\left(x_2^{k+1}\right)\hfill \\ +{\left(w-w^{k+1}\right)}^T\left\{F\left(w^{k+1}\right)+M\left(w^{k+1}-w^k\right)\right\}\ge 0,\forall w\in W\hfill \end{array}$$

(21)

where

$$M=\left(\begin{array}{ccc}\left(\beta -c\right)A^{T}A\hfill & -c{A}^{T}B& 0\\ -c{B}^{T}A\hfill & \left(\beta -c\right)B^{T}B& 0\\ 0\hfill & 0& \frac{1}{c}{I}_m\end{array}\right),\beta >2c$$

(22)

Proof of Lemma 2. 

According to the description of Lemma 1 and using variational inequality approach, solving (11) and (12) is equivalent to solving $\left(x_1^{k+1},x_2^{k+1}\right)$ which satisfies following inequalities,

$$\begin{array}{c}f\left(x_1\right)-f\left(x_1^{k+1}\right)+{\left(x_1-x_1^{k+1}\right)}^T\hfill \\ \left\{\left(\beta -c\right)A^T\left(A{x}_1-A{x}_1^k\right)+c{A}^T\left(A{x}_1+B{x}_2^k-b\right)-A^T{\lambda }^k\right\}\ge 0,\forall x_1\in {\mathsf{\Omega }}_1\hfill \end{array}$$

(23)

$$\begin{array}{c}g\left(x_2\right)-g\left(x_2^{k+1}\right)+{\left(x_2-x_2^{k+1}\right)}^T\hfill \\ \left\{\left(\beta -c\right)B^T\left(B{x}_2-B{x}_2^k\right)+c{B}^T\left(A{x}_1^k+B{x}_2-b\right)-B^T{\lambda }^k\right\}\ge 0,\forall x_2\in {\mathsf{\Omega }}_2\hfill \end{array}$$

(24)

Considering

$${\lambda }^{k+1}={\lambda }^k-c\left(A{x}_1^{k+1}+B{x}_2^{k+1}-b\right)$$

(25)

Thus, the following result is given by utilizing (23)–(25)

$$\begin{array}{c}f\left(x_1\right)+g\left(x_2\right)-f\left(x_1^{k+1}\right)-g\left(x_2^{k+1}\right)\hfill \\ +{\left(w-w^{k+1}\right)}^T\left\{F\left(w^{k+1}\right)+M\left(w^{k+1}-w^k\right)\right\}\ge 0,\forall w\in W\hfill \end{array}$$

(26)

Setting $w=w^{*}$ in (26), we get

$$\begin{array}{c}{\left(w^{*}-w^{k+1}\right)}^{T}M\left(w^{k+1}-w^k\right)\hfill \\ \ge f\left(x_1^{k+1}\right)+g\left(x_2^{k+1}\right)-f\left(x_1^{*}\right)-g\left(x_2^{*}\right)+{\left(w^{k+1}-w^{*}\right)}^{T}F\left(w^{k+1}\right)\hfill \end{array}$$

(27)

Mapping F is monotone, we have

$${\left(w^{k+1}-w^{*}\right)}^{T}F\left(w^{k+1}\right)\ge {\left(w^{k+1}-w^{*}\right)}^{T}F\left(w^{*}\right)$$

(28)

According to (8), we get

$${\left(w^{k+1}-w^{*}\right)}^{T}F\left(w^{*}\right)\ge 0$$

(29)

Combing (27)–(29), we get

$$\begin{array}{c}{\left(w^{*}-w^{k+1}\right)}^{T}M\left(w^{k+1}-w^k\right)\hfill \\ \begin{array}{c}\ge f\left(x_1^{k+1}\right)+g\left(x_2^{k+1}\right)-f\left(x_1^{*}\right)-g\left(x_2^{*}\right)+{\left(w^{k+1}-w^{*}\right)}^{T}F\left(w^{k+1}\right)\hfill \\ \ge f\left(x_1^{k+1}\right)+g\left(x_2^{k+1}\right)-f\left(x_1^{*}\right)-g\left(x_2^{*}\right)+{\left(w^{k+1}-w^{*}\right)}^{T}F\left(w^{*}\right)\hfill \\ \ge 0\hfill \\ \Rightarrow {\left(w^{*}-w^k+w^k-w^{k+1}\right)}^{T}M\left(w^{k+1}-w^k\right)\ge 0\hfill \\ \Rightarrow {\left(w^{*}-w^k\right)}^{T}M\left(w^{k+1}-w^k\right)\ge {\left(w^k-w^{k+1}\right)}^{T}M\left(w^k-w^{k+1}\right)\hfill \end{array}\hfill \end{array}$$

(30)

Using (30), we obtain

$$\begin{array}{c}{∥w^k-w^{*}∥}_M^2-{∥w^{k+1}-w^{*}∥}_M^2\hfill \\ ={∥w^k-w^{*}∥}_M^2-{∥w^k-w^{*}-(w^k-w^{k+1})∥}_M^2\hfill \\ =2{\left(w^{*}-w^k\right)}^{T}M\left(w^{k+1}-w^k\right)-{∥w^k-w^{k+1}∥}_M^2\hfill \\ \ge 2{∥w^k-w^{k+1}∥}_M^2-{∥w^k-w^{k+1}∥}_M^2\hfill \\ ={∥w^k-w^{k+1}∥}_M^2\hfill \end{array}$$

(31)

Based on the above discussion, the proof of Lemma 2 is completed.   □

If matrices A and B are full rank, for $\forall w\in W$, we can get ${∥w∥}_M=w^{T}Mw=\left(\beta -2c\right)\left({∥A{x}_1∥}^2+{∥B{x}_2∥}^2\right)+c{∥A{x}_1-B{x}_2∥}^2+\frac{1}{c}{∥\lambda ∥}^2\ge 0$, and the equality hold up if and only if $w=0$. It is clear that matrix M is positive definite matrix and (20) is Fejér monotone. We get

$$\underset{k\to \infty }{lim}{w}^k=w^{*}$$

(32)

Furthermore, for general matrices A and B, (20) can be rewritten as follows.

$${∥v^k-v^{*}∥}_N^2-{∥v^{k+1}-v^{*}∥}_N^2\ge {∥v^k-v^{k+1}∥}_N^2$$

(33)

where

$$v=\left(\begin{array}{c}A{x}_1\\ B{x}_2\\ \lambda \end{array}\right),N=\left(\begin{array}{ccc}\left(\beta -c\right)I& -cI& 0\\ -cI& \left(\beta -c\right)I& 0\\ 0& 0& \frac{1}{c}{I}_m\end{array}\right)$$

(34)

It is clear that (33) is Fejér monotone, so we get

$$\underset{k\to \infty }{lim}∥A{x}_1^{k+1}-A{x}_1^k∥=0,\underset{k\to \infty }{lim}∥B{x}_2^{k+1}-B{x}_2^k∥=0,\underset{k\to \infty }{lim}∥{\lambda }^{k+1}-{\lambda }^k∥=0$$

(35)

Lemma 3. 

Let sequence $\left\{w^k\right\}$ is generated by the iterative scheme APP. If

$$∥A{x}_1^{k+1}-A{x}_1^k∥=0,∥B{x}_2^{k+1}-B{x}_2^k∥=0,∥{\lambda }^{k+1}-{\lambda }^k∥=0$$

(36)

then, $w^{k+1}$ is the solution of VI problem (8).

Proof of Lemma 3. 

According to [14], solving (8) is equivalent to finding a zero point of e(w).

$$e\left(w\right)=\left[\begin{array}{c}{e}_{x_1}\left(w\right)\\ e_{x_2}\left(w\right)\\ e_{\lambda }\left(w\right)\end{array}\right]=\left[\begin{array}{c}{x}_1-P_{\mathsf{\Omega }1}\left\{x_1-\left[\nabla f\left(x_1\right)-A^T\lambda \right]\right\}\hfill \\ x_2-P_{\mathsf{\Omega }2}\left\{x_2-\left[\nabla g\left(x_2\right)-B^T\lambda \right]\right\}\hfill \\ A{x}_1+B{x}_2-b\hfill \end{array}\right]$$

(37)

where $P_{\mathsf{\Omega }}\left(·\right)$ denotes the projection on Ω. $\nabla f\left(·\right)$ denotes the gradient of $f\left(·\right)$.

Based on the iterative scheme APP and the projection equation, we obtain

$$\begin{array}{c}{x}_1^{k+1}=P_{\mathsf{\Omega }1}\left\{x_1^{k+1}-\left[\nabla f\left(x_1^{k+1}\right)-A^T\left({\lambda }^k-c\left(A{x}_1^{k+1}+B{x}_2^k-b\right)\right)\right.\right.\hfill \\ \left.\left.+\left(\beta -c\right)A^T\left(A{x}_1^{k+1}-A{x}_1^k\right)\right]\right\}\hfill \end{array}$$

(38)

$$\begin{array}{c}{x}_2^{k+1}=P_{\mathsf{\Omega }2}\left\{x_2^{k+1}-\left[\nabla g\left(x_2^{k+1}\right)-B^T\left({\lambda }^k-c\left(A{x}_1^k+B{x}_2^{k+1}-b\right)\right)\right.\right.\hfill \\ \left.\left.+\left(\beta -c\right)B^T\left(B{x}_2^{k+1}-B{x}_2^k\right)\right]\right\}\hfill \end{array}$$

(39)

Recall (37), we get,

$$e\left(w^{k+1}\right)=\left[\begin{array}{c}{e}_{x_1}\left(w^{k+1}\right)\\ e_{x_2}\left(w^{k+1}\right)\\ e_{\lambda }\left(w^{k+1}\right)\end{array}\right]=\left[\begin{array}{c}{x}_1^{k+1}-P_{\mathsf{\Omega }1}\left\{x_1^{k+1}-\left[\nabla f\left(x_1^{k+1}\right)-A^T{\lambda }^{k+1}\right]\right\}\hfill \\ x_2^{k+1}-P_{\mathsf{\Omega }2}\left\{x_2^{k+1}-\left[\nabla g\left(x_2^{k+1}\right)-B^T{\lambda }^{k+1}\right]\right\}\hfill \\ A{x}_1^{k+1}+B{x}_2^{k+1}-b\hfill \end{array}\right]$$

(40)

and hence,

$$∥e\left(w^{k+1}\right)∥\le ∥e_{x_1}\left(w^{k+1}\right)∥+∥e_{x_2}\left(w^{k+1}\right)∥+∥e_{\lambda }\left(w^{k+1}\right)∥$$

(41)

Replacing the first $x_1^{k+1}$ in $e_{x_1}\left(w^{k+1}\right)$ by (38) and using

$$∥P_{\mathsf{\Omega }}\left(x\right)-P_{\mathsf{\Omega }}\left(y\right)∥\le ∥x-y∥$$

(42)

We get

$$\begin{array}{c}∥e_{x_1}\left(w^{k+1}\right)∥=∥x_1^{k+1}-P_{\mathsf{\Omega }1}\left\{x_1^{k+1}-\left[\nabla f\left(x_1^{k+1}\right)-A^T{\lambda }^{k+1}\right]\right\}∥\hfill \\ \le ∥A^T\left\{\left({\lambda }^k-{\lambda }^{k+1}\right)-c\left(A{x}_1^{k+1}+B{x}_2^k-b\right)\right\}\hfill \\ -\left(\beta -c\right)A^T\left(A{x}_1^{k+1}-A{x}_1^k\right)∥\hfill \\ \le ∥A^T\left\{\left({\lambda }^k-{\lambda }^{k+1}\right)-c\left(A{x}_1^{k+1}+B{x}_2^{k+1}-b\right)+c\left(B{x}_2^{k+1}-B{x}_2^k\right)\right\}∥\hfill \\ +∥\left(\beta -c\right)A^T\left(A{x}_1^{k+1}-A{x}_1^k\right)∥\hfill \\ \le ∥A^{T}c∥∥B{x}_2^{k+1}-B{x}_2^k∥+∥\left(\beta -c\right)A^T∥∥\left(A{x}_1^{k+1}-A{x}_1^k\right)∥\hfill \end{array}$$

(43)

Similarly, replacing the first $x_2^{k+1}$ in $e_{x_2}\left(w^{k+1}\right)$ by (39) and using (42), we get

$$\begin{array}{c}∥e_{x_2}\left(w^{k+1}\right)∥=∥x_2^{k+1}-P_{\mathsf{\Omega }2}\left\{x_2^{k+1}-\left[\nabla g\left(x_2^{k+1}\right)-B^T{\lambda }^{k+1}\right]\right\}∥\hfill \\ \le ∥B^T\left\{\left({\lambda }^k-{\lambda }^{k+1}\right)-c\left(A{x}_1^k+B{x}_2^{k+1}-b\right)\right\}\hfill \\ -\left(\beta -c\right)B^T\left(B{x}_2^{k+1}-B{x}_2^k\right)∥\hfill \\ \le ∥B^T\left\{\left({\lambda }^k-{\lambda }^{k+1}\right)-c\left(A{x}_1^{k+1}+B{x}_2^{k+1}-b\right)+c\left(A{x}_1^{k+1}-A{x}_1^k\right)\right\}∥\hfill \\ +∥\left(\beta -c\right)B^T\left(B{x}_2^{k+1}-B{x}_2^k\right)∥\hfill \\ =∥B^{T}c\left(A{x}_1^{k+1}-A{x}_1^k\right)∥+∥\left(\beta -c\right)B^T\left(B{x}_2^{k+1}-B{x}_2^k\right)∥\hfill \\ \le ∥B^{T}c∥∥A{x}_1^{k+1}-A{x}_1^k∥+∥\left(\beta -c\right)B^T∥∥B{x}_2^{k+1}-B{x}_2^k∥\hfill \end{array}$$

(44)

Combining (41), (43) and (44), we obtain

$$\begin{array}{c}∥e\left(w^{k+1}\right)∥\le ∥e_{x_1}\left(w^{k+1}\right)∥+∥e_{x_2}\left(w^{k+1}\right)∥+∥e_{\lambda }\left(w^{k+1}\right)∥\hfill \\ \le \left(∥A^{T}c∥+∥\left(\beta -c\right)B^T∥\right)∥B{x}_2^{k+1}-B{x}_2^k∥\hfill \\ +\left(∥\left(\beta -c\right)A^T∥+∥B^{T}c∥\right)∥A{x}_1^{k+1}-A{x}_1^k∥+∥A{x}_1^{k+1}+B{x}_2^{k+1}-b∥\hfill \end{array}$$

(45)

and using

$${\lambda }^{k+1}={\lambda }^k-c\left(A{x}_1^{k+1}+B{x}_2^{k+1}-b\right)$$

(46)

Hence, we need only prove that if $w^{k+1}$ satisfies

$$\underset{k\to \infty }{lim}∥A{x}_1^{k+1}-A{x}_1^k∥=0,\underset{k\to \infty }{lim}∥B{x}_2^{k+1}-B{x}_2^k∥=0,\underset{k\to \infty }{lim}∥{\lambda }^{k+1}-{\lambda }^k∥=0$$

(47)

then, $w^{k+1}$ is the solution of problem (8).

Therefore, the proof of lemma 3 is completed.   □

3. The Convergence Rate Analysis of APP

In this section, we first introduce Lemma 4 which is originally described as Theorem 2.1 in [12]. Lemma 4 provides a basic property for the solution set of VI problem.

Lemma 4. 

The solution set of VI problem is convex and can be characterized as,

$$W^{*}=\underset{w\in W}{\cap }\left\{\tilde{w}\in W:\theta \left(u\right)-\theta \left(\tilde{u}\right)+{\left(w-\tilde{w}\right)}^{T}F\left(w\right)\ge 0\right\}$$

(48)

Lemma 4 demonstrates, for $\epsilon =O(1/n)$, if there is a point $\tilde{w}\in W$ satisfying

$$\theta \left(\tilde{u}\right)-\theta \left(u\right)+{\left(\tilde{w}-w\right)}^{T}F\left(w\right)\le \epsilon ,\forall w\in W$$

(49)

then, iterative scheme APP has $O(1/n)$ convergence rate.

Lemma 5. 

Let sequence $\left\{w^k\right\}$ be generated by APP algorithm, we get

$$\theta \left(u\right)-\theta \left(u^{k+1}\right)+{\left(w-w^{k+1}\right)}^{T}F\left(w\right)+\frac{1}{2}{∥w-w^k∥}_M^2\ge \frac{1}{2}{∥w-w^{k+1}∥}_M^2,\forall w\in W$$

(50)

Proof of Lemma 5.  

Using the following equation [12],

$${\left(a-b\right)}^{T}H\left(c-d\right)=\frac{1}{2}\left({∥a-d∥}_H^2-{∥a-c∥}_H^2\right)+\frac{1}{2}\left({∥c-b∥}_H^2-{∥d-b∥}_H^2\right)$$

(51)

where H is a symmetric and positive semidefinite matrix.

Here, setting $a=w,b=w^{k+1},c=w^k,d=w^{k+1}$, we get

$$\begin{array}{c}{\left(w-w^{k+1}\right)}^{T}M\left(w^k-w^{k+1}\right)\hfill \\ =\frac{1}{2}\left({∥w-w^{k+1}∥}_M^2-{∥w-w^k∥}_M^2\right)+\frac{1}{2}\left({∥w^k-w^{k+1}∥}_M^2-{∥w^{k+1}-w^{k+1}∥}_M^2\right)\hfill \\ =\frac{1}{2}\left({∥w-w^{k+1}∥}_M^2-{∥w-w^k∥}_M^2\right)+\frac{1}{2}{∥w^k-w^{k+1}∥}_M^2\hfill \\ \ge \frac{1}{2}\left({∥w-w^{k+1}∥}_M^2-{∥w-w^k∥}_M^2\right)\hfill \end{array}$$

(52)

Combining Lemma 2 and (52), we obtain

$$\theta \left(u\right)-\theta \left(u^{k+1}\right)+{\left(w-w^{k+1}\right)}^{T}F\left(w^{k+1}\right)+\frac{1}{2}{∥w-w^k∥}_M^2\ge \frac{1}{2}{∥w-w^{k+1}∥}_M^2$$

(53)

Based on the above discussion, the proof of Lemma 5 is completed.   □

Lemma 6. 

Let $\left\{w^k\right\}$ be generated by APP algorithm. For any integer $n>0$,

$$\theta \left({\tilde{u}}_n\right)-\theta \left(u\right)+{\left({\tilde{w}}_n-w\right)}^{T}F\left(w\right)\le \frac{1}{2\left(n+1\right)}{∥w-w^0∥}_M^2,\forall w\in W$$

(54)

where ${\tilde{w}}_n=\frac{1}{n+1}{\sum }_{k=0}^n{w}^{k+1}$, ${\tilde{u}}_n=\frac{1}{n+1}{\sum }_{k=0}^n{u}^{k+1}$, n is the iteration number, $w^0$ denotes the initial point.

Proof of Lemma 6. 

According to lemma 5, we sum the inequality (50) over $k=0,1,\cdots ,n$, we obtain

$$\begin{array}{c}{\displaystyle \sum _{k=0}^n}\left(\theta \left(u\right)-\theta \left(u^{k+1}\right)\right)+{\left(\left(n+1\right)w-{\displaystyle \sum _{k=0}^n}{w}^{k+1}\right)}^{T}F\left(w\right)+\frac{1}{2}{∥w-w^0∥}_M^2\ge \hfill \\ \frac{1}{2}{∥w-w^{k+1}∥}_M^2,\forall w\in W\hfill \end{array}$$

(55)

(55) can be rewritten as,

$$\frac{{∥w-w^0∥}_M^2}{2\left(n+1\right)}\ge \frac{1}{n+1}\sum _{k=0}^n\theta \left(u^{k+1}\right)-\theta \left(u\right)+{\left(\frac{1}{n+1}\sum _{k=0}^n{w}^{k+1}-w\right)}^{T}F\left(w\right),\forall w\in W$$

(56)

Because

$$\theta \left(u\right)=f\left(x_1\right)+g\left(x_2\right)$$

(57)

and $f\left(x_1\right)$, $g\left(x_2\right)$ are convex functions, we have,

$$\theta \left({\tilde{u}}_n\right)\le \frac{1}{n+1}\sum _{k=0}^n\theta \left(u^{k+1}\right)$$

(58)

Combining (56) and (58), we obtain,

$$\frac{{∥w-w^0∥}_M^2}{2\left(n+1\right)}\ge \theta \left({\tilde{u}}_n\right)-\theta \left(u\right)+{\left({\tilde{w}}_n-w\right)}^{T}F\left(w\right),\forall w\in W$$

(59)

Based on above discussion, the proof of Lemma 6 is completed.   □

According to Lemmas 4 and 5, it is found that iterative scheme APP has $O(1/n)$ convergence rate in an ergodic sense.

4. Numerical Experiments

In this section, we present the 40-unit test system to show the efficiency of the auxiliary problem principle. To be exact, the test system consists of two areas (area 1 and area 2). There are 25 units and 15 units in area 1 and area 2 respectively. The corresponding mathematical formulation can be expressed as follows.

$$min\left\{f\left(x_1\right)+g\left(x_2\right)\left|A{x}_1+B{x}_2\right.=b,x_1\in {\mathsf{\Omega }}_1,x_2\in {\mathsf{\Omega }}_2\right\}$$

(60)

where

$$A=\left(\underset{25}{\underbrace{0,\cdots ,0}},1\right),B=\left(\underset{15}{\underbrace{0,\cdots ,0}},-1\right),b=0$$

(61)

$$x_1={\left(P_1,P_2,\cdots ,P_{25},P_{b1}\right)}^T,x_2={\left(P_{26},P_{27},\cdots ,P_{40},P_{b2}\right)}^T$$

(62)

$$f\left(x_1\right)={\sum }_{i=1}^{25}\left(a_i^2{P}_i^2+b_i{P}_i+c_i\right),g\left(x_2\right)={\sum }_{i=26}^{40}\left(a_i^2{P}_i^2+b_i{P}_i+c_i\right)$$

(63)

$${\mathsf{\Omega }}_1=\left\{x_1\left|{\sum }_{i=1}^{25}{P}_i+P_{b1}=8000;P_{i,min}\le P_i\le P_{i,max},1\le i\le 25;\left|P_{b1}\right|\le 800\right.\right\}$$

(64)

$${\mathsf{\Omega }}_2=\left\{x_2\left|{\sum }_{i=26}^{40}{P}_i-P_{b2}=2000;P_{i,min}\le P_i\le P_{i,max},26\le i\le 40;\left|P_{b2}\right|\le 800\right.\right\}$$

(65)

$P_i$ is the active output of unit i in this test system. Both $P_{b1}$ and $P_{b2}$ denote transfer power flow between two areas. $P_{i,min}$, $P_{i,max}$ are given variable upper and lower limits, and $a_i,b_i,c_i$ are given fixed parameters for objective function as shown in Table 1 [15].

Table 1. Data for 40-Unit test sysem.

i	$P_{i,\min }$	$P_{i,\max }$	$a_i$	$b_i$	$c_i$
1	40	80	0.03073	8.336	170.44
2	60	120	0.02028	7.0706	309.54
3	80	190	0.00942	8.1817	369.03
4	24	42	0.08482	6.9467	135.48
5	26	42	0.09693	6.5595	135.19
6	68	140	0.01142	8.0543	222.33
7	110	300	0.00357	8.0323	287.71
8	135	300	0.00492	6.999	391.98
9	135	300	0.00573	6.602	455.76
10	130	300	0.00605	12.908	722.82
11	94	375	0.00515	12.986	635.2
12	94	375	0.00569	12.796	654.69
13	125	500	0.00421	12.501	913.4
14	125	500	0.00752	8.8412	1760.4
15	125	500	0.00708	9.1575	1728.3
16	125	500	0.00708	9.1575	1728.3
17	125	500	0.00708	9.1575	1728.3
18	220	500	0.00313	7.9691	647.85
19	220	500	0.00313	7.955	649.69
20	242	550	0.00313	7.9691	647.83
21	242	550	0.00313	7.9691	647.81
22	254	550	0.00298	6.6313	785.96
23	254	550	0.00298	6.6313	785.96
24	254	550	0.00298	6.6313	785.53
25	254	550	0.00298	6.6313	785.53
26	254	550	0.00277	7.1032	801.32
27	254	550	0.00277	7.1032	801.32
28	10	150	0.52124	3.3353	1055.1
29	10	150	0.52124	3.3353	1055.1
30	10	150	0.52124	3.3353	1055.1
31	20	70	0.25098	13.052	1207.8
32	20	70	0.16766	21.887	810.79
33	20	70	0.2635	10.244	1247.7
34	20	70	0.30575	8.3707	1219.2
35	18	60	0.18362	26.258	641.43
36	18	60	0.32563	9.6956	1112.8
37	20	60	0.33722	7.1633	1044.4
38	25	60	0.23915	16.339	832.24
39	25	60	0.23915	16.339	834.24
40	25	60	0.23915	16.339	1035.2

APP algorithm is employed to solve the problem. Here, parameters are selected as penalty parameter $c=0.01$ and auxiliary problem principle parameter $\beta =0.03$. Stop criterion is set to be

$$max\left(∥A{x}_1^{k+1}-A{x}_1^k∥,∥B{x}_2^{k+1}-B{x}_2^k∥,∥{\lambda }^{k+1}-{\lambda }^k∥\right)\le {10}^{-4}$$

(66)

Figure 1 and Figure 2 reflect the convergence characteristic of objective function and stop criterion for this test system, respectively. It is clear that objective function is converged to the optimal solution and the stop criterion is very close to zero when the number of iterations reaches 20. The effectiveness and correctness of the auxiliary problem principle have been demonstrated.

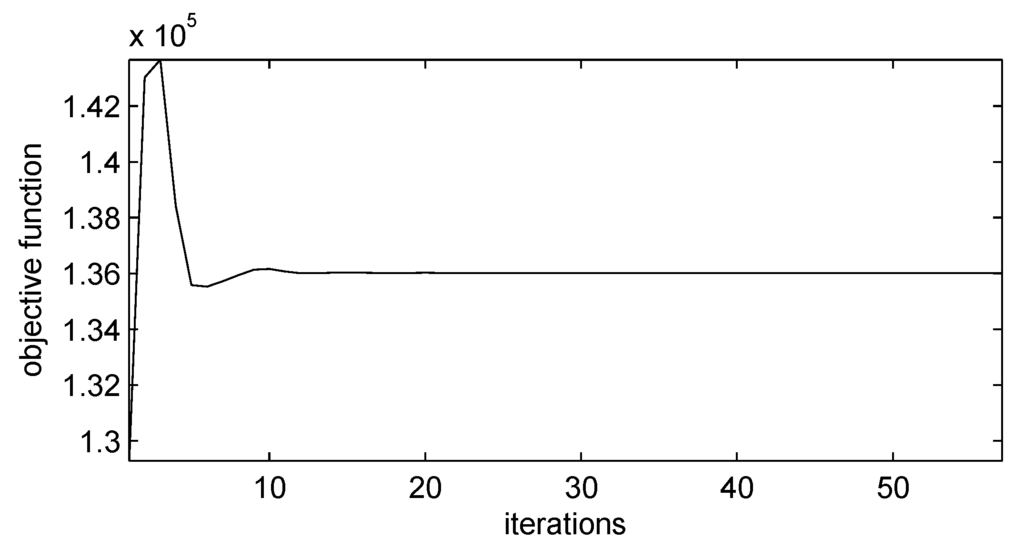
Figure 1. Convergence characteristic of objective function.

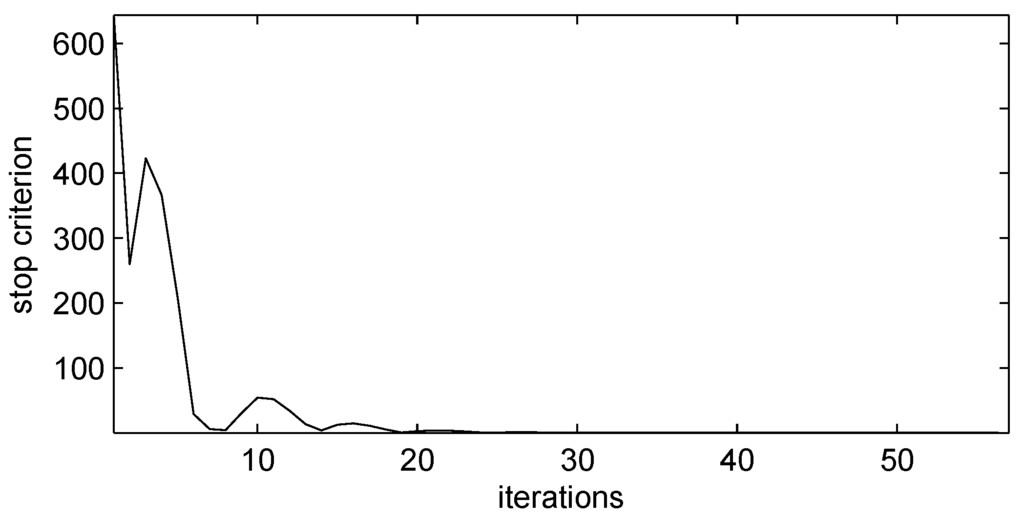
Figure 2. Convergence characteristic of stop criterion.

5. Conclusions

In this paper, taking advantage of special characterization of variational inequality solution set, we derive the $O(1/n)$ convergence rate of the auxiliary problem principle.