Abstract
The purpose of this work is to introduce a new kind of finite difference formulation inspired from Fourier analysis, for reaction-diffusion equations. Compared to classical schemes, the proposed scheme is much more accurate and has interesting stability properties. Convergence properties and stability of the scheme are discussed. Numerical examples are provided to show better performance of the method, compared with other existing methods in the literature.
1. Introduction
The movement of many individuals such as basic particles in physics or molecules can change under the effect of two important processes: chemical reactions in which the substances are transformed into each other, and diffusion mechanism which causes the substances to spread over a media. Such a process is governed by the following reaction-diffusion system
where is a matrix of diffusion coefficients, R is a vector valued function whose elements are the densities of the substances and represents reaction process. We are concerned with simulating the dynamics of single or many substances numerically in one dimension.
The analytical and numerical treatments of (1) attract the attention of many researchers with diverse backgrounds. Numerical analysis of several finite differences (FD) schemes for reaction-diffusion systems is given in the research monograph [1]. Apart from the classical approach, Ramirez et al. [2] derived nonstandard FD schemes for steady state reaction-diffusion equations based on Green’s integral formulation of the exact solution. In this work, we will derive so-called exponentially fitted finite difference schemes that can be obtained by only changing denominators in discrete derivative formulas.
2. Exponentially Fitted Finite Difference Formulation
Finite difference discretizations of ODEs and PDEs are widely used by the practitioners due to their easy analysis and implementation issues. However, many drawbacks, such as violation of positivity requirements and strict conditions on step sizes are encountered in the applications. To overcome these difficulties, some variants of FD schemes are developed. The very well known modification to FD schemes is nonstandard finite differences (NSFD) proposed by Mickens [3]. The rules of NSFD are based on complicated denominators and nonlocal representation of nonlinear terms in the equation. The other version of FD is exponentially fitted (EF) methods. In the last few decades, EF methods have become so popular that hundreds of papers have been published in theoretical and application-oriented journals. EF methods for differential equations date back to Gautschi [4], who proposed a method to integrate exactly appropriate trigonometric functions, just as classical methods integrate exactly algebraic polynomials. Paternoster [5] presents the overview of recent literature of EF methods. As for mathematical chemistry and physics, Anastassi and Simos [6] proposed EF methods for the numerical integration of the SchrÖdinger equation and related initial value problems with oscillating solution. The similarities and differences between NSFD and EF methods are discussed by Erdogan [7] and Gurski [8]. Other versions of EF methods are employed to solve singular perturbation problems which are numerically challenging. A historical review of these types of methods is given in [9]. Recent studies such as [10,11] present mathematical analysis and computational aspects of EF methods for singular perturbation problems.
EF methods include a fitting parameter, the so-called frequency that affects the convergence and stability properties of the method. For ordinary differential equations, the problem of how to choose fitting parameters are discussed in [12,13]. However, the usage EF method in the full discretization of PDE’s has not been well studied. In the recent work of the author [14], an exponentially fitted method is designed for solving advection type of initial boundary value problems by employing time and space frequencies in finite difference formulas. This approach does not only yield more accurate numerical results but also preserves the qualitative behavior of the equation under consideration.
In the construction of EF schemes, we will need the following EF based finite difference derivative formulas [15]
that are exact for the reference sets and respectively for the first and second derivatives. In the next chapters, these derivative approximations are inserted into the differential equation, and strategies for parameter selections are discussed.
2.1. Pure Diffusion
For the sake of clarity, we start with considering the diffusion equation
with initial condition and periodic boundary conditions. The separation of variables method for (3) gives
assuming the solution is of the form . It is clear that the time and spatial components of the solution are and . The relation between time and spatial components
is called dispersion relation [16]. However, classical finite difference methods never take this issue into account explicitly. Our contribution is to consider the dispersion relation through the construction of finite difference schemes. Fortunately, exponentially fitted methods and nonstandard finite differences provide us with a very useful tool: denominators in terms of non-polynomial functions [17,18]. We propose forward time derivative and the second space derivative in (2) to obtain an explicit EF scheme. The resulting scheme becomes
The assignments of ω and k and the relation between these parameters are of great importance. Ehrhardt and Mickens [18] obtained a similar scheme by sub-equation method. However, their motivation and procedure to determine ω and k were quite different. The main contribution of the present work is to describe a parameter selection strategy based on dispersion relation and local error formula. The local error of the scheme (6) is given by
where the derivatives etc. are computed at the point .
The selections
that vanish the first two terms in the local error formula and increase the time and space order. Furthermore, one can realize that these selections reveal the dispersion relation (5) by considering
In the implementation of (6), the classical finite difference approximations of and might be employed as follows for computing k numerically,
These approximations do not vanish the local error terms exactly. Nevertheless, this approach reduces the local error significantly. It is clear that k is updated at each .
k becomes constant within the time evolution and exact solution is obtained as long as initial profile is composed of only one Fourier component. However, in case of multi-frequency initial profile, k will not be constant any longer. It is also possible to take average values of parameters over time and space indices.
Stability of the Method
Both classical explicit finite difference scheme and EF scheme for the diffusion equation can be written as
where and stand for the CFL numbers for classical FD and EF schemes.
After the dispersion relation is substituted into , the limit
which tells us that classical FD formulation is employed in the implementation in case very small k values should be noticed.
Applying the well known stability arguments for time dependent PDEs [1,16], the stability requirement is found to be . After cumbersome algebra, it is verified that this requirement is satisfied when under the assumption , which prevents aliasing. In other words, stability of the method depends not only on step sizes but also on the parameters of the method. In order to overcome this drawback, we take (corresponding to classical FD) if computed values in (10) are very small or large in magnitude. Indeed, this precaution does not reduce the accuracy due to the fact that unwanted large and/or small values of parameters are caused by almost zero gradients that can be accurately resolved with classical FD formulas.
2.2. Reaction-Diffusion
In the presence of reaction term, the same derivative approximations are used to obtain the scheme
that corresponds to the original PDE
However, the dispersion relation (5) does not hold any longer. Considering (8), one computes k and ω as
For a coupled reaction-diffusion system, it is suggestive to use different space and time parameters for each of substances. Consider the system
with appropriate boundary and initial condition where D is 2 × 2 diffusion matrix. An explicit EF scheme for the coupled system can be written as
Apart from employing constant parameters in some special cases, local truncation errors for each line suggest that the selections
can decrease the error significantly. It is very usual to have stiffness in coupled reaction-diffusion systems. Explicit EF also fails in the case of stiffness. Therefore, an implicit version of EF finite differences should be used to deal with stiffness. By employing backward time difference in (2), one obtains an implicit version of (17). Local error based parameter selection strategy gives
Let us point out that parameter computations are performed explicitly although the proposed method is fully implicit.
3. Numerical Examples
3.1. Diffusion Equation
Consider the diffusion equation with periodic boundary conditions on
The initial condition leads to the exact solution . In Table 1, the EF method with the settings and , which will be denoted by , gives an exact solution up to machine accuracy. However, EF method performed by frequency search algorithm explained in the previous section could not catch the exact solution due to fluctuations in . Nevertheless, it is superior to the classical explicit finite difference scheme.

Table 1.
Errors in max norm at final time for example 1.
3.2. Nonlinear Diffusion
The proposed method is applied to nonlinear diffusion directly. Consider the problem
subject to initial condition
with exact solution [19]. The discretization of second derivative will be same as the linear case
The parameters k and ω are determined in terms of derivatives of not u itself. In Table 2, comparison of errors produced by EF and classical explicit finite difference methods is given. EF needs very moderate step sizes to get higher accuracy.

Table 2.
Errors in max norm at final time for example 2.
3.3. Fisher Equation
In this example, we will see that the proposed EF approach is not limited to linear equations with single dominant frequency. Consider the Fisher equation
with exact solution
EF solution is computed by Equations (15) and (13). Table 3 presents numerical solutions at and with , and for , . The wavelet method [20], which is a kind of spectral method, and B spline technique [21], that yields five points implicit stencil, are used for numerical comparison. Numerical time evolution of the initial profile by EF method is given in Figure 1.

Table 3.
Comparison of the methods for example 3.

Figure 1.
Numerical exponentially fitted (EF) solution of Fisher equation.
3.4. Coupled Nonlinear System
Consider the equation
with initial conditions , . Its exact travelling wave solution [22] is given by
where and . This problem is used to test some semi analytical approximation methods such as Adomian Decomposition Method [23].
A numerical experiment is performed for and . Explicit EF and classical FD schemes (central difference in space, forward difference in time) are employed. In Figure 2, the order plots are given. In Figure 2a, is fixed and several time steps within the stability region are considered. In Figure 2b, is fixed and numerical experiments are performed for different values. Figures indicate that the proposed parameter selection algorithm could not make leading order terms vanish in local error. This is because the exact solution does not consist of trigonometric space functions. However, the parameter selection strategy reduces the local errors considerably at each . The classical FD scheme can catch the accuracy that is obtained by EF only for very small and values.
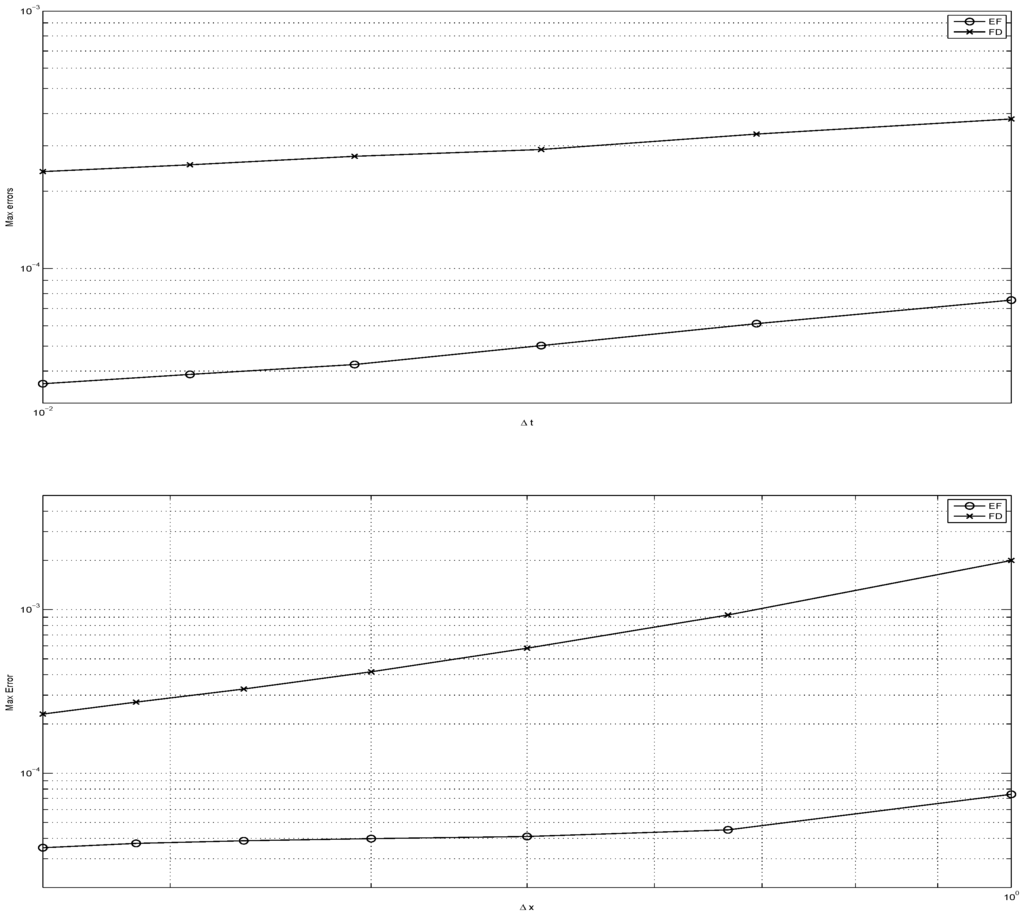
Figure 2.
(a) log log plot of values vs. max norm of errors at final time for fixed ; (b) log log plot of values vs. max norm of errors at final time for fixed .
3.5. Stiff Coupled System
Consider the initial- boundary value problem
with initial conditions , and homogenous Neumann conditions. Its exact solution is and . This example is used to test some implicit solvers such as those proposed in [24,25]. In this example, Implicit EF method with parameter selections in Equation (19) is compared with other implicit solvers. Table 4 presents errors in max norm for a fixed time step and various values. Although B spline method is based on five point stencil and employs Crank-Nicolson for time discretization, it falls behind Implicit EF.

Table 4.
Errors for and in max norm at final time with for example 5.
4. Conclusions
A simple modification of a classical explicit finite difference scheme, which is based on change of denominators, is described and convergence properties of the proposed scheme are discussed. This algorithmic approach has improved the accuracy without considerable computational work. A reader who is familiar with spectral methods [26] can realize that we are trying to include only dominant frequency into the finite difference formulation. The success of the proposed method for diffusion equations relies on the smoothing effect of the diffusion operator that damps high frequencies rapidly.
In a similar manner, all kinds of classical FD schemes can be converted to EF schemes by choosing a suitable reference set. A further study can be performed on the parameter selection strategies, possibly with the instruments of Fourier analysis.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments and suggestions to improve the quality of the paper.
Author Contributions
All authors have equally contributed to this paper. They have read and approved the final version of the manuscript. The second author as a Master Student simulated the numerical experiments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Multidisciplinary Digital Publishing Institute |
| TLA | Three letter acronym |
| LD | linear dichroism |
References
- Hundsdorfer, W.; Verwer, J. Numerical Solution of Time-Dependent Advection-Diffusion-Reaction Equations; Springer Series in Computational Mathematics; Springer-Verlag: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Alvarez-Ramirez, J.; Valdes-Parada, F.J.; Alvarez, J.; Ochoa-Tapia, J.A. A Green’s function formulation for finite-differences schemes. Chem. Eng. Sci. 2007, 62, 3083–3091. [Google Scholar] [CrossRef]
- Mickens, R.E. Nonstandard Finite Difference Schemes for Differential Equations. J. Differ. Equ. Appl. 2002, 8, 823–847. [Google Scholar]
- Gautschi, W. Numerical integration of ordinary differential equations based on trigonometric polynomials. Numer. Math. 1961, 3, 381–397. [Google Scholar] [CrossRef]
- Paternoster, B. Present state-of-the-art in exponential fitting. A contribution dedicated to Liviu Ixaru on his 70th birthday. Comput. Phys. Commun. 2012, 183, 2499–2512. [Google Scholar] [CrossRef]
- Anastassi, Z.; Simos, T. A family of two-stage two-step methods for the numerical integration of the Schrödinger equation and related IVPs with oscillating solution. J. Math. Chem. 2009, 45, 1102–1129. [Google Scholar] [CrossRef]
- Erdogan, U.; Ozis, T. A smart nonstandard finite difference scheme for second order nonlinear boundary value problems. J. Comput. Phys. 2011, 230, 6464–6474. [Google Scholar] [CrossRef]
- Gurski, K. A simple construction of nonstandard finite-difference schemes for small nonlinear systems applied to SIR models. Comput. Math. Appl. 2013, 66, 2165–2177. [Google Scholar] [CrossRef]
- Roos, H.G.; Stynes, M.; Tobiska, L. Robust Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion-Reaction and Flow Problems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 24. [Google Scholar]
- Öziş, T.; Erdoğan, U. An exponentially fitted method for solving Burgers’ equation. Int. J. Numer. Methods Eng. 2009, 79, 696–705. [Google Scholar] [CrossRef]
- Marušić, M. On ϵ uniform convergence of exponentially fitted methods. Math. Commun. 2014, 19, 545–559. [Google Scholar]
- Erdogan, U.; Kocak, H. Numerical study of the asymptotics of the second Painlevé equation by a functional fitting method. Math. Methods Appl. Sci. 2013, 36, 2347–2352. [Google Scholar] [CrossRef]
- Ramos, H.; Vigo-Aguiar, J. On the frequency choice in trigonometrically fitted methods. Appl. Math. Lett. 2010, 23, 1378–1381. [Google Scholar] [CrossRef]
- Erdogan, U. Improved upwind discretization of the advection equation. Numer. Methods Partial Differ. Equ. 2014, 30, 773–787. [Google Scholar] [CrossRef]
- Ixaru, L.; Berghe, G. Exponential fitting. In Mathematics and its Applications; Kluwer Academic Publishers: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Ascher, U.M. Numerical Methods for Evolutionary Differential Equations; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2008. [Google Scholar]
- Uddin, R. Comparison of the nodal integral method and nonstandard finite-difference schemes for the fisher equation. SIAM J. Sci. Comput. 2000, 22, 1926–1942. [Google Scholar] [CrossRef]
- Ehrhardt, M.; Mickens, R.E. A nonstandard finite difference scheme for convection–diffusion equations having constant coefficients. Appl. Math. Comput. 2013, 219, 6591–6604. [Google Scholar]
- Wazwaz, A.M. Exact solutions to nonlinear diffusion equations obtained by the decomposition method. Appl. Math. Comput. 2001, 123, 109–122. [Google Scholar] [CrossRef]
- Cattani, C.; Kudreyko, A. Mutiscale Analysis of the Fisher Equation. Comput. Sci. Appl. ICCSA 2008 2008, 5072, 1171–1180. [Google Scholar]
- Mittal, R.C.; Arora, G. Efficient numerical solution of Fisher’s equation by using B-spline method. Int. J. Comput. Math. 2010, 87, 3039–3051. [Google Scholar] [CrossRef]
- Feng, X. Exact wave front solutions to two generalized coupled nonlinear physical equations. Phys. Lett. A 1996, 213, 167–176. [Google Scholar] [CrossRef]
- El-Wakil, S.; Abdou, M. New applications of Adomian decomposition method. Chaos Solitons Fractals 2007, 33, 513–522. [Google Scholar] [CrossRef]
- Abbas, M.; Majid, A.A.; Ismail, A.I.M.; Rashid, A. Numerical method using cubic B-spline for a strongly coupled reaction-diffusion system. PLoS ONE 2014, 9. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.Y.; Sun, Z.Z. A second-order linearized difference scheme for a strongly coupled reaction-diffusion system. Numer. Methods Partial Differ. Equ. 2008, 24, 9–23. [Google Scholar] [CrossRef]
- Boyd, J. Chebyshev and Fourier Spectral Methods; Dover books on mathematics; DOVER PUBN Incorporated: New York, NY, USA, 2001. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).