A Novel Evolutionary Arithmetic Optimization Algorithm for Multilevel Thresholding Segmentation of COVID-19 CT Images

Abstract

One of the most crucial aspects of image segmentation is multilevel thresholding. However, multilevel thresholding becomes increasingly more computationally complex as the number of thresholds grows. In order to address this defect, this paper proposes a new multilevel thresholding approach based on the Evolutionary Arithmetic Optimization Algorithm (AOA). The arithmetic operators in science were the inspiration for AOA. DAOA is the proposed approach, which employs the Differential Evolution technique to enhance the AOA local research. The proposed algorithm is applied to the multilevel thresholding problem, using Kapur’s measure between class variance functions. The suggested DAOA is used to evaluate images, using eight standard test images from two different groups: nature and CT COVID-19 images. Peak signal-to-noise ratio (PSNR) and structural similarity index test (SSIM) are standard evaluation measures used to determine the accuracy of segmented images. The proposed DAOA method’s efficiency is evaluated and compared to other multilevel thresholding methods. The findings are presented with a number of different threshold values (i.e., 2, 3, 4, 5, and 6). According to the experimental results, the proposed DAOA process is better and produces higher-quality solutions than other comparative approaches. Moreover, it achieved better-segmented images, PSNR, and SSIM values. In addition, the proposed DAOA is ranked the first method in all test cases.

1. Introduction

One of the most often used image segmentation techniques is multilevel thresholding. It is divided into two types: bi-level and multilevel [1,2]. Multilevel thresholding is used to separate complex images, which can generate several thresholds, such as tri-level or quad-level thresholds, which break pixels into several identical parts depending on size. Bi-level thresholding divides the image into two levels, while multilevel thresholding divides the image into two classes [3,4]. When there are only two primary gray levels in an image, bi-level thresholding yields acceptable results; however, when it is expanded to multilevel thresholding, the main drawback is the time-consuming computation [5]. Bi-level thresholding cannot precisely find the optimum threshold, due to the slight variation between the target and the context of a complex image [6,7].

Medical imaging, machine vision, and satellite photography all use image segmentation [8,9,10]. The primary aim of image segmentation is to divide an image into relevant regions for a specific mission. The process of finding and isolating points of interest from the rest of the scene is known as the segmentation of pattern recognition systems [11,12]. Following image segmentation, certain features from objects are removed, and then objects are grouped into specific categories or classes, depending on the extracted features. Segmentation is used in medical applications to detect organs, such as the brain, heart, lungs, and liver, in CT or MR images [13,14]. It is also used to tell the difference between abnormal tissue, such as a tumor, and healthy tissue. Image segmentation techniques, such as image thresholding, edge detection, area expanding, stochastic models, Artificial Neural Network (ANN), and clustering techniques, have all been used, depending on the application [15,16].

Tsallis, Kapur, and Otsu procedures are the most widely used thresholding strategies [17,18]. The Otsu method maximizes the between-class variance function to find optimum thresholds, while the Kapur method maximizes the posterior entropy of the segmented groups. Due to exhaustive search, Tsallis and Otsu’s computational complexity grows exponentially as the number of thresholds increases [19]. Many researchers have worked on image segmentation over the years. Image segmentation has been tackled using a variety of approaches and algorithms [20]. Examples of the used optimization algorithms are the Bat Algorithm (BA) [21], Firefly Algorithm (FA) [22], Genetic Algorithm (GA) [23], Gray Wolf Optimizer (GWO) [24,25], Dragonfly Algorithm (DA) [26], Moth–Flame Optimization Algorithm (MFO) [27], Marine Predators Algorithm (MPA) [28], Arithmetic Optimization Algorithm (AOA) [29], Aquila Optimizer (AO) [30], Krill Herd Optimizer (KHO) [31], Harris Hawks Optimizer (HHO) [32], Red Fox Optimization Algorithm (RFOA) [33], Artificial Bee Colony Algorithm (ABC) [34], and Artificial Ecosystem-based Optimization [35]. Many other optimizers can be found in [36,37].

The paper [38] used Kapur and Otsu’s approaches to adjust the latest Elephant Herding Optimization Algorithm for multilevel thresholding. Its performance was compared to four other swarm intelligence algorithms, using regular benchmark images. The Elephant Herding Optimization Algorithm outperformed and proved more stable than other methods in the literature. Sahlol et al. in [39] introduced an improved hybrid method for COVID-19 images by merging the strengths of convolution neural networks (CNNs) to remove features and the MPA feature selection algorithm to choose the most important features. The proposed method exceeds several CNNs and other well-known methods on COVID-19 images.

The multi-verse optimizer (MVO), based on the multi-verse theorem, is a new algorithm for solving real-world multi-parameter optimization problems. A novel parallel multi-verse optimizer (PMVO) with a coordination approach is proposed in [40]. For each defined iteration, the parallel process is used to randomly split the original solutions into multiple groups and exchange the various groups’ details. This significantly improves individual MVO algorithm cooperation and reduces the shortcomings of the original MVO algorithm, such as premature convergence, search stagnation, and easy trapping into the local optimal search. The PMVO algorithm was compared to methods under the CEC2013 test suite to validate the proposed scheme’s efficiency. The experimental findings show that the PMVO outperforms the other algorithms under consideration. In addition, using minimum cross entropy thresholding, PMVO is used to solve complex multilevel image segmentation problems. In comparison with different related algorithms, the proposed PMVO algorithm seems to achieve better quality image segmentation.

For image segmentation, a modified artificial bee colony optimizer (MABC) is proposed [41], which balances the tradeoff between the search process by using a pool of optimal foraging strategies. MABC’s main goal is to improve artificial bee foraging behaviors by integrating local search with detailed learning, using a multi-dimensional PSO-based equation. With detailed learning, the bees combine global best solution knowledge into the solution quest equation to increase exploration. Simultaneously, local search allows the bees to thoroughly exploit across the promising field, providing a good combination of exploration and exploitation. The proposed algorithm’s feasibility was shown by the experimental findings comparing the MABC to several popular EA and SI algorithms on a series of benchmarks. The experimental findings verify the suggested algorithm’s efficacy.

For solving the image segmentation problem, a novel multilevel thresholding algorithm based on a meta-heuristic Krill Herd Optimization (KHO) algorithm is proposed in [42]. The optimal threshold values are calculated, using the Krill Herd Optimization technique to maximize Kapur’s or Otsu’s objective function. The suggested method reduces the amount of time it takes to calculate the best multilevel thresholds. Various benchmark images are used to illustrate the applicability and numerical performance of the Krill Herd Optimization-based multilevel thresholding. To demonstrate the superior performance of the proposed method, a detailed comparison with other current bio-inspired techniques based on multilevel thresholding techniques, such as Bacterial Foraging (BF), Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and Moth-Flame Optimization (MFO), was performed. The results confirmed that the proposed method achieved better results than other methods.

This paper presents a modified version of the Manta Ray Foraging Optimizer (MRFO) algorithm to deal with global optimization and multilevel image segmentation problems [43]. MRFO is a meta-heuristic technique that simulates the behaviors of manta rays to find food. The performance of the MRFO is improved by using fractional-order (FO) calculus during the exploitation phase. In this experiment, a variant of natural images is used to assess FO-MRFO. According to different performance measures, the FO-MRFO outperformed the compared algorithms in global optimization and image segmentation.

The concept “optimization” refers to the process of identifying the best solutions to a problem while keeping those constraints in mind [44,45]. The used optimization in solving the image segmentation problem is the method of finding the best threshold values for a given image. Swarm intelligence (SI) algorithms are used widely for multilevel thresholding problems to determine the optimal threshold values, using various objective functions to solve the problems of the computational inefficiency of traditional thresholding techniques. The primary motivation behind this paper is to find the optimal threshold values for image segmentation problems. At the same time, to address the weakness of the original AOA, it suffers from the local optimal problem and premature coverage in some cases. In this paper, an improved version of the Arithmetic Optimization Algorithm (AOA) by using Differential Evolution, called DAOA, is proposed. The proposed method uses Differential Evolution to tackle the conventional Arithmetic Optimization Algorithm’s weaknesses, such as being trapped in local optima and fast convergence. Thus, Differential Evolution is used to enhance the performance of the Arithmetic Optimization Algorithm. The proposed DAOA assists by using eight standard test images from different groups: two-color images, two gray images, two normal CT COVID-19 images, and two confirmed COVID-19 CT images. Peak signal-to-noise ratio (PSNR), structural similarity index test (SSIM), and fitness function (Kapur’s) are used to determine the accuracy of segmented images. The proposed DAOA method’s efficiency is evaluated and compared to other multilevel thresholding methods. The findings are presented with a number of different threshold values (i.e., 2, 3, 4, 5, and 6). According to the experimental results, the proposed DAOA process is better and produces higher-quality solutions than other approaches. The encouraging findings suggest that using the DAOA-based thresholding strategy has potential and is helpful.

The rest of this paper is organized as follows. Section 2 presents the procedure of the proposed DAOA method. Section 3 presents the definitions and procedures of the image segmentation problem. The experiments and results are given in Section 4. Finally, in Section 5, the conclusions and potential future work directions are given.

2. The Proposed Method

In this section, we present the conventional Arithmetic Optimization Algorithm (AOA), Differential Evolution (DE), and the proposed Evolutionary Arithmetic Optimization Algorithm (DAOA).

2.1. Arithmetic Optimization Algorithm (AOA)

In this section, we describe the exploration and exploitation phases of the original AOA [29], which is motivated by the main operators in math science (i.e., multiplication (M), division (D), subtraction (S), and addition (A)). The main search methods of the AOA are presented in Figure 1, which are illustrated in the following subsections.

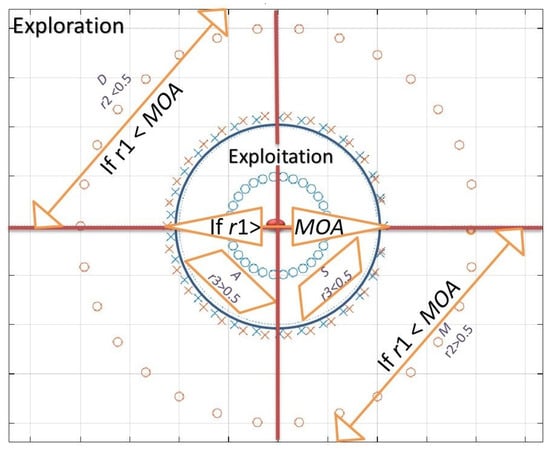
Figure 1. The search phases of the Arithmetic Optimization Algorithm.

The AOA should choose the search process before beginning its work (i.e., exploration or exploitation). So, in the following search steps, the Math Optimizer Accelerated ($MOA$) function is a coefficient determined by Equation (1).

$$MOA(C\_Iter)=Min+C\_Iter\times \left(\frac{Max-Min}{M\_Iter}\right)$$

(1)

where $MOA$(C_Iter) means the value at the $t\mathrm{th}$ iteration of MOA function, determined by Equation (1). $C\_Iter$ is the current iteration: [1 ………$M\_Iter$]. $Min$ and $Max$ are the accelerated function values (minimum and maximum), respectively.

2.1.1. Exploration Phase

The exploration operators of AOA are modeled in Equation (2). The exploration phase uses the D or M operators conditioned by $r1>$MOA. The D operator is prepared by $r2<$ 0.5, or, otherwise, by the M operator. $r2$ is a random number. The position updating process is determined as follows.

$$x_{i,j}(C\_Iter+1)=\left\{\begin{array}{cc}best(x_j)÷MOP\times ((U{B}_j-L{B}_j)\times \mu +L{B}_j),& r2<0.5\\ best(x_j)\times MOP\times ((U{B}_j-L{B}_j)\times \mu +L{B}_j),& otherwise\end{array}\right.$$

(2)

where $x_i$(C_Iter$+1)$ is the $i\mathrm{th}$ next solution, $x_{i,j}$(C_Iter) is the $j\mathrm{th}$ location of the $i\mathrm{th}$ solution, and $best(x_j)$ is the $j\mathrm{th}$ location in the best solution. $\mu$ is a control value (0.5) to tune the exploration search.

$$MOP(C\_Iter)=1-\frac{C\_Ite{r}^{1/\alpha }}{M\_Ite{r}^{1/\alpha }}$$

(3)

where $MOP$(C_Iter) denotes the coefficient value at the $t\mathrm{th}$ iteration. $\alpha$ is a control value (5) to tune the exploration search.

2.1.2. Exploitation Phase

The exploitation searching phase uses the S and A operators conditioned by the MOA function value. Subtraction (S) and addition (A) search strategies are represented in Equation (4).

$$x_{i,j}(C\_Iter+1)=\left\{\begin{array}{cc}best(x_j)-MOP\times ((U{B}_j-L{B}_j)\times \mu +L{B}_j),& r3<0.5\\ best(x_j)+MOP\times ((U{B}_j-L{B}_j)\times \mu +L{B}_j),& otherwise\end{array}\right.$$

(4)

The intuitive and detailed process of AOA is shown in Figure 2.

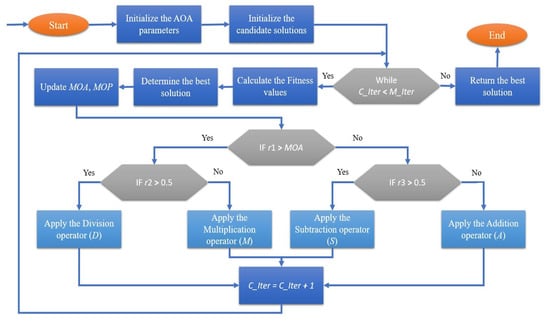
Figure 2. Flowchart of the conventional AOA.

2.2. Differential Evolution (DE)

In [46], Storn and Price introduced the DE as the first version to solve multiple optimization problems in 1997. DE stands out for its versatility, quick execution time, rapid acceleration pattern, and fast and accurate local operators [47,48]. In DE, the optimization process begins with a random selection of solutions for finding the majority of the points in the search space (initialization phase). The solutions can then be improved, using a series of operators called mutation and crossover. The new solution can be accepted if it has a higher objective value. For the current solution $X_i$, the mathematical model of the mutation operator $Z_i^t$ can be applied as follows:

$$Z_{i,j}=X{D}_{ran{d}_1}+F\times (X{D}_{r2}-X{D}_{r3}),$$

(5)

where $r_1,r_2$, and $r_3$ are random numbers, F is the mutation balancing factor, and F is greater than 0.

For the crossover operator, Equation (6) represents the new solution $V_i$, which is produced using the mutated operator through the crossover $Z_i$. The crossover is considered a mixture process among vectors $Z_i$ and $X{D}_i$.

$$V_{i,j}=\left\{\begin{array}{c}{Z}_{i,j}ifrand\le C_r\hfill \\ X{D}_{i,j}otherwise\hfill \end{array}\right.$$

(6)

$C_r$ is the crossover probability.

The DE algorithm improves its selected solutions according to the objective function values, where the generated $V_i,C\_Iter$ is replaced with the current one if it obtained a better fitness value, which is as follows.

$$X{D}_{i,j}=\left\{\begin{array}{c}{V}_{i,j}iff(V_{i,j})<f(X{D}_{i,j})\hfill \\ X{D}_{i,j}otherwise\hfill \end{array}\right.$$

(7)

2.3. The Proposed DAOA

In this section, the procedure of the proposed Evolutionary Arithmetic Optimization Algorithm (DAOA) is presented as follows.

2.3.1. Initialization Phase

When using the AOA, the optimization procedure begins with a number of random solutions (X) as designated in matrix (8). The best solution is taken in each iteration as the best-obtained solution.

$$X=\left[\begin{array}{cccccc}{x}_{1,1}& \cdots & \cdots & x_{1,j}& x_{1,n-1}& x_{1,n}\\ x_{2,1}& \cdots & \cdots & x_{2,j}& \cdots & x_{2,n}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ x_{N-1,1}& \cdots & \cdots & x_{N-1,j}& \cdots & x_{N-1,n}\\ x_{N,1}& \cdots & \cdots & x_{N,j}& x_{N,n-1}& x_{N,n}\end{array}\right]$$

(8)

2.3.2. Phases of the Proposed DAOA

In this section, the main details and procedures of the proposed Evolutionary Arithmetic Optimization Algorithm (DAOA) are given.

The DAOA is introduced mainly to develop the original AOA’s convergence ability, the quality of solutions, and the ability to avoid the local optima problem. Thus, the DE technique is introduced into the conventional AOA to form DAOA. This proposed DAOA method is introduced to perform the exploration search by the AOA and exploitation search by the DE. This also makes an excellent balance between the search strategies and guarantees that the proposed method averts the local optima.

Figure 3 depicts the proposed DAOA approach in this section. The DAOA procedure begins with (1) determining the values of the used algorithms’ parameters, (2) generating candidate solutions, (3) calculating fitness functions, (4) selecting the best solution, (5) if a given condition is true, the AOA is executed to update the solutions; otherwise, the DE is executed to update the solutions, and (6) then another condition is given to stop or continue the optimization process. Figure 3 shows the flowchart for the proposed DAOA. The pseudo-code of the DAOA algorithm is given in Algorithm 1.

Algorithm 1 Pseudo-code of the DAOA algorithm

1: Initialize the Arithmetic Optimization Algorithm parameters $\alpha$, $\mu$. 2: Initialize the solutions’ positions randomly. (Solutions: i = 1, …, N.). 3: Calculate the Fitness values. 4: while ($C\_Iter$<$M\_Iter$) do 5:  Find the best solution (determined best so far). 6:  Update the MOA value using Equation (1). 7:  Update the MOP value using Equation (3). 8:  Calculate the Fitness Function ($FF$) for the given solutions. 9:  for (i = 1 to $Solutions$) do 10:   if rand < 0.5 then 11:    Generate a random values between [0, 1] ($r1$, $r2$, and $r3$) 12:    if $r1>$ MOA then 13:     if $r2>$ 0.5 then 14:      Update the $i\mathrm{th}$ solutions’ positions using the first rule in Equation (2). 15:     else 16:      Update the $i\mathrm{th}$ solutions’ positions using the second rule in Equation (2). 17:     end if 18:    else 19:     if $r3>$ 0.5 then 20:      Update the $i\mathrm{th}$ solutions’ positions using the first rule in Equation (4). 21:     else 22:      Update the $i\mathrm{th}$ solutions’ positions using the second rule in Equation (4). 23:     end if 24:    end if 25:   else 26:    if rand < 0.5 then 27:     Update the $i\mathrm{th}$ solutions’ positions using Mutation operator as given in Equation (5). 28:    else 29:     Update the $i\mathrm{th}$ solutions’ positions using Crossover operator as given in Equation (6). 30:    end if 31:   end if 32:  end for 33:  C_Iter = C_Iter + 1 34: end while 35: Return the best solution (x).

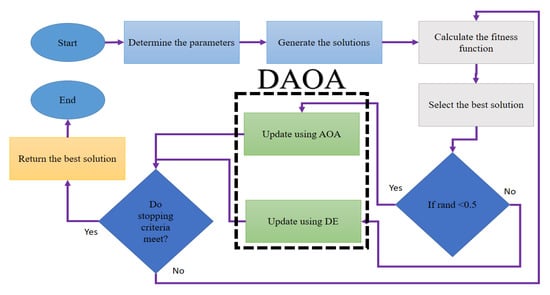
Figure 3. The flowchart of the proposed DAOA.

3. Definitions of the Multilevel Thresholding Image Segmentation Problems

In this section, we describe the main problem of multilevel thresholding. Let us suppose that I is a gray or color image that needs to be processed, where $K+1$ presents the classes that need to be produced. For segmenting the given image (I) into $K+1$ classes, the k thresholds’ values are required to progress in the image segmentation procedure; $\{t_k,k=1..........K\}$, and this can be expressed as follows [1,7,49].

$$\begin{array}{cc}\hfill & C_0=\{I_{i,j}\mid 0\le I_{i,j}\le t_1-1\},\hfill \\ \hfill & C_1=\{I_{i,j}\mid t_1\le I_{i,j}\le t_2-1\},\hfill \\ & \dots \hfill \\ \hfill & C_K=\{I_{i,j}\mid t_K\le I_{i,j}\le L-1\}\hfill \end{array}$$

(9)

where L indicates the highest gray levels and $C_K$ indicates the kth class of the image I. The $t_k$ is the k-th threshold, with $I_{i,j}$ being the gray level at the $(i,j)$th pixel. Furthermore, in Equation (10), multilevel thresholding is identified as a maximization optimization problem that needs to find the optimal threshold values.

K multilevel threshold values can be presented as follows.

$$t_1,\ast ,t_2,\ast ,\dots ,t_K,\ast =\arg \underset{t_1,\dots ,t_K}{\max }Fit(t_1,\dots ,t_K)$$

(10)

3.1. Fitness Function (Kapur’s Entropy)

For the purpose of thresholding, consider a digital image I with N pixels and L gray levels. Via thresholds, these L number of gray levels are divided into classes: Class1, Class2, …, Classk [1].

In this proposed DAOA, Kapur’s entropy is utilized for achieving optimum threshold values. Measurement of the bi-level thresholds needs the optimization process’s objective function, as shown in Equation (11).

$$Fit(t_1,\dots ,t_K)=\sum _{k=1},K{H}_i$$

(11)

$$H_k=-\sum _{i=0}^{L-1}\frac{p_i\times {\mu }_k(i)}{P_k}\times ln(\frac{p_i\times {\mu }_k(i)}{P_k}),$$

(12)

$$P_k=\sum _{i=0}^{L-1}{p}_i\times {\mu }_k(i)$$

(13)

$${\mu }_1(l)=\left\{\begin{array}{cc}1\hfill & l\le a_1\hfill \\ \frac{l-c_1}{a_1-c_1}\hfill & a_1\le l\le c_1\hfill \\ 0\hfill & l>c_1\hfill \end{array}\right.{\mu }_K(l)=\left\{\begin{array}{cc}1\hfill & l\le a_{K-1}\hfill \\ \frac{l-a_K}{c_K-a_K}\hfill & a_{K-1}<l\le c_{K-1}\hfill \\ 0\hfill & l>c_{K-1}\hfill \end{array}\right.$$

(14)

where $p_i$ is the probability distribution, $h(i)$ is the numbers of pixels for the used gray level L, and $N_p$ is the total numbers of pixels of the image I. $p_i$ presents the probability value for the distribution, determined as $p_i=h(i)/N_p$ ($0<i<L-1$). $h(i)$ and $N_k$ are the numbers of pixels for the used gray level L and total pixel of the image I. $a_1,c_1,\dots .,a_{k-1},c_{k-1}$ are the used fuzzy parameters, and $0\le a_1\le c_1\le \dots \le a_{K-1}\le c_{K-1}$.

Then, $t_1=\frac{a_1+c_1}{2},t_2=\frac{a_2+c_2}{2},...,t_{K-1}=\frac{a_{K-1}+c_{K-1}}{2}$. The best fitness function obtained is the highest value.

3.2. Performance Measures

We assess the proposed DAOA method performance, using three performance measures: the fitness function value, the Structural Similarity Index (SSIM), and the Peak Signal-to-Noise Ratio (PSNR) [50,51]. The following equations compute SSIM and PSNR:

$$SSIM(I,I_S)=\frac{(2{\mu }_I{\mu }_{I_S}+c_1)(2{\sigma }_{I,I_S}+c_2)}{({\mu }_I^2+{\mu }_{I_S}^2+c_1)({\sigma }_I^2+{\sigma }_{I_S}^2+c_2)}$$

(15)

where ${\mu }_{I_S}$ (${\sigma }_{I_S}$) and ${\mu }_I$(${\sigma }_I$) are the images’ mean intensity of $I_S$ and I, respectively, where ${\sigma }_{I,I_S}$ is the governance of I and $I_S$, and $c_1$ and $c_2$ coefficient values are equal to 6.5025 and 58.52252, respectively [1].

$$PSNR=20lo{g}_{10}(\frac{255}{RMSE}),RMSE=\sqrt{\frac{{\sum }_{i=1}^{N_r}{\sum }_{j=1}^{N_c}{(I_{i,j}-I_{S}i,j)}^2}{N_r\times N_c}}$$

(16)

where the $RMSE$ is the root-mean-squared error of each pixel, and $M\times N$ depicts the image’s size. $I_{i,j}$ is the gray pixel value of the initial image, and $I{s}_{ij}$ is the gray value of the pixel in the obtained segmented image.

4. Experiments and Results

4.1. Benchmark Images

In this section, the benchmark image data sets are presented in Figure 4 and Figure 5. Two image types were used in this paper’s experiments, taken from nature (as seen in Figure 4) and medical CT images (as seen in Figure 5). We chose eight images: two-color images from nature (i.e., Test 1 and Test 2), two gray images from nature (i.e., Test 3 and Test 4), two COVID-19 CT images (i.e., Test 5 and Test 6), and two normal COVID-19 CT images (i.e., Test 7 and Test 8). These benchmarks were taken from the Berkeley Segmentation Data Set: Images and BIMCV-COVID19 [52].

Figure 4. The nature benchmark images that have been used.

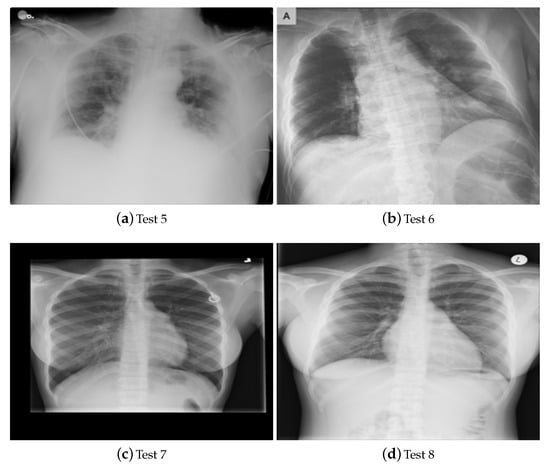
Figure 5. The CT benchmark images that were used.

4.2. Comparative Algorithms and Parameter Setting

The proposed DAOA is analyzed and compared with six recently well-known algorithms, including Aquila Optimizer (AO) [30], Whale Optimization Algorithm (WOA) [53], Salp Swarm Algorithm (SSA) [54], Arithmetic Optimization Algorithm (AOA) [29], Particle Swarm Optimization (PSO) [55], Marine Predators Algorithm (MPA) [56], and Differential Evolution (DE) [57].

These algorithms’ parameters are set in the same way as they were in their original papers. The values of different parameter settings used in the tested algorithms are shown in Table 1. These sensitive parameters can be tuned for further investigation to show the effect of each parameter on the performance of the tested methods. The algorithms are executed by using the MATLAB 2015a software. These algorithms are run on an Intel Core i7 1.80 GHz 2.30 GHz processor with 16 GB RAM. The number of solutions used is twenty-five. For a systematic comparison, the maximum number of iterations is set to one hundred. Each competitor algorithm generates thirty independent runs.

Table 1. Parameter settings.

No.	Algorithm	Reference	Parameter	Value
1	AO	[30]	$\alpha$	0.1
			/$\delta$	0.1
2	WOA	[53]	$\alpha$	Decreased from 2 to 0
			b	2
3	SSA	[54]	$v_0$	0
4	AOA	[29]	$\alpha$	5
			$\mu$	0.5
5	PSO	[55]	Topology	Fully connected
			Cognitive and social constant	(C1, C2) 2, 2
			Inertia weight	Linear reduction values [0.9 0.1]
			Velocity limit	10% of dimension range
6	MPA	[56]	$\gamma$	$\gamma$ > 1
			P	0.0
7	DE	[57]	Co	0.5
			Mu	0.5

4.3. Performance Evaluation

A comparison of the proposed DAOA for multilevel thresholding segmentation, using eight different images, is presented in this section. The following tables show the max, mean, min, and standard deviation of each test case’s PSNR and SSIM. Moreover, the summation, mean rank, and final ranking are given, using the Friedman ranking test to prove the proposed method’s significant improvement [58,59].

The PSNR and SSIM results of Test 1 are given in Table 2 and Table 3. It is clear that the proposed DAOA obtained excellent results in almost all the test cases in terms of PSNR. For threshold 2, the proposed DAOA obtained the best results, and it ranked first when compared to all other comparative methods, followed by AOA, SSA, PSO, WOA, MPA, AO, and finally, DE. In addition, for threshold 6, the proposed method obtained promising results compared to other methods. DAOA obtained the first rank, followed by WOA, PSO, SSA, AOA, AO, SSA, MPA, and DE. Overall, we can see that the proposed method obtained the first ranking, followed by AOA, PSO, SSA, WOA, AO, MPA, and DE. The obtained results in this table prove the ability of the proposed DAOA to solve the given problems effectively.

Table 2. The PSNR results of the test case 1.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	12.74479	13.20368	13.72521	13.27539	13.70085	12.02615	13.51551	14.55374
	Mean	11.43681	11.97746	12.58728	12.61579	12.51339	11.79407	11.25852	12.76203
	Min	10.60697	10.16222	10.98468	12.02184	11.85952	11.60000	10.33365	11.86358
	STD	1.14631	1.60401	1.42813	0.62935	1.03013	0.21560	0.65885	1.55167
	Ranking	7	5	3	2	4	6	8	1
3	Max	16.44011	14.27535	16.08140	16.89013	14.18813	15.13210	14.41440	15.73708
	Mean	15.19863	13.28605	14.43510	14.68456	13.49286	14.37895	12.22514	14.61015
	Min	14.28507	11.36665	12.18756	11.73528	12.53317	12.91041	11.02215	13.64585
	STD	1.11431	1.66251	2.01534	2.65668	0.85858	1.27194	0.56698	1.05506
	Ranking	1	7	4	2	6	5	8	3
4	Max	15.17656	17.95691	17.47235	17.16435	17.32833	16.30057	15.65854	17.94836
	Mean	14.00183	15.22041	16.87263	15.59121	16.52225	15.72838	14.25484	16.04748
	Min	13.30037	12.55354	15.90180	14.37544	16.09469	15.11861	13.95558	15.09213
	STD	1.02372	2.70236	0.84849	1.42839	0.69852	0.59188	0.47447	1.64622
	Ranking	8	6	1	5	2	4	7	3
5	Max	16.72622	16.42710	16.24110	17.90312	16.37420	16.30256	16.32254	18.67014
	Mean	15.54953	16.02096	15.54791	16.92259	15.84138	15.24571	15.22541	15.86760
	Min	14.49543	15.61807	14.88442	15.62385	15.34763	14.57955	14.02554	14.01993
	STD	1.12043	0.40452	0.67883	1.17248	0.51440	0.92557	0.65558	2.46778
	Ranking	5	2	6	1	4	7	8	3
6	Max	19.43582	20.61942	19.52344	20.43187	19.96838	18.86744	17.95101	20.03906
	Mean	18.38781	18.75391	17.85512	18.23439	18.71728	16.92716	16.25870	19.23425
	Min	16.37613	17.07040	14.78261	14.88956	17.44713	14.57855	15.33652	17.83410
	STD	1.74267	1.78149	2.66414	2.94391	1.26073	2.17340	1.25412	1.21708
	Ranking	4	2	6	5	3	7	8	1
Summation		25	22	20	15	19	29	39	11
Mean Rank		5	4.4	4	3	3.8	5.8	7.8	2.2
Final Ranking		6	5	4	2	3	7	8	1

Table 3. The SSIM results of the test case 1.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	0.269717	0.362146	0.380757	0.264672	0.454587	0.220516	0.374454	0.385465
	Mean	0.173575	0.223227	0.256072	0.231906	0.257714	0.1974	0.23555	0.277138
	Min	0.116657	0.019721	0.184588	0.204993	0.133367	0.1606	0.018985	0.122664
	STD	0.083731	0.180118	0.108367	0.030267	0.172455	0.032217	0.15415	0.137343
	Ranking	8	6	3	5	2	7	4	1
3	Max	0.417374	0.675072	0.673859	0.580374	0.631389	0.560641	0.64544	0.631938
	Mean	0.353685	0.44114	0.555818	0.511786	0.580212	0.504252	0.51445	0.588044
	Min	0.305838	0.217671	0.478485	0.417965	0.554552	0.438945	0.48554	0.53806
	STD	0.05743	0.22888	0.103854	0.084094	0.04432	0.061337	0.22252	0.047235
	Ranking	8	7	3	5	2	6	4	1
4	Max	0.417374	0.675072	0.631938	0.580374	0.631389	0.560641	0.58887	0.673859
	Mean	0.353685	0.44114	0.588044	0.511786	0.580212	0.504252	0.54414	0.555818
	Min	0.305838	0.217671	0.53806	0.417965	0.554552	0.438945	0.501141	0.478485
	STD	0.05743	0.22888	0.047235	0.084094	0.04432	0.061337	0.08885	0.103854
	Ranking	8	7	1	5	2	6	4	3
5	Max	0.577496	0.500592	0.535451	0.686032	0.685014	0.455519	0.55241	0.606479
	Mean	0.477899	0.461272	0.472833	0.604613	0.470727	0.406442	0.43525	0.483806
	Min	0.401935	0.390055	0.354047	0.545124	0.290476	0.317459	0.40125	0.387526
	STD	0.090135	0.061787	0.102922	0.072969	0.199459	0.077198	0.45452	0.111837
	Ranking	3	6	4	1	5	8	7	2
6	Max	0.716201	0.826943	0.751183	0.802334	0.768344	0.76727	0.59858	0.790498
	Mean	0.634075	0.674239	0.574338	0.641546	0.679048	0.575139	0.56555	0.736605
	Min	0.541354	0.522776	0.279256	0.394027	0.608891	0.388121	0.52555	0.669011
	STD	0.087904	0.152087	0.257223	0.217532	0.081431	0.189626	0.04414	0.061891
	Ranking	5	3	7	4	2	6	8	1
Summation		32	29	18	20	13	33	27	8
Mean Rank		6.4	5.8	3.6	4	2.6	6.6	5.4	1.6
Final Ranking		7	6	3	4	2	8	5	1

For threshold 2 in Table 3, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by PSO, SSA, DE, AOA, WOA, MPA, and finally, AO. In addition, for threshold 3, the proposed method obtained promising results, compared to other methods. DAOA obtained the first ranking, followed by PSO, SSA, DE, AOA, MPA, WOA, and AO. Overall, we can see that the proposed DAOA method obtained the first ranking, followed by PSO, AOA, SSA, DE, WOA, AO, and MPA. The obtained results in this table prove the ability of the proposed DAOA to solve the given problems effectively.

The PSNR and SSIM results of Test 2 are given in Table 4 and Table 5. The proposed DAOA achieved excellent results in almost all the test cases in terms of PSNR. For threshold 4, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by AO, MPA, AOA, SSA, DE, PSO, and finally, WOA. For threshold 5, the proposed method obtained promising results, compared to other methods. DAOA obtained the first rank, followed by AO, DE, PSO, WOA, AOA, SSA, and MPA. Overall, we can see that the proposed method obtained the first ranking, followed by AO, DE, SSA, PSO, MPA, WOA, and AOA. The achieved results in this table demonstrate the ability of the proposed DAOA to solve the given problems efficiently.

Table 4. The PSNR results of the test case 2.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	13.77491	12.63881	14.5297	10.51233	12.64124	13.99214	13.25145	13.27729
	Mean	11.98281	11.5817	12.11305	10.25692	11.54775	13.59189	12.2221	12.59842
	Min	10.73612	10.40495	10.15998	9.823369	10.95149	13.24731	12.01211	12.09539
	STD	1.591121	1.121728	2.221443	0.377446	0.948281	0.375522	0.25212	0.610259
	Ranking	5	6	4	8	7	1	3	2
3	Max	15.86388	16.44113	15.82975	14.47644	14.87275	14.35493	15.32521	16.8866
	Mean	14.94664	15.4703	15.49832	12.8352	13.88411	13.22512	14.14191	14.508
	Min	13.15776	14.64112	14.9623	11.6457	13.24925	11.88844	13.95478	12.02299
	STD	1.549381	0.908328	0.468519	1.468445	0.867645	1.24619	2.25141	2.433551
	Ranking	3	2	1	8	6	7	5	4
4	Max	16.53801	13.20085	17.12718	16.28012	17.27728	16.84103	16.5474	16.96062
	Mean	15.69685	12.29933	15.28839	15.53055	14.89734	15.66251	15.25145	16.84254
	Min	14.14842	11.1013	13.34897	14.77009	12.92993	14.78322	14.25114	16.71792
	STD	1.342654	1.080725	1.891116	0.755074	2.202842	1.06104	0.25496	0.121484
	Ranking	2	8	5	4	7	3	6	1
5	Max	17.94799	16.77612	16.58759	17.72468	17.66078	15.7246	18.25641	20.50293
	Mean	17.3332	16.14486	15.69308	15.81531	16.97316	15.13329	17.14954	17.45356
	Min	16.85601	15.47308	14.74147	12.33775	16.23477	14.29046	16.25415	15.26742
	STD	0.55884	0.652461	0.924385	3.016486	0.714359	0.749426	2.33365	2.722404
	Ranking	2	5	7	6	4	8	3	1
6	Max	18.41641	16.73333	17.63323	17.86417	16.98896	17.69201	17.54845	20.23421
	Mean	18.35135	16.26801	15.56212	16.33655	16.40105	15.7609	16.36652	19.55858
	Min	18.23814	15.46543	13.57085	14.13927	15.2753	12.90929	14.95854	18.29391
	STD	0.098406	0.697999	2.032367	1.950656	0.975254	2.52073	1.36945	1.096094
	Ranking	2	6	8	5	3	7	4	1
Summation		14	27	25	31	27	26	21	9
Mean Rank		2.80	5.40	5.00	6.20	5.40	5.20	4.20	1.80
Final Ranking		2	6	4	8	6	5	3	1

Table 5. The SSIM results of the test case 2.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	0.406268	0.372786	0.488313	0.098776	0.381066	0.416608	0.35652	0.388003
	Mean	0.247171	0.228951	0.26402	0.062589	0.260623	0.406156	0.32541	0.299891
	Min	0.055504	0.119071	0.090368	0.028341	0.156191	0.397245	0.32336	0.153948
	STD	0.177636	0.130221	0.203748	0.035257	0.113289	0.009773	0.45485	0.127294
	Ranking	6	7	4	8	5	1	2	3
3	Max	0.542502	0.591926	0.62208	0.469152	0.556273	0.429674	0.55241	0.577128
	Mean	0.48568	0.515704	0.385801	0.280354	0.407758	0.322274	0.51254	0.543097
	Min	0.382238	0.463366	0.116914	0.133011	0.319945	0.116597	0.46524	0.479899
	STD	0.089729	0.067526	0.254157	0.171862	0.12933	0.17818	0.51425	0.054785
	Ranking	4	2	6	8	5	7	3	1
4	Max	0.643506	0.372327	0.649426	0.569008	0.616709	0.630261	0.53652	0.609209
	Mean	0.540682	0.251443	0.515642	0.536243	0.469759	0.533684	0.51414	0.591323
	Min	0.343984	0.050187	0.373123	0.484871	0.345458	0.483908	0.46585	0.565499
	STD	0.170405	0.175466	0.138359	0.045049	0.137036	0.083651	0.25854	0.022911
	Ranking	2	8	5	3	7	4	6	1
5	Max	0.568273	0.535196	0.563217	0.613346	0.611966	0.810183	0.58475	0.647781
	Mean	0.53032	0.527867	0.529725	0.488084	0.578773	0.65271	0.54541	0.618783
	Min	0.455118	0.523047	0.467038	0.239554	0.556387	0.507866	0.51245	0.604212
	STD	0.065128	0.006451	0.054331	0.215235	0.029323	0.151553	0.25414	0.025113
	Ranking	5	7	6	8	3	1	4	2
6	Max	0.728985	0.589624	0.791703	0.692676	0.55024	0.64645	0.42541	0.666054
	Mean	0.688055	0.543363	0.751029	0.58507	0.505091	0.45092	0.42545	0.490001
	Min	0.658136	0.498046	0.689368	0.4474	0.427197	0.183286	0.40121	0.306101
	STD	0.036686	0.045797	0.054299	0.125371	0.067742	0.239853	0.15424	0.180105
	Ranking	2	4	1	3	5	7	8	6
Summation		19	28	22	30	25	20	23	13
Mean Rank		3.8	5.6	4.4	6	5	4	4.6	2.6
Final Ranking		2	7	4	8	6	3	5	1

For threshold 4 in Table 5, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by AO, AOA, MPA, SSA, DE, PSO, and finally, WOA. For threshold 3, the proposed method obtained promising results, compared to other methods. DAOA obtained the first ranking, followed by WOA, DE, AO, PSO, SSA, MPA, and AOA. Overall, we can see that the proposed DAOA method obtained the first ranking, followed by AO, MPA, SSA, DE, PSO, WOA, and AOA. The obtained results in this table confirm the performance of the proposed DAOA and its ability to solve the given problems efficiently.

The PSNR and SSIM results of Test 3 are given in Table 6 and Table 7. The proposed DAOA obtained new, promising results in almost all the test cases in terms of PSNR. For threshold 5, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by SSA, AO, PSO, AOA, MPA, and finally, DE. For threshold 6, the proposed method obtained promising results compared to other methods. DAOA obtained the first rank, followed by AO, PSO, DE, WOA, AOA, SSA, and MPA. Overall we can see that the proposed method obtained the first ranking, followed by WOA, DE, AO, AOA, MPA, PSO, and SSA. The achieved results in this table demonstrate the ability of the proposed DAOA to solve the given problems efficiently. As well, it is clear the proposed DAOA has this ability at different threshold levels.

Table 6. The PSNR results of the test case 3.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	16.43851	15.52329	16.17178	13.34026	10.70417	13.80156	11.25454	17.02237
	Mean	11.77337	13.62698	11.4258	10.90943	8.940243	11.97697	12.54562	13.0293
	Min	6.919499	10.52621	8.829951	8.362172	7.32234	10.25363	11.65856	10.1937
	STD	4.762311	2.707536	4.116175	2.491085	1.695636	1.776132	2.66525	3.558437
	Ranking	5	1	6	7	8	4	3	2
3	Max	16.32218	14.37629	19.8809	17.08167	18.01695	16.32078	17.54548	18.7061
	Mean	15.52933	13.1609	18.08332	15.15354	14.40812	12.59758	15.36525	14.62128
	Min	14.29581	11.73748	17.06783	12.61578	11.10578	8.576877	13.52541	11.41963
	STD	1.082679	1.331649	1.561118	2.294509	3.465768	3.880514	3.25414	3.722657
	Ranking	2	7	1	4	6	8	3	5
4	Max	17.09702	17.55333	17.6847	19.73127	19.45281	19.19681	18.56958	20.754
	Mean	16.23917	14.16665	16.1249	18.28651	15.02841	15.17751	16.52565	18.02446
	Min	14.73755	10.43243	13.88539	16.01418	9.874085	12.62804	15.96841	13.89724
	STD	1.30484	3.573146	1.988767	1.991944	4.830901	3.522425	2.59716	3.635777
	Ranking	4	8	5	1	7	6	3	2
5	Max	20.47295	20.08702	20.21561	19.42765	17.8608	20.6646	18.49371	20.41022
	Mean	17.9702	17.76647	18.04407	16.94888	17.74178	16.39606	16.46743	18.58232
	Min	15.06634	14.62097	15.09986	14.78632	17.57167	13.9744	15.45547	16.23457
	STD	2.725534	2.824863	2.643952	2.336768	0.151186	3.707817	2.65478	2.135811
	Ranking	3	4	2	6	5	8	7	1
6	Max	21.16341	21.39185	21.70955	20.93593	23.09058	19.19694	20.12154	21.98094
	Mean	19.12374	19.85058	16.84504	17.56936	16.8876	16.95177	18.15414	20.41186
	Min	16.5207	18.82027	12.89516	13.91389	12.51858	15.33711	16.36987	19.1292
	STD	2.372071	1.359806	4.477811	3.519921	5.519455	2.005675	1.64856	1.447282
	Ranking	3	2	8	5	7	6	4	1
Summation		17	22	22	23	33	32	20	11
Mean Rank		3.40	4.40	4.40	4.60	6.60	6.40	4.00	2.20
Final Ranking		2	4	4	6	8	7	3	1

Table 7. The SSIM results of the test case 3.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	0.810797	0.784223	0.737701	0.807984	0.729805	0.784964	0.74548	0.810173
	Mean	0.701346	0.726586	0.679275	0.652562	0.652503	0.748363	0.71254	0.777743
	Min	0.51097	0.614391	0.642633	0.512459	0.544859	0.707409	0.69584	0.738525
	STD	0.165486	0.097176	0.051142	0.148357	0.096133	0.03896	0.02514	0.036303
	Ranking	5	3	6	7	8	2	4	1
3	Max	0.858715	0.84955	0.879072	0.869936	0.846474	0.810939	0.801454	0.862403
	Mean	0.829113	0.82117	0.846587	0.810768	0.803586	0.714867	0.74125	0.826664
	Min	0.794989	0.799088	0.811991	0.7567	0.72253	0.656383	0.70215	0.798218
	STD	0.032103	0.025814	0.033591	0.05679	0.070237	0.083855	0.02193	0.032708
	Ranking	2	4	1	5	6	8	7	3
4	Max	0.835799	0.786265	0.889158	0.89639	0.831634	0.877477	0.81256	0.842558
	Mean	0.816523	0.765247	0.835175	0.863757	0.802387	0.856942	0.76585	0.820005
	Min	0.780192	0.748503	0.782824	0.807497	0.751995	0.824078	0.71369	0.776304
	STD	0.031483	0.019241	0.053186	0.04893	0.043828	0.028755	0.21454	0.037853
	Ranking	5	8	3	1	6	2	7	4
5	Max	0.869899	0.862851	0.864441	0.895398	0.889066	0.86625	0.85645	0.901137
	Mean	0.846835	0.858303	0.821075	0.863123	0.872182	0.862527	0.81021	0.874055
	Min	0.830022	0.850494	0.788281	0.836486	0.854754	0.856039	0.75645	0.837004
	STD	0.02066	0.006793	0.039165	0.029858	0.017162	0.005639	0.021114	0.033208
	Ranking	6	5	7	3	2	4	8	1
6	Max	0.897095	0.882473	0.910729	0.920257	0.898452	0.884757	0.84145	0.890175
	Mean	0.893914	0.868849	0.869001	0.850437	0.825776	0.87171	0.79568	0.874336
	Min	0.892161	0.848929	0.845306	0.787637	0.758887	0.848342	0.76582	0.855048
	STD	0.002759	0.017636	0.036248	0.066588	0.069962	0.020283	0.029447	0.017816
	Ranking	1	5	4	6	7	3	8	2
Summation		19	25	21	22	29	19	34	11
Mean Rank		3.8	5	4.2	4.4	5.8	3.8	6.8	2.2
Final Ranking		2	6	4	5	7	2	8	1

For threshold 2 in Table 7, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by MPA, WOA, DE, AO, SSA, AOA, and finally, PSO. For threshold 5, the proposed method obtained promising results compared to other methods. DAOA obtained the first ranking, followed by PSO, AOA, MPA, WOA, AO, PSO, and DE. Overall, we can see that the proposed DAOA method obtained the first ranking, followed by MPA, AO, SSA, AOA, WOA, PSO, and DE. The obtained results in this table confirm the performance of the proposed DAOA and its ability to solve the given problems efficiently. The following results prove and support that the proposed algorithm’s ability to solve such problems is strong and that it is capable of finding robust solutions in this field.

The PSNR and SSIM results of Test 4 are given in Table 8 and Table 9. The proposed DAOA obtained new promising results in almost all the test cases in terms of PSNR, as shown in Table 8. The proposed DAOA obtained the best results for two threshold values (i.e., 3 and 4 levels). For threshold 3, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by PSO, SSA, WOA, AOA, MPA, DE, and finally, AO. For threshold 4, the proposed method obtained promising results, compared to other methods. DAOA obtained the first rank, followed by WOA, SSA, AOA, MPA, AO, DE, and AOA. Overall, we can see that the proposed method obtained the first ranking, followed by WOA, PSO, SSA, MPA, AO, AOA, and DE. The achieved results in this table demonstrate the ability of the proposed DAOA to solve the given problems efficiently. As well, it is clear the proposed DAOA has this ability at different threshold levels.

Table 8. The PSNR results of the test case 4.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	0.810797	0.784223	0.737701	0.807984	0.729805	0.784964	0.74548	0.810173
	Mean	0.701346	0.726586	0.679275	0.652562	0.652503	0.748363	0.71254	0.777743
	Min	0.51097	0.614391	0.642633	0.512459	0.544859	0.707409	0.69584	0.738525
	STD	0.165486	0.097176	0.051142	0.148357	0.096133	0.03896	0.02514	0.036303
	Ranking	5	3	6	7	8	2	4	1
3	Max	0.858715	0.84955	0.879072	0.869936	0.846474	0.810939	0.801454	0.862403
	Mean	0.829113	0.82117	0.846587	0.810768	0.803586	0.714867	0.74125	0.826664
	Min	0.794989	0.799088	0.811991	0.7567	0.72253	0.656383	0.70215	0.798218
	STD	0.032103	0.025814	0.033591	0.05679	0.070237	0.083855	0.02193	0.032708
	Ranking	2	4	1	5	6	8	7	3
4	Max	0.835799	0.786265	0.889158	0.89639	0.831634	0.877477	0.81256	0.842558
	Mean	0.816523	0.765247	0.835175	0.863757	0.802387	0.856942	0.76585	0.820005
	Min	0.780192	0.748503	0.782824	0.807497	0.751995	0.824078	0.71369	0.776304
	STD	0.031483	0.019241	0.053186	0.04893	0.043828	0.028755	0.21454	0.037853
	Ranking	5	8	3	1	6	2	7	4
5	Max	0.869899	0.862851	0.864441	0.895398	0.889066	0.86625	0.85645	0.901137
	Mean	0.846835	0.858303	0.821075	0.863123	0.872182	0.862527	0.81021	0.874055
	Min	0.830022	0.850494	0.788281	0.836486	0.854754	0.856039	0.75645	0.837004
	STD	0.02066	0.006793	0.039165	0.029858	0.017162	0.005639	0.021114	0.033208
	Ranking	6	5	7	3	2	4	8	1
6	Max	0.897095	0.882473	0.910729	0.920257	0.898452	0.884757	0.84145	0.890175
	Mean	0.893914	0.868849	0.869001	0.850437	0.825776	0.87171	0.79568	0.874336
	Min	0.892161	0.848929	0.845306	0.787637	0.758887	0.848342	0.76582	0.855048
	STD	0.002759	0.017636	0.036248	0.066588	0.069962	0.020283	0.029447	0.017816
	Ranking	1	5	4	6	7	3	8	2
Summation		19	25	21	22	29	19	34	11
Mean Rank		3.8	5	4.2	4.4	5.8	3.8	6.8	2.2
Final Ranking		2	6	4	5	7	2	8	1

Table 9. The SSIM results of the test case 4.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	0.513176	0.446739	0.469347	0.303735	0.468033	0.472675	0.465855	0.493285
	Mean	0.420537	0.411645	0.379839	0.268241	0.395591	0.407972	0.432165	0.450537
	Min	0.297393	0.34853	0.312674	0.238732	0.353913	0.285825	0.415441	0.390067
	STD	0.111078	0.054773	0.080691	0.032912	0.062974	0.105845	0.065135	0.053842
	Ranking	3	4	7	8	6	5	2	1
3	Max	0.639969	0.518822	0.570567	0.642874	0.550295	0.516935	0.541685	0.638931
	Mean	0.539264	0.496794	0.476032	0.559045	0.522348	0.480253	0.451684	0.565094
	Min	0.483693	0.453509	0.406394	0.442666	0.507116	0.421783	0.401513	0.427189
	STD	0.087369	0.037488	0.084871	0.103997	0.024235	0.051181	0.165152	0.119529
	Ranking	3	5	7	2	4	6	8	1
4	Max	0.635584	0.520955	0.647437	0.629088	0.583309	0.567589	0.545438	0.59171
	Mean	0.558847	0.495081	0.624364	0.52697	0.542197	0.540923	0.484153	0.566602
	Min	0.496035	0.475477	0.612318	0.455541	0.49695	0.494102	0.351535	0.530519
	STD	0.070809	0.023378	0.019989	0.090753	0.043328	0.040678	0.91351	0.032038
	Ranking	3	7	1	6	4	5	8	2
5	Max	0.625459	0.722689	0.626088	0.678775	0.695846	0.682412	0.646849	0.752727
	Mean	0.574159	0.65505	0.608905	0.623735	0.681637	0.593452	0.568435	0.654905
	Min	0.544652	0.576303	0.589048	0.563386	0.661464	0.468945	0.515464	0.571449
	STD	0.044594	0.073823	0.018664	0.057878	0.01795	0.111084	0.51354	0.091489
	Ranking	7	2	5	4	1	6	8	3
6	Max	0.678699	0.761036	0.655062	0.693875	0.74922	0.721603	0.711543	0.765842
	Mean	0.655502	0.652531	0.558392	0.577277	0.735573	0.627711	0.658435	0.721667
	Min	0.613377	0.518519	0.460651	0.501179	0.727322	0.503922	0.615534	0.656329
	STD	0.036543	0.123255	0.09721	0.102534	0.011905	0.111878	0.153112	0.057742
	Ranking	4	5	8	7	1	6	3	2
Summation		20	23	28	27	16	28	29	9
Mean Rank		4	4.6	5.6	5.4	3.2	5.6	5.8	1.8
Final Ranking		3	4	6	5	2	6	8	1

Table 9 shows that the proposed DAOA method obtained better results in almost all the test cases in terms of SSIM for Test 4. The proposed DAOA obtained the best results for two threshold values (i.e., 2 and 3 levels). For threshold 2, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by DE, AOA, WOA, MPA, PSO, SSA, and finally, AOA. For threshold 3, the proposed method obtained promising results, compared to other methods. DAOA obtained the first ranking, followed by AOA, AO, PSO, WOA, MPA, SSA, and DE. Overall, we can see that the proposed DAOA method obtained the first ranking, followed by PSO, AO, WOA, AOA, MPA, SSA, and DE. The obtained results in this table confirm the performance of the proposed DAOA to solve the given problems efficiently. The following results prove and support that the proposed algorithm’s ability to solve such problems is strong and that it is capable of finding robust solutions in this field.

In Table 10 and Table 11, the PSNR and SSIM results of Test 5 are shown. As shown in Table 10, the proposed DAOA yielded new promising PSNR results in almost all test cases. For two threshold values, the proposed DAOA gave the best results (i.e., 2 and 5 levels). For threshold 2, the proposed DAOA produced the best results, placing it first among all other comparative methods, ahead of SSA, AOA, MPA, DE, AO, WOA, and PSO. In addition, when compared to other methods, the proposed method produced positive results for threshold 5. DAOA came first, followed by AOA, MPA, AO, WOA, PSO, and DE. Overall, we can see that DAOA came first, followed by SSA, DE, AO, AOA, PSO, MPA, and WOA. The obtained results in this table demonstrate the proposed DAOA’s ability to solve the given problems efficiently. Furthermore, it is evident that the proposed DAOA has the potential to operate at various threshold levels.

Table 10. The PSNR results of the test case 5.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	15.93985	14.4854	15.99861	17.14705	15.0977	16.05831	16.55749	17.53916
	Mean	14.10613	13.00072	15.294	14.79149	12.72877	14.46087	14.35989	15.82038
	Min	12.39387	11.27298	14.72307	11.8401	11.51447	13.62663	11.9752	13.42614
	STD	1.776107	1.619943	0.648191	2.703178	2.051771	1.383874	2.296871	2.138085
	Ranking	6	7	2	3	8	4	5	1
3	Max	19.40981	18.86115	17.48266	16.55749	17.95279	17.69139	19.44663	19.93627
	Mean	18.72279	17.28213	16.52113	14.35989	16.27857	17.1941	19.26877	18.13099
	Min	18.29158	15.95137	15.92209	11.9752	14.07194	16.51551	19.01602	15.35808
	STD	0.60141	1.470694	0.841066	2.296871	1.994456	0.608547	0.224857	2.437657
	Ranking	2	4	6	8	7	5	1	3
4	Max	18.13386	19.1223	18.90861	17.45745	19.1043	18.23407	18.83735	18.38066
	Mean	16.94739	16.40329	17.94929	15.50893	18.1176	16.67171	17.28304	17.01377
	Min	15.98498	14.81291	16.68311	13.37735	16.4206	14.93103	15.51976	15.35199
	STD	1.091819	2.366025	1.14404	2.046204	1.476127	1.658724	1.494198	1.535719
	Ranking	5	7	2	8	1	6	3	4
5	Max	20.21398	20.02404	21.27214	20.18245	18.91496	20.6886	20.25546	21.56663
	Mean	18.99103	18.67004	20.53727	20.04683	18.26845	19.69356	18.05347	20.9167
	Min	17.36811	17.86499	19.6089	19.85296	17.79804	18.97903	17.51354	20.14592
	STD	1.464489	1.179571	0.848332	0.172297	0.578907	0.888634	0.15434	0.718025
	Ranking	5	6	2	3	7	4	8	1
6	Max	21.09476	21.57137	21.3434	22.18733	23.89824	19.44663	21.54999	22.99988
	Mean	20.41811	20.42529	20.47827	21.60813	22.10233	19.26877	20.25987	21.55413
	Min	19.49805	19.07294	19.90813	21.16347	21.02315	19.01602	19.64856	19.98576
	STD	0.825716	1.261926	0.761747	0.525019	1.565831	0.224857	0.16655	1.510799
	Ranking	6	5	4	2	1	8	7	3
Summation		24	29	16	24	24	27	24	12
Mean Rank		4.80	5.80	3.20	4.80	4.80	5.40	4.80	2.40
Final Ranking		3	8	2	3	3	7	3	1

Table 11. The SSIM results of the test case 5.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	0.670559	0.663185	0.670191	0.656707	0.638999	0.641328	0.625454	0.652777
	Mean	0.615808	0.577209	0.627177	0.602737	0.588212	0.607857	0.58944	0.638984
	Min	0.554493	0.497657	0.570064	0.537508	0.547586	0.575353	0.523565	0.622532
	STD	0.058311	0.082951	0.051531	0.060392	0.046546	0.032998	0.051351	0.015297
	Ranking	3	8	2	5	7	4	6	1
3	Max	0.728918	0.677149	0.714839	0.663648	0.667938	0.717054	0.646841	0.704409
	Mean	0.719125	0.660935	0.666536	0.59634	0.629253	0.664745	0.551844	0.671047
	Min	0.712656	0.629315	0.6219	0.510537	0.576046	0.622826	0.493545	0.639151
	STD	0.008626	0.027387	0.046578	0.078213	0.047636	0.047965	0.050315	0.032654
	Ranking	1	5	3	7	6	4	8	2
4	Max	0.748435	0.70822	0.687422	0.729796	0.706817	0.729298	0.715434	0.720751
	Mean	0.676713	0.668007	0.675521	0.661629	0.681985	0.674847	0.698434	0.678177
	Min	0.633531	0.627958	0.660419	0.590072	0.636336	0.601496	0.651354	0.614625
	STD	0.062543	0.040131	0.013783	0.069924	0.039584	0.065964	0.05134	0.056087
	Ranking	4	7	5	8	2	6	1	3
5	Max	0.760316	0.744595	0.760228	0.722269	0.701088	0.713294	0.715469	0.754593
	Mean	0.735256	0.721088	0.707533	0.706524	0.686357	0.694403	0.694685	0.740905
	Min	0.719429	0.693768	0.680723	0.680577	0.665994	0.665244	0.645135	0.720782
	STD	0.021952	0.025627	0.045637	0.022641	0.018212	0.025618	0.100351	0.0178
	Ranking	2	3	4	5	8	7	6	1
6	Max	0.778606	0.802338	0.787056	0.759268	0.775117	0.754872	0.714354	0.759996
	Mean	0.745632	0.767851	0.728188	0.743422	0.760561	0.715035	0.69456	0.757846
	Min	0.717157	0.728973	0.685219	0.730438	0.737718	0.682379	0.646758	0.755781
	STD	0.030971	0.036879	0.052747	0.014627	0.02003	0.036776	0.14353	0.002109
	Ranking	4	1	6	5	2	7	8	3
Summation		14	24	20	30	25	28	29	10
Mean Rank		2.8	4.8	4	6	5	5.6	5.8	2
Final Ranking		2	4	3	8	5	6	7	1

In terms of SSIM for Test 5, Table 11 shows that the proposed DAOA system obtained better results in almost all test cases. For two threshold values, the proposed DAOA produced the best results (i.e., 2 and 5 levels). For threshold 2, the proposed DAOA received the best results, placing it first among SSA, AO, MPA, AOA, DE, PSO, and WOA. In addition, when compared to other methods, the proposed method produced positive results for threshold 5. The first-place winner was DAOA, followed by AO, WOA, SSA, AOA, DE, MPA, and PSO. Overall, we can see that the proposed DAOA method obtained the first ranking, followed by AO, SSA, WOA, PSO, MPA, DE, and AOA. The obtained results in this table confirm the performance of the proposed DAOA and its ability to solve the given problems efficiently. The following results prove and support that the proposed algorithm’s ability to solve such problems is strong and that it is capable of finding robust solutions in this field.

In Table 12 and Table 13, the PSNR and SSIM results of Test 6 are shown. As shown in Table 12, the proposed DAOA yielded new promising PSNR results in nearly all test cases. For two threshold values, the proposed DAOA gave the best results (i.e., 5 and 6 levels). For threshold 5, the DE produced the best results, placing it first among all other comparative approaches, ahead of DAOA, SSA, PSO, AOA, WOA, MPA, and AO. In addition, when compared to other methods, the proposed method produced positive results for threshold 6. DAOAO came first, followed by SSA, WOA, AOA, MPA, DE, AO, and PSO. Overall, we can see that DAOA came first, followed by AOA, DE, PSO, SSA, WOA, AO, and MPA. The obtained results in this table demonstrate the proposed DAOA’s ability to solve the given problems efficiently. Furthermore, it is evident that the proposed DAOA has the potential to operate at various threshold levels.

Table 12. The PSNR results of the test case 6.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	14.29003	14.99666	13.23076	14.2586	13.67276	13.88699	13.25669	13.62076
	Mean	12.13124	13.5679	12.00795	13.53452	12.69334	12.56354	12.76658	12.88169
	Min	11.02309	10.86625	10.71159	13.00777	11.90018	10.75974	11.81577	11.91395
	STD	1.86979	2.340995	1.261197	0.648342	0.900847	1.618015	0.727573	0.876084
	Ranking	7	1	8	2	5	6	4	3
3	Max	17.13609	13.26265	15.86297	16.70329	16.39937	16.77276	15.56435	16.70329
	Mean	14.80299	12.70421	14.27818	14.73781	15.54628	15.68245	14.56435	14.73781
	Min	11.88525	11.81721	13.19349	13.30319	14.95156	13.81152	13.54531	13.30319
	STD	2.673792	0.776716	1.40325	1.761111	0.757696	1.627652	0.35531	1.761111
	Ranking	3	8	7	4	2	1	6	4
4	Max	19.72094	16.65405	18.53668	18.36352	18.18219	16.8171	16.16153	17.29736
	Mean	17.42215	15.6372	16.4182	17.40203	16.17031	14.66404	15.61533	16.81609
	Min	14.47883	14.30732	14.08529	16.52227	14.97604	13.31745	14.65844	15.89593
	STD	2.679828	1.204274	2.233427	0.923342	1.752483	1.884058	0.513153	0.797164
	Ranking	1	6	4	2	5	8	7	3
5	Max	19.95971	18.41277	19.46272	20.77475	19.71927	18.09801	20.15615	21.7643
	Mean	16.21653	17.16753	18.12133	17.29533	17.30211	16.23449	19.56652	18.92589
	Min	12.15348	16.07533	17.44474	14.33996	15.60841	15.08771	18.91434	16.95589
	STD	3.912932	1.176211	1.161691	3.249246	2.148801	1.628114	0.44345	2.519088
	Ranking	8	6	3	5	4	7	1	2
6	Max	19.70338	18.99666	19.15752	19.97796	17.4372	20.54731	20.48618	21.16495
	Mean	17.55594	18.51687	18.95646	18.38941	16.73036	17.68373	17.67164	19.65434
	Min	14.92323	17.6852	18.62038	17.45989	16.33641	15.14494	14.56169	17.72153
	STD	2.426738	0.723084	0.292923	1.382353	0.613485	2.715789	3.51355	1.760107
	Ranking	7	3	2	4	8	5	6	1
Summation		26	24	24	17	24	27	24	13
Mean Rank		5.20	4.80	4.80	3.40	4.80	5.40	4.80	2.60
Final Ranking		7	3	3	2	3	8	3	1

Table 13. The SSIM results of the test case 6.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	0.585171	0.575848	0.507334	0.584204	0.554758	0.583274	0.545458	0.566448
	Mean	0.529789	0.511152	0.47466	0.558141	0.510173	0.517028	0.53251	0.551596
	Min	0.451429	0.421518	0.440468	0.528648	0.468501	0.418339	0.510512	0.540869
	STD	0.069769	0.08013	0.033459	0.027936	0.043202	0.087123	0.051651	0.013279
	Ranking	4	6	8	1	7	5	3	2
3	Max	0.633602	0.566445	0.593976	0.643107	0.624665	0.587316	0.584547	0.620738
	Mean	0.573218	0.53021	0.539426	0.586845	0.561226	0.554322	0.52548	0.6091
	Min	0.531603	0.476157	0.445784	0.557298	0.51424	0.500738	0.49522	0.590855
	STD	0.053527	0.047709	0.081464	0.048745	0.057022	0.046817	0.15479	0.015999
	Ranking	3	7	6	2	4	5	8	1
4	Max	0.625898	0.599759	0.688634	0.647084	0.588007	0.619283	0.60147	0.651858
	Mean	0.620455	0.584845	0.631581	0.584162	0.561247	0.577285	0.564549	0.631427
	Min	0.616739	0.561825	0.576099	0.541342	0.520971	0.552471	0.514625	0.594978
	STD	0.004818	0.020224	0.056284	0.055664	0.035503	0.036571	0.51556	0.031643
	Ranking	3	4	1	5	8	6	7	2
5	Max	0.639309	0.611599	0.670374	0.706368	0.662426	0.621919	0.61444	0.688438
	Mean	0.580397	0.593407	0.626018	0.659053	0.615559	0.601187	0.53255	0.657403
	Min	0.481486	0.57193	0.58953	0.596054	0.552583	0.585043	0.50144	0.634943
	STD	0.086179	0.020038	0.040992	0.056805	0.056666	0.018861	0.254516	0.027759
	Ranking	7	6	3	1	4	5	8	2
6	Max	0.732761	0.721116	0.702031	0.639447	0.669456	0.741237	0.62156	0.670238
	Mean	0.617062	0.675843	0.66037	0.614623	0.623098	0.698053	0.60156	0.621129
	Min	0.500442	0.628145	0.615404	0.582216	0.593419	0.632455	0.581685	0.555772
	STD	0.116162	0.046533	0.043408	0.029359	0.04067	0.057751	0.051617	0.058938
	Ranking	6	2	3	7	4	1	8	5
Summation		23	25	21	16	27	22	34	12
Mean Rank		4.6	5	4.2	3.2	5.4	4.4	6.8	2.4
Final Ranking		5	6	3	2	7	4	8	1

In terms of SSIM for Test 6, Table 13 shows that the proposed DAOA method obtained better results in almost all test cases. For one threshold value, the proposed DAOA produced the best results (i.e., three levels). For threshold 3, the proposed DAOA received the best results, placing it first, followed by AOA, AO, PSO, MPA, SSA, WOA, and DE. Overall, we can see that the proposed DAOA method obtained the first ranking, followed by AOA, SSA, MPA, AO, WOA, PSO, and DE. The obtained results in this table confirm the performance of the proposed DAOA to solve the given problems efficiently. The following results prove and support that the proposed algorithm’s ability to solve such problems is strong and that it is capable of finding robust solutions in this field.

The PSNR and SSIM results of Test 7 are given in Table 14 and Table 15. The proposed DAOA obtained new promising results in almost all the test cases in terms of PSNR, as shown in Table 14. The proposed DAOA obtained the best results for three threshold values (i.e., 3, 4, and 6 levels). For threshold 3, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by PSO, WOA, MPA, PSO, SSA, AOA, and finally, DE. For threshold 6, the proposed method obtained promising results, compared to other methods. DAOA obtained the first rank, followed by MPA, AO, AOA, SSA, PSO, DE, and WOA. Overall, we can see that the proposed method obtained the first ranking, followed by MPA, AO, AOA, SSA, PSO, WOA, and DE. The achieved results in this table demonstrate the ability of the proposed DAOA to solve the given problems efficiently. Furthermore, it is obvious that the proposed DAOA has the potential to operate at various threshold levels.

Table 14. The PSNR results of the test case 7.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	13.20515	14.81541	13.46643	15.49531	15.62603	15.20099	10.56165	11.17017
	Mean	12.41868	11.78621	13.27459	12.55658	13.52688	13.84887	8.68468	9.014158
	Min	11.32961	9.315363	13.00626	9.442963	9.675792	12.68271	7.51654	6.574355
	STD	0.973697	2.792211	0.239434	3.029961	3.339657	1.269397	2.26558	2.311011
	Ranking	5	6	3	4	2	1	8	7
3	Max	16.56695	17.57886	16.2908	16.58067	16.53626	15.88719	16.98971	18.01761
	Mean	15.69994	15.46688	14.50615	14.19241	14.84154	15.17141	14.15556	16.2308
	Min	15.1533	14.25297	13.45161	10.44799	12.24822	14.03169	10.44162	13.04052
	STD	0.759328	1.835835	1.554045	3.283571	2.280885	0.997755	3.255033	2.769505
	Ranking	2	3	6	7	5	4	8	1
4	Max	16.90963	17.97752	17.78105	17.43689	16.94918	19.34317	17.45543	19.60255
	Mean	15.08816	14.69292	16.45214	14.2211	12.8884	16.99385	14.22669	17.64468
	Min	11.44578	11.37666	14.68077	11.04897	8.255611	13.29746	11.4265	16.42001
	STD	3.154397	3.300544	1.596797	3.194184	4.374921	3.240157	3.143737	1.71328
	Ranking	4	5	3	7	8	2	6	1
5	Max	19.95651	19.11383	17.60007	20.11243	19.91776	20.2333	19.11482	20.05669
	Mean	17.89666	15.96258	16.58689	18.8553	17.88667	18.66736	15.96018	18.17262
	Min	16.75255	10.41909	15.4047	16.91343	15.05058	17.34947	10.42944	16.15425
	STD	1.78753	4.815784	1.1074	1.705889	2.531472	1.457831	4.39728	1.954685
	Ranking	4	7	6	1	5	2	8	3
6	Max	21.4354	20.29606	21.05977	22.61835	20.03635	21.47684	20.24338	21.70695
	Mean	19.4399	17.25886	19.58102	19.89625	19.37838	18.84269	17.35445	20.29721
	Min	17.7851	14.28299	17.61442	17.48669	18.99359	15.24118	14.23249	19.17387
	STD	1.848842	3.007007	1.773725	2.580068	0.572543	3.22842	3.234234	1.290597
	Ranking	4	8	3	2	5	6	7	1
Summation		19	29	21	21	25	15	37	13
Mean Rank		3.80	5.80	4.20	4.20	5.00	3.00	7.40	2.60
Final Ranking		3	7	4	4	6	2	8	1

Table 15. The SSIM results of the test case 7.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	0.73278	0.712288	0.560122	0.72505	0.733305	0.723576	0.564865	0.730313
	Mean	0.643606	0.617796	0.485729	0.645712	0.676013	0.683473	0.448642	0.710998
	Min	0.567798	0.478926	0.34029	0.519034	0.567055	0.639678	0.348649	0.691961
	STD	0.0833	0.122848	0.125965	0.110867	0.094402	0.042071	0.184476	0.019178
	Ranking	5	6	7	4	3	2	8	1
3	Max	0.773342	0.738051	0.693211	0.729915	0.747102	0.706363	0.694864	0.760805
	Mean	0.770604	0.721144	0.67817	0.65064	0.677895	0.700246	0.676463	0.725786
	Min	0.768211	0.698601	0.665159	0.495505	0.593947	0.693075	0.666456	0.672091
	STD	0.002582	0.02032	0.014136	0.134362	0.077634	0.006707	0.017743	0.047213
	Ranking	1	3	5	8	6	4	7	2
4	Max	0.742182	0.74847	0.727827	0.732508	0.782284	0.746116	0.728807	0.790683
	Mean	0.687277	0.664643	0.701216	0.669205	0.739291	0.579421	0.652713	0.763686
	Min	0.610196	0.549827	0.659058	0.632616	0.701494	0.394956	0.62996	0.719773
	STD	0.068731	0.102883	0.036927	0.055044	0.040645	0.176253	0.050762	0.038362
	Ranking	4	6	3	5	2	8	7	1
5	Max	0.79007	0.805645	0.822652	0.819285	0.748588	0.740407	0.791501	0.798539
	Mean	0.76336	0.699754	0.772285	0.780482	0.714524	0.728473	0.774441	0.775382
	Min	0.733348	0.508825	0.736218	0.751391	0.65435	0.707817	0.732424	0.760992
	STD	0.028505	0.165678	0.044956	0.034973	0.052264	0.01796	0.036023	0.020251
	Ranking	5	8	4	1	7	6	3	2
6	Max	0.767482	0.807074	0.769107	0.784627	0.803515	0.797439	0.762609	0.800054
	Mean	0.748283	0.77661	0.748259	0.768866	0.791177	0.766987	0.745271	0.762369
	Min	0.713817	0.723776	0.710988	0.751543	0.768949	0.742903	0.718795	0.741915
	STD	0.029913	0.045934	0.032353	0.016597	0.019288	0.02782	0.030372	0.032675
	Ranking	6	2	7	3	1	4	8	5
Summation		21	25	26	21	19	24	33	11
Mean Rank		4.2	5	5.2	4.2	3.8	4.8	6.6	2.2
Final Ranking		3	6	7	3	2	5	8	1

Table 15 shows that the proposed DAOA method obtained better results in almost all the test cases in terms of SSIM for Test 7. The proposed DAOA obtained the best results for two threshold values (i.e., 2 and 4 levels). For threshold 2, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by MPA, PSO, AOA, AO, WOA, SSA, and finally, DE. For threshold 4, the proposed method obtained promising results compared to other methods. DAOA obtained the first ranking, followed by PSO, SSA, AO, AOA, WOA, DE, and MPA. Overall, we can see that the proposed DAOA method obtained the first ranking, followed by PSO, AOA, AO, MPA, WOA, SSA, and DE. The obtained results in this table confirm the performance of the proposed DAOA to solve the given problems efficiently. The presented results demonstrate and declare the proposed algorithm’s ability to solve such problems and find reliable solutions in this area.

The PSNR and SSIM results of Test 8 are given in Table 16 and Table 17. The proposed DAOA obtained got new promising results in almost all the test cases in terms of PSNR, as shown in Table 16. The proposed DAOA obtained the best results for four threshold values (i.e., 2, 3, 4, and 5 levels). For threshold 2, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by DE, AOA, PSO, SSA, AO, MPA, and finally, WOA. For threshold 5, the proposed method obtained promising results, compared to other methods. DAOA obtained the first rank, followed by AO, DE, PSO, WOA, AOA, MPA, and SSA. Overall, we can see that the proposed method obtained the first ranking, followed by AO, AOA, PSO, DE, WOA, MPA, and SSA. The achieved results in this table demonstrate the ability of the proposed DAOA to solve the given problems efficiently. Furthermore, it is obvious that the proposed DAOA has the potential to operate at various threshold levels.

Table 16. The PSNR results of the test case 8.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	13.33503	12.70418	13.72589	13.87541	15.0179	13.22514	13.93463	14.2634
	Mean	11.87001	11.35382	11.90455	12.30024	12.0788	11.78679	11.15836	13.26591
	Min	9.627695	9.504035	10.85728	11.2966	9.738495	9.930564	10.85364	11.58005
	STD	1.972111	1.657497	1.583232	1.381142	2.690154	1.686571	1.547691	1.468158
	Ranking	5	7	4	2	3	6	8	1
3	Max	17.28625	16.57081	13.49278	14.92705	17.54352	15.13415	16.09049	16.35347
	Mean	14.74539	15.01544	12.50533	14.48463	14.21932	14.43299	15.04035	15.21107
	Min	9.822409	12.05905	11.30417	14.18863	12.3542	13.62575	12.05713	13.80324
	STD	4.264167	2.561471	1.109849	0.390375	2.885987	0.759773	2.554852	1.295669
	Ranking	4	3	8	5	7	6	2	1
4	Max	17.00622	17.0363	16.18631	17.26998	15.66957	17.89161	15.60819	18.921
	Mean	14.98358	12.94104	14.49141	15.41649	13.31057	14.87131	13.39887	15.69837
	Min	13.05113	8.268197	13.05194	13.97806	8.738069	11.04877	8.879347	13.14273
	STD	1.979087	4.412494	1.582717	1.684754	3.96057	3.491248	3.703273	2.946311
	Ranking	3	8	5	2	7	4	6	1
5	Max	19.33652	17.74905	19.68408	19.66732	20.9309	17.50957	17.83407	19.59432
	Mean	17.51972	16.46752	14.99745	15.68612	17.03271	15.38835	17.15497	17.61533
	Min	16.56115	14.43826	9.169088	8.179696	14.13458	12.63953	15.98558	15.74747
	STD	1.574189	1.777538	5.349667	6.504749	3.506793	2.494939	1.29808	1.925829
	Ranking	2	5	8	6	4	7	3	1
6	Max	22.35209	17.96208	20.45875	19.73508	19.56292	19.22911	19.91049	21.32792
	Mean	19.18047	17.28236	15.36816	17.47522	17.49288	16.85966	15.75105	18.93027
	Min	14.9198	15.96895	12.60476	14.82897	13.72243	12.6153	8.963192	16.39383
	STD	3.833964	1.137678	4.413974	2.475771	3.270534	3.684026	6.585767	2.46997
	Ranking	1	5	8	4	3	6	7	2
Summation		15	28	33	19	24	29	26	6
Mean Rank		3.00	5.60	6.60	3.80	4.80	5.80	5.20	1.20
Final Ranking		2	6	8	3	4	7	5	1
p-value		2.254 × 10${}^{-3}$	3.455 × 10${}^{-2}$	4.254 × 10${}^{-2}$	2.368 × 10${}^{-2}$	6.589 × 10${}^{-2}$	4.554 × 10${}^{-2}$	3.887 × 10${}^{-2}$	NaN
Wilcoxon sign		1	1	1	1	1	1	1	NaN

Table 17. The SSIM results of the test case 8.

Threshold	Metric	Comparative Methods
		AO	WOA	SSA	AOA	PSO	MPA	DE	DAOA
2	Max	0.576023	0.454896	0.60648	0.629978	0.625702	0.567363	0.699381	0.633192
	Mean	0.448062	0.416027	0.47257	0.542842	0.482223	0.501881	0.444351	0.525409
	Min	0.313677	0.343605	0.371043	0.424905	0.33731	0.400359	0.354733	0.383819
	STD	0.131291	0.062776	0.121013	0.10595	0.144201	0.089145	0.142674	0.128078
	Ranking	6	8	5	1	4	3	7	2
3	Max	0.62594	0.649127	0.606039	0.621	0.673756	0.482675	0.653015	0.670905
	Mean	0.521445	0.5597	0.577973	0.59104	0.509775	0.443829	0.570487	0.644174
	Min	0.328192	0.41791	0.533724	0.562574	0.411628	0.394558	0.52212	0.615842
	STD	0.167546	0.124184	0.038779	0.029241	0.142927	0.044974	0.020342	0.027566
	Ranking	6	5	3	2	7	8	4	1
4	Max	0.659553	0.689073	0.651031	0.688422	0.619171	0.654426	0.609938	0.702364
	Mean	0.585789	0.577215	0.572652	0.650246	0.538835	0.569699	0.444351	0.581725
	Min	0.457314	0.421803	0.524473	0.602193	0.438635	0.46478	0.373331	0.415275
	STD	0.111669	0.138856	0.068471	0.043955	0.091893	0.096422	0.144427	0.148926
	Ranking	2	4	5	1	7	6	8	3
5	Max	0.71179	0.653103	0.679673	0.728578	0.739026	0.654866	0.710614	0.723238
	Mean	0.667834	0.608033	0.628176	0.612995	0.625972	0.569295	0.65234	0.680701
	Min	0.645318	0.518308	0.529437	0.405271	0.535025	0.49256	0.543264	0.618906
	STD	0.038071	0.077705	0.085537	0.180276	0.103782	0.081513	0.020135	0.054767
	Ranking	2	7	4	6	5	8	3	1
6	Max	0.749897	0.758664	0.700491	0.739996	0.733031	0.674032	0.621232	0.726155
	Mean	0.700148	0.702408	0.625182	0.675597	0.681783	0.590369	0.60327	0.683228
	Min	0.614634	0.666246	0.567525	0.585931	0.60607	0.43936	0.513341	0.620501
	STD	0.074387	0.049377	0.068218	0.08008	0.066923	0.131032	0.780799	0.05554
	Ranking	2	1	6	5	4	8	7	3
Summation		18	25	23	15	27	33	29	10
Mean Rank		3.6	5	4.6	3	5.4	6.6	5.8	2
Final Ranking		3	5	4	2	6	8	7	1
p-value		3.856 × 10${}^{-2}$	2.669 × 10${}^{-2}$	2.665 × 10${}^{-2}$	2.814 × 10${}^{-2}$	6.665 × 10${}^{-2}$	3.854 × 10${}^{-2}$	3.225 × 10${}^{-2}$	NaN
Wilcoxon sign		1	1	1	1	1	1	1	NaN

Table 17 shows that the proposed DAOA method obtained better results in almost all the test cases in terms of SSIM for Test 8. The proposed DAOA obtained the best results for two threshold values (i.e., 3 and 5 levels). For threshold 3, the proposed DAOA obtained the best results, and it ranked as the first method, compared to all other comparative methods, followed by AOA, SSA, DE, WOA, AO, PSO, and finally, MPA. For threshold 5, the proposed method obtained promising results compared to other methods. DAOA obtained the first ranking, followed by AO, DE, SSA, PSO, AOA, WOA, and MPA. Overall, we can see that the proposed DAOA method obtained the first ranking, followed by AOA, AO, WOA, SSA, PSO, DE, and MPA. The obtained results in this table confirm the performance of the proposed DAOA and its ability to solve the given problems efficiently. The presented results demonstrate and declare the proposed algorithm’s ability to solve such problems and find reliable solutions in this area. We added a Wilcoxon sign test to show the significant improvement for test case number 8 as shown in Table 16 and Table 17. It is clear that the proposed method is more effective and better than the other methods.

The segmentation results (segmented images) of the proposed DAOA and the other comparative methods for Test 8 are shown in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 show the segmented images for all the tested methods, when the threshold values are 2, 3, 4, 5, and 6, respectively. According to these figures, we can recognize that the proposed DAOA showed good segmented images for various images (CT COVID-19 medical images) under different thresholds. Additionally, these figures prove that the segmented images are better in terms of quality when the threshold value is higher.

Figure 6. The segmented image (Test 8) by the comparative methods when the threshold value is 2.

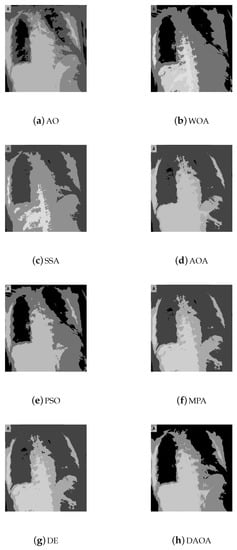
Figure 7. The segmented image (Test 8) by the comparative methods when the threshold value is 3.

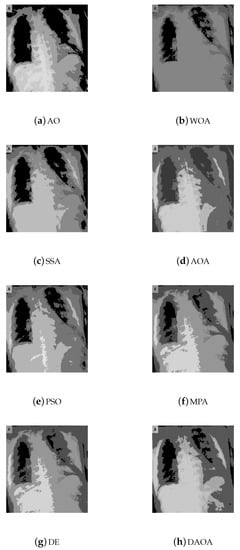
Figure 8. The segmented image (Test 8) by the comparative methods when the threshold value is 4.

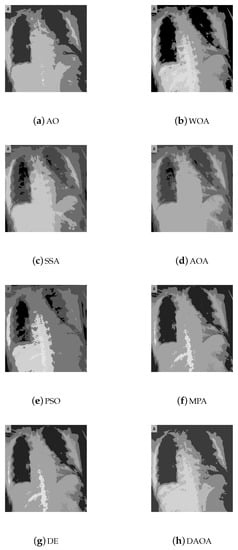
Figure 9. The segmented image (Test 8) by the comparative methods when the threshold value is 5.

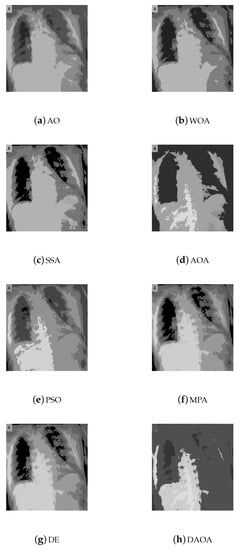
Figure 10. The segmented image (Test 8) by the comparative methods when the threshold value is 6.

The thresholds are shown in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, applied over the selected images. In Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, the histogram images are given with the best threshold values obtained by the comparative methods for Test 8, where the threshold values are taken (i.e., 2, 3, 4, 5, and 6). The X and Y axes present the threshold values and Kapur measure values, respectively. It is feasible to recognize that the histogram classes are uniformly created, even in complex situations from such images. This means that the proposed method has an excellent ability to find always the same threshold values. The complexity is different from case to case because of the various peaks displayed in the pixels’ distribution, which could create multiple classes or even carefully obtain the selection of the optimal thresholds.

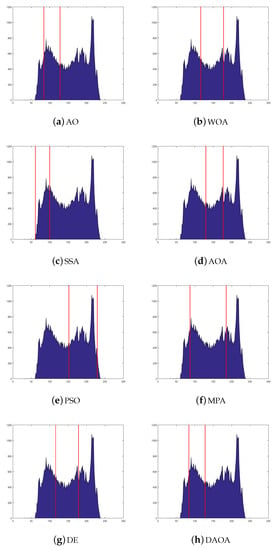
Figure 11. The histogram image (Test 8) by the comparative methods when the threshold value is 2.

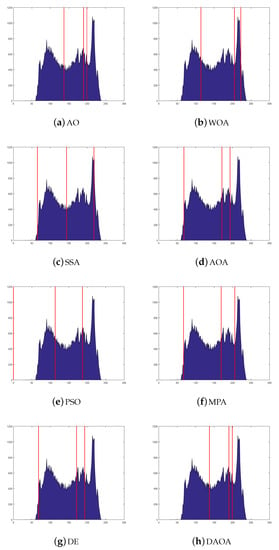
Figure 12. The histogram image (Test 8) by the comparative methods when the threshold value is 3.

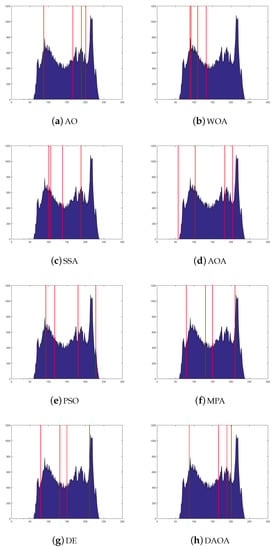
Figure 13. The histogram image (Test 8) by the comparative methods when the threshold value is 4.

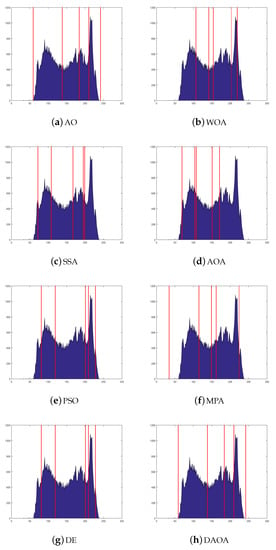
Figure 14. The histogram image (Test 8) by the comparative methods when the threshold value is 5.

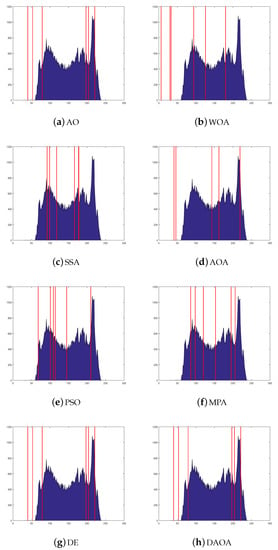
Figure 15. The histogram image (Test 8) by the comparative methods when the threshold value is 6.

Figure 16 shows the convergence curves of the proposed DAOA and its comparative optimization algorithms on eight tested images (i.e., Test 1 to Test 8); it can be seen that the proposed DAOA performs better than all involved other optimization methods in Test 8 when the threshold value is 6. For almost all the test images, the excellent optimized performance with accelerated convergence and more reliable accuracy achieved by the proposed DAOA can be seen as being remarkably smoothing behavior in the convergence curve. Moreover, we recognize that the curves of the proposed method always converge smoothly, reflecting the proposed DAOA’s ability to avoid the common problem (local optima). In the end, the proposed DAOA reached the best solutions almost in all the tested cases, compared to the other comparative methods, as clearly shown in Figure 16.

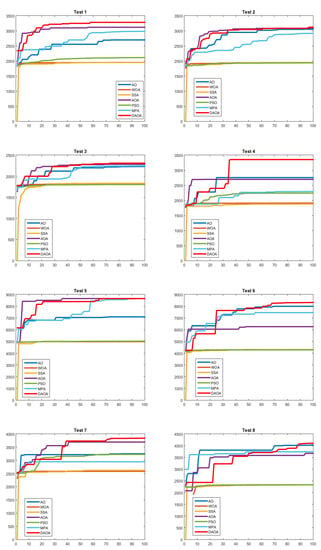
Figure 16. The convergence behavior of the comparative methods in solving Test 8 when the threshold value is 6.

5. Conclusions and Future Works

The most crucial aspect of image segmentation is multilevel thresholding. However, multilevel thresholding displays require increasingly more computational complexity as the number of thresholds grows. In order to address this weakness, this paper proposes a new multilevel thresholding approach based on using an improved optimization-based evolutionary method.

The Arithmetic Optimization Algorithm (AOA) is a recently proposed optimization technique to solve different complex optimization problems. An enhanced version of the Arithmetic Optimization Algorithm is proposed in this paper to solve multilevel thresholding image segmentation problems. The proposed method combines the conventional Arithmetic Optimization Algorithm with the Differential Evolution technique, called DAOA. The main aim of the proposed DAOA is to improve the local search of the Arithmetic Optimization Algorithm and to establish an equilibrium among the search methods (exploration and exploitation).

The proposed DAOA method was applied to the multilevel thresholding problem, using Kapur’s measure between class variance functions as a fitness function. The proposed DAOA evaluated eight standard test images from two different groups: nature images and CT medical images (i.e., COVID-19). The Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Test (SSIM) were used to determine the segmented images’ accuracy. The proposed DAOA method’s efficiency was evaluated and compared to other multilevel thresholding methods, including the Aquila Optimizer (AO), Whale Optimization Algorithm (WOA), Salp Swarm Algorithm (SSA), Arithmetic Optimization Algorithm (AOA), Particle Swarm Optimization (PSO), and Marine Predators Algorithm (MPA). The findings were presented, using a number of different threshold values (i.e., 2, 3, 4, 5, and 6). According to the experimental results, the proposed DAOA produced higher quality solutions than the other approaches. It achieved better results in almost all the tested cases, compared to other methods.

For future work, other fitness functions, evaluation measures, and benchmark images can be used. The conventional Arithmetic Optimization Algorithm can be improved, using other different optimization operations to enhance its performance further. As well, the proposed DAOA method can be used to solve other problems, such as text clustering, feature selection, photovoltaic parameter estimations, task scheduling in fog and cloud computing, appliances management in smart homes, advanced benchmark functions, text classification, text summarization, data clustering, engineering design problems, industrial problems, image construction, short-term wind speed forecasting, fuel cell modeling, damage identification, the prediction of the software vulnerability, knapsack problems, and others.