Abstract
Batch-type hot rolling planning highly affects electricity costs in a steel plant, but previous research models seldom considered time-of-use (TOU) electricity pricing. Based on an analysis of the hot-rolling process and TOU electricity pricing, a batch-processing plan optimization model for hot rolling was established, using an objective function with the goal of minimizing the total penalty incurred by the differences in width, thickness, and hardness among adjacent slabs, as well as the electricity cost of the rolling process. A method was provided to solve the model through improved genetic algorithm. An analysis of the batch processing of the hot rolling of 240 slabs of different sizes at a steel plant proved the effectiveness of the proposed model. Compared to the man–machine interaction model and the model in which TOU electricity pricing was not considered, the batch-processing model that included TOU electricity pricing produced significantly better results with respect to both product quality and power consumption.
1. Introduction
As a key link in steel production, hot rolling refers to a process in which the steel slabs sustain heating in a furnace, rough rolling, and fine rolling before becoming steel products (Figure 1). The main task of the batch-processing planning of hot rolling is to determine an appropriate sequence for the processing of multiple slabs, to achieve low power consumption, low cost of stack transfer, high efficiency, and high product quality, while the technical requirements of rolling are met [1]. Throughout the steel production process, the batch-processing plan of hot rolling directly determines the product quality and production efficiency of the steel plant. In the past, in most studies on the batch-processing planning of hot rolling, the penalty items relating to the differences (such as width, thickness, hardness, and delivery time) were only taken into consideration among adjacent slabs, while the differences in power consumption between slabs of difference sizes were ignored [2,3,4]. In fact, apart from guaranteeing product quality and production efficiency, a sound processing plan of rolling also served to reduce production cost through electricity cost cut-backs, thereby maximizing the economic benefits [5].
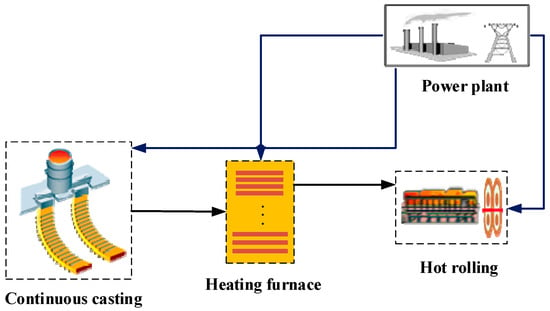
Figure 1.
Flow chart of the rolling process.
Throughout actual hot rolling, most electricity is used to drive the motor of the rolling mill and power various auxiliary electrical devices. The power consumption in hot rolling is closely related to the sizes and conditions of the devices, process parameters, as well as the types and sizes of the steel products [6]. Under the condition of time-of-use (TOU) electricity pricing, the sequence with which the slabs are processed has a major impact on power consumption. In the research area of hot rolling, only few studies were carried out regarding the impact investigation of TOU electricity pricing on the batch-processing planning of hot rolling. Most studies were focused on methods of better connection and matching during steelmaking, of continuous casting, and hot rolling processes. A charge-rolling plan coordination model based on the optimal furnace charge plan and optimal rolling plan models was presented [7,8], in which the tabu search algorithm was proposed for the corresponding solution. A steelmaking continuous-casting hot-rolling integrated planning model was proposed to enable an effective connection among the rolling unit plan [9], the furnace charge plan, and the casting plan. An integrated model on the production and logistics planning level was constructed [10], based on an analysis of the characteristics of steelmaking and hot rolling processes, as well as on the transition between the two processes, where the constraints of capacity and the conflicts between the two stages were taken into consideration. A mathematical model was presented for batch-processing optimization in the steelmaking and hot rolling processes [11]. This model was proposed for the model solution with the neighborhood search algorithm based on heuristic rules. The batch-processing planning problem of hot rolling was treated as a constraint compliant problem [12], while the vehicle routing problem with soft time windows (VRPSTW) constraint of uncertain plan number was constructed to satisfy the model. In certain studies, the effects of other factors on the rolling plan of hot-rolling planning were taken into consideration. As an example, the problem of slab stack transfer in the rolling plan was taken into consideration [13,14], whereas the solution was conducted with the improved genetic algorithm, resulting in reduced handling costs. The impact of TOU electricity pricing on the rolling planning was taken into consideration [6], but in the proposed model, the power consumptions of individual rolling units were only considered, instead of the influence of the rolling sequence on the electricity cost under TOU electricity pricing. Mao et al. [5] considered the influence of TOU electricity pricing when constructing a rolling unit as the production load unit, and a multi-objective optimization model for hot rolling was established and a multi-objective optimization algorithm was applied to solve this problem. However, all the goals were classified into one objective function in this paper.
In summary, in most previous studies, optimal rolling-plan models were proposed to be established, to produce products with the highest possible quality and production efficiency prior to the delivery deadline, indifferently to electricity cost reduction throughout production. Because the main characteristic of genetic algorithms is to directly operate the structural objects, only the objective function and the corresponding fitness functions that affect the search direction are needed. Therefore, the genetic algorithm provides a method for solving complex system problems. It does not depend on the specific fields and types of problems, and has strong robustness, so it has been widely used in many scientific fields. [15]. On the basis of previous studies, in this paper, a model for batch-processing planning of hot rolling under TOU electricity pricing was presented, resulting in a method of solving the model with an improved genetic algorithm.
2. Problem Description
2.1. Basic Principles of Hot Rolling Planning
Hot rolling constitutes the last link in the steelmaking continuous-casting hot-rolling process. The raw materials are the slabs resulting from continuous casting, while the products are strip steels (steel plates or steel coils). The strip steel could be directly sold as a finished product, or be further processed into high-quality cold-rolled strip steel. A key issue in hot rolling is the rolling plan formulation. A complete rolling unit generally consists of two parts: “roll heating pieces” and “principal pieces” (Figure 2). The roll-heating pieces are usually easy-to-process slabs, such as low-carbon steels as well as relatively thick and narrow strip steels. The number of slabs in this part is relatively low, while the main purpose of this part is to heat the rolled steel and lead it to reach heat equilibrium, creating conditions for the subsequent processing of principal pieces. Usually, the width of the slab increases gradually throughout rolling. The principal pieces are usually hard-to-process slabs, for thinner and wider products, whereas the width of the slab decreases gradually throughout hot rolling. Therefore, a complete rolling unit would have a dual trapezoidal structure, with the positive trapezoid as the roll-heated pieces and the inverted trapezoid as the principal pieces. In view of the fact that the numbers of roll-heated pieces in a rolling unit are small and the quality requirement is low, in this study, the principal pieces were focused on. The principal pieces processing met the following requirements [16,17].
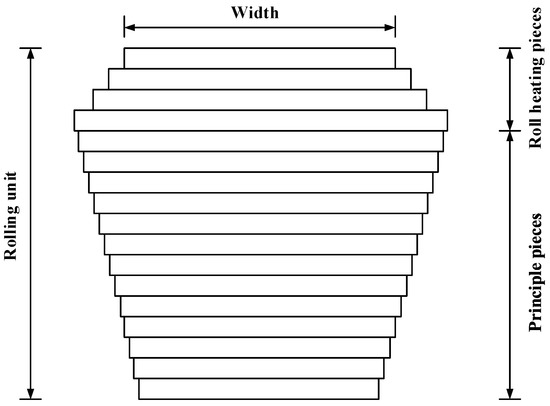
Figure 2.
Schematic diagram of rolling unit.
- (1)
- The length of each principal piece had a certain limit;
- (2)
- When the thickness of the principal piece changed in the non-increase direction, the step must be lower than 25 cm;
- (3)
- When the width changed inversely, the step did not generally exceed 15 cm;
- (4)
- When slabs of the same width were continuously processed, the total length should not exceed a certain limit;
- (5)
- The width, thickness and hardness were not allowed to jump at the same time;
- (6)
- The thickness jump should be smooth and repeated jumps were not allowed. Changes in the non-decrease direction were preferred.
- (7)
- The hardness change should be smooth. Both gradual increase and gradual decrease were allowed. Repeated jumps were not allowed.
Figure 3 presents the batch-processing plan formulation of hot rolling. Multiple slabs of different sizes were combined into a rolling unit in accordance with the process requirement, while multiple rolling units constituted a hot-rolling batch-processing plan (Figure 4). The hot-rolled batch processing plan was a rolling sequence of slabs arranged in accordance with the roll usage cycle. One rolling unit corresponded to the usage of one set of rolls. The hot-rolling batch-processing plan’s successful execution directly determines the product quality, delivery date, and production efficiency, and a sound hot-rolling batch-processing plan could improve production efficiency, reduce energy consumption (such as costs), and enhance the firm’s competitiveness.
Figure 3.
Batch-processing plan formulation of hot rolling.
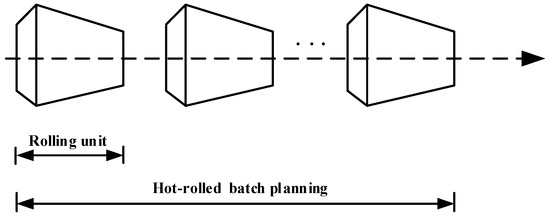
Figure 4.
Schematic diagram of a batch-processing plan for hot rolling.
2.2. Analysis of Energy Consumption in Rolling
Hot rolling is a typical energy-intensive process in steel production, mainly requiring electric energy and heat energy from gas consumption. The gas is mainly consumed in the heating furnace to heat the slabs to the temperature required for hot rolling. The gas used in the heating furnace is usually a mixture of blast furnace gas, Linz–Donawitz gas, and coke oven gas, while the calorific value of the mixed gas must meet the production requirement. The electric energy is mainly used to drive the rolling mill, while the power consumption in the rolling process varies depending on the slab size, steel type, and other factors. In a hot-rolling batch-processing plan, the rolling sequence change or positions exchange of two rolling units will change the energy consumption pattern. At many locations, the electricity price varies with time. As demonstrated with the TOU electricity pricing scheme presented in Figure 5, the highest electricity price was 2.43 times that of the lowest electricity price. Consequently, the rolling sequence in the rolling plan directly affected the electricity cost of hot rolling.
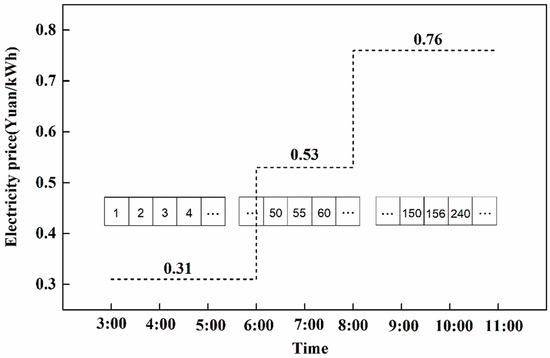
Figure 5.
Schematic diagram of production scheduling under time-of-use (TOU) electricity pricing.
At present, many batch-processing plans of hot-rolling steel plants are mainly prepared by human planners in human–computer interaction interfaces, based on their experience. The impact of the batch-processing plan on the power consumption has been often ignored. Besides, this mode of planning has the drawbacks of low efficiency, poor accuracy, and high labor cost. To compensate for this deficiency, in this paper, a model for batch-processing planning of hot rolling under TOU electricity pricing was proposed, with the aim of ensuring high quality and reducing power consumption at the same time.
3. Mathematical Model and Solution Method
3.1. Mathematical Model
3.1.1. Model Assumptions
- (1)
- The time required to process a single slab was roughly the same. In this paper, the processing time used was 2 min;
- (2)
- Basic properties, such as width, thickness, hardness, and length of each slab were known;
- (3)
- The change of the total attribute in the rolling unit could be determined through calculation.
3.1.2. Objective Function
In this paper, the optimizations of quality and power consumptions from different time periods were taken into consideration. On the basis of setting a certain weight coefficient, an objective function was formulated with the goal of minimizing the differences in width, thickness, and hardness among adjacent slabs of the same rolling unit, as well as the electricity cost of the rolling process. The objective function is presented as
where , , .
3.1.3. Constraints
Based on the above description, the constraints of the hot-rolled batch processing planning model are as follows:
where F represents the target penalty value, N represents the number of slabs, T represents the rolling period. , and are the penalty coefficients for the differences in width, thickness, and hardness among adjacent slabs of the same rolling unit, respectively. In the equations, represents the penalty coefficient for the electricity spent on the slab i, represent the prices of the electricity spent on the slab i, is the electricity spend on the slab i, is the length limit for each rolling unit, is the length limit for the continuously processed slabs of the same width in the same rolling unit, , , and are the upper limits for the differences in width, thickness and hardness among adjacent slabs from the same rolling unit. Constraint (2) ensured that each slab was assigned to one rolling unit; constraints (3) and (4) limited the total length of a single rolling unit and the length of continuously processed slabs of the same width; constraint (5) ensured that slabs of the same rolling unit were arranged in the descending order of width and that the width difference between two adjacent slabs did not exceed the upper limit; constraints (6) and (7) ensured that the differences in thickness and hardness between two adjacent slabs did not exceed the upper limits, respectively; constraint (8) signified that each slab could only be processed once; constraint (9) represented the prices of electricity from different time periods; and constraints (10)–(12) were the decision variables of values of 0, 1, respectively.
3.2. Method for Model Solution
3.2.1. Brief Description of Algorithm
The genetic algorithm (GA) is an algorithm that mimics the processes of inheritance, mutation, and natural selection in the evolution of biological organisms. Figure 6 presents the solution of the genetic algorithm. First, a set of initial feasible solutions were randomly selected, according to the characteristics of the problem. Following this, a new chromosome was obtained through crossover and mutation operations involving genetic operators. Next, the fitness of the new generation chromosome was calculated and evaluated. The chromosome with good adaptability would be passed on to the next generation. This solution process would be repeated until the preset number of iterations was reached or the convergence condition was met. The GA has the characteristics of randomness, implicit parallelism, and global optimization in the operation process. In the actual operation of steel plant, a requirement to prepare a large number of batch-processing plans exists. Consequently, it was difficult to achieve the expected result through the common search methods. To tackle this problem, in this paper, it was proposed that the batch-processing model was to be solved with the GA with improved genetic operators.
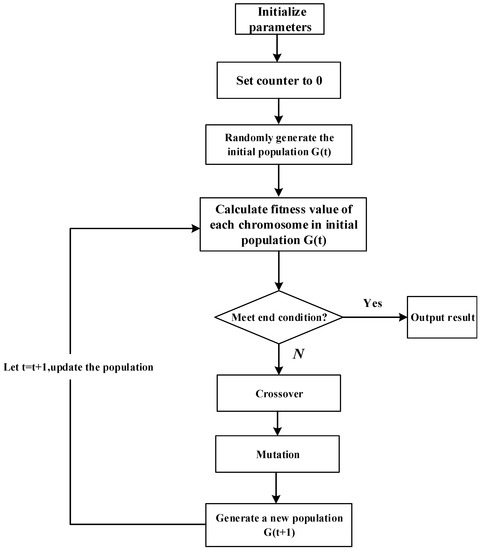
Figure 6.
Process of model solution through genetic algorithm.
3.2.2. Chromosome Coding
Throughout the hot-rolling planning model solution with GA, the chromosome was represented by a coding sequence consisting of decimal natural numbers. For a rolling plan, the serial numbers of the slabs represented the genes in the chromosome coding. The chromosome coding could be expressed as the sequence of , in which the chromosome length was the total number N of pre-processed slabs. Figure 7 presents a schematic diagram demonstrating the chromosomal coding of the rolling plan, in which, a1, a50 and a100 were the serial numbers of the slabs; A0, A1 and A2 were the slab sequences constituting the rolling units.
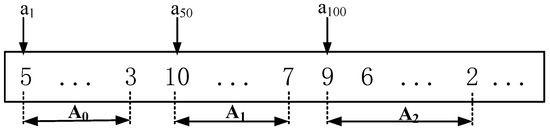
Figure 7.
Schematic diagram of rolling-plan chromosome coding.
3.2.3. Chromosome Decoding
In different chromosomes, the numbers represented the serial numbers of the slabs, while the order of appearance was the order of processing. Figure 8 presents the flowchart of chromosome decoding. The procedure of rolling plan chromosome decoding was as follows:
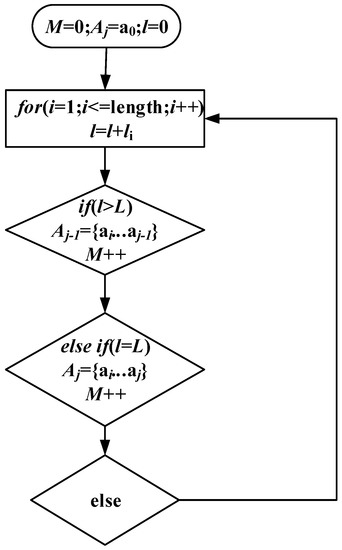
Figure 8.
Flow chart of chromosome decoding.
- Step 0:
- M = 0, = , l = 0;
- Step 1:
- Sequentially traversed the slab numbers from the th position of the chromosome, recording the length of the slab and recording in the arranged slab sequence , doing l = l + , and going to Step 2;
- Step 2:
- If l was larger than the length L of the rolling unit, the last element in the sequence was removed, turning the sequence into a rolling unit, and letting M = M + 1; if l was equal to the length L of the rolling unit, the sequence was turned into a rolling unit, and letting M = M + 1; otherwise, Step 1 was selected;
- Step 3:
- When i was equal to the length of the chromosome, the program exited.
3.2.4. Selection of Fitness Function
In this paper, a sorting-based allocation function was used as the fitness function. The equation was as follows:
where N is the number of chromosomes in the population, P is the sorting number of the chromosome in the population, Y is the selection pressure with a value in the range of [1.0, 2.0]. When the fitness function was applied, it was necessary to calculate at first the penalty value of each chromosome in the population, incurred by the differences in the width, thickness, and hardness among adjacent slabs, as well as the TOU electricity pricing. Following this, sorting was performed according to the penalty values, and the P value of the corresponding chromosome was obtained. Finally, the fitness values of different chromosomes were calculated. The smaller the objective function value was, the greater the fitness of the corresponding chromosome was. In this way, the high-quality chromosomes were picked from the population.
3.2.5. Genetic Operators
Genetic operators include selection operators, crossover operators, and mutation operators. In a rolling plan, each slab could only occupy one position in the sequence. In other words, no duplicate genes would appear in the same chromosome, which is different from the conventional GA. Therefore, it was necessary to improve the crossover and mutation operators. The selection operator used in the model solution method proposed in this paper was used to realize a selection operation similar to roulette according to the above-mentioned fitness function. The crossover operator was a secondary crossover operator. As illustrated in Figure 9, the crossover operator worked as follows. (1) Three contiguous genes on the chromosome were randomly selected and their positions are recorded; (2) the three genes were led to exchange positions with three corresponding genes on another chromosome without changing the original order. Finally, the mutation operator exchanged the positions of two randomly selected genes on the same chromosome, as presented in Figure 10.
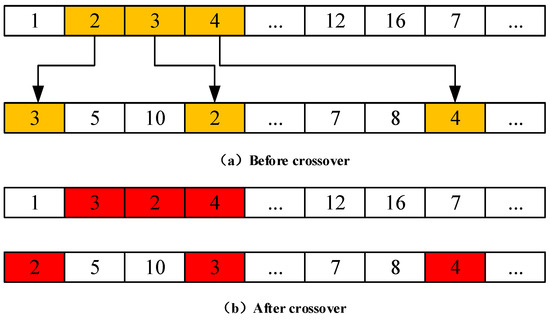
Figure 9.
Crossover operator.
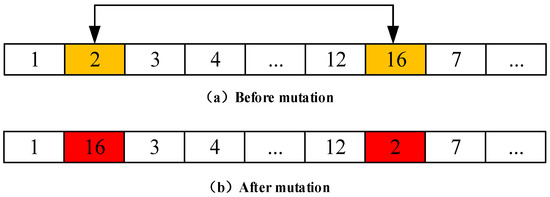
Figure 10.
Mutation operator.
4. Case Study
4.1. Basic Parameters
The total lengths of the slabs in a rolling unit were limited to 10 km, the lengths of the slabs of the same width were limited to 1 km, while the jump penalties for width, thickness, and hardness are presented in Table 1, Table 2 and Table 3 [18]. Throughout the model solution with genetic algorithm, the initial population size was 20, the crossover probability was 0.85, and the mutation probability was 0.15. The genetic algorithm was implemented through Visual C# programming.

Table 1.
Penalty of width jump.

Table 2.
Penalty of hardness jump.

Table 3.
Penalty of thickness jump.
Table 4 presents the different electricity prices charged to a typical steel plant during different periods within one day [19]. Each day was divided into six electricity price periods with three electricity prices (peak, flat, trough).

Table 4.
TOU electricity pricing in steel plant (24-h clock).
4.2. Analysis of Optimization Results
The subject of this case analysis was 240 slabs actually processed by a certain steel plant. The rolling operation started from 03:00. The genetic algorithm was used to solve the rolling batch-processing model under two conditions: considering the TOU electricity pricing, and not considering the TOU electricity pricing. Figure 11 presents the iteration curves under the two conditions. As it could be observed from Figure 11a, when TOU electricity pricing was not taken into consideration, the penalty value remained basically unchanged after 10 iterations. The initial penalty value was 23,537, and the value became 22,029 after optimization, amounting to an improvement of 6.4%. As presented in Figure 11b, when the TOU electricity pricing is taken into consideration, the penalty value remained basically unchanged after nine iterations. The initial penalty value was 27,880, while the value became 26,238 after optimization, amounting to an improvement of 5.9%. This indicated that a feasible solution with a low penalty value could be obtained through model optimization.
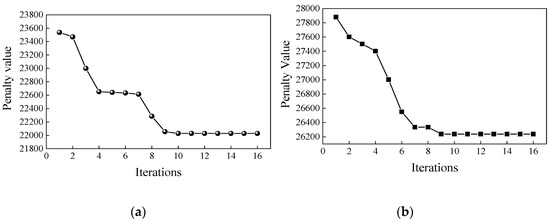
Figure 11.
(a) TOU electricity pricing not considered (b) TOU electricity pricing considered Convergence curve resulted from genetic algorithm iterations.
Table 5 presents the penalty values of three hot-rolling batch processing plans prepared with different methods. It could be observed that the two rolling plans formulated through the hot-rolling batch-processing model under two electricity pricing conditions (TOU plan, non-TOU plan) had apparently lower penalty values, compared to the rolling plan formulated by the man–machine interaction method (MMI plan), even though all three rolling plans had the same number of rolling units. This indicated that better slab arrangement (width, thickness, and hardness) could be achieved after the model-based optimization, which would further lead to a smoother hot-rolling operation. The optimization model, in which the TOU electricity pricing was considered, had higher penalty value compared to the optimization model without the TOU electricity-pricing consideration. This occurred because the penalty incurred by the electricity cost had been added to the objective function. The introduction of the electricity cost penalty created the condition for simultaneous quality and power consumption optimization for the hot-rolling process.

Table 5.
Penalty values of three hot-rolling batch-processing plans.
Figure 12 presets the electricity costs during rolling. The different colors represented different rolling units. The MMI plan induced an electricity cost of 11,230 yuan, the non-TOU plan induced 10,770 yuan and the TOU plan induced 10,230 yuan. In other words, the TOU plan induced 8.9% less electricity cost than the MMI plan and 5.0% less electricity cost than the non-TOU plan. Because the model considering the TOU electricity pricing is good for reducing peaks and filling valleys, the cost of electricity consumption is effectively reduced.
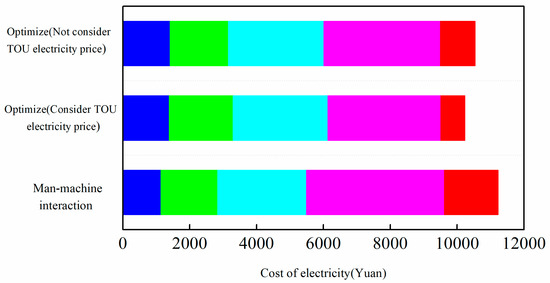
Figure 12.
Electricity costs of three rolling plans.
Figure 13 presents the power consumption data during the period from 04:00 to 10:00. The electricity price was 0.31 yuan/kWh in the period of 04:00–06:00, 0.53 yuan/kWh in the period of 06:00–8:00 and 0.76 yuan/ kWh in the period of 08:00–10:00. It could be observed that when the electricity price was 0.31 yuan/kWh, the MMI plan, non-TOU plan, and the TOU plan consumed 4293 kWh, 5134 kWh and 4808 kWh of electricity, respectively. When the electricity price was 0.76 yuan/kWh, the TOU plan consumed 4132 kWh, while the MMI plan consumed 5574 kWh. The former was 25.9% lower than the latter. This demonstrated the benefit of model-based optimization. After the model-based optimization, the high-load rolling units were arranged in the trough-price and flat-price periods, while the low-load rolling units were arranged in the peak-price period.
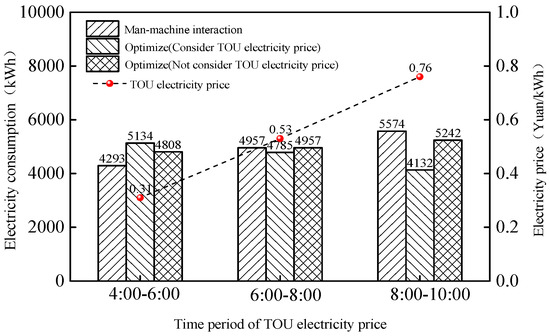
Figure 13.
Electricity consumptions at different time periods.
Figure 14 presents the electricity costs of three kinds of rolling plans at different time periods. It could be observed that when the electricity price was low (0.31 yuan/kWh), the MMI plan, TOU plan, and non-TOU plan induced electricity costs of 1331 yuan, 1592 yuan and 1490 yuan, respectively. When the electricity price was medium (0.53 yuan/kWh), the electricity costs induced by the three rolling plans were very close. When the electricity price was high (0.76 yuan/kWh), the MMI plan, non-TOU, and TOU plans induced costs of 4236 yuan, 3984 yuan and 3140 yuan, respectively. In other words, the TOU plan induced a 21.2% lower electricity cost than the non-TOU plan, and 25.9% lower than the MMI plan. Therefore, the TOU plan could effectively reduce the electricity cost and contribute to the power grid fluctuation reduction of electricity consumption.
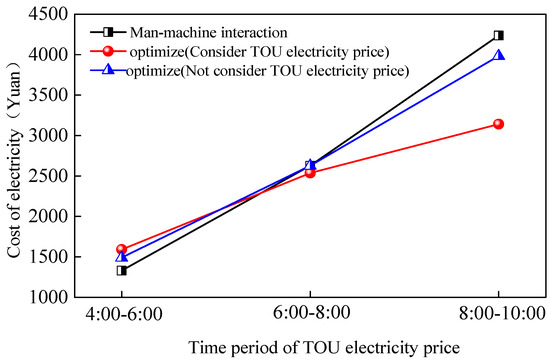
Figure 14.
Electricity costs at different TOU electricity pricing periods.
5. Conclusions
- (1)
- A hot-rolling batch-processing plan optimization model, in which TOU electricity pricing was taken into consideration was established. An objective function was used in the model that was aimed at the jump penalties minimizations of the jumps among adjacent slabs in width, hardness, and thickness, as well as in the electricity costs. The optimization method reduced the electricity cost of hot rolling, while ensuring the product quality and production efficiency, in addition to the extra benefit of power consumption fluctuation reduction.
- (2)
- In the proposed method, the crossover and mutation operators of the improved genetic algorithm were used to solve the model for batch-processing plan production for hot rolling. The algorithm was characterized by strong search ability and good convergence. The penalty value after optimization was significantly lower than before optimization, proving the actual value of the proposed method.
- (3)
- An experimental verification was carried out to check the electricity costs of processing of 240 slabs through three hot rolling batch processing plans, formulated under “TOU electricity-pricing consideration”, “TOU electricity-pricing absence” and “man–-machine interaction” models. The results demonstrated that the TOU plan induced 8.9% lower electricity cost than the MMI plan and 5.0% lower electricity cost than the non-TOU plan.
Author Contributions
Data curation, Z.H.; Formal analysis, Z.H.; Funding acquisition, D.H.; Methodology, K.F.; Project administration, D.H.; Resources, W.S. Software, W.S. and Z.H.; Writing—original draft, Z.H.; Writing—review & editing, D.H. and K.F. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful for the financial support provided by the General Programme of the National Natural Science Foundation of China (Grant No. 51574032, 51674030).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dong, G.J.; Li, K.T.; Wang, B.L. Adjustment model and algorithm of rolling plan based on real-time warehouse. Syst. Eng. Theory Pract. 2015, 35, 1246–1255. [Google Scholar]
- Chakraborti, N.; Kumar, B.S.; Babu, V.S.; Moitra, S.; Mukhopadhyay, A. A new multi-objective genetic algorithm applied to hot-rolling process. Appl. Math. Model. 2008, 32, 781–1789. [Google Scholar] [CrossRef]
- Tang, L.X.; Liu, J.Y.; Rong, A.Y.; Yang, Z.H. A review of planning and scheduling systems and methods for integrated steel production. Eur. J. Oper. Res. 2001, 133, 1–20. [Google Scholar] [CrossRef]
- Yadollahpour, M.R.; Bijari, M.; Kavosh, S.; Mahnam, M. Guided local search algorithm for hot strip mill scheduling problem with considering hot charge rolling. Int. J. Adv. Manuf. Technol. 2009, 45, 1215–1231. [Google Scholar] [CrossRef]
- Tan, M.; Duan, B.; Su, Y.X.; He, F. Optimizing production scheduling of steel plate hot rolling for economic load dispatch under time-of-use electricity pricing. Math. Probl. Eng. 2017, 145, 913–923. [Google Scholar] [CrossRef]
- He, D.F.; Liu, P.Z.; Feng, K.; Xu, A.J. Collaborative optimization of rolling plan and enemy dispatching in steel plants. China Metall. 2019, 29, 75–80. [Google Scholar]
- Cowling, P.; Ouelhadj, D.; Petrovic, S. A multi-agent architecture for dynamic scheduling of steel hot rolling. J. Intell. Manuf. 2003, 14, 457–470. [Google Scholar] [CrossRef]
- Cowling, P.; Rezig, W. Integration of continuous caster and hot strip mill planning for steel production. J. Sched. 2000, 3, 185–208. [Google Scholar] [CrossRef]
- Zheng, Z.; Liu, Y.; Chen, K.; Gao, X.Q. Unified modeling and intelligent algorithm of production planning for the process of steelmaking, continuous casting and hot rolling. J. Univ. Sci. Technol. Beijing 2013, 35, 687–693. [Google Scholar]
- Luo, Z.H.; Tang, L.X. Modeling and solution to integrated production and logistics planning of steel making and hot rolling. J. Manag. Sci. China 2011, 14, 16–23. [Google Scholar]
- Zhang, C.S.; Li, K.T. Optimization Model and Algorithm for Lot Planning Coordination between Steelmaking and Hot Rolling. Inf. Control 2017, 46, 122–128. [Google Scholar]
- Li, K.T.; Guo, D.F. Model and algorithm for hot-rolling batch plan based on constraint satisfaction. Control Decis. 2007, 22, 389–393. [Google Scholar]
- Tang, L.X.; Liu, J.Y.; Rong, A.Y.; Yang, Z.H. Modelling and a genetic algorithm solution for the slab stack shuffling problem when implementing steel rolling schedules. Int. J. Prod. Res. 2002, 40, 1583–1595. [Google Scholar] [CrossRef]
- Singh, K.A.; Srinivas; Tiwari, M.K. Modelling the slab stack shuffling problem in developing steel rolling schedules and its solution using improved Parallel Genetic Algorithms. Int. J. Prod. Econ. 2004, 91, 135–147. [Google Scholar] [CrossRef]
- Han, K.H.; Zhang, Q.; Shi, H.B.; Zhang, J.Y. An Improved Compact Genetic Algorithm for Scheduling Problems in a Flexible Flow Shop with a Multi-Queue Buffer. Processes 2019, 7, 302. [Google Scholar] [CrossRef]
- Hu, K.J.; Zhu, F.X.; Chen, J.F.; Noda, N.; Han, W.Q.; Sano, Y. Simulation of Thermal Stress and Fatigue Life Prediction of High Speed Steel Work Roll during Hot Rolling Considering the Initial Residual Stress. Metals 2019, 9, 966. [Google Scholar] [CrossRef]
- Yang, Y.J.; Jiang, Z.Y.; Zhang, X.X. Mathematical model and solving algorithm for the lot planning of slab hot rolling. J. Univ. Sci. Technol. Beijing 2012, 34, 457–463. [Google Scholar]
- Lu, Y.M.; Xu, A.J.; He, D.F.; Tian, N.Y. Hot-rolling batch planning method available to improve DHCR proportion. J. Univ. Sci. Technol. Beijing 2011, 33, 1301–1306. [Google Scholar]
- Zhao, X.C.; Bai, H.; Shi, Q.; Lu, X.; Zhang, Z.H. Optimal scheduling of a byproduct gas system in a steel plant concerning the time-of-use electricity pricing. Appl. Energy 2017, 195, 100–113. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).