Optimization of Distillation Sequences with Nonsharp Separation Columns

Abstract

Nonsharp distillation sequences are widely used in industrial separation processes; however, most current research has not discussed this topic, except in sequences with heat integration under special operating conditions, including complex columns. The sequence with nonsharp separation has the features of general distillation sequences, which are usually optimized by adjusting the separation sequence and the design/operation parameters of each column in the sequence, making the optimization a mixed integer nonlinear programming (MINLP) problem, which is usually hard to solve. With inclusion of nonsharp separation columns, the sequence optimization becomes even more complicated and computationally intensive. This work aimed to optimize the distillation sequence, including nonsharp distillation alongside simple columns and dividing wall columns. Inspired by the dynamic programing method for sharp distillation sequence, a framework for automatic optimization is proposed to decompose the MINLP problem into integer programming (IP) and nonlinear programming (NLP) problems. The optimization processes of sharp and nonsharp distillation sequences are compared and the solution space in terms of the possible number of distillation sequences with nonsharp separation is discussed. Two optimization cases, including an industrial one, are included to validate the proposed framework.

1. Introduction

In industrial processes [1], the nonsharp distillation sequences are widely used for obtaining nonsharp separated products. Compared to sharp separation sequences, nonsharp sequences are relatively understudied. Sequences with nonsharp separation have the features of the general distillation sequences, but with more options in terms of the choice of sequence and columns, which make their optimization complicated and computationally intensive. The distillation sequence is usually optimized by adjusting the discrete variables of the separation sequence and the continuous design/operation parameters of each column in the sequence. Column-associated equations contribute to the nonlinear part. All these make the problem a nonconvex MINLP problem with a discontinuous feasible region, making it difficult to find the global optimum.

Optimization algorithms based on numerical searching have been focused on solving the optimization problem of the distillation sequence. Floquet et al. [2] applied a simulated annealing algorithm on sequence synthesis, and their attention was focused on the definition and evolution of a local solution. Henrich et al. [3] combined an evolutionary algorithm with the rigorous modelling capabilities of Aspen Plus to optimize the distillation sequence. Similarly, Leboreiro et al. [4] combined the genetic algorithm with a sequential process simulator. Both Henrich’s and Leboreiro’s research combined numerical searching with a modelling tool. The convergence rate of numerical searching is fast, but global optimum solution could not be guaranteed.

Rather than random searching in the solution space, enumeration-like algorithms have been used to optimize distillation sequences. Xu et al. [5] improved 0–1 matrices into code matrices, but the information conveyed by code matrices is insufficient to describe the details of columns. Ni et al. [6] used a process simulation automation server to realize the optimization of heat-integrated sequences at both the sequence level and the column level. Proios et al. [7] proposed an improved generalized modular framework that can overcome the structural complexities of thermally-coupled columns, including dividing wall columns, through systematic and highly detailed structural models. However, the involved models significantly limit the scope of problems the framework can handle. None of the above-mentioned studies have considered nonsharp distillation sequences.

Heat exchanging within sequences has also been introduced to the research of distillation sequence optimization. Jain et al. [8] studied the synthesis of a heat-integrated thermally coupled distillation sequence with energy-capital economic trade-offs, thus enhancing the economy of the sequence. Caballero et al. [9] also synthesized the sequence in common with Jain’s via the Underwood–Fenske–Gilliland equations for column design and used a generalized disjunctive program (GDP) for model formulation, thus making the model more flexible. Zhang et al. [10] optimized the heat integrated nonsharp thermally coupled distillation sequence through an improved simulated annealing algorithm, thus increasing the searching efficiency. The energy is saved by heat integration in the heat exchanger network of the distillation sequence, but heat integration can only be used when there is a large pressure difference between the columns in the sequence [10]. Furthermore, thermal coupling or heat integration increase the complexity and instability of the system. Specific examples of heat integration and thermal coupling for energy saving were considered in the research of Jain, Caballero and Zhang, but their work is highly dependent on the corresponding configuration considered.

Optimization including a non-sharp distillation sequence has gradually received the attention of researchers. Among the relevant studies, Nath et al. [11] proposed a material allocation diagram, but this was not suitable for the optimization problem when the considered component number is more than three. Bamopoulos et al. [12,13] improved the material allocation diagram and combined the empirical rules with a depth-first search strategy, but the physical meaning of each element in the component recovery matrix is lost as the corresponding vector of each product is normalized every time the matrix is transformed. Muraki et al. [14] proposed a two-stage evolutionary method based on the achievements of Nath, but the computational load increases rapidly when this method is used to handle large-scale problems. The research of Nath, Bamopoulos and Muraki were based on material distribution diagrams, which are specified for each sequence.

Sargent and Gaminibandara [15] proposed a representation method for superstructures including nonsharp separation to make the whole MINLP problem for distillation sequence optimization modelled in a rigorous mathematical expression, and more details of a specific sequence can be optimized by this method. Compared to the achievements of Sargent and Gaminibandara, Floudas et al. [16] refined the representation method of the superstructure and proposed the MINLP model for superstructure optimization. Based on the mature representation of the superstructure, Yeomans and Grossmann [17,18] proposed two methods, the state task network (STN) and the state equipment network (SEN), to establish the superstructure; GDP was used to model the superstructure optimization problem, but structures which cannot be exclusively represented by Boolean variables are difficult to support in this method, e.g., side rectifiers and side strippers. Gaballero and Grossmann [19] used GDP to model the STN superstructure, verifying the feasibility of the method proposed by Yeomans and Grossmann. The methods based on the MINLP model needs complex solving algorithms, and the existing solving algorithms possibly fall into local optimum.

As distillation sequence optimization based on the superstructure representation method requires a rigorous mathematical foundation, optimization methods with simplified mathematical operations have been applied in distillation sequence optimization research. Rong et al. have proposed a series of heuristic and mathematically simplified methods for synthesis of sequences including dividing wall columns [20] and process intensification of sequences with respect to thermal couplings and heat integration [21,22,23,24,25,26], promoting optimization efficiency, improving the theoretical foundation of the optimization method and proposing new energy saving configurations of the sequence. Shah and Kokossis [27] proposed a method combining knowledge rules with mathematical programming to construct the search space. However, due to the limitation of empirical rules, some feasible distillation sequences have not been considered by this method, and the real optimal distillation sequence may not be obtained. Agrawal et al. [28,29] proposed a systematic mathematical method optimizing nonsharp distillation sequences with thermal coupling; however, with the increase of component number, the number of feasible distillation sequences is becoming larger and larger, resulting in unfeasible calculations.. In addition to the above conventional methods, Ulaganathan et al. [30] used a sequential minimization algorithm to optimize 3–5 components nonsharp distillation sequence, including complex columns, but when the component number is more than three, global optimization is hard to guarantee.

It can be observed that the representation of superstructures, the modelling of problems, the thermal coupled distillation sequences and the optimization algorithm have been investigated in previous research, which made the optimization of distillation sequence a very popular topic in process system engineering area. As Gibran said, we already walked too far, down to we had forgotten why embark. No matter how complicate the problem can be, the optimization of distillation sequence itself is still obtained via a good choice of column sequence with all columns optimized. Hendry et al. [31] proposed dynamic programming to optimize the distillation sequence. Based on the distillation sequence optimization method of Hendry, dividing wall columns were considered into the sharp distillation sequence by Zhang et al. [32]. By method used by Hendy, Zhang and Ni, the optimization problem is divided into two sub-problems at the sequence level and the column level, effectively separating the superstructure and column optimization. The solution is found by searching possible subsequences and ruling out the non-optimal ones sequentially to avoid random searching within non-continuous feasible domain. The optimization of individual columns is easy to obtained with the wide availability of commercial software such as Aspen Plus, while the ruling out is relatively hard for nonsharp distillation sequences as there are no unique subsequence in this situation any more, but the idea of ruling out significantly saves computational load if a proper strategy for ruling out can be proposed. Both the divide-and-conquer strategy and reliable column model are implied in the dynamic programing method, inspiring a way for this work.

In this work, the differences of subsequences in both sharp and nonsharp distillation sequences are illustrated in Section 2. A framework for separating the superstructure of nonsharp distillation problems is proposed in Section 3, in which modified ruling out is applied to speed up the sequence-level searching. Two cases are studied in Section 4 and conclusions are drawn at the end.

2. Difference Between Optimizations of Sharp and Nonsharp Distillation Sequences

In a nonsharp distillation column, there is one or more components distributed to both the top outflow and the bottom outflow. The nonsharp distillation sequence contains at least one nonsharp distillation column.

2.1. An Example of an Industrial Nonsharp Distillation Sequence

An industrial nonsharp distillation sequence is shown in Figure 1.

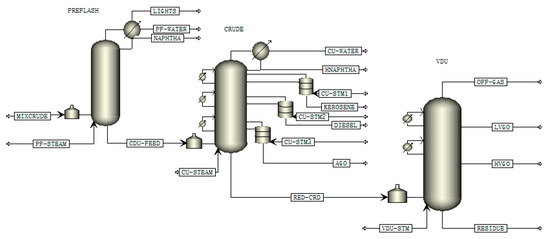
Figure 1. An industrial nonsharp distillation sequence.

As listed in Table 1, the crude oil is separated into several mixture products according to boiling point ranges by this sequence. In Figure 1, the left column is a prefractionator, the middle one is an atmospheric column, and the right one is a vacuum column. This kind of nonsharp distillation sequence is widely applied in petroleum refineries. Obviously, the adjacent products of this example overlap each other in composition.

Table 1. The composition of products of this example.

Product Name	Composition
lights	C1–C4
naphtha	C5–C7
heavy naphtha (HNAPHTHA)	C7–C11
kerosene	C9–C17
diesel	C10–C22
atmospheric gas oil (AGO)	C13–C30
light vacuum gas oil (LVGO)	C16–C40
heavy vacuum gas oil (HVGO)	C22–C60
residue	>C50

2.2. Hybrid Multiway Trees of Solution Space and Distillation Sequences

Rather than the representation of solution space for sharp distillation sequence by ordinary multiway tree, a hybrid tree illustrated in this section is more suitable to represent nonsharp distillation sequence solution space because it can store the extra information of nonsharp separation. Both kinds of hybrid multiway trees are built alternately by subgroup level and sub-problem level. As the solution space tree is built level by level, the sequence trees included in the solution space tree are also built level by level. The difference between these two kinds of trees is shown in Figure 2.

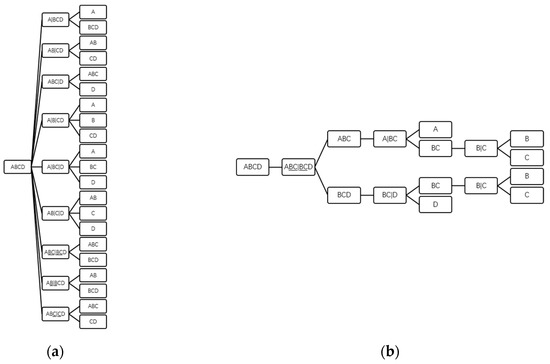
Figure 2. Two kinds of hybrid multiway tree structures for different representation functions are listed as: (a) A four-component non-sharp solution space with only three levels expanded and (b) a four-component non-sharp distillation sequence (the letters represent the components and the underlined ones represent the middle components).

The difference between them is that the subgroup node of a solution space tree expands all its sub-problem child nodes, but that of a sequence tree only expands one sub-problem child node. The hybrid multiway tree of the solution space contains all hybrid multiway trees for feasible distillation sequences in a specific split as outlined in this work. As the distillation sequence consisting of simple columns is the without-integration basic form for other more complex distillation sequences, the split to generate the solution space is assumed that for every subgroup node in the solution space tree, four kinds of columns (a sharp simple column (RadFrac module), a dividing wall column (Petlyuk module), a two-middle-components nonsharp simple column, and an one-middle-component nonsharp simple column, respectively) are attempted to expand its sub-problem child nodes. As at least one component must be ensured to be sharp separated at a split, the exception of this split is that the sub-problems like AB|ABCD or A|ABCD are forbidden. The purpose of the sequence is to get pure-component products. Using this split, the solution space contains both sharp sequences and nonsharp sequences. As we are focusing on theordinary situation of the distillation sequence, vacuum or pressurized distillations are not considered in this work.

2.3. Differences Between Optimization Direction of Sharp and Nonsharp Distillation Sequences

The sequence tree with only sharp distillations can be illustrated as a line structure, as Figure 3a shows, but the one with non-sharp distillations includes more possibilities, and therefore amore complicate structure is required, as Figure 3b shows. In Figure 3a, one end leaf node confirms a sharp sequence; but in Figure 3b, only one end leaf node is unable to confirm a nonsharp sequence, owing to its multi-branch structure. Before building the sharp sequence solution space tree, the sub-problems can be determined in advance, but due to more degrees of freedom in nonsharp separation, the sub-problems with the same components and the same split points may be slightly different in terms of feed flowrate and component ratio, such as sub-problem A|BC generated from sub-problem ABC|BCD and sub-problem A|BC generated from sub-problem ABC|D, as there is only the latter one in sharp distillation sequences; therefore, the sub-problems in nonsharp distillation sequences cannot be predicted at the beginning. Thus, the sub-problem calculation of sharp sequence optimization is conducted from the end leaf nodes to the root node in tree structures of a sharp sequence solution space, opposite to that of nonsharp sequence optimization. The end leaf nodes are signed in grey color in Figure 3.

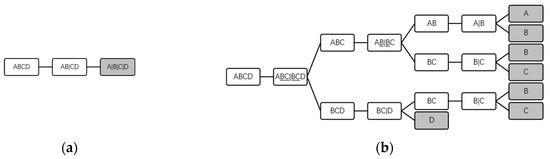
Figure 3. Two kinds of tree-like structures for the distillation sequence representation are listed as: (a) A completed sharp distillation sequence tree (line structure) and (b) A completed nonsharp distillation sequence hybrid multiway tree.

2.4. The Recurrence of Numbers of Sequence, Subgroup and Sub-Problem in the Assumed Split Described in Section 2.2

The purpose of the assumed split is to divide the R-components mixture into pure components. Assuming a simple column is first in the sequence, the component number of the top outflow is set as j, then the component number of the bottom outflow is R − j. If the sequence number of i-components mixture is $S_i$ for a specific split point, the sequence number is $S_j{S}_{R-j}$. Following this logic, the sequence number for a sharp simple column that is first in the sequence is Equation (1).

$$a_R={\displaystyle \sum _{j=1}^{R-1}{S}_j}{S}_{R-j}$$

(1)

Assuming that a dividing wall column is first in the sequence, as a dividing wall column has two splits, for the upper split, there are R − 2 split points to choose, and thus the upper limit of j in Equation (2) is R − 2. Similarly to the sharp simple column, the component numbers of the top outflow and middle outflow are set as j and k, then the component number of the bottom outflow is R − j − k. Therefore, the sequence number for the dividing wall column that is first in the sequence with a specific upper split point is $S_j{\sum }_{k=1}^{R-j-1}{S}_k{S}_{R-j-k}.$ Then, Equation (2) [32] is obtained by varying the upper split point.

$$b_R={\displaystyle \sum _{j=1}^{R-2}{S}_j}{\displaystyle \sum _{k=1}^{R-j-1}{S}_k{S}_{R-j-k} (R>2)}$$

(2)

According to the properties of two kinds of nonsharp simple column, Equation (3) for a two-middle-components nonsharp simple column first in the sequence and Equation (4) for an one-middle-component nonsharp simple column first in the sequence are similar to the form of Equation (1).

$$c_R={\displaystyle \sum _{j=2}^{R-2}{S}_{j+1}{S}_{R-j+1}}$$

(3)

$$d_R={\displaystyle \sum _{j=2}^{R-1}{S}_j{S}_{R-j+1} (R>2)}$$

(4)

Then the total sequence number is calculated by Equation (5).

$$S_R=a_R+b_R+c_R+d_R$$

(5)

The initial values of Equations (1)–(4) are listed below.

$$\begin{array}{l}{a}_1=1, b_1=0, c_1=0, d_1=0\\ a_2=1, b_2=0, c_2=0, d_2=0\\ a_3=2, b_3=1, c_3=0, d_3=1\\ a_4=9, b_4=3, c_4=16, d_4=8\end{array}$$

Table 2 is obtained by using recurrence Equations (1)–(5).

Table 2. Sequence number.

Component Number (R)	Sequence Number (SR, Including Nonsharp Sequences)	Sequence Number (Not Including Nonsharp Sequences)
1	1	1
2	1	1
3	4	3
4	36	10
5	471	38
6	7457	154
7	131,379	654
8	2,475,056	2871
9	48,806,969	12,925
10	994,831,083	59,345

Then by using a recurrence program, Table 3 for subgroup number and Table 4 for sub-problem number are also obtained.

Table 3. Subgroup number.

Component Number (R)	Subgroup Number (Including Nonsharp Sequences)	Subgroup Number (Not Including Nonsharp Sequences)
2	3	3
3	10	6
4	70	10
5	579	15
6	4761	21
7	37,852	28
8	293,580	36
9	2,242,401	45
10	16,971,043	55

Table 4. Sub-problem number.

Component Number (R)	Sub-Problem Number (Including Nonsharp Sequences)	Sub-Problem Number (Not Including Nonsharp Sequences)
2	1	1
3	8	5
4	56	15
5	397	35
6	2980	70
7	22,736	126
8	172,988	210
9	1,308,324	330
10	9,847,517	495

From Table 3 and Table 4, the conclusion is drawn that both the subgroup number and sub-problem number including nonsharp sequences will increase exponentially as the component number increases, because the subgroup nodes and sub-problem nodes with the same component and split point in the solution space including nonsharp sequences can not be merged due to the difference in flow rates of components.

3. Methodology

Inspired by the dynamic programing method for sharp distillation sequences, a bi-level distillation sequence optimization algorithm is proposed in this work to decompose the MINLP into an IP problem in the upper level and NLP problems in the lower level, by which the optimization of the separation sequence is implemented at the upper level and the single column within the sequence is simulated and optimized at the lower level.

3.1. The Framework with Aspen

The framework in Figure 4 is divided into three parts. The grey part, where the sequence is optimized, is edited by Python. The sparse oblique-line part, where column is optimized, is edited by VB.NET. The dense oblique-line part for the simulation and optimization of the column is the Aspen modules running in the background. The relationship among the three parts of the framework is shown in Figure 5.

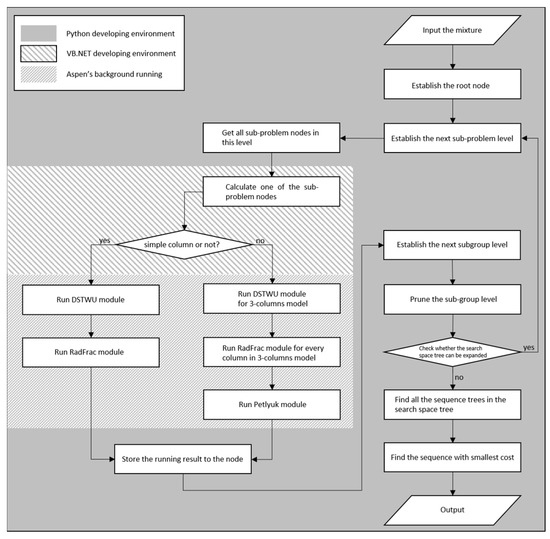
Figure 4. Diagram of framework.

Figure 5. The relationship among the three parts of the program framework (arrows represent data streams).

The VB.NET program (column optimization plug-in program) is applied to connect the Python program and the Aspen Plus background-running modules by manipulating the ActiveX interface of Aspen Plus. The Python language is an integrated language with many modules and functions encapsulated into packets, making the coding for sequence-level optimization easier.

There are two options to call and manipulate the Aspen modules automatically through the ActiveX interface. One is to code in Python language with a packet; the other is to code in VB.NET language. The later one is adopted in this work, because the Aspen help file [33] illustrates only the formats of VB.NET codes for manipulating the ActiveX interface, making coding in VB.NET rather than Python to operate Aspen modules more user-friendly.

The modules of Aspen used in this work can be divided into two categories. For simple columns and dividing wall columns (three outflows) respectively, as shown in the grey part of Figure 3, one includes the DSTWU (distillation-Winn-Underwood) module and RadFrac module, a module for rigorous distillation design, while another includes the DSTWU module, RadFrac module and Petlyuk module. The DSTWU module uses the Winn–Underwood–Gilliland (WUG) method for a short-cut. The Winn equations are cited as Equations (6) and (7).

$$N_{\min }=\frac{\ln \left[\frac{x_{LK,D}}{x_{LK,B}}(\frac{x_{HK,B}}{x_{HK,D}})\right]}{\ln {\beta }_{LK/HK}}$$

(6)

$${\beta }_{LK/HK}=\frac{K_{LK}}{K_{HK}{}^{{\theta }_{LK}}}$$

(7)

where subscripts D, B, LK, HK and x represent the top product, bottom product, light key component, heavy key component and liquid mole fraction, respectively. The minimum stage number N_min can be obtained by using Winn equations. The Underwood equations are cited as Equations (8) and (9).

$${\displaystyle \sum _{j=1}^N\frac{{\alpha }_j{f}_j}{{\alpha }_j-\phi }=F(1-q)}$$

(8)

$${\displaystyle \sum _{j=1}^N\frac{{\alpha }_j{\xi }_j{f}_j}{{\alpha }_j-\phi }=D(R_{\min }+1)}=V_{\min }$$

(9)

where α_j, f_j, φ, F, q, ξ_j and D represent the relative volatility of component j, flow rate of component j, the root of Underwood equations, the feed flow rate, the feed thermal state, the recovery of component j at the top of the column and the distillate flow rate, respectively. The minimum reflux ratio R_min can be obtained by using Underwood equations. The Gilliland correlation is cited as Equation (10).

$$\frac{N_t-N_{\min }}{N_t+1}=0.75\left[1-{\left(\frac{R-R_{\min }}{R+1}\right)}^{0.5668}\right]$$

(10)

The theoretical stage number N_t can be obtained by using the Gilliland correlation.

Many distillation sequence optimization works depend on using only the WUG method to simulate a single column. Based on the WUG method, a more rigorous module called RadFrac is used in this work to improve the simulation of a single column. The RadFrac module solves material balance, energy balance and phase equilibrium simultaneously by using two nested iteration loops and the Newton algorithm to converge.

The Petlyuk module can be regarded as a three-columns module with complete thermal coupling and it converges in the same way as the RadFrac module does. The prefractionator of the Petlyuk module is a nonsharp column, but the whole Petlyuk module is designed only for sharp separation. As the Petlyuk module is thermodynamically equivalent to the ideal dividing wall column, the dividing wall column is also for sharp separation only.

The Aspen Plus ActiveX automation server is used in this work as an interface to connect theVB.NET program and the Aspen Plus modules. This server exposes objects of Aspen Plus through the COM (component object model), and the vast majority of parameters are stored in a tree structure. Using VB.NET code in a specific format can navigate this tree structure and change the data on it. With this interface, the inputs and the results of Aspen Plus simulations can be connected to other applications.

In addition, this program framework can be further expanded to optimize distillation sequences with more complex structures.

3.2. The Search Space and the Pruning Operation

The scale of the solution space tree can be huge, and expanding the whole solution space tree consumes too much computing resource, therefore, a pruning method is proposed. The method can be implemented in two basic steps: first, once a subgroup level is finished, whether completed sequence trees are contained in the current incomplete solution space tree is determined; second, if there are completed sequence trees in the current incomplete solution space tree, the best one of them will be selected. All sequence trees contained in the current incomplete solution space tree will be compared with the best completed sequence tree while the ones worse than this one will not be expanded by deleting the nodes of the newest subgroup levels of them. In this method, the search space is generated. If the solution space tree is not pruned, the search space is equivalent to the solution space.

In Figure 6, after finishing the second subgroup level of the solution space tree, the black nodes make up a completed sequence tree earliest. If the cost of sequence tree ABC//AB|C//AB/C is greater than that of the black-nodes tree, the subgroup nodes AB and C of this sequence tree will be removed.

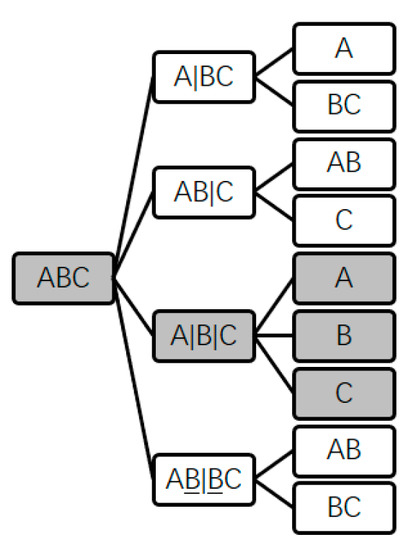
Figure 6. An example of pruning.

4. Results and Discussion

Using framework illustrated in Section 3, two cases including an industrial one were optimized in this section and their results were discussed. The sequences’ TACs of the two cases are all calculated according to Appendix A.

4.1. Four-Component Alkane Case

The original inflow composition of this case is listed in Table 5.

Table 5. The original inflow of the four-component alkane case.

Component	Flow Rate (kmol/h)
n-Hexane	200
n-Heptane	200
n-Octane	200
n-Nonane	200

The components n-Hexane, n-Heptane, n-Octane and n-Nonane are represented by the letters A, B, C and D respectively in this section. The costs of sharp and non-sharp sequences of this case are shown in Table 6 and Table 7 respectively.

Table 6. The costs of sharp sequences of the four-component alkane case. TAC = total annual cost.

Number	TAC (Dollar)	Containing Dividing Wall Column or Not
1	17,857,006	yes
2	22,639,012	no
3	22,057,879	yes
4	18,258,990	yes
5	18,613,382	yes
6	18,274,174	yes
7	22,199,609	no
8	23,752,499	no
9	25,522,719	no
10	26,919,693	no

Table 7. The costs of nonsharp sequences of the four-component alkane case.

Number	TAC (Dollar)	Containing Dividing Wall Column or Not
1	20,643,115	yes
2	19,645,301	yes
3	26,352,487	yes
4	25,823,053	no
5	25,314,930	no
6	26,053,113	no
7	28,598,757	no
8	28,090,634	no
9	28,828,817	no
10	23,960,076	yes
11	23,451,953	yes
12	22,506,092	yes
13	25,281,796	yes
14	25,989,749	yes
15	24,190,136	yes
16	29,306,710	no
17	28,798,587	no
18	29,536,771	no
19	24,814,920	no
20	29,052,332	no
21	23,895,168	no
22	24,144,968	no
23	24,599,039	no
24	28,781,709	no
25	31,205,129	no
26	31,941,852	no

The optimal one of the 36 sequences is shown as Figure 7.

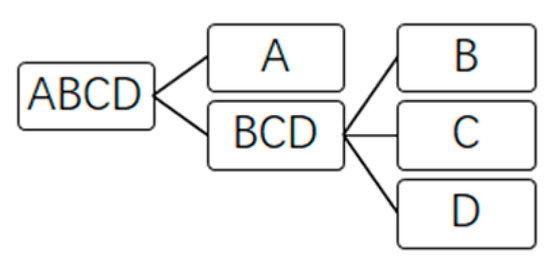
Figure 7. The optimal sequence of the four-component alkane case with 17,857,006 dollars TAC. n-Hexane = A; n-Heptane = B; n-Octane = C; n-Nonane = D.

The four-components case has 36 sequences (including 10 sharp ones) according to the split in Section 2.2. From Table 7, it can be concluded that most of the nonsharp sequences with relatively small costs contain dividing wall columns. Thus, thermal coupling is the most important factor for energy savings.

From Table 8, it can be noticed that after pruning, 12 of the 36 sequences remain. As concluded from Table 9, the scale of the search space tree is smaller than that of the solution space tree. Part of the possible sequences of this case are shown in Figure 8.

Table 8. Remaining sequences’ costs of the four-component alkane case after pruning.

Number	TAC (Dollar)	Sharp or Not
1	17,857,006	yes
2	22,639,012	yes
3	22,057,879	yes
4	18,258,990	yes
5	18,613,382	yes
6	18,274,174	yes
7	20,643,115	no
8	19,645,301	no
9	26,352,487	no
10	22,199,609	yes
11	23,752,499	yes
12	24,814,920	no

Table 9. Comparison of node numbers between the solution space tree (before pruning) and the search space tree (after pruning) of the four-component alkane case.

Level	Solution Space Tree	Search Space Tree
1	1	1
2	9	9
3	21	21
4	31	31
5	68	17
6	24	10
7	48	14

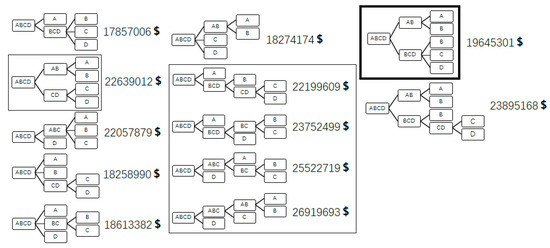
Figure 8. Part of the possible sequences of the four-component alkane case and their TACs.

From the four-component alkane case, it can be concluded that in this case, only one nonsharp sequence (enclosed in thick frame) with a smaller distillation rate nonsharp simple column and a dividing wall column is better than all sharp sequences without dividing wall columns (enclosed in slim frame). The cost of a smaller-distillation-rate simple column is less than that of the ones with larger distillation rates and same feeds, so as summarized from sequences enclosed in slim frame, the total distillation rate of the sequence is positively correlated to its TAC, showing that total distillation rate is an influencing factor of distillation sequence TAC. Energy can be saved by using dividing wall columns. Using nonsharp simple columns without any integration in the sequence to get all products finally sharp separated is ineffective (more nonsharp simple columns, more ineffective). Using a rigorous distillation model is so computationally intensive that only WUG equations are employed in other optimization methods based on MINLP problem solving. However, in this framework, the optimization efficiency is improved so that the rigorous model is used for computational efficiency.

Assuming that the component number of the origin mixture is R. According to the conclusion above, the split for the nonsharp separation requirement is proposed as follows.

• Using sharp distillation columns (simple column and dividing wall column) for sharp split points.
• Using nonsharp simple column for nonsharp split points.

The solution space generated by this split is a subset of that generated by the split in Section 2.2. Then the recurrence formula for sequence number S_R is Equation (11), similar to that of sharp distillation sequences [34].

$$S_R(\delta )=\{\begin{array}{c}1(R=1)\\ {\displaystyle \sum _{j=1}^{R-1}{S}_j}{S}_{R-j}(R=2)\\ {\displaystyle \sum _{j=1}^{R-1}{S}_j}({\delta }_{S_j})S_{R-j}({\delta }_{S_{R-j}})+{\displaystyle \sum _{j=1}^{R-r(\delta )-2}{S}_j}({\delta }_{S_j}){\displaystyle \sum _{k=1}^{R-r(\delta )-j-1}{S}_k({\delta }_{S_k})S_{R-r(\delta )-j-k}({\delta }_{S_{R-r(\delta )-j-k}})(R>2,r(\delta )\le R)}\end{array}$$

(11)

where δ is the split-point set of sequence number S_R(δ), and r(δ) is the number of nonsharp split points in δ.

4.2. Petroleum Refinery Case

This distillation sequence case is a part of a process in which a mixture containing mixed diesel oil, straight-run diesel oil, FCC (fluid catalytic cracking) diesel oil and diesel oil produced by residue hydrogenation is hydrogenated, then high-pressure-separation gas is separated from the product of the hydrogenation reaction as recycled hydrogen. Finally, the crude diesel oil after hydrogenation is fractionated to produce naphtha and diesel oil. In this distillation sequence case, a mixture is divided into four products by three nonsharp splits. The four products are gas mixtures containing hydrogen, non-condensing gas mixtures, naphtha, and diesel respectively. The purpose of this case is to get all products nonsharp separated. According to the conclusion of the four-component alkane case, the nonsharp simple column should only be employed for nonsharp separation requirement. In this way a nonsharp simple column can work effectively, and the solution space tree obtained is shown in Figure 9.

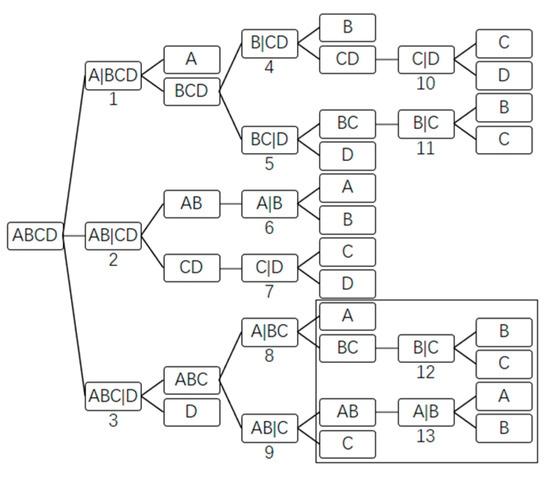
Figure 9. The solution space of the petroleum refinery case (the nodes enclosed in frame are pruned). Gas mixtures containing hydrogen = A; non-condensing gas mixture = B; naphtha = C; diesel oil = D.

The pruning operation is used to downsize this solution space tree. The pruning process is depicted below. The sequence 2\6\7 is the shortest completed sequence, and sequences 1\4, 1\5, 3\8 and 3\9 are compared with sequence 2\6\7. The costs of sequences 3\8 and 3\9 are more than that of sequence 2\6\7, so the child subgroup nodes of sub-problem nodes 8 and 9, sub-problem nodes 12 and 13 and child subgroup nodes of sub-problem nodes 12 and 13 are removed. The remaining sub-problem nodes’ costs and the remaining sequences’ costs of this case after pruning are shown in Table 10 and Table 11 respectively.

Table 10. Remaining sub-problem nodes’ costs of the petroleum refinery case after pruning.

Sub-Problem Node	TAC (Dollar)
1	42,927,499
2	66,525,092
3	104,910,383
4	37,352,492
5	66,867,845
6	6,954,837
7	39,054,059
8	32,594,510
9	69,679,308
10	41,435,554
11	9,448,464

Table 11. Remaining sequences’ costs of the petroleum refinery case after pruning.

Sequence	TAC (Dollar)
1\4\10	121,715,546
1\5\11	119,243,810
2\6\7	112,533,989

Obviously, the optimal sequence of the petroleum refinery case is the sequence 2\6\7. The actual sequence of the petroleum refinery case is 1\4\10. The optimal sequence saves 7.5% of the cost compared to the actual sequence. After pruning, 11 of the 13 sub-problem nodes remain and three of the five sequences remain. By this pruning result, we have shown that the pruning way is effective to reduce the computational load.

5. Conclusions

Under the same separation requirement, the scale of the solution space including both sharp and nonsharp distillation sequences is much larger than that of the solution space only including sharp distillation sequences. The optimization direction in the solution space tree structure of nonsharp distillation sequences is from the root node to the end leaf nodes, opposite to that of sharp distillation sequences. In nonsharp distillation sequences, nonsharp simple columns should be used to fit nonsharp separation requirements or form the thermal coupling column (like the Petlyuk module). The pruning method can reduce the computation required in both sharp and nonsharp distillation sequence optimization. The program framework proposed in this work is verified for automatic and effective optimization of distillation sequences including nonsharp separation.