Multi-Objective Large-Scale ALB Considering Position and Equipment Conflicts Using an Improved NSGA-II
Abstract
1. Introduction
2. Literature Review
- Modeling restrictive parallel constraints: This study explicitly incorporates restrictive parallel constraints, including conflicts associated with workers, equipment, and assembly positions, thereby providing a more realistic representation of large-scale product assembly lines.
- Multi-objective optimization framework: A multi-objective model is formulated with the aims of minimizing the number of workstations, reducing equipment investment costs, and balancing workloads among teams, thereby aligning with practical industrial needs.
- Improved NSGA-II algorithm: An enhanced version of the NSGA-II is developed to solve the proposed model, enabling efficient handling of complex constraints and improvement of solution quality.
- Case study validation: The effectiveness and superiority of the proposed approach are validated through a real-world-inspired case study, demonstrating its potential to reduce costs and enhance production efficiency in large-scale product assembly.
3. Problem Description
3.1. Restrictive Parallel Constraints and Balance Objectives
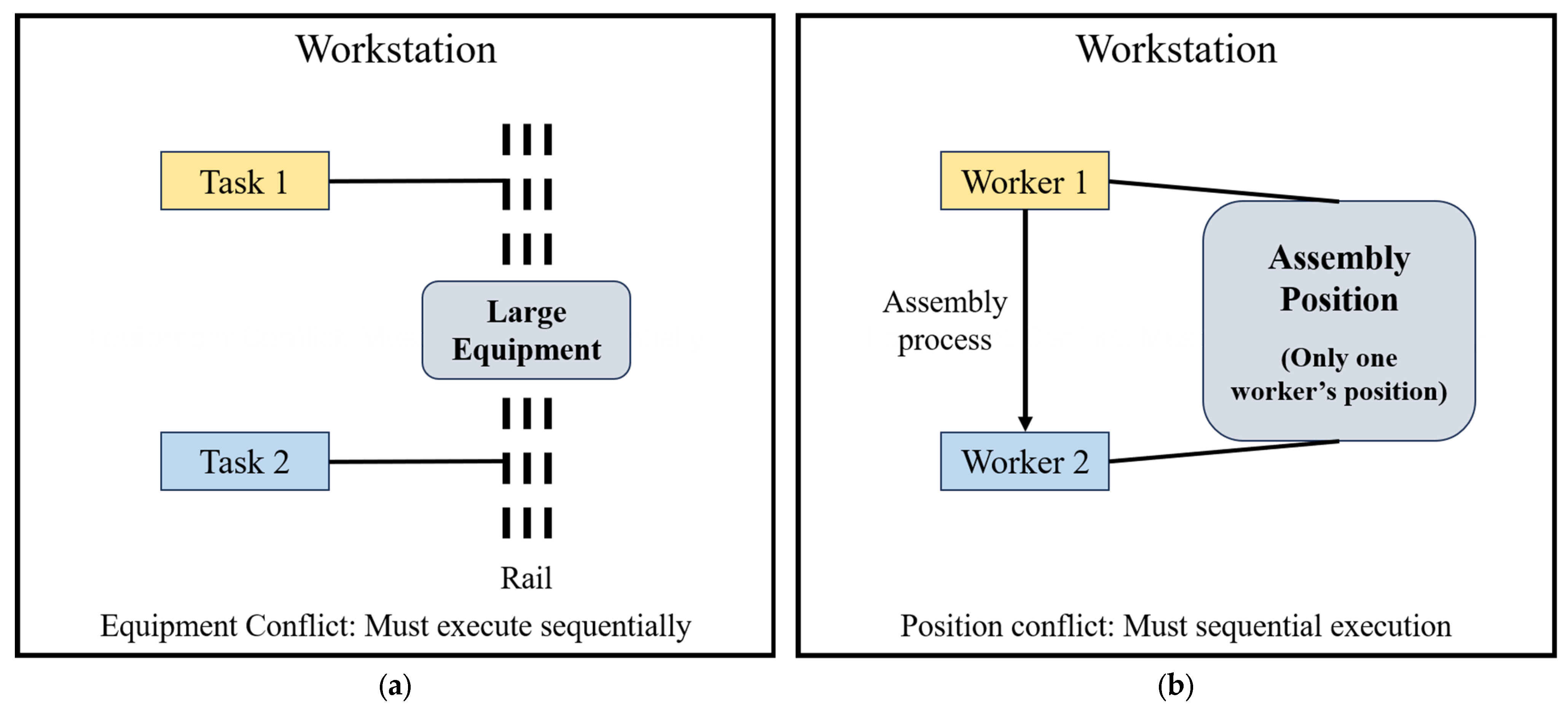
3.2. Assumptions
- The assembly line produces only a single type of product.
- The assembly line has a known and predetermined takt time requirement.
- The precedence relationships among tasks are known.
- The workstation positions and the equipment required for each assembly task are known.
- The processing time for each assembly task is predetermined and independent of the assigned workstation.
- Each workstation position or piece of equipment can perform only one task at a time.
- Workstations are arranged in series, and no parallel workstations are considered.
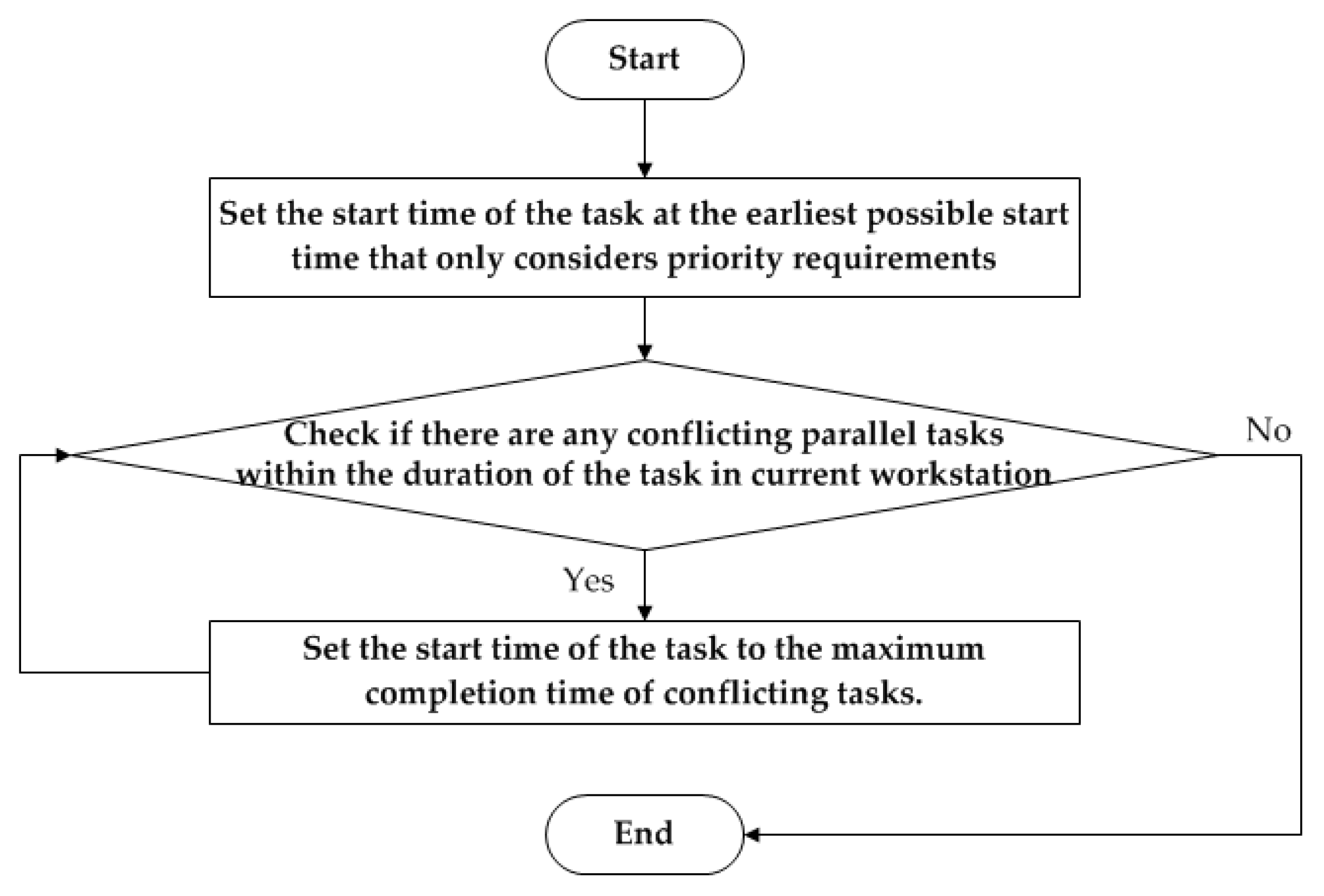
- Parallel tasks within the same workstation are scheduled as early as possible to maximize the number of tasks that can be executed within the workstation.
3.3. Notation and Variables Used in the Proposed Model
3.4. Mathematical Model
3.5. ASP Methods Within the Workstation
- (1)
- The parallel task processing principle of “parallelize as soon as possible if feasible” ensures that the initiation time of parallel tasks at the workstation is advanced to the earliest feasible point. This approach partially reduces the workstation cycle time and ensures that the workstation can accommodate as many tasks as possible under the given task assignment sequence, thereby minimizing the number of workstations and device procurement costs.
- (2)
- After the assembly line is balanced, the cycle time of the bottleneck workstation serves as the workstation cycle time constraint, while other workstations retain some idle capacity. When considering the goals of balancing workload within and between workstations, there remains potential for further optimization in ASP, which can also be addressed through worker reallocation across workstations. These optimizations do not affect the attainment of the balance objective in this study. Therefore, this study focuses on ALB, and it is appropriate to adhere to the parallel task processing principle of “parallelize as early as feasible” in ASP.
4. Improved NSGA-II Algorithm
4.1. NSGA-II Algorithm
4.2. Chromosome Coding
4.3. Chromosome Decoding
- Step 1: Starting from the first gene, check whether the corresponding task is assignable (a task is assignable when all its immediate predecessors have been assigned). If it is, mark the task as assigned and proceed to Step 2; otherwise, skip the gene and examine the next one until a feasible task is identified, then mark it as assigned and proceed to Step 2.
- Step 2: Insert the task corresponding to the gene into the last position of the new chromosome. If there are tasks preceding it, shift them forward by one position and proceed to Step 3.
- Step 3: Delete the gene from the original chromosome and shift subsequent genes forward by one position. Repeat Steps 1–3 until all genes in the original chromosome have been deleted, then proceed to Step 4.
- Step 4: Replace the original chromosome with the newly formed one to complete feasibility testing and repair.
- Step 1: Initialization. Let , , ; initialize the first workstation of the assembly line, and proceed to Step 2 ( is the set of tasks assigned to the -th workstation, is an empty set).
- Step 2: Initialize , indicating preparation to handle the corresponding task in the first gene sequence, and proceed to Step 3.
- Step 3: Determine whether is true. If it is, proceed to Step 4; otherwise, proceed to Step 11.
- Step 4: Because , it indicates the absence of an immediate predecessor task of in the currently assigned tasks within the -th workstation. Initialize , , turn to Step 5.
- Step 5: Determine whether is true. If it is, proceed to Step 6; otherwise, proceed to Step 10.
- Step 6: Determine whether is empty. If it is, proceed to Step 8; otherwise, proceed to Step 7.
- Step 7: Determine whether is true, where . If it is, proceed to Step 8; otherwise, proceed to Step 9.
- Step 8: Initialize , , turn to Step 17.
- Step 9: Find the task with the minimum end-time and its corresponding end-time in , denote them as and , respectively, let , and remove from . Then turn to Step 5.
- Step 10: Initialize ; initialize the subsequent workstation. Proceed to Step 3.
- Step 11: Initialize , , turn to Step 12.
- Step 12: Initialize , turn to Step 13.
- Step 13: Determine whether is true. If it is, proceed to Step 14; otherwise, proceed to Step 10.
- Step 14: Remove tasks with end-time less than in , then proceed to Step 15.
- Step 15: Determine whether is empty. If it is, proceed to Step 8; otherwise, proceed to Step 16.
- Step 16: Determine whether is true, where . If it is, proceed to Step 8; otherwise, proceed to Step 17.
- Step 17: Find the task with the minimum end-time in , let , and remove from . Then turn to Step 13.
- Step 18: Verify whether all tasks have been assigned. If so, proceed to Step 19; otherwise, return to Step 2.
- Step 19: Output the final task assignment results.
4.4. Population Initialization
- Step 1: Construct the task precedence relationship matrix. Based on the precedence relationships among tasks, define the relationship matrix such that if task is the immediate predecessor of task , then , otherwise, .
- Step 2: Initialize .
- Step 3: Randomly select a task from the set of tasks whose corresponding column sum in the matrix equals 0, and assign it to the -th gene position of the chromosome. Remove the corresponding row and column of this task from matrix , update accordingly, and increment by 1.
- Step 4: Repeat Step 3 until matrix becomes empty, thereby forming a feasible chromosome.
- Step 5: Repeat Steps 2–4 until the entire initial population is generated.
4.5. Genetic Operators
4.5.1. Selection Operator
- (1)
- Elite Pool Update: Identify chromosomes on the Pareto front in the current population, merge them with the existing elite pool, and select the Pareto-optimal chromosomes from the merged set. Add these selected chromosomes to the elite pool and remove others to complete the update.
- (2)
- Population Update: Inspired by the artificial immune algorithm [54], population updates are performed based on affinity. The affinity of a chromosome is defined as a function of its dominance rate and concentration:
4.5.2. Crossover Operator
- (1)
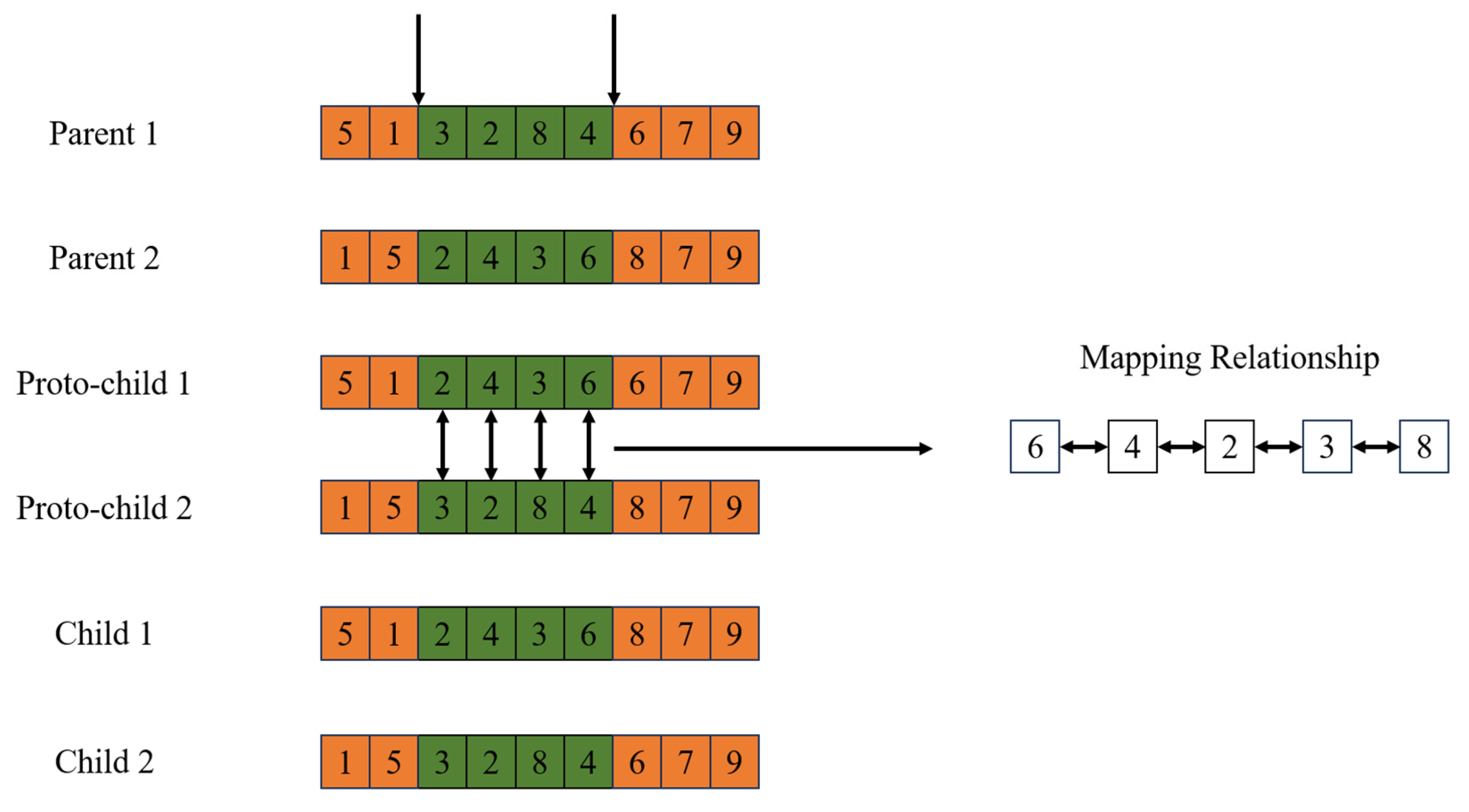
- Crossover Based on Sequence Features. This operator inherits the sequence features of the crossover fragments from the parent generation while ensuring the feasibility of the task assignment sequence after crossover. Consequently, no chromosome repair is required, which substantially reduces the algorithm’s computational workload. The specific crossover process is illustrated in Figure 5.
- (2)
- Crossover Based on Full Preservation of Crossover Segments. In this method, the offspring fully retain the parental crossover segment, although the positions of the segment and other genes may vary. This operator is capable of inheriting validated, effective local structures from the parent individual. The specific crossover process is illustrated in Figure 6.
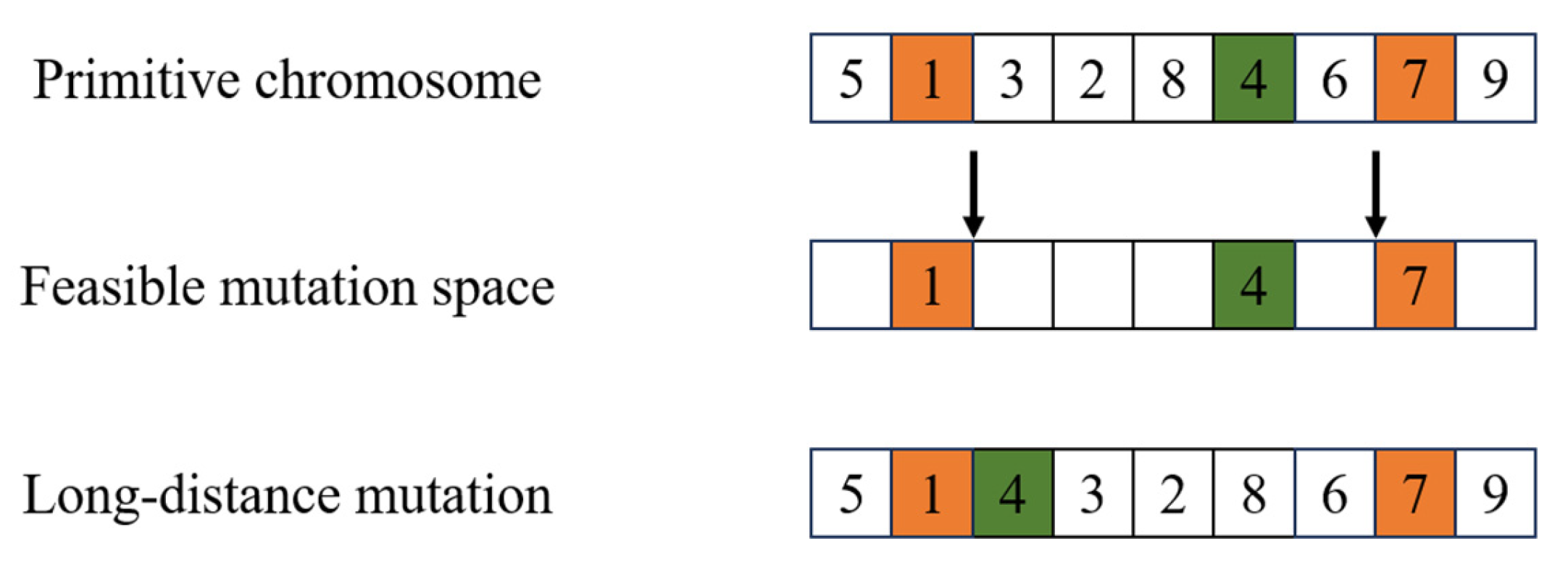
4.5.3. Mutation Operator
4.6. Iteration Termination Conditions
5. Case Study
5.1. Case Introduction
5.2. Calculation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Sample Calculation
| for gen = 1:max_gen |
| offspring = generate_offspring(pop_size, population, crossover_rate, mutation_rate, predecessors, ... |
| durations, m, conflict_jobs, required_equipment, … |
| equipment_types, equipment_cost_per_type); |
| combined_population = [population; offspring]; |
| for i = 1:size(combined_population, 1) |
| combined_population(i, :) = repair_chromosome(combined_population(i, :), predecessors); |
| end |
| combined_objectives = calculate_objectives(combined_population, predecessors, durations, m, conflict_jobs, required_equipment, equipment_types, equipment_cost_per_type); |
| [fronts, affinities] = non_dominated_sort_with_affinity(combined_objectives, gen); |
| population = tournament_selection(combined_population, affinities, pop_size); |
| current_combined_pareto = fronts{1}; |
| current_combined_elite = combined_population(current_combined_pareto, :); |
| current_combined_obj = combined_objectives(current_combined_pareto, :); |
| if isempty(current_elite_set) |
| merged_elite = current_combined_elite; |
| merged_obj = current_combined_obj; |
| else |
| merged_elite = [current_elite_set; current_combined_elite]; |
| merged_obj = [current_elite_objectives; current_combined_obj]; |
| [~, unique_indices] = unique(merged_elite, 'rows'); |
| merged_elite = merged_elite(unique_indices, :); |
| merged_obj = merged_obj(unique_indices, :); |
| end |
| [merged_fronts, ~] = non_dominated_sort_with_affinity(merged_obj, 1); |
| new_pareto_indices = merged_fronts{1}; |
| current_elite_set = merged_elite(new_pareto_indices, :); |
| current_elite_objectives = merged_obj(new_pareto_indices, :); |
| elite_count = size(current_elite_set, 1); |
| if ~isempty(current_elite_objectives) |
| min_stations = min(current_elite_objectives(:,1)); |
| min_cost = min(current_elite_objectives(current_elite_objectives(:,1) == min_stations, 2)); |
| max_load_balance = max(current_elite_objectives(current_elite_objectives(:,1) == min_stations & current_elite_objectives(:,2) == min_cost, 3)); |
| else |
| current_obj = calculate_objectives(population, predecessors, durations, m, conflict_jobs, required_equipment, equipment_types, equipment_cost_per_type); |
| min_stations = min(current_obj(:,1)); |
| min_cost = min(current_obj(current_obj(:,1) == min_stations, 2)); |
| max_load_balance = max(current_obj(current_obj(:,1) == min_stations & current_obj(:,2) == min_cost, 3)); |
| end |
| similarity_ratio = 0; |
| if gen > 1 && ~isempty(previous_elite_set) && elite_count > 0 |
| similarity_ratio = calculate_elite_similarity(current_elite_set, previous_elite_set); |
| end |
| consecutive_similar_count = 0; |
| end |
| previous_elite_set = current_elite_set; |
| end |
References
- Aguilar, H.; García-Villoria, A.; Pastor, R. A survey of the parallel assembly lines balancing problem. Comput. Oper. Res. 2020, 124, 105061. [Google Scholar] [CrossRef]
- Schmid, N.A.; Montreuil, B.; Limère, V. Modeling and solving integrated assembly line balancing, assembly line feeding, and facility sizing problems. Int. J. Prod. Econ. 2024, 277, 109354. [Google Scholar] [CrossRef]
- Gianassi, M.; Leoni, L.; Fantozzi, I.C.; De Carlo, F.; Tucci, M. Mixed-model and multi-model assembly lines: A systematic literature review on resource management. J. Manuf. Syst. 2025, 82, 632–657. [Google Scholar] [CrossRef]
- Şahin, M.C.; Tural, M. Robotic stochastic assembly line balancing. Flex. Serv. Manuf. J. 2023, 35, 1076–1115. [Google Scholar] [CrossRef]
- Tiacci, L. Simultaneous balancing and buffer allocation decisions for the design of mixed-model assembly lines with parallel workstations and stochastic task times. Int. J. Prod. Econ. 2015, 162, 201–215. [Google Scholar] [CrossRef]
- Hou, W.; Zhang, S. Assembly line balancing and optimal scheduling for flexible manufacturing workshop. J. Mech. Sci. Technol. 2024, 38, 2757–2772. [Google Scholar] [CrossRef]
- Kheirabadi, M.; Keivanpour, S.; Chinniah, Y.A.; Frayret, J. Human-robot collaboration in assembly line balancing problems: Review and research gaps. Comput. Ind. Eng. 2023, 186, 109737. [Google Scholar] [CrossRef]
- Huang, D.; Mao, Z.; Fang, K.; Fu, E.; Pinedo, M.L. An Improved Combinatorial Benders Decomposition Algorithm for the Human-Robot Collaborative Assembly Line Balancing Problem. INF. J. Comput. 2024, 37, 1267–1283. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, X.; Luo, H.; Xiong, J. An Improved Multi-Objective Evolutionary Approach for Aerospace Shell Production Scheduling Problem. Symmetry 2020, 12, 509. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, C.; Wang, J.; Zhang, L.; Hu, X.; Ma, X. Dynamic Modeling Method of Mission Reliability of a Multi-State Manufacturing System with Multiple Production Lines. IEEE Access 2020, 8, 57012–57023. [Google Scholar] [CrossRef]
- Telles, E.S.; Lacerda, D.P.; Morandi, M.I.; Piran, F.A. Drum-buffer-rope in an engineering-to-order system: An analysis of an aerospace manufacturer using data envelopment analysis (DEA). Int. J. Prod. Econ. 2020, 222, 107500. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, L.; Wang, J.; Zhu, T.; Jin, L. Investigating product innovation pathway from a modular standpoint: A case study of large aircraft assembly line. Heliyon 2023, 10, e23356. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.V. Optimally balancing large assembly lines with `FABLE’. Manag. Sci. 1988, 34, 240–253. [Google Scholar] [CrossRef]
- Martignago, M.; Battaïa, O.; Battini, D. Workforce management in manual assembly lines of large products: A case study. IFAC-Pap. 2017, 50, 6906–6911. [Google Scholar] [CrossRef]
- Liao, S.; Sang, C.; Liu, A.; Liu, H. Solving Type-I unpaced synchronous mixed-model two-sided assembly line balancing problem using a genetic algorithm. Comput. Oper. Res. 2025, 184, 107257. [Google Scholar] [CrossRef]
- Yin, X.; Yang, Y.; Li, X.; Wu, R.; Guo, A.; Zhao, Q. Research on the balancing problem of human-robot collaborative assembly line in SMEs considering ergonomic risk and cost. Comput. Ind. Eng. 2025, 204, 111091. [Google Scholar] [CrossRef]
- Jiao, Y.; Wang, Y.; Su, X.; Wang, F. An ant colony hybrid simulated annealing algorithm for collaborative optimization of robotic mixed-model parallel two-sided assembly lines balancing. Comput. Oper. Res. 2025, 182, 107113. [Google Scholar] [CrossRef]
- El Machouti, S.; Hlyal, M.; Babay, A.; Alami, J.E. Optimisation of Simple Assembly Line Balancing Problem Type E: A Systematic Literature Review. Manag. Syst. Prod. Eng. 2024, 32, 162–173. [Google Scholar] [CrossRef]
- Aguilar, H.; García-Villoria, A.; Pastor, R. Heuristic and metaheuristic procedures for the buffer sizing problem in parallel assembly lines balancing problem with multi-line workstations and different cycle times. Comput. Oper. Res. 2023, 157, 106285. [Google Scholar] [CrossRef]
- Lai, T.; Sotskov, Y.N.; Dolgui, A.; Zatsiupa, A. Stability radii of optimal assembly line balances with a fixed workstation set. Int. J. Prod. Econ. 2016, 182, 356–371. [Google Scholar] [CrossRef]
- Chao, Y.; Chen, X.; Chen, S.; Yuan, Y. An improved multi-objective antlion optimization algorithm for assembly line balancing problem considering learning cost and workstation area. Int. J. Interact. Des. Manuf. (IJIDeM) 2025, 19, 6691–6705. [Google Scholar] [CrossRef]
- Tiacci, L. Combining balancing, sequencing and buffer allocation decisions to improve the efficiency of mixed-model asynchronous assembly lines. Comput. Ind. Eng. 2024, 194, 110357. [Google Scholar] [CrossRef]
- Demiralay, Y.D.; Kara, Y. A Cost-Effective Balancing Model for Human-Robot Collaborative Assembly Lines. IEEE Int. Symp. Multimed. 2024, 253, 2766–2775. [Google Scholar] [CrossRef]
- Janardhanan, M.N.; Li, Z.; Bocewicz, G.; Banaszak, Z.A.; Nielsen, P. Metaheuristic algorithms for balancing robotic assembly lines with sequence-dependent robot setup times. Appl. Math. Model. 2019, 65, 256–270. [Google Scholar] [CrossRef]
- Junior, M.C.; Michels, A.S.; Magatão, L. An exact constraint programming method for the multi-manned assembly line balancing problem with assignment restrictions. Expert Syst. Appl. 2025, 259, 125294. [Google Scholar] [CrossRef]
- Abdous, M.; Delorme, X.; Battini, D.; Sgarbossa, F. Scenario-based optimization and simulation framework for human-centered Assembly Line Balancing. Int. J. Prod. Econ. 2025, 282, 109513. [Google Scholar] [CrossRef]
- Yang, H. Balance of mixed flow assembly line based on industrial engineering mathematics and simulated annealing improved algorithm. Results Eng. 2024, 22, 102071. [Google Scholar] [CrossRef]
- Nourmohammadi, A.; Arbaoui, T.; Fathi, M.; Dolgui, A. Balancing human-robot collaborative assembly lines: A constraint programming approach. Comput. Ind. Eng. 2025, 205, 111154. [Google Scholar] [CrossRef]
- Zamzam, N.; El-Kharbotly, A. Balancing two-sided multi-manned assembly line under time and space constraint. Ain Shams Eng. J. 2024, 15, 102464. [Google Scholar] [CrossRef]
- Nourmohammadi, A.; Fathi, M.; Ng, A.H. Balancing and scheduling human-robot collaborated assembly lines with layout and objective consideration. Comput. Ind. Eng. 2023, 187, 109775. [Google Scholar] [CrossRef]
- Alhomaidi, E.; Askin, R.G. Parallel Assembly Line Balancing Model with Tooling Consideration and Demand Fulfilment (ALBPTD). IFAC-Pap. 2022, 55, 103–108. [Google Scholar] [CrossRef]
- Alhomaidi, E.; Askin, R.G. Exact and approximation heuristic of mixed model assembly line balancing with parallel lines and task-dependent tooling consideration. Comput. Ind. Eng. 2024, 193, 110265. [Google Scholar] [CrossRef]
- Aguilar, H.; García-Villoria, A.; Pastor, R. Heuristic and metaheuristic procedures for the Parallel Assembly Lines Balancing Problem with multi-line workstations and buffer sizing. Comput. Oper. Res. 2024, 166, 106596. [Google Scholar] [CrossRef]
- Zhang, H. Assembly sequence planning: A Review. Recent Adv. Comput. Sci. Commun. 2022, 15, 531–539. [Google Scholar] [CrossRef]
- Kang, M.; Seo, J.; Chung, H. Ship block assembly sequence planning considering productivity and welding deformation. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 450–457. [Google Scholar] [CrossRef]
- Chen, Z.; Adel, A. Advancing robotic assembly in construction: Innovations, challenges, and opportunities. Autom. Constr. 2025, 178, 106370. [Google Scholar] [CrossRef]
- Parsi, S.S.; Whittaker, A.S.; Sivaselvan, M.V.; Velez-Lopez, E.; Stewart, W.R.; Shirvan, K. Experimental investigations into the rocking response of graphite-block assemblies in a HTGR core under horizontal earthquake shaking. Nucl. Eng. Des. 2025, 443, 114300. [Google Scholar] [CrossRef]
- Zhao, R.; Tao, S.; Li, P. Human-centric assembly planning framework for human-robot collaborative systems with efficient reinforcement self-learning multi-objective evolutionary optimizer. Adv. Eng. Inform. 2025, 67, 103508. [Google Scholar] [CrossRef]
- Tseng, H.; Wang, W.; Shih, H. Using memetic algorithms with guided local search to solve assembly sequence planning. Expert Syst. Appl. 2007, 33, 451–467. [Google Scholar] [CrossRef]
- Wan, X.; Liu, K.; Qiu, W.; Kang, Z. An Assembly Sequence Planning Method Based on Multiple Optimal Solutions Genetic Algorithm. Mathematics 2024, 12, 574. [Google Scholar] [CrossRef]
- Sheng, Z.; Chen, W.; Chen, Z.; Wen, H. Sequence planning for on-orbit robotic assembly based on symbiotic organisms search with diversification strategy. Acta Astronaut. 2024, 219, 941–951. [Google Scholar] [CrossRef]
- Watanabe, K.; Inada, S. Search algorithm of the assembly sequence of products by using past learning results. Int. J. Prod. Econ. 2020, 226, 107615. [Google Scholar] [CrossRef]
- Ab. Rashid, M.F.; Nik Mohamed, N.M.; Mohd Rose, A.N. A modified artificial bee colony algorithm to optimise integrated assembly sequence planning and assembly line balancing. J. Mech. Eng. Sci. 2019, 13, 5905–5921. [Google Scholar] [CrossRef]
- Rashid, M.F.; Tiwari, A.; Hutabarat, W. Integrated optimization of mixed-model assembly sequence planning and line balancing using Multi-objective Discrete Particle Swarm Optimization. Artif. Intell. Eng. Des. Anal. Manuf. 2019, 33, 332–345. [Google Scholar] [CrossRef]
- Yolmeh, A.; Kianfar, F. An efficient hybrid genetic algorithm to solve assembly line balancing problem with sequence-dependent setup times. Comput. Ind. Eng. 2012, 62, 936–945. [Google Scholar] [CrossRef]
- Murali, G.B.; Deepak, B.B.; Biswal, B.B.; Mohanta, G.B.; Rout, A. Robotic Optimal Assembly Sequence Using Improved Cuckoo Search Algorithm. Procedia Comput. Sci. 2018, 133, 323–330. [Google Scholar] [CrossRef]
- Petroodi, S.E.H.; Thevenin, S.; Kovalev, S.; Kovalev, S.; Dolgui, A. Robust multi-manned mixed-model assembly line balancing with dynamic task assignment considering product mix uncertainty. Int. J. Prod. Econ. 2025, 109756. [Google Scholar] [CrossRef]
- Ramezanian, R.; Khalesi, S. Integration of multi-product supply chain network design and assembly line balancing. Oper. Res. Int. J. 2021, 21, 453–483. [Google Scholar] [CrossRef]
- Nowicki, E.; Smutnicki, C. A Fast Taboo Search Algorithm for the Job Shop Problem. Manag. Sci. 1996, 42, 797–813. [Google Scholar] [CrossRef]
- Yijie, S.; Shen, G. Improved NSGA-II Multi-objective Genetic Algorithm Based on Hybridization-encouraged Mechanism. Chin. J. Aeronaut. 2008, 21, 540–549. [Google Scholar] [CrossRef]
- Hao, J.; Yang, X.; Wang, C.; Tu, R.; Zhang, T. An Improved NSGA-II Algorithm Based on Adaptive Weighting and Searching Strategy. Appl. Sci. 2022, 12, 11573. [Google Scholar] [CrossRef]
- Li, L.; Lin, Q.; Ming, Z. A survey of artificial immune algorithms for multi-objective optimization. Neurocomputing 2022, 489, 211–229. [Google Scholar] [CrossRef]
- Sener, A. Hybrid large neighbourhood search algorithm for capacitated vehicle routing problem. Expert Syst. Appl. 2016, 61, 28–38. [Google Scholar] [CrossRef]
- Hao, Y.; Zhao, C.; Zhang, Y.; Cao, Y.; Li, Z. Constrained multi-objective optimization problems: Methodologies, algorithms and applications. Knowl.-Based Syst. 2024, 299, 111998. [Google Scholar]
- Wang, L.P.; Ren, Y.; Qiu, Q.C.; Qiu, F.Y. Survey on performance indicators for multi-objective evolutionary algorithms. Chin. J. Comput. 2021, 44, 1590–1619. [Google Scholar]



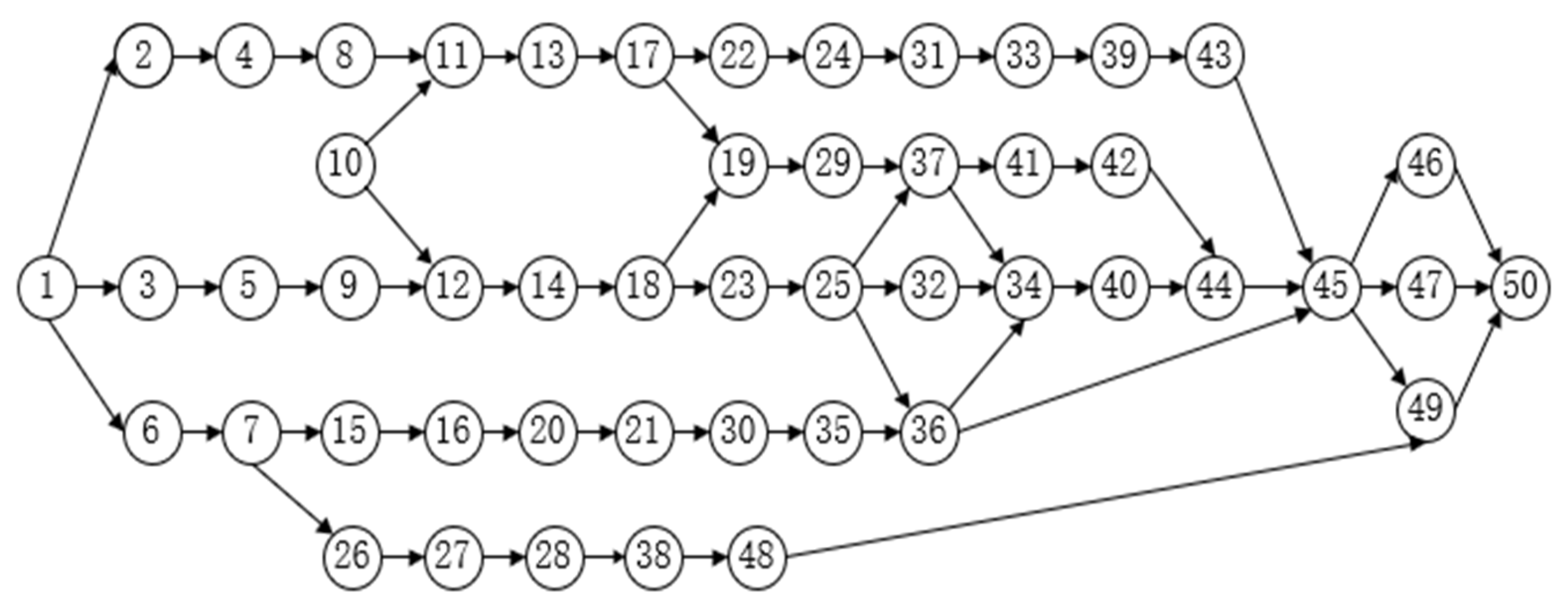
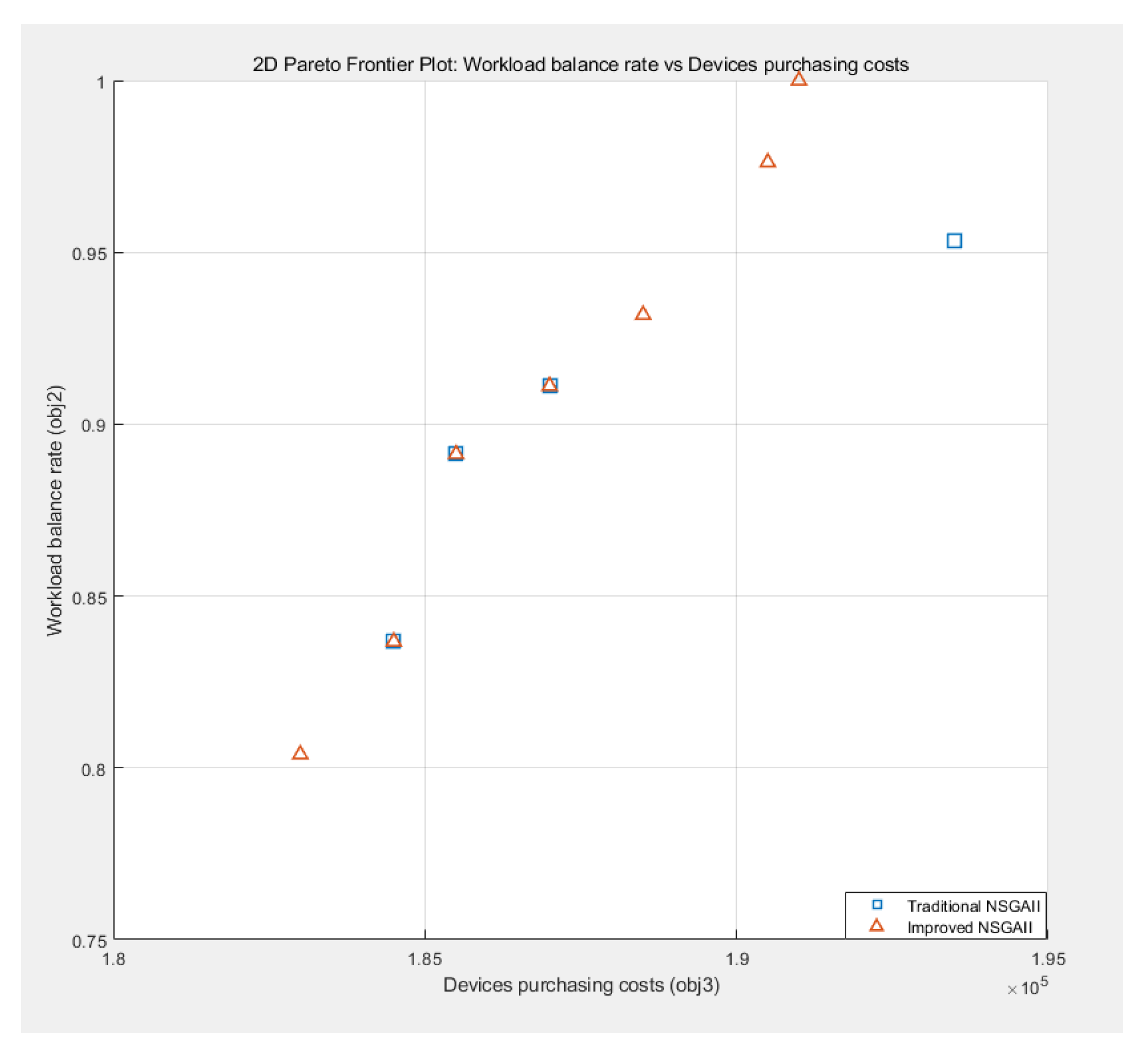


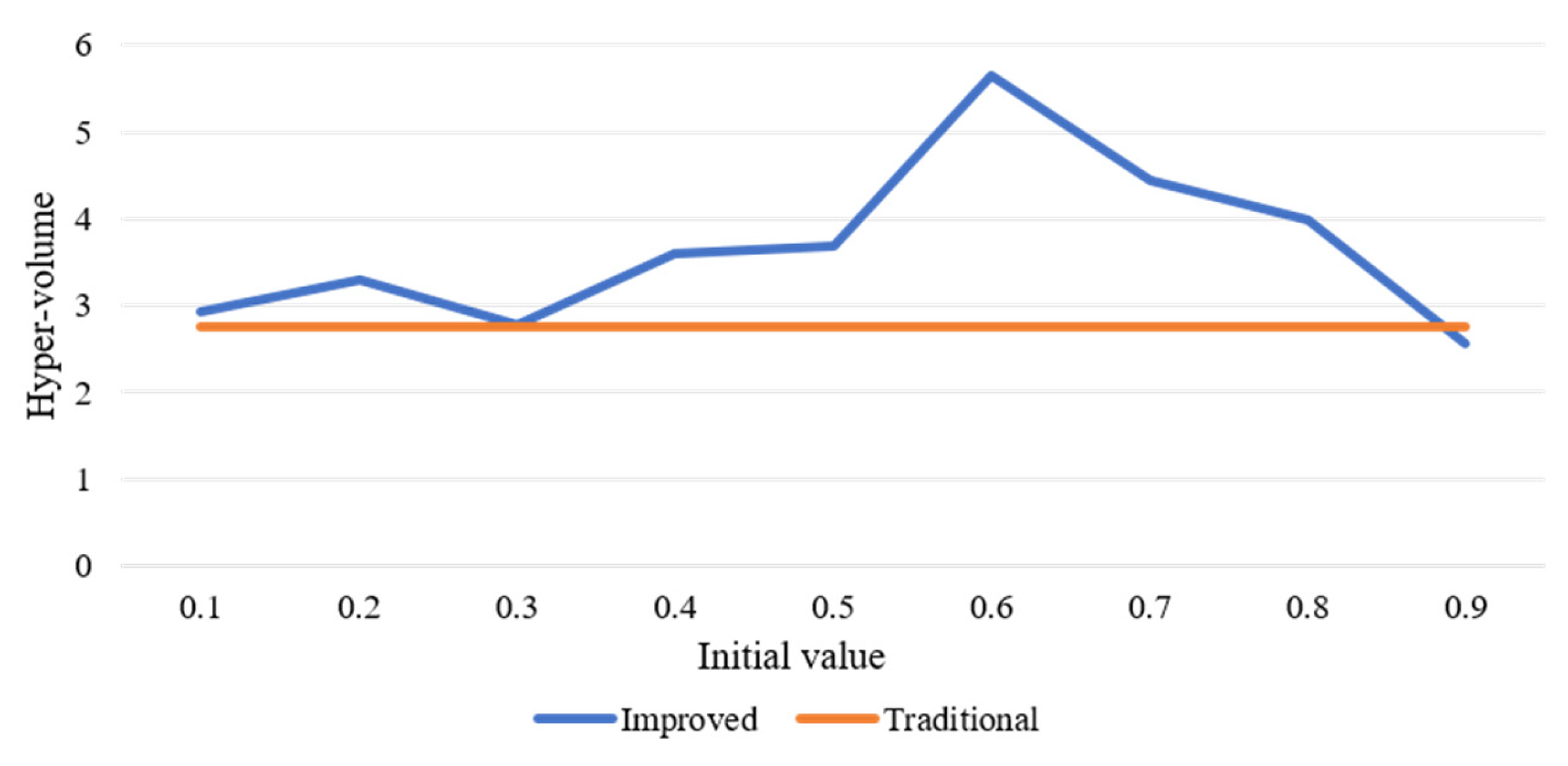
| Symbol | Description |
|---|---|
| Set of all tasks, . | |
| Takt time. | |
| Duration-time for task . | |
| Set of all workstations. | |
| Total number of workstations, . | |
| Purchase price of one device . | |
| Number of devices required for the entire assembly line. | |
| Set of all assembly positions. | |
| Set of fixed device types used in the entire assembly line. | |
| Set of movable device types used in the entire assembly line. | |
| Set of all device types used in the entire assembly line, . | |
| Set of immediate predecessor tasks for task . | |
| Cycle time of the -th workstation | |
| Total duration time of all tasks at the -th workstation | |
| Set of tasks in the -th workstation, | |
| 0 or 1 parameter. 1 indicates that at least one task has been assigned to the -th workstation, otherwise it is 0 | |
| 0 or 1 parameter. 1 means that the -th workstation uses the mobile device , otherwise it is 0. | |
| Set of tasks using mobile device . | |
| Set of tasks using fixed device | |
| 0 or 1 parameter. 1 indicates that task uses position , otherwise it is 0. | |
| 0 or 1 parameter. 1 indicates that task uses device , otherwise it is 0. | |
| Number of tasks using device . | |
| Set of tasks that are in the same workstation as task and have conflicts with task in terms of position, . | |
| Set of tasks that are in the same workstation as task and have conflicts with task in terms of devices, . | |
| A sufficiently large constant. | |
| 0 or 1 parameter. If there is a task using fixed device at position in the -th workstation, it is 1, otherwise it is 0. | |
| Number of fixed devices required for the -th workstation. | |
| Set of tasks assigned to position of the -th workstation. | |
| Task with the minimum end-time. | |
| Task corresponding to the -th gene locus in the chromosome. | |
| Set of assigned tasks for workstation . | |
| Set of tasks that have parallel conflicts with in current workstation. |
| Symbol | Description |
|---|---|
| Start-time for task . | |
| End-time for task . | |
| 0 or 1 variable. 1 indicates that task is assigned to the -th workstation, otherwise it is 0. | |
| 0 or 1 variable. 1 indicates that task is executed before task , otherwise it is 0. |
| Task | Task Position | Device Required | Device Property | Device Cost (Yuan) | Duration Time (Hours) | Task | Task Position | Device Required | Device Property | Device Cost (Yuan) | Duration Time (Hours) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | p1 | A | fixed | 5000 | 3 | 26 | p1 | A | fixed | 5000 | 2 |
| 2 | p2 | B | fixed | 3000 | 2 | 27 | p1 | B | fixed | 3000 | 3 |
| 3 | p3 | B | fixed | 3000 | 2 | 28 | p1 | E | fixed | 2000 | 1 |
| 4 | p2 | C | fixed | 1500 | 1 | 29 | p4 | H | fixed | 1500 | 5 |
| 5 | p3 | C | fixed | 1500 | 1 | 30 | p5 | D | fixed | 4000 | 3 |
| 6 | p1 | D | fixed | 4000 | 4 | 31 | p2 | H | fixed | 1500 | 2 |
| 7 | p1 | E | fixed | 2000 | 2 | 32 | p3 | H | fixed | 1500 | 2 |
| 8 | p2 | F | fixed | 1000 | 3 | 33 | p2 | None | - | 0 | 3 |
| 9 | p3 | F | fixed | 1000 | 3 | 34 | p3 | None | - | 0 | 3 |
| 10 | p4 | G | movable | 60,000 | 2 | 35 | p5 | F | fixed | 1000 | 3 |
| 11 | p2 | G | movable | 60,000 | 3 | 36 | p5 | C | fixed | 1500 | 1 |
| 12 | p3 | G | movable | 60,000 | 3 | 37 | p4 | G | movable | 60,000 | 4 |
| 13 | p2 | H | fixed | 1500 | 1 | 38 | p1 | E | fixed | 2000 | 2 |
| 14 | p3 | H | fixed | 1500 | 1 | 39 | p2 | None | - | 0 | 1 |
| 15 | p5 | A | fixed | 5000 | 5 | 40 | p3 | None | - | 0 | 1 |
| 16 | p5 | D | fixed | 4000 | 4 | 41 | p4 | H | fixed | 1500 | 5 |
| 17 | p2 | B | fixed | 3000 | 2 | 42 | p4 | D | fixed | 4000 | 2 |
| 18 | p3 | B | fixed | 3000 | 2 | 43 | p2 | B | fixed | 3000 | 2 |
| 19 | p4 | C | fixed | 1500 | 3 | 44 | p3 | B | fixed | 3000 | 2 |
| 20 | p5 | E | fixed | 2000 | 2 | 45 | p5 | None | - | 0 | 3 |
| 21 | p5 | G | movable | 60,000 | 3 | 46 | p5 | None | - | 0 | 1 |
| 22 | p2 | F | fixed | 1000 | 4 | 47 | p5 | None | - | 0 | 1 |
| 23 | p3 | F | fixed | 1000 | 4 | 48 | p1 | A | fixed | 5000 | 2 |
| 24 | p2 | C | fixed | 1500 | 2 | 49 | p1 | F | fixed | 1000 | 3 |
| 25 | p3 | C | fixed | 1500 | 2 | 50 | p1 | E | fixed | 2000 | 2 |
| Workstation | Traditional NSGA-II Algorithm Workload (Hours) | Improved NSGA-II Algorithm Workload (Hours) |
|---|---|---|
| Workstation 1 | 43 | 41 |
| Workstation 2 | 43 | 41 |
| Workstation 3 | 37 | 41 |
| Algorithm | Workstation | Number of Devices | Cost (Yuan) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | |||
| Traditional NSGA-II algorithm | Workstation 1 | 1 | 3 | 2 | 1 | 1 | 2 | 1 | 2 | 184,500 |
| Workstation 2 | 1 | 0 | 3 | 2 | 1 | 1 | 1 | 3 | ||
| Workstation 3 | 0 | 2 | 1 | 0 | 1 | 2 | 0 | 0 | ||
| Improved NSGA-II algorithm | Workstation 1 | 2 | 3 | 2 | 1 | 1 | 2 | 1 | 1 | 183,000 |
| Workstation 2 | 0 | 1 | 3 | 1 | 1 | 1 | 1 | 3 | ||
| Workstation 3 | 0 | 1 | 1 | 1 | 1 | 2 | 0 | 0 | ||
| Run Time | Normalized Hyper-Volume (Mean) | |
|---|---|---|
| Traditional NSGA-II | 3:11:02 | 2.7599 |
| Improved NSGA-II | 4:45:47 | 4.8474 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Cao, Y.; Kong, F.; Zhang, X.; Song, G. Multi-Objective Large-Scale ALB Considering Position and Equipment Conflicts Using an Improved NSGA-II. Processes 2025, 13, 3574. https://doi.org/10.3390/pr13113574
Li H, Cao Y, Kong F, Zhang X, Song G. Multi-Objective Large-Scale ALB Considering Position and Equipment Conflicts Using an Improved NSGA-II. Processes. 2025; 13(11):3574. https://doi.org/10.3390/pr13113574
Chicago/Turabian StyleLi, Haiwei, Yanghua Cao, Fansen Kong, Xi Zhang, and Guoqiu Song. 2025. "Multi-Objective Large-Scale ALB Considering Position and Equipment Conflicts Using an Improved NSGA-II" Processes 13, no. 11: 3574. https://doi.org/10.3390/pr13113574
APA StyleLi, H., Cao, Y., Kong, F., Zhang, X., & Song, G. (2025). Multi-Objective Large-Scale ALB Considering Position and Equipment Conflicts Using an Improved NSGA-II. Processes, 13(11), 3574. https://doi.org/10.3390/pr13113574







