An Integrated Approach of Fuzzy AHP-TOPSIS for Multi-Criteria Decision-Making in Industrial Robot Selection

Abstract

In recent times, industrial robots have gained immense significance and popularity in various industries. They not only enhance labor safety and reduce costs but also greatly improve productivity and efficiency in the production process. However, selecting the most suitable robot for a specific production process is a complex task. There are numerous criteria to consider, often conflicting with each other, making decision-making challenging. In order to tackle this problem, the multi-criteria decision-making (MCDM) method is employed, which aids in ranking decisions based on criteria weights. However, traditional MCDM methods are now considered outdated, and researchers are concentrating on hybrid models that include multiple MCDM techniques to tackle decision-making problems effectively. This study presents an effective MCDM model that integrates Fuzzy-AHP-TOPSIS to evaluate and choose the best robot. The Fuzzy-AHP is utilized to establish a set of weights for the evaluation criteria. Subsequently, the proposed technique analyzes, prioritizes, and chooses the best robot option from the ranking list for the factory. The experimental results demonstrate that by employing the integrated fuzzy analytical hierarchy process, taking into account parameter weights and expert judgment, the robots are identified in order of best to worst alternatives to factories. The outcomes of this research possess significant implications for robot selection and can be applied in various fields to cater to production requirements.

1. Introduction

The advancement of technology in the 4.0 industrial revolution has unlocked remarkable opportunities for heightened automation in production [1,2]. It is crucial to address the imperative of researching and implementing industrial robots to substitute human labor in production processes [3,4,5]. The utilization of robots in diverse industries such as automobile manufacturing, electronics, food and beverages, healthcare, and services has demonstrated notable impacts [6,7,8]. Especially in the manufacturing industry, the introduction of various robot types has resulted in a wide range of attributes, including functions, technical specifications, load capacity, speed, and price [9,10]. This diversity has presented challenges in choosing the best robot for a factory. The decision-making process for choosing the ideal robot aims not only to achieve cost effectiveness and efficient production but also to optimize other aspects of the production process, such as labor safety, productivity, product quality, space and resource optimization, flexibility, and reduced production time [11,12]. Making errors in decision-making regarding the selection of industrial robots can impact a factory’s ability to compete in the market for both productivity and product quality [13]. Consequently, choosing the appropriate robot for a certain industry application and production environment has become a complex challenge, particularly given the multitude of robot types available in the market. Decision makers must take into account subjective and objective factors, as well as the benefits and costs associated with each option [14,15]. In practice, the criteria for selecting industrial robots often conflict with each other, have different units of measurement, and require trade-offs, making it challenging to compare and make decisions [16,17,18]. To address this issue, researchers have put forth various methods and models for robot selection [19,20]. These models encompass computer-aided approaches, statistical methods, and optimization models for enhancing production system performance [21,22,23]. In 1991, the authors proposed a regression model to identify robots that outperformed others in terms of manufacturer specifications at a given cost [24]. Diagram and matrix methods have been utilized since 2006 to effectively compare and identify robots, as well as to store and retrieve robot data for various applications [25]. While these methods address the issue of robot selection, they may lack flexibility when dealing with complex variables, and the models can become intricate and confusing, particularly in large-scale factories. Conversely, determining the optimal robot involves a decision-making process that takes into account a number of competing subjective and objective factors, resembling an MCDM problem. MCDM techniques have proven to be valuable in handling such complicated problems, and researchers have employed various MCDM methods to tackle robot selection challenges [26,27,28,29]. The authors of one study employed the MCDM technique combined with the weighting technique for decision-making in the powder-mixed electrical discharge machining process [30]. The evaluation based on distance from average solution (EDAS) technique was effectively used to handle the robot selection problem [31]. Another MCDM technique, known as Analytic Hierarchy Process (AHP) secondary analysis, incorporates both subjective and objective criteria to make robot selections [32]. However, the traditional MCDM methods may not align with reality as decision-making for each option depends on the evaluator’s subjective opinion and related assessments, which are often vague and imprecise [33,34]. In many cases, accurately determining ratings and weights for performance is challenging. To address this issue, fuzzy set theory was created to represent uncertainties in predictions, human perception, and other factors. This led to the creation of Fuzzy MCDM (FMCDM) techniques [35]. Researchers have utilized FMCDM methods to tackle this problem [36,37,38]. The first people to introduce decision-making procedures in fuzzy contexts were Bellman and Zadeh (1970) [39]. Generally, a fuzzy function defines a fuzzy number, where each value in the set is assigned a membership degree ranging from 0 to 1 [40]. Octagonal fuzzy numbers are often considered the optimal solution for addressing load transmission problems in fuzzy environments [41]. The triangular fuzzy number (TFN), which represents the decision maker’s status in complex problems, can be an effective means of conveying information [42]. In MCDM models, fuzzy numbers are employed to manage the evaluator’s subjectivity and uncertainty. The novel hexagonal fuzzy approximation’s characteristics are examined, and a group MCDM issue using index matrices is used to show the practicality of the proposed method [43]. Multi-criteria selections are made using fuzzy numbers in MCDM approaches as Fuzzy-TOPSIS (Fuzzy Technique for Order Preference by Similarity to Ideal Solution), Fuzzy-AHP, Fuzzy-MOORA, etc. [44,45,46,47]. In order to prioritize the order for multi-criteria assessment of industrial robot systems, Cengiz Kahraman developed a fuzzy hierarchy approach based on the TOPSIS model [48]. In [49], the authors utilized the Fuzzy-AHP technique to achieve optimal robot selection. The utilization of fuzzy numbers in MCDM multi-criteria techniques offers a more objective, multi-perspective, and realistic assessment when considering criteria for selecting the optimal solution.

Several new MCDM models have been developed by researchers, which improve making choices, accuracy and strategy [50,51,52,53]. MCDM approaches are becoming more and more popular because of their capacity to evaluate and contrast many options. Meanwhile, traditional MCDM methods are progressively going out of style. For complicated decision-making scenarios, a single MCDM tool is often insufficient [54,55]. In order to achieve more effective decision-making, it is necessary to integrate two or more MCDM models together, in addition to combining MCDM with other methods [56,57]. The primary objective of merging these techniques is to leverage the advantages of each tool and overcome the drawbacks of individual models. To predict the ideal replacement robot, Goswani et al. [58] used a unique hybrid MCDM model that incorporates COPRAS and ARAS. For robot choosing, the authors integrated FAQT-2 and concluded that the suggested hybrid MCDM approach is more dependable and consistent compared to the traditional MCDM method [59]. Table 1 highlights a selection of notable research studies in the current body of literature pertaining to the evaluation of robots.

Table 1. Reference list for MCDM studies for robotics evaluation.

MCDM Method	Criteria for Evaluating Robots	Results	Reference
Entropy, TOPSIS	Mechanical Weight, Repeatability, Payload, Maximum Reach, Average Power Consumption.	The study determined that Robot-7 is the optimal selection for arc welding tasks. This robot has a mechanical weight of 501 kg, a repeatability of 0.15 mm, a load capacity of 6 kg, a maximum reach of 4368 mm, and a power consumption of 2.5 kW.	[60]
BW, EDAS	Load Capacity, Repeatability, Velocity Ratio, Degree of Freedom.	The proposed method offers several advantages, including increased consistency and reduced computational requirements.	[61]
EDAS	Purchase Cost, Load Capacity, Repeatability, Man–Machine Interface, Man–Machine Interface, Vendor’s Service Contract.	Compared with other MCDM methods (such as AHP, TOPSIS, VIKOR, ELECTRE, PROMETHEE, MOORA, WASPAS, GRA, ROV, and OCRA), the EDAS method is simpler and easier to apply in selecting industrial robots.	[62]
TOPSIS-ARAS, COPRAS-ARAS	Load Capacity, Repeatability Error, Handling Coefficient, Velocity, Cost.	Based on the evaluation, Robot-12 achieved the highest rating and was identified as the optimal choice. This study validates the effectiveness of the hybrid models TOPSIS-ARAS and COPRAS-ARAS in enhancing the accuracy of rankings and delivering consistent and dependable results in the selection of industrial robots.	[63]
SAW, TOPSIS, LINMAP, VIKOR, ELECTRE-III and NFM	Load Capacity, Repeatability Error, Cost, Vendor’s Service Quality, Programming Flexibility.	In case study 1, Robot 2 and Robot 3 emerged as the top choices for pick-and-place tasks. Case study 2 revealed that Robot 1 and Robot 3 received the highest ratings among the considered robots. In case study 3, Robot 2 was consistently identified as the optimal selection among the four robots considered by most MCDM methods.	[64]
CRITIC, MABAC	Load Capacity, Memory Capacity, Manipulator Reach, Maximum Tip Speed, Repeatability.	Robot R3 attained the highest ranking, signifying its suitability for pick-and-place operations in flexible manufacturing systems. Among the evaluated robots, Robot R1 received the lowest ranking. The study also conducted a comparison of the ranking results with other MCDM methods to validate the accuracy and reliability of the proposed method.	[65]
QFD, MPR	Payload Capacity, Workspace, Accuracy, Repeatability, Life Expectancy, Programmable Flexibility, Safety and Security, Purchase Cost, Maintenance Cost, Operation Cost.	The key criterion in the selection of an industrial robot is load capacity, and the most critical technical requirement is the drive system.	[66]
COCOSO, TOPSIS, VIKOR, MOORA	Load Capacity, Repeatability, Maximum Tip Speed, Memory Capacity, Manipulator Reach.	According to the COCOSO method, R3 emerges as the best robot based on the MW, SD, and CRITIC weight distribution methods. However, R1 is considered the best robot according to the EM method, and R3 is favored according to the AHP method.	[67]
SWARA, CoCoSo	Payload, Mechanical weight, Repeatability, Reach, Cost, Power Consumption.	The Fanuc P-350iA/45 robot has been selected as the most suitable robot for painting applications. These results have also been compared and cross-referenced with other popular MCDM methods such as TOPSIS, VIKOR, COPRAS, PROMETHEE, and MOORA, demonstrating a high degree of similarity in the ranking patterns among these methods, affirming the effectiveness of the SWARA-CoCoSo method.	[68]
Rough-MABAC	Payload, Horizontal Reach, Vertical Reach, Repeatability, Weight, Power Rating, Cost, Flexibility, Safety, Welding Performance, Maintainability, Ease of Programming.	The research findings indicate that Robot A6 is the most suitable choice, ranking at the top of the list, followed by Robots A3, A13, A10, A5, A9, A4, A11, A1, A14, A7, A12, A8, and finally Robot A2. The robots are categorized into two main groups, efficient and inefficient, based on their positions in the approximate boundary regions.	[69]
PIPRECIA-TOPSIS	Payload, Weight of Robot, Repeatability, Reach.	The PIPRECIA technique identifies payload as the most crucial criterion based on a predefined priority order, and the TOPSIS method recommends the FANUC 100iD/10L model as the best arc welding robot.	[70]
BWM, G-BWM	Velocity, Repeatability, Load Capacity, Cost, Quality, Memory Capacity, Manipulator Reach.	The results indicate that Robot 2 is the best robot. The G-BWM (group best–worst method) demonstrates greater effectiveness compared to the G-AHP (Group Analytic Hierarchy Process) method due to its lower overall violation and deviation, as well as requiring fewer comparisons, resulting in reduced computational requirements.	[71]
MCGDM-IP	Cost, Handling Coefficient, Load Capacity, Repeatability, Velocity.	Robot R11 achieved the highest ranking among the evaluated robots, while Robot R4 received the lowest ranking. The MCGDM-IP method improved the satisfaction level of the group by 2.12% compared to the simple additive weighting (SAW) method.	[72]
CODAS, COPRAS, COCOSO, MABAC, VIKOR	Payload, Speed, Reach, Mechanical Weight, Repeatability, Cost, Power Consumption.	The results indicate that the HY1010A-143 robot is evaluated as the most suitable for painting applications according to four out of the five methods used. The KF121 robot is evaluated as the least suitable for painting applications by all of the MCDM methods.	[73]
AHP	General Criteria, Structure/Architecture Criteria, Reliability Criteria, Application Criteria, Performance Criteria, Safety Criteria.	The AHP method is applied to evaluate the cobots based on the predefined criteria. The cobot with the highest overall priority weight (A1) is considered the most suitable based on the given criteria and AHP evaluation.	[74]
WSM, WPM, WASPAS, MOORA, MULTIMOORA	Load Capacity, Maximum Tip Speed, Repeatability, Memory Capacity, Manipulator Reach.	The results indicate that among the applied MCDM methods, the MULTIMOORA (MOORA with Complete Multiplicative Form) method is the most robust and less affected by changes in the criteria weights. The robot ranking results show that the Cybotech V15 Electric Robot (R3) is often the best choice in most of the methods.	[75]
COPRAS	Repeatability Error, Load Capacity, Maximum Tip Speed, Memory Capacity, Manipulator Reach.	The Cincinnati Milacrone T3-726 Robot (A2) achieved the highest ranking with a Qi value of 0.1946 and a Ui value of 100.00, securing first position. The COPRAS method has been demonstrated to be effective in the evaluation and selection of industrial robots, aligning well with the results from previous studies.	[76]
AHP	Load Capacity, Reach, Weight, Repeatability, Power Consumption, Dexterity, Service	Based on the AHP method, the robot structure R2 is selected as the most optimal choice.	[77]
GRA	Load Capacity, Repeatability Error, Velocity Ratio, Degrees of Freedom.	Robot R3 achieved the highest score with a grey relational grade of 0.9434 and was ranked first.	[78]
AHP	Technical Criteria: Movement, Shaft Speed, Reach, Repeatability, Allowable Moment, Load: Robot Mass, Robot Reach, Vertical Reach, Horizontal reach Other Criteria: Capacity, Cost, Flexibility, Mounting Type, Welding Type.	Among the analyzed 15 industrial robots, the robot with code A4 achieved the highest weight of approximately 16%, followed by A5 with approximately 15%, and A2 and A9 both scoring ≈ 10%. Robot A4 excelled in criteria such as repeatability (C1.2), robot weight (C2.2), and power (C3.1), obtaining the highest score in these aspects.	[79]

We introduced the hybrid approach of Fuzzy TOPSIS and Fuzzy AHP, which has not been previously explored in research on robot selection. Our results demonstrated the effectiveness of this evaluation method and the article not only brings practical value to robot selection in manufacturing but also contributes to the knowledge base of MCDM methods, particularly the combination of fuzzy AHP and fuzzy TOPSIS in modern production environments. In this study, the criterion weights are determined using the Fuzzy-AHP, while the robot alternatives are evaluated and ranked using the Fuzzy-TOPSIS. Specifically, we employ the Fuzzy-AHP-TOPSIS combination model to rank eight different robots based on their attributes, as evaluated by experts. The alternatives are organized in order of increasing closeness to both positive and negative ideal solutions. To address the uncertainty and subjectivity of the evaluators, we incorporate fuzzy numbers into the model. By integrating the Fuzzy-AHP-TOPSIS model, we successfully selected the optimal robot for our factory with a high degree of reliability. Moving forward, we plan to enhance this hybrid MCDM model by incorporating additional techniques and methods to ensure the best possible decision-making outcomes.

2. Materials and Methods

2.1. Fuzzy Numbers

Fuzzy set theory is employed to address uncertainty stemming from imprecision or ambiguous information. According to this theory, an ordered pair collection ($X$ being a subset of the real numbers $ℝ$) is referred to as a fuzzy set ($F=\left\{\left(\psi ,{\mu }_F\left(\psi \right)\right)|\psi \in X\right\}$). A membership function called ${\mu }_F\left(\psi \right)$ and ${\mu }_F\left(\psi \right)$ gives each element a number between 0 and 1. The pairwise comparison matrices of the AHP integrate fuzzy set theory. The triangular fuzzy number (TFN) is commonly utilized to represent the judgments of experts and is denoted by $F(\underset{\_}{f},f,\overline{f})$. The parameters $F(\underset{\_}{f},f,\overline{f})$ represent the minimum, intermediate (i.e., most favorable), and maximum values used to quantify uncertain judgments. The following determines the TFN’s membership function:

$${\mu }_F(\psi )=\{\begin{array}{l}0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \psi <\underset{\_}{f}\\ (\psi -\underset{\_}{f}){(f-\overline{f})}^{-1},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\underset{\_}{f}\le \psi <f\\ (\overline{f}-\psi ){(\overline{f}-f)}^{-1},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}f\le \psi \le \overline{f}\\ 0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \psi >\overline{f}\end{array}$$

(1)

A collection of criteria, represented as $C=\left\{c_1,c_2,c_3,\dots ,c_i\right\}$, and a set of alternatives, represented as $A=\left\{A_1,A_2,A_3,\dots ,A_j\right\}$, are taken into consideration while making a multi-criteria choice. Every alternative is analyzed using a specified set of criteria. The selection of each criterion is followed by the analysis of its utilization level for each alternative $A_j$. Thus, the value range analysis for each criterion can be expressed as $F_{Ai}^1,F_{Ai}^2,\dots ,F_{Ai}^m$ ($i=1,2,3,\dots ,n$), where $F_{Ai}^j(j=1,2,3,\dots ,m)$ represents the TFNs.

Utilizing fuzzy numbers facilitates improved the management of ambiguity and uncertainty within expert evaluations. By employing fuzzy numbers, experts can articulate their judgments using qualitative terms like “low”, “medium”, and “high”, which can then be translated into fuzzy numbers. This approach offers greater flexibility compared to traditional methods that demand precise score values, particularly beneficial when experts are uncertain about their assessments. Additionally, fuzzy numbers enable a more nuanced aggregation of diverse judgments, capturing the breadth of expert opinions and evaluations, a capability that conventional methods may lack. For instance, in a traditional scenario, an expert might assign a score of 3 out of 10 for the importance of the criterion “Cost”. In contrast, employing fuzzy numbers, the expert could rate this criterion as “Medium High”, resulting in a conversion to a triangular fuzzy number (2, 3, or 4). This method enhances the accuracy of representing the uncertainties and ambiguities inherent in the expert’s evaluation.

2.2. Fuzzy AHP

The AHP is a MCDM technique used in order to establish priorities among various criteria. It involves making pairwise comparisons between the criteria and alternatives, which are utilized to calculate the weights used to rank the alternatives (Figure 1).

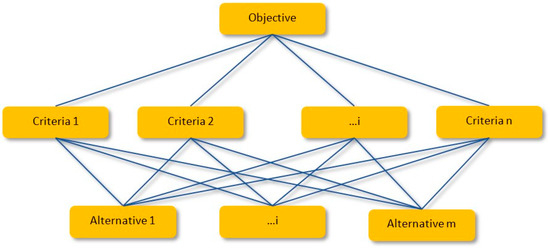
Figure 1. Hierarchical structure diagram.

However, in real-life decision-making scenarios, making clear and accurate comparisons can be challenging due to the presence of imprecision and subjectivity. Moreover, traditional AHP may not fully capture human reasoning and accurately represent expert opinions when comparing alternatives. The Fuzzy-AHP is an extension of the traditional AHP method that incorporates fuzzy number theory into its framework. This approach addresses the limitations of the conventional AHP by allowing decision makers to communicate their assessments utilizing linguistic variables or fuzzy numbers. By considering uncertainty in decision criteria and alternatives, the Fuzzy-AHP method facilitates a more flexible and diverse decision-making process. It is a widely employed method in the field of MCDM [80,81,82,83]. The Fuzzy-AHP approach makes use of a fuzzy pairwise comparison matrix. The priority weights are obtained by solving a fuzzy linear equation system. These resulting weights are then used to rank the alternatives based on their overall scores. In the Fuzzy-AHP method, the weight vector is determined by following these steps. $F={(\tilde{f})}_{n\times m}={({\underset{\_}{f}}_{ij},f_{ij},{\overline{f}}_{ij})}_{n\times m}$ is a fuzzy pairwise comparison matrix:

Step 1: Calculate the fuzzy aggregation range. For each object, the fuzzy synthetic extent value is computed as follows:

$$U_i={\displaystyle \sum _{j=1}^m{F}_{Ai}^j}\otimes {\left({\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{F}_{A_i}^j}}\right)}^{-1}=\left({\displaystyle \sum _{j=1}^m{\underset{\_}{f}}_j},{\displaystyle \sum _{j=1}^m{f}_j},{\displaystyle \sum _{j=1}^m{\overline{f}}_j}\right)\otimes {\left({\displaystyle \sum _{i=1}^n\left({\displaystyle \sum _{j=1}^m{\underset{\_}{f}}_j},{\displaystyle \sum _{j=1}^m{f}_j},{\displaystyle \sum _{j=1}^m{\overline{f}}_j}\right)}\right)}^{-1}$$

(2)

We calculate the fuzzy set value as follows:

$${\displaystyle \sum _{i=1}^n\left({\displaystyle \sum _{j=1}^m{\underset{\_}{f}}_j},{\displaystyle \sum _{j=1}^m{f}_j},{\displaystyle \sum _{j=1}^m{\overline{f}}_j}\right)}=\left({\displaystyle \sum _{i=1}^n{\underset{\_}{f}}_i},{\displaystyle \sum _{i=1}^n{f}_i},{\displaystyle \sum _{i=1}^n{\overline{f}}_i}\right)$$

(3)

Thus, Equation (2) becomes

$$U_i={\displaystyle \sum _{j=1}^m{F}_{Ai}^j}\otimes {\left({\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{F}_{A_i}^j}}\right)}^{-1}=\left({\displaystyle \sum _{j=1}^m{\underset{\_}{f}}_j},{\displaystyle \sum _{j=1}^m{f}_j},{\displaystyle \sum _{j=1}^m{\overline{f}}_j}\right)\otimes \left({\displaystyle \frac{1}{{\displaystyle \sum _{i=1}^n{\underset{\_}{f}}_i}}},{\displaystyle \frac{1}{{\displaystyle \sum _{i=1}^n{f}_i}}},{\displaystyle \frac{1}{{\displaystyle \sum _{i=1}^n{\overline{f}}_i}}}\right)$$

(4)

Step 2: The degree of possibility of $F_2=({\underset{\_}{f}}_2,a_2,{\overline{f}}_2)\ge F_1=({\underset{\_}{f}}_1,a_1,{\overline{f}}_1)$ is defined as follows:

$$V(F_2>F_1)=height(A_1\cap A_2)=\{\begin{array}{l}1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{f}_2\ge f_1\\ \\ 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\underset{\_}{f}}_1\le {\overline{f}}_2\\ {\displaystyle \frac{{\underset{\_}{f}}_1-{\overline{f}}_2}{(f_2-{\overline{f}}_2)-(f_1-{\underset{\_}{f}}_1)}} \hspace{1em}\mathrm{otherwise}\end{array}$$

(5)

To compare two fuzzy numbers $F_1$ and $F_2$, regarding the values of $V(F_1\ge F_2)$ or $V(F_2\ge F_1)$, we consider the highest intersection point $G$ between their corresponding membership functions ${\mu }_{F_1}$ and ${\mu }_{F_2}$, with corresponding value $g$ (Figure 2). The values of $V(F_1\ge F_2)$ and $V(F_2\ge F_1)$ can be calculated to compare between two fuzzy numbers of $F_1$ and $F_2$.

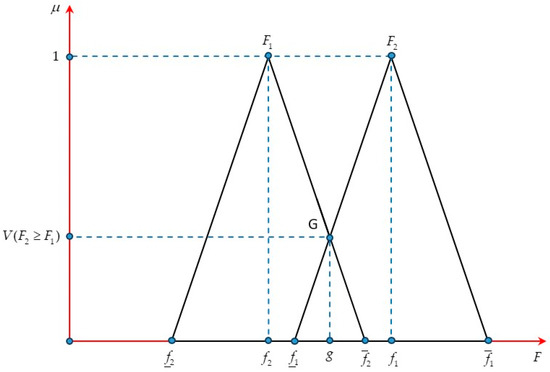
Figure 2. Value of fuzzy numbers $F_1$ and $F_2$.

Step 3: We calculate the minimum level at which fuzzy number $F$ is greater than fuzzy number $F_i(i=1,2,3,\dots ,k)$ as follows:

$$V(F\ge F_1,F_2,\dots ,F_k)=\min V(F\ge F_1)$$

(6)

The weight vector is given by

$$W={(\min V(F\ge F_1),\min V(F\ge F_2),\dots ,\min V(F\ge F_n))}^T$$

(7)

Step 4: We calculate the normalized weight vectors as follows:

$$W={(W_1,W_2,\dots ,W_3)}^T$$

(8)

where $W$ is a non-fuzzy number.

2.3. Fuzzy TOPSIS

The classic TOPSIS method operates under the assumption that if each local criterion increases or decreases monotonically, determining the ideal solution becomes straightforward. The ideal solution includes the highest achievable values for each local criterion, whereas the negative ideal solution includes the lowest obtainable values. To account for uncertainty and imprecision, the traditional TOPSIS approach was expanded to include a fuzzy variant [84,85,86,87,88]. The idea behind the Fuzzy-TOPSIS approach is that the chosen option ought to be closest to the positive ideal solution (PIS), which reduces the cost criteria and maximizes the benefit criterion, while being the furthest from the negative ideal solution (NIS). The implementation procedure for Fuzzy-TOPSIS is as follows (Figure 3):

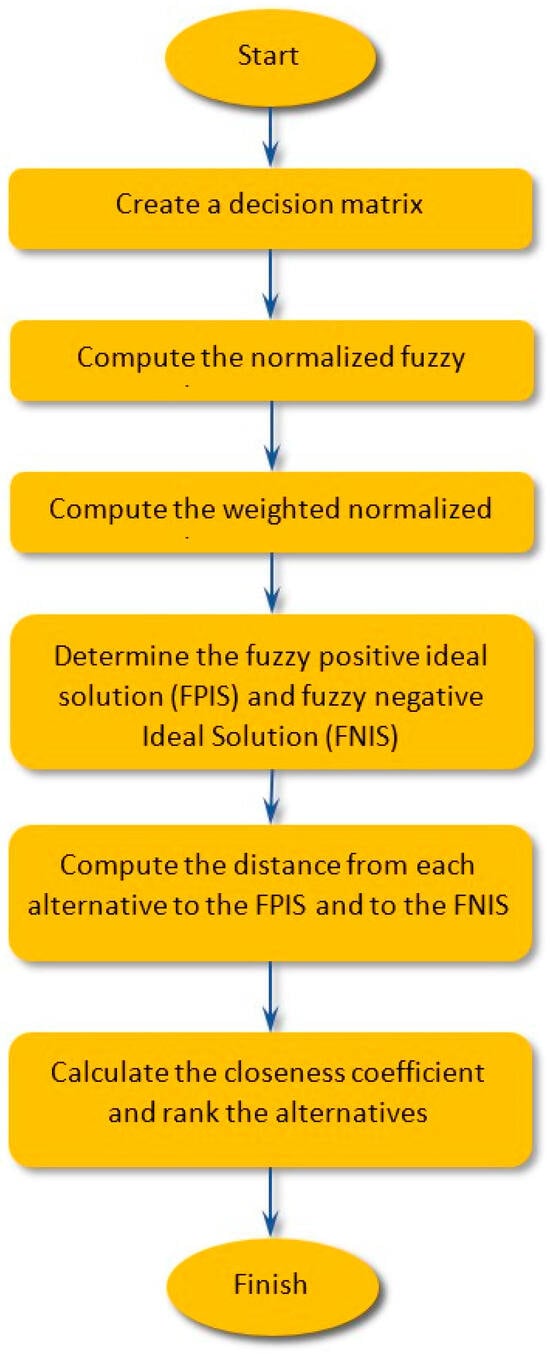
Figure 3. Flowchart of the fuzzy TOPSIS process.

Step 1: Determine the evaluation of criteria and alternative options. Suppose we have a decision group consisting of $K$ individuals. The fuzzy evaluation of the $C_j$ criterion for the $A_i$ alternative by the kth decision maker is represented by ${\tilde{x}}_{ij}^k=({a_1}_{ij}^k,{a_2}_{ij}^k,{a_3}_{ij}^k)$. The weight of the $C_j$ criterion is represented as ${\tilde{w}}_j^k=(w_{j1}^k,w_{j2}^k,w_{j3}^k)$.

Step 2: Determine the combined fuzzy weight for the criterion as well as the overall fuzzy ranking for the possibilities. The following approach may be used to obtain the aggregate fuzzy evaluation (abbreviated as ${\tilde{x}}_{ij}^k=({a_1}_{ij}^k,{a_2}_{ij}^k,{a_3}_{ij}^k)$) of the ith criteria that replaces the jth criterion:

$$\{\begin{array}{l}{a}_{1ij}=\underset{k}{\min }\left\{a_{1ij}^k\right\}\\ a_{2ij}={\displaystyle \frac{1}{K}}{\displaystyle \sum _{k=1}^K{a}_{2ij}^k}\\ a_{3ij}=\underset{k}{\max }\left\{a_{3ij}^k\right\}\end{array}$$

(9)

The aggregated fuzzy weight, ${\tilde{w}}_j=(w_{j1},w_{j2},w_{j3})$, for the $C_j$ criterion is given by

$$\{\begin{array}{l}{w}_{j1}=\underset{k}{\min }\left\{w_{j1}^k\right\}\\ w_{j2}={\displaystyle \frac{1}{K}}{\displaystyle \sum _{k=1}^K{w}_{j2}^k}\\ w_{j3}=\underset{k}{\max }\left\{w_{j3}^k\right\}\end{array}$$

(10)

Step 3: Compute the normalized fuzzy decision matrix $\tilde{R}=\left[{\tilde{r}}_{ij}\right]$, in which

$${\tilde{\psi }}_{ij}=\left({\displaystyle \frac{a_{ij}}{{\widehat{c}}_{ij}}},{\displaystyle \frac{b_{ij}}{{\widehat{c}}_{ij}}},{\displaystyle \frac{c_{ij}}{{\widehat{c}}_{ij}}}\right) \mathrm{and} {\widehat{c}}_{ij}=\underset{i}{\max }\left\{c_{ij}\right\} (\mathrm{for}\mathrm{the}\mathrm{benefit}\mathrm{criteria})$$

(11)

$${\tilde{\psi }}_{ij}=({\displaystyle \frac{{\widehat{a}}_{ij}}{c_{ij}}},{\displaystyle \frac{{\widehat{a}}_{ij}}{b_{ij}}},{\displaystyle \frac{{\widehat{a}}_{ij}}{a_{ij}}}) \mathrm{and} {\widehat{a}}_{ij}=\underset{i}{\min }\left\{a_{ij}\right\} (\mathrm{for}\mathrm{the}\mathrm{cost}\mathrm{criteria})$$

(12)

Step 4: Compute the matrix $\tilde{V}$ using the equation below:

$$\tilde{V}={\tilde{v}}_{ij}={\tilde{\psi }}_{ij}\times w_j$$

(13)

Step 5: Determine the fuzzy positive ideal solution (FPIS) and fuzzy negative ideal solution (FNIS) as described below:

$${\widehat{T}}_{\max }=({\widehat{v}}_{\max 1},{\widehat{v}}_{\max 2},{\widehat{v}}_{\max 3},\dots ,{\widehat{v}}_{\max n}), {\widehat{v}}_{\max j}=\underset{i}{\max }\left\{{\tilde{v}}_{ij}\right\}$$

(14)

$${\widehat{T}}_{\min }=\left({\widehat{v}}_{\min 1},{\widehat{v}}_{\min 2},{\widehat{v}}_{\min 3},\dots ,{\widehat{v}}_{\min n}\right), {\widehat{v}}_{\min j}=\underset{i}{\min }\left\{{\tilde{v}}_{ij}\right\}$$

(15)

Step 6: Compute the distance from each alternative to the FPIS and to the FNIS.

$$\{\begin{array}{l}{d}_i^{+}={\displaystyle \sum _{j=1}^{n}d({\tilde{v}}_{ij},{\widehat{v}}_{\max j}})\\ d_i^{-}={\displaystyle \sum _{j=1}^{n}d({\tilde{v}}_{ij},{\widehat{v}}_{\min j}})\end{array}$$

(16)

Step 7: Calculate the closeness coefficient $F{T}_i$ using the following formula:

$$F{T}_i={\displaystyle \frac{d_i^{-}}{d_i^{-}+d_i^{+}}}(i=1,2,3,\dots ,n)$$

(17)

Step 8: Rank the alternatives based on $F{T}_i$. The best choice is shown by the alternative with the highest $F{T}_i$.

3. Results and Discussion

In order to enhance the reliability of the MCDM model, we have incorporated two techniques, namely Fuzzy-AHP and Fuzzy-TOPSIS, to select the optimal robot for our factory based on specific criteria. Firstly, we utilize the Fuzzy-AHP to establish a set of weights for the evaluation criteria. Subsequently, we employ the Fuzzy-TOPSIS to assess and rank the available robot options. By employing the Fuzzy-AHP method to establish the weights for the evaluation criteria, we have achieved greater objectivity and accuracy compared to the conventional weight set determined by experts in Fuzzy-TOPSIS. The research process diagram is illustrated in Figure 4.

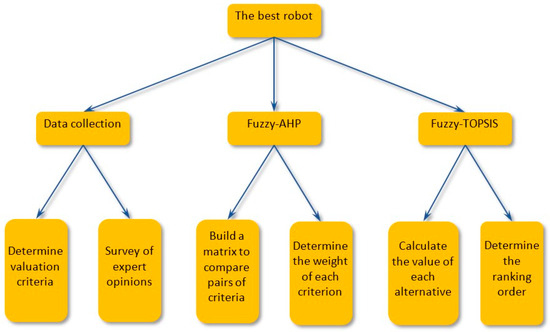
Figure 4. Components for calculating the optimal robots.

The Fuzzy-AHP-TOPSIS hybrid model is employed to assess and rank objects by evaluating criteria through a pairwise comparison matrix and ranking objects based on their proximity to positive and negative ideal solutions. Fuzzy numbers are utilized in the model to mitigate uncertainty and subjectivity associated with the evaluator. The model employs Fuzzy-AHP-TOPSIS to evaluate criteria, aiding in the selection of the optimal robot. The process involves the following steps:

Step 1: Determine evaluation criteria.

In order to make a decision in selecting the optimal robot, it is necessary to establish criteria that align with the factory’s requirements. These criteria represent the specific attributes that robot manufacturers have incorporated into their products. After careful consideration of the factory’s operations, we identified and defined the criteria, which are outlined in Table 2.

Table 2. List of criteria used in robot selection.

No.	Criteria	Units	Symbol
1	Mechanical Weight	Kg	MW
2	Velocity	m/s	VL
3	Payload	Kg	PL
4	Maximum Reach	Mm	MR
5	Average Power Consumption	Kw	APC
6	Cost	$	CO

The selection of criteria for evaluating and choosing the optimal robot in a manufacturing environment is crucial for the effectiveness and accuracy of the decision-making process. The six criteria chosen in this study are Mechanical Weight, Velocity, Payload, Maximum Reach, Average Power Consumption, and Cost. These criteria were selected based on their comprehensive relevance and critical importance in determining the suitability of a robot for industrial applications. Descriptions of these criteria are as follows:

Mechanical weight pertains to the weight of the robot itself, impacting aspects such as mobility, installation prerequisites, and the structural support essential in the production setting. This weight factor influences the ease of integration into existing systems and the overall adaptability for deployment across various sectors of the factory. Lighter robots may offer easier installation and relocation, whereas their heavier counterparts might necessitate sturdier infrastructure.

Velocity denotes the rate at which a robot can execute its assigned tasks, directly affecting production efficiency and cycle durations. Enhanced speeds can enhance productivity, diminishing the time needed for each operation and augmenting the factory’s output rate. This aspect holds particular significance in high-speed manufacturing scenarios where time optimization is paramount.

Payload signifies the maximum weight a robot can manage, a critical factor in ensuring its capability to execute tasks without mechanical strain. This capacity significantly influences the robot’s applicability for specific tasks, especially in handling hefty materials or products during manufacturing processes. A higher load capacity empowers the robot to handle larger or heavier components, thereby amplifying its versatility.

Maximum reach denotes the farthest distance a robot can extend to execute its tasks, influencing its access to different parts of the work area. This metric determines the robot’s operational range and its ability to function effectively in larger or more intricate setups. A greater reach enables the robot to cover more ground without requiring frequent repositioning, thereby enhancing its efficiency and adaptability across various applications.

Average power consumption quantifies the energy utilized by the robot during its operation, impacting operational expenses. Lower power consumption leads to reduced operational costs and contributes to a more sustainable production process. This criterion holds significance for factories striving to minimize energy usage and lower overall expenditures.

Cost encompasses the initial purchase price, installation expenses, and ongoing maintenance costs, all pivotal factors in any investment evaluation. It ensures that the investment aligns with the financial constraints of the factory and aids in comparing the economic viability of different robot options. Effectively managing costs is crucial for sustaining profitability and attaining a favorable return on investment.

Once the essential criteria were established, we conducted a thorough search to identify robots that possess the desired attributes. The robots, along with their corresponding attribute parameters, are listed in Table 3.

Table 3. Numerical data for robot selection [60].

Alternative	MW	VL	PL	MR	APC	CO
Robot 1	145	1.33	12	1441	1.0	722
Robot 2	27	1.11	8	911	0.5	485
Robot 3	170	1.26	4	1500	0.6	965
Robot 4	272	0.65	20	1650	3.4	671
Robot 5	250	0.04	25	2409	2	690
Robot 6	230	0.25	10	1925	5.6	325
Robot 7	501	1.01	6	4368	2.5	400
Robot 8	215	1.21	8	1801	5.05	690

Step 2: Survey experts’ opinions.

Initially, the study constructs a fuzzy evaluation table for the weight vector. The values corresponding to the semantic level, ranging from low to high, are presented in Table 4.

Table 4. Fuzzy evaluation scores for the weight vector.

Linguistic Terms	Scale of Fuzzy Number	Units
Absolutely strong (AS)	(2, 2.5, 3)	$\tilde{9}$
Very strong (VS)	(1.5, 2, 2.5)	$\tilde{8}$
Fairly strong (FS)	(1, 1.5, 2)	$\tilde{7}$
Slightly strong (SS)	(1, 1, 1.5)	$\tilde{6}$
Equal (E)	(1, 1, 1)	$\tilde{5}$
Slightly weak (SW)	(2/3, 1, 1)	$\tilde{4}$
Fairly weak (FW)	(0.5, 2/3, 1)	$\tilde{3}$
Very weak (VW)	(0.4, 0.5, 2/3)	$\tilde{2}$
Absolutely weak (AW)	(1/3, 0.4, 0.5)	$\tilde{1}$

To ensure practical applicability, we sought expert opinions by consulting individuals who are recognized as experts in the field of industrial robots. These experts possess extensive knowledge and experience in the domain, as listed in Table 5.

Table 5. List of the experts.

Experts	Age	Education	Experience in the Field (Years)
Decision maker 1 (DM 1)	58	Associate Professor of Mechanical Engineering	>15
Decision maker 2 (DM 2)	62	Associate Professor of Robotics Engineering	>20
Decision maker 3 (DM 3)	58	Associate Professor of Manufacturing Processes	>25
Decision maker 4 (DM 4)	65	Professor of Management Science and Engineering Management	>20
Decision maker 5 (DM 5)	66	Professor of Mechatronics Engineering	>30

The aforementioned experts assessed the criteria using a fuzzy evaluation table for the weight vector, as outlined in Table 6.

Table 6. Evaluation of criteria by experts.

Criteria	DM 1	DM 2	DM 3	DM 4	DM 5
MW	FS	FS	FS	VS	FS
VL	AS	VS	VS	AS	VS
PL	AS	AS	AS	AS	AS
MR	VS	VS	VS	VS	AS
APC	VW	VW	VW	FW	VW
CO	FW	FW	FW	FW	FW

Step 3: Construct a pairwise comparison matrix for the criteria.

For each pair of criteria A and B, we establish their relationship using the value scale determined by fuzzy numbers. Experts then assess the levels of superiority and inferiority between the criteria. The semantic relationship between the evaluation criteria is depicted in Table 7.

Table 7. Relationship between two criteria according to linguistic terms.

Criteria	High Priority				Equal	Low Priority				Criteria
A	$\tilde{9}$	$\tilde{8}$	$\tilde{7}$	$\tilde{6}$	$\tilde{5}$	$\tilde{4}$	$\tilde{3}$	$\tilde{2}$	$\tilde{1}$	B

Based on the established Fuzzy-AHP method, we have a pairwise comparison matrix between the criteria, as shown in Table 8.

Table 8. Pairwise comparison matrix between criteria.

Criteria	MW	VL	PL	MR	APC	CO
MW	(1, 1, 1)	(1, 15/14, 30/19)	(1, 15/13, 5/3)	(15/14, 30/19, 25/12)	(1, 8/5, 21/10)	(1, 11/10, 8/5)
VL	(19/30, 14/15, 1)	(1, 1, 1)	(1, 11/10, 8/5)	(1, 6/5, 17/10)	(8/5, 21/10, 13/5)	(1, 8/5, 21/10)
PL	(3/5, 13/15, 1)	(5/8, 10/11, 1)	(1, 1, 1)	(1, 15/14, 30/19)	(13/10, 9/5, 13/10)	(13/10, 9/5, 23/10)
MR	(12/25, 19/30, 14/15)	(10/17, 5/6, 1)	(19/30, 14/15, 1)	(1, 1, 1)	(1, 7/5, 19/10)	(1, 13/10, 9/5)
APC	(10/21, 5/8, 1)	(5/13, 10/21, 5/8)	(10/13, 5/9, 10/13)	(10/19, 5/7, 1)	(1, 1, 1)	(1, 7/5, 19/10)
CO	(5/8, 10/11, 1)	(10/21, 5/8, 1)	(10/23, 5/9, 10/13)	(5/9, 10/13, 1)	(10/19, 5/7, 1)	(1, 1, 1)

Step 4: Determine the fuzzy weight of each criterion.

Based on the evaluation of the criteria, we have a table of fuzzy weight values of each criterion, as seen in Table 9 below.

Table 9. Fuzzy weight value of each criterion.

$\mathbf{Fuzzy} \mathbf{Weight} {\tilde{\mathit{w}}}_{\mathit{j}}$	Value
${\tilde{w}}_1$	(0.132, 0.2, 0.33)
${\tilde{w}}_2$	(0.131, 0.206, 0.3190)
${\tilde{w}}_3$	(0.121, 0.192, 0.263)
${\tilde{w}}_4$	(0.098, 0.16, 0.247)
${\tilde{w}}_5$	(0.085, 0.121, 0.2)
${\tilde{w}}_6$	(0.076, 0.121, 0.195)

Step 5: Expert evaluation of alternative options based on criteria.

Initially, we have a fuzzy evaluation score table for the alternatives, which captures the expert assessments for each criterion listed in Table 10.

Table 10. Fuzzy evaluation scores for alternatives.

Linguistic Terms	Fuzzy Core
Very poor (VP)	(0, 0, 1)
Poor (P)	(0, 1, 3)
Medium poor (MP)	(1, 3, 5)
Fair (F)	(3, 5, 7)
Medium good (MG)	(5, 7, 9)
Good (G)	(7, 9, 10)
Very good (VG)	(9, 10, 10)

We consulted experts to gather their perspectives on alternative options for each criterion. Appendix A contains Table A1, Table A2, Table A3, Table A4, Table A5 and Table A6, which present the various issues discussed.

Step 6: Construct a decision matrix.

We establish a fuzzy decision matrix for the criteria, which summarizes the evaluations and scores for each criterion. The decision matrix for all criteria is depicted in Table 11.

Table 11. Decision matrix.

Alternative	MW	VL	PL	MR	APC	CO
Robot 1	(0, 0.6, 2.2)	(8.6, 9.8, 10)	(5.4, 7.4, 9.2)	(0, 0.8, 2.6)	(5.8, 7.8, 9.4)	(0, 0.6, 2.2)
Robot 2	(0, 0, 1)	(2.2, 4.2, 6.2)	(0, 0.8, 2.6)	(0, 0, 1)	(9, 10, 10)	(5.8, 7.8, 9.4)
Robot 3	(0, 1, 3)	(7.4, 9.2, 10)	(0, 0.6, 2.2)	(0, 1, 3)	(7.4, 9.2, 10)	(0, 0.2, 1.4)
Robot 4	(6.6, 8.6, 9.8)	(0, 0.4, 1.8)	(7.8, 9.4, 10)	(1.4, 3.4, 5.4)	(0, 1, 3)	(2.2, 4.2, 6.2)
Robot 5	(5.4, 7.4, 9.2)	(0, 0.8, 2.6)	(8.6, 9.8, 10)	(7.8, 9.4, 10)	(2.6, 4.6, 6.6)	(0.8, 2.6, 4.6)
Robot 6	(2.2, 4.2, 6.2)	(0, 0, 1)	(2.6, 4.6, 6.6)	(5, 7, 9)	(0, 0.2, 1.4)	(9, 10, 10)
Robot 7	(8.6, 9.8, 10)	(0.6, 2.2, 4.2)	(0.2, 1.4, 3.4)	(9, 10, 10)	(1.4, 3.4, 5.4)	(7.8, 9.4, 10)
Robot 8	(0.6, 2.2, 4.2)	(5.4, 7.4, 9.2)	(1, 3, 5)	(3.4, 5.4, 7.4)	(0, 0.4, 1.8)	(3.8, 5.8, 7.8)

Step 7: Compute the distance from each alternative to the FPIS and FNIS.

The values of the FPIS and FNIS are determined using Equation (16). The distances from the options to the FPIS and FNIS are presented in Table 12.

Table 12. Distance from alternatives to FPIS and FNIS.

Alternative	Robot 1	Robot 2	Robot 3	Robot 4	Robot 5	Robot 6	Robot 7	Robot 8
$d_i^{+}$	0.2656	0.4608	0.3525	0.2307	0.1653	0.3168	0.2131	0.2673
$d_i^{-}$	0.2803	0.0819	0.1953	0.3183	0.3835	0.2319	0.3301	0.2843

Step 8: Utilize the Fuzzy-TOPSIS method to evaluate the robots.

For each option $A_i$, we calculate a closeness coefficient $F{T}_i$, which is presented in Table 13, indicating the relative closeness of each option to the ideal solution.

Table 13. Ranking of alternatives.

Alternative	Robot 1	Robot 2	Robot 3	Robot 4	Robot 5	Robot 6	Robot 7	Robot 8
$F{T}_i$	0.5134	0.1508	0.3565	0.5798	0.6987	0.4227	0.6077	0.5154
Rank	5	8	7	3	1	6	2	4

Within the proposed model, a higher coefficient value $F{T}_i$ signifies a greater preference or optimality as per the decision maker’s inclinations. As per the closeness coefficients $F{T}_i$ detailed in Table 13, Robot 5 emerges as the most optimal choice to meet the factory’s needs, while Robot 2 is identified as the least favorable option. This ranking highlights the model’s efficacy in accurately distinguishing among alternatives. The key innovation of this method lies in its fusion of the strengths of both methodologies within a fuzzy logic framework, effectively addressing the inherent uncertainty and subjectivity in expert evaluations. Traditional methods often falter in handling the ambiguity and imprecision intrinsic to expert judgments, as they necessitate precise numerical inputs. In contrast, the fuzzy logic framework empowers experts to convey their preferences using linguistic terms that are subsequently transformed into triangular fuzzy numbers. This approach diminishes the reliance on exact figures and better encapsulates the uncertainty in expert evaluations. By employing this dual approach, the chosen robot optimizes benefits while minimizing costs and other adverse factors.

4. Conclusions

The solution to the problem of selecting optimal robots in production brought significant benefits to the factory. It not only alleviates the challenges associated with choosing the most suitable robot from a multitude of conflicting criteria but also delivers numerous advantages to the factory as a whole. Appropriately designed and selected robots can operate with enhanced efficiency, thereby increasing production output and labor productivity. In this study, the integrated Fuzzy-AHP-TOPSIS model is employed, leveraging the AHP technique to establish criteria weights and employing the TOPSIS method to evaluate and rank robot options. The proposed fuzzy solution enhances objectivity in evaluating criteria by utilizing nine fuzzy numbers for pairwise comparisons. Triangular fuzzy numbers are employed to expand the evaluation possibilities. The expert system is coordinated to construct a criteria comparison matrix, which is then used to determine the weights for the set of objective criteria. Based on the established fuzzy weight set, the TOPSIS fuzzification strategy is employed to select the option that is closest to the positive ideal solution (PIS), optimizing the benefit criterion while minimizing the cost criteria, and farthest from the negative ideal solution (NIS). The incorporation of fuzzy numbers mitigates uncertainty and subjectivity in the evaluation process, resulting in a more accurate ranking of alternatives compared to traditional MCDM methods. Based on this ranking, the optimal robot option can be selected for the factory, facilitating effective decision-making in manufacturing environments. However, it is important to note that this study has certain limitations. The number of robots included in the evaluation is relatively small. Nevertheless, this serves as a foundation for testing the Fuzzy-AHP-TOPSIS-integrated model and paves the way for its application to broader problems with a more diverse range of options. In the near future, we plan to implement this model with a larger dataset and enhance it by integrating additional MCDM methods to achieve the highest level of accuracy. Nevertheless, it is essential to acknowledge that this study has certain constraints. The evaluation includes a relatively small number of robots, potentially limiting the ability to comprehensively encompass the diversity and intricacies of available market options. Additionally, the model’s current applicability is restricted to a specific set of criteria and may necessitate adjustments for various industrial contexts or additional criteria. Despite these limitations, this study establishes the groundwork for testing the Fuzzy-AHP-TOPSIS-integrated model and sets the stage for its application to broader issues with a wider array of options, such as expanding the dataset, integrating additional MCDM methods, and incorporating real-time data.