Optimization of Synchronous Control Parameters Based on Improved Sinusoidal Gray Wolf Algorithm

Abstract

High precision control is often accompanied by many control parameters, which are interrelated and difficult to adjust directly. It is difficult to convert the system control effect directly into mathematical expression, so it is difficult to optimize it by intelligent algorithm. To solve this problem, we propose an improved sinusoidal gray wolf optimization algorithm (ISGWO). In this algorithm, a particle crossing processing mechanism based on the symmetry idea is introduced to maximize the retention of the position information of the optimal individual and improve the search accuracy of the algorithm. In addition, a differential cross-perturbation strategy is adopted to help the algorithm jump out of the local optimal solution in time, which enhances the development capability of ISGWO. Meanwhile, the position update formula with improved sinusoidal can better balance the development and exploration of ISGWO. The ISGWO algorithm is compared with three improved Gray Wolf algorithms on the CEC2017 test set as well as the synchronization controller. The experimental results show that the ISGWO algorithm has better selectivity, speed and robustness.

1. Introduction

Controller parameter tuning [1] is a major challenge in system control, following controller design. Usually, the designer relies on experience or fewer numerical attempts to determine the appropriate parameters. In fact, some adjustable parameters in the controller have a great influence on the final control effect, but it is more difficult to find the optimal values of the parameters mathematically. Meanwhile, in the case of multiple parameters affecting a system simultaneously, a direct solution is almost impossible. Therefore, it is necessary to design an optimization algorithm with both speed and high accuracy to seek the optimal parameters for the real-time changing control system.

Compared to other optimization problems, the optimization objective of a control system is difficult to be directly converted into a mathematical expression. Therefore, with the help of the concept of optimal control, the dynamic parameters such as the upward adjustment and response time of the system are expressed by performance indexes to measure the control effect. At the same time, due to the complexity of the optimization target and the performance index, the classical gradient-based algorithm takes a lot of time and easily falls into the complexity of the local optimum of the objective function, while the global optimum cannot be found. For this reason, to overcome the limitations of gradient-based, a meta-heuristic algorithm is introduced to solve this problem. As a whole, meta-heuristic algorithms can be roughly divided into two categories: (1) algorithms based on a single solution, such as the simulated annealing algorithm [2], in which the performance of the algorithm is continuously improved by simulating the temperature change in a hot object, and (2) population-based metaheuristic algorithms such as Black Widow Optimization Algorithm (BWO) [3], Seagull Optimization Algorithm (SOA) [4], Butterfly Optimization Algorithm (BOA) [5], Artificial Fishing Swarms Algorithm [6], Beluga Whale Algorithm [7] and African Vulture Optimization Algorithm (AVOA) [8]. Group-based algorithms exhibit intelligence through group cooperation. The gray wolf optimization algorithm is an excellent group meta-heuristic algorithm first proposed by Seyedali Mirjalili in 2014. GWO [9] is a search method to find the optimal solution, which is mainly achieved by simulating the social hierarchy and predatory behavior of gray wolf populations. It has the advantages of fast convergence speed, high convergence accuracy and a simple implementation process, and has been widely studied and emphasized. It has been widely applied in the fields of stress distribution [10], blood pressure monitoring [11], fault diagnosis [12], power systems [13], wind prediction [14], etc., and has achieved remarkable results.

GWO’s impressive optimization results in diverse fields prove the algorithm’s remarkable versatility and scalability in tackling problems of varying dimensions and objectives. The control parameter optimization problem is riddled with hidden constraints, making it challenging for classical metaheuristic algorithms like SA and GA to identify suitable parameters and achieve superior planning results. Meanwhile, some algorithms with relatively high computational time complexity and low accuracy, such as the Artificial Bee Colony Algorithm (ABC) [15], the Differential Evolutionary Algorithm (DE) [16] and the Particle Swarm Algorithm (PSO) [17], require high flight costs due to the short computational response time required for the control problem. GWO’s superior global search capability is a key advantage. It enables the algorithm to search globally for multiple objectives, maintaining diversity in the search space and avoiding local optima through group intelligence and competition. This ensures a high level of accuracy in the global search.

However, in practical applications, due to the complexity and variability of the optimization objectives of the control parameter optimization problem, the traditional GWO algorithm has limited adaptability when it comes to complex environmental factors and constraints, and it is easy for it to fall into local optimality, which affects the search accuracy. To solve the local optimum problem, researchers usually have the following two ideas to optimize the GWO algorithm:

(1) Optimize the position-update formula or form a new combined algorithm by introducing a simple adaptive mechanism into the GWO algorithm.

Xu et al. [18] developed a stochastic convergence factor, and Zhang et al. [19] assessed the performance of various adaptive convergence functions and identified the most suitable convergence function for the Gray Wolf algorithm. Liu et al. [20] introduced a nonlinear adaptive convergence factor strategy that balanced the algorithm’s global and local search capabilities, and Zheng et al. [21] applied tent chaotic mappings, which improved the diversity of the initial populations, thereby enhancing the algorithm’s global search capacity. Chuen et al. [22] designed a population initialization strategy based on SPM chaotic mapping. Madhiarasan et al. [23] partitioned the population into three groups and optimized the algorithm parameters, thereby boosting the convergence rate. Di et al. [24] proposed an adaptive search algorithm, which enhanced the algorithm’s global search capability and optimization search precision. To avoid the problem of random and blind searching in the iterative computation process, the chaotic mapping and the reverse learning mechanism are introduced into the improved optimization algorithm [25].

(2) Optimization by mixing the optimal search strategies and ideas of different algorithms.

Saurav et al. [24] integrate the reverse learning approach with the GWO algorithm, markedly enhancing the diversity of the initial population and expediting the algorithm’s precision. Liu et al. [20] incorporate Powell’s algorithm into the Gray Wolf algorithm, leveraging its robust local search capability to compensate for the shortcomings of late convergence precision. Deng et al. [26] introduce a damage repair operation in the large-scale domain search algorithm in the GA algorithm to address the deficiency in global search capability while further enhancing local search capability. Fariborz et al. [27] incorporate a hybrid optimization algorithm, which facilitates information exchange between individuals and addresses the issue of slow convergence in the late stage. Wang et al. [28] incorporate the somersault foraging strategy into the GWO algorithm to enhance population diversity, thereby preventing the algorithm from becoming trapped in a local optimum. She et al. [29] incorporate a dimension learning strategy, which augments the algorithm’s global search capability. Li et al. [30] improved the algorithm by integrating Levi’s flight and random swimming strategies, which augmented the algorithm’s local optimization capability and convergence speed. In Liang et al. [31], the PSO algorithm was combined with the GWO algorithm, which resulted in an enhanced local search capability and accelerated convergence speed. Huang et al. [32] improved the position update formula by combining the idea of individual superiority of the particle swarm algorithm, which led to an improved algorithmic model-solving ability. Zhang et al. [33] introduced individual coding and POX cross-operation to overcome local stagnation and enhance global search ability. Considering that there are numerous parameters to be optimized in ADRC, an improved moth-flame optimization (MFO) is proposed to obtain ADRC parameters [34].

Although the above methods provide two existing ideas and ways to solve the problem, the stability of single stratification may be insufficient, and the combination algorithm may affect the optimization searching effect to a certain extent due to the high time complexity and space complexity when performing the optimization objective calculation and parameter assignment. To address this problem, an improved sinusoidal gray wolf optimization algorithm (ISGWO) based on the improved sinusoidal algorithm combined with differential cross perturbation and symmetric particle crossing processing is proposed and applied to the optimization problem of control parameters.

The main contributions of this paper are as follows:

(1)

A novel position-update formulation based on an improved sinusoidal algorithm is used to balance the global exploration and local convergence of the algorithm;

(2)

The differential cross-perturbation strategy helps to improve the ability of the algorithm to please the local optimum;

(3)

The particle crossing processing mechanism based on the symmetry idea helps the algorithm retain the best individual information and improve the convergence accuracy;

(4)

The effectiveness of the ISGWO algorithm is verified through extensive statistical experiments, including CEC 2017 benchmarking and parameter-controlled optimization problems.

This paper is organized as follows. Section 2 gives the optimization object and parameter selection. Section 3 presents the basic mathematical model of GWO. Section 4 details the design and construction of ISGWO. Section 5 verifies the effectiveness of the ISGWO algorithm through simulation. Section 6 summarizes the conclusions of this paper.

2. Optimization Object and Parameter Selection

2.1. Optimization Objects

According to the literature [35], in the process of synchronous control of dual motors, the state space equation of the control object can be established as Equation (1). At the same time, the global reverse-step sliding mode angular velocity synchronous control is adopted for synchronous operation, and the controller is shown in Equation (2). In order to save space, detailed derivation is not carried out in this paper.

$$\left\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=-{\displaystyle \frac{B}{J}}-{\displaystyle \frac{K_m{K}_E+K_m{K}_v{K}_{pwm}{K}_e}{JR}}{x}_2+{\displaystyle \frac{K_m{K}_v{K}_{pwm}}{JR}}u\\ {\dot{x}}_3=x_4\\ {\dot{x}}_4=-{\displaystyle \frac{B}{J}}-{\displaystyle \frac{K_m{K}_E+K_m{K}_v{K}_{pwm}{K}_e}{JR}}{x}_4+{\displaystyle \frac{K_m{K}_v{K}_{pwm}}{JR}}u\end{array}\right.$$

(1)

where $x_1$ represents the output angle of the motor; $x_2$ represents the output angular speed of the motor; $K_E$ is the current loop feedback coefficient; $K_e$ is the speed loop feedback system; $K_v$ is the speed regulator proportionality coefficient; $K_{pwm}$ is the coefficient of pulse-width modulation; $K_m$ is the motor torque coefficient; $R$, $L$ is the resistance and inductance of the armature circuit, where $R\approx 0$ can be neglected in modeling; $J$ is the rotational inertia of the motor; and $B$ is the friction coefficient.

$$u={\displaystyle \frac{JR}{K_m{K}_v{K}_{pwm}}}(c_1{\dot{e}}_{11}+{\dot{x}}_{1d}+k_{2}s+k_{3}sgn(s)+a_1{x}_2-a_2{x}_4)$$

(2)

where $a_1=-{\displaystyle \frac{B}{J}}-{\displaystyle \frac{K_m{K}_E+K_m{K}_v{K}_{pwm}{K}_e}{JR}}$; $a_2={\displaystyle \frac{K_m{K}_v{K}_{pwm}}{JR}}$; $e_1=x_{1d}-x_1$; $e_2={\dot{x}}_{1d}+k_1{e}_1-x_2$; $x_{1d}$ is the expected value of $x_1$; $s=k_1{e}_1+k_2{e}_2$; $c_1, k_1, k_2, k_3$ are non-negative control parameters.

Several parameters in the controller affect the final control effect. To achieve the optimal control effect efficiently and accurately, the parameters need to be screened for parameter optimization.

2.2. Parameter Selection

Taguchi’s method [36] is a widely used local optimization method, which is able to comprehensively consider the influence of multiple parameters on the optimization objective Chengdu, with high efficiency and small computational volume. Four adjustable parameters $c_1, k_1, k_2$, and $k_3$ in the controller u are selected as alternative optimization factors, and the constraint ranges are given in Table 1 by combining the system stability conditions and the device technology level.

Table 1. Optimization factors and their constraint ranges.

Parameter	Numerical Value	Scope of Reasonable Constraints
$c_1$	1	0~4
$k_1$	5	0~20
$k_2$	5	0~20
$k_3$	1	0~4

Within this range, according to the general principle of Taguchi’s method for selecting the level values of optimization factors, four level values are selected equidistantly within the range of values, named level values I, II, III and IV, and the number of levels of the parameters to be optimized is shown in Table 2.

Table 2. Number of parameter levels to be optimized.

Parameter	Level I	Level II	Level III	Level IV
$c_1$	1	2	3	4
$k_1$	5	10	15	20
$k_2$	5	10	15	20
$k_3$	1	2	3	4

Considering the stability, speed and low energy consumption of the control algorithm, $J_1={\displaystyle {\int }_0^{t_f}\left|e^t\right|}dt$, $J_2={\displaystyle {\int }_0^{t_f}dt}$ and $J_3={\displaystyle {\int }_0^{t_f}{u}^{T}u(t)dt}$ are selected as the optimization objectives. $J_1$ is often used for given signal tracking problems. When targeting $J_1$, it seeks both dynamic quality and steady-state performance. With $J_2$ as the optimization goal, it emphasizes the dynamic quality, expects to optimize the time, and needs to complete the turnaround under the time-optimal condition under huge load consumption. When targeting $J_3$, it emphasizes steady-state performance, expecting a minimum control cost from initial state to final state.

With the help of Simulink simulation software to complete the sensitivity analysis of the main parameters, to obtain the Pearson correlation coefficient r of each parameter for a certain optimization target, and then according to the weight of the optimization target in the motor design, to obtain the sensitivity of a certain parameter $p_i$ for the optimization target $Q(p_i)$.

The Pearson correlation coefficient r and the sensitivity $Q(p_i)$ are defined as

$$r={\displaystyle \frac{{\displaystyle \sum _{i=1}^n\left(p_i-\overline{p}\right)\left(q_i-\overline{q}\right)}}{\sqrt{{\displaystyle \sum _{i=1}^n{\left(p_i-\overline{p}\right)}^2}}\sqrt{{\displaystyle \sum _{i=1}^n{\left(q_i-\overline{q}\right)}^2}}}}$$

(3)

$$Q(p_i)={\lambda }_1\left|r_1(p_i)\right|+{\lambda }_2\left|r_2(p_i)\right|+{\lambda }_3\left|r_3(p_i)\right|$$

(4)

where $q_i$ is the optimization target value corresponding to the control parameter $p_i$; $\overline{p}$ is the average value of the control parameter $p_i$; $\overline{q}$ is the average value of the optimization target value $q_i$; $r_j(p_i)$ is the Pearson correlation coefficient of each optimization target; and ${\lambda }_j$ is the weight coefficient of each optimization target. In this paper, the main premise is to maintain speed under the guarantee of stability, and finally to consider low energy consumption. According to the performance indexes of step response, six indexes of overshoot, delay time, rise time, peak time, adjustment time and error band are selected as the measurement standards. J1 can represent the delay time, rise time, peak time, adjustment time, error band and other five, J2 can represent the delay time, rise time, peak time, adjustment time and other four, and J3 can only represent the overshoot. Therefore, the weighting parameters in Equation (5) are: ${\lambda }_1=0.5$, ${\lambda }_2=0.4$, ${\lambda }_3=0.1$.

The Pearson correlation coefficients as well as the sensitivities of each control parameter were obtained in the single margin mode of operation as shown in Table 3.

Table 3. Summary of correlation coefficients and sensitivities of control parameters.

Parameter	${\mathit{c}}_1$	${\mathit{k}}_1$	${\mathit{k}}_2$	${\mathit{k}}_3$
Correlation coefficient 1	−0.9978	−0.99467	−0.93993	−0.9288
Correlation coefficient 2	−0.99923	−0.8582	−0.8733	−0.9923
Correlation coefficient 3	−0.1116	0.4181	0.5680	0.2522
Sensitivity	0.90698	0.85844	0.85474	0.88654

Therefore, the most sensitive control parameter was selected as the optimization parameter.

2.3. Optimization Algorithm Objective Function Selection

In the dual motor synchronization control process, the state space equation of the control object is established. The global backstepping sliding mode angular velocity synchronization control is used to synchronize the operation, and the controller as shown in Equation (2).

Among the integral-type performance metrics that are commonly used are shortest time control metrics, least fuel control and minimum energy control [37]. ITAE performance control is to minimize the performance metric $J={\displaystyle {\int }_0^{t_f}t\left|e(t)\right|dt}$, where $\left|e(t)\right|$ is the absolute value of the system error. In satisfying this performance metric, the control weights the unavoidable initial state error in a time-varying weighting manner to make the system have a fast yet smooth dynamic performance. However, the ITAE performance index cannot be solved analytically, and an optimization algorithm is needed to find the optimal parameters that minimize the performance index.

3. Basic Gray Wolf Optimization Algorithm

Under the harsh environment of nature, creatures, even if they do not have the high intelligence of human beings, have shown amazing group intelligence through continuous adaptation and cooperation under the incentive of the same goal, i.e., food. Based on the tightly organized system of wolf packs and their subtle collaborative hunting methods, a new group intelligence algorithm, the Gray Wolf Optimization Algorithm, is proposed in the literature.

The gray wolf population has a strict hierarchy, as shown in the diagram: the head wolf at the top of the pyramid is called $\alpha$, and is responsible for making decisions about hunting behavior, habitat, food allocation and other functions. Wolf $\alpha$ is not necessarily the strongest wolf, but is the best leader and manager. The second tier of the pyramid is called $\beta$, and $\beta$ is the replacement for $\alpha$ when $\alpha$ is missing from the peak. On the third level is $\delta$, and $\delta$ takes orders from $\alpha$ and $\beta$. Older (less well-adapted) $\alpha$ and $\beta$ are also relegated to the $\delta$ level. The lowest level, $\varpi$, is responsible for balancing relationships within the population.

The GWO algorithm simulates the hierarchy and hunting behavior of gray wolves in nature. The entire wolf pack is divided into $\alpha , \beta , \delta , \varpi$ four groups. The first three groups are the best adapted three groups in order, and these three groups guide the other wolves ($\varpi$) to search towards the target. During the optimization process, the wolves update the position of $\alpha , \beta , \delta , \varpi$. Equation (6) denotes the distance between individuals, and Equation (7) denotes the updating method of individual gray wolves:

$$D=\left|C\cdot X_p(t)-X(t)\right|$$

(5)

$$X(t+1)=X_p(t)-A\cdot D$$

(6)

where $D$ denotes the distance of an individual from the food; $t$ denotes the number of the current iteration; $A=2a\cdot r_2-a$. When $\left|A\right|<1$, the gray wolf pack expands its search range to find better food, which corresponds to local search; $\left|A\right|>1$, the gray wolf pack narrows its encirclement, which corresponds to local search; $C=2r_1$. The convergence factor $a$ is a linear decrease from 2 to 0 with the number of iterations. $X_p$ is the position of the prey and $X$ denotes the position vector for the gray wolf.

When the gray wolf judges the position of the prey, the head wolf $\alpha$ leads $\beta$ and $\delta$ to guide the pack to surround the prey, because $\alpha , \beta , \delta$ is the closest to the prey, so the position of the three wolves is used to judge the approximate position of the prey and gradually approach the prey; the mathematical description of this is as follows:

$$D_{\alpha }=\left|C_1\cdot X_{\alpha }(t)-X(t)\right|$$

(7)

$$D_{\beta }=\left|C_2\cdot X_{\beta }(t)-X(t)\right|$$

(8)

$$D_{\delta }=\left|C_3\cdot X_{\delta }(t)-X(t)\right|$$

(9)

where $X_{\alpha }$ denotes the current position of $\alpha$, $X_{\beta }$ denotes the current position of $\beta$ and $X_{\delta }$ denotes the current position of $\delta$. $C_1, C_2, C_3$ denotes a random vector, and $X(t)$ denotes the current gray wolf position vector. This Equation defines the length and direction of the front progress of wolf $\varpi$ towards $\alpha , \beta , \delta$, respectively.

After the fitness ranking, gray wolf individuals outside the top three randomly update their positions near prey (i.e., the optimal solution) under the guidance of the current best three wolves. The basic principle is the sum of three position difference vectors, adding random quantities to avoid falling into local optimal. The location update formula is shown below

$$X_1=X_{\alpha }-A_1\cdot D_{\alpha }$$

(10)

$$X_2=X_{\beta }-A_2\cdot D_{\beta }$$

(11)

$$X_3=X_{\delta }-A_3\cdot D_{\delta }$$

(12)

$$X(t)=(X_1+X_2+X_3)/3$$

(13)

4. Improved Gray Wolf Algorithm Guided by the Sinusoidal Algorithm

4.1. Improved Sinusoidal Algorithm

The improved sine algorithm strategy is inspired by various types of SCA-related algorithms, such as the sine-cosine algorithm, sine algorithm and exponential sine-cosine algorithm function, as well as the improved sine-cosine algorithm, which utilizes the sinusoidal function in mathematics to perform iterative search for optimization, with a strong global search capability. Meanwhile, the cosine algorithm is improved for the convergence factor, so that the algorithm can fully search the local area, so that the global search and local development ability achieve a good balance. The improved vector A formula is shown below:

$$A=2a\sin (r_2)-a$$

(14)

where $r_2$ is a random number on the interval $\left[0,2\pi \right]$.

A nonlinear decreasing mode is used to set the value of the convergence factor $a$ and a cosine function between 0 and $\pi$ is used to determine the change in value of $a$:

$$a=({\omega }_{\alpha }-{\omega }_{\delta })\cos {\displaystyle \frac{\pi t}{T_{\max }}}+{\omega }_{\alpha }+{\omega }_{\delta }$$

(15)

where $t$ denotes the current iteration number and $T_{\max }$ denotes the maximum iteration number.

The basic GWO algorithm updates gray wolf positions by calculating the average of the three best gray wolf positions. When the fitness values of the best gray wolves differ greatly, this position updating method takes a longer time to gather the wolves near the optimal point. To further speed up the local search of the algorithm, a weight factor can be designed using the fitness values of the first three gray wolves. Wolves with higher fitness should occupy higher weights accordingly.

$${\omega }_{\alpha }={\displaystyle \frac{f(x_{\beta })f\left(x_{\delta }\right)}{f(x_{\alpha })f\left(x_{\delta }\right)+f(x_{\alpha })f\left(x_{\delta }\right)+f(x_{\beta })f\left(x_{\delta }\right)}}$$

(16)

$${\omega }_{\beta }={\displaystyle \frac{f(x_{\alpha })f\left(x_{\delta }\right)}{f(x_{\alpha })f\left(x_{\beta }\right)+f(x_{\alpha })f\left(x_{\delta }\right)+f(x_{\beta })f\left(x_{\delta }\right)}}$$

(17)

$${\omega }_{\gamma }={\displaystyle \frac{f(x_{\alpha })f\left(x_{\beta }\right)}{f(x_{\alpha })f\left(x_{\delta }\right)+f(x_{\alpha })f\left(x_{\delta }\right)+f(x_{\beta })f\left(x_{\delta }\right)}}$$

(18)

Among them, the fitness value of a given gray wolf individual is the value of the control index after the operation of the system with changed individual parameters.

Therefore, the new updated position formula is obtained as follows:

$$X(t+1)={\displaystyle \frac{{\omega }_{\alpha }{X}_1+{\omega }_{\beta }{X}_2+{\omega }_{\delta }{X}_3}{3}}$$

(19)

4.2. Differential Cross-Talk

As the number of iterations of the GWO algorithm increases, the algorithm’s optimization search gradually converges, and it is difficult to jump out of the local optimum once it converges to it. To enhance the ability of the algorithm to jump out of the local optimum, a perturbation mechanism can be added to the population update of the algorithm. In this paper, we design a method that mimics the cross-perturbation of genetic algorithms for enhancing the population diversity of the algorithm at the later stage of the optimality search, to create favorable conditions for escaping from local convergence. Drawing on the crossover operation of the genetic algorithm, the three worst-adapted gray wolf individuals are perturbed as follows:

$$H_i(t)=\left\{\begin{array}{c}Cross\left[X_i(t),X_{\alpha }(t)\right],rand\le {\displaystyle \frac{1}{3}}\\ Cross\left[X_i(t),X_{\beta }(t)\right],{\displaystyle \frac{1}{3}}<rand\le {\displaystyle \frac{2}{3}}\\ Cross\left[X_i(t),X_{\delta }(t)\right],rand\ge {\displaystyle \frac{1}{3}}\end{array}\right.$$

(20)

where $t$ denotes the current moment, $Cross\left[\right]$ denotes the inter-individual crossover operator function and $rand$ is a random variable between 0 and 1.

To avoid falling into a local optimum solution, a moderate perturbation of the gray wolf individuals is required. However, perturbing all individuals will result in a longer processing time of the algorithm and affect the search speed. Therefore, we choose to perturb the three gray wolf individuals with the worst fitness. By retaining the dominant individuals among the gray wolves and performing random jumps globally, the potential optimal points can be searched.

When perturbing the worst assembled individuals with gray wolves $\alpha , \beta$ and $\delta$, respectively, regarding a particular segment of gene sequence, this results in a change in their own individuals, and ultimately in the evolution of the gray wolf population in the direction of diminishing fitness.

When the gray wolf individual is one-dimensional, crossover operations are not possible, so special definitions are required.

$$Cross[a,b]=\left\{\begin{array}{c}a+b/2,\left|b-a\right|>(X_{\max }-X_{\min })/2\\ \max \left(a,b\right)/2,\left|b-a\right|\le (X_{\max }-X_{\min })/2\end{array}\right.$$

(21)

Although the differential perturbation mutation strategy can enhance the algorithm’s ability to search globally and jump out of the local optimum, there is no way to determine that the new individual obtained after the mutation perturbation must be better than the original individual’s fitness value; therefore, after the mutation perturbation updating, the greedy rule is added, and by comparing the fitness values of the old and the new positions, we can determine whether or not we should update the position. The greedy rule is shown in Equation (23) $f(x)$ denotes the fitness value of position $x$.

$$X_i(t)=\left\{\begin{array}{c}{H}_i(t),f\left[H_i(t)\right]<f\left[X_i(t)\right]\\ X_i(t),f\left[H_i(t)\right]\ge f\left[X_i(t)\right]\end{array}\right.$$

(22)

4.3. Particle Transgression Handing Strategy Based on Symmetry Idea

In the process of solving problems, the position of the particles is constantly changing with the iteration of the algorithm, and it is inevitable that the particles will jump out of the feasible domain $\left[X_{\min },X_{\max }\right]$ of the boundary. If not dealt with, it will affect the convergence of the algorithm speed and accuracy. Usually there are three ways to deal with this problem: (1) “Reflection Boundary Method”: the velocity of the individual direction is reversed and the size is unchanged; (2) “Invisible Boundary Method”: give up the overstepping individual directly without participating in the subsequent algorithm optimization; (3) “Absorption Boundary Method”: take the boundary value directly when the particle overstepped the boundary. The literature [38] shows that all of the above three methods will cause a loss of population diversity in the wolf pack and affect the convergence accuracy of the particles. In order to improve the convergence accuracy of the algorithm, a symmetry-based individual boundary-crossing processing strategy is proposed, which is based on the principle of geometric symmetry: when an individual crosses the boundary, the boundary is used as the axis of symmetry (center of symmetry), the individual is transformed to the symmetric position as $2X_{\max }-x_i$ (or) $2X_{\min }-x_i$ and the distance from the individual to the boundary is computed as $X_{\max }-x_i$ (or) $X_{\min }-x_i$ and then processed in different situations. For instance, when an individual crosses the boundary upper limit and $X_{\max }>0$, the position of the individual after the process is the symmetric position plus the product of a random number and distance; when the individual crosses the upper boundary and $X_{\max }\le 0$, the position of the processed individual is the symmetric position minus the product of a random number and distance; when the individual crosses the lower boundary limit and $X_{\min }>0$, the position of the processed individual is the symmetric position minus the product of a random number and distance; when the individual crosses the lower boundary limit and $X_{\min }\le 0$, the position of the processed individual is the symmetric position plus the product of a random number and distance. The specific transformation process is shown in Equations (23) and (24), as shown below:

(1) $x_i>X_{\max }$:

$$x_i=\left\{\begin{array}{c}2X_{\max }-x_i+rand(0,1)\times (X_{\max }-x_i),X_{\max }>0\\ 2X_{\max }-x_i-rand(0,1)\times (X_{\max }-x_i),X_{\max }\le 0\end{array}\right.$$

(23)

(2) $x_i\le X_{\min }$:

$$x_i=\left\{\begin{array}{c}2X_{\min }-x_i-rand(0,1)\times (X_{\min }-x_i),X_{\min }>0\\ 2X_{\min }-x_i+rand(0,1)\times (X_{\min }-x_i),X_{\min }\le 0\end{array}\right.$$

(24)

As shown in Equations (24) and (25), random numbers on the $rand(0,1)\in (0,1)$, after this cross-border processing individuals will not be gathered on the boundary. The introduction of random numbers can ensure that the cross-boundary individuals are in the same position in this iteration, and different positions in the next iteration, increasing the diversity of the positions of the cross-boundary individuals after processing, thus increasing the diversity of the individual population, which can help the algorithm to find the optimal solution of the problem, and improve the convergence accuracy of the algorithm.

4.4. Flow Chart

First, the gray wolf population is initialized and the key parameters a, A and c are initialized. The fitness value of each individual is calculated according to the fitness function. Then, the three individuals with the highest fitness values are screened. Based on these three individuals, the position update formula of improved sine is applied to update the positions of other individuals. Then, it is judged whether the updated position is within the boundary, and the transgressed particle is rotated based on the idea of symmetry. In order to avoid the algorithm falling into local optimal, differential cross perturbation is added to the worst three individuals. Determine whether to update the position according to the greedy formula. Finally, nonlinear update parameters (a, A, c). The specific process is shown in Figure 1.

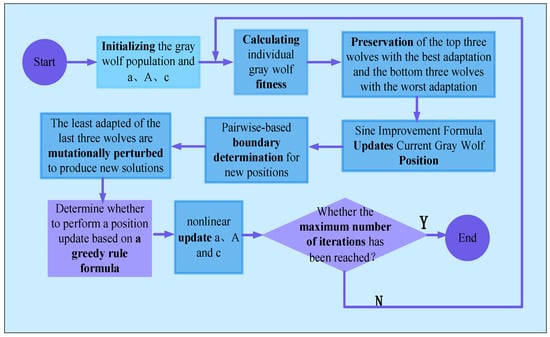
Figure 1. Algorithm Flow Chart.

5. Simulation Analysis

5.1. Experimental Environment and Parameter Settings

In this experiment, the test environment is a 64-bit Windows 10 operating system, and the experimental software is MATLAB R2016a to execute the algorithm operation. The processor is Intel(R) Core(TM)i7-8550U and RAM is 8192 MB. At the same time, to fully prove the feasibility and accuracy of the ISGWO algorithm, and also to ensure that the results of the algorithm operation are relatively fair, this paper will unify the test methods and test data of the algorithm in the simulation experiments. The number of populations is set to 100, the maximum number of iterations is 5000, and all experiments are run independently 20 times to prevent the influence of randomness in the algorithm running results, and the mean, standard deviation and average time of the experimental results are recorded.

5.2. Test Functions

In order to verify the applicability, effectiveness and efficiency of the ISGWO algorithm, 29 test functions in the CEC2017 test set are selected in this paper, and the specific information of the test functions is shown in Table 4. Among them, F1–F2 are single-peak functions, F3–F9 are simple multi-peak functions, F10–F19 are hybrid functions and F20–F29 are composite functions

Table 4. Test function of CEC2017.

Function	Functions	Search Range	Theoretical Optimum
F1	Shifted and Rotated Bent Cigar Function	[−100, 100] D	1.00 × 102
F2	Shifted and Rotated Zakharov Function	[−100, 100] D	3.00 × 102
F3	Shifted and Rotated Rosenbrock’s Function	[−100, 100] D	4.00 × 102
F4	Shifted and Rotated Rastrigin’s Function	[−100, 100] D	5.00 × 102
F5	Shifted and Rotated Expanded Scaffer’s F6 Function	[−100, 100] D	6.00 × 102
F6	Shifted and Rotated Lunacek Bi_Rastrigin Function	[−100, 100] D	7.00 × 102
F7	Shifted and Rotated Non-Continuous Rastrigin’s Function	[−100, 100] D	8.00 × 102
F8	Shifted and Rotated Levy Function	[−100, 100] D	9.00 × 102
F9	Shifted and Rotated Schwefel’s Function	[−100, 100] D	1.00 × 103
F10	Hybrid Function 1 (N = 3)	[−100, 100] D	1.10 × 103
F11	Hybrid Function 2 (N = 3)	[−100, 100] D	1.20 × 103
F12	Hybrid Function 3 (N = 3)	[−100, 100] D	1.30 × 103
F13	Hybrid Function 4 (N = 4)	[−100, 100] D	1.40 × 103
F14	Hybrid Function 5 (N = 4)	[−100, 100] D	1.50 × 103
F15	Hybrid Function 6 (N = 4)	[−100, 100] D	1.60 × 103
F16	Hybrid Function 6 (N = 5)	[−100, 100] D	1.70 × 103
F17	Hybrid Function 6 (N = 5)	[−100, 100] D	1.80 × 103
F18	Hybrid Function 6 (N = 5)	[−100, 100] D	1.90 × 103
F19	Hybrid Function 6 (N = 6)	[−100, 100] D	2.00 × 103
F20	Composition Function 1 (N = 3)	[−100, 100] D	2.10 × 103
F21	Composition Function 2 (N = 3)	[−100, 100] D	2.20 × 103
F22	Composition Function 3 (N = 4)	[−100, 100] D	2.30 × 103
F23	Composition Function 4 (N = 4)	[−100, 100] D	2.40 × 103
F24	Composition Function 5 (N = 5)	[−100, 100] Dvv	2.50 × 103
F25	Composition Function 6 (N = 5)	[−100, 100] D	2.60 × 103
F26	Composition Function 7 (N = 6)	[−100, 100] D	2.70 × 103
F27	Composition Function 8 (N = 6)	[−100, 100] D	2.80 × 103
F28	Composition Function 9 (N = 3)	[−100, 100] D	2.90 × 103
F29	Composition Function 10 (N = 3)	[−100, 100] D	3.00 × 103

Where, ^D represents the dimension.

5.3. Analysis of Experimental Data

To verify whether the ISGWO algorithm has a more prominent performance of optimization search and whether it can master enough competitiveness in the core field of optimization algorithms, this paper mainly selects GWO, BGWO and FGWO to conduct comparative experiments. From the experimental intuition, this paper took the control algorithm, and e test function to obtain the mean, standard deviation and time as shown in the statistics of Table 5. At the same time, the convergence curve of each test function is plotted for convergence analysis, and the intercepted part is shown in Figure 2 for space consideration.

Table 5. Experimental comparison of 4 different algorithms.

Function	Algorithm	Mean	Std	Time (s)
F1	GWO	6.90523 × 108	7.3323 × 107	7.7925
	BGWO	3.85216 × 108	1.1275 × 106	43.80995
	FGWO	9.89342 × 108	4.6709 × 105	5.017
	ISGWO	5.52135 × 108	8.4011 × 105	1.5474
F2	GWO	5571.2683	315.32	15.049
	BGWO	3760.4391	30.481	59.86
	FGWO	8554.8934	3.3215	6.0995
	ISGWO	2459.5781	1.6184	14.674
F3	GWO	25,921.29313	3913.3	7.834
	BGWO	12,854.846	2484.1	25.00796
	FGWO	23,850.89341	5314.4	2.0136
	ISGWO	27,195.00809	1364.2	1.23552
F4	GWO	546.9663281	254.23	13.119
	BGWO	537.0307179	67.09	44.3335
	FGWO	546.8461914	1.208	10.806
	ISGWO	570.4462098	8.1995	12.968
F5	GWO	589.6314228	65.197	9.4216
	BGWO	585.6479014	33.869	38.21547
	FGWO	583.2073571	25.959	6.18924
	ISGWO	576.547929	5.171	9.5044
F6	GWO	604.5017308	69.215	8.0232
	BGWO	602.726983	23.974	37.888
	FGWO	603.3626347	18.438	4.8796
F7	GWO	845.1886808	53.332	10.4956
	BGWO	827.9613051	20.001	43.4668
	FGWO	844.9241087	12.975	8.6448
	ISGWO	818.6132227	13.648	10.3744
F8	GWO	869.2234831	65.1897	7.372
	BGWO	872.531988	34.8695	37.0824
	FGWO	878.4351563	35.9592	4.3872
	ISGWO	873.6378075	5.17178	1.33872
F9	GWO	1347.90458	881.36	9.3536
	BGWO	1148.296602	225.74	40.6632
	FGWO	1260.235621	372.15	5.1232
	ISGWO	1379.978212	188.18	1.41336
F10	GWO	3813.596553	435.01	7.1344
	BGWO	3704.781305	623.72	41.1092
	FGWO	3629.050741	518.99	15.6356
	ISGWO	3805.474043	10.818	3.68228
F11	GWO	1350.296719	886.36	6.7384
	BGWO	1286.680082	284.44	36.8052
	FGWO	1342.023136	51.899	5.1516
	ISGWO	1335.148191	13.636	11.7544
F12	GWO	2.6986 × 107	1.9893 × 106	9.4508
	BGWO	1.8394 × 107	1.0302 × 106	42.2836
	FGWO	2.3565 × 107	5.3144 × 105	8.094
	ISGWO	1.5556 × 107	5.8676 × 105	9.3108
F13	GWO	2.7072 × 106	3.3548 × 105	5.834
	BGWO	4.6952 × 104	2.2197 × 103	30.04796
	FGWO	9.2827 × 104	7.5521 × 103	2.0136
	ISGWO	6.0144 × 104	2.6768 × 103	1.23552
F14	GWO	9.6319 × 104	4.6894 × 103	8.777
	BGWO	1.8212 × 104	6.1228 × 103	35.76934
	FGWO	1.13717 × 105	1.5084 × 104	5.73655
	ISGWO	1.9201 × 105	1.5303 × 104	6.8805
F15	GWO	1.4075 × 105	2.6049 × 104	5.918
	BGWO	2.8699 × 104	4.2609 × 103	51.3865
	FGWO	2.5117 × 105	5.3144 × 103	23.2945
	ISGWO	1.7599 × 105	8.0131 × 103	4.60285
F16	GWO	2234.32767	153.34	9.215
	BGWO	2331.459989	54.877	46.353
	FGWO	2355.28017	132.86	5.484
	ISGWO	2227.599117	41.373	1.7984
F17	GWO	1894.256886	466.91	11.647
	BGWO	1885.334288	600.28	42.76934
	FGWO	1906.436463	120.84	7.73657
	ISGWO	1896.082567	103.03	7.5805
F18	GWO	5.3140 × 105	2.6849 × 104	13.029
	BGWO	2.2563 × 105	4.2709 × 104	49.575
	FGWO	4.3349 × 105	5.3154 × 104	6.0995
F19	GWO	9.3538 × 105	3.854 × 104	11.1345
	BGWO	3.2154 × 105	2.519 × 104	45.1325
	FGWO	2.8086 × 105	7.5623 × 104	4.53825
	ISGWO	4.2901 × 105	1.8818 × 103	3.8275
F20	GWO	2313.493647	573.32	7.5076
	BGWO	2307.29724	254.12	29.298
	FGWO	2330.852595	139.75	3.6306
	ISGWO	2304.928113	176.36	8.6768
F21	GWO	2362.982928	999.465	11.9848
	BGWO	2369.789443	564.6	41.9
	FGWO	2365.578999	116.77	1.81592
	ISGWO	2366.097188	1.3636	10.2092
F22	GWO	3990.485265	184.34	9.4552
	BGWO	2423.382574	54.877	39.1933
	FGWO	4491.339793	132.23	3.979252
	ISGWO	3222.187367	7.1373	8.8648
F23	GWO	2742.025817	992.15	12.923
	BGWO	2718.251377	239.74	48.5005
	FGWO	2747.908115	284.38	6.4387
	ISGWO	2734.838013	258.57	14.693
F24	GWO	2929.15802	198.93	11.8133
	BGWO	2883.41147	173.02	42.8582
	FGWO	2909.911794	531.54	10.1175
	ISGWO	2882.435509	58.576	11.6385
F25	GWO	2952.882015	315.82	11.819
	BGWO	2938.074903	324.81	48.992
	FGWO	2948.599328	212.15	4.974065
	ISGWO	2960.889728	1.61174	11.081
F26	GWO	4458.104469	435.81	11.777
	BGWO	3948.745571	623.72	47.76934
	FGWO	4493.103783	418.99	7.73655
	ISGWO	4238.028442	1.5818	11.8303
F27	GWO	3231.424672	314.65	13.1345
	BGWO	3243.831139	108.49	49.1225
	FGWO	3235.252591	259.29	4.53825
	ISGWO	3253.695252	343.76	10.846
F28	GWO	3360.088798	491.33	14.983
	BGWO	3295.156013	241.41	52.375
	FGWO	3338.51627	558.99	4.7699
	ISGWO	3351.113638	1.3966	12.7615
F29	GWO	3621.138984	315.65	11.692
	BGWO	3545.933858	107.49	40.8415
	FGWO	3660.056807	384.38	6.3915
	ISGWO	3611.318771	343.74	1.7667
Control	GWO	12439.47	1670.293	9.03872
	BGWO	6562.99	993.2523	33.5226
	FGWO	12800.19	2100.485	3.204651
	ISGWO	1713.48	539.4944	2.284215

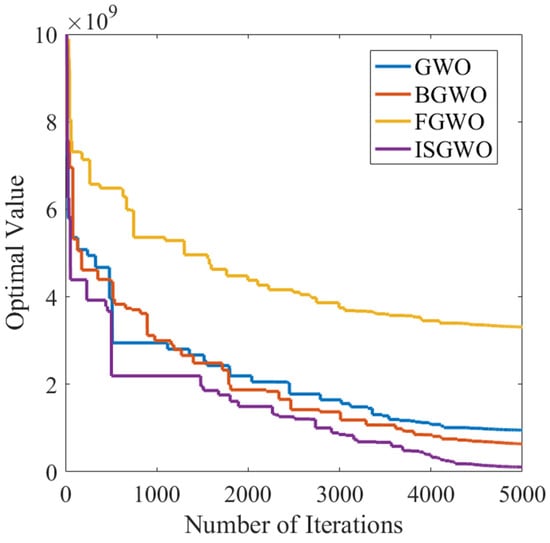
Figure 2. Convergence curve of F1.

Since the single-peak function has a unique global optimal solution, the data values of the F1–F2 counts can be used to determine the convergence of each of the tested algorithms during execution. Of the four compared algorithms, ISGWO has the best optimal solution search capability for the F2 function and exhibits the best accuracy in terms of standard deviation.

For simple multi-modal functions, i.e., the presence of multiple peaks in the function construction, this fully validates the algorithm’s ability to perform a global search. The statistical analysis of the test functions allows us to determine the accuracy of the algorithm. It can be seen that for simple multi-modal functions, there is a very small difference between the solution accuracies of the different algorithms, with an average difference of only one order of magnitude. Among the three evaluation metrics, ISGWO is in the leading position in terms of optimization accuracy and computation time in the test.

To test the optimization ability of the algorithms in large-scale and difficult environments, we will analyze the algorithmic accuracy for hybrid functions F5–F13 and combinatorial functions F14–F20. For hybrid functions, ISGWO shows good search ability and algorithmic stability. In F5–F13, the average solution accuracy of ISGWO in the F5 and F7 functions is closest to the theoretical optimal solution, showing the ability to find the optimal solution under large-scale complex conditions. The analysis results of the F16 function show that ISGWO outperforms the other algorithms in the three aspects of the mean, standard deviation and computational speed, demonstrating excellent robustness and stability in the hybrid test function.

Finally, by analyzing the accuracy values of complex functions F21–F29, we can see that as the difficulty of the test environment increases, the difference in the search accuracy of each comparative algorithm in the test function gradually decreases. In the F24 function, the mean and standard deviation values of the ISGWO algorithm reach the optimal values of the other algorithms. In the F21, F25, F26 and F28 functions, the ISGWO algorithm’s ability to solve these functions is significant and stable due to the small standard deviation values. However, ISGWO outperforms other algorithms in all aspects of control parameter tuning.

Combined with the convergence diagram, it can be seen that for the unimodal test function F1, the ISGWO algorithm not only has the fastest global convergence speed but also the smallest convergence value. This fully shows that ISGWO algorithm performs better in this kind of test function than other algorithms.

ISGWO also maintains the fastest convergence speed and small convergence value in the optimization process of multi-peak test function represented by F3 test function in Figure 3. At the same time, the F4 test function shows the ability of ISGWO algorithm to find the best through strong local search in the later stage in Figure 4. In addition, the optimization object in this paper is a complex system, and the performance of ISGWO in mixed functions and combined functions is more important.

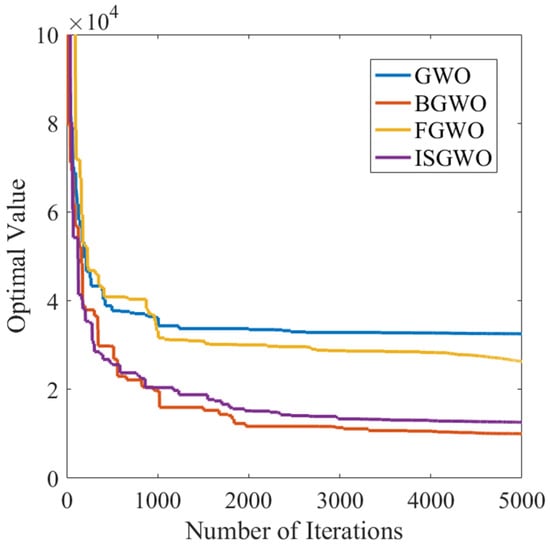
Figure 3. Convergence curve of F3.

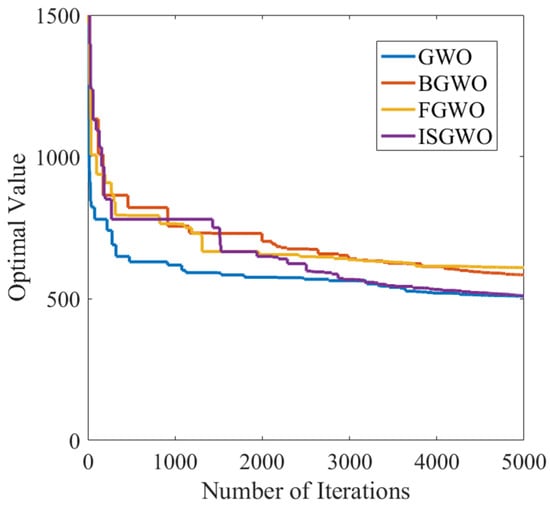
Figure 4. Convergence curve of F4.

In the optimization process of the mixed function F12 in Figure 5, ISGWO shows a fast convergence rate, which is not only fast in 10 iterations, but also far ahead in 800 iterations. In the optimization process of test function F16 in Figure 6, the ISGWO algorithm avoids the trap of local optimization and finds the optimal solution with smaller adaptation value while ensuring fast convergence.

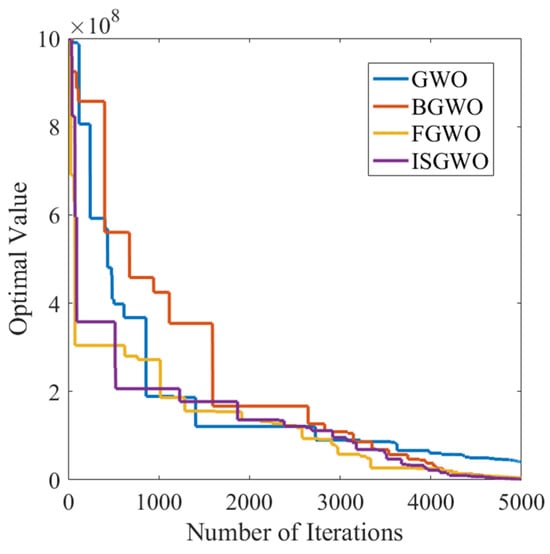
Figure 5. Convergence curve of F12.

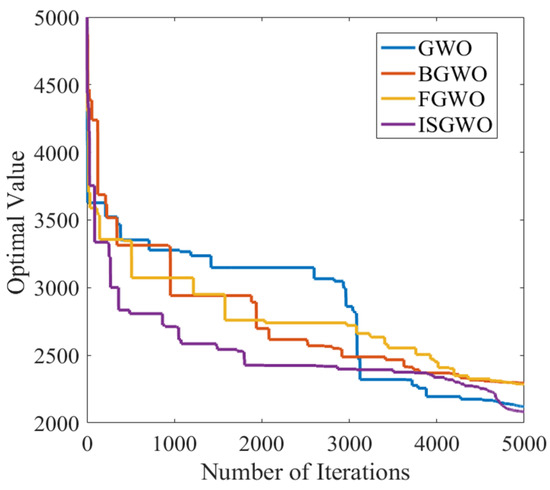
Figure 6. Convergence curve of F16.

Finally, in the convergence of F21 in Figure 7, the ISGWO algorithm shows a significant advantage in its ability to coordinate global and local search. This shows that ISGWO not only has a good balance of global exploration capability, but also has significant local exploitation performance in the optimization process of mixed function and combined function. The convergence analysis of the above four kinds of different test functions shows that ISGWO algorithm has good stable convergence and global searching ability from different angles.

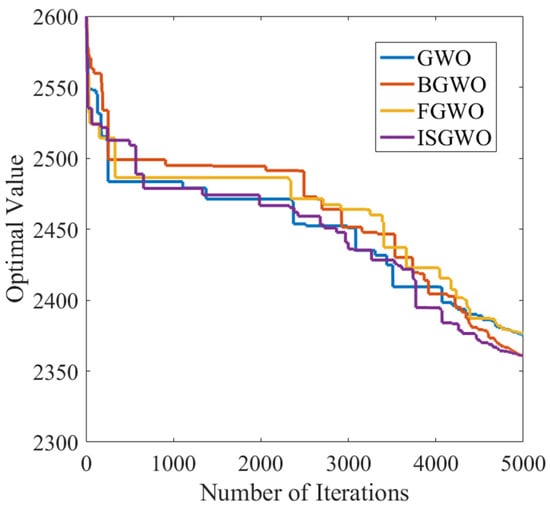
Figure 7. Convergence curve of F21.

5.4. Comprehensive Evaluation of Algorithms

According to CEC2017, the evaluation criteria will be divided into three sections:

1, The 25 points for the first part come from the sum of the mean error values for each test function

$$SE={\displaystyle \sum _{i=1}^{29}ef}$$

(25)

where $ef$ is the average of all counts and $SE$ is the combined error. The score for the first part can then be obtained:

$$Score1=(1-{\displaystyle \frac{SE-S{E}_{\min }}{SE}})\times 25$$

(26)

2, The 25 points for the second part come from the ordering of the different algorithms in each test function

$$SR={\displaystyle \sum _{i=1}^{29}rank}$$

(27)

where $SR$ is the composite of all the rankings. The score for the second part can then be obtained:

$$Score2=\left(1-{\displaystyle \frac{SR-S{R}_{\min }}{SR}}\right)\times 25$$

(28)

3, The 50 points for the third part come from the runtime of the different algorithms in each test function

$$ST={\displaystyle \sum _{i=1}^{29}time}$$

(29)

where $ST$ is the composite of all the rankings. The score for the second part is then available:

$$Score3=\left(1-{\displaystyle \frac{ST-S{T}_{\min }}{ST}}\right)\times 50$$

(30)

4, Finally, the three scores above are added together

$$Score=Score1+Score2+Score3$$

(31)

Table 6 shows that the BGWO algorithm performs the best in terms of accuracy but has the worst speed. On the other hand, the FGWO algorithm excels in speed but lacks precision. In contrast, the proposed ISGWO algorithm achieves a balance between accuracy and speed, demonstrating significant performance improvement in the same order of magnitude as the best algorithm.

Table 6. Combined scores of the four algorithms.

	GWO	BGWO	FGWO	ISGWO
SE	722,010,873.5	404,318,770.9	1,014,172,058	569,014,471.5
Score1	14.00	25	9.97	17.76
SR	86	51	83	70
Score2	14.83	25	15.36	18.21
ST	294.4	1232.4	191.3	220.5
Score3	32.49	7.76	50	43.38
Score	61.32	57.76	75.33	79.35

5.5. Optimization Analysis of Servo System Parameters

Although ISGWO performs well in test functions, performance in real systems is more important. According to literature [36], a control system is established as an optimization object, and the system parameters are shown in Table 7. The overall structure of the control system and optimization function established in Simulink is shown in Figure 8.

Table 7. Control parameter list.

Parameter	Value
$K_v$	2
$K_{pwm}$	10
$K_m$	6
$R$	8
$K_e$	0.11
$K_E$	0.16
$J$	0.065
$B$	1.5

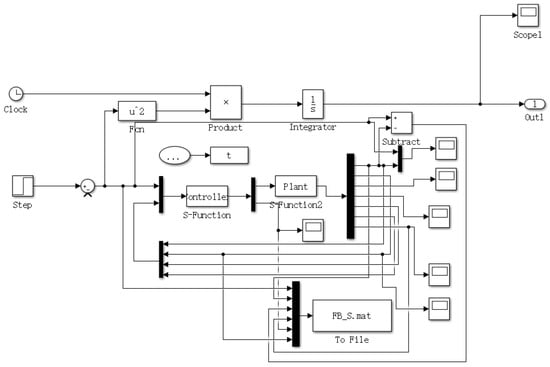
Figure 8. Program chart.

Considering the optimization parameters as individual population individuals, the number of population individuals in the algorithm is uniformly 1 and the maximum number of iterations is 500.

Under the step input, the four optimization functions perform 500 iterations of each of the four parameters. The initial parameter values and optimization values are shown in Table 8.

Table 8. Optimization results of the four optimization algorithms (step input).

	${\mathit{c}}_1$	${\mathit{k}}_1$	${\mathit{k}}_2$	${\mathit{k}}_3$
Initial response	1	5	5	1
GWO	0.92	7.56	9.14	0.57
BGWO	1.73	10.72	13.83	3.68
FGWO	1.54	8.46	11.75	2.49
ISGWO	2.38	9.78	9.46	1.75

To make the optimization more intuitive, the step response generated based on the optimized parameters is shown in Figure 9.

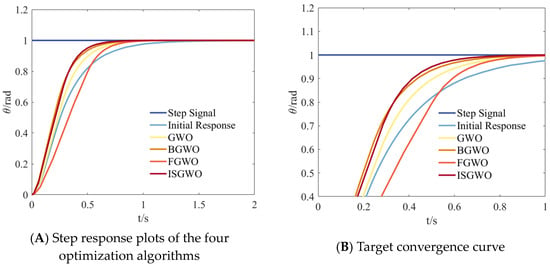
Figure 9. Parameter Optimization Comparison (Step Response).

In Figure 9A, comparing the initial response, each optimization algorithm generates a faster step response, FGWO algorithm has a slower initial response rate and ISGWO algorithm performs optimally in all aspects and can better achieve smooth and fast control of the system to meet the optimization requirements.

It can be seen from Figure 10 that the convergence speed of GWO decreases in steps, FGWO can reach convergence faster but with a larger convergence value, BGWO converges slower and has a larger final convergence value. The algorithm in this paper has the fastest convergence speed and the best convergence value.

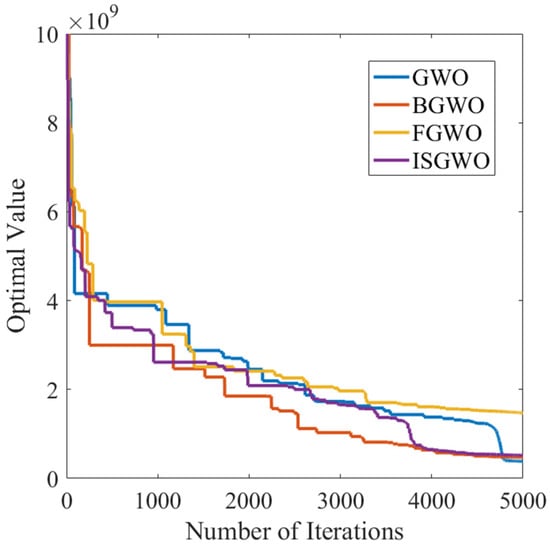
Figure 10. Parameter Optimization Target convergence curve (Step Response).

In Figure 11A, compared with the initial response, each optimization algorithm can produce a faster step response, while the GWO algorithm has a slower initial response speed, FGWO has the fastest response speed, but the convergence speed is slow, and ISGWO can achieve the fastest convergence and meet the optimization requirements.

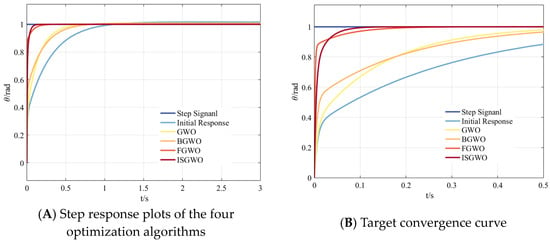
Figure 11. Parameter Optimization Comparison (Step Response).

As it can be seen from Figure 12, GWO has the slowest convergence speed, FGWO can achieve convergence faster, but the convergence value is large, and BGWO has a slower convergence speed, but the final convergence value is small. The algorithm in this paper has the fastest convergence speed.

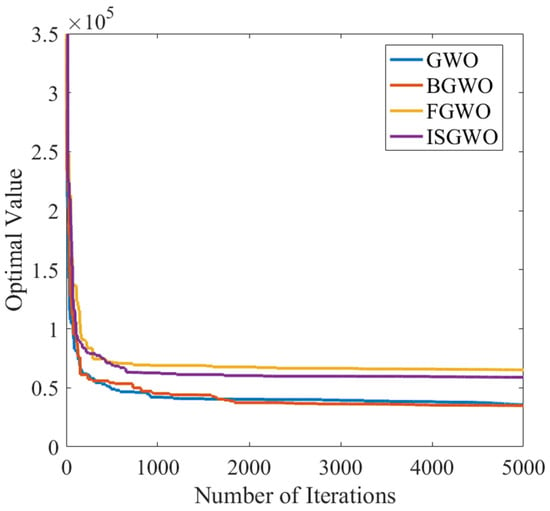
Figure 12. Parameter Optimization Target convergence curve (Step Response).

In Figure 13A, compared with the initial response, each optimization algorithm can produce a faster step response, while the initial response speed of GWO algorithm is slower but also improved. Although FGWO has the fastest response speed, its curve is not smooth enough, and ISGWO can achieve the fastest convergence and meet the optimization requirements.

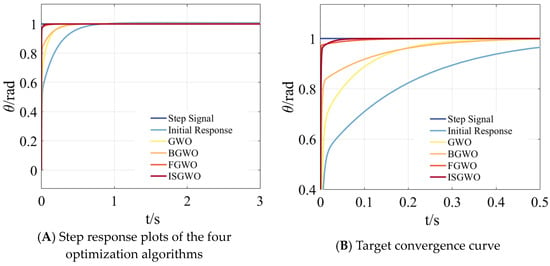
Figure 13. Parameter Optimization Comparison (Step Response).

As shown in Figure 14, FGWO can reach convergence faster, while BGWO has a slower convergence speed, but the final convergence value is small. The convergence rate of the algorithm in this paper is the fastest, and although the convergence value is large, it is maintained at a reasonable level.

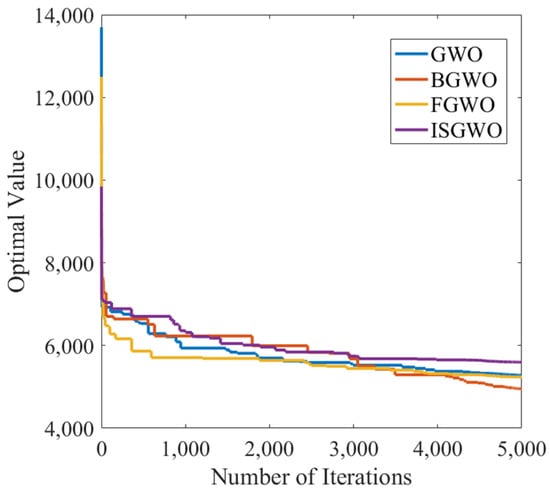
Figure 14. Parameter Optimization Target convergence curve (Step Response).

In Figure 15, compared with the initial response, each optimization algorithm can produce a faster step response, while the initial response speed of the GWO algorithm is slower, and FGWO has the fastest response speed but larger fluctuation. As shown in Figure 15B, ISGWO can achieve the fastest convergence and small overshoot, which meets the optimization requirements.

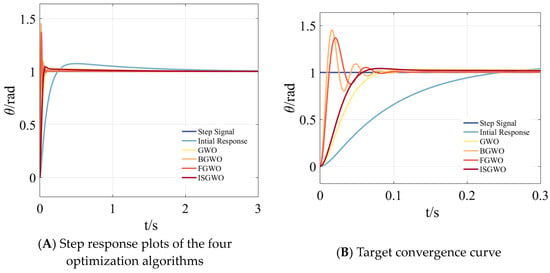
Figure 15. Target convergence curve (Step Response).

It can be seen from Figure 16 that GWO has the fastest convergence speed, but the convergence value is larger. FGWO has the slowest convergence speed, but the convergence value is small. The algorithm proposed in this paper has the fastest convergence speed and a smaller final value.

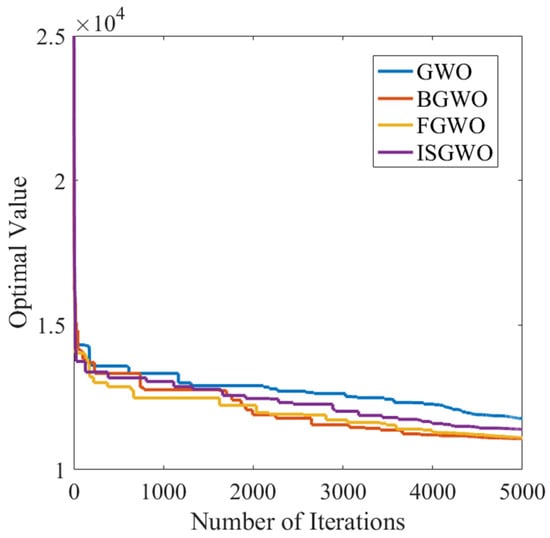
Figure 16. Parameter Optimization Target convergence curve (Step Response).

Under the sinusoidal input, the four optimization functions perform 500 iterations of each of the four parameters. The initial parameter values and optimization values are shown in Table 9.

Table 9. Optimization results of the four optimization algorithms (sinusoidal input).

	${\mathit{c}}_1$	${\mathit{k}}_1$	${\mathit{k}}_2$	${\mathit{k}}_3$
Initial response	1	5	5	1
GWO	0.95	7.75	9.68	0.49
BGWO	1.68	10.14	13.49	3.17
FGWO	1.41	8.57	11.32	2.84
ISGWO	2.17	9.83	8.62	1.46

In order to better verify the superiority of the ISGWO algorithm in parameter optimization, we change the input to a sinusoidal input.

In Figure 17A, comparing the initial responses, each optimization algorithm tracks the input sinusoidal curve better, the performance of the FGWO algorithm and ISGWO algorithm are not different from each other and the ISGWO algorithm has the smallest stabilization error, which satisfies the optimization requirements.

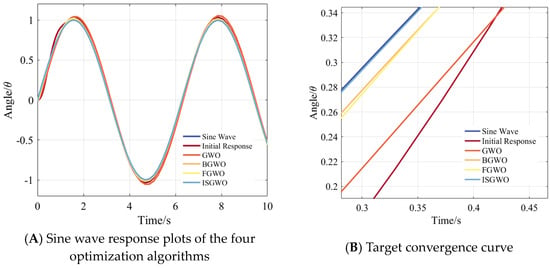
Figure 17. Parameter Optimization Comparison (Sine Wave Response).

From Figure 18, it can be seen that GWO has the fastest convergence speed, but the final convergence value is larger; FGWO can reach convergence faster, but the convergence value is larger. The algorithm in this paper has the smallest final convergence value and can reach a better convergence value in a shorter number of iterations.

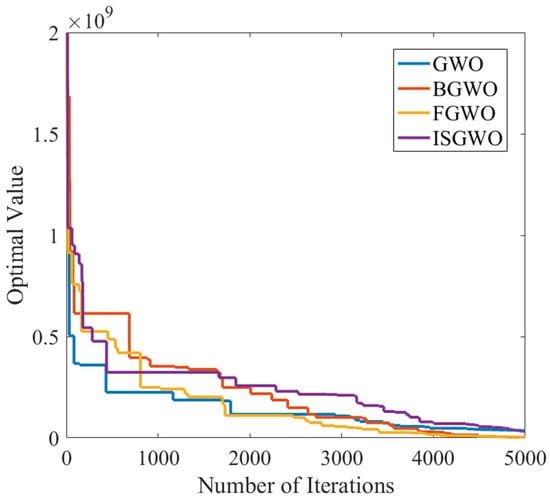
Figure 18. Parameter Optimization Target convergence curve (Sine Wave Response).

Similarly, we changed the input to a sinusoidal input to strengthen the verification of the superiority of the ISGWO algorithm. In Figure 19A, the stability error of each optimization algorithm is reduced compared to the initial response, and among them the ISGWO algorithm has the smallest stability error and converges faster to meet the optimization requirements.

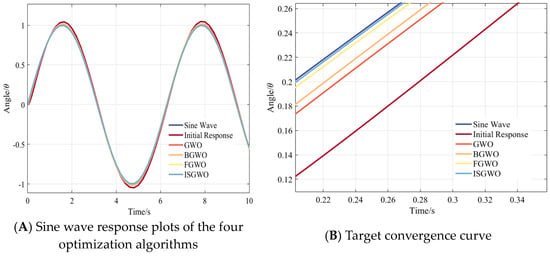
Figure 19. Parameter Optimization Comparison (Sine Wave Response).

From Figure 20, it can be seen that GWO has the slowest convergence speed and the largest convergence value, and FGWO has a slower convergence speed but a smaller convergence value. The algorithm in this paper not only has the fastest convergence speed, but also the final convergence value is not much different from the minimum convergence value.

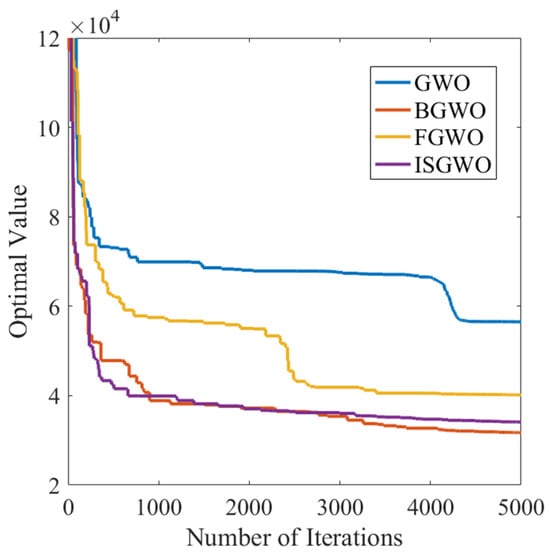
Figure 20. Parameter Optimization Target convergence curve (Sine Wave Response).

After changing the input to sinusoidal input, we can conclude from Figure 21A that each optimization algorithm fits the input curve better compared to the initial response, and that the GWO algorithm has a slower but improved initial response. ISGWO can achieve the fastest convergence speed and possesses the smallest stabilization error, which basically fits the input curve exactly and meets the optimization requirements.

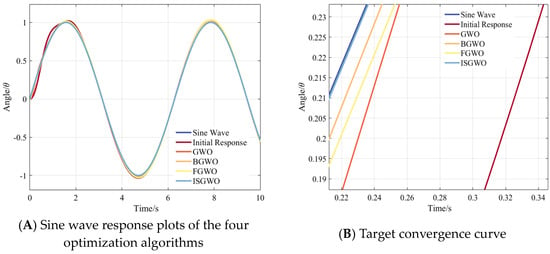
Figure 21. Parameter Optimization Comparison (Sine Wave Response).

As shown in Figure 22, GWO has the fastest convergence speed, but the late convergence is unstable. While BGWO has slower convergence speed, but the final convergence value is smaller. The algorithm in this paper has the fastest convergence speed, and the convergence value can reach a small level at a smaller number of iterations.

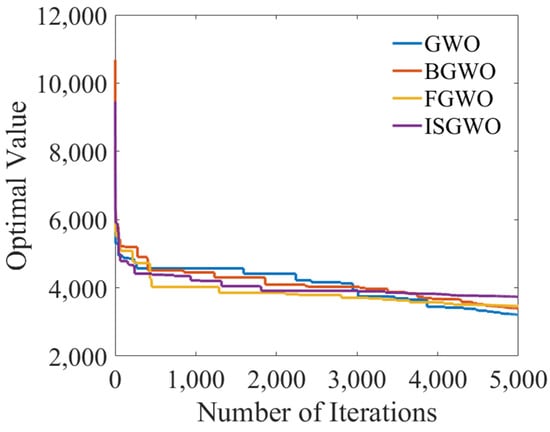
Figure 22. Parameter Optimization Target convergence curve (Sine Wave Response).

After replacing the input with sinusoidal input, from Figure 23A we can see that each optimization algorithm tracks the input curve better compared to the initial response. the GWO algorithm fluctuates more and the stabilization error of BGWO is larger. As shown in Figure 23B, ISGWO has the smallest stabilization error and less fluctuation, which satisfies the optimization requirements.

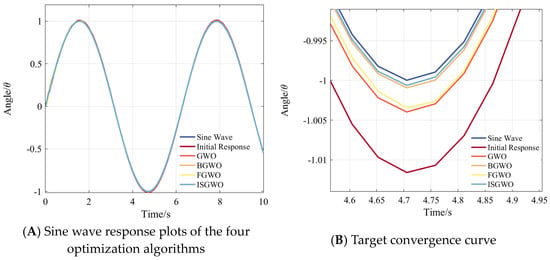
Figure 23. Target convergence curve (Sine Wave Response).

From Figure 24, it can be seen that GWO has the slowest convergence speed, but the final convergence value is smaller, and FGWO has the slowest convergence speed, but the convergence value is smaller. The algorithm proposed in this paper has the fastest convergence speed, and although the final convergence value is larger, a more objective convergence value can be achieved at a smaller number of convergence times. Combining the performance of different types, the algorithm in this paper converges faster, is not easy to fall into the local optimum, and can find the control parameters with better control effect in the complex control environment.

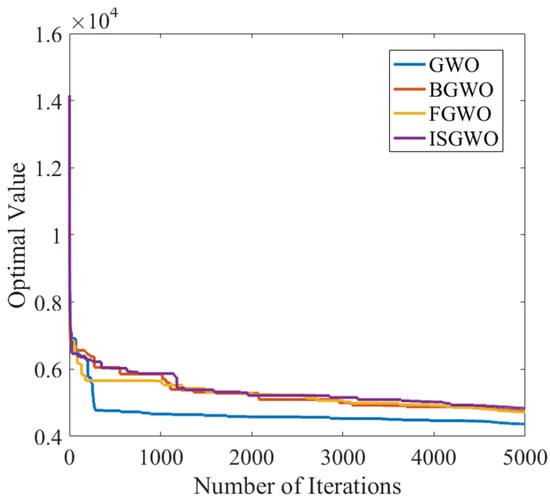
Figure 24. Parameter Optimization Target convergence curve (Sine Wave Response).

6. Conclusions

For the problem of optimizing the synchronous control parameters of permanent magnet synchronous motors, we propose an improved sinusoidal optimization Gray Wolf algorithm. In the algorithm design, we introduce a position-update formula based on the improved sinusoidal to balance the exploratory and exploitative abilities of the algorithm in the process of finding the optimal solution. Meanwhile, to prevent the population individuals from crossing the boundary during the optimization process, we adopt a particle-crossing processing strategy based on the symmetry idea, which can update the position of the crossing individuals in time and retain the position information of the optimal individuals to maximize the retention of the current optimal solution, to improve the convergence speed of the algorithm to the optimal solution. Finally, we use the differential cross-perturbation strategy to move the three gray wolf individuals with the worst fitness out of the local optimal position to help the algorithm jump out of the local optimal position, to improve the search accuracy of the algorithm.

To evaluate the performance and effectiveness of the algorithm, ISGWO was tested against three gray wolf-related algorithms such as GWO, BGWO and FGWO with the help of CEC2017 benchmark test functions on the ISGWO, and the experimental results show that ISGWO maintains the leading level in search accuracy, algorithmic performance as well as search speed, and achieves several balances. The algorithm is applied to the parameter optimization problem of synchronous control, and the same three algorithms are selected for comparison. The experimental results show that ISGWO can find the smallest cost function value as well as the optimal parameter value the fastest under the same environment, thus proving the effectiveness and significance of the ISGWO algorithm in the synchronous control parameter optimization problem.

Although ISGWO has made some contributions to the problem of algorithm design and control parameter optimization, there are some limitations. Although high convergence accuracy and short computation time can be guaranteed at the same time in the control parameter optimization in this paper, the algorithm is not universal enough for different types of functions.

In future work, we will try to optimize multiple parameters or multiple function indicators simultaneously. This places higher demands on the optimization algorithm and requires optimization of its process to improve convergence accuracy and computation time.