Abstract
The relaxation of a rigid particle suspended in a one-dimensional oscillating flow is calculated according to different drag models and the results are compared. Conditions are derived under which relaxation can be neglected or drag models can be substituted by simpler ones. This investigation is conducted analytically and graphically via the plane defined by the Reynolds number and amplitude parameter. This work matches various, mostly analytic drag models together to consider simple particle relaxation with a few, broad range input parameters and cover large parts of the plane spanned by Reynolds number and amplitude parameter.
1. Introduction
A rigid, spherical particle suspended in a harmonically oscillating one-dimensional flow is considered. This configuration can be found, for example, with ultrasonic levitators [1,2] or pulsation reactors [3,4,5]. In case the particle is fixed in position (or the particle executes harmonic oscillations in a fluid at rest), the interaction between the fluid and the particle as well as the resulting flow state is defined by two dimensionless numbers: the particle Reynolds number and the amplitude parameter . The particle Reynolds number expresses the ratio between inertial and viscous forces with the slip velocity amplitude U, the density of the fluid , the particle diameter d, and the dynamic viscosity of the fluid . The amplitude parameter sets the particle displacement A in relation to the particle diameter, while the particle displacement itself is the ratio of slip velocity amplitude to the angular frequency of the oscillating fluid. Reynolds number and amplitude parameter span a plane in which all flow states can be pinpointed, as shown in Figure 1. Note that the origin of Figure 1 has the coordinates . In case the particle is fixed in place, the slip velocity amplitude equals the far-field fluid velocity amplitude . Within this work, the far-field fluid velocity will be referred to as fluid velocity and can be described as . In case the particle is not considered fixed in place, the slip velocity differs from the flow velocity due to inertia and drag forces acting on the particle (relaxation). The particle will perform oscillations with the same frequency as the fluid, which is also true for the slip velocity. If harmonic behavior is assumed, the only unknown quantities, which are necessary to describe the slip velocity, are the slip velocity amplitude and the phase shift with respect to the fluid velocity [6]. The basic geometrical relations of these central quantities are displayed in Figure 2. In Section 2.1, several drag models are presented with their respective ranges of validity to calculate relaxation in large parts of the - plane. Afterward, in Section 2.2, the slip velocity is calculated and discussed. Distinguishing between cases where the particle can be considered fixed and where this is not the case is discussed in Section 2.3. In the last section (Section 3), criteria are derived under which the simple Stokes model can be applied in the validity ranges of the other models.
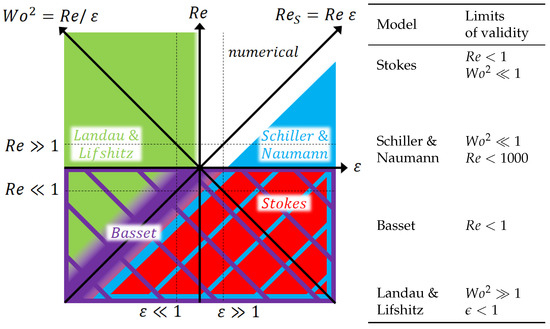
Figure 1.
Drag models considered for various combinations of Reynolds number , amplitude parameter , and Womersley number . (left) Various drag models displayed in the - plane. The striped patterns indicate the areas of validity, while the solid colors mark the preferable model in the area. Note that the origin has the coordinates . (right) Various drag models with their limits of validity.
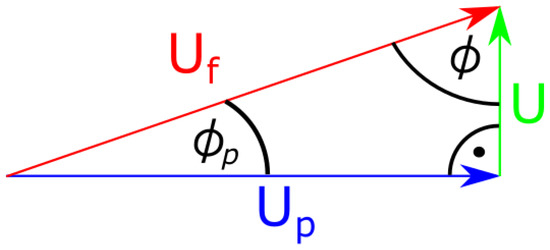
Figure 2.
Vector representation of fluid velocity amplitude , particle velocity amplitude , and slip velocity amplitude U, including phase shift angles in reference to the fluid oscillation of the particle velocity and slip velocity , respectively.
2. Method
2.1. Drag Models
If all quantities () but U are known and constant, U can be determined by equating the inertia of the particle (here treated as a mass point) with its drag when omitting all other forces. The slip velocity is not only central in working with the - plane (since it is part of and ), but it is also crucial for further considerations like flow patterns and heat and mass transfer, which are not subjects of this work. While the validity of the Navier-Stokes equations (NSE) is assumed, the complex process of solving them can be circumvented by applying various simplified drag models in their respected ranges of validity. Several drag models are necessary to cover large parts of the - plane, while the relations in Figure 2 holds true, independent of the applied drag model. It will now be investigated how these models behave and relate to each other. The expressions for the drag force of each drag model can be found in Table 1.

Table 1.
Amplitude ratio of slip to fluid velocity for several drag models dependent on the Womersley number and the density ratio .
While the described ranges of validity are listed on the right side of Figure 1, they are plotted in the - plane on the left side. In case two or three models are valid in the same area, the simplest one has a solid color, while the others have a striped pattern.
The first step is to distinguish between a steady and an unsteady flow. The main criterion for differentiating is whether the boundary layer thickness is larger or smaller than the particle itself. This phenomenon is expressed by the Womersley number [7]. The Womersley number is sometimes also referred to as Stokes number [8] or frequency parameter [9] in literature. While the Womersley number is one bisector of the - plane, the other one is the Streaming Reynolds number , which is central in the consideration of Steady Streaming [10]. If , the flow can be considered steady [11]. In case the Reynolds number is also smaller than unity , the viscous forces dominate and creeping flow can be assumed. This assumption enables the application of the simple Stokes drag model [12], which considers pure drag only and leads to closed analytic solutions. If , while the Reynolds number exceeds the validity limit of the Stokes model , the flow can still be considered steady, but a drag model with a larger range of validity regarding the Reynolds number has to be applied. In this case, the Schiller & Naumann model [13] (SN) was chosen, but for this case, many other drag models can be applied as well [14]. The SN model differs in nature from the Stokes model in two important aspects. On the one hand, it is an empirical model derived via the correlation of experimental data, rather than being derived from the NSE by omitting inertial forces. On the other hand, applying the SN drag model leads to a non-linear motion ODE, which can only be solved numerically. In the opposite case of , the drag model by Landau & Lifshitz [11] (LL) can be applied, which linearizes the NSE around small to ensure no detachment of the flow from the particle. In case neither nor , but , the drag model by Basset [15] is valid, which is explicitly derived for unsteady flow conditions. It is an extension of the Stokes model that, besides pure drag, also considers added mass and the pressure gradient. Additionally, the “history” of the fluid is factored in by a theoretically derived term. In this work, only the stationary state is considered, and therefore the lower boundary of the history integral is set to . A discussion of the transient case can be found with Coimbra & Rangel [16]. An uncolored area in the - plane is recognizable where none of the simplified models are valid. In this area, the NSEs need to be solved numerically to calculate the slip velocity. The introduced drag models are well established in the literature and have been validated via experiments (and DNS) several times. The SN model was derived from experimental data in the first place. Therefore, in this work, the drag models themselves and their minimal ranges of validity are considered valid.
Since the particle oscillates with the same frequency as the fluid, the particle velocity and, in extension, the slip velocity are bound by this condition and change only slightly with respect to the applied drag model. This is in contrast to a steady flow, where the differences between models tend to keep increasing over time and often grow exponentially. This means that the simple Stokes drag model is adequate over a wider parameter range in an oscillating flow than its perceived limit of validity of small Reynolds numbers in a steady flow. This phenomenon encourages the substitution of more complex models of drag with Stokes. This simplification is addressed in Section 3.
2.2. Slip Velocity Amplitude
The slip velocity amplitude can be calculated with each respected drag model under the assumption of a harmonic oscillating flow that can be described with , the results of which are displayed in Table 1. The derivation of the slip velocity amplitude with Stokes, SN, and the LL model is given in Appendix A, Appendix B and Appendix C, respectively, while the solution for the Basset model is taken from Hjelmfelt & Mockros [6].
Each solution in Table 1 contains only the Womersley number and the density ratio (In the case of the SN model also the Reynolds number). The density ratio is the ratio between the particle density and the fluid density. This implies that, in cases where relaxation needs to be considered, the above introduced - plane can still be utilized with as a parameter. The normalized slip velocity amplitude is displayed in Figure 3 for = 25,000, corresponding to iron particles in hot air (left), and = 8, corresponding to iron particles in water at STP (right). First, neglecting the particle relaxation will be discussed, followed by the comparison of drag models, both by means of Figure 3.
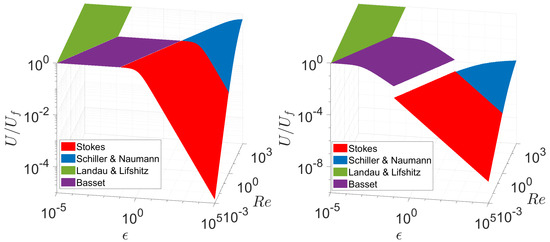
Figure 3.
Normalized slip velocity amplitude, calculated with various drag models. (left) = 25,000 (corresponds to iron particles in hot air); (right) (corresponds to iron particles in water at STP).
2.3. Particle Relaxation
The - plane can be loosely classified into two areas with respect to the slip velocity amplitude. In one part, related to large , holds true. In this area, relaxation can be neglected. The size of this area depends only on , while its border can be represented by a value of the Womersley number . This means each value of can be related to a density ratio value set (and vice versa) for which relaxation can be neglected. The lowest value of this set is now defined as the critical density ratio . Since relaxation is always present with this problem a cut-off criterion needs to be defined for neglecting particle relaxation. Depending on the specific applied case, the criterion can, for example, be set to , , or . The critical density ratio with respect to is displayed in Figure 4 for the suggested cut-off criteria. If the density ratio of a specific problem is above the line for the respective Womersley number, relaxation can be neglected, while the choice of the cut-off criteria becomes more important for high Womersley numbers, as can be derived from Figure 4. Graphically, it is even suggested that this finding is also valid for the white area of the - plane, where the NSEs need to be solved numerically.
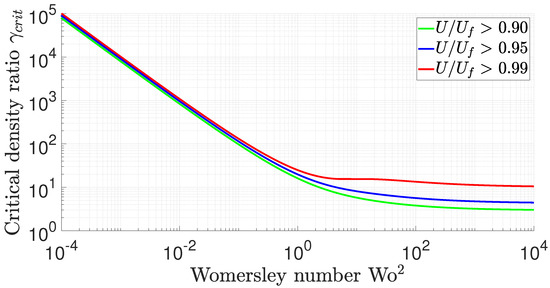
Figure 4.
Critical density ratio depending on the Womersley number for cut off criteria of , , and . Above the respected line, the particle motion is not affected by the flow and the slip velocity can be set equal to the fluid velocity (no relaxation case).
In the other part of the - plane, 1 and relaxation does need to be considered via adequate drag models.
3. Result and Discussion
For large , the quasi-steady approximation is valid for the entire relaxation part of the - plane, and the slip velocity amplitude can be calculated by Stokes or SN. This case is displayed on the left side of Figure 3, where is large enough for Stokes to reach 1, within its limit of validity . For small (right side of Figure 3) this is not the case. The same approach can be applied to the comparison between Stokes and SN. Here it is not , but rather the ratio between and that is the determining factor. This relates to the distinction of 1 being reached before or after becomes unity. Even though the limit was set here to , the slip velocity amplitude calculated with the Basset model still deviates substantially from the Stokes model. (Note here the logarithmic scale exaggerating the deviation between Basset and Stokes). Similar to the comparison between Stokes and Basset, on the right-hand side of Figure 3, the values at the model limits between Stokes and SN and even between Basset and LL do not match well, although this effect is not as pronounced. This is contrary to the high-density ratio case displayed on the left side of Figure 3, where the values at the model limits do match well. This raises the question of under which conditions the models connect to each other well or can even be applied interchangeably. The relation between Stokes and other models can be calculated with the expressions presented in Table 2, while harmonic particle velocities and slip velocities are assumed. The derivation of the deviation between Stokes and the SN model is given in detail in Appendix B. The expressions in Table 2 are derived from the expressions in Table 1 and also depend only on and . This time, however, the oscillation Stokes number is utilized [17]. It sets the characteristic time of the particle in relation to the characteristic time of the flow . It works as a criterion for how well the particle can adapt to the changing flow conditions. When the normalized slip velocity amplitude in an oscillating flow is calculated with the Stokes model, it is only dependent on the oscillation Stokes number . Therefore, the oscillation Stokes number is utilized in comparison of the Stokes model with the other models. The criterion for an acceptable deviation between the models was defined as 5%, and the parameter areas where the deviation is above and below this criterion are displayed in Figure 5 for the various models. The density ratio is the decisive parameter for the comparison between Stokes and Basset as well as Stokes and the LL model, while for the comparison between Stokes and the SN model it is the Reynolds number. Additionally, at least one criterion is presented in Table 2 for the deviation between Stokes and the other drag models to stay below 5%, while multiple criteria are set in relation to each other via logical operators. In this case, the Stokes model can be applied in the validity range of the respective model. These criteria are also plotted in Figure 5. Simple criteria were chosen for the sake of convenience, as they can not match the 5% error interface perfectly. This means that the deviation will stay below 5% if the criterion is met, but it can also stay below 5% if the criterion is violated, as can be seen in Figure 5. Stokes can be used in order to calculate the slip velocity amplitude in the entire colored area of the - plane when all criteria in Table 2 are met, hence .

Table 2.
Relations of the drag models listed in Table 1 to the Stokes model, expressed with the oscillation Stokes number and the density ratio . Additionally, the limit is given up to which the deviation stays below 5%, in which case the Stokes model can be applied in the validity range of the respective model. Multiple criteria are set in relation to each other via the logic operator ∧—‘and’.
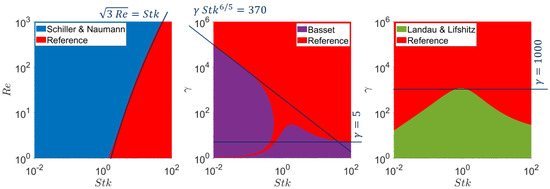
Figure 5.
Areas where the deviation between Stokes and the respective drag model is above (blue—Schiller & Naumann, purple—Basset, green—Landau & Lifshitz) and below (red) 5%. In the red areas, the Stokes model can be applied in the validity range of the respective model.
4. Conclusions
The special case of a rigid particle in a one-dimensional oscillating flow was considered. The - plane was introduced, in which all flow states of this problem are defined. The conditions under which particle relaxation can be neglected were derived. Subsequently, various drag models from the literature were considered to model particle relaxation as simply as possible in large parts of the - plane. It was pointed out under which conditions the simple Stokes model can be applied in the validity range of various other drag models. This was conducted graphically and analytically.
It was shown that the Stokes drag model can be applied validly for the calculation of particle relaxation for large sets of parameter combinations. This can even be true for , as long as other criteria, connected to high-density ratios between fluid and particle and/or high oscillating Stokes numbers, are met. These parameter combinations are found with many gas-solid multi-phase flows, which makes this work especially interesting for these kinds of systems.
Author Contributions
Conceptualization, methodology, writing—original draft preparation, writing—review and editing and visualization, S.H.; supervision, project administration and funding acquisition, S.U. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the Boysen-TU Dresden-Research Training Group for the financial support that has made this publication possible. The Research Training Group is co-financed by TU Dresden and the Friedrich and Elisabeth Boysen Foundation. Grant number: BOY-135.
Data Availability Statement
Data are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | displacement amplitude |
| a | particle acceleration |
| drag coefficient | |
| d | particle diameter |
| F | force |
| Reynolds number | |
| oscillation Stokes number | |
| t | time |
| u | velocity |
| U | velocity amplitude |
| Womersley number (frequency parameter) | |
| density ratio | |
| amplitude parameter | |
| dynamic viscosity | |
| density | |
| relaxation time | |
| phase shift | |
| angular frequency | |
| Abbreviations | |
| Landau & Lifshitz | |
| Navier-Stokes equations | |
| ordinary differential equation | |
| S | Stokes |
| Schiller & Naumann | |
| standard temperature and pressure | |
| Indices | |
| D | drag |
| I | inertia |
| p | particle |
| f | fluid |
| 0 | initial state |
Appendix A. Derivation of the Slip Velocity Amplitude Calculated with the Stokes Drag Model
Starting point is the ever-present force equilibrium on the particle between inertia and drag. The drag force predicted by the Stokes model, as listed in Table 1, is . A spherical particle is considered with an inertia of . Combining this with an oscillating flow around a zero mean that can be described with leads to the ordinary differential equation (ODE)
Here, is the slip velocity, the instantaneous acceleration, and the characteristic time of the particle. The solution to ODE (A1) is
Appendix B. Derivation of Slip Velocity Amplitude Calculated with SN and Deviation from the Stokes Model
Considering a spherical rigid particle and starting from the basic equilibrium between the drag force and the inertial force for Stokes (index S) and Schiller & Naumann (index SN):
Dividing (A4) by (A5) and rearranging leads to
For harmonic relations, the following statements with particle acceleration and particle velocity hold true:
Here, and denote the particle velocity amplitude and the particle acceleration amplitude, respectively. is the particle velocity derivation in respect of time. Relation (A6) also holds true for the extreme values and inserting (A8) leads to
is the maximum value of the drag coefficient when the slip velocity amplitude U is reached with the maximum Reynolds number
Using the relations gives the expression
When the Pythagorean theorem
is applied, which can be derived from Figure 2, Equation (A11) can be further simplified:
In order to set the slip velocity amplitude in relation to the fluid velocity amplitude, each side of Equation (A13) can be multiplied with the right side of Equation (A3):
Since only now are the different drag coefficients inserted, Equation (A14) can also be used in order to calculate the deviation between the Stokes drag model and any other drag model, which follows Newton’s drag formulation and can be expressed by a drag coefficient.
Appendix C. Derivation and Solution of Particle Motion with the Landau & Lifshitz Model
The point of origin is the constant equilibrium of the drag force and the inertia of the particle:
In combination with an oscillating flow around a zero mean that can be described with , Equation (A17) leads to the ODE
Solving ODE (A19) and recovering the slip velocity is achieved by applying the relation , while the extreme value is discovered by detecting zeros in the first differential, which leads to the expression for the normalized slip velocity amplitude
References
- Rothlisberger, M.; Schmidli, G.; Schuck, M.; Kolar, J.W. Multi-Frequency Acoustic Levitation and Trapping of Particles in All Degrees of Freedom. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 1572–1575. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wu, L.; Wang, Y. Study on Particle Manipulation in a Metal Internal Channel under Acoustic Levitation. Micromachines 2021, 13, 18. [Google Scholar] [CrossRef] [PubMed]
- Heidinger, S.; Spranger, F.; Dostál, J.; Zhang, C.; Klaus, C. Material Treatment in the Pulsation Reactor—From Flame Spray Pyrolysis to Industrial Scale. Sustainability 2022, 14, 3232. [Google Scholar] [CrossRef]
- Klaus, C.; Wegner, K.; Rammelt, T.; Ommer, M. New Challenges in Thermal Processing. Interceram Int. Ceram. Rev. 2021, 70, 22–25. [Google Scholar] [CrossRef]
- Hoffmann, C.; Ommer, M. Reactors for fluid-solid reactions: Pulsation reactors. In Handbuch Chemische Reaktoren; Reschetilowski, W., Ed.; Springer Reference Naturwissenschaften; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–19. [Google Scholar] [CrossRef]
- Hjelmfelt, A.T.; Mockros, L.F. Motion of discrete particles in a turbulent fluid. Appl. Sci. Res. 1966, 16, 149–161. [Google Scholar] [CrossRef]
- Womersley, J.R. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef] [PubMed]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Dover Publications: Mineola, NY, USA, 2013. [Google Scholar]
- Riley, N. On a Sphere Oscillating in a Viscous Fluid. Q. J. Mech. Appl. Math. 1966, 19, 461–472. [Google Scholar] [CrossRef]
- Riley, N. Steady Streaming. Annu. Rev. Fluid Mech. 2001, 33, 43–65. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Course of Theoretical Physics; Pergamon: Oxford, UK, 1987; Volume 6. [Google Scholar]
- Stokes, G.G. On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. In Mathematical and Physical Papers; Cambridge University Press: Cambridge, UK, 2009; pp. 1–10. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A. VDI Zeitung; VDI: Düsseldorf, Germany, 1935. [Google Scholar]
- Goossens, W.R. Review of the empirical correlations for the drag coefficient of rigid spheres. Powder Technol. 2019, 352, 350–359. [Google Scholar] [CrossRef]
- Basset, A.B. On the motion of a sphere in a viscous liquid. Philos. Trans. R. Soc. Lond. (A) 1888, 179, 43–63. [Google Scholar] [CrossRef] [Green Version]
- Coimbra, C.F.M.; Rangel, R.H. Spherical Particle Motion in Harmonic Stokes Flows. AIAA J. 2001, 39, 1673–1682. [Google Scholar] [CrossRef]
- Sazhin, S.; Shakked, T.; Sobolev, V.; Katoshevski, D. Particle grouping in oscillating flows. Eur. J. Mech. B/Fluids 2008, 27, 131–149. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





