Analytical Routes to Chaos and Controlling Chaos in Brushless DC Motors

Abstract

This study examines the dynamics in a brushless DC motor (BLDCM) and methods used to control potentially chaotic behavior or behavior similar to chaotic processes in these systems. Bifurcation diagrams revealed complex nonlinear behaviors over a range of parameter values. In the resulting bifurcation diagram, period-doubling bifurcation, period-three bifurcation, and chaotic behavior can clearly be seen. We used Lyapunov exponents and Lyapunov dimensions to show the occurrence of chaos in a BLDCM. We then used the state feedback method to control chaos behaviors in the same BLDCM. Numerical simulations show the feasibility of the suggested means. Analysis of robustness against parametric perturbation in a BLDCM was performed from the perspective of Lyapunov stability theory and by using numerical simulations. We believe that studying the nonlinear dynamics and controlling chaos in BLDCMs will help to advance the development of high-performance electric vehicles.

1. Introduction

Over the last decade, brushless DC motors (BLDCMs) have been widely adopted, such as in spacecraft applications [1], electrical vehicles [2], and unmanned aerial vehicles [3], due to their high efficiency, [4], torque [5], and robustness [6]. Modern nonlinear theory, which involves bifurcation and chaos [7,8], has been widely utilized to study the stability of nonlinear systems [9,10]. The stability of nonlinear dynamics of chaos in BLDCM have been extensively studied, such as bifurcation analysis in BLDCM [11] and chaotic dynamic analysis of BLDCM [12,13]. It has been observed that when the motor parameters fall within specific ranges, the motor drives a behavior that resembles a chaotic process and torque changes suddenly. In this study, we sought to elucidate the dynamics of BLDCM in order to develop an effective method by which to control chaotic vibrations.

This paper presents a variety of numerical analysis methods by which to reveal periodic and chaotic motions, namely bifurcation diagrams, Poincare maps, phase portraits, and frequency spectra. In the current study, we adopted the largest Lyapunov exponent to verify whether a given BLDCM exhibits chaotic motion. Algorithms have been developed to derive the Lyapunov exponents of smooth dynamical systems [14]. Note that a certain amount of chaotic behavior can be tolerated; however, it tends to have a negative effect on performances and restrict the operating ranges of many mechanical and electrical devices. Nonetheless, controlling chaos behavior in key variables in motors is difficult, as these systems feature multiple strongly coupled nonlinear variables. A number of methods by which to control chaotic motion in BLDCM have recently been developed, including anti-control [15], backstepping nonlinear control [16], and synchronization control [17].

Improving the performance of BLDCM by preventing chaotic motion involves the conversion of chaos behaviors into period motion in order to reach steady-state operating conditions. In this study, we employed the simple control method developed by Cai et al. [18] for controlling chaos by the linear state feedback. Numerous studies have addressed the application of linear state feedback to control the chaos behaviors in some nonlinear systems. Chang and Lin [19] employed this approach in an automobile wiper system. Chang [20] also succeeded in quenching chaos in a steer-by-wire using this method. Simulations were performed to confirm the feasibility and efficiency of these methods. Finally, we designed a feedback controller by which to ensure global stability in systems subject to nonlinear error based on the theory of Lyapunov stability [21,22,23].

2. Description and Bifurcation Analysis of BLDCM

The dynamic model of BLDCM was as in the literature [24,25,26]. By using an affine transformation and a single time-scale transformation [16], its governing equations can be transformed into a dimensionless mathematical model of BLDCM as follows:

$$\frac{d{\tilde{i}}_q}{d\tilde{t}}={\tilde{u}}_q-{\tilde{i}}_q-\tilde{\omega }{\tilde{i}}_d+\rho \tilde{\omega }$$

(1)

$$\frac{d{\tilde{i}}_d}{d\tilde{t}}={\tilde{u}}_d-\delta {\tilde{i}}_d+\tilde{\omega }{\tilde{i}}_q$$

(2)

$$\frac{d\tilde{\omega }}{d\tilde{t}}=\sigma \left({\tilde{i}}_q-\tilde{\omega }\right)+\eta {\tilde{i}}_q{\tilde{i}}_d-{\tilde{T}}_L$$

(3)

where ${\tilde{i}}_q$ and ${\tilde{i}}_d$ denote currents along the transformed direct axis and quadrature axis; $\tilde{\omega }$ denotes motor angular speed; ${\tilde{u}}_q$ and ${\tilde{u}}_d$ denote the voltages along the transformed direct axis and quadrature axis; ${\tilde{T}}_L$ is the load torque; and ρ, δ, σ, and η are structural parameters of the dynamic motor system after transformation; the state variables as $\left(\widetilde{.}\right)=T^{-1}(.)$ [16]. Setting $y_1={\tilde{i}}_q, y_2={\tilde{i}}_d \mathrm{and} y_3=\tilde{\omega }$ allows us to rewrite Equations (1)–(3) as Equations (4)–(6):

$${\dot{y}}_1={\tilde{u}}_q-y_1-y_1{y}_2+\rho y_3$$

(4)

$${\dot{y}}_2={\tilde{u}}_d-\delta y_2+y_1{y}_3$$

(5)

$${\dot{y}}_3=\sigma \left(y_1-y_3\right)+\eta y_1{y}_2-{\tilde{T}}_L$$

(6)

where the dot indicates derivation with respect to $\tilde{t}$. The parameter values of Equations (4)–(6) are summarized as follows in Table 1 [15].

Table 1. BLDCM system parameters [15].

Parameter	Value
$\rho$	60
${\tilde{u}}_q$	0.168
${\tilde{u}}_d$	20.66
$\delta$	0.875
$\eta$	0.26
${\tilde{T}}_L$	0.53

Simulations based on Equations (4)–(6) were used to clarify the dynamic characteristics of a BLDCM. IMSL FORTRAN subroutines (DIVPRK software suite) were used to solve the ordinary differential equations [27]. Here, DIVPRK with initial conditions (y₁(0) = 0.01, y₂(0) = 0.001, y₃(0) = 0.001) and time step (1 × 10⁻³) were used. An important conceptual tool for understanding the stability of periodic orbits is Poincaré map. Bifurcation diagrams are universally used to draw transitions from period to chaos motions in nonlinear dynamic systems. Figure 1 expresses a bifurcation diagram in which the first period-doubling bifurcation occurred when σ = 4.08, chaotic behavior appeared in region II, and period-three motion appeared in region III, eventually leading to chaos in region IV. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 detail system responses using Poincaré maps, phase portraits, and frequency spectra.

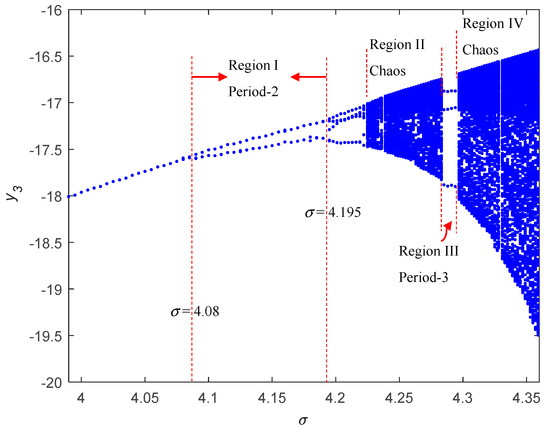
Figure 1. Bifurcation diagram of motor angular speed against σ.

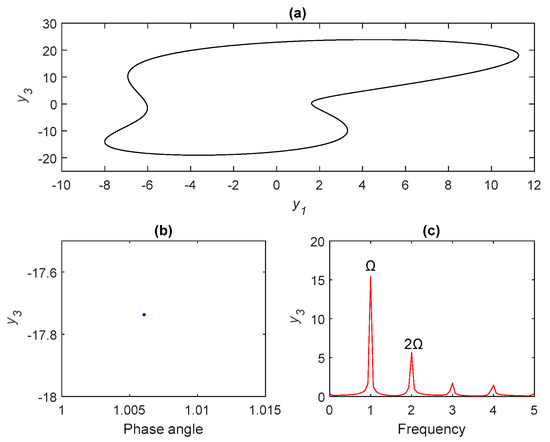
Figure 2. Period-1 orbit for σ = 4.05: (a) phase portraits, (b) Poincare maps, and (c) frequency spectra.

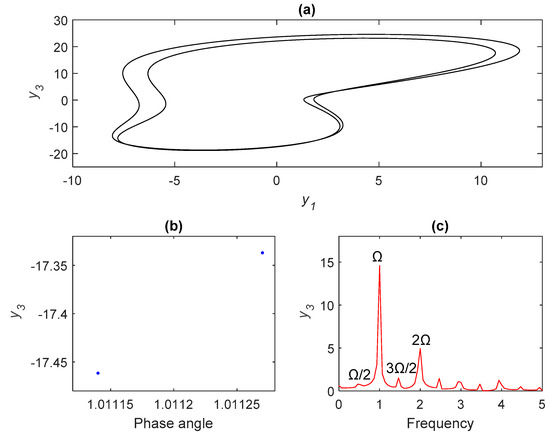
Figure 3. Period-2 motion for σ = 4.15: (a) phase portraits, (b) Poincare maps, and (c) frequency spectra.

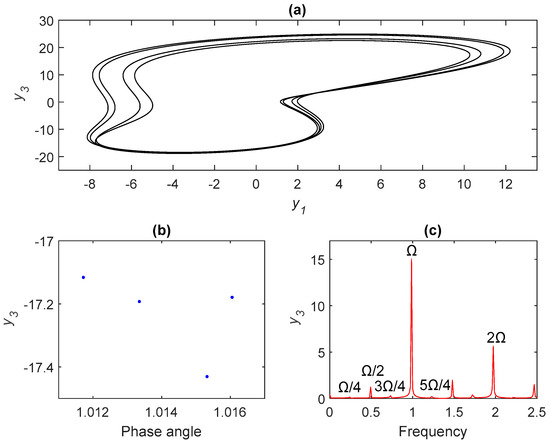
Figure 4. Period-4 orbit for σ = 4.205: (a) phase portraits, (b) Poincare maps, and (c) frequency spectra.

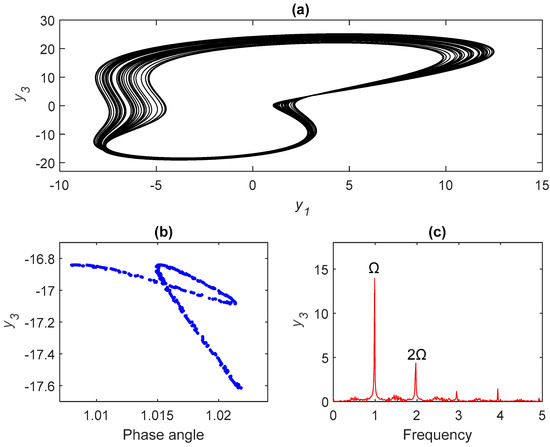
Figure 5. Chaotic orbit for σ = 4.26: (a) phase portraits, (b) Poincare maps, and (c) frequency spectra.

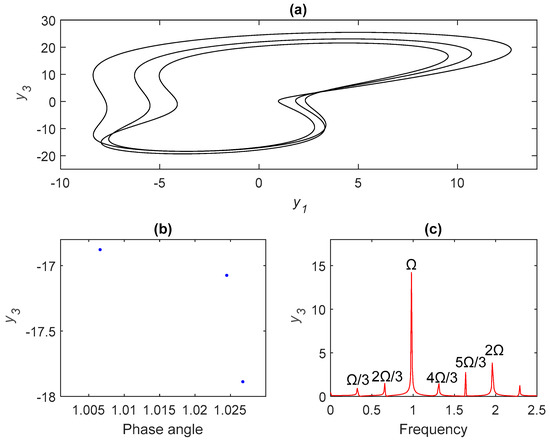
Figure 6. Period-3 orbit for σ = 4.2865: (a) phase portraits, (b) Poincare maps, and (c) frequency spectra.

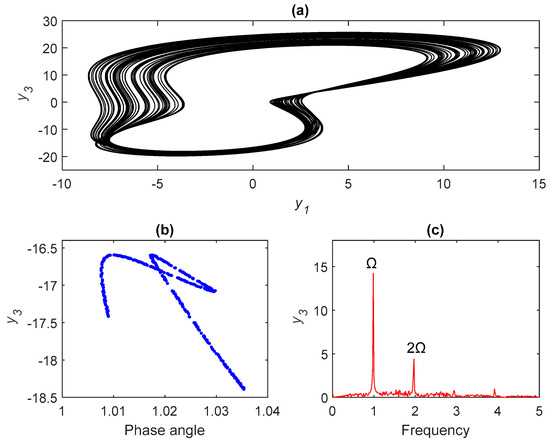
Figure 7. Chaotic motion for σ = 4.32: (a) phase portraits, (b) Poincare maps, and (c) frequency spectra.

Figure 2a–c illustrates period-1 motion, where σ < 4.08 indicates no chatter vibrations. Figure 3a–c delivers a cascade of period-doubling bifurcations with new frequencies at Ω/2, 3Ω/2, 5Ω/2, …, which generated a series of subharmonic components. Figure 4a–c depicts the period-4 bifurcation, which occurred when σ ≈ 4.195. As shown in Figure 1, a cascade of chaos-inducing period-doubling bifurcations occurred as σ continued to increase, resulting in a chatter vibration and potential instability. Poincaré maps and frequency spectra can be used to characterize the nature of chaotic behavior. Poincaré maps exhibit an infinite set of points referred to as strange attractors used to describe chaotic motion as a continuous frequency spectrum. The appearance of strange attractors and/or a continuous Fourier spectra are strong indicators of chaos [28]. Figure 5 indicates the characteristics of chaotic behavior. The period-three bifurcation occurs in region III in Figure 1, finally resulting in chaotic behavior. Period three is normally associated with chaos of dynamical systems and was first proved in [29]. Figure 6 depicts period-three motion and Figure 7 reveals these characteristics of chaotic behavior in detail.

3. Lyapunov Exponents and Lyapunov Dimension for Examining Chaos in a BLDCM

The analysis in Section 2 is inadequate to recognize chaos in BLDCM. In this section, we outline various methods based on Lyapunov exponents to affirm the onset of chaos in BLDCM. Lyapunov exponents, which are the average exponential rates of divergence or convergence of close orbits in phase space, can be used to characterize chaotic motions. Any bound motion of a system containing at least one positive Lyapunov exponent is defined to be chaos, whereas for period orbit, all Lyapunov exponents are negative. The algorithm for computing the Lyapunov exponents from an equation of motion has been described in detail in Wolf et al. [14]. The Lyapunov exponent spectrum from an equation of motion has been described in detail by the long-time evolution of axes of an infinitesimal sphere of states. The sphere will become an ellipsoid due to the locally deforming nature of the flow. The ith one-dimensional Lyapunov exponent is then defined in terms of the length of the ellipsoidal principal axis ρ_i(t) [14]:

$${\lambda }_i=\underset{t\to \infty }{\lim }{\log }_2\frac{{\rho }_i\left(t\right)}{{\rho }_i\left(0\right)}.$$

(7)

The largest Lyapunov exponent for BLDCM is shown in Figure 8, which indicates that the beginning of chaos arose at points P₃, P₄, and P₅, because the sign of the largest Lyapunov exponent converts from negative to positive when σ was increased. At P₁ and P₂, the largest Lyapunov exponent approached zero, at which point the system was prone to bifurcate.

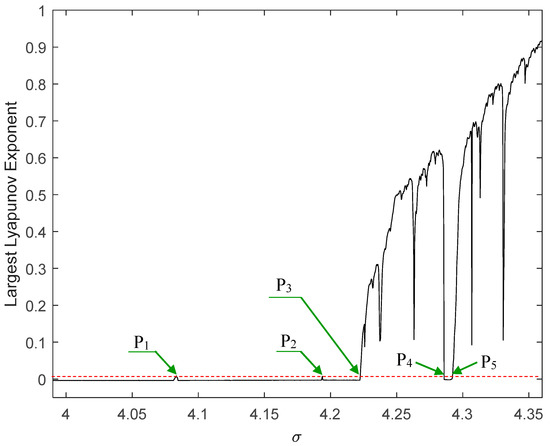
Figure 8. Evolutions of largest Lyapunov exponent.

When parameter σ increased across the bifurcation point P₂, for example σ = 4.1, the Lyapunov exponents were λ₁= −0.0035045, λ₂ = −0.2269056, and λ₃ = −8.3870359. This shows that the motion of the BLDCM at these parameter values will finally converge to a stable limit cycle. Kaplan and Yorke [30] utilized ${\lambda }_1\ge \dots \ge {\lambda }_n$ to assess Lyapunov dimension $d_L$:

$$d_L=j+\frac{1}{\left|{\lambda }_{j+1}\right|}{{\displaystyle \sum }}_{i=1}^j{\lambda }_i,$$

(8)

where j is the largest integer satisfying ${\displaystyle \sum }_{i=1}^j{\lambda }_i>0$. When σ = 4.1 in Equations (4)–(6), this manner yields a Lyapunov dimension of d_L = 1. Since the Lyapunov dimension was an integer, the variable behavior followed a periodic orbit. When the parameter σ increased across point P₃, such as at σ = 4.25, it resulted in Lyapunov exponents of λ₁ = 0.4994983, λ₂ = −0.0029595, and λ₃ = −9.3307454, and a Lyapunov dimension of d_L = 2.0535. The fact that the Lyapunov dimension is non-integer is evidence of chaotic motion. Accordingly, the Lyapunov dimension for a periodic system is an integer, whereas the Lyapunov dimension for a strange attractor is not necessarily an integer.

4. Controlling Chaos in BLDCM

Analyzing and predicting the behaviors of chaotic systems is beneficial; however, the final goal is performing chaos control. Ensuring reliable performance requires steady-state operating conditions, which can only be achieved by transforming chaotic motion to periodic motion. Cai et al. [18] suggested an easy approach to turning chaos into period orbit using linear state-feedback based on an available system variable. We describe this method for an n-dimensional dynamic system, namely:

$$\dot{x}=f(x,t),$$

(9)

where $x\left(t\right)\in R^n$ is the state vector, and $f=\left(f_1,\mathrm{\dots },f_i,\mathrm{\dots },f_n\right)$, where f includes at least one nonlinear function. Assume now that $f_k\left(x,t\right)$ is a nonlinear function that leads to chaos in Equation (9). One state feedback term of system state variable $x_m$ is added to the equation that includes $f_k$, namely:

$${\dot{x}}_k=f_k\left(x,t\right)+K{x}_m, k, m\in \left\{1, 2,\dots , n\right\},$$

(10)

where K denotes the feedback gain. Note that the other functions retain their original types.

Using state-feedback control, Equations (4)–(6) can be revised, namely:

$${\dot{y}}_1={\tilde{u}}_q-y_1-y_1{y}_2+\rho y_3+K{y}_1$$

(11)

$${\dot{y}}_2={\tilde{u}}_d-\delta y_2+y_1{y}_3+K{y}_2$$

(12)

$${\dot{y}}_3=\sigma \left(y_1-y_3\right)+\eta y_1{y}_2-{\tilde{T}}_L+K{y}_3$$

(13)

Equations (4)–(6) describes chaotic motion for σ = 4.26 in no state-feedback controller (i.e., K = 0). Figure 9 presents a bifurcation diagram resulting from the addition of state-feedback controller to the right-hand side of Equations (4)–(6). Chaotic motion appeared when K increased beyond −0.032, and a stable period motion appeared when K decreased beyond −0.032. Period-four orbit appeared when K decreased to approximately −0.055 and −0.032. Period-two orbit appeared when K decreased to approximately −0.19 and −0.055. A further decrease in K beyond −0.19 resulted in period-one motion. Stable period-one appeared when feedback gain (K) fell below −0.19. Figure 10 shows how the application of a control signal after 4 s can be used to assert control over chaotic oscillations. Therefore, to suppress the occurrence of chaos, the simple state-feedback controller can be used to disrupt the balance of dynamic behaviors in a chaotic system.

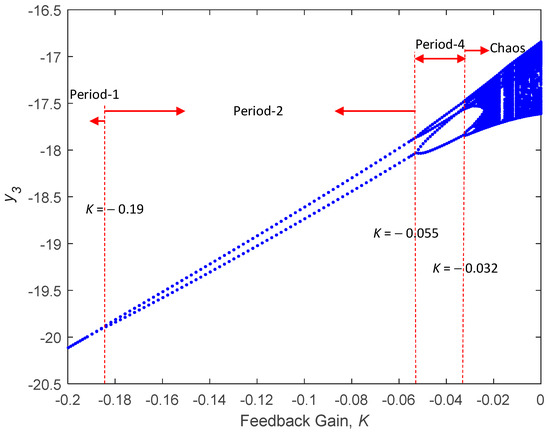
Figure 9. Bifurcation diagram of system with state-feedback control.

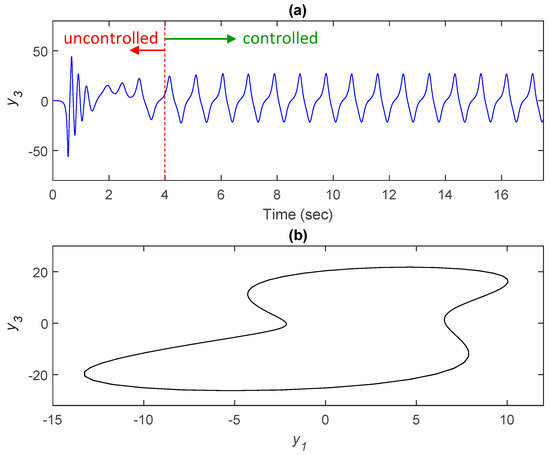
Figure 10. Converting chaos orbit to a period-1 motion for K = −0.195 and σ = 4.26: (a) time history of angular speed. State-feedback control signal is adopted after 4 s, (b) controlled orbit.

5. Study of Parametric Perturbation in BLDCM

The parameters ρ, δ, and η are the structure parameters of the BLDCM dynamic system. These parameters in Equations (4)–(6) are easily changed by the influence of temperature and noise in the working environment of BLDCM. In examining the effects of perturbated parameters on the manifestation of the suggested controller, we address the issue of linear state feedback by adding a sinusoidal perturbation to parameters ρ, δ, and η in the drive system addressed in Equations (4)–(6), with the aim of achieving synchronization. Thus, let Equations (4)–(6) be the drive system, the corresponding response system is given as follows:

$$\frac{d{v}_1}{dt}={\tilde{u}}_q-v_1-v_2{v}_3+\rho \left(1+\epsilon \sin \omega t\right)v_3+u_1,$$

(14)

$$\frac{d{v}_2}{dt}={\tilde{u}}_d-\delta \left(1+\epsilon \sin \omega t\right)v_2+v_1{v}_3+u_2$$

(15)

$$\frac{d{v}_3}{dt}=\sigma \left(v_1-v_3\right)+\eta \left(1+\epsilon \sin \omega t\right)v_1{v}_2-{\tilde{T}}_L+u_3,$$

(16)

where ε is the perturbated amplitude and ω is the perturbated angular frequency.

We subtract Equations (4)–(6) from Equations (14)–(16) to obtain error equations, namely:

$$\frac{d{e}_1}{dt}=-e_1-e_1{e}_2+\rho \epsilon \sin \omega t{e}_3+u_1,$$

(17)

$$\frac{d{e}_2}{dt}=-\delta \epsilon \sin \omega t{e}_2+e_1{e}_3+u_2$$

(18)

$$\frac{d{e}_3}{dt}=\sigma \left(e_1-e_3\right)+\eta \epsilon \sin \omega t{e}_1{e}_2+u_3$$

(19)

where $e_1=v_1-y_1$, $e_2=v_2-y_2$, and $e_3=v_3-y_3$.

We consider the Lyapunov function for Equations (17)–(19) as follows:

$$V\left(e\right)=\frac{1}{2}{e}^{T}e.$$

(20)

Thus, the first derivative of V(e) is given by

$$\dot{V}\left(e\right)=e_1{\dot{e}}_1+e_2{\dot{e}}_2+e_3{\dot{e}}_3.$$

(21)

If we select

$$u_1=e_1{e}_2-\rho \epsilon \sin \omega t{e}_3,$$

(22)

$$u_2=-e_2+\delta \epsilon \sin \omega t{e}_2-e_1{e}_3,$$

(23)

$$u_3=-e_3-\sigma \left(e_1-e_3\right)-\eta \epsilon \sin \omega t{e}_1{e}_2$$

(24)

then

$$\dot{V}\left(e\right)=-e_1^2-e_2^2-e_3^2,$$

(25)

such that $\dot{V}\left(e\right)<0$. Thus, $\dot{V}\left(e\right)$ is a negative defined function, namely, the error states $\underset{t\to \infty }{\lim }\parallel e\left(t\right)\parallel =0$. This means that the states of response system and drive system undergo globally asymptotic synchronization [31].

To explain the accuracy of the above theoretical analysis results, we performed simulations based on the following parameters: ε = 0.001 and ω = 125 rad/s. The detailed numerical results are presented in Figure 11a–c. Figure 11a displays the results for e₁ = v₁ − y₁, Figure 11b displays the results for e₂ = v₂ − y₂, and Figure 11c displays the results for e₃ = v₃ − y₃. Overall, the synchronization error converged to zero, thereby indicating that the two systems, which contained perturbated parameters, can synchronize the states of the drive system and the response system. This demonstrated that the suggested control approach is more robust to perturbated parameters in a BLDCM. Figure 12 presents a bifurcation diagram demonstrating the efficacy of the recommended control approach described in Equations (11)–(13) in suppressing chaotic behaviors under perturbed parameters.

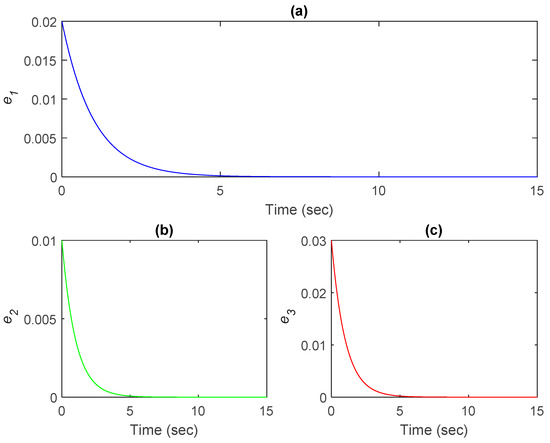
Figure 11. Dynamics of synchronization errors: (a) e₁ = v₁ − y₁, (b) e₂ = v₂ − y₂, and (c) e₃ = v₃ − y₃.

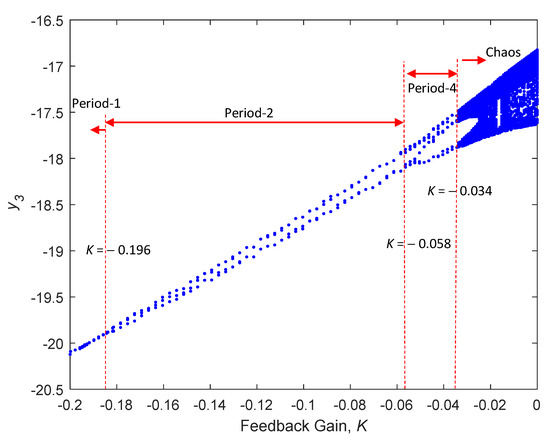
Figure 12. Bifurcation diagram of controlled system under $\rho +\rho \epsilon \sin \omega t$, $\delta +\delta \epsilon \sin \omega t$, and $\eta +\eta \epsilon \sin \omega t$.

6. Conclusions

Based on our analysis of nonlinear dynamics, we recommend an effective means to controlling chaos in BLDCM. The bifurcation diagram reveals that a BLDCM exhibits period-doubling bifurcation, period-three bifurcation, and chaotic motion. A period-doubling cascade is an infinite sequence of period-doubling bifurcations. Such cascades are a common route by which dynamical systems develop chaos. Period three implies chaos [29]. The most effective techniques to judging whether BLDCMs have chaotic motions involves Lyapunov exponents and Lyapunov dimensions. A BLDCM will produce chaos under certain electromechanical parameters, which greatly affects the operation quality and reliability of a BLDCM system. Therefore, it is very important to suppress a chaotic BLDCM. Our adoption of state-feedback control to suppress chaos in a BLDCM demonstrated the efficacy of the proposed controller in removing chaotic oscillations. We also analyzed and demonstrated the robustness of BLDCMs with state-feedback controller suppressing chaotic behaviors under parametric perturbation using bifurcation diagrams and Lyapunov stability theorem. The research results have a high reference value for stable operation and chaos control for BLDCMs. This study proposes that researching nonlinear dynamics and chaos control in BLDCMs could boost the progress of developing high-performance electric vehicles.