Abstract
Tourist flow prediction plays a crucial role in enhancing the efficiency of scenic area management, optimizing resource allocation, and promoting the sustainable development of the tourism industry. To improve the accuracy and real-time performance of tourist flow prediction, we propose a BP model based on a hybrid genetic algorithm (GA) and ant colony optimization algorithm (ACO), called the GA-ACO-BP model. First, we comprehensively considered multiple key factors related to tourist flow, including historical tourist flow data (such as tourist flow from yesterday, the previous day, and the same period last year), holiday types, climate comfort, and search popularity index on online map platforms. Second, to address the tendency of the BP model to get easily stuck in local optima, we introduce the GA, which has excellent global search capabilities. Finally, to further improve local convergence speed, we further introduce the ACO algorithm. The experimental results based on tourist flow data from the Elephant Trunk Hill Scenic Area in Guilin indicate that the GA-AC*O-BP model achieves optimal values for key tourist flow prediction metrics such as MAPE, RMSE, MAE, and R2, compared to commonly used prediction models. These values are 4.09%, 426.34, 258.80, and 0.98795, respectively. Compared to the initial BP neural network, the improved GA-ACO-BP model reduced error metrics such as MAPE, RMSE, and MAE by 1.12%, 244.04, and 122.91, respectively, and increased the R2 metric by 1.85%.
1. Introduction
As economic levels continue to rise and lifestyles evolve, tourism has become increasingly mainstream and plays a significant role in people’s daily lives. China’s tourism industry is currently in a phase of sustained rapid growth and has emerged as one of the world’s largest and fastest-growing tourism markets [1]. According to the statistical bulletin released in 2024, the total number of domestic tourists in China reached 5.62 billion, representing a year-on-year increase of 14.8%. Among these, urban residents accounted for 4.37 billion trips, up by 16.3%, while rural residents accounted for 1.25 billion trips, up by 9.9%. Meanwhile, total domestic tourism expenditure reached 5.8 trillion yuan, marking a year-on-year increase of 17.1%.
Against the backdrop of rapid development in the tourism industry, achieving timely and accurate predictions of tourist numbers at tourist attractions has become a key issue in promoting the operational efficiency of tourist attractions and the sustainable development of the tourism industry [2]. If the number of tourists on a given day far exceeds expectations and the tourist attraction is not adequately prepared, it can easily lead to regional congestion and traffic disruptions and, in severe cases, even safety incidents. Conversely, if tourist numbers drop significantly and the scenic area management fails to obtain advance information, this may result in waste of human and material resources, increasing unnecessary operational costs. Over the long term, this will have an adverse impact on the normal operations and healthy development of the scenic area. Therefore, establishing an efficient and reliable tourist flow prediction method is of great significance for enhancing the management efficiency of tourist scenic areas, ensuring tourist safety, and optimizing resource allocation.
Traditional tourist flow prediction methods, such as ARMA [3] and ARIMA [4], have certain forecasting capabilities under specific conditions, but their prediction results suffer from low accuracy, strong lag, and poor adaptability. Especially when dealing with complex nonlinear relationships, multivariate interactions, and dynamic changes in tourist flow, traditional prediction methods are significantly limited in their effectiveness and cannot meet the current tourism management requirements for high accuracy and real-time performance.
In recent years, the continuous advancement of artificial intelligence technology has provided new insights and methods for predicting tourist flow. Rob Law [5] used a back propagation (BP) neural network [6] to predict tourist demand and through empirical experiments demonstrated that this method outperforms regression models, time series models, and feedforward neural networks in terms of predictive accuracy. Li et al. [7] employed the long short-term memory (LSTM) [8] method to predict tourist flow and demonstrated through experiments that this method outperforms traditional ARIMA models [4] and BP neural networks [6] in terms of predictive performance. Chen et al. [9] proposed a road traffic flow prediction model based on least squares support vector machines (LSSVM) [10] to predict the traffic flow of a bus route in Changchun City. The experimental results showed that the predicted values of this model closely matched the actual observed values, with the coefficient of determination (R2) of the training set generally exceeding 0.90, verifying the effectiveness and feasibility of this method in bus passenger flow prediction. Liu et al. [11] proposed a hybrid model combining a deep neural network (DNN) initialized by a self-encoder (SAE) [12] to predict passenger flow at four rapid transit bus stations in Xiamen City. Experimental results showed that the SAE-DNN model demonstrated high prediction accuracy and good generalizability under different passenger flow characteristics at various stations. Hu et al. [13] proposed a multi-layer traffic flow prediction model (MTDLTFP) that integrates transformers [14] and deep learning. The model adopts the transformer’s encoder-decoder architecture to perform multi-layer feature extraction on raw traffic data and then inputs the extracted latent features into a neural network to generate prediction results. Experimental results show that the model achieves an RMSE of 0.191 and an MAE of 0.165 on the Workday dataset and an RMSE of 0.227 and an MAE of 0.192 on the Holiday dataset.
Given the limitations of artificial intelligence foundation models in tourist flow prediction, many scholars have improved the model structure and algorithms to enhance predictive performance and application effectiveness. Li et al. [15] combined web search data with the fruit fly optimization algorithm (FOA) [16] to optimize the BP neural network [6], constructing the FOA-BP model for predicting daily tourist flow in the Huangshan Scenic Area, China; experimental results showed that compared to the GA-BP and PSO-BP models, the FOA-BP model achieved higher prediction accuracy for tourist flow during peak seasons. Li et al. [17] combined seasonal K-means clustering with the particle swarm optimization (PSO) algorithm [18] to optimize the LSSVM [10], proposing a seasonal clustering-based tourist flow prediction method. This method effectively improved the accuracy of daily tourist flow predictions, with overall accuracy increasing by nearly 3% compared to the initial LSSVM model. Wang et al. [19] integrated attention mechanisms with 1DCNN-LSTM networks to construct a short-term traffic flow prediction model. This method combines the advantages of CNN [20] in time series feature extraction with the long-term dependency modeling capabilities of LSTM [8]. Experimental results demonstrated that compared with traditional neural network models, the proposed model achieved faster convergence and higher prediction accuracy, while the incorporation of attention mechanisms further enhanced its ability to capture key features. Lu et al. [21] proposed a CNN-LSTM prediction method optimized by genetic algorithms (GA-CNN-LSTM) for predicting the daily tourist flow in the Huangshan Scenic Area, China. This method constructs continuous feature maps from multi-modal data, such as web search data and meteorological data, extracts feature vectors through CNN [20], and inputs them into LSTM [8] for time series prediction. The experimental results show that this model exhibits high accuracy and stability in predicting daily tourist flow.
Although the aforementioned studies have achieved satisfactory results in tourist flow prediction, most researchers primarily rely on historical tourist flow data during the prediction process and pay little attention to objective environmental factors such as weather conditions and average temperature. These factors often significantly influence tourists’ willingness to travel, thereby causing fluctuations in tourist flow. In terms of base model selection, LSTM, LSSVM, and BP neural networks are frequently applied to tourist flow forecasting tasks due to their strong nonlinear modeling capabilities. LSTM effectively captures long-term dependencies in time series data; however, when handling tourist flow data containing discontinuous dates, it struggles to extract underlying information and correlations, resulting in limited predictive performance [22,23]. LSSVM demonstrates strong generalization capabilities when handling small-sample, high-dimensional data and converges quickly, but it is sensitive to parameter selection and may be affected by improper parameter settings, thereby impacting prediction accuracy [24,25]. In contrast, BP neural networks demonstrate greater adaptability when handling non-continuous, structurally complex data, making them highly suitable for complex tourist flow prediction tasks. However, BP neural networks also suffer from issues such as being prone to local optima and low training efficiency [26]. Therefore, research on model optimization for tourist flow prediction in scenic areas remains of significant theoretical and practical value.
We use a BP neural network as the base model to predict tourist flow in scenic spots. To address the issues that exist in real-world tourist flow prediction, we have made the following three improvements:
- To address the limitations of previous studies that relied too heavily on historical tourist flow data, we introduced multiple influencing factors, including holiday types, climate comfort, and search popularity index on online map platforms, in addition to historical data such as yesterday’s tourist flow, the previous day’s tourist flow, and tourist flow during the same period last year, to assess tourist travel intentions and improve the accuracy of tourist flow predictions.
- To address the issue of BP neural networks easily falling into local optima and affecting prediction accuracy, we introduce a genetic algorithm (GA) to optimize the initial weights and thresholds of BP neural networks. GA has good global search capabilities and can effectively solve the problem of BP neural networks easily falling into local optima, improving the prediction accuracy and training convergence stability of the model.
- To address the issue of low local convergence efficiency in GA when optimizing BP neural networks, we further introduce the ant colony optimization algorithm (ACO) to improve real-time prediction performance. ACO accelerates the model’s convergence speed in local regions by simulating the transmission and accumulation of pheromones to guide weight adjustment paths. Additionally, using GA’s optimization results as ACO’s initial solution to initialize pheromone distribution helps overcome the issue of slow global search speed in the early stages of ACO due to insufficient pheromones.
Section 2 of this paper introduces the dataset used, the basic structure of the BP neural network, and the optimization methods of GA and ACO for the network. Section 3 introduces the experimental environment, training parameters, and evaluation indicators and analyzes the experimental results. Section 4 discusses the experimental results and points out the limitations of the experiment and future research directions. Section 5 summarizes the experimental methods and implications.
2. Materials and Methods
2.1. Data Collection
To more comprehensively evaluate the performance of the tourist flow prediction model, this study constructed a dataset containing multi-dimensional features such as date, yesterday’s tourist flow, the previous day’s tourist flow, tourist flow during the same period last year, holiday type, climate comfort, and search popularity index. Tourist flow data was sourced from the Guilin Tourism Network, and we collected tourist flow data for the Elephant Trunk Hill Scenic Spot in Guilin from February 2023 to January 2025. For several discontinuous missing tourist flow values in the original data, we performed interpolation using linear interpolation based on the weighted average of tourist numbers from the preceding and following dates to ensure data continuity and minimize the impact of missing values on model training performance. For abnormal situations where the number of tourists on a given day exceeded the maximum daily capacity (35,000) of the scenic area, we adjusted it to the maximum capacity of the scenic area to ensure data rationality. To improve the accuracy of model predictions, daily tourist flow values were normalized using the following formula:
In the formula, represents the daily tourist flow, and and represent the minimum and maximum values of the daily tourist flow, respectively. is the normalized value, and and represent the lower and upper limits of the normalized value, respectively.
The type of holiday reflects the regulatory effect of holidays on tourist flow. Based on calendar information, we divide dates into three categories: weekdays, weekends, and national statutory holidays.
Climate comfort reflects tourists’ willingness to travel. We collected various climate indicators, including weather conditions, maximum and minimum temperatures, air quality, and wind speed, from the Guilin Meteorological Bureau website for the period from February 2023 to January 2025. For extreme readings of climate indicators caused by extreme weather events (such as typhoons and heavy rainfall), we used upper and lower limit truncation methods to control them within a reasonable range, thereby preventing unreasonable negative scores or extreme deviations. Based on these indicators, we divided climate comfort into five levels, using the following formula:
In the formula, are weighting coefficients, set to 0.3, 0.2, 0.2, 0.2, and 0.1, respectively; , , , , and are the scores for weather conditions, maximum temperature, minimum temperature, air quality, and wind speed, respectively, each with a maximum score of 100 points. The highest score is assigned when the indicator is at its optimal condition, specifically sunny weather (100 points), maximum temperature of (100 points), minimum temperature of (100 points), Air Quality Index (100 points), and wind speed of level 0 or 1 (100 points).
The search popularity index is used to measure changes in the level of interest in tourist attractions on online platforms, reflecting potential visitor trends. The tourist attraction search index used in this article is sourced from popular Chinese map search software, including Baidu Maps and Gaode Maps.
After preprocessing the data, we split the dataset chronologically to avoid information leakage and preserve temporal order. We used 516 data points from February 2023 to June 2024 as the training set, which covers multiple peak and off-peak seasons and holiday patterns to enable the model to learn long-term trends and seasonal cycles. The 153 data points from July 2024 to November 2024 served as the test set to evaluate generalization, while the 62 data points from December 2024 to January 2025 formed the validation set for hyperparameter tuning and the selection of BP network hidden layer nodes.
2.2. BP Neural Network Model
The BP neural network was proposed by British scholars Rumelhart, McClelland et al. in 1986 [6]. It is a feedforward neural network trained based on the error backpropagation mechanism. This model can effectively identify nonlinear relationships between inputs and outputs through learning from large amounts of data, making it very suitable for handling tourist flow prediction tasks involving complex nonlinear relationships.
The BP neural network consists of an input layer, hidden layers, and an output layer, as shown in Figure 1. The operation process of the BP neural network comprises two parts: forward propagation of input information and backward propagation of error. During the forward propagation of input information, input data is transmitted from the input layer to the hidden layers, processed, and then transmitted to the output layer to generate the model’s predicted values. Subsequently, the model’s predicted values are compared with the actual values to calculate the error. If the error meets the predefined target or reaches the maximum number of iterations, the training process terminates; otherwise, the process enters the error backpropagation phase, where the weights and thresholds between neurons in each layer are adjusted based on the error information to further optimize network performance. Through repeated iterations of this process, the BP neural network gradually converges toward the optimal solution, learning the complex nonlinear mapping relationship between input and output to achieve more accurate predictions.
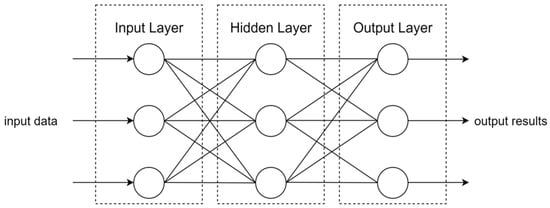
Figure 1.
BP neural network structure.
In the BP neural network, the input layer is used to receive external feature data, and the number of neurons typically corresponds to the dimension of the input features. In the tourist flow prediction experiment conducted in this study, the input data included six types of features: yesterday’s tourist flow, the previous day’s tourist flow, tourist flow during the same period last year, holiday type, climate comfort, and search popularity index. Therefore, the input layer of the BP neural network was set to six neurons to comprehensively reflect the main factors affecting tourist flow.
The hidden layer of the BP neural network is responsible for extracting and transforming input features, enabling the network to capture complex patterns in the data. The number of hidden layers can be one or multiple layers. In this study, it was set to one layer in the tourist flow prediction experiment. The number of neurons in the hidden layer typically needs to be determined through experimentation. Too few neurons may limit feature learning capabilities, while too many may lead to overfitting.
The output layer of the BP neural network is used to generate the final prediction results, and the number of neurons is determined by the dimension of the prediction target. In the tourist flow prediction experiment in this study, the prediction target was the daily tourist flow, so the output layer was set to 1 neuron.
In BP neural networks, the choice of activation function is critical to model performance. It not only introduces nonlinear factors but also directly affects the output of neurons, thereby helping to address nonlinear problems such as visitor traffic prediction. This study selected the Tansig function as the activation function and applied it to signal transmission from the input layer to the hidden layer and from the hidden layer to the output layer. The formula is as follows:
2.3. Improvements to the BP Model
2.3.1. Introduction of Genetic Algorithms
To address issues such as BP neural networks easily falling into local optima, we introduce genetic algorithms (GA) [27] to optimize the initial weights and thresholds of BP neural networks. GA simulates biological evolutionary processes to achieve global search and parameter optimization, which helps improve the prediction accuracy and training convergence stability of BP neural networks.
GA draws on Darwin’s concepts of natural selection and genetic mechanisms. Based on the rules of the fitness function, GA uses operations such as selection, crossover, and mutation to evaluate and screen each individual in the set, retaining the most optimal individuals. The specific process of GA is shown in Figure 2.
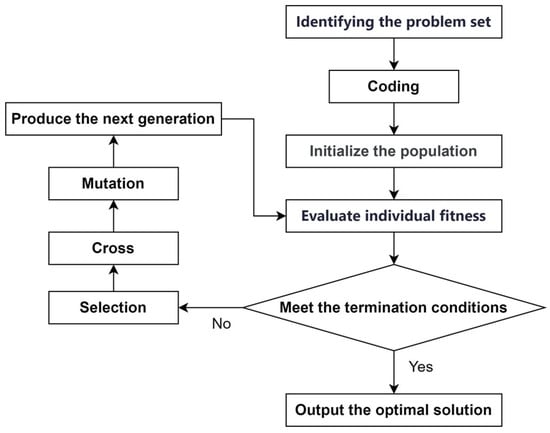
Figure 2.
Genetic algorithm flowchart.
The specific steps for optimizing the BP neural network using the GA are described below:
- 1.
- Initialize the population. Randomly generate an initial population of individuals. For each individual, use a linear interpolation function to generate a real number gene vector within a given data selection range as a chromosome of the GA. Use real number encoding to ensure that chromosomes can be directly mapped to the parameters of the BP neural network, thereby improving search efficiency and accuracy.
- 2.
- Evaluate individual fitness. Based on the optimized parameters of the BP neural network, assign the chromosomes generated in step 1 as the weights and thresholds of the network, and train using the training sample set. Then, calculate the sum of squared training errors to evaluate the fitness of each individual. If the fitness of the individual meets the termination condition, output the optimal solution. Otherwise, continue with the next step of genetic operation.
- 3.
- Perform individual selection operations based on the roulette wheel method using fitness ratios. The selection probability of each individual is related to its fitness, and the specific calculation method is shown in Formula (4):
In the formula, is the reciprocal of fitness, and is the population size.
- 4.
- Perform crossover operations. Crossover operations involve crossing genes at random positions on the chromosomes of two individuals to generate new offspring individuals. For example, the crossover operations for gene and gene at position are shown in Formula (5):
In the formula, is a random number between .
- 5.
- Perform mutation operations. Mutation operations adjust specific genes of individuals to enhance the global search capability of the algorithm. For example, select the jth gene of the ith individual for mutation operations. The specific calculation method is shown in Formula (6):
In Formula (6,) and are the upper and lower bounds of the values of gene , respectively, and is a random number between . In Formula (7), is a random number, is the current iteration count, and is the maximum number of evolutionary generations.
- 6.
- Select the individual with the optimal fitness as the optimal solution of GA and use the chromosome of that individual as the initial weight and threshold of the BP neural network.
Genetic operations such as selection, crossover, and mutation enable GA to perform global searches effectively, alleviating the problem of BP neural networks easily falling into local optima during training. However, GA needs to maintain a population consisting of multiple candidate individuals to search for the optimal solution. This population mechanism improves global search capabilities but also requires each iteration to evaluate multiple candidate individuals simultaneously, consuming more computational resources [28,29]. Especially when the population contains a large number of candidate individuals that are not concentrated in the optimal region, the convergence speed of GA in local regions tends to slow down.
2.3.2. Introduction of Ant Colony Optimization Algorithm
To address the shortcomings of GA in optimizing BP neural networks, such as low local convergence efficiency, we introduced the ant colony optimization algorithm (ACO). ACO was proposed by Marco Dorigo et al. [30], and its principle is based on simulating the foraging behavior of ants. During the process of searching for food, ants release pheromones along their paths, and other ants tend to choose paths with higher pheromone concentrations. Ants travel more frequently along shorter paths, leading to faster accumulation of pheromones, making these paths more likely to be chosen by other ants. Ultimately, all ants will select the shortest path. The process of the ACO is illustrated in Figure 3.
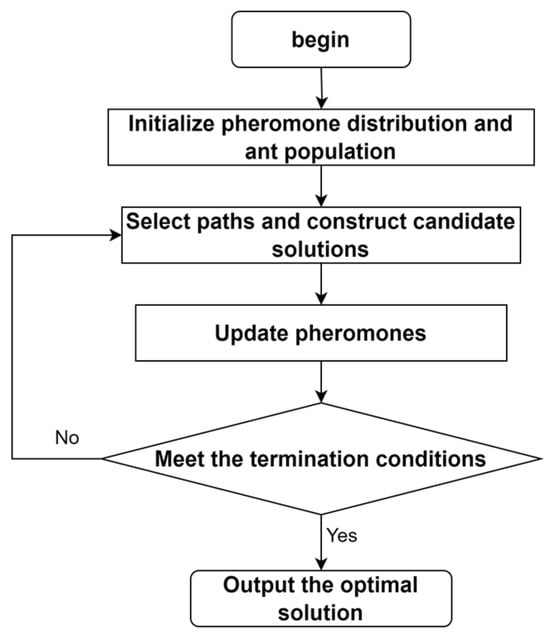
Figure 3.
Ant colony optimization algorithm flowchart.
The specific steps for optimizing the BP neural network using the ACO algorithm are described below:
- Initialize pheromone distribution and ant colony parameters. We treat the weights and thresholds in the BP neural network as nodes on the ant colony search path, and the pheromone concentration is used to represent the importance of the corresponding path. Randomly initialize the pheromone concentration on the path, and set the number of ants, pheromone evaporation rate, and maximum number of iterations according to the problem scale while determining the initial distribution position of the ants.
- Selecting paths and constructing candidate solutions. During the search process, ants use a probability transfer mechanism to determine their next move based on the pheromone concentration and heuristic information on the current path, gradually constructing candidate solutions. The path selection probability formula is as follows:
In the formula, is the pheromone concentration between paths and , is heuristic information, and and represent the importance of pheromones and heuristic information, respectively.
- 3.
- Update pheromones. Update the pheromone distribution along the search paths of all ants based on their search paths. Pheromones along shorter paths are enhanced to guide more ants toward that path. At the same time, pheromones along the path also evaporate over time to prevent the algorithm from getting stuck in a local optimum. The pheromone update formula is shown in Formula (9), and the pheromone evaporation formula is shown in Formula (10):
In Formula (8), represents the amount of pheromone between paths and , is a constant, and is the total length of the path. In Formula (9), is the pheromone evaporation rate, and is the pheromone concentration between paths and .
- 4.
- Determine whether the termination conditions are met, such as reaching the maximum number of iterations or the error of the solution being less than the preset target. If the termination conditions are met, end the search process. Otherwise, jump to step 2.
- 5.
- Output the optimal solution. Select the path with the highest pheromone concentration as the currently found global optimal solution and use its corresponding weight and threshold as the initial parameters of the BP neural network.
The pheromone positive feedback mechanism enables ACO to exhibit high efficiency in local searching, thereby accelerating the convergence speed of the BP neural network and improving the real-time nature of predictions. However, during the initial stages of searching, due to insufficient pheromone distribution, ants primarily rely on random search mechanisms, resulting in relatively slow global optimization speed in the initial stage [31,32]. Only when pheromones gradually accumulate along critical paths and form a significant guiding effect can the ant colony effectively transition to heuristic searching, thereby improving search efficiency and accelerating algorithm convergence.
2.3.3. GA-ACO-BP Neural Network Model
To fully leverage the complementary advantages of GA and ACO in optimizing performance, we propose a BP neural network model based on a hybrid GA and ACO, called the GA-ACO-BP model, for predicting tourist flow in scenic spots. This model combines the global search capabilities of genetic algorithms with the local efficient search capabilities of ant colony algorithms to improve the prediction accuracy and convergence efficiency of BP neural networks during the training process.
The core idea of the model is to use the weights and thresholds of the BP neural network as optimization objectives. First, the initial solution of the BP neural network is used as input for the genetic algorithm. Leveraging the genetic algorithm’s initial global search capability, a rough local range close to the optimal solution can be quickly identified, yielding a suboptimal intermediate solution. The convergence direction of the obtained intermediate solution is closer to the optimal solution and is independent of the initial values. Then, we use the intermediate solution obtained by the GA algorithm as the initial input for the ACO algorithm to initialize the pheromone distribution. Leveraging the ACO algorithm’s high efficiency in local convergence during the later stages, we can quickly compute the intermediate solution and obtain the optimal solution. The specific flowchart of the GA-ACO-BP model is illustrated in Figure 4:
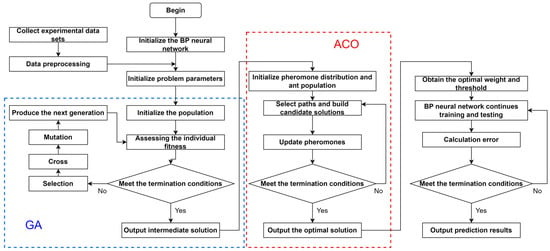
Figure 4.
The flowchart of the GA-ACO-BP neural network model.
3. Results
3.1. Experimental Environment and Training Parameters
Our experimental environment configuration mainly consists of hardware and software components. In terms of hardware, the experiment uses a 12th generation Gen Intel(R) Core(TM) i9-12900H processor with 16 GB of RAM. The software environment is a 64-bit Windows 10 Professional operating system, and the experiment is mainly conducted using MATLAB 2022a software.
All models were trained using uniform experimental parameters, with specific parameter settings shown in Table 1.

Table 1.
Training parameter settings.
The learning rate determines the step size for each weight update. If it is too high, it may cause gradient explosion; if it is too low, it will slow down the convergence speed. Considering the complexity of tourist flow prediction, we set the learning rate to 0.01. The target error is one of the stopping conditions for training, and we set it to 0.0001 to balance prediction accuracy and training efficiency. The maximum number of iterations is used to limit the number of training rounds, and we set it to 1000.
Population size directly affects the coverage of the algorithm’s search space and the diversity of solutions. A population that is too small may limit the search range, while a population that is too large may increase computational complexity. We set the population size for both the GA and ACO algorithms to 20 to balance search capability and computational efficiency. The maximum number of generations for GA and the maximum number of iterations for ACO are both set as the termination conditions for their respective algorithms. We uniformly set these to 50 to meet the requirements of the tourist flow prediction task and maintain consistency in parameter settings for subsequent comparative experiments.
In the GA algorithm, the cross probability determines the frequency of gene exchange between individuals. An excessively high cross probability may disrupt the genetic structure of superior individuals, while an excessively low probability may slow down the generation of new individuals. We set the cross probability to 0.8 to efficiently generate new individuals while maintaining population diversity. The mutation probability represents the likelihood of random changes in an individual’s genes, and we set it to 0.1 to introduce moderate randomness while maintaining population stability. In the ACO algorithm, the pheromone factor controls the importance of pheromones in path selection. We set it to 2 to ensure that the ant colony fully utilizes existing high-quality path information during the search process. The heuristic function factor reflects the weight of heuristic information in path selection. We set it to 3 to enhance the ant colony’s preference for locally optimal paths. The pheromone evaporation rate represents the rate at which pheromones decay over time. We set it to 0.5 to maintain search diversity while preventing premature convergence.
3.2. Evaluation Criteria
In previous studies evaluating the predictive performance of BP neural network models, common metrics such as the mean absolute percentage error (MAPE), root mean square error (RMSE), mean absolute error (MAE), and mean square error (MSE) have been used to assess the predictive performance of BP neural network models [33]. MAPE measures the average relative deviation between predicted values and actual values; RMSE reflects the overall variability of prediction errors; MAE represents the average absolute value of prediction errors and has strong resistance to outliers; MSE is commonly used to evaluate the training performance of models. Smaller values of MAPE, RMSE, MAE, and MSE indicate lower prediction errors and better overall predictive performance. To further assess the model’s goodness of fit, we also introduce the coefficient of determination (R2), which measures the model’s ability to fit the actual trend. A higher R2 value closer to 1 indicates better predictive performance. The formulas for these metrics are as follows:
In the above formula, represents the model’s predicted tourist flow value, represents the actual tourist flow, represents the average tourist flow value in the dataset, and represents the number of days with tourist flow in the dataset.
3.3. Comparative Experiment of Hidden Layer Nodes in BP Neural Networks
To analyze the impact of the number of hidden layer nodes on the prediction accuracy of the BP neural network, we designed a comparative experiment in the validation set to examine the mean absolute error (MAE) of the model under different node counts. The results are shown in Figure 5. The experimental results indicate that as the number of hidden layer nodes increases from 5 to 8, the MAE gradually decreases, suggesting that the prediction accuracy of the BP neural network for tourist flow has improved. When the number of hidden layer nodes exceeds 8, the MAE increases and becomes more volatile, indicating that the BP neural network faces the risk of overfitting, leading to reduced prediction stability. When the number of hidden layer nodes is set to 8, the MAE reaches its minimum value, at which point the BP neural network achieves the best tourist flow prediction performance. Therefore, in subsequent experiments, the number of hidden layer nodes is uniformly set to 8 to ensure fair comparison among models under identical structural conditions.
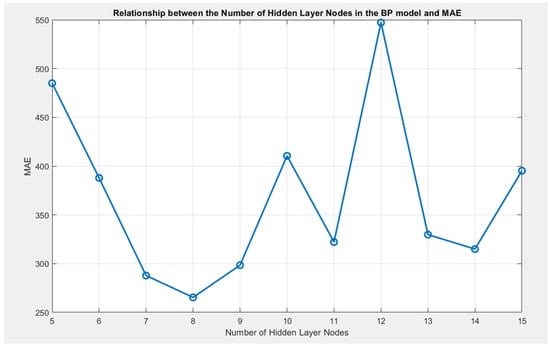
Figure 5.
Relationship between the number of hidden layer nodes in the BP model and MAE.
3.4. Tourist Flow Prediction Results of the GA-ACO-BP Model
Figure 6 shows the comparison between the prediction results of the GA-ACO-BP model on the test set and the actual tourist flow. Overall, the model’s predicted values are highly consistent with the actual data. In terms of three key error metrics, the model demonstrates low error rates: RMSE is 426.34, MAE is 258.80, and MAPE is 4.09%. A low RMSE indicates that the model has good fitting capability for data with significant fluctuations; a low MAE suggests that the model has minimal overall prediction bias; and a low MAPE further validates that the model maintains high stability and accuracy across different scales of tourist flow.
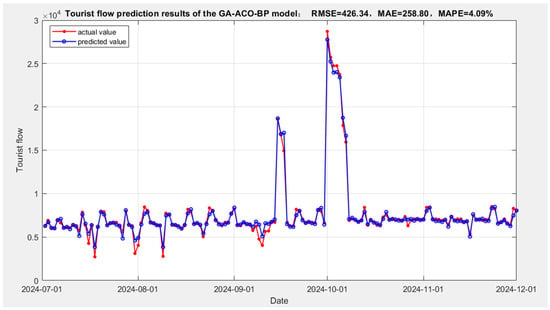
Figure 6.
Tourist flow prediction results of the GA-ACO-BP model on the test set.
Figure 7 shows the coefficient of determination (R2) of the GA-ACO-BP model on the training set and test set. The R2 for the training set is 0.98993, and that for the test set is 0.98795, both of which are close to 1. This indicates that the model has good fitting performance on different datasets, with prediction results highly consistent with actual tourist flow, demonstrating strong generalization capabilities.
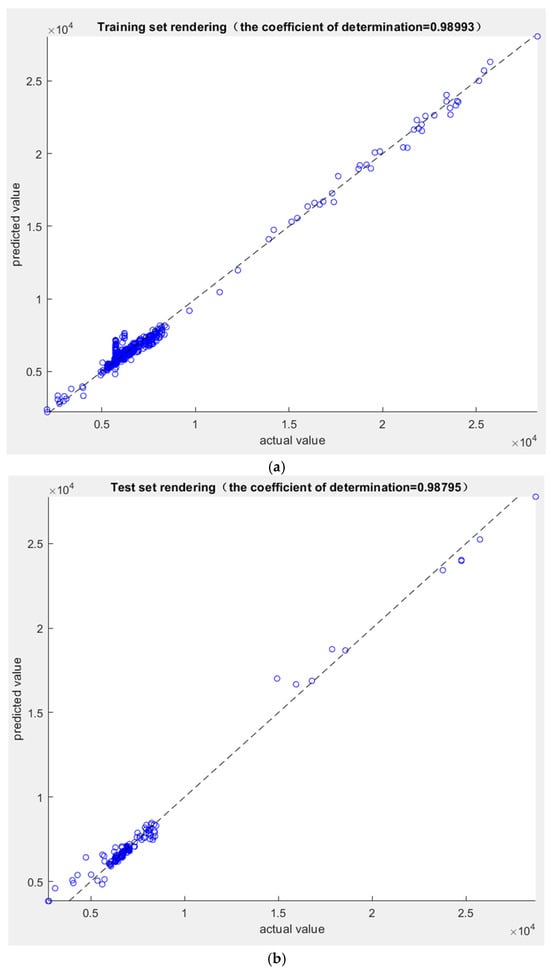
Figure 7.
(a) Training set rendering. (b) Test set rendering.
3.5. Comparative Experiments of Different Prediction Models
To validate the effectiveness of the GA-ACO-BP model, we compared it with several commonly used prediction models, including BP [6], LSSVM [10], LSTM [8], ELM [34], and PSO-BP [35]. The prediction performance of each model on the test set is shown in Table 2. Figure 8 shows the absolute error variation trends of different models on the test set for an intuitive comparison of their prediction accuracy and stability.

Table 2.
Prediction results of different prediction models on the test set.
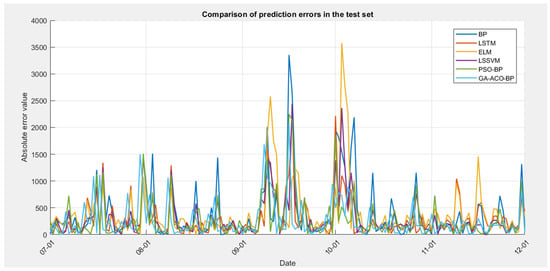
Figure 8.
Comparison of absolute errors on the test set for each prediction model.
As shown in Table 2, the GA-ACO-BP model outperforms other comparison models in all key prediction metrics, achieving MAPE, RMSE, MAE, and coefficient of determination (R2) values of 4.09%, 426.34, 258.80, and 0.98795, respectively, demonstrating the best tourist flow prediction performance. Compared to the basic BP neural network, the model shows significant improvements in error metrics, with MAPE, RMSE, and MAE decreasing by 1.12 percentage points, 244.04, and 122.91, respectively, and R2 increasing by 0.86 percentage points. This indicates that the GA-ACO-BP model is highly suitable for handling prediction tasks involving complex nonlinear relationships and interactions among multiple dependent variables, such as tourist flow forecasting.
3.6. Ablation Experiment
To verify the effectiveness of genetic algorithms (GA) and ant colony algorithms (ACO) in improving the performance of BP neural networks, we designed three sets of ablation experiments. The specific results are shown in Table 3.

Table 3.
Ablation experiment.
In the first round of experiments, we introduced GA into the basic BP neural network to obtain the GA-BP model. The results show that compared with the BP model, the GA-BP model decreased by 0.79%, 197.11, and 78.59 in error indicators such as MAPE, RMSE, and MAE, respectively, while R2 also increased by 1.56 percentage points. In the second round of experiments, we introduced ACO into the original BP model to obtain the ACO-BP model. This model outperformed the original BP model in all metrics, with MAPE, RMSE, and MAE decreasing by 1.04 percentage points, 227.95, and 96.8, respectively, and R2 increasing by 1.73 percentage points. In the third round of experiments, we introduced ACO into the GA-BP neural network, resulting in the optimized GA-ACO-BP model. This model outperformed the GA-BP model in all evaluation metrics, with MAPE, RMSE, and MAE decreasing by 0.33 percentage points, 46.93, and 44.32, respectively, while R2 improved by 0.28 percentage points. The above results indicate that both GA and ACO can effectively improve the predictive performance of the BP neural network, and their combination further enhances the overall performance of the model.
Figure 9 shows the fitness change curves of the GA, ACO, and GA-ACO algorithms. Fitness is an important metric for evaluating the quality of solutions in intelligent optimization algorithms; the smaller the value, the closer the solution is to the ideal state and the better the algorithm performance. In the initial stage, the GA algorithm has the lowest fitness value (0.00157), followed by the GA-ACO algorithm (0.00325), while the ACO algorithm has the highest fitness value (0.02239). The ACO algorithm, due to insufficient pheromone distribution in the initial stage, relies primarily on random search mechanisms, resulting in a higher initial fitness value. In contrast, the GA-ACO algorithm uses intermediate solutions obtained from the GA to initialize the pheromone distribution, resulting in a significantly lower initial fitness value compared to the standalone ACO algorithm. During subsequent iterations, the ACO algorithm converges significantly faster than the GA, due to its faster local convergence capability. The GA-ACO algorithm demonstrates superior convergence speed, achieving a final fitness value lower than that of the GA or ACO algorithms alone, indicating higher optimization efficiency. This characteristic makes it particularly suitable for real-time tourist flow prediction scenarios with high requirements for prediction speed. Specifically, the fitness value after convergence is for the ACO algorithm, for the GA algorithm, and for the GA-ACO algorithm, further validating the synergistic advantages of the GA-ACO algorithm in global search and local optimization.
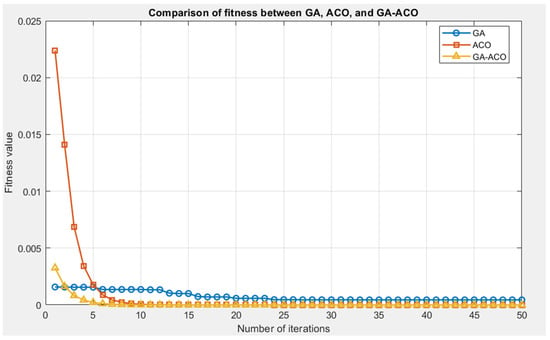
Figure 9.
Fitness comparison diagram for each algorithm.
Figure 10 illustrates the comparison of the mean square error (MSE) changes between the GA-ACO-BP model and the BP model during the training process. The GA-ACO-BP model achieves the best result on the validation set at the 8th iteration in 14 iterations, with an MSE of 0.00025532. In contrast, the BP model achieves the best effect on the validation set at the 20th iteration after 26 iterations, with an MSE of 0.00026964. The results show that the GA-ACO-BP model optimized by GA and ACO algorithms is better than the original BP model in terms of convergence speed and accuracy and is more suitable for tourist flow prediction scenarios that require high real-time performance and accuracy.
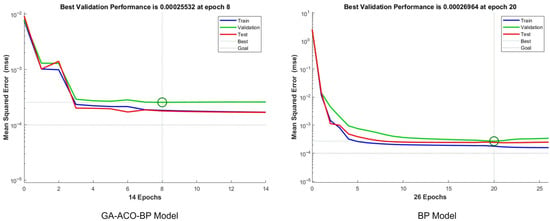
Figure 10.
Comparison of MSE variation during training between GA-ACO-BP and BP models.
4. Discussion
The results of the tourist flow prediction experiment conducted at the Elephant Trunk Hill Scenic Area in Guilin indicate that the GA-ACO-BP model achieved optimal values for key tourist flow prediction metrics such as MAPE, RMSE, MAE, and R2, compared to currently popular prediction models. These values were 4.09%, 426.34, 258.80, and 0.98795, respectively. Compared to the basic BP neural network, the improved GA-ACO-BP model reduced the error metrics MAPE, RMSE, and MAE by 1.12 percentage points, 244.04, and 122.91, respectively, and increased the R2 by 1.85 percentage points. Additionally, the GA and ACO optimization algorithms each have their own advantages in improving the performance of the BP neural network. GA enhances global search capabilities, while ACO improves local convergence speed. The combination of the two significantly improves the training convergence speed and model accuracy of the BP model, making it particularly suitable for tourist flow prediction tasks that require high real-time performance and accuracy.
Although the GA-ACO-BP model has demonstrated good performance in tourist flow prediction, it still has certain limitations. First, the parameter settings of the GA and ACO algorithms mainly rely on human experience and lack an adaptive adjustment mechanism. When applied to datasets with large fluctuations in data scale or obvious differences in feature distribution, we need to manually adjust the parameters according to the specific situation, which will affect the model’s generality and stability. Second, this study used the Guilin Elephant Trunk Hill Scenic Area as a case study for experimentation, and the model’s transferability and universality have not yet been systematically validated in other regions or different types of scenic areas. Future research will focus on the following areas: first, introducing automated hyperparameter optimization methods (such as Bayesian optimization) to enhance the model’s adaptability and generalization capabilities; second, expanding the model’s application scenarios to different geographical regions and multi-type scenic areas to validate its cross-regional predictive performance; and third, integrating more real-time data sources (such as social media dynamics and traffic flow) to enhance the model’s response capabilities to sudden events and complex environments. In addition, confidence intervals and hypothesis testing will be further explored to provide stronger statistical evidence and to more comprehensively assess the robustness of the model.
5. Conclusions
To address the shortcomings of traditional tourist flow prediction models in handling nonlinear features, prediction accuracy, and real-time response, we propose the GA-ACO-BP model to improve the accuracy and real-time response of tourist flow prediction in tourist attractions. First, in addition to historical tourist flow data (such as tourist flow from the previous day, the day before that, and the same period last year), we have introduced multi-dimensional features such as holiday type, climate comfort, and scenic area search index to enhance the model’s ability to perceive changes in visitor travel intentions, thereby improving the applicability and robustness of the prediction. Second, to address the issue of BP neural networks easily getting stuck in local optima, we have employed a genetic algorithm (GA) to optimize the initial weights and thresholds of the network, thereby enhancing its global search capability. Finally, to address the limitation of the GA’s relatively low local convergence efficiency when optimizing BP neural networks, we further introduced the ant colony optimization algorithm (ACO). The GA-ACO-BP model not only improves the accuracy and real-time nature of tourist flow predictions in scenic areas but also provides scientific decision-making support for optimizing scenic area management efficiency, rational resource allocation, and sustainable development of the tourism industry. At the same time, it provides referenceable ideas and methods for nonlinear time series prediction research based on intelligent optimization algorithms.
Author Contributions
Conceptualization, X.Y.; methodology, Y.C.; validation, Y.C.; writing—original draft, Y.C.; writing—review and editing, X.Y.; supervision, X.X. and M.D.; project administration, M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Natural Science Foundation of China (61563012); General Project of Guangxi Natural Science Foundation (2021GXNSFAA220074).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, H.; Wang, Q.; Zhang, L.; Cai, D. Big data in China tourism research: A systematic review of publications from English journals. J. China Tour. Res. 2022, 18, 453–471. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Yang, Y.; Tan, Y.; Geng, T.; Wang, S. Short-and long-term prediction and determinant analysis of tourism flow networks: A novel steady-state Markov chain method. Tour. Manag. 2025, 109, 105139. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Fan, L.; Shi, S.; Zhang, T.; Qi, M. Research on the prediction of dangerous goods accidents during highway transportation based on the ARMA model. J. Loss Prev. Process Ind. 2021, 72, 104583. [Google Scholar] [CrossRef] [PubMed]
- Alabdulrazzaq, H.; Alenezi, M.N.; Rawajfih, Y.; Alghannam, B.A.; Al-Hassan, A.A.; Al-Anzi, F.S. On the accuracy of ARIMA based prediction of COVID-19 spread. Results Phys. 2021, 27, 104509. [Google Scholar] [CrossRef] [PubMed]
- Law, R. Back-propagation learning in improving the accuracy of neural network-based tourism demand forecasting. Tour. Manag. 2000, 21, 331–340. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Li, Y.; Cao, H. Prediction for tourism flow based on LSTM neural network. Procedia Comput. Sci. 2018, 129, 277–283. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Chen, Q.; Li, W.; Zhao, J. The use of LS-SVM for short-term passenger flow prediction. Transport 2011, 26, 5–10. [Google Scholar] [CrossRef]
- Suykens, J.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Liu, L.; Chen, R. A novel passenger flow prediction model using deep learning methods. Transp. Res. Part C Emerg. Technol. 2017, 84, 74–91. [Google Scholar] [CrossRef]
- Sze, V.; Chen, Y.; Yang, T.; Emer, J. Efficient processing of deep neural networks: A tutorial and survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Hu, H.-X.; Hu, Q.; Tan, G.; Zhang, Y.; Lin, Z.-Z. A Multi-Layer Model Based on Transformer and Deep Learning for Traffic Flow Prediction. IEEE Trans. Intell. Transp. Syst. 2023, 25, 443–451. [Google Scholar] [CrossRef]
- Lin, T.; Wang, Y.; Liu, X.; Qiu, X. A Survey of Transformers. AI Open 2022, 3, 111–132. [Google Scholar] [CrossRef]
- Li, K.; Lu, W.; Liang, C.; Wang, B. Intelligence in tourism management: A hybrid FOA-BP method on daily tourism demand forecasting with web search data. Mathematics 2019, 7, 531. [Google Scholar] [CrossRef]
- Pan, Q.; Sang, H.; Duan, J.; Gao, L. An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl.-Based Syst. 2014, 62, 69–83. [Google Scholar] [CrossRef]
- Li, K.; Liang, C.; Lu, W.; Li, C.; Zhao, S.; Wang, B. Forecasting of short-term daily tourist flow based on seasonal clustering method and PSO-LSSVM. ISPRS Int. J. Geo-Inf. 2020, 9, 676. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Wang, K.; Ma, C.; Qiao, Y.; Lu, X.; Hao, W.; Dong, S. A Hybrid Deep Learning Model with 1DCNN-LSTM-Attention Networks for Short-Term Traffic Flow Prediction. Phys. A Stat. Mech. Appl. 2021, 583, 126293. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of Deep Learning: Concepts, CNN Architectures, Challenges, Applications, Future Directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Rui, H.; Liang, C.; Jiang, L.; Zhao, S.; Li, K. A Method Based on GA-CNN-LSTM for Daily Tourist Flow Prediction at Scenic Spots. Entropy 2020, 22, 261. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Siami-Namin, A. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar] [CrossRef]
- Wen, X.; Li, W. Time series prediction based on LSTM-attention-LSTM model. IEEE Access 2023, 11, 48322–48331. [Google Scholar] [CrossRef]
- Adankon, M.; Cheriet, M. Model selection for the LS-SVM. Application to handwriting recognition. Pattern Recognit. 2009, 42, 3264–3270. [Google Scholar] [CrossRef]
- Shahani, N.; Zheng, X. Predicting backbreak due to blasting using LSSVM optimized by metaheuristic algorithms. Environ. Earth Sci. 2025, 84, 156. [Google Scholar] [CrossRef]
- Hu, C.; Zhao, F. Improved methods of BP neural network algorithm and its limitation. In Proceedings of the 2010 International Forum on Information Technology and Applications, Kunming, China, 16–18 July 2010; Volume 1, pp. 11–14. [Google Scholar] [CrossRef]
- Holland, J. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Jiang, C. Research on optimizing multimodal transport path under the schedule limitation based on genetic algorithm. J. Phys. Conf. Ser. 2022, 2258, 012014. [Google Scholar] [CrossRef]
- Beg, A.; Islam, M. Advantages and limitations of genetic algorithms for clustering records. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016; pp. 2478–2483. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2007, 1, 28–39. [Google Scholar] [CrossRef]
- Blum, C. Ant colony optimization: Introduction and recent trends. Phys. Life Rev. 2005, 2, 353–373. [Google Scholar] [CrossRef]
- Yang, J.; Zhuang, Y. An improved ant colony optimization algorithm for solving a complex combinatorial optimization problem. Appl. Soft Comput. 2010, 10, 653–660. [Google Scholar] [CrossRef]
- Panda, S.; Panda, G. Performance evaluation of a new BP algorithm for a modified artificial neural network. Neural Process. Lett. 2020, 51, 1869–1889. [Google Scholar] [CrossRef]
- Huang, G.; Zhu, Q.; Siew, C. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, N.; Feng, Y.; Gong, D.; Hu, X. Comparison of BP, PSO-BP and statistical models for predicting daily global solar radiation in arid Northwest China. Comput. Electron. Agric. 2019, 164, 104905. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).