A Reverse Design Method for Convective PCR Chips Featuring Precise Control of Steady-State Flow Fields

Abstract

Convective Polymerase Chain Reaction (cPCR), owing to its enhanced thermal cycling efficiency, holds promise for application in the next generation of mainstream commercial PCR instruments. Despite its potential, existing capillary-based and annular reaction chamber designs encounter limitations in precisely controlling the internal flow field, which poses a significant barrier to the progression of cPCR. To overcome these obstacles, this work innovatively proposes a cPCR chip utilizing a “racetrack-shaped” reaction chamber, along with a reverse design approach tailored to meet diverse reaction requirements. Through modeling and simulation, we accurately obtained the relationship between the design parameters and the average flow velocity of the cPCR chip with a “racetrack-shaped” reaction chamber. By capturing the motion of fluorescent particles using a high-speed camera, we acquired the velocity distribution of the actual flow field. Further, we utilized these relationships to conduct a reverse design. Ultimately, a reaction chamber was designed based on the actual amplification needs of 2019-nCoV and hepatitis B virus, and successful amplification was achieved using a self-developed temperature control platform.

1. Introduction

Rayleigh–Bénard convection is a physical principle that describes the convection phenomenon in a fluid driven by a temperature gradient. When the temperature increases, the density of the fluid decreases, which imparts additional buoyancy, causing it to rise; conversely, fluids descend as their temperature drops [1]. Convection occurs due to changes in buoyancy and viscous forces, with the relationship between them described by the dimensionless Rayleigh number Ra [2,3],

$$Ra={\displaystyle \frac{g\alpha ∆T{d}^3}{v{D}_T}}.$$

(1)

wherein $g$ is gravitational acceleration, $\alpha$ is thermal expansivity, $d$ is geometric characteristic length, $v$ is kinematic viscosity, and $D_T$ is thermal diffusivity. Equation (1) reveals that when the temperature difference $∆T$ reaches a sufficient magnitude, natural thermal convection will be spontaneously triggered.

Rayleigh–Bénard convection is highly suited for biochemical reactions requiring continuous cycling between two temperatures. A prime application exploits its characteristics of temperature gradients, spontaneous occurrence, and the ability to form stable flow fields to create reaction chambers for PCR (Polymerase Chain Reaction). Convective PCR (cPCR) was initially proposed in 2002 and validated in a capillary tube heated from the bottom to 95 °C [4]. In 2003, Braun et al. suggested that laminar thermal convection could drive the cascade reactions involved in DNA replication [5]. In 2011, Lee et al. used cellphone cameras for DNA detection [6]. Furthermore, in 2013, Yang et al. developed a prototype cPCR reactor using capillary tubes [7]. Due to its unique features, cPCR often demonstrates superior performance advantages in applications, such as reducing reaction time, enhancing efficiency, simplifying procedures, and lowering costs [8,9,10,11,12,13,14].

However, the capillary-based reaction chambers frequently employed in cPCR exhibit at least two critical drawbacks. Firstly, the Rayleigh–Bénard thermal convection generated by heating the capillary from both ends results in the presence of a “dead zone” (with minimal flow velocity) in the middle section of the capillary, where the solution in dead zones will not participate the cycling, resulting in reduced amplification and severely affecting the reaction efficiency. Secondly, capillary-based convection has a limited ability to regulate flow rates in the capillary-based reaction chamber, where such a regulation can only be achieved by adjusting the aspect ratio—specifically, d in Equation (1). This significantly limits the editability of the flow field. To tackle these drawbacks, annular reaction chambers have been proposed. Compared to capillary-shaped reaction chambers, these chambers offer faster speeds and more portable equipment [15,16,17,18]. Earlier attempts were innovative in both structure and function. In 2004, Wheeler et al. designed a low-cost, disposable cPCR thermal chamber, achieving a significant breakthrough in efficiency compared to previous efforts [19]. In 2021, Khodakov et al. introduced a convection-based PCR device with a “doughnut”-shaped reaction chamber, which, combined with pre-quenched DNA microarray, demonstrated great potential for point-of-care diagnostics [17]. Unfortunately, these studies did not further analyze the internal flow field of the reaction chamber, and the final outcomes only included a single reaction chamber design. Due to the diversity of PCR reagents (such as DNA molecule chain length, enzyme activity, and reaction system volume), the optimal reaction conditions for efficient amplification vary. Using only one type of reaction chamber to meet all needs makes it urgent to customize different reaction chambers for different reaction conditions.

To achieve a more versatile and rapid application of the Rayleigh–Bénard convection phenomenon in PCR, a “racetrack-shaped” microfluidic chip tailored for convective PCR is introduced here, as shown in Figure 1. Distinct from the top-and-bottom heating approach used in capillary-based reaction chambers, this microfluidic chip utilizes lateral heating to drive the reaction chamber. The reaction channel creates a steady circular flow over 40 s, which triggers the amplification cycle. Unlike most annular reaction chamber designs, the “racetrack-shaped” chamber allows for adjustments to design parameters such as the vertical length of the reaction chamber L, inner ring width of the reaction chamber h, and channel width of the reaction chamber d, enabling effective control over fluid velocity within the microchannel. Furthermore, we model the convection by analyzing the energy characteristics of the steady-state circular flow, and establish the relationship between the design parameters and the fluid velocity. We constructed a temperature control platform, utilizing computer simulations and high-speed cameras to obtain the theoretical average flow velocity and the actual average flow velocity within the reaction chamber, thereby verifying the accuracy of the proposed relationship between target average flow velocity and design parameters. Based on such a relationship, we determined a unique set of racetrack-shaped reaction chamber parameters for 2019-nCoV and hepatitis B virus. Using the reaction chamber and temperature control platform fabricated with these parameters, high-efficiency DNA replication is demonstrated.

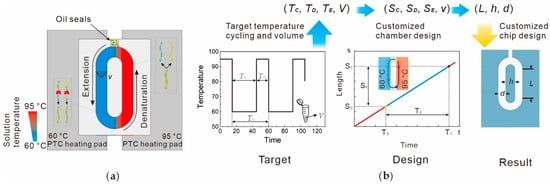
Figure 1. Principle and design of the “racetrack-shaped” cPCR chip. (a) Core principle of the microfluidic chip. After the PCR mixture is loaded into the “racetrack-shaped” chip, passive fluid flow is generated based on Rayleigh–Bénard convection. The temperatures of the left and right heating plates are set to 60 °C and 95 °C, respectively. DNA molecules undergo the extension and annealing processes in these two temperature zones. (b) Design steps for customizing the chip. Firstly, determine the denaturation time ($T_D$), extension time ($T_E$), cycle period ($T_C$), and sample volume (V) required for the target PCR reaction according to the reagent instructions. Subsequently, select the design parameters L, h, and d and the average flow velocity v based on the above requirements. Finally, fabricate the cPCR chip using the selected design parameters.

2. Materials and Methods

2.1. Modeling

In a cPCR operation under a constant temperature system ranging from 60 °C to 95 °C, the fluid within the reaction chamber undergoes two distinct phases: an initial accelerated turbulent flow followed by a steady-state laminar flow. The latter phase, characterized by a stable and uniform flow velocity, is typically the focus of attention for two primary reasons. Firstly, the acceleration phase, occurring within small-scale reaction chambers, is inherently transient, lasting for no longer than 10 s in experimental observations. Secondly, during the steady-state laminar flow phase, the flow field exhibits orderliness and stability, which favors repetitive temperature cycling of the fluid. This phase plays a pivotal role in the overall reaction efficiency, as it facilitates the primary working part of the process.

As illustrated in Figure 2, during the stable cycling phase of the reaction chamber, there are primarily three regions: region $A_H$, in direct contact with the high-temperature heating pad; region $A_L$, in direct contact with the low-temperature heating pad; and region $A_C$, where convection with air occurs. The liquid maintains a lower temperature in regions $A_L$ and $A_C$ to complete the annealing and extension steps, while in region $A_H$, it maintains a high temperature to complete the denaturation step. Therefore, within one cycle, the residence time of the liquid in region $A_H$ is defined as $T_D$, and the residence time in regions $A_L$ and $A_C$ is defined as $T_E$. Correspondingly, the characteristic length of region $A_H$ is defined as $S_D$, and the characteristic length of regions $A_L$ and $A_C$ is defined as $S_E$.

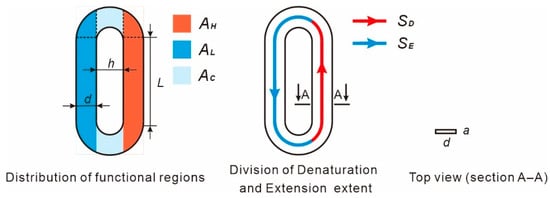
Figure 2. The functional region distribution within the reaction chamber, the characteristic lengths of the high- and low-temperature zones, and the cross-sectional shape of the reaction chamber.

During the stable cycling phase, an analysis of the fluid within the reaction chamber reveals that the fluid absorbs heat from its surroundings and performs work by overcoming the viscous forces within the boundary layer of the flow channel, thereby maintaining its velocity. Consequently, we can derive the following formula:

$$Q_{∆t}+E_{hf}=0.$$

(2)

In this equation, $Q_{∆T}$ represents the net input heat from the external environment, and $E_{hf}$ denotes the energy loss along the flow path within the channel. Given the conditions of minimal heat loss after system stabilization, and the incompressible and uniform flow of the liquid within the channel, Fourier’s law is utilized to calculate the heat transferred from the external environment:

$$Q=-{\lambda }_{q}A{\displaystyle \frac{dT}{d{x}^{\prime }}}$$

(3)

where $Q$ is the heat flow (W), ${\lambda }_q$ is the thermal conductivity coefficient (W/m·K), ${\displaystyle \frac{dT}{dx}}$ represents the temperature gradient (K/m), and $A$ is the contact cross-sectional area (m²). It is particularly noted that, due to the characteristics of the “racetrack-shaped” reaction chamber structure, during the calculation of the area of functional zones and the characteristic lengths of the heating zones, we further subdivided the zones and conducted approximate calculations. Specifically, as illustrated in the zone distribution diagram in Figure 2, the arcuate portion of the “racetrack-shaped” structure is divided into three parts. The two sector-shaped zones distributed in regions $A_H$ and $A_L$ are approximated as one-quarter circles with a radius of d. Therefore, the area of these two sector-shaped regions is calculated as $0.25\pi d^2$, and the characteristic length is calculated as $0.25\pi d$. Similarly, for the part distributed in $A_C$, the characteristic length used for calculation is h, with a width of d. For a “racetrack-shaped” reaction chamber, the contact area refers to the region where the reaction chamber directly interfaces with the heating plate, specifically,

$$A_H=A_L=dL+0.5\pi d^2,$$

(4)

wherein $A_H$ (m²) and $A_L$ (m²) represent the contact areas of the high-temperature heating plate and of the low-temperature heating plate, respectively. The Darcy–Weisbach equation is employed to calculate the energy loss of the fluid as it flows through the rectangular flow channel:

$$h_f={\lambda }_f{\displaystyle \frac{L_f{v}^2}{2d_f{g}^{\prime }}}$$

(5)

where $h_f$ is the head loss (m), ${\lambda }_f$ is the friction coefficient, $L_f$ is the characteristic length of the piping (m), $v$ is the average flow velocity (m/s), $d_f$ is the hydraulic diameter (m), and $g$ is the gravitational acceleration. For an annular reaction chamber, the length of the piping corresponds to the geometric circumference of one full revolution around the chamber, referring to the aforementioned method of approximate calculation:

$$L_f=S_D+S_E=2L+2h+\pi d,$$

(6)

where $S_D$ (m) and $S_E$ (m) represent the characteristic lengths of the denaturation zone and the extension zone, respectively. Additionally, since the actual cross-section of the reaction chamber is rectangular, with $a$ (m) and $d$ (m) denoting the length and width of the rectangular flow channel cross-section, respectively, and referring to the cross-sectional view in Figure 2, the hydraulic diameter $d_f$ (m) can be calculated as:

$$d_f={\displaystyle \frac{4ad}{2(a+d)}}.$$

(7)

Within a very short period of time $∆t$ (s), energy $Q_{∆T}$ (J) and $E_{hf}$ (J) are calculated using a variant of Fourier’s law and the Darcy–Weisbach equation, respectively:

$$Q_{∆T}=Q∆t,$$

(8)

$$E_{hf}=h_{f}g∆m,$$

(9)

$$∆m=ad\rho v∆t.$$

(10)

Solve for the average flow velocity $v$ (mm/s) by combining Equations (2)–(10):

$$v=\sqrt[3]{{\displaystyle \frac{2\left(2dL+\pi d^2\right){\lambda }_q}{\left(a+d\right)\left(2L+2h+\pi d\right){\lambda }_f\rho }}{\displaystyle \frac{dT}{dx}}}\times {10}^3.$$

(11)

In the equation, $a$, ${\lambda }_q$, ${\lambda }_f$, $\rho$ (kg/m³), and ${\displaystyle \frac{dT}{dx}}$ are all constants, while the design parameters $L$ (m), $d$, and $h$ (m) are variables. It is evident that the relationship between the average flow velocity and the design parameters is complex and nonlinear, posing difficulties in our analysis process. Therefore, to facilitate subsequent data processing and inverse design, we separate the constants and variables and decompose the right-hand side of the equation into two terms: a constant $c$ and a geometric parameter $x$, resulting in:

$$c=\sqrt[3]{{\displaystyle \frac{2{\lambda }_q}{{\lambda }_f\rho }}{\displaystyle \frac{dT}{dx}}}\times {10}^3,$$

(12)

$$x=\sqrt[3]{{\displaystyle \frac{2dL+\pi d^2}{\left(a+d\right)\left(2L+2h+\pi d\right)}}}.$$

(13)

Combine Equations (11)–(13):

$$v=cx.$$

(14)

In the equation, $v$ represents the characteristic average flow velocity within the reaction chamber, while x is an independent variable. Consequently, the relationship between the velocity and the design parameters $L$, $d$, and $h$ can be ultimately derived. After the above processing, only the fitting of $v$ and $x$ is required, and obtaining the slope of the directly proportional curve can accurately correspond to the relationship between the average flow velocity and the design parameters. In Section 3, we carried out the fitting work. Since x is a dimensionless number, the units for $L$, $d$, and $h$ in the subsequent text are all in millimeters (mm).

2.2. Chip Fabrication and Temperature Control Platform

Figure 3 illustrates the fabrication method of the “racetrack-shaped” microfluidic chip. The microfluidic chip is assembled in a “sandwich” configuration, consisting of two coverslips and an intermediate polymer spacer. The polymer spacer is constructed by stacking six layers of medical tape (3M 9965), resulting in a uniform thickness of 0.55 mm. In Section 2.1, it is mentioned that $a$ represents the length of the rectangular channel in the reaction chamber; thus, $a$ here is equal to the thickness of the polymer layer, which is 0.55 mm. The adoption of ultra-white glass coverslips with a thickness of merely 0.15 mm ensures both clarity for flow field observation and enhanced heat transfer efficiency. The contour of the polymer layer of the cPCR chip consists of a “racetrack-shaped” reaction chamber (as Figure 2) and an injection channel on top. The geometric contours of the chamber are achieved through laser cutting of the polymer layer using a Huagong Laser LSU5EI. In addition to the primary reaction chamber, an injection channel for introducing reactants is designed on top of the polymer layer of the microfluidic chip. The injection channel connects the reaction chamber to the external environment, and adding paraffin oil into the injection channel can achieve a sealing effect during the heating process.

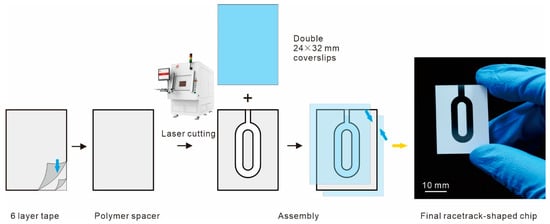
Figure 3. Fabrication of the “sandwich-structured” microfluidic chip. Initially, a polymer layer is obtained by stacking six layers of 3M 9965 medical tape. The polymer layer is then laser-cut to create reaction chamber contours with different design parameters (L, h, d). Two coverslips are adhered to the upper and lower surfaces of the polymer layer and pressed tightly to obtain the microfluidic chip.

One of the most critical aspects of PCR reaction is temperature control. One of the key challenges is how to make the temperature control system more stable and reliable [20]. Figure 4 illustrates the temperature control platform and its electrical diagram for the temperature controller. The two positive temperature coefficient (PTC) heating pads of the temperature control platform are arranged vertically, maintaining stable operating temperatures of 95 °C and 60 °C during the heating process. Our temperature control platform mainly consists of heating pads, temperature sensors, solid-state relays, a data acquisition module, and a control board. Both PTC heating pads are powered by a 12 V power supply. The surface of each heating pad is covered with a 1.5 mm-thick aluminum plate to ensure uniform temperature distribution during the heating process. Two thermocouple temperature sensors are respectively placed on the surfaces of the heating plates, and a data acquisition module is responsible for transmitting the temperature information fed back by the sensors to the control board. The control board adjusts the heating power of the heating pads through solid-state relays.

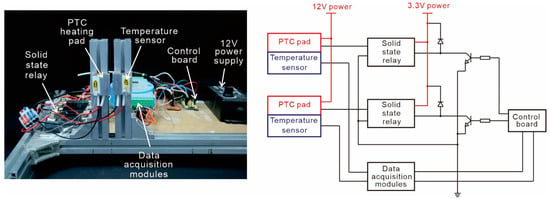
Figure 4. The temperature control platform and electrical diagram for the temperature controller.

The heating pads employ a dual-stage PID control algorithm, enabling it to reach a stable state within 40 s of activation. The point when the heating plate temperature is 10 °C away from the target temperature serves as a turning point in the temperature control program, which is shown in Figure 5 as point A and point B. The PID parameters before and after this turning point are different, ensuring that the heating time is shortened and the heating efficiency is improved without causing temperature overshoot. As illustrated by the kinetic traces depicted in Figure 5, the temperatures of both heating pads can be stably maintained at the preset values within 40 s. Thermal conductive tape is adhered to the backside of the microfluidic chip loaded with reaction fluids, ensuring that during operation, the chip is tightly pressed against the vertical surface of the heating plates, automatically initiating thermal convection. The status of the temperature control platform during its heating process is displayed in Figure 5. Through the temperature kinetic traces and thermal imaging, we can confirm that the temperatures of both heating pads precisely remain at the preset values and remain constant during operation.

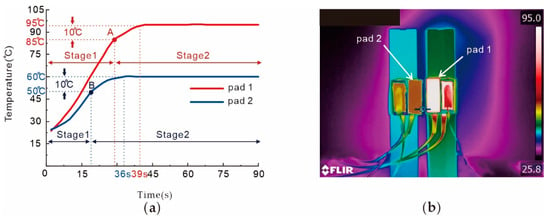
Figure 5. Control method for the temperature control platform and the actual temperature control effect. (a) Kinetic traces of the heating pads and the turning point of the dual-stage PID control algorithm. The turning points A and B, as well as the stages 1 and 2 divided by the turning points, are marked in the figure; (b) temperature distribution of the temperature control platform during the operational state. Photo was taken via a thermal imaging camera (FLIR T630SC).

2.3. Loading Process and Observation Method

Figure 6 illustrates the entire process of loading reagents onto the “racetrack-shaped” convective PCR chip. The chip consists of two main parts: an injection channel and a reaction chamber. It operates with single-sided heating, which is consistent with the simulation conditions. Due to the chip’s minimal thickness, we use a syringe needle with a diameter of 0.3 mm to quantitatively extract the reaction solution during reagent addition. Additionally, the inner walls of the reaction chambers, which have been laser-cut, are extremely smooth, effectively minimizing the potential for air bubbles to remain during the loading process. The paraffin oil used for the oil seal during the experiment has a melting point of −24 °C, a boiling point of 300 °C, and a density ranging from 0.827 to 0.890 g/mL. It is insoluble in water and biologically inert, allowing for safe and effective sealing of the reaction solution during the experimental process. To ensure accurate temperature control on both sides of the reaction chambers, we use thermally conductive tape to adhere the chip to the heating pads, preventing any air layers between them that could cause deviations in the actual temperature gradient within the reaction chambers compared to the simulated conditions. During the amplification experiment, loading is completed first, and switching on the temperature control platform is considered the start of the reaction. Simultaneously, the fluorescence intensity within the chip is collected in real time.

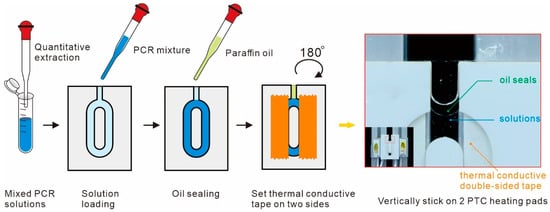
Figure 6. Loading process of convective PCR reaction. Firstly, the PCR solutions are mixed uniformly and fill the reaction chamber. Subsequently, paraffin oil is injected into the injection channel to complete the oil seal. After that, thermally conductive tape is attached to the backside of the chip. Finally, it is adhered to the PTC heating plate to initiate the cycling process.

To observe the actual flow velocity, we set up an observation system consisting of a high-speed camera (Ultrahigh-Speed Camera v1212, Phantom Inc., Wayne, NJ 07470, USA) equipped with an optical filter and a 470 nm blue light source (20 W). The high-speed camera is horizontally arranged and aligned to record videos of the front side of the chip. When measuring the actual flow velocity in the flow field, the solution containing fluorescent particles (13 μm) is first loaded into the reaction chamber and heating is initiated. Meanwhile, the high-speed camera records the movement of the particles in the reaction chamber. After the recording is completed, with the help of PCC software (Phantom Camera Control 3.9.40), we can analyze the displacement of the particles between adjacent frames and calculate the velocity of each particle accordingly. The overview of the whole system is shown in Figure 7.

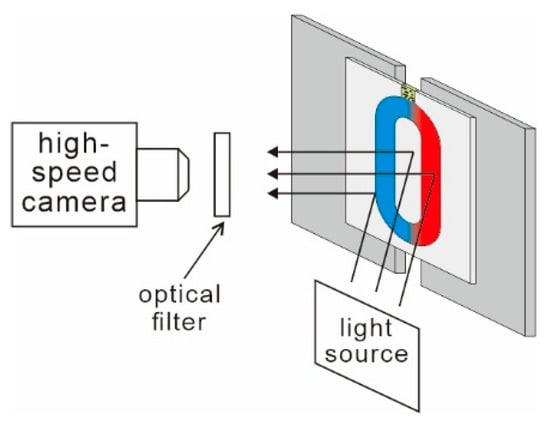
Figure 7. Overview of the observation system. The observation system includes a high-speed camera with an optical filter and a light source.

2.4. Simulation

Simulations were conducted using the Fluent module of ANSYS 19.2. The reactant fluid was modeled as an incompressible fluid and given the minimal temperature difference during operation (approximately 35 °C); the Boussinesq approximation was applied to initialize the fluid. Since the primary focus was on the constant-velocity circulation phase, simulations were computed and the average flow velocity after the system reached a steady state was recorded.

2.5. Reagents

In the experiment, various reagent kits were utilized for nucleic acid amplification, with their information presented as follows:

• For 2019-nCoV:

The 2019-nCoV one-step PCR reagent kit (Catalog No. 24009-2) was obtained from Sansure Biotech Inc. (Changsha, China). Each test requires 50 µL of reagent. This kit is designed for the detection of 2019-nCoV-specific polynucleotides using TaqMan fluorescent probe-based PCR technology. The probe, upstream primer, and downstream primer for the ORF1ab gene of the 2019-nCoV virus are labeled SEQ No. 1, SEQ No. 2, and SEQ No. 3, respectively. The probe, upstream primer, and downstream primer for the N gene of the 2019-nCoV virus are labeled SEQ No. 4, SEQ No. 5, and SEQ No. 6, respectively.

SEQ No. 1: 5′-ATAGTGAACCGCCACACATGACCA-3′;

SEQ No. 2: 5′-TGTAGCTTGTCACACCGTTT-3′;

SEQ No. 3: 5′-ATTAGCATAAGCAGTTGTGGCAT-3′.

SEQ No. 4: 5′-CTACTACCGAAGAGCTACCAGACGAA-3′;

SEQ No. 5: 5′-CTCACTCAACATGGCAAGG-3′;

SEQ No. 6: 5′-ACTGAGATCTTTCATTTTACCGTCAC-3′.

Each test solution set (50 µL) also includes Mg²⁺ (4 mM), dNTPs (0.25 mM), MMLV (10 U), and Taq polymerase (5 U).

• For Hepatitis B Virus:

The hepatitis B virus (HBV) one-step PCR reagent kit (Catalog No. 24009-2) was obtained from Sansure Biotech Inc. (Changsha, China). Each test requires 50 µL of reagent. This kit is designed for the detection of HBV-specific polynucleotides using TaqMan fluorescent probe-based PCR technology. The probe, upstream primer, and downstream primer for the S gene of the HBV are labeled SEQ No. 7, SEQ No. 8, and SEQ No. 9, respectively.

SEQ No. 7: 5′-CCTCTTCATCCTGCTGCTATGCCTCATCTTCTTATTGG-3′;

SEQ No. 8: 5′-ATCGCTGGATGTGTCTGCTGCGTTTT-3′;

SEQ No. 9: 5′-CTGGAATTAGAGGACAAACGGGCAACAT-3′.

Each test solution set (50 µL) also includes Mg2+ (4 mM), dNTPs (0.25 mM), UNG polymerase (1 U), and Taq polymerase (5 U).

3. Results

By adjusting the shape of the reaction chamber, the flow rate of the internal fluid can be regulated [21]. By varying the design parameters L, d, and h, 30 sets of reaction chambers were fabricated. After each microfluidic chip attained stable circulation, fluorescent particles were randomly selected for velocity measurements, yielding the actual average flow velocity corresponding to the respective geometric profile. The simulation result, the fluorescent particle velocimetry, and the particle velocity distribution are shown in Figure 8a. The experimentally obtained actual flow velocities and the theoretically simulated flow velocities are compiled in Figure 8b.

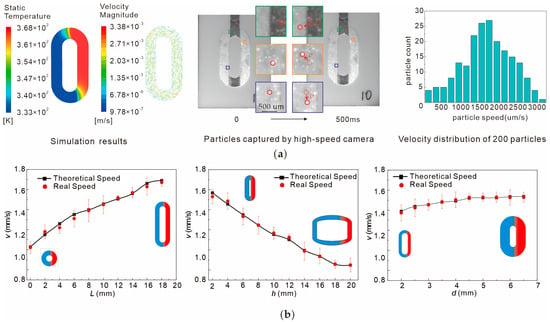
Figure 8. Measurement methodology for average flow velocity and comparison of theoretical and real average flow velocity results. (a) Simulation temperature contour, flow field distribution diagram, particle velocimetry method and local enlarged view (with tracked particles indicated by red circles), and particle velocity distribution for the reaction chamber with design parameters L = 10 mm, h = 4 mm, d = 3 mm. (b) Theoretical and actual flow rates with design parameters L ranging from 0 to 18 mm (with h = 4 mm, d = 3 mm remaining constant and unchanging), h ranging from 2 to 20 mm (with L = 10 mm, d = 3 mm remaining constant and unchanging), and d ranging from 2 to 6.5 mm (with L = 10 mm, h = 4 mm remaining constant and unchanging). L = 0, L = 18 mm, h = 2 mm, h = 20 mm, d = 2 mm, and d = 6.5 mm are demonstrated.

Figure 8 shows that the theoretically simulated flow rates are in close proximity to the experimentally measured flow rates. Geometric parameter $x$ was set as in Equation (13). Simulated flow velocities and x were substituted to obtain the fitting curve, through which the constant parameter c was calculated as 1.65468 ± 0.0473. Furthermore, the coefficient of determination (R²) for the fitted curve was 0.9927, which hints at a highly linear relationship between geometric parameter x and real average flow velocity v. The fitting results are presented in Figure 9.

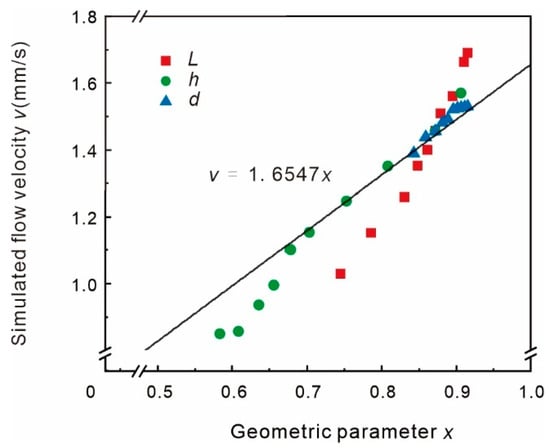
Figure 9. Fitting curve of geometric parameter x versus theoretical flow rate v.

4. Discussion

4.1. Reverse Design Methodologies

To perform reverse design on the reaction chamber, the first step involves correlating the temperature cycle time T with the characteristic length S of different zones within the reaction chamber, leading to the following equations:

$${\displaystyle \frac{S_E}{S_D}}={\displaystyle \frac{T_E}{T_D}},$$

(15)

$$S_E+S_D=S_C,$$

(16)

$$T_E+T_D=T_C,$$

(17)

where $T_E$, $T_D$, and $T_C$ represent the annealing time, extension time, and total cycle time, respectively; while $S_E$, $S_D$, and $S_C$ represent the characteristic length of the high-temperature zone, low-temperature zone, and overall reaction chamber, respectively. Referring to the method of approximate calculation mentioned in Section 2.1, we correlate the characteristic length S with design parameters L, h, and d, resulting in the following equations:

$$S_E=L+2h+0.5\pi d,$$

(18)

$$S_D=L+0.5\pi d.$$

(19)

Using data and expression methods in previous experiments,

$$\left\{\begin{array}{c}x=\sqrt[3]{{\displaystyle \frac{2dL+\pi d^2}{\left(a+d\right)\left(2L+2h+\pi d\right)}}}\\ a=0.55\\ c=1.65468\\ v=cx\end{array}.\right.$$

(20)

In specific application scenarios, the reaction conditions vary in different PCR experiments. When conducting the reverse design of the “racetrack-shaped” convection PCR chip for specific targets, we have Equation (21):

$$\left\{\begin{array}{c}{T}_C={\displaystyle \frac{S_c}{v}}\\ {\displaystyle \frac{T_D}{T_E}}={\displaystyle \frac{S_D}{S_E}}\\ V=a(A_H+A_L+A_C)\end{array}\right..$$

(21)

By setting different target V, $T_D$, and $T_E$ and substituting them into Equations (15)–(21) for solving, we can obtain the design parameters L, h, and d of the reaction chambers corresponding to these target conditions. Using this method, we have conducted seven sets of reverse designs for seven specific reaction requirements, and the results are shown in Table 1. The relative errors between the real average flow velocities of these seven reverse designs and the calculated flow velocities are also presented there.

Table 1. Reverse designs and errors for seven PCR reactions with different conditions.

No.	Target V (μL)	Target ${\mathit{T}}_{\mathit{D}}$(s)	Target ${\mathit{T}}_{\mathit{E}}$(s)	Designed L (mm)	Designed h (mm)	Designed d (mm)	Calculated v (mm/s)	Real v (mm/s)	Relative Error δ
1	50	15	30	17.11	9.77	1.55	1.30	1.28	1.53%
2	75	15	30	16.56	10.05	2.26	1.34	1.33	0.74%
3	100	15	30	15.77	10.21	2.97	1.36	1.39	2.21%
4	50	8	22	6.19	8.75	2.42	1.25	1.27	1.60%
5	50	10	20	9.86	6.70	2.26	1.34	1.37	2.24%
6	50	12	18	13.68	4.25	2.14	1.42	1.40	1.41%
7	50	14	16	17.65	1.49	2.04	1.49	1.45	2.68%

4.2. Analysis of PCR Amplification Results

In the first set of experiments, we used a lower concentration of 2019-nCoV reagents (8 × 10⁴ IU/mL) to explore the importance of the rational design of reaction chamber shapes for convective PCR. According to the manufacturer’s instructions, for rapid PCR, the heating program is typically set to cycles of 10 s at 95 °C followed by 20 s at 60 °C. The highest reaction efficiency can only be achieved under this temperature-cycling protocol. Variations in the shape of the reaction chambers directly influence the temperature-cycling protocol of convective PCR, thereby affecting the efficiency of DNA amplification.

In this experiment, we conducted a reverse design based on the temperature-cycling protocol recommended in the instructions and obtained the design parameters for the fifth group of reaction chambers shown in Table 1. While ensuring that the reaction cycle time remained unchanged, we also randomly designed two additional reaction chambers to simulate design parameters that were not optimized through reverse design, as shown in the sixth and seventh groups in Table 1. The design parameters of the sixth and seventh groups differed significantly from those of the fifth group obtained through reverse design. After calculation, we obtained the $T_D$ and $T_E$ values for the sixth and seventh groups, which are also presented in Table 1. We conducted amplification experiments using the reaction chambers of these three groups. Subsequently, we performed amplification experiments using a PCR machine according to the temperature-cycling protocols of the fifth, sixth, and seventh groups as controls. These three reverse designs are referred to as Convective A (V = 50 μL, $T_D$ = 10 s, $T_E$ = 20 s), Convective B (V = 50 μL, $T_D$ = 12 s, $T_E$ = 18 s), and Convective C (V = 50 μL, $T_D$ = 14 s, $T_E$ = 16 s), respectively. Correspondingly, three experiments were designed using a commercial PCR instrument with the same temperature-cycling protocol as controls, named Commercial A (V = 50 μL, $T_D$ = 10 s, $T_E$ = 20 s), Commercial B (V = 50 μL, $T_D$ = 12 s, $T_E$ = 18 s), and Commercial C (V = 50 μL, $T_D$ = 14 s, $T_E$ = 16 s), respectively.

Specifically, we also established a group named Test. The Test group utilized the same reagents and temperature protocol as Commercial A, and was deployed in the commercial PCR instrument for amplification. However, unlike the Commercial A group, for the Test group, the reagents were first injected into our cPCR chip and allowed to sit at room temperature for 30 min. After this period, the reaction mixture was extracted from the chip using a syringe and then amplified using the commercial PCR instrument. The purpose of setting up this experimental group was to investigate whether the surface of the reaction chamber had any impact on the biomolecules within the reagents.

In this experiment, the fluorescence intensity of the FAM channel (performing detection on the 2019-nCoV OFR1ab gene) was collected. In the real-time fluorescent quantitative PCR method, the fluorescence intensity serves as an indicator of the number of amplified target DNA molecules in the solution. In general, the intensity of the fluorescent signal in a successful PCR experiment typically initiates from a nearly horizontal baseline, undergoes an exponential growth phase and a linear growth phase, and ultimately stabilizes during the plateau phase, ultimately exhibiting an “S”-shaped curve. The duration required for the resultant “S”-shaped curve to reach the plateau phase reflects the amplification rate, whereas the fluorescence intensity during the plateau phase represents the quantity of the finally obtained DNA molecules. The results of the first experiment are shown in Figure 10; the convection cycle number is obtained by dividing the heating time by $T_C$.

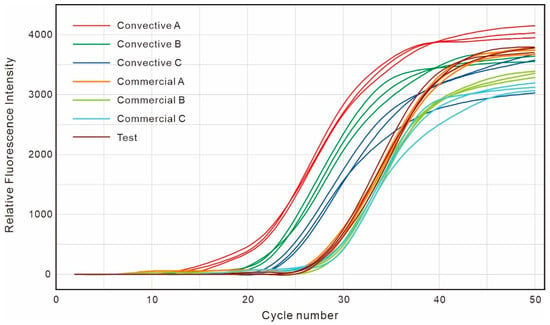
Figure 10. Fluorescence intensity during DNA amplification of 2019-nCoV using a commercial PCR instrument (NextPcr, Sansure Biotech Inc.) and the “racetrack-shaped” convective PCR chip. Cycle time were all set to 30 s.

The first experiment demonstrates that convective PCR is more sensitive to temperature cycling compared to commercial PCR, and blindly designing the reaction chamber can significantly affect experimental efficiency and consistency. Moreover, when adhering to the optimal temperature-cycling protocol specified in the instructions, the reaction velocity of Convective A exceeds that of Convective B and Convective C. The same pattern was observed in both our convective PCR and commercial PCR systems. Deviation from the optimal temperature cycling protocol specified in the instructions leads to a decrease in the final number of amplified DNA molecules, manifesting as a reduction in the maximum fluorescence intensity of the “S”-shaped curve depicted in Figure 9. An optimal reaction chamber design obtained through reverse design tailored to specific reactions is necessary to ensure amplification efficiency. Furthermore, the curves of the Test group and Commercial A are very close, almost overlapping, indicating that the material of the reaction chamber itself does not affect the activity of the biomolecules in the solution.

Furthermore, to validate the sensitivity, consistency, reproducibility, reliability, and robustness of the convective PCR instrument, we conducted amplification experiments using HBV at different concentration gradients. According to the instruction manual, the amplification temperature-cycling protocol for HBV reagents with a 50 μL reaction volume includes a denaturation time of 15 s and an extension and annealing time of 30 s per cycle, i.e., V = 50 μL, $T_D$ = 15 s, and $T_E$ = 30 s. Based on these target parameters, reverse design was conducted, and the design parameters were calculated as L = 17.11 mm, h = 9.77 mm, and d = 1.55 mm, corresponding to the first group of designs in Table 1. The reagents were divided into four concentration groups: A (4 × 10⁷ IU/mL), B (4 × 10⁶ IU/mL), C (4 × 10⁵ IU/mL), and D (4 × 10⁴ IU/mL), with three experiments conducted for each concentration. The fluorescence intensity of the ROX (performing detection on the HBV S gene) channel for convective PCR and commercial PCR at the four different concentrations were collected and are plotted in Figure 11. The analysis results of their $C_t$ values and absolute differences $\delta$ are presented in Table 2.

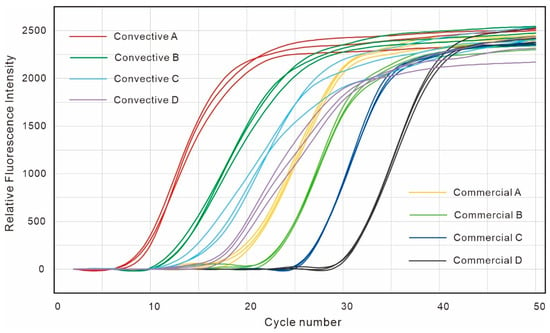
Figure 11. Fluorescence intensity during DNA amplification of HBV using a commercial PCR instrument (NextPcr, Sansure Biotech Inc.) and the “racetrack-shaped” convective PCR chip. Cycle time were all set to 45 s.

Table 2. Average cycle threshold and absolute differences in HBV PCR test performance.

	Convective A	Convective B	Convective C	Convective D	Commercial A	Commercial B	Commercial C	Commercial D
${\mathit{C}}_{\mathit{t}}$	9.82	13.04	16.23	20.10	20.25	23.96	27.41	30.88
$\mathsf{\delta }$	0.53	0.39	1.02	0.81	0.60	0.14	0.08	0.19

Upon comparison, it can be observed that when using the “racetrack-shaped” reaction chamber chip obtained through our precise customize reverse design, our convective PCR demonstrated significant improvement in reaction time compared to commercial PCR instruments. In reactions at any concentration, convective PCR completed amplification approximately 10 cycles (which is 450 s in this experiment) earlier than commercial PCR.

Prior research has demonstrated that the adoption of novel heating strategies in microfluidic PCR often leads to a substantial reduction in PCR amplification time [22,23]. Notably, the reaction velocities of all our “racetrack-shaped” cPCR chips exceeded those observed in commercial PCR instruments. This discrepancy is presumed to stem from the fact that cPCR achieves thermal cycling without the need for repeated changes in the temperature of the heating pads, thereby saving significant time compared to traditional commercial PCR instruments that require extensive temperature adjustment periods for both heating and cooling. This underscores the pivotal role of our reverse design method in achieving the highest reaction efficiency.

5. Conclusions

Contrary to existing convection-based PCR reaction chamber strategies, we have developed, analyzed, and tested an editable microfluidic chip featuring a ring-shaped reaction chamber with configurable geometric contours. Akin to other convection PCR reaction chamber chips, the racetrack-shaped microfluidic chip leverages the Rayleigh–Bénard thermal convection principle, enabling high thermal cycling efficiency, reducing the amplification time by 10 cycles. A vertical convection PCR temperature control platform was developed, upon which both experiments for measuring the average flow velocity in the flow field and DNA amplification experiments were successfully conducted. Furthermore, using the equations, we conducted multiple reverse designs tailored to different target reaction conditions. Ultimately, we successfully amplified 2019-nCoV DNA, demonstrating the accuracy of our proposed design method and the reliability of its application. The experimental results also indirectly confirmed the correctness of the theoretical modeling. With its robust editability, the “racetrack-shaped” microfluidic chip presents versatile application scenarios and is capable of flexibly adapting to various PCR requirements, thereby holding promise for commercialization, such as integration into point-of-care testing applications.