Abstract
The unrelated parallel machine scheduling problem aims to assign jobs to independent machines with sequence-dependent setup times so that the makespan is minimized. When many practical considerations are introduced, solving the resulting problem is challenging, especially when problems of realistic sizes are of interest. In this study, in addition to the conventional objective of minimizing the makespan, we further consider the burn-in (B/I) procedure that is required in practice; we need to ensure that the scheduling results satisfy the B/I ratio constrained by the equipment. To solve the resulting complicated problem, we propose a population-based simulated annealing algorithm embedded with a variable neighborhood descent technique. Empirical results show that the proposed solution strategy outperforms a commonly used commercial optimization package; it can obtain schedules that are better than the schedules used in practice, and it does so in a more efficient manner.
1. Introduction
The unrelated parallel machine scheduling problem aims to assign a set of jobs to a set of unrelated machines that can process the jobs in parallel without affecting each other. Unrelated parallel machine scheduling problems are of significant practical relevance, and they arise in many applications (i.e., the electronic assembly industry investigated in this study). However, many constraints and additional considerations need to be addressed in practice. For instance, jobs completed at machines need to go through a burn-in (B/I) process prior to being placed in service. The B/I process forces certain manufacturing failures to occur under supervised conditions so that the quality of the product can be examined and ensured. However, as B/I equipment is expensive, many companies have only a limited amount of this kind of equipment, and this becomes the bottleneck of this type of scheduling problem. In this study, we investigate the unrelated parallel machine scheduling problem that aims to minimize the makespan and maximize B/I equipment utilization. As each job has its own suitable B/I equipment, the maximization of B/I equipment utilization can be achieved by making the ratio of completed jobs match the number of B/I equipment available. Other than this additional consideration, the conventional constraints (i.e., sequence-dependent setup times) are also accommodated in the study. As the unrelated parallel machine scheduling problem possesses non-deterministic polynomial-time (NP)-hard complexity [1], solving problem instances with practical sizes is a challenging task, especially when many practical constraints need to be considered. To address this type of problem, we propose a population-based simulated annealing (PBSA) method embedded with a variable neighborhood descent (VND) heuristic to solve it. The proposed solution strategy is empirically applied to real-world problem instances. A comparison with a commercial optimization package demonstrates that the devised approach can determine the optimal schedules in small problem instances. When the problem size increases, we show that the designed approach can determine schedules that are better than the schedules used in practice, and it does so in a much more efficient manner than the commercial optimization package, which fails to obtain solutions.
The remainder of this paper is structured as follows. Section 2 critically overviews the related work regarding production schedules. Section 3 presents the mathematical formulation for the unrelated parallel machine scheduling problem considering various practical constraints. The solution strategy tailored for solving the resulting program is presented in Section 4. Empirical studies are summarized in Section 5 to demonstrate the efficiency and effectiveness of the proposed solution strategies. The final section offers conclusions and provides suggestions for future research.
2. Literature Review
In this section, we broadly categorize the production scheduling problem into single and multiple operation problems according to the production process. In a single operation problem, a job only needs to be processed/assembled once in a single and suitable machine to complete its production procedure. In a multiple operation problem, a job needs to go through various production/assembly steps. Each production/assembly step can only be performed in a specific machine. Only when a job goes through all the required steps is its production procedure completed in a multiple operation problem. Single operation problems can be further classified into single and parallel machine problems. Multiple operation problems can be further divided into flow shop, job shop and open shop problems.
2.1. Single Operation
In single operation production, the problem is considered as a single machine scheduling problem if all the jobs are completed by a single machine.
2.1.1. Single Machine Scheduling
Different research streams analyze single machine scheduling problems while considering various objective functions and constraints. Ref. [2] studied the single machine scheduling problem that aims to minimize both energy consumption and maximum tardiness, and they proposed a mixed-integer linear programming model to formulate it. A ε-constraint method that integrated local search, preprocessing, valid inequalities and solution space reduction techniques was developed to determine the Pareto optimal solution of the two obtained compromised objective functions. Ref. [3] considered the minimization of maximum costs, considering uncertain processing times. Various cost functions were analyzed, and polynomial algorithms were devised to solve the resulting problem. Ref. [4] investigated a single machine scheduling problem that takes release dates and inventory constraints into consideration. With the predetermined processing time of each job and each job’s known impact on the inventory level, the work aimed to determine the optimal sequence of jobs such that the makespan was minimized. It was shown that the problem is strongly NP-hard, and a series of algorithms were proposed to tackle it.
2.1.2. Parallel Machine Scheduling
When there are multiple machines with similar functionalities and these machines can work simultaneously without affecting each other, the problem is considered a parallel machine scheduling problem. Based on the features of the employed machines, parallel machine scheduling can be further classified into identical and unrelated parallel machine scheduling problems. The machines considered in identical parallel machine scheduling problems are homogeneous, and the processing time of a job at any machine is identical. The processing times of a job at the different machines considered in the unrelated parallel machine scheduling problem, however, can be different, and the processing times at different machines are not relevant.
Identical Parallel Machines
Ref. [5] presented a mathematical model for an identical parallel machine scheduling problem in which job splitting and sequence-dependent setup times were considered. Simulated annealing and genetic algorithm metaheuristic-based approaches were proposed with various encoding and decoding methods. The encoding effectively represented the solutions compactly, while the decoding heuristically split jobs in a different manner. The numerical results showed that the proposed approaches could determine solutions of good quality. Ref. [6] investigated the parallel machine scheduling problem that takes job tooling requirements and job-dependent setup times into consideration. A biased random-key genetic algorithm integrated with a variable neighborhood descent-based local search was proposed to solve the resulting NP-hard problem. Numerical results showed that the proposed solution approach outperformed benchmark methods.
One variant of the identical parallel machine problem is the uniform parallel scheduling problem. The processing times of a job at different machines considered in the uniform parallel scheduling problem can vary. However, the processing times are proportional to each other and are at a fixed rate. Ref. [7] examined a uniform parallel-machine scheduling problem with the objective of minimizing the total resource consumption subject to a bounded makespan. They developed a metaheuristic and showed that it could outperform the particle swarm optimization heuristic and approximate the theoretical lower bound.
2.2. Multiple Operation
There are three major types of problems in multiple production scheduling, namely, flow shop, job shop and open shop problems. In a typical flow shop scheduling problem, all jobs are required to complete an identical production process that can be processed at different machines. Conventional job shop scheduling is similar to flow shop scheduling, except that each job should complete the procedure in a specific order. In the open shop scheduling problem, jobs can be completed in random order.
2.2.1. Flow Shop scheduling Problem
Ref. [29] developed a greedy algorithm to solve the flow shop scheduling problem in two phases. The first phase, destruction, eliminates some jobs from the incumbent solution, while the second phase, construction, heuristically reinserts the eliminated jobs from the first phase into the sequence. It was shown that the greedy algorithm is easy to implement and can outperform many benchmarks. Ref. [30] studied the flow shop scheduling problem. First-in-first-out batch dispatching rules were designed to determine the initial solution, followed by mixed-integer program reoptimization techniques and local search heuristics to improve the solution quality. Ref. [31] adopted artificial immune system-based methods for solving a two-stage hybrid flow shop scheduling problem and showed that the proposed methods outperformed the existing lower bounds. Ref. [32] proposed a hybrid metaheuristic that integrated the GA and random sampling to solve the sequence-dependent flow-shop scheduling problem. Ref. [33] solved the distributed blocking flow shop scheduling problem with three hybrid iterative greedy algorithms.
2.2.2. Job Shop Scheduling Problem
Ref. [34] investigated the job shop scheduling problem to address the dynamic events that are inevitable in production environments. A GA embedded with various heuristic dispatching rules was devised to solve the problem. Ref. [35] studied the flexible job shop scheduling problem (FJSP) that allows a job to be processed at any machine from a given set. An algorithm that combines the advantages of the GA and tabu search was proposed to tackle the FJSP and was demonstrated to be effective in solving it. Ref. [36] improved the coding and decoding procedures in PSO and showed that the improvement was suitable for practical job shop scheduling. Ref. [37] utilized the GA and decentralization scheme to minimize the makespan in production scheduling. The proposed solution framework was compared with a shortest processing time rule-based approach (SPT) and was shown to outperform the SPT.
2.2.3. Open Shop Scheduling Problem
In solving the flexible open shop scheduling problem, ref. [38] proved the asymptotic optimality of the general dense scheduling (GDS) algorithm and showed that the proposed GDS-based heuristic could converge to good solutions in large problem instances. When using the minimization of the total flow time as the objective function in the open shop scheduling problem, ref. [39] adopted a GA and an ant colony optimization (ACO) method to solve the problem. For cases when the minimization of the makespan is the objective function, ref. [40] proposed using the GA to solve it.
2.3. Summary
In this work, the focus is on the unrelated parallel production scheduling problem. We summarize the studies we have discussed above in Table 1 to highlight the contribution of our work.

Table 1.
Literature comparison.
The obvious difference between the objective function in our work and those in past studies is the B/I procedure considered in our formulation. The differences in constraints can also be seen in the table. In terms of the solution approach, as suggested by [16], SA is an ideal choice for solving this problem. However, as the problem investigated in this work contains complicated constraints and objective functions, it is not rare to have different solutions with identical objective values (or multiple optimal solutions). As a standard SA needs the objective value to find the descent direction, having multiple solutions with identical objective values makes it difficult to identify the direction based on these values since they are all the same. To explore the neighborhood solutions in an efficient manner, we decide to adopt the population-based simulated annealing (PBSA) algorithm. Furthermore, as indicated by [20], replacing the local search process with VND can potentially increase the performances of various metaheuristics. Therefore, we further embed a VND procedure in the PBSA algorithm.
One of the most relevant studies in terms of the solution approach of our work is that of [19], which integrated SA and VNS in solving unrelated parallel machine scheduling problems. The primary difference between VNS and VND is that VNS introduces a shaking procedure into the solution framework. However, as the constraints considered in our work are rather complicated, so introducing a random shaking procedure can easily generate an infeasible solution. From our preliminary experiments, we believe that VND is more appropriate than VNS for solving our problem.
3. Mathematical Formulation
In this section, we formally define the problem under study, followed by the utilized notations, resulting in a mathematical and detailed explanation.
In each planning horizon, as illustrated in Figure 1, the master production schedule (MPS) outputs the jobs that need to be completed within the predefined time horizon. The jobs completed in the production lines are then sent to B/I equipment to finalize the manufacturing process. During the process, the daily production scheduling problem (DPS) aims to assign jobs to appropriate production lines so that the makespan can be minimized while meeting the B/I requirement as well as possible.
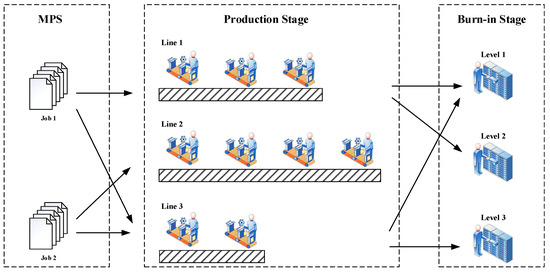
Figure 1.
Illustration of the production process considered in this study.
The current study focuses on the DPS. To focus on the core issues of the problem, the following assumptions are imposed.
- Each job contains only one kind of product. The products that need to be assembled in each job are provided by MPS.
- If two consecutive jobs processed in one production line are of different products, setup time is required.
- Each production line contains no job at the beginning of each day.
- The process time of each job on each production line is given and fixed.
- If a job begins in a production line, it will be completed without interruption.
The following practical constraints are considered in the mathematical formulation.
- Each production line has its own maximum number of daily production hours.
- Each product and its corresponding job have some production requirements and can only be processed in the predetermined/specified production lines.
- Each job has its own earliest starting time and can only start after that prespecified time.
- Each job requires a specific level of B/I equipment.
- There is an upper bound of the total production hours for all the production lines considered together.
Notations
Based on the abovementioned statements and assumptions, the problem studied corresponds to an unrelated parallel machine scheduling problem. The mathematical formulation is revised from [9] with some modifications of the constraints to meet the requirements imposed in practice.
Sets
| N | set of jobs |
| M | set of production lines |
| BI | set of burn-in levels |
| T | set of the planning horizon |
Parameters
| processing time of job on production line | |
| setup time between job and job on production line . = setup time if two consecutive jobs processed on production line belong to different job types; if two consecutive jobs processed on production line belong to identical job types. | |
| maximum daily processing hours for production line on day . | |
| maximum daily processing hours for all the production lines considered together. | |
| an extremely large number | |
| penalty parameter for burn/in ratio violations on day | |
| ,, | target ratio of jobs assigned to B/I levels 1, 2 and 3, respectively. Suppose that a company hopes to maintain three B/I levels of 5:4:1; we can set , , and . |
| number of products that need to be assembled in each job As the B/I level violations are calculated based on , this parameter is introduced. |
Decision Variables
| if job is processed immediately before job on production line on day otherwise. Note that if job or cannot be processed on production line , then . | |
| , if job has a B/I level of on day ; otherwise. | |
| completion time of job on production line on day | |
| complete time for each production line on day | |
| maximum completion time on day |
Mathematical Formulation
The objective function (1) aims to minimize the makespan ) and the B/I level violations . Parameters and are the weights of the corresponding terms, and these will be calibrated in the numerical experiments.
Equation (2) ensures that each job is assigned to a production line and that each job on this machine has only one preceding job . Equation (3) is the constraint that each job has at most one succeeding job . Each production line is assigned at most a dummy job 0 at the beginning that represents the first job of this production line. The design is described in Equation (4). Equation (5) defines the job order. If job is assigned to production line , there must be a preceding job on this production line. If job is the first job on this production line, then must be a dummy job. However, job may not have a succeeding job .
Equation (6) defines the completion time of the jobs. As job should be processed after job on production line , the completion time of job () must be greater than the completion time of job () plus the corresponding setup time and the processing time of job (). If , which means that job cannot be processed immediately after job on production line , this constraint becomes a redundant constraint. Equation (7) ensures that the completion time of each production line () is greater than or equal to the completion time of any job in that production line (). will be used to calculate the objective value later.
Equation (8) sets the maximum number of processing hours for each production line on each day . Equation (9) calculates the maximum completion time according to the statuses of all the jobs in all production lines. Equation (10) constrains the maximum number of processing hours for all the production lines considered together.
The limitation that any job can be assigned to a B/I level is enforced in Equation (11). Equation (12) establishes the relationship between a machine and the B/I level. Only if a job is assigned (i.e., any ) can a B/I level be assigned. The B/I ratio penalty is calculated based on Equation (13). Let us use the first term in that equation as an example to illustrate the proposed design. This term is designed as the absolute value of the number of products that need to be assembled in jobs that are assigned to B/I level 1 () minus the ratio of the number of products that need to be assembled in jobs that are assigned to B/I level 3 ). If the result of the first term is zero, then the ratio of the jobs assigned to levels 1 and 3 exactly matches the prespecified ratio . Otherwise, can serve as the measure of how far away the assignment is from the desired value and can be used as a penalty in the objective function to drive the assignment to match the desired value as closely as possible. The second and third terms can be interpreted in a similar manner. Finally, Equations (14) and (15) state that the decision variable considered in the formulation is of binary value.
As shown in [1], the unrelated parallel machine scheduling problem is an NP-hard problem. The mathematical formulation presented in this section is a parallel machine scheduling problem with additional side constraints. Therefore, it is at least of NP-hard complexity. Solving such problems of practical sizes can be a challenging task. To address this issue, we propose a metaheuristic-based solution approach in the following section.
4. Solution Approach
In this study, we propose population-based simulated annealing (PBSA), which is an extension of SA [41,42]. SA is the search heuristic analogous to the process of solid physical annealing. During the annealing process, a solid is heated and cooled down slowly until it achieves the most likely crystal lattice configuration so that the resulting solid has superior structural integrity. Similar to this process, SA compares the current solution with its neighborhood solution and accepts an improved solution in each iteration. Inferior solutions can also be accepted with a limited probability so that the search process can escape from local optima and finally approximate the global optimum. The probability of accepting inferior solutions depends on a nonincreasing temperature parameter with each iteration of the SA algorithm. In PBSA, instead of a single neighborhood solution, a population of neighborhood solutions are generated during each iteration, and only the best solution among them is used as the incumbent solution in the next iteration. With this improvement, the search for a neighborhood solution can be highly effective. To further enhance the performance of this approach, the traditional LS method employed in SA is replaced by VND in the proposed PBSA method. We next detail our critical algorithmic steps.
4.1. Initial Solution
The initialization step first sorts the jobs in descending order according to multiple attributes, namely, the earliest starting time, the number of allowable production lines and the total processing time. Then, the jobs are assigned according to the first-in-first-out (FIFO) rule to different production lines while satisfying all the assignment rules. Some of the jobs may be left unassigned after this procedure. However, the assigned and unassigned jobs together form an initial feasible solution. Note that the initial solution is designed to be the initial point for the following search procedure. The PBSA presented later can always converge to a good final solution regardless of the initial solution.
4.2. Algorithm Steps
There are four primary steps in the proposed PBSA algorithm, namely, initialization, neighborhood search, incumbent solution updating and termination.
4.2.1. Initialization
For ease of explanation, we introduce additional notations. We denote , and as the highest possible, current and lowest possible temperatures, respectively. We first initialize the current temperature as and reduce over iterations to simulate the “cooling down” process of solid physical annealing. The initial and incumbent solutions are both initialized as in the beginning. Starting from the initial solution found in the previous section, the PBSA algorithm enters the search procedure.
4.2.2. Neighborhood Search
In VND, three neighborhood search approaches/structures are employed in our solution framework. The first is single job switching (Figure 2), which switches one randomly selected job between two production lines ( and in this illustrative example). The second is moving jobs from one production line to another (illustrated in Figure 3). A job ( in this example) from one production line is randomly selected and inserted at the beginning of another production line. The final approach is one-to-two job switching (illustrated in Figure 4), which switches one job in a production line with two consecutive jobs in another production line. To reduce the number of setups, we sort the jobs so that jobs with the same job type can be grouped together after any of the above changes occur in any production line. Note that all the changes only take place when the scheduling rules are not violated. In other words, we explore the neighborhood solutions within the feasible region. As reported in the literature, there exist various alternative neighborhood search procedures. However, from our preliminary experiments, these three procedures yield the best performance and are incorporated in our solution framework.
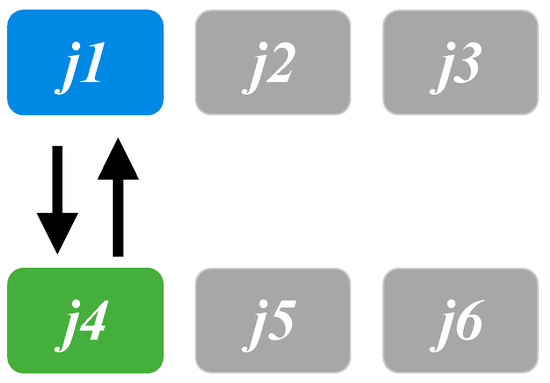
Figure 2.
Single job switching.
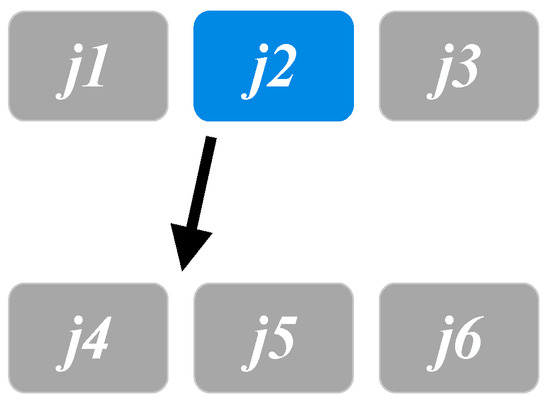
Figure 3.
Job moving.
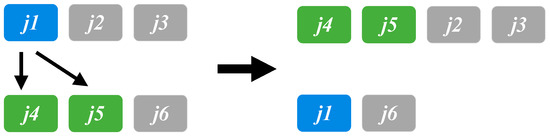
Figure 4.
One-to-two job switching.
In VND, we examine these three neighborhood structures sequentially. As we use the PBSA framework, we generate 5 neighborhood solutions by examining each neighborhood structure during each neighborhood search, and only the best solution is selected as a candidate. If a solution that is better than the incumbent solution is identified, we restart from the first structure and explore the neighborhood solutions with these structures again until a stopping criterion is met.
Specifically, we first define a maximum number of neighborhood structures that can be examined . When the neighborhood search begins, we examine each neighborhood structure sequentially, and a counter is used to keep track of the number of times a neighborhood structure is examined. If a superior solution is identified, we set and restart from the first neighborhood structure. If when examining a neighborhood structure, we examine the next neighborhood structure. If all the neighborhood structures are examined, we continue to the next iteration of the PBSA algorithm.
Over the PBSA iterations, the probability of accepting inferior solutions decreases due to the lowering temperature. Therefore, we increase gradually to increase the possibility of exploring a larger solution space. On the other hand, VND increases the chance of finding a superior solution during each neighborhood search. Based on our empirical experiment, the design balances the search procedure and is effective in solving the overall problem.
4.2.3. Incumbent Solution Updating
When a neighborhood solution is superior to the incumbent solution, we update the incumbent solution. To further improve the solution quality, after this update, we search the unassigned jobs and examine whether the insertion of additional jobs into the solution is possible. If yes, we insert the jobs and use the updated solution as the incumbent solution. If insertion is not possible, the superior solution is used as the incumbent solution directly.
Other than the above updating process, there is a limited probability (denoted as P in this study) of allowing the search procedure to accept inferior solutions. This probability is calculated based on the following modified Boltzmann function [41]:
In the function, is the difference between the objective value of the current solution () and that of the incumbent solution (). denotes the current temperature. If a randomly generated real number is greater than , the current inferior solution is accepted and becomes the incumbent solution in the next iteration. In this study, we reduce the temperature when the number of the searches for each neighborhood structure reaches the prespecified limit. The reduction of is controlled by:
where is the rate at which the temperature decreases. The value of is set between 0 and 1, and this causes the value of to decrease over multiple iterations. PBSA can converge effectively with the above cooling mechanism.
4.2.4. Termination
As many companies need solutions periodically so that they can adjust their scheduling results based on the current dynamic manufacturing environment, we terminate the search procedure and report the incumbent solution when the maximum allowed computational time is reached.
4.3. Summary
Overall, the proposed PBSA can be summarized as in Figure 5. With the generated initial solution and parameter settings, the search procedure examines the neighborhood solution with VND, and controls the PBSA framework based on the obtained results until the stopping criterion is met. Note that as VND is employed in the neighborhood search procedure, the iteration counter is reset to 0 only when the search procedure identifies a solution that is superior to the incumbent solution or when each neighborhood structure reaches the number of pre-specified limit. In other cases, .
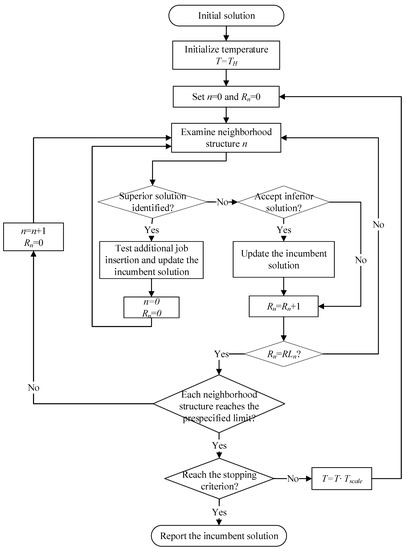
Figure 5.
Algorithmic steps of the population-based simulated annealing (PBSA) approach.
5. Solution Approach
To validate the effectiveness of the proposed solution framework and evaluate its performance, PBSA is empirically applied to problem instances of different sizes. In the experiments, the solutions from a commercial optimization package Gurobi 9.1.0 are used as the benchmark. Furthermore, we conduct a sensitivity analysis on the weights imposed in the objective function to capture the impact of these parameters. The proposed PBSA heuristic is implemented in the ANSI C++ programming language. The numerical experiments for both Gurobi and our solution method are conducted on a Windows-based machine with an Intel i7-8700 CPU at 3.20 GHz and 8 GB of memory. Note that the solutions reported for the proposed PBSA algorithm are averaged over 10 runs as the search process involves randomness.
5.1. Parameter Calibration
We first perturb the parameters and to evaluate their impacts on the objective value. The problem instance used contains 6 machines, 5 days for the planning horizon and 150 jobs. The results are summarized in Table 2 and Figure 6.

Table 2.
The impacts of α and β on the objective value.
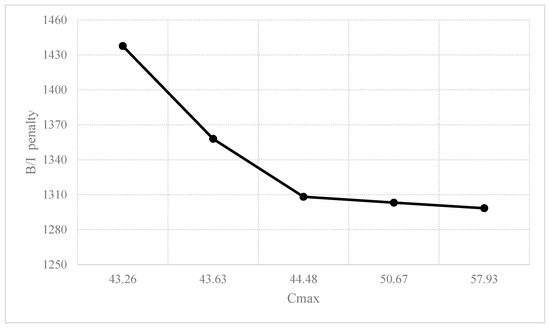
Figure 6.
The tradeoff between Cmax and the burn-in (B/I) penalty.
As expected, given a fixed , the result tends to improve the B/I penalty and worsen Cmax simultaneously when increases. We can see the apparent tradeoff between Cmax and the B/I penalty in Figure 6. However, as : goes beyond 1:0.01, the improvement in the B/I penalty is only marginal and almost ignorable. Therefore, we use and in the rest of the experiments. Furthermore, we conduct preliminary experiments with various parameter combinations of , , and using datasets obtained in practice and identify the parameter combination that performs best. The optimal values are , , and . Note that the Taguchi-based method may be used to calibrate the parameters [20,21,22]. However, we observe that no significant improvement can be obtained by that method for our cases. Therefore, we adopt the above parameters. For practical purposes, the maximum allowed computational time is limited to 1200 s. These parameters are used throughout the remaining experiments.
5.2. Validation
For validation purposes, we compare our solutions with the Gurobi solutions, which can be considered the optimal solutions. Note that Gurobi is used to solve the formulation presented in Section 3 with the default settings. The comparison is summarized in Table 3. As shown in the table, the proposed PBSA algorithm can determine the same optimal solutions as those obtained by Gurobi, demonstrating the efficacy of the proposed solution method. When the problem size increases, Gurobi fails to obtain feasible solutions for problem instances with more than 15 jobs. However, the proposed PBSA method can still determine solutions, thereby demonstrating its scalability. Furthermore, it is noted that PBSA with the two neighborhood structures explained in Figure 2 and Figure 3 (PBSA with 2VND) has a higher probability of finding improved solutions than PBSA with all three structures (PBSA with 3VND). It is suspected that the neighborhood structure depicted in Figure 4 makes it difficult for the search process to converge to an improved solution within the limited CPU time allowed. Let us depict the convergence of the proposed algorithm using the case with L/T/N = 6/3/100 as an example in Figure 7 to further discuss the results.

Table 3.
Validation of the proposed PBSA algorithm.
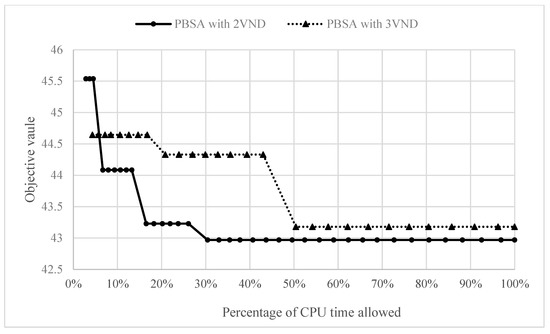
Figure 7.
Convergence of the algorithm.
As the computational time of each iteration required for PBSA with 3VND increases, the number of iterations that can be performed within the limited CPU time decreases, resulting in poor convergence when compared with that of PBSA with 2VND. Although PBSA can potentially explore large solution spaces, we still recommend PBSA with 2VND for practical purposes. As the actual production environment is rather dynamic, faster convergence to an ideal solution seems to be the most attractive option for most of the companies we encounter.
We next evaluate the impact of the numbers of production lines and scheduling days on the performance of the proposed algorithm. As Gurobi failed to determine feasible solutions in most of the cases, we only summarize our solutions in Figure 8.
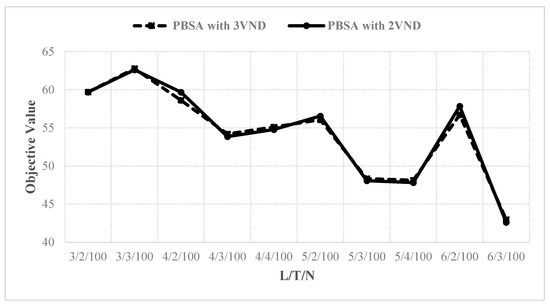
Figure 8.
Impacts of the numbers of production lines and scheduling days.
Nevertheless, PBSA with 2VND outperforms PBSA with 3VND in most cases. Note that, contrary to the mathematical formulation that assumes all jobs should be assigned, the proposed PBSA algorithm has the flexibility to allow for unscheduled jobs if some jobs cannot be inserted into the production schedule. For this reason, the objective values do not increase/decrease monotonically with increases in the numbers of production lines and scheduling days.
5.3. Practical Application Scenarios
Using the proposed PBSA algorithm with 2VND, we experiment with three application scenarios, namely, scenarios with various B/I ratios (summarized in Table 4), additional constraints (summarized in Table 5) and superhot runs.

Table 4.
The impacts of various B/I ratios.

Table 5.
Impacts of additional constraints.
From Table 4, we can see that the B/I ratio of 5:5:0 dominates 5:4:1 and 6:3:1 in terms of the objective values and number of scheduled jobs (NSJ) yielded. In the case where L/T/N = 6/3/100, the B/I penalty can reach zero, indicating that the ratio perfectly matches 5:5:0. In other words, it is possible to fully utilize the expensive B/I equipment, should we adjust the ratio properly.
In real-world applications, many supervisors may ask for additional constraints based on their past experiences, as they believe that the additional constraints can improve the scheduling performance of the algorithm. In Table 5, we introduce the additional constraint to fully utilize long production lines as much as possible, as many supervisors may think continuous processing without interruption can reduce the setup times and can improve the overall performance. However, the effect of this additional constraint drastically reduces the number of jobs that can be scheduled with the same setup and contradicts their intuition. Therefore, it is suggested to consider only the necessary constraints for practical purposes.
To manufacture products with a sudden surge in demand, customers may place urgent orders. For products such as this, the manufacturer may initiate a superhot run and charge a higher price for manufacturing the product. For such urgent orders, we believe that the proposed solution framework offers a possible pricing mechanism by charging based on the impact of the order on the original schedule. We illustrate this concept by inserting three urgent orders in the cases summarized in Table 6.

Table 6.
The impact of superhot runs.
As seen from the cases, there are 4 and 5 jobs that cannot be completed within this planning horizon due to the superhot runs. The impacts of the superhot runs on the rest of the jobs are 2.5% and 2.7%, respectively, so this provides an ideal guide for pricing based on superhot runs.
6. Concluding Remarks
In this study, we developed a PBSA algorithm for the unrelated parallel machine scheduling problem considering B/I constraints. The proposed PBSA algorithm integrates the advantages of SA and VND and was implemented for practical applications. Numerical results have shown that the proposed PBSA approach can solve the abovementioned problem optimally for small problem instances and is scalable to solve problem instances of realistic sizes. In practice, there are many industries that encounter the unrelated parallel machine scheduling problem (i.e., the electronic assembly industry investigated in the current study). For the unrelated parallel machine scheduling problem, we found that the PBSA and VND can solve problems of various practical sizes efficiently.
Although encouraging results are obtained, this research can be extended in several directions. First, it is apparent that this research can be extended to investigate the multi-objective optimization problem since there are two objective functions considered. Some practical techniques can be employed to approximate the Pareto-optimal solution set (i.e., [43]). Second, as each job can be split into smaller jobs, we can find the optimal splitting strategy for the jobs such that the overall scheduling performance can be improved. Third, as the production environment is highly uncertain and stochastic, processing time uncertainty can be incorporated in future research. Fourth, instead of minimizing the deviation from the desired burn-in levels, future research can consider the optimal assignment of jobs to the exact grids in burn-in machines, which may potentially improve the scheduling results further. Finally, as the production environment changes rapidly, developing a system that can rapidly respond to the dynamic and changing environment with the basis of this study can be another useful and interesting extension.
Author Contributions
Data curation, T.-Y.H.; Investigation, D.-Y.L.; Methodology, D.-Y.L. and T.-Y.H.; Software, T.-Y.H.; Validation, D.-Y.L.; Writing—original draft, D.-Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Ministry of Science and Technology, Taiwan, ROC grant number MOST 108-2410-H-007-097 -MY4.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest
Abbreviations
| B/I | burn-in |
| PBSA | population-based simulated annealing |
| VND | variable neighborhood descent |
| GA | genetic algorithm |
| SA | simulated annealing |
| LS | local search |
| ERD | earlier release date first |
| AIS | artificial immune system |
| PSO | particle swarm optimization |
| DWPSA | delay window-time parallel saving algorithm |
| DWGSA | delay window-time generalized saving algorithm |
| FJSP | flexible job shop scheduling problem |
| GDS | general dense scheduling |
| ACO | colony optimization |
| SPT | shortest processing time |
| MPS | master production schedule |
| DPS | daily production scheduling problem |
| NSJ | number of scheduled jobs |
References
- Karp, R.M. Reducibility among combinatorial problems. In Complexity of Computer Computations; Springer: Berlin/Heidelberg, Germany, 1972; pp. 85–103. [Google Scholar]
- Che, A.; Wu, X.Q.; Peng, J.; Yan, P.Y. Energy-efficient bi-objective single-machine scheduling with power-down mechanism. Comput. Oper. Res. 2017, 85, 172–183. [Google Scholar] [CrossRef]
- Fridman, I.; Pesch, E.; Shafransky, Y. Minimizing maximum cost for a single machine under uncertainty of processing times. Eur. J. Oper. Res. 2020, 286, 444–457. [Google Scholar] [CrossRef]
- Davari, M.; Ranjbar, M.; De Causmaecker, P.; Leus, R. Minimizing makespan on a single machine with release dates and inventory constraints. Eur. J. Oper. Res. 2020, 286, 115–128. [Google Scholar] [CrossRef]
- Kim, J.G.; Song, S.; Jeong, B. Minimising total tardiness for the identical parallel machine scheduling problem with splitting jobs and sequence-dependent setup times. Int. J. Prod. Res. 2020, 58, 1628–1643. [Google Scholar] [CrossRef]
- Soares, L.C.R.; Carvalho, M.A.M. Biased random-key genetic algorithm for scheduling identical parallel machines with tooling constraints. Eur. J. Oper. Res. 2020, 285, 955–964. [Google Scholar] [CrossRef]
- Lin, S.W.; Ying, K.C. Uniform Parallel-Machine Scheduling for Minimizing Total Resource Consumption With a Bounded Makespan. IEEE Access 2017, 5, 15791–15799. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems. An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence; ANAS: Roma, Italy, 1975. [Google Scholar]
- Vallada, E.; Ruiz, R. A genetic algorithm for the unrelated parallel machine scheduling problem with sequence dependent setup times. Eur. J. Oper. Res. 2011, 211, 612–622. [Google Scholar] [CrossRef]
- Joo, C.M.; Kim, B.S. Hybrid genetic algorithms with dispatching rules for unrelated parallel machine scheduling with setup time and production availability. Comput. Ind. Eng. 2015, 85, 102–109. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Huang, L.W. Minimizing total earliness and tardiness through unrelated parallel machine scheduling using distributed release time control. J. Manuf. Syst. 2017, 42, 1–10. [Google Scholar] [CrossRef]
- Yu, C.L.; Semeraro, Q.; Matta, A. A genetic algorithm for the hybrid flow shop scheduling with unrelated machines and machine eligibility. Comput. Oper. Res. 2018, 100, 211–229. [Google Scholar] [CrossRef]
- Jouhari, H.; Lei, D.M.; Al-qaness, M.A.A.; Abd Elaziz, M.; Ewees, A.A.; Farouk, O. Sine-Cosine Algorithm to Enhance Simulated Annealing for Unrelated Parallel Machine Scheduling with Setup Times. Mathematics 2019, 7, 1120. [Google Scholar] [CrossRef]
- Santos, H.G.; Toffolo, T.A.M.; Silva, C.; Vanden Berghe, G. Analysis of stochastic local search methods for the unrelated parallel machine scheduling problem. Int. Trans. Oper. Res. 2019, 26, 707–724. [Google Scholar] [CrossRef]
- Cota, L.P.; Haddad, M.N.; Souza, M.J.F.; Coelho, V.N. AIRP: A heuristic algorithm for solving the unrelated parallel machine scheduling problem. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (Cec), Beijing, China, 6–11 July; pp. 1855–1862.
- Wang, X.M.; Li, Z.T.; Chen, Q.X.; Mao, N. Meta-heuristics for unrelated parallel machines scheduling with random rework to minimize expected total weighted tardiness. Comput. Ind. Eng. 2020, 145, 106505. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N. An introduction to variable neighborhood search. In Meta-Heuristics; Springer: Berlin/Heidelberg, Germany, 1999; pp. 433–458. [Google Scholar]
- Fleszar, K.; Charalambous, C.; Hindi, K.S. A variable neighborhood descent heuristic for the problem of makespan minimisation on unrelated parallel machines with setup times. J. Intell. Manuf. 2011, 23, 1949–1958. [Google Scholar] [CrossRef]
- Al-Harkan, I.M.; Qamhan, A.A. Optimize Unrelated Parallel Machines Scheduling Problems With Multiple Limited Additional Resources, Sequence-Dependent Setup Times and Release Date Constraints. IEEE Access 2019, 7, 171533–171547. [Google Scholar] [CrossRef]
- Marinho Diana, R.O.; de Souza, S.R. Analysis of variable neighborhood descent as a local search operator for total weighted tardiness problem on unrelated parallel machines. Comput. Oper. Res. 2020, 117. [Google Scholar] [CrossRef]
- Afzalirad, M.; Rezaeian, J. Resource-constrained unrelated parallel machine scheduling problem with sequence dependent setup times, precedence constraints and machine eligibility restrictions. Comput. Ind. Eng. 2016, 98, 40–52. [Google Scholar] [CrossRef]
- Mir, M.S.S.; Rezaeian, J. A robust hybrid approach based on particle swarm optimization and genetic algorithm to minimize the total machine load on unrelated parallel machines. Appl. Soft. Comput. 2016, 41, 488–504. [Google Scholar] [CrossRef]
- Fleszar, K.; Hindi, K.S. Algorithms for the unrelated parallel machine scheduling problem with a resource constraint. Eur. J. Oper. Res. 2018, 271, 839–848. [Google Scholar] [CrossRef]
- He, Y.H.; Wang, L.B.; Wei, Y.; He, Z.Z. Optimisation of burn-in time considering the hidden loss of quality deviations in the manufacturing process. Int. J. Prod. Res. 2017, 55, 2961–2977. [Google Scholar] [CrossRef]
- Aghaee, N.; Peng, Z.B.; Eles, P. Temperature-Gradient-Based Burn-In and Test Scheduling for 3-D Stacked ICs. IEEE Trans. Very Large Scale Integr. (VlSI) Syst. 2015, 23, 2992–3005. [Google Scholar] [CrossRef]
- Kim, Y.D.; Kang, J.H.; Lee, G.E.; Lim, S.K. Scheduling Algorithms for Minimizing Tardiness of Orders at the Burn-in Workstation in a Semiconductor Manufacturing System. IEEE Trans. Semicond. Manuf. 2011, 24, 14–26. [Google Scholar] [CrossRef]
- Lee, C.Y.; Uzsoy, R.; Martinvega, L.A. Efficient Algorithms for Scheduling Semiconductor Burn-in Operations. Oper. Res. 1992, 40, 764–775. [Google Scholar] [CrossRef]
- Pearn, W.L.; Hong, J.S.; Tai, Y.T. The burn-in test scheduling problem with batch dependent processing time and sequence dependent setup time. Int. J. Prod. Res. 2013, 51, 1694–1706. [Google Scholar] [CrossRef]
- Ruiz, R.; Stutzle, T. A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem. Eur. J. Oper. Res. 2007, 177, 2033–2049. [Google Scholar] [CrossRef]
- Wang, I.L.; Yang, T.H.; Chang, Y.B. Scheduling two-stage hybrid flow shops with parallel batch, release time, and machine eligibility constraints. J. Intell. Manuf. 2012, 23, 2271–2280. [Google Scholar] [CrossRef]
- Komaki, G.M.; Teymourian, E.; Kayvanfar, V. Minimising makespan in the two-stage assembly hybrid flow shop scheduling problem using artificial immune systems. Int. J. Prod. Res. 2016, 54, 963–983. [Google Scholar] [CrossRef]
- Costa, A.; Cappadonna, F.A.; Fichera, S. A hybrid genetic algorithm for minimizing makespan in a flow-shop sequence-dependent group scheduling problem. J. Intell. Manuf. 2017, 28, 1269–1283. [Google Scholar] [CrossRef]
- Ying, K.C.; Lin, S.W. Minimizing Makespan in Distributed Blocking Flowshops Using Hybrid Iterated Greedy Algorithms. IEEE Access 2017, 5, 15694–15705. [Google Scholar] [CrossRef]
- Kundakci, N.; Kulak, O. Hybrid genetic algorithms for minimizing makespan in dynamic job shop scheduling problem. Comput. Ind. Eng. 2016, 96, 31–51. [Google Scholar] [CrossRef]
- Li, X.Y.; Gao, L. An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem. Int. J. Prod. Econ. 2016, 174, 93–110. [Google Scholar] [CrossRef]
- Ding, H.J.; Gu, X.S. Improved particle swarm optimization algorithm based novel encoding and decoding schemes for flexible job shop scheduling problem. Comput. Oper. Res. 2020, 121, 15. [Google Scholar] [CrossRef]
- Malega, P.; Rudy, V.; Kanasz, R.; Gazda, V. Decentralized optimization of the flexible production lines. Adv. Prod. Eng. Manag. 2020, 15, 267–276. [Google Scholar] [CrossRef]
- Bai, D.Y.; Zhang, Z.H.; Zhang, Q. Flexible open shop scheduling problem to minimize makespan. Comput. Oper. Res. 2016, 67, 207–215. [Google Scholar] [CrossRef]
- Ciro, G.C.; Dugardin, F.; Yalaoui, F.; Kelly, R. Open shop scheduling problem with a multi-skills resource constraint: A genetic algorithm and an ant colony optimisation approach. Int. J. Prod. Res. 2016, 54, 4854–4881. [Google Scholar] [CrossRef]
- Hosseinabadi, A.A.R.; Vahidi, J.; Saemi, B.; Sangaiah, A.K.; Elhoseny, M. Extended Genetic Algorithm for solving open-shop scheduling problem. Soft Comput. 2019, 23, 5099–5116. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Lin, D.Y.; Xie, C. The Pareto-optimal Solution Set of the Equilibrium Network Design Problem with Multiple Commensurate Objectives. Netw Spat. Econ. 2011, 11, 727–751. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).