A Note on On-Line Ramsey Numbers for Some Paths

Abstract

We consider the important generalisation of Ramsey numbers, namely on-line Ramsey numbers. It is easiest to understand them by considering a game between two players, a Builder and Painter, on an infinite set of vertices. In each round, the Builder joins two non-adjacent vertices with an edge, and the Painter colors the edge red or blue. An on-line Ramsey number $\tilde{r}(G,H)$ is the minimum number of rounds it takes the Builder to force the Painter to create a red copy of graph G or a blue copy of graph H, assuming that both the Builder and Painter play perfectly. The Painter’s goal is to resist to do so for as long as possible. In this paper, we consider the case where G is a path $P_4$ and H is a path $P_{10}$ or $P_{11}$.

1. Introduction

The terminology, definitions and some descriptions are taken from two previous works by the first author, namely [1,2].

Ramsey numbers and their generalizations have been a fundamentally important area of study in combinatorics for many years. Particularly well-studied are Ramsey numbers for graphs. Here, the Ramsey number of two graphs G and H, denoted by $r(G,H)$, is the least t such that any red-blue edge-coloring of $K_t$ contains a red copy of G or a blue copy of H.

In this paper, we consider the following generalization of Ramsey numbers defined independently by Beck [3] and Kurek and Ruciński [4]. Let G and H be two graphs. Consider a game played on the edge set of the infinite clique $K_N$ with two players, a Builder and Painter. In each round of the game, the Builder chooses an edge and the Painter colors it red or blue. The Builder wins by creating either a red copy of G or a blue copy of H, and wishes to do so in as few rounds as possible. The Painter wishes to delay the Builder for as many rounds as possible. (Note that the Painter may not delay the Builder indefinitely–for example, the Builder may simply choose every edge of $K_{r(G,H)}$).

The on-line Ramsey number $\tilde{r}(G,H)$ is the minimum number of rounds it takes the Builder to win, assuming that both the Builder and Painter play optimally. We call this game the $\tilde{r}(G,H)$-game. Note that $\tilde{r}(G,H)\ge e(G)+e(H)-1$ for all graphs G and H, as the Painter may simply colour the first $e(G)-1$ edges red and all subsequent edges blue.

Intuitively, it is not surprising that determining on-line Ramsey numbers exactly has proved even more difficult than determining classical Ramsey numbers exactly (the former are a generalization of the latter). The consequence of this is that there are very few known exact values of on-line Ramsey numbers. A significant amount of effort has been focused on the special case where G is a path $P_3$. Cyman, Dzido, Lapinskas and Lo [1] have determined $\tilde{r}(P_3,P_{\ell +1})$ and $\tilde{r}(P_3,C_{\ell })$ exactly (where $P_s$ is a path on s vertices).

Theorem 1.

In [1]. For all $\ell \ge 2$, we have $\tilde{r}(P_3,P_{\ell +1})=\lceil 5\ell /4\rceil$. As well,

$$\tilde{r}(P_3,C_{\ell })=\left\{\begin{array}{cc}\ell +2\hfill & if\ell =3,4,\hfill \\ \lceil 5\ell /4\rceil \hfill & if\ell \ge 5.\hfill \end{array}\right.$$

The best known bounds on $\tilde{r}(P_4,P_{\ell +1})$ were also proved in [1].

Theorem 2.

In [1]. For all $\ell \ge 3$, we have $(7\ell +2)/5\le \tilde{r}(P_4,P_{\ell +1})\le (7\ell +52)/5$.

Some new general lower and upper bounds for on-line Ramsey numbers $\tilde{r}(C_3,P_k)$ and $\tilde{r}(C_4,P_k)$ were proved in [2]. In this paper, we obtain two new exact values $\tilde{r}(P_4,P_{10})=13$ and $\tilde{r}(P_4,P_{11})=15$, furthermore we do so without help of computer algorithms. Our results agree with the following conjecture which was also proposed by Cyman, Dzido, Lapinskas and Lo.

Conjecture 1. 

In [1]. For all $\ell \ge 3$, we have $\tilde{r}(P_4,P_{\ell +1})=\lceil (7\ell +2)/5\rceil$.

This provides more evidence for the conjecture that the latter holds for all $l\ge 3$.

2. Determining $\tilde{\mathit{r}}({\mathit{P}}_{\mathbf{4}},{\mathit{P}}_{\mathit{l}})$ for $\mathit{l}\ge \mathbf{3}$

First note that $\tilde{r}(P_4,P_3)=4$, $\tilde{r}(P_4,P_5)=6$ and $\tilde{r}(P_4,P_4)=5$, as shown by Prałat [5] and Grytczuk, Kierstead and Prałat [6] respectively. The results $\tilde{r}(P_4,P_l)$ where $l\in \{6,7,8,9\}$ already required help of computer algorithms (see [5]). The first open cases are those of $\tilde{r}(P_4,P_{10})$ and $\tilde{r}(P_4,P_{11})$, which are determined later in this paper.

In the following discussion we take on the role of the Builder, and we will assume for clarity that the Painter will not voluntarily lose the game by creating a red $P_4$. We first observe that the Builder can obtain a long blue path by using the strategy for shorter paths twice.

Lemma 1.

We have $\tilde{r}(P_4,P_n)\le \tilde{r}(P_4,P_{\lfloor \frac{n}{2}\rfloor })+\tilde{r}(P_4,P_{\lceil \frac{n}{2}\rceil })+3$

Proof. 

First, the Builder will use at most $\tilde{r}(P_4,P_{\lfloor \frac{n}{2}\rfloor })$ and $\tilde{r}(P_4,P_{\lceil \frac{n}{2}\rceil })$ moves to construct two vertex-disjoint blue paths $P_{\lfloor \frac{n}{2}\rfloor }$ and $P_{\lceil \frac{n}{2}\rceil }$, respectively. Then, the Builder will join their endpoints together to form a blue $P_n$ in at most 3 rounds. □

Lemma 1 implies that $\tilde{r}(P_4,P_{10})\le 2\tilde{r}(P_4,P_5)+3=15$. However, the Builder may join the shorter paths more carefully than in the proof of Lemma 1, resulting in the following.

Theorem 3.

We have $\tilde{r}(P_4,P_{10})=13$.

Proof. 

Theorem 2 implies that $\tilde{r}(P_4,P_{10})\ge 13$. It therefore suffices to prove that Builder can win the $\tilde{r}(P_4,P_{10})$-game within 13 rounds.

The Builder starts with 2 disjoint $\tilde{r}(P_4,P_5)$-games. Recall that both the Builder and Painter play optimally, so the Painter wants to avoid a red $P_4$ and the Builder will force the Painter to create two separate blue $P_5$. At the beginning, let’s observe that if the Builder was able to construct a blue $P_5$ in at most 5 moves and a second, separate blue $P_5$ in at most 5 moves, then using similar reasoning as in the proof of Lemma 1 we have the result. Now we will be very carefully considering the strategy for the $\tilde{r}(P_4,P_5)$-game described by Prałat in [5]. We will use this strategy for the two above-mentioned $\tilde{r}(P_4,P_5)$-games.

In this strategy, the Builder first shows a path $P_4$. Therefore, one of the four possible color patterns appears: $bbb$, $bbr$, $brb$, and $rrb$. The Builder has to avoid the pattern $rbr$, otherwise, the Painter has a strategy to ‘survive’ to the end of the sixth round. In order to do that, the Builder can use the same strategy as for the $R(P_3,P_5)$ case described by Prałat in [5]. Finally, the Builder obtains a blue $P_5$ in the next three moves (the details as shown in Figure 3 in [5]).

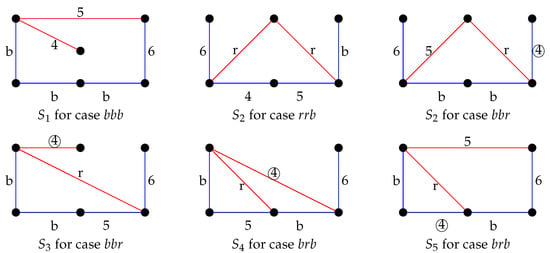
The Builder’s strategy for $\tilde{r}(P_4,P_5)$-game will be to build up one of the five nonisomorphic structures independent of the Painter’s choices, as shown in Figure 1.

Figure 1. All possible final structures in the strategy for $\tilde{r}(P_4,P_5)$-game.

Recall that the Builder’s start of the strategy for $\tilde{r}(P_4,P_{10})$-game is to play two separate $\tilde{r}(P_4,P_5)$-games with the strategy described in [5].

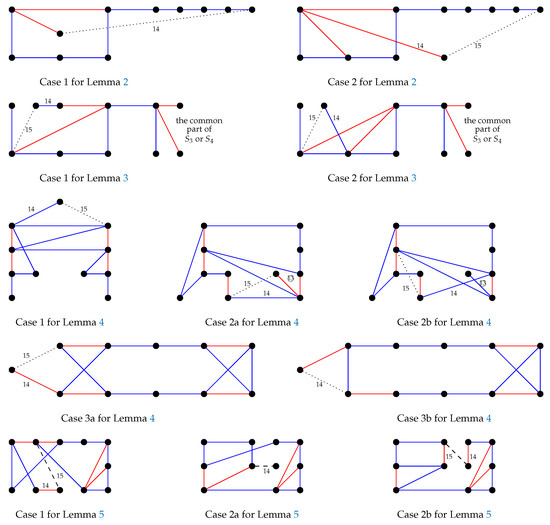
Lemma 2. 

Suppose that in the $\tilde{r}(P_4,P_{10})$-game, the Builder has already obtained a structure $S_1$ or $S_5$ in the first $\tilde{r}(P_4,P_5)$-game. Then, regardless of the strategy used by the Painter in the second $\tilde{r}(P_4,P_5)$-game, after the end of this game and one more move there is either a red copy of $P_4$ or a blue copy of $P_{10}$.

Proof. 

The Builder can join an endpoint of a red $P_3$ in $S_1$ or $S_5$, which is at the same time the endpoint of a blue path $P_5$, with an endpoint of a blue $P_5$ in the structure obtained after the end of the second $\tilde{r}(P_4,P_5)$-game. □

Lemma 3. 

Suppose that in the $\tilde{r}(P_4,P_{10})$-game, the Builder has obtained a structure $S_3$ or $S_4$ in both $\tilde{r}(P_4,P_5)$-games. Then, after one move there is either a red copy of $P_4$ or a blue copy of $P_{10}$.

Proof. 

The Builder can join an endpoint of a blue $P_5$ in the first structure, which is at the same time the middle of a red path $P_3$, with the vertex of the same type in the structure obtained in the second $\tilde{r}(P_4,P_5)$-game. □

Note that the structure $S_2$ could have occurred when the Painter started the $\tilde{r}(P_4,P_5)$-game from the configuration $rrb$ or $bbr$.

Lemma 4. 

Suppose that in the $\tilde{r}(P_4,P_{10})$-game, the Builder has obtained a structure $rrb$ or $bbr$ in both $\tilde{r}(P_4,P_5)$-games after 3 moves. Then, after 7 moves there is either a red copy of $P_4$ or a blue copy of $P_{10}$.

Proof. 

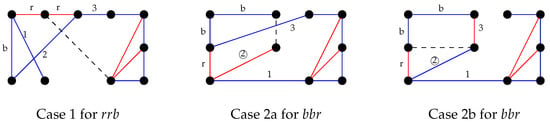
There are only three possible patterns that can appear. Let us consider these three cases depending on the Painter’s choice.

Case 1:

the Builder has obtained two structures $rrb$, say $v_0{v}_1{v}_2{v}_3$ and $v_4{v}_5{v}_6{v}_7$.

The Builder chooses the edges $v_2{v}_8$, $v_0{v}_8$, $v_0{v}_4$, $v_1{v}_4$, $v_1{v}_5$, $v_5{v}_9$ and $v_6{v}_9$, where $v_8$ and $v_9$ are new vertices. If the Painter colours any of the edges red, then we have a red $P_4$. Then the Painter colours them all blue and we obtain the blue $P_{10}$: $v_3{v}_8{v}_0{v}_4{v}_1{v}_5{v}_9{v}_6{v}_7$.

Case 2:

the Builder has obtained structures $rrb$ and $bbr$, say $v_0{v}_1{v}_2{v}_3$ and $v_4{v}_5{v}_6{v}_7$, respectively.

The Builder chooses the edges $v_2{v}_8$, $v_0{v}_3$, $v_0{v}_4$, $v_1{v}_6$ and $v_1{v}_7$, where $v_8$ is a new vertex. If the Painter colors any of the edges red, then we have a red $P_4$. Then the Painter colors them all blue. The Builder then chooses the edge $v_8{v}_9$, where $v_9$ is a new vertex. If the Painter colours $v_8{v}_9$ blue, then we have a blue $P_{10}$. So we may assume that the Painter colors $v_8{v}_9$ red. The Builder then chooses the edge $v_7{v}_9$ and we are done.

Case 3:

the Builder has obtained two structures $bbr$, say $v_0{v}_1{v}_2{v}_3$ and $v_4{v}_5{v}_6{v}_7$.

The Builder chooses the edges $v_2{v}_7$, $v_3{v}_6$, and $v_3{v}_7$. If the Painter colors any of the edges red, then we have a red $P_4$. Then the Painter colors them all blue. The Builder then chooses the edges $v_0{v}_8$ and $v_4{v}_9$, where $v_8$ and $v_9$ are new vertices. If the Painter colors them blue, then we have a blue $P_{10}$. If the Painter colors them red, then the Builder chooses the edges $v_0{v}_9$ and $v_4{v}_8$ and we are done. So we may assume that the Painter colors $v_0{v}_8$ red and $v_4{v}_9$ blue. The Builder then chooses the edge $v_9{v}_{10}$, where $v_{10}$ is a new vertex. If the Painter colours $v_9{v}_{10}$ blue, then we have a blue $P_{10}$. So we may assume that the Painter colors $v_9{v}_{10}$ red. The Builder then chooses the edge $v_8{v}_9$ and we are done.

□

Lemma 5. 

Suppose that after 3 rounds for $\tilde{r}(P_4,P_{10})$-game, the Builder has obtained a structure $rrb$ or $bbr$ in the first $\tilde{r}(P_4,P_5)$-game and after 3 rounds he has obtained a structure $bbb$ or $brb$ in the second $\tilde{r}(P_4,P_5)$-game. Then, after next 7 moves there is either a red copy of $P_4$ or a blue copy of $P_{10}$.

Proof. 

First, the Builder continues the second game and he forces the Painter to construct one of the structures $S_1$, $S_4$ or $S_5$. If he obtains structure $S_1$ or $S_5$, then by applying Lemma 2, we have the result. So we may assume that the Builder has structure $S_4$ after second $\tilde{r}(P_4,P_5)$-game. The Builder now is able to finish the game in the next 4 moves, as shown in Figure 2. The final edge is drawn with a dotted line and a circled number means that the Painter had a choice in that move, which led to branching into subcases. □

Figure 2. Three possible final structures in the strategy for $S_4$.

Finally, notice that since $\tilde{r}(P_4,P_5)=6$ and Lemmas 2–5 exhaust all possible situations of playing $\tilde{r}(P_4,P_5)$-games, then $\tilde{r}(P_4,P_{10})\le 13$. Taking into account the lower bound, the proof is complete. □

Now we prove that the Builder can obtain either a longer blue path or a red $P_4$ by simply extending an existing blue path.

Lemma 6.

Suppose Q is a non-trivial blue path with endpoints a and b. Then the Builder can force the Painter to construct either a red $P_4$ or a blue path of length $e(Q)+1$ in at most 3 moves.

Proof. 

Let c and d be the new vertices. The Builder chooses the edges $ac$, $bc$ and $bd$. If the Painter colors any of the edges blue, then we have a blue path of length $e(Q)+1$. Then the Painter colors them all red and we have a red $P_4$. □

Theorem 4.

We have $\tilde{r}(P_4,P_{11})=15$.

Proof. 

Theorem 2 implies that $\tilde{r}(P_4,P_{11})\ge 15$. It therefore suffices to prove that the Builder can win the $\tilde{r}(P_4,P_{11})$-game within 15 rounds.

The Builder starts with $\tilde{r}(P_4,P_{10})$-game and he uses it to force a blue copy of $P_{10}$ in at most 13 moves. If the Builder has achieved this goal in 12 or fewer moves, then by using Lemma 6 we have the result. The case that remains to be considered is when the $\tilde{r}(P_4,P_{10})$-game ends by forcing the Painter to create a blue $P_{10}$ in the 13th round. We will apply the strategy described in the proof of Theorem 3 and prove that in each of the cases considered in Lemmas 2–5, two moves are enough to force the Painter to create a red $P_4$ or a blue $P_{11}$.

The result is achieved by case-by-case analysis of the last two moves as shown in Figure 3. The final edge is drawn with a dotted line and a circled number means that the Painter had a choice in that move, which led to branching into subcases. □

Figure 3. All possible final structures in the strategy for $\tilde{r}(P_4,P_{11})$.

As a result of the application of Lemma 1 and known numbers we obtain new upper bounds for the numbers $\tilde{r}(P_4,P_n)$ where $12\le n\le 22$. The following Table 1 presents old bounds obtained by using Theorem 2 and new results.

Table 1. New upper bounds for the numbers $\tilde{r}(P_4,P_n)$ where $12\le n\le 22$

Number	Old Upper Bound	New Upper Bound
$\tilde{r}(P_4,P_{12})$	≤25	≤18 (by Lemma 6)
$\tilde{r}(P_4,P_{13})$	≤27	≤20
$\tilde{r}(P_4,P_{14})$	≤28	≤21
$\tilde{r}(P_4,P_{15})$	≤30	≤23
$\tilde{r}(P_4,P_{16})$	≤31	≤25
$\tilde{r}(P_4,P_{17})$	≤32	≤26
$\tilde{r}(P_4,P_{18})$	≤34	≤27
$\tilde{r}(P_4,P_{19})$	≤35	≤28
$\tilde{r}(P_4,P_{20})$	≤37	≤29
$\tilde{r}(P_4,P_{21})$	≤38	≤31
$\tilde{r}(P_4,P_{22})$	≤39	≤33

It remains an open question whether similar methods of finding the values of $R(P_4,P_{10})$ and $R(P_4,P_{11})$ could be used for longer paths. This would make it possible to confirm or disprove the hypothesis proposed by Cyman, Dzido, Lapinskas and Lo in [1].