Some Properties of the Exeter Transformation

Abstract

The Exeter point of a given triangle $ABC$ is the center of perspective of the tangential triangle and the circummedial triangle of the given triangle. The process of the Exeter point from the centroid serves as a base for defining the Exeter transformation with respect to the triangle $ABC$, which maps all points of the plane. We show that a point, its image, the symmedian, and three exsymmedian points of the triangle are on the same conic. The Exeter transformation of a general line is a fourth-order curve passing through the exsymmedian points. We show that each image point can be the Exeter transformation of four different points. We aim to determine the invariant lines and points and some other properties of the transformation.

1. Introduction

The Exeter point is one of the well-known triangle centers among the over 35,000 centers in the online Encyclopedia of Triangle Centers [1]. The Exeter point of a given triangle is defined from the centroid of the triangle by a drawing process. In this article, as a generalization of the definition of the Exeter point to the whole plane of the triangle, we define a so-called Exeter transformation with respect to a given triangle $ABC$. We show some properties of this transformation, we give the invariant figures, and we show that certain important points during the transformation lie on a conic.

Minevich and Morton [2] defined a similar, so-called “TCC-perspector”, transformation with respect to $△ABC$, and they gave a nice connection between the isogonal transformation and the “TCC-perspector”. For more details and the history of the Exeter point see, ex., in [1,2,3,4,5,6].

For verifying our statements we use an analytical way with barycentric coordinates. The base triples of this barycentric coordinate system we use the vertices of a given triangle. There are many interesting articles dealing with the use of barycentric coordinates, and among them the works in [7,8,9] may be useful.

2. Exeter Transformation

Let $ABC$ be a triangle and $A_t{B}_t{C}_t$ its tangential triangle.

Definition 1

(Exeter point). Let G be the centroid of a triangle $ABC$. Define $A^{\prime }$ to be the point (other than the polygon vertex A), where the triangle median through A meets the circumcircle of $ABC$, and define $B^{\prime }$ and $C^{\prime }$ similarly. Three lines—$A^{\prime }{A}_t,$ $B^{\prime }{B}_t$, and $C^{\prime }{C}_t$—intersect at a point $E_x$ called the Exeter point of triangle ABC.

Therefore, Exeter point is the perspector of the circum-medial triangle $A^{\prime }{B}^{\prime }{C}^{\prime }$, and the tangential triangle $A_t{B}_t{C}_t$.

In Figure 1, the centroid of the triangle $ABC$ is signed as G and the Exeter point as point $E_x$.

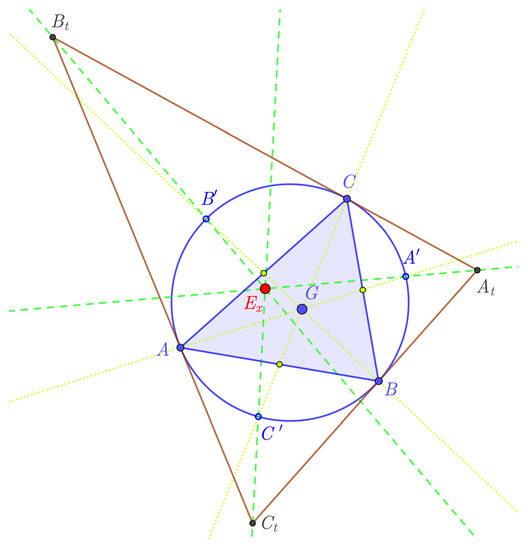
Figure 1. The Exeter point $E_x$.

The cevian properties of medians and its intersection (centroid) in the previous definition enable us to generalize the point construction process and obtain a new point transformation in connection to a triangle and its tangential triangle $A_t{B}_t{C}_t$:

Definition 2

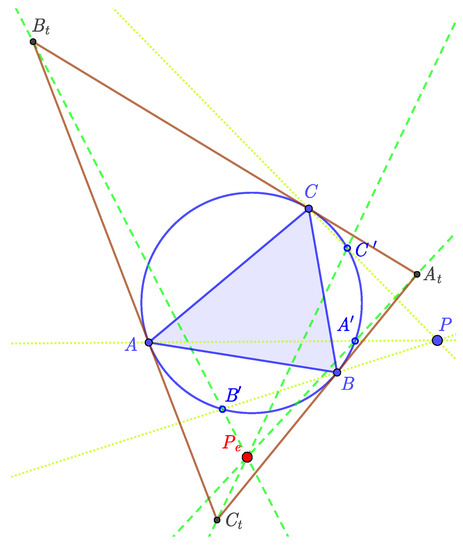
(Exeter transformation). Let P be an arbitrary point in the plane of the triangle $ABC$. Define $A^{\prime }$ to be the point (other than the polygon vertex A) where the line $AP$ meets the circumcircle of $ABC$, and define $B^{\prime }$ and $C^{\prime }$ similarly. Three lines—$A^{\prime }{A}_t,$ $B^{\prime }{B}_t$, and $C^{\prime }{C}_t$—intersect at a point $P_e$.

The transformation by which every point P is mapped onto the point $P_e$ by this process is called the Exeter transformation of the plane with respect to the triangle $ABC$ (see Figure 2).

Figure 2. The Exeter transformation.

The first question naturally arises: are such three lines concurrent and we have a unique point $P_e$ for each P? For verifying our statements, we use an analytical way with barycentric coordinates.

Let $△ABC$ be the fundamental non-degenerate triangle with sidelengths $a=\left|BC\right|$, $b=\left|CA\right|$, $c=\left|AB\right|$, where the barycentric coordinates of A, B and C are $(1,0,0)$, $(0,1,0)$, and $(0,0,1)$, respectively. Let the angle C be its largest (not smaller than the others) angle. Let $\mathcal{C}$ be the circumcircle of $△ABC$ with equation

$$a^{2}yz+b^{2}zx+c^{2}xy=0,$$

(1)

and let the triangle $A_t{B}_t{C}_t$ be the tangential triangle of $△ABC$. Now, the sides of $△A_t{B}_t{C}_t$ are on the tangent lines to $\mathcal{C}$ at the vertices of $△ABC$. Thus, if $△ABC$ is an acute triangle, then the incircle of $△A_t{B}_t{C}_t$ coincides with $\mathcal{C}$ (the triangle $ABC$ is known as the Gergonne triangle of $△A_t{B}_t{C}_t$). If $△ABC$ is an obtuse triangle, then $\mathcal{C}$ is one of the excircles of $△A_t{B}_t{C}_t$. If $△ABC$ is right angled, then $C_t$ is an ideal point. In all cases, the segment $A_t{B}_t$ touches the circle $\mathcal{C}$ at point C. In the projective sense, the lines of the sides of $△A_t{B}_t{C}_t$ divide the plane into four subsets. One is bounded, the others are unbounded in the affine sense. Let $\mathcal{R}$ denote the subset which contains $\mathcal{C}$.

The homogeneous barycentric coordinates of the vertices of $△A_t{B}_t{C}_t$ are

$$A_t(-a^2:b^2:c^2),B_t(a^2:-b^2:c^2),C_t(a^2:b^2:-c^2).$$

Points $A_t$, $B_t$ and $C_t$ are also known as exsymmedian points with respect to $▵ABC$. As usual, we denote the homogeneous barycentric coordinates by $(::)$ and the normalized (or absolute) barycentric coordinates by $(,,)$.

We consider an arbitrary point in the plane of triangle $ABC$

$$P(u:v:w)=\left(\frac{u}{s},\frac{v}{s},\frac{w}{s}\right),$$

where $s=u+v+w\ne 0$, $P\ne A$, $P\ne B$ and $P\ne C$, so at least two coordinates are not zero ($uv\ne 0$, $uw\ne 0$ or $vw\ne 0$). Let the lines $AP$, $BP$, and $CP$ meet $\mathcal{C}$ at $A^{\prime }$, $B^{\prime }$, and $C^{\prime }$, respectively.

Lemma 1.

The lines $A_t{A}^{\prime }$, $B_t{B}^{\prime }$ and $C_t{C}^{\prime }$ from Definition 2 are concurrent for all arbitrary point P.

Proof. 

The equation of the line $AP$ is $\left|\begin{array}{ccc}x& y& z\\ 1& 0& 0\\ u& v& w\end{array}\right|=wy-vz=0$. Similarly, the equations of lines $BP$ and $CP$ are $wx-uz=0$ and $vx-uy=0$, respectively. Their intersection points with the circumcircle $\mathcal{C}$ are $A^{\prime }(-a^{2}vw:v(b^{2}w+c^{2}v):w(b^{2}w+c^{2}v))$, $B^{\prime }(u(a^{2}w+c^{2}u):-b^{2}uw:w(a^{2}w+c^{2}u))$, and $C^{\prime }(u(a^{2}v+b^{2}u):v(a^{2}v+b^{2}u):-c^{2}vu)$.

The equation of line $A_t{A}^{\prime }$ is $\left|\begin{array}{ccc}x& y& z\\ -a^2& b^2& c^2\\ -a^{2}vw& v(b^{2}w+c^{2}v)& w(b^{2}w+c^{2}v)\end{array}\right|=(b^4{w}^2-c^4{v}^2)x+a^2{b}^2{w}^{2}y-a^2{c}^2{v}^{2}z=0$. Similarly, the equations of lines $B_t{B}^{\prime }$ and $C_t{C}^{\prime }$ are $-a^2{b}^2{w}^{2}x+(c^4{u}^2-a^4{w}^2)y+b^2{c}^2{u}^{2}z=0$ and $a^2{c}^2{v}^{2}x-b^2{c}^2{u}^{2}y+(a^4{v}^2-b^4{u}^2)z=0$, respectively. We then have from their coefficients that

$$\left|\begin{array}{ccc}{b}^4{w}^2-c^4{v}^2& a^2{b}^2{w}^2& -a^2{c}^2{v}^2\\ -a^2{b}^2{w}^2& -a^4{w}^2+c^4{u}^2& b^2{c}^2{u}^2\\ a^2{c}^2{v}^2& -b^2{c}^2{u}^2& a^4{v}^2-b^4{u}^2\end{array}\right|=0,$$

which implies the concurrency.  □

Let the point of concurrence of lines $A_t{A}^{\prime }$, $B_t{B}^{\prime }$, and $C_t{C}^{\prime }$ be $P_e$ (Figure 2). The image of a point P under the Exeter transformation with respect to triangle $ABC$ is the point $P_e$. We denote it by $ExTr(P)=P_e$. Let $G(1:1:1)$ be the centroid of $△ABC$ ($X_2$ in [1]). Then $ExTr(G)$ is the Exeter point ($X_{22}$ in [1]) of triangle $ABC$. That is why we call this transformation the Exeter transformation.

In the following, we examine the Exeter transformation and give some of its properties:

Theorem 1.

The barycentric coordinates of $P_e=ExTr(P)$, which is the image of $P(u:v:w)$ ($P\ne A$, $P\ne B$, $P\ne C$) over the Exeter transformation with respect to the triangle $ABC$, are

$$\left(a^2(-\mathfrak{p}+\mathfrak{q}+\mathfrak{r}):b^2(\mathfrak{p}-\mathfrak{q}+\mathfrak{r}):c^2(\mathfrak{p}+\mathfrak{q}-\mathfrak{r})\right),$$

(2)

where $\mathfrak{p}=a^4{v}^2{w}^2$, $\mathfrak{q}=b^4{w}^2{u}^2$ and $\mathfrak{r}=c^4{u}^2{v}^2$.

Proof. 

As the lines $A_t{A}^{\prime }$, $B_t{B}^{\prime }$, and $C_t{C}^{\prime }$ are concurrent according to Lemma 1, in order to determine the intersection point of lines $A_t{A}^{\prime }$, $B_t{B}^{\prime }$ we solve the system of their equations, and we obtain the concurrence point $P_e$ with barycentric coordinates (2).  □

Remark 1.

If $uvw\ne 0$ (P is not on any sideline of $▵ABC$), then from (2) we have $P_e=ExTr(P)=$

$$\left(a^2\left(-\frac{a^4}{u^2}+\frac{b^4}{v^2}+\frac{c^4}{w^2}\right):b^2\left(\frac{a^4}{u^2}-\frac{b^4}{v^2}+\frac{c^4}{w^2}\right):c^2\left(\frac{a^4}{u^2}+\frac{b^4}{v^2}-\frac{c^4}{w^2}\right)\right).$$

Remark 2.

If a triangle $ABC$ is equilateral, so $a=b=c=1$, then the barycentric coordinates of $P_e$ are $(u^2{v}^2+w^2{u}^2-v^2{w}^2:u^2{v}^2-w^2{u}^2+v^2{w}^2:-u^2{v}^2+u^2{v}^2+v^2{w}^2)$, and if $uvw\ne 0$, then the normalized barycentric coordinates of $P_e$ are

$$(1-\frac{\mathfrak{K}}{u^2},1-\frac{\mathfrak{K}}{v^2},1-\frac{\mathfrak{K}}{w^2}),$$

where

$$\mathfrak{K}=\frac{2u^2{v}^2{w}^2}{u^2{v}^2+u^2{v}^2+v^2{w}^2}=\frac{2}{\frac{1}{u^2}+\frac{1}{v^2}+\frac{1}{w^2}}.$$

If we used the planar by projective coordinates (obtained from a projective base given by the points $A,B,C,G$ where $A,B$, and C are triangle vertices and the centroid G is the “unit” point), instead of the barycentric with respect to the triangle $ABC$, we would notice that the projective coordinates are the same as barycentric in case $a=b=c=1$, but this way we would lose the Euclidean metrical properties of the Exeter transformation. However, we could extend Theorem 1 to the projective plane. Thus, the Exeter transformation works if we consider any circumconic $\mathcal{C}$ of a triangle A, B, C and its tangential triangle $A_t{B}_t{C}_t$.

Corollary 1.

The range of the Exeter transformation is $\mathcal{R}$.

Proof. 

We have to prove that $P_e$ is in $\mathcal{R}$. For this, we project the point $P_e$ from the vertices of $\mathcal{R}$ to the sidelines of $\mathcal{R}$, namely, from the vertices $A_t$, $B_t$ and $C_t$ to the sidelines of $△A_t{B}_t{C}_t$. We show that these projected points are on the sides of $\mathcal{R}$.

For example, the barycentric coordinates of each point of the line $A_t{B}_t$ are $(q{a}^2:-q{b}^2:c^2)$, where the parameter $q\in \mathbb{R}$. If $q=\pm 1$, then we have $A_t$ or $B_t$, and in the case of $q=0$ the point coincides with C, which is one of the points of the circle $\mathcal{C}$. Thus, the parameters $q\in [-1,1]$ describe one of the segments $A_t{B}_t$, which is the side of $\mathcal{R}$. Now, we consider the equation $a^2{c}^2{v}^{2}x-b^2{c}^2{u}^{2}y+(a^4{v}^2-b^4{u}^2)z=0$ of the line $C_t{P}_e$ (in the proof of Lemma 1, it is the line $C_t{C}^{\prime }$) and substitute $(q{a}^2:-q{b}^2:c^2)$ into the equation. After a short calculation, we express $t=-(a^4{v}^2-b^4{u}^2)/(a^4{v}^4+b^4{u}^2)$, where $\left|t\right|\le 1$. With similar calculation, we can prove that the other two projected points are on the sides of $\mathcal{R}$ as well.  □

Corollary 2.

If $P=(u:v:w)$ and $P^i=(\pm u:\pm v:\pm w)$, then $ExTr(P)=ExTr(P^i)$, because (2) contains only even powers of the coordinates of P (recall $(-u:v:w)=$$(u:-v:-w)$). Thus, generally, there are four points which have the same image with respect to the Exeter transformation. Let $P^0=P$, $P^1=(-u:v:w)$, $P^2=(u:-v:w)$, and $P^3=(u:v:-w)$.

Figure 3 shows the constructions of points $P^i$. For example, line $B^{\prime }{B}_t$ intersects $\mathcal{C}$ in point $\overline{B}$ as well, and the intersection point of lines $B\overline{B}$ and $A{A}^{\prime }$ is $P^1$. Follow the construction of the image of $P^1$ with respect to the Exeter transformation, then the result is $P_e$. Similarly, using $\overline{A}$ and $\overline{C}$ we obtain points $P^2$ and $P^3$.

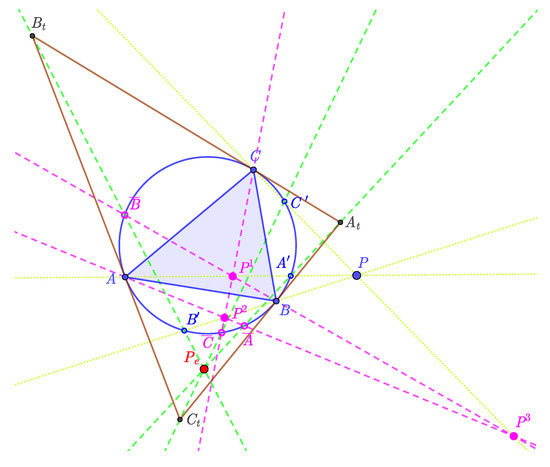
Figure 3. Four points (P, $P^1$, $P^2$, and $P^3$) have the same image $P_e$.

Corollary 3.

If we consider the centroid of $△ABC$ and the vertices of the anticomplementary triangle $A_1{B}_1{C}_1$ of $△ABC$ with coordinates $(1:1:1)$, $(-1:1:1)$, $(1:-1:1)$ and $(1:1:-1)$, respectively, then their common image is the point $(a^2(-a^4+b^4+c^4):b^2(a^4-b^4+c^4):c^2(a^4+b^4-c^4))$, which is the Exeter point ($X_{22}$) of $△ABC$.

Theorem 2.

The Exeter transformations of the lines $AB$, $BC$, and $CA$ (except points A, B, C) are the points $C_t$, $A_t$ and $B_t$, respectively.

Proof. 

The equation of line $AB$ is $z=0$, so if P is on line $AB$ then the coordinates are $(u,v,0)$. Therefore, from (2), as $p=q=0$, we have $ExTr(P)=(a^2\mathfrak{r}:b^2\mathfrak{r}:-c^2\mathfrak{r})=(a^2:b^2:-c^2)=C_t$, where $\mathfrak{r}=c^4{u}^2{v}^2\ne 0$. The proof is similar for the other lines.  □

Corollary 4.

If P is on one of the lines $AB$, $BC$ or $CA$, then some points from among $P^i$ for $i=0,1,2,3$ coincide.

Corollary 5.

If P, $P^1$, $P^2$, and $P^3$ are not on lines $AB$, $BC$, or $CA$, then they form a complete quadrangle with diagonal points A, B, and C.

Theorem 3.

The Exeter transformation of a line passing through neither points A, B, and C is a fourth-order curve incident with points $A_t$, $B_t$, and $C_t$.

Proof. 

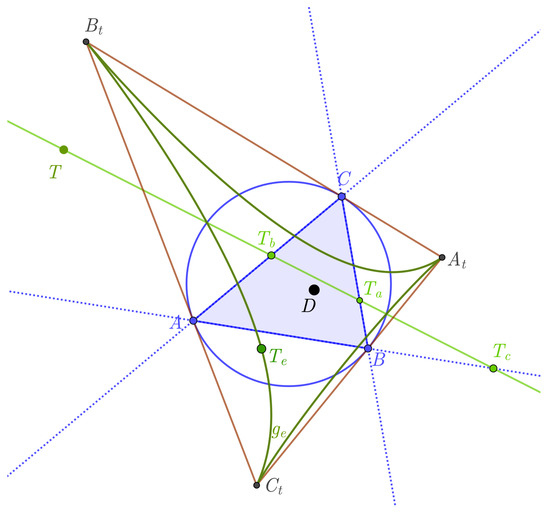
Without lost of generalization to give a general line g we take the points $T_a$, $T_b$ and $T_c$ on lines $BC$, $CA$ and $AB$, respectively, with baricentric coordinates $T_a(0:1:t_a)$, $T_b(t_b:0:1)$ and $T_c(1:t_c:0)$, where $t_a,t_b,t_c\in \mathbb{R}$ and $t_a{t}_b{t}_c\ne 0$ (Figure 4). As $\left|\begin{array}{ccc}0& 1& t_a\\ t_b& 0& 1\\ 1& t_c& 0\end{array}\right|=1+t_a{t}_b{t}_c,$ then $T_a$, $T_b$, and $T_c$ are collinear if and only if $t_a{t}_b{t}_c=-1$. Now, the equation of the line g given by the points $T_a$, $T_b$, and $T_c$ is, ex., $\left|\begin{array}{ccc}x& y& z\\ 0& 1& t_a\\ t_b& 0& 1\end{array}\right|=x+t_a{t}_{b}y-t_{b}z=0.$ Because the point $T(t+1:t_{c}t:t_a{t}_b)$, $t\in \mathbb{R}$ is incident with g, then the parametric system of equations of the line g with parameter t can be considered as $x(t)=t+1$, $y(t)=t_{c}t$, $z(t)=t_a{t}_b$, and the coordinates of the Exeter transformation of the point T give the parametric system of equations of the Exeter transformation of the line g. Thus, using for T the Equation (2) of the Exeter transformation, we have

$$T_e=\left(a^2(-\mathfrak{p}+\mathfrak{q}+\mathfrak{r}):b^2(\mathfrak{p}-\mathfrak{q}+\mathfrak{r}):c^2(\mathfrak{p}+\mathfrak{q}-\mathfrak{r})\right),$$

(3)

where $\mathfrak{p}=a^4{t}_a^2{t}_b^2{t}_c^2{t}^2$, $\mathfrak{q}=b^4{t}_a^2{t}_c^2{(t+1)}^2$, and $\mathfrak{r}=c^4{t}_c^2{t}^2{(t+1)}^2$. As the degree of the polynomial $\mathfrak{r}$ in variable t is four ($\mathfrak{p}$ and $\mathfrak{q}$ are second degree polynomials), then all coordinates of $T_e$ are polynomials in t having degree four. Thus, $g_e=ExTr(g)$ with points $T_e$, where $t\in \mathbb{R}$ is a fourth-order curve. Moreover, according to Theorem 2 the images of $T_a$, $T_b$ and $T_c$ are $A_t$, $B_t$, and $C_t$, respectively (Figure 4).  □

Figure 4. Exeter transformation of the line g.

2.1. Invariant Elements

Let D be the symmedian point of $△ABC$ ($X_6$ in [1]). (The point of concurrence of lines $A{A}_t$, $B{B}_t$ and $C{C}_t$. Thus, $△ABC$ is perspective with $△A_t{B}_t{C}_t$ at the point D. Furthermore, if $△ABC$ is acute, then D is the Gergonne point of $△A_t{B}_t{C}_t$, the point $X_7$ in [1].) It is well known that

$$D(a^2:b^2:c^2).$$

Theorem 4.

D is a fixed point of the Exeter transformation with respect to triangle $ABC$; moreover, $ExTr(D)=ExTr(A_t)=ExTr(B_t)=ExTr(C_t)=D$.

Proof. 

It follows directly from Corollary 2.  □

Theorem 5.

The lines $AD$, $BD$, and $CD$ are invariant lines with respect to the Exeter transformations. Their images are parts of $\mathcal{R}$. Moreover, if $△ABC$ is acute, then the Exeter transformations of lines $AD$, $BD$, and $CD$ are the segments $A{A}_t\subseteq \mathcal{R}$, $B{B}_t\subseteq \mathcal{R}$, and $C{C}_t\subseteq \mathcal{R}$, respectively.

Proof. 

For example, let P be on the line $AD$. As lines $AD$ and $A{A}_t$ are the same, then $A^{\prime }$ and $P_e$ are on that line. Analytically, the equation of line $AD$ is $c^{2}y-b^{2}z=0$ and the coordinates of its arbitrary point P is $(t:b^2:c^2)$, $t\in \mathbb{R}$ and its image with respect to (2) is $(a^2-2t^2/a^2:b^2:c^2)$, which is also on line $AD$.

The proof is similar for the case of the other lines.  □

Theorem 6.

The circumcircle of triangle $ABC$ is fixed (all of its points are fixed, except A, B, and C) over the Exeter transformation, so $ExTr(\mathcal{C})=\mathcal{C}$.

Proof. 

The barycentric equation of $\mathcal{C}$ is $a^{2}yz+b^{2}zx+c^{2}xy=0$. If $P(u:v:w)$ is a point of $\mathcal{C}$, then from $a^{2}vw+b^{2}wu+c^{2}uv=0$ we have

$$P(u:\frac{-b^{2}uw}{a^{2}w+c^{2}u}:w)=P(a^{2}uw+c^2{u}^2:-b^{2}uw:a^2{w}^2+c^{2}uw).$$

Using (2) we obtain $ExTr(P)=P$. Recall $P\ne B$, thus $a^{2}w+c^{2}u\ne 0$.  □

The points $A_t$, $B_t$, $C_t$, and D determine a pencil of conic $\mathcal{Q}$. Let $\mathcal{Q}(P)$ denote the element of the pencil $\mathcal{Q}$ on which the point P lies. If $△ABC$ is acute, then D is inside of the triangle $A_t{B}_t{C}_t$, and the conics of the pencil $\mathcal{Q}$ are hyperbolas.

Theorem 7.

The point and its image under the Exeter transformation with respect to triangle $ABC$ lie on the same conic of the pencil $\mathcal{Q}$, so $\mathcal{Q}(P)=\mathcal{Q}(ExTr(P))$, and the equation of $\mathcal{Q}(P)$ is

$$\alpha x^2+\beta y^2+\gamma z^2=0,$$

(4)

where

$$\alpha =b^4{w}^2-c^4{v}^2,\beta =-a^4{w}^2+c^4{u}^2,\gamma =a^4{v}^2-b^4{u}^2$$

(5)

and $(u:v:w)$ are the barycentric coordinates of P.

Proof. 

The equation of a conic is

$$\left(\begin{array}{ccc}x& y& z\end{array}\right)\left(\begin{array}{ccc}\alpha & \nu & \mu \\ \nu & \beta & \lambda \\ \mu & \lambda & \gamma \end{array}\right)\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=0.$$

(6)

Let $\gamma =1$, without loss of generality. Substituting points D, $A_t$, $B_t$, $C_t$, and P into (6) we have a system of five linear equations and after a homogenization the solution gives the Equation (4) of $\mathcal{Q}(P)$. Moreover, the coordinates of $ExTr(P)$ satisfy the Equation (4), so the image of P is on $\mathcal{Q}(P)$.  □

Remark 3.

If P is not on any sideline of $▵A_t{B}_t{C}_t$, so $\alpha \beta \gamma \ne 0$, then the conic $\mathcal{Q}(P)$ is non-degenerate.

Corollary 6.

All conics (or degenerate conics-crossing lines at points A, B, or C) lying through the points $A_t$, $B_t$, $C_t$ and D are invariant. Furthermore, their fixed points are D and the intersection points with the circumcircle of $▵ABC$.

Corollary 7.

The images of lines $A_t{B}_t$, $B_t{C}_t$, and $C_t{A}_t$ are parts of the lines $C{C}_t$, $A{A}_t$, and $B{B}_t$, respectively. Moreover, in the case of an acute $△ABC$ they are the segments $C{C}_t$, $A{A}_t$, and $B{B}_t$, respectively.

Theorem 8.

The image of the pencil of a line through A is a pencil of a line through $A_t$ and the corresponding lines intersect each other at the points of $\mathcal{C}$.

Proof. 

It is a simple corollary of the definition of the Exeter transformation.  □

Let the point sequence $P_i$ ($i\ge 0$) be the ith image of P. Thus, $P_i={(ExTr)}^i(P)$ and $P_0=P$.

Corollary 8.

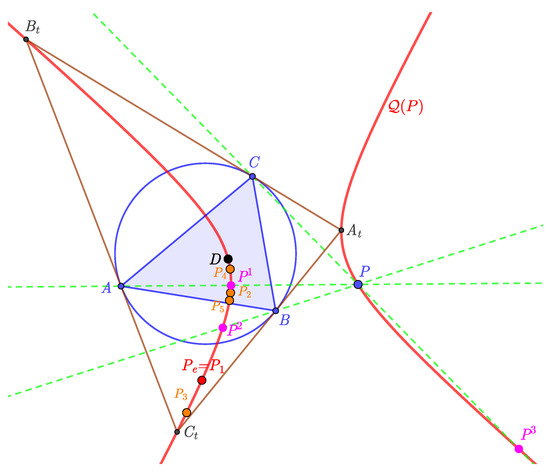
All elements of the point sequence $P_i$ ($i\ge 0$) are on the same conic $\mathcal{Q}(P)$ (see Figure 5).

Figure 5. Points on conic $\mathcal{Q}(P)$.

Proof. 

Every conic is clearly defined by five points. The conic $\mathcal{Q}(P)$ is given by $A_t$, $B_t$, $C_t$, D, and $P=P_0$. From Theorem 7, we have that the point $P_1$, the image of the point $P_0$ under the Exeter transformation, lies on the conic $\mathcal{Q}(P)$. Thus, $A_t$, $B_t$, $C_t$, D, and $P_1$ also define $\mathcal{Q}(P)$. Recursively—using Theorem 7—we can prove that the point $P_2$ (and so $P_3,P_4,\dots$) lies on the conic $\mathcal{Q}(P)$ as well.  □

From Theorem 7 and Corollaries 2 and 8 we gain

Corollary 9.

The points $P^0=P$, $P^1$, $P^2$ and $P^3$ are on the same conic $\mathcal{Q}(P)$.

Proof. 

If $P=(u:v:w)$ and $P^i=(\pm u:\pm v:\pm w)$, $i=0,1,2,3$, then not only P satisfies the Equation (4) of the conic $\mathcal{Q}(P)$, but also each $P^i$ does.  □

Corollary 10.

$P^1=AP\cap \mathcal{Q}(P)$, $P^2=BP\cap \mathcal{Q}(P)$, $P^3=CP\cap \mathcal{Q}(P)$ (See Figure 5).

Proof. 

From Corollary 9, we know that, for example, the points $P^0=P$ and $P^1$ are on the same conic $\mathcal{Q}(P)$. The point $P^1(-u:v:w)$ lies on the line $AP$ with the equation $wy-vz=0$. Thus, they are concurrent. As a line has maximum two intersection points with a non-degenerate conic, the other intersection point of the line $AP$ with $\mathcal{Q}(P)$ must be $P^1$.  □

Corollary 11.

The vertices of any complete quadrangle with diagonal points A, B, and C are on the same conic $\mathcal{Q}$.

Proof. 

According to Corollary 10 and Corollary 5 we know that $P^i$, $i=0,1,2,3$ lie on the same conic and (clearly) define a complete quadrangle with diagonal points A, B and C. Moreover, it is also well known that a complete quadrangle is clearly defined by three diagonal points and a vertex, i.e., A, B, C, and any point P, where P does not lie on the sidelines of the triangle $ABC$. The corollary summarizes these statements.  □

2.2. Tangent Lines

Let $\mathcal{Q}(P)$ be a non-degenerate conic of the pencil $\mathcal{Q}$. Let us denote by $t_X$ the tangent line to $\mathcal{Q}(P)$ at a point $X\in \mathcal{Q}(P)$.

Theorem 9.

If the points $P^i$, $i=0,1,2,3$ are mapped onto the same point by the Exeter transformation with respect to triangle $ABC$, then the intersection points of the tangent lines $t_{P^0}$, $t_{P^1}$, $t_{P^2}$, and $t_{P^3}$ are on the lines of the sides of triangle $ABC$.

Proof. 

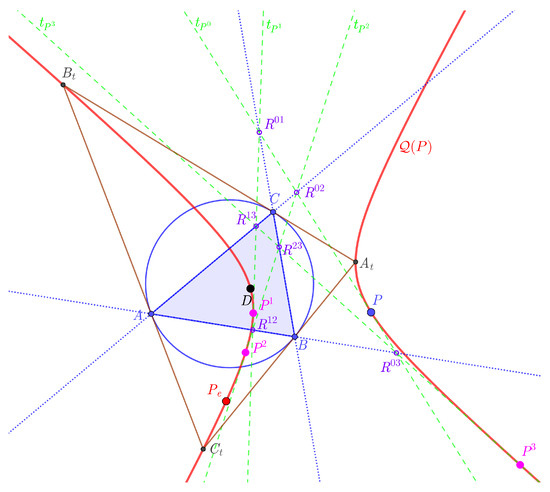
Let us consider an arbitrary line with barycentric equation $px+qy+rz=0$. If it is passing through the point $P=P^0$, then $-pu=qv+rw$. Moreover, the equation of the pencil of lines at $P^0$ is

$$(-qv-rw)x+uqy+urz=0,$$

(7)

where q and r are the barycentric coordinates of the lines from the pencil. To derive the tangent line among them, we consider the system of Equations (4) and (7). If its discriminant is zero and we put $x=1$, then using (5) we have $q=\left(v\beta /w\gamma \right)r.$ Finally, the equation of $t_{P_0}$ is

$$-\left(v^2\beta +w^2\gamma \right)x+uv\beta y+uw\gamma z=0.$$

Similarly, the equations of the pencil of lines at $P^1$, $P^2$ and $P^3$, respectively, are $(qv+rw)x+uqy+urz=0$, $(qv-rw)x+uqy+urz=0$ and $(-qv+rw)x+uqy+urz=0$. Moreover, the equations of lines $t_{P^1}$, $t_{P^2}$, and $t_{P^3}$, respectively, are $\left(v^2\beta +w^2\gamma \right)x+uv\beta y+uw\gamma z=0$, $\left(v^2\beta +w^2\gamma \right)x+uv\beta y-uw\gamma z=0$ and $\left(v^2\beta +w^2\gamma \right)x-uv\beta y+uw\gamma z=0$.

Let the point $R^{01}$ be the intersection of $t_{P^0}$ and $t_{P^1}$. From the equations of lines we have that $R^{01}=\left(0:w\gamma :-v\beta \right)$, which is on the line $BC$ (Figure 6).

Figure 6. Tangent lines at points $P^i$.

The proof is similar in the case of the other intersection points. Moreover, the intersection points are $R^{02}=\left(uw\gamma :0:v^2\beta +w^2\gamma \right)$, $R^{03}=\left(uv\beta :v^2\beta +w^2\gamma :0\right)$, $R^{12}=\left(-uv\beta :v^2\beta +w^2\gamma :0\right)$, $R^{13}=\left(-uw\gamma :0:v^2\beta +w^2\gamma \right)$, and $R^{23}=\left(0:w\gamma :v\beta \right)$.  □

Remark 4.

The points $R^{ij}$ and A, B, and C define a complete quadrilateral with diagonal points and projective harmonic conjugate point pairs with respect to the diagonal points. For example, in Figure 6, the points $R^{12}$, $R^{03}$, $R^{02}$, and $R^{13}$ form a complete quadrilateral with diagonal points A, $R^{23}$, $R^{01}$; B which is the projective harmonic conjugate of A with respect to $R^{03}$ and $R^{12}$; and C is the projective harmonic conjugate of A with respect to $R^{02}$ and $R^{13}$. Their cross-ratio is $-1$.

Corollary 12.

The intersection of any two lines $t_{A_t}$, $t_{B_t}$, $t_{C_t}$, and $t_D$ are on one of the sidelines of triangle $ABC$.

Proof. 

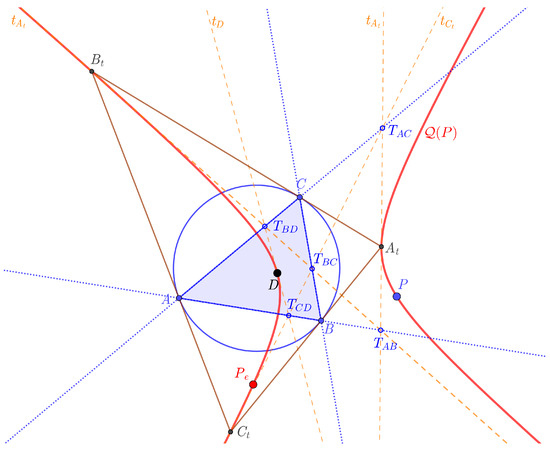
Considering Theorem 4, we obtain the statement from Theorem 9 (see Figure 7). Moreover, the equations of $t_{A_t}$, $t_{B_t}$, $t_{C_t}$, and $t_D$, respectively, are $\left(b^4\beta +c^4\gamma \right)x+a^2{b}^2\beta y+a^2{c}^2\gamma z=0$, $\left(b^4\beta +c^4\gamma \right)x+a^2{b}^2\beta y-a^2{c}^2\gamma z=0$, $\left(b^4\beta +c^4\gamma \right)x-a^2{b}^2\beta y+a^2{c}^2\gamma z=0$, and $-\left(b^4\beta +c^4\gamma \right)x+a^2{b}^2\beta y+a^2{c}^2\gamma z=0$. Their intersection points are $T_{AB}=\left(-a^2{b}^2\beta :b^4\beta +c^4\gamma :0\right)$, $T_{AC}=\left(-a^2{c}^2\gamma :0:b^4\beta +c^4\gamma \right)$, $T_{AD}=\left(0:c^2\gamma :-b^2\beta \right)$, $T_{BC}=\left(0:c^2\gamma :b^2\beta \right)$, $T_{AD}=\left(a^2{c}^2\gamma :0:b^4\beta +c^4\gamma \right)$, $T_{CD}=\left(a^2{b}^2\beta :b^4\beta +c^4\gamma :0\right)$.  □

Figure 7. Tangent lines at points $A_t$, $B_t$, $C_t$, and D.

Let $M_{AB1}$ and $M_{AB2}$ be the intersection points of line $AB$ and the non-degenerate $\mathcal{Q}(P)$. Let us define similarly the points $M_{AC1}$, $M_{AC2}$, $M_{BC1}$, and $M_{BC2}$. Their coordinates from Equation (4) are $M_{AB1}(\sqrt{-\frac{\beta }{\alpha }}:1:0)$, $M_{AB2}(\sqrt{-\frac{\beta }{\alpha }}:-1:0)$, $M_{AC1}(1:0:\sqrt{-\frac{\alpha }{\gamma }})$, $M_{AC2}(-1:0:\sqrt{-\frac{\alpha }{\gamma }})$, $M_{BC1}(0:\sqrt{-\frac{\gamma }{\beta }}:1)$, and $M_{BC2}(0:\sqrt{-\frac{\gamma }{\beta }}:-1)$. (Recall $\alpha \beta \gamma \ne 0$.) Naturally, $\mathcal{Q}(P)$ does not intersect the lines of the sides of $▵ABC$ at the same time, for example, $\alpha$ could not be positive and negative at the same time. Thus, at most four points exist at the same time among the above points. See Figure 8, when $\mathcal{Q}(P)$ intersects the lines $AC$ and $AB$, so $\frac{\alpha }{\gamma }<0$, $\frac{\gamma }{\beta }<0$ and then $\frac{\beta }{\alpha }<0$.

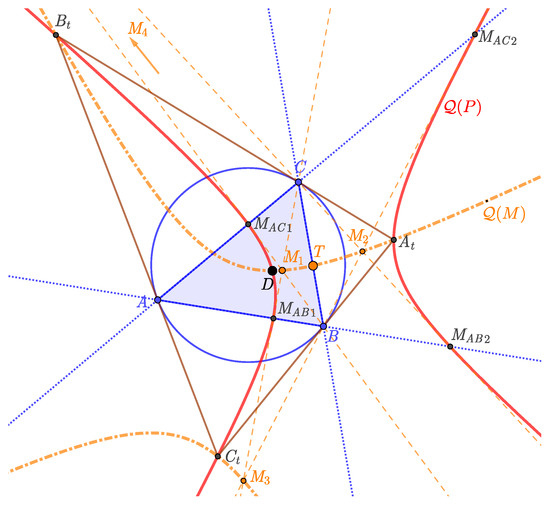
Figure 8. Tangent lines at intersection points.

Theorem 10.

The tangent lines to $\mathcal{Q}(P)$ at points $M_{AB1}$ and $M_{AB2}$ are passing through the point C. Similarly, the tangent lines to $\mathcal{Q}(P)$ at points $M_{AC1}$, $M_{AC2}$ or $M_{BC1}$, $M_{BC2}$ are passing through the points B or A, respectively.

Proof. 

The equations of the tangent lines at points $M_{AB1}$ and $M_{AB2}$ are $-x+\sqrt{-\frac{\beta }{\alpha }}y=0$ and $x+\sqrt{-\frac{\beta }{\alpha }}y=0$, respectively. Point C coincides with them.  □

Let $M_1$, $M_2$, $M_3$, and $M_4$ be the intersection points different from A, B, and C of the tangent lines at $M_{AB1}$, $M_{AB2}$, $M_{AC1}$, $M_{AC2}$, $M_{BC1}$, and $M_{BC2}$.

Theorem 11.

The points $M_1$, $M_2$, $M_3$ and $M_4$ are on the same conic $\mathcal{Q}(M)$ with one of the equations

$$\alpha \left(b^4\beta -c^4\gamma \right)x^2-\beta \left(a^4\alpha +c^4\gamma \right)y^2+\gamma \left(a^4\alpha +b^4\beta \right)z^2=0,$$

(8)

$$-\alpha \left(b^4\beta +c^4\gamma \right)x^2+\beta \left(a^4\alpha +c^4\gamma \right)y^2+z^2\gamma \left(a^4\alpha -b^4\beta \right)=0,$$

(9)

$$\alpha \left(b^4\beta +c^4\gamma \right)x^2+\beta \left(-a^4\alpha +c^4\gamma \right)y^2-z^2\gamma \left(a^4\alpha +b^4\beta \right)=0,$$

(10)

when $\mathcal{Q}(M)$ does not intersect lines $BC$, $AB$, or $AC$, respectively.

Proof. 

First, we consider the case of Figure 8. The points $M_1$, $M_2$, $M_3$, and $M_4$ define a complete quadrangle with diagonal points A, B, and C and according to Corollary 11 they are on the same conic of $\mathcal{Q}$. The barycentric coordinates of $M_i$ are $\left(\pm \sqrt{-\frac{\gamma }{\alpha }}:\pm \sqrt{\frac{\gamma }{\beta }}:1\right)$. The Equation (8) is determined similarly to the equation of $\mathcal{Q}(P)$ in Theorem 7.

Second, when $\mathcal{Q}(M)$ does not intersect the lines $AB$ or $AC$, respectively, the coordinates of $M_i$ are $\left(\pm \sqrt{-\frac{\gamma }{\alpha }}:\pm \sqrt{-\frac{\gamma }{\beta }}:1\right)$ or $\left(\pm \sqrt{\frac{\gamma }{\alpha }}:\pm \sqrt{-\frac{\gamma }{\beta }}:1\right)$. They yield the Equations (9) and (10).  □

Theorem 12.

The Exeter transformations of $M_1$, $M_2$, $M_3$, and $M_4$ are the same point T lying on one of the lines of $▵ABC$. Moreover, T coincides with $T_{AB}$, $T_{AC}$, or $T_{BC}$, when $\mathcal{Q}(P)$ does not intersect the lines $BC$, $AB$, or $AC$, respectively.

Proof. 

We use Corollaries 2 and 5. Analytically, for example, in case of Figure 8, $ExTr(M_1)=ExTr(M_2)=ExTr(M_3)=ExTr(M_4)=\left(0:c^2\gamma :b^2\beta \right)=T_{BC}=T$.  □

Let $\mathcal{N}$ be the nine-point conic determined by points $A_t$, $B_t$, $C_t$, and D [10]. Conic $\mathcal{N}$ is passing through the points A, B, C, and the midpoints of all segments of points $A_t$, $B_t$, $C_t$, and D. Moreover, it also well known that the center of a conic passing through points $A_t$, $B_t$, $C_t$, and D is on the nine-point conic $\mathcal{N}$ [10]. This proves the following theorem.

Theorem 13.

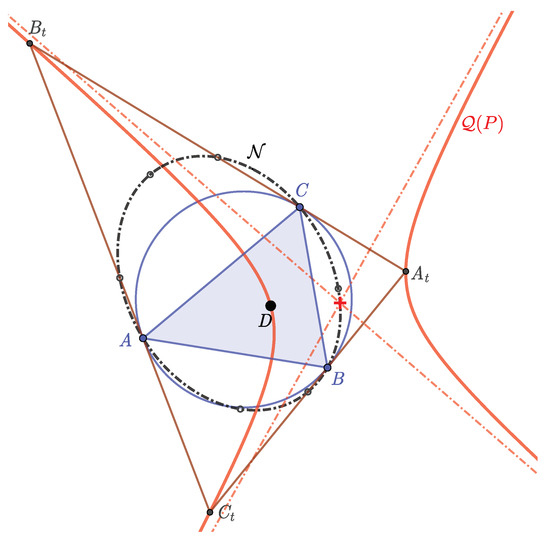
The center of the conic $\mathcal{Q}(P)$ is lying on the conic $\mathcal{N}$ (Figure 9).

Figure 9. Nine-point conic.

With a short calculation, we have $a^{4}yz+b^{4}xz+c^{4}xy=0$ for the equation of $\mathcal{N}$ and the coordinates of the center of $\mathcal{Q}(P)$ are

$$\left(\beta \gamma :\alpha \gamma :\alpha \beta \right).$$

3. Conclusions

With the help of the barycentric coordinates, we showed that the extension of the well-known process of the Exeter point from the centroid of a given triangle $ABC$ provides a so-called Exeter transformation for the whole plane. Each point P, its image $P_e$, the symmedian, and three exsymmedian points of the triangle are on the same conic $\mathcal{Q}(P)$. Moreover, three other points ($P^1$, $P^2$, and $P^3$) of this conic $\mathcal{Q}(P)$ have the common image point $P_e$ as well. The Exeter transformation is nonlinear, as the image of a general line is a fourth-order curve passing through the exsymmedian points of the triangle. We presented the images of some special lines, points, and we determined the invariant points and lines of the Exeter transformation. We particularly examined the intersection points of the tangent lines of the conic $\mathcal{Q}(P)$ at some special points. We think that this nonlinear transformation will reveal several interesting and useful properties during future investigations.